Der Titel meines Buches: „Philosophische
Betrachtungen. Alphabetisch nach ihren
Gegenständen || Themen geordnet || aneinandergereiht.” || ¤ nach Stichwörtern
angeordnet.” ¥ |
Wie kann man Vorbereitungen für die Ankunft von etwas eventuell
Existierendem treffen in dem Sinn in welchem Russell &
Ramsey das immer getan haben || tun
wollten¤? ¤ |
⍈
Ich drücke, was ich ausdrücken will doch immer nur „mit halbem
Gelingen” aus.
Ja auch das¤ nicht, sondern vielleicht nur mit einem Zehntel.
Das will doch etwas besagen.
Mein Schreiben ist oft nur ein „Stammeln”.
|
Nun kann man doch für die Existenz eines Dinges vorsorgen: ich mache
z.B. ein Kästchen um
den Schmuck hineinzulegen der vielleicht einmal gemacht werden
wird. Aber hier kann ich doch sagen, was der Fall sein muß, || – welcher Fall es ist für den ich vorsorge. Ich kann diesen Fall jetzt so gut beschreiben wie nachdem er eingetreten ist. (Lösung mathematischer Probleme.) Während Russell & Ramsey für eine eventuelle Grammatik x = a ⌵ x = b ⌵ … x = a ∙ y = b . ⌵ . x = c ∙ y = d . ⌵ x = a ∙ y = b ∙ z = c . ⌵ . … |
Man denkt z.B. einerseits daß es die
Arithmetik mit den Funktionen zu tun hat von deren Anzahlen sie
handelt.
Aber man will sich nicht durch die uns jetzt bekannten Funktionen binden
lassen und man weiß nicht ob es jemals eine geben wird die von 100
Gegenständen befriedigt wird:
also muß man vorsorgen
Was heißt es aber überhaupt „es findet sich (oder: es gibt) eine 100-stellige Relation”? Welchen Begriff haben wir von ihr? oder einer 2-stelligen?! – Als Beispiel einer 2-stelligen Relation gibt man etwa das der Beziehung zwischen Vater & Sohn. Aber welche Bedeutung hat dieses Beispiel für die weitere Behandlung des Gegenstandes? |
Hier handelt es sich um den Begriff der Anwendung.
Man hat etwa die
Vorstellung |
Aber was gibt die Anwendung der Rechnung?
Setzt sie ihr einen neuen Kalkül zu? dann ist sie ja
jetzt eine andere Rechnung.
Oder gibt sie ihr in irgend einem der Mathematik (Logik)
wesentlichen Sinne Substanz?
Wie kann man dann überhaupt auch nur zeitweise von der Anwendung
absehen? |
Nein, die Rechnung mit Äpfeln ist wesentlich dieselbe wie die mit Strichen
oder Ziffern.
Die Arbeitsmaschine setzt den Motor fort aber die Anwendung (in diesem
Sinne) nicht die Rechnung. |
Wenn ich nun sage „die Liebe ist z.B. eine
2-stellige Relation”, || – sage ich hier etwas
über die Liebe aus?
Natürlich nicht.
Ich gebe eine Regel für den Gebrauch des Wortes
„Liebe” & will etwa sagen
daß
|
Nun hat man aber doch das Gefühl daß mit
dem Hinweis auf die 2-stellige
Relation Liebe in die Hülse des Relationskalküls Sinn gesteckt
wurde. –
Denken wir uns eine geometrische
Demonstration statt an einer Zeichnung oder an analytischen Symbolen
an einem Lampenzylinder
vorgenommen.
Inwiefern ist hier von der Geometrie eine Anwendung
|
Wir haben mit verschiedenen Verwendungen des Wortes
„Anwendung” zu tun. „Die Multiplikation wird in dieser Rechnung angewandt”, „Der Glaszylinder |
Hier kann man nun sagen: Die Arithmetik ist ihre eigene
Anwendung.
Der Kalkül ist seine eigene Anwendung.
Wir können nicht in der Arithmetik für eine grammatische Anwendung vorsorgen. Denn ist die Arithmetik nur ein Spiel so ist für sie auch ihre Anwendung nur ein Spiel & entweder das gleiche Spiel (dann |
Wenn also der Logiker sagt, er habe für eventuell existierende
6-stellige Relationen in der Arithmetik vorgesorgt oder für
Funktionen die von 27 Dingen befriedigt werden, so können wir fragen:
Was wird denn nun zu dem was Du vorbereitet hast hinzutreten
wenn es nun
|
Die falsche || unrichtige Idee ist daß die
Anwendung eines Kalküls in der Grammatik der wirklichen Sprache ihm
eine Realität zuordnet || eine Wirklichkeit gibt die er
früher nicht hatte. || Die unrichtige Idee
|
Aber wie gewöhnlich in unserem Gebiet liegt hier der Fehler nicht darin
daß man etwas Falsches glaubt sondern darin daß man auf
eine nicht stimmende Analogie hinschielt. |
Was geschieht denn wenn die 6-stellige Relation gefunden
wird?
Wird quasi ein Metall gefunden das
nun die
gewünschte |
Das alles hängt auch mit dem falschen Begriff der
logischen Analyse zusammen den
Russell, ich &
Ramsey hatten.
So daß man auf
|
Die Grammatik ist für uns ein reiner Kalkül.
(Nicht die Anwendung eines auf die Realität.)
|
∣ ∣
Die Wörter sind nicht die Ingredienzien
eines Satzes. ∣ ∣ |
(∃2x) φx ∙ (∃2x) ψx ∙
Ind. . ⊃ . . ⊃ .
(∃4x) φx ⌵ ψx |
Weniger versprechen als man halten will ist oft schön, aber es
kann auch aus einer Anmaßung entspringen; dann, wenn man sich auch
etwas drauf einbildet weniger zu versprechen
als man halten wird. –
Ist es richtig oder unrichtig mein Buch nicht
„Philosophische Betrachtungen
etc.” zu nennen, sondern:
„Philosophische Bemerkungen,
nach
nach Stichwörtern alphabetisch geordnet”? || alphabetisch nach Stichwörtern angeordnet || geordnet”? |
∣
Was ich für die Sprache tue wenn ich einfache grammatische
Schemata neben sie stelle ist ähnlich dem was die Erfinder der Buchstaben
(Lautzeichen für die Lautsprache) getan haben. ∣
|
∣
Die Diskussionen über das Naturrecht, ein gutes Beispiel dafür
wie ein Problem || eine Schwierigkeit obsolet wird &
die
(No so soll er sich bessern!) ∣ |
Denken wir uns die Partitur des psychischen &
physischen Geschehens geschrieben, || – ist dann das Glauben (Erwarten, Hoffen, Fürchten,
etc.) wie ein Orgelpunkt oder ein Basso
ostinato? |
∣ Die philosophische Klarheit wird auf das
Wachsen der Mathematik den gleichen Einfluß
|
∣
Eine der wichtigsten Ideen unsrer Ideen wie die Idee
der Disposition.
„Ich kann das A-B-C hersagen wenn ich
will.”
Ich habe es gleichsam in mir aufgeschrieben und zwar
tut's da nicht irgend ein Bild das ich in mir trage
sondern es handelt sich nur um ganz bestimmte. ∣
|
Worin besteht es eine Absicht zu haben?
(Siehe Glauben
|
Wenn man jemandem sagt: „denk' nur was daraus
würde wenn alle das
|
Der Disput darüber ob schon Eins oder erst Zwei die erste Zahl
sei. |
Was bedeutet ein Satz der Art (∃n)
4 + n = 7?
Nun
|
Wie wäre es wenn ein Satz seinen Sinn selber nicht ganz
erfaßte.
Wenn er sich quasi selber zu hoch wäre.
Und das nehmen eigentlich die Logiker an. |
„Alle Zahlen haben vielleicht diese
Eigenschaft”. |
Ein unbewiesener Satz || mathematischer Satz – ein Wegweiser der mathematischen Forschung. |
Der Beweis eines Satzes ist ein Teil seiner Grammatik.
Und wenn er unbewiesen ist so hat er eine andere Funktion als, wenn er
(oder ein Kalkül in dem er) bewiesen ist. Der unbewiesene Satz ist immer ein Gleichnis mit einem nicht mathematischen Satz. |
Wir haben von einer Zahlenreihe „1, 2, 3, 4, 5, Viele” gesprochen & ihrer Arithmetik; aber es gibt natürlich auch eine Arithmetik (oder: ich kann natürlich auch eine Arithmetik konstruieren) für die Reihe „1, 2, 3, 4, 5” ohne dem abschließenden unbestimmten Zahlwort. |
Ich verliere mich jetzt leicht in einem Wald möglicher Notationen
& Kalküle in dem ich mich im Kreis
|
Das jüdische “Genie” ist nur ein Heiliger.
Der größte jüdische Denker ist nur ein Talent.
(Ich z.B.) |
Es ist, glaube ich eine Wahrheit darin wenn ich denke, daß ich eigentlich
in meinem Denken nur reproduktiv bin.
Ich glaube ich habe nie eine Gedankenbewegung erfunden
sondern sie wurde mir immer von jemand anderem gegeben & ich habe
sie nur sogleich
|
Als ich seinerzeit den Kopf für Drobil
modellierte so war auch die Anregung
wesentlich ein Werk Drobils
& meine Arbeit war eigentlich wieder die des Klärens.
|
Der Jude muß im eigentlichen Sinn „sein Sach' auf nichts
stellen”.
Aber das fällt gerade ihm besonders schwer, weil er, sozusagen, nichts
hat.
Es ist viel schwerer freiwillig arm zu sein, wenn man arm sein
muß als, wenn man auch reich sein könnte. |
Man könnte sagen
Es ist dem jüdischen Geiste typisch das Werk eines Andern besser zu verstehen als der es selbst versteht. |
Ich habe mich oft dabei ertappt wenn ich ein Bild entweder
richtig hatte rahmen lassen oder in die
richtige Umgebung gehangen hatte so stolz zu sein als hätte ich das
Bild gemalt.
Das ist eigentlich
Der Vorgang der Entstehung auch des winzigsten & |
Das genaueste Bild eines ganzen Apfelbaumes hat in gewissem Sinne
unendlich viel weniger Ähnlichkeit mit
ihm als das kleinste Maßliebchen mit dem Baum
hat.
Und in diesem Sinne ist eine Brucknersche Symphonie mit einer Symphonie der heroischen Zeit
unendlich näher verwandt als eine Mahlerische.
Wenn diese ein Kunstwerk ist, dann eines gänzlich andrer
Art.
(Diese Betrachtung aber selbst ist eigentlich
|
Als ich übrigens in Norwegen war, im Jahre 1913-14
hatte ich eigene Gedanken, so scheint es mir jetzt
wenigstens.
Ich meine, es kommt mir so vor, als hätte ich damals in mir neue
Denkbewegungen geboren
(Aber vielleicht irre ich mich).
Während ich jetzt nur mehr alte anzuwenden scheine.
|
~(∃φ):(Еx) φx
(∃x) φx ∙ ~ (∃xy) φx ∙ φy φxε1 φxε5 |
Der Satz ~(∃φ):(Еx) φx muß von der Art dessen sein:
Es gibt keinen Kreis auf dieser Fläche der nur einen schwarzen Fleck
enthält.
|
Wenn nun aus zwei || den Sätzen
~(∃φ):(Еx)
φx &
~(∃φ):(Еx,y) φx ∙ φ || ρy
folgt daß 1 = 2 ist so kann hier mit „1”
& „2” nicht dasselbe gemeint sein || ist hier mit „1” & „2” nicht das
gemeint was wir gemeinhin damit meinen, denn die Sätze
ρ &
σ würden gewöhnlich || in der gewöhnlichen Wortsprache
lauten: Es gibt keine Funktion die nur von einem Ding
& keine die nur von zwei Dingen befriedigt wird.
Und dies sind nach der Regel unserer Sprache verschiedene Sätze und
diese Regel stützt sich
|
‒ ‒ ‒ Aber dieses Vorkommen des Paradigmas der & der
Klasse im Symbolismus bedeutet nicht, daß ein bestimmter Satz des
Symbolismus wahr sein muß. |
Rousseau hat
etwas Jüdisches in seiner Natur. |
Aber die Gleichung 1 = 2 in dieser
Auffassung hat ja nichts Erstaunliches denn sie
besagt: der
|
Daß Dein Satz
(∃x,y)x = a ∙ y = b wahr ist, ist doch nicht das was mich in Stand setzt „(∃x,y) φx ∙ φy” zu sagen! |
Kann man sagen ein
|
Oder kann man sagen der Satz
(∃φ):(Еx) φx ist sein eigener Beweis, da der Satz || das Zeichen selber so ein Ding enthält. |
Wenn manchmal gesagt wird die Philosophie
(eines Menschen) sei Temperamentssache, so ist auch darin
eine Wahrheit.
Die Bevorzugung gewisser
|
„Betrachte diese Warze || Beule als ein
regelrechtes Glied deines Körpers!”
Kann man das, auf Befehl?
|
Ist es in meiner Macht willkürlich ein Ideal von meinem Körper zu haben
oder nicht?
Die Geschichte der Juden wird darum in der Geschichte der europäischen Völker nicht mit der Ausführlichkeit behandelt wie es ihr Eingriff in die europäischen Ereignisse eigentlich verdiente, weil sie als eine Art Krankheit, Anomalie, in dieser Geschichte empfunden werden & niemand gern eine Krankheit mit dem normalen Leben gleichsam auf eine Stufe stellt. || & niemand Man kann sagen: diese Beule kann nur dann als ein Glied des Körpers betrachtet werden, wenn sich das ganze Gefühl für den Körper ändert (wenn sich das ganze Nationalgefühl für den Körper ändert). Sonst kann man sie höchstens dulden. Vom einzelnen Menschen kann man so eine Duldung erwarten oder auch |
Macht & Besitz sind nicht dasselbe.
Obwohl uns der Besitz auch Macht gibt.
Wenn man sagt die Juden hätten keinen Sinn für
|
Zwischen Brahms &
Mendelssohn herrscht entschieden eine gewisse Verwandtschaft;
& zwar meine ich nicht
|
Frege glaubte daß wir durch
Aufgeben der logischen
|
Man hat manchmal gesagt daß die
fortwährende Verfolgung der
Juden & ihre Heimlichkeit & Verstecktheit hervorgebracht hat || Heimlichkeit & Verstecktheit der Juden durch
ihre || die lange Verfolgung hervorgebracht worden sei.
Das ist gewiß unwahr; dagegen ist es gewiß, daß
|
Die Musik Bruckners
|
Die alles gleich machende Gewalt der Sprache die sich am krassesten
im Wörterbuch zeigt & die es möglich macht daß
die Zeit personifiziert werden konnte, was
|
a b c d Im logischen Sinne des Wortes möglich ist der Schluß vom esse ad posse nicht gerechtfertigter als der vom non esse ad posse. |
Seine Handlungsweise darauf einrichten daß es immer so weitergehen
wird. |
Glauben, erwarten, hoffen
|
Wenn wir sagen möchten die Unendlichkeit ist eine Eigenschaft
der Möglichkeit nicht der Wirklichkeit oder das Wort
„unendlich” gehört immer zum Wort
„möglich”
u. dergl. so kommt das darauf
hinaus zu sagen, das Wort
„unendlich”
sei immer Teil einer Regel nicht eines Erfahrungssatzes.
|
Man kann sagen ich mache Vorbereitungen für die nächsten 3
Tage
|
Wenn ich aber „Vorbereitungen auf unbestimmte Zeit
mache” dann läßt sich ein Zeitraum (nachträglich)
finden für den ich jedenfalls keine Vorbereitungen mehr mache.
|
D.h. aus dem Satz „ich mache
Vorbereitungen für unbestimmte Zeit” folgt nicht jeder beliebige Satz „ich mache Vorbereitungen für unbestimmte
Jahre”. |
Damit daß gesagt wird daß aus der unendlichen Hypothese
(u) ∙
(∃ux) φx wie ich sie nur der Kürze
wegen jetzt schreiben will jeder beliebige Satz
(∃ux) φx folgt
& sie selbst aus keinem dieser Sätze ist natürlich noch gar nichts
über den weiteren Gebrauch dieses Spiels gesagt. |
Denken wir gar an den Satz: ich vermute daß das immer so weitergehn
wird. |
Der komische Klang der Widerlegung: Du hast gesagt die Uhr werde
immer so weitergehen, und sie steht jetzt schon. Wir fühlen daß ja Es ist nämlich Unsinn zu sagen: „sie ist nicht unendlich weitergegangen sondern nach zehn Jahren stehen geblieben” oder noch komischer: „sondern schon nach zehn Jahren stehen geblieben”. |
Wie seltsam wenn
|
„Ich glaube das wird immer so weitergehen”.
„Ist es nicht genug wenn Du sagst Du
glaubst es werde noch 100000 Jahre so weitergehen?”
–
„Ja, das tut's auch”. |
„For all practical purposes” ist es genug zu
sagen, „ich glaube es werde …
Jahre dauern”. |
Wir müssen nämlich fragen: kann es Gründe zu diesem Glauben
geben?
Welches sind sie.
Welches sind die Gründe zur Annahme daß die Uhr noch 10000 Jahre
weitergehen wird welche für die Annahme daß sie noch
100000 Jahre gehen wird
– || – & welche nun die Gründe
zur unendlichen Annahme?! Das ist es ja was den Satz |
Denken wir an den Satz „dieser Komet wird sich in einer Parabel
mit der Gleichung … bewegen.”
Wie wird dieser Satz gebraucht? Er kann nicht verifiziert werden (d.h. wir haben keine Er wird auch gewisse Handlungen bestimmen z.B. wird || könnte er uns dann verhindern den Die Unendlichkeit der Annahme besteht nicht in ihrer Größe sondern in ihrer Unabgeschlossenheit. |
[Verschiedene Beunruhigungen des Verstandes || Geistes werden durch verschiedene Mittel beruhigt (eben alle
nennen wir Probleme & sprechen von Suchen &
Finden ihrer Lösung). Manche durch Erklärungen manche durch Gleichnisse manche durch Vereinfachungen.] |
Wenn man von || vom
Begriff „Unendlichkeit” redet muß man sich
daran erinnern daß dieses Wort eine Unzahl von verschiedenen
Bedeutungen hat & von welcher wir jetzt gerade reden.
Ob z.B. gerade von der
Unendlichkeit der Zahlenreihe & der Kardinalzahlen
insbesondere.¤
Wenn ich also sage „unendlich” sei eine
Charakteristik einer Regel oder der
Möglichkeit & nicht der Wirklichkeit so beziehe ich
mich auf eine bestimmte Bedeutung des Worts.
Wir könnten z.B. sehr wohl sagen ein
kontinuierlicher Farbübergang sei ein
Andres Beispiel: Die Geraden treffen sich im Unendlichen wenn sie parallel sind oder das Lineal hat einen unendlichen Krümmungsgrad. |
(Die besondere Beruhigung welche eintritt wenn wir einem Fall den wir
für einzigartig hielten andere ähnliche Fälle an die Seite
stellen tritt in unserer Untersuchung immer wieder
|
Warum ist man denn versucht das Wort „unendlich” ganz in die Regeln zu verweisen? Und fühlt es ungemütlich wenn es in einer Hypothese vorkommt? Aber auch in der Hypothese, möchte ich sagen, steht es nur für die Möglichkeit. – Das wogegen man sich wehrt Wir wehren uns gegen die Auffassung des Unendlichen als einer ungeheuern Größe. (Die wir merkwürdigerweise ohne Schwierigkeit erfassen während eine große endliche Zahl zu groß sein |
Denken wir uns wir erzählten jemandem „Gestern kaufte ich
mir ein Lineal mit unendlichem
Krümmungsradius”.
(Ach, Du meinst, es war gerade, – ja das verstehe
ich. –)
Aber hier kommt doch das Wort
„unendlich”
|
Ich meine: wenn das Wort „Gerade” oder
„Parallel” oder
„Längengleich”
etc. etc. in einem Erfahrungssatz stehen
darf dann auch das Wort
„Unendlich”. |
Und wie wenn ich nun sagte: „gerade
ist nur die Möglichkeit, nicht die Wirklichkeit”? Aber das hätte nur insofern Sinn ‒ ‒ ‒ |
Unendlich ist nur die Möglichkeit heißt:
„unendlich” ist ein Zusatz vor
„u.s.w.”
Wenn ich nun sage „dieser Komet bewegt sich in einer Parabel”. |
Soweit „unendlich” ein Zusatz zu
u.s.w. ist gehört es in eine Regel, ein
Gesetz.
Aber doch nicht notwendig in die Grammatik! |
In die Erfahrung gehört es insofern nicht als die Erfahrung die
einem Gesetz entspricht eine endliche Reihe von
Erfahrungen sind. |
„Das Wort
‚unendlich’ ist nur die
Möglichkeit
Das Wort bekämpft einen Fehler, legt aber auch einen nahe. Man kann sagen: „unendlich ist hier nur die Möglichkeit”. Und man fragt mit Recht: was ist denn an dieser Hypothese unendlich? Ist an dieser Annahme, an |
Es wundert mich nicht daß das Wort
„inf.” das in
„u.s.w. ad
inf.” vorkommt, nirgends sonst || anders vorkommt.
Denn „u.s.w. ad
inf.” ist, sozusagen, kein Wort.
|
Denken wir es sagte uns ein Kommis in einem
Geschäft: „davon können
Sie jede Menge haben” & nehmen wir an
es wäre mir erlaubt nur einmal eine Zahl zu nennen.
Denken wir uns die Fee im Märchen sagte: „Du kannst so viel Goldstücke haben als Du Dir wünscht aber Du darfst nur einmal wünschen.” Ist ihre Prophezeiung nicht erfüllt wenn ich kriege was ich wünsche? Und war meine Wahl nicht unbeschränkt? Wäre der Fall nicht ein andrer gewesen wenn sie mir eine Grenze gesetzt hätte wie weit immer sie sie gezogen hätte? Kann ich nun nicht sagen: die Freiheit die |
Man könnte das auch so sagen: Wenn man den Begriff der
Unendlichkeit auf die || in der Beschreibung
der Realität anwendet so ist in solchen Beschreibungen
z.B. nicht von unendlich langen
Linealen die Rede sondern von Linealen mit unendlichem
Krümmungsradius.
Und nicht
Wenn wir sagen: die Möglichkeit der Bildung von Dezimalstellen in der Division
|
Wenn man sagt daß dieses Gebiet unseres Gegenstandes
außerordentlich schwer ist so ist das insofern nicht wahr als nicht
etwa von schwer
vorstellbaren oder komplizierten Dingen
die Rede ist, sondern nur insofern als es außerordentlich schwer ist an den
unzähligen Fallen die hier in der Sprache für uns aufgestellt
sind vorbeizukommen.
|
Und es bleibt natürlich in diesen Erfahrungssätzen
„unendlich” die Eigenschaft einer Regel wenn man es so
ausdrücken will & das heißt nichts anderes als daß es
auch hier durch „u.s.w.
ad inf.” wiedergegeben werden kann &
zugleich ist das auch alles was damit gemeint ist; die
Unendlichkeit sei eine Eigenschaft || ein Produkt der
Möglichkeit. |
∣
Muß man sagen die Konstruktion des 7-Ecks ist
unmöglich?
Wie wenn es nicht so nahe läge zu versuchen
Dies ist nicht anders als wenn man sagt die Division von 2 durch 4 ist im System der Kardinalzahlen nicht möglich d.h.: es |
Die Reihe der
n-Eck-Konstruktionen
enthält kein 17-Eck. So wie die
Reihe der Kombinationszahlen nicht die Zahl 3 enthält.
Hat man einmal den „strengen” Begriff der
n-Eckskonstruktion so gibt es für diese keine Versuche der
Konstruktion des n-Ecks & ehe man ihn hatte war unser Begriff
ein anderer.
Denn die mathematische Form ist in der Mathematik das || entspricht in der Mathematik dem Zeichen des Begriffs.
Und verschiedene Formen sind verschiedene
mathematische Begriffe
|
Denken wir uns jemand stellte sich
folgendes Problem.
Ich
will ein Spiel || Erst ein Spiel zu erfinden, das folgenden
Bedingungen gemäß auf einem Schachbrett gespielt
wird.
Jede Seite || Die eine Seite soll 6 Steine haben
darunter gleichberechtigte die ich Bürger nenne &
zwei die ich Konsulen nennen will.
Diese beiden sollen etwas andere Züge machen dürfen
als die Bürger.
Man nimmt einen Stein des andern indem man den eigenen
an die Stelle des fremden setzt.
Der hat verloren
Denken wir uns es stellte sich das Problem in der Form: Wie kann man in so einem Spiel gewinnen? Das wäre eine ganz analoge Problemstellung wie die der Mathematik. |
Man könnte sagen: Der bewiesene mathematische Satz hat in seiner Grammatik zur Wahrheit hin ein Übergewicht. Denn wenn ich sage: „Wenn wir seinen Sinn verstehen wollen so fragen wir, wie er bewiesen wird” so ist da doch ein Fehler: Es müßte |
Ist er nun bewiesen, was ist dann der Sinn seines Gegenteils.
D.h. Ist die Analogie zwischen mathematischen & andern Sätzen nicht nur dort vorhanden wo der Zweifel ob ein Satz wahr oder falsch ist eine bestimmte Form annimmt, z.B. in Sätzen der Art 25 × 25 = 625? Wo nämlich zwar 25 × 25 nicht 624 ist aber dafür 20 × 31˙2 = 624. |
a + (b + c) = (a + b) + c
Wenn ich das negiere so hat das nur einen Sinn wenn ich etwas sagen kann wie: Es ist nicht a + (b + c) = (a + b) + c sondern = (a + b) + (c + 1)! Was ist der Raum in welchem ich den Satz ausschließe & was ist um ihn herum das nicht ausgeschlossen wird. Oder welches ist der Raum in dem mein Satz eine Grenze zieht? Nun der Fermatsche Satz: Es ist so & nicht wie? |
Es gibt etwas
1 + 1 = 2 Def. |
Das Wesentliche an der Möglichkeit der
Ausrechnung
Z.B. ist (a + b)² = a² + 2ab + b² nicht
a³ + 4ab aber
(a + b)² =
log a wäre kein möglicher Rechenfehler in diesem
System.
|
Insofern man die Unmöglichkeit der 3-Teilung als eine
wirkliche Unmöglichkeit darstellen kann, indem man
z.B. sagt: „Versuch
nicht den Winkel in 3 Teile
|
a + (b + c) = (a + b) + c
Man kann nicht sagen „ich werde ausrechnen daß es so ist” sondern „ob es so ist”. Also ob so oder anders. |
Ich könnte ja auch ganz beiläufig (siehe
„25 × 64 = 160 64 × 25 = 160, das beweist daß a × b = b × a ist” (& diese Redensart ist nicht vielleicht lächerlich & falsch; sondern man muß sie nur richtig || recht deuten¤). Und man kann richtig daraus schließen: also läßt sich a ∙ b = b ∙ a in gewissem Sinne beweisen. |
Und ich will sagen nur in dem Sinn in welchem die
Ausrechnung so eines Beispiels Beweis des algebraischen Satzes
|
Nun redet man vom Beweis des Satzes ~(∃n) ∙ x3 + y³
= zn ∙ n ˃ 2.
Das ist also wohl die Art & Weise wie man ausrechnet daß das so
ist. |
∣
Die Philosophie prüft nicht die Kalküle der Mathematik sondern nur
das was die Mathematiker über diese |
„Ich habe ausgerechnet daß es keine Zahl gibt …”
In welchem Rechnungssystem kommt diese Rechnung vor? Dies wird uns zeigen in welchem Satzsystem der errechnete Satz ist. (Man fragt auch: „wie rechnet man so etwas aus”.) |
„Ich habe gefunden daß es eine solche Zahl
gibt.” „Ich habe ausgerechnet daß es keine solche Zahl gibt.” |
Und wie wenn ich im zweiten statt „keine” „eine” setze? Nehmen wir an die Rechnung ergibt nicht den Satz ~(∃) etc. sondern (∃ …) etc. Hat es dann etwa Sinn zu sagen: nur Mut, jetzt mußt Du einmal auf eine solche Zahl kommen wenn Du nur lang genug probierst? Das hat nur Sinn wenn der Beweis nicht (∃ …) etc. ergeben hat sondern dem Probieren Grenzen gesteckt hat Es hat zwar keinen Sinn vom Beweis des Gegenteils von 28 × 15 = 618 zu reden || eines Satzes zu reden der bewiesen wurde da es diesen Beweis eo ipso nicht gibt wohl aber vom Beweis des Gegenteils eines analogen Satzes im selben System (d.h. eines Satzes den wir als analogen Satz im selben System auffassen wodurch der erste Satz erst den Charakter des Satzes erhält). & || Und der Vergleich mathem. Sätze mit dem was wir sonst Sätze nennen ist nur möglich solange wir von Verneinungen & Beweisen des entgegengesetzten Satzes in D.h. was das Gegenteil eines Satzes ist muß ich aus den Rechnungsregeln |
Der Existenzbeweis (in unserm Sinne) ist |
Man sollte glauben in den Beweis des Gegenteils von
(∃‒ ‒ ‒) sollte sich
eine Negation verirren können irrtümlicherweise
~(∃x)
beweist.
Gehen wir doch einmal, umgekehrt, von den Beweisen aus & nehmen wir an sie wären uns ursprünglich gezeigt worden & wir wären dann gefragt worden: was beweisen diese Sätze, würden wir sagen der eine beweist das Gegenteil des andern? || der eine beweist die entgegengesetzte Art von Satz als der andere? |
Ich sage z.B.: Ich weiß wie man
37 × 18 = 426
kontrolliert; kommt auf die & die Weise 426 heraus so
stimmt Hier mache ich überhaupt einen Fehler indem ich den Existenzbeweis im allgemeinen Fall mit dem des Probierens im Intervall im besondern Fall verwechsle. Auch wenn mir ein Existenzbeweis zuerst das Intervall gewiesen hat so beweist doch die Existenz die gefundene besondere Sieh auf die Beweise & entscheide dann was sie beweisen! |
Das was ich über die unendliche Teilbarkeit des Gesichtsraumes gesagt habe beruht glaube ich auf einem Irrtum. Wir müssen ja wohl an den Fall denken wenn wir eine Strecke sehen etwa die Länge eines länglichen schwarzen Fleckes an einer weißen Wand. Wenn ich nun z.B. sage: er läßt sich in die Hälfte teilen, so bezieht sich mein Satz unmittelbar auf den mir gegenwärtigen Fleck. Verschwindet dieser so (Erinnere Dich hier an die Sprachspiele mit grüner & roter Laterne & den Sinn von wahr
und falsch.) |
Wenn man sagt die Strecke im Gesichtsraum sei unendlich teilbar so meint
man etwas Analoges wie wenn man
sagt ein Fleck könne im Gesichtsraum unendlich viele Lagen einnehmen
was nur heißt daß keine Anzahl von Lagen in irgend einem Sinn
|
Kontrolle ist eine Methode die man anwenden kann
unabhängig davon ob der Satz wahr oder falsch ist.
„Das werden wir gleich ausrechnen.” |
Die Methode der Kontrolle kann ich beschreiben.
Wenn ich sie nun für einen bestimmten Fall beschreiben wollte so
könnte ich nicht sagen ergibt |
So beschreibe ich die Kontrolle der Teilbarkeit
(etc.).
Ist die Zahl durch 8 teilbar so … nicht
„ist 128 durch 8 teilbar so …”.
So gibt es für die Sätze (∃x) etc. & ~(∃x) eine Kontrolle wenn es sich um endliche Klassen von Zahlen handele. Denken wir nun an die Frage: hat die Gleichung x² + ax + b = 0 eine reelle Lösung? Hier gibt es wieder eine Kontrolle & die Kontrolle scheidet zwischen den Fällen (∃) etc. & ~(∃) etc. Kann ich aber in demselben Sinne auch fragen & kontrollieren ob die Gleichung eine Lösung hat, es sei denn daß ich diesen Fall wieder mit anderen zusammenstelle, in ein System bringe? |
Der Satz daß dieser Beweis rekursiv ist, ist in einem ganz
andern Sinne Satz der Mathematik als der welcher eine Kontrolle
zuläßt. |
Der Beweis antwortet im
ersten Fall auf eine Frage & die |
◇◇◇
Ich kann freilich fragen „ist
25 × 25 625 oder
nicht”; aber darauf erfolgt gleich die
Frage: Wie wirst || kannst Du das herausfinden
& die Antwort darauf ist die Beschreibung der allgemeinen Methode der
Kontrolle. |
In Wirklichkeit schafft „der Beweis des
Hauptsatzes” eine neue Art Zahlen. |
Die Philosophie der |
Die Frage ist immer worin besteht die Beschreibung des Gegenteils, worauf
stützt sie sich auf welche Beispiele & wie sind diese Beispiele mit
einem besondern Fall verwandt.
Dies ist nicht vielleicht nebensächlich „Jede Gleichung hat eine Wurzel” & wie ist es wenn sie keine hat? Können wir diesen Fall beschreiben wie den wenn sie keine rationale Lösung hat? |
Sehen wir uns einen Induktionsbeweis an
etwa den des Satzes daß keine Zahl die größer als 1 ist mit
3 multipliziert 5 ergibt
3 × 2 = 5 + 1 3 × a = (5 + b) 3 × (a + 1) = (5 + (b + 3)) 3 × (a + 1) = (3 × a) + 3 = (5 + b) + 3 = 5 + (b + 3) Wurde also in einem Satz ein Rechenfehler gemacht so kann durch Richtigstellung dieses Fehlers das Gegenteil von dem bewiesen werden was hätte bewiesen werden sollen. Dagegen kann kein Rechenfehler in der zweiten Gleichung den Satz zum || ¤ Beweis ins Gegenteil |
D.h. Wenn mir nachgewiesen wird daß ich mich
in der zweiten Gleichung geirrt habe so bin ich damit
nicht im Stande das Gegenteil des Satzes ~(∃)
etc. zu behaupten.
Nun, das könnte man freilich auch von einem Fehler in
der Rechnung 25 × 25 etc. sagen denn damit daß ein Fehler gemacht || nachgewiesen wäre, wäre das Resultat nicht als falsch erwiesen, aber nur, weil vielleicht noch ein zweiter Fehler |
∣
Der allgemeine geometrische
Beweis der Euklidischen Art ist das
was alle besonderen Beweise etwa für bestimmte Dreiecke
gemeinsam haben.
Nur beweist er es erst dann für das Dreieck … wenn dieses Dreieck
gegeben wird. ∣ |
Der Induktionsbeweis ist die allgemeine Aber das Gegenteil des Vorhandenseins dieser Form ist nicht etwa der Besitz einer Form die ihr widerspricht. |
Ich will doch sagen wenn der Beweis für ~(∃‒ ‒ ‒)
etc. geliefert wäre & wäre unique so wäre er
auch nicht der Beweis eines Satzes.
Denn dann würde man fragen können: Wie wäre es wenn es anders
wäre?
Oder: Was ist das System in welchem es nur für das Gegenteil
Raum gibt? |
Der Beweis sieht sein eigenes Gegenteil vor durch das Rechensystem zu dem
er gehört (gehören wird). |
Man muß bedenken, daß der Satz, daß es keine Zahl gibt die …, nicht
extensional zu verstehen ist sondern wesentlich das ist, was
der Induktionsbeweis beweist. || zeigt. Was aber zeigt er? Was ist sein Resultat? Er zeigt sich nur selbst. |
Der Induktionsbeweis |
Kann man sagen „prüfen wir ob dieser Satz für
alle n gilt oder ob er für irgendwelche nicht
gilt”? |
Denken wir Einer sagte: „prüfen wir
einmal nach ob f für alle n gilt.”
Nun fängt er an & sagt nach ein paar Versuchen „ich sehe
schon daß es für alle gilt”.
Darauf sage ich ja wenn Du das mit dem Satze
(x)
f(x) meintest!
Aber so hat er also nachgeprüft ob er eine Induktion findet Denn die Kontrolle würde lauten: Sehen wir nach ob sich eine Induktion findet oder ein Fall für den das Gesetz nicht gilt. Aber diese beiden sind ja nicht Alternativen. (Satz des ausgeschlossenen Dritten!) |
Wenn das Gesetz des ausgeschlossenen
Dritten nicht gilt so heißt das nur |
Man kann wohl sagen wenn die Induktion stimmt dann kann ich keine Zahl
finden die den Bedingungen nicht entspricht weil
die Induktion der Beweis jedes besonderen Satzes ist.
Und anderseits, wenn ich einen Wert von a gefunden
habe so daß ~ fn dann kann die Induktion erst
hinter a anfangen.
|
Die Induktion ist die gemeinsame Form von
Beweisen denen jedem die
Auffindung einer
Form || eines Satzes ~fa widersprechen
würde.
Darum sage ich sie beweisen einen Satz (n)
f(n).
Denn das Verhältnis zwischen Induktion &
~fa ist nun ähnlicher wie
das von „alle Menschen sind
sterblich” &
„ist ein Mensch & nicht
sterblich”. |
Im Fall des Beweises von
25 × 25 = 625
sage ich, vielleicht habe ich mich geirrt &
25 × 25 ist nicht
625.
Aber im Falle des Beweises von (n)f(n) in ‒ ‒ ‒. |
Statt „es gilt für alle” kann ich sagen „es
gilt für jeden den Du aufschreibst”. & nicht „die Induktion beweist daß es für alle n gilt” sondern daß jeder Satz fn den Du aufschreibst stimmt. Oder richtiger die Induktion beweist jeden Satz von der Form fn den Du anschreibst. |
(n) fn heißt dann
jeder Satz fn den Du angibst ist
richtig. |
Die Induktion ist kein Beweis sondern die Konstruktion einer Reihe
von Beweisen.
Daher wenn diese Konstruktion nicht vorhanden ist ist keiner der Sätze
negiert deren Beweise die Induktion zusammengehalten hätte. |
Man kann die Induktion nicht mit einem Beweis vergleichen.
|
Ich kann nicht den Fall beschreiben wo diese Division ausgeht
& nicht ausgeht, aber den Fall wo eine Division ausgeht
oder nicht ausgeht |
„Hat diese Gleichung eine Lösung?” –
Welches |
∣ ∣
Den Motor eines Autos umgekehrt laufen zu lassen ist unmöglich, oder würde
die größten Änderungen bedingen, aber den Wagen verkehrt
laufen zu lassen genügt ein leichter Handgriff.
So schaut es manchmal aus als ob Menschen die das
Entgegengesetzte tun fundamental entgegengesetzt
sein müßten & man dann oft sagen muß, der
Gegensatz sei nur im Getriebe basiert in den tieferen Schichten
|
Wie kommt es daß ich diesen Satz (den geometrischen
oder arithmetischen) nicht für jeden Fall wieder beweisen
muß?!
Aber Du mußt es ja, indem Du nämlich den Satz hinschreibst
denn das Übrige ist nur was allen Beweisen solcher
Sätze gemeinsam ist.
(Du mußt den Satz für jedes Dreieck wieder beweisen denn er
|
(Warum nenne ich || nennst
Du denn diesen Beweis (die Induktion) den Beweis dafür daß
(n)~f(n)?!
Nun, siehst Du denn nicht daß der Satz wenn
er für 2 gilt auch für
3 gilt & dann
auch für 4 &
daß es immer so weitergeht.
(Was erkläre ich dem, dem ich das Funktionieren des induktiven Beweises
erkläre?)
Du nennst ihn also |
Analogie dazu daß es Sinn haben muß zu sagen die Induktion beweise daß
es sich so verhält || dies & nicht das
Gegenteil der Fall ist.
Welches wäre || ist aber das Gegenteil.
Nun daß (∃n)fn der Fall
ist.
Damit verbinde ich nun zwei Begriffe: den einen den ich aus meinem
gegenwärtigen Begriff des Beweises vom Begriff n herleite &
einen andern der von der Analogie mit
(∃x)fx hergenommen
ist.
(Du mußt ja bedenken 3 × 2 = 5 + 1 ist und z.B. nicht 3 × 1 = 6 + 1. Wir lernen daß a + … = ‒ ‒ ‒ ist & nicht … aber dieses Gegenteil entspricht |
Es hätte keinen Sinn zu sagen ~
((a + b)² =
a² + 3ab + b²) wenn man das nicht
ausdrücklich als einen Satz erlaubt hätte oder
25 × 25 ≠ 620
wenn man diesen Satz nicht ausdrücklich in den Kalkül
hineingenommen |
Darum || Daraus weil ich diesen
Ausdruck in gewissen Verbindungen gebrauche folgt nicht daß ich ihn in
allem analog dem Ausdruck „der
Satz (∃x)fx”
gebrauche. |
Wenn wir nocheinmal die Analogie des
„Induktionsbeweises” mit den andern Beweisen besehen
so ergibt sich folgendes: 3 × 2 = 5 + 1 3 × 2 ˃ 5 3 × (2 + 1) = (3 × 2) + 3 = (5 + 1) + 3 = 5 + (1 + 3) 3x 3 × (2 + 2) = (3 × (2 + 1)) + 3 = (5 + (1 + 3)) + 3 = ¤5 + (1 + 3 + 3) Jeder dieser Beweise ist von der Art dessen von 25 × 25 = 625 oder etwa 25 × 25 = 125 × 5. Sie endigen in Sätzen die wir nach den Regeln kontrollieren. ◇◇◇ Diese Beweise nun bilden ein bestimmtes Muster¤ (was man z.B. durch Unterstreichen & Verbindungsstriche sichtbar machen kann). |
Und ich kann nun die Beweise abkürzen 0'(3 × 2 = 5 + 1) statt der zweiten 02'(3 + 2 = 5 + 1) ((2 + 2)) ˃ 5 u.s.w. |
Am Schluß wird jeder dieser Beweis zu weiter nichts als dem
bewiesenen Satz der gleichsam den Index enthält & die
allgemeine Form.
Das Beweisen besteht dann nur darin daß man den gegebenen Satz als einen
Fall der Form Wir sehen etwa auf den Satz hin & sagen: Ja die linke Seite ist von der Art dieser linken Seite so müßte die rechte Seite nun dies sein & das ist sie auch. Jeder dieser Beweise kontrolliert eine durch Sätze beantwortete Frage. Nun sagt man aber die allgemeine Beweisform sei der Beweis eines allgemeinen Satzes. Das soll heißen daß sie die Beweisform |
Wenn es hier eine Prüfung gibt so ist es immer ◇◇◇ ob alle n
die oder jene || nicht die Eigenschaft haben aber nicht ob
alle sie haben oder einige sie nicht haben.
Wir haben dann ein System von Induktionen &
|
Daher wir es seltsam finden wenn uns gesagt wird die
Induktion beweise den allg. Satz da
wir das richtige Gefühl haben daß wir ja in terms der
Induktion die allgemeine Frage gar nicht hatten stellen
können.
Da uns ja nicht zuerst eine Alternative gestellt war (oder nur zu
sein schien solange |
Die Frage nach der Allgemeinheit hatte vor dem Beweis noch gar keinen Sinn
also war sie auch keine Frage denn die hätte nur Sinn gehabt
wenn eine allgemeine Methode bekannt war ehe der besondere Beweis
bekannt war. |
Denken wir uns es hätten sich Menschen || Leute
darüber gestritten ob die Division
1 : 3 lauter Dreier plötzlich fällt dem Einen die induktive Beziehung in der Division
|
Der Ausdruck d, a, a, u.s.w. ist
der unexakte Ausdruck nicht
unexakter als der des allgemeinen Gliedes.
Denn auch dieses verläßt sich auf die Kenntnis der
Zahlenreihe & diese kann nicht durch ein allgemeines Glied etwa
n vermittelt werden!
Vielmehr ist n wesentlich die unabhängige Variable.
Und worin unterscheidet sich
x
Wir schreiben die Form der ungeraden Zahlen heute 2n + 1 aber die Form der Kardinalzahlen könnte geschrieben werden
|
In der Welt der Euklidischen Elemente kann ich ebensowenig nach der
3-Teilung fragen als ich nach ihr suchen
kann.
Es ist von ihr einfach nicht die Rede.
|
Man kann nur in einem System fragen wo es sowohl die 3-Teilung als auch die Geometrie mit Lineal &
Zirkel gibt. |
Ich kann erst dann fragen wenn ich fragen kann: wo ist die
3-Teilung? |
Ich kann ja auch nicht fragen ob die 4 unter den
Kombinationszahlen
Wenn also in |
Die Wirkung einer in der Sprache eingeschlossenen falschen
Analogie.
Sie bewirkt einen ständigen Krampf & Beunruhigung (quasi einen
ständigen Reiz).
Es ist wie wenn ein Ding aus der
¤ Entfernung etwas
anderes zu sein scheint als aus der Nähe betrachtet;
wir sagen dann: Ach ja das ist ein Baum¤.
Kaum entfernen wir uns ein wenig & verlieren die Erklärungen aus
dem Auge so erscheint uns eine Gestalt gehen wir darauf
näher zu so sehen wir eine andere nun entfernen wir uns wieder
u.s.w. |
Denken wir uns der beschriebene Konstruktionsvorgang wäre der der
fortgesetzten 2-Teilung
einer
Strecke mit Lineal & Zirkel Denn es
könnte ja an die Konstruktion mit Lineal &
Zirkel eine weitere Bedingung
geknüpft sein. in
der euklidischen Weise.
Man würde nun fragen: gibt es in
diesem Prozeß eine
3-Teilung der Strecke.
Man könnte die Reihe der Teilungen etwa durch Zeichen
|
Das Problem der
3-Teilung
ist kein
euklidisches.
(Wir wollen |
„Ist die 2-Teilung
im
euklidischen
System möglich?”
Wie geht man diese Frage an wenn man die
2-Teilung
noch nicht kennt.
Als physikalische Frage ist sie natürlich
möglich.
Denn im System der physikalischen Teilungen habe ich ja
die 2-Teilung (& auch die
3-Teilung¤
etc.). Das Problem lautet dann: Gibt es eine Konstruktion mit Zirkel und Lineal 3 Denken wir uns der Zirkel in unserer Geometrie hätte eine konstante Öffnung. |
Wenn man fragt: ist die
Konstruktion der
3-Teilung des ∢ möglich,
so könnte ich antworten: Was heißt das: ist sie
möglich? ist was möglich? ich kann
sie ja nicht einmal beschreiben.
Und ich kann nicht fragen: ist die
2-Teilung
möglich, denn indem ich angebe
wonach ich frage habe ich ja die 2-Teilung
beschrieben.
(Ich kann natürlich fragen: ist die physikalische
3-Teilung
oder 2-Teilung
möglich.) |
Buch ˃ Man kann also || nun fragen: ist diese Konstruktion 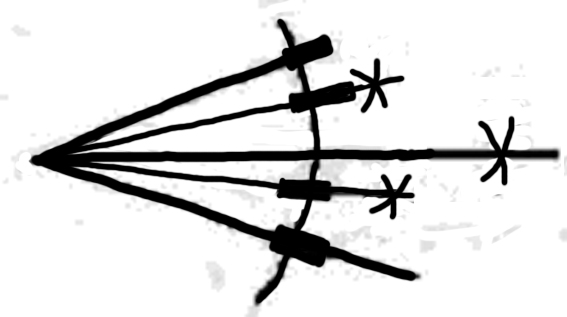 ?
Wir könnten uns denken er sähe die Konstruktion durch ein
verzerrendes Medium & die 3 Teile erschienen ihm gleich.
Und die Antwort ist natürlich nein diese Konstruktion erzeugt nicht
gleiche Teile, denn sie
erzeugt …. –
Aber man kann nicht fragen: „Wie teilt man den
∢ mit
Lineal &
Zirkel in 3 Teile?” noch:
„ist eine 3-Teilung
…
möglich?”. ?
Wir könnten uns denken er sähe die Konstruktion durch ein
verzerrendes Medium & die 3 Teile erschienen ihm gleich.
Und die Antwort ist natürlich nein diese Konstruktion erzeugt nicht
gleiche Teile, denn sie
erzeugt …. –
Aber man kann nicht fragen: „Wie teilt man den
∢ mit
Lineal &
Zirkel in 3 Teile?” noch:
„ist eine 3-Teilung
…
möglich?”. |
Das Wort „möglich” ist
irreführend.
Es sollte heißen, gibt es eine
3-Teilung im
euklidischen |
Gibt es die 3-Teilung
der Strecke im
α System?
Das kann heißen: kommt die Zahl 3 unter den Zahlen 2, 2², 2³ … vor? oder ist es möglich eine Strecke mit dieser Operation in 3 gleiche Teile zu teilen. Auch das kann beantwortet werden & zwar durch eine Induktion. Die erste Frage handelt eigentlich nicht von 3 Teilen die Welcher Art sind diese Fragen? Für die erste gibt es eine Methode des Suchens. Die zweite Frage ist: ist eine der Zahlen 2, 2², 2³ etc. durch 3 teilbar. Eine Induktion wird uns die Antwort ihrer Art geben. |
„Kann man den Winkel mit Lineal
& Zirkel
3-teilen?”
Wenn es unmöglich ist (logisch unmöglich)
wie kann man dann überhaupt danach fragen?
Wie kann man das logisch
Unmögliche beschreiben & nach seiner
Möglichkeit fragen?
D.h. wie kann man logisch
unzusammenpassende Begriffe zusammenstellen & sinnvoll nach ihrer
Möglichkeit fragen?
Es kann nicht heißen die 3-Teilung
mit Zirkel &
Lineal ist unmöglich wie es
etwa heißen könnte sie ist nicht erlaubt; sondern die
3-Teilung liegt nicht im Gebiet von
Zirkel & Lineal
|
Die Frage ist hier vor allem was verstehe ich hier unter
„3-Teilung”? physische Teilung? Teilung
durch eine andere Konstruktion?
Die 3-Teilung von der ich spreche muß ja
doch möglich sein d.h. es muß Sinn haben
diesen Ausdruck zu gebrauchen, welche 3-Teilung ist gemeint? |
In dem Sinne z.B. in dem man sagen kann das Produkt
3 × α ist in 3
Teile geteilt kann man ja von einem konstruierten Mittel
etwa des Winkels |
∣ (Wir sprechen von einer Teilung des Kreises in 7 gleiche
Teile & von einer Teilung eines Kuchens in 7 gleiche
Teile.) |
Ich kann in dem System α wirklich
nicht von einer
Dies wäre der Fall wenn „eine 3-Teilung im System α gibt es nicht” heißt es gibt da eine 4-Teilung oder die 3 kommt auf solche Weise nicht vor womit eben nichts gemeint ist als daß in der Reihe 2, 2² … nicht vorkommt oder 2 ≠ 3, 2² ≠ 3, 2³ ≠ 3 u.s.w. Dann aber könnte „eine 3-Teilung gibt es nicht” heißen: nicht in diesem Und das kommt darauf hinaus zu fragen welche Art der 3-Teilung ist gemeint wenn man sagt es gebe sie nicht. Wenn man die Geometrie mit Quadratwurzelausdrücken betriebe so käme man gar nicht auf eine ∛. Wie könnte man nun in dieser Geometrie nach der 3-Teilung fragen? oder nach der ∛? Nun es hat natürlich einen Sinn zu sagen daß wir durch Superposition von ²√ nicht Das ist derselbe Fall wie der des Systems α. |
„Ist die 3-Teilung …
möglich” wie kann man denn nach ihr fragen etc.
etc.
Nun das kommt auf dasselbe hinaus wie zu fragen: wie kann man fragen
ob
25 × 25 = 624
ist wenn es nicht so ist da es doch dann logisch unmöglich ist,
ich kann ja nicht schreiben wie es wäre wenn –.
Ja, der Zweifel über
25 × 25 = 624
oder |
Der Beweis des Satzes daß ◇◇◇ für alle Zahlen gilt wäre
eine Konstruktion der Induktion aus allgemeinen Prinzipien.
a + (b + 1) = (a + b) + 1 (b + (c + 1)) = (a + (b + c)) + 1 (a + b) + (c + 1) = ((a + b) + c) + 1 |
Die allgemeine Form eines Rekursionsbeweises ist das allgemeine Glied
einer Reihe von Beweisen.
Diese Reihe könnte ich ebensogut in der Form a1, a2,
a3 u.s.w.
schreiben.
|
a + (b + c) = (a + b) + c |
Die Konstruktion der Induktion ist nicht ein Beweis sondern eine
bestimmte Zusammenstellung von Beweisen. |
Wenn ich drei Sätze von den Formen α, β, γ bewiesen habe,
dann sage ich ich habe fc = φc bewiesen.
Welches weiter nichts ist als eine Definition |
Man kann auch nicht sagen ich beweise eine Gleichung wenn ich drei
beweise. Wie die Sätze einer Sonate || Suite nicht einen Satz ergeben. |
Steht nun A zu B im
Verhältnis von Sätzen zu einer
Ausrechnung?
¥
Steht es nicht im Verhältnis von
|
Wäre B die Ausrechnung von A so hätte ich
B ◇◇◇ A nicht allgemeiner beschreiben
können. |
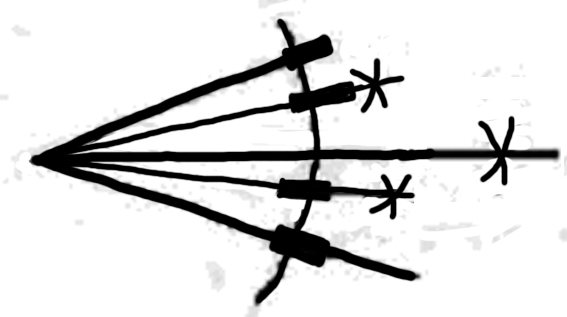
4 Sprungfedern. |
Aber das heißt schon daß wir A nicht in demselben Sinne
bewiesen haben wie etwa einen der
Sätze α, β, γ.
Die Frage ist A der Fall ist also die Frage ist α, β, & γ |
Ich habe jetzt das Wort „Beweis”
neu definiert mit Hilfe des Begriffes des Beweises einer Gleichung &
dem Muster α
β γ.
|
a + (b + 1) = (a + b) + 1 Def
a + (1 + 1) = (a + 1) + 1 a + ((1 + 1) + 1) = ((a + …
x + iy =
a = 2x √ ‒ 1y = √
y = √b ‒
y² +
|
Ich kann ruhig von „meinem
Gesichtsraum” & dem
„Gesichtsraum des Andern”
reden es wird sich schon in der Grammatik dieser Ausdrücke zeigen, daß es
sich hier nicht um einen Unterschied handelt wie zwischen meinem
Taschenmesser & dem des Andern. |
Man stellt sich den Gesichtsraum gern als eine Art ◇◇◇ vor
den jeder mit || vor sich herumträgt. |
|
Begriff & Gegenstand¤ sind
Subjekt &
Prädikat. fa = a ε
f(ξ) Dieser Körper ist ein Stück Eisen. Herr N ist ein Franzose. Dieses || Das Blatt ist ein Rosenblatt. Das ist ein Kanonenschuß. „Das ist ein Haus” kann heißen „hier ist ein Haus”. |
Ist „hier” ein Name?
Nein.
Es läßt sich ja auch nicht durch einen Namen
ersetzen. Es hat nur soweit Sinn einem Gegenstand einen Namen zu geben als ich sagen kann das ist derselbe Gegenstand welcher … |
Wenn ich in der Geometrie sage, der Kreis K0 … so heißt das, der
Kreis an diesem Ort.
Es hätte keinen Sinn wenn dieser
Kreis mir entschwände & einer an einer andern Stelle auftaucht
zu fragen: ist das wieder der Kreis K? Was ist das Kriterien dafür, daß ein Gegenstand |
Im Falle des Gebrauchs eines Personennamens z.B. ist
es wesentlich daß die Frage Sinn hat: ist dieser Gegenstand
der den Du A genannt hast.
Denn die hinweisende Def. lautet: Dies ist
A & insofern könnte also A einfach statt des Hinweises
stehen.
Statt „A
wächst” kann ich dann einfach sagen
„dieses wächst”.
Aber die Technik des Gebrauchs von A ist gerade daß ich A dort
gebrauche wo die |
Die Schreibweise (∃x) nimmt sich
von der Ausdrucksform der gewöhnlichen Wortsprache her „es gibt
…”
Aber obwohl wir z.B. || etwa sagen: „Es gibt einen
Menschen der 8 Fuß hoch ist” so sagen wir doch nicht „es
gibt ein Ding, das ein Mensch & 8 Fuß hoch
ist”.
Wir Wenn ich nun sage „In dem großen Kreis  ist konzentrisch ein
kleiner” so hieße das in der
(∃)-Notation
es sei ein Ding im großen Kreis
das ein konzentrischer Kreis ist || sei.
Nun welches Ding ist denn das? –
Die Notation wie Russell sie
versteht mußte immer den Satz erlauben ist konzentrisch ein
kleiner” so hieße das in der
(∃)-Notation
es sei ein Ding im großen Kreis
das ein konzentrischer Kreis ist || sei.
Nun welches Ding ist denn das? –
Die Notation wie Russell sie
versteht mußte immer den Satz erlauben Die Notation der gewöhnlichen Sprache „Im Viereck sind 3 Kreise” ist viel korrekter. Sie macht mehr relevante Unterschiede als die Russellsche. |
„Mann” ist freilich ein Begriffswort
& nicht eine Bezeichnung für einen Mann &
„Kreis” nicht der Name eines
Kreises (soweit ein Kreis überhaupt einen Namen haben kann).
Aber roter Kreis vom
|
„Ergibt die Operation z.B. eine
rationale Zahl.”
Wie kann das gefragt werden wenn man keine Methode der
Entscheidung der |
Die Frage „ist π =
π'” hat daher keinen Sinn.
π & π' sind mit
einander nicht vergleichbar.
Wenn π ein Punkt der Zahlengeraden ist, ist π' keiner.
Man kann nicht sagen „π' ist ein Punkt
den ich nicht kenne”, denn π' ist nur was ich
kenne & sollte ich einmal etwas |
So weit ich auch das Intervall verkleinere so
komme ich nicht nur zu keiner Entscheidung
sondern bleibe immer gleich weit von der Entscheidung.
|
Wenn man sagt: „die Menschen meinen mit dem Ausdruck …
das (oder eigentlich
das)” so will man meist sagen daß sie sich
auf bestimmte Weise dazu bringen lassen zu sagen, sie meinten das.
Wenn man ihnen z.B. eine Definition eines Begriffes
gibt an die sie früher nicht gedacht hatten & sie diese nun
annehmen. |
❘ ❘• ❘ ❘ Würde sich die Zahl π dadurch ändern, daß eine Methode gefunden würde zu berechnen an welcher Stelle der Entwicklung 777 777 auftritt. |
Was für großartige Menschen wir sind diese alten Probleme gelöst zu
haben! –
Nein die Zeit hat uns geändert & die Probleme
sind verschwunden. |
Stetigkeit. |
Gleichheit im Gesichtsraum im Gegensatz zum
Euklidischen.
S 72 |
Gecto Plotj
–|––––|––||||–|–– |
Editorial notes
1) For the dating of Ms-154 see the corresponding parts in Ms-113.
2) Between leaf 24 and leaf 25 one leaf seems to have been cut out.
3) The remark is preceded by geometric drawing drafts, including of angle trisection.
4) The first of the three elastic spring drawings is deleted.
5) On page 91v.