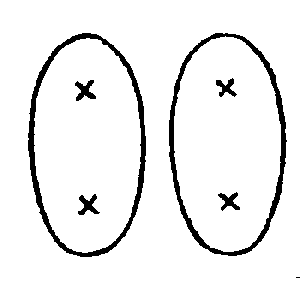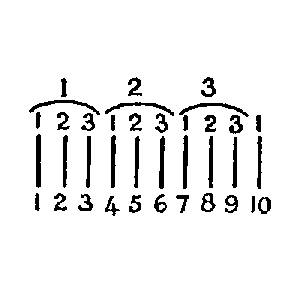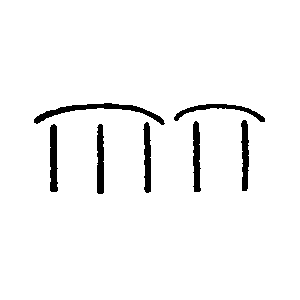138
“Aber1 sind die Übergänge
also durch die algebraische Formel nicht
bestimmt?” – In der Frage liegt ein
Fehler. Wir verwenden den Ausdruck: “die Übergänge sind durch die Formel ..... bestimmt”. Wie wird er verwendet? Wir können etwa davon reden, daß Menschen durch Erziehung (Abrichtung) dahingebracht werden, die Formel y = x² so zu verwenden, daß Alle, wenn sie die gleiche Zahl für x einsetzen, immer die gleiche Zahl für y herausrechnen. Oder wir können sagen: “Diese Menschen sind so abgerichtet, daß sie alle auf den Befehl ‘+3’ auf der gleichen Stufe den gleichen Übergang machen.” Wir könnten dies so ausdrücken: “Der Befehl ‘+3’ bestimmt für diese Menschen jeden Übergang von einer Zahl zur nächsten völlig.” (Im Gegensatz zu andern Menschen, die auf diesen Befehl nicht wissen, was sie zu tun haben, oder deren jeder zwar mit Sicherheit, aber in anderer Weise auf ihn reagieren.) || , oder die zwar mit Sicherheit, aber ein jeder in anderer Weise auf ihn reagieren.) Wir können anderseits verschiedene Arten von Formeln und zu ihnen gehörige verschiedene Arten der Verwendung (verschiedene Arten der Abrichtung) einander entgegensetzen. Wir nennen dann Formeln einer bestimmten Art (und der dazugehörigen Verwendungsweise) “Formeln, welche eine Zahl y für ein gegebenes x bestimmen”, und Formeln anderer Art, solche, “die die Zahl y für ein gegebenes x nicht bestimmen”. (y = x² + 1 wäre etwa von der ersten Art, y ˃ x² + 1, y = x² ± 1, y = x² + Z von der zweiten.) Der Satz “die Formel ..... bestimmt eine 139 Zahl
y” ist dann eine Aussage
über die Form der Formeln und es ist nun zu unterscheiden ein
Satz wie: “die Formel, die ich hingeschrieben
habe, bestimmt y” oder “hier steht
eine Formel, die y bestimmt”, von einem Satz
wie: “die Formel
y =
x² bestimmt die Zahl
y
für ein gegebenes x”. Die
Frage: “Steht dort eine Formel, die
y bestimmt?” heißt dann
dasselbe wie: “Steht dort eine Formel dieser
Art, oder jener Art?”, was wir aber mit der Frage
anfangen sollen: “Ist
y =
x² eine Formel, die y für ein
gegebenes x bestimmt?” ist nicht ohne
weiteres klar. Diese Frage könnte man etwa an einen
Schüler stellen, um zu prüfen, ob er die Verwendung des
Ausdrucks “bestimmen” versteht; oder es
könnte eine mathematische Aufgabe sein, zu
berechnen, ob auf der rechten Seite der Formel nur eine
Variable steht, wie
z.B. im Fall
y =
(x² + Z)² ‒
Z(2x² + Z).
Man kann nun sagen: “Wie die Formel
gemeint wird, das bestimmt, welche
Übergänge zu machen
sind.” Was ist das Kriterium dafür, wie
die Formel gemeint ist? Doch wohl die Art und Weise,
wie wir sie ständig gebrauchen, wie uns gelehrt wurde, sie zu
gebrauchen. Wir sagen z.B. Einem, der ein uns unbekanntes Zeichen gebraucht: “Wenn Du mit ‘
So kann also das Meinen die Übergänge zum voraus bestimmen. 140 |
“Worin liegt
dann aber die eigentümliche
Unerbittlichkeit der Mathematik?” –
Wäre für sie nicht ein
gutes Beispiel die
Unerbittlichkeit, mit der auf 1 || eins zwei
folgt, auf zwei drei, auf drei vier,
usw.? ‒ ‒ Das heißt doch
wohl: in der
Kardinalzahlenreihe folgt, – denn in einer
andern Reihe folgt ja etwas anderes? Und ist denn
diese Reihe nicht eben durch diese Folge
definiert? – “Soll das
also heißen, daß es
gleich richtig ist, wie immer man zählt und
daß jeder zählen kann, wie er
will?” – Wir würden es wohl nicht
“zählen” nennen, wenn jeder
irgendwie Ziffern nacheinander ausspricht; aber es
ist freilich nicht einfach eine Frage der Benennung. Denn
das, was wir “zählen” nennen, ist ja ein
wichtiger Teil der Tätigkeiten unseres Lebens. Das
Zählen, und Rechnen, ist doch,
z.B.,
nicht einfach ein Zeitvertreib. Zählen
(und das heißt: so
zählen) ist eine Technik, die täglich in den
mannigfachsten Verrichtungen unseres Lebens verwendet wird.
Und darum lernen wir zählen, so wie wir es lernen:
mit endlosem Üben, mit erbarmungsloser
Genauigkeit; darum wird unerbittlich darauf gedrungen,
daß wir Alle auf “eins”
“zwei”, auf “zwei”
“drei”, sagen
u.s.f.
– “Aber ist dieses Zählen
also nur ein Gebrauch; entspricht dieser Folge nicht
auch eine Wahrheit?” Die
Wahrheit ist, daß das
Zählen sich sehr gut bewährt hat. –
“Willst du also sagen, daß
‘wahr-sein’
heißt: brauchbar (oder
nützlich) sein?” – Nein;
sondern, daß man von der natürlichen
Zahlenreihe – ebenso wie von unserer Sprache – nicht
sagen kann, sie sei wahr, sondern:
141
sie sei brauchbar und, vor
allem, sie werde verwendet. |
“Aber folgt es nicht mit
logischer Notwendigkeit, daß Du
Ziffer 2 || zwei
erhältst, wenn Du zu eins eins
zählst und drei, wenn Du zu zwei eins
zählst,
u.s.f.; und ist diese
Unerbittlichkeit nicht dieselbe, wie die des logischen
Schlusses?” – Doch! Sie ist
dieselbe. – “Aber entspricht denn der
logische Schluß nicht einer
Wahrheit? Ist es nicht wahr,
daß das aus diesem folgt?”
– Der Satz: ‘es ist wahr,
daß das aus diesem folgt’,
heißt einfach: das folgt aus
diesem. Und wie verwenden wir diesen Satz? – Was würde denn geschehen, wenn wir anders
schlössen – wie würden wir mit der Wahrheit in
Konflikt geraten?
|
Da muß man
sich klar machen, worin Schließen denn
eigentlich besteht. Man wird etwa sagen, es besteht im
Übergang von einer Behauptung zu einer
andern. Aber was heißt
das? Heißt es,
daß Schließen etwas
ist, was stattfindet beim Übergang
von der einen zur andern Behauptung, also ehe die
andere ausgesprochen ist – oder heißt
es, daß Schließen
darin besteht, die eine Behauptung auf die andere folgen zu lassen,
d.h., nach ihr
auszusprechen? Wir stellen uns, verleitet durch die
besondere Verwendung des Verbums
“schließen”, gern vor,
das Schließen sei eine
eigentümliche Tätigkeit,
142 ein Vorgang
im Medium des Verstandes, gleichsam ein Brauen der Nebel, aus
welchem dann die Folgerung auftaucht. Sehen wir aber
doch zu, was dabei geschieht! Einerseits gibt es da
einen Übergang von einem Satz zum andern auf
dem Weg über andere Sätze, also durch eine
Schlußkette, – aber von diesem
Übergang brauchen wir nicht zu
reden, da er ja eine andere Art von
Übergang voraussetzt, nämlich von
einem Glied der Kette zum nächsten. || , da er ja aus andern
Übergängen
zusammengesetzt ist, nämlich von einem Glied der Kette zum
nächsten. Und auch hier
gibt es einen Vorgang, den man
Übergang zwischen Gliedern
nennen kann. An diesem
Vorgang ist nun nichts Okkultes; es ist ein
Ableiten des einen Satzzeichens aus dem andern nach einer
Regel, ein Vergleichen der beiden mit irgendeinem Paradigma, das
uns das Schema des Übergangs
darstellt, oder dergleichen. Es kann auf dem Papier,
mündlich, oder ‘im Kopf’,
d.h. in der Vorstellung vor sich gehen.
Der Schluß kann aber auch so gezogen
werden, daß der eine Satz ohne einen
Vorgang der Überleitung nach dem
andern ausgesprochen wird; oder die
Überleitung besteht nur darin,
daß wir sagen;
“Also:”, oder:
“Daraus folgt:”, oder
dergl. Man nennt es dann
“Schluß”, wenn der
gefolgerte Satz sich tatsächlich aus der
Prämisse ableiten
läßt. |
Was heißt es
nun, daß sich ein Satz aus einem andern,
vermittels einer Regel, ableiten
läßt?
Läßt sich nicht alles aus allem
vermittels irgend einer Regel ableiten? – Was heißt es, wenn ich
z.B. sage: diese Zahl
läßt sich durch die Multiplikation
jener beiden erhalten? Dies ist
offenbar eine
143 Regel, die sagt,
daß Du diese Zahl erhalten
mußt, wenn anders Du
richtig multiplizierst; und
diese Regel können wir dadurch erhalten,
daß wir die beiden Zahlen
multiplizieren, oder auch auf andere Weise (obwohl man auch
jeden Vorgang, der zu diesem Ergebnis führt, eine
‘Multiplikation’ nennen
kann). Man sagt nun, ich habe
multipliziert, wenn ich die Multiplikation
165 × 363
ausgeführt habe, aber auch, wenn ich sage:
“4 mal 2 ist
8”, obwohl hier kein
Rechnungsvorgang zum Produkt geführt hat (das ich aber auch
hätte ausrechnen können). Und
so sagen wir auch, es werde ein Schluß
gezogen, wo er nicht errechnet wird. |
Aber die
Schlußregel muß doch
so sein, daß die Folgerung wahr sein
muß, wenn die
Prämisse wahr ist.
Wenn ich also die Prämisse
als wahr erkannt habe, so muß der
Schluß ein solcher sein,
daß ein
Nicht-Übereinstimmen der Folgerung mit
der Realität ausgeschlossen ist. ‒ ‒ Und
das ist nur dadurch möglich, daß ich
nichts als ein solches
Nicht-Übereinstimmen gelten lasse,
wenn die Realität mit den
Prämissen
übereinstimmt. |
“Ich darf aber doch nur
folgern, was wirklich folgt!”
– Soll das heißen: nur das,
was den Schlußregeln
gemäß folgt, – oder soll es
heißen: nur das, was solchen
Schlußregeln
gemäß folgt, die irgendwie mit der
Realität übereinstimmen?
144 Hier schwebt uns
in vager Weise vor, daß diese Realität
etwas sehr Abstraktes, sehr Allgemeines und sehr
Hartes ist. Die Logik ist eine Art von
Ultraphysik, die Beschreibung des ‘logischen
Baus’ der Welt, den wir durch eine Art Ultraerfahrung
wahrnehmen (mit dem Verstande etwa). Es
schweben uns hier vielleicht Schlüsse vor wie dieser:
“Der Ofen raucht, also ist das Ofenrohr wieder
verlegt.” (Und so wird dieser
Schluß gezogen! Nicht
so: “Der Ofen raucht, und wenn immer der Ofen
raucht, ist das Ofenrohr verlegt;
also .....”.) |
Das, was wir ‘logischer
Schluß’ nennen, ist nichts als
eine Transformation des Ausdrucks. Die Umrechnung
von einem Maß auf ein anderes. Auf
der einen Kante des || eines
Maßstabes sind Zoll aufgetragen, auf der
andern
cm. Ich messe den Tisch in
Zoll und gehe dann auf dem
Maßstab
zu
cm über. –
Oder so: ich fülle ein
Gefäß mit Wasser, dann leere ich das
Wasser in ein Meßglas und endlich wäge
ich dieses Wasser, um einen andern Ausdruck
für den Inhalt des Gefäßes zu
erhalten. Und freilich gibt es auch beim
Übergang von einem
Maß zum andern richtig und falsch; aber mit
welcher Realität stimmt hier das Richtige
überein? Wohl mit einer
Abmachung, oder einem Gebrauch, und
etwa mit den praktischen Bedürfnissen.
|
Wie würden wir mit der
Wahrheit in Konflikt
145 geraten, wenn unsere
Zollstäbe aus weichem Gummi wären, statt aus Holz und
Stahl? – “Nun, wir würden nicht das
richtige Maß des Tisches kennen
lernen.” – Du meinst, wir würden
nicht, oder nicht zuverlässig, die
Maßzahl erhalten, die wir mit
unsern harten Maßstäben
erhalten. Der wäre also im Unrecht,
der den Tisch mit dem dehnbaren Maßstab
gemessen hätte und behauptet, er
mäße nun 1.80
m nach
unserer gewöhnlichen Meßart;
sagt er aber bloß,
der Tisch mißt 1.80
m nach
seiner Meßart, so stimmt das. – “Aber das ist dann doch überhaupt kein
Messen!” –
Gewiß, es ist nicht, was wir
‘messen’ nennen; kann aber unter Umständen
auch ‘praktische Zwecke’ erfüllen.
Einen Maßstab, der sich bei der || geringer Erwärmung außerordentlich stark ausdehnte, würden wir – unter gewöhnlichen Umständen – deshalb unbrauchbar nennen. Wir könnten uns aber Verhältnisse denken, in denen gerade dies das Erwünschte wäre. Ich stelle mir vor, daß wir die Ausdehnung mit freiem Auge wahrnehmen; und Körpern in Räumen von ungleicher Temperatur die gleiche Maßzahl der Länge beilegen, wenn sie auf dem Maßstab, der fürs Auge bald länger bald kürzer ist, gleich weit reichen. Man kann dann sagen: Was hier “messen” und “Länge” und “längengleich” heißt, ist etwas Anderes, als was wir so nennen. Der Gebrauch dieser Wörter ist hier ein anderer, als der unsere; aber er ist mit ihm verwandt und auch wir gebrauchen diese Wörter auf vielerlei Weise. Plinius sagte, es sei eine Eigenschaft der Zahlen, daß nach je zehn eine höhere Art beginne. (Die logische Struktur der Welt. –) 146 |
“Aber
muß denn nicht
z.B. aus
‘(x).fx’
fa
folgen, wenn “‘Alle’2 heißt doch: alle!” möchten wir sagen, wenn wir sie erklären sollen; und dabei machen wir eine gewisse Geste und Miene. Hacke alle diese Bäume um! ‒ ‒ Ja, verstehst Du nicht, was ‘alle’ heißt? (Er hatte einen stehen gelassen.) Wie hat er gelernt, was ‘alle’ heißt? Doch wohl durch Übung. – Und freilich diese Übung hat nun nicht nur bewirkt, daß er auf den Befehl das tut, sondern sie hat das Wort mit einer Menge von Bildern (visuellen und andern) umgeben, von denen das eine oder das andere auftaucht, wenn wir das Wort hören und aussprechen. (Und wenn wir Rechenschaft darüber geben sollen, was die ‘Bedeutung’ des Wortes ist, greifen wir zuerst ein Bild aus dieser Masse heraus – und verwerfen es dann wieder als unwesentlich, wenn wir sehen, daß einmal dies, einmal jenes auftritt, und manchmal keines.) Man könnte sagen: Man lernt die Bedeutung von “alle” indem man lernt, daß aus ‘(x).fx’ fa folgt. – D.h., die Übungen, die den Gebrauch dieses Wortes einüben, seine Bedeutung lehren, zielen immer dahin, daß eine Ausnahme nicht gemacht 147 werden darf.
|
“Aus
‘alle’, wenn es so gemeint ist,
muß doch das
folgen.” – Wenn es wie gemeint
ist?
Überlege es Dir, wie meinst Du
es? Da schwebt Dir etwa noch ein Bild vor – und
mehr hast Du nicht. – Nein, es
muß nicht – aber es
folgt: Wir vollziehen diesen
Übergang. Und wir sagen: Wenn das nicht folgt, dann waren es eben nicht alle! – – und das zeigt nur, wie wir mit Worten in so einer Situation reagieren. – |
Wir könnten es auch so
sagen: Es kommt uns vor, daß,
wenn aus (x).fx nicht mehr
fa folgen soll,
außer dem Gebrauch des
Wortes “alle” noch etwas anderes sich
geändert haben muß, etwas, was dem Worte
unmittelbar || selbst
anhängt. Ist das nicht ähnlich, wie wenn man sagt: “Wenn dieser Mensch anders handelte, dann müßte auch sein Charakter ein anderer sein.” Nun das kann in manchen Fällen etwas heißen und in manchen nicht. Wir sagen: “aus dem Charakter fließt die Handlungsweise”, und so fließt aus der Bedeutung der Gebrauch. |
Das zeigt Dir – könnte man sagen
– wie fest
148 verbunden gewisse Gesten,
Bilder, Reaktionen, mit einem ständig geübten Gebrauch
sind. ‘Es drängt sich uns das Bild auf .....’. Es ist sehr interessant || bemerkenswert, daß sich uns Bilder || Bilder sich aufdrängen können. |
Wichtig ist,
daß in unserer Sprache – in
unserer natürlichen Sprache –
‘alle’ ein Grundbegriff ist und ‘alle
außer einem’ weniger fundamental;
d.h., es gibt dafür nicht
ein Wort, auch nicht eine charakteristische
Geste. |
Der
Witz des Wortes “alle” ist ja,
daß es keine Ausnahme
zuläßt. – Ja, das ist
der Witz seiner Verwendung in unserer Sprache; aber welche
Verwendungsarten wir als ‘Witz’ empfinden, das
hängt damit zusammen, welche Rolle diese Verwendung in
unserem || unserm ganzen
Leben spielt.
(Damit hängt diese Bemerkung zusammen: Wir möchten manchmal sagen, “es muß doch einen Grund haben, warum auf dieses Thema – in einer Symphonie etwa – gerade das Thema folgt”. Als Grund würden wir eine gewisse Beziehung der beiden Themen, eine Verwandtschaft, einen Gegensatz, oder dergleichen, anerkennen. – Aber wir können ja eine solche Beziehung konstruieren: sozusagen eine Operation, die das eine Thema aus dem andern erzeugt; aber damit ist uns nur gedient, wenn diese Beziehung eine uns wohlbekannte ist. Es ist also, als müßte die Folge dieser Themen einem in uns 149 schon vorhandenen Paradigma
entsprechen. Von einem Gemälde, das zwei menschliche Gestalten zeigt, könnte man ähnlich sagen: “Es muß einen Grund haben, warum gerade diese zwei Gesichter uns einen solchen Eindruck machen.” Wir möchten – heißt das – diesen Eindruck der beiden Gesichter wo anders wieder finden – in einem anderen Gebiet. – Aber ob er wieder zu finden ist? Man könnte auch fragen: Welche Zusammenstellung von Themen hat eine Pointe, welche keine? Oder: Warum hat diese Zusammenstellung eine Pointe und die keine? Das mag nicht leicht zu sagen sein! Oft können wir sagen: “Diese entspricht einer Geste, diese nicht.”) |
Auf die Frage, worin denn das
Schließen besteht, hören wir
etwa: “Wenn ich die Wahrheit der Sätze
...... erkannt habe, so bin ich nun berechtigt, ......
hinzuschreiben.” – Inwiefern
berechtigt? Hatte ich früher kein Recht, es
hinzuschreiben? ‒ ‒ “Jene
Sätze überzeugen mich von der Wahrheit dieses
Satzes.” – Aber darum handelt
sich's natürlich auch nicht. ‒ ‒
“Nach diesen Gesetzen vollführt der Geist die
besondere Tätigkeit des logischen
Schließens.” – Das
ist gewiß interessant und wichtig;
aber ist es denn auch wahr? schließt
er immer nach diesen Gesetzen? Und
worin besteht die besondere Tätigkeit des
Schließens? ‒ ‒
Darum
ist es notwendig, zu schauen, wie wir denn in der Praxis der
Sprache
Schlüsse vollziehen, – was denn das
Schließen im Sprachspiel für ein
Vorgang ist. Z.B.: In einer Vorschrift steht: “Alle, die über 1.80 m hoch sind, sind in die ..... Abteilung aufzunehmen.” Ein Kanzlist verliest die Namen der Leute, dazu ihre Höhe. Ein anderer teilt sie den und den Abteilungen zu. – N.N., 1.90 m. – “Also N.N. in die ..... Abteilung.” Das ist Schließen. 151 |
Was
nennen wir,
z.B.,
‘Schlüsse’ bei
Russell,
oder bei Euklid? Soll ich
sagen: die Übergänge von einem
Satz zum nächsten im Beweis? Aber wo steht der
Übergang? –
Ich sage, bei Russell folge dieser Satz p aus
jenem q || p
aus q, wenn
p
aus q
gemäß der
Stellung der beiden in einem ‘Beweise’, und den
ihnen beigefügten Zeichen, abzuleiten ist, wenn wir das Buch
lesen. Denn, dieses Buch zu lesen ist ein Spiel,
welches gelernt sein will. |
Man ist sich oft im Unklaren, worin das
Folgen und Folgern eigentlich besteht; was
für ein
Sachverhalt oder Vorgang es ist. Und dies kommt von der
eigentümlichen Verwendung dieser Verben. Es
wird uns nahe gelegt, daß Folgen das
Bestehen einer Verbindung zwischen Sätzen ist, der wir beim
Folgern nachgehen. Diese Unklarheit zeigt sich
sehr lehrreich in
Russell's Darstellung (‘Principia
Mathematica’). Daß
ein Satz ⊢p aus
einem Satz ⊢p ⊃ q.p
folgt, ist hier ein logisches Grundgesetz:
⊢p ⊃ q.p. ⊃ .⊢q
Dieses berechtige uns nun, heißt es,
⊢q aus
⊢p ⊃ q.p
zu schließen. Aber worin
besteht denn ‘schließen’,
diese Prozedur, zu der wir berechtigt werden? Doch
darin, den einen Satz – in irgendeinem Sprachspiel –
nach dem andern als Behauptung auszusprechen, anzuschreiben und
dergl., und wie
kann mich jenes
Grundgesetz dazu berechtigen?
152 |
Russell will doch sagen:
“So werde ich
schließen und so ist es
richtig.” Er will uns also einmal
mitteilen, wie er schließen will: das
geschieht durch eine Regel des
Schließens. Wie lautet
sie? Daß dieser Satz jenen impliziert?
Doch wohl, daß in den Beweisen
dieses Buchs ein solcher Satz nach einem solchen stehen
soll. – Aber es soll ja ein logisches Grundgesetz
sein, daß es richtig
ist, so zu schließen! –
Dann müßte das Grundgesetz
lauten: “Es ist richtig vom .....
auf ..... zu
schließen”; und dieses
Grundgesetz sollte nun wohl einleuchten; aber dann wird uns eben
die Regel selbst als richtig, oder berechtigt, einleuchten.
“Aber diese Regel handelt
doch von Sätzen in einem Buch, und das gehört doch nicht
in die Logik!” – Ganz richtig; die Regel
ist wirklich nur eine Mitteilung, daß in
diesem Buche nur dieser
Übergang von einem Satz zum andern
gebraucht wird, denn die Richtigkeit des
Übergangs muß an
Ort und Stelle einleuchten; und der Ausdruck des
‘logischen Grundgesetzes’ ist dann
die Folge || das
Aufeinanderfolgen der Sätze
selbst. || selbst.
|
Russell scheint mit jenem Grundgesetz von einem Satz
q zu sagen:
“Er folgt schon – ich brauche ihn nur noch zu
folgern.”
Ganz analog
heißt es einmal bei
Frege, die Gerade, welche
je zwei Punkte verbindet, sei eigentlich schon da, ehe
wir sie zögen und so ist es auch, wenn wir sagen, die
Übergänge der
Reihe +2 etwa wären
eigentlich bereits gemacht, ehe wir sie
153
mündlich oder schriftlich
machen, – gleichsam nachzögen. |
Einem, der dies sagt, könnte man
antworten: Du verwendest hier ein Bild: Man
kann die
Übergänge, die
einer in einer Reihe machen soll, dadurch
bestimmen, daß man sie ihm
vormacht. Indem man
z.B. die Reihe,
die er schreiben soll, in einer anderen Notation hinschreibt,
daß er sie nur noch zu
übertragen hat, oder indem man sie
wirklich ganz dünn vorschreibt und er hat sie
nachzuziehen. Im ersten Fall können wir auch sagen,
wir schreiben nicht die Reihe an, die er zu schreiben
hat, machen also die
Übergänge
dieser Reihe selbst nicht; im zweiten Falle aber
werden wir gewiß sagen, die Reihe, die er
schreiben soll, sei schon vorhanden. Wir würden
dies auch sagen, wenn wir ihm, was er hinzuschreiben hat,
diktieren, obwohl wir dann eine Reihe von Lauten
hervorbringen und er eine Reihe von Schriftzeichen. Es
ist jedenfalls eine sichere Art, die
Übergänge, die
Einer zu machen hat, zu bestimmen, sie
ihm, in irgendeinem Sinne, schon vorzumachen. –
Wenn wir daher diese Übergänge in
einem ganz andern Sinne bestimmen, indem wir nämlich unsern
Schüler einer Abrichtung unterziehen, wie
z.B. unsere Kinder sie im Einmaleins und im
Multiplizieren erhalten, so nämlich,
daß Alle, die so abgerichtet sind, nun
beliebige Multiplikationen, die sie nicht in ihrer Lehrzeit gemacht
haben, auf die gleiche Weise und mit übereinstimmenden
Resultaten ausführen – wenn also die
Übergänge, die
Einer auf den Befehl +2 zu machen hat,
154 durch Abrichtung so
bestimmt sind, daß wir mit Sicherheit
voraussagen können, wie er gehen wird, auch wenn er
diesen Übergang bis jetzt
noch nie gemacht hat, – dann kann es uns natürlich sein,
als Bild dieses Sachverhalts den zu gebrauchen: die
Übergänge seien
bereits alle gemacht, er schriebe sie nur noch hin. |
Wird es nun
experimentell festgestellt, ob sich ein Satz
aus dem andern ableiten
läßt? – Es scheint,
ja! Denn ich schreibe gewisse Zeichenfolgen hin,
richte mich dabei nach gewissen Paradigmen – dabei ist es
¤
allerdings wesentlich, daß ich kein
Zeichen übersehe, oder daß es
sonstwie abhanden kommt – und was bei diesem Vorgang entsteht,
davon sage ich, es folge. ‒ ‒ Dagegen ist ein
Argument dies: Wenn 2 und 2
Äpfel nur 3 Äpfel
geben,
d.h., wenn 3
Äpfel daliegen, nachdem ich zwei und
wieder zwei hingelegt habe, sage ich nun nicht:
“2
+ 2 ist also doch nicht immer 4”;
sondern: “Einer muß
irgendwie weggekommen sein”. |
Aber inwiefern mache ich ein Experiment,
wenn ich dem schon hingeschriebenen Beweis nur
folge? Man könnte sagen:
“Wenn Du diese Kette von Umformungen ansiehst,
– kommt es Dir nicht auch so
vor, als stimmten sie mit den
Paradigmen?”
– 155 – |
Wenn das also ein Experiment genannt werden soll, dann wohl ein
psychologisches. – Der Anschein des Stimmens kann
ja auf einer Sinnestäuschung beruhen. Und so ist es ja
auch manchmal, wenn wir uns verrechnen.
Man sagt auch: “Das kommt mir heraus.” Und es ist doch wohl ein Experiment, das zeigt, daß dies mir herauskommt. |
Man könnte sagen: Das Resultat des Experiments
ist dies, daß ich, am Ende beim Resultat des
Beweises angelangt, mit Überzeugung
sage: “Ja, es stimmt.” |
Was ist die charakteristische
Verwendung des Vorgangs der Ableitung als
Rechnung – im Gegensatz zur Verwendung des
Vorgangs als Experiment? Wir betrachten die Berechnung als Demonstration einer internen Eigenschaft (eine Eigenschaft des Wesens) der Strukturen. Aber was heißt das? Als Urbild der ‘internen Eigenschaft’ könnte dieses dienen:
Wenn ich nun sage: 10 Striche bestehen notwendig aus 3 mal 3 Strichen und einem Strich – das heißt doch nicht: wenn 10 Striche dastehen, so stehen immer die Ziffern und Bogen rund herum. – – 156
– Setze ich sie aber zu den Strichen
hinzu, so sage ich, ich demonstrierte nur das Wesen jener Gruppe
von Strichen. – Aber bist Du sicher,
daß sich die Gruppe
beim Dazuschreiben
jener Zeichen nicht verändert hat? –
“Ich weiß nicht; aber
eine bestimmte Zahl von Strichen stand da; und wenn
nicht 10, so eine andre und dann hatte die eben andre
Eigenschaften. –” ¤ |
Man
sagt: die Rechnung ‘entfaltet’ die
Eigenschaft der Hundert. Was
heißt es eigentlich: 100 bestehe aus
50 und 50? Man sagt: der Inhalt der Kiste besteht
aus fünfzig || 50
Äpfeln und
50 || fünfzig Birnen.
Aber wenn Einer sagte: “der Inhalt der
Kiste besteht aus fünfzig || 50
Äpfeln und 50 || fünfzig || 50
Äpfeln” –, wir
wüßten zunächst nicht, was er
meint. – Wenn man sagt: “Der
Inhalt der Kiste besteht aus 2 mal 50
Äpfeln”, so
heißt das entweder, es seien da zwei
Abteilungen zu 50 Äpfeln; oder es handelt
sich etwa um eine Verteilung, in der Jeder 50
Äpfel erhalten soll, und ich höre nun,
daß man aus dieser Kiste zwei Leute
beteilen kann. |
“Die 100 Äpfel in der Kiste
bestehen aus 50 und 50” – hier ist wichtig der
unzeitliche Charakter von ‘bestehen’.
Denn es heißt nicht, sie bestünden
jetzt, oder für einige Zeit aus 50 und
50.
– 157
– |
Was ist denn das
Charakteristikum der ‘internen
Eigenschaften’? Daß sie
immer, unveränderlich in dem Ganzen bestehen, das sie
bilden; gleichsam unabhängig von allen
äußeren Geschehnissen. Wie
die Konstruktion einer Maschine auf dem Papier nicht bricht, wenn
die Maschine selbst äußeren
Kräften erliegt. – Oder ich möchte
sagen: daß sie nicht Wind und Wetter
unterworfen sind, wie das Physikalische der Dinge; sondern
unangreifbar wie Schemen. |
Statt, “100 bestehen aus
50 und 50”, könnte man ¤ sagen: “ich
lasse 100 aus 50 und 50 bestehen”. |
“Aber bin ich also in
einer Schlußkette nicht gezwungen, zu
gehen, wie ich gehe?” –
Gezwungen? Ich kann doch wohl gehen, wie ich
will! – “Aber wenn Du im
Einklang mit den Regeln bleiben willst,
mußt Du so
gehen.”
– Durchaus nicht; ich nenne etwas anderes
‘Einklang’. – Ja, aber dann
veränderst Du eben den Sinn des Wortes
‘Einklang’, oder den Sinn der Regel.”
– Nein, – wer sagt, was hier
‘verändern’ und was
‘gleichbleiben’
heißt? Wieviele Regeln immer Du mir angibst – ich gebe Dir eine Regel, die meine Verwendung Deiner Regeln rechtfertigt. |
“Du darfst
doch das Gesetz jetzt nicht auf einmal
– 158 – anders
anwenden!” – Wenn ich darauf
antworte: “Ach ja, ich hatte es ja
so angewandt!” oder:
“Ach, so sollte ich es anwenden –
!”; dann spiele ich mit. Antworte ich
aber einfach: “Anders? – Das
ist doch nicht anders!” – was
willst Du tun? |
Inwiefern ist das logische Argument ein Zwang? –
“Du gibst doch das zu, – und
das zu; dann mußt Du auch
das zugeben!” Das ist die Art,
jemanden zu zwingen.
D.h., man
kann so tatsächlich Menschen zwingen, etwas zuzugeben. – Nicht anders, als wie man Einen etwa dazu
zwingen kann, dorthin zu
gehen, indem man gebietend mit dem Finger dorthin zeigt.
Denke, ich zeige in so einem Fall mit zwei Fingern zugleich in zwei verschiedenen Richtungen und stelle es damit den Andern frei, in welcher der beiden Richtungen er gehen will – ein andermal zeige ich nur in einer Richtung; so kann man das auch so ausdrücken: mein erster Befehl habe ihn nicht gezwungen, in einer Richtung zu gehen, wohl aber der zweite. Das ist aber eine Aussage, die angeben soll, welcher Art meine Befehle waren; aber nicht, in welcher Art sie wirken, ob sie den und den tatsächlich zwingen, d.h., ob er ihnen gehorcht. |
Ist eine Berechnung ein
Experiment? – Ist es ein Experiment, wenn ich
morgens aus dem Bett steige? Aber könnte dies
nicht ein Experiment sein, – welches zeigen soll, ob ich nach
so und soviel Stunden Schlafes die Kraft habe, mich zu
erheben?
– 158
– “Du darfst doch das Gesetz jetzt nicht auf einmal3 anders anwenden!” – Wenn ich darauf antworte: “Ach ja, ich hatte es ja so angewandt!” oder: “Ach, so sollte ich es anwenden –!”; dann spiele ich mit. Antworte ich aber einfach: “Anders? – Das ist doch nicht anders!” – was willst Du tun? |
Inwiefern ist das logische Argument ein
Zwang?
“Du gibst doch
das || das zu, – und
das zu; dann mußt du auch
das zugeben!” Das ist die
Art, jemanden zu zwingen.
D.h., man
kann so tatsächlich Menschen zwingen, etwas
zuzugeben. – Nicht anders, als wie man Einen etwa
dazu zwingen kann, dorthin zu gehen, indem man gebietend mit
dem Finger dorthin zeigt. Denke, ich zeige in so einem Fall mit zwei Fingern zugleich in zwei verschiedenen Richtungen und stelle es damit dem Andern frei, in welcher der beiden Richtungen er gehen will – ein andermal zeige ich nur in einer Richtung; so kann man das auch so ausdrücken: mein erster Befehl habe ihn nicht gezwungen, in einer Richtung zu gehen, wohl aber der zweite. Das ist aber eine Aussage, die angeben soll, welcher Art meine Befehle waren; aber nicht, in welcher Art sie wirken, ob sie den und den tatsächlich zwingen, d.h., ob er ihnen gehorcht. |
Ist eine
Berechnung ein Experiment? – Ist es ein
Experiment, wenn ich morgens aus dem Bett steige?
Aber könnte dies nicht ein Experiment sein, – welches
zeigen soll, ob ich nach so und soviel Stunden Schlafes die Kraft
habe, mich zu erheben?
– 158 – Und was fehlt dieser
Handlung dazu, dies Experiment zu sein? –
Bloß, daß sie nicht zu diesem Zwecke,
d.h., in der Verbindung mit einer solchen
Untersuchung ausgeführt wird.
Experiment ist etwas durch den Gebrauch,
der davon gemacht wird. |
Wäre es möglich, daß Leute
heute eine unserer || unsrer Berechnungen durchgingen und von den Schlüssen
befriedigt wären, morgen aber ganz andere Schlüsse ziehen
wollen, und einen andern Tag wieder
andere? Ja, kann man sich nicht denken, daß dies mit einer Gesetzmäßigkeit so geschähe; daß, wenn er einmal diesen Übergang macht, er ‘eben darum’ das nächste Mal einen andern macht, und darum (etwa) das nächste Mal wieder den ersten? (Ähnlich, wie wenn in einer Sprache die Farbe, die einmal “rot” genannt wird, darum beim nächsten Male anders genannt würde und beim übernächsten wieder “rot”, u.s.f.; dies könnte Menschen so natürlich sein. Man könnte es ein Bedürfnis nach Abwechslung nennen.) |
Ist es
nicht so: Solange man denkt, es kann nicht anders sein,
zieht man logische Schlüsse. Das heißt wohl: Solange || solange das und das gar nicht in Frage gezogen wird. Die Schritte, welche man nicht in Frage zieht, sind logische Schlüsse. Aber man zieht sie nicht darum nicht – 159 – in Frage, weil sie
‘sicher der Wahrheit entsprechen’ – oder
dergl. – sondern, dies ist eben, was man
‘Denken’, ‘Sprechen’,
‘Schließen’,
‘Argumentieren’, nennt. Es handelt sich
hier garnicht um
irgendeine Entsprechung des Gesagten mit der
Realität; vielmehr ist die Logik vor einer
solchen Entsprechung; nämlich in dem Sinne, in welchem die
Festlegung der Methode || Meßmethode vor der
Richtigkeit oder Falschheit einer Längenangabe ist. |
“Nach Dir könnte also
jeder die Reihe fortsetzen, wie er will; und also auch auf
irgend eine || eine
Weise schließen!” Wir
werden es dann nicht “die Reihe fortsetzen”
nennen und auch wohl nicht
“schließen”.
Denn, daß ihn Schlußgesetze nicht zwingen, das und das zu reden, oder zu schreiben, darüber sind wir ja einig. Und wenn Du sagst, er könne es zwar reden, aber er kann es nicht denken, so sage ich nur, das heiße nicht: er könne es, quasi trotz aller Anstrengung, nicht denken, sondern es heißt: zum ‘Denken’ gehört für uns wesentlich, daß er – beim Reden, Schreiben, etc. – solche Übergänge macht. Und ferner sage ich, daß die Grenze zwischen dem, was wir noch ‘denken’ und dem, was wir nicht mehr so nennen, so wenig scharf gezogen ist, wie die Grenze zwischen dem, was noch “Gesetzmäßigkeit” genannt wird und dem, was wir nicht mehr so nennen. Nun muß ich dies aber qualifizieren: Denn man kann ja doch sagen, daß die Schlußgesetze uns zwingen; in dem – 160 – Sinne
nämlich, wie andere die
Sätze || Gesetze in der
menschlichen Gesellschaft. Der Kanzlist, der so
schließt, wie in ( ),
muß es so tun, er wäre
bestraft worden, wenn er anders schlösse. Wer
anders schließt, kommt allerdings in
Konflikt:
z.B. mit der Gesellschaft;
aber auch mit andern praktischen Folgen. Und auch daran ist mehr, als ich oben zugab, wenn Einer sagt: “Er kann es nicht denken.” Man will etwa sagen: Er kann es nicht mit persönlichem Inhalt erfüllen: er kann nicht wirklich mitgehen – mit seinem Verstand, mit seiner Person. Es ist ähnlich, wie man sagt: Diese Tonfolgen geben keinen Sinn, ich kann sie nicht mit Ausdruck singen. Ich kann nicht mitschwingen. Oder, was hier auf dasselbe hinauskommt: ich schwinge nicht mit. “Wenn er es ¤ redet – könnte man sagen – kann er es nur gedankenlos reden”. Und hierzu muß nur bemerkt werden, daß das ‘gedankenlose’ Reden sich von einem anderen wohl auch manchmal durch das unterscheidet, was beim Reden im Redenden an Vorstellungen, Empfindungen und anderem vor sich geht, daß aber diese begleitenden Vorgänge nicht das ‘Denken’ ausmachen und ihr Fehlen noch nicht die ‘Gedankenlosigkeit’. |
Wenn man einen Beweis als
Experiment auffaßt, so ist das Resultat
des Experiments jedenfalls nicht das, was man das Resultat des
Beweises nennt. Das Resultat der Rechnung ist der Satz,
mit welchem sie abschließt; das Resultat
des
– 161
– Experiments ist:
daß ich von diesen Sätzen durch diese
Regeln zu diesem Satz geführt wurde. |
Aber nicht daran haftet unser
Interesse, daß die und die (oder alle)
Menschen von diesen Regeln so geleitet worden sind (oder so
gegangen sind); es gilt uns als selbstverständlich,
daß die Menschen – ‘wenn sie
richtig denken können’ – so
gehen. Wir haben jetzt aber einen Weg
erhalten, sozusagen durch die
Fußstapfen derer, die so gegangen
sind. Und auf diesem Weg geht nun der Verkehr vor sich
– zu verschiedenen Zwecken. |
Wenn wir sagen: “dieser Satz
folgt aus jenem”, so ist hier
“folgen” wieder unzeitlich
gebraucht. (Und das zeigt,
daß dieser Satz nicht das Resultat eines
Experiments ausspricht.) |
Vergleiche damit:
“Weiß ist heller als
Schwarz”. Auch dieser Ausdruck ist
zeitlos ||
unzeitlich und auch er
spricht das Bestehen einer internen
Relation aus.
– 162 – |
“Diese Relation besteht aber eben”
– möchte man sagen. Aber die Frage ist:
Hat dieser Satz einen Gebrauch – und welchen?
Denn einstweilen weiß ich nur,
daß mir dabei ein Bild vorschwebt (aber
dies garantiert mir die Verwendung nicht) und
daß die Worte einen deutschen Satz
geben. Aber es fällt Dir auf,
daß die Worte hier anders gebraucht
werden, als im alltäglichen Fall einer nützlichen
Aussage. (Wie etwa der
Radmacher bemerken kann,
daß die Aussagen, die er gewöhnlich
über Kreisförmiges und Gerades macht, anderer Art sind,
als die, die im Euklid
stehen.) Denn wir sagen: dieser
Gegenstand ist heller als jener, oder, die Farbe
dieses Dings ist heller als die Farbe jenes, und dann ist etwas
jetzt heller und kann später dunkler sein.
Woher die Empfindung, “Weiß ist heller als Schwarz” sage etwas über das Wesen der beiden Farben aus? – Aber ist die Frage überhaupt richtig gestellt? Was meinen wir denn mit dem ‘Wesen’ von Weiß oder Schwarz? Wir denken etwa an ‘das Innere’, ‘die Konstitution’, aber das ergibt hier doch keinen Sinn. Wir sagen etwas auch: “Es liegt in Weiß, daß es heller ist ....”. Ist es nicht so: das Bild eines schwarzen und eines weißen Flecks dient uns zugleich als Paradigma dessen, was wir unter “heller” und “dunkler” verstehen und als Paradigma für “weiß” und für “schwarz”. In so fern ‘liegt’ nun die Dunkelheit – 163 – ‘im’
Schwarz, als sie beide von diesem Fleck dargestellt
werden. Er ist dunkel, dadurch
daß er schwarz ist. –
Aber richtiger gesagt: er
heißt
“schwarz” und damit, in unserer Sprache, auch
“dunkel”. Jene Verbindung, eine
Verbindung der Paradigmen und Namen ist in unsrer Sprache
hergestellt. Und unser Satz ist unzeitlich, weil er
nur die Verbindung der Worte
“weiß”,
“schwarz” und “heller” mit einem
Paradigma ausspricht. Man kann Mißverständnisse vermeiden, dadurch daß man erklärt, es sei Unsinn, zu sagen: “die Farbe dieses Körpers ist heller, als die Farbe jenes”, es müsse heißen: “dieser Körper ist heller als jener”. D.h., man schließt jene Ausdrucksform aus unserer Sprache aus. |
Wir
könnten auch sagen: Wenn wir den
Schlußgesetzen
(Schlußregeln) folgen, so
liegt in einem Folgen immer auch ein Deuten. |
“Aber wir folgern doch
diesen Satz aus jenem, weil er tatsächlich folgt!
Wir überzeugen uns doch, daß er
folgt.” Wir überzeugen uns,
daß, was hier steht, aus dem folgt, was
dort steht. Und dieser Satz ist zeitlich
gebraucht.
– 164
– |
Wie ist es aber,
wenn ich mich davon überzeuge, daß
das Schema dieser Striche
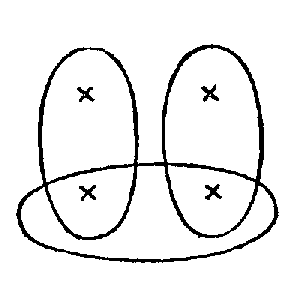
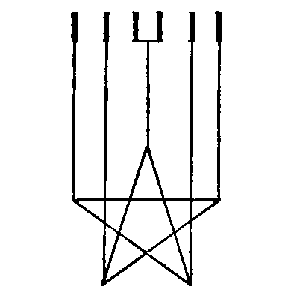
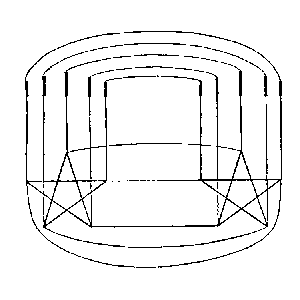
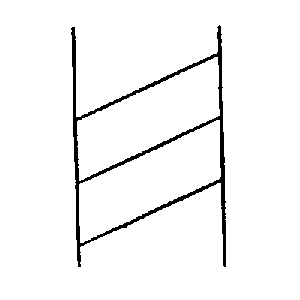
❘ ❘ ❘ ❘ ❘ (a gleichzahlig ist dem Schema dieser Eckpunkte: (ich habe die Schemata absichtlich einprägsam gemacht), indem ich zuordne: Nun, wovon überzeuge ich mich denn, wenn ich diese Figur ansehe? Ich sehe einen Stern mit fadenförmigen Fortsätzen. – |
Aber ich kann von der Figur
so Gebrauch machen: Fünf Leute stehen im
Fünfeck aufgestellt; an der Wand stehen Stäbe, wie die
Striche in (a); ich sehe auf die Figur
(c) und sage: “ich kann
jedem der Leute einen Stab geben.” Ich könnte die Figur (c) als schematisches Bild davon auffassen, daß ich fünf Leuten je einen Stab gebe. |
Wenn ich
nämlich erst ein beliebiges Vieleck zeichne
– 165 – und dann
eine beliebige Reihe von Strichen❘ ❘ ❘ ❘ ❘ ❘ ❘ ❘ ❘ ❘ ❘ ❘ ❘ ❘ ❘ ❘ ❘ ❘ so
kann ich nun durch Zuordnung herausfinden, ob ich oben soviele
Ecken habe, wie unten Striche. (Ich
weiß nicht, was herauskommen
würde.) Und so kann ich auch sagen, ich habe
mich durch das Ziehen der Projektionslinien davon überzeugt,
daß am oberen Ende der Figur
(c) soviele Striche stehen, wie der Stern
unten Ecken hat. (Zeitlich!) In dieser
Auffassung gleicht die Figur nicht einem mathematischen Beweise
(so wenig, wie es ein mathematischer Beweis ist, wenn ich
einer Gruppe von Leuten einen
Sack Äpfel austeile und finde,
daß Jeder gerade
einen Apfel kriegen kann). Ich kann die Figur (c) aber als mathematischen Beweis auffassen. Geben wir den Schemata (a) und (b) Namen! (a) heiße “Hand” (H.), (b) “Drudenfuß”, (D.)¤ Ich habe bewiesen, daß H. soviel Striche hat, wie D. Ecken. Und dieser Satz ist wieder unzeitlich. |
Der || Ein
Beweis – kann ich sagen – ist eine Figur,
an deren einem Ende gewisse Sätze stehen und an deren anderm Ende ein Satz
stehe || steht
(den wir den ‘bewiesenen’ nennen).
Man kann als Beschreibung so einer Figur sagen: in ihr folge der Satz ..... aus ..... und..... Das ist eine Form der Beschreibung eines Musters, das z.B. auch ein Ornament (Tapetenmuster) sein könnte. Ich kann also sagen: “In – 166 – dem Beweise, welcher
auf jener Karte || Tafel
steht, folgt der Satz p aus
q
und r”, und das ist einfach eine
Beschreibung dessen, was dort zu sehen ist. Es ist aber
nicht der mathematische Satz, daß
p
aus q und
r
folgt. Dieser hat eine andere
Anwendung. Er sagt – so könnte man es
ausdrücken – daß es Sinn hat,
von einem Beweise (Muster) zu reden, in welchem
p
aus q und
r
folgt. Wie man sagen kann, der Satz
“Weiß || weiß
ist heller als
Schwarz || schwarz”
sage aus, es habe Sinn, von zwei Gegenständen zu reden, von
denen der hellere weiß, der andere schwarz
sei, aber nicht von zwei Gegenständen, von denen der
hellere schwarz, der andere weiß sei.
|
Denken wir uns, wir
hätten das Paradigma für “heller” und
“dunkler” in Form eines
weißen und schwarzen Flecks gegeben, und
nun leiten wir mit seiner Hilfe – sozusagen – ab:
daß Rot dunkler ist als
Weiß. |
Der durch (c)
bewiesene Satz dient nun als neue Vorschrift zum Konstatieren der
Gleichzahligkeit: Hat man eine Menge von
Gegenständen in Form der Hand angeordnet und eine andere als
die Ecken eines Drudenfußes, so sagen wir,
die beiden Mengen seien gleichzahlig. |
“Aber ist das nicht
bloß, weil wir H. und D.
schon einmal zugeordnet haben und gesehen,
daß sie gleichzahlig
– 167 –
sind?” – Ja aber, wenn sie es in
einem Fall waren –
wie weiß ich,
daß sie es jetzt wieder sein
werden? – “Weil es eben im
Wesen der H. und des D. liegt,
daß sie gleichzahlig
sind.” – Aber wie konntest Du
das durch die Zuordnung herausbringen?
(Ich dachte, die Zählung, oder Zuordnung ergibt nur,
daß diese beiden Gruppen, die ich jetzt vor
mir habe, gleichzahlig – oder ungleichzahlig –
sind.) – “Aber wenn er nun eine H. Dinge hat und einen D. Dinge und er ordnet sie nun tatsächlich einander zu, so ist es doch nicht möglich, daß er etwas anderes erhält, als daß sie gleichzahlig sind. – Und, daß es nicht möglich ist, das sehe ich doch aus dem Beweis.” – Aber ist es denn nicht möglich? Wenn er z.B. – wie ein Anderer sagen könnte – eine der Zuordnungslinien zu ziehen übersieht. Aber ich gebe zu, daß er in der ungeheuren Mehrzahl der Fälle immer das gleiche Resultat erhalten wird und, erhielte er es nicht, sich für irgendwie gestört halten würde. Und wäre es nicht so, so würde dem ganzen Beweis der Boden entzogen. Wir entscheiden uns nämlich, das Beweisbild statt einer Zuordnung der Gruppen zu gebrauchen; wir ordnen sie nicht zu, sondern vergleichen statt dessen die Gruppen mit denen des Beweises (in welchem allerdings zwei Gruppen einander zugeordnet sind.) (Wie wir uns entscheiden..... |
Ich könnte als Resultat des Beweises auch
– 168 – sagen:
“Eine H. und ein D.
heißen
‘gleichzahlig’”. || heißen von
nun an ‘gleichzahlig’”.
Oder: Der Beweis erforscht nicht das Wesen der beiden Figuren, aber er spricht aus, was ich von nun an zum Wesen der Figuren rechnen werde. ‒ ‒ Was zum Wesen gehört, lege ich unter den Paradigmen der Sprache nieder. |
Wenn ich sage:
“Dieser Satz folgt aus jenem”, so ist das
die Anerkennung einer Regel. Sie geschieht auf
Grund des Beweises.
D.h., ich
lasse mir diese Kette (diese Figur) als Beweis
gefallen. ‒ ‒ “Aber könnte ich
denn anders? Muß
ich mir sie nicht gefallen lassen?” –
Warum sagst Du, Du
müßtest? Doch
darum, weil Du am Schlusse des Beweises etwa sagst:
“Ja – ich
muß diesen Schluß
anerkennen.” Aber das ist doch nur der
Ausdruck Deiner unbedingten Anerkennung. –
D.h., glaube ich: die Worte “Das muß ich zugeben” werden in zweierlei Fällen gebraucht: wenn wir einen Beweis erhalten haben – aber auch in Bezug auf den einzelnen Schritt selber des Beweises. |
Und
worin
äußert es sich denn,
daß der Beweis mich
zwingt? Doch darin,
daß ich so und so darauf vorgehe,
daß ich mich weigere, einen anderen Weg zu
gehen. Als letztes Argument, gegen Einen, der so nicht
gehen wollte, würde ich nur noch
sagen: “Ja siehst Du denn
nicht
– 169
– .....!” – und das
ist doch kein Argument. |
“Aber, wenn Du recht hast,
wie kommt es dann,
daß sich alle Menschen (oder doch alle
normale Menschen) diese Figuren als Beweise dieser
Sätze gefallen lassen?” – Ja, es
besteht eine große – und interessante
– Übereinstimmung. |
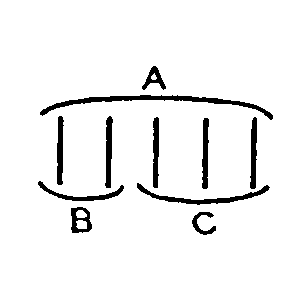
Denk' Dir, Du hättest
eine Reihe von Kugeln vor Dir; Du numerierst sie
nun mit arabischen Ziffern und es geht von 1 bis 100;
dann machst Du nach je 10 ((die sich in der Numerierung
nun deutlich hervorheben) einen
größern Abstand; in jedem
Reihenstück von je 10 machst Du einen etwas
kleineren Abstand in der Mitte, also zwischen 5 und 5
– so werden die 10 übersichtlich; nun nimmst Du die
Zehnerstücke und legst sie eines
unter das
andere || unter einander
und machst in der Mitte der Kolonne einen etwas
größeren Abstand, also zwischen
fünf Reihen und fünf Reihen; nun numerierst Du die Reihen
von 1 bis 10. Ich kann sagen, ich habe Eigenschaften der
hundert Kugeln
entfaltet || gezeigt. –
Nun aber denke Dir, daß dieser ganze
Vorgang, dies Experiment mit den hundert Kugeln, gefilmt
wurde. Ich sehe nun auf der Leinwand doch nicht ein
Experiment, denn das Bild eines Experiments ist doch nicht selbst
ein Experiment. – Aber das
‘mathematisch
Wesentliche || Mathematische’ sehe ich
nun auch in der Projektion! Denn es erscheinen da
zuerst 100 Flecken, dann werden sie in Zehnerstücke eingeteilt,
usw.,
usw.
– 170 – Ich könnte also sagen: der Beweis dient mir nicht als Experiment, wohl aber als Bild eines Experiments. |
Lege 2
Äpfel auf die leere Tischplatte, schau
daß niemand in ihre Nähe kommt und der
Tisch nicht erschüttert wird; nun lege noch 2
Äpfel auf die Tischplatte; nun zähle
die Äpfel, die da liegen.
Du hast ein Experiment gemacht; das Ergebnis der
Zählung ist wahrscheinlich 4. (Wir würden
das Ergebnis x so darstellen: wenn man unter den und
den Umständen erst 2 dann noch 2
Äpfel auf einen Tisch legt,
verschwindet zumeist keiner, noch kommt einer dazu.)
Und analoge
Experimente
kann man, mit dem gleichen Ergebnis, mit allerlei festen
Körpern ausführen. – So lernen ja die Kinder
bei uns rechnen, denn man läßt sie 3
Bohnen hinlegen und noch 3 Bohnen und dann zählen, was da
liegt. Käme dabei einmal 5, einmal 7
heraus (weil, wie wir jetzt sagen
würden, einmal von selbst eine dazu, einmal eine
weg käme), so würden wir
zunächst Bohnen als für den Rechenunterricht ungeeignet
erklären. Geschähe das
Gleiche aber mit Stäben, Fingern,
Strichen und den meisten
anderen || andern
Dingen, so hätte das Rechnen damit ein Ende.
“Aber wäre dann nicht doch noch 2 + 2 = 2?” – Dieses Sätzchen wäre damit unbrauchbar geworden. – – 171 – |
Wenn
wir Geld in eine Lade legen und später finden wir es nicht
mehr dort, so sagen wir: “Von selbst ist es
nicht verschwunden.” Dies ist ein wichtiger
Satz der Physik. |
Wir lehren jemand eine
Methode, Nüsse unter Leute zu verteilen; ein Teil dieser
Methode ist das Multiplizieren zweier Zahlen im
Dezimalsystem. Wir lehren jemand ein Haus errichten; dabei auch, wie er sich die genügenden Mengen von Material, etwa Brettern, anschaffen soll, hiezu eine Technik des Rechnens. Die Technik des Rechnens ist ein Teil der Technik des Hausbaues. Leute verkaufen und kaufen Scheitholz; die Stöße werden mit einem Maßstab gemessen, die Maßzahlen der Länge, Breite, Höhe multipliziert, und was dabei herauskommt, – 172 – ist die Zahl der
Groschen, die sie zu fordern und zu geben haben. Sie
wissen nicht, ‘warum’ dies so geschieht, sondern
sie machen es einfach so: so wird es gemacht. –
Rechnen diese Leute nicht? |
Aber in welchem Verhältnis steht dann
die Begründung eines Rechenvorgangs zu der
Rechnung selbst? |
“Ja, ich verstehe, daß dieser
Satz aus diesem folgt.” – Verstehe ich,
warum er folgt, oder verstehe ich
nur, daß er folgt?
|
Wie, wenn ich gesagt
hätte: Jene Leute zahlen für's Holz
auf Grund der Rechnung; sie lassen sich die Rechnung
als Beweis dafür gefallen,
daß sie soviel zu zahlen haben. – Nun, es ist einfach eine Beschreibung ihres Vorgehens
(Benehmens).
– 173
– |
Wer uns erinnert:
“Die Kette der Gründe hat ein Ende”,
stellt den Ursprung der Kette mit ihrer Mitte zusammen,
daß wir den Unterschied wahrnehmen,
‘Schau das an – und
schau das an! Präg'
Dir diese beiden Formen ein!’ |
Die Logik – kann
man sagen – zeigt, was wir unter “Satz” und
unter “Sprache” verstehen. – |
Trenne die Gefühle
(Gebärden) der
Übereinstimmung, von dem, was Du mit
dem Beweise machst! |
Jene Leute –
würden wir sagen – verkaufen das Holz nach dem
Kubikmaß – – aber haben sie darin
recht? Wäre es nicht richtiger, es nach dem
Gewicht zu verkaufen – oder nach der Arbeitszeit des
Fällens – oder nach der Mühe des Fällens,
gemessen am Alter und an der Stärke des
Holzfällers? Und warum sollten sie es nicht
für einen Preis hergeben, der von alledem unabhängig
ist: jeder Käufer zahlt ein und dasselbe, wieviel immer
er nimmt (man hat gefunden, daß man so
leben kann). Und ist etwas dagegen zu sagen,
daß man das Holz einfach
verschenkt? |
Gut;
aber wie, wenn sie das Holz in Stöße
von
– 174
– beliebigen, verschiedenen Höhen
schlichteten und es dann zu einem Preis proportional der
Grundfläche der
Stöße verkauften?
Und wie, wenn sie dies sogar mit den Worten begründeten: “Ja, wer mehr Holz kauft, muß auch mehr zahlen.” |
Wie könnte ich ihnen nun zeigen, daß
– wie ich sagen würde – der nicht wirklich mehr Holz
kauft, der einen Stoß von
größerer Grundfläche kauft? – Ich würde
z.B. einen, nach
ihren Begriffen, kleinen Stoß nehmen und ihn
durch Umlegen der Scheiter in einen
‘großen’
verwandeln. Das könnte sie
überzeugen – vielleicht aber würden sie sagen:
“ja, jetzt ist es viel Holz und kostet
mehr” – und damit wäre es
Schluß. – Wir würden in
diesem Falle wohl sagen: sie meinen
¤ mit “viel
Holz” und “wenig Holz” einfach nicht das
Gleiche, wie wir; und sie haben ein ganz anderes System der
Bezahlung als wir. |
Frege sagt im Vorwort
der Grundgesetze
der Arithmetik: “..... hier haben wir eine
bisher unbekannte Art der Verrücktheit” –
aber er hat nie angegeben, wie diese
‘Verrücktheit’ wirklich aussehen
würde. |
(Eine
Gesellschaft, die so handelt, würde uns vielleicht an die
“Klugen Leute” in dem Märchen
erinnern.)
– 175
– |
Worin besteht die
Übereinstimmung der Menschen
in Bezug auf die || bezüglich
der Anerkennung einer Struktur als der eines Beweises?
Darin. daß sie Worte als
Sprache gebrauchen? Als das, was wir
“Sprache” nennen.
Denke Dir Menschen, die Geld im Verkehr gebrauchten, nämlich Münzen, die so aussehen wie unsere Münzen, aus Gold oder Silber sind und geprägt; und sie geben sie auch für Waren her – – aber jeder gibt für die Waren, was ihm gerade gefällt und der Kaufmann gibt dem Kunden nicht mehr, oder weniger, je nachdem er bezahlt; kurz, dies Geld, oder was so aussieht, spielt bei ihnen eine ganz andere Rolle als bei uns. Wir würden uns diesen Leuten viel weniger verwandt fühlen, als solchen, die noch gar kein Geld kennen, und eine primitive Art des Tauschhandels treiben. – “Aber die Münzen dieser Leute werden doch auch einen Zweck haben!” – Hat denn alles, was man tut, einen Zweck? Etwa religiöse Handlungen –. Es ist schon möglich, daß wir geneigt wären, Menschen, die sich so benehmen, Verrückte zu nennen. Aber doch nennen wir nicht alle die Verrückte, die in den Formen unserer Kultur ähnlich handeln, Worte ‘zwecklos’ verwenden. (Denke an die Krönung eines Königs!) |
Zum Beweis gehört
Übersichtlichkeit. Wäre
der Prozeß, durch den ich das Resultat
erhalte, unübersehbar, so könnte ich zwar
das Ergebnis, daß diese Zahl herauskommt,
vermerken – 176
– – welche Tatsache aber soll es
mir bestätigen? ich weiß
nicht: ‘was herauskommen
soll’. |
Aber ist es denn unmöglich,
daß ich mich in der Rechnung geirrt
habe? Und wie, wenn mich ein Teufelchen irrt, so
daß ich irgend etwas immer wieder
übersehe, so oft ich auch, Schritt für Schritt
nachrechne. Sodaß, wenn ich aus
der Verhexung erwachte, ich sagen würde: “ja, war
ich denn blind!” – Aber welchen
Unterschied macht es, wenn ich dies
‘annehme’? Ich könnte dann
sagen: “Ja ja, die Rechnung ist
gewiß falsch – aber so rechne
ich. Und das nenne ich nun addieren, und diese Zahl die
Summe dieser beiden.” |
Denke, jemand würde so behext,
daß er rechnete:
Nun soll er seine Rechnung anwenden. Er nimmt viermal 3 Nüsse und noch 2, und verteilt sie unter 10 Leute; und jeder erhält eine Nuß: denn er teilt sie, den Bögen der Rechnung entsprechend, aus und so oft er Einem eine zweite Nuß gibt, ist sie verschwunden. |
Man könnte auch sagen; Du schreitest in dem Beweis von
Satz zu Satz; aber läßt Du Dir
dann || denn
auch eine
– 177
– Kontrolle dafür gefallen,
daß Du richtig gegangen bist? – Oder sagst Du bloß,
“Es muß
stimmen” und mißt alles andere
mit dem Satz, den Du erhältst? |
Denn, wenn es so ist, dann
schreitest Du nur von Bild zu Bild. |
Es könnte praktisch sein, mit einem
Maßstab zu messen, der die Eigenschaft
hat, sich auf etwa die Hälfte seiner Länge zusammen zu
ziehen, wenn er aus diesem Raum in jenen gebracht wird.
Eine Eigenschaft, die ihn unter andern Verhältnissen
zum Maßstab untauglich machen
würde. Es könnte praktisch sein, beim Abzählen einer Menge, unter gewissen Umständen, Ziffern auszulassen; sie abzuzählen: 1, 2, 4, 5, 7, 8, 10. |
Wovon
überzeuge ich Einen, der jene Abbildung im Film des Versuchs
mit den hundert Kugeln verfolgt? Man könnte sagen: davon, daß sich dies so zugetragen hat. – Aber das wäre keine mathematische Überzeugung. ‒ ‒ Aber kann ich denn nicht sagen: ich präge ihm einen Vorgang ein? Dieser Vorgang ist die Umgruppierung einer Reihe von 100 Dingen in 10 Reihen zu 10. Und dieser Vorgang ist tatsächlich immer wieder leicht durchzuführen. Und davon kann er mit Recht überzeugt sein. – 178
– |
Und so prägt
der Beweis durch Ziehen der Projektionslinien
Aber kann ich denn nicht sagen, die Figur zeige, wie eine solche Zuordnung möglich ist – und muß sie darum nicht auch zeigen, daß sie möglich ist? – |
Was
war denn damals der Sinn davon, daß wir
– 179 – vorschlugen,
den Formen der 5 parallelen Striche und des Fünfecksterns
Namen beizulegen? Was ist damit geschehen,
daß sie Namen erhalten haben? Es
wird dadurch etwas über die Art des
Gebrauchs dieser Figuren
angedeutet. Nämlich –
daß man sie auf einen Blick als die und die
erkennt; Man denkt nicht
dran, ihre Striche oder Ecken abzuzählen, sondern erkennt sie
als Gestalten, wie man Messer und Gabel, die Buchstaben und
Ziffern erkennt. || ; man || . Man
zählt dazu nicht ihre Striche oder Ecken; sie sind für
uns Gestalttypen, wie Messer und Gabel, die Buchstaben und
Ziffern. Ich kann also auf den Befehl: “Zeichne eine H.” (z.B.) diese Form unmittelbar wiedergeben. – Nun lehrt mich der Beweis eine Zuordnung der beiden Formen. (Ich möchte sagen, es seien in dem Beweis nicht bloß diese individuellen Figuren zugeordnet, sondern die Formen selbst; aber das heißt doch nur, daß ich mir jene Formen gut einpräge. || als Paradigmen einpräge.) Kann ich nun, wenn ich die Formen H. und D. einander so zuordnen will, nicht in Schwierigkeiten geraten – indem etwa eine Ecke unten zuviel, oder oben ein Strich zuviel ist? – “Aber doch nicht, wenn Du wirklich wieder H. und D. gezeichnet hast! – Und das läßt sich ja beweisen; sieh diese Figur an!” – Diese Figur lehrt mich eine neue Art der Kontrolle dafür, daß – 180 – ich wirklich die
gleichen Figuren hingezeichnet habe; aber kann ich, wenn ich mich nun
nach dieser Vorlage richten will, nicht dennoch in Schwierigkeiten
geraten? Ich sage aber, ich bin sicher,
daß ich normalerweise in keine
Schwierigkeiten kommen werde. Was tut nun diese Überlegung? – |
Es gibt ein Geduldspiel, das darin besteht,
eine bestimmte Figur,
z.B. ein Rechteck aus
gegebenen Teilen
(Plättchen) || Stücken
zusammenzusetzen. Die Teilung der Figur ist eine solche,
daß es uns schwer wird, die richtige
Zusammenstellung der Teile zu finden. Sie sei etwa
diese
Was findet der, dem die Zusammensetzung gelingt? –
Er findet: eine Lage – an welche er früher nicht
gedacht hat. – Gut; aber kann man also nicht
sagen: er überzeugt sich davon,
daß man diese Dreiecke so zusammensetzen
kann? – Aber diese
Dreiecke: bilden sie schon das Rechteck, oder noch nicht, und
sollen erst so zusammengesetzt
werden? || Aber diese
Dreiecke: sind es die, welche oben das Rechteck bilden, oder
Dreiecke, die erst so zusammengesetzt werden
sollen? |
Wer sagt: “Ich
hätte nicht geglaubt, daß man
– 181 – diese
Figuren so zusammensetzen kann”, dem kann man
doch nicht, auf das zusammengesetzte Geduldspiel zeigend,
sagen: “So, Du hast nicht geglaubt,
daß man die Stücke so zusammensetzen
kann?” – Er würde antworten:
“Ich meine, ich habe an diese Art der
Zusammensetzung garnicht
gedacht.” |
Denken wir uns die physikalischen Eigenschaften der Teile des
Geduldspiels so || solcher Art,
daß sie || die Teile
desgleichen in die gesuchte
Lage nicht kommen können.
Ich meine
aber || Aber nicht,
daß man einen Widerstand empfindet, wenn man
sie in diese Lage bringen will, sondern man macht einfach alle
andern Versuche, nur den nicht, und
die Stücke kommen auch durch Zufall nicht in diese
Lage. Es ist gleichsam diese Lage aus dem Raum
ausgeschlossen. Als wäre hier ein ‘blinder
Fleck’, etwa in unserem Gehirn. – Und
ist es denn nicht so, wenn ich glaube, alle
möglichen Stellungen versucht zu haben und an
dieser, wie durch Verhexung, immer vorbeigegangen bin.
Kann man nicht sagen: die Figur, die uns || Dir die Lösung zeigt, beseitigt eine Blindheit; oder auch, sie ändert Deine Geometrie? Sie zeigt Dir gleichsam eine neue Dimension des Raumes. (Wie wenn man einer Fliege den Weg aus dem Fliegenglas zeigte.) |
Ein Wesen hat diese Lage mit einem Bann
– 182 – umzogen und
aus unserm Raum ausgeschlossen. |
Die neue Lage ist wie aus dem Nichts
entstanden. Dort, wo früher nichts war, dort
ist jetzt auf einmal etwas. |
Inwiefern hat Dich denn die Lösung
davon überzeugt, daß man dies und
dies kann? – Du konntest es ja früher
nicht – und jetzt kannst Du es etwa. –
|
Es schien zuerst, als sollten diese
Überlegungen zeigen,
daß, ‘was ein logischer Zwang zu
sein scheint, in Wirklichkeit nur ein psychologischer
ist’ – und da fragte es sich doch: kenne ich
also beide Arten des Zwanges?! –
Denke Dir, es würde der Ausdruck gebraucht: “Das Gesetz § ..... bestraft den Mörder mit dem Tode.” Das könnte doch nur heißen, dieses Gesetz laute: u.s.w. Jene Form des Ausdrucks aber könnte sich uns aufdrängen, weil das Gesetz Mittel ist, wenn der Schuldige der Bestrafung zugeführt wird. – Nun reden wir von ‘Unerbittlichkeit’ bei denen, die jemand bestrafen. Da könnte es uns einfallen, zu sagen: das Gesetz ist unerbittlicher als alle Menschen, denn sie können den Schuldigen laufen lassen, das Gesetz richtet ihn hin. || : das Gesetz ist unerbittlich: die Menschen können den Schuldigen – 183 – laufen lassen, das
Gesetz richtet ihn hin.
(Ja auch: “das Gesetz richtet ihn
immer hin”.) – Wozu ist so
eine Ausdrucksform zu gebrauchen? – Zunächst
sagt dieser Satz ja nur, im Gesetz stehe das und das, und die
Menschen richten sich manchmal nicht danach. Dann aber
zeigt er doch das Bild des
einen || einen unerbittlichen – und
vieler laxer Richter. Er dient darum als Ausdruck des
Respekts vor dem Gesetz. Endlich aber kann man die
Ausdrucksform auch so gebrauchen, daß man ein
Gesetz ‘unerbittlich’ nennt, wenn es eine
Möglichkeit der Begnadigung nicht vorsieht, und im
entgegengesetzten Fall etwa
‘einsichtig’. Wir reden nun von der ‘Unerbittlichkeit’ der Logik; und denken uns die logischen Gesetze unerbittlich, unerbittlicher noch, als die Naturgesetze. Wir machen nun darauf aufmerksam, wie das Wort “unerbittlich” auf mehrerlei Weise angewendet wird. Es entsprechen unsern logischen Gesetzen sehr allgemeine Tatsachen der täglichen Erfahrung. Es sind die, die es uns möglich machen, jene Gesetze immer wieder auf einfache Weise (mit Tinte auf Papier z.B.) zu demonstrieren. Sie sind zu vergleichen mit jenen Tatsachen, welche die Messung mit dem Metermaß leicht ausführbar und nützlich machen. Das legt den Gebrauch gerade dieser Schlußgesetze nahe, und nun sind wir unerbittlich in der Anwendung dieser Gesetze. Weil wir ‘messen’; und es gehört zum Messen, daß Alle das gleiche Maß haben. Außerdem aber kann man unerbittliche, d.h., eindeutige, von nichteindeutigen Schlußregeln unterscheiden, ich meine von solchen, die uns eine Alternative freistellen. – 184
– |
Ich sagte,
‘ich lasse mir das und das als Beweis eines Satzes
gefallen’ – aber kann ich mir die Figur, die die
Stücke des Geduldspiels zusammengefügt zeigt,
nicht als Beweis dafür gefallen lassen,
daß man jene Stücke zu diesem
Umriß zusammensetzen kann? |
Aber denk nun, eines der
Stücke liege so, daß es das
Spiegelbild des entsprechenden Teils der Vorlage
ist. Er will nun die Figur nach der Vorlage
zusammensetzen, sieht, es muß gehen, kommt
aber nicht auf den Einfall, das Stück umzuwenden und findet,
daß ihm das Zusammensetzen nicht
gelingt. |
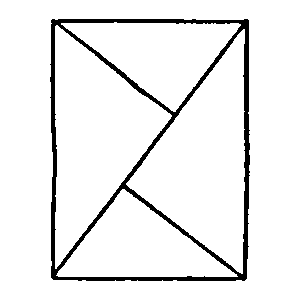
Man kann ein
Rechteck aus zwei Parallelogrammen und zwei Dreiecken
zusammensetzen. Beweis:
Ein
Kind würde die Zusammensetzung eines Rechtecks aus diesen
Bestandteilen schwer treffen und davon überrascht sein,
daß zwei Seiten der Parallelogramme in
eine gerade Linie fallen, wo doch die Parallelogramme schief
sind. – Es könnte ihm vorkommen,
daß das Rechteck gleichsam durch Zauberei aus
diesen Figuren wird. Ja, es
muß zugeben, daß sie
nun ein Rechteck
– 185
– bilden, aber durch einen Trick, durch eine
vertrackte Stellung, auf unnatürliche Weise.
Ich kann mir denken, daß das Kind, wenn es die beiden Parallelogramme in der Weise zusammengelegt hat, seinen Augen nicht traut, wenn es sieht, daß sie so zusammenpassen. ‘Sie sehen nicht aus als ob sie so zusammenpaßten.’ Und ich könnte mir denken, daß man sagte: Es erscheint uns nur durch ein Blendwerk, als gäben sie das Rechteck – in Wirklichkeit haben sie ihre Natur verändert, sie sind nicht mehr die Parallelogramme. |
Aber kann ich den Satz der Geometrie nicht auch ohne Beweis
glauben,
z.B. auf die Versicherung eines
Andern hin? – Und was verliert der Satz, wenn er
seinen Beweis verliert? – Ich soll hier wohl
fragen: “Was kann ich mit ihm
anfangen || machen?”,
denn darauf kommt es an. Den
Satz auf die Versicherung des Andern annehmen –
wie zeigt sich das? Ich kann ihn
z.B. in weiteren Rechenoperationen
verwenden, oder ich verwende ihn bei der Beurteilung eines
physikalischen Sachverhalts. Versichert mich jemand
z.B., 13 mal 13 sei 396, und ich glaube ihm, so
werde ich mich nun wundern, daß ich 396
Nüsse nicht in 13 Reihen zu je 13 Nüssen legen kann und
vielleicht annehmen, die Nüsse hätten sich von selbst
vermehrt. Aber ich fühle mich versucht zu sagen: – 186
– man könne nicht
glauben, daß
13 ×
13 = 396 ist, man könne diese Zahl
nur mechanisch vom Andern annehmen. Aber
warum soll ich nicht sagen, ich glaube es? Ist denn,
es glauben, ein geheimnisvoller Akt, der sozusagen unterirdisch
mit der wahren || richtigen
Rechnung in Verbindung
ist || steht? Ich
kann doch jedenfalls sagen: “ich
glaube es”, und nun danach handeln. Man möchte fragen: “Was tut der, der glaubt, daß 13 × 13 = 396 ist?” Und die Antwort kann sein: Nun, das wird davon abhängen, ob er z.B. die Rechnung selber gemacht und sich dabei verschrieben hat, – oder ob sie zwar ein Anderer || Andrer gemacht hat, er aber doch weiß, wie man so eine Rechnung macht, – oder ob er nicht multiplizieren kann, aber weiß, daß das Produkt die Zahl der Leute ist, die in 13 Reihen zu je 13 stehen, – kurz davon, was er denn mit der Gleichung 13 × 13 = 396 anfangen kann. Denn, sie prüfen, ist etwas mit ihr anzufangen. |
Denkt man nämlich an
die arithmetische Gleichung als den Ausdruck einer internen
Relation, so möchte man sagen: “Er kann
ja garnicht glauben, daß 13
× 13 dies ergibt, weil das ja
keine Multiplikation von 13 mit 13, oder kein Ergeben
ist, wenn 396 am Ende steht.” Das
heißt aber, daß
man das Wort “glauben” für den Fall einer
Rechnung und ihres Resultats nicht anwenden will, – oder nur
dann, wenn man die richtige Rechnung vor sich hat.
– 187 – |
“Was glaubt der, der glaubt 13
× 13 ist 396?” –
Wie tief dringt er – könnte man sagen, mit seinem Glauben
in das Verhältnis dieser Zahlen ein? Denn bis zum
Ende – will man sagen – kann er nicht dringen, –
oder er könnte es nicht glauben. Aber wann dringt er in die Verhältnisse der Zahlen ein? Gerade während er sagt, daß er glaubt ......? Darauf wirst Du nicht bestehen – denn es ist leicht zu sehen, daß dieser Schein nur durch die Oberflächenform unserer || unsrer Grammatik – wie man es nennen könnte – || (wie man es nennen könnte) erzeugt wurde || wird. |
Denn ich will sagen: “Man
kann nur sehen, daß
13 ×
13 = 369 ist, und man kann auch das nicht
glauben. Und man kann – mehr oder
weniger blind – eine Regel
anwenden || annehmen.”
Und was tue ich, wenn ich dies sage? Ich mache
einen Schnitt; zwischen
der || einer Rechnung mit
ihrem Resultat (d.i. einem bestimmten
Bild, einer bestimmten Vorlage) und einen Versuch mit seinem
Ergebnis || Ausgang. || zwischen einer Rechnung mit ihrem
Resultat –
d.i. einem bestimmten Bild,
einer bestimmten Vorlage– –und dem
Experiment (mit seinem
Ausgang). |
Ich möchte sagen: “Wenn ich glaube,
daß x × y =
z ist, – und es kommt ja vor,
daß ich so etwas glaube, sage,
daß ich es glaube – so glaube ich
nicht den mathematischen Satz, denn der steht am Ende eines
Beweises, ist das Ende eines
Beweises;
– 188
– sondern ich glaube:
daß dies die Formel ist, die dort und
¤ dort steht, die ich so und so
erhalten werde
u. dergl.” –
Und dies klingt ja, als dränge ich in den Vorgang des
Glaubens eines solchen Satzes ein. Während ich nur
– in ungeschickter Weise – auf den
fundamentalen Unterschied der
Rollen deute – eines arithmetischen Satzes und eines
Erfahrungssatzes, im Gegensatz zu ihrer scheinbaren
Ähnlichkeit. || bei scheinbarer Ähnlichkeit der
Rollen deute – eines arithmetischen Satzes und eines
Erfahrungssatzes. Denn ich sage eben unter gewissen Umständen: “ich glaube daß x × y = z ist”. Was meine ich damit? – Was ich sage! ‒ ‒ Wohl aber ist die Frage interessant: unter was für Umständen sage ich dies, und wie sind sie charakterisiert im Gegensatz zu denen einer Aussage: “ich glaube, es wird regnen”? Denn was uns beschäftigt, ist ja dieser Gegensatz. Wir verlangen danach, ein Bild zu erhalten von der Verwendung der mathematischen Sätze und der Sätze “ich glaube, daß .....”, Wo || wo ein mathematischer Satz der Gegenstand des Glaubens ist. |
“Du glaubst
doch nicht den mathematischen Satz. –” Das
heißt: “mathematischer
Satz” bezeichnet mir eine Rolle für den
Satz, eine Funktion, in der ein Glauben nicht
vorkommt. || bezeichnet mir eine Rolle,
ein Sprachspiel, worin ein Glauben nicht
vorkommt.
Vergleiche: “Wenn du sagst: ‘ich glaube, daß das Rochieren so und so geschieht’, so glaubst Du nicht die Schachregel, sondern Du glaubst etwa, daß so eine – 189
– Regel des
Schach lautet.” |
“Man kann nicht glauben, die
Multiplikation 13
× 13 liefere 369, weil das Resultat
zur Rechnung gehört.” – Was nenne ich
“die Multiplikation
13 ×
13”? Nur das richtige
Multiplikationsbild, an dessen unterem Ende 369 steht? oder
auch eine ‘falsche Multiplikation’?
Wie ist festgelegt, welches Bild die Multiplikation 13 × 13 ist? – Ist es nicht durch die Multiplikationsregeln bestimmt? – Aber wie, wenn Dir mit Hilfe dieser Regeln heute etwas anderes herauskommt, als was in den || allen Rechenbüchern steht? Ist das nicht möglich? – “Nicht, wenn Du die Regeln anwendest, wie sie!” – Freilich nicht! aber das ist ja ein Pleonasmus. Und wo steht, wie sie anzuwenden sind – und wenn es wo steht: wo steht, wie dies anzuwenden ist? Und das heißt nicht nur: in welchem Buch steht es, sondern auch, in welchem Kopf? – Was ist also die Multiplikation 13 × 13 – oder, wonach soll ich mich beim Multiplizieren richten: nach den Regeln, oder nach der Multiplikation, die in den Rechenbüchern steht – – wenn diese beiden nämlich nicht übereinstimmen? – Nun, es kommt tatsächlich nie vor, daß der, welcher rechnen gelernt hat, bei dieser Multiplikation hartnäckig etwas anderes herausbringt, als was in den Rechenbüchern steht. Sollte es aber geschehen; so würden wir ihn für abnorm erklären, und von seiner Rechnung weiter keine Notiz nehmen. – 190
– |
“Du
gibst das zu – dann mußt
Du das zugeben.” – Er
muß es zugeben – und dabei
ist es möglich, daß er es nicht
zugibt. || ! Oder
willst Du sagen: “er kann es sagen, aber er kann es
nicht denken”. || Du
willst sagen, “Wenn er denkt
muß er es zugeben”.
“Ich werde Dir zeigen, warum Du es zugeben mußt. –” Ich werde Dir einen Fall vor Augen führen, welcher, wenn Du ihn bedenkst, Dich bestimmen wird, so zu urteilen. |
Wie können ihn denn die
Manipulationen des Beweises dazu bringen, etwas
zuzugeben? |
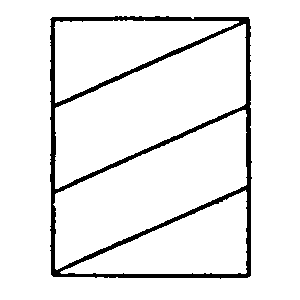
Man
könnte
z.B. die Figur
als Beweis
dafür nehmen, daß 100 Parallelogramme,
so zusammengesetzt, einen geraden Streifen geben
müssen. Wenn man dann wirklich 100
zusammenfügt, erhält man nun etwa einen schwach
– 191 – gebogenen
Streifen. – Der Beweis aber hat uns bestimmt, das
Bild und die Ausdrucksweise zu gebrauchen: Wenn sie
keinen geraden Streifen geben, waren || sind sie ungenau hergestellt. |
Denke nur, wie kann mich das
Bild, das Du mir zeigst, (oder der Vorgang) dazu
verpflichten, nun so und so immer zu urteilen!
Ja, liegt hier ein Experiment vor, so ist eines ja doch zu wenig, mich zu irgendeinem Urteil zu verbinden. |
Der Beweisende sagt:
“Schau diese Figur an! Was wollen wir
dazu sagen? Nicht, daß ein
Rechteck aus ..... besteht? –”
Oder auch: “Das nennst Du doch ‘Parallelogramme’ und das ‘Dreiecke’ und so sieht es doch aus, wenn eine Figur aus andern besteht. –” |
“Ja, Du hast mich
überzeugt: ein Rechteck besteht immer aus
.....” – Würde ich auch sagen:
“Ja Du hast mich überzeugt:
dieses Rechteck (das des Beweises) besteht
aus .....”? Und dies wäre ja doch der
bescheidenere Satz; den auch der zugeben sollte, der etwa
den allgemeinen Satz noch nicht zugibt. Seltsamerweise
aber
– 192
– scheint der, der das zugibt,
nicht den bescheideneren geometrischen Satz zuzugeben, sondern gar
keinen Satz der Geometrie. Freilich, – denn
bezüglich des Rechtecks des Beweises hat er mich ja von nichts
überzeugt. (Über
diese Figur, wenn ich sie früher gesehen hätte, wäre
ich ja in keinem Zweifel gewesen.) Ich habe aus
freien Stücken, was diese Figur anbelangt, alles
zugestanden. Und er hat mich nur mittels
ihrer überzeugt. – Aber anderseits, wenn er
mich nicht einmal bezüglich dieses Rechtecks von
etwas überzeugt hat, wie dann erst von einer Eigenschaft
anderer || andrer
Rechtecke? |
Wenn ich ein Rechteck als auf diese Weise
zusammengefügt sehe, so vergleiche ich dies dem Fall:
meine Blicke dringen in das Innere und sehen dort diese
Zusammensetzung. Man kann ja auch sagen:
“Ich könnte es nicht so zusammengesetzt sehen,
wenn es nicht so zusammengesetzt wäre.” |
“Ich habe nicht
gewußt, daß die
Rechtecksform aus diesen Formen besteht.”
Es ist, als wäre die Form aus diesem Formen gemacht, geschweißt. |
“Ich wußte
nicht, daß die Form aus diesen Formen
besteht.” – So hat's Dich das Bild
gelehrt.
– 193
– |
Du hast etwas Neues gesehen – und
willst sagen, Du habest gesehen, daß das
Alte so und so zusammengesetzt ist. |
Du vergleichst also Dein Erstaunen
dem: Du siehst ein rechteckiges Brett und findest,
daß es auf diese seltsame Weise
zusammengesetzt ist. |
“Ja, die Form sieht nicht so aus,
als könne sie aus zwei windschiefen Teilen
bestehen.” Was überrascht Dich? Doch nicht, daß Du jetzt diese Figur vor Dir siehst! Mich überrascht etwas in dieser Figur. – Aber in dieser Figur geht ja nichts vor! Mich überrascht die Zusammenstellung des Schiefen mit dem Geraden. Mir wird, gleichsam, schwindlig. |
Ich sehe ein
Bild und umgebe es in der Vorstellung hartnäckig
mit einem Vorgang, von welchem ich meine Ausdrucksformen
hernehme. Ich habe ein geteiltes Rechteck vor
mir; ich gebe vor, ich habe es aus diesen Teilen
zusammengesetzt und sei durch das Ergebnis überrascht.
Ich gebe vor, ich sei davon überzeugt worden,
daß Teile – die nicht
danach ausgesehen haben – sich zu dieser Figur
– 194 –
zusammenfügen. |
Ich sage aber doch wirklich:
“Ich habe mich überzeugt,
daß man die Figur aus diesen Teilen legen
kann”, wenn ich nämlich etwa die Abbildung der
Lösung des Geduldspiels gesehen habe.
Wenn ich nun Einem das sage, so soll es doch heißen: “Versuch nur! diese Stücke, richtig gelegt, geben wirklich die Figur.” Ich will ihn aufmuntern etwas zu tun und sage ihm einen Erfolg voraus. Und die Vorhersage beruht auf der Leichtigkeit, mit der man die Figur aus den Stücken zusammensetzen kann, sobald man nur weiß wie. |
Du sagst, Du bist erstaunt
über das, was Dir der Beweis zeigt. Aber bist Du
erstaunt darüber, daß sich diese
Striche haben ziehen lassen? Nein. Du
bist erstaunt nur, wenn Du Dir sagst, daß
zwei solche Stücke diese Form geben.
Wenn Du Dich also in die Situation hineindenkst, Du habest Dir
etwas anderes erwartet und nun sähest Du das Ergebnis.
|
“Aus
dem folgt unerbittlich
das.” Ja, in dieser
Demonstration geht es aus ihm hervor. Und eine Demonstration ist dies für den, der sie als Demonstration anerkennt. Wer sie nicht anerkennt, wer ihr nicht als Demonstration folgt, der trennt sich – 195 – von uns,
noch ehe es zu der Sprache kommt. || ,
der trennt sich von uns eben, ehe es zu einer Sprache
kommt.
¥(Insert p. 209, all except last line, ¥and middle paragraph of page 214) |
Ich habe einen Beweis gelesen –
nun bin ich überzeugt. – Wie wenn ich diese
Überzeugtheit sofort
vergäße!
Denn es ist ein eigentümliches Vorgehen: daß ich den Beweis durchlaufe und dann sein Ergebnis annehme. ‒ ‒ Ich meine: so machen wir es eben. Das ist so bei uns der Brauch, oder eine Tatsache unserer Naturgeschichte. |
‘Wenn ich fünf habe, so habe
ich drei, und zwei.’
‒ ‒ Aber woher weiß ich,
daß ich fünf habe? –
Nun, wenn es so ❘ ❘ ❘ ❘ ❘ ausschaut. – Und ist es auch gewiß,
daß, wenn es so ausschaut, ich
es immer in solche Gruppen zerlegen kann?
Es ist Tatsache, daß wir das folgende || dies Spiel spielen können: Ich lehre Einen, wie eine Zweier-, Dreier-, – 196
– Vierer-,
Fünfergruppe aussieht, und ich lehre ihn, Striche einander
eins-zu-eins zuzuordnen; dann lasse ich ihn immer je
zweimal den Befehl ausführen: ‘Zeichne eine
Fünfergruppe” – und dann den Befehl:
“Ordne die beiden Gruppen einander zu”; da
zeigt es sich, daß er, so gut wie
immer, die Striche restlos einander zuordnet.
Oder auch: es ist Tatsache, daß ich bei eins-zu-eins Zuordnung dessen, was ich als Fünfergruppen hinzeichne, so gut wie nie in Schwierigkeiten komme. |
Ich soll das Geduldspiel zusammenlegen, ich versuche hin
und her, bin zweifelhaft, ob ich es zusammenbringen
werde. Nun zeigt mir jemand das Bild der Lösung:
Nun sage ich – ohne irgendeinen Zweifel –
“jetzt kann ich's!” –
Ist es denn sicher, daß ich
es nun zusammenbringen werde? – Aber die
Tatsache ist: ich zweifle nicht daran. Wenn nun jemand fragte: “Worin besteht die Fernwirkung jenes Bildes?” – Doch in seiner Anwendung, wo immer es sei. || darin daß ich es anwende. |
Ich
sagte || schrieb einmal,
es sei keine Erfahrungstatsache:
daß die Tangente einer visuellen Kurve
ein Stück mit dieser gemeinsam läuft; und wenn dies eine
Figur zeige, so nicht als das Resultat eines Experiments.
– 197 –
Man
könnte auch sagen: Du siehst hier,
daß Stücke einer kontinuierlichen
visuellen Kurve gerade sind. – Aber sollte ich
nicht sagen: – “Das nennst Du doch eine
‘Kurve’. – Und nennst
Du dieses Stückchen nun ‘krumm’ oder
‘gerade’? – Das nennst Du doch
eine ‘Gerade’, und sie enthält dieses
Stück.”
Aber warum sollte man nicht für visuelle Streckeneiner Kurve, die auch in einer Geraden liegen können || , die in einer Kurve liegen, aber auch in einer Geraden liegen können, ein neues Wort gebrauchen? || für visuelle Strecken einer Kurve, die allein keine Krümmung zeigen, einen neuen Namen gebrauchen? “Das Experiment des Ziehens dieser Linien hat doch gezeigt, daß sie sich nicht in einem Punkt berühren.” – Daß sie sich nicht in einem Punkt berühren? Wie sind ‘sie’ definiert? Oder: kannst Du mir ein Bild davon zeigen, wie es ist, wenn sie sich ‘in einem Punkt berühren’? Denn warum soll ich nicht einfach sagen: das Experiment hat ergeben, daß sie – nämlich eine krumme und eine gerade Linie – einander berühren? Denn ist dies nicht, was ich “Berührung” solcher Linien nenne? |
Wie, wenn jemand sagte:
“Die Erfahrung lehrt Dich,
daß diese Linie
 krumm ist”? – Da wäre zu sagen, daß hier die Worte “diese Linie”, den auf dem Papier gezogenen Strich bedeuten. Man kann ja tatsächlich den Versuch anstellen und diesen Strich verschiedenen Menschen zeigen, und fragen: “was siehst Du; eine gerade, oder eine krumme Linie?” – Wenn aber jemand sagte: “Ich stelle mir jetzt eine krumme Linie vor”, und wir ihm darauf sagen: “Da siehst Du also, daß diese Linie eine krumme ist” – was für einen Sinn hätte das? Nun kann man aber auch sagen: “Ich stelle mir einen Kreis vor aus schwarzen und weißen Stücken, eines ist groß, gekrümmt, die folgenden werden immer kleiner, das sechste ist schon gerade.” Wo liegt hier das Experiment? In der Vorstellung kann ich rechnen, aber nicht experimentieren. – 199
– |
In
einer Demonstration einigen wir uns mit
jemand. Einigen wir uns in ihr nicht, so trennen sich
unsere Wege, ehe es zu einem Verkehr mittels dieser Sprache
kommt. Es ist ja nicht wesentlich, daß der Eine den Andern mit der Demonstration überrede. Es können ja beide sie sehen (lesen), und anerkennen. |
“Du siehst doch – es kann
doch keinem Zweifel unterliegen, daß eine Gruppe wie A
wesentlich aus einer wie
B und einer wie C besteht!” –
Ich sage auch –
d.h., ich drücke mich auch || Auch
ich sage –
d.h. auch ich drücke
mich so aus – daß die Gruppe,
die Du hingezeichnet hast, aus den beiden kleineren besteht; aber
ich weiß nicht, ob jede Gruppe, die ich
eine von der Art (oder Gestalt) der ersten nennen würde,
unbedingt aus zwei Gruppen von der Art jener kleineren
zusammengesetzt sein wird. ‒ ‒ Ich glaube aber,
es wird wohl immer so sein (meine Erfahrung hat mich dies
vielleicht gelehrt) und darum will ich als Regel annehmen:
Ich will eine Gruppe dann, und nur dann, eine von der Gestalt
A nennen, wenn sie in zwei Gruppen wie B und C
zerlegt werden kann. |
Und so wirkt auch die Zeichnung
⇒282 als Beweis.
– 200 – “Ja
wahrhaftig! zwei Parallelogramme stellen
sich in || zu dieser Form
zusammen!” (Das ist sehr ähnlich, wie
wenn ich sagte: “Ja wirklich! eine
Kurve kann aus geraden Stücken
bestehen.”) – Ich hätte es nicht
gedacht. Ja – nicht, daß die
Teile dieser Figur diese Figur ergeben. Das
heißt ja nichts. – Sondern
ich staune nur, wenn ich denke, ich hätte das obere
Parallelogramm ahnungslos auf das untere gestellt und sähe
nun dieses Ergebnis. |
Und man könnte sagen: Der
Beweis beweist eben das, was Dich überrascht.
|| der Beweis hat mich
von dem überzeugt –
was mich überrascht.
|
Wenn man sagt: “Diese Form besteht
aus diesen Formen” – so denkt man sich die Form als
eine feine
– 201
– Zeichnung, ein feines Gestell von dieser
Form, auf das gleichsam die Dinge gespannt sind, die diese Form
haben. (Vergleiche:
Platos Auffassung der
Eigenschaft als Ingredientien eines
Dings.) |
Hiermit ist in Zusammenhang, daß
ich oben schrieb: ..... daß eine
Gruppe wesentlich aus .....
besteht”. Wann besteht denn eine Gruppe ‘wesentlich aus .....? Das hängt natürlich von der Art der Verwendung der Bezeichnung ab, die ich der Gruppe gebe. – Meine Hand hat zwar 5 Finger, aber ich hätte nicht gesagt: die Finger meiner Hand bestehen aus 3 und 2. Nun, wesentlich ist es, ‘wenn es nicht anders sein kann’; und es kann nicht anders sein, wenn die Gruppe mit ihrer Teilung als Paradigma dienen soll || dient. Der wesentliche Zug ist ein Zug der Darstellungsart. |
“Diese Form besteht aus diesen Formen.
Du hast mir eine wesentliche Eigenschaft dieser Form
gezeigt.” – Du hast mir ein neues
Bild gezeigt. Es ist, als hätte Gott sie so zusammengesetzt. ‒ ‒ Wir bedienen uns also eines Gleichnisses. Die Form wird zum ätherischen – 202 – Wesen, welches diese
Form hat; es ist, als wäre sie ein für
allemal so zusammengesetzt worden (von dem, der die
wesentlichen Eigenschaften in die Dinge gelegt hat).
Denn, wird die Form zum Ding, das aus Teilen besteht, so ist der
Werkmeister der Form der, der auch Licht und Dunkelheit, Farbe und
Härte,
etc., gemacht hat.
(Denke, jemand fragte: “Die Form .....
ist aus diesen Teilen zusammengesetzt; wer hat sie
zusammengesetzt? Du?)5 Man hat das Wort “Sein” für eine sublimierte, ätherische Art Existieren || des Existieren gebraucht. Betrachte nun den Satz: “Rot ist || ist” (z.B.). Freilich, niemand gebraucht ihn je. Wenn ich mir aber doch einen Gebrauch für ihn erfinden sollte, so wäre es: als einleitende Formel zu Aussagen, die dann vom Wort “rot” Gebrauch machen sollen. Beim Aussprechen der Formel blicke ich auf ein Muster der Farbe Rot. Einen Satz, ¤wie “Rot ist.” ist man versucht auszusprechen, wenn man die Farbe mit Aufmerksamkeit betrachtet: also in der gleichen Situation in welcher man die Existenz eines Ding's feststellt (eines blattähnlichen Insekts z.B.). Und ich will sagen: wenn man den Ausdruck gebraucht, “der Beweis hat mich gelehrt, – hat mich davon überzeugt – daß es sich so verhält”, ist man noch immer in jenem Gleichnis. – 203 – |
Ich hätte auch sagen
können: Wesentlich ist nie die Eigenschaft des
Gegenstandes, sondern das Merkmal des Begriffes. |
“War die Gestalt der Gruppe
dieselbe, so muß sie dieselben Aspekte,
Möglichkeiten der Teilung, haben. Hat sie andere,
so ist es nicht die gleiche Gestalt; sie hat Dir dann vielleicht
irgendwie den gleichen Eindruck gemacht; aber dieselbe
Gestalt ist sie nur, wenn Du sie auf gleiche Weise zerteilen
kannst.” Es ist doch, als würde dies das Wesen der Gestalt aussprechen. – Aber ich sage doch: Wer über das Wesen spricht –, konstatiert bloß eine Übereinkunft. Und da möchte man doch entgegnen: es gibt doch nichts Verschiedeneres, als ein Satz über die Tiefe des Wesens und einer – über eine bloße Übereinkunft. Wie aber, wenn ich antworte: der Tiefe des Wesens entspricht das tiefe Bedürfnis nach der Übereinkunft. Wenn ich also sage: “es ist, als spräche dieser Satz das Wesen der Gestalt aus” – so meine ich: es ist doch, als spräche dieser Satz eine Eigenschaft des Wesens Gestalt aus! – Und man kann sagen: Das Wesen, von dem er eine Eigenschaft aussagt, und das ich hier das Wesen ‘Gestalt’ nenne, ist das Bild, das mir mit dem Wort “Gestalt” untrennbar verbunden scheint. || das Bild, das ich nicht umhin – 204 – kann, mir
beim Wort “Gestalt” zu
machen. |
Wie lernen wir denn Schließen? Oder lernen wir es nicht –? Weiß das Kind, daß aus der doppelten Verneinung die Bejahung folgt? – Und wie überzeugt man es davon? Wohl dadurch, daß man ihm einen Vorgang zeigt (eine doppelte Umkehrung, zweimalige Drehung um 180, u. dergl.) den es nun als Bild der Verneinung annimmt. Und man macht den Sinn von “(x).fx” klar, indem man darauf dringt, daß aus ihm “fa” folgt. |
Ist ein Experiment, in
welchem wir die Beschleunigung beim freien Fall beobachten, ein
physikalisches Experiment, oder ist es ein psychologisches,
das zeigt, was Menschen, unter solchen Umständen,
sehen? ‒ ‒ Kann es nicht beides
sein? Hängt das nicht von seiner
Umgebung ab: von dem, was wir damit machen,
darüber sagen? Könnte man nicht sagen: ein bestimmtes Experiment ist etwas erst im Raum einer Theorie? |
“Das ist ein überraschendes
Resultat!” – Wenn es Dich
überrascht, dann hast Du es noch nicht verstanden.
Denn die Überraschung ist hier nicht
legitim, wie beim
– 205
– Ausgang eines Experiments.
Da – möchte ich sagen – darfst Du
Dich ihrem Reiz hingeben; aber nicht, wenn sie Dir am Ende einer
Schlußkette zuteil wird. Denn da
ist sie nur ein Zeichen dafür,
daß noch Unklarheit, oder ein
Mißverständnis herrscht.
“Aber warum soll ich nicht überrascht sein, daß ich dahin geleitet worden bin?” – Denk Dir Du hättest einen langen algebraischen Ausdruck vor Dir; es sieht zuerst aus, als ließe er sich nicht wesentlich kürzen; dann aber siehst Du eine Möglichkeit der Kürzung und nun geht sie weiter, bis der Ausdruck zu einer kompakten Form zusammenschrumpft. Können wir hier nicht über dies Resultat überrascht sein? (Beim Patience-Legen geschieht ähnliches.) Gewiß, und es ist eine angenehme Überraschung; und sie ist von psychologischem Interesse, denn sie zeigt ein Phänomen des Nicht-Überblickens und der Änderung des Aspekts eines gesehenen Komplexes. Es ist interessant, daß man es diesem Komplex nicht immer ansieht, daß er sich so kürzen läßt; ist aber der Weg der Kürzung übersichtlich vor unsern Augen, so verschwindet die Überraschung. Wenn man sagt, man sei eben überrascht, daß man dahin geführt worden sei, so ist dies keine ganz richtige¤ Darstellung des Sachverhalts. Denn diese Überraschung hat man doch nur dann, wenn man den Weg noch nicht kennt. Nicht, wenn man ihn ganz vor sich sieht. Daß dieser Weg, den ich ganz vor mir habe, da anfängt, wo er anfängt, und da aufhört, wo er aufhört, das ist keine Überraschung. Die Überraschung und das – 206 – Interesse kommen dann
sozusagen von außen. Ich meine
– man kann sagen: “Diese mathematische
Untersuchung hat großes psychologisches
Interesse”, oder “großes
physikalisches Interesse”. |
Ich staune immer wieder bei dieser Wendung
des Themas; obwohl ich es unzählige Male gehört habe und
es auswendig weiß. Es ist
vielleicht sein Sinn, Staunen zu erwecken.
Was soll es dann heißen, wenn ich sage: ‘Du darfst nicht staunen!’? Denke an mathematische Rätselfragen. Sie werden gestellt, weil sie überraschen; das ist ihr ganzer Sinn. Ich will also sagen: Du sollst nicht glauben, es sei hier etwas verborgen, in das man nicht Einsicht nehmen kann – – als seien wir durch einen unterirdischen Gang gegangen und kämen nun irgendwo ans Licht, ohne aber wissen zu können, wie wir dahin gekommen sind, oder welches die Lage des Anfangspunkts zum Ausgang des Tunnels ist. Wie aber konnte man denn überhaupt in dieser Einbildung sein? Was gleicht in der Rechnung einer Bewegung unter der Erde? Was konnte uns denn dieses Bild nahe legen? Ich glaube: daß kein Tageslicht auf diese Schritte fällt; daß wir den Anfangs- und Endpunkt der Rechnung in einem Sinne verstehen, in dem wir den übrigen Gang der Rechnung nicht verstehen. – 207 –
“Hier ist kein Geheimnis!” – aber wie konnten wir denn glauben, daß eines sei? – Nun, ich bin immer wieder den Weg gegangen und war immer wieder überrascht; und auf den Gedanken, daß man hier etwas verstehen kann, bin ich nicht gekommen. “Hier ist kein Geheimnis”, heißt also: Schau Dich doch um! |
Ist es nicht, als sähe man in einer Rechnung eine Art
Kartenaufschlagen? Man hat die Karten gemischt; man
weiß nicht, was dabei vor sich ging:
aber am Ende lag obenauf der Zehner, und das bedeutet .....
|
Unterschied zwischen
dem Werfen des Loses und dem Auszählen vor einem
Spiel. Könnten aber nicht naive Menschen auch
im Ernstfalle statt einen Mann auszulosen sich des Auszählens
bedienen? |
Was
tut der, der uns darauf aufmerksam macht,
daß beim Auszählen das Ergebnis
abgekartet ist? |
Ich will sagen: “Wir haben keinen
Überblick über das, was wir gemacht
haben, und deshalb kommt es uns geheimnisvoll
vor”. Denn nun steht ein Resultat vor uns, und wir
wissen nicht mehr, wie wir dazu gekommen sind, aber wir sagen
(wir haben
– 208
– gelernt zu sagen):
“also muß es so
sein” || “so
muß es sein”;
und wir nehmen es hin, und staunen darüber.
Könnten wir uns nicht denken, daß
ein Mensch verschiedene Befehle von der Form “Du
mußt jetzt das und das tun”, einzeln
auf Karten geschrieben hätte, daß er
die Karten dann mischt, und die, welche obenauf zu liegen kommt,
liest und sagt: Also, ich
muß das tun! –
Denn das Lesen eines geschriebenen Befehls macht nun einmal
einen bestimmten Eindruck, hat eine bestimmte Wirkung.
Und ebenso auch das Anlangen bei einer
Schlußfolgerung. – Man
könnte aber vielleicht den Bann eines solchen Befehls brechen,
indem man noch einmal klar vor Augen führt, wie man
zu diesen Worten gelangt ist, und diesen Vorgang
mit anderen vergleicht¤ || und, was da geschehen ist, mit andern Fällen
vergleicht – indem man
z.B. sagt: “Es hat Dir doch
niemand den Befehl gegeben!” Und ist es nicht auch so, wenn ich sage: “Hier ist kein Geheimnis”? – Er hatte ja, in gewissem Sinne, nicht geglaubt, daß ein Geheimnis vorliegt. Aber er war unter dem Eindruck des Geheimnisses (wie der Andere unter dem Eindruck eines Befehles). In einem Sinne kannte er ja die Situation, aber er verhielt sich zu ihr (im Gefühl und im Handeln) ‘als läge ein andrer Sachverhalt vor’ – wie wir sagen würden. |
⍈
*Die logischen Gesetze sind
allerdings
– 209
– der Ausdruck von
‘Denkgewohnheiten’, aber auch von der
Gewohnheit zu denken || des
Denkens.
D.h., man
kann sagen, sie zeigten: wie Menschen denken und auch,
was Menschen “denken”
nennen. |
⍈
Frege nennt
‘ein Gesetz des menschlichen
Fürwahrhaltens’: “Es ist
den Menschen .... unmöglich, einen Gegenstand als von ihm
selbst verschieden anzuerkennen”. – Wenn ich
denke, daß mir das unmöglich ist, so
denke ich, daß ich versuche,
es zu tun. Ich schaue also auf meine Lampe und
sage: “diese Lampe ist verschieden von ihr
selbst”. (Aber es rührt sich
nichts.) Ich sehe nicht etwa,
daß es falsch ist, sondern ich kann damit
garnichts anfangen.
Außer, wenn die Lampe im Sonnenlicht
flimmert, dann kann ich das ganz gut durch diesen Satz
ausdrücken. – Man kann sich auch in eine Art
Denkkrampf versetzen, in welchem man tut, als versuchte
man, das Unmögliche zu denken || etwas
‘Unmögliches’ zu denken und
es gelänge nicht.
Ähnlich, wie man auch
tun kann, als versuchte man (vergeblich)
einen Gegenstand aus der Ferne durch
bloßes Wollen an sich zu ziehen.
(Dabei schneidet man gewisse Gesichter, so, als wollte man
dem Ding durch Mienen zu verstehen geben, es solle
herkommen.) |
Wie kann man die
Zeit schätzen –
– 210 – da das Leben doch
fern von einer Uhr ist? –
Daß uns die
Zeiten übereinstimmend mit der Uhr einfallen,
daß wir die Zeit
schätzen können,
ist ein Grund, warum, was die Uhr mißt,
die Zeit, so wichtig ist. |
Denk Dir ein Material härter und fester als
irgend ein anderes. Aber wenn man einen Stab aus diesem
Stoff aus der horizontalen in die vertikale Lage bringt, so zieht
er sich zusammen; oder denk Dir, er biegt sich, wenn man ihn
aufrichtet und ist dabei so hart, daß man ihn
auf keine andere Weise biegen kann. – Ein
Mechanismus aus diesem Stoff, etwa eine Kurbel, Pleuelstange und
Kreuzkopf. Andere Bewegungsweise des
Kreuzkopfs. Oder: eine Stange biegt sich, wenn man ihr eine gewisse Masse nähert; gegen alle Kräfte aber, die wir auf sie wirken lassen, ist sie vollkommen starr. Denk Dir, die Führungsschienen biegen sich und strecken sich wieder, wenn die Kurbel sich ihnen nähert und sich wieder entfernt. Ich nähme aber an, daß keinerlei besondere äußere Kraft dazu nötig ist, dies hervorzurufen. Dieses Benehmen der Schienen würde wie das, eines lebenden Wesens anmuten. Wenn wir sagen: “Wenn die Glieder des Mechanismus ganz starr wären, würden sie sich so und so bewegen”, was ist das Kriterium dafür, daß sie ganz starr sind? Ist es, daß sie gewissen Kräften widerstehen? oder, daß sie sich so – 211 – und so
bewegen? Denke, ich sage: “das ist das Bewegungsgesetz des Kreuzkopfes (die Zuordnung seiner Lage – zur Lage der Kurbel etwa), wenn sich die Länge der Kurbel und der Pleuelstange nicht ändern”. Das heißt wohl: Wenn sich die Lagen der Kurbel und des Kreuzkopfes so zueinander verhalten, dann sage ich, daß die Länge der Pleuelstange gleich bleibt. |
“Wenn die Teile ganz starr wären, würden sie
sich so bewegen”: ist das eine Hypothese?
Es scheint, nein. Denn wenn wir
sagen: “die Kinematik beschreibt die Bewegungen des
Mechanismus unter der Voraussetzung, daß
seine Teile vollkommen starr sind”, so geben wir
einerseits zu, daß diese Voraussetzung
in der Wirklichkeit nie zutrifft, anderseits soll es keinem Zweifel
unterliegen, daß vollkommen starre Teile
sich so bewegen würden. Aber woher diese
Sicherheit? Es handelt sich hier wohl nicht um
Sicherheit, sondern um eine Bestimmung, die wir getroffen
haben. Wir wissen nicht,
daß Körper, wenn sie (nach den und
den Kriterien) starr wären, sich so bewegen
würden; wohl aber würden wir (unter Umständen)
Teile ‘starr’ nennen, die sich so bewegen –
denke in so einem Fall immer daran, daß ja
die Geometrie (oder Kinematik) keine
Meßmethode spezifiziert, wenn sie von
gleichen Längen oder vom Gleichbleiben einer Länge
spricht. Wenn wir also die Kinematik etwa die Lehre von der Bewegung vollkommen starrer Maschinenteile nennen, so – 212
– liegt hierin einerseits eine Andeutung
über die (mathematische) Methode: wir bestimmen
gewisse Distanzen als die Längen der
Maschinenteile¤ || von
Maschinenteilen, die sich nicht ändern;
anderseits eine Andeutung über die Anwendung des
Kalküls. |
“Aber willst Du sagen, daß der
Ausdruck ‘+2’ es für
Dich zweifelhaft läßt, was Du, nach 234
z.B., schreiben sollst?”
– Nein; ich sage ohne Bedenken:
“236”; aber darum ist es ja
überflüssig || unnötig,
daß darüber schon früher etwas
bestimmt wurde – daß ich keinen
Zweifel habe, wenn die Frage an mich herantritt,
– heißt das,
daß sie früher bereits beantwortet
worden ist? || heißt
eben nicht, daß sie früher schon
beantwortet worden war. Aber ich weiß doch auch, daß, welche Zahl immer man mir geben wird, ich die folgende gleich mit Sicherheit werde angeben können. – Ausgenommen ist doch gewiß der Fall, daß ich sterbe, ehe ich dazu komme, die nächste Zahl zu nennen, und natürlich auch viele andere Fälle. Daß ich aber so sicher bin, daß ich fortsetzen kann, || daß ich werde fortsetzen können, ist natürlich sehr wichtig. – |
“Eine Definition führt Dich doch nur wieder einen
Schritt zurück, zu etwas anderem nicht
Definiertem.” Was sagt uns das?
Wußte das irgend jemand nicht? – Nein; aber
– 213
– konnte er es nicht aus dem Auge
verlieren? |
Oder: “Wenn Du schreibst ‘1, 4, 9, 16, ....’, so hast Du nur vier Zahlen angeschrieben, und vier Pünktchen” – worauf machst Du da aufmerksam? Konnte jemand etwas anderes glauben? Man sagt Einem in so einem Falle auch: “Damit hast Du weiter nichts hingeschrieben als vier Zahlzeichen und noch ein fünftes Zeichen, die Pünktchen”. Ja, wußte er das nicht? Aber kann er nicht doch sagen: Ja wirklich, ich habe die Pünktchen nie als ein weiteres Zeichen in dieser Reihe || als ein Zeichen nach dem Zahlzeichen aufgefaßt, – das hier so allerdings so aussieht, wie weitere flüchtig geschriebene Ziffern, aber auch anders geschrieben werden könnte, daß es den Charakter eines Buchstabens oder Zahlzeichens hätte. |
Oder wie ist es, wenn man darauf aufmerksam
macht, daß eine Linie im Sinne
Euklids eine Farbengrenze ist und
nicht ein Strich; und ein Punkt der Schnitt solcher
Farbengrenzen und kein Tupfen? (Wie oft ist
gesagt worden, daß man sich einen Punkt
nicht vorstellen kann.) |
Man kann in der Einbildung leben, denken,
daß es sich so und so verhält, ohne es
zu glauben;
d.h.: wenn
man gefragt wird, so weiß man es, hat man
aber nicht auf die Frage zu antworten, so
weiß man es nicht,
– 214 – sondern man
handelt und denkt dann nach einer andern Ansicht. |
Denn eine Ausdrucksform
läßt uns so und so
handeln. Wenn sie unser Denken beherrscht, so möchten
wir trotz aller Einwendungen sagen: “in gewissem
Sinne verhält es sich doch so.”
Obwohl es gerade auf den ‘gewissen Sinn’
ankommt. (Ähnlich
beinahe, wie es uns die Unehrlichkeit eines Menschen bedeutet, wenn
wir sagen: er sei kein Dieb.) |
⍈
Die Sätze der
Logik sind ‘Denkgesetze’, ‘weil sie das
Wesen des menschlichen Denkens zum Ausdruck bringen’
– richtiger aber: weil sie das Wesen, die Technik, des
Denkens zum Ausdruck bringen, oder zeigen. Sie zeigen, was
das Denken ist, und auch Arten des Denkens.
|
Das Überraschende
kann in der Mathematik || in der
Behandlung der
Mathematik zweierlei völlig verschiedene
Rollen spielen. Man kann den Wert einer mathematischen Gedankenreihe darin erblicken, daß sie etwas Überraschendes || etwas uns überraschendes zutage fördert: weil es von großem Interesse, von großer Wichtigkeit ist, zu sehen, wie ein Sachverhalt durch die und die Art seiner Darstellung überraschend, oder paradox, wirkt || wird || überraschend, erstaunlich, oder auch paradox wird. – 215
– |
Hievon ganz
verschieden ist die gegenwärtig gepflogene
Darstellungsweise || heute herrschende Auffassung der
Mathematik, der das
Überraschende, das Erstaunliche, darum
als Wert gilt, weil es zeige || zeigt, in
welche Tiefe die mathematische Untersuchung dringt; wie
wir den Wert eines Teleskops daran ermessen
können || könnten, daß
es uns Dinge zeigt, die wir ohne dieses Instrument nicht
hätten ahnen können. Der
Mathematiker sagt gleichsam: “Siehst Du, das
ist doch wichtig, das hättest Du ohne mich nicht
gewußt.” – So
als wären durch diese Überlegungen,
als durch eine Art höheren Experiments, erstaunliche, ja die
erstaunlichsten Tatsachen ans Licht gefördert worden.
Der Mathematiker ist kein Entdecker, sondern ein Erfinder. |
“Ich kann doch nur folgern, was wirklich
folgt!” –
D.h.: was die logische
Maschine wirklich hervorbringt. Die
logische Maschine, das wäre ein Art Weltäther; ein
alles durchdringender ätherischer Mechanismus. – Und vor diesem Bild muß man
warnen. |
“Ich habe gemeint .....”
heißt hier: ich habe dies
in petto gehabt. Aber dies ist doch
ein Bild. “Die Maschine hat es in sich, sich so zu bewegen.” Der Fall wird also verglichen dem, daß wir etwas aus einem Behälter holen, was dort lag. (Dieses – 216
– Bild liegt in einer Menge von Wendungen
unserer Sprache, wird immer wieder von uns ausgesprochen;
kein Wunder, wenn es große Gewalt
über uns hat.) |
Wenn
jemand eine ihm wohl bekannte Melodie singt, || Es singt einer
eine ihm wohl bekannte Melodie; wir unterbrechen ihn an
irgendeiner Stelle und fragen dann:
“Hast du gewußt, wie es weiter
geht; wolltest Du so fortsetzen, oder
so?” – (indem
wir ihm die richtige und eine falsche Fortsetzung angeben)
– er antwortet: “Freilich
wußte ich, wie es weiter geht und ich
wollte natürlich so
fortsetzen .....”. Es drängt sich
uns das Bild auf, die Fortsetzung der Melodie habe schon
existiert, und zwar in uns gleichsam hinter der
Mundöffnung. Dies Bild wird verstärkt
dadurch, daß wir nach der Unterbrechung noch
ein Stückchen der Melodie mit dem innern Ohr hören
und es ist, als sähen wir noch ein Stück der Reihe jener
Töne entlang, die bereit lagen, ans Licht zu
kommen. Und dies ist wieder ganz ähnlich dem, was
beim Zählen vor sich geht, oder beim Anschreiben einer Reihe
mit ‘Pünktchen’, die
‘u.s.w. ad inf.’ bedeuten.
|
“Es ist aber doch
ein entscheidender Unterschied zwischen einem Reihenstück,
welches ein bestimmtes Ende haben soll, und jenen Anfängen
einer Reihe, die endlos ist, ich meine, ein
wesentlicher || wesenhafter Unterschied in unserer
Auffassung von dem hingeschriebenen
Reihenstück. Endlos – möchte ich sagen
– ist eben wirklich endlos. Und hier
kann doch die Bedeutung
– 217
– nicht im Gebrauch bestehen, denn der
Gebrauch ist ja endlich, und wenn man auf ihn schaut, so kommt
man eben auf
finitistische Gedanken! Sieht man aber auf die
Bedeutung, das, was wir uns bei dem Wort
denken, so sieht man, wovon hier die Mathematik
redet.” – Erstens, wenn du sagst, der
Gebrauch des Wortes ist ein endlicher, was
heißt das? Wie sieht denn
ein unendlicher Gebrauch aus? – Also kann man
wohl ‘endlich’ und ‘unendlich’
garnicht auf die Verwendung || den
Gebrauch eines Wortes anwenden. – Ist nun
aber der Gebrauch, den wir von
“u.s.w. ad inf.” machen, der
gleiche, wie der, den wir von
“u.s.w. ad
734” machen? Offenbar nein. Nur ist
der Unterschied der Verwendung
von: “u.s.w.
ad 734” und
“u.s.w. ad
100” nicht von der gleichen Art, wie
der zwischen der Verwendung eines dieser Zeichen und
des Zeichens “u.s.w. ad inf.”. |
Wie
z.B. auch
die Verwendung der Befehle “zeichne ein Kreisstück
vom Radius 25
cm.”,
“zeichne ein Kreisstück vom Radius 6
cm.” nicht von gleicher Art ist,
wie die des Befehles: “zeichne ein Kreisstück
vom Radius ∞”. In den
beiden ersten Fällen benutzen wir einen Zirkel, im dritten ein
Lineal. |
An der
Verwendung des Wortes “endlos”, oder
“unendlich”, ist weiter nichts zu beanstanden, als
der Geist, in dem sie verwendet werden.
Der
hocus-pocus,
der, bei aller
– 218
– scheinbaren Nüchternheit, in den
Worten liegt, mit denen Mathematiker ihre Kalküle
begleiten. Zeige uns statt der
Bilder, die dieses Wort und diese
Sätze hervorrufen, ihre
Verwendung! |
Wenn man sich nun nach dem Gebrauch des
Zeichens “u.s.w. ad inf.” umschaut, so
fällt einem freilich auf, daß das
Eigentümliche dieses Gebrauches ja nicht darin bestehen
kann, daß er, in irgendeinem Sinne,
ausgedehnter ist, als der, jener andern
Zeichen || als der, der Zeichen
“u.s.w. ad
n.”. Er
unterscheidet sich eben nicht durch die
‘Länge’ von dem des begrenzten
“u.s.w.”. |
Aber was für Eigenschaften
der 100 Kugeln hast Du entfaltet, oder gezeigt? –
Nun, daß man diese Dinge mit ihnen tun
kann. – Aber welche Dinge?
Meinst Du: daß Du sie hast so
bewegen können, daß sie nicht an der
Tischfläche festgeleimt waren? – Dies
auch, aber hauptsächlich, daß keine
von ihnen verschwand, daß man sie
verschieben, und der Verschiebung mit den Augen folgen konnte,
daß sie dabei ihre Form beibehielten. – Aber warum hast Du den Ausdruck
“entfalten” gebraucht? Du
hättest doch nicht gesagt, Du entfaltest die Eigenschaften
einer Eisenstange, indem Du zeigst, daß
sie bei so und soviel Grad
schmilzt? || . Und nimm
einen einfachern Fall: ‘entfalte die
Eigenschaften’ einer Reihe von 4
Äpfeln, indem Du sie erst
so: – 219 – Könntest Du
nicht ebenso gut sagen, Du entfaltest die Eigenschaften unseres
Zahlengedächtnisses (z.B.)?
Was Du eigentlich entfaltest, ist ja wohl die
Reihe der Kugeln. – Und Du zeigst,
daß, wenn eine Reihe so und so
ausschaut,
z.B. so und so
römisch numeriert ist, daß sie dann auf
einfache Weise, und ohne daß eine dazu- oder wegkommt, in jene andere
einprägsame Form gebracht werden kann. Aber
ebensogut könnte das
doch ein psychologisches Experiment sein, das zeigt,
daß Du jetzt || jetzt gewisse Formen einprägsam findest, in
die 100 Flecke durch bloßes Verschieben
gebracht werden. “Ich habe gezeigt, was sich mit 100 Kugeln machen läßt.” Du hast gezeigt, daß sich diese 100 Kugeln so entfalten ließen. Das Experiment war eines des Entfaltens (im Gegensatz z.B. zu einem des Verbrennens). Und das psychologische Experiment konnte z.B. zeigen, wie leicht man Dich betrügen kann; daß Du es nämlich nicht merkst, wenn man Kugeln zu der Reihe dazu-, oder wegschmuggelt. Man könnte ja auch so sagen: Ich habe gezeigt, was sich mit einer Reihe von 100 Flecken durch scheinbares Verschieben machen läßt, – welche Figuren sich durch scheinbares Verschieben aus ihr erzeugen lassen. – Was aber habe ich in diesem Fall entfaltet? Es kann doch z.B. nicht gut ein Entfalten der Eigenschaften von 100 römisch numerierten Kugeln genannt werden, daß sie sich arabisch bis zur Zahl 100 numerieren lassen! Wie, wenn ich sagte: “Ich habe die Eigenschaften – 220
– dieser Formation (von
Leuten) entfaltet”? |
Denk Dir, man sagte: wir
entfalten die Eigenschaften eines Polygons
indem wir je 3 Seiten durch eine Diagonale
zusammennehmen. Es zeigt sich dann etwa als
15-Eck. Will ich sagen: ich habe eine
Eigenschaft des 15-Ecks entfaltet?
Nein. Ich will sagen, ich habe eine Eigenschaft
dieses (hier gezeichneten) Vielecks entfaltet.
Ist dies ein Experiment? Gewiß. Ich wußte ja nicht, was herauskommen würde, ja noch weiß ich, ob das Gleiche beim nächsten Versuch herauskommen wird. Ja; wie aber, wenn ich so einen Versuch an einem Fünfeck anstelle, das ich ja schon übersehen kann? – Nun, nehmen wir einen Augenblick an, ich könnte es nicht übersehen, was z.B. geschehen kann, wenn es zu groß ist und ich zu nahe bin. Dann wäre das Ziehen der Diagonalen ein Mittel, um mich davon zu überzeugen, daß da ein Fünfeck steht. Ich könnte wieder sagen, ich habe die Eigenschaften des Polygons, das da gezeichnet ist, entfaltet. – Kann ich es nun übersehen, dann kann sich doch daran nichts ändern. Es war etwa überflüssig, diese Eigenschaft zu entfalten, wie es überflüssig ist, zwei Äpfel, die vor mir liegen, zu zählen. Soll ich nun sagen: “es war wieder ein Experiment, aber ich war des Ausgangs sicher”? Aber bin ich des Ausgangs in der Weise sicher, wie des Ausgangs der Elektrolyse einer Wassermenge? Nein, – sondern anders! Er¤gäbe die Elektrolyse – 221 – der Flüssigkeit
nicht H2O so würde ich
mich nicht für
närrisch halten, oder sagen, ich wisse jetzt überhaupt
nicht mehr, was ich sagen soll. Denk Dir, ich sagte: “Ja, hier steht ein Quadrat – aber schauen wir noch nach, ob es durch eine Diagonale in zwei Dreiecke zerlegt wird!” Ich ziehe sie dann und sage: “Ja, hier haben wir zwei Dreiecke.” Da würde man mich fragen: Hast Du denn nicht gesehen, daß es in zwei Dreiecke zerlegt werden kann? Bist Du erst jetzt überzeugt, daß hier ein Viereck steht; und warum traust Du jetzt Deinen Augen mehr als früher? Aber dann ist es ja auch ein Experiment, wenn ich die Linien garnicht ziehe, sondern nur ‘mit dem Auge’ immer so und soviele Seiten zusammennehme. Freilich, auch es so zu prüfen ist ein Experiment. – Und so ist es auch ein Experiment, wenn ich Analoges an einem Quadrat ausführe || mit einem Quadrat tue; es zeigt, daß ich dies (jetzt) an der Figur, die hier steht, ausführen kann – was immer das zeigen mag. Man könnte es ja auch “die Eigenschaften einer Reihe von Kugeln entfalten” nennen, wenn ich sie einfach zähle; und anderseits könnte man das mehrmalige Umgruppieren einer Reihe auch “ein mehrmaliges Zählen auf verschiedene Arten” nennen. Aber dann ist das Umgruppieren der Bilder im Film auch nur ein Zählen der Flecke. Dann muß es ja aber auch ein Experiment sein. Denk Dir, es würde im Film – 222 – gezählt, indem das
Numerieren der Reihe nach gefilmt würde; dann zählt hier
also der Film selbst die Reihe der Flecke – aber damit es mich
überzeugt, muß ich mitzählen,
d.h., das gefilmte Zählen kontrollieren;
denn wenn im Film falsch gezählt würde, so
kämen wir zwar dennoch zu der und
der Zahl, aber ich dürfte sie nicht als Ergebnis der
Zählung anerkennen. Mein Zählen besteht hier
darin, die Reihenfolge der auftauchenden Ziffern
zu prüfen. |
Aufgaben: Zahl der ¤
Töne, die innere Eigenschaft einer Melodie; Zahl
der Blätter, – äußere
Eigenschaft eines Baumes. Wie hängt das mit der
Identität des Begriffes zusammen? |
Was wir liefern, sind eigentlich
Bemerkungen zur Naturgeschichte des Menschen; aber nicht
kuriose Beiträge, sondern solche Feststellungen, an denen
niemand gezweifelt hat, und die dem Bemerktwerden nur entgehen,
weil sie ständig vor unsern Augen sind. || weil sie sich ständig vor unsern Augen
herumtreiben. |
Was zeigt uns der, der 4 Kugeln in 2 und 2
trennt, sie wieder zusammenschiebt || vereinigt, wieder trennt
etc.? Er prägt uns ein Gesicht ein
und eine typische Veränderung dieses Gesichts.
– 223
– |
Denke an die
möglichen Stellungen einer Gliederpuppe. Oder
denk, Du hättest eine Kette mit, sagen wir 10 Gliedern und
Du zeigst, was für charakteristische
(d.h. einprägsame) Figuren man mit
ihr legen kann. Die Glieder seien numeriert; dadurch
werden sie zu einer leicht einprägbaren Struktur, auch wenn
sie in gerader Reihe liegen. Ich präge Dir also charakteristische Lagen und Bewegungen dieser || der Kette ein. Wenn ich nun sage: “Sieh', man kann auch das aus ihr machen” (und es vorführe), zeige ich Dir da ein Experiment? – Im gewissen Sinne ja; ich zeige z.B., daß man sie in diese Form bringen kann; aber daran hast Du nicht gezweifelt. Und was Dich interessiert, ist nicht etwas, was diese individuelle || eine Kette betrifft. – Aber ist, was ich vorführe, nicht doch eine Eigenschaft dieser Kette? Gewiß; aber ich führe nur solche Bewegungen, solche Umformungen, vor, die einprägsamer Art sind; und Dich interessiert, diese Umformungen zu lernen. Es interessiert Dich aber darum, weil es so leicht ist, sie immer wieder, an verschiedenen Gegenständen vorzunehmen. |
Die Worte “Sieh, was
ich aus ihr machen kann –” sind allerdings dieselben,
die ich auch verwenden würde, wenn ich Dir zeigte, was ich
alles aus einem Klumpen Ton
z.B. formen
kann. Hier würde Dich nicht so sehr interessieren,
daß
sich solche Dinge aus diesem Klumpen formen
lassen, als daß ich etwa geschickt genug
bin, es zu tun. In einem andern Fall
– 224 – etwa:
daß dies Material sich so
behandeln läßt. Hier
würde man kaum sagen: ich ‘mache Dich darauf
aufmerksam’, daß ich
dies machen kann, oder daß das Material dies
aushält, – während man im Fall der Kette sagen
würde: ich mache Dich darauf aufmerksam,
daß sich dies mit ihr machen
läßt. – Denn Du
hättest es Dir auch vorstellen
können. Aber Du kannst natürlich keine
Eigenschaft der Kette durch Vorstellen erkennen.
Das Experimenthafte verschwindet, indem man den Vorgang bloß als einprägsames Bild ansieht. |
Man kann
daher sagen: Wir entfalten die
Rolle, die “100” in unserm
Rechensystem spielt. Inwiefern kann man denn sagen: die Rechnung analysiert das Zeichen “100”? sie setzt dem Zeichen ja etwas hinzu. |
(Ich schrieb einmal:
“In der Mathematik sind
Prozeß und Resultat einander
äquivalent.”) |
Und doch fühle ich,
daß es eine Eigenschaft von
“100” sei, daß es so
erzeugt wird, oder werden kann. Aber wie kann es denn
eine Eigenschaft der Struktur “100” sein,
daß sie so erzeugt wird, wenn sie
z.B. garnicht so
erzeugt würde? Wenn niemand so
multiplizierte? Doch nur, wenn man sagen könnte,
– 225 – es ist eine
Eigenschaft dieses Zeichens, Gegenstand dieser Regel zu
sein. Es ist Eigenschaft der “5”,
Gegenstand der Regel
“3
+ 2 = 5” zu
sein. Denn nur als Gegenstand der Regel ist die Zahl
das Resultat der Addition jener andern Zahlen.
Wenn ich aber nun sage: es ist Eigenschaft der Zahl ....., das Resultat der Addition von ..... nach der Regel ..... zu sein? Es ist also eine Eigenschaft der Zahl, daß sie bei der Anwendung dieser Regel auf diese Zahlen entsteht. Die Frage ist: würden wir es “Anwendung der Regel” nennen, wenn diese Zahl nicht das Resultat wäre? Und das ist dieselbe Frage wie: “Was verstehst Du unter der ‘Anwendung dieser Regel’: das, was Du etwa mit ihr machst (und Du magst sie einmal so, einmal so anwenden), oder ist ‘ihre Anwendung’ anders definiert || erklärt.” |
“Es ist eine Eigenschaft
dieser Zahl, daß
dieser Prozeß zu ihr
führt.” – Aber
mathematisch gesprochen führt kein
Prozeß zu ihr, sondern sie ist das Ende eines
Prozesses (gehört noch zum
Prozeß). |
Ich entfalte die Rolle der
“100” im Spiel. (Und es ist hier ganz gleichgültig, ob ich die Ziffer “100” betrachte, oder, z.B., 100 Striche.) “Zugegeben, ich interessierte mich nicht für die Eigenschaften: daß keine der Kugeln verschwindet, daß man sie verschieben kann, etc. – die nehme ich alle als – 226 –
selbstverständlich hin – aber ist es nicht
dennoch eine Eigenschaft der Reihe, daß
wir sie so zerlegen und zu diesen Gestalten
umgruppieren können – gegeben,
daß die Kugeln jene andern Eigenschaften
haben? Denn ich könnte doch sehr wohl
überrascht sein, zu sehen, daß die 100
Kugeln ein solches Viereck bilden,
etc.”
– Wohl; aber wenn ich Dir diese Umformung einmal gezeigt hätte, wärest Du da ein zweites Mal wieder überrascht, daß man sie machen kann? |
Wenn Du
die Eigenschaften, von denen wir oben sprachen, als
selbstverständlich hinnimmst, hast Du weiter || auch weiter keine Eigenschaften der Reihe
demonstriert. |
“Diese Reihe gibt durch derlei
Umformungen || Umformung
diese Formation.” Liegt hier das Gewicht darauf,
daß sie nicht eine andere
Formation ergibt? – So
muß es doch sein. Aber
konstituiert dies nicht eben die Tatsache,
daß nichts weg und nichts
dazukommt? |
Aber
warum fühle ich, es werde eine Eigenschaft der Reihe
entfaltet, gezeigt? – Weil ich abwechselnd, was
gezeigt wird, als der Reihe wesentlich, und nicht wesentlich
ansehe. Oder: weil ich an diese Eigenschaften
abwechselnd als externe
– 227
– und interne denke. Weil ich
abwechselnd etwas als selbstverständlich hinnehme und es
bemerkenswert finde. |
Es ist eine Eigenschaft der Reihe, sich so
zu bewegen. |
“Du entfaltest doch die Eigenschaften der 100,
indem Du zeigst, was aus ihr || ihnen gemacht
werden kann.” – Wie gemacht werden
kann? Denn, daß das aus ihnen
gemacht werden kann, daran hat ja niemand
gezweifelt, es muß also um die Art und
Weise gehen, wie dies aus ihnen erzeugt wird.
Aber sieh' diese an! ob sie nicht etwa das
Resultat schon voraussetzt. – Denn denke Dir, es entsteht auf diese Weise einmal dies, einmal ein anderes Resultat; würdest Du das nun hinnehmen? Würdest Du nicht sagen: “Ich muß mich geirrt haben; auf diese || dieselbe Art und Weise mußte immer das Gleiche entstehen.” Das zeigt, daß Du das Resultat der Umformung mitrechnest zur Art und Weise der Umformung. || , daß Du das Resultat in die Art und Weise der Umformung miteinrechnest. |
Die Härte des logischen
Muß. Wie, wenn man
sagte: das Muß der Kinematik ist
viel härter, als das kausale
Muß, das einen Maschinenteil zwingt, sich
so zu bewegen,
– 228
– wenn der andere sich so
bewegt? – Denk Dir, wir würden die Bewegungsweise des ‘vollkommen starren’ Mechanismus durch ein kinematographisches Bild, einen Zeichenfilm, darstellen. Wie, wenn man sagen würde, dies Bild sei vollkommen hart, und damit meinte, wir hätten dieses Bild als Darstellungsweise genommen, – was immer die Tatsachen seien, wie immer sich die Teile des || eines wirklichen Mechanismus biegen, oder dehnen mögen. – Das wäre ähnlich, als dächte man sich die Länge des Meters unendlich hart: weil sie gleichbleibe, wie immer auch die Längen der Dinge sich änderten, weil sie, von den Kräften, die die Dinge ausdehnen und zusammendrücken, unbeeinflußt sei. |
Die Maschine (ihr Bau) als Symbol
für ihre Wirkungsweise: Die Maschine –
könnte ich zuerst sagen, – ‘scheint ihre
Wirkungsweise schon in sich zu haben’. Was
heißt das? Indem wir die Maschine kennen, scheint alles Übrige, nämlich die Bewegungen, die sie machen wird, schon ganz bestimmt zu sein. “Wir reden so, als könnten sich diese Teile nur so bewegen, als könnten sie nichts andres tun.” Wie ist es –: vergessen wir also die Möglichkeit, daß sie sich biegen, abbrechen, schmelzen können, etc.? Ja; wir denken in vielen Fällen garnicht daran. Wir gebrauchen eine Maschine, oder das Bild einer Maschine, als Symbol für eine bestimmte Wirkungsweise. Wir teilen z.B. Einem – 229
– dieses Bild, mit und setzen voraus,
daß er die Erscheinungen der Bewegungen
der Teile aus ihm ableitet. (So wie wir jemand eine
Zahl mitteilen können, indem wir sagen, sie sei die
fünfundzwanzigste der Reihe: 1, 4, 9, 16 ....)
“Die Maschine scheint ihre Wirkungsweise schon in sich zu haben” heißt: Du bist geneigt, die künftigen Bewegungen der Maschine in ihrer Bestimmtheit Gegenständen zu vergleichen, die schon in einer Lade liegen und von uns nun herausgeholt werden. So aber reden wir nicht, wenn es sich darum handelt, das wirkliche Verhalten einer Maschine vorauszusagen; da vergessen wir, im allgemeinen, nicht die Möglichkeiten der Deformation der Teile etc. Wohl aber, wenn wir uns darüber wundern, wie wir denn die Maschine als Symbol einer Bewegungsweise verwenden können – da sie sich doch auch ganz anders bewegen kann. Nun, wir könnten sagen, die Maschine, oder ihr Bild, stehe als Anfang einer Bilderreihe, die wir aus diesem Bild abzuleiten gelernt haben. Wenn wir aber bedenken, daß sich die Maschine auch anders hätte bewegen können, so erscheint es uns leicht, als müßte in der Maschine als Symbol ihre Bewegungsart noch viel bestimmter enthalten sein, als in der wirklichen Maschine. Es genüge da nicht, daß dies die erfahrungsmäßig vorausbestimmten Bewegungen seien || sind, sondern sie müßten eigentlich – in einem mysteriösen Sinne – bereits gegenwärtig sein. Und – 230
– es ist ja wahr: die Bewegung des
Maschinensymbols ist in anderer Weise vorausbestimmt, als die einer
gegebenen wirklichen Maschine. |
“Es ist,
als könnten wir die ganze Verwendung des Wortes mit einem
Schlag erfassen.” – Wie was
z.B.? – Kann
man sie nicht – in gewissem Sinne – mit einem Schlag
erfassen? Und in welchem Sinne
kannst Du dies nicht? Es ist eben, als könnten
wir sie in einem noch viel direkteren Sinne mit einem Schlag
erfassen. Aber hast Du dafür ein
Vorbild? Nein. Es bietet sich
uns nur diese Ausdrucksweise an. Als das Resultat sich
kreuzender Bilder || Gleichnisse. |
Du hast kein Vorbild dieser
übermäßigen Tatsache, aber
Du wirst dazu verführt, einen
Über-Ausdruck || Über-Ausdruck zu
gebrauchen. |
Wann
denkt man denn: die Maschine habe ihre
möglichen Bewegungen schon in irgend einer mysteriösen Weise
in sich? – Nun, wenn man philosophiert.
Und was verleitet uns, das zu denken? Die Art und
Weise, wie wir von der Maschine reden. Wir sagen
z.B., die Maschine habe
(besäße) diese
Bewegungsmöglichkeiten, wir sprechen von der ideal
starren Maschine, die
sich nur so und so bewegen könne. ‒ ‒ Die Bewegungsmöglichkeit,
was ist sie? Sie ist nicht die Bewegung;
aber sie scheint auch nicht die bloße
physikalische
– 231
– Bedingung der Bewegung zu
sein, etwa, daß zwischen Lager und Zapfen
ein gewisser Zwischenraum ist, der Zapfen nicht zu streng ins Lager
paßt. Denn dies ist zwar || nur
erfahrungsmäßig die
Bedingung der Bewegung, aber man
könnte sich die Sache auch
anders vorstellen. Die Bewegungsmöglichkeit
soll mehr wie ein Schatten der Bewegung selber sein.
Aber kennst Du so einen Schatten? || Aber hier wieder: Kennst Du so
einen Schatten? Und unter Schatten
verstehe ich nicht irgendein Bild der Bewegung; denn dies Bild
müßte ja nicht das Bild gerade
dieser Bewegung sein. Aber die
Möglichkeit dieser Bewegung muß die
Möglichkeit gerade dieser Bewegung sein.
(Sieh', wie hoch die Wellen der Sprache
hier gehen.) Die Wellen legen sich, so wie wir uns fragen: wie gebrauchen wir denn, wenn wir von einer Maschine reden, das Wort “Möglichkeit der Bewegung”? – Woher kamen aber dann diese || die seltsamen Ideen? Nun, ich zeige Dir die Möglichkeit der Bewegung etwa durch ein Bild der Bewegung: ‘also ist die Möglichkeit etwas der Wirklichkeit Ähnliches’. Wir sagen: “es bewegt sich noch nicht, aber es hat schon die Möglichkeit sich zu bewegen”, ‘also ist die Möglichkeit etwas der Wirklichkeit sehr Nahes’. Wir mögen zwar bezweifeln, ob die und die physikalische Bedingung, diese Bewegung möglich macht, aber wir diskutieren nie, ob dies die Möglichkeit dieser oder jener Bewegung sei: ‘also steht die Möglichkeit der Bewegung zur Bewegung selbst in einer einzigartigen Relation, enger, als die des Bildes zu seinem Gegenstand’, denn es kann bezweifelt – 232 – werden, ob dies das
Bild dieses oder jenes Gegenstandes ist. || denn es kann gefragt werden, wessen Bild dies Bild
ist. Wir sagen: “die
Erfahrung wird lehren, ob dies dem Zapfen diese
Bewegungsmöglichkeit gibt”, aber wir sagen nicht:
“die Erfahrung wird lehren, ob dies die
Möglichkeit dieser Bewegung ist”:
‘also ist es nicht Erfahrungstatsache,
daß diese Möglichkeit die
Möglichkeit gerade dieser Bewegung ist’.
Wir achten auf unsere eigene Ausdrucksweise, diese Dinge betreffend, verstehen sie aber nicht, sondern mißdeuten sie. Wir sind, wenn wir philosophieren, wie Wilde, wie primitive Menschen, die die Ausdrucksweise zivilisierter Menschen hören, sie mißdeuten und nun die seltsamsten Schluß || Schlüsse aus dieser || ihrer Deutung ziehen. Denke Dir, es verstünde Einer unsere || unsre Vergangenheitsform nicht: “er ist hier gewesen”. ‒ ‒ Er sagt: “‘er ist’, das ist die Gegenwart, also sagt jener || der Satz, daß die Vergangenheit in einem gewissen Sinne gegenwärtig ist”. |
“Aber
ich meine nicht,
daß, was ich jetzt (beim Erfassen)
tue, die künftige Verwendung kausal und
erfahrungsgemäß bestimmt, sondern
daß, in einer seltsamen
Weise diese Verwendung selbst in irgendeinem Sinne,
gegenwärtig ist.” – Aber ‘in
irgend einem Sinne’ ist sie es
ja! (Wir sagen ja auch: “die Ereignisse
der vergangenen Jahre sind mir
gegenwärtig”.) Eigentlich ist an dem, was
Du
– 233
– sagst, falsch nur der Ausdruck:
“in seltsamer Weise”. Das
Übrige ist richtig; und seltsam erscheint
der Satz nur, wenn man sich zu ihm ein anderes Sprachspiel
vorstellt, als das, worin wir ihn tatsächlich
verwenden. (Jemand sagte mir, er habe sich als Kind
darüber gewundert, wie denn der Schneider ein Kleid
nähe – er dachte, dies
heißt, es werde durch
bloßes Nähen ein Kleid erzeugt, indem
man etwa Faden an Faden legt und
aneinander näht.) |
Die unverstandene Verwendung des Wortes wird als Ausdruck eines
seltsamen Vorgangs gedeutet. (Wie man
sich die Zeit als seltsames Medium, die Seele als seltsames Wesen
denkt.) Die Schwierigkeit aber entsteht hier in allen Fällen durch die Vermischung || Verwechslung von “ist” und “heißt”. |
Die Verbindung, die keine kausale,
erfahrungsmäßige, sondern eine
viel strengere und härtere sein soll, ja, so fest,
daß das Eine irgendwie schon das Andere
ist, ist immer eine Verbindung in der
Grammatik. |
Woher
weiß ich, daß dies
Bild meine Vorstellung von der Sonne ist? – Ich nenne es Vorstellung
von der Sonne. Ich verwende es als Bild der
Sonne.
– 234 – |
“Es ist, als könnten wir die ganze Verwendung des
Wortes mit einem Schlag erfassen.” – Wir
sagen ja, daß wir es tun.
D.h., wir beschreiben ja, manchmal, was
geschieht || was wir tun, mit diesen
Worten. Aber es ist an dem, was geschieht, nichts
Erstaunliches, nichts Seltsames. Seltsam wird es, wenn
wir dazu geführt werden, zu denken, daß
die künftige Entwickelung auf irgendeine Weise schon im Akt
des Erfassens gegenwärtig sein
muß und doch nicht gegenwärtig ist. – Denn wir sagen, es bestehe || sei kein
Zweifel, daß wir das Wort .....
verstehen und anderseits liegt seine¤ Bedeutung in seiner
Verwendung. Es ist kein Zweifel,
daß ich jetzt Schach spielen
will; aber das Schachspiel ist dies Spiel durch alle seine
Regeln (u.s.f.).
Weiß ich also nicht, was ich spielen
wollte, ehe ich gespielt habe? Oder
aber, sind alle Regeln in meinem Akt der Intention
enthalten? Ist es nun Erfahrung, die mich lehrt,
daß auf diesen Akt der Intention für
gewöhnlich diese Art des Spielens folgt? Kann ich
also doch nicht sicher sein, was ich zu tun beabsichtigte?
Und wenn dies Unsinn ist, welcherlei über-starre
Verbindung besteht zwischen dem Akt der Absicht und dem
Beabsichtigten? ‒ ‒ Wo ist die Verbindung
gemacht zwischen dem Sinn der Worte “Spielen wir eine
Partie Schach!” und allen Regeln
des Spiels? – Im Regelverzeichnis des Spiels, im
Schachunterricht, in der täglichen Praxis des
Spielens. |
Aber ist
nicht gleich: gleich?
– 235 – Für die
Gleichheit scheinen wir ein unfehlbares Paradigma zu haben in der
Gleichheit eines Dinges mit sich selbst. Ich will
sagen: “Hier kann es doch nicht verschiedene
Deutungen geben. Wenn er etwas || ein
Ding vor sich sieht, so sieht er auch
Gleichheit.” Also sind zwei Dinge gleich, wenn sie so sind, wie ein Ding? Und wie soll ich nun das, was mir das eine Ding zeigt, auf den Fall der zwei anwenden? |
“Ein Ding
ist mit sich selbst
identisch.” – Es gibt kein schöneres
Beispiel eines nutzlosen Satzes, der aber dabei mit einem Spiel der
Vorstellung verbunden ist. Es ist, als legten wir
das Ding, in der Vorstellung, in seine eigene Form hinein und
sähen, daß es
paßt. || Es ist,
als legten wir in der Vorstellung die Gestalt des
Ding's in sich selbst hinein, und
sähen || sehen, daß sie
paßt. Wir könnten auch sagen: “Jedes Ding paßt in sich selbst.” – Oder anders: “Jedes Ding paßt in seine eigene Form hinein.” Man schaut dabei ein Ding an und stellt sich vor, daß der Raum dafür ausgespart war und es nun genau hineinpaßt. ‘Paßt’ dieser Fleck 236 man dies
aber, so könnte man leicht diesen Satz
aufstellen: ¤ || so könnte
man leicht dahinkommen, den Satz
aufzustellen: “Jeder
Farbfleck paßt genau in seine
Umgebung.” |
Wann sagen wir denn: der Vollzylinder
paßt in den
Hohlzylinder? Da gibt es viele verschiedene
Fälle; aber ein wichtiger ist der: wir
stecken sie zusammen, probieren, ob sie
passen. Passen sie dann, so sagen wir, sie passen;
d.h., auch dann, wenn sie wieder getrennt sind
– nämlich unter bestimmten Bedingungen.
Probieren wir nun wieder, und sie passen nicht, – wann, sollen wir sagen, haben sie zu passen aufgehört. Diese Frage wird manchmal so beantwortet: der Zeitpunkt der Änderung sei der einer anderen Änderung (als wir den Zylinder erhitzten, da hat er aufgehört, zu passen). Wenn wir aber kein solches Kriterium für diesen Zeitpunkt haben; wenn wir – sozusagen – garnicht wissen, was in dem Intervall zwischen den Proben mit den Dingen geschieht?: passen sie nun, oder passen sie nicht. |
Man sagt:
“Es ist schwer zu wissen, ob diese Medizin wirklich
hilft, oder nicht, weil man nicht weiß, ob
der Schnupfen länger gedauert hätte, oder ärger gewesen
wäre, wenn man sie nicht genommen
hätte.” Wenn man dafür wirklich
keinen Anhaltspunkt hat, ist es dann bloß
schwer zu wissen?
– 237
– Denke, ich hätte eine Medizin
erfunden; ich sage: diese Medizin, einige Monate hindurch
genommen, verlängert das Leben jedes Menschen um
einen Monat. Hätte er sie nicht genommen, so
wäre er einen Monat früher gestorben.
“Man kann nicht wissen, ob es wirklich
die Medizin war; ob er nicht ohne sie ebenso lang gelebt
hätte.” – Ist diese Ausdrucksweise nicht
irreführend? Sollte es nicht besser
heißen: “Es
heißt nichts, von dieser Medizin zu sagen,
sie verlängere das Leben; wenn eine Prüfung der
Behauptung || des Satzes in dieser Weise ausgeschlossen
wurde || ist.”
Nämlich: wir haben hier zwar einen richtigen
deutschen Satz nach Analogie oft gebrauchter Sätze gebildet,
aber Du bist Dir nicht klar über den
grundlegenden Unterschied in den Verwendungen
dieser Sätze. Diese zu überblicken, ist nicht
leicht. Der Satz liegt Dir vor Augen, aber nicht eine
übersichtliche Darstellung der Verwendung.
Mit “Es heißt nichts .....” will ich also sagen || will also gesagt werden: dies sind Worte, die Dich irreführen, sie spiegeln einen Gebrauch vor, den sie nicht haben. Sie rufen wohl auch eine Vorstellung hervor (der Verlängerung des Lebens, etc.), aber das Spiel mit dem Satz ist so eingerichtet, daß es die wesentliche Pointe nicht hat, die dem Spiel mit ähnlich gebauten Sätzen seinen Nutzen gibt. (Wie der ‘Wettlauf zwischen dem Hasen und dem Igel’ zwar aussieht wie ein Wettlauf, aber keiner ist.) |
Du mußt Dich
fragen: was nimmt man als
– 238
– Kriterium dafür,
daß eine Medizin geholfen hat?
Es gibt verschiedene Fälle. In welchen
Fällen sagt man: “Es ist schwer zu sagen,
ob sie geholfen hat”. In welchen Fällen
ist die Redeweise als sinnlos zu verwerfen: “Man
kann natürlich nie sicher sein, ob es die Medizin war, die
geholfen hat”. |
Wann nennen wir zwei Körper gleich schwer?
Wenn wir sie gewogen haben, oder nur während wir sie
wägen? Wenn Wägen das einzige Kriterium für das Gewicht wäre, – wann hat nun ein Körper sein Gewicht geändert, wenn er bei einer Wägung mehr wiegt, als bei der vorhergehenden? Der Sprachgebrauch könnte so sein: der Körper hat das und das Gewicht, bis er beim Wägen ein anderes zeigt; auf die Frage: “wann hat er sein Gewicht geändert?” gibt man den Zeitpunkt dieser Wägung an. – Oder: man sagt: “Man kann nicht wissen, wann er sein Gewicht ändert, wir wissen nur: bei der ersten Wägung hatte er dieses, bei der zweiten jenes Gewicht.” – Oder: “Es ist sinnlos, zu fragen, wann er sein Gewicht geändert hat; man kann nur fragen, wann sich die Gewichtsänderung gezeigt hat”. |
“Aber der Körper hatte
doch zu jeder Zeit irgend ein Gewicht, also war doch
die Antwort die richtige: wir
wüßten
nicht, wann er es
geändert habe.” – Und wie, wenn wir
sagten, ein Körper habe gar kein Gewicht,
außer dann,
– 239
– wenn es sich irgendwie zeigt, oder, er habe
kein bestimmtes Gewicht,
außer, wenn es gemessen wird?
Könnten wir nicht auch dieses Spiel spielen?
Denke, wir verkaufen ein Material ‘nach dem Gewicht’ und das Herkommen ist so: Wir wägen das Material alle fünf Minuten und berechnen dann den Preis nach dem Resultat der letzten Wägung. Oder ein anderes Herkommen: Wir berechnen den Preis auf diese Weise nur, wenn das Gewicht bei der Wägung nach dem Kauf das gleiche ist, hat es sich dann geändert, so berechnen wir den Preis nach dem arithmetischen Mittel der beiden Gewichte. Welche Art der Preisbestimmung ist die richtigere? – (Wenn sich der Preis einer Ware von gestern auf heute geändert hat, wann hat er sich geändert? Wie hoch stand er um zwölf Uhr Mitternacht, als niemand kaufte?) Resultat: Die Verbindung der Ausdrücke: “der Körper hat jetzt das Gewicht .....”, “der Körper wiegt jetzt ungefähr .....”, “ich weiß nicht, wieviel er jetzt wiegt”, – mit den Ergebnissen der Wägung || mit dem Ergebnis einer Wägung ist keine ganz einfache, hängt von diversen Umständen ab, wir können mit der Wägung, und also mit diesen Sätzen, uns leicht verschiedene Spiele gespielt denken. || wir können uns leicht verschiedene Rollen denken, die die Wägung in den Verrichtungen des Lebens spielen könnte und also verschiedene Rollen für die Ausdrücke, die das Wägspiel begleiten. Und das Gleiche gilt von der Rolle des – 240 Wortes
“passen” in unsern Sprachspielen.
|
Es ist sehr schwer,
Gedankenbahnen zu beschreiben, wo schon viel Fahrgeleise sind,
ob Deine eigenen, oder andere, und nicht in eins der ausgefahrenen
Gleise zu kommen. Es ist schwer: nur
wenig von einem alten Gedankengleise
abzuweichen. |
Was
geht da vor, wenn Einer versucht, eine Figur mit ihrem Spiegelbild
durch Verschieben in der Ebene zur Deckung zu bringen und
es ihm nicht gelingt? Er legt sie in verschiedener
Weise aufeinander, blickt auf die Teile, die sich nicht decken, ist
unbefriedigt, sagt etwa: “es
muß doch
gehen”, und legt die Figuren wieder anders
zusammen. Was geht vor, wenn Einer versucht ein Gewicht aufzuheben und es ihm nicht gelingt, weil das Gewicht zu schwer ist? Er nimmt die und die Stellung ein, faßt das Gewicht an und spannt die und die Muskeln an, dann läßt er es los und gibt etwa Zeichen der Unbefriedigung. Worin zeigt sich die geometrische, logische, Unmöglichkeit der ersten Aufgabe? “Nun er hätte doch an einem Bild oder in andrer Weise zeigen können, wie das aussieht, was er im zweiten Versuch anstrebt.” Aber er behauptet, das auch im ersten Fall zu können, indem er zwei gleiche, kongruente, Figuren mit einander zur – 241 –
Deckung bringt. – Was
sollen wir nun sagen? Daß diese
beiden Fälle eben verschieden sind? Aber
so || das sind ja auch Bild und Wirklichkeit im
zweiten Fall. |
In
der Philosophie kann man eine Frage durch hundert
andere beantworten. |
Erfahrung lehrt mich freilich, wie die Rechnung ausgeht;
aber damit erkenne ich sie noch nicht an. |
Die Erfahrung hat mich gelehrt,
daß das diesmal herausgekommen ist,
daß es für gewöhnlich
herauskommt; aber sagt das der Satz der Mathematik?
Die Erfahrung hat mich gelehrt, daß ich
diesen Weg gegangen bin. Aber ist das die
mathematische Aussage? – Was
sagt er aber? In welchem Verhältnis steht er zu
diesen Erfahrungssätzen? Der
mathematische Satz hat die Würde einer
Regel. Das ist wahr daran, daß Mathematik logisch || Logik ist: sie bewegt sich in den Regeln unsrer Sprache. Und das gibt ihr ihre besondere Festigkeit, ihre abgesonderte und unangreifbare Stellung. |
Aber wie
–, dreht sie sich in diesen Regeln hin und
her? – Sie schafft immer
neue und neue Regeln:
– 242 – baut immer neue
Verkehrsstraßen || Straßen des
Verkehrs; indem sie die alten
verlängert. |
Was ist Mathematik? – Nun, was in den
Mathematikbüchern steht. |
Aber bedarf sie denn dazu nicht einer
Sanktion? Kann sie das Netz denn beliebig
weiterführen? Nun, ich könnte ja
sagen: der Mathematiker erfindet immer neue
Darstellungsformen. Die einen, angeregt durch praktische
Bedürfnisse, andre aus ästhetischen
Bedürfnissen, und noch mancherlei anderen.
Und denke Dir hier einen Gartenarchitekt, der Wege für eine Gartenanlage entwirft; es kann wohl geschehen || sein, daß er sie bloß als ornamentale Bänder auf dem Reißbrett zieht und garnicht daran denkt, daß jemand je || einmal auf ihnen gehn wird. |
Erfahrung lehrt, daß beim
Auszählen, wenn wir die Finger einer Hand brauchen, oder
irgend eine Gruppe von Dingen, die so
– 243
– sieht, in der die beiden Mittelstriche
verschmolzen sind und dementsprechend den Mittelstrich zweimal
zählt. (Ja, das Gewöhnliche ist es
nicht. –) |
Wie aber ist es, wenn ich Einen erst
drauf || darauf aufmerksam mache,
daß das Ergebnis des Auszählens durch
den Anfang vorausbestimmt ist, und er es nun versteht und
sagt: “Ja freilich, – es
muß ja so
sein!” Was ist das für eine
Erkenntnis? – Er hat sich etwa das Schema
aufgezeichnet: Und sein Raisonnement wäre || ist etwa: “Es ist doch so, wenn ich auszähle. – Also muß .....” |
Denk Dir diese seltsame
Möglichkeit: Wir hätten uns bisher immer in
der Multiplikation 12
× 12 verrechnet. Ja, es ist
unbegreiflich, wie das geschehen konnte, aber es ist
geschehen. Also ist alles falsch, was man so
ausgerechnet hat! ‒ ‒ Aber was macht
das || es? Es macht ja
garnichts! – Dann
muß also etwas falsch sein in unsrer Idee von
Wahrheit und Falschheit der mathematischen || arithmetischen Sätze. |
Wir sagen: “es
paßt,
ich habe
es probiert”, nicht nur: “es hat
gepaßt, ich habe es
probiert”. Und ebenso:
“er wiegt 50
kg, ich habe ihn
gewogen”, “er ist
– 244 – 1
m lang, ich
habe ihn gemessen”, und auch: “ich kann es,
ich habe es probiert.” Wir sagen:
“der Schuh paßt”, auch
wenn wir ihn nicht anhaben. |
Was für einen Sinn hätte es, anzunehmen,
daß ein Stück Stahl, wann immer man
seine Festigkeit gerade nicht prüft, || gerade auf keine Weise
beansprucht, es seine Festigkeit verliert,
oder sie sich ändert. Das hängt mit der Idee
zusammen, daß die Körper um uns nur
solange existieren, als sie wahrgenommen werden. Das ist
wirklich: das Zifferblatt mit dem Zeiger kuppeln; denn
hier kuppelt man in der Grammatik die Aussage eines Tatbestandes
mit der Bedingung der Nichtkontrollierbarkeit. Man hat
die Annahme dadurch zu einem leerlaufenden Rad
der Sprache gemacht; und sie stört nun den
Mechanismus der Sprache jedenfalls nicht. |
Hat es einen Sinn, zu fragen:
“Hat dieses Stück Eisen nur dann diese
Festigkeit, oder Elastizität, wenn sie geprüft wird, oder
auch sonst?” Dies ist doch eine gut deutsche
Frage! Und, daß wir
empfinden: “das heißt ja
nichts!” – weist uns darauf hin, den
eigentlichen Gebrauch des Ausdrucks, “eine
Festigkeit haben” aufzusuchen, seinen Zusammenhang mit den
Erfahrungen, die uns die Festigkeit zeigen. (Von so
einer Frage sagen wir: ‘sie treibe das Problem auf
die Spitze’.)
– 245 – |
Vergleiche den ‘Zustand’, diese
Festigkeit zu haben, mit dem ‘Zustand’, diese
Farbe zu haben. Und wieder mit dem
‘Zustand’, diese Länge zu haben:
a) die gesehene, b) die gemessene. –
Und nun mit dem ‘Zustand’, einer bestimmten
Fähigkeit:
z.B.,
der Fähigkeit dieser Feder, diesen Druck auszuüben;
meiner Fähigkeit, dies Gewicht zu stemmen; meiner
Fähigkeit dies Gedicht aufzusagen; meiner Fähigkeit diese
Reihe fortzusetzen.
|
Unter welchen
Umständen sagt man: “x ist
in diesem Zustande”.
D.h., wie, unter welchen Umständen,
braucht man hier die Gegenwart des Verbums; unter welchen, die
andern Zeitformen? Es gibt Umstände, unter denen man sagt: “ich kann es”, während man es nicht gerade tut. – Andere, unter denen man in so einem Fall sagt: “ich glaube, ich kann es”. Es gibt auch Fälle, in welchen man nur dann sagt: “ich kann es”, wenn man es gerade tut. |
Was sind unsere Kriterien
dafür, ‘daß wir etwas
können’? Daß wir
es früher getan haben; daß wir
etwas anderes (etwa
‘Schwereres’) früher getan haben;
daß wir es jetzt tun;
daß wir jetzt gerade etwas getan haben, was
als Probe der Fähigkeit gilt. (Sich das Gedicht
leise vorsagen, als Probe dafür, daß
man es laut aufsagen kann.)
– 246 – |
Man kann sich leicht eine Sprache denken, in der es keine
Frage- und keine Befehlsform gibt,
sondern in der Frage und Befehl in der Form || Formen
der Behauptung ausgedrückt wird, in Formen
z.B.,
entsprechend unserem: “Ich möchte wissen,
ob .....” und “Ich wünsche,
daß
.....”.
Niemand würde doch von einer Frage (etwa, ob es draußen regnet) sagen, sie sei wahr oder falsch. Es ist freilich deutsch, dies von einem Satz, “ich wünsche zu wissen, ob .....”, zu sagen. Wenn nun aber diese Form immer statt der Frage verwendet wird || würde? – |
Die große
Mehrzahl der Sätze, die wir aussprechen, schreiben
und lesen, sind Behauptungssätze.
Und – sagst Du – diese Sätze sind wahr oder falsch. Oder, wie ich auch sagen könnte, mit ihnen wird das Spiel der Wahrheitsfunktionen |
– 247
– Denke, man sagte: Ein
Befehl besteht aus einem Vorschlag
(‘Annahme’) und dem Befehlen des
Vorgeschlagenen. |
Könnte man nicht Arithmetik treiben, ohne auf
den Gedanken zu kommen, arithmetische Sätze
auszusprechen, und ohne daß uns die
Ähnlichkeit einer Multiplikation mit
einem Satz je auffiele? Aber würden wir nicht den Kopf schütteln, wenn Einer uns eine falsch gerechnete Multiplikation zeigte, wie wir es tun, wenn er uns sagt, es regne, wenn es nicht regnet? – Doch; und hier liegt ein Punkt der Anknüpfung. Wir machen aber auch abwehrende Gesten, wenn ein Hund sich nicht benimmt, wie wir es wünschen. Wir sind gewohnt, zu sagen “2 mal 2 ist 4” und das Verbum “ist” macht dies zum Satz und stellt scheinbar eine nahe Verwandtschaft her mit allem, was wir ‘Satz’ nennen. Während || ; während es sich nur um eine sehr äußerliche || oberflächliche Beziehung handelt. |
Wo es bei Euklid
heißt: das und das sei zu
konstruieren und am Schluß
“q.e.c.”,
könnte man auch setzen: es sei zu
beweisen, daß das die
Konstruktion dieser Figur sei und am
Schluß schreiben
“q.e.d.”, also das
Resultat auf die Form des bewiesenen
Satzes bringen. 248 |
Gibt es wahre Sätze in
Russell's
System, die nicht in seinem System zu beweisen sind? – Was nennt man denn einen wahren Satz in
Russell's
System? |
Was heißt denn, ein Satz
‘ist wahr’?
p ist wahr
= p. (dies ist die
Antwort.) Man will also etwa fragen: unter welchen Umständen behauptet man einen Satz? oder: wie wird die Behauptung des Satzes im Sprachspiel gebraucht? Und die “Behauptung des Satzes” ist hier entgegengesetzt dem Aussprechen des Satzes etwa als Sprachübung, – oder als Teil eines andern Satzes, u. dergl.. Fragt man also in diesem Sinne: “Unter welchen Umständen behauptet man in Russell's Spiel einen Satz”, so ist die Antwort: Am Ende eines seiner Beweise, oder als ‘Grundgesetz’ (p.p.). Anders werden in diesem System Behauptungssätze in den Russell'schen Symbolen nicht verwendet. |
“Kann es aber nicht wahre Sätze
geben, die in diesem Symbolismus angeschrieben sind, aber in dem
System Russell's nicht beweisbar?” –
‘Wahre Sätze’, das sind also Sätze, die
in einem andern System wahr sind,
d.h. in einem andern Spiel mit Recht
behauptet werden können.
Gewiß; warum soll es keine solchen
Sätze geben; oder vielmehr: warum soll man nicht Sätze
– der Physik¤
z.B. – in
Russell's
Symbolen anschreiben? Die Frage ist ganz analog
der: Kann es wahre
– 249
– Sätze in
Euklids Sprache geben, die in seinem
System nicht beweisbar, aber wahr sind? – Aber es
gibt ja sogar Sätze, die in
Euklid's System
beweisbar, aber in einem andern System falsch
sind. Können nicht Dreiecke – in einem andern
System – ähnlich
(sehr ähnlich)
sein, die nicht gleiche || die gleichen Winkel
haben? – “Aber das ist doch ein
Witz! sie sind ja dann nicht im selben Sinne einander
‘ähnlich’!” –
Freilich; und ein Satz, der nicht in
Russell's
System zu beweisen ist, ist im andern Sinne
“wahr” oder “falsch”, als ein
Satz, der ‘Principia
Mathematica’. |
Ich stelle mir vor, es fragte mich Einer um Rat;
er sagt: “Ich habe einen Satz (ich will ihn
mit “P”
bezeichnen) in Russell's Symbolen konstruiert, und den kann man durch
gewisse Definitionen und Transformationen so deuten,
daß er sagt:
‘P
ist nicht in Russell's System beweisbar’. || auch in der Form aussprechen: ‘P ist (in
Russell's
System) nicht beweisbar’.
Muß ich nun von diesem Satz nicht
sagen: einerseits, er sei wahr,
andererseits || anderseits
er sei unbeweisbar? Denn angenommen, er wäre
falsch, so ist es also wahr, daß er
beweisbar ist! Und das kann doch nicht sein.
Und ist er bewiesen, so ist bewiesen, daß
er nicht beweisbar ist! So kann er also nur wahr, aber
unbeweisbar sein.” So wie wir fragen: “in welchem System ‘beweisbar’?”, so müssen wir auch fragen: “in welchem System ‘wahr’?”. ‘In Russell's System wahr’ heißt, wie gesagt: in Russell's – 250
– System bewiesen; und ‘in
Russell's
System falsch’ heißt: das
Gegenteil sei in Russell's System bewiesen. – Was
heißt nun Dein:
“angenommen, er sei falsch”? In
Russell's Sinne heißt
es: “angenommen das Gegenteil sei in
Russell's System bewiesen”; ist das Deine
Annahme, so wirst Du jetzt die Deutung, er sei unbeweisbar,
wohl aufgeben. Und unter dieser Deutung verstehe ich
die Übersetzung in diesem deutschen
Satz. – Nimmst Du an, der Satz sei in
Russell's
System beweisbar, so ist er damit in
Russell's Sinne wahr und die Deutung “P ist nicht
beweisbar” ist wieder aufzugeben. Nimmst Du an,
der Satz sei in Russell's Sinne wahr, so folgt das
Gleiche.
Ferner: soll der Satz in einem andern als
Russell's
Sinne falsch sein: so widerspricht dem nicht,
daß er in
Russell's
System bewiesen ist. (Was im Schach
“verlieren” heißt,
kann doch in einem andern Spiel das Gewinnen
ausmachen.) || , darin kann doch in einem
andern Spiel das Gewinnen bestehen. |
Was heißt
es denn: “P” und
“P ist
unbeweisbar” seien der gleiche Satz? Es
heißt, daß diese
zwei deutschen Sätze in der und der Notation
einen Ausdruck haben. |
“Aber
P kann doch nicht
beweisbar sein, denn, angenommen es wäre bewiesen, so
wäre der Satz bewiesen,
– 251
– er sei nicht beweisbar.”
Aber wenn dies nun bewiesen wäre, oder wenn ich glaubte
– vielleicht durch Irrtum – ich hätte es bewiesen,
warum sollte ich den Beweis nicht gelten lassen und sagen, ich
müsse meine Deutung “unbeweisbar”
zurückziehen? |
Nehmen wir an, ich beweise die
Unbeweisbarkeit (in
Russell's
System) von P; so habe ich mit
diesem Beweis P bewiesen.
Wenn nun dieser Beweis einer in
Russell's System wäre, – dann hätte ich also
zu gleicher Zeit seine
Zugehörigkeit und Unzugehörigkeit zum
Russell'schen System bewiesen. – Das kommt
davon, wenn man solche Sätze bildet. – Aber hier
ist || wäre ja ein Widerspruch! –
Nun so ist hier ein Widerspruch. Schadet er hier
etwas? |
Schadet
der Widerspruch, der entsteht wenn Einer sagt:
“Ich lüge. – Also lüge ich
nicht. – Also lüge ich.
Etc.” Ich meine: ist unsere
Sprache dadurch weniger brauchbar,
daß man in diesem Fall aus einem Satz nach
den gewöhnlichen Regeln sein Gegenteil und daraus wieder
ihn folgern kann? – der Satz selbst ist
unbrauchbar, und ebenso dieses Schlüsseziehen; aber
warum soll man es nicht tun? – Es ist eine brotlose
Kunst! – Es ist ein Sprachspiel, das
Ähnlichkeit mit dem Spiel des
Daumenfangens hat.
– 252 – |
Interesse
erhält so ein Widerspruch nur dadurch,
daß er Menschen gequält hat und dadurch
zeigt, wie aus der Sprache quälende Probleme wachsen
können; und was für Dinge uns quälen
können. |
Ein
Beweis der Unbeweisbarkeit ist quasi ein geometrischer Beweis; ein
Beweis, die Geometrie der Beweise betreffend. Ganz
analog einem Beweise etwa, daß die und die
Konstruktion nicht mit Zirkel und Lineal ausführbar
ist. Nun enthält so ein Beweis ein Element der
Vorhersage, ein physikalisches Element. Denn als Folge
dieses Beweises sagen wir ja einem Menschen:
“Bemüh' Dich nicht, eine
Konstruktion (der Dreiteilung des Winkels, etwa) zu
finden, – man kann beweisen, daß es
nicht geht.” Das
heißt: es ist wesentlich,
daß sich der Beweis der
Unbeweisbarkeit in dieser Weise soll anwenden
lassen. Er muß – könnte
man sagen – für uns ein triftiger Grund
sein, die Suche nach einem Beweis (also einer Konstruktion der
und der Art) aufzugeben. |
Ob etwas mit Recht der Satz genannt wird
“X ist unbeweisbar”,
hängt davon ab, wie wir diesen Satz beweisen. Nur
der Beweis zeigt, was als das Kriterium der Unbeweisbarkeit
gilt. Der Beweis ist ein Teil des Systems von
Operationen, des Spiels, worin der Satz gebraucht wird, und zeigt
uns seinen ‘Sinn’.
– 253 –
Der Satz “p ist unbeweisbar” hat einen andern Sinn, nach dem, – als ehe er bewiesen ist. Ist er bewiesen, so ist er die Schlußfigur des Unbeweisbarkeitsbeweises. – Ist er unbewiesen, so ist ja noch nicht klar, was als Kriterium seiner Wahrheit zu gelten hat, und sein Sinn ist – kann man sagen – noch verschleiert. |
Wie, soll ich nun annehmen, ist
P bewiesen?
Durch einen Unbeweisbarkeitsbeweis? oder auf eine
andere Weise? Nimm an, durch einen
Unbeweisbarkeitsbeweis. Nun, um zu sehen,
was bewiesen ist, schau auf den Beweis!
Vielleicht ist hier bewiesen, daß die und
die Form des Beweises nicht zu
P führt. – Oder, es sei P auf eine direkte
Art bewiesen – wie ich einmal sagen will –, dann
folgt also der Satz “P ist
unbeweisbar”, und es muß sich nun
zeigen, wie diese Deutung der Symbole von
P mit der Tatsache des
Beweises kollidiert und warum sie hier aufzugeben sei.
Angenommen aber, ~ P sei bewiesen. – Wie bewiesen? Etwa dadurch, daß P direkt bewiesen ist – denn daraus folgt, daß es beweisbar ist, also ~ P. Was soll ich nun aussagen: “P”, oder “~ P”? Warum nicht beides? Wenn mich jemand fragt: “Was ist der Fall – P, oder nicht-P?”, so antworte ich: “⊢ P” steht am Ende eines Russell'schen Beweises, Du schreibst also im Russell'schen System: “ ⊢ P”; anderseits ist es aber eben beweisbar und dies drückt man durch “ ⊢ ~ P” – 254 – aus, dieser
Satz aber steht nicht am Ende eines
Russell'schen Beweises, gehört also nicht zum
Russell'schen System. – Als die Deutung
“P ist
unbeweisbar” für P gegeben
wurde, da kannte man ja diesen || den Beweis
für P nicht und man
kann || muß also nicht
sagen: “P”
sage: dieser Beweis existierte nicht. – Ist der Beweis
hergestellt || konstruiert, so ist damit eine neue
Lage geschaffen: Und wir haben nun zu
entscheiden, ob wir dies einen Beweis
(noch einen Beweis), oder ob wir
dies noch die Aussage der Unbeweisbarkeit nennen
wollen. Angenommen ~ P sei direkt bewiesen; es ist also bewiesen, daß sich P direkt beweisen läßt! Das ist also wieder eine Frage der Deutung – es sei denn, daß wir nun auch einen direkten Beweis von P haben. Wäre es nun so, nun, so wäre es so. – (Die abergläubische Angst und Verehrung der Mathematiker vor dem Widerspruch.) |
“Aber angenommen, der Satz wäre
nun falsch – und daher beweisbar!
–” Warum nennst Du ihn
‘falsch’? Weil Du einen Beweis
siehst? – Oder aus andern Gründen?
Dann macht es ja nichts. Man kann ja den Satz des
Widerspruchs sehr wohl falsch nennen, mit der Begründung
z.B., daß wir sehr oft
mit gutem Sinn auf eine Frage antworten: “Ja,
und nein.” Und ebenso || desgleichen
den Satz “p ≡
~~p”: weil wir
die Verdoppelung der Verneinung als eine
Verstärkung der Verneinung
verwenden und nicht bloß als ihre
Aufhebung. |
– 255
– Du sagst: “.....” also ist P wahr und unbeweisbar.” Das heißt wohl: “Also ⊢ P.” Von mir aus – aber zu welchem Zweck schreibst Du diese ‘Behauptung’ hin? (Das ist, als hätte jemand aus gewissen Prinzipien über Naturformen und Baustil abgeleitet, auf den Mount Everest, wo niemand wohnen kann, gehöre ein Schlößchen im Barockstile.) Und wie könntest Du mir die Wahrheit der Behauptung plausibel machen, da Du sie ja zu nichts weiter brauchen kannst als zu jenen Kunststückchen? |
Man muß sich hier daran erinnern,
daß die Sätze der Logik so
konstruiert sind, daß sie als
Information keine Anwendung in der Praxis
haben. Man könnte also sehr wohl sagen, sie seien
garnicht Sätze; und
daß man sie überhaupt hinschreibt,
bedarf einer Rechtfertigung. Fügt man diesen
‘Sätzen’ nun ein weiteres
satzartiges Gebilde andrer Art hinzu, so
sind wir hier schon erst recht im Dunkeln darüber, was dieses
System von Zeichenkombinationen nun für eine
Anwendung, für einen Sinn haben soll, denn der
bloße Satzklang dieser
Zeichenverbindungen gibt ihnen ja eine Bedeutung noch
nicht.
256 |
Könnte ich nicht sagen, zwei Wörter
– schreiben wir sie “non” und
“ne” – hätten dieselbe
Bedeutung, sie seien beide Verneinungszeichen –
aber non non p =
p
und
ne ne p =
ne p. – In den
Wortsprachen bedeutet eine doppelte Verneinung sehr oft eine
Verneinung. – Warum nenne ich dann aber beide
“Verneinungen”? Was haben sie
miteinander gemein? Nun, es ist klar,
daß ein großer Teil
ihres Gebrauchs beiden gemeinsam ist. Das
löst
aber unser Problem noch nicht. Denn wir möchten doch
sagen: Auch, daß die doppelte
Verneinung eine Bejahung ist, muß für
beide stimmen, wenn wir nur die Verdoppelung entsprechend
auffassen. Aber wie? – Nun so, wie es
z.B. durch Klammern
ausgedrückt werden kann.
(ne ne) p =
ne p, ne (ne
p) = p Wir denken gleich an einen analogen Fall der Geometrie: “Zwei halbe Drehungen addiert heben einander auf”, “Zwei halbe Drehungen addiert sind eine halbe Drehung”. Es kommt eben darauf an, wie wir sie addieren. (Ich könnte es ebenso wohl “sie addieren” nennen, einen Gegenstand zweimal zu drehen, wie das Schema eins || I zeigt; oder auch, ihn einmal um 180˚ zu drehen und dann, gleichsam, um diese Drehung zu bekräftigen, ihn in die erste Stellung zurück, und noch einmal im ersten Sinn zu drehen (II). 257 |
Hier
stoßen wir auf eine merkwürdige und
charakteristische Erscheinung in philosophischen
Untersuchungen: Die Schwierigkeit – könnte
ich sagen – ist nicht, die Lösung zu finden, sondern,
etwas als die Lösung anzuerkennen, was aussieht, als
wäre es erst eine Vorstufe zu ihr. “Wir haben
schon alles gesagt. – Nicht etwas, was daraus
folgt, sondern eben das ist die
Lösung!” Das hängt, glaube ich, damit zusammen, daß wir fälschlich eine Erklärung erwarten; während eine Beschreibung die Lösung der Schwierigkeit ist, wenn wir sie richtig in unsere Betrachtung einordnen. Wenn wir bei ihr verweilen und nicht versuchen, über sie hinauszukommen. Die Schwierigkeit ist hier: Halt zu machen. |
“Das ist bereits alles, was sich darüber sagen
läßt.” –
“non non
p” als Verneinung des verneinten Satzes
auffassen, das ist etwa: eine
Erklärung der Art
“non
non p = non (non
p)” zu geben.
“Wenn ‘ne’ eine Verneinung ist, so muß ‘ne ne p’, wenn es nur richtig aufgefaßt wird gleich p sein.” “Wenn man ‘ne ne p’ als Negation von p nimmt, muß man die Verdoppelung anders auffassen.” Man möchte sagen, “‘Verdoppelung’ heißt dann etwas anderes, darum ergibt sie jetzt eine Verneinung”, also: daß sie jetzt eine Verneinung ergibt ist die Folge ihres anderen Wesens || ihrer anderen Bedeutung. “Ich meine sie jetzt als Verstärkung”, würde man sagen. Wir setzen statt der Meinung den 258 Ausdruck der Meinung.
|
Worin mag das gelegen haben,
daß, als ich die doppelte Verneinung
sagte, ich sie als Verstärkung meinte? In den
Umständen, unter denen ich den Ausdruck gebrauche, im Bild,
das mir etwa dabei vorschwebt, im Ton meiner Rede (so wie ich
auch im Ton die Klammern in “ne (ne
p)” wiedergeben kann). Die
Verdoppelung als Verstärkung meinen, ist dann von der Art,
es als Verstärkung aussprechen. Die
Verdoppelung als Aufhebung meinen,
heißt
z.B. Klammern
setzen (auch im gesprochenen Ausdruck). –
“Ja, aber diese Klammern selbst können doch
verschiedene Rollen spielen;
denn wer sagt, daß sie in
‘non (non p)’
im gewöhnlichen Sinn als Klammern aufzufassen seien und
nicht irgendwie anders; etwa die erste als Trennungsstrich
zwischen den beiden
‘non’, die zweite als
Schlußpunkt des Satzes?”
– Niemand sagt es. Und Du hast ja Deine
Auffassung wieder durch Worte ersetzt. Was die Klammern
bedeuten, wird sich in ihrem Gebrauch zeigen und, in
anderm Sinn, liegt es etwa im Aspekt (gesehenen Rhythmus) des
Gesichtseindrucks von ‘non (non-p)’. |
Soll ich nun sagen: die
Bedeutung
von “non” und
“ne” sei || Bedeutungen von
“non” und “ne”
seien etwas verschieden? Sie seien
verschiedene Abarten der Verneinung? – Das
würde niemand sagen. Denn, würde man
einwenden, heißt dann “geh nicht
in dieses Zimmer!” vielleicht nicht
genau dasselbe, wenn wir die Regel aufstellen “nicht
nicht” solle als
259 Verneinung gebraucht werden und nicht
als Bejahung? – Dagegen aber möchte man
einwenden: “Wenn die beiden Sätze
‘ne p’ und
‘non p’ ganz
dasselbe sagen, wie kann dann ‘ne ne’
nicht dasselbe bedeuten wie
‘non
non’?” Aber hier
setzen wir eben einen Symbolismus voraus,
d.h., nehmen ihn zum Vorbild, in welchem aus
‘ne p = non
p’ folgt, daß die beiden
Wörter in allen Fällen
gleich verwendet
werden. Die Drehung um 180˚ und die Verneinung sind im besonderen Fall tatsächlich dasselbe, und die Anwendung des Satzes ‘non non p = p’ von der Art der Anwendung einer Geometrie. |
Denken
wir, ich fragte: Zeigt es sich uns klar, wenn wir die
Sätze aussprechen “dieser Stab ist 1
m
lang” und “hier steht 1 Soldat”,
daß wir mit ‘1’
verschiedenes meinen, daß
‘1’ verschiedene Bedeutungen hat? –
Es zeigt sich uns garnicht. Besonders, wenn wir einen Satz sagen
wie: “auf je 1
m steht 1 Soldat, auf
2
m 2 Soldaten
u.s.w.”. Gefragt,
“meinst Du dasselbe mit den beiden
Einsern”, würde man etwa
antworten: “freilich meine ich dasselbe:
– eins!” (wobei man etwa
einen Finger in die Höhe hebt). |
Was meint man damit:
‘ne ne
p’, auch wenn es nach dem
Übereinkommen
‘ne p’
bedeutet, könnte auch als aufgehobene Verneinung
gebraucht werden? – Man möchte sagen:
“‘ne’, mit der
Bedeutung, die wir ihm gegeben haben, könnte sich
260 selbst aufheben, wenn wir es nur
richtig applizieren”. Was meint man
damit? (Die beiden halben Drehungen in der gleichen
Richtung könnten einander aufheben, wenn sie entsprechend
zusammengesetzt würden.) “Die
Bewegung der Verneinung
‘ne’ kann
sich selbst aufheben || ist imstande, sich selbst
aufzuheben”. Aber wo ist diese
Bewegung? Man möchte natürlich von einer
geistigen Bewegung der Verneinung reden, zu deren Ausführung
das Zeichen ‘ne’ nur das
Signal gibt. |
Wir
können uns leicht Menschen mit einer
‘primitiveren’ Logik denken, in der es etwas
unserer Verneinung Entsprechendes nur für
gewisse Sätze gibt; für solche etwa, die keine
Verneinung enthalten. In der Sprache dieser
Menschen könnte man dann einen Satz wie “Er
geht in dieses Haus” verneinen; sie würden aber eine
Verdoppelung der Verneinung immer nur als Wiederholung der
Verneinung, nie als ihre Aufhebung, verstehen. |
Die Frage, ob für diese
Menschen die Verneinung dieselbe
Deutung || Bedeutung
hat, wie für uns, wäre dann analog der, ob die Ziffer
‘2’ für Menschen, deren Zahlenreihe mit 5
endigt dasselbe bedeutet wie
für uns. |
Wer
“~~p =
p” (oder auch
“~~p ≡
p”) einen “notwendigen
Satz der Logik” nennt (nicht, eine Bestimmung
über die von uns angenommene Darstellungsart) der
hat auch die Tendenz zu sagen,
261 dieser Satz gehe aus der Bedeutung
der Verneinung hervor. Wenn in einer
dialektischen Redeweise die doppelte Verneinung als
Verneinung gebraucht wird, wie in “er hat nirgends
nichts gefunden”, so sind wir geneigt zu sagen:
eigentlich heiße das, er
habe überall etwas gefunden.
Überlegen wir, was dieses
“eigentlich”
heißt! – |
Unser Problem könnte man sehr klar so
stellen: Angenommen, wir hätten zwei Systeme der
Längenmessung; eine Länge wird in beiden durch ein
Zahlzeichen ausgedrückt, diesem folgt ein Wort, welches das
Maßsystem angibt. Das eine System
bezeichnet eine Länge als “n
Fuß” und
Fuß ist eine Längeneinheit im
gewöhnlichen Sinne; im andern System wird eine Länge
mit “n W” bezeichnet und
1
Fuß = 1
W. Aber
2 W = 4
Fuß,
3 W = 9
Fuß,
usw. –
Also heißt der Satz “dieser
Stock ist 1 W lang” dasselbe wie, “dieser
Stock ist 1 Fuß lang”.
Frage: Hat in diesen beiden
Sätzen “W” und
“Fuß” dieselbe
Bedeutung? |
Die Frage ist falsch
gestellt. Das sieht man, wenn wir Bedeutungsgleichheit
durch eine Gleichung ausdrücken. Die Frage kann
dann nur lauten: “ist
W =
Fuß, oder nicht?”
– Die Sätze, in denen diese Zeichen
stehen, verschwinden in dieser Betrachtung. – Ebenso wenig kann
man natürlich in dieser Terminologie
262 fragen, ob “ist”
das gleiche bedeutet wie “ist”; wohl aber, ob
“ε” das gleiche bedeutet wie
“ = ”. Nun, wir sagten ja:
1
Fuß = 1 W, aber
Fuß ≠ W. |
Hat nun
“ne” dieselbe Bedeutung wie
“non”? – Kann ich
“ne” statt
“non” setzen? –
“Nun, an gewissen Stellen wohl, an andern
nicht.”¤ – Aber danach fragte ich
nicht. Meine Frage war: kann man, ohne
weitere Qualifikation “ne” statt
“non” gebrauchen? –
Nein. |
“‘ne’ und
‘non’ heißen in
diesem Fall genau dasselbe.” –
Und zwar, was? – “Nun, man solle das und
das nicht tun.” – Aber damit
hast Du nur gesagt, daß in diesem Fall
ne p = non
p ist und das leugnen wir nicht.
Wenn Du erklärst ne ne p = ne p, non non p = p, so gebrauchst Du die beiden Wörter eben in verschiedener Weise; und hält man dann an der Auffassung fest, daß, was sie in gewissen Kombinationen ergeben, von ihrer Bedeutung ‘abhängt’, der Bedeutung, die sie mit sich herumtragen, dann muß man also sagen, sie müssen verschiedene Bedeutungen haben, wenn sie, auf gleiche Weise zusammengesetzt, verschiedene Resultate ergeben können. |
Man
möchte etwa von der Funktion des Wortes in diesem Satz
reden. Aber worin besteht diese Funktion?
Wie
263 tritt sie zutage? Denn
es ist ja nichts verborgen! wir sehen ja den ganzen
Satz. Die Funktion muß sich im
Laufe des Kalküls zeigen. Man will aber sagen: “‘non’ tut dasselbe mit ‘p’, was ‘ne’ tut: es kehrt ihn um”. Aber das sind nur andere Worte für: “non p = ne p” (was nur gilt, wenn “p” nicht selbst ein verneinter Satz ist). Immer wieder der Gedanke, daß, was wir vom Zeichen sehen, nur eine Außenseite zu einem Innern ist, worin sich die eigentlichen Prozesse des Sinnes und der Bedeutung abspielen || die eigentlichen Operationen der Meinung abspielen. |
Ist es nun nicht merkwürdig,
daß ich sage, das Wort
“ist” werde in zwei verschiedenen Bedeutungen
(als ‘ε’ und
‘ = ’) gebraucht, und nicht sagen möchte,
seine Bedeutung sei sein Gebrauch als
‘ε’ und
‘ = ’? || seine Bedeutung sei
sein Gebrauch als Kopula und
Gleichheitszeichen? Man möchte sagen, diese beiden Arten des Gebrauchs geben nicht eine Bedeutung; die Personalunion durch das gleiche Wort sei ein unwesentlicher Zufall. |
Aber wie kann ich entscheiden, welches ein
wesentlicher und welches ein unwesentlicher, zufälliger
Zug der Notation ist? Liegt denn eine
Realität hinter der Notation, nach der sich ihre Grammatik
richtet? Denken wir an einen ähnlichen Fall im Spiel: 264 Im Damespiel wird eine Dame
dadurch gekennzeichnet, daß man zwei
Spielsteine aufeinanderlegt. Wird man nun nicht
sagen, es sei für das Spiel unwesentlich,
daß eine Dame aus zwei Steinen
besteht? |
Sagen
wir: die Bedeutung eines Steines (einer
Figur) ist ihre Rolle im Spiel. – Nun werde vor
Beginn jeder Schachpartie durch das Los entschieden, welcher der
Spieler Weiß erhält. Dazu
halte der eine Spieler in jeder geschlossenen Hand einen
Schachkönig und der andere wähle auf gut Glück
eine der beiden Hände. Wird man es
nun zur Rolle des Königs im Schachspiel rechnen,
daß er so beim Auslosen verwendet
wird? |
Ich bin
geneigt || also geneigt auch im
Spiel zwischen wesentlichen und unwesentlichen Regeln zu
unterscheiden. Das Spiel, möchte ich sagen, hat
nicht nur Regeln, sondern auch einen Witz. |
Wozu das gleiche Wort?
Wir machen ja im Kalkül keinen Gebrauch von dieser
Gleichheit! Wozu für Beides die gleichen
Steine? – Aber was heißt es
hier “von der Gleichheit Gebrauch
machen”? Ist es denn nicht ein Gebrauch, wenn
wir eben das gleiche Wort gebrauchen? |
Hier scheint es nun, als
hätte der Gebrauch des gleichen Worts,
des gleichen Steines, einen Zweck – wenn die
Gleichheit nicht zufällig, unwesentlich, ist. Und als
sei der
265 Zweck, daß
man den Stein wiedererkennen, und wissen könne, wie man zu
spielen hat. Ist da von einer physikalischen oder einer
logischen Möglichkeit die Rede? Wenn das
Letztere, so gehört eben die Gleichheit der Steine zum || ins Spiel. |
Das Spiel soll doch durch die Regeln bestimmt sein!
Wenn also eine Spielregel vorschreibt, daß
zum Auslosen vor der Schachpartie die Könige
zu nehmen sind, so gehört das, wesentlich,
zum Spiel. Was könnte man dagegen
einwenden? Daß man den Witz
dieser Vorschrift || Regel nicht einsähe.
Etwa, wie man auch den Witz einer Vorschrift nicht
einsähe, jeden Stein dreimal umzudrehen, ehe
man mit ihm zieht. Fänden wir diese Regel in einem
Brettspiel, so würden wir uns wundern und Vermutungen
über den Zweck zu einer Regel anstellen.
(“Sollte diese Vorschrift verhindern,
daß man ohne Überlegung
zieht?”) |
“Wenn ich den Charakter des Spiels richtig
verstehe”, könnte ich sagen, “so gehört
das nicht wesentlich dazu”. |
Denken wir uns aber die beiden
Ämter in einer Person vereinigt als ein
altes Herkommen. |
Man sagt: der Gebrauch des gleichen Wortes ist
hier unwesentlich, weil die Gleichheit keine
Übergänge
überbrückt. || weil die Gleichheit der
Wortgestalt hier nicht dazu dient, einen
Übergang zu
vermitteln. Aber damit beschreibt man nur
den Charakter des
266 Spiels, welches man spielen
will. 267 |
Aufgabe: Soll ich es Erfahrungstatsache
nennen, daß dieses Gesicht durch diese
Veränderung zu jenem wird? |
Ist die Eigenschaft, die ich
‘entfalte’ eine externe oder interne?
|
Man
‘entfaltet’, was schon in der Sache liegt.
|
Die Eigenschaften der
Hundert entfalten heißt, durch
Entfalten von 100 Gegenständen Merkmale des Begriffs 100 vor
Augen führen. |
Man entfaltet eine Reihe (Formation)
– – nicht physikalische
Eigenschaften der || einer Reihe. Und man
sagt, man entfalte interne Eigenschaften der
Reihe || Formation (das sind Merkmale, die den
Begriff dieser Reihe || Formation kennzeichnen), wenn
man vorführt, was alles Umformung
dieser Formation durch Entfalten der
Formation genannt wird. |
Habe ich gezeigt, daß
da ein Fünfeck steht, und war es nur
überflüssig? Wenn das Ziehen der Diagonalen hier ein Experiment war, war das ‘Ergebnis’ dasselbe, wie im vorigen Fall? |
Man
sagt: diese Einteilung macht klar, was
268 da für eine Reihe von
Kugeln steht. Macht sie klar, was für eine Reihe
vor der Einteilung da stand, oder macht sie klar, was
für eine Reihe jetzt da steht? |
‘Ich sehe auf den ersten Blick,
wieviele es sind.’ Nun wieviele sind
es? So viele? – Nein, das
ist nicht die Antwort. Es
sind ‘50’, oder
‘100’,
etc. |
“Die Einteilung macht mir klar, was
da für eine Reihe steht”. Nun, was
für eine steht da?
“Diese.” – Es
muß natürlich
heißen: “Eine von 100
Kugeln”, “Eine, die durch
drei || 3 teilbar ist”, oder
dergleichen. |
Habe
ich gezeigt, daß da ein Fünfeck
steht, und war es nur überflüssig?
Wenn das Ziehen der Diagonalen hier ein Experiment war, war das ‘Ergebnis’ dasselbe wie im vorigen Fall? Oder: berechtigt mich das Ziehen der Diagonalen nun, zu sagen: “da steht ein Fünfeck”? – Aber kann es mich nicht dazu berechtigen, obwohl ich dieser Berechtigung garnicht bedarf? – |
Auf dieser Stütze liegt im Sprachspiel
kein Gewicht; daher trägt sie
auch nicht. |
Ich entfalte doch die geometrischen
Eigenschaften
269 dieser Kette auch, indem ich die
Umformungen einer andern, gleich gebauten Kette
vorführe. Aber dadurch zeige ich doch
nicht, was ich tatsächlich mit der ersten tun kann,
wenn diese sich nämlich tatsächlich als unbiegbar, oder
sonstwie physikalisch ungeeignet erweist.
Also kann ich doch nicht sagen: ich entfalte die Eigenschaften dieser Kette. |
Wie kann man denn Eigenschaften der Kette
entfalten, die sie garnicht
hat || besitzt. |
‘Wir entfalten die Eigenheiten des
hier gezogenen Vielecks.’ Nehmen wir an, das
Vieleck wäre aus Draht gewoben, statt gezeichnet; wären
wir noch geneigt, zu sagen: wir entfalten die
Eigenschaften des gebogenen Drahtes? Wir entfalten sie, soll hier doch heißen, wir führen sie vor Augen, machen sie deutlich, was früher nicht zu sehen || deutlich war. |
Ich messe einen Tisch, und er ist
1
m lang. – Nun lege ich meinen Meterstab
an einen andern Meterstab. Messe ich ihn
dadurch? Finde ich, daß jener
zweite Meterstab 1
m lang ist? Mache ich das
gleiche Experiment der Messung, nur mit dem Unterschied,
daß ich des Ausgangs sicher bin?
|
Ja, wenn ich den
Maßstab an den Tisch anlege, messe
270 ich immer den Tisch;
kontrolliere ich nicht manchmal den
Maßstab? Und worin liegt der
Unterschied zwischen dem einen Vorgehen und dem andern?
|
Ich entfalte die
Eigenschaften dieses Vielecks, heißt hier,
ich zeige
z.B., daß es
15 Ecken hat. Ähnlich,
als sagte ich: ich entfalte die Länge und Breite dieses
Papiers, indem ich das Papier
auseinanderfalte. |
Das Entfalten ist hier eine Art
Zählen. |
Das
Experiment des Entfaltens einer Reihe kann uns, unter
anderem, zeigen, aus wievielen Kugeln die
Reihe besteht, oder aber, daß wir diese
(sagen wir) 100 Kugeln so und so bewegen können.
Die Rechnung aber des Entfaltens zeigt uns, was wir eine ‘Umformung durch bloßes Entfalten’ nennen. |
“Ich entfalte die Eigenschaften dieser Kette, ich
zeige, was man alles aus ihr machen kann.” –
Was man alles durch bloßes
Biegen in
ihren || den Gelenken aus ihr machen kann.
Nun, ich könnte sagen || ich möchte
vielleicht sagen, ich zeige nicht nur
physikalische, sondern auch geometrische Eigenschaften der
Kette. Könnte man sagen: Die Glieder dieser Kette sind zwar so zusammengeschweißt, daß man sie nicht in diese Stellung bringen kann, aber es ist doch eine geometrische Eigenschaft dieser 271 Kette,
daß man sie in diese Stellung bringen
kann. |
“Ich zeige Dir, was man alles aus dieser Kette machen
kann.” Dabei nehme ich als selbstverständlich
an, daß die Glieder sich bewegen lassen,
nicht brechen, sich nicht vermehren,
etc. –
Zeige ich Dir nun nicht eine Eigenschaft der Kette?
Aber welche von den vielen Eigenschaften der Kette
zeige ich? Ist es denn noch eine Kette, wenn sie – aus irgend einem Grunde – steif ist wie ein Stock? |
Editorial notes
1) Ts-221a contains a great number of handwritten additions and corrections which are not in Wittgenstein's hand. Partly they fill in graphics and notation, partly they copy over (Wittgenstein's) corrections from Ts-222, partly they contain instructions (see for example pages 184 and 195). They stem probably from Rush Rhees, possibly made in the context of the trustees' work on editing RFM, Part I, and are here included throughout this transcription.
2) See facsimile; arrow pointing left, probably indicating that the indentation shall be canceled.
3) Three pages are paginated 158; they are here called 158, 158a and 158b. 158a repeats the text of 158 (but is not simply a copy of it) while 158b continues from 158 / 158a with new text.
4) See facsimile; line connecting this part of the sentence with the following one, indicating that the space left for the graphic shall be removed.
5) See facsimile; line connecting this sentence with the following one.