​

Im Falle meines Todes vor der Fertigstellung oder Veröffentlichung dieses Buches sollen meine Aufzeichnungen fragmentarisch veröffentlicht werden unter dem Titel: “Philosophische Bemerkungen” und mit der Widmung: “Francis Skinner zugeeignet” Er ist, wenn diese Bemerkung nach meinem Tode gelesen wird, von meiner Absicht in Kenntnis zu setzen, an die Adresse: Trinity College Cambridge.

​

X. Philosophische Grammatik.

​

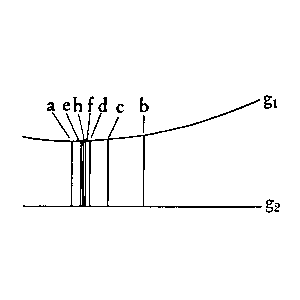
27.5.32. Ich1 kann die Regel R a + (1 + 1) a + (ξ + 1) a + ((ξ + 1) + 1) = (a + 1) + 1 (a + ξ) + 1 ((a + ξ) + 1) + 1 (Ƒ) auch so schreiben: a + (1 + 1) a + (ξ + 1) a + ((ξ + 1) + 1) = (a + 1) + 1        (a + ξ) + 1 ‒ ‒ ‒ S (a + (ξ + 1)) + 1 (Ƒ) oder auch so: a + (b + 1) = (a + b) + 1⌊,⌋ wenn ich R oder S als Erklärung oder Ersatz für diese Form nehme.   Wenn ich nun sage, in α β γ                         a + (b + 1) a + (b + (c + 1)) (a + b) + (c + 1) = = = (a + b) + 1 a + ((b + c) + 1) = (a + (b + c)) + 1 ‒ ‒ ‒ B ((a + b) + c) + 1 (Ƒ)  seien die Übergänge durch die Regel R gerechtfertigt, – so kann man mir drauf antworten: „[w|W]enn Du das eine Rechtfertigung nennst, so hast Du die Übergänge gerechtfertigt. Du hättest uns aber ebensoviel gesagt, wenn Du uns nur auf die Regel R & ihre formale Beziehung zu ˇα (ˇoder zu α, β & γ) aufmerksam gemacht hättest.”     Ich hätte also auch sagen können: Ich nehme die Regel R in der & der Weise als Paradigma meiner Übergänge.     Wenn nun Skolem etwa nach seinem Beweis für das associative Gesetz übergeht zu: a + 1 a + (b + 1) (b + 1) + a = = = 1 + a (a + b) + 1) ‒ ‒ ‒ C (b + (1 + a) = b + (a + 1) = (b + a) + 1 (Ƒ) & sagt der erste & dritte Übergang in der dritten Zeile seien nach dem bewiesenen associativen Gesetz gerechtfertigt, – so erfahren wir damit nicht mehr, als … sagt er uns damit nicht mehr als wenn er sagte, die Übergänge seien nach dem Paradigma a + (b + c) = (a + (b) + c) gemacht (ˇd.h. sie entsprechen dem Paradigma) & es außerdem sei ein Schema α, β, γ ab mit Übergängen nach dem Paradigma α abgeleitet. – „Aber rechtfertigt B nun diese Übergänge oder nicht?” – „Was meinst Du mit dem Wort „rechtfertigen”?” – „Nun, der Übergang ist gerechtfertigt, wenn wirklich ein Satz, der für alle Zahlen gilt, bewiesen ist.” – „Aber in welchem Falle wäre das geschehen? Was nennst Du einen Beweis davon, daß ein Satz für alle KardinalZahlen gültig ist? Wie weißt Du ob der Satz ⌊(⌋wirklich⌊)⌋ für alle Kardinalzahlen giltig ist, da Du es nicht ausprobieren kannst. Dein einziges Kriterium ist ja der Beweis. Du bestimmst also wohl eine die Form & nennst sie die, des Beweises, daß ein Satz für alle Kardinalzahlen gilt. Dann haben wir eigentlich gar nichts davon, daß uns ˇzuerst die allgemeine Form dieser Beweise zuerst gezeigt wird; da ja dadurch nicht gezeigt wird, daß nun der besondere Beweis wirklich das leistet, was wir von ihm verlangen; ich meine: da hiedurch der besondere Beweis nicht als einer gerechtfertigt, erwiesen, ist, der einen Satz für alle Kardinalzahlen beweist. ˇ Der recursive Beweis muß vielmehr seine eigene Rechtfertigung sein. Wenn wir unsern Beweisvorgang wirklich als den Beweis einer solchen Allgemeinheit rechtfertigen wollen tun wir vielmehr etwas anderes, ⌊:⌋ wir gehen Beispiele einer Reihe durch & diese Beispiele & das Gesetz was wir in ihnen erkennen befriedigt uns nun & wir sagen: ja, unser Beweis leistet wirklich was wir wollten. Aber wir müssen nun bedenken, daß wir mit der Angabe dieser Beispielreihe die Schreibweise B & C nur in eine andere ⌊(⌋Schreibweise⌊)⌋ übersetzt haben. (Denn die Beispielreihe ist nicht die Anwendung unvollständige Anwendung der allgemeinen Form, sondern ein anderer Ausdruck dieser Form [ des Gesetzes ] .) Und weil die Wortsprache wenn sie den Beweis erklärt, erklärt was er beweist, nur den Beweis nur in eine andere Ausdrucksform übersetzt, so können wir diese Erklärung auch ganz weglassen. Und wenn wir das tun so werden die mathematischen Verhältnisse viel ◇ klarer, nicht verwischt durch die mehrdeutigen i [ vieles bedeutenden ] Ausdrücke der Wortsprache. Wenn ich z.B. B unmittelbar neben A setze, ohne [d|D]azwischenkunft des Wortes „alle” [ ohne Vermittlung durch d[as|en] Ausdruck der Wortsprache „für alle Zahlen ˇKardinalzahlen ⌊ etc.⌋” ] , so kann kein falscher Schein eines Beweises von A durch B entstehen. Wir sehen dann ganz nüchtern wie weit die Beziehungen von B zu A ˇ& zu a + b = b + a reichen & wo sie aufhören. [ Wir sehen dann die nüchternen, ⌊(⌋nackten⌊)⌋ Beziehungen zwischen A & B, & wie weit sie re⌊i⌋chen. ] Man lernt so erst, unbeirrt von der alles gleichmachenden Form Gewalt der Wortsprache die St eigentliche Struktur dieser Beziehung kennen & was es mit ihr auf sich hat.   Man sieht hier vor allem, daß wir an in dem Baum der Strukturen B, C, etc. interessiert sind, ˇ& daß aber an ihm zwar allenthalben die Form φ 1 = ψ 1 φ (n + 1) = F (φ n) ψ (n + 1) = F (φ n) zu sehen ist, gleichsam eine bestimmte Astgabelung ein bestimmtes Asttrippel , daß aber diese dieses Gebilde in verschiedenen Anordnungen & Verbindungen untereinander auftreten[,| &] daß sie nicht in dem Sinne Konstruktionselemente sind bilden , wie die Paradigmen im Beweis, daß ⌊oder⌋ (a + b)² = a² + 2ab + b² ⌊.⌋ ist. von a + (b + (c + 1)) = (a + (b + c)) + 1 Der Zweck, & die Rechtfertigung, der „rekursiven Beweise” ist ja, den algebraischen Kalkül mit dem der Zahlen in Verbindung zu setzen bringen . Und der Baum der rekursiven Beweise „rechtfertigt” den algebraischen Kalkül nur, wenn das heißen soll, daß er ihn mit dem Ar arithmetischen in Verbindung bringt. Nicht aber in dem Sinne in welchem die Liste der Paradigmen den ˇalgebraischen Kalkül, d.h. die Übergänge in ihm, rechtfertigt. Wenn man also die Paradigmen der Übergänge tabuliert so hat das dort Sinn wo das Interesse darin liegt zu zeigen daß die & die Transformationen alle bloß mit Hilfe jener – im übrigen willkürlich gewählten – Übergangsformen zu Stande gebracht sind. Nicht aber dort, wo sich die Rechnung in einem andern Sinne rechtfertigen soll wo also das Anschauen der Rechnung – ganz abgesehen von dem Vergleich mit einer Tabelle vorher festgelegter Normen – uns lehren muß ob wir sie zulassen sollen oder nicht. Skolem hätte uns also keinen Beweis des assoziativen & kommutativen Gesetzes versprechen sollen brauchen sondern einfach sagen können, er werde uns einen Zusammenhang der Paradigmen der Algebra mit den Rechnungsregeln der Arithmetik zeigen. Aber ist das nicht Wortklauberei? hat er denn nicht die Zahl der Paradigmen reduziert & uns z.B. statt jener beiden Gesetze eines, nämlich a + (b + 1) = (a + b) + 1 gegeben? Nein. Wenn wir z.B. (a + b)⁴ = [ …| etc.] ⌊(k⌋ ˇbeweisen so könnten wir dabei von dem vorher bewiesenen Satz (a + b)² = [ …| etc.] (𝓁 gebrauch machen. Aber in diesem Fall lassen sich die Übergänge in k die durch 𝓁 gerechtfertigt wurden auch durch jene Regeln Rechtfertigen mit denen 𝓁 bewiesen wurde. Und es Verhält sich dann 𝓁 zu jenen ersten Regeln wie ein durch Definition eingeführtes Zeichen zu den primären Zeichen mit deren Hilfe es definiert wurde. Man kann die Definition immer auch elliminieren & auf die primären Zeichen übergehen. Wenn wir aber in C einen Übergang machen der durch B gerechtfertigt ist so können wir diesen Übergang nun nicht auch mit a + (b + 1) = (a + b) + 1 allein machen. Wir haben eben mit dem was hier Beweis genannt wird nicht einen Übergang Schritt in Stufen zerlegt, sondern etwas ganz andres getan.

​

Wenn gefragt würde: ist die Verneinung Negation in der Mathematik etwa in ~(2 + 2 = 5) 2 + 2 ≠ 5 die gleiche wie die nicht-mathematischer Sätze? so müßte erst bestimmt werden was als Charakteristikum dieser der Verneinung ˇals solcher aufzufassen ist. Die Bedeutung eines Zeichens liegt ja in den Regeln die seinen Gebrauch vorschreiben nach denen es verwendet wird . Welche dieser Regeln machen das Zeichen „~” zur Verneinung? Denn es ist klar daß gewisse Regeln die sich auf „~” beziehen für beide Fälle die gleiche sind; z.B. ~~p = p. Man könnte ja auch fragen: ist die Verneinung eines Satzes „ich sehe einen roten Fleck” die gleiche wie die von „die Erde bewegt sich in einer Elipse um die Sonne”; & die Antwort müßte auch sein: „Wie hast Du „Verneinung” definiert, durch welche Klasse von Regeln? ⌊–⌋ daraus wird sich ergeben ob wir in beiden Fällen „die gleiche Verneinung” haben. Wenn die Logik allgemein von der Verneinung redet, oder einen Kalkül mit ihr treibt, so ist die Bedeutung des Verneinungszeichens nicht weiter festgelegt, als sein die Regeln seines Kalküls. Wir dürfen hier nicht vergessen daß ein Wort seine Bedeutung nicht als etwas ihm ein für allemal verliehenes mit sich herumträgt sodaß wir sicher sind wenn wir nach dieser Flasche ◇◇◇ greifen auch die bestimmte Flüssigkeit etwa Spiritus vielleicht Schwefelsäure zu erwischen. [ – – – auch die bestimmte Flüssigkeit ˇ z.B. Spiritus in der Hand zu halten. ]

​

Irrtümliche Anwendung unserer physikalischen Ausdrucksweise auf Sinnesdaten. „Gegenstände” d.h. Dinge, Körper im Raum des Zimmers & „Gegenstände” im Gesichtsfeld, der Schatten eines Körpers an der Wand als Gegenstand! Wenn man gefragt wird: „existiert der Kasten noch, wenn ich ihn nicht anschaue”, so ist die korrekte Antwort: „ich glaube nicht, daß ihn jemand ger⌊a⌋de dann wegtragen ˇwird oder zerstören⌊.”⌋ wird”. Die Sprachform „ich nehme x wahr” bezieht sich ursprünglich auf einen Körper Phänomen (als Argument), das im physikalischen Raum (ich meine hier: im „Raum” de[s|r] alltäglichen Ausdrucksweise). Ich kann daher diese Form nicht unbedenklich auf das Anwenden, was man Sinnesdatum nennt ˇetwa auf ein Nachbild optisches Nachbild. (Vergleiche auch, was wir über die Identifizierung von Körpern & anderseits von Farbflecken im Gesichtsfeld gesagt haben.) Was es heißt: ich⌊, ⌋ stehe das Subject, stehe dem Tisch, als Object, gegenüber, kann ich leicht verstehen; in welchem Sinne aber stehe ich meinem optischen Nachbild des Tisches gegenüber?      „[i|I]ch kann diesen Tisch Glasscheibe nicht sehen aber ich kann ihn sie fühlen”. Kann man sagen: „ich kann das Nachbild nicht sehen, aber …”? ˇVergleiche: „Ich sehe einen den Tisch deutlich”; „[i|I]ch sehe das Nachbi⌊l⌋d deutlich”; „Ich höre die Musik deutlich”; ich höre das Ohrensausen deutlich”. Vergleiche die Grammatik Ich sehe den Tisch ˇnicht deutlich heißt etwa: ich sehe ˇnicht alle Einzelheiten des Tisches; – was aber heißt es: „ich sehe nicht alle Einzelheiten des Nachbildes”, oder: „ich höre nicht alle Einzelheiten des Ohernklingens”? Könnte man nicht sehr wohl statt „ein Nachbild sehen” sagen: „ein Nachbild haben”? Denn: ein Nachbild „sehen”? im Gegensatz wozu? – „Wenn Du mich auf den Kopf schlägst, sehe ich Kreise”,⌊. –⌋ „[s|S]ind es genaue Kreise, hast Du sie gemessen?” (Oder: „sind es gewiß Kreise, oder täuscht Dich Dein Augenmaß?”) – Was heißt es nun, wenn man sagt: „wir können nie einen genauen Kreis sehen”? Soll das eine Erfahrungstatsache sein, oder die Konstatierung einer logischen Unmöglichkeit? – Wenn das letztere, so heißt es also, daß es keinen Sinn hat vo[n|m] einem [s|S]ehen eines genauen Kreises zu reden. Nun, das kommt drauf an, wie man das Wort gebrauchen will. „Genauer Kreis” im Gegensatz zu einem Gesichtsbild da[ß|s] wir eine sehr kreisähnliche Elipse nennen würden kann man doch gewiß sagen. D[er|as] Kreis Gesichtsbild ist dann ein genauer Kreis welches uns wirklich ˇwie wir sagen würden kreisförmig erscheint & nicht vielleicht nur sehr ◇◇◇ ˇähnlich einem Kreis. Ist anderseits von einem Gegenstand die Rede der gemessen werden kann der Messung die Rede, so gibt es wieder verschiedene Bedeutungen des Ausdrucks „genauer Kreis” je|nach|dem welches Erfahrungs Kriterium ˇwelches ich dafür bestimme gebe , daß ⌊.⌋ daß der der gemessene Gegenstand genau kreisförmig ist. [ – – – je nach dem Erfahrungskriterium, das ich für die genaue Kreisförmigkeit des Gegenstandes bestimme. ] Wenn wir sagen ich nun sage : „keine Messung ist absolut genau⌊”⌋, so erinnern wir hier an einen Zug in der Grammatik der Angabe von Messungsresultaten. Denn sonst könnte uns Einer sehr wohl antworten: „Wie weißt Du das, hast Du alle Messungen untersucht?” – „Es gibt Man kann nie einen genauen Kreis sehen” kann die Hypothese sein daß we genauere Messung eines kreisförmig aussehenden Gegenstandes immer zu dem Resultat führen wird, daß der Gegenstand von der Kreisform abweicht. – Wenn man sagt ˇDer Satz „[m|M]an kann ein 100-Eck nicht von einem Kreis unterscheiden” hat nur Sinn, wenn man die beiden auf irgend eine Weise unterscheiden kann, & sagen will man könne, so unterschiedene, sie etwa mit freiem den Auge⌊n⌋ nicht visuell nicht unterscheiden. Wäre keine Methode der Unterscheidung vorgesehen, so hätte es also keinen Sinn zu sagen, daß diese zwar wie ein Kreis zwei Figuren ⌊(⌋zwar⌊)⌋ gleich aussehen aber „ tatsächlich in Wirklichkeit ” verschieden sind. Und jener Satz wäre dann etwa die Definition 100-Eck = Kreis. Ist in irgend einem Sinne ein genauer Kreis im Gesichtsfeld undenkbar, dann muß der Satz „ich sehe nie einen genauen Kreis im Gesichtsfeld” von der Art des Satzes sein: „ich sehe nie ein hohes C im Gesichtsfeld”. [ … , dann muß der Satz „im Gesichtsfeld ist nie ein genauer Kreis” von der Art des Satzes sein: „im Gesichtsfeld ist nie ein hohes C”. ]

​

Verschwommenheit, [U|u]nklarheit, unscharf. „Die Linien dieser Zeichnung sind unscharf”, „meine Erinnerung an die Zeichnung ist unklar ˇverschwommen”, „die Gegenstände am Rande meines Gesichtsfeldes sehe ich verschwommen”. – Wenn man von der Verschwommenheit der Gegenstände Bilder am Rande des Gesichtsfeldes spricht so schwebt einem oft ein Bild dieses Gesichtsfeldes vor wie es etwa Mach entworfen hat. Die Verschwommenheit aber die die Kontu Ränder eines Bildes auf der Papierfläche haben können der Ränder eines Bildes … ist von gänzlich andrer Natur, als die die man von den Rändern des Gesichtsfeldes aussagt. So verschieden wie die Blässe der Erinnerung an eine Zeichnung von der Blässe einer Zeichnung selbst. Wenn seinerzeit im Film eine Erinnerung oder ein Traum dargestellt werden sollte, so gab man den Bildern einen bläulichen Ton. Aber die ˇTraum- & Erinnerungsbilder haben natürlich keinen bläulichen Ton – sowenig wie unser Ge⌊s⌋ichtsbild verwaschene Ränder hat– ⌊;⌋ also sind die bläulichen Projektionen auf der Leinwand Bilder [ bläulichen Bilder auf der Leinwand nicht ˇunmittelbar anschauliche Bilder der Träume, sondern Bilder in ˇnoch einem andern Sinn. [ D – Bemerken wir im gewöhnlichen Leben, wo wir doch unablässig schauen, die Verschwommenheit an den Rändern des Gesichtsfeldes? Ja, welcher Erfahrung entspricht sie eigentlich, denn im normalen Sehen kommt sie nicht vor! Nun, wenn wir den Kopf nicht drehen & wir beobachten etwas, was wir durch drehen der Augen gerade noch sehen können, dann sehen wir etwa einen Menschen, können aber sein Gesicht nicht erkennen, sondern sehen es in gewisser Weise verschwommen. Die Erfahrung hat nicht die geringste Ähnlichkeit mit dem Sehen einer Scheibe auf welcher der Bilder gemalt sind die in der Mitte der Scheibe ˇmit scharfe⌊n⌋ Umrisse⌊n⌋ haben & etwa nach dem Rand zu mehr & mehr verschwimmend etwa in ein allgemeines Grau ˇ unmerklich übergehen⌊d⌋. Wir denken an so eine Scheibe, wenn wir z.B. fragen: könnte man sich nicht ein das Gesichtsfeld auch so denken mit gleich bleibender Klarheit der Umrisse etc. denken? Es gibt keine Erfahrung ˇdie im Gesichtsfeld die der entspräche, wenn man den Blick einem Bild entlanggleiten läßt das von scharfen Figuren zu immer verschwommeneren übergeht.

​

Die visuelle Gerade berührt den visuellen Kreis nicht in einem Punkt sondern in einer visuellen Strecke. – Wenn ich einen eine die die Zeichnung eines Kreises & einer Tangente ansehe, so wäre ist nicht das merkwürdig daß wenn ich etwa niemals einen vollkommenen Kreis & eine vollkommene Gerade mit einander in Berührung sehe; interessant wird wäre ist es erst, wenn ich sie sehe, & dann die Tangente mit dem Kreis ein Stück zusammenläuft.

∕∕

30.    Denken wir uns folgendes psychologisches Experiment: Wir zeigen dem Subject zwei Linien g1, g2 durch welche quer die Gerade a gezogen ist. [d|D]as Stück dieser Geraden welches zwischen g1 & g2 liegt werde ich die Strecke auch a nennen. Wir ziehen nun in beliebiger [e|E]ntfernung von a & parallel dazu b & fragen ob er die Strecke b größer sieht als a oder ob er die beiden Längen nicht mehr unterscheidet. Er antwortet, b erscheine größer als a. Darauf nähern wir uns a, indem wir die Distanz von a zu b halbieren mit unsern Meßinstrumenten halbieren & ziehen c. „Siehst Du c größer als a?” . ⌊–⌋ „Ja”. Wir halbieren die Distanz c–a & ziehen d. „Siehst Du d größer als a?” . ⌊–⌋ „Ja”. Wir halbieren a–d. „Siehst Du e größer als a⌊?⌋” . – „Nein”. Wir halbieren daher e–d. „Siehst Du f größer als e?” – „Ja”. Wir halbieren also e–f & ziehen g ⌊ h⌋. Wir könnten uns so auch von der linken Seite der Strecke a nähern, & dann sagen daß einer gesehenen Länge a im [e|E]uklidischen Raum nicht eine Länge sondern ein Interval von Längen entspricht, und in ahnlicher Weise einer gesehenen Lage eines Strichs (etwa des eines Zeigens eines Instruments) ein Interval von Lagen im Euklidischen Raum; aber dieses Interval hat nicht scharfe Grenzen. Das heißt: es ist nicht von Linien be Punkten begrenzt sondern von konvergierenden Intervalen die nicht gegen einen Punkt konvergieren. (Wie die Reihe der Dualbrüche die wir durch Werfen von Kopf & Adler erzeugen). Das Charakteristische zweier Intervale, die so nicht durch Punkte sondern durch unscharf begrenzt sind, ist, daß auf die Frage, ob sie einander übergreifen oder getrennt von einander liegen in gewissen Fällen die Antwort lautet: „unentschieden”. Und daß die Frage ob sie einander berühren, einen Endpunkt mit einander gemein haben, ˇimmer sinnlos ist⌊,⌋ (da sie ja keine Endpunkte haben. Man könnte aber sagen: sie haben vorläufige Endpunkte. In dem Sinne in welchem die Entwicklung von π ein vorläufiges Ende hat. An dieser Eigenschaft des ‚unscharfen’ Intervals ist natürlich nichts geheimnisvolles sondern das etwas Paradoxe liegt klärt sich durch die doppelte Verwendung des Wortes Interval auf. Es ist dies der gleiche Fall wie der der doppelten Verwendung des Wortes Schach, wenn es einmal die Gesamtheit der jetzt geltenden Schachregeln bedeutet, ein andermal: das Spiel welches N.N. in Persien erfunden hat & welches sich so & so entwickelt hat. In einem Fall ist es unsinnig von einer Entwicklung Änderung der Schachregeln zu reden, im andern Fall nicht. Wir können „Länge einer gemessenen Strecke” entweder das nennen, was bei einer bestimmten Messung her die ich heute um 5 Uhr durchführe herauskommt – dann gibt es für diese Längenangabe kein „ ± etc.” –, oder etwas dem sich Messungen nähern etc.; in den zwei Fällen wird das Wort „Länge” mit mit ganz verschiedener Grammatik gebraucht. Und ebenso das Wort „Interval l ” wenn ich einmal etwas Fertiges, einmal etwas sich [e|E]ntwickelndes ein Interval nenne. I: Die Intervalle liegen getrennt II sie liegen getrennt & berühren sich vorläufig III unentschieden IV unentschieden V unentschieden VI sie übergreifen VII sie übergreifen Wir können uns aber nicht wundern, daß nun ein Interval so seltsame Eigenschaften haben soll; das wir eben etwas das Wort Interval jetzt in einem nicht gewöhnlichen Sinn gebrauchen. Und wir können nicht sagen wir haben neue Eigenschaften gewisser Intervalle entdeckt. So wenig wie wir neue Eigenschaften des Schachkönigs entdecken würden, wenn wir die Regeln des Spiels änderten aber die Bezeichnung „Schach” & „König” bei[g|b]ehielten. (Vergl. dagegen Brouwer über das Gesetz des ausgeschlossenen Dritten.)        Jener Versuch ergibt also wesentlich, was wir ein „unscharfes” Interval genannt haben, dagegen wären sind natürlich andere Experimente möglich [ denkbar ] die statt dessen ein scharfes Interval ergeben. Denken wir etwa, wir bewegten ein Lineal ⌊(⌋langsam⌊)⌋ von der Anfangsstellung b, & parallel zu dieser, gegen a hin, bis et in unserm Subjekt irgend eine bestimmte Reaktion einträte; dann könnten wir den Punkt an dem die Reaktion beginnt die Grenze unseres Streifens nennen. – So könnten wir natürlich auch ein Wägungsresultat „das Gewicht eines Körpers” nennen & es gäbe dann in diesem Sinn eine absolut genaue Wägung d.i. eine deren Resultat nicht die Form „G ± g” hat. Wir haben damit unsere Ausdrucksweise geändert, & müssen nun sagen daß der Körper sein das Gewicht des Körpers schwankt & zwar nach einem uns unbekannten Gesetz. (Die Unterscheidung zwischen „absolut genauer” Wägung & „wesentlich ungenauer” Wägung ist ein grammatischer & bezieht sich auf zwei verschiedene Bedeutungen des Ausdrucks Wortes „Wägung” oder „ Ergebnis Resultat ) der Wägung”.)

∕∕

Die Unbestimmtheit des Wortes „Haufen”. Ich könnte definieren: ein Körper von gewisser Form & [k|K]onsistenz etc. sei ein Haufe wenn er ˇsein Volumen K m ³ beträgt, oder darüber mehr , was darunter liegt will ich ein Häufchen nennen. Dann gibt es kein größtes Häufchen; das heißt: dann ist es sinnlos von dem einem „größten Häufchen” zu reden. Umgekehrt könnte ich bestimmen: Haufe solle alles das sein, was größer als K m ³ ist & dann hätte der Ausdruck ⌊„[„|d]er⌋ kleinste Haufe” keine Bedeutung. Ist aber diese Unterscheidung nicht müßig? Gewiß, – wenn wir ˇunter dem Volumen ein mit Meßungsresulta[t|]ten im gewöhnlichen Sinne verstehen; denn dieses Resultat hat die Form „V ± v”. [ Gewiß, – wenn wir unter dem Resultat der Messung des Volumens einen Ausdruck von der Form „V ± v” verstehen. ] Sonst aber wäre diese könnte die Unterscheidung so brauchbar sein wie nicht müßiger als die zwischen einem Schock Äpfeln & 61 Äpfeln.

∕∕

Die Verschwommenheit, Unbestimmtheit unserer Sinneseindrücke ist nicht etwas dem sich abhelfen läßt, eine Verschwommenheit, der auch völlige Schärfe entspricht (oder entgegensteht). Vielmehr ist diese allgemeine Unbestimmtheit, Ungreifbarkeit, dieses Schwimmen der Sinneseindrücke, das, was mit dem Worte „alles fließt” bezei bezeichnet worden ist. Wir sagen „man sieht nie einen genauen Kreis”, & wollen sagen, daß, auch wenn wir keine Abweichung von der Kreisform sehen, das nicht ˇuns keinen genauen Kreis gibt. (Es ist als wollten wir sagen: wir können dieses Werkzeug nie genau führen denn wir halten nur den Griff & das Werkzeug sitzt im Griff lose.) Was aber verstehen wir dann unter dem Begriff ‚genauer Kreis’? Wie sind wir zu diesem Begriff überhaupt gekommen? Nun, wir denken z.B. an eine genau gemessene Kreisscheibe aus einem sehr harten Stahl. Aha – also dorthin zielen wir mit dem Begriff ‚genauer Kreis’. Freilich, davon finden wir im Gesichtsbild nichts. Wir haben eben die Darstellungsform gewählt, die die Stahlscheibe als genauer nennt als die Holzscheibe & die Holzscheibe genauer als die Papierscheibe. Wir haben den Begriff „genau” durch eine Reihe bestimmt, & reden von den Sinneseindrücken als ˇBildern, ungenauen Bildern, der physikalischen Gegenstände.

​

Die Gallstonesche [F|Ph]otographie, das Bild einer Wahrscheinlichkeit. Das Gesetz der Wahrscheinlichkeit, das Naturgesetz, was man sieht wenn man blinzelt.

​

In den Theorien & Streitigkeiten der Philosophie finden wir die Worte deren Bedeutungen uns vom alltäglichen Leben her wohlbekannt sind in einem ultraphysischen Sinne angewandt.

​

2 + 3 + 4       5             9      2 + 4 + 3       6             9      4 + 3 + 2       7             9 (Ƒ) „Siehst Du, es kommt tatsächlich immer dasselbe heraus”, möchte man sagen. So aufgefaßt, haben ist war die Rechnung ein Experiment. Wir haben die Regeln des Eins-&-Eins angewendet & denen sieht man es nicht unmittelbar an, daß sie in den drei Fällen zum gleichen Resultat führen. Man wundert sich gleichsam, daß die Ziffern, losgelöst von ihren Definitionen so richtig funktionieren. Oder vielmehr: daß die Ziffernregeln so richtig arbeiten, wenn sie nicht von den Definitionen kontrolliert werden. – Denken wir an den Schritt, der zu machen ist von der gelernten Regel des Eins-&-Eins zu der Anwendung der Regel in dem speziellen Fall. –

​

Könnten die Berechnungen eines Ingenieurs ergeben, daß eine Dimension die Stärke eines eine Maschinenteils bei gleichmäßig wachsender Belastung ⌊in⌋ d[ie|er] Reihe der Primzahlen fortschreiten müsse? [ daß die Stärken eines Maschinenteils … müssen? ]

​

Ist nicht 1 : 3 = 0,3   1 entscheidet durch ihre Periodizität nichts, was früher offen gelassen war. Wenn vor der Entdeckung der Periodizität [e|E]iner vergebens nach einer 4 in der Entwicklung von 1 : 3 gesucht hätte, so hätte er doch die Frage „gibt es eine 4 in der Entwicklung von 1 : 3” nicht sinnvoll stellen können; d.h., abgesehen davon daß er tatsächlich zu keiner 4 gekommen war, können wir ihn davon überzeugen, daß er keine Methode besitzt seine Frage zu entscheiden. Oder auch wir könnten auch sagen: abgesehen von dem Resultat seiner Tätigkeit könnten wir ihn über die Grammatik seiner Frage & die Natur seines Suchens aufklären[.| (]wie einen heutigen Mathematiker der über das Goldba analoge Probleme.) „Aber als Folge der Entdeckung der Periodizität hört er nun doch gewiß auf ˇnach einer 4 zu suchen! Sie überzeugt ihn also, daß er nie eine finden wird.” – Nein. Die Entdeckung der Periodizität bringt ihn vom Suchen ab, wenn er sich nun neu einstellt. Man könnte ihn nun fragen: „Wie ist es nun, willst Du noch immer nach einer 4 suchen?” (Oder hat Dich, sozusagen, die Periodizität, auf andere Gedanken gebracht.)     Und die Entdeckung der Periodizität ist in Wirklichkeit die Konstruktion eines neuen Zeichens & Kalküls. Denn es ist irreführend ausgedrückt wenn wir sagen sie bestehe darin daß es uns aufgefallen sei, daß der erste Rest gleich dem Dividenden ist. Denn hätte man [e|E]inen, der die periodische Division nicht kannte gefragt ist in dieser Division der erste Rest gleich dem Dividenden, so hätte er natürlich „ja” gesagt; es wäre ihm also aufgefallen. Aber damit hätte ihm nicht die Periodizität auffallen brauchen: d.h.: er hätte damit nicht den K[ä|a]lkül mit den Zeichen aa : b = c gefunden.      Ist nicht, was ich hier sage im G immer dasselbe das , was Kant meinte damit meinte, daß 5 + 7 = 12 nicht analytisch sondern synthetisch a priori sei?

Der Satz, daß eine Klasse einer ihrer Subklassen nicht ähnlich ist, ist für endliche Klassen nicht wahr, sondern eine Tautologie. Die ˇgrammatischen Regeln über die Allgemeinheit der generellen Implication in dem Satz daß „k ist eine Subklasse von K” ist enthalten das was der Satz, K sei eine unendlich Klasse, sagt. [ Die grammatischen Regeln über die Allgemeinheit jener der generellen Implication im Satz „k ist eine Subklasse von K” … ] .

\

​

Unzulänglichkeit der Frege- & Russellschen Allgemeinheitsbezeichnung.    Es hat Sinn zu sagen „schreib eine beliebige Kardinalzahl hin”, ist aber Unsinn zu sagen: „schreib alle Kardi- nalzahlen hin”. „In dem Viereck befindet sich ein Kreis” ˇ ((∃x) ∙ φx) hat Sinn, aber nicht ˇ also ~ (∃x) ~φx: „in dem Viereck befinden sich alle Kreise”. Und was sollte der Satz (∃x) ~φx bedeuten: „es gibt einen Kreis der nicht im Viereck ist”? „Auf einem andersfarbige[m|n] Hintergrund befindet sich ein roter Kreis” hat Sinn, aber nicht „es gibt keine ˇvon rot verschiedene Farbe eines Hintergrundes auf der sich kein roter Kreis befindet”.     „In diesem Viereck ist ein ˇschwarzer Kreis”: Wenn dieser Satz die Form „(∃x) ∙ x ist ein schwarzer Kreis ˇim Viereck” hat, welcher Art was ist so ein Ding x das welches die Eigenschaft hat ein schwarzer Kreis zu sein (& also auch die haben kann kein schwarzer Kreis zu sein)? Ist es etwa ein Ort im Quadrat? dann aber gibt es keinen Satz „(x) ∙ x ist ein schwarzer …” Anderseits könnte jener Satz bedeuten „es gibt einen Fleck de im Quadrat, der ein schwarzer Kreis ist”. Wie verifiziert man diesen Satz? Nun, man geht die verschiedenen Flecken im Quadrat durch & untersucht sie darauf hin ob sie ganz schwarz & kreisförmig sind. Welcher Art Satz ist aber der Satz: „Es gibt ist keinen Fleck i[m|n] dem Quadrat”? Denn, wenn das ‚x’ in ‚(∃x)’ im vorigen Fall ‚Fleck im Quadrat’ hieß, dann kann es zwar einen Satz „(∃x) ∙ φx” geben, aber keinen ⌊„⌋~(∃x)⌊”⌋ oder ⌊„⌋~(∃x)⌊”⌋. Oder, ich könnte wieder fragen: Was ist das für ein Ding, das die Eigenschaft haben ka hat (oder nicht hat) ein Fleck im Quadrat zu sein?     Und wenn man sagen kann „ein Fleck ist in dem Quadrat”, hat es damit dann auch schon Sinn zu sagen „alle Flecken sind in dem Quadrat”? Welche alle?

​

1.6. Was heißt es: „die Punkte die das Experiment liefert, liegen durchschnittlich auf einer Geraden”? oder: „wenn ich mit einem guten Würfel würfle so werfe ich durchschnittlich alle 6 Würfe eine 1”? Ist dieser Satz mit jeder Erfahrung die ich etwa mache vereinbar? Wenn er das ist so sagt er nichts. Habe ich ⌊(⌋vorher⌊)⌋ angegeben mit welcher Erfahrung er nicht mehr vereinbar ist, welches die Grenze ist bis zu der die Ausnahmen von der Regel gehen dürfen, ohne die Regel umzustoßen? Nein. Hätte ich aber nicht eine solche Grenze aufstellen können? Gewiß. – Denken wir uns die Grenze wäre [die :| ] Wenn unter 6 aufeinander folgenden Würfen 4 gleiche auftreten ist der Würfel schlecht. Nun fr[ä|a]gt man aber: „Wenn das aber nur selten genug geschieht, ist er dann nicht doch gut?” – Darauf lautet die Antwort: Wenn ich das Auftreten von 4 gleiche Würfen unter 6 aufeinanderfolgenden für eine bestimmte Zahl von Würfen erlaube, so ziehe ich damit eine andere Grenze als die erste war. Wenn ich aber sage „jede Anzahl gleicher aufeinanderfolgender Würfe ist erlaubt, wenn sie nur selten genug auftritt, dann habe ich damit die Güte des Würfels im strengen Sinne ˇals unabhängig von den Wurfresultaten erklärt. Es sei denn daß ich unter der Güte des Würfels nicht eine Eigenschaft des Würfels sondern eine Eigenschaft einer bestimmten Partie im Würfelspiel verstehe. Denn dann kann ich allerdi⌊n⌋gs sagen: Ich nenne den Würfel in einer Partie gut wenn unter den N wu Würfen der Partie nicht mehr als log N gleiche aufeinanderfolgende vorkommen. H Hiermit wäre aber eben kein Test zur Überprüfung von Würfeln gegeben, sondern ein Criterium zur Beurteilung einer Partie des Spiels.

​

Man sagt, wenn der Würfel ˇganz gleichmäßig & sich selbst überlassen ist m dann muß die Verteilung der Würfresultate Ziffern 1, 2, 3, 4, 5, 6 in unter den Wurfresultaten gleichförmig sein, weil kein Grund vorhanden ist, weshalb die eine Ziffer öfter vorkommen sollte als die andere. Aber wie ist es mit den Werten der Funktion (x ‒ 3)² für (1 ‒ 3)², (2 ‒ 3)², (3 ‒ 3)², (4 ‒ 3)², (5 ‒ 3)², (6 ‒ 3)²; ist ein Grund vorhanden für die Argumente von 1 bis 6; ist ein Grund vorhanden, warum einer dieser Werte öfter unter den Wurfresultaten vorkommen sollte als ein anderer. Könnte ich nicht ebensogut das als das a priori Wahrscheinliche Erklären? Stellen wir nun aber die Wurfresultate statt durch die Ziffern 1 bis 6 durch die Werte der Funktion (x ‒ 3)² für die Argumente 1 bis 6 dar also durch die Ziffern 0, 1, 4, 9. Ist ein Grund vorhanden, warum eine dieser Ziffern öfter in den ˇneuen Wurfresultaten fungieren soll als eine andere? Dies lehrt uns, daß das Gesetz a priori der Wahrscheinlichkeit eine Form von Gesetzen ist, wie die der Minimumsgesetze der Mechanik etc.. Hätte man durch Versuche herausgefunden, daß die Verteilung der Würfe ˇ1 – 6 eines gleichmäßigen mit einem regelm Würfels so ausfällt, daß die Verteilung der Werte (x ‒ 3)² eine gleichmäßige wird, so hätte man nun diese Ver Gleichmäßigkeit als fürc die Gleichmäßigkeit a priori erklärt.     So machen wir es auch in der ˇkinethischen Gastheorie, ⌊:⌋ wir stellen die Verteilung der Molekülbewegungen in der Form ˇirgend einer gleichförmigen Verteilung dar was aber gleichförmig verteilt ist – so wie an andrer Stelle was zu einem Minimum wird – wählen wir so daß unsere Theorie mit der Erfahrung übereinstimmt.

​

„Die Moleküle bewegen sich blos nach den Gesetzen der Wahrscheinlichkeit”, das soll heißen: die Physik tritt ab, & laß überläßt die Moleküle sich selbst bewegen sich jetzt quasi bloß nach Gesetzen der Logik. Diese Meinung ist der verwandt der, daß das Trägheitsgesetz ein Satz a priori ist, & auch hier redet man davon, was ein Körpert tut, wenn er sich selbst überlassen ist. Was ist das Criterium dafür, daß er sich selbst überlassen ist? Ist es am Ende das, daß er sich gleichförmig in einer Geraden bewegt? Oder ist es ein anderes. Wenn das letztere dann ist es eine Sache der Erfahrung ob das Trägheitsgesetz stimmt; im ersten Fall aber war es gar kein Gesetz, sondern eine Definition. Und analoges gilt von einem dem Satz S: „wenn die Teilchen Körper sich selbst überlassen sind, dann ist die Verteilung ihrer Bewegungen die & die”. Welches ist das Criterium dafür daß sie sich selbst überlassen sind? etc..

​

⌊[⌋ Wenn die Messung ergiebt, daß der Würfel genau & homogen ist Wenn man sagt: der Würfel ist gleichmäßig , & ich nehme an, daß die Vert Ziffern auf seinen Flächen die Wurfresultate nicht beeinflußen, so folgt & & daß die werfende Hand ˇbewegt sich – gleichmäßig – bewegt regellos folgt daraus die ˇdurchschnittlich gleichmäßige Verteilung der Würfe 1 bis 6? Woraus sollte man die das schließen? Über die Bewegung beim Werfen hat man keine Annahme gemacht & die ˇ Premisse der [ Annahme der ] Genauigkeit des Würfels ist doch von ganz anderer Art Multiplizität , als eine durchschnittlich gleichförmige Verteilung von Resultaten Ziffern . (Die Premisse ist gleichsam einfärbig, die Konklusion gesprenkelt.) Warum hat man gesagt, der Esel werde zwischen den beiden gleichen Heubündeln verhungern, & nicht, er werde von beiden durchschnittlich gleich oft fressen? durchschnittlich sooft von dem einen wie von dem andern fressen? ]2

​

Behaviourism. „Mir scheint, ich bin traurig, ich lasse den Kopf so hängen”. Warum hat man kein Mitleid, wenn eine Tür ungeölt ist & beim auf- & zumachen schreit quietscht ? Haben wir mit dem Andern der sich benimmt wie wir, wenn wir Schmerzen haben, Mitleid, auf philosophische Erwägungen hin, die zu dem Ergebnis geführt haben, daß er leidet wie wir? Ebensogut könnten uns die Physiker damit Furcht einflößen daß sie uns versichern, der Fußboden sei gar nicht kompakt, wie er scheine, sondern bestehe aus losen Partikeln die [R|r]egellos herumschwirren. „Aber wir hätten doch mit dem Andern nicht mitleid, wenn wir wüßten daß er nur eine Puppe ist oder seine Schmerzen blo [ß|s] heuchelt.” Freilich– ⌊,⌋ aber wir haben auch ganz bestimmte Kriterien dafür daß einer etwas eine Puppe ist oder daß [e|E]iner seine Schmerzen heuchelt & diese Kriterien stehen eben im Gegensatz zu denen die wir Kriterien dafür nennen, daß etwa keine Puppe (sondern etwa ein Mensch) ist & seine Schmerzen nicht heuchelt (sondern wirklich welch Schmerzen hat).

​

Die Untersuchung der Regeln des Gebrauchs unserer Sprache, die Erkenntnis dieser Regeln & übersichtliche Darstellung läuft auf das hinaus, d.h., leistet dasselbe, was man oft durch die Konstruktion einer phänomenologischen Sprache erzielen leisten will.   Jedesmal wenn wir erkennen, daß die & die Darstellungsweise auch durch eine andre ersetzt werden kann, machen wir einen Schritt zu diesem Ziel.

∕∕

Wie kommt es daß die Philosophie ein so komplizierter Bau Aufbau ist. Sie sollte doch ganz gänzlich einfach sein wenn sie jenes Letzte von aller Erfahrung Unabhängige ist, wofür Du sie ausgibst. – Die Philosophie löst Knoten in unserem Denken auf; … auf die wir in unser Denken gemacht haben; daher muß ihr Resultat einfach sein, ihre Tätigkeit aber so kompliziert wie derselben Knoten, die sie auflöst.

Hat es Sinn zu sagen, zwei Menschen hätten den⌊|⌋selben Körper? Welches wären die Erfahrungen, die wir mit diesem Satz beschrieben? Daß ich darauf käme daß das was ich meine Hand nenne & bewege an dem Korper eines Andern sitzt ist natürlich denkbar, denn ich sehe während ich jetzt schreibe die Verbindung meiner Hand mit meinem übrigen Körper nicht & ich könnte wohl daraufkommen daß sich die frühere Verbindung gelöst hat & also auch daß meine Hand jetzt an dem Arm eines Andern sitzt. Angenommen ich & mein Freund sitzen nebeneinander ohne uns einander anzuschauen, ich schreibe ohne meinen rechten Arm zu sehen. Plötzlich sehe ich mich um & werde gewahr daß meine Hand an seinem Arm sitzt. Ich mache ihn darauf aufmerksam, & er sagt: „ich habe gerade mit dieser Hand geschrieben, allerdings nicht auf sie geschaut & habe nicht gewußt daß sie jetzt ausschaut wie Deine & Du ein Gefühl in ihr hast”.

✓

​

Die Geometrie ist nicht die Wissenschaft (Naturwissenschaft) von den geometrischen Ebenen, ˇgeometrischen Geraden & ˇgeometrischen Punkten, im Gegensatz etwa zu einer andern Wissenschaft die von den groben physischen Geraden, Strichen, Flächen etc. handelt & deren Eigenschaften angibt. Der Zusammenhang der Geometrie mit Sätzen ˇdes praktischen Lebens, die von Strichen, Farbgrenzen, Kanten& ⌊,⌋ Ecken ˇ etc handeln ist nicht der, daß in ihr ähnliche Sätze über ähnliche, wenn auch ideale Dinge (Kanten, Ecken etc) sie aus allgemeinen besteht spricht sie über ähnliche Dinge wie diese spricht, wie diese Sätze, wenn auch über ideale Kanten, Ecken, etc.., sondern derc, zwischen diesen Sätzen & ihrer Grammatik. Die angewandte Geometrie ist die Grammatik der Aussagen über die ˇräumlichen Gegenstände, daß⌊.⌋ Die sogenannte geometrische Geraden verhalt sich zu einer Farbgrenze nicht wie etwas Feines zu etwas Grobem, sondern wie Möglichkeit zur Wirklichkeit. (Denke an die Auffassung der Möglichkeit als Schatten der Wirklichkeit.)

​

Der Name den ich eine[s|m] Körpers ˇgebe, einer Fläche, eine[s|m] Ortes, einer Farbe, hat jedesmal andere Grammatik. Der Name „a” in „a ist gelb” hat h eine andere Grammatik wenn a der Name eines Körpers & wenn es der Name der Oberflä⌊Flä⌋che eines einer Fläche eines Körpers ist, ob nun ein Satz „dieser Körper ist gelb” sagt daß die Oberfläche des Körpers gelb ist, oder daß er durch & durch gelb ist. „Ich zeige auf a” hat hat eine verschiedene Grammatik, je nachdem wenn a ein Körper, eine Fläche, eine Farbe ist etc.. Und so hat auch das hinweisende Fürwort „dieser” (diese, dieses) andere Bedeutung (d.h. Grammatik) wenn es ˇsich auf Hauptwörter verschiedener Grammatik bezieht.

∕∕

Zu sagen, die Punkte, die dieses Experiment liefert, liegen durchschnittlich auf dieser Linie, z.B. einer Geraden, sagt etwas Ahnliches wie: „aus dieser Entfernung gesehen, scheinen sie in einer Geraden zu liegen”. ⌊⌊ Ausdruck eines Gesichts unter diesen Umständen. ⌋⌋ Ich kann von einer Strecke Linie sagen, der allgemeine Eindruck ist der einer Geraden; aber nicht von der Linie a 〰; obwohl es möglich wäre, die es sie als Stück einer längeren Linie zu sehen in der sich die Abweichung⌊en⌋ ˇdes Stückes a von der Geraden verlieren würde⌊n⌋. Ich kann nicht ˇvon jenem a sagen: „jenes Stück „die Linie schaut gerade aus, denn sie kann das Stück einer Linie sein die mir als Ganzes den Eindruck der Geraden macht.” ⌊ (Berge auf der Erde & auf dem Mond. Erde eine Kugel.) ⌋

✓ \

​

Von Sinnesdaten in dem Sinne dieses Wortes, in dem es undenkbar ist, daß der Andere sie hat, kann man eben aus diesem Grunde auch nicht sagen, daß der Andere sie nicht hat. Und eben darum ist es auch sinnlos zu sagen, daß ich, im Gegensatz zum Andern, sie habe. – Wenn man sagt „seine Zahnschmerzen kann ich nicht fühlen”, meint man damit, daß man die Zahnschmerzen des Andern bis jetzt nie gefühlt hat? Wie unterscheiden sich seine Zahnschmerzen von den [M|m]einen? Wenn das Wort „Zahnschmerzen” in den Sätzen „ich habe Z.” & „er hat Z.” die gleiche Bedeutung hat, was heißt es dann zu sagen, daß er nicht dieselben Zahnschmerzen haben kann, wie ich? Wie können sich den verschiedene Z. von einander unterscheiden? Durch Stärke, durch den Charakter des Schmerzes (stechend, bohrend, etc) & durch die Lokalisation im Kiefer Kopf . Wenn nun aber diese Charakteristica bei beiden dieselben sind? – Wenn man aber einwendet, ihr der [u|U]nterschied der Schmerzen sei eben der, daß in einem Falle ich sie habe, im andern Fall er! – dann ist also die besitzende Person eine Charakteristik der Zahnschmerzen selbst. Aber was wie ist es dann mit dem Satz „ich habe [z| Z].” oder „er hat Z.” ausgesagt? – Wenn das Wort „Z” in beiden Fällen die gleiche Bedeutung hat, dann muß man die Z der beiden mit einander vergleichen können & wenn sie in Stärke etc. etc. mit einander übereinstimmen, so sind sie die gleichen; wie zwei Anzüge die gleiche Farbe besitzen, wenn sie in [b|B]ezug auf Helligkeit, Sättigung etc. miteinander übereinstimmen.    Wenn man fragt „ist es denkbar daß ein Mensch die Z. des andern fühlt?” so schweben einem dabei die Z. des [a|A]ndern gleichsam als ein Körper ein Volumen vor im Mund des [a|A]ndern & die Frage scheint zu fragen ob wir an diesem Schmerzvolumen teil haben können. Etwa dadurch daß sich unser beider Wangen durchdrängen. Aber auch das scheint dann nicht zu genügen & wir müßten ganz mit ihm zusammenfallen [ & wir müßten uns ganz mit ihm decken. ]

∕∕

Das Experiment des Würfelns dauert eine gewisse Zeit, & unsere Erwartungen, für über die Zukünftigen Ergebnisse des Würfelns können sich nur auf Tendenzen gründen, die wir in den Ergebnissen des Experiments wahrnehmen. D.h., das Experiment kann nur die Erwartung begründen, daß es so weitergehen wird, wie ⌊(⌋es⌊)⌋ das Experiment gezeigt hat. Aber wir können nicht erwarten, daß das Experiment, wenn fortgesetzt, nun Ergebnisse liefern k wird, die mehr als die des wirklich ausgeführten Experiments mit einer vorgefaßten Meinung über seinen Verlauf übereinstimmen. Wenn ich also z.B. Kopf & Adler werfe & in den Ergebnissen des Experiments keine Tendenz der Kopf- & Adlerzahlen finde, sich weiter einander zu nähern, so gibt das Experiment mir keinen Grund zur Annahme, daß seine [f|F]ortsetzung eine solche Annäherung zeigen wird. Ja die Erwartung dieser Annäherung muß sich selbst auf einen bestimmten Zeitpunkt beziehen, denn man kann nicht sagen, „ich man erwarte daß ein Ereignis einmal – in der unendlichen Zukunft – eintreten werde. [ Ja, die Erwartung dieser Annäherung

​

3. Ein Gedanke über die Darstellbarkeit der unmittelbaren Realität durch die Sprache:     „Der Strom des Lebens, oder der Strom der Welt, fließt dahin, & unsere Sätze werden, sozusagen, nur in Augenblicken verifiziert. Unsere Sätze werden nur von der Gegenwart verifiziert. – Sie müssen also so gemacht sein, daß sie von ihr verifiziert werden können. Sie müssen das Zeug haben, um von ihr verifiziert werden zu können. Dann haben sie also in irgend einer Weise die Kommensurabilität mit der Gegenwart [ Dann sind sie also in irgend einer Weise mit der Gegenwart kommensurabel ] & diese dies können sie nicht haben sein trotz ihrer raum-zeitlichen Natur, sondern diese muß sich zur Kommensurabilität verhalten, wie die Körperlichkeit eines Maßstabes zu seiner Ausgedehntheit, mittels mit der er mißt. Im Fall des Maßstabes kann man auch nicht sagen: „‚Ja, der Maßstab mißt die Länge trotz seiner Körperlichkeit; freilich, ein Maßstab, der nur Länge hätte, wäre das Ideal, wäre, der reine Maßstab’. Nein, wenn ein Körper Länge hat, so kann es keinen Körper ohne Länge ohne einen Körper geben – & wenn ich auch verstehe, daß in einem bestimmten Sinn nur die Länge des Maßstabs mißt, so bleibt doch kein Beistrich was ich in die Tasche stecke der Maßstab[;|,] – der Körper, & nicht die Länge.”

∫

Die Anschauungen neuerer Physiker stimmen mit den meinen Ich stimme mit den überein, wenn sie sagen, daß die Zeichen in ihren Gleichungen keine „Bedeutung⌊en⌋” mehr haben, & daß die Physik zu keinen solchen Bedeutungen gelangen könne, sondern bei den Zeichen stehen bleiben müsse: Ssie sehen nämlich nicht, daß diese Zeichen insofern Bedeutung haben – & nur insofern – als ihnen, auf welchen Umwegen immer, das beobachtete Phänomen entspricht, oder nicht entspricht.

​

Darstellung einer Linie als Gerade mit Abweichungen. Die Gleichung der Linie enthält einen Parameter, dessen d ◇◇◇ Verlauf die Abweichungen von der Geraden ausdrückt. Es ist nicht wesentlich, daß diese Abweichungen „gering” seien. Sie können so groß sein, daß die Lin⌊i⌋e einer Geraden nicht ähnlich sieht. Die „Gerade mit Abweichungen” ist nur eine Form der Beschreibung. Sie erleichtert es mir, einen [B|b]estimmten Teil der Beschreibung auszuschalten, zu vernachlässigen, wenn ich will. (Die Form „Regel mit Ausnahmen”.)

​

Alle „begründete Erwartung” ist Erwartung, daß eine bis jetzt beobachtete Regel weiter weiterhin gelten wird. [kein neuer Absatz] (Die Regel aber muß beobachtet worden sein & kann nicht selbst wieder blo [ß|s] erwartet werden.)

​

Die Logik der Wahrscheinlichkeit hat es mit dem Zustand der Erwartung nur soweit zu tun, wie die Logik überhaupt mit dem Denken.

​

Von der Lichtquelle Q wird ein Lichtstrahl ausgesandt, der die Scheibe AB trifft, dort einen Lichtpunkt erzeugt & dann die die Scheibe AB AC trifft⌊.⌋ & auf ihr einen Lichtpunkt erzeugt. Wir haben nun keinen Grund zur Annahme, daß der Lichtpunkt auf AB ˇwerde rechts von der Mitte M liegen, noch zur entgegengesetzten; aber auch keinen Grund anzunehmen, der Lichtpunkt auf AC werde auf der & nicht auf jener Seite von der Mitte m liegen. [ Wir haben nun keinen Grund, anzunehmen, daß der Lichtpunkt auf AB eher auf der einen Seite der Mitte M als auf der andern liegen wird; aber auch keinen Grund, anzunehmen, daß der Lichtpunkt auf AC werde auf der einen & nicht auf der andern Seite von ˇder Mitte m liegen. ] Das gibt also wiedersprechende Wahrscheinlichkeiten. 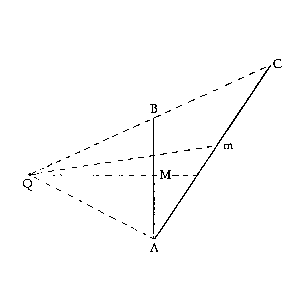Wenn ich nun eine Annahme über den Grad der Wahrscheinlichkeit mache, daß der eine Lichtpunkt in AM im Stück AM liegt, wie wird diese Annahme verifiziert? Wir meinen denken doch durch einen Häufigkeitsversuch. Angenommen nun dieser bestätigt die Auffassung, daß die Wahrscheinlichkeiten für das Stück A[m|M] & BM gleich sind ˇ(also für Am & Cm verschieden), so ist sie damit als die richtige erkannt & erweist sich also als eine physikalische Hypothese. Die [G|g]eometrische Konstruktion zeigt nur, daß die [g|G]leichheit der Strecken AM & BM kein Grund zu Annahme gleicher Wahrscheinlichkeit war.

∕∕

Was heißt es: den Goldbachschen Satz glauben? Worin besteht dieser Glaube? In einem Gefühl der Sicherheit, wenn wir den Satz aussprechen, oder hören? Das interessiert uns nicht. Ich weiß ja auch nicht wie weit dieses Gefühl durch den Satz selbst hervorgerufen sein mag. Wie greift der Glaube in diesen Satz ein? Sehen wir nach, welche Konsequenzen er hat, wozu er uns bringt. „Er bringt mich zum Suchen nach einem Beweis dieses Satzes”. – Gut, jetzt sehen wir noch nach, worin Dein Suchen eigentlich besteht; dann werden wir wissen wie es sich mit Deinem Glauben an den Satz verhält. [ … worin Dein was es mit dem Glauben an den Satz auf sich hat. ]

​

„Der Kretische Lügner”. Statt zu sagen „ich lüge”, könnte er auch hinschreiben „dieser Satz ist falsch”. Die Antwort darauf wäre: „Wohl, aber welchen Satz meinst Du?” – „Nun diesen Satz.” – „ich verstehe, aber von welchem Satz ist in ihm die Rede?” – „Von diesem.” – „Gut, & ˇauf welchen Satz spielt dieser an?” u.s.w. Er könnte uns so ◇ nicht erklären, was er meint ehe bis er zu einem kompletten Satz übergeht. – Man kann auch sagen: Der [F|f]undamentale Fehler liegt darin, daß man glaubt denkt ein Wort, z.B. „dieser Satz”, könne auf seinen Gegenstand gleichsam anspielen (aus der Entfernung hindeuten) ohne ihn vertreten zu müssen.

​

(Ein Satz der von allen Sätzen oder allen Funktionen handelt. Was meint man damit? stellt man sich darunter vor? Es wäre wohl ein Satz der Logik. Denken wir nun nur daran, wie wir de[n|r] Satz ~2n p = p bew[ei|ie]sen wird.)

​

Wenn ich annehme, die Messung ergebe, daß der Würfel genau & homogen ist, & die Ziffern auf seinen Flächen die Wurfresultate nicht beeinflussen, & die Hand die ihn wirft, bewegt sich ohne bestimmte Regel; folgt daraus eine die durchschnittlich gleichförmige Verteilung der Würfe 1 bis 6 unter den Wurfergebnissen? – Woraus sollte sie hervorgehen? Daß der Würfel genau & homogen ist kann doch keine durchschnittlich gleichförmige Verteilung von Resultaten begründen (Die Voraussetzung ist sozusagen homogen, die Folgerung ˇwäre gesprenkelt.) Und über die Bewegung beim Werfen haben wir ja keine Annahme gemacht. Mit der Gleichheit der beiden Heubündel hat man zwar begründet, daß der Esel zwischen in ihrer Mitte verhungern werde, aber nicht, daß er ungefähr gleich oft von jedem fressen. werde.) – Mit unseren Annahmen ist es auch vollkommen vereinbar daß mit dem Würfel 100 Einser nach einander geworfen werden, wenn Reibung, Handbewegung, Luftwiderstand so zusammentreffen. Die Erfahrung, daß das nie geschieht, ist eine, die diese diese Faktoren betrifft [ ist eine diese Faktoren betreffende ] . Und die Vermutung der gleichmäßigen Verteilung der Wurfergebnisse ist eine Vermutung über das Arbeiten dieser Faktoren [ Einflüsse ] .     Wenn wir man sag[e|t]n ein gleicharmiger Hebel auf den sy⌊m⌋metrische Kräfte wirken müsse werde in Ruhe bleiben, so heißt das weil keine Ursache vorhanden ist weshalb er ˇsich eher auf die eine als auf die andre Seite neigen sollte, so heißt das nur, daß, wenn wir ˇgleiche Hebelarme & symetrische Kräfte konstatiert haben & nun der Hebel sich nach der einen Seite neigt, wir dies aus den uns bekannten – oder von uns angenommenen – Voraussetzungen nicht erklären können. (Die Form die wir „Erklärung” nennen muß auch assy⌊m⌋metrisch sein); wie die Operation die aus „a & b” „2a & 3 b” macht.) Wohl aber können wir die ˇandauernde Ruhe des Hebels aus unsern Voraussetzungen erklären. – Aber etwa auch eine [S|s]chwingende Bewegung, die durchschnittlich gleich oft von der Mittellage Mitte nach rechts & von der Mittellage Mitte nach links gerichtet ist? Die Schwingende Bewegung nicht, denn in der ist ja wieder Assym⌊m⌋etrie. Nur die Sym⌊m⌋etrie in dieser Assymmetrie. Hätte sich der Hebel gleichförmig nach von rechts gedreht, so könnte man analog sagen: Mit der Symmetrie der Bedin- gungen kann ich die Gleichförmigkeit der Bewegung aber nicht ihre Richtung erklären.      Eine Die Ungleichförmigkeit der Verteilung der Wurfresultate ist mit der Symmetrie des Würfels nicht zu erklären. Und nur insofern erklärt diese Symmetrie die Gleichförmigkeit der Verteilung. – Denn man kann natürlich sagen: Wenn die Ziffern auf den Würfelflächen keine Wirkung haben, dann kann ihre Verschiedenheit nicht nicht eine Ungleichförmigkeit der Verteilung erklären; & gleiche Umstände können selbstverständlich nicht Verschiedenheiten erklären; soweit insofern also könnte man auf eine Gleichförmigkeit schließen. Aber woher dann überhaupt verschiedene Wurfresultate? Was diese … Gewiß, was diese erklärt muß ˇnun auch ihre ˇdurchschnittliche Gleichförmigkeit erklären. Die Regelmäßigkeit des Würfels stört nur eben diese Gleichformigkeit nicht.

​

Angenommen Einer der täglich im Spiel würfelt würde ˇetwa eine Woche lang nichts als Einser werfen, & zwar mit Würfeln die nach allen anderen Arten [ Methoden ] der Prüfung Untersuchung sich als gut erweisen & wenn ein [a|A]ndrer sie wirft auch die gewöhnlichen Resultate liefern geben. Hat er nun Grund zu denken, daß hier ein Naturgesetz besteht anzunehmen dem gemäß er immer Einser werfen muß wirft ; hat er Grund⌊:⌋ zu glauben, daß das nun so weitergehen wird, oder ˇvielmehr Grund anzunehmen, daß diese Regelmäßigkeit nicht lange mehr andauern wird kann ? Hat er also Grund das Spiel aufzugeben, da es sich gezeigt hat, daß er nur Einser werfen kann, oder weiterzuspielen, da es jetzt nur um so wahrscheinlicher ist, daß er beim nächsten Wurf eine höhere Zahl werfen wird? – Z In Wirklichkeit wird er sich weigern die Regelmäßigkeit als ein Naturgesetz anzuerkennen; zum mindesten wird sie lang andauern müssen, ehe er diese Auffassung in Betracht zieht. Aber warum? – Ich glaube, weil so viel frühere Erfahrung ˇseines Lebens gegen ein solches das Gesetz spricht, die alle – sozusagen – erst überwunden werden muß, ehe wir eine ganz neue Betrachtungsweise annehmen.

​

Wenn wir aus der relativen Häufigkeit eines Ereignisses auf seine relative Häufigkeit in der Zukunft Schlüsse ziehen, so können wir das natürlich nur nach der bisher tatsächlich beobachteten Häufigkeit tun. Und nicht nach einer, die wir aus der beobachteten durch irgend einen Prozess der Wahrscheinlichkeitsrechnung erhalten haben. Denn die berechnete Wahrscheinlichkeit stimmt mit jeder beliebigen tatsächlich beobachteten Häufigkeit überein, da sie die Zeit offen lässt.

​

Wenn sich der Spieler, oder die Versicherungsgesellschaft, nach der Wahrscheinlichkeit richten, so richten sie sich nicht nach der Wahrscheinlichkeitsrechnung, denn nach dieser allein kann man sich nicht richten, da, was immer geschieht, mit ihr in Uebereinstimmung zu bringen ist; sondern die Versicherungsgesellschaft richtet sich nach einer tatsächlich beobachteten Häufigkeit. Und zwar ist das notürlich eine absolute Häufigkeit.

​

Was zum Wesen der Welt gehört, kann die Sprache nicht ausdrücken.     Daher kann sie nicht sagen, dass alles fliesst. Nur was wir uns auch anders vorstellen könnten, kann die Sprache sagen.

​

Daß alles fließt, muß im in dem Wesen der Anwendung der Sprache auf die Wi[i|r]klichkeit liegen. [ Daß alles fließt, muß im Wesen der Berührung der Sprache mit der Wirklichkeit liegen. ] Oder ˇbesser: daß alles fließt, muß im Wesen der Sprache liegen.   Und, erinnern wir uns, : im gewöhnlichen Leben fällt uns das nicht auf – (sowenig wie die verschwommenen Ränder unseres Gesichtsfelds („weil wir so daran gewöhnt s⌊i⌋nd” wird mancher sagen). Wie, bei welcher Gelegenheit, glauben wir denn darauf aufmerksam zu werden? Ist es nicht, wenn wir Sätze gegen die Grammatik der Zeit bilden wollen?

​

4. „Nur die Erfahrung des gegenwärtigen Augenblicks hat Realität”. – Soll das heißen, daß ich heute [F|f]rüh nicht aufgestanden bin? – Oder, daß ein Ereignis, dessen ich mich in diesem Augenblick nicht entsinne erinnere , nicht stattgefunden hat? – Und „‚gegenwärtige Erfahrung’ – im Gegensatz wozu? Hier ist offenbar das Wort ‚gegenwärtig’ überflüssig Soll ◇ hier ‚gegenwartige’ Erfahrung’ im Gegensatz stehen zu zukunftiger & vergangener Erfahrung? Oder ist es ein Beiwort wie das Wort „rational” in „rationale Zahl” so daß man die beiden Wörter auch durch eines ersetzen könnte & das [b|B]eiwort auf eine grammatische Eigentümlichkeit hinweist. Und was wird in diesem Falle vom Subjekt ausgesagt wenn ihm Realität zugesprochen wird? Betonen wir hier nicht wieder eine grammatische Eigentümlichkeit , etwa als wenn man sagte: „… nur die Kardinalzahlen sind wirkliche Zahlen” (Kronecker soll gesagt haben, nur die Kardinalzahlen seien von Gott erschaffen, alles andere⌊n⌋ seien Menschenwerk.) – Heißt es ‚gegenwärtige Erfahrung’ im Gegensatz zu zukünftiger & vergangener, dann ist meint man mit diesen Erfahrungen etwa physikalische Vorgänge; & wenn ich das Bild von der Laterna magica gebrauche & dem Filmstreifen gebrauche & die Zeitlichen Beziehungen in räumliche übersetze so ist die gegenwärtige Erfahrung im physikalischen Sinn das Bild auf dem Filmstreifens das sich vor dem Objectiv der Laterne befindet (ich kann nicht sagen: „das sich jetzt vor dem Objectiv der Laterne befindet”.) Auf der einen Seite dieses Bildes liegen sind die vergangenen auf der andern die zukünftigen Bilder (die beiden Seiten sind durch Eigentümlichkeiten des Apparates charakterisiert). Das Bild auf de[m|r] Streifen Leinwand gehört der Zeit des Filmstreifens nicht an[. M|; m]an kann von ihm nicht in dem eben beschriebenen Sinne sagen, es sei gegenwärtig. (Im Gegensatz wozu? – Wenn man [d|D]as Wort [„|‚]gegenwärtig’⌊,⌋ ˇwenn man es hier benützt, so bezeichnet man nicht einen Teil eines Raumes im Gegensatz zu andern Teilen, sondern charakterisiert einen Raum.) Der Satz, nur die gegenwärtige Erfahrung habe Realität, wäre nun hier der Satz, daß nur das Bild vor dem Objektiv dem Bild auf der Leinwand entspricht. Und das wäre könnte allerdings ein Erfahrungssatz sein⌊&⌋ Aber hier läßt uns das Gleichnis ˇläßt uns hier in Stich, wenn wir nicht festsetzen, ˇdie Projektionsmethode nicht so festlegensetzen, daß das der Projektion „entsprechende” Bild des Filmstreifens das Bild von dem Objektiv heißen soll. die Entsprechung zwischen Film & Leinwand nicht (die Projektionsart) nicht so festsetzenlegen , daß sich dadurch das Bild auf dem Film welches dem Bild auf der Leinwand entspricht als das Bild vor dem Objektiv der Laterne ergibt.

​

Wer den Satz, nur die gegenwärtige Erfahrung sei real, bestreiten will (was ebenso falsch ist, wie ihn zu behaupten) wird etwa fragen, ob denn ein Satz wie „Julius Cäsar ging über die Alpen” nur den gegenwärtigen Geisteszustand desjenigen beschreibt, der sich mit dieser Sache beschäftigt. Und die Antwort ist natürlich: Nein! er beschreibt ein Ereignis, da[ß|s], wie wir glauben, vor ca 2000 Jahren stattgefunden hat. ⌊–⌋ (Wenn nämlich das Wort „beschreibt” so aufgefaßt wird, wie in dem Satz „der Satz ‚ich schreibe’ beschreibt, was ich gegenwärtig tue”.) Der Name Julius Cäsar bezeichnet eine Person. – Aber was sagt denn das alles? Ich scheine mich ja um die eigentliche philosophische Antwort drücken zu wollen! – Aber Nun , Sätze die von Personen handeln, d.h. Personennamen enthalten, können ˇebenc auf sehr verschiedene Weise verifiziert werden. – ⌊⌊ˇ Fragen wir uns nur, warum wir den Satz glauben. ⌋⌋ – Daß es ˇ z.B. denkbar ist, die Leiche Cäsars noch zu finden, hängt unmittelbar mit dem Sinn des Satzes über Julius Cäsar zusammen. Aber auch, daß es denkbar möglich ist, eine Schrift zu finden, aus der hervorgeht, daß so ein Mann nie gelebt hat & seine Existenz zu bestimmten Zwecken erdichtet worden ist. sei. Solche Diese Möglichkeiten gibt es ˇaber nicht für einen Satz: „ich sehe einen roten Fleck über einen grünen dahinziehen” ˇnicht; und das ist es, was wir damit meinen, wenn wir sagen, dieser Satz habe in … Sinn, als … daß dieser Satz in unmittelbarerer Art Sinn hat, als der jener über Julius Cäsar. [ … Und das meinen wir, wenn wir sagen, dieser Satz habe … ]

​

5. 1) „Ich habe Schmerzen”   „N hat Schmerzen” dagegen ⌊2)⌋: „Ich habe graue Haare”              „N hat graue Haare” Die verschiedenen ˇphilosophischen Schwierigkeiten & Confusionen in Verbindung mit dem ersten Beispiel lassen sich zum größten Teil auf die Verwechslung der Grammatik der Fälle 1 & 2 zurückführen.     Es hat Sinn zu sagen: „ich sehe seine Haare, aber nicht die meinen” oder ˇanalog „ich sehe meine Hände Kinder täglich, aber nicht die seinen” & dieser Satz ist analog dem: „ich sehe meine Kinder Wohnung täglich, aber nicht die seinen seine.” – Dagegen ist Unsinn: „ich fühle meine Schmerzen aber nicht die seinen”    Die Ausdrucksweise unserer Sprache wie sie in den einzelnen Fällen 1 & 2 ist natürlich nicht ‚falsch’ aber ˇsie ist irreführend. „Eine herrenlose Wohnung”, „herrenlose Zahn⌊-⌋Schmerzen”. Es gibt Menschen die Untersuchungen darüber anstellen „ob es ungesehene Gesichtsbilder gibt” & sie glauben, daß das eine Art wissenschaftlicher Untersuchung ⌊(⌋über diese Phänomene⌊)⌋ ist.   „Wie ein Satz verifiziert wird, das sagt er”⌊:⌋ & nun sieh Dir darauf hin die Sätze an: „Ich h⌊a⌋be Schmerzen”, „N hat Schmerzen”. Wenn nun aber ich der N bin?! – Dann haben dennoch die beiden Sätze verschiedenen Sinn.    „Die Sache ist doch ganz einfach: ich spüre freilich seine Zahnschmerzen nicht, aber er spürt sie eben (& so sind alle Verhältnisse ˇdoch symmetrisch).” Aber dieser Satz ist eben Unsinn. – Um nun die Assymmetrie in der Erfahrung mit Bezug auf mich & den Andern klar deutlich zum Ausdruck zu bringen, könnte ich man nun eine assymetrische Ausdrucksweise vorschlagen: [a|A]lte Ausdrucksweise: L.W. hat Schmerzen L.W. hat Schmerzen in seiner linken Hand. N. hat Schmerzen N. heuchelt Schmerzen in seiner Hand Ich bedauere N., weil er Sch. hat [n|N]eue Ausdrucksweise: Es sind Schmerzen vorhanden Es sind Schmerzen in der linken Hand des L.W. N. benimmt sich wie L.W. wenn Sch. vorhanden sind N heuchelt das ein Benehmen des L.W. wenn Sch. in seiner Hand sind. Ich bedauere N, weil er sich benimmt, wie etc.

​

Da wir für jeden ˇsinnvollen Ausdruck der alten Ausdrucks- weise einen der neuen setzen & für verschiedene alte, verschiedene neue, so muß, was Eindeutigkeit & Verständlichkeit anbelangt, die neue Ausdrucksweise der alten gleichwertig sein. – Aber könnte man denn nicht eine solche assymetrische Ausdrucksweise au ebensogut für Sätze der Art „ich habe graue Haare„, „N hat graue Haare” konstruieren? Nein[; m|. M]an muß nämlich verstehen daß der N Name „L.W.” in den Sätzen der rechten Seite sinnvoll muß durch andere Namen ersetzt werden können. Und ist das nicht der Fall dann braucht weder „L.W.” noch ein anderer Name in diesen Sätzen vo⌊r⌋zukommen. Ersetzt man nämlich L.W. durch den einen andern Namen eines andern Menschen, so heißt das wird etwa gesagt daß ich in der Hand eines anderen Körpers als des meinigen Schmerzen empfinde. Es wäre z.B. denkbar, daß ich mit einem Andern Körper wechsle, etwa aufwache, meinen ˇalten Körper mir gegenüber auf einem Sessel sitzen sehe & mich im Spiegel sehend fände daß ich d[en|as] Ko Gesicht & den Körper meines Freundes angenommen habe. Ich betrachte nun den Personennamen als Name des Körpers. Und in diese es hat nun Sinn zu sagen: „ich habe im Körper des N (oder im Körper N) Zahnschmerzen (in der assymmetrischen Ausdrucksweise: ⌊„⌋i[m|n] Körper des einem Zahn des N sind Schmerzen”); aber ˇes hat keinen Sinn zu sagen „ich habe auf dem Kopf des N. graue Haare”, außer, das soll dasselbe heißen, wie ⌊:⌋ „N hat graue Haare”.     Aber ist ⌊(⌋denn⌊)⌋ die vorgeschlagene assymmetrische Ausdrucksweise richtig? Warum sage ich „N benimmt sich wie L.W wenn er …”? Wodurch ist denn L.W. charakterisiert? Doch durch die Formen etc seines Körpers & durch dessen kontinuierliche Existenz im Raum. Sind aber diese Dinge für die Erfahrung der Schmerzen wesentlich? Könnte ich mir nicht folgende Erfahrung denken: ich wache mit Schmerzen in der linken Hand auf & finde, daß sie ihre Gestalt geändert hat & jetzt so aussieht wie die Hand meines Freundes, während er meine Hand erhalten hat. Und worin besteht die Kontinuität meiner Existenz im Raum? Wenn mir jemand verläßlicher erzählte, er sei während ich geschlafen habe bei mir gesessen, plötzlich sei mein Körper verschwunden & sei plötzlich wieder erschienen – ist es unmöglich das zu glauben? – Und worin besteht etwa die Kontinuität meines Gedächtnisses? In welcher Zeit ist es kontinuierlich? O Oder besteht die Kontinuität darin, daß im Gedächtnis keine Lücke ist. Wie im Gesichtsfeld keine ist. (Denn überlege nur, wie wir den blinden Fleck merken!) Und was hätte diese Kontinuität mit der zu tun die für den Gebrauch des N Personennamens L.W. wesentlich ist [ von Bedeutung ist ] ? Die Erfahrung der Zahnschmerzen läßt sich in ganz anderer Umgebung als der von uns gewohnten denken. (Denken wir doch nur⌊,⌋ daran daß man tatsächlich Schmerzen in der Hand d.h. im Ort der Hand haben kann obwohl es diese sie im physikalischen Sinne gar nicht mehr gibt, weil sie einem amputiert worden ist.) In diesem Sinne könnte man Zahnschmerzen ohne Zahn, Kopfschmerzen ohne Kopf etc. haben. Wir machen eben hier einfach eine Unterscheidung wie die zwi⌊s⌋chen Gesichtsraum & physikalischen Raum oder Gedächtniszeit & physikalischer Zeit. – Danach nun ist es unrichtig die Ausdrucksweise einzuführen „N benimmt sich wie L.W. wenn …” Man könnte vielleicht sagen „N benimmt sich wie der Mensch in dessen Hand [s|S]chmerzen sind”. Warum sollte man aber überhaupt die Erfahrung der Schmerzen zur Beschreibung des bewußten Benehmens heranziehen? – Wir wollen doch einfach zwei verschiedene Erfahrungsgebiete tre trennen; wie wenn wir Tasterfahrung & Gesichtserfahrung an einem Körper trennen. Und verschiedener kann nichts sein, als die Schmerzerfahrung & die Erfahrung einen menschlichen Körper sich winden sehen, Laute ausstoßen zu hören etc.. Und zwar besteht hier kein Unterschied zwischen meinem Körper & dem des Andern, denn es gibt auch die Erfahrung die Bewegungen des eigenen Körpers zu sehen & die von ihm ausgestoßenen Laute zu hören.

​

Denken wir uns unser Körper würde aus unserem Gesichtsfeld entfernt, etwa indem man ihn gänzlich durchsichtig machte; er behielte aber die Fähigkeit bei in einem geeigneten Spiegel in der uns gewohnten Weise zu erscheinen so daß wir etwa die sichtbaren Äußerungen unserer Zahnschmerzen wesentlich wie die eines fremden Körpers wahrnähmen. Dies ergäbe auch eine ganz andere Koordination zwischen sehendem Auge & Gesichtsraum als die uns selbstverständlich erscheinende alltägliche. (Denke an das Zeichnen eines Vierecks mit seinen Diagonalen im Spiegel.) Wenn wir uns aber so die Moglichkeit denken können, daß wir unsern ˇsichtbaren Körper nur als Bild in einem Spiegel kennten so ist einem auch denkbar daß dieser Spiegel wegfiele & wir ihn nicht anders sähen als irgend einen andern menschlichen Körper. – Wodurch wurd wäre er dann aber als mein Körper charakterisiert? Nun nur dadurch daß ich ˇ z.B. die Berührung dieses Körpers fühlen würde nicht aber die eines andern, etc.. So ist es auch nicht mehr wesentlich daß der Mund unterhalb des sehenden Auges meine Worte spricht. (Und das ist von großer Wichtigkeit). Auch wenn ich meinen Körper sehe wie ich ihn jetzt sehe d.h. von seine[m|n] Auge⌊n⌋ aus ist es denkbar daß ich mit Andern den Körper tausche. Die Erfahrung bestünde einfach in einer darin in dem, was man als eine S⌊s⌋prunghafte Änderung meines Körpers & seiner Umgebung nennen beschreiben würde. •E •A •D •C •B Ich würde einmal die Körper A B C D von E aus & E von seinen A den Augen dieses Körpers sehen & plötzlich etwa C D E A von B aus & B aus dessen Augen, etc. Noch einfacher aber wird die Sache wenn ich alle Körper meinen, sowie die fremden, überhaupt nicht aus Augen sehe & sie mir also, was ihre visuelle Erscheinung betrifft alle auf gleicher Stufe stehen. Dann ist es klar, was es heißt, daß ich im Zahn des Andern Schmerzen haben kann; – wenn ich dann überhaupt noch bei der Bezeichnung bleiben will, die einen Körper „meinen” nennt & also einen andern den „eines Andern”. Denn es ist nun vielleicht praktischer die Körper nur einfach mit Eigennamen zu bezeichnen. – Es gibt also jetzt eine Erfahrung, die der Schmerzen in einem Zahn eines der existierenden menschlichen Körper; das ist nicht die die wir ich in der unserer gewöhnlichen Ausdrucksweise mit den Worten „A hat Zahnschmerzen” beschriebe, sondern mit den Worten „ich habe in einem Zahn des A [s|S]chmerzen”. Und es gibt die andere Erfahrung einen Körper, sei es meiner oder eine anderer sich winden zu sehen. Denn, vergessen wir nicht: Die Zahnschmerzen haben zwar einen Ort in einem Raum, sofern man z.B. sagen kann, sie wandern oder seien an zwei Orten zugleich, etc.: Ab aber ihr Raum ist nicht der visuelle oder physikalische. – Und nun haben wir zwar eine neue Ausdrucksweise, sie ist aber nicht mehr assymetrisch. Sie bevorzugt nicht einen Körper, einen Menschen auf zum Nachteilc der andern, ist also nicht solipsistisch. – So ist alle Erfahrung alles ohne Ansehen der Person verteilt. Aber wir teilen anders wir teilen anders. Es werden die Dinge in unsrer Betrachtungsweise anders zusammengefaßt. Wie wenn man einmal die Zeit zum Raum rechnet & einmal nicht, oder wie wenn man einen Wald als Holzblock mit Löchern ansähe. Oder die Bahn des Mondes um die Sonne einmal als Kreis Kreisbahn um die Erde die sich verschiebt, ein andermal als Wellenlinie die um die Sonne läuft. (Wäre die Erde etwa nicht sichtbar, so wäre könnte es eine merkwürdige neue Betrachtungsweise sein die Be Wellenbewegung um die Sonne als Kreisbahn um einen kreisenden Körper [ um ein kreisendes Centrum ] zu aufzufassen.) Man könnte auf diese Weise gewisse Vorurteile zerstören die auf die besondere uns geläufige Betrachtungsart aufgebaut wären. – Sehr klar wird der Charakter der anderen Betrachtungsweise wenn man an die analoge Veränderung Verschiebung der Grenzen durch die Einführung des Bgriffs der Gedächtniszeit denkt. Es ist ganz ähnlich der veränderten Betrachtung der Mondbewegung Eine Grenze die früher mit anderen in der Zeichnung zusammen lief wird plötzlich stark ausgezogen & hervorgehoben. ‒ ‒ ‒ ‒ ‒ ‒

​

Die mathematische Frage muß so exact sein wie der mathematische Satz. Wie irreführend die Ausdrucksweise der Wortsprache den Sinn der mathematischen Sätze darstellt, sieht man wenn man sich die Multiplizität eines mathematischen Beweises vor Augen führt stellt & bedenkt daß der Beweis zum Sinn des bewiesenen Satzes gehört d.h. den Sinn bestimmt. Also nicht etwas ist, was uns gezeigt wird damit wir was bewirkt daß wir einen bestimmten Satz glauben, sondern etwas was uns zeigt, was wir glauben, wenn hier von Glauben eine Rede sein kann. Begriffswörter in der Mathematik: Primzahl, Kardinalzahl etc.. Es scheint darum unmittelbar Sinn zu haben wenn gefragt wird: „Wieviel Primzahlen gibt es⌊?⌋” „Es glaubt der Mensch wenn er nur Worte hört …”) In Wirklichkeit ist diese Wortzusammenstellung ˇeinstweilen Unsinn; bis für sie eine besondere Syntax gegeben wurde. Sieh den Beweis dafür an,, „daß es unendlich viele Primzahlen gibt” & dann die Frage, die er zu beantworten scheint. Das Resultat eines intrikaten Beweises kann nur in sofern einen einfachen Wortausdruck haben, als das System von Ausdrücken dem dieser Ausdruck angehört in seiner Multiplizität einem System solcher Beweise entspricht. – Die Confusionen in diesen Dingen ist sind ganz darauf zurückzuführen, daß man die Mathematik als eine Art Naturwissenschaft behandelt. Und das wieder hängt damit zusammen, daß sich die Mathematik von der Naturwissenschaft abgelöst hat. Denn solange sie in unmittelbarer Verbindung mit der Physik betrieben wird [es|is]t es klar, daß sie keine Naturwissenschaft ist. (Etwa, wie man einen Besen nicht für ein Einrichtungsstück des Zimmers halten kann, solange man ihn dazu benützt die Einrichtungsgegenstände zu säubern.)

​

In der Mathematik gibt es kein „noch nicht” & kein „bis auf weiteres” (außer in dem trivialen Sinne in welchem mann ˇsagen kann man habe noch nicht 1000-stellige Zahlen mit einander multipliziert⌊).⌋ hat).

​

Der Punkt √2 ist wesentlich der Endpunkt der Konstruktion. 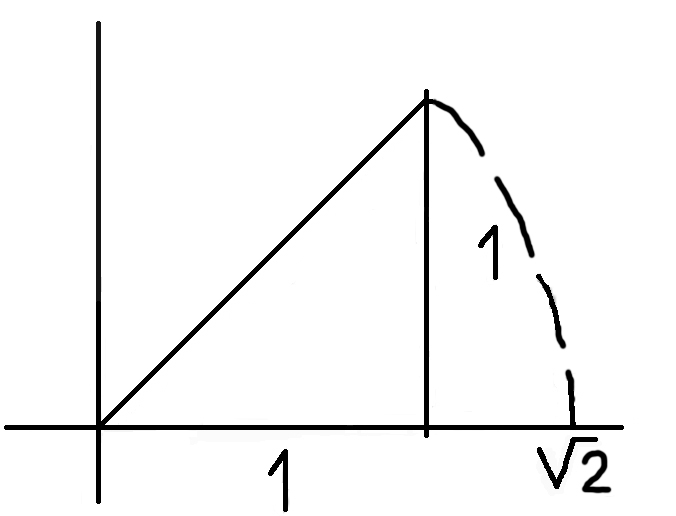Und der Ausdruck „der Endpunkt der Konstruktion ist hier keine Beschreibung im Russellschen Sinne. Es ist nicht von einer bestimmten Länge die Rede, die auch so gewonnen werden kann. Und wie der mathematische Satz die Endfläche eines Beweiskörpers so ist wie hier das Resultat der Konstruktion der Endpunkt der Konstruktion & sonst nichts. Wie auch das 5-Eck das Ende der 5-Ecks-Konstruktion.

​

Daher kann ich auch von einer Klasse von Punkten die dem Punkt √2 analog sind nur reden wenn ich von einer Klasse analoger Konstruktionen spreche rede .

​

Wenn mir eine endliche Reihe von Ziffern gegeben ist so kann ich offenbar jede der folgenden Fragen fra stellen: ⌊1)⌋ Findet sich in ihnen eine Periode? ⌊2)⌋ Welche? 3) Ist es die Periode ⌊(⌋z.B.⌊) ⌋ 1414 … Da hier jede dieser Fragen zu stellen ist, glaubt man, es müssen auch dort wo eine von ihnen in einem neuen Sinn gestellt wird sich die andern eo ipso stellen lassen. So sagt man, die periodische Division 1 : 3 = 0˙3̇ habe die Frage beantwortet ob in der Entwicklung des Quotienten 1 : 3 lauter 3 stehen werden. Und die Division scheint nun alle die Fragen beantwortet zu haben: „Gibt es hier eine Periode?” „Welche?”, “„Ist es z.B. die Periode 1414 …?’ „Geht der Dezimalbruch ohne Periode in's Unendliche fort?” Folgt nun daraus daß einen die periodische Division verstanden hat indem er, wie wir sagen würden, einsieht daß 1 : 3 = 0,3   1 nun immer so weiter gehn muß, – folgt daraus, daß er nach einer Periode suchen kann wenn noch keine zu sehen ist? Kann er also, nach dem er 1 : 3 = 0,3   1 periodisch verstan aufgefasst hat damit auch die Periode von 1 : 7 finden? finden? d.h. kann er sie suchen? Offenbar nicht. D.h., die Frage „Ist 1 : 7 periodisch”, hat für Ihn ihn keinen Sinn, wohl aber nicht die Frage „Wird 1 : 7 nach den ersten 2, 3, 4 Stellen periodisch”. „Kommt die Entwicklung von 1 : 7 jemals zu einem Ende” ist für ihn [S|s]innlos, ebenso ˇsinnlos wie die Frage „liefert 1 : 7 einen endlosen nicht periodischen Dezimalbruch oder einen periodischen”; dagegen hat die Frage Sinn “„wird 1 : 7 nach den ersten 4 Stellen periodisch”? & natürlich auch die Frage “„ist die Periode 0˙14̇ 14 …”.   Wenn er aber nun die Periode von 1 : 7 gefunden hätte, hätte er dann nicht doch alle jene Fragen damit beantwortet? Nein, nur die, nach deren Antwort er hat suchen können. Oder auch: die andern f Fragen hatten nur den Sinn den die gefundene Antwort ihnen gibt. Erklären wir dies auf andere Weise: Angenommen wir hatten jemandem multiplizieren gelehrt, aber nicht dividieren. Er hätte nun gefunden daß 14 × 15 = 210 ist & ich sagte ihm „, dieses Resultat können wir auch so ausdrücken: „210 : 15 = 14”. Hätte damit nun die Fragestellung auf die das Dividieren antwortet einen Sinn erhalten? Nein, die ist eine ganz andere deren Grammatik uns erst die Methode des Dividierens gibt. Ich hätte auch einen Menschen nicht multiplizieren gelehrt dem ich die Definition 1 × 1 = 1 gegeben hätte.

​

Die mathematischen Sätze als Mittel um die Beweise zu katalogisieren. (Ursell)

​

Eine Hypothese als unumstößliche Regel der Darstellung angenommen, wird zum Koordinatensystem.

​

“Schnitt” ist nach der üblichen Erklärung wirklich das, was sich mit allen den Rationalzahlen vergleichen läßt. Denn wenn man den Schnitt z.B. an der √2 am Beispiel der √2 erklärt, so zeigt man nur daß man in diesem Falle eine Definition von ‘größer’ & ‘kleiner’ geben kann die der der für die Rationalzahlen ähnlich [ analog ] ist. Nämlich √2 ≷ n ≝ 2 ≷ n²(Ƒ) .

​

Unbewußte Zahnschmerzen. Was heißt der Satz: „ich bin mir meiner Zahnschmerzen bewußt”. „Ich bin mir meiner Armut bewußt” ist ≠ „ich bin arm”. Dagegen: ich bin mir meiner Zahnschmerzen bewußt = ich habe Zahnschmerzen. Es sei denn ich führe eine neue Alternative in meiner Ausdrucksweise ein; dann aber muß ich erst ihre Anwendung zeigen sonst habe ich ihr noch keinen Sinn gegeben.

​

[zu „Schmerzen”] Muß sich denn nicht eine Welt beschreiben lassen, worin der solipsistische Fehler uns weniger nahe liegt. Wo die Tatsachen solche sind, daß wir weniger leicht zu einer einseitigen Grammatik verführt werden?

​

In meinen Betrachtungen der Mathematik [ über die Mathematik ] spielen winzige Veränderungen der symbolischen Ausdrucksweise eine Rolle. Was so gesagt [ dargestellt ] klar & durchsichtig ist, kann, ein wenig anders gesetzt, undurchsichtig oder irreführend sein.

​

‚Jemandem für etwas dankbar sein’ analog ‚jemanden erwarten’, etc..

​

Zeichnung eines 4Dimensionalen Würfels (als Erklärung meiner Auffassung der perspektivischen Zeichnung als 3-dimensionaler). [Gehört vielleicht zur Betrachtung des math. Beweises als Ornament]

​

Das Gesichtsbild wenn man feinen Regen niedergehn sieht: man sieht eine Bewegung, aber nicht etwas Bestimmtes sich bewegen.

​

Schädlichkeit der Ausdrucksform „Sinn”, „Bedeutung”, die immer wieder die Idee von Schatten (Geistern) hinter den Wörtern & Sätzen geben.

​

„Ich denke mir viel mehr, als ich sage” – wie kann man das vergleichen?

​

Was heißt „Gegenstände zählen”?

​

Wir mischen uns nicht in das, was der Mathematiker tut, erst wenn er behauptet Metamathematik zu treiben, dann kontrollieren wir ihn.

​

Wenn wir uns einige male rasch im Kreis herumdrehen & dann stehen bleiben, so scheint sich das Zimmer um uns zu drehen & doch sehen wir nicht, daß Gegenstände um uns dabei unserm Blick entschwinden & andere in unser Gesichtsfeld treten, wie es doch bei einer Drehung des Zimmers der Fall sein müßte. Ganz ähnlich dem ist es aber, wein ein Musikstück so gespielt wird, daß es uns scheint, es würde schneller & schneller gespielt & dabei müssen wir uns sagen daß sich das Tempo im Ganzen nicht merkbar verändert.

​

Man kann zu dem ersten Fall sagen: es gibt eben nicht nur visuelle Bewegung.

​

Schwanken des Begriffs ‚Wortart’. Ist “3” die gleiche Wortart wie ‘4’?

​

1 Umarbeitung. ⇒Zweite Umarbeitung im großen Format

​

Wie kann man von vom ‘vVerstehen’ & ‘nicht vVerstehen’ eines Satzes reden, – ist er es nicht erst ein Satz, wenn man ihn versteht?

​

D.h.: [k|K]ann denn nicht, eine Zusammenstellung von Sesseln, z.B., ein Satz sein, wenn man sie als solchen versteht & andernfalls hat sie doch nicht das Geringste mit einem Satz zu tun & man kann nicht davon reden, ‘sie zu verstehen’.

​

Man kann sagen: eine chinesische Aufschrift sagt mir so wenig wie ein Tapetenmuster oder etwa die Stellung von Sesseln in meinem einem Zimmer. – Und anderseits könnte auch das Tap⌊e⌋tenmuster & die Gruppe von Stellung der Sesseln mir ˇnach gehöriger Übereinkunft etwas mitteilen.

​

Das zeigt an daß ich die Bedeutungen des Wortes ‘verstehen’ & des Wortes ‘Satz’ hier zu wenig spezialisiert habe.

​

Es hat, wie wir das Wort ‘verstehen’ gebrauchen, keinen Sinn zu fragen “verstehst Du diese Baumgruppe” es sei ◇ denn daß jemand im Begriffe sei eine Sprache zu lernen 2 deren Ausdrucke etwa Gruppierungen von Bäumen wären.

​

“Das Verstehen fängt erst mit dem Satz an.”   Dadurch hat man die Bedeutung des Wortes “verstehen” auf ein bestimmtes Gebiet festgelegt.

​

Es gibt keine Metalogik. Auch das Wort “verstehen”, der Ausdruck “einen Satz verstehen”, sind nicht metalogisch.

​

Es ist doch seltsam, daß die Wissenschaft & die Mathematik die Sätze gebraucht : , aber vom Verstehen dieser Sätze nicht spricht.

​

Man sieht im Vers⌊t⌋ehen das Eigentliche, im Zeichen das Nebensächliche. – Übrigens, wozu dann das Zeichen überhaupt? – Nur um sich Anderen verständlich zu machen? Aber wie ist das möglich? – Man sieht da Es wird da das Zeichen als eine Medizin an angesehen, die im Andern die gleichen Zustände hervorrufen soll, die ich habe. wie ich sie habe.

​

Auf die Frage: “was meinst Du?” (etwa mit dieser Handbewegung) ist die Antwort: “ich meine p” ( ich meine, etwa: Du sollst hinausgehen) & nicht “ich meine, was ich mit dem Satz ‘p’ meine”.

​

3 Wenn Frege gegen die formale Auffassung der Arithmetik spricht, so sagt er gleichsam: diese kleinlichen Erklärungen, die Zeichen Symbole betreffend, sind müßig, wenn wir die Zeichen verstehn. Und das Verstehn wäre quasi das Sehen eines Bildes, aus welchem demc alle Regeln folgen⌊,⌋ (wodurch sie verständlich werden. Frege scheint schien aber nicht zu sehen, daß dieses Bild selbst wieder ein Zeichen ist, oder ein Kalkül, der uns den geschriebenen Kalkül erklärt.    Und, was wir ˇ im Allgemeinen ‘ [V|v] erstehen einer Sprache’ nennen, ist im Allgemeinen überhaupt von der Art des Verständnisses, welches das wir für einen Kalkül kriegen, wenn wir z.B. den Grund seiner Entstehung oder seine praktische … seinen Ursprung, seine Genesis, oder seine praktische Anwendung kennen lernen. Und auch da lernen wir einen übersichtlichern Symbolismus statt des fremdern kennen. (Wie wenn Denken wir es hätte [e|E]iner das Schachspiel zuerst als Schreibspiel kennen lernte gelernt hätte & ihm später erst ˇwäre ihm die ‘Deutung’ dieses Spiels als eines Brettspiels gezeigt würde worden.) Verstehen heißt hier etwas [ä|Ä]hnliches wie Übersehen.

​

Wenn ich jemandem einen Befehl gebe, so ist es mir ganz genug, ihm Zeichen zu geben. Und ich würde ˇeinen Befehl hörend nie sagen: das sind ja nur Worte, & ich muß hinter die Worte dringen. Und wenn ich jemand etwas gefragt hätte & er gibt mir eine Antwort (also ein Zeichen), bin ich zufrieden – das war es gerade, was 4 ich erwartete – & wende nicht ein: “das ist ja eine bloße Antwort”. (Es ist klar, daß nichts andres erwartet werden konnte, & daß die Antwort den Gebrauch einer Sprache, eines bestimmten Sprachspiels, voraussetzte; wie alles was wir sagen können.

​

Wenn man aber sagt: “wie soll ich wissen, was er meint, ich sehe ja nur seine Zeichen?”, – so sage ich: “wie soll er wissen, was er meint; er hat ja auch nur seine Zeichen”.

​

Die Sprache muß für sich selbst sprechen

​

Gesprochenes kann man nur durch die Sprache erklären, darum kann man die Sprache selbst als solche in diesem Sinne nicht erklären.     Die ganze Sprache kann man nicht interpretieren. Eine Interpretation ist immer nur eine im Gegensatz zu einer anderen. Und jede hängt sich an das erklärte Zeichen & erweitert vergrößert die Sprache.

​

Man kann auch sagen: Die Meinung fällt aus der Sprache heraus; denn wenn gefragt wird, man fragt, was ein Satz meint, ⌊(⌋so⌊)⌋ wird dies wieder durch einen Satz gesagt. // ; denn die Frage, was ein Satz meint, wird durch einen Satz beantwortet. // // denn was ein Satz meint, wird wieder durch einen Satz gesagt //

​

5 “Was hast Du mit diesen Worten gemeint?” “ Hast Du gemeint, was Du gesagt hast Hast Du diese Worte gemeint ?” (oder nur gesagt).

​

Die zweite Frage steht zur ersten nicht in dem Verhältnis, wie die Frage “bist Du verliebt?” zu der “wen liebst Du?”.   Auf die erste Frage kommt ein Satz (ein weiteres Zeichen) zur Antwort; das was man eine Erklärung des Sinnes nennt. [ … zur Antwort, eine Erklärung des Sinnes der ursprünglichen Worte. ]

​

Die erste dieser Fragen ist nicht eine genauere Bestimmung zur zweiten. (Es ist also nicht der Fall “bist Du verliebt, & wen liebst Du”.)   Auf die erste Frage kommt ein Satz (ein weiteres Zeichen) zur Antwort der den ersten ersetzt; eine Erklärung ˇdes Sinnes des ursprünglichen Zeichens. Die zweite Frage fragt nicht nach einer Erklärung.

​

Der zweiten Frage ähnlich ist die: “hast Du das im Ernst oder im Spaß gemeint?”

​

Dem Worte “meinen” analog wird das Wort “verstehen” gebraucht.

​

6   Das Wort “verstehen”, wie das Wort “meinen”, wird in mit verschiedenen Bedeutungen verwendet. // in mehrfacher Bedeutung verwendet. // In einer Art der Anwendung bedeutet es eine psychische Reaktion beim Hören, Lesen, Aussprechen etc. des Satzes. Das Verstehen ist dann hier das Phänomen, welches sich einstellt, wenn ich den Satz einer mir geläufigen Sprache höre oder lese & das welches ausbleibt, sich nicht einstellt, wenn ich etwa einen chinesischen Satz höre.

​

Das Lernen der Sprache steht zu dem Verstehen in diesem Sinne im Verhältnis der Ursache zur Wirkung.

​

Und wenn man das Verstehen des geschriebenen Satzes die seelische Reaktion nennt, die der Satz, wie er an uns vorbeiläuft, hervorruft erzeugt , dann ist dieses Verstehen ⌊(⌋wieder⌊)⌋ die Wirkung des Satzzeichens auf den, der es liest. uns.     Dieses Das Verständnis // Verstehen // geschieht nur so wie das Hören des Satzes & begleitet das Hören. es.     Ich kann in diesem Sinn von einem ‘erleben’ des Satzes reden.     Der Satz, wenn ich ihn verstehe, bekommt für mich Tiefe    “Ich sage das nicht nur, ich meine auch etwas damit”. – Wenn man überlegt, was dabei in uns vorgeht, wenn wir Worte meinen (& nicht bloß sagen), so ist es uns, als wäre dann etwas mit diesen Worten 7 gekuppelt, während sie sonst leer liefen. – Als ob sie, etwa gleichsam , in uns eingriffen.

​

¥ ⌊ ⋎ p. 21⌋

​

Ich verstehe einen Befehl als Befehl, d.h. ich sehe in ihm nicht nur diese Struktur von Lauten oder Strichen, sondern sie hat – sozusagen – einen Einfluß auf mich. Ich reagiere auf einen Befehl (auch ohne ihn zu befolgen) anders, als auf eine Mitteilung oder Frage. (Ich lese ihn auch mit anderem Tonfall, mit anderer Geste.)

​

Dem Das Verstehen, in diesem Sinne, eines Satzes ist das mit dem Verstehen eines Bildes ähnlich. zu vergleichen. Und hier gibt es wieder verschiedene Fälle. Denken wir uns eine ◇◇◇ Zeichnung die eine Gruppe von Gegenst. im Raum räumlicher Gegenstände darstellen soll; aber wir seien sind unfähig einen ˇbestimmten Teil des Bildes raumlich als räumliche Darstellung zu sehen sondern sehen nur Flecke & Striche in auf der Bildfläche. Wir können dann sagen, wir verstehen diesen Teil des Bildes nicht. – Ich sage aber auch, ich verstehe das Bild nicht, wenn ich zwar alles räumlich sehe, die räumlichen Gestalten aber solche sind nicht als mir wohlbekannte Gegenstande (Bäume, Tiere, Häuser etc.) wiedererkenne.    Angenommen etwa das Bild stellte eine Gruppe von Menschen dar & die Menschen darauf wären etwa einen Zoll lang. Gäbe es nun ˇwirkliche Menschen ˇvon dieser Länge so könnten 8 wir sie in dem Bild erkennen, das Bild als lebensgroße [d|D]arstellung empfinden; & es würde uns nun einen ganz anderen Eindruck machen, obwohl doch die Illusion der dreidimensionalen Gegenstände ganz die gleiche wäre, als im Falle wie wenn das Bild Menschen der gewöhnlichen Größe darstellen sollte. Und der Eindruck , den das Bild macht, des Bildes, die Art wie ich es auffasse, existiert ˇnun unabhängig davon daß ich Menschen der gewöhnlichen Größe oder Zwerge von einem Zoll Länge gesehen habe, wenn auch dies die Ursache des dieses Eindrucks sein mag. (Ebenso, wie ich zwar ˇ vielleicht die Zeichnung eines Würfels ˇvielleicht nur darum räumlich als Würfel sehe, weil ich ˇso oft ˇ einen wirkliche⌊ n ⌋ Würfel gesehen habe; aber die Beschreibung des räumlichen Gesichtsbildes ˇenthält nichts von dem, enthält, was einen ‘wirklichen’ Würfel von einem gemalten gezeichneten unterscheidet.)

​

Den verschiedenen Erlebnissen, wenn ich ein Bild einmal so, ⌊–⌋ einmal so, sehe, ist es zu vergleichen, wenn ich einen Satz einmal mit Verständnis, & einmal ohne Verständnis lese. (Erinnere Dich daran, wie es ist, wenn man einen Satz mit falscher Betonung liest, ihn daher nicht versteht, & nun auf einmal darauf kommt, wie er zu lesen ist.)    (Lesen einer schleuderhaften Schrift.)

​

Wenn man eine Uhr abliest, so sieht 9 man einen Komplex von Strichen, Flecken, etc.; aber man sieht ihn auf bestimmte Weise, wenn man ihn als Zifferblatt & Zeiger auffaßt. (Wie man den Orion Mond als Mann Gesicht, aber auch anders sehen kann.)

​

Denke auch an den Unterschied des Verständnisses, wenn man in einem Satz ein Wort einmal als dem einen Wort, einmal als dem andern Wort zugehörig empfindet.

​

Als den ‘gelesenen Satz’ können wir nun das Schriftzeichen, aber auch das besondere Erlebnis, ⌊–⌋ das Zeichen so gesehen, so aufgefaßt – bezeichnen. (Hier ist eine Quelle von Verwechslungen.)

​

Erinnern wir uns nun an eine Mehrdeutigkeit des Wortes verstehn. Wenn ich in einem Buch lese: “nachdem er das gesagt hatte, verließ er sie, wie am vorigen Tage” – fragt man mich ob ich diesen Satz verstehe so ist es nicht leicht darauf zu antworten. Es ist ein deutscher Satz & insofern verstehe ich ihn: Ich wüßte, wie man diesen Satz etwa gebrauchen könnte. Ich könnte selbst einen Zusammenhang für ihn erfinden. Und doch verstehe ich ihn nicht in dem Sinne, in dem wie ich ihn verstünde, wenn ich eine Erzählung gelesen hätte, in welcher er so steht. (Vergleiche: [V|v]erschiedene Sprachspiele.)

​

10 Verstehen wir Lewis Carroll's Gedicht “Jabberwocky”[?|,] oder Gedichte von Christian Morgenstern?

​

Es sei mir ein Satz in einer mir nicht geläufigen Chiffre gegeben & zugleich auch der Schlüssel zu ihrer [e|E]ntzifferung. Dann ist uns ⌊(⌋natürlich⌊)⌋ in gewissem Sinne [a|A]lles zum Verständnis des Satzes gegeben. Und doch würde ich auf die Frage ob ich den Satz verstehe etwa antworten: “ich muß ihn erst entziffern”; & wenn ich ihn als deutschen Satz entziffert vor mir hätte, würde ich sagen: “jetzt verstehe ich ihn”.    Wenn man nun die Frage stellt: “in welchem Augenblick der Übertragung (aus der Chiffre ins Deutsche) beginnt das Verstehen // der Zustand des Verstehens // des Satzes”, so erhält man einen Einblick in das Wesen dessen, was wir “verstehen” nennen.

​

Ich sage einen Satz “ich sehe dort einen schwarzen Kreis”; ich kann nach Übereinkunft die Wörter dieses Satzes durch andre Zeichen ersetzen & der ⌊ein⌋ Satz in den neuen Zeichen wird dann den selben Sinn erhalten. Schreiben wir also statt der 6 Wörter des Satzes die ersten 6 Buchstaben des Alphabets. Dann heißt der Satz: “a b c d e f”. Aber nun zeigt [s|e]s sich, daß ich – wie man sagen möchte – den Sinn des oberen Satzes nicht ohne weiteres in dem Ausdruck “a b c d e f” denken kann. Ich könnte 11 es auch so sagen: ich bin nicht gewöhnt statt ‘ich’ ‘a’ zu sagen & statt ‘sehe’ ‘b’, statt ‘dort’ ‘c’, etc.. Aber damit meine ich nicht, daß⌊,⌋ ◇◇◇ wenn ich daran gewöhnt wäre, ich mit dem Zeichen ‘a’ sofort das Wort ‘ich’ assoziieren würde; sondern, daß ich nicht gew ich bin nicht gewöhnt ‘a’ an Stelle von ‘ich’ zu gebrauchen.

​

“Einen Satz verstehen”, kann heißen im Sinne von kann soviel heißen wie: “wissen, was der Satz besagt”, & das heißt, : ⌊,⌋ die Frage “was ⌊be⌋sagt er dieser Satz ” beantworten können.     Den Sinn eines Satzes verstehen soll dann heiß[en|t]t: die Frage ‘was ist sein Sinn’ beantworten können.

​

Verstehen (in dieser Bedeutung) ist das Korrelat einer Erklärung des Sinnes.

​

Es ist eine sehr ◇◇◇ häufige häufig erscheinende Auffassung: daß Einer Man meint oft, daß Einer … sein Verständnis nur unvollkommen zeigen kann. Daß er gleichsam nur immer aus der Ferne darauf deuten, auch sich ihm nähern, kann es aber nie mit der Hand berühren kann. Und das Letzte immer ungesagt bleiben muß.3    Man fragt: Ist denn das Verständnis nicht etwas anderes als der Ausdruck des Verständnisses? – Ist es nicht so, daß 12 der Ausdruck des Verständnisses eben ein unvollkommener Ausdruck // eine unvollkommene Äußerung des V. // ist? –    Das heißt doch wohl, ein Ausdruck, der etwas ausläßt, – was aber wesentlich unausdrückbar sein müßte ist [; d|. d]enn sonst könnte ich ja eben einen bessern finden.

​

Uns interessie[r|t]en die ˇdie Tatsache daß gewisse psychischen Vorgänge einen Satz erfahrungsgemaß begleiten nicht; wohl aber das Verstehen, die Auffassung , die in einer , so weit sie in einer Erklärung des Sinnes ⌊(⌋der Bedeutung⌊)⌋ niedergelegt sind ist .

​

Es ist schwierig die Grammatik des Wortes “meinen” klar zu sehen. Aber der Weg dazu führt über die Frage “welches ist das Kriterium dafür, daß wir etwas so meinen”,⌊,⌋ & welcher Art ist der Ausdruck den dieses “so” vertritt. Die Antwort auf die Frage “wie ist das gemeint” stellt die Verbindung zwischen zwei sprachlichen Ausdrücken her. Also fragt auch die Frage nach dieser Verbindung ⌊⌊ Als hätte man zwei Bilder die dieselbe Person darstellen, diese selbst aber könnte ich nicht zeigen. ⌋⌋      Der Gebrauch der Hauptwörter “Sinn”, “Bedeutung”, “Auffassung” & anderer Wörter verleitet uns zu glauben, daß dieser Sinn,. etc, dem Zeichen so gegenübersteht, wie das Wort – der Name – dem Ding, das sein Träger ist. So daß man sagen könnte: “[d|D]as Zeichen hat eine ganz bestimmte Bedeutung, ist in einer ganz bestimmten Weise gemeint, 13 die ich nur in Ermanglung eines direkten Weges wieder durch ein Zeichen ausdrücken muß”. Die Meinung, die Intention, wäre gleichsam seine Seele die ich am liebsten selbst zeigen möchte, auf die ich aber leider nur indirekt durch ihren Körper hinweisen kann. – ⇒ 487          Wenn ich ˇum den Sinn eines Pfeiles zu erklären sage: “ich meine diesen Pfeil so, dass man ihm durch eine Bewegung in der Richtung vom Schwanz zur Spitze folgt”, so gebe ich eine Definition (ich setze ein Zeichen für ein andres), während es scheint, als hätte ich sozusagen die Aussage // Angabe // , die der Pfeil macht des Pfeils ergänzt. Ich habe den Pfeil durch ein neues Zeichen ersetzt, das wir statt des Pfeiles gebrauchen können. – Gebrauchen können –. Während es scheint, als wäre der Pfeil selbst wesentlich unvollständig // unvollkommen // , ergänzungsbedürftig, und als hätte ich ihm nun die nötige Ergänzung gegeben. Wie man eine Beschreibung eines Gegenstandes als unvollkommen erkennt und vervollständigt // vervollständigen kann // . Als hätte der Pfeil die Beschreibung angefangen und wir sie durch den Satz vollendet. – Auch so: Wenn ich,, wie oben, sage “ich meine diesen Pfeil so, dass …”, so ﹖– macht es den Eindruck –﹖, als hätte ich jetzt erst das Eigentliche beschrieben, die Meinung; als wäre der Pfeil gleichsam nur das Musikinstrument, die Meinung aber die Musik, oder besser: der Pfeil das Zeichen – das heisst in diesem Falle – die Ursache des inneren, seelischen, Vorgangs und die Worte der Erklärung erst die Beschreibung dieses Vorgangs. Hier spukt die Auffassung des Satzes als eines des Zeichens des Gedankens; und des Gedankens als eines Vorgangs in der Seele, oder im Kopf. ))

​

Der Vorgang den wir … Was wir ‘verstehen’ nennen, ist manchmal ein Vorgang des Nachziehens Übersetzens des Zeichens in ein anderes Bild.      Das Verstehen einer Beschreibung kann 14 man mit dem Zeichnen eines Bildes nach dieser Beschreibung vergleichen.

​

Wir reden von dem Verständnis eines Satzes als der Bedingung dafür, daß wir ihn anwenden können. Wir sagen “wir können einen Befehl nicht verstehen befolgen wenn wir ihn nicht verstehen”, oder “ˇich muß ihn verstehen⌊,⌋ ehe ⌊ich⌋ wir ihn verstehen befolge”.

​

Damit hängt es zusammen, daß wir sagen: “Ich verstehe dieses Bild genau[:|,] ich könnte es plastisch darstellen”. “Ich verstehe diese Beschreibung genau, ich könnte ein Bild nach ihr zeichnen. ¥ •

​

Wir reden von dem Verständnis eines Satzes als der Bedingung dafür, daß wir ihn anwenden können. Wir sagen: “ich kann einen Befehl nicht befolgen, wenn ich ihn nicht verstehe”, oder “ich muß ihn verstehen, ⌊“⌋ehe ich ihn [befolge|verstehe]”.

​

⍈ ↺ Man könnte es in gewissen Fällen ⌊(⌋offiziell⌊)⌋ als das Kriterium des Verständnisses ˇeines Befehls festsetzen, daß der welcher ihn erhält bekommt seinen Sinn muß zeichnerisch wiedergeben darstellen können.

​

“Muß ich wirklich einen Satz verstehen, um nach ihm handeln zu können?” – “Gewiß, ! , sonst wüßtest Du ja nicht, was Du zu tun hast.” – “Aber was nützt mich dieses Wissen? vom Wissen zum Tun ist ja wieder ein Sprung.”

​

15 Wenn “einen Satz verstehen” heißt, in bestimmter Weise nach ihm handeln, dann kann das Verständnis nicht die logische Bedingung dafür sein, daß wir nach ihm handeln.

​

⍈ ↻ Aber der Satz “ich muß den Befehl verstehen, ehe ich nach ihm handeln kann” hat natürlich einen guten Sinn Aber jedenfalls keinen ; nur keinen metalogischen. Denn auch das Verstehen ist kein metalogischer Begriff.

​

Der Begriff, welchen man vom Verstehen hat, ist etwa, daß man dadurch damit vom Zeichen näher an die dargestellte Realität kommt, von den Worten des Befehls näher an die Befolgung. Und in einem psychologischen Sinn kann das richtig sein.

​

“Ich muß doch einen Befehl verstehen, um nach ihm handeln zu können” – hier ist das ‘muß’ verdächtig. Wenn das ein logisches Muss ist, so so ist der Satz eine Grammatische Anmerkung.     Auch wäre das könnte man da fragen: “Wie lange vor dem Befolgen mußt Du den Befehl versteh⌊e⌋n?”

​

¥ • Wenn mit dem Verstehen ein psychischer Vorgang gemeint ist & gesagt wird werden soll , daß dieser Prozess Vorgang erfahrungsgemäß ˇimmer eintritt ehe ein Mensch einen Befehl befolgt, so interessiert uns diese Aussage nicht. (Eine Erklärung “den Befehl befolgen” wolle man es nur nennen, wenn jener psychische Vorgang eing⌊e⌋treten sei, wäre 16 müßig.)

​

Soll “verstehen” heißen: erklären können, – warum sollte das notwendig sein, um den Befehl zu befolgen. (Es handelt sich hier natürlich nicht um logische Notwendigkeit.)

​

Wenn das Verstehen eine Vorbereitung des Befolgens Folgens war, so hat es der Wahrnehmung des Zeichens dem Zeichen des Befehls etwas hinzugefügt; aber etwas, was jedenfalls nicht die Ausführung ⌊(⌋des Befehls⌊)⌋ war.

​

Es scheint uns “Ich kann den Befehl nicht ausführen, weil ich nicht verstehe, was Du meinst. Ja, jetzt verstehe ich Dich.” – Was ging da vor, als ich plötzlich den Andern verstand?    Da gibt gab es viele Möglichkeiten. Der Befehl konnte z.B. in einer mir bekannten Sprache, aber mit falscher Betonung gegeben worden sein & es fiel mir plötzlich die richtige Betonung der Worte ein. Einem Dritten würde ich dann sagen: “jetzt verstehe ich ihn, er meint …” & nun würde ich den Befehl in richtiger Betonung wiederholen. Und mit dem Erfassen des wohlbekannten Satzes hätte ich nun den Befehl verstanden; ich meine: ich müßte nun nicht erst erst noch einen abstrakten Sinn erfassen. // Und mit dem Erfassen des richtig bettonten Satzes hätte ich nun den Befehl verstanden. Ich meine: ich müßte nun nicht erst noch einen abstrakten Sinn erfassen, sondern es genügt mir 17 das Erleben des wohlbekannten Wortlautes [–| // ] – Oder aber der Befehl wäre mir in verstandlichem Deutsch gegeben worden, schiene mir aber ungereimt, da ich irgend etwas in ihm mißverstanden habe; dann fiel mir eine Erklärung ein “ach, er meint …” & nun kann ich den Befehl ausführen.       (Der Zerstreute, der auf den Befehl “rechtsum” sich nach links gedreht hätte und nun, an die Stirne greifend, sagte “ach so, ‘rechtsum’!” & rechtsum machte.)

​

Es konnten mir auch vor dem Verstehen mehrere mögliche Deutungen, das heißt, mehrere Erklärungen, vorschweben, für deren eine ich mich dann entscheide.

​

(Denke auch an den Fall: Es macht mir jemand Zeichen & ich sage: “er meint, ich soll etwas tun; aber was er wünscht, weiß ich nicht”.)

​

Es scheint uns, als ob wir dem Befehl durch das Verstehen etwas hinzufügen (ˇetwa dem Befehl “ x x² 1 2 3 ” z.B.) (etwa dem: “ x x² 1 2 3 ”) etwas durch das Verstehen etwas hinzufügen, was die Lücke zwischen Befehl & Ausführung füllt. So daß wir Einem der sagt sagte “aber Du verstehst ihn ja, er ist also nicht unvollständig”, antworten können: 18 “Ja, aber ich verstehe ihn⌊,⌋ ˇaber nur, weil ich noch etwas hinzufüge; die Deutung nämlich”.        Aber was veranlaßt Dich gerade zu dieser Deutung? Ist es der Befehl, –⌊,⌋ dann war er ja schon eindeutig, da er diese Deutung befahl. Oder hast Du die Deutung willkürlich hinzugefügt⌊,⌋ –, dann hast Du ja auch den Befehl nicht verstanden, sondern erst das, was Du aus ihm gemacht hast.

​

Eine Interpretation ist doch etwas, was in Zeichen gegeben wird. Es ist diese Interpretation im Gegensatz zu einer anderen (die anders lautet. Wenn man also sagte: “jeder Satz bedarf noch einer Interpretation,” – so hieße das: kein Satz kann ohne einen Zusatz verstanden werden.

​

Es geschieht wohl daß ich ˇein Zeichen deute, ihm eine Deutung hinzufüge, aber durchaus nicht immer, wenn ich Zeichen verstehe.    Wenn man mich fragt “wieviel Uhr ist es”, so geht in mir keine Arbeit des Deutens vor ; sondern . Sondern ich reagiere ˇ einfach auf das, was ich sehe & höre. (Wie ich, wenn Einer das Messer auf mich zückt, ich nicht sage: “ich deute das als eine Drohung.”)

​

Wir sehen in der Philosophie dort immer Probleme, wo keine sind. Und die Philosophie soll zeigen daß dort keine sind. kein Problem ist.

​

19   ‘Ein Wort verstehen’ im Sinne von: Wissen, wie es gebraucht wird.

​

‘Wissen wie ein Wort gebraucht wird’ heißt das Gleiche wie ‘es anwenden können.

​

Man gebraucht das Wort “können” so, daß die Ausführung als das Kriterium der Fähigkeit ist; aber auch so, daß sich das Kriter nicht die Ausführung das Kriterium ist.     “Kannst Du diese Kugel heben?” – [i|I]ch sage “ja”. Dann versuche ich, sie zu heben & es gelingt mir nicht. – Da werde ich in einem Fall sagen: „ich hatte mich geirrt; ich konnte es nicht”; aber es gibt auch den Fall: “jetzt kann ich sie nicht heben, weil ich müde bin; als ich sagte, ⌊ ‘⌋ich k[ö|a]nn sie heben’, da konnte ich es ⌊(⌋auch⌊)⌋”. Ebenso: “ich dachte ich könnte Schach spielen, aber ich habe es schon vergessen” aber auch “als ich sagte ich könne es, da konnte ich's, jetzt aber habe ich ist mir durch den Schrecken alles vergessen entfallen”[; e|. E]tc..    Gefragt, ‘wie weißt Du, daß Du es damals konntest”, würde ich man etwa antworten: “ich konnte so ein leichtes Gewicht immer heben”, “ich hatte es gerade zuvor gehoben”, “ich habe vor we ku wenigen Jahren Schach gespielt & mein Gedächtnis ist gut”, “ich hatte mir gerade die Regeln rekapituliert”, u.s.w..      Was ich als Beweis des Könnens betachte Was uns als Anzeichen des Könnens gilt zeigt uns, in welcher Weise wir das Wort “können” // dieses Wort // gebrauchen. 20   In keinem dieser Fälle ist die Fähigkeit ein bewußter Zustand, wie etwa Muskelschmerzen.

​

Vergleiche folgende Sätze mit einander, von denen deren jeder in anderem Sinne einen Zustand beschreibt: „ich habe den ganzen Tag Zahnschmerzen gehabt” „ich habe mich den ganzen Tag nach ihm gesehnt” „ich habe ihn den ganzen Tag erwartet” „ich wußte schon seit gestern den ganzen Tag , daß er kommen werde” „ich kann konnte seit gestern Schach spielen”. ¥ • In welchen dieser Sätze könnte man würden wir das Wort “ununterbrochen” mit Sinn einsetzen? ⍈ ↺ Kann man sagen: “ich ◇◇◇ wußte seit gestern ununterbrochen, daß er kommen werde”?

​

Wenn man das Wissen einen ⌊‘⌋Zustand⌊’⌋ nennt, dann in dem Sinn, in welchem man vom Zustand eines physikalischen Körpers oder eines physikalischen Modells redet (also im physiologischen Sinn, oder ˇauch im Sinn einer Psychologie, die von unbewußten Zuständen eines Seelenmodells redet). Und das würde freilich auch jeder zugeben; aber nun muß man noch verstehen sehen nun muß man sich noch darüber klar sein, daß man sich dam⌊i⌋t ˇaus dem grammatischen Bereich der seelischen bewußten Zustände (Zahnschmerzen etc.) in ein anderes grammatisches Gebiet begeben hat. Ich kann sehr wohl von unbewußten Zahnschmerzen reden, wenn der Satz “ich habe unbewußte Zahnschmerzen”, vielleicht nun etwa , bedeuten soll, was wir gewöhnlich du⌊r⌋ch den Satz “ich habe einen schlechten Zahn, der mir keine Schmerzen verursacht bereitet ” ausdrücken. so ausdrücken: “ … Der ‘bewußte Zustand’ (im früheren Sinn) steht nun nich zum ‘unbewußten ˇZustand’ nun nicht in dem grammatischen Verhältnis, wie ‘ein Sessel, den ich sehe’ zu einem ‘Sessel den ich nicht 21 sehe, weil er im Nebenzimmer steht”. // Ich kann wohl von “unbewußten Zahnschmerzen” reden, wenn der Satz “ich habe unbewußte Z.” etwa bedeuten soll: “ich habe einen schlechten Zahn, der mir keine Schmerzen verursacht”. Man muß nun sehen, daß der Ausdruck “bewußter Zustand” (im früheren Sinne) zum Ausdruck “unbewußter Zustand” nicht in dem ˇgrammatischen Verhältnis steht wie “ein Sessel, den ich sehe” zu “ein Sessel, den ich nicht sehe, weil er versteckt ist”.

​

Etwas wissen kommt für unsere Zwecke auf das Gleiche hinaus wie ist damit zu vergleichen : ˇeinen Zettel in meiner Tasche tragen, auf dem es aufgeschrieben steht.

​

¥ ⋎ S. 35 A

​

Auf die Frage “verstehst Du das Wort “⌊‘⌋rot⌊’⌋”, weißt Du, welche Farbe “⌊‘⌋rot⌊’⌋” heißt?” kann würde ◇◇◇ man antworten: “Ja; wenn hier etwas Rotes wäre, so würde ich es erkennen”.

​

Es sei Ist etwa a b c d e f g h mein Wörterbuch, &⌊.⌋ [i|I]ch übersetze mit ihm den Satz “b d c a” in den Satz “f h g e”; nun habe ich gezeigt, daß ich den Gebrauch des Wörterbuchs verstehe & kann sagen, daß ich auf gleiche Weise den Satz “c d a b” übersetzen kann, wenn ich will.

​

¥ ⋎ S. 35 A

​

⍈ [Zu p. 7]        Das Verstehen eines Satzes der Sprache ist dem Verstehen eines Musikstücks viel 22 verwandter, als man glauben möchte. – Warum möchte sollen d müssen diese Takte gerade so gespielt werden? Warum bringe ich den Rhythmus Wechsel der Stärke & des Zeitmaßes gerade auf dieses ganz bestimmte Ideal? Man möchte sagen: “weil ich weiß, was das alles heißt”, – aber was heißt es denn? – – Ich wüßte es nicht zu sagen, außer wieder durch eine Übersetzung in einen Ausdruck vom mit dem gleichen Rhythmus. // … außer wieder durch indem ich die Musik in einen ˇandern Ausdruck vom gleichen Rhythmus ˇjenes Ideals übersetze. //

​

A “Ich kann das Wort “⌊‘⌋gelb⌊’⌋” ‘Kugel’ anwenden”, – ist das auf einer andern Stufe als: “ich kann den König weiß, wie man den König im Schachspiel verwenden” verwendet.”? // “ich kann mit dem König im Schachspiel ziehen” // ? // “Ich weiß, wie ein Bauer ziehen darf”. “Ich weiß, wie das Wort ‘Kugel’ gebraucht werden darf”.

​

¥ ⋎ p. 23 D ¥ p. 24 A

​

B Ein Paradox schwieriges Problem scheint der Gegensatz, das Verhältnis zu sein, zwischen dem Operieren mit der Sprache im Laufe ihrer Anwendung & dem momentanen Erfassen des Sinnes Satzes .     Aber wann erfassen wir, oder verstehen, wir den Satz?! – Wenn Nachdem wir ihn ausgesprochen haben? – Oder während wir ihn aussprechen? – Und ist das Verstehen ein artikulierter Vorgang, wie das 23 bilden sprechen oder schreiben des Satzes[?|,] oder ein unartikulierter? Und wenn ein artikulierter: ⌊,⌋ – entspricht seine Articulation der des Satzes oder ist sie von ihr unabhängig? ist er projektiv mit dem andern verbunden? oder ist seine Artikulation von der des Satzes unabhängig? –

​

¥ • [Absatz]

​

⌊ ⌊⌊A⌋⌋ ⌋ “Er sagt das, & meint es”. Vergleiche das mit dem Satz: “er sagt das & schreibt es nieder”, – & anderseits mit: “er schreibt sagt das & unterschreibt es”.

​

⍈ ↺ Wie lange braucht es : , einen Satz verstehn? ⌊⌊ B ⌋⌋ Und ˇwenn man ihn eine Stunde lang versteht, beginnt man das immer wieder von neuem? frischem?

​

⌊ C ⌋ Ist das Verstehen eines Satzes nicht dem Verstehen eines Schachzuges als Zug des bestimmten Spieles analog des dieses Spiels ähnlich vergleichbar? // Ist das Verstehen eines Satzes nicht vergleichbar analog dem …? // Wer das Spiel gar nicht kennt & sieht jemand ziehen, der wird … einen Zug machen, der wird die Handlung nicht verstehn, d.h. nicht als Zug eines Spiels. (Oder ˇauch, nicht als Zug dieses Spiels.) Und es ist etwas a Anderes den dem Zug mit Verständnis des Spiels sehen folgen , als ihn ohne dieses Verständnis zu sehen.

​

⍈ [zu p. 22] ⌊⌊ D ⌋⌋ Wie, wenn man fragte: wann kannst Du Schach spielen? Immer? oder ˇjetzt während Du es sagst? sagst, daß Du es kannst? oder während jedes ˇeines SchachZuges? – Und wie seltsam, daß Schachspielen-Können so kurze Zeit braucht & eine Schachpartie so viel länger!   (Augustinus: “Wann messe ich einen Zeitraum.”)

​

24 ⍈ [zu p. 22]      ⌊⌊ A ⌋⌋ Wenn “das Wort ‘gelb’ verstehen” heißt, es anwenden können, so ist die gleiche Frage: wann kannst Du es anwenden? Redest Du von einer Disposition? Ist es eine Vermutung?

​

[Ordnung der Sätze: 22A, 23D, 24A, 22B, 23B, 23A, 23C]

​

Das Verständnis der Sprache – quasi des Spiels – scheint wie ein Hintergrun[g|d], auf dem der einzelne Satz erst Bedeutung gewinnt. (siehe § 25)⇒

​

Man könnte sagen: Mich interessiert nur der Inhalt eines des Satzes; & der Inhalt des Satzes ist in ihm. nicht ◇◇◇    Seinen Inhalt hat der Satz als Glied eines Kalküls.       Einen Satz verstehen bedeutet: einen Kalkül verstehen Ist also “einen Satz verstehen” ˇnicht von gleicher Art, wie “einen Kalkül verstehen” ? also wie: “multiplizieren können”?

​

Was ist es aber dann, was uns immer das Gefühl gibt, daß das Verstehen des Satzes das Erfassen von etwas außerhalb ihm Liegenden ist; aber nicht von der Welt außerhalb der Zeichen, wie sie eben ist, sondern von der Welt, wie sie das Zeichen sie – gleichsam – wünscht. ¥ •     Das Übersetzen in die Vorstellung & das Eingreifen des Satzes in uns bilden jenes Außerhalb.

​

⍈ • Man möchte etwa sagen: “Ich sage ja nicht nur ‘Zeichne einen Kreis’, sondern ich wünsche 25 doch daß der Andre etwas tut.” (Freilich!)

​

Das Verständnis der Sprache – quasi des Spiels – scheint wie ein Hintergrund, auf dem der einzelne Satz erst Bedeutung gewinnt.

​

Wenn “die Bedeutung eines Wortes verstehen” heißt, die Möglichkeiten seiner grammatischen Anwendung kennen– ⌊,⌋ so kann ist die Frage entstehen denkbar: “Wie kann ich man dann gleich wissen, was ich mit ‘Kugel’ meine, ich kann doch nicht die ganze Art der Anwendung des Worts auf einmal im Kopf haben?”    In einem Sinne kann man sagen, ich wisse die Regeln des Schachspiels (‘habe sie im Kopf’) wenn während ich spiele. Aber ist dieses “im Kopf haben” nicht nur eine Hypothese? Gewiß, dieses Wissen ist nur das hypothetische Reservoir, woraus das wirklich gesehene Wasser fließt.

​

¥ ⋎ S. 27/A✓ , ¥ S. 31/A

​

Wenn Du von Rot gesprochen hast, hast Du das gemeint, wovon man sagen kann, es sei hell, aber nicht, es sei grün, auch wenn Du an diese Regel nicht gedacht hast noch von ihr Gebrauch gemacht hast? – Hast Du das ~ verwendet, wofür ~~~p = p ist? auch wenn Du diese Regel nicht verwendet hast? Ist es etwa eine Hypothese, 26 daß es das ~ war? Kann es zweifelhaft sein, ob es dasselbe war & durch die Erfahrung bestätigt werden?

​

Das Schachspiel ist gewiß durch seine Regeln (sein Regelverzeichnis) charakterisiert. Wenn ich Schach nun durch seine Regeln definiere ( vom Damespiel von Dame unterscheide), so gehören diese Regeln zur Grammatik des Wortes “Schach” Muß nun dem, der das Wort “Schach” sinnvoll gebraucht (etwa im Satz wenn er sagt: “ich möchte jetzt Schach spielen”) eine Definition des Wortes vorschweben? Gewiß nicht. – Gefragt, was er unter “Schach” versteht, wird er erst eine geben.    Wenn ich nun fragte: “Wie Du das Wort ausgesprochen hast, was hast Du damit gemeint?” – Wenn er mir darauf antwortet: “Ich habe das Spiel gemeint, das wir so oft gespielt haben etc. etc.”, so weiß ich, daß ihm diese Erklärung in keiner Weise beim Gebrauch des Wortes vorgeschwebt hatte, & daß seine Antwort meine Frage nicht in dem Sinn beantwortet, daß sie mir sagt, was “in ihm vorgegangen ist” als er das Wort aussprach.

​

Denn die Frage ist eben, ob unter der “Bedeutung, in der man ein Wort gebraucht” ein Vorgang verstanden werden soll, den wir beim Sprechen oder Hören des Wortes erleben.

​

Statt “ich habe das Spiel gemeint, welches …” hätte er auch sagen können: “ich setze ⌊(⌋jetzt⌊)⌋ statt des Wortes ‘Schach’ – das ich fruhe vorhin gebraucht 27 habe – den Ausdruck ‘ …’”.

​

¥ ⋎ 27/B

​​

Die Quelle der Verwirrung ist vielleicht der Begriff vom Gedanken, der den Satz begleitet (Oder seinem Ausdruck vorangeht.) Dem Wortausdruck kann natürlich der Gedanke in anderer Form vorangehen, aber für uns kommt der Unterschied Artunterschied dieser beiden Ausdrücke, oder Gedanken, nicht in Frage. [kein ◇ neuer Absatz] (“Er hat diese Worte gesagt, sich aber dabei gar nichts geda[g|ch]t.” – “Doch, ich habe mir etwas dabei gedacht.” – “Und zwar was denn?” – Nun, was ich gesagt habe.”)

​

Auf die Aussage “dieser Satz hat Sinn” kann man nicht wesentlich fragen “welchen?”. So wie man ˇja auch auf den Satz “diese Worte sind ein bilden einen Satz” nicht fragen kann “welcher?”.

​

“Ich meine aber doch mit diesen Worten etwas”. Gewiß: im Gegensatz zu dem Falle, wo ich nichts meine, wo ich etwa die Silben ihres komischen Klangs wegen aneinanderreihe. (Der Satz “ich meine etwas …”, nicht metalogisch.)

✓

⍈ ⌊⌊ A ⌋⌋       Es handelt sich beim Verstehen, Meinen, nicht um einen Akt eines des momentanen, sozusagen nicht-diskursiven Erfassens der Grammatik. Als könnte man sie gleichsam auf einmal hinc her unterschlucken.

​

⍈ ⌊⌊ B ⌋⌋ Das ⌊ (⌋ also ⌊)⌋ , was der macht, der ein Zeichen, das welches man ihm ihm ein Anderer gegeben hat, ˇin einem Sinne deutet, ˇauffasst, ist ein Schritt in einem eines Kalkül⌊s⌋ (quasi einer Rechnung). 28 Er tut ungefähr was er sagt, wenn er seiner Deutung Ausdruck gibt. – Und wenn ich sage “was er macht, ist der Schritt eines Kalküls”, so meine ich, daß ich diesen Kalkül schon kenne; in dem Sinne, in dem ich die deutsche Sprache kenne, oder das Einmaleins. Welche⌊s⌋ ich ja auch nicht so in mir habe, als wären die ganze deutsche Grammatik & alle die ge Einmaleinssätze zusammengeschoben auf [E|e]twas, was ich nun als Ganzes besitze.

​

Es können ⌊(⌋nun⌊)⌋ die grammatischen Regeln als die Auseinanderlegung dessen erscheinen, was Es kann uns vorkommen erscheinen, als wären die gr. Regeln ˇin irgend einem Sinne die die Auseinanderlegung dessen, was … wir beim im Gebrauch des Wortes auf einmal erleben.

​

⇒ Fortsetzung von S. 14 Großes Format

? ∫

Kann ich das, was die grammatischen Regeln von einem Worte sagen, auch anders beschreiben, nämlich durch die Beschreibung des Vorgangs, der beim Verstehen stattfindet?     Wenn also die Grammatik – z.B. – die Geometrie der Verneinung ist, kann ich sie durch die Beschreibung dessen ersetzen, was bei der Anwendung sozusagen ‘hinter’ dem Wort “nicht” steht?     Wir sagen: “Wer die Negation versteht, der weiß, daß die doppelte Negation eine Bejahung ergibt”.

?

Das klingt so wie: “Kohle & Sauerstoff gibt Kohlensäure Sauerstoff ”. Aber in Wirklichkeit gibt die doppelte 29 Negation nichts, sondern ist etwas.     Es täuscht uns da etwas eine physikalische Tatsache vor. Als sä[g|h]en wir ein Ergebniss des logischen Processes. Während das Ergebnis nur das des physischen physikalischen Processes ist.

∕∕

Man möchte sagen: “die Verneinung hat die Eigenschaft verdoppelt eine Bejahung zu ergeben.” Während die Regel die Verneinung nicht näher beschreibt sondern konstituiert.    Die Negation hat keine andere die Eigenschaft, als, etwa, die, in gewissen den & den einen Satz wahrheitsgemäß zu verneinen. // , … der Wahrheit gemäß zu verneinen. //     So hat ein Kreis – etwa ein auf einer Fläche Papier gemalter – die Eigenschaft,, da oder dort zu stehn, diese Farbe zu haben, von einer Geraden (Farbgrenze) geschnitten zu werden, etc.; aber nicht Eigenschaften, die ihm die Geometrie zuzuschreiben scheint. (Nämlich, jene Eigenschaften haben zu können.) Und die Eins hat nicht die Eigenschaft zu sich selbst addiert zwei zu ergeben.

∕∕

Die Geometrie spricht sowenig von Würfeln, wie die Logik von der Verneinung.     Sie definiert die Würfelform aber beschreibt sie nicht. Sagt die Beschreibung eines Würfels, daß er rot & hart ist, dann ist ‘Beschreibung der Würfelform’ ein Satz wie: “diese Kiste ist würfelförmig”.     Aber wenn ich nun beschreibe, wie man eine würfelförmige Kiste macht, ist hierin nicht auch eine Beschreibung der Würfelform enthalten? Nur inˇ Eine Beschreibung nur sofern, als von diesem Ding gesagt wird, es sei würfelförmig, 30 ⌊&⌋ im Übrigen aber ˇist dies eine Definition ˇAnalyse, des Begriffs Würfel. Nicht die Würfelform hat die Eigenschaft lauter gleiche Seiten zu besitzen; aber ein Holzklotz hat diese Eigenschaft. Noch hat “die Eins die Eigenschaft, zu sich selbst addiert zwei zu ergeben”.

​

“Dieses Papier ist nicht schwarz, & ‘nicht’ zwei solche Verneinungen geben eine Bej[ä|a]hung”.    “Dieses Buch ist rot & die Rose ist rot, & die beiden Wörter ‘rot’ haben die gleiche Bedeutung.”     “Und zwei solche Verneinungen geben eine Bejahung” das ˇDer Zusatz erinnert an: “ˇund zwei solche Pferde können den Wagen fortbewegen”. Aber in ihm jenem Zusatz wird nichts über die Verneinung ausgesagt; sondern er ist eine Regel über die Ersetzung eines Zeichens durch ein anderes.

∕∕ ∕∕

“Daß zwei Verneinungen eine Bejahung ergeben, muß doch schon im Wesen in der Verneinung, die ich jetzt gebrauche, liegen.” Hier bin ich Bin ich hier nicht im Begriffe eine Myt⌊h⌋ologie ˇdes Symbolismus zu erfinden?       Es hat den Anschein, als könnte man aus der Bedeutung der Negation schließen, daß “~~p” p bedeutet. Als würden aus der Natur der Negation die Regeln über das Negationszeichen folgen. So daß, in gewissem Sinne, die Negation zuerst vorhanden ist, & dann die Regeln der Grammatik.     Es ist also, als hätte das Wesen der Negation einen zweifachen Ausdruck in der Sprache: dasjenige was denjenigen welchen dessen Bedeutung ich erfasse, wenn ich den Ausdruck der Negation, etwa das Wort “nicht”◇◇◇, wenn ich das Wort “nicht” in einem 31 Satz verstehe, & die Folgen des erfaßten dieses Wesens dieser Bedeutung in der Grammatik.

​

⍈ A [zu S. 25]          Man ist versucht etwa folgenden Einwand zu machen: Man Ich möchte ˇetwa auch sagen: Wenn mir jemand sagt: “sieh' dort ist eine Kugel”, oder “dort ist eine Halbkugel”, so kann die Ansicht ˇdie ich erhalte zu beidem passen; & wenn ich nun sage “ja, ich sehe sie”, so unterscheide ich doch zwischen den beiden Hypothesen. – Wie ich in der Schachpartie im Schachspiel zwischen einem Bauer & dem König unterscheide, auch wenn der gegenwärtige Zug einer ist, den beide machen könnten, & wenn selbst eine Königsfigur als Bauer fungierte.4      Das Wort “Kugel” ist mir bekannt & steht in mir für etwas : ; d.h. es bringt mich in eine gewisse Haltung Stellung zu sich (wie ein Magnet eine Nadel in seine Richtung bringt).        Man ist in der Philosophie immer in Gefahr, eine Mythologie des Symbolismus zu geben, oder der Psychologie; statt einfach zu sagen, was man weiß.

∕∕

⍈ ˇ [Zu S. 32] B     Es scheint so, ˇuns als wäre in einem Satzˇ, der, z.B., das Wort “Kugel” enthält, schon der Schatten anderer Sätze mit diesem Wort Verwendungen des dieses Worts enthalten. – Nämlich eben die Möglichkeit, jene andern Sätze zu bilden. Wem scheint es so? und unter welchen Umständen?

∕∕

Was heißt es nun, wenn ich sage, wenn daß im Satze “die Rose ist rot” das “ist” eine andere Bedeutung hat, als in “2 mal 2 ist 4”? Wenn man antwortet, es heiße, daß verschiedene Regeln von diesen beiden Wörtern gelten, so ist 32 zunächst zu sagen, daß wir hier nur ein Wort haben. – Und wenn ich nur auf die grammatischen Regeln achte, so erlauben diese eben die Verwendung des Wortes “ist” in beiden Zusammenhängen. – Die Regel aber, welche zeigt, daß das Wort “ist” in den zwei Sätzen verschiedene Bedeutung hat, ist die, welche erlaubt im zweiten Satz das Wort “ist” durch den Aus “ist gleich” zu ersetzen, & die aber diese Ersetzung im ersten Satz verbietet.

/

“Ist nun diese Regel nur die Folge des Ersten: daß das Wort ‘ist’ in den beiden zwei Sätzen verschiedene Bedeutungˇgen hat[;|?] Oder ist es so, daß es so, daß diese diese Regel eben ein der der Ausdruck dafür ist ist , daß das Wort ‘ist’ ˇin den beiden Sätzen Zusammenhängen Verschiedenes bedeutet?”

​

¥ ⋎ S. 31B

/

Es liegt hier der Vergleich nahe, daß das Wort “ist” in verschiedenen Fällen verschiedene einen andern Bedeutungskörper hinter sich hat; daß es ˇetwa beidemale die gleiche eine quadratförmige Flächec ist, ⌊(⌋etwa jedesmal ein Quadrat⌊)⌋ , das aber ⌊das⌋ ein[m|em]al ˇdie Endfläche einer Pyramide⌊.⌋ ist.      Denken wir uns ˇnun diesen Fall: Wir hätten Glaswürfel, die vollkommen durchsichtig sein sollen wärenˇwären , deren eine Seitenfläche aber ˇsei rot gefärbt⌊.⌋ wäre. Wenn wir diese Würfel im Raume zusammenstellen gruppieren , so werden nur ganz bestimmte Anordnungen roter Quadrate im Raum entstehen können, bedingt durch die Form Würfelform der Glaskörper. Ich könnte nun die Regel, nach der die roten Quadrate angeordnet sein können auch ohne Erwähnung 33 der Würfel angeben ausdrücken , aber in ihr wäre dennoch das Wesen der Würfelform enthalten präjudiziert . Freilich nicht, daß gläserne Würfel hinter den ˇroten Quadraten stehen sind , wohl aber die Geometrie des Würfels.        Wenn wir nun aber einen solchen Würfel sehen, sind damit wirklich schon die Gesetze der möglichen Zusammenstellung gegeben?⌊;⌋ Aalso die Geometrie des Würfels? Kann ich die Geometrie des Würfels von einem Würfel ablesen?

​

Der Würfel ist dann ein Ausdruck eine Notation der Regel. Und hätten wir eine solche Regel gefunden, so könnten wir sie wirklich nicht besser notieren, als mittels der durch die Zeichnung eines Würfels. (Und daß es hier auch eine Zeichnung ˇstatt des Würfels tut, ist sehr bedeutsam.)        Wie kann aber der Würfel (oder die Zeichnung) als Notation einer geometrischen Regel dienen? Nur sofern er als Satz ˇoder Teil eines Satzes einem System von Sätzen angehört.

​

¥ ⋎ S. 93 ¥ ⋎ S. 52D ¥ oder großes Format S. 26A

​

Das Zeichen der Negation, z.B. “ p W F F W ”⌊, z.B.,⌋ ist gleichwertig jedem andern Negationszeichen; es ist ebenso ein Komplex von Strichen, wie der Ausdruck “nicht p” das Wort “nicht” , & zum N Zeichen für die Negation wird es nur durch die Art, wie es ‘wirkt’, – ich meine: wie es im Spiel gebraucht wird. ⌊ (Analoges⌊,⌋ gilt die S für die W-F-Schemata der Tautologie & Contradiktion.) ⌋

​

Ich möchte sagen: Nur dynamisch ist etwas ein wirkt das Zeichen, nicht statisch.

∫

Es scheint hier ˇleicht, als ob das Zeichen die ganze Grammatik zusammenfaßte; daß sie in ihm 34 enthalten wäre, ˇwie die Perlˇenschnur in einer Schachtel & wir sie nur herausziehen müßten. (Aber ein solches dieses Bild ist es eben, welches was⌊das⌋ uns irreführt.) | Als wäre das Verständnis ein momentanes Erfassen von etwas, wovon später mir die Konsequenzen gezogen werden, & zwar so, daß diese Konsequenzen bereits in einem, ideellen Sinn existieren, ehe sie gezogen werden. | c ⌊⌊ Wird geschrieben⌋⌋ Als ob der Würfel schon die Geometrie des Würfels enthielte & ich sie nur noch auszubreiten hätte. Aber welcher Würfel? Der Gesichtswürfel, oder ein Eisenwürfel? Oder gibt es einen idealen geometrischen Würfel? Es schwebt uns offenbar Offenbar schwebt uns der Vorgang vor, wenn wir aus einer Zeichnung, ˇeiner Vorstellung (oder einem Modell) Sätze der Geometrie ableiten. // Wir denken hier offenbar an den Vorgang, wenn … // Aber welche Rolle spielt dabei das Modell? Doch wohl die des Zeichens; [. D|d]es Zeichens, das in einem bestimmten Spiel verwendet wird. – Und es ist interessant & merkwürdig, wie dieses Zeichen verwendet wird, wie wirˇ, etwa, die Zeichnung des Würfels wieder & wieder benützenc, mit in immer andern Zutaten. immer anderen ◇◇◇ Verbindungen. – Einmal sind die Diagonalen gezogen, einmal mehrere Würfel aneinandergereiht, etc. etc.. Und es ist dieses Zeichen (mit der Identität eines Zeichens), welches wir für jenen Würfel nehmen, in dem die geometrischen Gesetze bereits liegen. (Sie liegen in ihm so wenig, wie im Schachkönig die Dispositionen in gewisser Weise gebraucht benützt zu werden.)

​

Man ist in der Philosophie immer in der Versuchung Gefahr , 35 eine Mythologie des Symbolismus zu geben, oder der Psychologie ˇaufzustellen; statt einfach zu sagen, was man weiß.

​

⍈ A [Zu S. 21]            Es ist ⌊(⌋so⌊)⌋, wie wenn wir ich mir im Werkzeugkasten der Sprache Werkzeuge zum künftigen Gebrauch herrichtete. Der Dieser Werkzeugkasten ist die Grammatik mit ihren Regeln. Denke an den Gebrauch des Bildes einer Kugel (der Vorstellung oder eines Bildes auf dem Papier). Ein solches Bild wird nicht immer gebraucht werden, wenn von einer Kugel die Rede ist (wenn das Wort ‘Kugel’ sinnvoll gebraucht wird), aber es wird in gewissen Fällen gebraucht & dann sozusagen aus dem Werkzeugkasten gezogen // hervorgezogen // . werden. ¥ ⋎ S. 52 in der Reihenfolge: A C D B E

​

Der Begriff der Bedeutung, wie ich ihn ˇin meine philosophischen Erörterungen Gedanken übernommen überkommen habe, stammt aus einer primitiven Philosophie der Sprache her.

​

Was wir “Bedeutung” nennen, scheint mit der primitiven Gebärdensprache (Zeigesprache) zusammenzuhängen. “Bedeutung” kommt von “deuten”.

​

Augustinus, wenn er vom Lernen der Sprache redet, redet nur davon, wie wir den Dingen Namen beilegen, oder die Namen der Dinge verstehen. Hier scheint [d|D]as Benennen das ˇscheint hier das 36 Fundament & Um & Auf der Sprache zu sein.    Diese Betrachtungsweise ist wohl die, welcher Es ist die Auffassung, der die Erklärungsform “das ist …” im Fundament der Sprache zu liegen scheint. Von einem Unterschied der Wortarten redet Augustinus nicht & meint mit “Namen” offenbar Wörter wie “Baum”, “Tisch”, “Brot” , & gewiß die Eigennamen der von Personen; dann aber wohl auch “essen”, “geben”, “hier”, “dort”, kurz alle Wörter. Gewiß aber denkt er zunächst an Hauptwörter, & an die übrigen als etwas, was sich finden wird. (Und Plato sagt, daß der Satz aus Haupt- & Zeitwörtern besteht.)     Sie beschreiben eben das Spiel einfacher als es ist.     Aber das Spiel, welches das Augustinus beschreibt, kommt wohl auch in der Wirklichkeit vor wird wohl auch in der Wirklichkeit gespielt. ein Teil der ist allerdings ein Teil der Sprache. Denken wir, ich wollte aus Bausteinen, die mir ein Andrer zureichen soll, einen Bau ein Haus aufführen; so könnten wir zuerst ein Übereinkommen dadurch treffen, indem daß ich, auf einen Baustein zeigend, sage: “das ist eine Säule”, auf einen andern zeigend: “das heißt ein ‘Würfel’”, – “das heißt ‘Platte’”, u.s.w.. Und nun bestünde die Anwendung riefe ich die Wörter “Säule”, “Platte” etc. aus in der Ordnung, wie ich die Steine brauche.

​

Augustinus beschreibt einen Kalkül unserer Sprache, nur ist nicht alles, 37 was wir Sprache nennen, dieser Kalkül.  (Und das muß man in sehr vielen Fällen sagen, wo die Frage ist ˇuns entgegentritt ˇvor uns steht: “ist diese Darstellung brauchbar, oder unbrauchbar”. Die Antwort ist istlautet : “ja, brauchbar, – aber nur dafür; nicht für das ganze Gebiet, das Du darzustellen vorgabst”.) ¥ ⌊ ⋎ S. 179 A ⌋

​

Es ist so, wie wenn jemand erklärte: “Ein Spiel spielen besteht darin, daß man Dinge, gewissen Regeln gemäß, auf einer Fläche verschiebt …”; und wir ihm sagten: Du denkst da gewiß an die Brettspiele & auf die ist Deine Beschreibung anwendbar; aber das sind nicht alle Spiele. Du kannst also Deine Erklärung dadurch richtigstellen, daß Du sie ausdrücklich auf diese Spiele einschränkst. ⌊⌊Besser in der Maschinschrift⌋⌋ ⌊ ⋎ S. 179 B ⌋

​

¥ ⋎ S. 179 B ˇIch wollte sagen: Wie Augustinus das Lernen der Sprache beschreibt, das kann uns zeigen, woher diese Auffassung eigentlich kommt.      Man könnte den Fall ˇunserer Sprache mit dem einer Schrift vergleichen, in der Buchstaben zum Bezeichnen von Lauten benützt würden, aber auch zur Bezeichnung der Betonung des Accentes & ˇetwa als Interpunktionszeichen. Fassen wir S[e|ie]h[e|t]n man dann diese Schrift als Sprache zur Beschreibung des Lautbildes auf an, , so kann man sich denken, daß ei Einer sie so mißverstünde versteht , als entspräche einfach jedem Buchstaben ein Laut, & als hätten die Buchstaben nicht auch ganz andere Funktionen.

​

38 ⍈ ↻ Hierher gehört auch: Man kann – für Andere leicht verständlich⌊,⌋ – von Kombinationen von Farben mit Figuren Formen sprechen (etwa der Farben rot & blau mit den Figuren Formen Quadrat & Kreis), ganz ebenso wie von Kombinationen verschiedener Figuren Formen oder Körper. Und hier ist haben wir die Wurzel des schlechten irreleitenden Ausdrucks, : die Tatsache sei ein Komplex von Gegenständen. Es wird hier also , daß ein Mensch kl krank ist verglichen mit der Zusammenstellung zweier Dinge, wovon das eine der Mensch, das andere die Krankheit wäre. Hüten wir uns davor zu vergessen, daß das ein Vergleich ist.

​

Wie ˇmit die Handgriffen i[n|m] dem Stellwerk Führerstand einer Lokomotive sehr verschiedene Dinge ausgeführt werden Arten der Betätigung haben, so mit den die Wörtern der Sprache, die in gewissem Sinne Handgriffen gleichen entsprechen . Einer ist der Handgriff Ein Handgriff etwa gehört zu einer Kurbel, die sie kann kontinuierlich verstellt werden kann , denn sie betätigt ein Ventil; ein anderer Handgriff bewegt betätigt betätigt einen Schalter, der zweier Stellungen fähig ist hat; ein dritter ist der Handgriff einer Pumpe & wirkt nur wenn er auf & ab bewegt wird; etc.. Aber alle sehen einander ähnlich, denn sie werden mit der Hand angefaßt. ¥ •

​

Wer Jeder, der einen Satz einer ihm geläufigen Sprache liest, nimmt empfindet die Wörter der verschiedenen Wortarten in ˇganz verschiedener Weise⌊.⌋ auf., obwohl sich ihr Bild & Klang der Art nach 39 nicht unterscheidet. (Das Gleichnis vom Bedeutungskörper.) Wir vergessen ganz, daß ˇdie Laut- oder Schriftbilder “nicht” & “Tisch” & “grün” gleichartige Dinge sind als Laut- oder Schriftbilder sich nicht ihrem Wesen nach von einander unterscheiden & sehen dies // & sehen die Einförmigkeit der Wörter // nur klar in einer uns fremden Sprache. (Das Gleichnis vom Bedeutungskörper der hinter dem Wort steht, drängt sich uns hier auf) (Vergleiche auch William James über die Gefühle die Worten wie “nicht”, “aber”, etc. entsprechen.)

​

¥ ⋎ [S. 26 großes Format B als neuer Absatz] Vergleich der Linien auf einer Landkarte mit verschiedener Funktion auf einer Landkarte ˇ(Grenzen, Straßen, Meridiane, Schichtenlinien) mit den verschiedenen Wortarten im Satz. Der Unbelehrte sieht eine Menge von Linien & kennt nicht die Verschiedenheit ihrer der Bedeutungen.     Denken wir uns ˇauf der Karte auch einen Strich, der ein Zeichen durchstreicht, um zu zeigen, daß es ungiltig ist.

​

Der Unterschied der Wortarten ist dem Unterschied der Spielfiguren im Schach zu vergleichen, aber oder auch dem noch größeren einer Spielfigur & des Schachbrettes.

​

Man kann erklären könnte sagen : Dc d er Ort eines Wortes in der Grammatik ist seine Bedeutung. ⌊⌊ Absatz ⌋⌋ Man würde [I|i]n der alten Ausdrucksweise ◇◇◇ sag[t|en ] man: Das Wesentliche ˇam Wort ist die seine Bedeutung des Wortes, nicht das Wort. Wir können also das 40 Man sagt: Das Wesentliche am Wort ist seine Bedeutung. Man kann das Wort durch ein anderes ersetzen, das die gleiche Bedeutung hat. Damit ist gleichsam sozusagen ein Platz für das Wort fixiertc, & man kann ein Wort für ein anderes setzen, wenn man es an den gleichen Platz setzt.

​

Wenn ich mich entschlösse (auch in meinen Gedanken) statt “rot” ein neues Wort zu sagen, wie würde es sich zeigen daß dieses an dem Platz des Wortes “rot” steht? – Sind es etwa immer Vorstellungen die den Platz der Wörter halten?      Wenn man übereinkäme im Deutschen statt “nicht” “non” zu sagen & dafür “nicht” statt des Wortes “rot” ˇ “nicht” ; so bliebe das Wort “nicht” in der Sprache, & doch könnte man sagen, daß “non” ˇjetzt so gebraucht wird, wie früher “nicht”, & daß jetzt “nicht” anders gebraucht wird⌊.⌋ als früher.

​

Wäre es das es nicht ähnlich, wenn ich mich entschlösse, die Formen der Schachfiguren zu ändern, oder, die eine Figur eines Pferdchens als König zu verwenden? Wie würde es sich nun zeigen, daß das Pferdchen Schachkönig ist? Kann ich hier nicht sehr gut von einem Wechsel der Bedeutung reden?

​

⇒ Fortsetzung S. 15 Großes Format Ist es, anderseits, eine unwesentliche Änderung wenn ich so in einem Gedicht // in einem Satz der Lyrik // ein Wort durch ein anderes ersetze? – Welche Art von Unterschied macht es, wenn ich, etwa, in einem Lehrbuch der Physik das Wort Geschwindigkeit 41 ˇsystematisch durch ein beliebiges andere oder den Buchstaben v durch einen hebräischen ersetzte? Und & welchen Unterschied, anderseits, wenn ich etwa ein Wort eines lyrischen Stücks durch das Zeichen “A” ersetzte & erkläre A solle die Bedeutung jenes Wortes haben. – Das wäre, als wollte ich die Stirn runzeln & erklären, daß es das gleiche bedeuten solle, wie ein freundliches Lächeln.

​

[Dazu gehört: Die Bedeutung des Worts, der Sinn des Satzes liegt in ihm, im Kalkül ⌊⌊dem er angehört. Dieser ist sozusagen⌋⌋ ⌊⌊autonom. Die Sprache, Der Satz muß für sich selber sprechen. Uns interessiert der Inhalt des Satzes u.s.w.. ⌋⌋    Die Bedeutung eines Namens ist nicht sein Träger. – Der Ausdruck “der Träger des Namens ‘N’” hat die gleiche Bedeutung wie der Name ‘N’. Der Ausdruck kann statt des Namens eingesetzt werden. “Der Träger des Namens ‘N’ ist krank” heißt: N ist krank. Man sagt Aber wir sagen nicht, die Bedeutung des Wortes N sei ◇ krank. Der Träger des Namens ‘N’ hört etwa auf zu existieren, wenn er ˇvernichtet wird, ˇ ◇◇◇ stirbt; wenn aber der Name ˇverliert seine Bedeutung verliert, so etwa dadurch, daß wir seinem Träger einen anderen Namen gegeben haben. wenn wir ihn abschaffen & durch einen andern ersetzen.     Aber heißt es nicht dasselbe zu sagen “zwei Namen haben einen Träger” & “zwei Namen haben dieselbe Bedeutung”? Gewiß Wohl – ⌊,⌋ denn statt der Gleichung:        der Träger des Namens A = der Träger des Namens B kann man ja schreiben: A = B

​

Wir weisen zur Erklärung der Bedeutung des Namens auf seinen Träger. Man kann dadurch den Gebrauch des Wortes 42 lehren, wenn dieser Gebrauch, sozusagen, schon bis auf eine letzte Bestimmung bekannt ist.     Erinnere Dich daran, daß durch dieselbe hinweisende Geste auf den gleichen Körper die Bedeutung von Wörtern verschiedener Art erklärt werden kann. Z.B.: “das (worauf ich zeige) heißt ‘Holz’”, “das heißt ‘braun’”, “das heißt ‘Stab’”, “das heißt ‘Federstiel’”.      Der erklärende Hinweis entscheidet da nur noch eine Frage von der Art: “Welcher dieser Leute ist Herr N”, “Welche Farbe heißt ‘lila violett’”, “welcher Ton ist das hohe C” .

​

⍈   [Zu S. 59] Wenn ich sage “die Farbe dieses Gegenstands heißt ‘violett’”, so muß ich die Farbe mit dem Hinweis den Worten “die Farbe dieses Gegenstands” schon bezeichnet haben, sie schon zur Taufe gehalten haben, damit die eine Namengebung geschehen kann. Denn ich könnte auch sagen: “der Name dieser Farbe ist von Dir zu bestimmen”; & der den Namen gibt müßte nun schon wissen, wem er ihn geben soll (an welchen Platz der Sprache er ihn stellt).         Ich könnte so erklären: die Farbe dieses Flecks heißt “rot”, die Form “Elipse”. Und hier stehen die Wörter “Farbe” & “Form” stehen hier für die Anwendungsarten der gegebenen Namen & bezeichnen in Wirklichkeit Wortarten wie “Hauptwort” & “Eigenschaftswort”. Man könnte sehr wohl in der gebräuchlichen Grammatik die Bezeichnungen “Farbwort”, “Formwort”, “Stoffwort” einfüh 43 ren. (Aber mit demselben Recht auch “Baumwort”, “Buchwort”?)

​

Denken wir aber an das Zeigen & Benennen von Gegenständen, wenn man Kindern die Anfänge der Sprache lehrt. Hier kann man nicht sagen, diese Erklärung (wenn man das eine Erklärung nennen will) gebe noch eine letzte Bestimmung über den Gebrauch des Wortes (des Wortes “Papa” etwa); & das Kind kann auch noch nicht fragen “wie heißt das”. (Diese ‘Erklärung’ ist nicht die Antwort auf die Frage “wie heißt dieser Gegenstand”.)

​

Der Name, den ich einem Körper gebe, ˇoder aber einer Gestalt, einem Ort, einer Farbe, hat in jedem Fall jedesmal eine andere Grammatik. “A” in “A ist gelb” hat eine andere Grammatik, wenn es einmal der Name eines Körpers, ein andermal der Name der einer F Oberfläche eines Körpers ist. (Es hat z.B. Sinn zu sagen der Körper sei durch & durch gelb, aber nicht, die Fläche sei es.) Und man zeigt in anderm Sinne auf einen Körper, auf seine Länge, & auf seine Farbe. Es ist etwa eine Definition möglich: auf eine Farbe zeigen heißt: ⌊,⌋ auf den Körper zeigen der sie hat. (Wie, ⌊–⌋ wer der, welcher Geld he⌊i⌋ratet, es nicht in demselben Sinne heiratet, wie er die Frau heiratet, die es besitzt.)

​

Man könnte sagen: Die Bedeutung eines Wortes ist das, was die Erklärung der Bedeutung erklärt.     Und soweit ˇdie Bedeutung in der Erklärung n⌊i⌋edergelegt ist, tritt der Begriff der Bedeu- 44 tung in den Kalkül ein, den wir mit den Zeichen betreiben. ¥ •    Verstehen wir unter “Bedeutung” aber ein charakteristisches Gefühl, das durch's beim beimc Hören eines Wortes wachgerufen wird, dann ist die Bedeutung in der Erklärung des eines Wortes nicht niedergelegt, aber durch sie vielleicht etwa bewirkt, wie die Krankheit durch die Verkühlung. ⌊Speise.⌋

​

↺ ⍈ (Dazu: “Das, was 1cm³ Wasser wiegt, hat man ‘1 Gramm’ genannt.” – “Ja, was wiegt er denn?”)

​

¥ ⋎ S. 45 A In dem ersten Sinn könnte kann man die Erklärung der Bedeutung die Ausschließung von Mißverständnissen nennen ˇwollen. Sie sagt Die Erklärung sagt ˇetwa, das Wort hat diese Bedeutung, nicht jene. Aber das gilt nur von Gewissem, was wir die Erklärung der Bedeutung eines Wortes nennen, wenn wir etwa erklären: “diese Farbe heißt ‘orange’” (nicht jene), “dieser Mann heißt ‘N.N.’” (nicht der [a|A]ndere).      ‘Erklärung der Bedeutung’ aber, nennen wir vielerlei.       // Die Erklärung eines Zeichens muß jede Meinungsverschiedenheit in Bezug auf seine Bedeutung beseitigen können.       Mißverständnisse nenne ich das, was durch eine Erklärung zu beseitigen ist, ⌊.⌋ Die Erklärung der Bedeutung eines Wortes schließt Mißverständnisse aus.       Die Aufklärung kann nur verstanden werden, wenn sie in einer Sprache gegeben wird, die unabhängig von dem 45 Mißverständnis besteht. Die Aufklärung sagt etwa: das Wort hat diese Bedeutung, nicht jene. Aber das gilt … //     Aber wir nennen sehr verschiedenes ‘Erklärung der Bedeutung’. ‘Erklärung der Bedeutung’ aber, nennen wir vielerlei. Zur Erklärung des Wortes “Blatt” zeigen wir wohl auf verschiedene Blätter; zur Erklärung des Wortes “violett”c auf einen violetten Gegenstand; zur Erklärung des Wortes “wehe!” machen wir etwa vielleicht eine Geste & sprechen in bestimmtem Tonfall; zur Erklärung des Zeichens “ ⊃ ” schreiben wir “p ⊃ q = p ⌵ ~q ” u.s.f.. ¥ [neue Zeile ⋎ S. 46 A], ¥ B ] ¥ ⋎ S. 48 ⌊ B ⌋ nach S 46 A]     Man sagt dem Kind: “nein, kein Stück Zucker mehr!” & nimmt es ihm weg. So lernt es die Bedeutung des Wortes “kein”. Hätte man ihm mit denselben Worten ein Stück Zucker gereicht, so hätte es gelernt, das Wort anders zu verstehn. (Es hat damit gelernt das Wort zu gebrauchen, aber auch ein bestimmtes Gefühl mit ihm zu verbinden, es in gewisser bestimmter Weise zu erleben.)

​

¥ [Neuer Absatz ⋎ S. 48 A ⍈ [Zu S. 44] A Die Erklärung der Bedeutung ist ein Teil des Kalküls mit den Worten. Und man kann sagen, sie sei das was uns in der Philosophie wenn von der Bedeutung eines Wortes die Rede ist, angeht. an der Bedeutung eines Wortes interessiert. Denn diese Erklärung ist ein weiteres Stück Sprache.       Man könnte auch so sagen. Fragen wir nicht, was Bedeutung sei, sondern sehen wir uns an, was man die “Erklärung der Bedeutung” nennt.

​

46 ⍈ [Zu S. 45] A          Man sagt: “der Name ‘Mont Blanc’ ˇauf der Karte bedeutet diesen Berg”, “das Wort ‘violett’, diese Farbe”, “das Wort ‘Tisch’ ‘Blatt’ so einen Gegenstand”, aber ˇes gibt nichts Analoges für das Wort “nicht”.    Aber auch vom Wort “hallo” oder “ach” sagt man es hat eine Bedeutung zum Unterschied etwa von einer in unserer Sprache nicht gebrauchten Bildung ( etwa wie “ech”).    Von manchem Wort werden wir sagen, es sei gleichbedeutend einer Geste; & wenn wir von der Bedeutung des Wortes “hehe!” reden wollten, so im [S|s]elben Sinne wie von der des Lachens [⋎

​

⍈ [Zu S. 45] B           Was man Erklärung der Bedeutung eines Wortes nennt, eine Definition z.B., lehrt uns den Gebrauch des Wortes. Und die meisten Worte wurden uns nicht in diesem Sinne erklärt, durch Definition erklärt, sondern wir lernten ihren Gebrauch auf andere Weise. // , sondern ihr Gebrauch uns auf andere Weise gelehrt. //

​

Man möchte nun sagen: Gewiß, die Bedeutung eines Wortes ist seine Wirkung. Denn die Sätze, die wir sagen, haben einen bestimmten Zweck, sie sollen gewisse Wirkungen hervorbringen herbeiführen . Also sind sie offenbar Teil eines Mechanismus (vielleicht eines psychologischen) ˇzur Herbeiführung dieser Wirkung & die W[o|ö]rte⌊r⌋ sind auch solche Teile // Bestandteile // (Hebel, Zahnräder u. dergl.). Und das einfachste Beispiel wäre die Wirkung 47 einer Gruppe von Löchern in dem Tonstreifen eines Pianola. Wie aber, wenn das Pianola nicht richtig funktioniert, weil sein Mechanismus in Unordnung geraten ist? Wenn also diese Gruppe von Löchern statt einer musikalischen Phrase ein Klopfen & Zischen hervorruft. Vielleicht sagt man, der Sinn der Zeichen sei die Wirkung ˇjener Löcher in einem auf ein Pianola in gutem Zusta⌊n⌋d (der Sinn eines Befehls sei seine Wirkung auf einen willigen Menschen). Aber was soll hier als Kriterium der Willigkeit dienen?

​

Nicht der Wirkung entspricht der Sinn, sondern dem Zwe⌊c⌋k (der Zweck wird festgesetzt, die Wirkung ist Sache der Erfahrung.)    Die Bedeutung eines Wortes wird festgesetzt. Die Wirkung wird die Erfahrung lehren.    Soll ich also sagen, der Zweck eines Wortes ist seine Bedeutung? – Was ist nun also der Zweck des Wortes “Gras”? (Sage nicht, es sei einfach der, in uns im Hörenden eine Vorstellung von Gras hervorzurufen.) – Nach dem Zwe⌊c⌋k der Löcher auf der Pianolarolle gefragt, werde ich wohl ihre Wirkungsweise im Pianola beschreiben. Aber ich könnte nicht den Zwe⌊c⌋k dieser Löcher als Teil des Zwecks des Pianolas darstellen, ˇetwa des Zwecks vielleicht, etwa, einen Menschen aufzuheitern. Man könnte sagen, es sei die Funktion des Schachspiels uns Vergnügen zu machen; aber kann man die Funktion des Rössels damit beschreiben, daß man den Teil des ˇganzen Vergnügens zeigt, der auf das 48 Rössel entfällt // zeigt, den uns das Rössel macht? //

​

¥ ⋎ Absatz, dann S. 51 A ⍈ ˇ[Zu S. 45] A Wie lernt ein Kind den Gebrauch etwa des Wortes “vielleicht”? – Es spricht etwa einen Satz nach, wie es ihn ähnlich den es von einem Erwachsenen gehört hat: “sie wird vielleicht kommen”; im gleichen Tonfall wie der Erwachsene. (Dies ist gleichsam ein Spiel.) Dann fragt man sich manchmal: versteht es das Wort “vielleicht” schon, oder spricht es es nur nach? – Was ist das Anzeichen dafür, daß es das Wort wirklich versteht? – Daß es es das Wort in verschiedenen Fällen richtig – (das heißt doch[;|,] den [r|R]egeln gemäß) – gebraucht, & danach auch auch danach handelt.

​

⍈ [Zu S. 45 nach dem Satz S 46 A] A B Geld, & was man dafür kauft. In gewissen Fällen einen Gegenstand (einen Apfel), aber auch die Erlaubnis auf einem Platz im Theater zu sitzen, oder einen Titel, oder schnelle Fortbewegung, oder das Leben, etc..

​

Man möchte mit dem Gedächtnis & der Assoziation den Mechanismus des Bedeutens erklären.        Aber wir fühlen, daß es uns nicht auf eine die Erklärung eines Mechanismus ankommen kann. Denn diese Erklärung ist wieder eine Beschreibung von Phänomenen durch die Sprache. Sie sagt etwa: wenn das Wort “rot” gehört wird, springt 49 die Vorstellung rot hervor[.| (]eine Tafel durch den Druck eines Knopfes). Nun, wenn das eintritt, – was weiter? – Wir wollen eben die Erklärung eines Kalküls hören. Und die Erklarung des Mechanismus stellt sich außerhalb des Kalküls. Sie ist selbst eine Beschreibung in der Sprache, & eine, die in den Kalkül, der uns erklärt werden soll, nicht eingreift. Während wir eine Erklärung brauchen, die ein Teil des dieses Kalküls ist.

​

(Die psychologischen – trivialen – Erörterungen über Assoziation, Wiedererkennen, etc. lassen immer das für uns eigentlich Merkwürdige aus & man merkt ihnen an, daß sie herumreden, ohne den springenden Punkt zu berühren.)

​

“Wie soll er wissen, welche Farbe er zu wählen hat, wenn er das Wort ‘rot’ hört?” – “Sehr einfach: er soll die Farbe nehmen, deren Bild ihm beim Hören des Wortes einfällt”. – Aber wie soll er wissen, was das heißt & welche das ist “die ihm beim dem Wort ‘rot’ einfällt”?    (Es gibt freilich auch ein Spiel: die Farbe wählen die Dir bei diesem Wort einfällt.) Und: “‘rot’ bedeutet: die Farbe die mir beim Hören des Wortes ‘rot’ einfällt” wäre eine Definition.)      Wenn ich sage, das “Symbol ist das, was diesen bestimmten Effekt hervorruft”, – so fragt es sich eben, wie ich von “diesem Effekt” reden kann. Und wie ich weiß, daß es er der ist, den ich gemeint habe, wenn er eintritt. 50   Es ist drum darum keine Erklärung, die die Wurzel unseres Problems unserer Schwierigkeit trifft, zu sagen: sehr einfach, wir vergleichen ihn mit unserem Erinnerungsbild; – denn wie ist uns die Vergleichsmethode gegeben nach der wir vergleichen sollen? D.h., wie wissen wir was das Wort “vergleichen” bedeutet?     Was ist denn das Kriterium dessen // dafür // , daß ich die Farbe rot richtig wiedererkannt habe?     Und es ist ⌊g⌋a[g|r] nicht notwendig die Wirkungsweise eines Worts durch Assoziation & Gedächtnis zu erklären, weil man statt dieser Fähigkeiten immer einen Zettel mit einer Tabelle bei sich ⌊t⌋ragen kann.

​

Ich könnte auch so fragen: Warum verlangst Du ˇkausale Erklärungen? Wenn diese gegeben sein werden, wirst Du ja doch wieder vor einem Ende stehen. Sie können Dich nicht weiter führen, als Du jetzt bist.

​

Ich wünsche mir, einen Apfel zu bekommen; kann ich sagen, daß erst die Erfüllung des Wunsches mir zeigt, was ich gewünscht habe? daß sie mich erst die Bedeutung des Wortes “Apfel” lehrt? – Diese Bedeutung wird durch eine Worterklärung gegeben // Das Verständnis dieses Wortes wird durch eine Worterklärung gegeben // , welche nicht die Erfüllung des Wunsches ist.

​

¥ ⋎ Absatz, dann S. 59 A   Es ist eine Funktion des Wortes “rot” uns 51 die ˇbestimmte Farbe in Erinnerung zu rufen , ja & es könnte auch z.B. es könnte z.B. gefunden werden, daß sich dazu das Wort “rot” besser eignet als ein anderes, daß seine Bedeutung etwa nicht so leicht vergessen oder verwechselt wird. Aber wir hätten uns, wie schon gesagt, statt des Mechanismus der Assoziation einer Tabelle (oder dergleichen) bedienen können; & nun müßte unser Kalkül eben mit dem assoziierten, oder gesehenen, Farbmuster weiterschreiten. Die psychologische Wirksamkeit Eignung Zweckmäßigkeit eines Zeichens beschäftigt mich uns nicht. (Dagegen heißt es im , z.B., Kratylos: “Bei weitem & ohne Frage ist es vorzüglicher, Sokrates, durch ein Ähnliches darzustellen, was jemand darstellen will, als durch das erste beste.”)

​

⍈ ˇ[Zu S. 48] A Die Verwendung eines Planes, einer Landkarte besteht darin, daß wir uns in irgendeiner Weise nach ihr richten; daß wir ihr Bild in unsere Handlungen übertragen. Es ist klar, daß da kausale Zusammenhänge stattfindenhaben; aber würde man sagen, sie sind es, die den Plan zum Plan machen?

​

Die Untersuchung, ob die Bedeutung eines Zeichens seine Wirkung ist, sein Zweck, etc. ist eine grammatische Untersuchung. 52 ⌊⌊ [Zu S. 35] ⌋⌋ ⍈ [Zu S. 35] A       Anderseits sagt man: “ich verstehe diese Geste”, wie “ich verstehe dieses Thema”, “es sagt mir etwas”, & das heißt hier: ich erlebe es, es greift in mich ein. Ich folge ihm mit bestimmtem Erlebnis        ¥ • ⌊ B ⌋ Wenn ich sage, bei irgend einer Gelegenheit, sage: “ich verstehe diese Geste”, meine ich da, daß ich sie in Worten oder andere Zeichen übersetzen kann? Gewiß nicht immer. Ich charakterisiere ˇauch ein Erlebnis. ⌊ (Die Geste macht einen Eindruck auf mich) ⌋

​

[Zu S.◇◇◇]

​

↺ ⌊ C ⌋ Es ist sonderbar: das Verstehen einer Geste werden // möchten // wir als durch ihre Übersetzung in Worte erklären & das Verstehen von Worten, als durch eine Übersetzung in Gesten. // : das Verstehen einer Geste möchten wir …          Und wirklich werden wir Worte durch eine Geste & eine Geste durch Worte erklären. //   Das ⍈ [Zu S. 33]       ⌊ D ⌋ (Gefragt, was ich mit dem Wort “und” im Satz “gib mir das Brot und die Butter” meine, würde ich mit einer ˇzusammenfassenden Gebärde antworten; & diese Gebärde würde, was ich meine, illustrieren. Ähnlich, wie das ein grüne⌊s⌋ Täfelchen ˇdie Bedeutung von “grün” illustriert & die W-F-Notation die Bedeutung von “nicht”, “und”, etc..) ⌊ (Die Geste des Wortes “vielleicht”; des Wortes “bitte” & ˇ“danke”.) ⌋

​

E      Das “nicht” macht eine abwehrende Geste. Ja, es ist … Es ist eine abwehrende Geste. Und man könnte ˇwohl sagen: das Verstehen der Verneinung ist 53 das Verstehen einer abwehrenden (verneinenden) Geste. (Wie lernt man das Kopfschütteln der Verneinung verstehen.)

​

Es ist möglich daß Einer die Bedeutung eines Wortes, etwa des Wortes “blau”, vergißt. Was hat er da vergessen? ⌊–⌋ Wie äußert sich das?       Da gibt es verschiedene Fälle. ˇ Z.B. [E|e]r zeigt etwa auf ve Täfelchen verschiedener Farben & sagt: “ich weiß nicht mehr, welche von diesen man ‘blau’ nennt”. Oder aber, er weiß überhaupt nicht mehr, was das Wort bedeutet, & nur, daß es ein Wort der deutschen Sprache ist.      Wenn wir ihn nun fragen “weißt Du, was das Wort ‘blau’ bedeutet”– ⌊,⌋ & er sagt “ja”, – da konnte er verschiedene Kriterien anwenden, um sich “zu überzeugen”, daß er die Bedeutung wisse. (Denken wir an die entsprechenden Kriterien dafür, daß er das Alphabet hersagen kann.) Vielleicht ruft er sich ein blaues Vorstellungsbild vor die Seele, vielleicht sah er nach einem blauen Gegenstand im Zimmer, vielleicht fiel ihm das englische “blue” ein, oder er dachte an einen ˇSchlag der einen “blauen Fleck”, den er sich geholt hatte. erzeugt hatte,. ⌊etc..⌋       Wenn gefragt würde: wie kann er sich denn zur Probe seines Verständnisses ein blaues Vorstellungsbild vor die Seele rufen hervorrufen ? Denn, wie kann ihm das Wort “blau” zeigen, zeigen welche Farbe aus dem Farbenkasten 54 seine Vorstellung er zu wählen hat, – so ist zu sagen, daß es sich da eben zeigt, daß das Bild vom Wählen, etwa, eines blauen Gegenstandes nach einem mittels einesc blauen Mustertäfelchens hier unpassend // ungeeignet // ist. versagt. Und der Vorgang eher mit dem zu vergleichen ist, wenn beim [d|D]rücken eines Knopfes, der die “Aufschrift “blau” trägt, auf dem das Wort ‘blau’ geschrieben steht, automatisch ein blaues Täfelchen hervorspringt; oder, wenn der Mechanismus versagt, nicht vorspringt.      Man könnte nun sagen: Der, welcher die Bedeutung des Wortes “blau” vergessen hat & aufgefordert wurde, einen blauen Gegenstand aus anderen auszuwählen, fühlt beim Ansehn dieser Gegenstände, daß die Verbindung zwischen dem Wort “blau” & jenen Farben nicht mehr besteht (daß sie unterbrochen ist). Und die Verbindung wird wieder angeknüpft hergestellt , wenn wir ihm die Erklärung des Wortes wiederholen. Aber wir konnten die Verbindung auf mannigfache Weise wieder herstellen: Wir konnten, auf einen blauen Gegenstand zeigend, ⌊&⌋ sagen “das ist blau”, oder ihm sagen “erinnere Dich an Deinen blauen Fleck”, oder wir erinnerten ihn an das Wort “blue” // oder wir flüsterten ihm sagten das Wort “blue” zu ein // , etc.. Und wenn ich sagte, wir konnten die Verbindung auf diese verschiedenen Arten herstellen, so liegt der Gedanke nahe, daß ich ein bestimmtes Phänomen, welches ich die Verbindung zwischen Wort & Farbe, oder das 55 Verständnis des Wortes nenne, auf alle diese verschiedenen Arten hervorgerufen habe, wie ich etwa sage, daß ich die Enden zweier Drähte durch Dinge [ von verschiedener Form & aus versch. Material ] verschiedener Formen & Materialien verschiedene Gegenstände leitend mit einander verbinden kann. Aber von so einem Phänomen ˇder Verbindung, dem Entstehen eines blauen Vorstellungsbildes etwa, muß keine Rede sein, & das Verständnis wird sich dann dadurch zeigen, wird darin bestehen, daß er die blaue Kugel aus den andern tatsächlich auswählt; oder sagt, er könne es nun tun, wolle es aber nicht; ˇoder etc., etc.,⌊.⌋ etc.. Wir können dann immer ein Spiel festsetzen, welches eine Möglichkeit so eines Vorgangs darstellt, & müssen nicht vergessen, daß in Wirklichkeit unzählige verschiedene & ihre Kreuzungen mit den Worten “die Bedeutung vergessen”, “sich der Bedeutung erinnern”, “die Bedeutung kennen” beschrieben werden. ¥ •

​

Welche Wirkung hat⌊te⌋ ˇnun die hinweisende Erklärung? Wird sie beim Gebrauch des Worts immer wieder herangezogen, oder wirkte wirkt sie wie eine Impfung, die uns bis auf weiteres geändert hat?

​

↺ ⍈     Die Art des Erlernens der Sprache // [d|D]ie Wei ◇ se, wie wir die Sprache erlernten, // ist in ihrem Gebrauch nicht enthalten. (Wie die Ursache eben c﹖ nicht in ihrer Wirkung.)

​

Die Erklärung als Teil des Kalküls kann 56 nicht in die Ferne wirken. Sie wirkt nur, sofern sie angewandt wird.

​

⇒ [Bis hierher M.S. großes Format S. 39]   Ist es nicht so, daß eine ˇErklärung, eine Tabelle, zuerst so gebraucht wird werden , daß man sie “nachschlägt”, – daß man sie dann gleichsam im Kopf nachschlägt, sie sich vors innere Auge ruft (oder dergleichen), & daß man endlich ohne diese Tabelle arbeitet, – also so, als wäre sie nie dagewesen. – In diesem letzteren Falle spielt man nun ˇaber ein anderes Spiel. Denn es ist nicht so, ist nun nicht so, daß jene Tabelle ja doch im Hintergrund steht (& man immer auf sie zurückgreifen kann); sie ist aus unserm Spiel ausgeschieden, & wenn ich auf sie “zurückgreife”, so tue ich, was der Erblindete tut, der auf den Tastsinn zurückgreift. Eine Erklärung fertigt eine Tabelle an, & sie wird zur Geschichte, wenn ich die Tabelle nicht mehr benütze.

​

Ich muß unterscheiden zwischen den Fällen: wenn ich ˇmich, einmal, nach der Tabelle richte, &, ein andermal in Übereinstimmung mit der Tabelle⌊,⌋ (Regel, handle, ohne sie die Tabelle zu benützen. – Die Regel, deren Erlernung uns veranlasste, jetzt so & so zu handeln, ist als Ursache unserer Handlungsweise, als ihre Vorgeschichte ohne Interesse für uns. – Sofern sie aber eine allgemeine Beschreibung unsrer Handlungsweise ist, ist sie eine Hypothese. Es ist die Hypothese, daß diese beiden Leute, die am Schach- 57 brett sitzen, so & so handeln (ziehen) werden. ([w|W]obei auch ein Verstoß gegen die Spielregeln unter die Hypothese fällt, denn sie sagt dann etwas über das Verhalten der Spieler darüber aus, wie sich die Beiden benehmen werden , wenn sie auf den Verstoß aufmerksam werden.) Die Spieler könnten aber die Regeln auch so benützen, daß sie in jedem besonderen Fall nachschla ü gen, was zu tun ist; hier träte die Regel in die Spielhandlung selbst ein & verhielte verhält sich zu ihr nicht, wie eine Hypothese zu ihrer Bestätigung. – Hier gibt es aber eine Schwierigkeit: Denn der Spieler, der ohne [b|B]enützung eines Regelverzeichn⌊i⌋sses spielt, ja, der nie eins gesehen hat, könnte dennoch, wenn es verlangt würde, ein Regelverzeichnis Regeln seines Spiels angeben; & zwar nicht, indem er durch wiederholte Beobachtung festsetzte feststellte, wie er in dieserm & jener Spielsituation Situation gehandelt hat, sondern, indem er, vor einem Zug stehend, sagte: “in diesem Fall zieht man so”. – Aber, wenn das so ist, so zeigt es doch nur, daß er unter gewissen Umständen eine Regel aussprechen wird, nicht, daß er von ihr beim [s|S]pielen expliziten Gebrauch macht.    Daß er ein Regelverzeichnis anlegen wird, wenn man es verlangt, ist eine Hypothese; & wenn man eine Disposition, ein Vermögen dazu in ihm annimmt, so ist es eine psychische Disposition analog einer physiologischen. Wenn gesagt wird, diese Disposition charakterisiere t den Vorgang des Spiels, so charakterisiert sie ihn als einen psychologischen psychischen oder 58 physiologischen, was er tatsächlich ist. (I[m|n] unser⌊e⌋m Studium des Symbolismus gibt es keinen Vordergrund & Hintergrund, nicht ˇwesentlich ein greifbares Zeichen & ein es begleitendes ungreifbares Vermögen oder Verständnis.)

v

Das, was uns in am Zeichen an der Sprache interessiert, die Bedeutung, die für maßgebend ist, ist das, was in der Grammatik des Zeichens niedergelegt ist.

v

Wir fragen: Wie gebrauchst Du das Wort, was machst Du damit ? , – Das das wird uns z lehren, wie Du es verstehst.

v

Die Grammatik, das sind die Geschäftsbücher der Sprache, aus denen alles zu ersehen sein muß, was nicht begleitende Empfindungen Gefühle betrifft,sondern unsere die tatsächlichen ˇsprachlichen Transaktionen. // , sondern // , sondern die unsere tatsächlichen Transaktionen in mitc der Sprache. //

∫

Man könnte in gewissem Sinne sagen, daß ⌊es⌋ uns es nicht auf Nuancen ankommt. ˇ [Neuer Absatz] (Ich könnte mir einen Philosophen denken, der glaubte, einen Satz⌊,⌋ ˇüber das Wesen des Erkennensˇ, etwa ◇◇◇⌊,⌋ in roter Farbe drucken lassen zu müssen, da er sonst nicht wirklich er erst so ganz das sage ausdrücke, was er sagen ausdrücken solle.)

​

Die Deutung von Schrift- & Lautzeichen 59 durch hinweisende Erklärungen ist nicht Anwendung der Sprache, sondern Teil der … sondern ein Teil der Sprachlehre. Die Deutung vollzieht sich noch im Allgemeinen, als Vorbereitung auf jede Anwendung.

​

¥ • ⌊ Man kann die hinw. Erkl. auffassen als eine Regel der Übersetzung aus einer Gebärdensprache in die Wortsprache ¥ ˇ ⋎ S. 42 A [Dann Absatz]⌋

∫

Zur Grammatik gehört nicht, daß dieser Erfahrungssatz wahr, jener falsch ist Zu ; zu ihr gehören alle Bedingungen (die Methode) des Vergleichs des Satzes mit der Wirklichkeit. Das heißt, alle Bedingungen des Verständnisses (des Sinnes).

∫

⍈ [Zu S. 50] A Soweit sich die Bedeutung der Wörter in der eingetroffenen Erwartung, ˇin der Erfüllung des Wunsches⌊,⌋ in der Befolgung des Befehls, etc., zeigt, erweist, zeigt kommt sie in der Beschreibung der jeder Tatsache⌊n⌋ zum Vorschein. (D.h., in einem im Ausdruck der Erwartung, des Befehls.) zeigt sie sich immer schon in einer sprachlichen Darstellung der Erwartung etc.⌊.⌋ (Sie wird also ganz in der Sprachlehre bestimmt. (In dem, was sich hat voraussehen lassen; worüber man schon vor dem Eintreffen der Tatsache reden konnte.)

​

↺ ⍈   Ist nicht der Grund, weshalb wir glauben, mit der hinweisenden Erklärung das Gebiet der Sprache, der Zeichen, zu verlassen, daß wir dieses Heraustreten aus den Schriftzeichen mit einer Anwendung der Sprache, etwa mit der Beschreibung eines gesehenen Gegenstandes verwechseln?

∫

60     Besteht nun unsere Sprache wesentlich aus primären Zeichen (hinweisenden Gesten) & sekundären Zeichen (Worten)? Man möchte fragen, ob ˇes in unsere⌊r⌋ Sprache nicht diese primären Zeichen geben müsse, während sie auch ohne die sekundären anderen auskommen könnte.   (Der falsche Ton in dieser Frage liegt ⌊(⌋schon⌊)⌋ darin, daß sie eine Erklärung der wirklichen bestehendenˇwirklich bestehenden Sprache⌊,⌋ ˇwie sie existiert ⌊,⌋ erwartet, statt der bloßen einfachen Beschreibung.) ˇ Absatz     Es klingt ˇnatürlich wie eine lächerliche Selbstverständlichkeit, wenn ich sage, daß der, welcher glaubt sagt , die Gebärden Gesten seien die primären Zeichen, die allen andern zu Grunde liegen, außer Stande wäre, den gewöhnlichsten Satz durch Gebärden zu ersetzen.

∫

Man möchte zwischen Regeln der Grammatik unterscheiden, die “eine Verbindung von Sprache & Wirklichkeit” herstellen, & solchen, die es nicht tun. Von ˇEine Regel der ersten Art ˇist: “diese Farbe heißt ‘rot’”, – eine Regel von der zweiten ˇArt: “~~p = p”. Über Aber über diesen Unterschied besteht ein Irrtum ; : die Sprache ist nicht etwas, was dem eine Struktur gegeben,⌊,⌋ & das dann der Wirklichkeit aufgepaßt wird. // … ein Irrtum: der Unterschied scheint prinzipieller Natur zu sein, & die Sprache etwas, dem eine Struktur … //

​

Man könnte fragen wollen: Ist es denn aber ein Zufall, daß ich zur Erklärung 61 von Zeichen, also zur Vervollständigung des Zeichensystems, aus den Schrift- & Lautzeichen heraustreten muß? Trete ich damit nicht eben in das Gebiet, worin sich dann das zu Beschreibende abspielt? – Aber ist es nicht seltsam, daß ich dann überhaupt mit de[m|n] Schriftzeichen etwas anfangen kann? – Man sagt etwa, daß die Schriftzeichen bloß die Vertreter jener Dinge sind, ⌊ aufc ⌋ diec die hinweisende Erklarung man c in den zeigtc. der Dinge sind. – Aber wie seltsam, daß diese so eine Vertretung möglich ist. // Aber wie ˇdenn ist diese Vertretung möglich? // (Ich kann nicht sagen: statt Milch trinke ich Wasser & esse statt Brot Holz, indem ich Wasser die Milch⌊,⌋ & Holz das Brot vertreten lasse.)     (Es hat natürlich einen guten Sinn, zu sagen, das definierte Zeichen Definiendum verträte das definierende; & auch in d[er|ie] hinweisenden Erklärung könne mache ein Wort zum Vertreter des Hinweises auf einen Gegenstand.) Übrigens aber: nicht die Farbe rot wird vom Wort “rot” vertreten, sondern etwa ein rotes Täfelchen.) ¥ ⋎ S. 180 A

∫

Man sagt möchte sagen : ein rotes Täfelchen⌊,⌋ (oder dergleichen⌊,⌋) ist das primäre Zeichen für die Farbe Rot, das ein Wort ˇ“rot” oder ein sekundäres Zeichen : , denn es erklärt die Bedeutung des Wortes “rot”, wenn ich auf ein rotes Täfelchen weise, etc., aber nicht, wenn ich sage “rot” bedeute dasselbe wie “rouge”. ¥ ⌊⌊ ⋎ S 184 ⌋⌋ Aber ist das unter allen Umständen so? Muß immer ein roter Gegenstand oder ein rotes 62 ⌊⌊ Zu S. 73 ⇒ ⌋⌋ Vorstellungsbild gegenwärtig sein, wenn ich das Wort “rot” verstehen soll? Denke an den Befehl: “stelle Dir einen roten Kreis auf weißem Grund vor”! Und was ist welches sind die primären Zeichen für Bindewörter, Präpositionen, Interjektionen, etc.?

​

¥ ⋎ S. 63 A    Welches Was ist das Kriterium des unseres Verständnisses: das Aufzeigen eines des roten Täfelchens Gegenstands, wenn gefragt wurde, welcher von diesen Gegenständen ist rot, – oder das Wiederholen der hinweisenden Erklären: “diese Farbe heißt ‘rot’”?      // Welches ist ⌊(⌋aber⌊)⌋ das Zeichen Kriterium des unseres ˇ Des Andern, oder des eigenen? Verständnisses ˇbeim Andern: [E|e]inen roten Gegenstand aus anderen auswählen auszuwählen , wenn es verlangt wird, oder, die hinweisende Erklärung des Wortes “rot” geben? //     Beides betrachten wir als Zeichen des Verständnisses. Hören wir jemand das Wort “rot” gebrauchen & bezweifeln, daß er es versteht, so können wir ihn zur Prüfung fragen: “welche Farbe nennst Du ‘rot’”. Anderseits, wenn wir jemandem die hinweisende Erklärung ˇdes Wortes gegeben hätten & nun sehen wollten, ob er sie richtig verstanden hat, würden wir nicht ˇvon ihm verlangen, daß er ˇsolle sie wiederhol[t|e]⌊n⌋, sondern wir gäben ihm etwa die Aufgabe, aus einer Reihe von Dingen die roten herauszusuchen. In jedem Fall ist das, was Was wir Wie wir das Wort ⌊“⌋Verständnis⌊”⌋ nennen, gebrauchen,, ist durch das dadurch bestimmt, was wir als Probe des Verständnisses ansehen. (Denke auch an den 63 Fall wenn in dem wir sagen: “ja, wenn das Wort das bedeutet, ist der Satz wahr.”) ⌊ // … das bedeuten soll, so stimmt es, was er sagt.”)⌋ ⌊⌊ Wie aber wenn er das Wort nach dem einen Test versteht & nach dem andern nicht? ⌋⌋

​

⍈ ˇ[Zu S. 62] ⌊ A ⌋   Wenn [e|E]iner sagte: “es gilt mit Recht als ⌊(⌋ein⌊)⌋ Zeichen des Verständnisses Verstehens des Wortes “rot”, einen roten Gegenstand ˇauf Befehl aus andersgefärbten herausgreifen ⌊(⌋zu⌊)⌋ können; dagegen ist das richtige Übersetzen des Wortes “rot” in's Französische kein Beweis des Verstehens”, – so antworte ich: Das zeigt, was Du … so würde ich antworten: Das zeigt nur, was Du mit “verstehen” meinst. Was heißt: “[e|E]s gilt mit Recht”? sollte soll doch wohl nicht heißen⌊:⌋, daß wenn ein Mensch einen roten Gegenstand auf Befehl etc. etc., dann hat er, erfahrungsgemäß, das Wort verstanden. (War das gemeint, so kann man ˇweiter fragen: welche andere Erfahrung gilt als der spezifische Test des Verständnisses.)

∫

Wie ist es nun mit dem, was man “primäre Zeichen” nennen möchte : , sind sie ˇSind die Zeichen, die man ‘primäre’ nennen möchte unmißverständlich // unmißdeutbar // ?     Kann man etwa ˇsagen sie müßten eigentlich nicht mehr verstanden werden? – Wenn das heißen soll, sie mü[ss|ß]ten nicht weiter gedeutet werden, so gilt das auch vom Wort; heißt es aber, sie könnten nicht weiter gedeutet werden, dann ist es falsch. (Denke an die Erklärung der Gesten durch Worte u. u..)

​

¥ ⋎ S. 185 64 ⌊⌊ Hier [Hierher gehört eine Bemerkung, daß die hinw. Def. ein Zeichen für ein anderes setzt] ⌋⌋

​

ˇWie ist es [W|w]enn ich eine Bezeichnungsweise festsetze; wenn ich, z.B. für den eigenen Gebrauch, Farb[en|tö]nen Namen geben will, : Ich werde will: – Ich werde das etwa mittels einer Tabelle tun –; und nun werde ich doch nicht den Namen zur falschen Farbe schreiben (zu der Farbe, der ich ihn nicht geben will). Aber warum nicht? Warum soll nicht “rot” gegenüber dem grünen Täfelchen stehen & “grün” gegenüber dem roten, etc.? Wenn die hinweisende Definition nur ein Zeichen statt eines andern setzt so sollte das doch keinen Unterschied machen. – Da gibt es jedenfalls zwei verschiedene Fälle: Es kann die Tabelle, mit grün gegenüber “rot” etc., so gebraucht werden, daß der, der sie ‘nachschlägtc’, vom Wort “rot” schräg auf das rote Täfelchen übergeht & vom Wort “grün” auf das grüne u.s.f.. Wir würden dann sagen, die Tabelle sei nur anders angeordnet als die gewöhnliche // gewohnte // (nach einem andern räumlichen Schema), aber sie verbinde die Zeichen, wie die gewohnte. – Es könnte aber auch sein, daß der welcher die Tabelle sie benützt, von der einen Seite horizontal zu andern blickt & nun in irgend welchen Sätzen das Wort “rot” durch ein grünes Täfelchen ersetzt; aber nicht etwa auf den Befehl “gib mir das rote Buch” ein grünes bringt, sondern ganz richtigc ein rotes (d.h. das, welches auch wir “rot” nennen). Dieser hat nun die Tabelle anders benützt, als der [e|E]rste, aber doch so, daß 65 das Wort “rot” für ihn die gleiche Farbe bedeutet, wie für uns.      Es ist nun der zweite Fall, der uns interessiert, & die Frage ist: Kann ein grünes Täfelchen als Muster für rot dienen? –      Ich kann mir eine Abmachung denken, nach welcher Einer, dem ich eine grüne Tafel zeige & sage male mir diese Farbe, mir ein Rot malen soll; zeige ich ˇihm mit diesen Worten auf blau, so hat er gelb zu malen; ⌊ (⌋etwa immer die komplementäre Farbe[.|⌊)⌋]. Und daher ist es auch möglich daß Einer meinen Befehl, auch ohne eine solche Abmachung, so deutet. Ich kann Die Abmachung hätte er könnte auch gelautet haben: “wenn ich sage, male diese Farbe, dann male immer eine etwas dunklere”; & wieder können wir uns denken, daß der Befehl auch ohne diese Verabredung so gedeutet würde. – Aber kann man sagen: es kopiere Einer das Rot des Täfelchens, indem er einen bestimmten Ton von grün (oder ein anderes Rot als malt? Und & zwar ˇetwa so, wie er eine geometrische Figur, nach verschiedenen Projektionsmethoden, verschieden & genau kopieren kann? – Kann ich hier Farben mit Gestalten vergleichen & sagen kann ein grünes Täfelchen einerseits als Name einer bestimmten Schattierung von [r|R]ot verwendet werden, anderseits als ihr Muster? wie ein Kreis als Name einer bestimmten Elipsengestalt dienen kann, aber auch als ihr Muster.

​

66    Es ist klar: das Muster wird nicht verwendet wie das Wort[.| (]der Name). Und die [H|h]inweisende Erklärung, die Tabelle, sofern sie uns Muster uns von Worten zu Mustern führt anders, als die Verbaldefinition Tabelle die einen Namen durch einen andern ersetzt.

​

Das Wort “kopieren” hat aber in verschiedenen Fällen verschiedene Bedeutung & dem entsprechend wechselt ist das , was ich “Muster” nenne. Was heißt es “eine Figur genau kopieren”?: sie nach dem Augenmaß ˇgenau kopieren? oder mit Meßinstrumenten? und mit welchen? Welches wollen wir die gleiche Farbe wie die des Musters nennen? [d|D]enke an verschiedene Vergleichsmethoden. Inwiefern läßt sich die Regel dunkler zu kopieren mit der vergleichen eine Figur in vergrößertem ˇoder verkleinertem Maßstab zu kopieren?

​

Denken wir uns einen Menschen, der vorgäbe, “ er könne Schattierungen von Rot in grün kopieren, & der nun, das rote Muster ins Auge fassend ansehend , mit allen äußeren Zeichen des genauen Kopierens einen grünen Ton mischte. Der wäre für uns auf gleicher Stufe, wie Einer, der ˇ(genau hinhorchend) Farben nach Violintönen mischte. Wir würden in dem Fall sagen: “ich weiß nicht, wie er es macht”; aber nicht in 67 dem Sinne, als // aber nicht, als // verstünden wir nicht die verborgenen Vorgänge in seinem Gehirn oder in seinen Muskeln, sondern, wir verstehen nicht, was es heißt “dieser Farbton sei die Kopie dieses Violintons”. Es sei denn, daß damit nur gemeint ist wird , ein daß ein Mensch assoziiert erfahrungsgemäß einen bestimmten Farbton mit einem bestimmten Klang assoziiert (ihn vor sich sieht, malt, etc.). Der Unterschied zwischen dem der Bedeutung⌊en⌋ von ⌊“⌋Assoziieren⌊”⌋ & ⌊“⌋Kopieren⌊”⌋ zeigt sich besteht darin, daß es ˇkeinen Sinn hat für die assoziierte Gestalt (oder Farbe) keinen Sinn von einer Projektionsmethode oder ⌊(⌋Regel des Übertragens Kopierens ⌊)⌋ der Assoziation zu reden. Wir sagen Es hat Sinn zu sagen : “Du hast nicht richtig kopiert”, – aber nicht “Du hast nicht richtig assoziiert”.

​

¥ ⋎ S. 185    Bringt unsere die Tabelle das Wort mit einem Muster in Zusammenhang, so ist es nun nicht gleichgültig mit welchem Täfelchen beim Aufsuchen Nachschlagenc das Wort verbunden wird⌊.⌋ (denke daran, daß eine Farbe der andern nicht in dem ˇgleichen Sinne als Muster dien[e|t]n kann wie sich selbst). – “Aber dann gibt es also willkürliche Zeichen & solche, die nicht willkürlich sind!” – Denken wir nur an die Verständigung durch Landkarten, Zeichnungen, – & anderseits durch Sätze. Die Sätze sind so wenig willkürlich, wie die Zeichnungen; nur die Worte sind willkürlich. Und anderseits ist die Proje[c|k]tionsmethode der Landkarte willkürlich[. Und| ; ; und ] wie sollte ˇman bestimmen, was 68 willkürlich ist.

​

Ich kann allerdings wohl die Festsetzung von Wortbedeutungen vergleichen der Festsetzung einer Projektionsart // Projektionsmethode // , ˇwie der zur Abbildung räumlicher Gebilde (“der Satz ist ein Bild”); dies ist ein guter Vergleich : , aber er enthebt uns nicht davon, das Funktionieren der Bezeichnung durch Worte zu untersuchen, der Untersuchung des Funktionierens der Worte, welches seine eigenen Regeln hat. Wir können freilich sagen – d.h. es entspricht dem Sprachgebrauch – daß wir uns durch Zeichen verständigen, ob wir nun Wörter oder Muster verwenden; aber das Muster ist kein Wort, & das Spiel, sich nach Worten zu richten ˇist ein anderes, als das : , sich nach Mustern richten. (Wörter sind dem was wir “Sprache” nennen einer Sprache als solcher nicht wesentlich, & Muster auch nicht.)      Die Wortsprache ist nur eine unter vielen möglichen Arten der Sprache & es gibt Übergänge von einer zur ihr in die andern. (Denke an zwei Darstellungsarten Arten de[s|n] Satzes “ich sehe einen roten Kreis” ˇzu schreiben: es könnte z.B. dadurch geschehen, daß ich einen Kreis schreibe & ihm die entsprechende Farbe (rot) gebe; aber auch so, daß ich einen Kreis & daneben einen roten Fleck schreibe.) Betrachte die Landkarte daraufhin, was in ihr der B Ausdrucksform einer derc Wortsprache entspricht.)

​

“Ich will nicht verlangen, daß in der erklären- 69 den Tabelle das rote Muster horizontal gegenüber dem Wort “rot” stehen soll, aber irgend ein Gesetz des Lesens der Tabelle muß es doch geben”, denn sonst verliert sie ja ihren Sinn”. Aber Ist es aber gesetzlos wenn die Tabelle so aufgefaßt wird, wie die Pfeile des Schemas andeuten? – “Aber muß dann nicht eben das Schema der Pfeile vorher gegeben werden?” – Muß denn vor der gewöhnlichen Gebrauchsweise das Schema gegeben werden?       “Wird aber dann nicht wenigstens eine zeitliche Regelmäßigkeit im Gebrauch der Tabelle gefordert? würde es angehen, wenn wir eine Tabelle einmal nach diesem, einmal nach jenem Schema zu gebrauchen hätten? Und wie Wie soll man denn wissen, wie man die Tabelle zu gebrauchen ist?” – Ja, weiß man es denn sonst heute ? Die Zeichenerklärungen haben doch irgendwo ein Ende.     Ich würde natürlich freilich ein Mißverständnis hervorrufen, wenn ich, ohne eine besondere Abmachung, jemandem einen den Weg wiese, indem ich mit dem Finger nicht in der Richtung zeigte, in der er gehen soll, sondern in der entgegengesetzten. Aber auch diese Art des Zeigens könnte richtig ver- 70 standen werden. Es liegt in der menschlichen Natur, das Zeigen mit dem Finger so zu verstehen. (Wie es in ihr liegt Brettspiele zu spielen & Zeichensprachen zu benützen erfinden , die aus Schriftzeichen geschriebenen Zeichen auf einer Fläche bestehnen.)

​

⌊Die⌋ Tabelle garantiert die Gleichheit der Übergänge, die in mit ihr gemacht werden, nicht. Sie zwingt mich ja nicht, sie immer gleich zu gebrauchen. Sie ist da, wie ein Feld, durch das Wege führen; aber ich kann ja auch querfeldein gehen. – Ich mache den Übergang in der Tabelle bei jeder Anwendung von Neuem. Er ist nicht, quasi, ein für allemal in der Tabelle gemacht (sie verleitet mich nur ihn zu machen.).    (Von welcher Art sind diese Sätze? – Wohl von derselben, wie die Bemerkung, daß die Zeichenerklärungen doch einmal ein Ende haben. Und das ist etwas ähnlich, wie wenn man sagt: “was nützt Dir die Annahme eines Schöpfers am Anfang der Welt, sie schiebt doch das Problem des Anfangs der Welt nur hinaus”. Diese Bemerkung hebt einen Aspekt meiner Erklärung hervor, den ich vielleicht nicht bemerkt hatte. Man könnte auch sagen: “Sieh' Deine Erklärung doch so ◇◇◇ an! – bist Du jetzt noch immer von ihr befriedigt?”

​

71    Kann man etwas Rotes nach dem Wort “rot” suchen? braucht man ein Erinnerungsbild dazu?

∕∕ \

Kann man sagen, daß das Wort “rot”, um ein brauchbares Zeichen zu sein, ein Supplement – etwa im Gedächtnis – braucht?     Wenn ich eine Erfahrung mit den Worten beschreibe “vor mir liegt ein rotes Buch”, ist die Rechtfertigung der Wahl ⌊(⌋des Gebrauchs⌊)⌋ dieser Worte, außer der ˇbeschriebenen Erfahrung, die in den Worten beschrieben wird, noch eine die Erinnerung, daß ich ˇmich erinnere das Wort “rot” immer für diese Farbe verwendet ˇzu habe⌊n⌋? ⌊ ( Der Befehl: “Stelle Muß das die Rechtfertigg. sein? ⌋

∕∕ \

¥ ⋎ S. 74 A ¥ S. 186    Wenn es beim Gebrauch des Wortes “rot” auf das Bild ankommt, das mein Gedächtnis beim Klang dieses Wortes automatisch reproduziert, so bin ich dieser Reproduktion geradeso ausgeliefert, als wäre ich entschlossen, die Bedeutung durch Nachschlagen in einer Tabelle zu bestimmen, wobei ich mich dem, was ich in ihr fände, dieser, quasi, auf Gnade & Ungnade ergeben würde.

∕∕ \

Wenn mir das Farbmuster, nach dem ich mich richten will, dunkler vorkommt als es meiner Erinnerung nach gestern war, so muß ich nicht dem Gedächtnis recht geben & tue es auch nicht immer. Und ich könnte in sehr wohl von einem Nach- 72 du⌊n⌋keln meines [g|G]edächtnisses reden.

​

Wenn ich jemandem sage: “male die Farbe Deiner Zimmertür nach dem Gedächtnis”, so bestimmt das, was er zu tun hat, nicht eindeutiger als der Befehl: “male das Grün, welches Du auf dieser Tafel siehst”. Auch den ersten dieser Sätze Befehle könnte man sich so aufgefaßt denken, daß wie, normalerweise⌊,⌋ˇ, etwa, den Satz “male einen Farbton, etwas lichter als den, welchen Du Dich erinnerst dort gesehen zu haben”; und anderseits wird der, wel dem man den Befehl gibt, den Farbton nach einem Muster zu malen für gewöhnlich nicht über die Projektionsmethode im Zweifel sein.

​

Wenn mir befohlen worden wäre, : “suche mir eine rote Blume auf dieser Wiese & bringe sie mir”, & ich fände nun eine, – vergleiche ich sie da mit meinem Erinnerungsbild von der roten Farbe? – Und muß ich auch ein weiteres Bild zu rate ziehen um zu sehen ob das erste noch stimmt? – Und warum wozu soll ich dann unbedingt das erste brauchen? – Ich sehe die Farbe der Blume & erkenne sie. (Es wäre natürlich der Fall denkbar, daß [e|E]iner das Muster einer Farbe haluziniert & es wie ein Wirkliches mit dem gesuchten Gegenstand vergleicht.) 73   Auch wenn ich sage “nein, diese Farbe ist noch nicht die richtige, sie ist heller als die, die ich dort gesehen habe”, so sehe ˇist nicht gesagt daß ich diese nicht vor mir ˇsehe & der Vorgang ˇder ist nicht der des Vergleichens zweier gleichzeitig gesehener Farbtöne. Und es ist auch nicht so, als klingelte es irgendwo in meinem Geiste, wenn der richtige Farbton gefunden wäre & als hätte ˇtrüge ich nun ständig ein Bild dieses Klingelns mit mir herum[.|,] ˇum beurteilen zu können, wenn es klingelt.

​

Es ist ein anderes Spiel, mit einem Muster auf die Suche gehn, es an die Gegenstände anlegen & ⌊(⌋soc⌊)⌋ die Farbengleichheit prüfen, & anderseits: ˇohne ein solches Muster nach Wörtern einer Wortsprache hand⌊e⌋ln. Denken wir an das laute Lesen nach der Schrift (oder das Schreiben, nach dem Gehör). Wir könnten uns freilich natürlich eine Art Tabelle denken, nach welcher wir die uns dabei führen könnte. Aber es führt uns keine; kein Akt des Gedächtnisses, nichts, vermittelt zwischen dem geschriebenen Zeichen & dem Laut.

​

⋎ S. 62   Würde Wenn ich nun gefragt werde: “warum wählst Du diese Farbe auf diesen Befehl hin”; wie rechtfertigst Du diese Deine Wahl?”, – so kann ich in dem einen Fall antworten: “Weil diese Farbe in meiner Tabelle gegenüber dem Wort ‘rot’ steht”. Im andern Fall hat diese gäbe es auf diese Frage keine Antwort & 74 die Frage hat keinen Sinn. Aber im ersten Spiel hat ⌊(⌋wieder⌊)⌋ die Frage keinen Sinn: “[w|W]arum nennst Du die Farbe ‘rot’” die in der Tabelle gegenüber dem Worte ‘rot’ steht”. Ein Grund läßt sich nur innerhalb eines Spiels angeben. Die Kette der Gründe kommt zu einem Ende & zwar an der Grenze des Spiels. (Grund & Ursache.)

​

⍈ [Zu S. 71] A Betrachten wir den Befehl: Ich kann sagen: “Tu jetzt, was Du, Deiner Erinnerung nach, gestern um diese Zeit getan hast”. Wie weiß er, was die Worte dieses Befehls von ihm verlangen, – wenn wir annehmen, es sei immer ein Erinnerungsbild das den Worten ihre Bedeutung gibt? ⌊⌊ Diese Worte können ihm nur den Ort sagen wo er nach einem Bild suchen soll; aber um diese Worte zu verstehen braucht er ja wieder ein Bild u.s.f.. ⌋⌋ – Wenn er sich daran erinnert, kann er seiner Erinnerung folgen; erinnert er sich aber nicht, so ha[b|t]en der Befehl keinen Sinn für ihn. Der Befehl ist also ähnlich dem: “tu, was auf diesem Zettel geschrieben steht”. Wenn der Zettel leer ist, so ist dies kein Befehl. (Denken wir uns, daß auf dem Zettel eine sinnlose Wortverbindung steht.⌊)⌋ Etwa “iß n Äpfel & n² + 2n + 2 = 0.”)

​

Und, wenn man sich in die Erinnerung ruft, “daß die Tabelle uns nicht zwingt”, sie auf eine bestimmte Weise⌊,⌋ , ⌊–⌋ noch, sie immer auf die gleiche Weise zu benützen, – so wird es Jedem ⌊(⌋ganz⌊)⌋ klar, daß unser Gebrauch des Wortes “Regel” & “Spiel” ein schwankender ist (nach den Rändern zu verschwimmender) ist.

​

75 ¥ • ¥ ⋎ S. 77 A, ¥ B ¥   ⌊ A ⌋ Es ist falsch ist unwahr wäre unrecht zu ˇ Es ist nicht richtig zu Man sollte nicht sagen: die Übereinstimmung (und Nichtübereinstimmung) zwischen Satz & Welt // Außenwelt // ist sei willkürlich durch eine Zuordnung der beiden erzeugt. geschaffen. Denn, wie ist die Zuordnung auszudrücken? Sie soll darin bestehen besteht darin , daß der Satz “p” sagt, es sei gerade das der Fall. Aber wie ist dieses ‘gerade das’ ⌊(⌋im besondern Fall⌊)⌋ in uns gegeben (ˇd.h. ausgedrückt)? Wenn durch ˇandern einen Satz, so gewinnen wir nichts dabei; wenn aber durch ein Factum eine Tatsache der Außenwelt, dann muß dieses schon in bestimmter Weise artikuliert aufgefaßt werden sein dann gehört dieses als Erklärung der Sprache mit zur Sprache. D.h., ⌊:⌋ es gibt keine hinweisende Definition eines Satzes, ⌊–⌋ oder richtiger: die die hinweisenden Erklärungen müssen werden vor der Anwendung des Satzes gegeben werden & sind verschieden von der Anwendung. // von der Anwendung ad hoc. // // von der Anwendung im besondern Fall⌊.⌋ // )

​

↺ ⍈ B    Die “Verbindung zwischen “Sprache & Wirklichkeit” ist durch die Worterklärungen gemacht, – welche zur Sprachlehre gehören[. So| ; ⌊so⌋] daß die Sprache in sich geschlossen, autonom, bleibt.

∫

Wenn ich das Klangbild eines chinesischen Satzes auswendig lernte kennte & wüßte, daß dieser Satz, etwa in einem 76 Bilderbuch, als Titel unter einem jenem ˇbestimmten Bild steht, so würde mich das könnte ich dadurch noch nicht befähigen einen chinesischen Satz zu bilden. Ich könnte sagen: es befähigt mich nicht einen Sachverhalt auf chinesisch zu portraitieren.

​

Wenn man jemanden fragte “wie weißt Du, daß diese Beschreibung // dieser Wortausdruck // wiedergibt, was Du siehst”, so könnte er vielleicht geneigt sein so wäre er vielleicht …, zu antworten “ich meine das mit diesen Worten”. Und damit könnte er glauben sich in die Psychologie gerettet zu haben. Aber “ich meine das” ist der Ausdruck einer Zeichengebung. Aber was ist dieses “das”, wenn es nicht selbst wieder artikuliert also schon Sprache ist? – ˇUnd [A|a]lso war ist “ich meine das” gar keine Antwort. Die Antwort ist eine Erklärung der Bedeutungen der Worte.

∫

Wenn ich eine Beschreibung nach festgesetzten Regeln bilde, die Wirklichkeit nach ihnen in die Beschreibung übertrage, dann übersetze ich sie wie aus einer Sprache in eine andere. Und wenn ich die Beschreibung Übertragung durch Berufung auf die Grammatik rechtfertige, so tue ich nichts, als eine [b|B]eziehung zwischen Wirklichkeit & Beschreibung (eine projektive Beziehung) festzustellen : ; von der Intention aber, meiner Beschreibung, als einem psychischen Vorgang, ist hiebei dabeic keine Rede. (D.h., ich kann eben nur die Ähnlichkeit des Portraits [P|p]rüfen, nichts weiter. ]

​

77 ⍈ [Zu S. 75 nach S. 75 B zwischen S. 75 A & S. 75 B ] A Könnte ich Man könnte sagen: mich interessiert nur der Inhalt des Satzes , – ; & der Inhalt des Satzes ist in ihm. –        ⌊ [Keine neue Zeile.] ⌋ Seinen Inhalt hat der Satz als Glied eines Kalküls.        Die Sprache muß für sich selber sprechen.

/

⍈ ˇ[Zu S. 75 nach S. 77 A] B Denken wir an eine Gebärdensprache, mit der wir uns Menschen verständlich machen, die keine Wortsprache mit uns gemeins haben[:|.] Fühlen wir hier auch das Bedürfnis aus der Sprache heraus zu treten, um ihre Zeichen mit der Wirklichkeit zu verbindenknüpfen? // Fühlen wir da nun auch das Bedürfnis, zur Erklärung der Zeichen jener Sprache aus ihr herauszutreten? //

∫ ∫

“Die Verbindung von Wort & Sache durch das Lehren der Sprache hergestellt”. Was ist das für eine Verbindung, welcher Art? Eine mechanische, elektrische, psychische Verbindung kann funktionieren oder nicht funktionieren. Mechanismus & Kalkül.        Die Zuordnung von Gegenstand & Namen ist keine andere als die durch d eine Tabelle, hinweisende Geste & gleichzeitiges Aussprechen des Namens, u. dergl, erzeugte. Sie ist ein Teil des Symbolismus. Einem Gegenstand einen Namen geben ist wesentlich von gleicher Art wie ihm ein Namenstäfelchen umhängen. 78    Es ist der Ausdruck einer unrichtigen Auffassung, wenn man sagt: die Verbindung wischen Name & Gegenstand sei eine P psychologische.

​

Denken wir uns, daß jemand eine Figur im Maßstab 1 : 10 kopiert; ist dann in dem Vorgang des Kopierensc schon das Verständnis der allgemeinen Regel dieses Abbildens enthalten? – Mein Stift wurde von mir quasi ganz voraussetzungslos gehalten & nur von der Länge der Vorlage geführt (beeinflußt). – Ich würde sagen: wäre die Vorlage länger gewesen, so wäre ich mit dem Stift noch weiter gefahren & wenn kürzer, weniger weit. Aber ist, gleichsam, der Geist, der sich hierin ausspricht, schon im Nachziehen des Strichs enthalten?       Ich kann mir vornehmen: “i I ch gehe solange, bis ich den N. ihn finde” ( ⌊–⌋ ich will etwa jemand auf einer Straße treffen –; & nun gehe ich die Straße entlang & treffe ihn an einem bestimmten Punkt, & bleibe stehn. War in dem Vorgang des Gehens, oder einem andern gleichzeitigen das Handeln nach der allgemeinen Regel, die ich mir vorgesetzt hatte, enthalten? Oder war der Vorgang nur in Übereinstimmung mit dieser Regel, aber also auch ˇin Übereinstimmung mit andern Regeln?       Ich gebe jemandem den Befehl von A eine Linie parallel zu a zu ziehen. Er versucht (beabsichtigt) es zu 79 tun, aber mit dem Erfolg, daß die Linie parallel zu b wird. War der Vorgang des Kopierens derselbe, als hätte er beabsichtigt eine Linie parallel zu b zu ziehen, & seine Absicht ausgeführt?

​

Und wenn es mir gelungen ist, eine Vorlage nach der vorgesetzten Regel zu kopieren // wiederzugeben // , ist es dann möglich den Vorgang des Nachbildens Kopierens , wie er stattgefunden hatte, auch durch eine andere allgemeine Regel zu beschreiben? Oder kann ich diese Beschreibung ablehnen mit den Worten: “nein, ich habe mich von dieser Regel leiten lassen – & nicht von der andern, die in diesem Falle allerdings das gleiche Resultat ergeben hätte”?

∫

Man möchte sagen: Wenn ich absichtlich eine Form nachzeichne, so hat der Vorgang des Kopierens mit der Vorlage diese Form gemein. Sie ist eine Fassette des Vorgangs des Kopierens; eine Fassette, die an dem p kopierten Gegenstand anliegt & sich dort mit ihm deckt.    Wenn auch mein Bleistift die Vorlage nicht trifft, die Absicht trifft sie immer.

​

Wenn ich auf dem Klavier ein Stück nach Noten spielen will, so wird muß die Erfahrung zeigen lehren , was welche Tonfolge // welche Töne // ich t[ä|a]tsächlich spielen werde; & die Beschreibung des Gespielten muß nichts mit der Beschreibung des Notenbildes gemein haben. Wenn ich dagegen meine Absicht beschreiben will, so muß es heißen: ich sagen, daß ich dieses Notenbild 80 in Tönen wiedergeben wollte. – Und nur das kann der Ausdruck dafür sein, daß die Absicht an die Vorlage heranreicht & eine allgemeine Regel enthält.

​

Der Ausdruck der Absicht beschreibt die Vorlage ˇder Abbildung; die Beschreibung des Abbildes nicht.

∫

Es kann nie essentiell für unsere Betrachtungen sein, daß ein symbolisches Phänomen in der Seele sich abspielt & nicht auf dem Papier, für jeden Andere den Andern sichtbar. Immer wieder ist man in Versuchung, einen symbolischen Vorgang durch einen besondern psychischen Vorgang erklären zu wollen; als ob die Psyche “in dieser Sache viel mehr tun könnte”, als die Zeichen. Es mißleitet ◇ uns da die Idee eines Mechanismus ein falscher Vergleich mit einem Mechanismus , der mit besonderen andern Mitteln arbeitet, & daher besondere Bewegungen erklären kann. Wie wenn wir sagen: diese Bewegung kann nicht durch eine Anordnung von Hebeln erklärt werden.

​

Die Beschreibung des Psychischen muß sich ja wieder als Symbol verwenden lassen.      ⌊⌊ Absatz ⌋⌋ Hierher gehört, daß es eine wichtige Einsicht ist in das Wesen der Zeichenerklärung, daß sich das Zeichen durch seine Erklä- 81 rung ersetzen läßt. Das bringt den Begriff dieser Erklärung in Gegensatz zu dem der Kausalerklärung.

∫

Man kann sagen daß es sich nicht durch äußere Beobachtung entscheiden läßt, ob ich lese oder nur Laute hervorbringe, während ein Text an meinen Augen vorbeiläuft. Aber was uns am Lesen interessiert, … Aber das Lesen ist kann nicht wesentlich eine innere Angelegenheit sein. Das Ableiten der Übersetzung von der Vorlage kann auch ein sichtbarer Vorgang sein. Man muß z.B. den Vorgang dafür nehmen können der sich auf dem Papier abspielt, wenn die Glieder der Reihe 1, 4, 9, 16 100, 121, 144, ⌊169⌋ durch die Rechnungen 10 × 10   00 100 , 11 × 11   11 121 , 12 × 12   24 144 , 13 × 13   39 169 , aus den Gliedern der Reihe 10, 11, 12, 13 abgeleitet erscheinen. ¥ ⌊ ⋎ S. 82 B [neue Zeile, nicht Absatz] ⌋

​

Das Gefühl, welches man bei jeder solchen – gleichsam behaviouristischen – Darstellung hat, daß sie roh (unbeholfen) ist, leitet irre; wir sind versucht, nach einer “besseren” Darstellung zu suchen[. D|; d]ie gibt es aber gar nicht. Eine ist so gut wie die andere & jedesmal stellt das System dar, worin ein Zeichen verwendet wird (“Darstellung dynamisch, nicht statisch”.) ¥ ⋎ S. 82 A [Neue Zeile, nicht neuer Absatz.]

​

82 ⍈ ˇ[Zu S. 81] B (Der Unterschied zwischen ‘innen’ & ‘außen’ interessiert uns nicht.)

​

⍈ [Zu S. 81] A (Auch der psychische Prozess kann nichts in wesentlich anderem Sinne ‘offen lassen’, als eine leere Klammer im Symbolismus eine Argumentstelle offen läßt.)

∫ v

Man kann nicht fragen: Welcher Art sind die geistigen Vorgänge, daß sie wahr & falsch sein können, was die außergeistigen nicht können. Wenn, wenn es die ‘geistigen’ können, so müssen's auch die anderen können; & umgekehrt. – Denn, können es die seelischen Vorgänge, so muß es auch ihre Beschreibung können. Denn in ihrer Beschreibung muß es sich zeigen, wie es möglich ist.

v

Wenn man sagt, der Gedanke sei eine seelische Tätigkeit, oder eine Tätigkeit des Geistes, so denkt man an den Geist als an ein trübes, gasförmiges Wesen, in dem manches geschehen kann, das außerhalb dieser Sphäre nicht geschehen kann. Und von dem man manches erwarten kann, das sonst nicht möglich ist.    (Der Vorgang des Denkens im menschlichen Geist, & der Vorgang der Verdauung.)

​

83     Jedes Abbilden (Handeln nach – nicht bloß in Übereinstimmung mit – gewissen Regeln), Ableiten einer Handlung aus einem Befehl, Rechtfertigen einer Handlung mit einem Befehl, ist von der Art des schriftlichen Ableitens eines Resultats aus einer Angabe, des Hinweises auf eine Tabelle // auf die Gegenüberstellung von Zeichen in einer Tabelle // .    (Der Begriff des Abbildens ist kein metalogischer Begriff.)

​

¥ ⋎ S. 84 A    Wenn die Aufgabe ist die Quadrate, Kuben, etc., der natürlichen Zahlen zu bilden, so kann man sagen: “ich schreibe in der Tabelle ⌊hierher die Zahl 16,⌋ x x² x³ 1, 2, 3, 4 16 an diesen Ort die Zahl 16, weil dort x² steht” Wie aber, wenn ich sagte: “ich schreibe hierhin ein “ + ”, weil dort x² steht”? Man würde fragen: “Schreibst Du überall ein “ + ” wo ein “x²” steht?” – – d.h., man würde nach einer allgemeinen Regel fragen; ⌊;⌋ forschen; ⌊;⌋ und das “weil” in meinem Satze gäbe sonst keinen Sinn. das “weil” in meinem Satze gäbe // gibt // sonst keinen Sinn. “Ich habe geschrieben schreibe ‘16’ weil dort ‘x²’ steht”. – ⌊Oder man könnte fragen: “⌋ “Woher weißt Du denn, daß Du es deswegen geschrieben 84 hast?”    Hier hat man das “weil” als Einleitung einer Angabe der Ursache aufgefaßt, statt des Grundes.

​

⍈ ˇ[Zu S. 83] A “Ich schreibe hierher die Ziffer Zahl ‘16’, x x² x³ 1 2 3 4 16 64 weil dort ‘x²’ steht & hier ‘64’ weil dort ‘x³’ steht”. So sieht jede Rechtfertigung aus. In gewissem Sinne bringt uns das nicht weiter. Aber es kann uns ja nicht weiter, d.h., zu dem Metalogischen bringen.     (Die Schwierigke⌊i⌋t ist hier : , das nicht zu rechtfertigen versuchen, was keine Rechtfertigung zuläßt hat .)

​

Wenn ich der Regel folgend unter ‘4’ ‘16’ schreibe, so könnte es scheinen, als wäre hier eine Kausal⌊i⌋tät im Spiel, die nicht hypothetisch, sondern unmittelbar wahrgenommen ˇ(erlebt) wäre. (Verwechslung der Begriffe vonc ‘Grund’ & ‘Ursache’)

​

Welche Art von Nexus mei meine ich in dem Satz: ““ich geh' hinaus, weil er es befielt” … ”? ist in dem Satz: “ich geh' hinaus, weil er es befielt”, gemeint?       Und wie vergleicht sich dieser Satz mit dem: “ich geh' hinaus, obwohl er es ˇmir befohlen hat”. ⌊(⌋ Oder: Oder: “ Iich geh' hinaus, aber nicht, weil er es befohlen hat”, “ich geh' hinaus, weil er mir befohlen hat, es nicht zu tun”.⌊)⌋ // 85 // Welchen Nexus meine ich in dem Satz: “ich geh' hinaus, weil er es befielt”? Und wie verhält sich dieser Satz zu: … //

∫

“Das soll er sein” (dieses Bild stellt ihn vor), darin liegt ist das ganze Problem der Darstellung.      Was ist das Kriterium dafür, wie ist es zu verifizieren, daß dieses Bild das Porträt dieses jenes Gegenstandes ist( , – d.h., ihn darstellen soll? Die Ähnlichkeit macht das Bild nicht zum Portrait. (es könnte dem Einen täuschend ähnlich sein & dabei das Portrait eines Andern sein, dem es weniger ähnlich sieht.)    Wie kann ich wissen daß er das Bild als Porträt des N meint? – Nun⌊,⌋ ˇetwa indem er's sagt, oder drunter schreibt.      Welchen Zusammenhang hat sein P das Portrait des N mit ihm. Etwa den, daß der Name darunter steht mit dem er angeredet wird.

/

Wenn ich mich an meinen Freund erinnere, ihn “vor mir sehe”, was ist hier der Zusammenhang des Erinnerungsbildes mit seinem Gegenstand? Die Ähnlichkeit?     Nun die Vorstellung als Bild kann ihm nur ähnlich sein.

​

Die Vorstellung von ihm ist ein ungemaltes Portrait. 86 Ich mußte auch in der Vorstellung seinen Namen unter das Bild schreiben, damit es zur Vorstellung von ihm wurde.

​

Ich habe den Vorsatz eine bestimmte Handlung auszuführen, ich hege einen Plan aus. Der Plan ˇin meiner Seele soll darin bestehen, daß ich mich das & das tun sehe. Aber wie weiß ich, daß ich es bin den ich sehe? Nun ich bin es ja nicht, sondern etwa ein Bild. Aber warum nenne ich es mein Bild?    “Wie weiß ich, da[s|ß] ich es bin”, ⌊:⌋ die Frage hat Sinn, wenn es z.B. heißt: “wie weiß ich, daß ich es bin, den ich dort im Spiegel sehe”. Und die Antwort gibt Merkmale, nach denen ich zu erkennen bin.    Daß aber mein Vorstellungsbild mich vertritt ist meine eigene Bestimmung. Und ich könnte ebensogut fragen: “woher weiß ich, daß das Wort ‘ich’ mich vertritt?”, denn meine Gestalt im Bild war nur ein anderes Wort “ich”.

v

“Ich kann mir vorstellen daß du zur Türe hinausgehen wirst”⌊.⌋ – die ˇWir unterliegen einer seltsame⌊n⌋ Täuschung, der wir unterliegen, daß im Satz⌊,⌋ ˇim Gedanken⌊,⌋ die Gegenstände das tun, was der Satz von ihnen aussagt[!|.] – Es ist, als ob im Befehl ein Schatten der Ausführung läge. Aber ein Schatten eben dieser Ausführung. Du gehst im Befehl dort & dort hin. – Sonst wäre es aber eben ein ◇◇◇ andrer Befehl. 87    Gewiß diese Identität ist die, die der Diversität zweier verschiedener Befehle entspricht // entgegengesetzt ist // .

v

“Ich dachte Napoleon sei im Jahre 1805 gekrönt worden.” – Was hat Dein Gedanke mit Napoleon zu tun? Welcher Zusammenhang Welche Verbindung besteht zwischen Deinem Gedanken & Napoleon? – Es kann, z.B., die sein, daß das Wort “Napoleon” in dem Ausdruck meines Gedankens vorkommt, plus dem Zusammenhang, den dieses Wort mit seinem Träger hatte; also etwa, daß er sich so unterschrieb, so angeredet wurde etc., etc..    “Aber mit dem Wort ‘Napoleon’ bezeichnest Du doch, wenn während Du es aussprichst, eben diesen Menschen”. – “Wie geht denn, Deiner Meinung nach, dieser Akt des Bezeichnens vor sich? Momentan? oder braucht er Zeit?” – “Ja aber, wenn man Dich fragt: ‘hast Du jetzt eben den Mann gemeint, der die Schlacht bei Austerlitz gewonnen hat’, wirst Du doch sagen: ‘ja’”. – Also hast Du diesen Mann gemeint, als Du den Satz, worin sein Name vorkommt, aussprachst?” – Wohl, aber nur etwa in dem Sinn, in welchem ich damals auch wußte, daß 6 × 6 = 36 ist.     Die Antwort “ich habe den Sieger von Austerlitz gemeint” ist ein neuer Schritt in unserm Kalkül. Täuschend ist an ihm dieser Antwort die vergangene Form, die eine Beschreibung dessen zu geben scheint, was “in mir” während des Aussprechens vor- 88 gegangen warging. ⌊ [Absatz] ⌋    (“Aber ich habe ihn gemeint”. Sonderbarer Vorgang, dieses Meinen! Kann man ˇ(in Europa) jemanden meinen, der auch wenn er in Amerika ist? Oder gar Und gar auch, wenn er ˇgar nicht mehr existstiert?)

v

Man ist (irregeführt durch unsere Grammatik) versucht, zu fragen: “wie denkt man einen Satz, wie erwartet man daß das & das ein[f|t]reffen wird? (wie macht man das?)”      “Wie arbeitet der Gedanke, wie bedient er sich seines Ausdrucks?” – [d|D]iese Frage scheint analog der: “wie arbeitet der Musterwebstuhl, wie bedient er sich der Karten”.      Aber man könnte antworten: “Weißt Du es denn wirklich nicht? Du siehst es doch, wenn Du denkst.” Es ist ja nichts verborgen. ¥ • ⋎ ¥ ⋎ S. 89 A [nach S. 88 A]

v

Aber auf die Antwort “Du weißt ja, wie es der Satz es macht, es ist ja nichts verborgen” möchte man sagen: “ja, aber es fließt alles so rasch vorüber & ich möchte es gleichsam breiter auseinandergelegt seh⌊e⌋n”. (“Alles fließt.”)

v

• ⍈ ⌊⌊ A ⌋⌋ Unser Gefühl ist dann, daß in dem Satz “ich glaube, daß p der Fall ist” etwas 89 das Westentliche, der eigentliche … Wesentliches, der eigentliche Vorgang des Glaubens⌊,⌋ ˇnicht dargestellt, nur angedeutet sei, daß sich diese Andeutung durch eine Beschreibung des Mechanismus ˇdes Glaubens müsse ersetzen lassen. ⌊Eine⌋ Beschreibung, in der worin die Wortfolge “p”ˇ vorkäme, wie die Karten in der Beschreibung des Musterwebstuhls⌊.⌋ vorkäme Und daß nun diese Beschreibung erst der volle Ausdruck des Gedankens Glaubens wäre.     Vergleichen wir das Glauben mit dem Aussprechen des Satzes; es gehen auch da äußerst sehr komplizierte Vorgänge in unserm Kehlkopf, in den Sprechmuskeln, Nerven, etc., vor sich. Diese begleiten den ausgesprochenen Satz ; und . Und er bleibt das Einzige was uns interessiert, ⌊–⌋ nicht als Bestandteil eines Mechanismus, sondern eines Kalküls.

​

⍈ [Zu S. 88] A “Wie macht der Gedanke das, daß er darstellt?” – Die Antwort könnte sein: “Weißt Du es denn wirklich nicht? Du siehst es doch, wenn Du denkst.”. Es ist ja nichts verborgen.    Wie macht der Satz das? – Weißt Du es denn nicht? Es ist ja nichts versteckt.

​

Es ist uns, als ginge es uns mit dem Gedanken so, wie mit einer Landschaft, die wir gesehen haben & beschreiben sollen, aber wir erinnern uns ihrer nicht genau genug, um sie mit in allen ihren Zusammenhängen beschreiben zu können. So, meinen wir, können wir das Denken nachträglich nicht beschreiben, weil uns die vielen feineren Vorgänge dann 90 verloren gegangen sind. Diese feinen Ver ◇ häkelungen möchten wir sozusagen unter der Lupe sehen. (ˇDenke an den Satz: “Alles fließt”.) ¥ • [nach S. 90 A ¥ ⋎ S. 91 A ¥ 188]

​

“Aber könnte eine Maschine denken?” – Könnte sie [s|S]chmerzen haben? Hier kommt es drauf an, was man unter dem Ausdruck darunter versteht “Schmerzen haben”. // … , was man darunter versteht: “etwas habe Schmerzen”. // Ich kann den Andern als eine Maschine ansehen die Schmerzen hat, d.h.: den andern Körper. Und ebenso, natürlich, meinen Körper. Dagegen setzt das Phänomen der Schmerzen, wie welches ich es beschreibe, wenn ich etwa sage, “ich habe Zahnschmerzen”, einen ˇphysikalischen Körper nicht voraus. (Ich kann z Zahnschmerzen haben ohne Zähne.) Und hier hat nun die Maschine gar keinen Platz. – Es ist klar, die Maschine kann nur einen physikalischen Körper ersetzen. Und in dem Sinne, in welchem man von einem solchen sagen kann, er habe [s|S]chmerzen, kann man es auch von einer Maschine sagen. Oder wieder: die Körper, von denen wir sagen, sie hätten Schmerzen, können wir mit Maschinen vergleichen, & auch Maschinen nennen.

​

↺ ⍈ ⌊ A ⌋ Wir fragen: “Was ist ein Gedanke; welcher Art muß etwas sein, um die Funktion des Gedankens verrichten zu können?” Und diese Frage ist analog der: was ist, oder, wie funktioniert eine Nähmaschine? – Aber die Antwort, die der unsern analog wäre, würde würde 91 sein laute[t|n]: schau “Schau den Strich an, den sie nähen soll; alles, was der Maschine wesentlich ist, ist in an ihm zu sehen; alles andre kann so, oder anders sein.”     Was ist denn die Funktion, Bestimmung, des Gedankens? – Wenn sie seine Wirkung ist, dann interessiert sie uns nicht.     Wir sind nicht im Bereiche der Kausalerklärungen & jede solche Erklärung klingt ˇfür uns trivial.

​

⍈ [Zu S. 90] A Wenn man an den Gedanken, als etwas spezifisch Menschliches, Organisches, denkt, möchte man fragen: “Könnte es eine Gedankenprothese geben?” – Nun, die Rechenmaschine kann man als Ersatz d[er|ie] zehn Finger beim Rechnen ersetzen; aber von einem anorganischen Ersatz für die Rechnung kann man ˇnatürlich nicht reden.

​

Es ist hier, merkwürdigerweise, eine der ˇfür unsere Betrachtungen gefährlichsten Ideen, daß wir mit dem Kopf, oder im Kopf, denken.     Die Idee von einem Vorgang im Kopf, in dem gänzlich abgeschlossenen Raum, gibt dem Denken etwas Okultes.    “Das Denken geht im Kopf vor sich” heißt eigentlich nichts anderes⌊,⌋ als, ⌊:⌋ der Kopf steht in Zusammenhang mit dem Denken. hat etwas mit dem Denken zu tun. – Man sagt freilich auch “ich denke mit der Feder” & diese Ortsangabe ist mindestens ebensogut. so gut wie die erste.    Zu sagen: Denken sei eine Tätigkeit unseres des Geistes, 92 wie Schreiben eine Tätigkeit der Hand, ist eine Travestie der Wahrheit.    ( Die Liebe im Herzen. Das Herz als Ort der Liebe. Kopf & Herz als Örtlichkeiten Lokalitäten der Seele.)

​

¥ ⋎ S. 188 A, ¥ 189 B, ¥ 190 C     Denken nennen wir den Gebrauch von, das Operieren mit Symbolen.     Man kann etwa sagen, das Denken rechne auf Grund von Daten & ende in einer Handlung. ‘Denken’ ist aber ein wechselnder Begriff. (Die Berechnung der Wandstärke eines Kessels & die seine Verfertigung der Berechnung entsprechend ist gewiß ein Beispiel des Denkens & seiner Funktion. Anwendung. )

​

ˇWenn wir vom Gedanken & seinem Ausdruck reden so ist [D|d]er Gedanke ist nicht eine Art von Stimmung, die durch den Satz seinen Ausdruck , wie durch einen Trank eine Droge hervorgerufen wird. Und die Verständigung, die Vermittelung des Gedankens durch die Sprache, ist nicht der Vorgang, daß ich durch ein Gift im Andern die gleichen Schmerzen hervorrufe, wie ich sie habe.     (Was für einen Vorgang könnte kann man “Gedankenübertragung” & “Gedankenlesen” nennen?)

​

Ein französischer Politiker unserer Tage hat einmal gesagt, die französische Sprache sei dadurch ausgezeichnet, daß in ihren Sätzen ihr die Wörter in der Reihenfolge stünden, wie man denkt.        Die Idee, daß eine Sprache eine Wortfolge 93 haben kann, die der Reihenfolge des Denkens entspricht, im Gegensatz zu anderen Sprachen, rührt von der Auffassung her, daß das Denken vom Ausdruck der Gedanken getrennt vor sich geht; & ein wesentlich anderer Vorgang ist. (Nach dieser Auffassung könnte ich vielleicht sagen: ⍈ “D[as|ie] grammatischen Möglichkeiten des Negationszeichens offenbaren sich freilich erst nach & nach im Gebrauch des Zeichens, aber ich denke die Negation auf einmal. Das Zeichen ‘nicht’ ist ja nur ein Hinweis auf den Gedanken ‘nicht’; es stößt mich nur, daß ich das Rechte denke (ist nur ein Signal). ) Zu S. 33 [Neue Zeile, nicht Absatz.]5

​

(Niemand würde fragen, ob das schriftliche Multiplizieren die Multiplikation zweier Zahlen im Dezimalsystem gleichläuft mit dem Gedanken ˇder Multiplikation.)

​

¥ ⋎ S. 94   Das Denken ist diskursiv. – ‘Intuitives Denken’, das wäre so, wie ‘eine Schachpartie, auf die Form eines dauernden, gleichbleibenden Zustandes gebracht’.    (Es stört uns nun, daß der Gedanke eines Satzes in keinem Moment ganz vorhanden ist. Hier sehen wir, daß wir den Gedanken mit einem Ding vergleichen, das wir erzeugen, & das wir nie als Ganzes besitzen; sondern kaum entsteht ein Teil, so verschwindet ein andrer. Das hat, gewissermaßen, etwas Unbefriedigendes, weil wir, durch ein naheliegendes Gleichnis verführt, uns etwas Anderes erwarten.)

​

94 ⍈ [Zu S. 93]        “Ich habe etwas bestimmtes damit gemeint, als ich sagte …”. – “Hast Du bei jedem Wort etwas anderes gemeint, oder während des ganzen Satzes dasselbe?”      Übrigens seltsam: wenn man bei jedem deutschen Wort etwas meint, daß dann eine Zusammenstellung solcher Wörter Unsinn sein kann! –      “Dachtest Du denn, als Du den Satz sagtest, daran, daß …” – “Ich dachte nur, was ich sagte.”

∕∕ /

(Lernt das Kind auch nur sprechen, oder auch denken? Lernt es den Sinn des Multiplizierens vor, ⌊–,⌋ oder nach dem Multiplizieren?)

​

Ist es, quasi, eine Verunreinigung des Sinnes, daß wir ihn ein einer bestimmten Sprache, mit ihren Zufälligkeiten, ausdrücken, & nicht gleichsam körperlos & rein?     Spiele ich eigentlich doch nicht das Schachspiel selbst, da die Figuren auch anders sein könnten?!    (Ist ein B mathematischer Beweis in der allgemeinen Theorie der [i|I]rrationalzahlen we darum dadurch weniger allgemein ˇoder streng, weil daß wir ihn mit Bezug auf die Dezimalnotation dieser Zahlen führen?) Gilt etwa auch die Gleichung 25 × 25 = 625 Beeinträchtigt es vielleicht auch die Strenge & Reinheit des Satzes 25 × 25 = 625, daß er in einem be- 95 stimmten Zahlensystem hingeschrieben ist?)

v

Der Gedanke kann nur muß etwas ganz hausbackenesˇ, gewöhnliches, sein. (Man pflegt sich ihn als etwas Aetherisches, Unerforschtes, zu denken; als handle es sich um Etwas, dessen Außenseite bloß wir kennen, dessen Inneres Wesen aber noch unbekannt ist, etwa wie … unerforscht ist, ⌊–⌋ etwa wienicht bekannt ist, etwa … unser Gehirn.)                      (Man möchte sagen: “Der Gedanke, welch ein seltsames dieses seltsame Wesen”) ¥ ⌊ ⋎ S. 190. ⌋        Wir können wieder nur die Grammatik des Wortes “denken” explizit machen. (Und ebenso de[s|r] Wortes “erwarten”, “glauben”, etc..)

v

Wozu denkt der Mensch? Wozu ist es nütze? Warum berechnet er ˇdie Wandstärke eines Dampfkessel⌊s⌋ & überläßt sie nicht de[m|n] Zufall, oder d[er|ie] Laune? ◇◇◇ , sie bestimmen? Es ist doch bloß Erfahrungstatsache, daß Kessel, die berechnet wurden, nicht so oft explodieren. Aber, wie er alles eher täte, als die Hand ins Feuer stecken, das ihn früher gebrannt hat, so wird er alles eher tun, als den Kessel nicht berechnen. Da uns nun Ursachen nicht interessieren, so können wir sagen: die Menschen denken tatsächlich; sie gehen z.B. auf diese Weise vor, wenn sie einen Dampfkessel bauen. – Kann nun ein so erzeugter Kessel nicht explodieren? Doch, gewiß!

​

Wir überlegen uns Handlungen, ehe wir sie 96 ausführen. Wir machen uns Bilder von ihnen; aber wozu? Wir Es gibt doch kein “Gedankenexperiment”!      Wir erwarten etwas, & handeln der Erwartung gemäß; muß die Erwartung eintreffen? Nein. Warum aber handeln wir nach der Erwartung? Weil wir dazu getrieben werden, wie dazu, einem Automobil auszuweichen, uns niederzusetzen, wenn wir müde sind, aufzuspringen, wenn wir uns auf einen Dorn gesetzt haben.

v

Was es mit dem Glauben an die Gleichförmigkeit des Geschehens auf sich hat, wird vielleicht am klarsten, wenn wir Furcht f vor dem erwarteten Ereignis empfinden. Nichts könnte mich bewegen, meine Hand in die Flamme ins Feuer zu stecken, obwohl ich mich doch nur in der Vergangenheit verbrannt habe.      Der Glaube, daß mich das Feuer brennen wird, ist von der Natur der Furcht, daß es mich brennen wird.      Hier sehe ich auch was “es ist sicher” bedeutet.

v

Wenn man mich in's Feuer zöge, so würde ich mich wehren & ˇwürde nicht gutwillig gehn; & ebenso würde ich schreien “es wird mich brennen!” & nicht: “es wird vielleicht ganz angenehm sein!”

v

“Aber Du glaubst doch auch, daß es 97 mehr Dampfkesselexplosionen geben würde, wenn man die Kessel nicht berechnete!” – Ja, ich glaube es; – aber was will das sagen? Folgt daraus, daß tatsächlich weniger sein werden? – Und was ist denn die Grundlage dieses Glaubens?

​

Ich nehme an, daß dieses Haus⌊,⌋ ˇin dem ich schreibe nicht i[n|m] einer Laufe der nächsten halben Stunde ˇnicht einstürzen wird. – Wann nehme ich das an; die ganze Zeit? Und was für eine Tätigkeit ist dieses Annehmen?   Es kann damit eine psychologische Disposition gemeint sein; aber auch das Denken, [a|A]usdrücken, bestimmter Gedanken. eines bestimmten Gedankens. Im zweiten Falle wird der Satz, den ich etwa werde ich etwa einen ausspreche ⌊n⌋ ˇich etwa einen Satz aus, der wieder ein Glied einer Überlegung (Kalkulation) ist. Nun sagt man: Du mußt aber doch einen Grund haben, das anzunehmen, sonst ist die Annahme ungestützt & wertlos. – (Erinnere Dich daran, daß wir zwar auf der Erde stehen, die Erde aber nicht wieder auf etwas; & Kinder glauben, sie müsse fallen, wenn sie nicht gestützt ist.) Nun, ich habe auch Gründe zu meiner Annahme. Sie lauten etwa: daß das Haus schon jahrelang gestanden hat, aber nicht solange, daß es schon baufällig sein könnte; etc., etc.. – Was als Grund einer Annahme gilt, kann von vornherein angegeben werden, & bestimmt einen Kalkül; ein System von Übergängen. Wird nun aber nach einem Grund dieses Kalküls gefragt, so sehen wir, daß er nicht vorhanden ist.      Ist der Kalkül also willkürlich 98 von uns angenommen? So wenig, wie die Furcht vor dem Feuer, oder einem wütenden Menschen, der sich uns nähert.       “Gewiß sind doch die Regeln der Grammatik, nach denen wir vorgehen & operieren, nicht willkürlich!” – Gut, also, warum denkt denn ein Mensch, wie er denkt, warum geht er denn durch diese Denkhandlungen? (Gefragt ist hier natürlich nach Gründen, nicht nach Ursachen.) Nun, da lassen sich Gründe in dem Kalkül angeben, & ganz zum Schluß & zum Schluß ist man dann versucht zu sagen: “es ist eben sehr wahrscheinlich, daß sich die Dinge jetzt so verhalten, wie sie sich immer verhalten haben”, – oder dergleichen. Eine Redewendung, die den Anfang der Begründung verhüllt. (Der Schöpfer ˇals Erklärung am Beginn der Welt.)      Das was so schwer einzusehen ist, kann so ausgedrückt werden: lautet etwa: daß, solange wir im Bereich der Wahr-Falsch-Spiele bleiben, eine Änderung der Grammatik uns nur von einem solchen Spiel zu einem andern führen kann, aber nicht von etwas Wahrem zu etwas Falschem. Und wenn wir anderseits aus dem Bereich d⌊i⌋e[r|s]er Spiele heraustreten, so nennen wir es nicht mehr ‘Sprache’ & ‘Grammatik’, & zu einem Widerspruch mit der Wirklichkeit kommen wir wieder nicht.

​

Was ist ein Satz? – Wovon unterscheide ich denn 99 einen Satz? Oder, wovon will ich ihn denn unterscheiden? Von Satzteilen in seinem grammatischen System (wie eine Gleichung von ihren Teilen), oder von Allem, was wir nicht ‘Satz’ nennen, also diesem Sessel, meiner Uhr, etc., etc.?

​

Wenn ich frage: “wie ist der ˇallgemeine Begriff des Satzes begrenzt”, – so muß dagegen zuerst gefragt werden: “ja, haben wir denn einen allgemeinen Begriff vom Satz?”     “Aber ich habe doch einen bestimmten Begriff von dem was ich ‘Satz’ nenne.” – “Nun, wie würdest Du ich ihn denn einem Andern, oder Dir mir selbst, erklären? Denn in dieser Erklärung wird sich ja zeigen, was Dein mein Begriff ist (ein das Wort ‘Satz’ begleitendes Gefühl geht mich ja nichts an).” Ich würde den Begriff durch Beispiele erklären. – Also geht mein Begriff, soweit die Beispiele gehn. – Aber es sind doch eben nur Beispiele & ihr Gebiet soll ja eben … & der Begriff, der nur sie allein umschließt, soll ja eben ausdehnungsfähig sein. – Gut, dann mußt Du mir sagen, was das Wort “ausdehnungsfähig” hier bedeutet. Die Grammatik dieses Wortes muß bestimmte Grenzen haben.

​

“Aber ich kenne doch einen Satz, wenn ich ihn sehe, also muß ich auch die Grenzen des Begriffes scharf ziehen können.” Ist aber wirklich kein Zweifel möglich? – Denken wir uns eine Sprache in der alle Sätze Befehle sind in bestimmter Richtung 100 zu gehn. (Sie würde etwa von einer Art primitiver Menschen ◇◇◇ ausschließlich im Kriege gebraucht. Denken wir daran, wie beschränkt einmal der Gebrauch der geschriebenen Sprache war.) Nun, Befehle “geh' hierhin!”, “geh dorthin!” würden wir noch Sätze nennen; wie aber wenn die Sprache nun nur aus dem Zeigen mit dem Finger in irgend einer Richtung bestünde? Wäre dieses Zeichen noch ein Satz? – Und wie wäre ist es mit einer Sprache d[ie|er]en Zeichen ˇnur das Verlangen nach gew bestimmten Gegenständen ausdrückte (ähnlich der ersten Sprache der Kinder) & die bloß aus Zeichen für diese Gegenstande besteht (gleichsam aus Hauptwörtern)? Oder denken wir an ein System aus zwei Zeichen bestehend, deren eines Annahme, das andre Ablehnung dargebotener Gegenstände ausdrückt. Ist dies eine Sprache, besteht sie aus Sätzen?      Und anderseits: fällt alles was den Satzklang der deutschen Sprache hat unter unsern den Satzbegriff? “Ich bin müde”, “2 × 2 ist 4”, “die Zeit vergeht”, “es gibt nur eine 0”?

​

Das Wort “Satz” bezeichnet noch keinen scharf begrenzten Begriff. Wollen wir unserm Gebrauch dieses Wortes einen Begriff mit scharfen Grenzen an die Seite stellen, so steht es uns frei ihn zu definieren, ˇähnlich wie es uns freisteht d[en|as] primitiven Längenmaß ⌊“⌋Schritt⌊”⌋maß einen Schritt von 75 cm Länge dem Längenmaße “ein Schritt” außer seiner primi- 101 tiven die [b|B]edeutung des primitiven Längenmaßes “ein Schritt” auf [7|e]ine Längeneinheit das Maß von 75 cm zu präzisieren. einzuengen.

​

“Was geschieht, wenn ein neuer Satz in die Sprache aufgenommen wird: was ist das Kriterium dafür, daß es er das neue Gebilde // das Neue // ein Satz ist?” Denken wir uns so einen ˇsolchen Fall. Wir lernen ˇetwa eine neue Erfahrung kennen, etwa das Wir lernen, etwa, einen neuen Hautreiz kennen, das Bremseln des elektrischen Schlages, & sagen davon aus, es sei Un unangenehm. Mit welchem Rechte nenne ich diese neu gebildete Aussage einen “Satz”? Nun, mit welchem Rechte habe ich denn von einer neuen “Erfahrung” geredet, oder, noch genauer, von einer neuen “Muskelempfindung”? Doch wohl, nach Analogie meines früheren Gebrauches dieser Wörter. Mußte ich aber, anderseits, das Wort “Erfahrung” & das Wort “Satz” ˇin dem neuen Fall gebrauchen? Ist denn damit schon etwas über die Empfindung des elektr. Schlages das Bremseln ausgesagt, daß man sagt es sei eine ich dafür das Wort Erfahrung ˇgebrauche? // daß ich es eine Erfahrung nenne? // Und was läge daran, wenn ich // die ◇◇◇ Aussage // ˇden Ausdruck “das Bremseln ist [U|u]nangenehm” aus dem Satzbegriff ausschlösse, weil ich seine dessen Grenzen schon früher endgültig fest gezogen hätte?

​

Vergleiche mit dem Satzbegriff den Begriff ‘Zahl’, & anderseits den Begriff der ‘Kardinalzahl’. Zu den Zahlen rechnen wir die Kardinalzahlen, Rationalzahlen, irrationalen Zahlen, komplexen Zahlen; ob wir noch andere Konstruktionen, nach ihrer Ahnlichkeit mit 102 diesen⌊,⌋ Zahlen nennen⌊,⌋ wollen oder die Grenze hier oder anderswo endgültig ziehen wollen, steht uns frei. Der Zahlbegriff ist darin analog dem Begriff des Satzes. Dagegen Anderseits ist sind die ist der kann man den Begriffe der Kardinal- & Rationalzahlen Kardinalzahl [1, ξ, ξ + 1] einen streng umschriebenen nennen, d.h. & er ist ‘Begriff’ in einem andern Sinne dieses Wortes.

∕∕

Wie bin ich denn zum Begriff ‘Satz’, oder zum Begriff ‘Sprache’ gekommen? Doch nur durch die Sprachen, die ich gelernt habe. – Aber die scheinen mich in gewissem Sinne über sich selbst hinausgeführt zu haben, denn ich bin jetzt im Stande, eine neue Sprache zu konstruieren, z.B., Wörter zu erfinden. – Also gehört diese Konstruktion noch zum Begriff der Sprache. Aber nur, wenn ich ihn so festlegen will. festlege. Immer wieder hat der ist der Sinn des meines “u.s.w” eine Grenze⌊.⌋ in der Grammatik. grammatisch begrenzt.

​

Ich kann in der Logik ( in innerhalb einer exakten Grammatik) nicht ins Blaue verallgemeinern. Ich rede denke aber hier nicht von einer an die Einschränkung durch eine “Theorie der Typen”. // Ich meine ˇhier aber nicht eine Einschränkung durch “ˇlogische Typen”. // , [s|S]ondern, ⌊:⌋ die Verallgemeinerung ist ein Zeichen mit bestimmte[n|r] [g|G]rammati[s|k]chen⌊.⌋ Regeln. D.h. die Unbestimmtheit der Allgemeinheit ist keine logische Unbestimmtheit. Sie ist ˇeine Bewegungsfreiheit i[n|m] einem Raum, nicht eine die Unbestimmtheit der Geometrie 103 des Raumes. // Sie ist eine Bewegungsfreiheit, nicht eine Unbestimmtheit der Geometrie. // ⌊⌊ ¥ ⋎ S. 191 B ⌋⌋ ¥• ⋎ ⌊ S.⌋ 103 A, ¥ S. 123 A

​

Über sich selbst führt uns kein Zeichen hinaus, & auch kein Argument.

​

Was tut der, der eine neue Sprache konstruiert (erfindet)[?|,] nach welchem Prinzip geht er vor? Denn dieses Prinzip ist der Begriff der ‘Sprache’. – Erweitert (verändert) jede neu konstruierte Sprache den Begriff der Sprache? – Überlege, welches Verhältnis sie zum früheren Begriff hat. Das kommt darauf an, wie dieser Begriff festgelegt wurde. – Denken wir an das Verhältnis der Komplexen Zahlen zum ältern Zahlbegriff; & anderseits, an den Fall, wenn zum ersten Mal zwei bestimmte (etwa sehr große) Kardinalzahlen hingeschrieben & mit einander multipliziert werden, & an das Verhältnis dieser neuen Multiplikation zum allgemeinen Begriff der Multiplikation von Kardinalzahlen.

​

↺ ⍈ A     Das ist es auch, was ich damit gemeint habe, “daß es “ zwar in der Wirklichkeit überraschungen gibt, aber nicht in der Grammatik”.

​

¥ ⋎ S. 191 A    Aber, wenn so der allgemeine Begriff der Sprache, sozusagen, zerfließt, zerfließt da nicht auch die Philosophie? Nein, denn ihre die Aufgabe der Philosophie ist nicht, eine neue, die richtige ideale, [s|S]prache zu schaffen, sondern den Sprachgebrauch unserer Sprache – der bestehenden – zu klären. Ihr Zweck ist es beson- 104 dere Mißverständnisse zu beseitigen; nicht, etwa, ein eigentliches Verständnis erst zu schaffen.

​

Der welcher darauf aufmerksam macht, daß ein Wort in mehreren zwei verschiedenen Bedeutungen gebraucht wurde, oder, daß bei dem Gebrauch eines Ausdrucks uns dieses irreführende Bild vorschwebt, & der überhaupt die Regeln feststellt (tabuliert), nach denen ˇgewisse Worte gebraucht werden, hat gar nicht die Pflicht übernommen eine Erklärung (Definition) des Wortes “Regel”, oder “Satz”, oder “Wort”, etc. zu geben.       Es ist mir erlaubt das Wort “Regel” zu verwenden, ohne erst zuerst die Regeln des Gebrauchs dieses Wortes zu tabulieren. Und diese Regeln sind nicht Über-Regeln.

​

Und die Philosophie hat es in demselben Sinn mit Kalkülen zu tun, wie sie es mit Gedanken, Sätzen & [s|S]prachen zu tun hat. Hätte sie's aber wesentlich mit dem Begriff des Kalküls zu tun, also mit dem Begriff des Kalküls vor allen Kalkülen, so gäbe es eine Metaphilosophie. (ˇAber die gibt es nicht. . Man könnte alles, was wir zu sagen haben, so darstellen, daß das als ein leitender Gedanke erschiene.)

​

105     Wie gebrauchen wir denn das Wort “Regel”, wenn wir etwa von Spielen reden? Im Gegensatz wozu? – Wir sagen z.B. “das folgt aus dieser Regel”, aber dann könn⌊t⌋en wir ja die betreffende Regel Regel des Spiels zitieren & so das Wort “Regel” vermeiden ersetzen . Oder wir sprechen von “allen Regeln des Spiels” & müssen haben sie dann entweder aufgezählt haben (& dann liebt wieder der erste Fall vor), oder wir sprechen von den Regeln als einer Gruppe ˇvon Ausdrücken, die deren Glieder ˇdie auf bestimmte Art aus gegebenen Grundregeln erzeugt werden, & dann steht das Wort “Regel” für den Ausdruck dieser Grundregeln & Operationen. Oder wir sagen: “das ist eine Regel, das nicht”, – wenn etwa das zweiteˇ, etwa, nur ein einzelnes Wort ist ⌊⌊ + (oder ein nicht vollständiger Satz im Sinne der deutschen Grammatik)⌋⌋, oder ˇdie Illustration einer Stellung Konfiguration der Spielfiguren. Spielsteine. (Oder: “nein, das ist nach der neuen Abmachung auch eine Regel”.) – Wenn wir etwa das Regelverzeichnis des Spiels aufzuschreiben hätten, so könnte so etwas gesagt werden & dann bedeutete es: hieße es: das gehört hinein, das nicht. Aber nicht vermöge einer bestimmten Eigenschaft, der nämlich, eine Regel zu sein; wie … Eigenschaft (nämlich der, eine Regel zu sein.); wie wenn man lauter Äpfel in eine Kiste packen möchte, & sagt: “nein, das gehört nicht hinein, das ist eine Birne”.      Ja, aber wir nennen doch manches “Spiel”, & manches nicht, & manches “Regel”, & manches nicht! – Aber auf die Abgrenzung alles dessen, was wir Spiel nennen gegen alles [a|A]ndere, kommt es ja nie an. – Die Spiele sind für uns die Spiele, von denen wir gehört haben, die wir aufzählen können, & etwa noch einige nach Analogie neu gebildete; & wenn jemand etwa ein Buch über die Spiele schriebe, 106 so brauchte er eigentlich das Wort “Spiel” auch im Titel des Buches nicht zu verwenden unbedingt , sondern als Titel könnte eine Aufzählung der Namen der einzelnen Spiele stehen.    Und gefragt: Was ist denn aber das Gemeinsame aller dieser Dinge, weswegen Du sie zusammenfaßt? – könnte er sagen: ich weiß es nicht ohne weiteres in einem Satz anzugeben, – aber Du siehst ja viele Analogien. Im übrigen scheint mir die diese Frage müßig, da ich auchˇ wieder,, nach Analogien fortfahrend, fortschreitend, durch unmerkbare Stufen, zu Gebilden kommen kann, die niemand mehr im gewöhnlichen Leben “Spiel” nennen würde. Ich nenne daher “Spiel” das, was auf dieser Liste steht, wie auch, was diesen Spielen bis zu einem gewissen (von mir nicht näher festgelegten bestimmten ) Grade ähnlich ist. Übrigens behalte ich mir Und ich behalte mir vor, in jedem neuen Fall zu entscheiden, ob ich etwas zu den Spielen rechnen will oder nicht.

​

Und so verhält es sich mit dem Begriff ‘Satz’, ‘Regel’, ‘Satz’, ‘Sprache’, etc.. Nur in besonderen Fällen (d.h., nicht immer, wenn wir das Wort “ Regel Satz ” gebrauchen) handelt es sich darum ⌊die⌋ Regeln Sätze von etwas abzugrenzen, was nicht Regel Satz ist, & dann können leicht [g|G]renzen gezogen werden. & in allen diesen Fällen ist es leicht das unterscheidende Merkmal zu geben. Wir brauchen das Wort “Regel” im Gegensatz zu “Wort”, “Abbildung” & einigem Andern, & diese Abgrenzungen können klar gezogen werden. sind klar zu ziehen. 107 Dagegen ziehen wir dort ˇmeist keine Grenzen, wo wir sie nicht brauchen. (Es ist, wie wenn man für gewisse Spiele nur einen Strich mitten durchs Spielfeld zieht um die Parteien zu trennen // scheiden // , das Feld aber im übrigen nicht begrenzt, weil es nicht nötig ist.)      Wir können das Wort “Pflanze” in unmißverständlicher Weise gebrauchen, aber es lassen sich unzählige Grenzfälle konstruieren, für welche die Entscheidung, ob etwas noch unter den Begriff ‘Pflanze’ fällt falle , erst zu treffen wäre. Ist aber deshalb die Bedeutung des Wortes “Pflanze” in allen andern Fällen mit einer Unsicherheit behaftet, unsicher, sodaß man ◇ sagen könnte, wir verstehen das Wort eigentlich nicht? gar nicht? // … könnte, wir gebrauchen das Wort, ohne es zu verstehen? // Ja, würde uns eine Definition, die diesen den Begriff nach mehreren Seiten hin begrenzte, die Bedeutung des Wortes in allen Sätzen klarer machen, & würden wir also daher alle Sätze, in denen es vorkommt, ˇ ◇◇◇ besser verstehn?

∕∕

⌊ ¥ ⋎ [S. 192 und das Folgende bis S 196 zum Strich.] ⌋    Der Gebrauch des Wortes “Spiel”, “Satz”, “Sprache”, etc. hat die Verschwommenheit des normalen Gebrauchs der aller Begr⌊i⌋ffswörter unserer Sprache. Zu glauben, sie wären darum unbrauchbar, oder doch ihrem Zweck nicht ideal ganz entsprechend, wäre so so , als wollte man sagen: “der Duft dieser Rose Blumen die Wärme die dieser Ofen gibt ist nichts nutz, weil man nicht weiß, wo er sie anfängt & wo er sie aufhört”.       Will ich zur Aufklärung & zur Vermeidung von Mißverständnissen im Gebiet eines solchen Sprachgebrauchs scharfe Grenzen ziehen, so werden sich diese zu den verfließenden 108 Grenzen im ˇnatürlichen Sprachgebrauch ⌊(⌋◇◇◇⌊)⌋ verhalten, wie die scharfen Konturen in einer Federzeichnung zu den allmählichen Übergängen ˇvon Farbflecken in der dargestellten Wirklichkeit.

​

Unsere Betrachtungsweise ist entgegengesetzt der Platos. Sokrates weist den Schüler zurecht, der, nach dem Wesen auf die Frage der Erkenntnis gefragt, Erkenntnisse aufzählt. & Und er läßt dies diese Aufzählung ˇauch nicht als ◇◇◇ einen vorläufigen Schritt zur Beantwortung der Frage gelten.    Während unsere Antwort gerade eine solche Aufzählung & die Angabe einiger Analogien ist. // Und Sokrates er sieht darin auch nicht einen vorläufigen Schritt zur Beantwortung der Frage.      Während unsere Antwort in einer solchen Aufzählung & der Angabe einiger Analogien besteht. // (Wir machen es uns in der Philosophie ˇin gewissem Sinne immer leichter & leichter.)

∕∕ /

Die Philosophie der Logik redet in keinem andern Sinn von Sätzen ˇ& Wörtern, als wir es im gewöhnlichen Leben tun, wenn wir sagen “hier steht ein ˇchinesischer Satz aufgeschrieben”, oder “nein, das sieht nur aus wie ein Satz, ⌊ein⌋ W[ö|o]rter ein Schriftzeichen, ist aber keiner” ˇsondern ein Ornament”,, etc. etc..       Wir reden von dem räumlichen & zeitlichen Phänomen der Sprache, nicht von einem unräumlichen & unzeitlichen Unding. Aber wir reden von ihr so, wie von den Figuren des Schach- 109 spiels, indem wir Regeln für ihren Gebrauch angeben // indem wir Spielregeln für sie angeben // , nicht ihre physikalischen Eigenschaften beschreiben.     Die Frage “was ist ein Wort” ist analog der: “was ist eine Schachfigur (etwa der Schachkönig)”.

​

⍈         Zu Bd. XI./49/1     Wir können leicht, beim Nachdenken über die Sprache & Bedeutung, dahin kommen , daß wir zu denken, wir man redeten dürften redete ˇin der Philosophie eigentlich nicht eigentlich nicht von Wörtern & Sätzen im ganz hausbackenen Sinn, oder, sondern in einem sublimierten, abstrakten Sinn. ⌊–⌋ So als wäre ein bestimmter Satz nicht eigentlich das, was irgend ein Mensch ausspricht, sondern ein Idealwesen (die “Klasse aller gleichbedeutenden Sätze”, oder dergleichen). Aber ist auch der Schachkönig von dem die Schachregeln handeln ein solches Idealding, ein abstraktes Wesen? ⌊ ¥ [Dazu der Satz ‘Spinnennetz …’] ⇒ [“Hier ist es schwer den Kopf …”] ⌋ [neue Zeile], nicht Absatz] ¥ S. 110 A

​

Wir können in der Philosophie ˇauch keine größere Allgemeinheit erreichen, als in dem, was wir im Leben & in der Wissenschaft sagen. Auch hier (wie in der Mathematik) lassen wir alles, wie es ist.

∕∕

Wenn ich über Sprache[,| (]Wort, Satz, etc.) rede, muß ich die Sprache des Alltags reden. Ist diese Sprache etwa zu grob, materiell, für das, was wir sagen wollen? Und wie wird eine denn eine andere Wie ist eine andere 110 gebildet? – Und ˇwiec merkwürdig, daß wir dann mit der unsern überhaupt etwas anfangen können!       Daß ich in beim den philosophischen Erklärungen über die der Sprache schon die volle Sprache (nicht etwa eine vorbereitende, vorläufige) anwenden muß, zeigt schon, daß ich nur Äußerliches über die Sprache vorbringen kann.       “Ja, aber wie können uns diese Ausführungen dann befriedigen?⌊”⌋ – ⌊–⌋ Nun, Deine Fragen w[ä|a]ren ja auch schon in dieser Sprache abgefaßt! – Und Deine Skrupel sind Mißverständnisse. – Deine Fragen beziehen sich auf Wörter, so muß ich von Wörtern reden.    Man sagt: Es kommt nicht auf's Wort an, sondern auf seine Bedeutung; & denkt dabei an die Bedeutung, wie an eine Sache von der Art des Worts, wenn auch vom Wort verschieden. Hier das Wort, hier die Bedeutung. (Das Geld & die Kuh, die man dafür kaufen kann. (Anderseits aber: das Geld, & sein Nutzen.)

​

⍈ [Zu S. 109] A (Über unsre Sprache sind nicht mehr Bedenken // Skrupel // gerechtfertigt, als ein Schachspieler über das Schachspiel hat, nämlich keine.)

​

Wenn wir nach der allgemeinen Satzform fragen, –, bedenken wir, daß die gewöhnliche Sprache zwar einen bestimmten ◇◇◇ ˇSatzrhythmus⌊,⌋ Satzklang hat, 111 daß wir aber nicht alles , was ‘wie ein Satz klingt’, “Satz” nennen , was diesen Satzklang hat, einen Satz nennen . – Daher spricht man auch Es vom sinnvollen & unsinnigen “Satz”.       Anderseits aber ist dieser Satzklang dem was wir in der Logik Satz nennen natürlich nicht wesentlich. Der Ausdruck “gut Zucker” klingt nicht wie ein deutscher Satz, kann aber doch sehr wohl den Satz “Zucker schmeckt gut” ersetzen. Und zwar nicht etwa so, daß etwa nur, wenn wir uns etwas Fehlendes Worte hinzudenken müßten. (Vielmehr kommt es nur auf das Ausdrucksystem Sprachsystem an dem der Ausdruck “gut Zucker” angehört.)     Es fragt sich also, ob wir abgesehen von diesem irreführenden Satzklang noch einen allgemeinen Begriff vom Satz haben.

​

Denken wir uns die deutsche Sprache so geändert daß die Reihenfolge der Wörter im Satz die umgekehrte der gegenwärtig richtigen ist. Das Ergebnis wären also Sätze, wie Wortfolgen welche wir sie erhalten, wenn wir die Sätze eines deutschen Buches von rechts nach links durchlesen. Es ist klar, daß die Mannigfaltigkeit der Ausdrucksmöglichkeiten dieser neuen Sprache genau die gleiche wie die der deutschen sein muß; aber wir könnten einen längeren Satz, wenn er so gelesen würde nur äußers äußerst schwer verstehen & würden vielleicht nie lernen “in dieser Sprache zu denken”. (Das Beispiel einer solchen Sprache kann manches Wesentliche am Gedanken am Wesen des Gedankens dessen, was wir “Gedanken” nennen, klar machen.)

​

Die Erklärung: “Satz sei alles, was wahr oder 112 falsch sein kann” bestimmt den Begriff des Satzes in einem ˇ besondern Sprachsystem als das, was in diesem System Argument einer Wahrheitsfunktion sein kann.      Und wenn wir von dem sprechen, was der Satzform als solcher wesen⌊t⌋lich ist, // sprechen, was den Satz zum Satz macht, // so sind wir geneigt die Wahrheitsfunktionen zu meinen.     “Satz ist alles, was wahr oder falsch sein kann” heißt dasselbe wie: “Satz ist alles, was sich verneinen läßt”.

​

“p” ist wahr = p    “p” ist falsch = ~p ¥ • Man könnte sagen: Wahr die Worte “wahr” & “falsch” sind nur Glieder einer besti bestimmten Notation der Wahrheitsfunktionen. ⍈     ↺ “Was er sagt, ist wahr” = Es verhält sich so, Es ist so, wie er sagt

​

Ist es denn richtig, zu schreiben ““p” ist wahr”, “‘p’ ist falsch”[?|;] muß es nicht heißen “ p ist wahr” (oder falsch)? Der Tintenstrich ist doch nicht wahr; wie er schwarz & krumm ist.   Sagt denn “‘p’ ist wahr” etwas über das Zeichen ‘p’ aus? – “Ja, es sagt, daß ‘p’ mit der Wirklichkeit übereinstimmt.” – Denken wir uns Betrachten wir, statt eines Satzes der Wortsprache, ein nach exakten Regeln einer objektiven Projektionsregeln gezeichnetes Bild das nach exakten Projektionsregeln mit der Wirklichkeit zu vergleichen ist. 113 Hier muß es sich gewiß am deutlichsten zeigen, was “‘p’ ist wahr” von dem Bild ‘p’ aussagt. Man kann also den Satz “‘p’ ist wahr” mit dem vergleichen: “dieser Gegenstand hat die Länge dieses Meterstabes Maßstabes ”; & “p” dem Satz: “dieser Gegenstand ist 1 m lang”. Aber der Vergleich ist falsch, denn “dieser Meterstab” ist eine Beschreibung, weil “Meterstab” eine Begriffsbestimmung⌊.⌋ ist. Dagegen tritt in “‘p’ ist wahr” der Maßstab selbst unmittelbar in den Satz ein. ‘p’ representiert hier einfach die Länge & nicht den Meterstab. Denn die darstellende Zeichnung ist ja auch gar nicht ‘wahr’, außer nach einer bestimmten Projektionsmethode, die den Maßstab zu einem rein geometrischen Anhängsel der gemessenen Strecke macht.

​

Man kann es auch so sagen: Den Satz “‘p’ ist wahr” kann man nur dann verstehen wenn man die Grammatik des Zeichens “‘p’” als eines Satzzeichens versteht; nicht, wenn man “‘p’” einfach der Name der Gestalt eines bestimmten Tintenstriches ist. – Und endlich kann man sagen die Anführ[ü|u]ngszeichen im Satz “‘p’ ist wahr” sind einfach überflüssig.

​

Wenn man erklärt, ⌊:⌋ “(x) ∙ fx” sei wahr, wenn “f( )” für alle Substitutionen einen wahren S[a|ä]tz⌊e⌋ ergibt, – so bedenken wir, daß der Satz “(x) ∙ fx” aus dem Satz “‘f( )’ gibt für alle Substitutionen wahre Sätze” folgt, & umgekehrt dieser aus jenem. Die beiden Sätze sagen also das selbe.    Jene Erklärung setzt also den Mechanis- 114 mus der Verallgemeinerung nicht erst aus seinen Teilen zusammen. –

​

Man kann natürlich nicht sagen, Satz sei dasjenige, wovon man “wahr” & “falsch” aussagen kann, in dem Sinne, als könnte man versuchen, zu welchen Symbolen die Wörter “wahr” & “falsch” paßten & danach entscheiden, ob etwas ein Satz ist. Denn dieser Versuch // … als könnte man versuchsweise zum Versuch Symbole mit den Wörtern “wahr” & “falsch” zusammenstellen um zu & sehen ob sie Sinn ergeben. Denn dieser mit diesem Versuch könnte man nur dann etwas entscheiden, bestimmen, wenn “wahr” & “falsch” schon bestimmte Bedeutungen haben, & das können sie nur wenn der Zusammenhang in dem sie vorkommen dürfen bereits festgelegt ist.   (Denke auch an die Bestimmung von Redeteilen durch Fragen. “Wer oder was …?”)

​

¥ ⋎ S. 115 A, ¥ B “Kann man die allgemeine Form des Satzes angeben?“ – Warum nicht? Wie man ja auch die allgemeine Form der Zahl angeben den Begriff Zahl festlegen könnte, durch das Zeichen “[0, ξ, ξ + 1]” z.B.. Es steht mir ja doch frei nur das “Zahl” zu nennen, & so kann ich kann ich auch, eine analoge Vorschrift ˇauch zur Bildung von Sätzen oder Gesetzen zu geben & das Wort “Satz” oder “Gesetz” als Äquivalent dieser Vorschrift zu gebrauchen. – Wehr⌊t⌋ man sich dagegen & sagt, es sei doch klar, daß dadurch nur gewisse Gesetze von andern abgegrenzt worden seien, so antworte ich: Du kannst freilich nicht 115 eine Grenze ziehen, wenn Du von vornherein entschlossen bist keine anzuerkennen! Die Frage bleibt natürlich … Es bleibt dann natürlich die Frage: Wie gebrauchst Du das Wort Satz? Im Gegensatz wozu? –

​

(“Kann ein Satz von allen Sätzen handeln, oder allen Satzfunktionen, handeln?” – Was meint man damit? Denkt man an einen Satz der Logik? – Wie s⌊i⌋eht denn der Beweis des ˇeines solchen Satzes ◇◇◇ aus?)

​

⍈ [Zu S. 114] B       Wenn ich übrigens “es verhält sich so & so” als allgemeine Satzform gelten lasse, dann muß ich “2 + 2 = 4” unter die Sätze rechnen. Es braucht weitere Regeln, um die Sätze der Arithmetik auszuschließen.

​

⍈ [Zu S. 114] A         In dem Schema “es verhält sich so & so” ist das der Ausdruck “es verhält sich” eigentlich der Angriff für die Wahrheitsfunktionen.    “Es verhält sich” ist also ein Ausdruck aus einer Notation der Wahrheitsfunktionen. Ein Ausdruck der uns zeigt, welcher Teil der Grammatik hier in Funktion tritt.

​

Eine allgemeine Satzform bestimmt den Satz als Glied eines Kalküls.

​

Die Regeln, welche sagen, aussagen, daß die & die Zusammenstellungen von Wörtern Worten keinen Sinn ergibt, sind sie mit den Festsetzungen für das Schachspiel zu vergleichen, daß ˇes, z.B., keine Spiel- 116 stellung ist, wenn zwei Figuren auf demselben Feld stehen, oder eine Figur auf der Grenze zweier Felder, etc.? Diese Sätze sind wieder ähnlich gewissen Handlungen; wie wenn man z.B. ein Schachbrett aus einem größeren Stück eines karierten Papiers herausschnitte. Sie ziehen eine Grenze. – Was heißt es denn, zu sagen: “diese Wortzusammenstellung ist sinnlos // besitzt hat keinen Sinn // ”? Von einem Namen (einer Lautreihe) Wort kann man sagen: “diesen Namen habe ich niemandem gegeben”; & das Namengeben ist eine bestimmte [h|H]andlung (Umhängen eines Täfelchens). Denken wir Denke an die Darstellung der Reiseroute Reise eines Forschers durch eine Linie, die wir in die in den den beiden Projektionen der beiden Erdhalbkugeln ziehen. gezogen ist. Wir können nun sagen: Ein Linienstück, welches das auf der Zeichenebene die Grenzkreise dieser Projektionen verläßt, ist in dieser Darstellung sinnlos. Man könnte es auch so sagen ausdrücken : Nichts ist darüber vereinbart worden. Keine Vereinbarung ist darüber getroffen worden.

​

“Wie mach' ich's denn, um ein Wort immer sinnvoll anzuwenden?; schaue ich immer in der Grammatik nach? Nein, daß ich etwas meine, – was ich meine, hindert mich Unsinn zu sagen”. – Aber was meine ich denn? – Ich möchte sagen: Ich rede vom Teilen eines Apfels, aber nicht vom Teilen der Farbe Rot, weil ich bei den Worten “teilen eines Apfels” mir etwas denken kann, etwas vorstellen, etwas wollen kann, – beim Ausdruck “teilen der 117 Farbe Rot” nicht. (Und ist es etwa so, daß man bei diesen Worten nur noch keine Wirkung auf andere Menschen beobachtet hat?) Richtiger wäre es zu sagen[;|,] daß ich mir bei den Worten “teilen eines Apfels” mir etwas denke, vorstelle, etwas will, aber nicht beim Ausdruck “teilen der Farbe rot”.       Der [a|A]usdruck “ich teile Rot” kann aber doch einen Sinn haben (z.B. den des Satzes “ich teile etwas Rotes”). – Was, wenn ich fragte: welches Wort, welcher Fehler, macht den S Ausdruck zum Unsinn? Da sieht man, daß wir bei diesem Ausdruck, trotz seiner Sinnlosigkeit, an ein ganz bestimmtes grammatisches System denken. Daher sagen wir auch “[r|R]ot kann man nicht teilen”, geben also eine Antwort; während man auf eine Wortzusammenstellung wie “ist hat gut” nichts antworten würde. – Denkt man nun aber an ein bestimmtes System, Sprachspiel mit seiner Anwendung, dann sagt, daß “ich teile rot” unsinnig ist, vor allem, daß dieser Ausdruck nicht z zu dem bestimmten Spiel gehört, zu dem es, auf den ersten Blick seinem Aussehen nach zu gehören scheint.

​

Was machen wir nun // [w|W]ie machen wir es nun // , wenn wir der Wortgruppe “ich teile Rot” einen Sinn geben? – Ja wir könn⌊t⌋en doch ganz Verschiedenes aus ihr machen: E einen Erfahrungssatz, einen Satz der Arithmetik (wie 2 + 2 = 4), einen unbewiesenen Satz der Mathematik (wie den Goldbachschen Satz), einen Ausruf, und anderes. Ich habe 118 also eine beliebige Auswahl; & wie ist die begrenzt? Das ist schwer zu sagen –: durch allerlei Arten von Nützlichkeit, & auch durch die formelle Ähnlichkeit der Gebilde mit gewissen primitiven Satzformen, & alle diese Grenzen sind verschwommen.

​

“ Wie Woher weiß ich, daß man Rot nicht teilen kann⌊?⌋” – Die Frage selbst Das ist ˇselbst gar keine Frage. –      Ich möchte sagen: “ Ich Man muß mit der Unterscheidung von Sinn & Unsinn anfangen. Vor ihr ist nichts möglich. Ich kann sie nicht begründen.”

​

Kann man fragen: “wie müssen die grammatischen Regeln für die Wörter beschaffen sein, damit sie einem Satz Sinn geben”?      Ich sage z.B.: “[h|H]ier liegt kein Buch, aber es könnte eins da liegen”; dagegen ist es unsinnig zu sagen, ˇdie Farben grün & rot könnten zu gleicher Zeit an einem Ort sein. Aber, wenn der Satz dadurch sinnvoll wird, daß er mit den grammatischen Regeln in Einklang ist, ◇◇◇ so machen wir eben die Regel, die den Satz “rot & grün sind zugleich an diesem Fleck” zuläßt. Gut; aber damit ist nun die Grammatik dieses Ausdrucks noch nicht festgelegt. Es müssen erst noch weitere Bestimmungen darüber getroffen werden, wie ein solcher Satz zu gebrauchen ist; wie er z.B. verifi- 119 ziert wird.

​

Wenn man auch den Satz als Bild des beschriebenen Sachverhalts auffaßt & sagt, der Satz zeige eben, wie sich die Dinge verhalten, wenn … wie es ist, wenn er wahr ist, er zeige also die Möglichkeit des behaupteten Sachverhalts; so kann der Satz doch bestenfalls tun, was ein gemaltes, oder modelliertes, Bild tut, & er kann also jedenfalls nicht das wirklich hinstellen, was nun einmal nicht der [f|F]all ist. Also hängt es ganz von unserer Grammatik ab, was möglich genannt wird & was nicht, nämlich eben was sie zuläßt. Aber das ist doch willkürlich! – Gewiß; aber grammatische Gebilde, welche wir Erfahrungssätze nennen, z.B die, welche eine ˇsichtbare Verteilung von Körpern im Raum beschreiben & sich durch eine zeichnerische Darstellung ersetzen ließen, haben eine bestimmte Anwendung, einen bestimmten Nutzen. Aber nicht jede Konstruktion, die einem solchen Erfahrungssatz Satz ihrer äußern Form nach, ähnlich ist & die in einem Kalkül eine ˇirgendwie ähnliche Rolle spielt, hat eine analoge Anwendung einen analogen Nutzen , & wir werden dann nicht geneigt sein diese Konstruktion einen Satz zu nennen.

​

“Möglich” heißt hier soviel wie “denkbar”; aber “denkbar” kann heißen “malbar”, “modellierbar”, “vorstellbar”, also: darstellbar in einem bestimmten System. Nun, da kommt es auf das System an. – 120 Man fragt z.B.: “ist es denkbar, daß eine Baumreihe in gerader Richtung endlos weiterläuft, ohne je zu einem Ende zu kommen?” – Warum soll das nicht ‘denkbar’ sein, es ist doch ˇjedenfalls in einem grammatischen System aussprechbar. Aber was ist nun die Anwendung des so eines Satzes, wie wird er verifiziert, welche Beziehung hat d seine Verifikation zu der eines Satzes wie: “diese Baumreihe läuft bis zum endet mit dem 100sten Baum”⌊?⌋ Baum weiter. Das wird uns zeigen wie viel diese Denkbarkeit– ⌊,⌋ sozusagen– ⌊,⌋ wert ist. ⌊ chemisch möglich O | O – – O H – H ⌋

​

“Ich habe tatsächlich nie gesehen, daß ein schwarzer Strich nach & nach immer heller wird, bis er weiß ist, & dann immer rötlicher bis er rot ist; aber ich weiß, daß es möglich ist, weil ich es mir vorstellen kann.” – Die Ausdrucksweise “ich weiß, daß es möglich ist, weil …” ist von Fällen hergenommen, wie: “ich weiß, daß es möglich ist diese die Tür mit diesem Schlüssel aufzusperren, weil ich es schon einmal getan habe”. Vermute ich also in dem Sinn, ⌊:⌋ daß jener Farbenübergang möglich sein wird, weil ich mir ih[m|n] vorstellen kann? – Muß Ist es nicht vielmehr heißen so: “der Farben⌊ü⌋bergang ist möglich” heißt hier dasselbe wie “ ich kann mir ih[m|n] vorstellen”? – Wie ist es damit: “Das Alphabet läßt sich laut hersagen, weil ich es mir im Geiste hersagen kann”?    Und “ich kann mir den Farbenübergang vorstellen” ist hier keine Aussage über 121 meine besondere Vorstellungskraft, wie der Satz “ich kann diesen Stein 50 kg heben” eine Aussage über meine Muskelkraft. Der Satz “ich kann es mir ˇden Übergang vorstellen”, verb ebenso wie der “dieser Sachverhalt läßt sich zeichnen”, verbindet die Sprachliche Darstellung mit einer anderen Darstellungsweise; er ist als Satz der Grammatik zu verstehn.

​

¥ ⋎ S. 122 A   Wenn man die Sinnlosigkeit einer, Erfahrungssätzen ähnlichen, gewisser metaphysischer Redeweisen dartun will, sagt man oft: “ich könnte mir das Gegenteil davon nicht vorstellen”, oder: “wie wäre es denn, wenn's anders wäre”. (Wenn z.B. jemand gesagt hätte, daß meine Vorstellungen privat seien, daß nur ich allein es wissen kann, wenn ich Schmerzen empfinde, etc..) Kann ⌊Nun,⌋ [W|w]enn ich mir nicht vorstellen ˇkann, wie es anders wäre, so kann ich mir auch nicht vorstellen, es wäre so. daß es so wäre. wie es so sein kann. // , daß es so ist. // Denn, “ich kann mir nicht vorstellen” heißt hier nicht, was es im Satz “ich kann mir keinen Totenkopf vorstellen” heißt bedeutet (Ich will damit ˇdeutet hier nicht auf eine auf eine mangelnde Vorstellungskraft). Ich kann ja auch nicht ebensowenig versuchen, es mir vorzustellen: Es ergibt keinen Sinn, zu sagen, “ich stelle es mir vor”. Und das heißt : , eine Verbindung zwischen diesem Satz & der Darstellungsweise der Vorstellung (oder Zeichnung) ist nicht gemacht.       Warum sagt man aber ˇgerade: “ich kann mir nicht vorstellen, wie es anders sein könnte wäre ” & nicht “ich kann mir das nicht vorstellen”? Man sieht den unsinnigen Satz ˇ(z.B. “dieser Stab hat eine Länge” hier als eine 122 ⌊(⌋Art⌊)⌋ Tautologie an, im Gegensatz zu einer Kontradiktion. Man sagt gleichsam: “Ja, er hat eine Länge; aber wie könnte es denn anders sein; also, wozu es sagen!”   Wir sind versucht werden auf den Satz “dieser Stab hat eine Länge” nicht “Unsinn!” zu antworten ˇ“Unsinn!”, sondern: “Freilich!”. Wir könnten es auch so sagen: Wenn wir die Bei beiden Sätze “dieser Stab hat eine Länge” & seine Verneinung “dieser Stab hat keine Länge” hören, so sind wir parteiisch & neigen dem ersten Satze zu; statt beide für Unsinn zu erklären. Der Grund dieser Einseitigkeit aber ist eine Verwechslung: Wir sehen den ersten Satz verifiziert (& den zweiten falsifiziert) dadurch, “daß der Stab 4 m hat”. “Und 4 m ist doch eine Länge”, – aber man vergißt, daß dies ˇein Satz der Grammatik ist.

​

⍈ [Zu S. 121 ˇ[neuer Absatz]] A Es scheint, als könnte man sagen: die Wortsprache läßt unsinnige Wortzusammenstellungen zu, die Sprache der Vorstellung aber nicht unsinnige Vorstellungen. Also die Sprache der Zeichnung auch nicht unsinnige Zeichnungen; – aber so ist es nicht: denn eine Zeichnung kann auf gleiche Weise unsinnig sein, wie ein Satz. Denken wir an eine Werkzeichnung nach der welcher der Dreher arbeiten soll; hier ist es sehr leicht sich das exakte Analogon zu einem unsinnigen [s|S]cheinsatz vorzustellen. Denken wir auch an das Beispiel vom Einzeichnen einer Reiseroute in die Projektionen der Erdkugel.

​

123 ⍈ [Zu S. 103] A “Aber die Sprache kann sich doch erweitern.” – Gewiß; aber wenn dieses Wort “erweitern” hier einen Sinn hat, so muß ich jetzt schon wissen, was damit gemeint ist // was ich damit meine // , muß angeben können, wie ich mir so eine Erweiterung vorstelle. Und was ich jetzt nicht denken kann, das kann ich jetzt auch nicht ausdrücken, & auch nicht andeuten. Und das Wort “jetzt” bedeutet hier: “in diesem Kalkül, oder: “wenn die Worte nach diesen grammatischen Regeln gebraucht werden”.    Hier haben liegt auch haben wir auch dieses bohrende Problem: wie es möglich ist, an die Existenz von Dingen auch nur zu denken, wenn wir immer nur Vorstellungen – ihre Abbilder – sehen. – Zu dieser Frage ist ganz richtig der Nachsatz zu denken –abgeschrieben – Wir fragen: “Wie bin ich denn aber überhaupt zu diesem Begriff gekommen?” Zu dieser Frage ist ganz richtig der Nachsatz zu denken: “ich konnte doch nicht mein eigenes Denken transzendieren”, “ich konnte doch nicht sinnvoll das transzendieren, was für mich Sinn hat”. Es ist das Gefühl: daß ich nicht auf Schleichwegen (hinterrücks) dahin kommen kann, etwas zu denken, was ˇauf direktem Wege zu denken mir eigentlich verwehrt ist[;|.] daß es hier keine Schleichwege gibt, auf denen ich weiter kommen könnte, als auf dem direkten Weg. (ˇDenke an die Mengenlehre & Ähnliches.)

​

124     Man kann oft auch zeigen, daß ein Satz metaphysisch gemeint ist, indem man fragt: Ist “Soll was Du behauptest das eine Erfahrungstatsache sein? Kannst Du Dir denken (vorstellen), daß es anders wäre?” – Willst Du sagen, Substanz sei noch nie zerstört worden, oder, es sei undenkbar, daß sie zerstört werde?” ⌊ Willst Du sagen daß die ˇ ◇◇◇ Erfahrung lehre, daß der Mensch immer das [a|A]ngenehmere dem [u|U]nangenehmeren ˇvorziehe? ⌋

​

Seltsam, daß man sollte sagen können, der & der Sachverhalt sei undenkbar! Auch wenn wir im Denken wesentlich eine Begleitung des Ausdrucks sehen, so müssen also doch die Worte, die den undenkbaren Sachverhalt ˇin dieser Aussage angeben unbegleitet sein. Was soll sie also für einen Sinn haben? es sei denn, daß sie aussagt, diese Worte seien sinnlos. Aber dann ist nicht, quasi, ihr Sinn sinnlos; sondern sie werden aus unserer Sprache ausgeschaltet, ausgeschlossen, wie ˇetwa irgend ein beliebiges Geräusch, & der Grund zu ihrer ausdrücklichen Ausschließung kann nur darin liegen, daß wir versucht sind, sie das Gebilde mit einem Satz unserer Sprache zu verwechseln.

​

Welche Rolle der Satz im Kalkül spielt, das ist sein Sinn.       Die Methode des Messens[,| (]des Messens 125 einer Länge z.B.[,|)] verhält sich zu einer bestimmten Messung genau so, wie der Sinn eines Satzes zu seiner Wahr- oder Falschheit. // Die Methode des Messens ( ⌊–⌋ einer Länge z.B.) ⌊–⌋ verhält sich zur Richtigkeit eines einer ⌊(⌋bestimmten⌊)⌋ Messungsresultats einer Maßangabe genau so, wie der Sinn eines Satzes zu seiner Wahr- oder Falschheit. //

∕∕ v

Was heißt es denn: “entdecken, daß eine Aussage keinen Sinn hat”? – Und was heißt das: “wenn ich etwas dam⌊i⌋t meine, muß es doch Sinn haben ˇdas zu sagen”? –“ ⌊‘⌋Wenn ich etwas ˇdamit meine’ – wenn ich Was damit meine?! – Man will sagen: der sinnvolle Satz ist der, den ich man nicht nur sagen⌊⌊, sondern ˇden man auch denken kann.⌋⌋ ⌊⌊ Oder heißt es: Das sagte wäre etwa als sagte man: das sinnvolle Bild ist das, was ich nicht nur zeichnen sondern auch modellieren kann. Und dies zu sagen, hätte Sinn. ⌋⌋ ⌊⌊Aber das Denken des Satzes⌋⌋ ⌊ist nicht eine Tätigkeit die man nach den Worten vollzieht (wie etwa das Singen nach den Noten).⌋ ⌊ Das folgende Beispiel zeigt dies. ⌋      Hat es Sinn zu sagen: “ich habe soviele Freunde, als soviel die eine Lösung von x³ + 2x ‒ 3 = 0 ergibt”? Hier , könnte man meinen, wir hätten wir hätten wir ˇwäre // ist // eine Notation, deren Grammatik allein es nicht bestimmt, ob ein Satz Sinn hat oder nicht. So daß es also nicht von vornherein bestimmt … von vornherein überhaupt nicht bestimmt wäre. ¥ •     Wenn der Ausdruck “die Wurzel der Gleichung …” eine Beschreibung im Russell'schen Sinne wäre, so hätte der Satz “ich habe n Äpfel & 2 + n = 6” einen andern Sinn, als der Satz “ich habe 4 Äpfel”.

​

↺ ⍈ Dies gibt ein herrliches Beispiel dafür, was es heißt, ⌊:⌋ einen Satz zu verstehen.

​

Der Sinn eines Satzes ist nicht pneumatisch (wie der Gedanke es nicht ist), sondern er ist das, was auf die Frage nach 126 der Erklärung des Sinnes zur Antwort kommt. Oder: der eine Sinn unterscheidet sich vom andern, wie die Erklärung des einen von der Erklärung des andern. Also auch: der Sinn des einen Satzes unterscheidet sich vom Sinn des andern, wie der eine Satz vom andern.        Der Sinn des Satzes ist keine Seele.

​

Etwas ist ein Satz nur in einer Sprache Einen Satz verstehen, heißt, eine Sprache verstehen.     Ein Satz ist ein Zeichen in einem System von Zeichen. Er ist eine Zeichenverbindung unter mehreren möglichen & im Gegensatz zu andern möglichen. Gleichsam eine Zeigerstellung im Gegensatz zu andern möglichen.

​

“Geh' in der Richtung, in der der Pfeil zeigt.”      “Geh' so viele meter wieviele m als 100 mal soweit als der Pfeil lang ist.”      “Mach soviele Schritte als ich Pfeile zeichne.”      “Zeichne diesen Pfeil nach.”      “Geh' um die Zeit von      “Komm' um die Zeit die dieser Pfeil anzeigt wenn er der Stundenzeiger einer Uhr ist.”    Für jeden dieser Befehle könnte kann der gleiche Pfeil stehen.   ↑ im Gegensatz zu ↗ ist ein andres Zeichen, als ↑ im Gegensatz zu ↑.

​

127     Das Symbol (der Gedanke) scheint als solches unbefriedigt zu sein.     Der Wunsch, die Vermutung, der Glaube, der Befehl , scheint etwas Unbefriedigtes⌊,⌋ ˇErgänzungsbedürftiges ⌊[.|z]u sein.⌋ Ich So möchte ˇich mein Gefühl ˇdes Verstehens // Erfassens // , dem Befehl gegenüber als ˇdas einer Innervation bezeichnen. Aber auch die Innervation an sich ist nicht unbefriedigt, läßt nichts offen, ist nicht ergänzungsbedürftig.      Und ich will sagen meine : “die der Wunsch ist unbefriedigt, weil er der Wunsch nach Etwas ist; die Meinung unbefriedigt, weil sie die Meinung ist, es sei etwas der Fall, ⌊–⌋ etwas Wirkliches; etwas außerhalb dem Vorgang der Meinung.”

​

Ich möchte sagen: “Meine Erwartung ist so gemacht, daß, was immer kommt, mit ihr übereinstimmen muß, oder nicht.” ⌊    [Neuer Absatz.] ⌋ Der Satz scheint uns als Richter hingestellt & wir fühlen uns vor ihm verantwortlich. – Er scheint die Realität zu fordern sich mit ihm zu vergleichen.

​

Ich sagte, der Satz wäre wie ein Maßstab an die Wirklichkeit angelegt . Und der Maßstab : aber ⌊das ist,⌋ wie alle logischen Gleichnisse des Satzes, selber ˇein besonderer Fall ein⌊es⌋ Satzzeichen⌊s⌋ // selber ein Satzzeichen in einem besonderen Fall // . Man möchte nun sagen: “Lege den Maßstab an einen Körper an; er sagt nicht, daß der Körper so lang ist. 128 Vielmehr ist er gleichsam tot & leistet nichts von dem, was der Gedanke leistet.” Es ist, als hätten wir uns eingebildet, das Wesentliche am lebenden sei die äußere Gestalt, & hätten nun einen Holzblock hergestellt in dieser Gestalt hergestellt verfertigt & sähen mit Beschämung Enttäuschung den toten Klotz, der auch keine Ähnlichkeit mit dem Leben hat.

∕∕

Ich will sagen: “Wenn [e|E]iner die Erwartung // den Vorgang der Erwartung // sehen könnte, müßte er sehen, was erwartet wurde.” – Aber so ist es ja auch: Wer den Ausdruck der Erwartung sieht, sieht was erwartet wird. Und wie könnte man es auf andere Weise, in anderem Sinne, sehen?!

​

¥ ⋎ S. 196.    Der Befehl die Zahlen 1 bis 4 zu quadrieren, wenn ich ihn etwa durch die Tabelle → ausdrücke, kommt uns in gewissem Sinne unvollständig unvollkommen vor; es ist uns, als wäre etwas nur angedeutet, was nicht ausgesprochen ist. ⌊(⌋Nämlich ˇeben die Befolgung⌊.⌋⌊)⌋ des Befehls.⌊)⌋      Es scheint uns, als ob, wenn wir den Befehl verstehen, wir etwas hinzufügen, was die Lücke füllt. So daß wir dem, der uns sagte “aber Du verstehst ihn ja, also ist er ˇja vollständig” antworten können: “Ja, 129 aber nur, weil ich noch etwas hinzufüge: die Deutung nämlich.” – Aber was veranlaßt Dich denn zu gerade dieser Deutung? Ist es der Befehl, dann war er ja schon eindeutig, da er diese Deutung forderte befahl . Oder hast Du die Deutung willkürlich hinzugefügt –, dann hast Du auch den Befehl nicht verstanden, sondern erst das, was Du aus ihm, auf eigene Faust, gemacht hast.    Wir möchten sagen, es sei nur angedeutet, das Zeichen suggeriere nur undeutlich, was wir zu tun hätten. Es sei etwa undeutlich in dem Sinn, in welchem wie der Pfeil → weniger nicht so deutlich ist, als wie ⌊der Pfeil⌋ ↣ Das Zeichen scheint sucht sich wie ein Stummer durch allerlei suggestive Gebärden ⌊ [Neuer Abs] ⌋ Der Dieser Schein von der Unbeholfenheit, mit welcher das Zeichen wie ein Stummer durch allerlei suggestive Gebärden sich verständlich zu machen sucht, – verschwindet, wenn wir bedenken, daß das Zeichen nur in einem grammatischen System seine Funktion hat erfüllt . Für uns ist ˇdann der Befehl vollständig eindeutig deutlich , wenn er unzweideutig ist;c & einen deutlichern gibt es nichtc // & deutlicher kann er nicht sein // . Wir werden den Befehl dann deutlich nennen, wenn er unzweideutig ist.    (Was in der Logik nicht nötig ist, hilft auch nicht.) 130

∕∕

In wiefern kann man den Wunsch als solchen, die Erwartung den Glauben , – ‘unbefriedigt’ nennen? Was ist unser Urbild das Vorbild der Unbefriedigungˇ, das wovon wir unsern Begriff nehmen. Ist es ein Hohlraum eine Hohlform? und würde man von eine[r|m] solchen sagen, sie er er sei unbefriedigt; wäre das nicht auch eine Metapher? Ist es nicht ein Gefühl, was wir Unbefriedigung nennen[?|;] etwa der den Hunger?   Wir können aber in einem bestimmten System des Ausdrucks einen Gegenstand mittels der Worte “befriedigt” & “unbefriedigt” beschreiben. Wenn wir, z.B., festsetz⌊t⌋en den Hohlzylinder den “unbefriedigten Zylinder” zu nennen & den ihn ergänzenden Vollzylinder, seine “Befriedigung”.

∕∕

Es scheint: Die Erwartung & die Tatsache, die die Erwartung befriedigt, passen doch irgendwie zusammen. Man möge soll nun eine Erwartung beschreiben & eine Tatsache, die zusammenpassen, damit man sieht, worin diese Übereinstimmung besteht. Da denkt man sofort an das Passen einer Vollform in eine entsprechende Hohlform. Aber wenn man diese beiden beschreiben will, so sieht man, daß, soweit sie passen eine Beschreibung für beide gilt. (Vergleichen wir dagegen, was es heißt: “diese Hose paßt nicht zu diesem Rock”.)

∕∕ ∕∕

¥ ⋎ S. 133 A Das Seltsame Paradoxe ist darin ausgedrückt, daß, wenn das Ereignis eintritt // wenn dies das Ereignis ist // welches ich erwartet habe, 131 es sich nicht von dem unterscheidet, welches ich erwartet habe. Wenn man also fragt: “Wie unterscheidet sich denn dieser Mensch von dem, den Du erwartet hast; denn in Deiner Erwartung war doch der wirkliche Mensch nicht vorhanden, sonst hättest Du ihn nicht erwarten können”, so ist die Antwort dennoch: dieser Mensch ist der, den ich erwartet habe.   Ich sage: “[g|G]enau so habe ich mir's vorgestellt”; & jemand antwortet etwa: “Das ist unmöglich, denn das eine war eine Vorstellung & das andere ist keine; & hast Du etwa Deine Vorstellung für Wirklichkeit gehalten?” ⌊ Absatz ⌋      Ich sehe wie [e|E]iner das Gewehr anlegt & ich sage: “ich erwarte mir einen Knall Schuß ”. Der Schuß fällt. – Wie, das hast Du Dir erwartet; was also dieser Krach irgendwie schon in Deiner Erwartung? Oder stimmt Deine Erwartung nur in anderer Hinsicht mit dem Eingetretenen überein; war dieser Lärm nicht in Deiner Erwartung enthalten & kam nur als ein Accidens hinzu, als die Erwartung erfüllt wurde? Aber nein, wenn der Lärm nicht eingetreten wäre, so so wäre meine Erwartung nicht erfüllt worden; der Lärm hat sie erfüllt; er kam nicht zu der Erfüllung hinzu, wie ein zweiter Gast zu dem einen den ich erwartet hatte. – War das am Ereignis, was nicht auch in der Erwartung war, ein Accidens, eine Beigabe der Schickung? – Aber was war denn dann nicht Beigabe, – kam den⌊n⌋ irgend etwas vor dem Schuß schon in meiner Erwartung vor? – Und was 132 war denn b Beigabe, – denn hatte ich mir nicht den ganzen Schuß erwartet?     “Der Knall war leiser als ich mir ihn erwartet hatte.” – “Hat es also es in Deiner Erwartung lauter geknallt?”

​

Wie komisch wäre es, zu sagen: ein Vorgang sieht anders “Das Rot, das Du Dir vorstellst, ist doch gewiß nicht [d|D]asselbe – dieselbe Sache – wie das, was Du vor Dir siehst; – wie kannst Du dann sagen , es sei das, was Du Dir vorgestellt hattest?” ‘das ist dasselbe, was ich mir vorgestellt habe’?” – Aber verhält es sich nicht analog ebenso in den Sätzen ist es nicht ähnlich in den Sätzen … “hier ist ein roter Fleck” & “hier ist kein roter Fleck”? In beiden kommt das Wort “rot” vor, also kann dieses Wort nicht das Vorhandensein von etwas Rotem anzeigen. Das Wort “rot” hat eben nur im Satzzusammenhange seine Funktion[; &| . Und] ist nicht das Mißverständnis ˇdies, daß man die Bedeutung des Wortes “rot” für den Sinn eines Satzes nimmt⌊,⌋? welcher sagt, etwas sei rot?

∕∕

¥ ⋎ S 139 A dann ¥S. 138 A   Komisch wäre es, zu sagen: “ein Vorgang sieht anders aus, wenn er geschieht, als wenn er nicht geschieht”. Oder: “Ein roter Fleck sieht anders aus, wenn er da ist, als wenn er nicht da ist; aber die Sprache abstrahiert von diesem diesem Unterschied, denn sie spricht von einem roten Fleck, ob er da ist, oder nicht.”

∕∕

Die Realität ist keine Eigenschaft, die dem 133 Erwarteten noch fehlt & die nun hinzutritt, wenn das Erwartete die Erwartung eintrifft. – Sie Die Realität ist auch nicht wie das Tageslicht, das den Dingen erst Farbe gibt, wenn sie im Dunkeln schon, gleichsam farblos, vorhanden sind.

​

“Wie weißt Du, daß Du einen roten Fleck erwartest[. D.h.| ]:, wie weißt Du, daß ein roter Fleck die Erfüllung dessen ist, was Du Dir erwartest?” Aber ebensogut könnte ich fragen : , “wie weißt Du, daß das ein roter Fleck ist?”    Wie weißt Du, daß, was Du getan hast, wirklich war: das Alphabet im Geist herzusagen? – Aber wie weißt Du, daß, was Du laut hersagst, nun wirklich das Alphabet ist?    Das ist natürlich die gleiche Frage wie die: “Woher weißt Du, daß, was Du [“|‘]rot’ nennst, wirklich dasselbe ist, was der Andre so nennt”. Und die eine Frage ist, wenn sie hat, als eine metaphysisch⌊e⌋ gebraucht wird, ebenso unsinnig, wenig Sinn wie eine andere.

​

⍈ [Zu S. 130] A Die Erwartung verhält sich eben zu ihrer Befriedigung nicht, wie der Hunger zu seiner Befriedigung. Ich kann den Hunger beschreiben, & das was ihn stillt, & sagen, daß es ihn stillt. ¥ ⋎ S. 134 A

​

Du siehst also, möchte ich sagen, an diesen Beispielen, wie die Worte wirklich gebraucht 134 werden.

​

⍈ Zu [Fortsetzung von 133 A zu S. 130] A Und Aber es ist auch nicht so: ich habe den Wunsch nach einem Lust auf einen Apfel; was immer also diesen Wunsch diese Lust stillen wird, werde ich einen “Apfel” nennen.

​

Man könnte meinen: Welcher sonderbare außerordentliche Prozess muß das Wollen sein, daß ich das jetzt wollen kann, was ich erst in fünf Minuten tun werde!    Wie kann ich das Ereignis erwarten; es ist ja noch gar nicht da[!|?]

∕∕

“Sokrates: Wer also vorstellt; was nicht ist, der stellt nichts vor? – Theaitetos: So scheint es. – S.: Wer aber nichts vorstellt, der wird gewiß überhaupt gar nicht vorstellen? – Th.: Offenbar, wie wir sehen.”   Setzen wir in diesem Argument statt des Wortes “vorstellen” etwa das Wort “ bekämpfen töten ”, so gibt es eine Regel für den Gebrauch dieses Worts; es hat keinen Sinn zu sagen: “ich töte etwas, was nicht existiert”. Ich kann mir einen Hirsch auf dieser Wiese vorstellen, der nicht da ist, aber keinen töten, der nicht da ist. Und “sich einen Hirsch ˇauf dieser Wiese vorstellen” heißt: sich vorstellen, daß ein Hirsch da ist. Einen Hirsch töten aber heißt nicht: töten, daß etc.. Wenn aber jemand sagt: “um damit ˇ ◇◇◇ ˇich mir einen Hirsch vorzustellen ˇkann,, muß es ihn doch in einem gewissen Sinne geben”, – so ist die Antwort: nein, es 135 muß ihn dazu in keinem Sinne geben. Und wenn geantwortet würde: “aber die braune Farbe ˇ z.B. muß es doch geben, damit ich sie mir vorstellen kann”, – so ist zu sagen: “es gibt die braune Farbe” heißt überhaupt nichts; außer etwa, daß sie da oder dort als Färbung eines Gegenstands vorhanden ist erscheint , & das ist nicht nötig, damit ich mir einen braunen Hirschen vorstellen kann.

∕∕

⍈ [Zu S. 147]    Etwas tun können erscheint wie ein Schatten des wirklichen Tuns, gerade d wie der Sinn des Satzes als Schatten seiner Verifikation Tatsache, oder das Verstehen des Befehls als Schatten seiner Ausführung. Der Im Befehl wirft die Tatsache gleichsam “ihren Schatten schon voraus”. Dieser Schatten aber, was immer er sein möge, wäre, ist nicht das Ereignis.      Das Dieses schattenhafte antizipieren der Tatsache besteht also darin, daß wir jetzt denken können, daß das eintreffen wird, was erst eintreffen wird. Oder, wie es in irreführender Weise ausgedrückt wird heißt: daß wir jetzt das (oder, an das) denken können, was erst eintreffen wird.     Dieser Fehler ist tief in unsrer Sprache verankert

∕∕

Wir sagen, der Ausdruck der [e|E]rwartung ‘beschreibe’ die erwartete Tatsache, die 136 Erfüllung, ⌊⌊ // Wir reden vom Ausdruck der Erwartung als der Beschreibung der erwarteten Tatsache // ⌋⌋ & denken an sie wie an einen Gegenstand oder Komplex der mit der als Erfüllung ⌊⌊ // & denken an einen Gegenstand oder Komplex der als Erfüllung … // ⌋⌋ der Erwartung in die Erscheinung tritt. – Aber der Erwartete ist nicht die Erfüllung, sondern daß er kommt gekommen ist. .      Der Dieser Fehler ist tief in unserer Sprache verankert: Wir sagen “ich erwarte ihn” & “ich erwarte sein Kommen” & “ich erwarte, daß er kommt”.       ⌊ [Absatz] ⌋ Es ist uns schwer, von der Analogie dem Vergleich loszukommen: Der Mensch tritt ein – das Ereignis tritt ein. Als wäre das Ereignis schon vorgebildet vor der Tür der Wirklichkeit & würde nun in diese (wie in ein Zimmer) eintreten.

∕∕

Ich kann ihn suchen, wenn er nicht da ist, aber ihn nicht hängen auf ihn zeigen, wenn er nicht da ist.    Man könnte sagen wollen: “da muß er doch auch dabei sein, wenn ich ihn suche”. – Dann muß er auch dabei sein, wenn ich ihn nicht finde, & auch, wenn es ihn nicht gibt.

​

Ihn (etwa meinen Stock) suchen, ist eine Art des Suchens & unterscheidet sich davon, daß man etwas anderes sucht, durch das, was man beim Suchen tut (sagt, denkt), nicht durch das was man findet.      Und trage ich beim Suchen ein Bild mit mir oder eine Vorstellung des Gesuchten, – nun 137 gut. Und sage ich, das Bild sei das Bild des Gesuchten, so sagt das nur, welchen Platz das Bild im Vorgang des Suchens einnimmt. Und finde ich ihn & sage “da ist er! den habe ich gesucht”, so sind diese Worte nicht etwa eine Worterklärung für die Bezeichnung des gesuchten Gegenstands (etwa für die Worte “mein Stock”), die erst jetzt, wo er gefunden ist, gegeben werden könnte.

∕∕

“Den hast Du gesucht? Du konntest ja nicht einmal wissen, ob er da ist!” Vergleiche dagegen das Suchen nach der Dreiteilung des Winkels.)

∕∕ /

Man kann vom Träger eines des Namens sagen, daß er nicht existiert; & das ist natürlich keine Tätigkeit, obwohl man es mit einer vergleichen verwechseln könnte & sagen, ⌊:⌋ er müsse doch dabei sein, wenn er nicht existiert. (Und das ist von einem Philosophen bestimmt schon einmal geschrieben worden.)

∕∕

Der Gedanke, daß uns erst das Finden zeigt, was wir gesucht, erst die Erfüllung des Wunsches was wir gewünscht haben, heißt den Vorgang so beurteilen, wie die Symptome der Erwartung, oder des Suchens bei einem Andern. Ich sehe ihn unruhig in seinem Zimmer auf & ab gehen; da kommt jemand zur Tür herein 138 & er wird ruhig & gibt Zeichen der Befriedigung; & nun sage ich: “er hat offenbar diesen Menschen erwartet”.   Die Symptome der Erwartung sind nicht der Ausdruck der Erwartung.

∕∕

⍈ ˇ[Zu S. 132] ⌊ A ⌋ ˇHierher gehört auch: Wenn wir Einem sagen “stelle Dir die Farbe Rot vor” so soll wird er etwa versuchen sich etwa einen roten Gegenstand Fleck vorzustellen, aber nicht: sich einen grünen⌊,⌋ vorzustellen, weil er dieser nich⌊t⌋ rot ist.   ⌊(⌋Könnte man zur Erklärung des Wortes “rot” auf etwas weisen, was nicht rot ist? Das wäre ähnlich w⌊i⌋e wenn man Einem, der der deutschen Sprache nicht mächtig ist, das Wort “bescheiden” erklären sollte & man zeigte zur Erklärung auf einen sehr arroganten Menschen & sagte: “dieser ist nicht bescheiden.”. Es ist kein Argument gegen eine solche Erklärungsweise, daß sie vieldeutig ist. Jede Erklärung kann mißverstanden werden. (Vergleiche: Der Wegweiser dessen Hand entgegen der Wegrichtung weist.) ¥ ⌊ ⋎ S. 197 ⌋    ( Es könnte z.B. Menschen geben, die zur Erklärung … Man könnte z.B. zur Erklärung eines Farbworts ˇimmer auf die komplementäre Farbe weisen zeigen ; aber ohne vorher abzumachen, daß man auf sie die komplementäre zeigen werde: wie man ja jetzt heute auch nicht abmacht, daß man auf d die gleiche Farbe zeigt. einen Gegenstand von der Farbe selbst zeigt. ) Vergleiche auch den Wegweiser dessen 139 Hand entgegen der Wegrichtung zeigt weist .⌊)⌋

​

⍈ [Zu S. 132] A Unser ˇDie Möglichkeit dieses Mißverständnis⌊ses⌋ liegt äußert sich auch darin, daß es doppelsinnig ist, in dem Doppelsinn der Ausdrucksweise vo[m|n] “Vorkommen ⌊“⌋der Farbe Rot in zwei Sachverhalten als deren dem dem gemeinsamen Bestandteil” zu reden zweier Tatbestände”⌊.⌋ zu reden. Dies kann heißen, daß in beiden etwas rot ist, die Farbe rot hat. // In dem einen Fall heißt das es , daß sowohl da wie dort etwas rot ist, ˇetwas die Farbe Rot hat // Im andern Fall handelt es sich nicht um eine Gemeinsamkeit der Farbe (die ja durch eine Farbangabe ausgedrückt würde). // Dies kann heißen, daß in beiden etwas rot ist, die Farbe [r|R]ot hat; aber auch, daß zwei Sätze von der Farbe Rot handeln. //    Diese Gemeinsamkeit ˇim letzteren Fall ist die Harmonie zwischen Wirklichkeit & Gedanken, welcher der in Wahrheit eine Form unserer Sprache entspricht.

∕∕

In der Sprache berühren sich Erwartung & Erfüllung.

∕∕

Man hat vielleicht das Gefühl, daß man sich im Satz “ich erwarte, daß er kommt” der Worte “er kommt” in anderem Sinne bedient, als in der Behauptung “er kommt”. Aber wäre es so, wie könnte ich davon reden, daß meine Erwartung 140 in Erfüllung gegangen ist? ¥ • ⌊⌊ Aber nun sage ich vielleicht beim auf & ab gehen “Ich erwarte, daß er herein kommt”. – Nun ist eine [a|A]hnlichkeit vorhanden! Aber welcher Art ist sie?! ⌋⌋    Nun könnte man aber fragen: Wie schaut das aus, wenn er kommt? – Es geht die Tür auf, ein Mann tritt ein, etc.. Wie schaut das aus, wenn ich erwarte, daß er kommt? – Ich gehe im Zimmer auf & ab, sehe vielleicht z⌊u⌋weilen nach der Tür auf die Uhr, etc.. – Aber der eine Vorgang hat ja mit dem andern nicht die geringste Ähnlichkeit! Wie kann man dann dieselben Worte zu ihrer Beschreibung gebrauchen? ⌊ Wo ist denn hier Hohlform & Vollform? ◇◇◇ ⌋   Aber in meinem Zimmer auf- & ab gehen konnte ich doch auch ohne zu erwarten, daß er kommen werde, & auch auf die Uhr sehen, etc.. Diese Vorgänge würde ich nicht mit den Worten “ich erwarte, daß er kommt” beschreiben. Worin läge es denn z.B., daß ich gerade ihn erwarte? Ich sagte doch, der Vorgang der Erwartung sollte ein solcher sein, daß man ich aus ihm ersehen müßte, was erwartet wird.    Will Nennt man jene erwartenden Handlungen die Erwartung nennen , dann ,, dann ist sie ein Hunger & die Erfüllung der Erwartung ist das, was den Hunger stillt.     Was uns interessiert ist die Erwartung als Gedanke, also als Ausdruck der Erwartung. ⍈ ↺      Und die Worte “er kommt” bedeuten dasselbe im Ausdruck der Erwartung & in der Beschreibung der Erfüllung, denn wenn ich die beiden Worte erklären wollte, etwa durch eine hinweisende Erklärungen % 141 so würden diese die gleichen Erklärungen für beide Sätze gelten.

​

¥ ⋎ S. 149 A   Wenn wir sagen: “[i|I]ch habe ihn den ganzen Tag erwartet⌊.⌋”, so Hier ist hier mit “erwarten” kein Dauerzustand gemeint der den Erwarteten & sein Kommen als Bestandteile enthielte, sondern eine eine Folge von Handlungen, Gefühlen & Gedanken gemeint; kein Dauerzustand der den Erwarteten & sein Kommen als Bestandteile enthielte. Kein Gedanken in amorpher Form.

​

Wir fragen also Wenn wir den Satz “ich erwarte, daß er kommt” verstehen wollen, – fragen wir uns : Was ist das Kriterium dafür, daß, was wir tun, ist, ihn zu erwarten?   Wie weiß ich, daß ich: ihn erwarte?    Und das gleiche selbe kann ich von der Intention sagen. Warum nennen wir das was wir in dieser Situation tun “ihn erwarten”? Welche Bestimmungen treffen wir über den Gebrauch des Worts “erwarten”? Nennen Wollen wir unsere Gedanken die Erwartung ˇnennen, , oder ist soll es eine Hypothese ˇsein, daß wir gerade das erwarten; geht, was wir erwarten, aus gewissen Handlungen hervor (z.B. daraus, daß ich die Speise vorbereite zu einer Mahlzeit statt nur eines Gedeckes ⌊für mich⌋ zwei Gedecke vorbereite & die Speise, die N.N. besonders gerne hat), oder heißt nenne ichist es, den N. erwarten, wenn ich unter ganz bestimmten Umständen, etwa z.B. nachdem ich mich mit ihm auf 5 Uhr verabredet habe, 142 um diese Stunde allein in meinem Zimmer sitze etc. etc.?

​

¥ ⋎ [S. 198 & das Folgende ˇbis S. 201 zum Strich] ¥ ⋎ S. 150 A ¥ B , ¥ S. 201 A, B.]    Das Gleiche ist von der Intention zu sagen. Wenn eine Vorrichtung als Bremse wirken soll, tatsächlich aber, aus irgend_welchen Ursachen den Gang der Maschine nicht verzögert, so ist die Absicht, der die Vorrichtung dienen soll aus ihr & ihrer Wirkungsweise allein nicht ˇunmittelbar zu erkennen. Wenn man sagt: “das ist eine Bremse, sie funktioniert aber nicht”, so spricht man von der Absicht. – Wenn es nun aber so wäre, daß immer dann, wenn die Vorrichtung nicht als Bremse funktioniert, eine bestimmte Person ärgerlich würde, –◇◇◇ wäre nun in dieser Wirkungsweise die Intention der Vorrichtung ˇnicht ausgesprochen? Nein, denn nun könnte man sagen, daß der Hebel einmal die … ˇaber Bremse, einmal den Ärger betätigt? Denn Denn wie drückt es … Wie nämlich drückt es sich aus, daß jener Mensch er darüber ärgerlich wird ist , daß der Hebel die Bremse nicht betätigt. Denn, argerlich “[s|S]ich darüber ärgern, daß die Vorrichtung nicht so funktioniert”, heißt nämlich wieder doch etwas ähnliches wie, “wünschen, daß sie so funktioniert”. – Und wir haben hier das alte Problem, welches wir so ausdrücken möchten : :⌊,⌋ “daß der Gedanke, daß p der Fall ist, nicht voraussetzt, daß es der Fall sei ist ; daß aber ande⌊r⌋seits doch etwas 143 an der Tatsache für die Möglichkeit des Gedankens den Gedanken selbst [v|V]oraussetzung sein muß, – ⌊ (⌋ich kann nicht denken, daß etwas rot ist, wenn die Farbe Rot nicht existiert)”. Es ist das Problem der Harmonie zwischen Welt & Gedanken. – Man kann darauf antworten, daß die Gedanken im selben sind sein müssen, wie das Zweifelhafte & an diesem anligen wie der Maßstab an dem Gemessenen. , wenn auch an einer andern Stelle. Im Raum der Sprache nämlich. ⌊ [Absatz] ⌋   Denn eigentlich will ich doch sagen, : daß der Wunsch, ‘er möchte kommen’ der Wunsch ist, daß: wirklich er wirklich kommen möge Und ; & wollte man eine weitere Erklärung dieser Beteuerung Versicherung haben, so würde⌊n⌋ würde man man ich wir sagen: “& unter “‘er’” verstehe ich diesen da, & mit ‘“kommen”’ meine ich diese Handlung das …”[:|.] Aber das sind eben Erklärungen der Grammatik, Erklärungen, die die Sprache schaffen. konstituieren. [Absatz] ¥ • Der Satz “ich könnte nicht denken, daß etwas rot ist, wenn Rot nicht existierte” meint wirklich die bezieht sich wirklich auf die Vorstellung von etwas Rotem, oder die Existenz eines roten Musters, als Teil unserer Sprache. Aber natürlich kann man auch nicht sagen, unsere Sprache müsse ein solches Muster enthalten. Enthält sie es nicht, so ist sie eben eine [a|A]ndere. Aber man kann sagen & betonen, daß sie es enthält.

​

⍈ ↺ [Als eigener Absatz] In der Sprache wird alles ausgetragen.

​

Es ˇkann nun schein[t|e]⌊n⌋ nun als Es kann nun scheint nun, ˇ irgendwie, : als würde man die Intention, von 144 außen betrachtet, nie als Intention erkennen; als müsste man sie selbst meinen intendieren , um sie als Meinung zu verstehen. (Und das ist einesteils so, als wollte man sagen, man könne Zahnschmerzen nur von innen betrachtet als solche erkennen.) – Es heißt die Intention nicht als Phänomen, nicht als Tatsache zu betrachten. Und hier erinnert die Intention an den Willen (auch im Schopenhauer'schen Sinn). Jedes Phänomen scheint uns tot im Gegensatz Vergleich zum lebenden Gedanken.   Man muß aber den Gedanken, die Intention⌊,⌋ ˇ “von außen betrachtet”⌊,⌋ als solche verstehen: ; ohne ˇnämlich über eine die Bedeutung ˇin ihnen unterrichtet zu werden. D.h.: Wenn man den Gedanken betrachtet, so kann nicht mehr von einem Verstehen die Rede sein; denn, sieht man ihn, so muß man ihn als den Gedanken dieses Inhalts erkennen; es ist nichts zu deuten. – Aber so ist es ja wirklich: wenn wir denken, da wird nicht gedeutet. –

∕∕

¥ ⋎ [von S 202 nach dem Strich bis S. 227 zum Strich]        In der Sprache wird alles ausgetragen.       Die Erfüllung der Erwartung besteht nicht darin, daß ein Drittes geschieht, das man, außer eben als “die Erfüllung dieser Erwartung” auch noch anders beschreiben könnte, also z.B. etwa als ein Gefühl der Befriedigung, oder der Freude, oder wie immer. Die Erwartung, daß p der Fall 145 sein wird ist das Gleiche wie die Erwartung der Erfüllung jener der Erwartung.    Könnte die Rechtfertigung einer Handlung als Befolgung eines Befehls so lauten: “Du hast gesagt ‘bring mir eine gelbe Blume’, & diese hier hat mir daraufhin ein Gefühl der Befriedigung gegeben, darum habe ich sie gebracht”? Müßte man da nicht antworten: “Ich habe Dir doch nicht geschafft, mir die Blume zu bringen, die Dir auf meine Worte hin ein solches Gefühl geben wird!”

​

(Ich gehe die gelbe Blume suchen. Auch wenn mir während des Suchens ein Bild vorschwebt, – brauche ich es denn, wenn ich die gelbe Blume – oder eine andere – sehe? – Und wenn ich sage: “sobald ich eine gelbe Blume sehe, schnappt, gleichsam, etwas in dem Gedächtnis ein”, – wie etwa im Schlagwerk einer Uhr ein Hebel in die ◇◇◇ ˇ Nut eines Zahn[r|R]ades kann ich denn dieses Einschnappen eher voraussehen, erwarten, als die gelbe Blume? – Wenn es auch in einem bestimmten Fall wirklich so ist, daß ich nicht das Gesuchte, sondern ein anderes (indirektes) Kriterium erwarte, so ist dies jedenfalls keine Erklärung des Erwartens.)

​

Aber geht nicht mit dem Eintreffen des Erwarteten immer ein Phänomen der Zustimmung (oder Befriedigung) zusammen? – Ist dieses Phänomen ein anderes, als das Eintreten des Erwarteten? Wenn ja, dann weiß ich nicht, ob so ein Phäno- 146 men die Erfüllung immer begleitet.     Wenn ich sage: der, dem die Erwartung erfüllt wird, muß doch nicht ausrufen “ja, das ist es”⌊,⌋ (oder dergleichen, – so kann man mir antworten: “Gewiß, aber er muß doch wissen, daß die Erwartung erfüllt ist”. – Ja, soweit das dieses Wissen dazu gehört, daß sie erfüllt ist. – “Wohl, aber wenn Einem eine Erwartung erfüllt wird, so tritt doch immer eine Entspannung ein auf !” – Woher weißt Du das? // Wie kann man das wissen? //

∕∕ ?

Eine Die Beschreibung der Sprache muß dasselbe leisten, wie die Sprache. “Denn dann kann ich wirklich aus dem Satz, der Beschreibung der Wirklichkeit, ersehen, wie es sich in ˇder Wirklichkeit verhält.” – – Aber nur das nennt man ja “Beschreibung”, & nur das nennt man ja “ersehen, wie es sich verhält”! ˇUnd [E|e]twas anderes ist es ja nicht, was wir je damit sagen: gesagt wird: daß wir aus der Beschreibung ersehen, wie es sich in Wirklichkeit verhält.    “ ⌊“⌋Du beziehst von dem Befehl die Kenntnis dessen, was Du zu tun hast. Und doch gibt Dir der Befehl nur sich selbst, & auf seine Wirkung kommt es nicht an.” Aber hier werden wir eben von der Ausdrucksweise unserer Sprache irregeleitet, wenn sie sagt “die Kenntnis dessen”, oder “die Kenntnis der Handlung”. Denn es ist also, als ob dieses Etwas, die Handlung, ein Ding wäre, das in der Befolgung des Befehls in ⌊(⌋die⌊)⌋ Existenz 147 treten solle, & als ob der Befehl uns eben dieses Ding kennen lehrte, also zeigte; so daß er es also schon in irgend einem Sinne in die Existenz riefe. (Wie kann der Befehl – die Erwartung – uns einen Menschen zeigen, ehe er in unser Zimmer eingetreten ist?!)

/? / \

Wenn man sagt, aus dem Befehl ist sei die Handlung zu entnehmen, die ihn befolgt, aus dem Satz die Tatsache die ihn wahr macht, – was ist denn aus dem Satz zu entnehmen, außer er selbst. [o|O]der wie kann man denn aus ihm dem Befehl die Handlung ableiten ehe sie geschieht? außer man meint eine andere Form der Beschreibung jener Handlung, wie wenn ich etwa nach dem Befehl eine Zeichnung der Handlung anfertige. – Aber auch diese weitere Beschreibung ist erst da, wenn ich sie abgeleitet habe & nicht steckt nicht schon schattenhaft im Befehl selbst.

​

¥ ⋎ S. 135 [neuer Absatz]    Das Denken mit seiner Anwendung geht [sc|Sc]hritt für Schritt als Kalkül vor sich. – Wieviele Zwischenstufen ich auch zwischen den Gedanken & die Anwendung setze, immer folgt eine Zw⌊i⌋schenstufe der nächsten – & die Anwendung der letzten – ohne Zwischenglied. Hier haben wir den gleichen Fall, wie wenn wir zwischen Entschluß 148 & Tat durch Zwischenglieder vermitteln möchten // wollen // .

∕∕ v

Die Doppeldeutigkeit Zweideutigkeit unserer Ausdrucksweise: Wenn uns ein Befehl in einer Chiffre gegeben wäre & auch der Schlüssel zur Übersetzung in's Deutsche, so würden wir könnten wir das den Vorgang des Bildens de[s|n] deutschen Befehls nennen zu bilden, mit den Worten bezeichnen: “aus der Chiffre ableiten, was wir zu tun haben” ˇoder “ableiten, was die Befolgung des Befehls ist”.. Wenn wir anderseits nach dem Befehl handeln, ihn befolgen, so kann man auch hier von einem Ableiten der Befolgung reden.

v

Wir können die Brücke zur Befolgung nicht überschreiten, ehe als bis wir bei ihr angelangt sind. // ehe wir dort sind. //

​

⌊ ⌋ Wenn der Gedanke ein Bild ist, so ersch[ei|ie]n[t|e] unsere die Beschäftigung mit diesem Bild // Die Unsere Beschäftigung mit dem Bild des Gedankens erscheint als ˇbloßes Spiel, wenn sie sich nicht mit der uns interessierenden Wirklichkeit befaßt // , wenn sie nicht mit der … Wirklichkeit operiert // . Wenn ich erwarte daß er zur Tür hereintreten Man kann sagen, die Erwartung ist eine vorbereitende Handlung. – Und Wenn unsere Erwartung, unser Denken, ein Spiel ist, // ein selbständiges Spiel ist, // warum sollte unsc gerade dieses Bild Phantasiebild interessieren, wo wir uns doch sonst mit Seelenzuständen, 149 Magenschmerzen, etc. nicht b⌊e⌋fassen. ((Wozu denken wir, wozu ist es nütze?)) ⌊⌊ Was wir wissen wollen ist: Was hat der Gedanke mit dem zu tun, was außerhalb dem Gedanken vorfällt? ⌋⌋ Was hat das, was ich denke, mit dem zu tun, was der Fall ist?

​

¥ ⋎ S. 228    Der Kalkül des Denkens knüpft mit der Wirklichkeit außerhalb dem Denken des Denkens an. ⌊ Absatz ⌋       Von der Erwartung zur Erfüllung ist … Vom Befehl zu seiner Ausführung ist ein Schritt einer Rechnung. Ja, die Rechnung 25 × 25 50 125 steht zu ihrem Resultat 625 genau im Verhältnis des Befehls der Erwartung zur Ausführung Erfüllung. Und soweit – & nur soweit – als diese Rechnung ein Bild des Resultats ist, ˇist auch der Befehl die Erwartung ein Bild der Ausführung Erfüllung. Und … (die Erwartung ein Bild der Erfüllung). soweit das Resultat von durch die Rechnung bestimmt ist, soweit ist die Befolgung Erfüllung durch den Befehl die Erwartung bestimmt.

​

⍈ ˇ[Zu S 141 A Von der Erwartung ⌊,⌋ ˇder Erwartung als Gedanke kann man sagen, daß sie eine vorbereitende, erwartende, Handlung ist. Sie streckt, wie ein Ballspieler, die Hände aus, richtet sie vor her , um den Ball zu empfangen⌊.⌋, der kommen soll.

​

150 ⍈ ˇ[Zu S. 142 ⌊ A ⌋ Wenn ich jemanden erwarte, – was geschieht? – Ich finde etwa in meinem Kalender beim heutigen Datum seinen Namen N & den Vermerk “5 h ”. Ich sage zu jemand anderem “ich kann heute nicht zu Dir kommen, weil ich N erwarte.” Ich mache Vorbereitungen ˇwie zum Empfang eines Gastes. Ich überlege: “raucht N?” & erinnere mich, ihn rauchen gesehen zu haben & stelle Zigarren zurecht. Nahe an 5 h sage ich zu mir: “jetzt wird er gleich kommen”, & dabei stelle ich mir einen Menschen vor der ungefähr aussieht wie N; dann stelle ich mir vor, wie er in's Zimmer tritt & wie ich ihn begrüße & beim Namen nenne. Das & ähnliches heißt: Das ˇSo ein Vorgang & vieles mehr oder weniger Ähnliche heißt: … “das Kommen des N erwarten”. ⌊ Nein! Denn “ich erwarte Dich” heißt nicht daß ich in dieser Weise handle. Solche Vorgänge & ähnliche sind Vorgänge des Erwartens. ⌋

​

⍈ [Zu S. 142 B        Ist der Hunger der Wunsch nach dem Essen? Aber warum nicht bloß der Wunsch nach dem Aufhören des Hungers [?|,] , wodurch immer dies es bewirkt werden mag? – Aber welche Erscheinung ist der Wunsch, – we⌊l⌋che nennt man “den Wunsch nach dem Essen”? Wenn ich Hunger habe; & ich suche in einer Lade, wo gewöhnlich etwas Essbares zu finden ist; & die Lade ist leer & ich werde ärgerlich; & nun sage ich vielleicht zu mir: “wo könnte ich noch etwas finden⌊?⌋”; endlich kommt jemand & ich sage: “ich möchte etwas essen”. 151

∕∕

Wenn ich in der Sprache denke, so schweben mir nicht neben ⌊dem⌋ sprachlichen Ausdruck noch die Bedeutungen vor; sondern die Sprache selbst ist das Vehikel der Gedanken // des Denkens // .       In der Sprache wird alles ausgetragen.

∕∕ v

Inwiefern nimmt antizipiert denn der Befehl die Ausführung? – Dadurch, daß er das jetzt befielt, was später ausgeführt wird? Aber es müßte ja heißen: “⌊…⌋ was später ausgeführt wird, oder nicht ausgeführt wird”. Und das sagt nichts.      “Aber, wenn auch mein Wunsch nicht bestimmt, was der Fall sein wird, so bestimmt er doch sozusagen das Thema einer Tatsache, ob die nun den Wunsch erfüllt, oder nicht.” Wir wundern uns – gleichsam sozusagen – nicht darüber, daß Einer die Zukunft weiß, sondern darüber, daß er überhaupt prophezeien kann (richtig oder falsch).     Als nähme die bloße Prophezeiung, (ˇgleichgültig ob richtig oder falsch)⌊,⌋ schon einen Schatten der Zukunft voraus⌊.⌋, – Während sie über die Zukunft nichts weiß; & weniger als nichts nicht wissen kann.

∕∕ v

Wenn man nun fragt: Ist also die Tatsache durch die Erwartung auf ja & nein bestimmt, oder nicht, – d.h., ist es bestimmt, in welchem Sinne die Erwartung durch ein Ereignis – welches immer 152 eintrifft eintreffen mag – beantwortet werden wird, – so muß man antworten: Ja! [u|U]nbestimmt kann man das Ereignis nennen wenn nicht der Ausdruck der Erwartung unbestimmt ist, insofern er z.B. eine Disjunktion verschiedener Möglichkeiten enthält. ist.

​

In der Sprache wird alles ausgetragen.

v

“Der Satz ‘p’ bestimmt doch schon im Voraus, was ihn wahr machen wird”. Gew⌊i⌋ß, der Satz ‘p’ bestimmt, daß p der Fall sein muß um ihn wahr zu machen; & das heißt:     (der Satz p) = (der Satz, den die Tatsache p wahr macht) Und die Aussage, daß der Wunsch, daß p der Fall sein möge, p möge der Fall sein, durch das Ereignis p befriedigt wird, sagt nichts . Es sei denn ; außer als ˇeine Zeichenregel: (der Wunsch daß p der Fall sein möge) = (der Wunsch, der durch das Ereignis die Tatsache p befriedigt wird)

∕∕ v

Wie alles Metaphysische ist die Harmonie zwischen Gedanken & Wirklichkeit in der Grammatik der Sprache aufzufinden.

v ∕∕

Was macht uns glauben Statt ˇHarmonie, Übereinstimmung der von Gedanken mit der & Wirklichkeit 153 könnte man hier ruhig sagen: Bildhaftigkeit der Gedanken. Ist aber die Bildhaftigkeit eine Übereinstimmung? In der Abhandlung hatte ich so etwas gesagt wie: sie ist eine Übereinstimmung der Form. Das ist aber irreführend. Alles    Alles kann ein Bild von allem sein: wenn wir den Begriff des Bildes entsprechend ausdehnen. Und sonst müssen wir eben erklären sagen , was wir ein Bild von etwas nennen, & damit auch, was wir noch die Übereinstimmung der Bildhaftigkeit, die Übereinstimmung der Formen nennen wollen.    Denn, was ich sagte, kommt ja eigentlich darauf hinaus: daß jede Projektion, nach welcher Methode immer, etwas mit dem Projizierten gemeinsam haben muß. Aber das sagt nur, daß ich hier den Begriff des ‘gemeinsam habens’ ausdehne & ihn dem allgemeinen Begriff des Projizierens äquivalent mache. Ich mache also nur auf eine Moglichkeit der Verallgemeinerung aufmerksam (was freilich sehr wichtig sein kann). ⌊ Die Übereinstimmung von Gedanken & Wirklichkeit liegt darin, daß, wenn ich fälschlich sage, etwas sei rot, es doch immerhin nicht rot ist. Und wenn ich Einem das Wort “rot” im Satze “[d|D]as ist nicht rot” erklären will, ich dazu auf etwas Rotes zeige. ⌋

∫ ∫ ∫ ∫

In welchem Sinne kann ich sagen, der Satz sei ein Bild? Wenn ich darüber denke, möchte ich sagen: er muß ein Bild sein, damit er mir zeigen kann, was ich tun soll; damit ich mich nach ihm richten kann. Aber dann willst Du also bloß sagen, daß Du Dich nach dem Satz richtest 154 in dem Sinne, in welchem Du Dich nach einem Bild richtest.      Zu sagen, daß der Satz ein Bild ist, hebt gewisse Züge in der Grammatik des Wortes “Satz” hervor. ⌊⌊ Absatz ⌋⌋     Das Denken ist ganz dem Zeichnen von Bildern zu vergleichen. ⌊⌊ Absatz ⌋⌋     Man kann aber auch sagen, daß das, was wie ein Vergleichsobjekt erscheint des Gedankens, oder des Satzes, erscheint, in Wirklichkeit ein besonderer Fall ⌊,⌋ ˇein Beispiel ⌊,⌋ der unseres allgemeinern Idee ◇◇◇ ˇBegriffs ist. Wenn ich den Satz mit einem Maßstab verglichen habe, so habe ich, strenggenommen, einen Satz, der mit Hilfe eines Maßstabs die Länge eines Gegenstands angibt, // so habe ich, strenggenommen, eine die Längenangabe mit Hilfe eines Maßstabes // als Beispiel für alle Sätze gebraucht herangezogen .

∕∕

Sinn des Satzes, Sinn eines Bildes. Wenn wir den Satz mit einem Bild vergleichen, so müssen wir bedenken, ob mit einem Portrait (einer historischen Darstellung), oder mit einem Genrebild. Und beide Vergleiche haben Sinn. (Sätze in Dichtungen entsprechen Genrebildern.)      “Wenn ich ein Genrebild anschaue, so ‘sagt es mir etwas’, auch wenn ich keinen Augenblick glaube (mir einbilde), die Menschen, die ich darin sehe seien wirklich, oder, es habe wirkliche Menschen 155 in dieser Situation gegeben,⌊.⌋ von denen dies ein verkleinertes Bild sei ist ” ‘Es sagt mir etwas’ kann aber hier nur heißen, es ich habe eine bestimmte Einstellung dazu, sehe es in bestimmter Weise. Denn wie, wenn ich fragte: “was sagte es mir denn?” ⌊ ¥ ⋎ S. 228 ⌋      Bedenke die gänzlich verschiedene Grammatik der Ausdrücke:        “dieses Bild stellt Leute in einer Dorfschenke dar”, und        “dieses Bild stellt die Krönung Napoleons dar”.

​

(Sokrates: “Und wer vorstellt, sollte nicht etwas vorstellen?” – Theaitetos: “Notwendig.” – Sok.: “Und wer etwas vorstellt, nichts Wirkliches?” – Th.: “So scheint es.”)

​

¥⋎ [S. 228 und ¥S. 1 – 34 Bd XI zum Strich]     Wenn man es für selbstverständlich hält, daß sich der Mensch ⌊an⌋ seiner Phantasie vergnügt, so bedenke man man , daß diese Phantasie nicht einem gemalten Bild oder … ähnlich ist; sondern … wie ein gemaltes Bild oder plastisches Modell ist; sondern ein kompliziertes Gebilde aus heterogenen Bestandteilen: Wörtern, Bildern, u.a.. Man wird dann das Operieren mit Schrift – & Laut[z|z]eichen nicht mehr in Gegensatz stellen zu dem Operieren mit “Vorstellungsbildern” der Ereignisse.

∫ ∫

Die Illustration in einem Buch gesellt sich zum Wort, wie ein verwandter Behelf zu⌊m⌋ 156 einem andern . (Die Häßlichkeit eines Menschen kann im Bildˇ, im gemalten, abstoßen, wie in der Wirklichkeit, aber auch in der Beschreibung, in den Worten.)

​

Die Stellungnahme zu dem Bild (dem Gedanken), – wie wir das Bild erleben, das macht uns das Bild es uns zur Wirklichkeit⌊.⌋, verbindet es mit der Wirklichkeit D.h., ˇdas verbindet es mit der Wirklichkeit; stellt eine Kontinuität mit der Wirklichkeit her.   (Die Furcht verbindet das Bild mit den dem Schrecken der Wirklichkeit.)

∕∕ v

Kann eine hinweisende Erklärung mit den übrigen Regeln der Anwendung eines Wortes kollidieren? Denn so könnte es scheinen; aber Regeln können doch … – Denn Regeln können doch nicht kollidieren, außer sie widersprechen einander. Denn im Übrigen bestimmen sie ja eine Bedeutung, & sind keiner verantwortlich, so daß sie ihr widersprechen könnten.

∫

Die Grammatik ist keiner Wirklichkeit Rechenschaft schuldig. Die grammatischen Regeln bestimmen erst die Bedeutung (konstituieren sie) & sind darum keiner Bedeutung verantwortlich & ⌊in⌋sofern willkürlich. 157

∕∕

Es kann keine Diskussion darüber geben, ob diese Regeln oder andere die richtigen für das Wort “nicht” sind (d.h. ob sie seiner Bedeutung gemäß sind). Denn das Wort hat ohne diese Regeln noch keine Bedeutung, & wenn wir die Regeln ändern, so hat es nun eine andere Bedeutung (oder keine) & wir können dann ebensogut auch das Wort ändern. Daher sind diese Regeln willkürlich, weil die Regeln erst das Zeichen machen.

​

⍈     “Das einzige Korrelat in der Sprache zu einer Naturnotwendigkeit ist eine willkürliche Regel. Sie ist das einzige, was man von dieser Notwendigkeit in einen Satz abziehen kann.” ⌊ [Vielleicht zu dem Paradox daß die Mathem. aus Regeln besteht.] ⌋

​

Warum nenne ich die Regeln des Kochens nicht willkürlich; & warum bin ich versucht, die Regeln der Grammatik willkürlich zu nennen? Weil das Kochen durch seinen Zweck definiert ist, die S dagegen die Sprache nicht. Weil ich den Begriff des ⌊‘⌋Kochens⌊’⌋ durch den Zweck des Kochens definiert denke, dagegen den Begriff der ⌊‘⌋Sprache⌊’⌋ nicht durch den Zweck der Sprache. Darum ist der Gebrauch der Sprache in ˇeinem gewisse[m|n] Sinne autonom, in dem das Kochen & Waschen es nicht ist. Wer Denn, wer sich beim Kochen nach andern als den richtigen Regeln richtet kocht schlecht; aber wer sich nach andern Regeln als denen des Schach richtet, spielt ein 158 anderes Spiel; & wer sich nach andern grammatischen Regeln richtet, als etwa den üblichen, spricht darum nichts Falsches, sondern von etwas Anderem.

​

Wenn ich dem Holzblock eine bestimmte Form geben will, so ist der Hieb der richtige, der diese Form erzeugt. Ich nenne aber nicht das Argument das richtige, das die gewünschten Folgen hat. (Pragmatism.) Vielmehr nenne ich die Rechnung falsch, obwohl die Handlungen, die dem Resultat entsprungen sind, zum gewünsch⌊t⌋en Ende geführt haben. (Vergleiche den Witz: “Ich mach' den Haupttreffer & er will mich belehren⌊!⌋”.) Das Zei zeigt, daß die Rechtfertigungen in den beiden Fällen verschieden sind, & also daß “Rechtfertigung” verschiedenes in den beiden bedeutet. In einem Fall kann man sagen: “Wart' nur, Du wirst schon sehen, daß [s|d]as Rechte ˇ(d.h. gewü[ü|n]schte) herauskommt”; im andern ist dies keine Rechtfertigung.

​

Wenn man von der Willkürlichkeit der grammatischen Regeln spricht, so bedeutet das, daß es die Rechtfertigung, die in der Grammatik als solcher liegt, nicht für die Grammatik gibt.

​

Die Regeln der Kochkunst hängen mit der 159 Grammatik des Wortes “Kochen” anders zusammen, als die Regeln des Schachspiels mit der Grammatik des Wortes “Schachspielen” & als die Regeln des Multiplizierens mit der Grammatik des Wortes “multiplizieren”.

​

Die Regeln der Grammatik sind in demselben Sinne willkürlich, wie die Wahl einer Maßeinheit. Aber das kann doch nur heißen, daß sie von der Länge des Objekts der Messung unabhängig ist[.|;] Uund daß nicht die Wahl der einen Einheit ‘wahr’, der andern ‘falsch’ ist, wie die Angabe der Länge wahr oder falsch ist. Das ist natürlich nur eine Bemerkung über die Grammatik des Wortes “Längeneinheit”.

​

Man ist versucht, die Regeln der Grammatik durch Sätze zu ◇ rechtfertigen, indem man z.B. sagt: “aber es gibt doch wirklich 4 primäre Farben”. Und gegen die Möglichkeit dieser Rechtfertigung richtet es sich, wenn wir sagen, daß … sich das Wort, daß die Regeln der Grammatik willkürlich sind. Kann man aber nicht doch sagen, daß die Grammatik der Farbwörter die Welt, wie sie tatsächlich ist, charakterisiert? Man möchte sagen: kann ich nicht wirklich vergebens nach einer fünften primären Farbe suchen? (Und wenn man suchen kann, dann ist ein Finden denkbar.) Nimmt nicht die Grammatik man nicht die primären Farben zusammen, weil sie eine 160 Art von Ähnlichkeit haben? oder doch die Farben im Gegensatz zu den Formen & Tönen? Oder habe ich, wenn ich diese Einteilung der Welt als die richtige hinstelle, schon eine vorgefaßte Idee als Paradigma im Kopf? Von der wir ich dann sagen kann: “das ist die Weise, wie wir die Dinge betrachten”; oder “wir wollen eben ein solches Bild der Dinge machen”. Wenn ich nämlich sage: “die ˇprimären Farben haben doch eine bestimmte gewisse Ähnlichkeit miteinander”, – woher nehme ich den Begriff dieser Ähnlichkeit? Nicht nur von den 4 primären Farben? Ist nicht so, wie der Begriff ‘primäre Farbe’ nichts andres ist als ‘blau[,| o]der rot oder grün oder gelb’, auch der Begriff jener Ähnlichkeit nur durch die vier Farben gegeben? ⌊ // Ist nicht so, wie der Begriff ‘prim. Farbe’ nur die Disjunktion ‘blau oder … ’, auch der Begriff jener Ähnlichkeit nur durch die diese vier Elemente gegeben? // ⌋ Ja, sind diese Begriffe sie nicht die gleichen! (Denn hier kann man sagen: “Wie wäre es wenn diese Farben diese Ähnlichkeit nicht hätten?!”) (Denken wir an die Zusammenfassung der vier primären Farben mit weiß & schwarz, & an die Zusammenfassung der ˇsichtbaren Farben mit Ultraviolett & Infrarot.)

​

Ich nenne ˇdie Regeln Vorschriften der Darstellung nicht Konventionen, wenn sie die wenn sie sich dadurch rechtfertigen lassen, indem daß man das Dargestellte beschreibt & zeigt, daß die Darstellung, ˇwenn sie jenen Regeln Vorschriften gemäß ˇist, ˇmit der Wirklichkeit gemäß ist übereinstimmt. Die Regeln Konventionen der Grammatik lassen sich nicht durch eine Charakterisie- 161 rung des Darzustellenden rechtfertigen. Denn, was die Grammatik dieser Charakterisierung zuläßt, warum soll es nicht auch die Grammatik zulassen, die ich zu rechtfertigen versuche. ∣ ¥ ⌊⌊ ⋎ S. 34 Bd XI A ⌋⌋ Und, Denn, was diese Sprache dieser Charakterisierung ˇDarstellung Rechtfertigung sagen ˇUnd was diese Rechtfertigung sagen kann, was ihre Grammatik zuläßt, – warum soll es nicht auch die Grammatik zulassen, die ich zu rechtfertigen versuche. Warum sollen beide Ausdrucksweisen Sprachen nicht die selbe Freiheit der Ausdrucksweise haben? Und wie kann, was die eine sagt, einschränken, was die andre sagen darf?

​

¥ ⋎ S. 34 Bd XI B    Wer es ablehnt, daß man die Regeln der Grammatik Spielregeln nennt, hat in dem Sinne recht, als daß er das, was das Spiel zum Spiel macht, die Konkurrenz der Spielenden, der Zweck der Unterhaltung & Erholung, u.a., in der Grammatik nicht vorhanden ist. Aber n Niemand wird leugnen, daß das Studium des Wesens der Spielregeln für das Studium der grammatischen Regeln nützlich sein muß, da irgend eine Ähnlichkeit zweifellos besteht. – Es ist das Richtige Es ist überhaupt besser , ohne ein vorgefaßtes Urteil– ⌊,⌋ oder Vorurteil– ⌊,⌋ über die Analogie zwischen Grammatik & Spiel, & nur getrieben von dem sicheren Instinkt, daß hier eine Verwandtschaft vorliegt, die Spielregeln zu betrachten. Und hier wieder soll man einfach berichten, was man sieht & nicht fürchten, daß man damit eine bedeutungsvolle & richtige Anschauung untergräbt; oder auch, seine Zeit mit etwas Über- 162 flüssigem verliert.

​

Man kann natürlich die Sprache als einen Teil eines psychischen // psychologischen Mechanismus betrachten. Am einfachsten ist das wenn man den Sprachbegriff so einschränkt daß die Sprache aus Befehlen besteht. auf Befehle einschränkt.      Man kann dann daran denken, wie ein Vormann die Arbeiten von einer Schar von Leuten durch Zurufe lenkt.

∕∕

Man kann sich denken, daß ein Mensch die Sprache erfindet; daß er die Erfindung macht andere menschliche Wesen für sich // statt seiner // arbeiten zu lassen indem er sie durch Strafe & Belohnung abrichtet auf Zurufe hin gewisse Tätigkeiten zu verrichten. Diese Erfindung wäre ganz von analog der ˇErfindung einer der Dampf[m|M]aschine etwa.

​

Das System von Zurufen, Signalen, welches er verwendet, wäre analog dem System der Durchlöcherung des Papierstreifens eines Pianola. (Ich denke mir hier übrigens ein solches welches auch stärke & Schwäche des Tons selbsttätig nach den ‘Zeichen’ auf dem Papierstreifen regelt.) Der Mensch der nach Noten spielt kann dann auch als eine Spielmaschine aufgefaßt werden & wir könnten 163 uns auch eine Spielmaschine denken, die das Musikstück von den gewöhnlichen gedruckten Noten ‘herunterläse’.      (Jede solche Vorrichtung wie der ˇgelochte Streifen eines Pianolas ist dem Bart eines Schlüssels zu vergleichen)⌊,⌋ & man könnte von der Sprache des Schlüsselbartes reden.)

∕∕

Kann man sagen die Grammatik beschreibe die Sprache; die Sprache, jenen Teil des psycho-physischen psychologischen Mechanismus mittels dessen wir durch das Aussprechen von Worten gleichsam wie durch das Drücken auf die Knöpfe einer Tastatur gewisse Knöpfe ⌊eine⌋ menschliche Maschinen für uns arbeiten lassen machen? Die Grammatik nun beschreibe jenen Teil der ganzen Maschine⌊.⌋, wie man einen Teil einer Setzmaschine, etwa, beschreiben könnte. Diejenige Sprache, dann, wäre die richtige, die die gewünschte Tätigkeit veranlassen würde⌊.⌋ die also funktionierte, eine Sprache die das nicht tut, wäre wie eine nach falschen Prinzipien gebaute Dampfmaschine[.| (]also eigentlich keine Dampfmaschine)

∕∕ /

Es ist klar ich kann durch Erfahrung feststellen, daß ein Mensch (oder Tier) auf ein Zeichen so reagiert wie ich es will, auf ein anderes nicht. Daß z.B. ein Mensch auf das Zeichen „→” hin 164 nach rechts, auf das Zeichen „←” nach links geht; daß er aber auf das Zeichen „⊣” nicht so reagiert wie auf „→” etc..      Ja ich brauche gar keinen Fall zu erdichten & nur den tatsächlichen Fall zu betrachten daß ich einen Menschen der nur Deutsch gelernt hat, nur mit der [D|d]eutschen Sprache lenken kann. (Denn das Lernen der deutschen Sprache betrachte ich nur als ein Einstellen des Mechanismus auf eine gewisse Art der Beeinflussung & es macht keinen prinzipiellen Unterschied ob er der Andere die Sprache gelernt hat oder vielleicht schon mit von Natur so gebaut ist daß er auf die Sätze der deutschen Sprache so reagiert wie [E|e]iner der gewöhnlichere Mensch, wenn er der sie gelernt hat.)

∕∕

Ich hätte nun die Entdeckung gemacht, daß Einer etwa auf einen Wink verbunden mit dem Aus Ruf „Zu” mir Zucker bringt auf den Wink & den Ruf “Mi” ˇmir Milch bringt, & daß er dies auf ein andere Worte hin nicht tut. Kann ich dann sagen, es zeige sich, daß “Zu” das richtige (einzig richtige) Zeichen für Zucker, s “Mi” das richtige für Milch sei?      Wenn Nun wenn ich das sage, so 165 gebrauche ich d[as|en] ◇◇◇ Ausdruck “Zeichen für Zucker” so wie anders, als man es für gewöhnlich gebraucht & anders als ich es gebrauchen will[.| // ] zu gebrauchen die Absicht habe. wünsche // .

∫

“Dieses ist das Zeichen für Zucker” konstatiert nicht eine Wirkung dieses Zeichens sondern drückt eine Absicht aus. D.h. verbindet das Wort “Zucker” mit einem andern Ausdruck der Sprache.     “Dieses ist das Zeichen für Zucker” verwende ich also nicht analog dem Satz: “wenn ich diesen Knopf drücke so erhalte ich ein Stück Zucker”.

​

Vergleichen wir nun aber dennoch die Sprache mit einem System solcher Knöpfe, mit einer Tastatur, mittelst welcher ich durch drücken verschiedener Komb⌊i⌋nationen von Tasten einen Menschen oder eine Maschine lenken kann. Was entspricht in diesem Fall der Grammatik der Sprache?      Es ist leicht sich eine solche Tastatur durch die der Maschine verschiedene [“|‘]Befehle’ zu geben sind zusammenzustellen. Sehen wir uns eine ganz einfache an: sie bestehe aus zwei Tasten; auf der einen steht “geh” auf der andern “komm”. Nun könnte man meinen eine Regel der Grammatik müsse 166 offenbar sein, die beiden Tasten dürfen nicht zugleicherzeit niedergedrückt werden (das ergäbe einen Widerspruch). Aber was geschieht den[m|n], wenn wir beide zugleich drücken? Nehme ich an, daß dies eine Wirkung hat? oder keine? – In jedem Fall kann ich die Wirkung oder das Ausbleiben einer Wirkung als den ˇZweck & Sinn des ˇgleichzeitigen Niederdrückens beider Knöpfe bezeichnen.

∕∕

Oder: Wenn ich sage der Befehl “bring mir Zucker” & “bring mir Milch” hat Sinn aber nicht die Kombination “Zucker mir Milch”, so heißt das nicht, daß das aussprechen dieser Wortverbindung keine Wirkung hat. Und wenn sie nun die Wirkung hat, daß der Andre mich anstarrt & den Mund aufmacht, so nenne ich sie nicht deswegen den Befehl mich anzustarren etc.. ⌊auch wenn ich gerade diese Wirkung hätte hervorbringen wollen.⌋

∕∕ \ \

“Diese Wortverbindung hat keinen Sinn” heißt nicht, sie hat keine Wirkung. ⌊ Und auch nicht, ⌊“⌋sie hat nicht die gewünscht Wirkung”. ⌋

∕∕

Zu sagen “diese Wortverbindung hat keinen Sinn” schließt sie aus dem Bereich der Sprache aus & umgrenzt dadurch das Gebiet der Sprache. Wenn man aber eine Grenze zieht, so kann das verschiedenerlei Gründe haben. Wenn ich einen Platz mit einem Zaun einem Strich oder sonst irgendwie umziehe, so kann das den Zweck haben 167 irgend jemand nicht hinaus, oder nicht hinein zu lassen; es kann aber auch zu einem Spiel gehören // ein Teil eines Spiels sein // & die Grenze soll etwa von den Spielenden übersprungen werden; oder es kann andeuten, wo der Besitz des A aufhört & der des B anfängt; etc. etc.. Ziehe ich also eine Grenze, so ist damit noch nicht gesagt, weshalb ich sie ziehe.

∕∕

Die Sprache ist für uns nicht als Einrichtung definiert, die einen bestimm⌊t⌋en Zweck erfüllt. Sondern “Sprache” ist für mich ein Sammelname & ich verstehe darunter die deutsche Sprache, die englische Sprache, u.s.w & noch plus verschiedenen Zeichensystemen die mit diesen Sprachen eine größere oder geringere Verwandschaft haben.

∫

Die Sprache interessiert mich als Erscheinung & nicht nur als ˇdas bloße Mittel zu einem bestimmten Zweck. Die Sprache ist durch die Sprachhandlungen

​

Die Grammatik besteht aus Vereinbarungen. [s|S]o eine Vereinbarung ist es, z.B., wenn sie sagt: “das Wort ‘rot’ bedeutet diese Farbe”. Eine solche Vereinbarung kann also etwa in einer Tabelle enthalten sein. – Nun, Nun [w|W]ie könnte denn diese Vereinbarung ⌊(⌋also⌊)⌋ 168 in einem Mechanismus (einem dem Pianola analogem) Platz finden? Nun, es ist wäre doch möglich, daß in dem Mechanismus sich ein Teil von der Art einer Tabelle sich befindet, der zwischen das einer der Sprache [a|A]naloge & den übrigen Mechanismus eingeschaltet ist.

​

“Sinn haben” bezeich bedeutet die Zugehörigkeit zu einem bestimmten System.     Wenn man bei der Pianolarolle vom Zweck ihrer Perforierung (nicht ihrer Wirkung spricht, so ist es leicht auf “Sinn” & “Unsinn” überzugehn. Denn der Zweck wird zum Voraus beschrieben & ist unabhängig von der Erfahrung.

​

Freilich stellt eine hinweisende Erklärung eines Worts eine Verbindung her zwischen einem Wort & ‘einer Sache’ & der Zweck dieser Verbindung ist etwa daß der Mechanismus dessen Teil unsre Sprache ist auf gewisse Weise funktioniert. Die Erklärung bewirkt kann also das richtige Arbeiten bewirken, wie die Verbindung zwischen Taste & Hammer im Klavier; aber die Verbindung besteht nicht darin, daß das Hören des Worts nun die Wirkung hat, wenn es vielleicht auch diese Wirkung 169 hat, weil die Verbindung ⌊(⌋so⌊)⌋ gemacht wurde. Und die ◇ Verbindung, nicht die Wirkung, bestimmt die Bedeutung.

​

⍈ ˇ[Zu S. 171 ⌊ A ⌋ Wenn ich sagte für uns sei Sprache nicht das, was einen bestimmten Zweck erfülle, sondern den Begriff bestimmen gewisse Systeme die wir “Sprachen” nennen & solche die nach [a|A]nalogien zu jenen gebildet seien, – so könnte ich das auch so ausdrücken:, daß ich mir erlaube ˇmir kausale Zusammenhänge für die Wirkungsweise der Sprache auch zu erdichten.

∫

¥ ⋎ S. 171 A Wenn Einem die eine Sprache gelehrt wird, lernt er da, was Sinn & was Unsinn ist? Inwieweit benützt er die Grammatik & insbesondere die Unterscheidung zwischen von Sinn & Unsinn wenn er die Sprache verwendet?

∕∕

Wenn er die Notenschrift lernt, so wird ihm eine Art Grammatik beigebracht. Es heißt da: diese Note, entspricht dieser Taste am Klavier, das Zeichen # erhöht einen Ton, das Zeichen ♮ hebt die 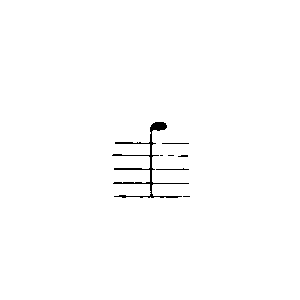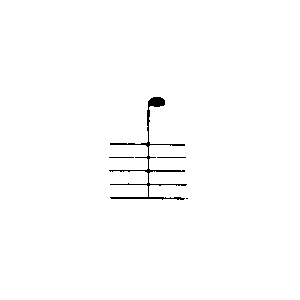Kraft Wirkung des # auf etc. etc.. Wenn der Schüler fragte ob ein Unterschied zwischen & sei oder was das Zeichen 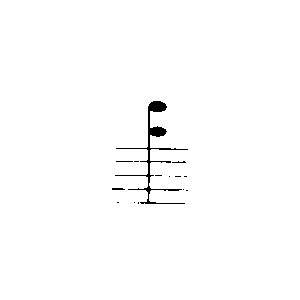bedeute, so würden wir ihm sagen, daß die Entfernung des 170 Notenkopfes von den Linien nichts ausdrücke, u.s.f.. Diese Belehrungen kann man so auffassen, daß sie ein Teil der Vorbereitung sind die den Schüler zur Spielmaschine machen. sie dazu dienen den Schüler zu einer Spielmaschine (Pianola) zu machen. Und so ist, was im Pianola der Grammatik der Sprache des seines Tonstreifens entspricht, im Bau des Pianolas verkörpert.      So[fern|weit] Sofern man den Zweck aus dem Bau ablesen kann, ist die Grammatik in ihm im Bau ausgedrückt. Die Wirkung kann man nicht ablesen.

​

Kann man denn auch von einer Grammatik reden, sofern die eine Sprache einem dem Menschen durch ein reines Abrichten gelehrt wird? Es ist klar, daß ich da das Wort “Grammatik” nur in einem “degenerierten” Sinn gebrauchen kann, wenn ich es gebrauchen will: denn wie kann ich hier von “Erklarung” reden oder von “Übereinkommen”? // denn nur in einem degenerierten Sinn könnte ich …. nur so könnte ich auch von “Erklärung” reden, oder von “Übereinkommen”. //       Ein abgerichtetes Kind ˇoder Tier kennt auch noch keine Probleme der Philosophie Philosophie .

​

Worin besteht denn die überwältigende Bedeutung der Grammatik? Worin besteht die Bedeutung der Grammatik für uns?     Wir erinnern immer daran, welche 171 Abmachungen über ein Wort in der Grammatik geschlossen worden sind.

​

¥ ⋎ S. 169 A ⍈ ˇ[Zu S. 169] ⌊ A ⌋ Denken wir uns es würde Einer erklären: “Sprache ist alles, womit man sich verständigen kann”. Worin besteht es aber, sich mit einander verständigen? ⌊–⌋ Zur Erklärung müßten wir einen Vorgang der Verständigung beschreiben[. U|; u]nd in diesem Vorgang würden gewisse kausale Verbindungen, erfahrungs[m|gem]äß[i|e]ge Regelmäßigkeiten auftreten. Aber gerade die würden mich nicht interessieren; d.h. ich würde mich nicht scheuen solche Zusammenhänge zu fingieren. Ich würde also “Schlüsselbart” nicht das nennen, was die Tür öffnet sondern das, was eine bestimmte Form, Struktur, hat. ⌊ ¥ ⋎ [S.35 Bd XI. A] ⌋

​

“Ein Zeichen ist doch immer für ein lebendes Wesen da, also muß das etwas dem Zeichen wesentliches essentielles sein”. Ja, wie ist ein “lebendes” Wesen definiert? Es scheint daß ich hier bereit bin, das Lebewesen durch die ˇFähigkeit zur Benützung einer Zeichensprache zu definieren.    Und der Begriff des Lebewesens hat wirklich eine ganz ähnliche Unbestimmtheit wie der der Sprache // wie der Begriff ‘Sprache’ // . 172

∕∕

Eine Sprache erfinden könnte heißen, auf Grund von Naturgesetzen (oder in Übereinstimmung mit ihnen) eine Vorrichtung zu bestimmtem Zweck erfinden; es kann hat aber auch den andern Sinn, dem analog, wenn wir von der Erfindung eines Spiels reden.      Ich sage damit hier etwas über die Grammatik des Worts “Sprache” aus, indem ich sie mit der des Wortes “[E|e]rfinden” in Verbindung bringe. ⍈ ↻         ¥ ⋎ S. 35 Bd XI. B

​

Sind die Regeln des Schachspiels willkürlich? Denken wir uns den Fall, es stellte sich heraus, daß nur das Schachspiel, mit den Regeln nach denen wir es heute spielen, die Menschen unterhalte & befriedige. Dann sind doch diese Regeln, wenn der Zweck des Spiels erfüllt werden soll, nicht willkürlich. Wenn wir aber von diesem Zweck absehen, so können wir die Regeln mit Beziehung auf eine andere Bestimmung willkürlich nennen. ¥ • In einem analogen Sinne So ist die Maßc[e|E]cinheit Maßeinheit Maßeinheit in der wir eine Länge ausdrücken in einem Sinne willkürlich, in einem andern die Wahl der Einheit beschränkt, oder bestimmt.

​

Die Grammatik der Sprache macht ihr Wesen aus. Die Sprache ist eben für uns ein Kalkül; sie ist durch die 173 Sprachhandlungen charakterisiert⌊.⌋, nicht durch deren praktischen Zweck.

​

Der Zweck der Grammatik ist nur der Zweck der Sprache.      Der Zweck der Grammatik ist der Zweck der Sprache.

​

Woher die Bedeutung der Sprache? Kann man sagen: “Ohne Sprache könnten wir uns nicht miteinander verständigen”? Nein[;|.] dieser [d|D]er Fall ist nicht dem analog: Ohne ˇdas Telefon könnten wir nicht von Europa nach Amerika sprechen. ¥ • Wahr ist es aber Wohl aber kann man sagen : Ohne Sprache könnten wir die Menschen nicht bewegen unsern Willen zu tun, ohne Sprache könnten wir nicht Häuser LokomotiStraßenLokomotiven bauen⌊.⌋, etc..

​

↺ ⍈    Wohl aber kann man sagen: “ ohne den mit dem Mund könnten sich die Menschen nicht ˇmit einander verständigen”. Der Begriff der Sprache ˇdagegen liegt bereits im Begriff der Verständigung.

​

Warum interessiere ich mich nun sosehr für die Sprache? Ist es nicht, als interessierte ich mich für Bilder, in denen wir die Welt um uns darstellten?     Und könnten philosophische ˇProbleme, Beunruhigungen, auch in Menschen entstehen, die ihre Umwelt durch eine Sprache gezeichneter Bilder darstellten 174 auch auch in einer Sprache der den gezeichneten Bildern unserer Umwelt erwachsen? So ein Fall ließe sich schon ausdenken.

​

Es wurde mir einmal die ˇfolgende Erfindung eines neuen Systems einer neuen Benzinstraßenwalze Motor ˇgemacht mitgeteilt; das Wesentliche der Erfindung war folgendes: Die Walze ist war ein [H|h]ohler Zylinder durch dessen Mitte eine Welle läuft lief die an beiden Enden der Walze mit dem Walzenrand durch Speichen fest verbunden war. Die Welle ist war gekröpft & als Kurbelwelle ausgebildet & an der Kurbel greift griff eine Pleuelstange samt Kolben an & der dazugehorige Zylinder ist war innen a[m|n] Walz der hohlen Walze befestigt. – Das ganze ist mithin ein starres System & der Kolben kann sich in seinem Zylinder nicht ˇaus & ein bewegen. // [D|d]as Wesentliche der Erfindung bestand darin daß dieser Erfindung war, daß … [d|D]er Motor ˇsollte sich im Innern der ho[l|h]len Walze saß bef[a|i]nd ⌊en⌋ sollte. Die Kurbelwelle lief durch die Mitte der Walze & war an beiden Enden durch Speichen mit de[r|m] Walze Walzenrande fest verbunden. Der Zylinder des Benzin[m|M]otors Motors aber war an der Innenseite der Walze befestigt. – Auf den ersten Blick sieht diese Konstruktion wie eine Maschine aus. In Wirk ˇTatsächlich aber ist [D|d]as Ganze war also ein starres System & der Kolben des Benzinmotors k[o|a]nnte sich i[n|m] seinem Zylinder nicht aus & ein bewegen. Der Irrtum des Erfinders hat mit einem philosophischen Irrtum Verwandtschaft. ⌊⌊ Die Konstruktion schaut ˇganz so aus wie eine Maschine & ist doch keine. Wir haben sie selbst ◇◇◇ jeder Bewegungsmöglichkeit beraubt & wissen es nicht. ⌋⌋ 175 ¥ [⋎ S. 35 Bd XI C] als eigener Absatz.]

​

Ich könnte mir eine Orgel denken deren Register durch Tasten zu betätigen wären, die den Spieltasten des Manuals ganz gleichgeformt wären & ˇso unter diese verstreut wären daß das Manual wie ein gewöhnliches aussähe . Und es könnte nun so ein philosophisches Problem entstehen; daß etwa: “wie sind stumme Töne möglich”. Und der würde das Problem lösen, der auf den Gedanken käme die Registertasten durch Züge zu ersetzen, die mit den Spieltasten keine Ähnlichkeit hätten haben . ¥ ⋎[S. 36 Bd XI A anschließend ˇneue Zeile] c

​

¥ ⋎[S. 36 Bd XI B eigener Absatz]    “Könnte eine Sprache aus lauter unabhängigen Signalen bestehen?” Statt dessen könnte ◇ man fragen: Wollen wir eine Reihe von einander unabhängigen Signale noch eine “Sprache” nennen? – Wenn gefragt würde: Kann so eine Sprache dasselbe leisten, wie eine die aus Sätzen also Kombinationen von Zeichen, besteht, müßte man antworten: die Erfahrung wird es lehren, ob z.B. die Wirkung dieser Spra jener Signale auf die Menschen eine ähnliche ist wie die der Sätze. Aber die Wirkung interessiert uns nicht; wir betrachten die Erscheinung, den Kalkül, der Sprache.     Denken wir uns etwa ein Tagebuch mit unabhängigen Signalen geführt. Eine Seite ist in Abschnitte für die Stunden des Tages eingeteilt ˇnach Art eines Stundenplans,. Das Zeichen “A” heißt: ich schlafe; “B” 176 heißt “ich arbeite”; “C”, “ich esse; u.s.w., u.s.w.. Aber da kommt es nun drauf an: werden diese Erklärungen ausdrücklich gegeben, daß sie also die Signale mit einer andern Sprache verbinden; werden hinweisende Erklärungen der Signale gegeben die die Signalsprache vervollstandigen? [o|O]der soll die Sprache wirklich nur aus den Zeichen A, B, C, etc. bestehen?     Wie, wenn mich [e|E]iner fragte: “wie weißt Du daß Du jetzt dasselbe tust, wie vor einer Stunde”, & ich antwortete: “ich hab mir's ja aufgeschrieben, hier steht ja ein ‘C’.”. – Kann man fragen ob ˇdas Zeichen “A” immer das gleiche bedeutet; & unter welchen Umständen kann diese Frage, im einen oder andern Sinn mit ja oder nein , beantwortet werden? (Man kann sich eine Sprache denken in der die Wörter, die Farbnamen etwa z.B. , mit den Wochentagen ihre Bedeutung wechseln; diese Farbe heißt Montag “rot”, [d|D]ienstag “blau”. “A = A” kann besagen, daß es in den Sprachen, auf die sich die Regel bezieht, keinen Wechsel … in der betreffenden Sprache keinen Wechsel der Bedeutung des Zeichens “A” gibt.)

​

Denken wir uns wieder eine Sprache die aus Befehlen besteht. Man soll mit ihr die Bewegungen eines Menschen leiten können[. D|; d]ie Befehle bestehen aus Ziffern einer Längenangabe bestünden etwa im Nennen einer Anzahl von Schritten verbunden mit den Wörtern “vor”, “rückwärts”, “rechts”, “links” & den Wörtern “schnell” & “langsam”. Man könnte 177 nun natürlich alle diejenigen Befehle die man wirklich gebrauchen wird durch von einander unabhängige Zeichen, Signale, ersetzen. Es wäre dann m könnte Einer diese Signale zuerst erst als Abkürzungen ˇder Sätze jener ersten Sprache lernen, die Signale sie⌊sie⌋ auch in sie diesec zurückübersetzen, ehe er sie befolgt, später aber unmittelbar nach den Signalen handeln. – Man könnte dann von zwei Sprachen reden & die erste bildhafter nennen als die zweite. Man ˇnämlich würde nicht sagen, daß ich aus einer Reihe solcher Signale allein d[ie|er] ein Bild Bewegung des Menschen, der ihnen folgte, ableiten kann, wenn nicht zu den Signalen noch das tritt, was man eine allgemeine Regel der Übersetzung in die Zeichnung nennen würde. Wir würden nicht sagen : , aus dem Zeichen abbcd läßt sich die Figur ↑ → → ← ↓ ableiten; wohl aber aus abbcd und der Tabelle a b c d ↑ → ↓ ← Man

​

Man kann nun sagen: die Grammatik erklärt die Bedeutung der Zeichen & dadurch macht sie die Sprache bildhaft. Die Grammatik bestimmt die Bedeutung der Wörter & bestimmt ihnen damit den Platz, den sie beim Portraitieren eines 178 Sachverhalts einnehmen dürfen. Denn wonach richte ich mich, wenn ˇich hier “rot” sage & nicht “blau”, hier “oder und & nicht “und” “oder”? Doch woh nach der Bedeutung der Wörter, nach dem, was in Abmachungen über sie, also in der Grammatik festgehalten ist. Denn warum sollte ich sonst ein Wort einem andern vorziehen.    Das heißt will sagen: Wenn [i|I]ch ˇkann die Wahl eines Wortes rechtfertige, dann so geschieht es durch die Grammatik ˇrechtfertigen. Das heißt aber nicht, daß ichˇ die Worte, wenn die ich Worte gebrau ˇsie etwa bei in einer Beschreibung, gebrauche ich sie durch Erklärungen rechtfertige, oder rechtfertigen muß.

​

Wir reden vielmehr von der Möglichkeit dieser Rechtfertigung. Und die verhält sich zum wirklich eintretenden Fall ähnlich wie ein Gedankengang, in dem ich die Überlegung m 12 × 12 = 144 mache, zu einer Wiedergabe des Gedankengangs, worin diese Multiplikation Rechnung auf dem Papier wirklich durchgeführt ist.      Wir vergleichen den tatsächlichen Vorgang beim Gebrauch des Zeichens mit dem einem solchen, in welchem eine Rechtfertigung gegeben wird. Wir ergänzen das tatsächlich Ausgeführte zu einem bestimmten Kalkül, um es von diesem bestimmten Gesichtspunkt anzusehen. Ähnlich, wie die 179 ˇDamit ist es zu vergleichen wenn die gewöhnliche Grammatik einen eliptischen Satz ergänzt, also dieses Gebilde als einen verkürzten Satz auffaßt.

​

⍈ [Zu S. 37] A Man könnte also sagen, Augustinus stelle die Sache zu einfach dar; aber auch: er stelle eine einfachere Sache dar.

​

⍈ [Zu S. 37] B Wie Augustinus das Lernen der Sprache beschreibt, das kann uns zeigen, von welcher Auffassung der Sprache der Begriff von der Bedeutung der Wörter sich herleitet.

​

Ich will erklären: Der Ort eines Worts in der Grammatik ist seine Bedeutung.

​

Ich kann das auch so sagen: der Gebrauch des Wortes in der Sprache ist seine Bedeutung.

​

ˇIch kann aber auch sagen: Die Bedeutung eines Wortes ist das, was die Erklärung der Bedeutung [E|e]rklärt.

​

Die Erklärung der Bedeutung aber erklärt den Gebrauch des Wortes.   Der Gebrauch des Wortes in der Sprache ist seine Bedeutung

​

180 ⍈ [Zu S. 61 anschließend an: “zeigt. –”] Aber wie ist denn diese Vertretung möglich? Ich kann doch nicht ein beliebiges Ding ein anderes vertreten lassen. – Es ist dann eben bedeutsam, daß diese Vertretung möglich ist; denn das Vertretende der Vertreter muß dann, in bestimmten Fällen wenigstens, ebensogut taugen wie das Vertretene.

​

[Das Folgende bis zum Strich ˇauf S. 184 gehört zu S. 38 gr. Format]

​

Wir reden von einem Verstehen (einem Vorgang des Verstehens, oder auch einem Zustand des Verständnisses Verstehens ) & auch von gewissen Vorgängen, die Kriterien dieses Verstehens sind.      Das Verstehen möchte man einen geistigen Vorgang oder einen Zustand der Seele nennen & charakterisiert es damit als hypothetischen Vorgang etc. oder richtiger als Vorgang (oder Zustand) im hypothetischen Sinn. D.h. man verweist das Wort “Verstehen” in ein bestimmtes Gebiet der Grammatik.

​

Und zwar ist die Grammatik des seelischen Zustands oder Vorgangs ˇin mancher Beziehung ähnlich der etwa des Gehirnvorgangs. Der Hauptunterschied ist vielleicht der, daß im Falle des Gehirnvorgangs eine direkte Kontrolle ˇals möglich zugelassen wird; wenn man etwa den ˇbetreffenden Vorgang durch öffnen des Schädels 181 sieht. Während ein solches von so einem ‘unmittelbare[s|n] Wahrnehmen’ das in der Grammatik des seelischen Vorgangs nicht die Rede ist. (Diesen Zug gibt es in diesem Spiel nicht.)

​

Welches ist das Kriterium dafür, daß wir das Wort “rot” verstehen? Daß wir einen roten Gegenstand aus anderen auswählen, wenn es verlangt wird, oder daß wir die hinweisende Definition des Wortes “rot” geben können?    Beides betrachten wir als Zeichen des Verständnisses. Hören wir jemand das Wort “rot” gebrauchen & bezweifeln daß er es versteht, so können wir ihn zur Prüfung fragen: “welche Farbe nennst Du ‘rot’”. Anderseits, wenn wir jemandem die hinw. Erklärung ˇdes Wortes gegeben hätten & nun sehen wollten, ob er sie richtig verstanden hat, würden wir nicht von ihm verlangen, daß er sie wiederhole, sondern wir gäben ihm etwa die Aufgabe, aus einer Reihe von Dingen die roten herauszusuchen.

​

Hier kann g vor allem gefragt werden: “ist von meinem Verstehen oder vom Verständnis des Andern die Rede?” “Nur ich kann wissen, ob ich verstehe, der Andere kann es nur vermuten.” 182 “Daß ich verstehe ist keine Hypothese, daß der [a|A]ndere versteht ist eine.” Wenn wir das sagen, so fassen wir “Verstehen” als ein Erlebnis auf analog ˇ z.B. dem der Zahn[s|S]chmerze[n|s] eines etwa.     Man sagt: “Du kannst nicht wissen ob ich verstehe (ob ich mich freue etc); Du kannst nicht in mich hineinschauen”. “Du kannst nicht wissen, was ich denke”. Wohl, aber das gilt nur dann, wenn Du nicht laut denkst; & der Unterschied zwischen dem lauten (oder schriftlichen) Denken & dem Denken in der Vorstellung interessiert uns hier nicht.

​

Darauf kann man einwenden daß das Denken auch wenn es nur das visuelle Erlebnis des Schreibens wäre, doch privat ist & daß der Andere zwar w sehen kann was meine physische Hand schreibt aber nicht mein Seherlebnis haben kann. Diese Fragen müssen uns an einer andern Stelle beschäftigen.

​

Aber können wir für unseren gegenwärtigen Zweck statt “er versteht” & “ich verstehe” nicht sagen “er schreibt” & “ich schreibe”?      Wir lassen dann die Frage des Erlebens ganz aus dem Spiel. Und also etwa auch die Frage 183 privaten Verständnisses. Sie erscheint uns dann hier unwichtig. // Sie erscheint uns dann an dieser Stelle unwichtig. //

​

Wir nennen “verstehen” nicht die Handlung – welche immer – die uns das Verständnis zeigt, sondern einen Zustand, für den diese Handlung ein Anzeichen ist. Und das ist eine Aussage über die Grammatik der Bezeichnung eines solchen Zustandes.

​

Wir können das Aussprechen Hersagen der Regel allein ‘Kriterium des Verstehens’ nennen oder auch Proben des Gebrauchs allein.    In einem Fall wird dann “er versteht” heißen: “wenn Du ihn nach der Regel fragst wird er sie sagen”; im andern Fall: “wenn Du eine Anwendung der Regel von ihm verlangst wird er Deinen Befehl ausführen.    Oder aber wir betrachten das das Angeben der Regel als ein Symptom dafür daß er etwas Anderes tun kann als die Regel angeben. So also, wie wir die Uhr an's Ohr halten, sie ticken hören & sagen, ⌊:⌋ sie geht. Wir erwarten dann nicht bloß daß sie auch weiterhin ticken wird, sondern auch, daß sie die Zeit zeigen wird. 184

​

Man könnte sagen: “das Hersagen der Regel ist ein Kriterium des Verständnisses, wenn er die Regel mit Verständnis ausspricht & nicht rein mechanisch.” Aber hier kann wieder die sinnvolle Betonung beim Aussprechen als Verständnis gelten; & warum dann nicht einfach das Aussprechen selbst?

​

Verstehen = be-greifen = einen bestimmten Eindruck von dem Gegenstand erhalten, ihn auf sich wirken lassen. Einen Satz auf sich wirken lassen; Konsequenzen von ihm des Satzes betrachten, sich vorstellen; etc..

​

“Verstehen” nennen wir ein psychisches Phänomen das speziell mit den Erscheinungen der Erscheinung des Lernens & Gebrauchs unserer, der menschlichen, Wortsprache verbunden ist.

​

⍈ [Zu S. 61] anschließend an die letzte nicht durchstrichene Zeile] Aber erkläre ich nicht einem Franzosen die Bedeutung des Wortes “rot” auf eben diese Weise? “Ja, aber nur, weil er die Bedeutung von [“|‘] rouge [”|’] durch hinweisende Definition gelernt hat.” Aber muß ihm diese Definition gegen- 185 wärtig sein (& sonst andernfalls ist sie nur Geschichte), oder ein rotes Vorstellungsbild, wenn er meine Erklärung “rot = rouge” versteht? Muß so ein Bild gegenwärtig sein, wenn er, wie wir sagen würden, das Wort “rouge” mit Verständni[g|s] gebraucht? (Denke an den Befehl: “[s|S]telle Dir einen ˇkreisförmigen roten Kreis vor roten Fleck vor!”)

​

⍈ [Zu S. 63 als neuer Absatz]     Ist es richtig, & in welchem Sinne, von hinweisenden Definition zu sagen, sie setze wie die Verbaldefinition ein Zeichen für ein anderes; das Wort für den Hinweis?

​

⍈ [Zu S. 67 als neuer Absatz] Anderseits ist es wohl denkbar, daß Menschen in den Farben die sie mit Violintönen assoziieren Asso[t|z]iationen von Farben mit Violintönen so genau übereinstimmten daß Einer zum Andern sagen könnte: “Nein, diesen ˇViolinTon hast Du nicht richtig dargestellt gemalt , er war gelblicher als Du ihn gemalt hast”; & der Andere würde nun nicht etwa antworten: “Du hast recht es hat mir selber so geschienen”. –

​

Wie kann, wenn ich klingle, das jemandem befehlen zu mir zu kommen? 186 Ist es nur dadurch möglich, daß ich das Klingelzeichen nach dem Gedächtnis (oder nach einer Tabelle) in Worte übersetze? Und können wieder diese Worte nur dadurch etwas sagen, daß ich sie (nach dem Gedächtnis oder nach einer Tabelle) in ein Bild übersetze? (Wie weiß ich wie dieses Bild anzuwenden ist?)

​

⍈ [Zu S 71 als neuer Absatz]   Brauchen wir etwa nur einen gesprochenen Befehl zu befolgen ˇzu können ein Erinnerungsbild dessen, was wir taten als wir ihn das letzte Mal befolgten?    Befielt er uns also eigentlich, : “Tu jetzt das, was Du, Deiner Erinnerung nach, damals getan hast”? Auch diesen Befehl könnte man geben. Aber brauche ich also um ihn befolgen zu können ein Erinnerungsbild davon vom Suchen in der Erinnerung?     Der Befehl “[t|T]u jetzt das was Du Deiner Erinnerung nach damals getan hast” sagt mir, ich solle an einem bestimmten Ort nach einem Bild suchen, welches mir sagen wird, was ich zu tun habe. Der Befehl ist also ganz analog dem: “Tu das was auf dem Zettel in dieser Lade aufgeschrieben steht”. Steht nichts 187 auf dem Zettel so ist der Befehl sinnlos.

​

⍈ [Zu S. 75 als neuer Absatz nach S. 77 B] Es wäre nicht richtig zu sagen: “die Übereinstimmung & Nichtübereinstimmung zwischen Satz & Wirklichkeit Welt sei ist willkürlich durch eine Zuordnung von sprachlichem Ausdruck & Wirklichkeit erzeugt”: Die Zuordnung besteht bestünde doch darin, daß der Satz ‘p’ sagt, es sei gerade das der Fall. Aber wie ist uns diesesc ‘gerade das’ im besondern Fall gegeben? Ob [d|D]urch einen andern Satz der Wortsprache oder durch einen Hinweis auf die ‘Wirklichkeit’. Beides sind Erklärungen der Sprache als Vorbereitung zu ihrem Gebrauch. Aber was ist dieses ‘gerade das’ in einem besonderen Fall? Ist es durch einen Hinweis auf die ‘Wirklichkeit’ gegeben, dann ist dieser Hinweis die Erklärung eines sprachlichen Ausdrucks, & selber ein solcher. Der erklärende Hinweis bereitet auf die Anwendung der Sprache vor; er übersetzt eigentlich aus einer Sprache in eine andere. Er ist ein Akt der Zeichengebung & verschieden von dem Urteil, daß ein Satz mit der Wirklichkeit übereinstimmt (oder das Gegenteil).

​

188 ⍈ [Zu S. 90. neuer Absatz]     Wenn man an den Gedanken, als etwas spezifisch [m|M]enschliches, [o|O]rganisches denkt, möchte man fragen: “Könnte es denn eine Gedankenprothese geben, einen anorganischen Ersatz für den Gedanken?” Aber wenn das Denken nun im Schreiben oder Sprechen besteht, warum soll dies nicht eine Maschine tun? – “Ja, aber die Maschine weiß von nichts!” – Freilich, von einer Prothese des Sehens & Hörens zu reden hat keinen Sinn. Man redet zwar von einem k⌊ü⌋nstlichen Fuß, aber nicht von künstlichen Fußschmerzen. [Variante]    Wenn man den Gedanken als etwas spezifisch [m|M]enschliches, Organisches auffaßt, möchte man fragen: “Könnte es eine Gedankenprothese geben, könnte denken von einer leblosen [v|V]orrichtung vollbracht werden? Nun, die Rechenmaschine kann die zehn Finger beim Rechnen ersetzen; aber von einem anorganischen Ersatz für die Rechnung kann natürlich nicht geredet werden.

​

⍈ [Zu S. 92 neuer Abs.] A     Wir können sagen: Denken ist das Operieren mit Symbolen. Aber ‘[d|D]enken’ ist ein fließender Begriff, & welcher das ‘Operieren mit Symbolen’ ist, muß in jedem besondern Fall eigens betrachtet werden. 189    Ich könnte auch sagen: Denken ist operieren mit der Sprache[.|;] ⌊a⌋ Aber ‘Sprache’ ist wieder ein fließender Begriff.

​

⍈ ⌊⌊ B ⌋⌋ Wenn gesagt wird: “[d|D]enken ist ein geistiger Vorgang”, so stimmt ist das wohl nur ˇrichtig, insofern man auch das sehen eines geschriebenen Satzes oder das Hören eines gesprochenen einen geistigen Vorgang nennt. Also in dem Sinne in welchem man Schmerzen einen geistigen Zustand nennt. Man will dann mit dem Wort “geistiger Vorgang” das ‘Erlebnis’ vom ‘physikalischen Vorgang’ unterscheiden. – Anderseits deutet freilich das Wort “geistiger Vorgang” an, daß es sich hier um etwas unverstandene Vorgänge in einer uns nicht zugänglichen Sphäre handelt.     Ferners redet die Psychologie auch von ‘unbewußten Gedanken’ & meint gebraucht hier das Wort mit “Gedanken” als einen Vorgang in einem Seelenmodell. (‘Modell’ in dem Sinn, in welchem man von einem mechanischen Modell der elektrischen Vorgänge spricht.)     Wenn dagegen Frege vom Gedanken spricht, den ein Satz ausdrückt, so ist hier das Wort “Gedanke” etwa gleichbedeutend dem Wort “Sinn des Satzes”. 190

∕∕

⍈ C     Man könnte sagen: in allen Fällen meint man mit “Gedanken” das Lebende am Satz. Das, ohne welches er tot, ein⌊e⌋ bloßer Lautfolge oder Folge von geschriebene[n|r] Figuren ist.      Wenn ich aber ebenso von einem Etwas spräche, welches einer Konfiguration von Schachfiguren Bedeutung gibt, d.h., & sie von einer beliebigen andern Zusammenstellung von Holzklötzchen unterscheidet, oder von dem Etwas welches den Geldstücken ihre Bedeutung, ihr Leben was könnte ich da nicht alles meinen! Die Regeln die die Schachkonfiguration zu einer Situation eines Spiels machen, die besonderen Erlebnisse die wir mit solchen Spielstellungen verbinden, den Nutzen des Spiels.     Oder wenn wir von einem Etwas sprächen, welches das Papiergeld von bloßen bedruckten Zetteln unterscheidet & ihm seine Bedeutung, sein Leben gibt!

​

⍈ [Zu S. 95 anschließend an: “Wesen.””] Aber wenn ich sage der Gedanke sei etwas ganz [h|H]a⌊u⌋sbackenes, so meine ich, es gehe uns mit diesem Begriff wie mit dem der Zahl oder Begriff etwa der Zahl [1| Eins]. Es scheint etwas geheimnisvoll an ihm zu sein, weil wir die seine Grammatik mißverstehn 191 & ein greifbares Ding vermissen was dem Dingwort entspricht. (Es ist uns da Das ist beinah ähnlich zu mute, wie wenn wir aus dem leeren Raum vor uns eine menschliche Stimme hörten, aber keinen Menschen vor uns sähen.)        ¥ • [Anschließend in eine neue Zeile.]

​

⍈       [Zu S. 103 als eigener Absatz] A      Ich könnte sagen: “‘Sprache’ das ist ein Sammelname für die Sprachen; & die Sprachen sind auf vielerlei Weise mit einander verwandt.”

​

↺ ⍈   Die Erklärungen, die ich das Denken & den Gedanken betreffend zu geben habe, sind nur Darstellungen der Grammatik der Wörter “denken” & “Gedanke”.

​

⍈ [Zu S. 103] B     Man kann in der Logik nicht allgemein sein ins Blaue. Lege ich die Grammatik meiner Allgemeinheit fest so gibt es keine logischen Überraschungen ˇmehr. Und lege ich sie nicht fest so bin ich nicht mehr im Reich einer exakten Grammatik.     D.h.: die Unbestimmtheit der Allgemeinheit ist keine logische Unbestimmtheit. Die Unbestimmtheit ihrer Grammatik. Die Allgemeinheit ist eine Bewegungsfreiheit, keine Unbestimmtheit der Geometrie.

​

192 [Zu S. 107 als neuer Absatz.]   Wie haben wir denn das Wort “Pflanze” verstehen gelernt? Wenn ich davon absehe, daß wir vielleicht eine Definition des Begriffs, in der Botanik etwa, gelernt haben, die dann auch nur in der Botanik eine Rolle spielt, so ist es klar, daß wir die Bedeutung des Wortes durch Beispiele gelernt haben. Und wenn wir nun von hypothetischen Dispositionen absehen, so stehen diese Beispiele nur für sich selbst. Hypothesen über das Lernen & Gebrauchen der Sprache & kausale Zusammenhänge interessieren uns ja nicht. Wir nehmen daher nicht an, daß die Beispiele im Lernenden etwas hervorrufen, ein Wesen vor seine Seele stellen rufen , die Bedeutung des Begriffswortes, den Begriff ‘Pflanze’. Sollten die Beispiele eine Wirkung haben indem sie, sagen wir, ein bestimmtes Gesichtsbild im Lernenden erzeugen hervorrufen , so geht uns der kausale Zusammenhang zwischen den Beispielen & diesem Bild nichts an, & für uns stehen sie nebeneinander. Und wir können etwa dann von den Beispielen ganz absehen & nur das Bild als Symbol des Begriffes ansehen; oder auch Bild & Beispiele zusammen.       Wenn man sagt “wir verstehen das Wort ‘Sessel’, indem weil wir wissen, was allen Sesseln gemeinsam ist” –, was heißt es, daß wir das wissen? Etwa daß wir bereit sind es zu sagen (wie im 193 Fall “wir wissen, daß 6 × 6 36 ist”)? Und was ist also das Gemeinsame? Oder sagen wir hier nicht nur darum, wir wissen das Gemeinsame, weil wir das Wort “Sessel” anwenden können? Verführt uns da nicht etwa eine Analogie wie diese: Nehmen wir an, ich erklärte das Wort “rot” indem ich auf eine rote Wand, ein rotes Buch, ein rotes Stück Tuch zeigte & jemand fertigte nach dieser Erklärung danach ein Muster der Farbe Rot an indem er ein Rotes Täfelchen herstellte. Man könnte in diesem Falle sagen, er habe gezeigt daß er begriffen habe, was das [g|G]emeinsame aller Beispiele war, die ich ihm gegeben hatte.

​

Der grammatische Ort des Wortes “Spiel”, “Regel” etc. ist durch Beispiele etwa so gegeben, wie der Ort einer Zusammenkunft durch die Angabe sie werde bei diesem & diesem Baum stattfinden.

​

Man denkt sich die Bedeutung als etwas, was uns bei dem Wort vorschwebt.    Was uns bei dem Wort vorschwebt charakterisiert jedenfalls die Bedeutung. Was mir aber vorschwebt ist ein Beispiel, ein Fall der Anwendung des Worts. Und das Vorschweben besteht nicht eigentlich darin, 194 daß, wenn immer ich das Wort ◇ ausspreche oder höre eine bestimmte Vorstellung gegenwärtig ist, sondern daß mir, wenn ich nach der Bedeutung des Wortes gefragt werde, Anwendungen des Wortes einfallen.

∕∕

Jemand sagt mir: “Zeige den Kindern ein Spiel!” Ich lehre sie nun Geld würfeln & der Andere sagt mir: “Ich habe nicht so ein Spiel gemeint”. Mußte ihm da, als er mir den Befehl gab der Ausschluß des Würfelspiels vorschweben?

​

Nehmen wir an jemand sagte: “Nein, so ein Spiel habe ich nicht gemeint; ich habe “‘Spiel’ in der engeren Bedeutung gebraucht”. Wie zeigt es sich daß er das Wort in einer engeren Bedeutung g⌊e⌋braucht?

​

Kann man aber das Wort “Spiel” nicht auch in seiner weitesten Bedeutung gebrauchen? Aber welches ist die? Es sind ja keine Grenzen gezogen außer wir legen eigens solche fest.    Ein Satz wie der: “Die Assyrer kannten verschiedene Spiele”, wenn wir ohne jede weitere Qualifikation etwa in einem Geschichtsbuch fänden, würde 195 uns sehr seltsam anmuten; weil wir nicht sicher wären ein Beispiel angeben zu können was auch nur beiläufig der Bedeutung des Wortes “Spiel” in diesem Fall entspricht.

​

Es will etwa jemand in das Regelverzeichnis eines Spieles den Satz aufnehmen schreiben , das Spiel sei in dem & dem Jahre erfunden worden. Ich sage: “ ⌊(⌋Nein,⌊)⌋ das gehört nicht ins Regelverzeichnis, das ist keine Regel”. Ich schließe hier also Sätze der Geschichte aus den Regeln // aus dem Gebiet der Regeln // aus. Und ebenso würde ich einen Satz wie: “dieses Spiel ist nur durch lange Übung zu erlernen” als einen Erfahrungssatz aus den Regeln ausschließen. Aber es würde uns leicht irreführen zu sagen, man hätte damit um das Gebiet der Regeln Grenzen gezogen.

​

Wenn ich jemandem den Gebrauch eines Wortes, etwa des Wortes “wünschen”, durch ˇcharakteristische Beispiele klar zu machen suche, so liegt es nahe, daß der Andere in Form eines Einwands ˇgegen das von mir Vorgebrachte ein Beispiel Beispiele anführt das auf eine ˇnoch andere Gebrauchsart hindeutet. Meine Antwort ist dann, daß das neue Beispiel für unsre Betrachtung nützlich werden kann, daß es 196 aber kein Einwand gegen meine Beispiele ist. Denn ich wollte ja gar nicht sagen, diese Beispiele seien die Darstellung des Wesens dessen was man “wünschen” nennt Höchstens Darstellungen verschiedener Wesenheiten die alle man wegen gewisser Verwandtschaften mit diesem Wort bezeichnet. Der Irrtum ist, daß angenommen wird, wir wollten durch diese Beispiele das Wesen, des Wünschens etwa, illustrieren, & die Gegenbeispiele zeigten nun, daß dieses Wesen noch nicht richtig erfaßt sei. Das ist, als wäre unser Ziel, eine Theorie des Wünschens zu geben, die dann eben alle Fälle des Wünschens erklären müßte.     Darum sind aber anders⌊e⌋its die herangezogenen Beispiele nur dann von Nutzen, wenn sie klar ausgeführt, & nicht blos vag angedeutet sind.

∕∕

⍈ [Zu S. 128 als neuer Absatz]   Wenn wir einen Befehl geben, so kann es scheinen, als ob das Letzte was der Befehl wünscht ⌊(⌋doch⌊)⌋ unausgedrückt bleiben muß, da immer noch eine Kluft zwischen dem Befehl & seiner Befolgung bleibt. Ich wünsche etwa, daß Einer eine bestimmte Bewegung macht, etwa den Arm hebt. Damit es ganz deutlich wird mache ich ihm die Bewegung vor. Dieses Bild scheint unzweideutig bis auf die 197 Frage: wie weiß er daß er diese Bewegung machen soll? – Wie weiß er überhaupt, wie er die Zeichen, welche immer ich ihm gebe, gebrauchen soll? Ich werde nun etwa trachten den Befehl durch ˇweitere Zeichen zu ergänzen, indem ich von mir etwa auf den Andern denke, Gebärden der Aufmunterung mache, etc.. Hier scheint es als finge der Befehl zu stammeln an.      Denken wir, ich wollte jemandem vorschreiben die Zahlen von 1 bis 4 zu quadrieren & täte es mit dem Schema: x x² 4 ? Ich bin nun versucht zu sagen, daß mit dem Fragezeichen doch nur etwas angedeutet aber nicht ausgesprochen ist.    Als trachte das Zeichen sich uns verständlich zu machen. Aber wenn wir es nun verstehen // Als trachte das Zeichen mit unsicheren Mitteln in uns ein Verständnis hervorzurufen. // Aber wenn wir es nun verstehen, in welchen Zeichen tun wir das?

​

⍈ [Zu S. 138 anschließend] Wohl aber könnte man fragen: sollen wir das noch eine “Erklärung” nennen? – Denn sie spielt im Kalkül natürlich eine andere 198 Rolle als was wir gewöhnlich hinweisende Erklärung des Wortes “rot” nennen auch wenn sie dieselbe praktische Folge dieselbe Wirkung auf den Lernenden hätte.

​

[Zu S. 142]    Ich kann wohl sagen: In meinem Zimmer unruhig auf & ab⌊|⌋gehen, zur Tür schau⌊e⌋n, bei einem Geräusch aufhorchen heißt: den N. erwarten. – Das ist eben eine Definition des Ausdrucks “den N erwarten”. Freilich ist es keine Definition des Wortes “erwarten”, denn es ist ja damit z.B. nicht e⌊r⌋klärt was es heißt “den M erwarten”. Nun, dafür können wir sorgen; wir sagen etwa: den X N erwarten heißt die angegebenen Handlungen ausführen & dabei den Namen “X” “N” aussprechen. Nach dieser Definition ist der den ich erwarte, der, welcher den ausgesprochenen Namen hat. Oder ich definiere: den Menschen X erwarten heißt: das tun was ich im zweiten Beispiel angegeben habe & die Zeichnung eines Menschen anfertigen. Der Erwartete ist nun, wer den Namen X trägt & der Zeichnung entspricht. – Damit wäre natürlich nicht erklärt, was es heißt “das Gehen des N” erwarten” & ich müßte dafür entweder eine neue ˇunabhängige Definition geben, oder eine allgemeinere Erklärung die Gehen & Kommen umschließt. Und mit 199 der wäre etwa nicht erklärt, was es heißt “ein Gewitter erwarten”; etc. etc..

​

Was alle diese Fälle char⌊a⌋kterisiert ist, daß, was erwartet wird aus der erwartenden Handlung mittels der Definition abgelesen werden kann. Nicht eine spätere Erfahrung entscheidet darüber, was wir erwarten.      Und ich kann sagen: In der Erf Sprache berühren sich Erwartung & Erfüllung.

​

Die Handlung des Erwartenden ist hier also eine, die ich nach gegebenen Regeln in den Satz “er erwartet, daß p geschieht” übertragen kann. Und also ist das einfachste typische Beispiel für diese Fälle diesen F[a|ä]lle // für diesen Gebrauch des Wortes “erwarten” // , daß die Erwartung des Eintreffens von p darin besteht, daß der Erwartende sagt: “ich erwarte daß p geschieht”. ⌊ Daher klärt es in sovielen Fällen die grammatische Situation, zu sagen: Setzen wir statt der Erwartung den Ausdruck der Erwartung. Statt des Gedankens, den Ausdruck des Gedankens. // Den Ausdruck des Gedankens statt des Gedankens. // ⌋

​

Die Erwartung kann man auffassen als eine erwartende, vorbereitende Handlung. Sie streckt wie ein Ballspieler die Hände aus, richtet sie, um den Ball zu empfangen. 200 Und die Erwartung des Ballspieles kann darin bestehen, daß er die Hände ˇin bestimmter Haltung ausstreckt & auf den Ball blickt.

/

Mancher wird vielleicht sagen wollen: “[d|D]ie Erwartung ist ein Gedanke.” Und gewiß Das entspricht das offenbar einem Gebrauch des Wortes “erwarten”. Und wir wollen uns nur erinnern, daß der Vorgang eines desc Gedankens sehr verschiedenerlei sein kann.     Und ist die Erwartung der Gedanke: “ich erwarte daß p geschieht”, so ist es unsinnig zu sagen, ich werde vielleicht erst später erkennen, was ich erwartet habe.

​

Analoges Dasselbe ließe sich könnte man von Wunsch, Furcht & ⌊,⌋ Hoffnung sagen. (Plato nennt die Hoffnung “eine Rede”.)

​

Anders ist es aber, wenn man den Hunger “einen “Wunsch” nennt & etwa zwar den Wunsch ˇdes Körpers nach der Speise, die ihn s⌊t⌋illen wird. Dann ist es eine Hypothese, daß gerade das den Wunsch befriedigen wird & es gibt eine Vermutung ˇdarüber & einen Zweifel⌊.⌋ darüber.    Und so ist es auch wenn ich “Erwartung” ein Gefühl nenne, etwa eins der Unruhe, Unbefriedigung. Aber natürlich sind diese Gefühle nicht Gedanken 201 in amorpher Form.

​

Die Vorstellung, daß der Gedanke ein unerklärter seltsamer Vorgang im menschlichen Geist sei macht es möglich, sich ihn in einen amorphen Dauerzustand verwandelt zu denken.

∫

Wenn ich sage “ich habe ihn den ganzen Tag erwartet”, so ist mit “erwarten” kein Dauerzustand gemeint, der den Erwarteten & sein Kommen als Bestandteile enthielte, wie ein Teig Mehl, Zucker, Eier gleichmäßig verrührt enthält. Die Erwartung bestand vielmehr in einer Folge von Handlungen, Gedanken , ⌊(⌋&⌊)⌋ Gefühlen.

​

[Zu S 142, wie das Vorige, aber nach S. 150 A.] ⌊⌊ A ⌋⌋   Ich werde aber vielleicht auch dann sagen “ich habe den N erwartet”, wenn die einzige Verbindung meiner [E|e]rwartenden Tätigkeiten mit ihm, die ist, daß ich z.B. an einem bestimmten Tage Vorbereitungen für eine Malzeit für mich & eine andere Person treffe & daß sich N für diese Mahlzeit bei mir angesagt hat.

​

⌊⌊ B ⌋⌋ Worin besteht der Vorgang oder Zustand des Wunsches einen Apfel zu essen? Vielleicht empfinde ich Hunger oder Durst oder beides, 202 vielleicht & stelle ich mir dabei einen Apfel vor ˇoder erinnere mich, daß mir gestern einer geschmeckt hat,, vielleicht sage ich: “ich möchte einen Apfel essen”, vielleicht gehe i gehe ich & schaue ich in einen Schrank wo in dem gewöhnlich Äpfel liegen. Vielleicht verbinden sich alle diese Zustände & Tätigkeiten & andere.

/

Es scheint nun irgendwie, als würde man die Intention von außen betrachtet nie als Intention erkennen; als müßte man sie selbst intendieren // meinen // um sie als Meinung zu verstehen. Das hieße aber sie nicht als Phänomen, nicht als bloß gegebene Tatsache, zu … Tatsache an & für sich, zu // nicht als Erscheinung // // Das hieße aber sie nicht als Erscheinung, nicht als Tatsache zu … // betrachten[.|;] (Hier erinnert die Intention an den Willen in der Schopenhauerschen Auffassung.) sondern als etwas [i|I]ntendiertes, – dem eine Richtung gegeben wurde. Und was diese Richtung ist, das wissen wir nicht. ˇ(Es ist etwas, was der Erscheinung als solcher fehlt)⌊. –⌋ [Hineinrücken]6 Das ist natürlich wieder das vorige Problem[.|;] Ddenn der Witz ist, daß man es dem Gedanken ansehen muß, daß er der Gedanke ist, daß das & das der Fall ist. Kann man es ihm nicht ansehen (sowenig wie den Magenschmerzen woher sie rühren) so hat er kein logisches Interesse. – Das kommt auch darauf hinaus, ⌊:⌋ daß man den Gedanken mit der Realität muß unmittetelbar vergleichen können & es nicht erst einer Erfahrung bedürfen kann        Meine Auffassung scheint 203 unsinnig, wenn man sie so ausdrückt: Man soll sehen können, worüber Einer denkt, wenn man ihm den Kopf aufmacht[. W|; w]ie ist ˇdenn das möglich? die Gegenstände, über die er denkt, sind ja gar nicht in seinem Kopf⌊ ! ⌋ (eE﹖bensowenig wie in seinen Gedanken)⌊ (!) ⌋ ﹖[Siehe ursprüngliches M.S.]     Man muß die Gedanken, Intentionen, etc. “von außen betrachtet” als solche verstehen, ohne über eine Bedeutung von etwas unterrichtet zu werden. Denn die Relation des Bedeutens das Bedeuten gehört dann eben mit zum Phänomen des Gedankens.

/

Wenn man den Gedanken betrachtet, so kann also von einem Verstehen keine Rede mehr sein; denn, sieht man ihn, so muß man ihn als den Gedanken dieses Inhalts erkennen , ; es ist nichts zu deuten. – Aber so ist es ja wirklich; wenn wir denken, da wird nichts gedeutet. –

​

Wenn ich sagte: ⌊“⌋[“D|d]as hieße aber die Intention nicht als Phänomen zu betrachten”, so erinnerte hier die Intention an den Willen in der Schopenhauerschen Auffassung. Jedes Phänomen scheint uns [T|t]ot im Gegensatz zum lebenden Gedanken.

​

“Die Intention von außen gesehen”, 204 das hat mit der Frage zu tun, ob eine Maschine denken könnte. “We⌊l⌋ches Phänomen immer man sähe, es könnte nie die Intention sein. Denn die muß ja das Intendierte enthalten. Und jedes Phänomen, wäre ein in sich Vollstandiges, sich um nichts auß ihm [b|B]ekümmerndes, das tot daläge wenn man es für sich betrachtet.”      Und dem analog ist es wenn wir sagen: “Der Wille kann kein Phänomen sein, denn jedes Phänomen geschieht wieder nur, wird von uns hingenommen, ist aber nicht etwas, was wir tun. Der Wille ist nicht ˇetwas, was ich ich geschehen sehe, sondern er besteht darin gleichsam darin, daß wir in der Handlung sind; daß wir die Handlung sind.” Schau auf Deinen Arm & bewege ihn & Du wirst das sehr stark empfinden: “Du beobachtest nicht, wie es sich bewegt beobachtest nicht w⌊i⌋e er sich bewegt, Du machst keine Erfahrung – oder keine bloße Erfahrung – sondern Du tust etwas.” Du kannst Dir dann sagen, daß Du Dir sehr wohl auch den Fall denken könntest, wo daß ganz dasselbe mit Deiner Hand geschehe, aber von Dir beobachtet, nicht ˇvon Dir gewollt. – Aber schließe Deine Augen & bewege den Arm; dann machst Du doch auch eine Erfahrung & nun frage Dich, ob Du Dir wieder vorstellen könntest, Du machest 205 die gleiche Erfahrung, aber ohne sie zu wollen.

​

Wenn man willkürliche von unwillkürlichen Bewegungen unterscheiden will & es wird etwa ausgesprochen, daß sich die willkürlichen Bewegungen des Armes, z.B., von den unwillkürlichen durch ein Gefühl der Innervation unterscheiden, so drängt es Einen zu sagen: “[a|A]ber ich erleide doch diese Erfahrung nicht, ich tue sie doch!” – Aber kann man bei der Erfahrung der Innervation auch noch von einem Unterschied zwischen erleiden & tun reden? Ich möchte sagen: “Wenn ich will so geschieht doch nichts mit mir, weder die Bewegung noch ein Gefühl, sondern ich bin das Agens.” Gut, aber es ist doch sicher daß Du auch Erfahrungen machst, wenn Du den Arm willkürlich bewegst; denn Du siehst (& fühlst) ihn doch sich bewegen ob Du Dich nun beobachtend dazu verhältst oder nicht. Dann versuche ˇalso einmal zu unterscheiden zwischen allen Erfahrungen des Handelns plus dem Tun (das keine Erfahrung ist) & allen diesen Erfahrungen ohne das Element des Tuns. Überlege, ob Du dieses so ein Element auch weiter noch für bedarfst, oder ob es Dir 206 nun obsolet erscheint. – Und freilich kannst Du mit Recht sagen, daß wenn Du etwas tust, nichts mit Dir geschieht; denn, die Phänomene des tu Tuns in diesen Fällen sind eben andere, als die des Beobachtens⌊,⌋ ˇetwa⌊,⌋ einer Reflexbewegung. Klar wird dies übrigens erst, wenn man die ˇsehr verschiedenen Fälle dessen ˇbetrachtet, was man willkürliche gewollte Handlungen & was man ungewollte ˇoder unwillkürliche Vorgänge Phänomene unseres Lebens nennt. (Davon an mehr an einer anderen Stelle.)

∕∕

Mit “Intention” meine ich hier das, was das Zeichen im Gedanken verwendet. Die Intention scheint zu interpretieren, die [E|e]ndgültigec endliche Interpretation zu geben, aber nicht ein weiteres Zeichen oder Bild, sondern etwas Anderes, das, was man nicht wieder interpretieren kann. Aber ein psychologisches Ende ist erreicht, kein logisches.      Denken wir eine Zeichensprache, eine ‘abstrakte’, ich meine eine die uns fremd ist, in der wir uns nicht heimisch fühlen⌊,⌋ (in der, wie wir sagen würden, wir nicht denken.) (wir haben früher einmals so ein Beispiel erwähnt), & denken wir uns diese Sprache interpretiert durch eine Übersetzung in eine, wie wir sagen möchten, unzweideutige Bildersprache, eine Sprache die aus perspektivisch gemalten Bildern des Darzustellenden besteht. Es 207 ist ganz klar, daß es viel leichter ist, sich verschiedene Deutungen der Schriftzeichen zu denken, als eines in gewohnter Art gemalten Bildes⌊,⌋ ˇdas etwa ein Zimmer mit gewöhnlichen Mobeln darstellt. Hier werden wir auch geneigt sein zu denken sagen , es gebe hier keine andere [m|M]öglichkeiten der Deutung mehr.

∕∕

Wir könnten da auch sagen, wir lebten nicht in der Zeichensprache, wohl aber im gemalten Bilde.

​

(Das hängt auch damit zusammen daß, was wir ein ‘ähnliches Portrait’ nennen, nicht ein Bild nach in irgend einer beliebig festgesetzten Projektionsart ist. “Ähnlichkeit” bedeutet hier etwas Ähnliches wie “Verwechselbarkeit”.)

∕∕

“Nur das intendierte Bild reicht als Maßstab an die W⌊i⌋rklichkeit heran. Von außen betrachtet steht es gleich tot & isoliert da”. Es ist als hätten wir ein Bild erst so angeschaut, daß wir in ihm leben & die Gegenstände in ihm uns als wirkliche umgeben, & dann träten wir zurück & wären nun außerhalb, sähen den Ra h men & das Bild wäre eine bemalte Fläche. So, wenn wir intendieren, umgeben uns die Bilder der Intention & wir leben unter ihnen. Aber wenn 208 wir aus der Intention heraustreten, so sind es bloße Flecke auf einer Leinwand, ohne Leben & ohne Interesse für uns. ⌊(⌋Wir könnten auch sagen:⌊)⌋ Wenn wir intendieren, leben wir im Raum der Intention unter den Schatten der Intention // unter den Bildern (Schatten) der Intention // zugleich mit den wirklichen Dingen. Denken wir, wir sitzen im verdunkelten Kino & leben im Film // im Vorgang des Films // . Der Saal werde nun erhellt aber das Lichtspiel auf der Leinwand gehe weiter. Aber jetzt sehen wir es plötzlich “cvon außen”c // Aber jetzt stehen wir plötzlich außerhalb als Bewegungen von lichten & dunkeln Flecken auf einer Leinwand. // Aber jetzt stehen wir plötzlich außerhalb & sehen es als Bewegungen … // (Im Traum geschieht es manchmal, daß wir eine Geschichte erst lesen, & dann auf einmal in ihr selbst agieren. Und nach dem Aufwachen aus einem Traum ist es manchmal als wären wir aus dem Traum heraus zurück getreten & sehen ihn jetzt, als ˇein fremdes bloßes Bild, vor uns.) Und es heißt auch etwas “in den Seiten eines Buches leben”. (Das hängt damit zusammen, daß ˇdas Dasein unser ⌊es⌋ Körper ⌊s⌋ für das Dasein unserer Erfahrung ganz unwesentlich ist. ⇒ (Siehe: Auge & Gesichtsraum.)   (Damit vergleiche man auch die Bemerkung: Wenn wir einen Satz verstehen, 209 erhält er für uns Tiefe.)

∕∕

Nicht das findet statt, daß sich dieses Symbol nicht mehr deuten läßt, sondern: ich deute nicht. ∣ Denn das Symbol, worin ich gegenwärtig bin, ist eine Stufe auf meinem Gedankenwege. Und wenn ich deute, so schreite ich von einer Stufe zur andern nächsten . ∣ Ich deute nicht, wenn weil ich mich in dem gegenwärtigen Bild natürlich fühle. Wenn ich deute, so schreite ich auf meinem Gedankenweg von Stufe zu Stufe.

∕∕

Sehe ich das gedachte Symbol “von außen” an, so kommt es mir zum Bewußtsein daß es so & so gedeutet werden könnte; ist es eine Stufe meines Gedankenweges, so ist es ein mir natürlicher Aufenthalt & es beschäftigt (& beunruhigt) mich seine weitere Deutbarkeit nicht. – Wie ich die Tabelle, den Eisenbahnfahrplan, bei mir habe ohne daß es mich beschäftigt, daß eine Tabelle auf verschiedene Art deutbar ist.

​

Wenn ich davon redete, daß meine Vorstellung, um ein Portrait zu sein auch den Namen des Dargestellten tragen muß, so 210 meinte ich nicht, daß ich mir ihn mit seinem Namen zugleich vorstellen muß. Denn wenn ich etwa sage: “ich sehe doch nicht bloß ein Bild vor mir, daß dem N (aber vielleicht auch andern Leuten) ähnlich sieht, sondern ich weiß doch, daß es er ist, ihn darstellt”, so könnte ich fragen: wann weiß ich das, & was heißt es das zu wissen? Aber es muß auch während des Vorstellens gar nichts statthaben was ich dieses “Wissen” nennen könnte. So etwas kann etwa nach der Vorstellung vor sich gehen, indem ich dann vom Bild zum Namen übergehe, vielleicht sage ich hätte mir den N vorgestellt, während zur Zeit der Vorstellung nichts sie als die Vorstellung des N charakterisierte, als etwa eine Ähnlichkeit. Auch konnte der Vorstellung etwas Der Vorstellung konnte etwas vorangehen, welches den Bezug auf N ausmacht ausmachte . // welches Und so ist die Intention nicht eine Begleitung der Vorstellung sondern liegt in deren Vorgeschichte oder Folgen. Und so begleitet die Interpretation die Vorstellung nicht, sondern liegt in dem Weg, auf dem die Vorstellung liegt. der über die Vorstellung führt. // sondern der Weg, auf dem die Vorstellung liegt, gibt ihr die Interpretation. //      Alles das erscheint klarer, wenn man statt des Vorstellens das Zeichnen eines Bildes annimmt. // Alles das wird würde klarer, wenn man sich denkt, das Vorstellen werde bei 211 einem Menschen ersetzt, dadurch daß er Bilder zeichnete. // Das Alles wird klarer wenn man sich das Vorstellen ersetzt denkt durch ein Zeichnen von Bildern, wenn man sich ˇetwa Menschen denkt bei denen das Vorstellen durch so einen Vorgang vertreten wird. //

∕∕

Wenn ich den Vorgang der Intention beschreiben will, so fühle ich vor allem, daß sie noch am ehesten leisten kann, was sie soll // , wenn sie ein äußerst getreues Bild von dem enthält, was sie intendiert. Aber ferner, daß auch das nicht ausreicht, weil ja das Bild, was immer es ist, sich verschieden deuten läßt; daß also dieses Bild doch wieder isoliert dasteht. Wie man das Bild allein in's Auge faßt, ist es plötzlich tot & es ist, als wäre ihm etwas genommen worden, was es zuvor belebt hatte. Es ist kein Gedanke, keine Intention & wie immer wir es uns begleitet denken, durch artikulierte oder unartikulierte Vorgänge & durch welche Empfindungen immer, es bleibt isoliert, weist nicht aus sich heraus auf eine Realität außer ihm sich . ˇ [Neue Zeile] Nun sagt man: “Freilich intendiert das Bild nicht, sondern wir müssen mit ihm ⌊(⌋etwas⌊)⌋ intendieren”. Aber wenn dieses Intendieren⌊,⌋ ˇMeinen ⌊(⌋wieder⌊)⌋ etwas ist was mit dem Bild geschieht, so sehe ich nicht ein, warum der das an einen Menschen gebunden sein soll. Man kann ja auch den Vorgang der 212 Verdauung als chemischen Prozess studieren unabhängig davon, ob er in einem [l|L]ebewesen stattfindet. Wir wollen sagen: “Das Meinen Intendieren ist doch wesentlich ein geistiger, lebender Vorgang, ein Vorgang des // Bewußtseins, Lebens // ˇbewußten Lebens , nicht der toten Materie”. Aber was soll einen solchen so einen ausmachen, als die besondere spezifische Art dessen, was vorgeht, ⌊–⌋ solange wir an einen Vorgang denken. wir eben von einem Vorgang reden. Wenn Und nun kommt es uns soc vor, daß als ob gar kein Vorgang, welcher Art immer, das Intendieren sein kann. – Wir sind eben ˇhier mit der Grammatik des Vorgangs nicht zufrieden, & nicht mit der spezifischen Art eines Vorgangs. – Man könnte sagen: jeden Vorgang würden wir in diesem Sinne ‘tot’ nennen!

​

Denken wir uns, Sagen wir, denr Wunsch, daß dieser Tisch ˇum ein Stück höher wäre, sei der Akt daß ich meine Hand über den Tisch halte, so hoch als ich ihn wünschte. Nun ist der Einspruch Einwand : “Die Hand über dem Tisch kann nicht der Wunsch sein: sie drückt nicht aus, daß der Tisch höher sein sollte; sie ist wo sie ist & der Tisch ist wo er ist. Und es würde auch nichts ändern, nützen, wenn ich irgend eine andere Geste machte⌊.⌋”. –

∕∕

“Die Meinung hat eine Richtung (einen Sinn), den kein bloßer Vorgang hat.” (Fast könnte man sagen: “die Meinung 213 geht, während jeder Vorgang steht”.)

​

ˇNun aber: Denke ich mir das Aussprechen des Wunsches als den Akt des Wunsches, so erscheint mir das Problem als gelöst; weil ich im System der Sprache das Medium zu haben scheine, worin der Satz nicht tot ist.

​

Wenn wir uns den Ausdruck des Wunsches als Wunsch denken, so ist das ˇ ungefähr // beinahe // , wie wenn wir uns, zu in gewissen Zwe⌊c⌋ken Überlegungen, Lebewesen vorstellen, die sich etwa nur entlang den Linien eines gewissen Netzes auf der Erde fortbewegten, oder dergleichen.

​

Nun aber würde man sagen: Auch wenn das Aussprechen des Wunsches der Wunsch ist, so ist doch nicht die ganze Sprache bei diesem Aussprechen zugegen, & ist es dann der Wunsch!      Wie hilft dann die Sprache? Nun es ist eben nicht nötig, daß etwas außer dem Ausdruck zugegen sei.

​

Man könnte quasi in der Grammatik der Sprache die ganzen Zusammenhänge auffinden (nachschlagen). Das ganze Netz in das der Satz gehört, 214 ist da zu sehen.

​

Fragt man: Wenn man fragt: “[W|w]arum stoßen wir uns denn nicht an den bloßen Bildern Vorgängen an dem bloßen Bild, wenn wir denken, meinen, etc.?”, so müssen wir uns sagen: wir denken dann ja ja dann nicht, ob das Bild der Gedanke⌊,⌋ ˇdie Meinung ist, etc., sondern wir gebrauchen, durchlaufen,, Bilder, Sätze etc..

​

Aber freilich, wenn Du das Bild den Wunsch nennst (z.B. daß dieser der Tisch höher wäre), was Du dann tust ist, das Bild mit einem Ausdruck unserer Sprache der Sprache vergleichen, & dem entspricht es allerdings freilich nicht, so wie wir es wünschen außer es ist Teil eine[r|s] Sprache System⌊s⌋⌊,⌋ & kann das in unsere Sprache übertrag[en|ba]⌊r⌋ werden kann. ist.

∕∕

Man sagt: wie kann den diese Haltung der Hand, dieses Bild, der Wunsch sein, daß das & das der Fall wäre; sie ist weiter nichts als eine Hand über einem Tisch & steht allein & ohne Sinn da! Wie eine einzelne Kulisse aus der einer Aufführung eines Theaterstücks, die allein stehen geblieben ist. // Wie eine einzelne Kulisse, die von der Aufführung eines Theaterstücks, allein in einem Zimmer Raum stehen geblieben ist. // Sie hatte Leben nur im Stück. Nun diese Stellung einer Hand 215 über einem Tisch ist auch nicht der Wunsch, der Tisch möge höher sein, wenn sie nicht systematisch in diesen Ausdruck übersetzt werden kann.

​

Wir sehen in der Geste den eigentlichen Schatten der Erfüllung nicht; den unzweideutigen, oder nicht mehr deutbaren.

​

Wir fragen: “wünscht eine Hand über einem Tisch?” Und wünscht irgend etwas, was wir, ob es geistiger oder materieller Natur ist, hinzufügen mögen? Ist in irgend so einer Situation oder einem Vorgang wirklich das was gewünscht wird da? – Und was ist unser Vorbild für dieses Dasein? Ist es nicht unsere Sprache? Wo ist denn das gegeben, was den Wunsch zu diesem Wunsche macht, obwohl er doch nur Wunsch ist? Eben im ausgedrückten Wunsch.

∕∕

“Das Wünschen muß doch ˇzeigen was gewünscht wird, es muß doch, was gewünscht wird in der Wunschsphäre vorbilden.” Aber welcher wirkliche Vorgang schwebt Dir denn hierfür als Vorbild vor? (Welches ist denn der Spiegel in welchem dem Du Dir das Gewünschte gesehen denkst?)

∕∕

“Die Geste versucht vorzubilden,” möchte 216 man sagen, “aber kann es nicht”.

​

Kann man sagen, daß während wenn ich wünsche, mein Wunsch die Erfullung vorzubilden scheint? Er scheint dann gar nichts zu tun // gar nicht etwas zu tun // [. E|; e]s fäl⌊l⌋t mir nichts [s|S]eltsames an ihm auf. Nur wenn wir die sprachliche Äußerung des Wunsches betrachten, werden wir dessen gewahr. fällt uns so etwas auf. // entsteht dieser Schein.

∕∕

Wir betrachten einen Vorgang, den wir einen den Vorgang des Wunsches nennen würden, daß dieser Tisch höher wäre. Aber in diesem Vorgang ist die Erfüllung auch nicht scheinbar enthalten vorhanden . Nun sagt man[;|:] “Aber dieser Vorgang soll ja ein Schatten gerade der gewünschten Tatsache sein & das sind doch diese Handlungen nicht.” Aber warum sagst Du denn, daß der Wunsch das sein soll?! “Nun, weil er der Wunsch ist, es möge gerade das der Fall sein.” Ja, & das ist die einzige Antwort, die Du darauf geben konntest. Und nun ist jener Vorgang also doch der Schatten, soweit er dem Ausdruck des Wunsches in der Wortsprache systematisch entspricht. Dieser Schatten ist im Wunschvorgang der Wortsprache. ⌊ (In der Sprache treffen sich Wunsch & Erfüllung.) ⌋

​

217 Bedenke, daß der Ausdruck des Wunsches der Wunsch sein kann & dieser Ausdruck seinen Sinn nicht durch die Anwesenheit eines besonderen Geistes hat!

​

Denke auch an den dem unsern ˇganz analogen Fall: “dieser Tisch ist nicht 80 cm hoch”; muß die Tatsache daß er 90 cm, also nicht 80 cm hoch ist, den Schatten der Tatsache enthalten daß er 80 cm hoch ist? Warum macht es diesen Eindruck? Macht etwa der Tisch der [8|9]0 cm hoch ist, wenn ich ihn sehe, auch den schatten[f|h]aften Eindruck, daß er die Höhe hat, die er nicht hat?   Das wäre etwa als mißverstünden wir die Behauptung “⊢~p” dahin, sie enthielte die Behauptung “⊢p”; etwa wie “⊢ p ∙ q” in einem Sinne “⊢p” enthält

​

Es beschreibt mir jemand die Vorgänge seine Handlungen als er, wie er sagt, den Wunsch hatte, der Tisch möge 10 cm höher sein. Er sagt, er habe die Hand 10 cm über den Tisch gehalten. Ich antworte: “Aber wie weißt Du daß Du nicht bloß den Wunsch hattest, der Tisch solle höher sein, denn auch dann hättest Du die Hand in irgend einer Höhe über dem Tisch gehalten”. Nun sagt er: “[i|I]ch werde doch wissen, was ich gewünscht habe”. Ich: “Gut, aber ich will wissen woran Du Dich erinnerst, wenn Du Dich an Deinen Wunsch erinnerst; was Du die Handlung der Vorgang 218 Deines Wunsches war; & was Dich sagen macht, Du hättest gerade das gewünscht.” Er: “Ich weiß, daß ich absichtlich die Hand gerade 10 cm hoch gehalten habe.” Ich: “Aber worin bestand gerade diese Absicht?” – Ich könnte auch fragen: “Hast Du auch ˇgewiss im Maßstab 1 : 1 gewünscht? & wie weißt Du das?”      Hätte er den Wunschvorgang so beschrieben: “[I|i]ch habe gesagt, ‘ich möchte den Tisch 10 cm höher haben’”, so wäre die Frage, wie konnte er wissen, was er wünschte; … wie er wissen konnte was er wünschte, nicht aufgetreten. (Außer man hätte etwa weiter gefragt: “Hast Du di⌊e⌋se Worte auch so gemeint, wie sie gewöhnlich gemeint werden?”)       Und es läuft endlich immer darauf hinaus, daß er den & den diesen Vorgang ohne weitere Meinung eben den Wunsch nennt, daß das geschehen möge. ⌊ [Äußerung, nicht Beschreibung!] ⌋

​

“Wie weiß ich, daß ich mich an ihn erinnere, wenn die Erinnerung ein Bild ist?” Aber inwiefern weiß ich es denn?   (“Wie kann ich mich an einen bestimmten von zwei Menschen erinnern, die ganz gleich aussehn?”)

∕∕

Wir sagen “der Satz ist keine bloße ◇ Lautreihe, er ist mehr”; wir denken daran daß ein chinesischer Satz für uns ein⌊e⌋ bloße Lautreihe Reihe von Lauten ist, daß 219 das eben heißt, daß wir ihn nicht verstehn & wir sagen, das kommt daher daß wir beim chinesischen Satz keinen Gedanken haben (ˇZ.B. das chinesische Wort für ‘rot’ bringt in uns z.B. keine rote Vorstellung hervor). “Also ist das, was den sinnvollen Satz von bloßen Lauten unterscheidet der hervorgerufene seelische Vorgang // der hervorgerufene Gedanke // .” Der Satz ist wie ein Schlüsselbart dessen einzelnen Auszahnungen so angeordnet gewisse Hebel der Seele in gewisser Weise bewegen. Der Satz spielt gleichsam auf dem Instrument der Seele ein Thema ( den einen Gedanken). Wozu aber soll ich jetzt außer dem systematischen Spiel der Worte noch ein mit diesem parallel laufendes Spiel geistiger Elemente annehmen. Es vermehrt ja nur die Sprache um etwas Gleichartiges.

​

Der Satz sei: “N ging heute nachmittag ins Senathaus”. Der Satz ist für mich kein bloßer Schall // Klang // Laut , er ruft in mir eine Vorstellung hervor etwa eines Mannes in der Nähe des Senathauses. Aber der Satz & diese Vorstellung ist nicht bloß ein Klang & eine schwache Vorstellung; sondern der Satz hat es sozusagen in sich diese Vorstellung hervorzurufen, aber auch andere Konsequenzen, & das ist sein Sinn. Die Vorstellung scheint nur ein schwaches Abbild dieses Sinnes, oder, sagen wir, nur eine Ansicht dieses Sinnes. – 220 Aber was meine ich denn damit; sehe ich eben den Satz ˇeben nicht als Glied in einem System von Konsequenzen?

​

Nehmen wir an der obige Satz riefe in mir ein sehr deutliches Bild des N auf dem Wege zum Senathause hervor; in diesem Bild sei auch die untergehenden Sonne (“abend”) & zu sehen & ein Kalenderblatt mit dem heutigen Datum. Wenn ich dieses Bild, statt es durch den Satz hervorrufen zu lassen, malte & es dem Andern als Mitteilung statt des Satzes zeigte, so würde kann er ˇwieder geneigt sein zu sagen es müsse drücke einen Gedanken aus, man er müsse es verstehen; & als Akt des Verstehens würde er wahrscheinlich an eine Übersetzen in die Wortsprache denken.

​

“Ich komme am 24ten Dezember nach ⌊in⌋ Wien” an”, das sind doch nicht bloße Worte! Gewiß nicht; wenn ich sie lese, geht außer dem Wahrnehmen der Worte noch verschiedenes in mir vor sich: ich empfinde etwa Freude, stelle mir etwas vor & dergleichen. – Aber ich meine doch nicht bloß⌊,⌋ ˇdaß der Satz vom ˇdaß mit dem Satz verschiedenen mehr oder weniger unwesentlichen Begleiterscheinungen vor sich gehn sollen; ich meine, der Satz hat doch einen bestimmten Sinn & den nehme ich wahr. erfassen ich. Aber was ist denn dieser bestimmte Sinn? Nun, daß diese 221 bestimmte Person, die ich kenne, dort & dort hin kommt, etc.. Ja, & wenn Du den Sinn angibst, bewegst Du Dich in der ◇ grammatischen Umgebung des Satzes umher. Du siehst dann die verschiedenen Tra⌊n⌋sformationen & Konsequenzen des Sa⌊t⌋zes als präformiert an; & das sind sie, sofern sie in einer Grammatik niedergelegt sind. (Du betrachtest eben den Satz, wie einen Zug eines gegebenen Spiels.)

​

Ich sagte, es sei das System der Sprache, welches den Satz zum Gedanken macht & ihn uns zum Gedanken macht.    Es heißt nicht: es ist das System der Sprache, welches uns den Satz, wenn wir ihn gebrauchen aussprechen , zum Gedanken macht, denn das System ist dann nicht anwesend & es braucht gar nichts, das uns den Satz lebendig macht, da die Frage der Lebendigkeit gar nicht auftaucht. Wenn wir dagegen fragen: “warum kommt uns der Satz nicht isoliert & tot vor, wenn wir nämlich über sein Wesen ihn , seinen Sinn, den Gedanken, etc., nachdenken”, so kann man sagen, daß wir uns dann im System der Sprache weiterbewegen.

​

Gemäß den Worten “ich erfasse den Sinn” oder “ich denke den Gedanken dieses Satzes, nimmst Du einen Vorgang an, der zum Unterschied vom bloßen Satzzeichen 222 diese Konsequenzen beinhaltet.

∕∕ ∫

“Der Gedanke, dieses seltsame Wesen”: aber er kommt uns nicht seltsam vor wenn wir ˇihn denken. Er kommt uns seltsam vor, wenn wir uns sagen: daß er die Gegenstände im Geist zusammenstellt, weil es eben der Gedanke ist, daß dieser Mensch das tut; er ist nicht ein Zeichen oder Bild, denn davon müßte ich erst wieder wissen, wie es gemeint ist; der Gedanke ist nicht etwas Totes, denn für mich geschieht dann wirklich, was ich denke.       Was es macht Woher diese seltsame Betrachtungsweise?     Was es macht, daß man meint, der Gedanke, der gedachte Satz, enthalte die Realität, ist, daß man bereit ist von ihm zur Realität überzugehen & diesen Übergang als etwas bereits in ihm potentiell enthaltenes empfindet (wenn man nämlich darüber nachdenkt), denn wir sagen: “dieses Wort meinte ihn”. Wir empfinden diesen Übergang ⌊(⌋als⌊)⌋ legitim, wie den erlaubten Zug eines Spiels.

∕∕ /

Der Gedanke kommt uns nicht geheimnisvoll vor während wir denken, sondern nur, wenn wir, gleichsam retrospektiv, sagen: “wie war das möglich?” Wie war es möglich, daß der Gedanke von diesem 223 Menschen selbst handelte? Aber hier wundere ich mich // Aber hier erstaune ich // nur über meinen einen sprachlichen Ausdruck, den ich jetzt mißverstehe.

∕∕ /?

Der Gedanke kommt uns geheimnisvoll vor. Aber nicht während wir denken. Auch meinen wir nicht psychologisch merkwürdig . Wir ; wir sehen in ihm nicht nur eine besondere Art, Bilder & Zeichen zu machen // herzustellen // ; sondern das Denken erscheint uns als eine Art die Realität einzufangen. // ; sondern wir scheinen mit ihm die Realität einzufangen. // ; sondern es scheint uns, als hätten wir in mit ihm die Realität eingefangen //

∫

Er scheint uns ein seltsamer Vorgang nicht wenn wir ihn ansehen; sondern wenn wir uns von der Sprache führen lassen, wenn wir ⌊(⌋das⌊)⌋ ansehen, was wir über ihn sagen.     Dieses Geheimnis verlegen wir in die Natur des Vorgangs. (Wir deuten das Rätselhafte das durch unser Nicht-Verstehen das Unverständnis der Grammatik unserer Sprachformen unserer Sprachform hervorgebracht wird, als // das durch unser ein Mißverstehen unserer Sprachform hervorgebracht wird, … der Grammatik unserer Sprachformen hervorgebracht wird, als … // … das durch [ Unklarheit ] [ Trübe unseres Blicks ] [ Dunkelheit ] unser Unverständnis unserer sprachlichen Ausdrucksform … // ˇdas Rätselhafte eines uns unverständlichen Vorgangs.)

​

224    “Das Denken ist ein merkwürdiger Vorgang, denn wenn ich daran denke, was morgen geschehen wird, so bin ich im Geiste in der Zukunft.” Man muß eben die Grammatik Grammatik des Satzes “ich bin im Geiste in der Zukunft” verstehen, um nicht zu glauben, daß hier die Zukunft in seltsamer Weise im Sinn eines Satzes, in der Bedeutung von Worten der Worte erfaßt wird. So meint man auch die unendliche Reihe der Kardinalzahlen sei irgendwie vor unserm geistigen Auge, wenn wir jenen Ausdruck sinnvoll gebrauchen können

​

Was heißt: “dieses Portrait Bild ist für mich er”? Ich habe dieselbe Einstellung zum zu dem Portrait, wie zu dem Menschen selber. Denn die unterscheide doch zwischen ihm & seinem Bild.

​

Ein Gedankenexperiment, ⌊(⌋das⌊)⌋ kommt auf dasselbe hinaus, wie ein Experiment, welches das man, statt es auszuführen, aufzeichnet, malt oder beschreibt. Und das Ergebnis des ˇGedanken[E|e]xperiments ist dann das erdichtete Ergebnis des erdichteten Experiments.

​

“Der Sinn dieses Satzes war mir gegenwärtig”, was geschah da?

∕∕ /?

225 “Das kann nur Einer jemand sagen, der davon überzeugt ist”. Wie hilft ihm die Überzeugung ⌊(⌋dabei⌊)⌋, wenn er es sagt? – Ist sie dann neben dem gesprochenen Ausdruck vorhanden? (Oder wird sie von diesem gleichsam zugedeckt, wie ein leiser Ton von einem lauten, so daß, so daß sie gleichsam nicht mehr gehört werden kann, wenn man sie laut ausdrückt?) Wie, wenn Einer sagte: “damit man eine Melodie nach dem Gedächtnis singen kann, muß man sie im Geiste hören & sie nachsingen”?

​

Versuche folgendes: Sage einen Satz, etwa: “das Wetter ist heute sehr schön” ; so, & nun ; & nun denke den Gedanken dieses Satzes, aber ohne Satz, sondern rein.

​

“Es scheint als würde man die Intention von außen betrachtet nie als Intention erkennen; a⌊l⌋s müßte man sie selbst meinen, um sie als Meinung zu verstehen erkennen ”   Kann man Magenschmerzen, von außen betrachtet, als solche verstehen? Was sind Magenschmerzen von außen betrachtet? Es gibt doch hier gar kein außen & innen! Freilich, sofern das Meinen eine spezifische Erfahrung ist, kann wird man keine andere “meinen” nennen. Nur erklärt keine Besonderheit der Empfindung der Erfahrung ˇdie den Satz begleitet die Richtung der 226 Meinung. // Nur erklärt keine Besonderheit der Empfindung die Richtung der Meinung // Und wenn wir sagten “von außen betrachtet kann man die Intention nicht als Intention erkennen etc.”, so wollten wir auch gar nicht sagen, die Meinung sei eine besondere Erfahrung, sondern sie sei nicht etwas was geschähe oder uns geschähe (denn das wäre ja tot) aber etwas was wir tun. (Das Subjekt falle hier nicht aus der Erfahrung heraus, sondern sei so in ihr involviert, daß sich die Erfahrung nicht beschreiben ließe.)

​

Es ist beinahe als sagte man: wir können uns nicht dort & dort hin dorthin // an einen Ort // gehen sehen, da wir selbst gehen[.|⌊(⌋]und also nicht stehen & zuschauen können.⌊)⌋. Aber hier laborieren wir eben, wie so sehr oft, an einer Ausdrucksweise, die inadaequat ist, die wir abschütteln wollen, & doch aber zugleich gebrauchen, & ˇwir kleiden den Protest gegen unsere eigene Ausdrucksweise in einen Satz in dieser Ausdrucksweise. , der ihr angehört. // in eine sachliche Kritik in dieser Ausdrucksweise. // in einen scheinbar sachlichen wissenschaftlichen Satz ⌊(⌋in⌊)⌋ dieser Ausdrucksweise. // Denn, wenn man sagt, “wir sehen uns dorthin gehen”, so meint man eben, daß wir sehen man sieht , was man sieht, wenn man selbst geht, & nicht was man sieht wenn ein Anderer geht. Und man hat auch eine bestimmte Seherfahrung wenn man selbst geht.

​

227 D.h., man redet von einem Fall, der Erfahrung entgegengesetzt, in welchem das Subjekt inextrikabel involviert ist // in dem welchem das Subjekt wie ein Element in einer chemischen Verbindung gebunden ist. Aber woher nimmt man diese Idee? Den Begriff des lebenden Tuns im Gegensatz zum toten Phänomen.

​

Denken wir uns, jemand würde nun sagen: “selbst gehen ist keine Erfahrung”.

​

Wir wollen sagen: “Wenn wir meinen, so ist hier kein totes Bild (welcher Art immer), sondern es ist als gingen wir auf jemand zu. Wir gehen auf das Gemeinte zu.

​

Aber hier konstruieren wir fälschlich einen Gegensatz zwischen der Erfahrung & etwas anderem, als ob die Erfahrung das wäre, wenn man ruhig sitzt & die Bilder an sich vorüberziehen läßt.

​

“Wen[m|n] man meint, so meint man selber”; so bewegt man sich selber. “Man stürmt selber vor & kann daher das Vorstürmen nicht auch beobachten”. Gewiß nicht.

​

Ja, meinen ist, wie wenn man auf jemanden zugeht.

​

228 ⍈ [Zu S. 149] Uns interessiert das Denken als Kalkül; nicht als Tätigkeit der menschlichen Phantasie.

​

⍈ [Zu S. 155] Sagt es mir, z.B., “in einer Schenke sitzen zwei Leute & trinken Wein”? Nur dann, wenn dieser Satz in irgend einer Form außer dem Bild im Vorgang des Verstehens auftritt. Wenn ich mir also etwa beim Betrachten des Bildes sage: “hier sitzen zwei Leute etc.”. ∣ S Aber so einen Fall meine ich ja nicht. Sondern ich meine den, in welchem das Bild uns nur sich selber selbst gibt. Dann heißt “es sagt mir etwas” etwas [ä|Ä]hnliches wie “diese Formen sind mir wohlvertraut” ∣ Wenn mir das Bild in diesem Sinne etwas sagt, so sagt es mir Worte. Aber inwiefern erklärt es sich in mit diesen Worten? Für die Realität ist es doch ein Umweg, sich über durch die Sprache zu [E|e]rklären.    Also ist der Tatsache, daß das Bild mir etwas sagt nicht wesentlich, daß mir bei seinem Anblick Worte einfallen. Denn das Bild sollte doch die direktere Sprache sein. Hier ist es wichtig zu verstehen, daß man statt eines Bildes auch einen Ausschnitt aus der Körperlichen Wirklichkeit hätte betrachten können. Denn die Beziehung die wir zu einem gemalten Tisch haben hat zwar historisch ihren Ursprung in unserer Beziehung zu wirklichen Tischen, aber diese tritt in jene nicht ein. 7

Editorial notes

1) Continuation from Ms-113,144r.

2) See facsimile; arrow pointing right.

3) See facsimile; line connecting this sentence with the following one.

4) See facsimile; line connecting this sentence with the following one.

5) See facsimile; line connecting this remark with the following one.

6) See facsimile; arrow pointing right, indicating that the line shall be indented.

7) Continuation in Ms-115,1.