| | | | | |
Prof. L. Wittgenstein Trinity
College Cambridge
1 | | |
| | | | | | ⌊⌊ Nun,
was würde er ein ‘bloßes Deuten’
nennen? Etwa wenn er sagte: “Das
sieht nicht wie ein  aus aber es soll eins
sein.” Der andre Fall wäre:
“Doch das ist ein aus aber es soll eins
sein.” Der andre Fall wäre:
“Doch das ist ein  ; nur ein bißchen
anders geschrieben.” ⌋⌋ ; nur ein bißchen
anders geschrieben.” ⌋⌋
| | |
| | | ✢ | | |
6.6.41.
 einmalc als einmalc als
 , einmalc
oder als sein
Spiegelbild . –
Wenn mir ein ein vertrauenswürdiger Mensch sagt,
daß mich versichert: daß
seine Erfahrung ganz so ist, wie wenn er einmal einen,
einmal einen andern Gegenstand sieht, – kann ich das
als Evidenz dafür,
daß es sich hier um ein verschieden Sehen
(& nicht, etwa, um ein verschieden
Denken) handelt? Und warum kann ich
nicht? Wenn er intelligent ist,
& die Sprache versteht, sollte er es doch wissen! , einmalc
oder als sein
Spiegelbild . –
Wenn mir ein ein vertrauenswürdiger Mensch sagt,
daß mich versichert: daß
seine Erfahrung ganz so ist, wie wenn er einmal einen,
einmal einen andern Gegenstand sieht, – kann ich das
als Evidenz dafür,
daß es sich hier um ein verschieden Sehen
(& nicht, etwa, um ein verschieden
Denken) handelt? Und warum kann ich
nicht? Wenn er intelligent ist,
& die Sprache versteht, sollte er es doch wissen!
| | |
| | | | | | Ich kann sein Zeugnis
nicht annehmen, weil es kein Zeugnis ist.
| | |
| | | | | | “Geneigt sein zu
sagen …” vergleiche “Vouloir
dire”.
2
| | |
| | | / | | |
Kann “ich bin geneigt zu sagen: ‘ich habe
Schmerzen’” die Aussage “ich habe
Schmerzen” ersetzen? – Warum
nicht? Das ist kein Einwand: daß die
Sätze von [v|V]erschiedenem handeln.
| | |
| | | ∫ / | | |
Bald hätte ich gesagt: “dieser Ersatz ließe
sich auch der alten Auffassung
”! Aber
was ist die ‘alte Auffassung’? Sie ist,
glaube ich, durch ein Bild charakterisiert: Das
des Sehens, des Anschauens eines Gegenstandes, der nicht unter
den physikalischen Gegenständen, sondern wo anders
sich befindet
seinen Platz hat |
.
(Denn warum soll ich mir die Anwesenheit
dieses Gegenstands vor meinem geistigen Auge nicht eben als den Reiz
denken, der die Geneigtheit, das & und das zu sagen,
ausmacht?)
| | |
| | | ? / | | | ¤
Das Beispiel von dem ‘Wissen, wie man zu antworten
hat’ zeigt 3
| | |
| | | | | | Da ich aus
Versehen zwei Seiten überblättert habe so will ich den Raum
als Tagebuch benutzen. Ich hatte den Gedanken, noch jemals
fur mich über
philosophi⌊s⌋che Probleme nachzudenken schon
ganz aufgegeben. So war es ganz
unerwartet, daß ich wieder, wenn noch so schwach,
denken konnte. Und
Gott weiß wie lange es dauern
wird. – Ich habe viele
Herzschmerzen gehabt. Und
ware ich starker,
könnte ich verdauen, was kommt, so
ware alles das zum Guten.
| | |
| | | | | | Unsere
größten Dummheiten können sehr weise
sein.
| | |
| | | | | |
Meine Nerven sind in schlechtem Zustand. Ich weiß
nicht warum. Ich bin häufig, ohne
G[i|r]und innerlich aufgeregt; zittere und
vibriere gleichsam 4 innerlich, daß ich mich
furchte, wenn dieser Zustand
stärker wird ich könnte ganz außer mir geraten,
oder meine Seele könnte sozusagen
überschnappen. Wie ein Körper der auf
einer seiner Flächen im Gleichgewicht ist, wenn er
weit genug aus der dieser
Gleichgewichtslage herausgehoben wird, in eine
andere fallen kann.
Ich fürchte mich, wie schon so oft im Leben, vor
Müdigkeit, vor Erschopfung.
Welchen Grund, allerdings, ich zur Erschöpfung
haben soll, weiß ich nicht.
| | |
| | | | | | Unterschätze nie Deine
Nebenbuhler! – ihren Verstand, ihr Talent, ihr
Können! | | |
| | | | | |
21.6. I've got to be able
to take it. Wenn ich ein
Waschlappen bin, ich mir nichts
gutes erwarten. – Willst Du Güte und Stärke
in der Welt, warum willst Du sie nicht selber liefern?5 | | |
| | | ? / | | |
¤ nur, daß man bei Beschreibung der
Mathematik nicht von Wissen & Mitteilung
reden muß﹖
| | |
| | | ∕∕ \ | | |
7.6.41.
Der Gegenstand vor dem
geistigen (inneren) Sinnesorgan ist
Erklärung,
Schein⌊-⌋[e|E]rklärung,
der Äußerung. Das Scheingesims, das das Auge
fordert, nichts
traägt. | | |
| | | / \ ✢ | | |
Wir fordern oft eine
Erklärung, weil wir die Form der Erklärung // Erklärungsform // fordern; aber
auch wenn sie nichts trägt.
⌊⌊ Erinnere Dich, daß wir
oft Erklärungen fordern nichts ihres Gehalts wegen,
sondern der Form der Erklärung wegen. Die Forderung
ist eine architektonische & die Erklärung eine Art
Scheingesims.⌋⌋
| | |
| | | ? / | | |
Aber bist Du nicht doch nur ein
verkappter Behaviourist? Denn Du
sagst, daß nichts hinter der Äußerung der
Empfindung steht.
Sagst Du nicht doch im
Grunde, daß alles Fiktion ist, außer dem
Benehmen? –
Fiktion? So
glaube ich also, daß wir nicht wirklich etwas empfinden, sondern
nur Gesichter ?!
Aber Fiktion ist der Gegen-6 stand hinter der
Äußerung. Fiktionˇ ist es, daß
unsre Worte, um etwas zu bedeuten,
Bedeutung zu haben |
auf ein Etwas anspielen müssen, das ich, wenn nicht einem Andern,
doch mir selbst zeigen kann. (Grammatische
Fiktion.)
¤
| | |
| | | ∕∕ \ | | |
Der Satz: “Hinter der Äußerung der
Empfindung steht nichts” ist ein grammatischer
– er sagt also nicht, daß wir nichts empfinden.
| | |
| | | / | | | Meine Kritik
besteht darin, daß ich die gewöhnliche, primitive Auffassung
der Funktion der Wörter im Sprachspiel // im Gebrauch der Sprache // als zu eng
hinstelle. //
bezeichne. //
| | |
| | | ∕∕ | | |
¤↺ //
Fiktion? So glaube ich also, daß wir nicht
eigentlich empfinden; sondern bloß so tun? Fiktion aber ist
wirklich die Erklärung der Äußerung mit
dem mittels des privaten
Gegenstands. vor unserm innern Sinne.
// 7
| | |
| | | ∕∕ \ ? | 1 ∕∕ \ ? | |
Aber
sagst Du nicht doch daß ‘Seele nur etwas am
Körper’ sei? – Daß, wenn Du das
Benehmen der Menschen (eines Stammes) beschrieben hast, Du
alles beschrieben hast? – Aber der, der
die Äußerung des Schmerzes macht, beschreibt
doch nicht sein ˇeigenes Benehmen!
| | |
| | | ∕∕ \ ? | 2 ∕∕ \ ? | |
Aber
wenn nichts hinter der Äußerung steht, das nicht doch, daß sie nicht
etwas ausdrückt // nicht der Ausdruck von etwas
ist // ? Nein, denn, was sie
ausdrückt, ist nicht, was wir uns geeinigt haben, so
﹖ zu nennen. | | |
| | | / | 3 / | |
8.6.
Die Rolle
der Sätze, die von den Maßen handeln & nicht
‘Erfahrungssätze’ sind. –
Jemand sagt mir: ‘[d|D]iese
Lange Strecke ist
8 240 lang’. Ich sage:
‘Das sind 20 Fuß, also ungefähr 7 Schritte
& habe nun einen Begriff von der Länge erhalten. – Die Umformung beruht
darauf
, daß arithmetischen Satzen
& auf dem Satz, daß 12 Zoll = 1 Fuß ist.
| | |
| | | ? / | 1 ? / | |
Diesen letzteren Satz
wird niemand für gewöhnlich, als Erfahrungssatz
aussprechen. Man sagt er ein Übereinkommen aus. Aber das
Messen würde seine[m|n] gegenwärtigen
Charakter gänzlich verlieren
// verändern //
ändern |
, wenn nichtˇ,
Z.B., die
z.B. Aneinanderreihung von 12
Zollstücken für gewöhnlich eine Länge
ergäbe, die sich wieder einfach aufbewahren
wieder besonders aufbewahren |
läßt.
| | |
| | | ? / | 2 ? / | |
Muß ich darum sagen, der Satz “12 Zoll = 1
Fuß” sage alle diese Dinge aus, die dem Messen seine
gegenwärtige Pointe geben?
9
| | |
| | | / | 1 / | |
Nein. Der Satz ruht
in einer Technik. Und, wenn Du willst, in den
physikalischen und psychologischen Tatsachen, die diese Technik
möglich machen. Aber darum ist sein Sinn nicht diese
Sätze Bedingungen
auszusprechen. Das Gegenteil Satzes, ‘12 Zoll ≠ 1 Fuß’
sagt nicht, daß die Maßstäbe nicht
starr genug sind, oder wir nicht Alle ˇin gleicher Weise
zählen & rechnen.
Der Satz
ruht in einer Technik, beschreibt sie aber
nicht.
| | |
| | | ∕∕ | 2 ∕∕ | |
Der Satz spielt die
typische (damit aber nicht einfache) Rolle der
Regel.
| | |
| | | / | 3 / | |
Ich kann mittels des Satzes 12 Zoll =
1 Fuß eine Voraussage machen; nämlich daß 12 zoll-lange
Stücke Holz anei-10 nander gelegt sich gleichlang mit einem
auf andere Weise gemessenen Stück erweisen
wird. Also ist der Witz jener Regel etwa, daß man
ˇmittels ihrer gewisse Voraussagen machen kann.
Verliert sie nun dadurch den Charakter der
Regel? –
| | |
| | | / | 1 / | |
Warum kann man
jene Voraussagen machen? Nun, – alle
MaßZollstäbe sind gleich gearbeitet; sie verändern ihre
Längen nicht beträchtlich; Stücke Holz, die man
nach auf einen nach einem Zoll oder Fuß zugeschnitten
hat, tun dies auch nicht; unser Gedächtnis ist gut
genugc, wir beim
Zählen bis ‘12’ Ziffern nicht
& nicht auslassen; u.a..
| | |
| | | / | 2 / | | Aber
kann man denn nun nicht die Regel durch einen Erfahrungssatz
ersetzen, der [S|s]agt, daß Maßstäbe so
& so gearbeitet sind, 11 daß Leute so mit
sie so handhaben? // Leute
dies mit ihnen tun? // Man
gäbe etwa eine [E|e]thnologische des Messens. // der Gepflogenheit des
Messens.
des G menschlichen
Gebrauchs des Messens. |
// // der
menschlichen Verrichtung Einrichtung des
Messens. // // Darstellung dieser
menschlichen Einrichtung. //
| | |
| | | / | 1 / | | Nun
es ist offenbar, daß diese Darstellung die Funktion
d Regel
übernehmen könnte.
| | |
| | | / \
? ∫ | 2 / \
? ∫ | |
Ist die hinweisende
Definition die , daß
diese Farbe “grün” heißt,
keine Regel – sondern ein Satz über den Gebrauch
der Wörter, das Arbeiten unsers Gedächtnisses,
usw.?
| | |
| | | ? / | 3 ? / | |
Wer einen
math. Satz weiß, soll noch
nichts wissen. Ist Verwirrung in unserm n
Rechnen Operationen, rechnet jeder anders
& einmal 12 so, einmal so, so liegt noch kein
Rechnen vor; stimmen wir überein, nun dann haben wir nur unsre
Uhren , doch noch keine Zeit
gemessen.
Wer einen
math. Satz weiß, soll noch
nichts wissen.
D.h. der
math. Satz // Beweis // soll nur das Gerüst liefern
für eine Beschreibung.
| | |
| | | | 1 | | Wie kann die bloße
transformation // Umformung // des
Ausdrucks von praktischer Konsequenz sein?
| | |
| | | | 2 | | Daß ich
25 × 25
Nüsse habe, läßt sich verifizieren indem ich
625 Nüsse
zähle, aber es läßt sich auch auf andre Weise
herausfinden, die mit der Zahlangabe
‘25 ×
25’ näher verknüpft
ist. // , die der Ausdrucksform
‘25
× 25’ näher
steht. // // , die zum Ausdruck
‘25 ×
25’ in 13 direkterer Beziehung
steht. // , // in einer
unmittelbareren Beziehung steht. // Und es
ist natürlich die Verknüpfung dieser beiden Arten der
Zahlbestimmung, in der der ein Zweck des
Multiplizierens ruht beruht.
9.6.
| | |
| | | / | 1 / | | Die
Regel ist, als Regel, losgelöst, & steht, sozusagen,
selbstherrlich da; obschon, was sie wichtig macht // was ihr Wichtigkeit gibt // , die Tatsachen der täglichen Erfahrung
sind.
| | |
| | | / | | | Was ich zu tun habe,
ist , das Amt eines
Königs zu beschreiben
wobei ich ˇnun nicht in den Fehler darf, aus
Nützlichkeit zu erklären
noch die Nützlichkeit zu vergessen
außer Acht zu lassen |
. // Was ich
zu tun habe, ist etwas, wie: das Amt eines des Königs zu beschreiben. ; – wobei ich nicht 14 in den Fehler verfallen darf,
d[as|ie] königliche Amt Würde
(streng) aus seiner
der der Nützlichkeit ˇdes AmtsKönigs zu
erklären; & doch weder Nützlichkeit noch Würde
außer [a|A]cht lassen darf. //
| 2 | |
| | | | 1 | | Ich richte mich
beim praktischen Arbeiten nach dem Resultat der
des Ausdrucks.
| | |
| | | | 2 | | Wie kann ich
dann aber noch sagen, daß es dasselbe heißt, ob ich sage
“hier sind 625 Nüsse”, oder “hier sind
25 × 25
Nüsse”?
| | |
| | | / | 3 / | |
Wer den Satz “hier
sind 625 …” verifiziert, verifiziert auch “hier sind
25 × 25
…”; u.u..
Doch steht die eine Form der eine[n|r] ˇArt
der Verifikation, die andre einer andern Art der
Verifikation näher.
| | |
| | | / | 4 / | |
Wie kannst Du
, daß 15 “…
625 …”
&
“…25
× 25 …” dasselbe sagen?
– Erst durch unsere Arithmetik werden sie
.
| | |
| | | | 1 | | Erst als Glieder des Systems
der Arithmetik werden sie Eins.
| | |
| | | | 2 | |
Ich kann einmal die eine, einmal die andere
Art der Beschreibung, durch Zählen
z.B., erhalten. // ,
unmittelbar erhalten. //
D.h., ich kann jede der beiden Formen auf
jede Art erhalten; aber auf verschiedenem Weg.
| | |
| | | | 3 | | Man könnte nun
fragen: Wenn der Satz F
“…625 …” einmal so, einmal anders
verifiziert wurde, sagte er da
beidemale dasselbe?
Oder: Was geschieht, wenn eine Methode
des Verifizierens ‘625’,
die andere nicht
‘25 ×
25’ ergibt? – Ist da
“…
625 …”
wahr 16 & “ … 25 ×
25 …” falsch? Nein! – Das eine anzweifeln heißt, das andre anzweifeln:
[d|D]Das
ist die Grammatik, die unsre Arithmetik diesen Zeichen
gibt.
| | |
| | | | 1 | |
Wenn die beiden Arten als die Begründung einer
Zahlangabe gebraucht werden, sein
sollen, dann ist nur eine
Zahlangabe, wenn auch in verschiedenen Formen,
vorgesehen möglich // da // . Dagegen kann man
ohne Widerspruch sagen: “Mir kommt bei der einen
Art des Zählens 25
× 25 [& also
625] heraus,
bei der anderen nicht
625 [also
nicht 25 ×
25]”.1
(Die
Arithmetik hat hiergegen keinen Einwand.)
| | |
| | | | 2 | | Daß die Arithmetik die
beiden Ausdrücke einander gleichsetzt, ist, könnte man
sagen, ein grammatischer Trick.
Sie
sperrt damit eine be-17 stimmte Art der Beschreibung ab
& leitet sie in andere Kanäle. (Und daß
dies mit den Tatsachen der Erfahrung zusammenhängt braucht
nicht ˇerst gesagt zu werden.)
| | |
| | | / | 1 / | | Nimm
an, ich habe jemand multiplizieren gelehrt, aber nicht
mittels ˇmit Hilfe einer
allgemeinen ausgesprochenen formulierten
allgemeinen Regel, sondern nur dadurch
daß er
zusieht
ich ihn zuschauen lasse |
wie ich ihm Beispiele vorrechne. Ich
kann ihm dann eine neue Aufgabe stellen anschreiben, & sagen:
“[M|m]ach dasselbe mit diesen beiden Zahlen, was ich mit
den früheren getan habe”. Aber ich kann auch
sagen: “Wenn Du mit diesen beiden machst, was ich
mit den andern gemacht habe, so wirst Du ˇzu der Zahl
… kommen”. Was ist das für ein
Satz?
“Du wirst das
& das schreiben” ist eine physikalische
Vorhersage. 18 ‘Wenn Du das & das
schreiben wirst, wirst Du's so gemacht haben, wie ich
Dir's habe’
bestimmt, was er “seinem Beispiel folgen”
nennt.
| | |
| | | | 1 | |
‘Die Lösung dieser Aufgabe ist …’
– Wenn ich das lese, ehe ich die Aufgabe gerechnet habe,
– was ist das für ein Satz?
| | |
| | | ∫ | 2 ∫ | |
10.6. Das
Vorurteil muß man besiegen, – &
doch, Und doch, // besiegen ‒ ‒und doch,
… // wenn man's aber seine Kraft
aber es ist die Kraft die philosophische Arbeit leistet. nicht
hat, kann man nicht keine philosophische Arbeit
leisten.
| | |
| | | / | 3 / | |
“Wenn Du mit diesen Zahlen machst, was ich Dir mit den
andern vorgemacht habe, wirst Du … erhalten” –
das heißt doch ‘[d|D]as Resultat dieser Rechnung ist
…” – & das ist keine Vorhersage, sondern
ein mathematischer Satz. Aber es ist dennoch auch
eine Vorhersage! 19 – Eine Vorhersage besonderer
Art. Wie der, der am Ende findet daß sich beim Addieren
der Kolumne wirklich das & das ergibt, wirklich
überrascht sein kann; z.B. ausrufen
kann: ja, bei Gott, es kommt
heraus!
Denke Dir nur
diesen Vorgang des Vorhersagens & der Bestätigung
als ein besonderes Sprachspiel meine: isoliert von dem Übrigen der
Ar⌊i⌋thmetik & ihrer Anwendung.
| | |
| | | ∕∕ \ | | |
‘Zu sagen: “er hat Schmerzen”
heißt etwas ganz & gar anderes als zu sagen:
“er benimmt sich so & so”!’
– das ist völlig richtig. Ja, der Unterschied ist
in gewisse[r|m] Beziehung
Sinne
noch größer als man sich ihn vorstellt.
Und wieder: der Satz, der ein Benehmen
beschreibt, kann von einer Empfindung (des Andern)
20 reden – & wenn
er dies tut: so spielt er nicht indirekt auf sie
an. – Wenn wir so reden //
uns so ausdrücken // meinen wir nicht
ˇeigentlich etwas anderes, als was wir sagen. Noch
wir sagen: wir meinen zwar
das Benehmen, aber einer
Atmosphere die wir nicht eigens
erwähnen.
| | |
| | | ∕∕ \ | | |
Die
Ausdrücke “Schmerzen haben” &
“sich so & so benehmen” werden – im
allgemeinen – nicht auf die gleiche Weise
ganz
verschieden |
gebraucht! Ja, ihr Gebrauch ist
verschiedener, als die Philosophen, welche gegen
den Behaviourism
sprechen, es darstellen. //
verschiedener, als die Philosophie es darstellt,
die gegen den
Behaviourism
spricht﹖. //
Denn wenn diese die Verschiedenheit
betont betonen // hervorheben
wollen // // uns zeigen wollen // ,
so stellen sie doch
den Gebrauch beidemale nach demselben
Schema dar. // Denn, wenn diese
21 die Verschiedenheit des
Gebrauchs zeigen will wollen, so stellt stellen sie ihn doch
beidemale nach demselben Schema
dar. // // Denn wenn diese die
Verschiedenheit uns vor Augen führen will wollen, so
stellt stellen sie doch den Gebrauch
beidemale … //
| | |
| | | ∫ | | | “Ich kann
mir doch vorstellen, daß Einer Schmerzen hat, & auch,
daß er sich so & so benimmt – & die
beiden sind doch etwas ganz anderes!” Da macht man meistens
den Fehler, daß man sich nicht klar darüber ist
daß den Satz “ich stelle mir vor …“
ˇfür eine Beschreibung ansieht, während er eine
Äußerung ist⌊.⌋, keine Beschreibung
. // Da macht man meistens den
Fehler “[i|I]ch stelle mir …
vor” für eine Beschreibung eines Bildes anzusehen,
während er eine Äußerung ist.
//
22
| | |
| | | ∫ / | | | Wie soll
ich denn den Gebrauch der Sprache mittels etwas erklären,
was Du selbst für privat erklärst & was also
für den Gebrauch der Sprache irrelevant sein müßte. – Ich sage “müßte”,
weil die ganze Idee des privaten Gegenstands auf einem
Mißverständnis beruht.
| | |
| | | ∫ | | | In unserm
Schema der Erklärung der Sprache können wir
nicht den Schmerz die Empfindung als Rechtfertigung der
Schmerzäußerung ihrer Äußerung
einführen. Denn so funktioniert das Wort
“Schmerz” einfach nicht.
| | |
| | | ∕∕ \ | | |
Nur die intime Bekanntschaft
Vertrautheit |
mit dem Gebrauch eines Wortes bringt
die Erfahrung hervor, daß das Wort eine Seele hat.
Einer könnte sagen, daß 23 ein Tennis-
& ein Cricketball
(für ihn)
ˇjeder eine ganz
verschiedenecen andere
[b|B]edeutung⌊en⌋ Sinn Dazu aber
muß er mit den Regeln der beiden Spiele nicht nur
oberflächlich bekannt sein &
die Spiele müssen in Leben eingreifen.
Man könnte sagen: ‘ich hätte
keinen Eindruck von dem Zimmer als ganzes, könnte ich nicht
meinen Blick schnell in ihm dahin & dorthin schweifen
lassen & mich nicht frei in ihm herumbewegen.
Aber dennoch ist an dem allen etwas unklar.
| | |
| | | | 1 | | Es ist eine
interessante Tatsache, daß die Regeln der
meisten unserer
wichtigsten |
Spiele sehr konservativ behandelt werden. Daß,
z.B., normalerweise niemand dran denkt,
die Regeln des Schach zu variieren, etwa 24 dem König eine andere
Bewegungsfreiheit zu geben; daß man
interessant, oder lustig findet, sondern eher ungehörig &
sogar dumm.
| | |
| | | | | |
11.6.
⇒[Zu
18/3] Was ist an diesem
Vorhersagespiel so sonderbar? Was mir sonderbar
würde
fortfallen
// entfernt //
wegfallen |
, wenn
die Vorhersage lautete: “[w|W]enn
Du glauben wirst, meinem Beispiel gefolgt zu sein,
wir[d|st] Du das
herausgebracht haben.”
– , oder: “Wenn Dir alles richtig scheinen wird, wird das das
Resultat sein.” Dies Spiel konnte
z.B. man sich
(,z.B.,) mit dem eingeben z.B. mit dem
Eingeben … verbunden sein. eines bestimmten Giftes verbunden
denken vorstellen, & die Vorhersage wäre, daß
die Injektion unsre Fähigkeiten unser Gedächtnis z.B.,
in der & der Weise beeinflußt. – Aber, wenn wir uns das Spiel mit dem
Ein-25 geben eines Giftes denken können,
warum nicht mit dem Eingeben eines
Heilmittels⌊?⌋ ,oder auch
ohne. Aber auch dann kann das
Schwergewicht der Vorhersage noch immer darauf ruhen, daß
der gesunde Mensch das als Resultat
ansieht. Oder vielleicht: daß den gesunden
Menschen das befriedigt.
| | |
| | | | 1 | | ∣ Es ist
unglaublich, wie eine neue
La[g|d]e Lade, an geeignetem Ort, in
unserem filing-cabinet, hilft. ∣
| | |
| | | | 2 | | “Folge mir, so wirst
Du das herausbringen.”
natürlich nicht:
“[f|F]olge mir, dann wirst Du mir folgen” –
noch: “[r|R]echne so dann wirst Du so
rechnen”. – Aber was heißt
“Folge, mir”? Im
Sprachspiel kann es einfach ein Befehl sein:
“Folge mir jetzt!”.
26 | | |
| | | | 1 | |
Was ist der Unterschied zwischen den Vorhersagen:
“Wenn Du richtig rechnest, wirst Du das
erhalten” – &
“[w|W]enn Du glauben wirst, daß Du richtig
rechnest, wirst Du das erhalten”?
Wer sagt nun, daß in meinem
ˇobigen Sprachspiel die Vorhersage nicht eben
das letztere bedeutet? Es scheint, sie bedeutet das nicht
‒ ‒ ‒ aber wie zeigt sich das? ⌊⌊ˇ
Frage Dich unter welchen Umständen würde die
Vorhersage das eine, unter welchen das andere vorherzusagen
scheinen. Denn es ist klar: es kommt hier auf die
übrigen Umstände an. ⌋⌋
| | |
| | | / | 3 / | | Wer mir
vorhersagt, daß ich das herausbringen werde, sagt der
mir nicht eben vorher daß ich dieses Resultat für
richtig halten werde? –
“Aber” – sagst Du vielleicht –
“nur eben weil es ˇwirklich richtig
ist!” – Aber was heißt
das: “Ich halte die Rechnung für richtig,
weil, sie richtig ist”?
| | |
| | | / | 4 / | | Und
doch kann man sagen: 27 [i|I]n in meinem Sprachspiel denkt der
Rechnende nicht daran, daß die Tatsache, – daß er
dies herausbringt, – eine Eigentümlichkeit
seines Wesens ist; sie erscheint ihm
// die Tatsache erscheint
ihm nicht als eine
psychologische // . |
Eher
stelle ich mir ihn unter dem Eindruck vor, daß er nur einem
bereits vorhandenen Faden .
Und das Wie des Folgens als eine
Selbstverständlichkeit hinnimmt; & nur
eine Erklärung seiner Handlung kennt,
nämlich: den Lauf des Fadens.
| | |
| | | | 1 | | Er läßt
sich allerdings ablaufen, indem er der Regel, oder den Beispielen
folgt, aber was er hervorbringt
(–wenn es ihm richtig erscheint
–)
tut |
betrachtet er nun nicht als Besonderheit
seines 28 Ablaufs, er sagt nicht:
“also so bin ich abgelaufen
–!”, sondern: “also
so läuft es ab –”.
| | |
| | | / | 1 / | |
Aber wenn nun [e|E] dennoch am Ende der Rechnung in unserm
Sprachspiel sagte: “also so bin ich
abgelaufen!” – oder: “also
dieser Ablauf befriedigt mich!” –
Kann ich nun sagen, er habe das (ganze) Sprachspiel
mißverstanden? Doch gewiß nicht! er nicht sonst
eine unerwünschte Auffassung zeigt.
Anwendung von ihm macht. |
| | |
| | | / | 2 / | | Ist es nicht die
Anwendung der Rechnung, die jene Auffassung
hervorruftbringt daß die Rechnung abläuft und nicht
wir?
| | |
| | | | 3 | |
Du mußt Neues sagen & doch lauter Altes.
⌊(N.)⌋
| | |
| | | | 4 | | Du mußt allerdings nur Altes sagen
– aber doch etwas Neues! 29
| | |
| | | / | | | Die
verschiedenen ‘Auffassungen’ müssen
verschiedenen Anwendungen entsprechen.
| 1 | |
| | | | 2 | | ∣ Auch der Dichter muß
sich immer fragen: ‘ist denn, was ich schreibe,
wirklich wahr?’ – was nicht heißen
muß: ‘geschieht es so in
Wirklichkeit?’. ∣
| | |
| | | / | 3 / | | Denn es
ist allerdings ein Unterschied dazwischen: überrascht
zu sein, das ich davon befriedigt
bin –; überrascht zu sein, daß die Ziffern ˇauf
dem Papier sich so zu benehmen scheinen; &
überrascht zu sein darüber, daß das
herauskommt. Aber in jedem Fall sehe ich die
Rechnung // das Ergebnis // in
anderm Zusammenhang.
| | |
| | | / | 4 / | | Ich
Gefühl des
‘Herausbekommens’, wenn wir etwa eine längere
Kolumne ˇvon Zahlen verschiede-30 ner Gestalt addieren & eine runde Zahl
&
ˇso eine Zahl |
wie 1000000
herauskommt – , wie es uns zuvor
gesagt worden war. “Ja, bei
Gott, wieder eine Null –”
sagen wir.
“Man sähe es den Zahlen
nicht an –”, könnte ich auch sagen.
| | |
| | | | 1 | | Wie wäre es, wenn wir
sagten, ⌊–⌋ statt:
‘6 ×
6 ergibt
36’
– : ‘Das Ergeben der Zahl
36 durch
6 ×
6’? – Den Satz ersetzen
durch einen substantivischen Ausdruck. (Der Beweis zeigt
das Ergeben)
| | |
| | | / | 2 / | |
Du mußt freilich Altes herbeitragen. Aber
zu einem Bau. –
⌊(W.)⌋
| | |
| | | | 3 | | Warum willst Du die
Mathematik immer unter dem Aspekt des Findens & nicht
des Tuns betrachten?
| | |
| | | | 4 | | Von großem Einflusse muß es sein,
daß wir die Wörter “richtig”,
& “wahr” &
“falsch” & die Form der Aussage im Rechnen
gebrauchen. (Kopfschütteln &
Nicken) 31
| | |
| | | | | |
Warum soll ich sagen, daß das [w|W]issen, daß alle
Menschen, die gelernt haben,
so rech⌊n⌋en, kein mathematisches Wissen
ist? Weil es auf Zusammenhänge
(einen)
ˇandern Zusammenhang |
hinzudeuten scheint
hindeutet |
. // Weil es auf Zusammenhänge
hindeutet, die anders sind als die des mathematischen
Wissens. //
| | |
| | | / | | |
12.6. Die Berechnung des
des Resultats des menschlichen Rechnens.
// des Ergebnisses ⌊ // ⌋ einer
Rechnung, die ein Mensch Einer ausführt
anstellt. //
| | |
| | | / | | | Ist also
⌊Be⌋[R|r]echnen, was Einer durch Rechnung herauskriegen wird,
schon angewandte Mathematik? – & also
auch: Berechnen, was ich selbst herauskriegen werde?
| | |
| | | | | | (Im Alter
entschlüpfen uns wieder die Probleme, so wie in
32 der Jugend. Wir
können sie nicht nur nicht , wir können sie auch nicht
halten.)
| | |
| | | | | | Für uns könnten die
Rechnungen im Himmel aufgeschrieben sein.
| | |
| | | / | | |
‘Warum möchte ich immer das & das
sagen?’ – Das
einen guten Grund
haben.: [e|E]s wird die Beschreibung in
einer primitiven Form primitiver, von grammatischen ,
grammatischer Tatsachen sein.
| | |
| | | | | | Ist es ein typisches Beispiel der
Anwendung der , wenn wir
berechnen, was ˇfür einen Rechenvorgang durchlaufen
wird? // berechnen, welchen Rechenvorgang
ein Andrer durchlaufen wird? //
| | |
| | | / | | |
Über das Einleuchten der Axiome. Die
Axiome eines mathematischen Systems müssen
33 selber
math. Sätze
sein. Und was macht sie dazu?
Daß sie einleuchten? Und wie stark müssen sie
einleuchten? Wenn sie nun einleuchten & die
Erfahrung ihnen widerspricht – wer gewinnt dann?
Oder stellen wir uns ihre Anwendung immer so vor, daß
Erfahrung ihnen nicht widersprechen kann, weil wir sie zu
grammatischen Sätzen machen? Aber damit sie gute
grammatische Satze sind muß sich doch
wieder viel Erfahrung leicht nach ihnen darstellen
lassen.
Warum ist z.B.
der Satz ‘der Teil ist kleiner als das Ganze’ so
einleuchtend, obwohl man in vielen Fällen auch sein
Gegenteil für wahr erklären
könnte? (Man z.B. sagen: ich sehe den
Berg größer als das Fenster, durch ich ihn sehe ⌊ // ⌋, durch
er mir
erscheint⌊ // ⌋.) 34
| | |
| | | / | | | 13.6. Es ist ja gar
kein Zweifel, daß math.
Sätze in gewissen Sprachspielen die Rolle von
Regeln der Darstellung spielen, im Gegensatz zu Sätzen, welche
beschreiben.
Sätzen
der Darstellung. |
| | |
| | | / | | | Es ist ja gar
kein Zweifel, daß math.
Sätze in gewissen Sprachspielen Schemata der
Darstellung sind, im [g|G]egensatz zu den Sätzen,
welche beschreiben.
| | |
| | | / | | | Aber das sagt nicht, daß
dieser Gegensatz nicht nach allen
Richtungen // allen möglichen
Richtungen // hin abfällt.
Und das wieder nicht,daß Gegensatz er nicht von
Wichtigkeit ist. // , daß er nicht von großer
Wichtigkeit ist. //
| | |
| | | | | | Die Schwierigkeit ist, daß
grammatische Terrain zu schildern; zu sehen. 35
| | |
| | | | | |
Das piédestal
der Mathematik auf dem die
Math. steht, ist eine bestimmte Rolle
ist die Rolle |
, welche ihre Sätze in unsern
Sprachspielen spielen. // Das
piédestal, auf welchem
die Math. ˇfür uns
steht, kommt von hat sie vermöge einer
bestimmten Rolle her, welche
die Sätze der Math. in unsern
Sprachspielen spielen. // // Das
piédestal, auf welchem die
Math. für uns steht, hat sie
vermöge einer bestimmten Rolle, die ihre Sätze in
Sprachspielen
spielen. //
| | |
| | | / \ | | |
Die Sätze, welche Hardy in seinem – elenden – Buch,
“Apology of a
Math.”, als Ausdruck seiner
Philosophie der Mathematik
ausspricht hinstellt
// hinschreibt //
|
, sind
noch gar nicht Philosophie, sondern , wie alle ähnlichen
Ergüsse, allerdings das als
Rohmaterial des Philosophierens , & sollten dann nicht in der Form von
Meinungen, Feststellungen, oder Axiomen, aus-36 gesprochen werden, sondern in der
Form: “Ich bin geneigt zu sagen …”, oder
“Ich möchte immer
sagen: …”. Worauf das Philosophieren
erst beginnen soll; uns diese
….
, (um) uns nämlich diese
seltsame Neigung zu erklären. |
// sondern können – wie
alle ähnlichen Ergüsse – Rohmaterial
des Philosophierens sein; & sollten …
//
| | |
| | | | | | Was
der math. Beweis
, wird als
interne Relation hingestellt & dem Zweifel
entzogen.
| | |
| | | | | | Was
ist einem mathematischen Satz & einem mathematischen
Beweis gemein, daß sie beide
“mathematisch” heißen?
Nicht daß der
math. Satz mathematisch bewiesen
sein muß; nicht daß der
math. Beweis einen
math. Satz beweisen
muß.
Was hat der unbewiesene Satz
(das Axiom) mMathematisches? 37
(&) was hat er gemein mit einem
mathematischen Beweis?
| | |
| | | ∫ | | | Soll ich
antworten: ‘Die Schlußregeln des
math. Beweises sind immer
math.
Sätze’? Oder:
‘Math.
Sätze & Beweise dienen dem
Schließen’? Das wäre schon näher
dem Wahren
| | |
| | | | | | Der
Beweis muß eine interne Relation , nicht eine . Denn wir könnten uns auch einen
Vorgang der Transformation eines Satzes durchs
Experiment &
eine, die zu⌊m⌋ Vorhersagen des vom transformierten Satz
Behaupteten benützt würde. Man könnte sich
z.B. (ganz gut)
denken, daß Zeichen durch hinzulegen anderer Zeichen sich
verschöben, daß
sie eine wahre Vorhersage bilden auf der Grundlage der in ihrer
Ausgangslage ausgedrück-38 ten Bedingungen. Ja, wenn Du
willst, kannst Du den rechnenden Menschen als einen Apparat
für ein solches Experiment
dieser Art |
betrachten.
| | |
| | | | | |
Denn, daß ein Mensch das Resultat
errechnet in dem
Sinne: daß er nicht gleich das Resultat, sondern erst
verschiedenes anderes macht ihn nicht
weniger zu einem physikalisch-chemischen Hilfsmittel,
eine Zeichenreihe
// Zeichenfolge //
Zahl |
zu erzeugen, wenn
gewisse andere ihm zugebracht werden. // gewisse andere
seine[m|r]
Einwirkung ausgesetzt werden. //
// eine Zeichenfolge zu erzeugen, man eine
Zeichenfolge seiner Einwirkung aussetzt. // c // eine Zeichenfolge zu erzeugen,
indem man ihn auf ˇeine Zeichenfolge sie
einwirken läßt. // // eine
Zeichenfolge aus einer Zeichenfolge zu erzeugen. //
| | |
| | | | | | Ich müßte also sagen:
Der bewiesene Satz ist nichtˇ:
die // diejenige //
Zeichenfolge, der so
& so 39 trainirte
geschulte
abgerichtete |
Mensch unter den
& den [u|U]mständen erzeugt.
| | |
| | | | | |
14.6. Wenn wir
so betrachten, ändert sich, was wir erblicken,
gänzlich. Die Zwischenstufen werden ein
uninteressantes Nebenprodukt.
(Wie im Innern
des
Wie in einem |
Automaten ein Geräusch, er uns Ware zuwirft.) // (Wie ein Geräusch im Innern eines
Autmaten, ehe er uns die Ware
zuwirft.) //
| | |
| | | | | | ∣ Das Durchstreichen von
Ausdrücken als Schriftzeichen. ∣
| | |
| | | | | | Ja, wenn nun die Bedingungen
erfüllt wären & der Eine erzeugte dies, der
Andre jenes Resultat, & wenn nun jeder sein Resultat
anwendete & die Anwendung es rechtfertigte –
wie ganz leicht möglich wäre! –
| | |
| | | ∕∕ | | | Wir
sagen: der Beweis sei ein Bild. Aber dies Bild bedarf
doch der 40
Approbationierung, die wir ihm
(nämlich) beim Nachrechnen
erteilen. –
| | |
| | | ∕∕ | | | Wohl wahr; aber wenn es
von dem Einen die Approbation erhielte, von dem Andern nicht &
sie sich nicht verständigen könnten
– hätten wir ein
Rechnen? // –wäre da ein
Rechnen? //
Also ist es nicht
die Approbation allein, die es zur Rechnung macht, sondern
die Gleichheit // Übereinstimmmung //
der Approbationen.
| | |
| | | ∕∕ | | | Denn es ließe sich ja
auch ein Spiel denken, in welchem durch Menschen durch
Ausdrücke, etwa ˇ[keine⌊n⌋
Beistriche] ähnlich denen allgemeiner
Regeln, angeregt, für bestimmte praktische Aufgaben,
also ad hoc, sich Zeichenfolgen einfallen lassen, &
daß sich dies sogar bewährte. Und hier brauchen die
‘Rechnungen’, wenn man sie so nennen wollte, nicht
miteinander übereinstimmen. (Hier könnte man
von ‘Intuition’ reden.) 41
| | |
| | | | | |
Die Übereinstimmung der Approbationen ist die Vorbedingung
unseres des Sprachspiels, sie wird nicht in ihm
konstatiert.
| | |
| | | | | |
Nehmen wir (im ‘rein mathematischen’
Sprachspiel ˇvon vorhin) an, daß die Antwort
en auf die gleiche Frage immer & von Allen
die gleiche ist [,| (]oder, daß es sich
doch nur ausnahmsweise anders verhält) &
die Ausnahmen etwa aus der Gesellschaft ausgestoßen
werden)?
Gehört dies nicht dazu,
daß unser Sprachspiel der Arithmetik ähnlich
wird?
Oder auch: nur im ersten Fall die Leute arithmetische
? Und wenn dies
diese , das Benehmen der Menschen betreffend, sind,
warum dann nicht auch im zweiten Fall? //
Und wenn d es Sätze, das 42 Benehmen … warum lernen sie nicht auch im zweiten
Fall arithmetische Sätze? //
| | |
| | | | | |
Man könnte sich aber doch auch
die Rechnung als Experiment behandelt denken!
Denke Dir
eine Kaste, die nicht rechnen kann (dwie die
Ritter nicht schreiben konnten), Sklaven haltend,
die sich Sklaven
hält, // sich Sklaven
haltend // |
die, sagen wir, rechnen; manchmal
richtig, manchmal falsch, von ihren Herren aber nicht
kontrolliert. Diese ihnen
Aufgaben (&) die Sklaven
geben Antworten; vorher ˇehe sie
antworten schreiben sie ˇmeistens,
gewöhnlich noch meistens
noch etwas ˇhin; aber ihre Herren verstehen
das nicht. Sie richten sich nach den Antworten der
Sklaven & betrachten sie als eine Art Orakel.
Man könnte sich au[f|c]h ferners denken, daß die Herrn jene Sklaven
, wenn der das praktische
Erfolg Ergebnis unbefriedi-43 gend war, sie gut , wenn er glücklich ist.
| | |
| | | ∕∕ | | |
15.6. Der Gebrauch von
Wörtern, wie ‘pas’ oder
‘point’ in ‘ne …
pas’, ‘ne … point’,
etc.. Das
ˇHaupt[W|w]ort ˇ“ne” pas” könnte hinweisend definiert
werden & dann davon der Gebrauch als Teil der Negation
gemacht. – Was heißt es: Niemand
denkt, wenn er ‘ne … pas’
sagt an einen Schritt? – Nun, man
sagt: ‘Ich wußte nicht einmal, daß das
dasselbe Wort ist!’. Aber was
heißt das? Was war uns nicht
aufgefallen? (Dies Beispiel ist höchst
wichtig für das Verständnis dessen, was man
‘Bedeutung’ nennt.)
| | |
| | | | | | Eine Sprache, in der die Schriftzeichen
von der Art der t
eines Rebus sind, so daß das Wort “kann”
“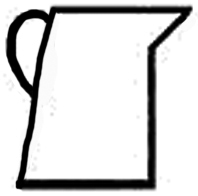 ”
geschrieben , oder
“wollen” Bild eines
Wollknäuls
& // mit
einem ihm // eines ˇdem angehängten
Zeichenns, ”
geschrieben , oder
“wollen” Bild eines
Wollknäuls
& // mit
einem ihm // eines ˇdem angehängten
Zeichenns,
44
. Auch wird
die Bedeutung der Wörter so beigebracht, daß die Beziehung
zu⌊r⌋ den Kanne, Wolle,
etc., immer lebendig bleibt. Kennten wir
// diese Sprache, (dann)
könnten sehr eigentümliche philosophische
Probleme für uns existieren.
| | |
| | | ∕∕ \ \ | 1 ∕∕ \ \ | |
Ist, was wir “einer Regel folgen”
nennen, etwas, was nur [E|e]in Mensch, &
nur einmal im Leben, tun ? – Das ist natürlich eine Anmerkung zur
Grammatikc “
Regel folgen”.
| | |
| | | | | | Wenn die Rechnung ein Experiment ist
& die Bedingungen sind erfüllt dann müssen
wir als Ausgang nehmen // anerkennen // , was kommt; & wenn die Rechnung ein
Experiment ist, so ist doch der Satz, daß sie das &
das ergibt, der Satz, daß unter solchen Bedingungen diese Art von
45 Zeichen entsteht.
Und entsteh[e|t]n also unter diesen Bedingungen einmal ein,
einmal ein anderes Resultat, so darf man nun nicht
sagen: “das stimmt etwas
nicht”, oder “beide Rechnungen können nicht in
Ordnung sein”, sondern man müßte
sagen: diese Rechnung ergibt nicht immer das gleiche Resultat
(warum, muß nicht bekannt sein). Aber
obwohl der Vorgang nun nun das Experiment ebenso interessant, ja
vielleicht noch interessanter , ist, haben wir
nun keine Rechnung mehr. // , ja
vielleicht noch interessanter geworden ist, ist keine Rechnung
mehr vorhanden. // Und das ist
natürlich wieder eine grammatische Bemerkung
über den Gebrauch des Wortes
“Rechnung”. Und natürlich hat diese
Grammatik eine Pointe.
46
| | |
| | | | | | Was
heißt es sich über einen Unterschied
im Resultat einer Rechnung verständigen?
Es heißt doch zu einem gleichförmigen Rechnen zu
gelangen. Und kann man das nicht // man sich nicht verständigen // so
kann nun Einer nicht sagen, der Andre rechne auch; nur eben mit
anderen Ergebnissen. // Und können sie
sich nicht verständigen, so kann nun Einer nicht sagen
… //
| | |
| | | | | | Wie ist es nun, – soll ich
sagen: Der gleiche Sinn könne nur
einen Beweis haben? Oder: wenn ein Beweis
gefunden wird, ändere sich der Sinn?
Freilich würden Einige sich dagegen wehren, sagen:
‘So kann man also nie den Beweis eines Satzes finden,
denn, hat man ihn gefunden, so ist er nicht mehr ˇder
Beweis dieses Satzes.’ Aber das sagt
noch gar nichts. – 47
| | |
| | | | | |
Es kommt eben darauf an, was den Sinn des Satzes
festlegt. Wovon wir sagen wollen, es lege den Sinn des
Satzes fest. Der Gebrauch muß ihn
festlegen. Aber was rechnen wir zum
Gebrauch? – // Der Gebrauch der
Zeichen muß ihn festlegen; aber was rechnen …? //
| | |
| | | | | |
16.6. Zwei Die
Beweise beweisen denselben Satz, heißt etwa: beide
erweisen ihn ˇfür uns als ˇein
Instrument zu dem
Gleichen. // gleichen
Zweck // . // als ein
Instrument zum gleichen
Zweck. //
| | |
| | | | | | Und der Zweck ist eine Anspielung
auf Außermathematisches.
| | |
| | | | | | Ich sagte einmal:
‘Wenn Du wissen willst, was ein
math. Satz sagt,
, was sein Beweis
beweist. Nun, ist darin nicht 48 Wahres & Falsches?
Sinn, der Witz eines
math. Satzes wirklich klar, wenn man nur seinen Beweis
? //
sieht & versteht? // // , sobald wir nur dem Beweis folgen
können? //
| | |
| | | | | |
Dem Russellschen “~f(f)”
fehlt vor allem die Anwendung, & daher der Sinn.
Wendet man diese Form aber dennoch an, dann ist nicht
gesagt, daß ‘~f(f)’
ein Satz ˇin irgendeinem gewohnten Sinne sein muß, oder
‘f(ξ)’ eine
Satzfunktion. Denn der Begriff des Satzes, außer der des
Satzes der Logik, ist ja durch Russell nur in allgemeinen, ganz konventionellen
herkömmlichen |
◇◇◇ Zügen
erklärt.
Man sieht hier auf die Sprache,
ohne auf das Sprachspiel zu sehen.
| | |
| | | | | | Wenn wir von verschiedenen 49 Bilderreihen sagen, sie
demonstrierten, z.B., ˇdaß
25 × 25 =
625, so ist leicht genug zu erkennen, was den Ort
dieses Satzes fixiert, den beide Wege erreichen.
| | |
| | | | | | ∣ Welche seltsame
Stellungnahme der Wissenschaftler–: “Das
wissen wir noch nicht aber es läßt sich
wissen, & es ist nur eine Frage der Zeit, so wird man es
wissen”! Als ob es sich von selbst
verstünde. – ∣
| | |
| | | | | | Der Beweis
reiht den Satz in eine
Ordnung ein; dabei findet oft ein Übersetzen einer
Art von Operation in eine gänzlich andere statt. Wie
wenn wir Gleichungen in Kurven Linien // Linienformen
// übertragen. Und dann sehen wir
etwas für die ein & dadurch für die
Gleichungen.
Aber mit welchem Rechte
überzeugen wir uns durch ˇeinen
Gedankeng[ä|a]ange, der dem Gegenstand unsrer Gedanken
scheinbar ganz heterogen ist? // Aber mit
welchem Rechte überzeugt uns 50 der dem Gegenstand unsrer
Gedankenn scheinbar ganz Gedankengang? // // Aber mit welchem Rechte überzeugen wir uns
durch Gedankengänge, die dem Gegenstand unsrer Gedanken scheinbar
ganz fernliegen? //
Nun,
unsre Operationen liegen jenem Gegenstand auch nicht
ferner, als, etwa, das Dividieren im Dezimalsystem
mit Dezimalzahlen |
, dem verteilen von
G Nüssen // Gegenständen // .
Besonders, wenn man sich (was man leicht kann), daß
Operation ursprünglich zu
einem ganz
anderen Zweck als
dem des Teilens ˇu.
dergl. erfunden worden
wäre.
| | |
| | | | | |
Fragst Du: “Mit welchem Recht
Recht?” so ist die Antwort:
Vielleicht
﹖﹖ mit gar keinem. – Mit welchem Recht sagst Du daß die Fortsetzung dieses
Systems mit jenem immer parallel laufen 51 wird? (Es ist, als ob
Du Zoll & Fuß beide als Einheit
festsetztest & behauptetest,
12n Zoll werden immer mit
n Fuß gleich lang
sein.)
| | |
| | | | | |
17.6. Wenn zwei Beweise denselben Satz
beweisen, so kann man sich allerdings Umstände denken, in denen
die ganze diese Beweise verbindende Umgebung wegfiele, sodaß
sie allein & nackt dastünden & kein Grund
vorhanden wäre, zu sagen sie hätten eine gemeinsame
Pointe, sie bewiesen denselben Satz.
Man
muß sich nur denken, daß die beiden Beweise ohne
den ungeheuren, sie beide umhüllenden
& verbindenden, Organismus der Anwendungen,
d sozusagen nackt & und bloß,
dastünden. (Wie zwei
Knochen ohne die Unzahl Muskeln aus dem ˇungeheuer
mannigfachen Zu-52 sammenhang des Organismus
gelöst;) in allein
wir gewohnt sind, an sie zu denken.)
| | |
| | | / | | |
Nimm an, man rechnete mit Zahlen & verwendet
manchmal auch die Division durch Ausdrücke von der Form
(n ‒ n), & erhielte
auf diese Weise hie & da andere als
normalen Resultate des Multiplizierens, etc.
Das störe aber niemand. – Vergleiche
damit: Man legt Listen, Verzeichnisse, von Personen
an, aber nicht wie wir es tun, alphabetisch; & so kommt es,
daß der gleiche Name in mancher Liste öfters als einmal
figurirt steht // vorkommt // . –
Aber nun kann man annehmen, : daß das
niemandem auffällt; oder, daß die Leute es sehen,
es ihnen aber ˇweiters nichts macht. // ,
es aber ruhig hinnehmen. // Wie man
Leute eines Stammes denken könnte, die, wenn sie
zur Erde
fallen lassen, es nicht der 53 Mühe Wert halten sie
aufzuheben. (Sie haben dann etwa eine
Redensart: “Es gehört den
Andern”), oder dergleichen.)
| | |
| | | | | | Nun aber ändert sich die
Zeit, & die Menschen fangen an (zuerst nur wenige)
Exactheit zu fordern. Mit
Recht mit Unrecht? – Waren
die früheren
eigentlich nicht eigentlich
? –
| | |
| | | | | | Sagen wir, wir erhielten
manche unsrer Rechenresultate auf durch einen versteckten
Widerspruch. dadurch illegitim? – Aber
wenn wir nun solche Resultate durchaus nicht anerkennen wollen
& doch fürchten, es könnten uns welche
könnten welche |
durchschlüpfen – Nun dann haben wir
also eine Idee die einem neuen Kalkül als
vorbild dienen soll. // dienen .
// 54 Wie man die Idee zu einem Spiel
haben kann.
| | |
| | | | | |
Der R'sche Widerspruch ist nicht, weil er ein
Widerspruch ist, beunruhigend, sondern weil das ganze Gewächs,
dessen Ende er , ein
Krebsgewächs ist, [Z|z]weck-
& [S|s]innlos ohne Zweck & Sinn
aus dem normalenc Körper herauszuwachsen
scheint.
| | |
| | | | | | Kann
man nun sagen: “Wir wollen einen Kalkül, der
uns sicherer die Wahrheit
”? // anzeigt”? //
| | |
| | | | | |
18.6. Aber Du kannst doch einen
Widerspruch nicht gelten lassen! – Warum
nicht? Wir gebrauchen ja
manchmal in unsrer Rede, freilich selten – aber man
könnte sich eine Sprachtechnik denken, in der er ein
ständiges Implemet ist // wäre // .
Man könnte z.B. von einem Objekt in
Bewegung sagen, es existiere & es existiere nicht an
diesem Ort; Verände-55 rung könnte durch den Widerspruch
ausgedrückt werden.
| | |
| | | | | |
Nimm ein Thema, wie das
Haydensche
(Chorale St.
Antoni), nimm den Teil einer
der Brahmsschen Variationnen
d[ie|er] dem ersten Teil des Themas entspricht & stell die
Aufgabe den zweiten Teil der Variation im Stil ihres ersten Teiles zu
konstruieren. Das ist ein Problem
(sehr) ähnlich von ähnlicher Art
den mathematischen Problemen. // Das ist ein
Problem einer Art ähnlich der, der von math.
Probl. // // Das ist ein Probl von
der Art mathematischer
Pr.
der math.
Probl. |
// Ist die
Lösung gefunden, etwa wie Brahms sie gibt, so zweifelt man nicht, daß dies die
Lösung . // so
ist es uns klar zweifelt man nicht, so ist es uns
klar, daß dies … // so zweifelt man nicht
dies ist die Lösung. //
| | |
| | | | | | Mit diesem Weg sind wir
einverstanden. Und doch ist es hier klar, daß
56 es leicht verschiedene Wege
geben kann, kann mit deren
jedem wir einverstanden sein
konnen,
wir uns einverstanden erklären
konnen, |
deren jeden wir
consequent nennen .
| | |
| | | ∕∕ | | |
∣ Ich konnte mir denken, daß [e|E]iner
meinte die Namen “Fortnum”
& “Mason” paßten
zusammen. ∣
| | |
| | | | | | ‘Wir machen lauter legitime
– d.h. in den Regeln erlaubte –
Schritte, & auf einmal kommt ein Widerspruch
heraus. Also ist das Regelverzeichnis, wie es ist,
nichts nutz, denn der Widerspruch wirft das ganze Spiel
um.’ Warum laßt Du
ihn es umwerfen?
Aber ich will, daß man
auch nach der Regel soll mechanisch weiter
schließen können, ohne je zu widersprechenden Resultaten
zu gelangen. Nun, welche Art der Voraussicht willst
Du? Eine, die Dein gegenwärtiger
Kalkül nicht zuläßt? Nun, dadurch ist er
nicht 57 ein schlechtes Stück
Mathematik oder
nicht im vollsten Sinne Mathematik. Der Sinn des
Wortes “mechanisch” verführt Dich.
| | |
| | | ∕∕ | | |
∣ Die philosophische Betrachtung der Mathematik hat eine andere
Pointe, als die mathematische mathematischer
Sätze & Beweise. ∣
| | |
| | | | | | Wenn Du zu einem praktischen Zweck
einen Widerspruch mechanisch vermeiden willst, wie Dein
Kalkül es jetzt ˇbis jetzt nicht
kann, so ist das etwa, wie wenn Du nach einer Konstruktion des
…-Ecks suchst, das Du
bis jetzt nur durch Probieren hast zeichnen können;
oder nach einer Lösung der Gleichung 3ten Grades, die
Du bisher nur appoximiert hast.
Nicht schlechte Mathematik wird hier verbessert,
sondern ein neues Stück Mathematik .
| | |
| | | | | |
19.6. Nimm an, ich wollte eine
Irratio-58 nalzahl so bestimmen, daß in ihrer
Entwicklung nicht die Figur ‘777’
vorkommt. Ich könnte π nehmen &
bestimmen: wenn jene Figur entsteht setzen wir statt ihr
‘000’. Nun sagt man mir: das
genügt nicht, denn der, welcher die Stellen berechnet, ist
verhindert, auf die früher berechneten vorhergehenden // früheren
// zurückzuschauen. Nun brauche
ich einen andern Kalkül; einen in dem ich mich zum Voraus
versichere
versichern kann |
, er könne
‘777’ nicht liefern. Ein mathematisches
Problem.
| | |
| | | | | | ‘Solange
die Widerspruchsfreiheit nicht bewiesen ist, kann ich nie ganz
sicher sein, daß mir jemand, der gedankenlos, aber gemäß
den Regeln, rechnet, nicht irgend etwas Falsches
herausrechnen
wird.
herausrechnet. |
’ So lange also jene Voraussicht nicht
gewonnen ist, ist der Kalkül 59
unzuverläßig. – Aber
denke, ich fragte: “Wie
unzuverläßig?– // ‘Wie
unzuverläßig ist
er? – // Wenn wir
von Graden der Unzuverläßigkeit redeten,
könnten wir ihr dadurch nicht den metaphysischen Stachel
nehmen?
Waren d⌊i⌋e ersten Regeln des
Kalküls nicht gut? Nun, wir gaben sie nur,
weil sie gut waren. – Wenn sich
später ein Widerspruch ergibt, – haben sie
nicht ihre Pflicht getan?
Nein // Nicht
doch, // sie Sie waren für diese Anwendung nicht gegeben
worden.
| | |
| | | | | | Ich kann meinem
Kalkül eine bestimmte Art der Voraussicht geben
wollen. Sie macht ihn nicht zu einem
eigentlicheren Stück Mathematik, aber, etwa gewissem Zweck
brauchbarerembarern.
| | |
| | | | | | Die Idee des
[m|M]echanisierens 60 der
Math.. Die Mode des
Axiomatischen Systems.
| | |
| | | | | | Ein reflexives Fürwort,
das sich auf den Satz in dem es steht bezieht.
Gebra⌊u⌋chen wir das Wort “ich” – so
daß “[i|I]ch bin 5 cm
lang” dadurch zu prüfen ist, daß man diesen Satz
mißt. Eine solche Form wird meines Wissens nie
gebraucht; könnte aber
auch eine
aber unter Umständen eine |
wichtige Rolle spielen. Satzform // Form von Sätzen //
sein. Oder: “Ich bestehe aus 5
Wörtern.”
| | |
| | | | | | “Ich bin aus den
S[a|ä]tzen … nicht beweisbar.”
– Nicht paradox ist dagegen:
“Ich bin aus den Sätzen … nicht
erhältlich.”
| | |
| | | | | | Aber nehmen wir an, die ‘Axiome’
& ‘Schlußweisen’ seien nicht nur
irgendwelche Konstruktionsweisen, sondern sie
überzeugten uns auch durchaus von dem Konstruierten! // , sondern auch durchaus
überzeugende! // Nun, 61 dann heißt das, daß es
Fälle gibt, in denen die Konstruktion aus diesen Bausteinen Bauelementen // Elementen
// nicht überzeugt.
Und tatsächlich sind die logischen Axiome gar
nicht überzeugend, wenn wir für die
Satzvariablen Strukturen einsetzen, die niemand
ursprünglich vorhergesehen hat, als …
als mögliche Werte vorhergesehen hat |
, als man nämlich ihrer der
Wahrheit ˇder Axiome (im Anfang) die unbedingte Anerkennung
gab.
| | |
| | | | | | Wie
aber wenn man sagt: die Axiome und Schlußweisen sollen doch
so gewählt werden, daß sie keinen falschen Satz beweisen
können?
| | |
| | | | | |
‘Wir wollen nicht nur einen ziemlich
zuverläßigen, sondern einen
absolut zuverläßigen
Kalkül. Die Mathematik muß absolut
sein.’
| | |
| | | | | | Nimm an, ich
hätte die Regeln 62 für's Spiel
‘Fuchs & Jäger’ aufgestellt –
stellte mir das Spiel unterhaltlich & hübsch vor
– später finde ich // .
Später aber finde ich // , daß die
Jäger immer gewinnen können, wenn man einmal .
Ich bin nun, sagen wir, mit meinem Spiel unzufrieden.
Die von mir gegebenen Regeln haben ein Resultat gezeitigt,
daß ich nicht vorausgesehen hatte // voraussah // &
(das) mir das Spiel verdirbt.
| | |
| | | | | |
20.6.
‘N. N. kam darauf,
daß man bei den Berechnungen oft durch Ausdrücke der Form
‘(n ‒
n)’ gekürzt hatte. Er wies die
dadurch entstehende Diskrepanz der Resultate nach &
zeigte, wie Menschenleben durch diese Art des Rechnens verloren
worden waren.’
| | |
| | | | | | Aber nehmen wir an, auch die Andern
hätten jene Widersprüche gemerkt, nur sich nicht
darüber 63 Rechenschaft geben können woher
sie . Sie hätten
sozusagen mit schlechtem Gewissen gerechnet. Sie
hätten zwischen widersprechenden Resultaten eins
gewählt, aber mit Unsicherheit, während ihnen
N's Entdeckung vollkommene Sicherheit gegeben
hätte. – Aber sagten sie sich:
‘mit unserm Kalkül ist etwas nicht in
Ordnung’? War ihre Unsicherheit von der Art der
unsern, wenn wir eine physikalische Berechnung anstellen, aber nicht
ganz sicher sind, ob die⌊se⌋
benützten
Formeln hier wirklich das richtige Resultat ergeben?
Oder war es ein Zweifel darüber, ob ihr Rechnen
ihre Mathematik |
wirklich sei? In diesem Falle: was taten sie,
um den
Übelstand abzustellen
sich davon zu überzeugen |
?
| | |
| | | / | | | Ich versuche
nicht, den Gegenstand in's
Futeral zu pressen, noch Stücke wegzuschneiden, bis
er paßt, 64 sondern ich will ihn
drehenc ˇumlegen, –
vielleicht um 180˚ – damit er passe.
bis er
paßt. |
⌊
[gehört eigentlich zu Betrachtungen der Grundlagen der
Mathem.]⌋
| | |
| | | | | | Die Leute haben bisher nur
verhältnismäßig selten vom Kürzen durch
Ausdrücke vom
Werte 0 Gebrauch
gemacht.
entdeckt daß sie auf diese
Weise wirklich jedes beliebige Resultat ausrechnen können. – Was tun sie nun? Nun, wir könnten uns
sehr verschiedenes vorstellen.
Sie können, z.B., nun erklären,
diese Art des Rechnens habe (damit)
ihren Witz verloren, & so sei künftig
nicht (mehr) zu rechnen.
| | |
| | | | | | ‘Er glaubt, er rechnet –
möchte man sagen – er rechnet tatsächlich
nicht.’
| | |
| | | | | |
Wenn die Rechnung für mich ihren Witz verloren hat, sobald ich
weiß, wie ich nun alles Beliebige errechnen kann –
hat sie keinen gehabt, so 65 lang ich das nicht
wußte?
| | |
| | | | | | Ich
mag freilich jetzt alle diese Rechnungen als nichtig erklären
– ich führe sie eben jetzt nicht mehr aus – aber waren
es darum keine Rechnungen?
| | |
| | | | | | Ich habe (einmal), ohne es zu
wissen, über einen Widerspruch // versteckten Widerspruch //
geschlossen. Ist mein Resultat nun falsch, oder doch
unrecht erworben?
| | |
| | | | | | Wenn der Widerspruch wirklich so gut
versteckt ist, daß wir ihn nicht merken, // daß ihn niemand merkt, // warum
sollen wir nicht das, was wir jetzt tun, das eigentliche Rechnen
nennen?
| | |
| | | | | | Wir
sagen, der Widerspr. würde den
Kalkül vernichten. Aber wenn er nun
sozusagen in winzigen Dosen aufträte, gleichsam 66 blitzweise, nicht als ein
ständiges Rechenmittel, würde er da auch vernichten?
| | |
| | | | | |
21.6. Denk' Dir,
ˇdie Leute hätten sich eingebildet
(a +
b)² sei gl müsse gleich
sein a² +
b². (Ist das eine Einbildung von der
Art: es müsse eine Dreiteilung des Winkels mit Lineal und
Zirkel geben?) Kann man sich also so einbilden, zwei
Rechnungsweisenwege
müssten dasselbe ergeben, wenn
sie es nicht ˇder Fall ist tun?
| | |
| | | | | | Ich addiere eine
Kolumne, addiere sie auf verschiedene Weise, nehme
z.B. die Zahlen in verschiedener
Reihenfolge & kriege immer wieder,
scheinbar regellos, etwas andres heraus. – Ich werde vielleicht sagen: “Ich bin
ganz verwirrt; ich mache entweder regellos Rechenfehler,
67 oder ich mache
gewisse Rechenfehler in bestimmten
Verbindungen etwa, auf
‘6 + 3
= 9’ sage ich immer
‘7 + 7 =
15’.
Oder ich könnte
mir denken, daß ich plötzlich einmal in der
Rechnung subtrahiere statt zu addieren, aber nicht denke, daß
ich da nun etwas anderes tue.
| | |
| | | | | | Nun könnte es sein,
daß ich den Fehler nicht fände & mich für
geistesgestört hielte. Aber das müßte meine
Reaktion nicht sein.
| | |
| | | | | | ‘Der Widerspruch hebt den
Kalkül auf,’ – woher diese
Sonderstellung? Sie ist, glaube ich, durch etwas
Phantasie gewiß zu erschüttern.
| | |
| | | ∕∕ | | | Um
diese philosophischen Probleme zu lösen muß man Dinge
miteinander vergleichen, 68 die zu vergleichen noch niemand
ernstlich miteinander verglichen hat. // , die zu
vergleichen noch niemand ernstlich eingefallen
ist. //
| | |
| | | ∫ / | | | Man
kann auf diesem Gebiete allerlei fragen, was zwar zur Sache
gehört, aber nicht durch die Mitte ˇder Sache // derselben // führt.
Eine bestimmte Reihe von Fragen führt
durch die Mitte, ins Freie. Die andern werden nebenbei
beantwortet.
Den Weg durch die Mitte zu
finden, ist ungeheuer schwer.
| | |
| | | ∫ / | | | Er geht
über neue Beispiele & Vergleiche.
Die abgebrauchten zeigen ihn nicht. // diesen Weg
nicht. // // zeigen uns Weg nicht. // // zeigen uns ihn nicht. //
| | |
| | | | | |
22.6. Der Widerspruch ist
so speziell, wie die Wahrheitsfunktionen, wie ‘ja’
& ‘nein’.
69
| | |
| | | / | | | 23.6.
Nehmen wir an, der
R'sche
Widerspruch wäre nie
gefunden worden. Nun – ist es ganz klar, daß wir
dann einen falschen Kalkül besessen hätten?
Gibt es denn hier nicht verschiedene
Möglichkeiten?
| | |
| | | / | | | Und wie, wenn man den
Widerspr. zwar gefunden, sich aber
weiter nicht über ihn aufgeregt, & etwa bestimmt
hätte, es seien aus ihm keine Schlüsse zu ziehen.
(Wie ja auch niemand aus dem ‘Lügner’
Schlüsse zieht.) Wäre das ein offenbarer
Fehler gewesen?
| | |
| | | / | | | “Aber
dann ist doch das kein eigentlicher Kalkül! Er
verliert ja alle Strenge!” Nun nicht
alle. Und er hat nur dann nicht die volle
Strenge, wenn man ein bestimmtes Ideal der Strenge hat // verfolgt // , einen bestimmten Stil
70 der Mathematik
.
| | |
| | | | | | ‘Aber ein
Widerspr. in der
Math. verträgt sich doch nicht
mit ihrer Anwendung // mit der
Anwendg. der Mathematik // .
Er macht, wenn er
konsequent, d.h. beliebiger Resultate
verwendet wird, die Anwendung der
Math. zu einer Farce, oder
einer Art überflüssiger Zeremonie. Seine
Wirkung ist etwa die, unstarrer Maßstäbe, die durch
[d|D]ehnen & [z|Z]usammendrücken
verschiedene Messungsresultate zulassen.’
Aber war das Messen durch Abschreiten kein
Messen? Und wenn die Menschen mit Maßstäben aus
Teig arbeiteten, wäre das an sich schon falsch zu
nennen?
| | |
| | | | | | Könnte man
sich nicht leicht Gründe denken, weshalb eine gewisse Dehnbarkeit
der Maßstäbe erwünscht sein könnte?
71
| | |
| | | | | |
‘Aber ist es nicht richtig, die Maßstäbe aus immer
härterem, unveränderlicherem Material
herzustellen? Gewiß ist es richtig; wenn man es
so will.’
| | |
| | | / | | | ‘Also
redest Du dem Widerspruch das Wort?!’
Durchaus nicht; so wenig, wie den weichen
Maßstäben.
| | |
| | | | | |
Ein Fehler ist zu vermeiden: Man denkt, der
Widerspruch muß sinnlos sein:
d.h., wenn man z.B. die
Zeichen ‘p’,
‘~’, ∙
konsequent benützt, so kann
‘p ∙ ~p’
nichts sagen. – Aber denke was heißt, den & den Gebrauch
‘konsequent fortsetzen’?
(‘Dieses Kurvenstück konsequent
fortsetzen’.)
| | |
| | | / | | | Wozu braucht
die Mathematik eine Grundlegung?! Sie braucht sie,
glaube ich, ebenso wenig, wie die
Sätze über physikalische Gegenstände oder
Sinnesdatenempfindungen eine
Analyse. // wie die Sätze, die von
physikalischen Gegenständen 72 handeln, oder von
Sinneseindrücken, eine Analyse. // // wie die Sätze, die von physikalischen
Gegenständen, – oder die, welche von
Sinneseindrücken handeln, eine Analyse. // Wohl aber bedürfen die mathematischen,
sowie jene andern Sätze eine Klarlegung ihrer
Grammatik.
| | |
| | | ∕∕ | | | Die
mathematischen Probleme der sogenannten Grundlagen liegen
für uns der Math.
so wenig zu
Grunde, wie der gemalte Fels einer
gemalten Burg. // wie der gemalte Fels die
gemalte Burg trägt. //
| | |
| | | | | |
‘Aber wurde die
Fregesche Logik durch den
Widerspr. zur Grundlegung
der Arithmetik nicht untauglich? Doch!
⌇ Aber wer sagte denn auch, daß sie zu diesem Zweck
tauglich sein müsse?!⌇
| | |
| | | | | |
24.6.
Man könnte sich sogar denken,
daß man die Fregesche Logik
einem Wilden 73 als Instrument gegeben hätte, um
damit arithm. Sätze
abzuleiten. Er habe den
Widerspr. abgeleitet, ohne zu
merken, daß es einer ist, & aus ihm nun beliebige wahre
& falsche Sätze.
| | |
| | | | | | ‘Ein guter Engel hat uns
bisher bewahrt, diesen Weg zu gehen.’
Nun, was willst Du mehr? Man könnte, glaube
ich, sagen: Ein guter Engel wird immer nötig sein,
was immer Du tust.
| | |
| | | | | |
Man sagt: das Rechnen sei ein Experiment, um
dadurch seine praktische Anwendbarkeit zu erklären // – um dadurch zu zeigen, wie es so
praktisch sein kann // . Denn vom
Experiment weiß man, daß es realen Wert
hat // daß es wirklich
Wert hat // . Nur vergißt man, daß es
diesen Wert besitzt vermöge einer Technik, die (wohl)
ein naturgeschichtliches Faktum ist, deren Regeln aber
74 nicht die Rolle von
Sätzen der Naturgeschichte haben.
| | |
| | | ∕∕ | | |
“Die Grenzen der
Empirie” – (Leben wir, weil es praktisch ist zu
leben? Denken wir, weil Denken praktisch
ist?
, weil zu denken praktisch
ist? |
)
| | |
| | | / | | | 25.6.
Daß ein Experiment praktisch ist, das weiß er; also ist die
Rechnung ein Experiment.
| | |
| | | / | | | Unsre
experimentellen Handlungen haben allerdings ein charakteristisches
Gesicht. Wenn ich jemand in einem Laboratorium eine
Flüssigkeit in eine Proberöhre gießen &
über einer Bunsenflamme erhitzen sehe, bin ich geneigt zu sagen,
er mache ein Experiment.
| | |
| | | / | | | Nehmen wir an,
Leute, die ˇwelche zählen
können, wollen so wie
wir zu
verschiedenendenerlei praktischen Zwecken . Und dazu fragen sie gewisse
, die, wenn ihnen das
75 praktische Problem
erklärt wurde, die Augen schließen, & sich die dem
Zweck entsprechende Zahl einfallen ließen;
‒ ‒ ‒ läge hier keine
Rechnung vor, wie verläßlich immer die Zahlangabe sein
mag. Ja diese Zahlbestimmung könnte ˇpraktisch
viel verläßlicher sein, als jede Rechnung.
| | |
| | | / | | | Eine
Rechnung – könnte man sagen – ist ˇetwa ein Teil
der Technik eines Experiments, aber allein Experiment.
| | |
| | | / | | | 27.6.
Vergißt man denn, daß das
Experiment in bestimmter Weise angewendet ? // Experiment eine
Anwendung hat? // // daß
das Experiment dies durch eine // daß zum Experiment eine bestimmte Anwendung
der [e|E]xperimenthandlung des
experimentellen Vorgangs gehört? // // daß zum Experiments eine
bestimmte Anwendung des Vorgangs gehört?
// Und die Rechnung vermittelt die
Anwendung.
76
| | |
| | | ∕∕ | | | Würde denn jemand
daran denken, das Übersetzen einer
sChiffre mittels eines Schlüssels ein
Experiment zu nennen?
| | |
| | | | | | Das normative Spiel – im
Gegensatz, etwa, zum beschreibenden.
| | |
| | | ∕∕ | | | Wenn ich
zweifle, ob die Zahlen n und m multipliziert
𝓁
ergeben werden, so bin ich nicht darüber im
Zweifel, ob eine Verwirrung in unserm Rechnen ausbrechen wird
& etwa die Hälfte der Menschen eines – die andere
Hälfte etwas andres für richtig werden.
| | |
| | | / | | |
‘Experiment’ ist eine Handlung nur von
einem gewissen Gesichtspunkt gesehen. Und es ist
klar, daß die Rechnungshandlung auch ein Experiment sein
kann.
Ich kann z.B.
prüfen wollen, was dieser Mensch unter solchen Umständen,
auf diese Aufgabenstellung 77 hin, rechnet. –
Aber, zum Teufel, das ist es ja doch
ist nicht eben das, was Du untersuchst
fragst, wenn Du ihn rechnen läßt! //
untersuchst, fragst, um zu erfahren, , wenn Du
erfahren wissen willst, wieviel 52 × 63
ist! // Ja
[d|D]as mag ich
wohl fragen – d.h.: meine Frage
mag sogar in diesen Worten ausgedrückt sein.
(Vergl. damit: Ist der Satz
“der Arme Horch, sie stöhnt!“
einer ein Satz über das ihr Benehmen,
oder das über ihr Leiden?
des)
Aber wie ist es nun, wenn ich seine Rechnung
vielleicht nachrechne? – ‘Nun,
dann mache ich noch ein Experiment um ganz sicher
herauszufinden, daß alle normalen Menschen so
reagieren.’ – Und wenn sie nun
nicht gleichförmig reagieren –:
welches ist das Rechnungsresultat? // das mathematische Resultat?
//
| | |
| | | / | | | “Soll
die Rechnung praktisch sein, so muß sie Tatsachen
herauskriegen . Und das kann man nur
durchs das
Experiment.”
Aber welches sind
‘Tatsachen’? 78 Glaubst Du, Du kannst zeigen,
was eine welche Tatsache
ˇgemeint ist, indem Du ˇetwa mit dem Finger
Finger zeigst? drauf ˇsie
hinzeigst? Macht das schon die Rolle klar, welche
die ‘Feststellung’ einer Tatsache spielt? – Wenn nun die Mathematik erst den
Charakter dessen bestimmte, was Du
‘Tatsache’ nennst?!
‘Es ist interessant zu wissen wieviele Schwingungen dieser Ton
hat.’ Aber die Arithmetik hat Dich diese Frage erst
gelehrt.
lehrt Dich
erst, was wieviele heißt. |
Sie
lehrt hat Dich, gelehrt, nach dieser Art von Tatsachen
fragen; diese Art von Tatsachen zu sehen.
| | |
| | | / | | | Die Mathematik – will
ich sagen – lehrt Dich nicht die Antwort auf eine Frage;
sondern ein ganzes Sprachspiel, mit Fragen Frage &
Antworten Antwort.
| | |
| | | | | |
Sollen wir sagen, die Mathematik lehre uns
zählen? 79 | | |
| | | | | | ⌊⌊
Kann man von der Mathematik sagen, sie lehre uns experimentelle
Forschungsweisen? Oder sie helfe uns, solche
Forschungsweisen finden? ⌋⌋
| | |
| | | / ? ? | | |
‘Die Mathematik, um praktisch zu sein, muß uns
Tatsachen lehren.’ – Aber müssen diese
Tatsachen die mathematischen Tatsachen sein? – Aber warum soll sie nicht, statt uns
‘Tatsachen’ zu lehren‘, die
Formen dessen schaffen ˇschaffen helfen,
was wir Tatsachen nennen?
| | |
| | | ? / | | |
“Ja aber es
bleibt doch empirische Tatsache, daß die Menschen soc
rechnen! – Ja, aber damit werden
Rech⌊e⌋nungsätze nicht zu empirischen
Sätzen.
| | |
| | | ? / | | |
“Ja, aber es muß doch Rechnen auf empirischen Tatsachen
beruhen!” Gewiß.
Der Zusammenhang besteht (eben) darin,
daß die Rechnung ein das Bild eines
Experiments ist; den
Gang zeigend, den
; & zwar den Gang zeigt, den |
es so gut wie immer nimmt. // Gewiß. Aber welche meinst Du
jetzt? Die psychologischen &
physiologischen, die es möglich machen, oder die, die es zu einer
nützli
80 zu etwas Nützlichem machen?
nützlichen Tätigkeit
machen? |
Der Zusammenhang mit diesen besteht darin,
daß die Rechnung das Bild eines Experiments ist, so wie
es ˇnämlich, so gut wie immer,
abläuft. // Von den anderen erhält
es seine Pointe, seine Physiognomie: aber das sagt durchaus
nicht, daß die Sätze der Mathematik die
Rollen ⌊der⌋ Funktionen der
empirische[r|n] Sätze spielen haben. [Das Wort ‘Rolle’
ist mir unangenehm. Es ist zu
facil.] (Das wäre
ˇbeinahe, als glaubte Einer: weil doch nur die
Schauspieler im Stücke eine Rolle⌊e⌋
spielen // auftreten // agieren // handeln // , so
könnten auch keine andern Leute nützlich auf
der Bühne des Theaters beschäftigt sein beschäftigt sein.) // so gäbe es auf ˇauch für
andre Leute auf der Bühne nichts nützliches zu
tun.) //
| | |
| | | / | | | In der Rechnung
sind die Zusammenhänge
nicht kausal.
gibt es keine kausalen Zusammenhänge, nur die
Zusammenhänge des Bildes. |
81
| | |
| | | | | | Und daran
ändert es nichts, daß wir die Beweisfigur nachrechnen, um sie
anzuerkennen. Daß wir also versucht sind, zu
sagen, wir ließen sie durch ein psychologisches Experiment
entstehen. Denn der Ablauf wird beim Rechnen nicht
psychologisch untersucht.
| | |
| | | ∕∕ | | | Aber
können wir uns keine menschliche Gesellschaft denken, in
der es ebensowenig ein Rechnen, ganz in unserm Sinn, wie ein
Messen, ganz in unserm Sinn, gibt? – Doch. – Aber wozu will ich mich dann bemühen, was Mathematik
ist herauszuarbeiten?
Weil es bei uns eine
Mathematik gibt & eine besondere Auffassung derselben, ein
Ideal, ˇgleichsam⌊,⌋ ihrer Stellung & Funktionc, – & dieses
muß klar herausgearbeitet
werden.
| | |
| | | | | | ˇErwäge⌊:⌋
‘Unsre Mathematik wandelt Experimente in
Definitionen um.’
82
| | |
| | | | | |
Fordere nicht zuviel, & fürchte nicht, daß Deine
gerechte Forderung in's Nichts zerrinnen
wird.
| | |
| | | / | | | Meine Aufgabe ist es nicht,
Russells Logik von
innen anzugreifen, sondern von außen.2
| | |
| | | / | | |
D.h.: nicht, sie mathematisch
anzugreifen – sonst triebe ich Mathematik – sondern
ihre Stellung, ihr Amt. // ihre
Stellung, ihr Prestige. //
| | |
| | | / | | | 2.7.
‘Die Minute hat 60 Sekunden.’ Das ist
ein Satz ganz ähnlich﹖ einem
mathematischen. Hängt seine Wahrheit von der
Erfahrung ab? – Nun: könnten ˇwir
von Minuten und Sekunden reden, wenn es keinen Zeitsinn gäbe;
wenn es keine Uhren gäbe, oder, aus physikalischen Gründen,
nicht geben könnte; wenn alle die Zusammenhänge nicht
statt hätten, die unsern Zeitmaßen Sinn & Bedeutung
geben? In diesem Falle – würden wir sagen
– hätte das Zeitmaß seine Pointe 83 verloren (wie die Handlung des
Matsetzens ohne das
Schachspiel. , wenn das Schachspiel
verschwändeohne die Institution des
Schachspiels.) – oder es hätte dann
einen ganz anderen . – Macht aber die eine so beschriebene Erfahrung den
Satz falsch, die andre wahr? Nein; das
beschriebe nicht seine Funktion. Er
funktioniert ganz anders.
| | |
| | | ∫ | | | Ich will einen
bestimmten Aspekt der Mathematik herausarbeiten; & zwar den,
der – meiner Meinung nach – offenbar gemacht
die Art & Weise beeinflußt, wie Mathematiker
& Philosophen (heute) die Mathematik
betrachten. // – klar
die Art &
Weise … //
//
| | |
| | | | | | ‘Der psychologische Ablauf der
Rechnung’ – oder soll ich ihn einen physiologischen
nennen? Will ich die Gefühle der Billigung eines
Rechenübergangs beschreiben? Wenn wir statt der
Billigung hier den Ausdruck der Billigung setzen:
– was interessiert er uns? 84 Er ist bloß eine
Umgebung des Rechnens. (Beachte das
Benehmen beim Rechnen!)
| | |
| | | | | | ‘Das Rechnen, um praktisch
sein zu können, muß auf empirischen Tatsachen
beruhn.’ – Warum soll es nicht
lieber bestimmen, was wir empirische Tatsachen nennen?
// bestimmen helfen, was emp. Tats. sind?
// // bestimmen, was emp. Tatsachen
sind? //
| | |
| | | | | |
Meine Aufgabe ist es nicht über
den Gödelschen Beweis
,(z.B.), zu reden; sondern an ihm vorbei zu
reden.
| | |
| | | | | | Die
Aufgabe, die Zahl der Wege zu finden, auf denen man
d[ie|en]
Fugen dieser Mauern ˇohne abzusetzen & ohne
Wiederholung
nachentlangfahren kann, erkennt
als mathematische
Aufgabe. –
| | |
| | | | | | Wäre die
vielc
komplizierter & größer, nicht zu
überblicken, so könnte man annehmen sie ändere sich,
ohne das wir's merken, &
dann wäre die Auf-85 gabe,
jene Zahl (die sich vielleicht
gesetzmäßig ändert) zu finden, keine
mathematische mehr. Aber auch wenn sie gleichbleibt,
ist die Aufgabe dann nicht mathematisch. – Aber auch
wenn das Netz der Fugen
die Mauer |
zu
überblicken ist, so heißt das nicht, die
Aufgabe ist eine
mathematische als
sagte man: diese Aufgabe ist nun eine der
Embryologie. Vielmehr , so kann man nicht
sagen die Aufgabe wird dadurch zu einer
mathematischen – wie man sagt:
…. // zu überblicken ist, tritt
die Aufgabe dadurch ˇnun nicht in's
Gebiet der Mathematik über – wie man sagt:
diese … // Vielmehr:
hier brauchen wir eine [M|m]athematische
Lösung. (Wie: ist, was wir , eine Vorlage.)
| | |
| | | | | |
‘Erkannten’ wir das Problem als mathematisches,
weil, die Mathematik vom Nachfahren von Zeichnungen
handelt?
| | |
| | | | | | Warum sind wir
also geneigt, dieses Problem ˇschlechtweg ein
‘mathematisches’ zu nennen? Weil wir es
ihm ˇgleichc ansehen, daß hier die 86 Beantwortung einer
mathematischen Frage alles ist, was wir
brauchen. Obschon man das Problem,
z.B., leicht als als ein
psychologisches sehen könnte.
Ähnliches von der Aufgabe, aus einem Blatt Papier das
& das zu falten.
| | |
| | | | | | Es kann so ausschauen, als ob die
Mathematik hier eine Wissenschaft ist, die mit
Einheiten
[e|e]xperiment[i|e]ert macht
ˇExperimente, bei es
ˇnämlich nicht auf die Arten der Einheiten
nicht ankommt, also
nicht darauf, ob Erbsen,
Glaskugeln, Striche, usw. sind. – Nur
was von allen diesen gilt, findet sie heraus.
über ihren Schmelzpunkt, aber, daß 2 und 2
ˇvon ihnen 4 sind. Und das Problem der Mauer
⌊№ 1⌋ ist eben ein
mathematisches, d.h.: kann
durch diese Art von Experiment gelöst werden. – Und worin das math.
Experiment besteht? Nun, im [h|H]inlegen
& Verschieben von Dingen, [z|Z]iehen von
Strichen, [a|A]nschreiben von Ausdrücken,
Sätzen, etc. Und man 87 muß sich
dadurch nicht stören lassen, daß die äußere
Erscheinung dieser Experimente nicht die physikalischer
& anderer chemischer,
etc. hat, es sind eben andersartige.
ist eben eine völlig andre
Art. |
Nur eine
Schwierigkeit ist da: das, was
vorgeht
der Vorgang |
ist leicht genug zu sehen, zu beschreiben –
aber wie ist es als Experiment anzuschauen?
Welches ist hier der Kopf, welches der Fuß des
Experiments?c ⌊Welches sind die
Bedingungen des Experiments, welches das Resultat?⌋ ⌊⌊ˇ Welches sind die Bedingungen des Experiments, welches
sein Resultat?⌋⌋ ⌊⌊ˇIst das Resultat
das Rechnungsergebnis, oder das Rechnungsbild, oder die
Zustimmung (worin immer diese besteht) des Rechnenden?
⌋⌋
| | |
| | | | | | Werden aber,
etwa, die Prinzipien der Dynamik zu Sätzen der reinen Mathematik
dadurch, daß man ihre Interpretation offen läßt &
sie nur zum Erzeugen eines Maßsystems verwendet?
| | |
| | | | | | “Der
math. Beweis muß
übersichtlich sein” – das hängt mit der
Übersichtlichkeit jener Figur zusammen.
| | |
| | | | | | Vergiß nicht: der Satz, der von
sich selbst aussagt, er sei unbeweisbar, ist als
mathematische Aussage auf-88 zufassen, ‒ ‒ ‒ denn das ist
nicht selbstverständlich.
Es ist nicht selbstverständlich, daß der
Satz, die & die Struktur sei: so & so nicht
konstruierbar, als als mathematischer Satz aufzufassen
.
| | |
| | | | | |
D.h.: wenn man
sagt: “er sagt von sich selbst aus”
– so ist das auf eine spezielle Weise zu verstehen,. Hier nämlich entsteht leicht Verwirrung
durch den bunten Gebrauch des Ausdrucks “dieser Satz
sagt etwas von … aus“.
| | |
| | | | | | In diesem Sinne ˇsagt der Satz
625 = 25 ×
25 auch etwas über sich selbst aus: daß
nämlich die linke Ziffer erhalten wird, wenn man die rechts
stehenden multipliziert.
| | |
| | | | | |
Der
Gödelsche Satz, der
etwas über sich selbst aussagt, erwähnt sich
selbst nicht. 89
| | |
| | | | | | Kann man
nicht ebenso sagen, der Satz
3 + 2 =
5 sage von sich aus, er könne in eine Gruppe von 3
& eine von 2 Zeichen zerlegt werden? // ,
er bestehe aus einer Gruppe von 3 & einer von 2
Zeichen? //
| | |
| | | | | | ‘Der Satz sagt, daß diese
Zahl aus diesen Zahlen auf diese Weise nicht erhältlich
ist.’ – Aber bist Du auch sicher, daß Du
ihn recht ins Deutsche übersetzt hast? Ja gewiß,
es scheint so. – Aber kann man da nicht
fehlgehen?
| | |
| | | | | |
∣ Ein Stil, Maschinen zu bauen, in welchem man die wirksamen
Räder, Hebel, etc. einer Zahl unwirksamer umgibt, die,
z.B., nur eines ästhetischen Eindrucks
wegen angebracht sind. (Ähnlich wie Scheinfester in
einer Fassade.) ∣
| | |
| | | | | |
Könnte man sagen:
Gödel sagt, daß man
einen math.
Beweis auch trauen
muß,
muß trauen können, |
wenn man ihn, prak-90 tisch, als den Beweis
seiner der Konstruierbarkeit ˇder
Satzfigur nach den Beweisregeln
auffassen will?
Oder: Ein
math. Satz muß als Satz einer
auf sein eigenes Zeichen
sich selbst |
wirklich
anwendbaren Geometrie aufgefaßt werden können. Und
tut man das so zeigt es sich, daß man
sich auf einen Beweis in gewissen Fällen nicht
verlassen kann
| | |
| | | | | | | Wir erwarten dies & werden
das
eine & werden |
von dem überrascht
von dem
andern überrascht |
; aber die
Kette der Gründe hat ein Ende. ∣
| | |
| | | | | | ∣ Die Grenzen der Empirie sind
nicht unverbürgte Annahmen, oder intuitiv als richtig erkannte;
sondern Arten & Weisen des
Vergleichschens
& des Handelns.
| | |
| | | | | |
3.7. ‘Nehmen wir an, wir haben
einen arithmetischen Satz, der sagt, eine bestimmte Zahl
⌊ … ⌋ könne nicht aus den Zahlen … , … ,
… , durch die & die Operationen 91 gewonnen werden. Und nehmen
wir an, es ließe sich eine Übersetzungsregel geben, dieser
arithm. Satz in die Ziffer
jener ersten Zahl , – die Axiome,
unseres
Beweissystems in die …
aus denen wir versuchen ihn zu beweisen, in die |
Ziffern jener andern Zahlen –
& unsere Schlußregeln in die im Satz erwähnten
Operationen sich übersetzen ließen. –
Hätten wir dann den arithm
Satz aus den Axiomen nach unsern Schlußregeln
abgeleitet, so hätten wir dadurch seine
Ableitbarkeit demonstriert, aber auch einen Satz bewiesen, den
man nach jener Übersetzungsregel dahin aussprechen
: dieser
arithm. Satz (nämlich
unserer) sei unableitbar.
Was
wäre nun da zu tun? Ich denke mir, wir schenken
unserer Konstruktion des Satzzeichens
glauben, also dem geometrischen Beweis.
Wir sagen also, diese ‘Satzfigur’ ist aus jenen
so & so gewinnbar. Und übertragen, nur, in
eine andre Notation heißt das: diese Ziffer
ist mittels dieser Operationen aus jenen zu ge-92 winnen. Soweit hat der Satz
& sein Beweis nichts mit einer besonderen Logik zu
tun. Hier war jener konstruierte Satz einfach eine
andere Schreibweise der konstruierten Ziffer; sie hatte die
Form eines Satzes aber wir verglichen nicht mit andern Sätzen als
Zeichen, welches dies oder jenes sagt, einen Sinn
hat.
| | |
| | | | | | Aber
freilich ist zu sagen daß jenes Zeichen weder als Satzzeichen noch
als Zahlzeichen angesehen werden
braucht muß. –
Frage Dich: was macht es zu dem einen, was zu dem
anderen?
| | |
| | | | | |
Lesen wir nun den konstruierten Satz (oder die Ziffer) als
Satz der mathematischen Sprache (etwa auf Deutsch), so spricht
er das Gegenteil von dem, was wir eben als bewiesen
betrachtet. Wir haben also den ˇwörtlichen Sinn
des Satzes als falsch 93 demonstriert & ihn zu gleicher
Zeit bewiesen – wenn wir nämlich seine
Konstruktion aus den ˇzugelassenen Axiomen mittels der
zugelassenen Schlußregeln als Beweis betrachten.
| | |
| | | | | | (Wenn jemand uns
einwürfe, wir könnten solche Annahmen nicht
machen, das es logische oder
mathematische Annahmen wären, so antworten wir,
daß nur nötig ist anzunehmen jemand habe einen Rechenfehler
gemacht & sei dadurch zu dem Resultat
gelangt, das wir ‘annehmen’, & er
könne diesen Rechenfehler vorderhand nicht finden.
| | |
| | | | | |
∣ Die Menschen
die immerfort ‘warum’ fragen, sind wie die
Touristen, die, im
Bädeker lesend, vor einem Gebäude stehen & durch
das Lesen der Entstehungsgeschichte
etc etc
gehindert werden, das Gebäude zu
sehen. ∣
94
| | |
| | | | | | Hier
kommen wir wieder auf den Ausdruck “der Beweis überzeugt
uns” zurück. Und was uns ˇhier an
der Überzeugung interessiert, ist weder ihr Ausdruck durch
Stimme und Gebärde, noch das Gefühl, der
Befriedigung, oder ähnliches; sondern ihre
Betätigung in der Verwendung des Bewiesenen.
| | |
| | | | | |
Man mit Recht fragen, welche Wichtigkeit
Gödel's Beweis
für unsre Arbeit habe. Denn ein kann
Stück Mathematik kann ein Probleme Problem
dieser Untersuchung von der Art der unsern
nicht // kann Probleme von der Art, die
uns beunruhigen, nicht lösen. // // kann kein Problem von der Art, die uns
beunruhigt lösen. // // kann nicht
Probleme von der Art, die uns beunruhigt,
lösen. // – Die Antwort ist:
daß die Situation uns interessiert, in die ein solcher
Beweis uns bringt. ‘Was sollen nun sagen?’ – das ist unser
Thema. 95
| | |
| | | | | |
4.7. Es kommt uns viel zu
selbstverständlich vor, daß wir
“wieviele?” fragen & darauf
zählen & rechnen!
| | |
| | | | | |
So seltsam es klingt, so scheint meine Aufgabe
ˇdas Gödelsche
Theorem betreffend (bloß) darin
zu bestehen, klar zu stellen, was in der Mathematik so ein Satz
bedeutet, wie: “angenommen, man könnte dies
beweisen”.
| | |
| | | | | |
Zählen wir weil es praktisch ist zu zählen?
Wir zählen! – Und so rechnen wir
auch. ⌊⇒ Siehe Seite
74⌋
| | |
| | | ∫ | | |
:
“‘Einfach hersagen:
“eins, zwei, drei, vier,”
… ” – ist reine Mathematik treiben; Dinge
zählen, angewandte.’
| | |
| | | | | | Man kann auf Grund eines Experiments – oder wie
man es sonst nennen will – manchmal die Maßzahl des
[g|G]emessenen, manchmal aber auch das geeignete Maß
bestimmen. 96
| | |
| | | | | |
So ist also die Maßeinheit das Resultat von
Messungen? Ja & nein. Nicht das
Messungsresultat, aber vielleicht die Folge von
Messungen.
| | |
| | | | | | Es
wäre also eine Frage: “hat uns die
Erfahrung , so zu
rechnen?” – & eine andre:
“ist die Rechnung ein Experiment?”.
| | |
| | | / \ | | |
5.3.44
Aber
läßt sich nicht alles aus allem nach irgend einer Regel –
ja nach jeder Regel mit entsprechender Deutung –
ableiten? Was heißt es, wenn ich
z.B. sage:
Ddiese Zahl
läßt sich aus jenen beiden durch
Multiplikation jener beiden ? Frage Dich: W
wann gebraucht man diesen
Satz? Nun, es ist z.B.
kein psychologischer Satz, der sagen soll, was Menschen unter
gewissen Bedingungen tun werden, was sie befriedigen wird; es ist auch
kein physikalischer das Benehmen von Zeichen auf dem Papier
97 betreffend. Er
wird nämlich in einer andern Umgebung, als ein
psychologischer, oder physikalischer, angewandt.
| | |
| | | | | | Nimm an Menschen lernen
rechnen, ungefähr, wie sie es tatsächlich tun; aber stell
Dir nun verschiedene ‘Umgebungen’ vor, die das
Rechnen einmal zu einem psychologischen Experiment, einmal zu einem
physikalischen mit den Rechenzeichen, einmal zu etwas anderem
macht!
Wir nehmen an die Kinder lernen
zählen & die ein⌊f⌋achen Rechnungsarten durch
Nachahmen, Aufmunterung & Zurechtweisung. Aber von
einem gewissen Punkt wird nun die
Nichtübereinstimmung der Rechnenden (also etwa die
Rechenfehler) nicht als etwas [s|S]chlechtes, sondern
als etwas psychologisch
[i|I]nteressantes behandelt. “Also das
hieltest Du damals für richtig?” heißt es,
“wir Andern haben es alle so
gemacht”.
98
| | |
| | | | | | Ich
will sagen: daß das, was wir Mathematik, die
mathematische Auffassung des [s|S]atzes
13 × 14 =
182, nennen, mit der besondern
Stellungnahme zusammenhängt, die wir gegen
⌊zu⌋ dieer Tätigkeit des Rechnens einnehmen. Oder,
die besondere Stellung, die die Rechnung – in unserm
Leben, in unsern ˇübrigen Tätigkeiten hat.
Das Sprachspiel in dem sie steht.
| | |
| | | / | | | Man kann ein
Musikstück auswendig lernen, um es ˇrichtig spielen
zu können; aber auch, in einem psychologischen Experiment,
um des
ˇmusikalischen Gedächtnisses zu untersuchen.
Man könnte es aber auch dem Gedächtnis
einprägen um danach ˇirgendwelche Veränderungen
in der Partitur zu beurteilen.
| | |
| | | | | | Ein Sprachspiel: Ich rechne
Multiplikationen & sage dem Andern: wenn Du
richtig rechnest wird das & das herauskommen; worauf er die
Rechnung ausführt und sich der Richtigkeit, 99 & manchmal der Falschheit,
meiner Voraussage freut. Was setzt dieses
Sprachspiel voraus? Daß
‘Rechenfehler’ leicht zu finden sind &
immer Übereinstimmung über Richtigkeit, oder
Falschheit der Rechnung rasch erzielt wird.
| | |
| | | | | | “Wenn Du mit jedem
Schritt übereinstimmen wirst, wirst Du zu diesem
Resultat gelangen.”
| | |
| | | | | | Was ist das
Kriterium dafür, daß ein Schritt der
Rechnung richtig ist; ist es nicht, daß mir der Schritt richtig
erscheint, & anderes von der gleichen Art?
Was ist das Kriterium dafür, daß ich zweimal
die gleiche Ziffer hinschreibe? Ist es nicht,
daß mir die Ziffern gleich erscheinen, &
ähnliches?
| | |
| | | | | |
Was ist das Kriterium dafür, daß ich hier dem Paradigma
gefolgt bin? 100
| | |
| | | | | |
“Wenn Du sagen wirst, daß jeder Schritt richtig
ist, wird das
herauskommen.
, wirst Du das herausbekommen. |
”
| | |
| | | | | | Die Voraussage ist eigentlich: Du
wirst, Du Dein Tun
für richtig hälst, das tun.
Du wirst, sofern Du jeden Schritt für
richtig , diesen
Weg gehen. – Daher auch zu diesem Ende
gelangen.
| | |
| | | / | | |
Logis⌊c⌋h wird geschlossen, // Ein logischer Schluß wird
, // wenn keine
Erfahrung dem Resultat
// dem Schlußresultat //
der Konklusion |
widerstreiten kann, widerstreite denn den
Premissen.
D.h., wenn der Schluß nur eine Bewegung
in der Darstellung ist. // in den
Darstellungsmitteln ist. // // in den
Mitteln der Darstellung ist. //
| | |
| | | | | | In einem Sprachspiel werden Sätze gebraucht;
Meldungen, Befehle, u. dergl. Und nun
101 werden auch
Rechensätze von den Personen verwendet. Sie sagen sie
etwa zu sich selbst, zwischen den Befehlen und Meldungen.
| | |
| | | | | |
6.3.44 Ein
Sprachspiel, in dem Einer nach einer Regel rechnet &
danach ˇden Rechnungsresultaten Steine eines Baues
setzt. Er hat gelernt mit Schriftzeichen nach Regeln zu
operieren. – Wer den Vorgang
Lehrens Lernens besch
ein beschreibt hat alles gesagt, was sich über das
richtige Handeln nach der Regel sagen läßt.
Wir können nicht weiter gehen. Es nützt
z.B. nichts zum Begriff der
Übereinstimmung ˇzurück zu gehen, weil es nicht
sichererc ist, daß [e|E]iner der Regel
gefolgt ist, als daß eine Handlung mit einer andern
übereinstimmt, als daß
Regel
gemäß geschehen ist. Es ist ja, nach
einer Regel vorgehen, auch auf eine Übereinstimmung
// Es beruht ja, nach einer Regel vorgehen,
102 auch auf einer
Übereinstimmung. //
| | |
| | | | | | Wie gesagt, was worin einer
Regel (richtig) folgen besteht, kann man
nicht näher beschreiben, als man das Lernen des
‘Vorgehens nach der Regel’ beschreibt.
Und diese Beschreibung ist natürlich eine
ˇalltägliche Beschreibung, wie die
ˇetwa des Kochens, oder Nähens
ˇetwa.
Sie setzt schon soviel voraus wie diese. Sie
unterscheidet Eins vom Andern; informiert alsoc einen
Menschen, der etwas ganzc bestimmtes nicht
weiß. (Vergl. Bemerkung: die
Philosophie verwende keine vorbereitende Sprache
etc.)
| | |
| | | | | |
7.3.44
Denn wer mir beschreibt, wie Leute zum Befolgen einer Regel
abgerichtet werden & wie sie richtig drauf reagieren,
wird selber ˇin der Beschreibung eine Regel
gebrauchen & ihr Verständnis bei mir
voraussetzen. // wird selbst in der Beschreibung
den Ausdruck einer Regel verwenden & sein Verständnis bei
mir 103
voraussetzen. //
| | |
| | | / | | | Wir haben also
jemand die Technik des Multiplizierens beigebracht. Dabei
verwenden wir der
& der
Zurückweisung. Wir werden ihm auch manchmal das
Ziel der Multiplikation anschreiben.
“Das mußt Du erhalten, wenn es richtig sein
soll.” können wir ihm sagen.
| | |
| | | / | | |
Kann nun der Schüler aber widersprechen &
sagen: ‘Woher weißt Du das? Und
ist, was Du willst, daß ich der Regel folgen soll, oder daß ich
dies Resultat erhalten soll? Denn die beiden brauchen ja
nicht zusammen⌊|⌋zu⌊|⌋treffen.” Nun, wir nehmen nicht an, daß
der Schüler das sagen kann; wir nehmen an, daß er die
Regel von beiden Seiten her gelten läßt.
Daß er den einzelnen Schritt & das
Rechnungsbild – & also das Rechnungsresultat – als
Kriterien der Richtigkeit auffaßt, & daß, wenn diese
nicht Übereinstimmen er an eine
Verwirrung 104 der Sinne glaubt.
| | |
| | | | | |
Ist es nun denkbar, daß einer der Regel richtig folgt &
zu verschiedenen Malen ˇbeim
Multiplizieren 15
× 13 doch verschiedenes errechnet?
Daß kommt darauf an, welche Kriterien für das richtige Folgen gelten läßt.
In der Mathematik ist das Resultat selbst auch ein Kriterium des
richtigen Rechnens. Da ist es also
So aufgefaßt ist es also |
undenkbar der Regel richtig zu folgen
& verschiedene Rechnungsbilder zu .
| | |
| | | | | |
Das Nicht-Geltenlassen des Widerspruchs charakterisiert die
Technik Verwendung
Wahrheitsfunktionen.
Lassen wir den Widerspruch gelten, so das eine Änderung der
Auffassung der Wahrheitsfunktionen
daß wir die Verwendung der
Wahrheitsfunktionen ändern |
; als faßten wir
z.B. eine doppelte Verneinung nicht mehr als
Bejahung auf. Und keine Änderung ist // Lassen wir den Widerspruch ˇin unsern
Sprachspielen gelten, so das eine
Änderung jener Technik. // // Lassen wir den Widerspruch in unsern 105 Sprachspielen gelten, so ändern
wir jene Technik – so, als giengen wir davon ab, eine
doppelte Verneinung als Bejahung anzusehen. Und diese
Änderung wäre von Bedeutung, da die Technik unserer Logik
ihrem Charakter nach zusammenhängt mit ‒ ‒ ‒
| | |
| | | | | | “Die Regeln
zwingen mich zu etwas”, nun das kann man schon sagen, weil,
was mir mit der Regel übereinzustimmen scheint ja nicht von
meine[m|r] freien
Willenkür abhängt. Daher kann
es ja geschehen daß ich die Regeln eines Brettspiels ersinne
& nachträglich herausfinde daß in diesem
Spiel wer anfängt gewinnen muß. Und so
ähnlich ist es ja, wenn ich finde, daß die Regeln zu einem
Widerspruch führen
| | |
| | | | | |
[7|8].3.44. Ich bin nun gezwungen
anzuerkennen, daß, das eigentlich kein Spiel ist.
106
| | |
| | | | | |
‘Die Regeln des Multiplizierens, einmal angenommen,
zwingen mich nun anzuerkennen, daß … × …
gleich … ist.’ Angenommen, daß es mir
unangenehm wäre,
anzuerkennen. Soll ich sagen: “Nun,
das kommt von dieser Art Abrichtung. Menschen, die so
[A|a]bgerichtet, so conditioniert
sind, kommen dann in solche Schwierigkeiten.”?
| | |
| | | | | | ‘Wie
im
Dezimalsystem?’ – “Wir schreiben
auf 1, 2, auf 2, 3 … – auf 13 14 … auf 123 124,
u.s.f.” – Das ist eine
Erklärung für den, der ˇzwar irgend etwas
andres als das nicht wußte, verstand, das
’u.s.f.’ aber versteht. aber das
’u.s.f.’ ˇaber verstand. Und es verstehen, heißt,
es nicht als Abkürzung verstehen; es heißt nicht,
daß er jetzt im Geiste eine viel längere Reihe als die meiner
Beispiele sieht., Daß er es versteht, zeigt
sich darin, daß er nun gewisse Anwendungen macht, in gewissen
Fällen 107 dies sagt &
so handelt.
| | |
| | | | | |
“Wie zählen wir im Dezimalsystem?”
– … – Nun ist das keine Antwort?
Aber nicht für den, der das
“u.s.f.” nicht
. – Aber kann
unsere Erklärung es ihm nicht begreiflich gemacht
haben? Kann er durch sie nicht die Idee der Regel
erhalten haben? – Frage Dich, was die Kriterien
dafür sind, daß er diese Idee ˇnun erhalten
hat.
| | |
| | | | | |
Was zwingt mich denn? – Der
Ausdruck der Regel? – Ja; wenn ich einmal so
erzogen bin. Aber kann ich sagen, er zwingt mich, ihm zu
folgen? Ja; wenn dies nicht schon man sich
hier die Regel nicht als Linie denkt, der ich nachfahre, sondern als
Zauberspruch der uns alle im Bann hält.
[“schlichter Unsinn, & Beulen
…”]
| | |
| | | | | |
Warum soll man nicht sagen 108 der Widerspruch,
z.B. ‘heteronom’
∊heteronom ≡ =
~(‘heteronom’∊ heteronom), zeige
etwas eine logische Eigenschaft des Begriffs
‘heteronom’?
| | |
| | | | | |
“‘Zweisilbig’ ist heteronom”,
oder “dreisilbig ist nicht heteronom” sind
[e|E]rfahrungssätze. Es
könnte ˇin irgend einem Zusammenhang wichtig
sein, herauszufinden, ob Eigenschaftswörter die
Eigenschaften ˇbesitzen, die sie bezeichnen,
ˇoder nicht selber haben Man gebraucht dann in einem Sprachspiel das
Wort “heteronom”. Aber soll nun der
[s|S]atz
“‘h’∊h”
ein Erfahrungssatz sein? Er ist es offenbar nicht
& wir würden ihn, auch,, wenn wir den
Widerspruch nicht gefunden haben, nicht als einen Satz
unsres in unserm
ˇSprach[S|s]piels .
| | |
| | | | | |
[8|9]
.3.44. ‘h’ ∊
h ≡ ~(‘h’ ∊
h) könnte man ‘eine wahre
Kontradiktion’ nennen. –Aber diese
Kontradi[c|k]tion ist doch kein sinnvoller Satz!
Wohl, aber die Tautologien der Logik sind
ja 109 auch nicht.
| | |
| | | | | | ‘Die Kontradiktion
ist wahr’ heißt hier, sie ist bewiesen; abgeleitet aus den
Regeln des für das Wort
“h”. Ihre Verwendung ist, zu
zeigen, daß “‘h’∊h”
kein Satz ist“h” eines jener
Wörter ist ein Wort ist, welches
welches in “ξ ∊ b”
eingesetzt keinen Satz ergibt ergeben ergibt
| | |
| | | | | |
“Die Kontradiktion ist wahr” heißt:
Das ist wirklich ein Widerspruch, & Du
darfst also das Wort ‘h’ so als Argument
von ‘ξ∊
h’ nicht verwenden.
| | |
| | | | | | Ich bestimme ein Spiel &
sage: “[m|M]achst Du diese Art Zug,
soc ziehe ich so, machst Du jene, so ziehe ich
so. – Jetzt spiele!”
Und nun macht er einen Zug, oder etwas, was ich auch als Zug
ge anerkennen muß, & wenn ich
nach meinen Regeln daraufhin ziehen
weiterspielen |
will, so erweist sich, was immer ich tue, als
unrichtig // als Regeln
nicht gemäß // . 110 Wie konnte das
geschehen? Als ich Regeln aufstellte, da sagte
ich etwas. Ich folgte einem gewissen Brauch. Ich
sah nicht voraus, was wir weiter tun würden, oder sah nur eine
bestimmte Möglichkeit. Es war nicht anders,
als hätte ich [e|E]inem Farbtöpfe gegeben &
gesagt: “damit kannst Du nun jede Landkarte
erzeugen”. // Es war
nicht anders als hätte ich ˇEinem gesagt:
“ˇGib das Spiel auf;
[M|m]it diesen Figuren kannst Du nicht mattsetzen”
& hätte dabei eine bestehende
Möglichkeit des Mattsetzens //
| | |
| | | | | | Die verschiedenen,
halbs scherzhaften, Einkleidungen des logischen
Paradoxes sind nur in sofern interessant als sie einen daran erinnern,
daß eine ernsthafte Einkleidung des Paradoxes von Nöten
ist, um es seine Funktion eigentlich zu
verstehen. Es fragt sich: Welche Rolle kann ein
solcher ‘logischer Irrtum’ 111 in einer
Sprachanwendung
einem Sprachspiel |
spielen?
| | |
| | | | | | Man gibt jemandem etwa
Instruktionen, wie er in dem & dem Fall zu handeln hat;
& diese Instruktionen erweisen sich als unsinnig.
| | |
| | | | | | Das logische Schließen ist
ein Teil eines Sprachspiels. Und zwar folgt, der
im Sprachspiel logische Schlüsse ausführt, gewissen
Instruktionen, die beim Lernen des Sprachspiels gegeben wurden. Baut der Gehilfe
etwa nach gewissen Befehlen ein Haus, so hat er das Herbeitragen
der Baustoffe etc. von Zeit zu Zeit zu unterbrechen
& gewisse operationen mit
[z|Z]eichen auf einem Blatt Papier
auszuführen; worauf er dem Resultat entsprechend, wieder
seine Bauarbeit
aufnimmt
zu seiner Bauarbeit zurückkehrt |
.
112
| | |
| | | | | |
Denke Dir einen Vorgang, in welchem jemand, der einen Karren
schiebt darauf gekommen ist, daß er die Radachse reinigen muß,
wenn der Karren sich zu schwer schieben läßt. Ich
meine nicht, daß er zu sich sagt: “immer, wenn der
Karren sich nicht schieben laßt,
…”. Sondern er handelt einfach
so. Und nun kommt er darauf einem Andern
zuzurufen: “Der Karren geht nicht; reinige
die Achse”, oder auch:
“[d|D]er Karren geht nicht. Also
mußt Du die Achse
⌊ge⌋reinig[e|t]n ˇwerden. Nun das ist ein Schluß. Kein
logischer, freilich.
| | |
| | | | | | Kann
ich nun sagen: “Der nicht-logische
Schluß kann sich als falsch erweisen; der logische
nicht“?
| | |
| | | | | |
Ist der logische Schluß richtig, wenn er den Regeln
gemäß gezogen wurde; oder, wenn er
richtigen Regeln ge-113 mäß gezogen wird?
Wäre es z.B. falsch, wenn man sagte, aus
~p solle immer p
gefolgert werden? Aber warum soll man nicht lieber
sagen: so eine Regel gäbe den Zeichen
“~p” &
“p” nicht ihre gewöhnliche
Bedeutung?
| | |
| | | | | |
Man kann es so auffassen – will ich sagen –
daß die Schlußregeln den Zeichen ihre Bedeutung , weil sie Regeln der Verwendung Zeichen sind.
Daß die
Schlußregeln zur [b|B]estimmung der Bedeutung der
Zeichen gehören. In diesem Sinne können die
Schlußregeln nicht falsch⌊,⌋ ˇoder richtig
sein.
| | |
| | | | | | A
hat beim Bau die Länge & Breite einer Fläche
gemessen & gibt dem B Befehl: “Bring 15 ×
18 Platten”. B ist dazu abgerichtet
ˇin diesem Fall zu multiplizieren & dem Resultat
entsprechend eine Menge von Platten abzuzählen.
| | |
| | | | | | Der Satz
“15 × 18
= 270” braucht 114 natürlich nie ausgesprochen zu
werden.
| | |
| | | | | |
[9|10].3.44. Man könnte
sagen: Experiment – Rechnung sind Pole, zwischen
welchen sich menschliche Handlungen bewegen.
| | |
| | | | | | Wir konditionieren einen Menschen in
dieser & dieser Weise; wirken dann auf ihn durch eine Frage
ein; & erhalten eine Zahlzeichen
Zahl. Diesese
verwenden wir weiter zu unsern Zwecken & es erweist sich als
praktisch. Das ist das Rechnen. – Noch
nicht! Dies könnte ein sehr
Zweckmäßiger Vorgang sein
– muß aber nicht sein, was wir ‘rechnen’
nennen. Wie man sich denken könnte, daß zu Zwecken
denen heute unsere Sprache dient Laute ausgestoßen würden, die
doch keine Sprache bildeten.
Zum Rechnen
gehört, daß alle die richtig rechnen dasselbe Rechnungsbild
. Und
‘richtig rechnen’ heißt nicht: bei klarem
Verstande, oder ungestört rechnen, sondern so
rechnen. 115
| | |
| | | | | |
Das Unphilosophische an
Gödels Aufsatz
darin, daß er das Verhältnis
der Mathematik ihrer
Anwendung nicht .
Er hat hier die schleimigen Begriffe der
Mathematiker.
| | |
| | | | | |
Jeder math. Beweis stellt
das math. Regelgebäude Gebäude gibt dem …
einen auf einen
weitern
Stützpunkt
neuen Fuß |
. [Ich dachte an
die Füße eines Tisches]
| | |
| | | | | | Ich habe mich gefragt: Ist
Mathematik mit rein phantastischer Anwendung nicht auch wirkliche
Mathematik? – Aber es frägt sich:
[n|N]ennen wir es ‘Mathematik’
nicht etwa nur darum weil es hier Übergänge,
Brücken gibt von der phantastischen zur nichtphantastischen
Anwendung?
D.h., ⌊:⌋
würden wir sagen, Leute besäßen eine Mathematik, die das
Rechnen, Operieren mit Zeichen, bloß zu
okulten Zwecken benützten?
| | |
| | | | | | Aber ist es dann doch nicht unrichtig zu
sagen, ⌊:⌋ das ˇder
Mathematik Wesentliche sei, daß 116 sie Begriffe bilde? –
Denn die Mathematik ist doch ein anthropologisches
Phänomen. Wir können es also als das
Wesentliche einem großen
der Mathematik (dessen was
‘Mathematik’ genannt wird) erkennen
& doch sagen, es spiele keine Rolle in anderen
Gebieten. Diese Einsicht allein wird freilich nicht ohne
Einfluß aud die sein, die die Mathematik nun
so sehen lernen. Die Mathematik ist also eine
Familie; aber das sagt nicht daß es uns also gleich sein wird, was
alles in
aufgenommen wird.
| | |
| | | ∕∕ | | | Man könnte
sagen: verstündest Du keinen mathematischen Satz
besser als (Du) das Mult.
Ax.
(verstehst), so
verstündest Du Mathematik nicht.
| | |
| | | | | | Gibt es nicht ein Versuchen ob
()²
(wo p und q Kardinalzahlen sind) 2 ergibt?
Nun worin besteht es, ⌊:⌋ das prüfen. 117 Er rechnet für verschiedene
Werte ()²
& verglei sieht, ob das
Resultat 2 ist, oder sich 2 nähert, etc.
Aber ist es klar, worin dies
[n|N]achsehen & Vergleichen
besteht? Nein.
Und wie ist
es: ist es etwas anders zu prüfen, ob
()² =
2 & zu prüfen ob (²) ≠ 2
ist?
| | |
| | | | | | Aber was
prüfe ich nun: ist es das Zeichen
“()² =
2”, oder der Inhalt dieses Satzes? –
Nun, was tue ich? Ich operiere mit
diesem Zeichen. Wenn Du das ein
‘Prüfen’ nennen willst so sage meinetwegen Du
prüfest dies, oder jenes;
solange Du nur
weißt, was wirklich geschieht.
| | |
| | | | | | Übrigens ist ˇhier die
Gleichung, die man prüft nicht notwendigerweise als der
Satz aufzufassen, es gäbe zwei Zahlen p & q
für welche ….
| | |
| | | | | | –Hier ist ein
Widerspruch[,|:] [a|A]er wir sehen ihn nicht &
ziehen Schlüsse aus 118 ihm. Etwa auf
mathematische Sätze; & auf falsche. Aber wir
erkennen diese Schlüsse an. – Und bricht nun eine
von uns berechnete Brücke zusammen, so finden wir
dafür eine andere Ursache, oder sagen,
Gott habe es so gewollt. War
nun unsre Rechnung falsch; oder ware es keine
Rechnung?
Gewiß, wenn wir ˇals
Forschungsreisende nun die Leute ˇbeobachten
betrachten, die es so machen, ˇvon
außen⌊,⌋ als Reisende, betrachten, werden
wir vielleicht sagen: diese Leute rechnen überhaupt
nicht[;|.] [o|O]der ,
⌊:⌋ in ihren Rechnungen sei ein Element der
Willkür, welches das ganze Wesen ihrer Mathematik von dem
der unsern unterscheidet.
verschieden macht. |
Und doch würden wir
nicht leugnen können daß die Leute eine Mathematik
haben.
| | |
| | | | | | Was
für Regeln muß der König geben, damit er ˇin
Zukunft von nun an der unangenehmen Situation ˇvon nun
an entgeht,
in die ihn sein Gefangener ⌊ge⌋brachte?
⌊hat⌋⌊?⌋ – Was für eine Art Problem ist
das? – Es ist doch 119 ähnlich diesem: Wie
muß ich die Regeln dieses Spiels abändern, daß die
& die Situation nicht eintreten kann. Und das
ist eine mathematische Aufgabe.
| | |
| | | | | | Aber kann es denn eine mathematische Aufgabe
sein, die Mathematik zur Mathematik zu machen?
| | |
| | | / | | | Kann
man sagen: “Nachdem dies mathematische Problem
gelöst war, begannen die Menschen eigentlich zu
rechnen”?
| | |
| | | ∕∕ | | |
11.3.44.
Was ist das für eine
Sicherheit, wenn sie darauf beruht, daß unsre Banken
tatsächlich im allgemeinen
einfach |
nicht plötzlich von allen ihren Kunden ˇauf
einmal überrannt werden; aber bankrott
würden, wenn es doch geschähe?! Nun es
ist eine andere Art von Sicherheit als die
primitivere; aber es ist doch auch eine
Sicherheit.
Ich meine: wenn nun
wirklich in der Arithmetik ein Widerspruch ge-120 funden würde – nun so
bewiese das nur, daß eine Arithmetik mit einem solchen
Widerspruch sehr gute Dienste leisten konnte; & es besser sein
wird, wenn wir unsern Begriff der Sicherheit modifizieren, als zu sagen, das
wäre eigentlich ˇnoch gar keine ˇrechte
Arithmetik gewesen.
| | |
| | | | | |
“Aber es ist doch nicht die ideale
Sicherheit?” – Ideal, – für
welchen Zweck?
| | |
| | | | | |
Die Regeln des logischen Schließens sind Regeln des
Sprachspiels.
| | |
| | | | | | “Ist der Satz ‘18 × 15 = 270’
ein Erfahrungssatz?” – Beruht er
nicht auf einer Erfahrung⌊,⌋ ?
[A|a]ber der,
daß die Rechnung dies ergab? Richtiger freilich,
daß das Rechnen dies ergab, denn
“Rechnung” darf hier nicht bedeuten: das
Rechnungsbild. Es war eine Erfahrung diese Rechnung machen, dies Rechnungsbild (& also auch sein )
erzeugen. 121 A
Aber
beschreibt der Satz diese Erfahrung? Ist es also
wahr, wenn ich so gerechnet habe, ob das nun richtig oder falsch
war?
| | |
| | | | | | Kann
also ein Satz auf einer Erfahrung beruhen & doch kein
Erfahrungssatz sein?
| | |
| | | | | | Der Satz beruht auf der
Erfahrung, daß ich so abgelaufen bin, oder, daß wir so
ablaufen. Aber, “er sagt, daß wir so
ablaufen” bedeutet eine bestimmte Verwendung
Sprachspiel.
| | |
| | | | | | Zu sagen “der Satz beruht auf
der Erfahrung”
sagt: der Satz wird von Menschen
[E|e]rzeugt, die die so & so abgerichtet
sind.
| | |
| | | | | | Und die
Verwendung des Rechensatzes ist nicht die des
psychologischen Satzes.
122
| | |
| | | | | |
12.3.44. Was für
eine Art ˇvon Satz ist: ist
dies ist es: “Die Klasse
der Löwen Katzen ist kein Löwe keine
Katze, aber die Klassen der Klasse eine
Klasse”. Wie wird er verifiziert? Wie
könnte man ihn verwenden? – So viel
ich sehe nur als grammatischeen Aussage
Satz. Um
[j|J]emandc drauf aufmerksam zu machen // Ich mache jemand auf die Verschiedenheit der
Verwendung aufmerksam // , daß man
von ‘einer Klasse von Löwen’ & einer
‘Klasse von Klassen’ daß der Ausdruck “die
Klasse der Löwen” nicht die Bezeichnung
einesc Löwen ist, daß aber Klassen eine Klasse
bilden können.
// daß aber Klassen
Klassen bilden. //
|
//
daß “Klasse” reflexiv gebraucht wird, aber
Löwe nicht. // ⌊⌊ˇ // Jemand drauf aufmerksam zu machen, daß
“die Klasse der Katzen” nicht eine Katze bezeichnet,
noch auch ˇnur ähnlich wie die Bezeichnung
einer Katze verwendet wird; das Wort “Klasse” aber so ganz
anders gebraucht wird, daß von ‘Klassen von
Klassen’ zu reden ˇeinen Sinn hat. Die
Verwendung der Worte “Klasse” &
“Katze” kann natürlich nur an den Sprachspielen
mit diesen Worten klar werden. // ⌋⌋ ¤
| | |
| | | | | | Man kann
sagen, daß Wort “Klasse” reflexiv gebraucht, auch wenn man,
z.B., die Russellsche Theorie der Typen anerkennt.
Denn es wird ja doch auch in ihr reflexiv verwendet.
| | |
| | | | | | Freilich ist, in diesem Sinn
zu sagen, die Klasse der Löwen sei kein Löwe
etc., ähnlich, als sagte jemand, er habe ein
“e” für ein “n”
gehalten, wenn er eine Kugel für einen 123 Kegel ansieht.
| | |
| | | | | | Das plötzliche Umwechseln
der Auffassung des Bilds eines Würfels & die
Unmöglichkeit “Löwe” &
“Klasse” als vergleichbare Begriffe
| | |
| | | | | | Der Widerspruch sagt:
“Nimm Dich in Acht …”.
| | |
| | | | | | Wie aber wenn man einem
bestimmten Löwen (dem König der Löwen etwa) den
Namen “Löwe” gibt? Nun wirst Du
sagen: aber es ist doch klar daß im Satz “Löwe
ist ein Löwe” das Wort “Löwe” auf
zwei verschiedene Arten gebra⌊u⌋cht wird.
(Log. Phil. Abh.) Aber
kann ich sie nicht zu einer Art des Gebrauchs
zählen?
| | |
| | | | | | Aber wenn in
dieser Weise ˇder Satz “Löwe ist ein
Löwe” gebraucht würde, ⌊:⌋ würde ich
[e|E]inen den auf nichts
aufmerksam 124 machen, den ich auf die
Verschiedenheit der Verwendung der beiden
“Löwe”
des ersten & des
Zweiten Substantivs |
aufmerksam machte?
| | |
| | | | | | ⌊⌊ Man kann ein Tier
daraufhin untersuchen, ob es eine Katze ist. Aber den
Begriff Katze kann man so jedenfalls nicht untersuchen. ⌋⌋
| | |
| | | | | | Wenn auch “die
Klasse der Löwen ist kein Löwe” wie ein Unsinn
erscheint, dem man nur aus Höflichkeit ⌊einen⌋ Sinn
beilegen könnte, so will ich diesen Satz doch nicht so
auffassen, sondern als (einen) rechten Satz, wenn er
nur richtig aufgefaßt wird. (Also
nicht so wie in
Log. Phil. Abh.) Meine
Auffassung ist also hier s⌊o⌋zusagen
anders. Das heißt aber, ich sage:
Aber das heißt, daß
ich sage: |
es gibt auch ein Sprachspiel mit diesem Satz.
| | |
| | | | | | “Die Klasse der
Katzen ist keine Katze.” –
[o|W]oher weißt Du das?
| | |
| | | | | |
13.3.44 In der Tierfabel heißt es:
“[d|D]er Löwe ging mit dem Fuchs
spazieren”, nicht “einc Löwe mit
einem Fuchs; noch auch der Löwe so & so mit dem Fuchs so
& so. 125
Und hier ist es doch wirklich ˇso,
als ob die Gattung Löwe als ein Löwe gesehen
würde.
(Es ist nicht so, wie
Lessing sagt, als
ob statt irgendeinem Löwen ein bestimmter gesetzt
würde. “Grimmbart der
Dachs” heißt nicht: ein Dachs mit Namen
Grimmbart”.)
| | |
| | | | | | ¤
// Was für eine Art von Satz ist dies:
“Die Klasse der Löwen ist doch kein nicht ein Löwe, aber die Klasse der Klassen
aber, eine Klasse”? Wie wird er
verifiziert? Wie könnte man ihn
verwenden? – So viel ich sehe, nur als
grammatischen Satz. Einen darauf aufmerksam zu machen,
daß das Wort “Löwe” grundverschieden
gebraucht wird von dem Namen eines Löwen; das Gattungswort
“Klasse” aber ähnlich wie die Bezeichnung
für eine der Klassen, für die Klasse Löwe
etwa. //
126
| | |
| | | | | | Denk
Dir eine Sprache, in der die Klasse Löwen “der Löwe aller Löwen genannt
wird”, die Klasse der Bäume “der Baum
aller von allen Bäume”, etc.
– weil sie sich vorstellen alle Löwen bildeten
einen ˇgroßen Löwen. // einen, großen, Löwen. //
[(|[]Wir sagen:
“Gott hat den Menschen
geschaffen”.[)|]]
Dann könnte jemand das Paradox aufstellen, es gäbe
bestimmte Anzahl aller
Löwen. [e|E]tc.
| | |
| | | | | | Wäre es aber etwa
unmöglich, in so einer Sprache zu zählen & zu
rechnen?
| | |
| | | | | |
Man könnte sich fragen: Welche Rolle kann ein
Satz, wie “[i|I]ch lüge
immer”, im menschlichen Leben spielen? Und da
kann man sich Verschiedenes vorstellen. | | |
| | | | | |
14.3.44. Ist die Umrechnung von Zoll auf
cm ein logischer Schluß? “Der
ist 2 Zoll
lang. – Also ist er ungefähr 50 mm
lang.” Ist das ein logischer
Schluß? 127
| | |
| | | | | |
Ja aber ist nicht eine Regel etwas willkürliches?
Etwas, was ich festsetze? Und könnte
ich festsetzen, daß die Multiplication
18 × 15
nicht 270 ergeben solle? – Warum
nicht? – Aber dann ist sie eben nicht nach der Regel
geschehen, die ich zuerst festgesetzt, & deren
Gebrauch ich eingeübt hatte.
Ist denn
etwas, was aus einer Regel folgt, eine Regel? Und wenn nicht, – was
für eine Art von Satz soll ich es nennen?
| | |
| | | | | | “Es ist den Menschen
… unmöglich einen Gegenstand als von sich selbst
verschieden anzuerkennen.” Ja, wenn ich nur eine
Ahnung davon hätte, wie es gemacht wird, – ich
versuchte es gleich! – Aber wenn es uns
unmöglich ist einen Gegenstand von sich selbst verschieden
anzuerkennen, so ist es also wohl möglich
zwei Gegenstän-128 de als von einander verschieden
anzuerkennen? Ich habe also zwei Sessel vor mir &
erkenne ˇan daß es zwei sind. Aber da
kann ich doch unter Umständen auch glauben, daß es ˇnur
einer ist; & in diesem Sinne kann ich auch
einen für zwei halten. – Aber damit erkenne ich
doch nicht den Sessel als von sich selbst verschieden an!
Wohl; & in aber dann habe ich auch nicht die
zwei als voneinander verschieden anerkannt. Denn
indem ich sie “zwei” nannte zwei = zwei
verschiedene, so wie ein = ein & derselbe.
Wer glaubt, er könne dies tun– (,
& eine Art psychologisches Spiel spielt ), der
übersetze dies ein
Spiel der Gesten. Wenn er die zwei
Gegenstände vor sich hat, zeige er mit jeder Hand auf einen von
ihnen; gleichsam als wolle er ,
andeuten daß j sie autonom . Hat er nur einen Gegenstand vor
sich, so deutet er mit beiden Händen auf ihn um anzudeuten,
daß man keinen 129 Unterschied zwischen ihm &
ihm selbst machen kann. – Warum soll man nun aber
nicht das Spiel in umgekehrter Weise spielen?
| | |
| | | | | |
15.3.44. Die Worte
“richtig” & “falsch”
werden beim Unterricht ˇdes Schülers in der
Regel // im nach der Regel //
gebra⌊u⌋cht. Das Wort “richtig”
läßt
gehenc, das Wort “falsch” hält ihn
zurück. Könnte man nun statt
dieser
W[ö|o]rter ihrer auch setzen: “das stimmt mit der Regel
überein”, “das stimmt nicht mit der Regel
überein”? Warum nicht? Aber
wären diese ˇAusdrücke nun eine Erklärung jener
Wörter? dem Schüler diese
W[ö|o]örter ˇdadurch erklären, indem
daß man statt ihrer setzt: “das stimmt mit
der Regel überein – das nicht”? // Könnte man nun dem Schüler diese Worte
durch die Ausdrücke erklären: “das
stimmt mit der Regel überein”, “das
nicht? // // Könnte
man nun dem Schüler diese Worte erklären durch die
Ausdrücke 130 …? // Nun, wenn er einen
Begriff vom Übereinstimmen hat. Aber wie, wenn dieser
eben erst gebildet werden muß? ⌊ (Es kommt
darauf an, wie er auf das Wort “übereinstimmen”
reagiert.) ⌋
| | |
| | | | | |
Man lernt nicht einer Regel folgen, indem man zuerst die Bedeutung
den
Gebrauch |
des Wortes
“Übereinstimmung” lernt.
| | |
| | | | | | Vielmehr lernt man die Bedeutung von
“Übereinstimmen”, indem man einer Regel
folgen lernt. // indem man die Technik das
nach einer Regel
erlernt.[)| // ]
| | |
| | | | | | Wer verstehen will, was es heißt:
“einer Regel folgen”, der muß doch selbst einer
Regel folgen können.
| | |
| | | | | |
“Wenn Du diese Regel annimmst, mußt Du das
tun.” – Das kann heißen: die Regel
läßt Dir hier nicht zwei Wege offen. (Ein
mathematischer Satz.) Ich meine aber: die Regel
führt Dich wie 131 ein Gang festen Mauern. gemauerter
Gang. Aber dagegen kann man doch
einwenden, die Regel ließe sich auf alle mögliche Weisen
deuten. – Die Regel steht hier wie ein
Befehl[.|;]! Und
und
wirkt auch wie ein Befehl.
| | |
| | | / \ | | |
Ein Sprachspiel: Etwas [a|A]nderes
bringen; das Gleiche bringen. Nun wir können
uns vorstellen, wie es gespielt wird. – Aber wie kann
ich es 's
[e|E]inem erklären? Wie
weiß Ich kann ihm diesen Unterricht
geben. – Aber wie weiß er ˇdann, was er das
nächste Mal als ‘Gleiches’ bringen soll –
wie ˇmit welchem Recht kann
ich sagen, daß er das richtige, oder falsche, gebracht
hat? – Ja, ich weiß freilich, daß
(hier) in gewissen Fällen
auf mich
würden mit den Zeichen des Widersprechens
der Mißbilligung |
⌊ // Menschen mit den
Zeichen des Widersprechens auf mich einstürmen
würden // ⌋.
Und
heißt das nun etwa, die Definition von
“Gleich” wäre die: gleich sei,
was alle Menschen für gleich hielten? –
Freilich nicht. // gleich sei 132 was alle ˇoder die meisten
Menschen übereinstimmend “gleich”
nenntcen? so ansehen? – Freilich
nicht. //
| | |
| | | | | | Denn, um Gleichheit zu
konstatieren benütze ich ja
(natürlichc) nicht
die Übereinstimmung der Menschen. // Denn Kriterium der
Gleichheit benütze ich ja natürlich nicht die
Übereinstimmung der Menschen. Welches Kriterium
verwendest Du also? Gar keins.
| | |
| | | / \ | | | Das Wort ohne
Rechtfertigung zu gebrauchen, heißt nicht, es zu Unrecht
gebrauchen.
| | |
| | | ∫ ∫ | | | Soll ich sagen:
das Kriterium der Gleichheit sei, daß gleich ? – Aber wie weiß ich,
daß ich den Ausdruck “gleich vorkommen”
in gleicher Weise
? – Aber sage ich nicht es ist gl⌊e⌋ich, weil es
mir gleich ?
Worin besteht es, daß mir diese Farbe gleich jener
erscheint 133 erscheint? Kann die
charakteristische Reaktion nicht die sein, daß ich
sage diese gleich der?
| | |
| | | / | | | Das Problem des
vorigen Sprachspiels [№ … ]
gibt es natürlich auch in Bringe mir etwas Rotes. Denn
woran erkenne ich, daß etwas rot ist? An der
Übereinstimmung der Farbe mit einem Muster? –
Mit welchem Recht sage ich: “Ja, das ist
rot.”? Nun, ich sage es; & es
läßt sich nicht rechtfertigen. Und auch
für dieses Sprachspiel, wie für
das vorige, ist es charakteristisch,
daß es sich unter der ruhigen Zustimmung aller Menschen
vollzöge.
| | |
| | | k | | |
16.3.44.
Die Verteilung der Primzahlen wäre ein ideales Beispiel
für das, was man synthetisch a priori nennen
, denn man kann sagen, daß sie
jedenfalls durch eine Analyse des Begriffs der Primzahl nicht zu
finden ist.
134
| | |
| | | k | | |
Ich lese in
“The chemical history of a
candle”: “Water is one
individual thing – it never changes”.
| | |
| | | k | | | Eine
Definition ist doch gewiß eine Begriffsbestimmung – aber wie
ist es mit dem bloßen Schema einer Definition?
| | |
| | | k | | | Eine Definition
muß nicht zur eines
Zeichenausdrucks dienen. Sie könnte auch zur
Verlängerung, oder zur Verschönerung ˇdes
Zeichens dienen. // oder zu[m|r]
Ersetzung durch ein schöneres Zeichen
dienen. //
| | |
| | | k | | | Könnte man
sich die Definitionen im Kalkül nicht ausgelassen denken –
& nur die ˇihr entsprechende Substitution,
die ihr entspricht gemacht, mit
dem Vermerk dies möge eine gestattete Substitution
sein?
| | |
| | | k | | | “Wer
dieser Regel folgt, der folgt auch einer Regel, …”
Z.B.: “der folgt auch einer
Regel, die verbietet, daß …”
| | |
| | | k | | | Wer eine
neue Regel einführt, der führt 135 einen neuen Begriff ein.
Denn einer neuen Regel folgt, hat einen neuen Begriff
gebildet. Denn … eine neue Regel ist eine neue
Art die Dinge zu sehen.
Und hier gibt es
triviale und folgenreiche Fälle. Heißt
‘die Dinge anders sehen’ auch anders
handeln?
| | |
| | | k | | | Ein
unentschiedener Satz der Mathematik ist weder als Regel, noch als das Gegenteil einer
Regel anerkannt ist & die Form einer mathematischen Aussage
hat. – Ist diese Form aber ein klar
umschriebener Begriff?
| | |
| | | k | | | Denke Dir den
limn→∞φn =
l als eine Eigenschaft eines Musikstücks
(etwa). Aber natürlich nicht so,
daß das Stück endlos weiterliefe, sondern als eine dem Ohr
erkennbare Eigenschaft (gleichsam algebraische
Eigenschaft) des Stückes.
| | |
| | | k | | | wenn man die Stätigkeit
als Eigenschaft Zeichens
“x² +
y² = r²” ansähe –
natürlich nur, wenn diese Gleichung & 136 andere
gewohnheitsmäßig einer bestimmten
Art der Prüfung unterzogen würden.
“So stellt sich diese Regel (Gleichung) zu
dieser bestimmten Prüfung.” Eine
Prüfung, die mit einem Streifblick auf
eine Art Extension geschieht
vorgenommen wird |
.
| | |
| | | k | | | Es wird bei jener
Prüfung der Gleichung etwas vorgenommen, was mit gewissen
Entwicklungen (Extensionen) zusammenhängt.
Aber nicht als handelte es sich (da) um eine Extension, die
der Gleichung irgendwie äquivalent wäre. Es wird
nur auf gewisse Entwicklungen, sozusagen, angespielt. – Nicht die Extension ist hier das Eigentliche, das nur
faute de mieux
intensional beschrieben wird; sondern die Intension wird beschrieben
– oder dargestellt – vermittels gewisser Extensionen, die
sich da & dort aus ihr ergeben.
| | |
| | | k | | | Der Verlauf
gewisser Extensionen wirft ein Streiflicht auf die algebraische
Eigenschaft der Funktion. In diesem Sinne könnte
man 137 also sagen, es werfe die Zeichnung
einer Hyperbel ein Streiflicht auf die
Hyperbelgleichung.
| | |
| | | | | |
Denk Dir Gleichungen als Ornamente (Tapetenmuster) verwendet;
& nun eine Prüfung dieser Ornamente daraufhin,
ob welcher Art Kurven sie entsprechen. Die
Prüfung wäre
ˇder kontrapunktischen Eigenschaften eines
Musikstücks.
| | |
| | | k | | | Dem widerspricht
nicht, daß jene Extensionen die wichtigste Anwendung der Regel
wären; denn es ist eines eine
Elipse zeichnen, & ein anderes, sie mittels
ihrer Gleichung konstruieren.
| | |
| | | k | | |
Wie, wenn ich
sagte, ⌊:⌋ Die extensionalen
Überlegungen (z.B. der
Heine-Borelsche Satz) zeigen: so sollen die
Intensionen behandelt werden. // : so soll man die Intensionen
behandeln. //
Das Theorem gibt
uns in großen Zügen eine Methode, wie mit Intensionen zu
verfahren ist. Es sagt etwa:
“So wird 138 es ausschauen
müssen”.
Und man wird dann
etwa zu einem Verfahren mit bestimmten Intensionen eine
bestimmte Illustration zeichnen können. Die
Illustration ist ein Zeichen, eine Beschreibung, die besonders
übersichtlich, einprägsam, ist.
| | |
| | | k | | | Die Illustration
wird hier eben ein Verfahren angeben.
Eine Prozedur.
| | |
| | | | | | Ein Beweis der zeigt, daß
die Figur “777” in der von π vorkommt aber nicht zeigt
wo. Nun, so bewiesen wäre dieser
‘[e|E]xistenzsatz’ als Regel
für gewisse Zwecke keine Regel. Aber
könnte er nicht z.B. als Mittel der
Einteilung von Entwicklungsregeln dienen. Es wäre etwa
bewie auf analoge Art bewiesen daß
“777” in π² nicht vorkomme, wohl aber
in π ∙ e. etc.
Die Frage wäre nun: [i|I]st es
vernünftig von dem betreffenden Beweis zu sagen: er beweise
139 die Existenz von
“777” in dieser
Entwicklung. Dies kann einfach irreführend
sein. Das ist eben der Fluch der Prosa, & besonders
der Russellschen Prosa, in
der Mathematik.
| | |
| | | k | | | Was schadet es,
z.B., zu sagen,
Gott kenne alle irrationalen
Zahlen? Oder: sie seien schon alle da, wenn wir
auch nur gewisse kennen? Warum sind diese Bilder nicht
harmlos?
Einmal verstecken sie gewisse
Probleme. – [Im
⇒Buch F. Dazu einige Sätze die diesem
vorhergehen.]
| | |
| | | k | | |
Wenn ich von der Mathematik
sagte, ihre Sätze Begriffe, so
ist das vag; denn
“2 + 2 =
4” bildet einen Begriff in anderem Sinne,
als “p
⊃ p”,
“(x).fx ⊃
fa”, oder der Dedekindsche Satz. Es gibt hier eben eine
Familie von Fällen.
| | |
| | | k | | | Der Begriff der
Regel zur Bildung eines 140 unendlichen Dezimalbruchs ist –
natürlich – kein spezifisch mathematischer.
Es ist ein Begriff in Zusammenhang mit einer bestimmten
Tätigkeit im menschlichen Leben. Der
Begriff dieser Regel ist nicht mathematischer, als der: der
Regel zu folgen. Oder auch: dieser letztere ist nicht
weniger scharf definiert, als der Begriff so einer Regel selbst. – Ja, der Ausdruck der Regel & sein Sinn ist
nur ein Teil des Sprachspiels: Der Regel
folgen.
| | |
| | | k | | | Man kann mit dem
gleichen Recht allgemein von solchen Regeln reden,
von den Tätigkeiten, ihnen zu
folgen.
| | |
| | | k ∕∕ | | | Man
sagt freilich “das liegt alles schon in unserm
Begriff” von der Regel, z.B. –
aber das heißt nur: zu diesen Begriffsbestimmungen
neigenc wir. Denn was haben wir denn im Kopf,
was alle diese Bestimmungen schon enthält?!
| | |
| | | k | | |
Die Zahl ist, wie Frege
sagt, eine Eigenschaft 141 eines Begriffs – – aber in
der Mathematik ist sie ein Merkmal eines mathematischen
Begriffs. ℵo ist ein
Merkmal des Begriffs (der) Kardinalzahl; & die
Eigenschaft einer Technik. 2ℵo
ist ein Merkmal des Begriffs des unendlichen Dezimalbruchs, aber wovon
ist diese Zahl eine Eigenschaft?
D.h.: von welcher Art von Begriff kann
man sie empirisch aussagen?
| | |
| | | k | | | Der Beweis des Satzes zeigt
mir, was ich auf den Satz
hin
die Wahrheit des Satzes hin |
wagen will // kann // . Und verschiedene
Beweise können mich wohl dazu bringen dasselbe zu wagen.
| | |
| | | k | | | Das
Überraschende, Paradoxe, ist paradox nur in einer
gewissen, gleichsam mangelhaften, Umgebung. Man
muß diese Umgebung so ergänzen, daß, was paradox
schien nicht länger so erscheint.
| | |
| | | k | | | Wenn ich bewiesen habe, daß
18 × 15 =
270 ist, so habe ich damit auch den geome-142 trischen Satz bewiesen, daß man
durch Anwendung
Transformationsregeln auf das Zeichen “18 ×
15” das Zeichen “270”
erhält. – Angenommen nun, die Menschen, durch
irgendein Gift am klaren Sehen, oder richtigen Erinnern
gehindert (wie wir uns jetzt
ausdrücken
jetztc sagen |
wollen) erhielten bei dieser Rechnung nicht
“270”. – Ist die Rechnung, wenn man
ihr nicht voraussagen kann, was Einer unter normalen
Umständen herausbringen wird, nicht nutzlos?
Nun, auch wenn sie es ist, so zeigt das nicht daß der Satz
18 × 15 =
270 der Erfahrungssatz sei: die Menschen rechneten im
allgemeinen so
| | |
| | | ∕∕ | | | Anderseits ist es nicht
klar, daß die allgemeine Übereinstimmung der Rechnenden ein
charakteristisches Merkmal alles dessen ist was man
“Rrechnen” nennt. Ich könnte mir
denken, daß Leute die rechnen gelernt haben unter bestimmten
Umständen, etwa 143 unter dem Einfluß
eines des Opiums, anfingen
[e|E]iner verschieden vom Andern zu rechnen, & von
diesen Rechnungen gebrauch machten; &
daß man nun nicht sagte, sie rechneten ja gar nicht & seien
unzurechnungsfähig, sondern daß man ihre
Rechnungen als berechtigtes Vorgehen hinnähme.
Aber müssen sie nicht wenigstens zum
gleichen Rechnen abgerichtet werden? Gehört
das nicht zum Begriff des Rechnens? Ich glaube,
man könnte sich auch Abweichungen vorstellen.
–
| | |
| | | k | | |
17.3.44.
Verschiedene Arten, zu zeigen, daß eine Zahl durch
7 teilbar
ist. Der eine Beweis zeigt, daß es eine Beweisfigur der
andern Art geben muß. Andererseits: Ein
Beweis des Fundamentalsatzes der Algebra – zeigt er, daß eine
Beweisfigur der andern Art möglich ist? Nun, man
kann das sagen, wenn diese Beweisfigur von vornherein genügend
bestimmt ist. 144
Wenn eine
Überlegung dahin führt, dann kann eine Überlegung, die
auf diesen Prinzipien beruht, nicht dorthin
führen. D.h., ⌊:⌋ wenn man die Sache nach
diesen Prinzipien überlegt, kann nicht das
herauskommen.
| | |
| | | ∫ | | | “Zum Beweis
gehört Übersichtlichkeit” heißt
eigentlich: Im Beweis schreitet man von Bild zu Bild; man
muß ihn reproduzieren können, ob er richtig oder falsch ist;
er ist etwas was man ˇkopieren, oder auswendig lernen
kann.
| | |
| | | | | | Kann man
sagen, daß die Mathematik eine experimentelle Forschungsweise,
Fragestellung, lehrt?
⇒⌊[S.
79]⌋ Nun kann man nicht sagen, sie lehre
mich z.B. zu fragen, ob ein gewisser Körper
einer Parabelgleichung gemäß bewegt? – Was tut aber die Mathematik in diesem Fall?
Ohne sie ˇoder ohne die Mathematiker wären wir freilich
nicht zur Definition dieser Kurve gelangt. War aber,
diese Kurve definieren schon Mathema-145 tik? Bedingte es
z.B. Mathematik, wenn Leute die Bewegung von
Körpern darauf hin untersuchten, ob ihre Bahn
sich durch
Elipsenkonstruktion mit einem Faden & zwei
Nägeln in den Brennpunkten darstellen lasse?
Wer diese Art der Untersuchung erfunden hätte, hätte der
Mathematik getrieben?
Er hat
uns doch einen neuen Begriff
.
Aber war es auf die Art wie die Mathematik dies tut?
War es, wie uns die Multiplikation
18 × 15 =
270 einen neuen Begriff gibt?
| | |
| | | | | | Kann man also nicht
sagen, die Mathematik lehrt uns zählen?
Wenn sie uns aber zählen lehrt, warum nicht auch Farben
miteinander vergleichen?
| | |
| | | | | | Es ist klar: wer uns die
Elipsengleichung lehrt, lehrt uns einen neuen
Begriff. Wer uns aber beweist, daß diese
Elipse & diese Gerade sich in
diesen Punkten schnei-146 den; nun der gibt uns auch einen neuen
Begriff.
| | |
| | | | | | Uns die
Elipsengleichung lehren ist ähnlich
wie, uns zählen lehren. Aber auch
ähnlich wie, uns fragen
lehren
uns die Frage lehren |
: “sind hier hundertmal soviel Kugeln als
dort?“.
| | |
| | | | | | Wenn ich nun jemand in einem
S[ch|pr]achspiele diese Frage & Methode sie zu beantworten gelehrt hätte,
hätte ich ihn Mathematik gelehrt? Oder nur wenn er
mit Zeichen operiert hat?
| | |
| | | | | | (Wäre das
etwas als
fragte man: “wäre auch das eine Geometrie, die
nur aus den Euklidschen
Axiomen bestünde?”)
| | |
| | | | | | Ist was ich hier sehe, bloß der
natürliche Abfall des Begriffs
‘Mathematik”?
(ˇSo [W|w] wenn ich fragte: ist das Bellen der
Hunde auch ?)
Oder ist hier etwas was mich beunruhigen sollte? 147
| | |
| | | | | |
Wenn uns die Arithmetik die Frage
“wieviele?”
lehrt, warum nicht auch die Frage “Wie
dunkel?”?
| | |
| | | | | | Aber die Frage “sind hier
hundertmal soviel Kugeln als dort” ist doch keine
mathematische Frage ˇ& ihre Antwort kein mathematischer
Satz. Eine solche ˇmathematische
Frage wäre: “[i|I]st
Sind 170 ˇKugeln hundertmal soviel 3
Kugeln?” (Und zwar ist dies eine
Frage der reinen, nicht der angewandten Mathematik.)
| | |
| | | | | | Soll ich nun sagen, daß, wer uns
ˇDinge zählen lehrt, & ähnliches, uns neue
Begriffe gibt, & auch der, welcher uns reine
Mathematik mit solchen Begriffen lehrt?
| | |
| | | | | | Ist eine neue Begriffsverknüpfung eine
neuer Begriff? Und schafft die Mathematik
Begriffsverknüpfungen?
| | |
| | | | | | Das Wort “Begriff” ist ganz & gar
zu vag. 148
| | |
| | | | | |
Die Mathematik lehrt uns mit den Begriffen // arbeiten. // Und
man kann daher sagen, sie ändert unser begriffliches
Arbeiten.
unsere
Begriffstätigkeit. // unsern
Begriffsapparat. // |
// , sie
ändert die Art & Weise uns⌊e⌋rer
Begriffsarbeit. //
| | |
| | | | | | Aber erst der bewiesene, oder als
[p|P]ostulat angenommene mathematische Satz tut das, nicht
der problematische.
| | |
| | | | | | Kann man
aber nicht doch mathematisch experimentieren?
Z.B. versuchen, ob sich aus einem
quadratischen Papier ein Katzenkopf falten läßt, wobei
die physikalischen Eigenschaften des Papiers, seine
Festigkeit, Elastizität Dehnbarkeit,
etc. nicht in Frage gezogen werden? Nun
man redet doch hier gewiß von einem Versuchen. Und warum
nicht von einem Experimentieren? Dieser Fall ist doch
der gleiche ähnlich dem,
Zahlenpaare ver-149 suchsweise in die Gleichung
x ² + y
² = 25 einzusetzen, um eines zu finden das die
Gleichung befriedigt. Und kommt man also endlich auf
3² +
4² = 25, ist dieser Satz nun das Resultat eines
Experiments? Warum nannte man den Vorgang denn ein
?
Hätten wir es auch so genannt, wenn Einer immer aufs
erste Mal mit völliger Sicherheit (den Zeichen der
Sicherheit), aber ohne Rechnung, solche Probleme
löste? Worin bestünde hier das
Versuchen? Experimentieren? Angenommen, ehe er die
Lösung gibt, erscheint sie ihm als Vision. –
| | |
| | | / | | | 18
.3.44. Wenn eine
Regel Dich nicht zwingt, so folgst Du keiner Regel.
| | |
| | | / ∫ | | | Aber
wie soll ich ihr denn folgen; wenn ich ihr doch folgen kann, wie ich
will?
| | |
| | | ∫ | | | Wie soll
ich dem Wegweiser folgen, wenn 150 alles was ich tue ein Folgen
ist?
| | |
| | | ∫ | | |
Aber daß alles (auch) als ein Folgen
gedeutet werden kann, heißt doch nicht, daß alles ein
Folgen ist.
| | |
| | | | | | Aber wie deutet
denn also der Lehrer dem Schüler die Regel? (Denn
der soll ihr doch gewiß eine bestimmte Deutung geben.)
– Nun, wie anders, als durch Worte &
Abrichtung?
Und der Schüler hat die
Regel (so gedeutet) inne, wenn er so
& so auf sie reagiert.
Das
aber ist wichtig, daß diese Reaktion, die uns das
Verständnis verbürgt, nur unter
bestimmten Umständen, bestimmte
Lebens- & Sprachformen als Umgebung,
voraussetzt. (Wie es keinen Gesichtsausdruck gibt ohne
Gesicht.)
Dies ist eine wichtige
Gedankenbewegung.)
| | |
| | | | | |
[Zu dem
⇒Typescript
“ … – was willst Du tun?] D.h. er kann antworten, wie ein
151 verständiger Mensch
& doch das Spiel mit uns nicht spielen.
| | |
| | | | | | [Zu dem
⇒Typescript … .
Wir werden es dann nicht “die Reihe fortsetzen”
nennen & auch wohl nicht
“schließen”.] Und
dDenken &
sSchließen (sowie das
Zählen) ist für uns natürlich nicht durch eine
willkürliche Definition
, sondern durch
natürliche Grenzen, dem Körper dessen entsprechend,
was wir die Rolle des Denkens & Schließens in unserm Leben
nennen können.
| | |
| | | ⌇ | | | Zwingt3 mich eine Linie dazu
ihr nachzufahren? – Nein; aber wenn ich mich
dazu entschlossen habe sie so als Vorlage zu gebrauchen,
dann zwingt sie mich. – Nein; dann zwinge
ich mich sie so zu gebrauchen. Ich halte mich
gleichsam an ihr fest. – Aber wichtig ist hier doch,
daß ich sozusagen ein für allemal den Entschluß mit
der (allgemeinen) Deutung 152 fassen & halten
kann, & nicht bei jedem Schritt von frischem
deute. // Deutungsarbeit
vollziehe. //
| | |
| | | | | | Die Linie, könnte man sagen,
gibt's mir ein, wie ich gehen soll. Aber das ist
natürlich nur ein Bild. Und gäbe sie mir jedesmal
etwas anderes ein,
so folgte ich ihr nicht als Regel. Und was
“anderes”, & was “das
Gleiche” heißt, das kann nur das Leben
entscheiden.
| | |
| | | | | | “Die Li⌊n⌋ie gibt mir ein, wie ich
gehen soll”, : das paraphrasiert nur, daß sie meine
letzte Instanz dafür ist ist : – sie
sei ist meine letzte,
wie ich gehen soll.
| | |
| | | | | | Denke dir Einer folgte einer Linie als
Regel auf diese Weise: Er hält einen Zirkel, dessen
eine Spitze er der entlang
führt, während die andre Spitze die Linie zieht,
die der Regel folgt. Und wie er so der Regel-Linie
geht, öffnet & schließt
er den Zirkel, anscheinend 153 mit großer
, wobei er
immer auf die Regel schaut, als bestimme sie Wir nun,
die wir ihm zusehen, sehen keinerlei Regelmäßigkeit
in . ˇdarin⌊.⌋ˇin diesem Öffnen &
Schließen Wir können daher
seine Art der Re Linie zu folgen, ˇvon
ihm auch nicht von ihm lernen. Wir glauben ihm aber, die
Linie habe ihm eingegeben, was er tat.
| | |
| | | | | | Wir würden hier
(vielleicht) wirklich sagen: “Die
Vorlage scheint ihm einzugeben, wie er zu gehen
hat. Aber sie ist keine Regel.”
| | |
| | | | | | Nimm an einer folgt der Reihe
x =
1, 3, 5, 7, … indem er die Reihe der
y =
x² + 1 hinschreibt; &
& er fragte sich: “aber tue ich auch
immer das Gleiche, oder jedesmal etwas anderes?”
(Wer von einem Tag auf den andern
verspricht: “morgen ich das
Trink Rauchen aufgeben”, sagt der jeden
Tag das Gleiche; oder jeden Tag etwas anderes?
| | |
| | | ∫ | | | Wie ist das zu
entscheiden, ob er immer das 154 gleiche tut, wenn ihm die Linie
eingibt, wie er gehen soll?
| | |
| | | ∫ | | | Wollte ich nicht sagen:
Nur das gesamte Bild der Verwendung des Wortes
“gleich” in seiner Verwebung mit den Verwendungen
der andern Wörter kann entscheiden, ob er das Wort verwendet wie
wir?
| | |
| | | ? / | | | Tut er nicht immer
das Gleiche, nämlich, es sich von der Linie eingeben zu lassen,
wie er gehen soll? Wie aber, wenn er sagt, die Linie gebe
ihm einmal dies, einmal jenes ein? Könnte er nun
nicht sagen: er tue in einem Sinne immer das Gleiche,
aber Regel folge er doch
nicht? Und kann aber auch nicht der, der einer Regel
folgt, doch sagen, in einem gewissen Sinne tue er jedesmal etwas
Anderes? So bestimmt also, ob er das Gleiche tut,
oder immer
, nicht, ob er einer Regel
folgt.
| | |
| | | / | | |
Nur so kann man den Vorgang, einer Regel folgen
beschreiben, daß man in anderer Weise beschreibt, was wir
dabei tun. 155 [Dazu die Bemerkung
ˇim großen weißen
M.S. über die Schwierigkeit in der
Philosophie Halt zu machen.]
| | |
| | | / | | | Hätte es einen Sinn zu
sagen: “Wenn er jedesmal etwas anderes
täte, würden wir nicht sagen: er folge einer
Regel”? Das hat keinen Sinn.
| | |
| | | / \ | | |
Einer Regel folgen ist ein bestimmtes Sprachspiel. Wie
kann man es be beschreiben? Wann sagen wir,
er habe die Beschreibung verstanden? – Wir tun dies
& das; wenn er nun so & so reagiert hat er das Spiel
verstanden.
dieses ‘dies & das’ & ‘so
& so’ enthält
“und so weiter”. – Oder:
verwendete ich bei der Beschreibung ein “unddiv
sodivweiter” & würde ˇich gefragt,
Einer fragte
mich, |
was das
bedeutet,
“was heißt das”, |
so müßte ich es wieder durch eine
Aufzählungc von Beispielen erklären; oder etwa
durch eine Geste;. dash
Und ich
würde es dann als Zeichen des Verständnisses ansehen,
wenn er die Geste ˇetwa mit einem verständnisvollen
Gesichtsausdruck wiederholte, & auch
eine Z Anzahl 156 von Beispielen
ausfuhrte. &
in speziellen Fällen so & so handelte.
| | |
| | | / \ | | |
“Aber reicht denn nicht das Verständnis weiter,
als alle Beispiele?” Ein sehr merkwürdiger
Ausdruck, & ganz natürlich.
| | |
| | | / \ | | |
Wenn man Beispiele aufzählt & dann sagt “und
so weiter”, so wird dieser letztere Ausdruck nicht auf die gleiche Weise
auf andere
Weise |
erklärt,
die Beispiele.
| | |
| | | / \ | | |
Denn das “und so weiter” könnte man
einerseits durch einen Pfeil ersetzen der anzeigt, daß das Ende der
Beispielreihe nicht das Ende ihrer Anwendung bedeuten soll.
Anderseits heißt “und so weiter” auch:
es ist genug⌊,⌋ ˇDu hast mich verstanden; wir brauchen
keine weiteren Beispiele.
| | |
| | | / \ | | |
Wenn wir den Ausdruck durch eine Geste ersetzen, so könnte es
ja sein, daß die Menschen unsre Beispielreihe 157 nur dann
wie sie
sollten, (nur dann also ihr richtig
folgten,) wenn wir am Schluß diese Geste
machten. wäre also
ganz analog der des [z|Z]eigens auf
einen Gegenstand, oder Ort.
| | |
| | | | | | Nimm an, eine Linie gebe mir ein, wie ich ihr folgen
soll; d.h., wenn ich ihr mit den Augen nachgehe,
so sagt mir etwa eine innere Stimme: zieh so. – Nun, was ist der Unterschied zwischen diesem
Vorgang, des einer Art Inspiration zu
folgen & demVorgang ⌊,⌋ einer
Regel zu folgen? Denn sie sind doch nicht das
Gleiche. Nun In dem Fall der Inspiration
warte ich auf die Anweisung. Ich werde
einen Anderen nicht
‘Technik’ lehren können, der Linie zu
folgen. Es sei denn, ich lehre ihm eine Art des
Hinhorchens, der Rezeptivität, etc. Aber
dann kann ich natürlich nicht ,
daß er der Linie so folgte, wie ich.
| | |
| | | | | | Man könnte sich auch
so einen 158 Unterricht in einer Art von Rechnen
denken. Die Kinder können dann, ein jeder auf seine
Weise, rechnen; solange sie nur auf die innere Stimme
horchen & ihr folgen. – Dieses Rechnen
wäre wie ein Komponieren.
| | |
| | | | | |
Denn gehört nicht zum Befolgen einer Regel die
einen Andern im
Folgen abzurichten? Und zwar durch Beispiele.
Und das Kriterium seines Verständnisses muß die
Übereinstimmung der einzelnen Handlungen sein. Also
nicht wie beim Unterricht in der Rezeptivität.
| | |
| | | | | | Wie folgst Du der Regel? – “Ich mach es so: “ … ” & nun folgen allgemeine
Erklärungen & Beispiele. ‒ ‒
Wie folgst Du der Stimme
dem, als Einfluß |
der Linie? –
“Ich sehe auf sie hin, schließe alle Gedanken aus,
etc. etc.”
| | |
| | | | | | “Ich würde nicht sagen,
daß sie mir immer etwas anderes eingebe
wenn ich ihr als Regel folgte.’ Kann man das
sagen? 159
| | |
| | | | | |
“Das Gleiche tun” ist mit “der Regel
folgen” verknüpft.
| | |
| | | k / \ | | |
19.3.44.
Kannst
du Dir absolutes Gehör vorstellen, wenn Du es nicht
hast? Kannst Du es Dir vorstellen, wenn Du es
hast? –Kann ein Blinder sich das Sehen von rot
vorstellen? Kann ich mir es vorstellen? Kann
ich mir vorstellen, daß ich so & so spontan reagiere, wenn
ich's nicht tue? Kann ich mir's
besser vorstellen, wenn ich's tue?
| | |
| | | k
/ \ | | | Kann ich aber das Sprachspiel
spielen, wenn ich nicht so reagiere?
| | |
| | | / \ | | |
20.3.44.
Man
fühlt nicht, daß man immer des
Winkes (der Einflüsterung
der
Eingebung |
) der Regel
gewärtig sein muß. Im
Gegenteil. // Man fühlt nicht, man
müsse immer des Winks der Regel gewärtig sein. Im
Gegenteil. // Wir sind nicht gespannt
darauf was sie uns jetzt sagen wird,
sondern vielmehr ⌊sie⌋ sagt sie uns immer dasselbe & wir tun, was sie uns
sagt. 160
Man könnte
sagen: wir sehen, was wir beim Folgen nach der Regel
Befolgen der
Regel |
tun, unter dem
Gesichtspunkt des ˇimmer Gleichen
an. // unter dem Gesichtspunkt des
immer [G|g]leichen Handelns
an. //
| | |
| | | / \ | | | Man
könnte dem, den man abzurichten anfängt, sagen:
“Sieh, ich tu(e)
immer das Gleiche: … ”.
| | |
| | | | | | Wann sagen wir:
“Die Linie gibt mir das als Regel ein –
immer das Gleiche.” Und anderseits:
“Sie gibt mir immer wieder ein, was ich zu
tun habe – sie ist keine Regel.“
Im ersten Fall heißt es: ich habe keine weitere Instanz
dafür, was ich zu tun habe. Die Regel tut es ganz
allein; ich brauche ihr nur zu folgen (& folgen ist eben
eins). Ich fühle nicht
z.B., es ist seltsam, daß mir die Linie immer
etwas sagt. – Der andre Satz sagt: Ich
weiß nicht, zum was ich tun werde; die Linie
wirds mir sagen.
| | |
| | | ∕∕ | | | Die Kunstrechner, die zum
richtigen Resultat gelangen, aber nicht sagen können,
wie. 161 Sollen wir sagen: sie
rechnen nicht? (Eine Familie von
Fällen.)
| | |
| | | | | |
Diese Dinge sind feiner gesponnen, als grobe Hände
ahnen.
| | |
| | | | | | Kann ich
nicht einer Regel zu folgen glauben? Gibt es
diesen Fall nicht?
Und kann ich dann nicht
auch keiner Regel zu folgen glauben & doch einer
folgen? Würden wir nicht auch etwas so
nennen?
| | |
| | | / \ | | | Wie kann ich
das Wort “gleich” erklären? –
Nun, durch Beispiele. – Aber ist das
alles? gibt es nicht
eine noch tiefere Erklärung; oder muß nicht doch das
Verständnis der Erklärung tiefer
sein? – Ja, hab ich denn selbst ein tieferes
Verständnis? Habe ich mehr, als ich in der
Erklärung gebe?
Woher aber
ˇ(dann)
das Gefühl, ich hätte mehr, als ich sagen kann?
Ist es, daß ich das nicht Begrenzte (die
nicht begrenzte als Länge deute, die über jede
Länge hinausreicht? (Die
un nicht
begrenzte
Erlaubnis, als Erlaubnis zu etwas 162 Grenzenlosem)
| | |
| | | | | | Die Vorstellung die mit dem
Grenzenlosen geht, ist die von etwas so großem, daß wir
sein Ende nicht sehen können. // , daß
wir davon kein Ende sehen können. //
| | |
| | | / | | |
Die Verwendung des Wortes “Regel” ist mit der
Verwendung des Wortes “gleich” verwoben.
| | |
| | | / | | |
Überlege Dir: Unter welchen Umständen wird
der Forschungsreisende sagen: Das Wort
“ … ” dieses Stammes heißt soviel wie unser
“und so weiter”? Stelle Dir
Einzelheiten ihres Lebens & ihrer Sprache vor, die ihn dazu
berechtigen würden.
| | |
| | | | | | “Ich weiß doch, was
‘gleich’ heißt!” –
Daran zweifle ich nicht; ich weiß es auch.
| | |
| | | | | | “Die Linie
gibt's mir ein …” Hier ist der Ton auf
dem Ungreifbaren
Eingebens. Eben darauf, daß nichts meine
Handlung von der Regel trennt, daß nichts zwischen ihr &
der Handlung steht. // Eben darauf, daß
nichts zwischen 163 der Regel & meiner Handlung
steht. //
| | |
| | | | | |
– – – ein Bild. Und urteile ich, sie gebe
mir, gleichsam verantwortungslos, dies, oder das ein, so würde
ich nicht sagen, ich folgte ihr als Regel.
als einer
Regel. |
| | |
| | | ∕∕ | | | Mann könnte
sich aber denken, daß einer mit solchen Gefühlen
multipliziert, richtig multipliziert; immer wieder sagt:
“Ich weiß nicht – jetzt gibt mir die Regel auf
einmal das ein!” & daß wir
antworten: “Freilich; Du gehst ja ganz nach der
Regel vor.”
| | |
| | | | | | Einer
Regel folgen: das läßt sich verschiedenem
entgegensetzen. Der Forschungsreisende wird, unter
anderm, auch die Umstände beschreiben
(können), unter denen ein
Einzelner von diesenr
Leuten
nicht von sich selbst sagt, er folge einer Regel[,|.] ˇNämlich
auch ˇdann⌊,⌋ wenn es so ˇin mancher Beziehung
so aussieht, als täte er⌊'s⌋
es // Nämlich auch,
wenn es in der einen, oder andern Beziehung
164 so
aussieht. // // … dieser Leute
nicht von sich selbst sagen will, er folge einer Regel.
Wenn es in dieser, oder jener Beziehung auch so
ausschaut. //
| | |
| | | ∕∕ | | | Aber könnten
wir nicht auch rechnen, wie wir rechnen (Alle
übereinstimmend, etc.) & doch bei
jedem Schritt das Gefühl haben, von den Regeln wie von einem
Zauber geleitet zu werden; etwa erstaunt
darüber, ˇvielleicht⌊,⌋ daß wir
übereinstimmen? (Der Gottheit etwa für
diese Übereinstimmung dankend.)
| | |
| | | ∕∕ | | | Daraus
siehst Du nur, wieviel zu der Physiognomie dessen gehört, was wir
im alltäglichen Leben “einer Regel folgen”
nennen!
| | |
| | | | | | Man
folgt der Regel
‘mechanisch’. Man
vergleicht sich also mit einem Mechanismus.
| | |
| | | | | |
“Mechanisch”, das heißt: ohne zu
denken. Aber ganz ohne zu denken?
Ohne nachzudenken. 165
| | |
| | | | | |
Der Forscher könnte sagen: “Sie folgen
Regeln, aber es sieht doch ganz anders aus, als bei
uns.”
| | |
| | | | | |
“Sie gibt mir, verantwortungslos, dies, oder das
ein” heißt: ich kann es Dich
nicht lehren, wie ich der Linie folge. Ich setze
nicht voraus, daß Du ihr folgen wirst wie ich, auch wenn Du ihr
folgst.
| | |
| | | k | | |
21.3.44.
Eine Addition von Formen, in der gewisse Glieder verschmelzen
spielt in unserm Leben eine sehr geringe Rolle. – Wie
wenn
 &
△ die Figur &
△ die Figur
 ergeben. Aber wäre dies eine wichtige
Operation, so hätten wir vielleicht einen andern geläufigen
Begriff von der arithmetischen Addition.
ergeben. Aber wäre dies eine wichtige
Operation, so hätten wir vielleicht einen andern geläufigen
Begriff von der arithmetischen Addition.
| | |
| | | k | | | Daß man ein
Boot, einen Hut, etc. aus einem quadratischen
Stück Papier (nach gewissen Regeln) falten kann, ist uns
natürlich als Angelegenheit der
Geometrie
geometrische Tatsache |
zu betrachten, nicht der Physik. Aber ist
166 Geometrie, so verstanden,
nicht ein Teil der Physik? Nein; wir spalten die
Geometrie von der Physik ab. Die geometrische
Möglichkeit von der physikalischen. Aber wie, wenn man
sie beisammen ließe? Wenn man einfach sagte:
“wenn Du das & das & das mit dem Papier tust,
wird dies herauskommen”? Was zu
tun ist, könnte durch einen Reim gegeben werden. Ist
es denn nicht möglich, daß jemand zwischen den beiden
Möglichkeiten gar nicht unterscheidet? Wie
etwa ein Kind, das diese Technik lernt. Es weiß nicht,
& denkt nicht darüber nach, ob diese Resultate des
Faltens nur möglich sind weil das Papier ˇdabei sich
dabei in der
& der Weise dehnt& , verzerrt,
oder, weil es sicht nicht verzerrt.
| | |
| | | | | | Und ist es nun nicht auch so in der
Arithmetik? Warum sollten Leute nicht rechnen lernen
können ohne einen Begriff von einer mathematischen &
einer physikalischen Tatsache. Sie wissen nur, daß das
immer herauskommt, wenn sie ˇgut gut
achtgeben & tun was man sie gelehrt hat.
Denken wir uns, während wir rechneten
veränderten sich die Ziffern ˇsprungweise auf dem
167 Papier. Eine
Eins würde plötzlich zu einer 6 dann zu einer 5, dann wieder
zu einer 1 u.s.f. Und ich will
einmal annehmen, das änderte an der Rechnung gar nichts,
weil, sowie ich eine Ziffer ablese um mit ihr zu rechnen, ˇoder sie
anzuwenden⌊,⌋ sie wieder zu der würde, die wir bei
unserm Rechnen vor uns haben. Dabei sähe man
aber wohl während des Rechnens wie die Ziffern sich ändern;
wir sind aber instruiert uns darum weiter nicht zu
kümmern.
Dieses Rechnen
könnte natürlich, auch wenn wir die obige Annahme nicht
machen, zu brauchbaren Resultaten führen.
Wir rechnen hier streng nach einer Regel // nach Regeln // ,
& doch muß dieses Resultat nicht herauskommen.
– Ich nehme an, daß wir keinerlei
Gesetzmäßigkeit in dem Wechsel der Ziffern sehen.
| | |
| | | | | | Ich will sagen:
Man könnte dieses 168 Rechnen wirklich als ein
Experimentieren auffassen, & z.B.
sagen: “versuchen wir was jetzt herauskommt, wenn ich
diese Regel anwende”.
| | |
| | | | | |
Oder auch: “Machen wir dieses
Experiment: schreiben wir die Ziffern mit einer Tinte von
der & der dieser Zusammensetzung ˇ …
& rechnen nach Regel … .
| | |
| | | | | | Nun könntest Du natürlich sagen:
“In
diesem Fall ist das Manipulieren … kein Rechnen. “
Dieses Manipulieren von Ziffern nach Regeln ist
(nun) kein Rechnen. |
| | |
| | | | | | “Wir rechnen nur, wenn hinter dem
Resultat ein Muß steht.” , wenn das
Resultat erhalten werden
muß.” // – Aber
wenn wir nun nur dieses Muß nicht wissen, – liegt es da
dennoch in der Rechnung? Oder rechnen wir nicht,
wenn wir es, sozusagen, ganz naïf
tun?
| | |
| | | | | | Wie ist
es damit: Der rechnet nicht, der, wenn ihm
einmal das, einmal jenes herauskommt & er einen Fehler nicht
169
kann, sich damit abfindet &
sagt das zeige eben,
es zeige sich
eben, |
daß gewisse noch unbekannte
Umstände das
beeinflussen.
| | |
| | | | | | Man
könnte das so ausdrücken: Wer die Rechnung
zum Finden eines kausalen Zusammenhangs verwendet, rechnet
nicht. // : Wem die Rechnung
einen kausalen Zusammenhang
aufdeckt entdeckt //
aufzeichnet // , der rechnet
nicht. //
| | |
| | | | | |
Kinder werden nicht nur im
Rechnen geübt, sondern auch in einer ganz bestimmten
Stellungnahme gegen einen Rechenfehler. // gegen eine Abweichung von der
Norm. //
| | |
| | | | | | Was ich sage, kommt darauf hinaus, die
Mathematik sei normativ. Aber
“Norm” bedeutet nicht dasselbe, wie
“Ideal”.
| | |
| | | | | | Denke Dir Menschen, die eine
Linie immer impressionistisch nachzeichneten.
| | |
| | | / | | |
“[In| Mit] Zungen reden”.
Könnte man sich auch 170 denken, daß das die ganze Sprache
der Menschen wäre? Wäre so eine Sprache dann
ähnlich wie die von Tieren?
| | |
| | | / | | | Hätte ich
das Sprachspiel (2) fundamentaler beschreiben können,
als ich es tat? Nein. – Aber was
könnte verleiten,
zu denken? Ist es, weil wir keinem
Grund trauen wollen, der nicht begründet ist?
| | |
| | | | | | Statt “ich
deute sie mir so” möchte ich
lieber
sollte ich |
sagen: “sie deutet sich mir nun
so”.
| | |
| | | | | |
Warum aber nicht sagen, was wir tatsächlich in solchen
Fällen sagen;? nämlich:
“Das heißt ich muß nun
so handeln … ”?
| | |
| | | / | | | Was kann die
Beschreibung des Sprachspiels mehr tun, als ihm ein Bild zu
zeichnen? – Und wenn er mehr will; was will er
dann?
| | |
| | | k | | |
Die Lösung mancher Probleme 171 nicht
durch denken, sondern nur durch üben
erhalten. // ˇkannst Du nicht durch denken
allein erhalten, sondern nur durch
üben. //
| | |
| | | k | | | 22
.3.44. Die
Einführung einer neuen Schlußregel kann man als Übergang
zu einem neuen Sprachspiel auffassen. Ich stelle mir eines
vor, in welchem etwa eine Person ‘p ⊃
q’ aussagt, eine andere
‘p’, & eine dritte den
Schluß zieht.
| | |
| | | | | | Ist es
möglich, zu beobachten, daß eine halb rot & halb blau
ˇgefärbt ist; & nicht zu beobachten, daß sie
rot ist? Denk Dir, man verwende eine Art
Farbadjektiv für eine Fläche Dinge, die
halb rot halb blau ist sind: Man sagt (dann) sie seien
‘bu’. Könnte nun
jemand nicht darauf trainiert sein, zu beobachten, ob bu ist, oder nicht;
& nicht darauf, ob rot ? Dieser würde dann nur zu melden
wissen: “bu”, oder
“nicht bu”. Und wir
aus de[m|r]
ersten ˇMeldung den Schluß ziehen, rot. 172
| | |
| | | | | |
23.3.44. Ich stelle mir ˇhier
vor, daß die Beobachtung durch ein psychologisches Sieb
geschieht, das z.B. nur das
Factum durchläßt, die Fläche
blau-weiß-rot (französische
tricolore), oder sei es
nicht.
| | |
| | | | | | Ist es nun eine
besondere Beobachtung, die Fläche sei zum Teil rot, wie kann
[es| dies] logisch aus dem Vorigen folgen. Die
Logik kann uns doch nicht sagen, was wir beobachten
müssen.
| | |
| | | | | | Jemand
zählt Äpfel in einer Kiste; er zählt bis 100.
Ein Andrer sagt: “also sind jedenfalls 50
Äpfel in der Kiste” (das ist alles, was ihn
interessiert). Das ist doch ein logischer Schluß; ist
es aber nicht auch eine besondere Erfahrung?
| | |
| | | | | | Eine
geteilte Fläche⌊,⌋ ˇdie in
Stücke von, die in eine Anzahl von Streifen
ˇeingeteilt, ist wird ˇvon mehreren
Leuten beobachtet. Die Farben ⌊⌊ // Wir beobachten eine Fläche, die in eine
Anzahl von Streifen abgeteilt ist. Die Farben …
// ⌋⌋ Streifen ändern sich, alle
 zu gleicher Zeit, immer
nach je einer Minute. zu gleicher Zeit, immer
nach je einer Minute. 173 Jetzt sind
Farben: rot, grün,
blau, [weiß| schwarz], [weiß| schwarz],
blau.
Es wird beobachtet daß jedesmal
rot ∙ blau ⊃ schwarz
. ⊃ . weiß
Es wird auch beobachtet:
~grün ⊃ ~
weiß
und Einer zieht den
Schluß: ~grün ⊃ rot ∙ blau
∙ ~ schwarz Und
diese Implikationen sind ‘material
implications’ im Sinne in
Russell's Sinn
| | |
| | | | | | Aber kann man denn,
daß r.b ⊃ s . ⊃ .
w, beobachten?
Beobachtet man nicht
Farben[z|Z]usammenstellungen,
& schließt etwa also etwa,
ˇdaß r ∙
b ∙ s ∙ w; & schließt
leitet dann jeden Satz ab?
Aber
kann Einer bei der Beobachtung einer Fläche nicht ganz von
der Frage eingenommen sein, ob sie sich grün, oder nicht
grün färben wird; & wenn er nun sieht:
~g, muß er auf die
ˇbesondere Farbe aufmerksam 174 werden sein, die
die der Fläche zeigte, aufmerksam
sein?
Und könnte einer nicht ganz von dem Aspekt
r ∙ b ⊃ s
. ⊃ . w eingenommen
sein[;|?] [w|W]enn er z.B. dazu
angelernt worden wäre, alles andere vergessend, nur unter diesem
Gesichtspunkt die Färbung der Fläche zu
betrachten. (Es könnte ˇden Menschen unter
bestimmten Verhältnissen ganz gleichgültig sein, ob
Gegenstände rot, ˇsind, oder grün sind
sind; von ˇgroßer Wichtigkeit aber,
daß ob sie rot oder grün sind eine
dieser beiden Farben, oder eine dritte besitzen. Und
es könnte in diesem Falle ein Wort für Farbwort für “rot oder grün”
geben.)
| | |
| | | | | | Wenn
es man aber eine echte Beobachtung gibt
beobachten kann, daß r ∙ b ⊃ s
. ⊃ . w & eine
daß
~g ⊃ ~w ,
dann kann ˇman ja auch beobachtetn, &
nicht bloß geschlossen ß werden
schließen, daß
~g ⊃
r ∙ b ∙ ~s
175
| | |
| | | | | | Wenn
dies drei (echte)
B⌊e⌋obachtungen sind,
muß es ˇauch möglich sein, daß , was
d[er|ie] Dritte ˇdritte Beobachtung
sieht, nicht mit dem logischen Schluß
ˇaus dem aus den beiden ersten
übereinstimmt.
•
| | |
| | | | | | Angenommen die Menschen berechnen
die Entwicklung von π ˇimmer weiter &
weiter. Der allwissende Gott
weiß ˇalso, daß ob sie bis zum
bis zur Zeit des Weltuntergang⌊s⌋
die zu einer Figur 777 entwickelt haben.
gekommen sein werden. Aber weiß er mehr?
[K|k]ann seine Allwissenheit entscheiden, ob die
Menschen nach dem Weltuntergang zu jener Figur gekommen
wären? Ich will sagen:
Sie kann es nicht[!| .] Ich will
sagen: Auch Gott
Mathematisches nur durch
Mathematik entscheiden. Auch für ihn kann die bloße
Regel des Entwickelns nichts entscheiden, was sie für uns nicht
entscheidet.
| | |
| | | | | |
Man könnte das so sagen: Ist uns die Regel der
Entwicklung gegeben, so kann uns nun eine Rechnung lehren,
daß an der 100sten fünften Stelle 176 die Ziffer “2”
steht. Hätte Gott dies,
ohne diese Rechnung, bloß aus der Entwicklungsregel wissen
können? Ich will sagen: Nein.
| | |
| | | | | |
24.3.44.
⇒← Ist
es denn also denkbar, daß einer beim Beobachten einer Fläche
die Verbindung
sieht (etwa als Flagge), aber, , wenn er sich
(nun) drauf einstellt, eine der beiden Hälften zu
sehen, statt des Rot ˇein Blau sieht? Nun, Du
hast's ja es gerade beschrieben. – Es
wäre etwa so, wie wenn jemand auf eine Gruppe von Äpfeln
schaute & sie ˇihm immer als ˇzwei Gruppen von
je zwei Äpfel & zwei Äpfel⌊n⌋
sähe ˇerschienen, so wie er aber versuchte,
sie mit dem Blick zusammenzufassen, erschienen sie ihm als
5. Dies wäre ein sehr merkwürdiges
Phänomen. Und es ist keines von denen, von
deren Möglichkeit wir Notitz nehmen.
| | |
| | | | | |
25.3.44. Erinnere Dich dran, daß ein
Rhombus, als Raute angesehen, nicht wie ein
Parallelogram ausschaut. Nicht
aber, als schienen seine gegenüberliegenden Seiten nicht parallel
177 zu sein, sondern der
Parallelismus fällt uns nicht auf.
| | |
| | | | | | Ich könnte mir denken, daß
Einer sagt, er sähe einen weiß & gelben
Stern aber nichts Gelbes – weil er den Stern gleichsam
als eine Verbindung von Farbteilen sieht, die er
nicht zu trennen vermag.
| | |
| | | | | | Er hatte z.B.
Figuren vor sich, wie diese
Gefragt, ob
er ein rote fünfeck sieht
& würde er ‘ja’ sagen; gefragt ob er
ein gelbes sieht: ‘nein’. Ebenso
sagt er er sehe ein blaues Dreieck, aber kein rotes. –
Aufmerksam gemacht sagte er etwa: “Ja, jetzt
seh ich's; ich hatte die Sterne nicht so
aufgefaßt.”
Und so könnte es
ihm auch vorkommen, man könne die Farben im Stern nicht
trennen, weil man die Formen nicht trennen kann.
| | |
| | | ∕∕ | | | Der kann die
Geographie einer Landschaft 178 nicht übersehen lernen, der sich so langsam in ihr bewegt, // , der so langsam in ihr
sich
fortbewegt
weiterkriecht |
, // daß er das eine
Stück längst vergessen hat, wenn er zu einem andern
kommt. | | |
| | | | | |
2[5|6]
.3.44. Denke es gebe kein schriftliches
Rechnen ˇ(oder es wäre verboten). Wir
rechnen alles mündlich, & bei längeren Rechnungen
gibt es oft [d|D]iskrepanzen⌊.⌋ in den
Resultaten. Wir würden
ˇdiese durch verschiedene Maßregeln bis zu einem gewissen
Grade herabdrückencc
niedrig ˇzu halten ˇtrachten
ˇsuchen suchen; dann aber ¤ nicht sagen eine Multiplikation
könne habe natürlich nur ein
ˇrichtiges Ergebnis haben,
wir nicht ˇmit Sicherheit kennen;
sondern: die Technik des Multiplizierens ergebe nicht
immer genau dasselbe
gleiche Resultat,
sei aber brauchbar für unsere Zwecke.
(Ja, vielleicht gerade deswegen.)
¤ // Wir
würden diese durch verschieden Maßregeln klein zu halten
suchen; dann aber … //
| | |
| | | | | |
2[7|9]
.3.44. Warum rede ich immer vom Zwang
durch die Regel; warum nicht davon, daß ich ihr folgen 179 wollen kann?
Denn das ist ja ebenso wichtig.
Aber ich
will auch nicht sagen, die Regel zwinge mich so & so zu
handeln, sondern sie mache es mir möglich, mich an ihr
anzuhalten & von ihr zwingen zu lassen.
| | |
| | | | | | Und wer, z.B., ein
Spiel spielt, der hält sich an seine Regeln. Und es
ist eine interessante Tatsache, daß Menschen zum
Vergnügen Regeln aufstellen & sich dann nach ihnen
halten.
| | |
| | | | | |
Meine Frage war eigentlich:
“[W|w]ie
kann man sich an eine Regel
anhalten?” // an eine Regel
halten?” // Und
das (paradoxe) Bild, das einem hier vorschweben
könnte, wäre das eines kurzen
Stückes Geländer, vorschwebt, könnte
das eines kurzen Stücks Geländer sein, durch
, von dem ich mich
weiter ˇsoll führen lassen
soll, als reicht. [Aber da ist
doch nichts; aber da ist doch nicht nichts!]
Denn wenn ich Frage “wie kann man sich
…?”
an eine Regel halten?” |
, 180 so heißt es, daß mir hier etwas
paradox erscheint; also ein Bild mich verwirrt.
| | |
| | | | | | “Daß das
auch rot ist, daran habe ich gar nicht gedacht; ich habe es nur als
Teil des mehrfärbigen Ornaments gesehen.”
| | |
| | | | | | Logischer Schluß ist ein
Übergang der gerechtfertigt ist, wenn er einem bestimmten
Paradigma folgt & dessen Rechtmäßigkeit von sonst
nichts abhängt.
| | |
| | | | | | Wir sagen: “Wenn
ihr beim Multiplizieren wirklich der Regel folgt,
muß das Gleiche herauskommen.”
Nun, wenn dies nur die etwas hysterische Ausdrucksweise der
Universitätssprache ist, so braucht sie uns nicht sehr zu
interessieren.
Es ist aber der Ausdruck einer
Einstellung zu der Technik des Rechnens, die sich überall
in unserm Leben zeigt. Die Emphase des Muß
entspricht nur der Unerbittlichkeit Einstellung sowohl zur Technik
des Rechnens, als auch zu unzähligen verwandten
Techniken. 181
| | |
| | | | | |
Das mathematische Muß ist nur ein andrer Ausdruck
dafür, daß die Mathematik Begriffe bildet.
Und Begriffe dienen zum Begreifen. Sie
entsprechen einer bestimmten Behandlung der
Sachlagen.
| | |
| | | | | | Die Mathematik bildet ein Netz von
Normen.
| | |
| | | | | | Es ist
wie wenn ein Maßkörper mehrere Facetten hätte &
mit ihnen verschiedene Gegenstände zugleich & ihre
gegenseitige Lage mäße. // beurteilen
hülfe. //
| | |
| | | | | |
Wir messen Längen von Gegenständen mit
Eisenstäben & nicht mit Teigstäben.
| | |
| | | | | | Es ist möglich, den
Komplex aus A & B sehen, ohne A, oder
B, zu sehen. Es ist auch möglich, den Komplex
einen “Komplex von A & B” zu
nennen & zu denken, diese Benennung deutete nur auf eine
Art Verwandtschaft dieses Ganzen mit A & mit
B hin. Es ist also 182 möglich, zu sagen, man sehe den
Komplex von A & B, aber weder A noch
B. Etwa wie man sagen könnte, es sei hier ein
rötlich-gelb, aber weder rot noch gelb.
| | |
| | | | | | Kann ich nun A
& B vor mir haben & ˇauch beide sehen,
aber nur A ⌵ B
beobachten? Nun, in gewissem Sinne ist das doch
möglich. Und zwar dachte ich mir es so, daß der
Beobachter von einem gewissen Aspekt eingenommen sei; daß er etwa
eine bestimmte Art von Paradigma vor
sich habe, in einer bestimmten Routine
der Anwendung begriffen sei. – Und wie er
nun auf
A ⌵ B eingestellt sein
kann, so (doch) auch auf A ∙ B. Es
fällt ihm also nur A ∙ B auf &
nicht, z.B., A. Auf
A ⌵ B eingestellt
sein heiße, könnte man sagen, mit dem Begriff
‘A ⌵ B’ auf die & die Situation
zu reagieren. Und genauso kann man's
natürlich auch mit A ∙ B tun.
| | |
| | | | | | Sagen wir: es
interessiert Einen nur A ∙ B, & er
urteilt also, was immer geschieht, nur
“A ∙ B”, oder
“~(A ∙ B)”;
so kann ich mir denken, daß er “A ∙ B” urteilt
& auf die Frage “siehst Du B?”
sagt “nein, ich sehe A ∙ B”.
183 Etwa wie mancher der
A ∙ B sieht nicht zugeben
wird, er sehe A ⌵ B.
| | |
| | | | | |
30.3.44. Aber die Fläche ‘ganz
rot sehen’ & ‘ganz blau sehen’ sind
doch gewiß ‘echte’ Erfahrungen, & doch
sagen wir, Einer könne sie nicht zugleich haben.
| | |
| | | | | | Wenn er uns nun
versicherte, er sehe diese Fläche ganz rot & zugleich
ganz blau? Wir müßten sagen: “Du
machst Dich uns nicht
verstandlich”.
| | |
| | | | | | Der Satz 1 Fuß =
… cm ist bei uns zeitlos. Man könnte
sich aber auch den Fall denken, in welchem sich das Fußmaß
& das Metermaß nach & nach etwas veränderten
& dann immer wieder verglichen werden müßten um
sie in einander
umzugerechnent ⌊zu
werden⌋.
| | |
| | | | | |
Ist aber nicht auch bei uns das Verhältnis der Längen des
Meters & Fußes experimentell bestimmt
worden? Doch; aber das Ergebnis wurde zu einer Regel
gestempelt.
184
| | |
| | | | | | Die Mathematik hat
schon alles vorbereitet.
| | |
| | | / | | | “Eine Reihe hat
doch für uns ein Gesicht!” Wohl;
aber welches? – Nun doch das algebraische, &
das eines Stücks der Entwicklung. Oder hat sie sonst
noch eins? – “Aber in dem liegt doch schon
alles!” – Aber das ist keine
Feststellung über das Reihenstück, oder über
etwas, was wir darin ;
sondern ein Ausruf; & ˇes
ist der Ausdruck dafür, daß wir nur auf den Mund der
Regel schauen & tun[;| ,] & an
keine weitere Anleitung appellieren.
| | |
| | | ∫ | | | Der Vorgang des Ableitens hat
einen Grund (Boden).
| | |
| | | / | | | “Aber
Du siehst doch …” Nun das ist eben die charakteristische Äußerung Eines, der
von der Regel gezwungen ist.
| | |
| | | | | | Also so, ein Bild kommt Dir
vor Augen! – könnte ich sagen.
| | |
| | | | | | “Aber darin liegt doch schon
alles!” Nun, was willst Du mehr?
Das ist eben der Ausruf 185 den diese
Situation hervorbringt. ˇin mir
erzeugt. – // in mir
hervorbringt. // //
erzeugt. // Und
es ist nun eine andere Frage warum
⌊ich⌋ wir geneigt sind
bin
diese Worte zu
gebrauchen
so zu reagieren |
. ˇ⌊gerade⌋ dies zu
sagen. Denn zur Anwendung der Regel
gehört[e|t]e sie esdas ja nicht. // Das ist eben
der Ausruf, den diese Situation erzeugt. – Und es ist
nun eine andere Frage, : warum ich
gerade dies zu sagen geneigt bin. – Denn zur Anwendung
der Regel gehört ja
nicht. //
| | |
| | | / \ | | | Woher die
Idee, wäre die angefangene Reihe ein
sichtbares Stück unsichtbar bis in's unendliche
gelegter Geleise?
| | |
| | | / \ | | |
Warum aber: “es liegt doch schon alles in
ihr”? – Ich brauche nur noch die
Kurbel zu drehen, alles übrige macht die Maschine.
Und die Kurbel drehen ist etwas so Einfaches: ich kann
es automatisch tun.
| | |
| | | / \ | | | Ich glaube im
Reihenstück ganz fein eine Zeichnung zu erblicken, die nur
mehr das
“u.s.w”
bedarf um in die Unendlichkeit zu reichen.
| | |
| | | ∫ | | | “Ich erblicke ein
Charakteristikum in ihr.” – 186 Nun, doch etwas, was dem
algebraischen Ausdruck entspricht. –
“Ja, aber nichts Geschriebenes, sondern förmlich
etwas aetherisches.” –
Welches seltsame Bild. – “Etwas, was nicht
der algebraische Ausdruck ist, sondern wofür dieser nur
eben der Ausdruck ist.”
| | |
| | | | | | Ich erblicke etwas in ihr –
ähnlich wie die Gestalt im Vexierbild. Und sehe ich
das, so sage ich: “das ist alles, was ich
brauche.” – Wer den Wegweiser findet, sucht
nun nicht nach einer weiteren Instruktion, sondern er
geht nun. ⌊.⌋
(Und sagte ich; statt “er geht
nun” “er
richtet sich nun nach ihm”; ⌊,⌋
so könnte der [u|U]nterschied der beiden nur
sein, daß der zweite Ausdruck auf gewisse psychologische
Begleiterscheinungen
Erscheinungen |
anspielt.)
| | |
| | | | | |
Die Regel kann mich in mehr als einem Sinne zwingen.
Z.B. [d|D]urch die Macht der Gewohnheit,
ˇz.B. oder einer menschlichen Institution
menschlicher Gesetze |
. Aber an diesen
Zwang denke ich nicht[; s|. S]ondern an
den⌊,⌋jenigen durch welchen mit welchem
⌊Zwang,⌋ der darin liegt, daß die Regel
alles vorgemacht hat, was ich ihr nachmachen 187 kann; ˇdaß sie
schon alles in logischer Schrift ˇschon
alles vorgeschrieben
hat.
| | |
| | | ∫ | | | Einer Regel
folgen: da gibt es viele verschiedene
charakteristische Arten des Benehmens. // da gibt es viele verschiedene charakteristische
Erscheinungen. // [Lesen.]
| | |
| | | ∫ | | | “Wie kann
ich einer Regel folgen?” Nun, was kann ich
mehr tun, als zu beschreiben, wie man ihr folgt; als
einen Fall
beschreiben? – Und ist das nun eine
Erklärung? – Manche ist es eine. – Und habe ich mehr
als ich gebe? Nein; mehr habe ich
nicht.
| | |
| | | | | | Das
ist eben eine Beschreibung des Vorgangs ‘einer
Regel [F|f]olgen’.
| | |
| | | /
\ | | | Wenn ich auf dem Mars ein Wesen
beobachtete das auf einen
Wegweiser-ähnlichen Gegenstand schaut
& ihm dann parallel geht, so hätte ich keine
Berechtigung zu sagen, es folge ihm, auch wenn ich alle seine
Gefühle in diesem Augenblick 188 kennte. ”Aber er
muß doch wissen, ob er dem Zeichen folgt!”
– Nicht durch Introspektion!
| | |
| | | / \ | | |
Man kann einer Regel nicht einmal folgen.
| | |
| | | /
\ | | | Wenn ˇin der Geschichte einmal
ein einziges Mal ein Mensch einmal
Multiplikation, ˇsagen wir,
127 × 938,
aus schriftlich ausgeführt
hätte, dann hätte er, was immer seine gedanklichen
Prozesse zu ⌊da⌋bei diesem Vorgang
waren, nicht multipliziert.
| | |
| | | ∕∕ | | | Damit
es mir erscheinen kann, als hätte die Regel alle ihrer
Folgesätze erzeugt, müssen sie mir
selbstverständlich . So selbstverständlich, wie
es mir ist,
diese Farbe “blau” zu nennen. | | |
| | | | | |
31.3.44. Wozu spielt die
Mathematik mit den Begriffen? –
Sie macht sie für unsere Zwecke brauchbar.
| | |
| | | \ | | |
13.4.44.
Was wir
“Sprache” nennen ist eine Institution.
189 Es könnte nicht
in der Geschichte
der Menschheit ein Satz ausgesprochen, & verstanden,
werden. Und so auch kein Befehl & keine
Regel. (Vergleiche damit den Gedankengang
über ˇIdealismus & Solipsismus & die
Möglichkeit einer ’privaten
Sprache’⌊.⌋,⌊)⌋ zusammenhängend mit
Idealismus & Solipsismus.)
| | |
| | | | | | Inwiefern kann man sagen, ein Satz der
Arithmetik gebe uns einen Begriff? Nun, denken
wir uns ihn nicht als Satz, als Entscheidung einer Frage, sondern als
eine, irgendwie anerkannte, Verbindung von Begriffen.
| | |
| | | | | |
Die
mathematischen Sätze als Katalognummern der
Beweise (Ursell). Wie
wüßte man sonst, welchen Satz wir den vom Beweis bewiesenen
nennen sollten?
Wie ist es aber mit
unbewiesenen Sätzen? Nun, die warten eben noch auf
Beweise, die sie katalogisieren, oder sie sind ihre eigenen Beweise
(Axiome).
190
| | |
| | | | | | Der
Beweis verschafft dem Satz Anerkennung.
| | |
| | | | | | Der Beweis knüpft eine Kette von
Begriffsverbindungen.
| | |
| | | | | | Der Beweis reiht den Satz in ein System
ein.
| | |
| | | | | | Könnte man sagen,
daß der Beweis von
25² = 625
zeigt inwiefern
25² = 625
ist? – Das heißt eigentlich:
“könnte man den Sinn ˇ(den Gebrauch) eines
math. Satzes
ˇdadurch erklären, indem
daß man zeigt, was als sein Beweis gelten
soll?” Es ist zweifellos, daß der Beweis
in dem Satz nicht nur diesem Satz im
gegensatz zu einem andern Anerkennung verschafft,
sondern uns auch zeigt warum man so einen Satz überhaupt
ausspricht. Kinder, wenn sie den Anfang
der Arithmetik lernen, werden nicht drauf aufmerksam gemacht daß
4 + 5 auch
etwas andres sein könnte als 9. Sie lernen aus
von 4
ˇKugeln & ˇeiner von 5 Kugeln eine
Gruppe von 9 machen, & eine von 9 in eine von 4 & 5 zerlegen.
Sie 191 üben einen Vorgang ein &
lernen (dabei) einen Satz sagen. Den Vorgang kann man
den Beweis des Satzes nennen, aber er gibt vor allem dem Satz seine
Anwendung.
| | |
| | | | | | Der
Satz & der Beweis müssen jeder in
anderem Sinne eine Begriffsverbindung sein. –
Das will eigentlich sagen daß man den Satz & den Beweis
auf wesentlich Weise
verwendet. Nun, ich beweise den Satz zuerst & dann verwende ich ihn
() als Paradigma
für Urteilsübergänge. Der Beweis
überredet mich dazu, den Satz zu gebrauchen, oder:
überzeugt mich davon, daß ich den Satz gebrauchen
darf.
| | |
| | | | | | Das
[G|g]leichgesetzte 25² & 625 gibt mir nun,
könnte man sagen, einen neuen Begriff. Und der Beweis
zeigt, was es mit dieser Gleichheit für eine
Bewandnis hat. – “Einen
neuen Begriff geben”, kann nur heißen, eine neue
Begriffsverwendung einführen, eine neue Praxis.
192
| | |
| | | | | |
“Wie kann man den Satz von seinem Beweis
loslösen?” zeigt natürlich eine falsche
Auffassung.
| | |
| | | | | | Der
Beweis ist eine Umgebung des Satzes.
| | |
| | | | | | ‘Begriff’ ist ein
[V|v]ager Begriff.
| | |
| | | | | | Nicht in jedem Sprachspiel gibt es
etwas, was man “Begriffe” nennen wird.
| | |
| | | | | | Begriff ist etwas einem Bild vergleichbares,
etwas wie ein
Bild, |
womit man
Gegenstände vergleicht. Und man
urteilt
| | |
| | | | | | Gibt es im Sprachspiel (2) Begriffe? Aber man
könnte es leicht so erweitern // auf solche Art erweitern // , daß
“Platte”, “Würfel”,
etc. zu
Begriff[en|s]ˇwörtern würden. // , daß “Platte“,
“Würfel”,
unzweifelhaft
Begriffe würden bezeichneten // .
Z.B. durch eine Technik des
Beschreibens oder abbildens jener
Gegenstände. Es
natürlich keine scharfe Grenze zwischen Sprachspielen, die mit
Begriffen arbeiten, & andern. Wichtig ist,
daß 193 das Wort “Begriff”
sich auf eine Art von Behelf im Mechanismus der Sprachspiele
bezieht.
| | |
| | | | | |
Betrachte einen
Im
Denke an einen |
Mechanismus
Während
der Punkt A einen Kreis beschreibt, beschreibt B eine Achterfigur
eine
Acht |
. Wir schreiben das
ˇnun als ˇeinen kinematischen Satz auf.
◇◇◇ Indem ich den
Mechanismus umtreibe
in Gang setze
bewege |
beweist beweist mir das Bild
seiner Bewegung diesen den Satz er mir
diesen Satz;
wie etwa eine Konstruktion auf dem Papier es
täte. Und
[d|D]en Satz könnte man ein Bild ˇder
Bewegung des Mechanismus nennen. Die Methode der Abbildung
aber wäre eben jene Konstruktion, oder die Bewegungen von A
& B, ich sehe, wenn
der Mechanismus im Gang
ist.
ich das Rad umtreibe. |
Ich kann ja auch den Mechanismus mit dem Satz
vergleichen & prüfen ob 194 er ein richtiges Bild des Mechanismus
ist. Der Satz entspricht etwa einem Bild des Mechanismus
mit den eingezeichneten Bahnen der Punkte A &
B. Er ist also in gewisser Beziehung ein Bild jener
Bewegung. Er hält das fest, wovon mich der Beweis
überzeugt. Oder wozu er
mich überredet
| | |
| | | | | | Wenn mir nun der Beweis einen neuen
Begriff gibt; was tut der bewiesene Satz? Man könnte
sagen: der ˇbewiesene Satz spielt spielt auf
diesen Begriff an.
| | |
| | | | | |
Wenn der Beweis das Vorgehn nach der Regel
registriert, so erzeugt er (dadurch) einen neuen
Begriff.
| | |
| | | | | | Indem er einen
neuen Begriff erzeugt, überzeugt er mich von etwas.
Denn zu dieser Überzeugung ist es wesentlich, daß das
Vorgehn nach diesen immer das gleiche Bild erzeugen
muß. (‘Gleich’ nämlich nach
unsern gewöhnlichen Regeln 195 des Vergleichens &
Kopierens.)
| | |
| | | | | | Damit
hängt es zusammen, daß man sagen kann, der Beweis müsse
das [b|B]estehen einer internen Relation
zeigen. Denn die interne Relation von ist
die Operation, die eine Struktur aus der andern erzeugt ˇals
äquivalent betrachtet
// angeschaut //
angesehen |
mit dem Bild
d⌊i⌋eses Übergangs selbst – so daß nun der
Übergang dieser Bilderreihe gemäß eo ipso ein
Übergang jenen Regeln // Operationsregeln //
gemäß ist.
| | |
| | | | | | Indem der
Beweis einen Begriff erzeugt, überzeugt er mich von
etwas. Das Wovon er mich überzeugt, ist in dem
Satz ausgesprochen, den er bewiesen hat.
| | |
| | | | | | ∣ Problem:
Bedeutet das
“mathematisch” jedesmal das Gleiche:
wenn wir von ‘mathematischen’ Begriffen,
⌊von⌋ ‘mathematischen’ Sätzen
& ⌊von⌋ ‘mathematischen’ Beweisen
reden?| // wenn wir von
‘mathematischen’ Begriffen reden, von
‘mathematischen’ Sätzen & von
196 mathematischen
Beweisen? // |
| | |
| | | | | |
19.4.44. Was hat nun der
bewiesene Satz mit dem Begriff zu tun den der Beweis schuf?
Oder was hat der bewiesene Satz mit der
internen Relation zu tun, die der Beweis demonstrierte?
| | |
| | | | | | Das ist ein Instrument des Überzeugens.
| | |
| | | | | | Es ist klar, man
auch den unbewiesenen math.
Satz anwenden; ja auch den falschen.
Der
math. Satz sagt mir dann:
Verfahre so!
| | |
| | | | | | “Überzeugt
Wenn uns der Beweis überzeugt, dann müssen wir auch von den
Axiomen überzeugt sein“. Nicht
aber als von empirischen Sätzen; das ist ihre
Rolle nicht. Sie sind im Sprachspiel von der
Verification durch die Erfahrung
ausgeschlossen. Sind nicht Erfahrungssätze
sondern Prinzipien des Urteilens. 197
| | |
| | | | | |
Der Beweis überredet mich, so zu verfahren.
Der bewiesene Satz sagt: “verfahre
so!”
| | |
| | | ∕∕ | | | Ein Sprachspiel:
Wie habe ich mir eins vorzustellen, in dem Axiome, Beweise
& bewiesene Sätze auftreten!4
| | |
| | | | | |
Wer in der Schule zum erstenmal
ein bißchen von der Logik hört, der ist sogleich davon
überzeugt, wenn man ihm sagt, ein Satz implizierte sich selbst,
oder wenn er nun den Satz vom Widerspruch
, oder des
ausgeschloßenen Dritten. –
Warum ist er gleich davon überzeugt? Nun, diese
Gesetze passen ganz in den Gebrauch der Sprache, der ihm so
geläufig ist.
Dann lernt er etwa
kompliziertere Sätze der Logik beweisen. Die
Beweise werden ihm [f|v]orgeführt, & er ist
wieder überzeugt; oder er erfindet einen Beweis
selber.
Er lernt so neue Techniken des
Schließens. Und auch, auf welche Rechnung es zu
setzen ist, wenn (nun) Fehler 198 sich zeigen.
| | |
| | | | | | Der Beweis überzeugt ihn, daß
er an dem Satz, an der Technik, die
vorschreibt, festhalten muß; aber er zeigt ihm wie er an dem Satz festhalten kann, ohne Gefahr zu
laufen mit einer Erfahrung in Konflikt zu geraten.
| | |
| | | | | | ∣ Der
Philosoph ist der, der in sich viele Krankheiten des Verstandes heilen
muß, ehe er zu den Notionen des gesunden Menschenverstandes kommen
kann.
| | |
| | | | | | Jeder Beweis in der
angewandten Mathematik kann aufgefaßt werden als ein
Beweis der reinen Mathematik, welcher beweist daß
dieser Satz aus diesen Sätzen folgt, oder aus
ihnen durch die & die Operationen zu erhalten ist;
etc.
| | |
| | | | | | Der Beweis
ist ein bestimmter Gang. Wenn wir ihn
beschreiben, so werden Ursachen nicht genannt.
199
| | |
| | | | | | Ich handle auf den Beweis hin. – Aber wie? – Dem Satz gemäß der
bewiesen wurde.
| | |
| | | | | | Der Beweis hat mich
eine Technik des
Approximierens gelehrt. Aber er hat
doch etwas bewiesen, mich von etwas überzeugt.
Das spricht der Satz aus. Er sagt,
was ich nun auf den Beweis hin tun werde.
| | |
| | | | | | Der Beweis gehört zum Hintergrund des
Satzes. Zum System, in dem der Satz wirkt.
| | |
| | | | | | Sieh', so
geben 3 & 2 5.
Merk Dir diesen
Vorgang!
| | |
| | | | | |
Jeder S Erfahrungssatz kann als Regel dienen
wenn man ihn ˇ– wie einen Maschinenteil – feststellt,
d.h. unbeweglich macht, so daß sich nun
alle Darstellung um ihn dreht & er zu einem Teil des
Coordinatensystems wird &
unabhängig von den Tat-200 sachen.
| | |
| | | | | | “So ist es, wenn dieser Satz aus diesen
abgeleitet wird. Das mußt Du doch
zugeben.” – Was ich zugebe ist, daß ich so
einen Vorgang so nenne.
| | |
| | | ∫ | | |
–
– – Und ist denn diese Reihe nicht
eben durch diese Folge definiert? –
Nicht durch
Folge; aber durch eine Regel; durch die Abrichtung zum
Gebrauch Regel.
| | |
| | | / \ | | | Ich
kann jemand dazu abrichten, einer Regel zu folgen. Und als
Einleitung dazu lehre ich ihn, ˇetwa gewisse
gleichmäßige Tätigkeiten
auszuführen: Z.B. eine
Linie der Art wie diese
–– ∙ ∙ –– ∙ ∙ –– ∙ ∙ –– ∙ ∙ –– ∙ ∙
weiter &
weiter .
201
| | |
| | | | | |
“Die Regel bestimmt, was ich auf jeder Stufe zu schreiben
habe.” Das kann man so auffassen, wie:
“Die Konstruktion des Mechanismus bestimmt die Bewegung
dieses Teils für jede Lage Kurbel ˇdie ihn
antreibt”. Der Mensch ist die Maschine, die mit Hilfe der Regel, des
Befehls, der die Regel enthielt, der Abrichtung im Befolgen von
Befehlen (etc.) gezwungen wurde, auf dieser
Stufe, dies zu schreiben (so zu
handeln).
| | |
| | | | | | “Aber
auch ohne den Zwang des Befehls die Regel doch wie eine endliche, oder
unendliche Vorlage, nach der ich mich richten
kann.” Z.B. wenn
die Regel ist, im Dezimalsystem von einer Kardinalzahl zur
nächsten fortzuschreiten. – Nun, der Ausdruck der
Regel ist entweder ein allgemeiner, etwa algebraischer, oder er ist
etwa ein Stück der Reihe mit dem Und-202 so-weiter. Wie aber
kann man das eine Vorlage nennen eine, die dazu dient diese Zeichen zu
kopierten? ? nach
der wir ein beliebig langes Stück der Reihe
angeschrieben werden kann (Hier ist
es nun so leicht zu denken, daß die
eigentliche Vorlage in unsererm Seele
Geist
existiere. Aber denke daran daß ja diese geistige
Vorla[l|g]e selbst durch Zeichen hervorgerufen werden
mußte; & auch, daß die erst noch in ihre Kopie übersetzt werden
will.) Und wenn sich mein Geist nach den Zeichen
richten konnte, warum dann nicht gleich meine
Hand?)
| | |
| | | | | | ⌊⌊ Nun,
eines ist gewiß: Man kann nach der Regel eine
Zeichenfolge aufschreiben & die als Vorlage
gebrauchen. Und das ist wichtig. ⌋⌋
| | |
| | | | | | Wie führt mich also die Regel?
([e|E]twa
ˇdie Werte von hinzuschreiben, wenn x
die Kardinalzahlen durchläuft.), –
Ich sehe die Regel immer wieder
an, murmle gewisse Rechnungen ˇvor mich hin &
schreibe ˇeine Folge von Zahlen. Ferner: würde
ich Ich gebe Einem der mit meinen Zahlen nicht
einverstanden wäre ist dem, was ich tue, nicht
einleuchtet, gewisse ˇGründe &
Erklärungen geben. Z.B.: “4 folgt
doch auf 3; 203 4 x 4 ist doch 16; etc.“
meines Handelns .
Wie aber, wenn diese
Gründe & Erklärungen niemand
überzeugten? Wenn
[a|A]lle sagten, ich
schriebe ˇdie Zahlen regellos & ohne Rechtfertigung
⌊.⌋ ⌊eine⌋ Zahl auf Zahl hin nach der
andern. Nun, das wäre , wie wenn die Menschen plötzlich
meine Sprache nicht mehr verstünden; Wie wenn ich
etwa eines [m|M]orgens aufwachte & alle Menschen um mich
sprächen eine mir völlig
Sprache & gäben Zeichen des Erstaunens, sobald sie mich
reden hörten. Was würde ich da sagen?
Daß alle Andern ihre Sprache geändert hätten
& die alte vergessen
; oder daß ich
irgendwie närrisch geworden bin meine Sprache
übernacht geändert habe,
oder überhaupt keine Sprache ˇmehr spreche.
ˇNun [E|e]s würde darauf ankommen, ob ich im Stande wäre
ihre Sprache zu lernen & sie meine, oder
ob es jeder Versuch der zu keiner
Verständigung käme. 204
In diesem
Fall ich nicht, was ich
sagen würde. // Was ich in
diesem Falle sagen würde, weiß ich
nicht. // Wie sollte
ich sagen, was wahr ist. Sie würden mich
vielleicht in ein Irrenhaus sperren, & ich
wu daraus zu entrinnen suchen.
Ich kann mir aber vorstellen, daß ich von der Veränderung
so erschüttert wäre, daß ich mich nicht trauen
würde, ein Urteil auszusprechen.
205
| | |
| | | / \ | | |
⌊⌊3.7.44.⌋⌋
“Aber
wie kann mich eine Regel lehren, was ich an dieser Stelle zu tun
habe? – Was immer ich tue, ist doch durch
irgend eine Deutung mit der Regel zu
vereinbaren.” Nein; so sollte es nicht
heißen. Sondern so: “Jede Deutung
hängt, mitsamt dem Gedeuteten, in der Luft & kann
also nicht an
eine[r|m] en Stelle
Platz
festhalten.”
| | |
| | | / \ | | | “Also
ist, was immer ich tue, mit
Regel vereinbar?” – Laß mich
soc fragen: Was hat denn der Ausdruck
der Regel (der Wegweiser z.B.), wieviele
Deutungen immer ich ihm
, mit meinen Handlungen zu tun?
Welche Beziehung besteht denn da überhaupt? – Nun, [e|E]twa die die,: daß
ich ˇbin zu einem bestimmten Reagieren auf diese Zeichen
abgerichtet wurde, & nun ˇich auf sie so
& so ⌊.⌋ reagiere.
206
| | |
| | | / \ | | |
Denn ist klar:
Es ist nicht möglich, daß in der Geschichte der
Menschheit nur einmal ˇnur einer Regel
(einem Wegweiser etwa) gefolgt
.
Es ist auch
nicht unmöglich daß nur nur
einmal ˇnur in der
Geschichte der Menschheit eine Mitteilung gemacht; ein
Befehl gegeben & verstanden, würde oder
ein Gedanke gedacht worden wäre. Und die
Unmöglichkeit ist hier die logische.
Einen Satz ˇaussprechen & verstehen heißt eine
Sprache ˇsprechen & verstehen.
| | |
| | | / \ | | | So
wie es auch unmöglich ist, daß nur einmal in der Geschichte
Menschen ein Spiel gespielt hätten. – Aber ist es
denn undenkbar, daß zwei nur einmal
z⌊w⌋ei Leute sich zu einem Schachbrett gesetzt & eine
Schachpartie gespielt hätten? Es ist natürlich
denkbar, daß diese Leute alle Handlungen einer
Schachpartie 207 vollzogen hätten. Ja,
wenn Du irgend welche Vorgänge &
Zustände für eine Schachpartie wesentlich hältst,
auch diese
stattgehabt haben. Aber mit welchem Recht könnte man
das alles ein Spiel nennen. Es könnte
ebensowohl die ˇzwecklose Handlung zweier Wahnsinniger
sein.
Was wir “Spiel”
nennen ist eine menschliche Gepflogenheit mit einem bestimmten Platz
unter andern menschlichen Gepflogenheiten. Und ebenso ist
das auch die Sprache in allen ihren Formen.
| | |
| | | ∫ | | | Bedenke auch dies.
Ich kann heute ein Spiel erfinden, & das dann
ˇeben nie von mir, oder Andern gespielt wird. –
Wie wäre aber das:
“[d|D]ie
Menschen hätten ˇhaben nie Spiele
gespielt, ˇaber einmal allerdings
zwar ein Mensch ein
Spiel erfunden; es ist dann nicht gespielt 208 worden”?
| | |
| | | ∫ | | | Einer Regel
folgen, das ist analog dem:,⌊,⌋
einem Befehl zu zu folgen.
Auch dazu abgerichtet.
Und nun reagieret ich man auf ihn in bestimmter Weise. Wie aber,
wenn Andere anders der Eine so der Andre anders auf den
Befehl & die Abrichtung reagierent? Wer hat dann Recht?
Wie, wenn [i|I]ch
ˇkäme zu einem fremden Stamm käme &
[e|E]iner gäbe
scheinbar in der mir unbekannten Sprache einen Befehl; seine
Gebärde, Stimme, & die Situation sei etwa
die, daß ich glaube einen Befehl zu hören. legt
es mir nahe es ein Befehl war. ist. Ich höre diese Laute ˇoder
Worte bei verschiedenen Menschen bei verschiedenen
Gelegenheiten im gleichen Ton ausgesprochen, sehe aber keine
Regelmäßigkeit in den Reaktionen ⌊der⌋
[a|A]ndere[r|n], an die die Worte gerichtet werden. Werde
ich sie dann
209 einen Befehl
nennen?
In den Reaktionen auf einen Befehl
muß es Gleichförmigkeit geben.
| | |
| | | / \ | | |
So erkläre ich also, was Befehl & was Regel heißt
durch Gleichförmigkeit also durch
Regelmaßigkeit?!
Wie erkläre ich “gleich”, wie
erkläre ich “regelmäßig”?
Nun, Einem der ˇz.B. Französisch
spricht werde ich diese Worte durch die entsprechende
französischen erklären. Einem aber der, wie wir
sagen könnten, diese Begriffe noch nicht hat, werde ich die Wörter durch
Beispiele & Übung gebrauchen
lehren. Und dabei gebe ich ihm nicht weniger als
ich selbst habe. Ich werde ihm also in diesem Unterricht
gleiche Farben, gleiche Längen, gleiche Gesichter
usw. zeigen;
u.s.w.. Ich werde ihm
‘regelmäßige’ Figuren 210 zeigen, ihn a⌊n⌋leiten,
Figurenreihen regelmäßig fortzusetzen. Etwa eine
Reihe –– ∙ ∙ ∙ –– ∙ ∙ ∙ –– ∙ ∙ ∙ ––
u.s.w.
u.s.w.
Es wird mir
aber vielleicht auch gelingen ihm eine andere Art der
Regelmäßigkeit zu lehren so daß er etwa die Reihe
–– ∙ –– ∙ ∙ –– ∙ ∙ ∙ –– so fortsetzt
–– ∙ ∙ ∙ ∙ –– ∙ ∙ ∙ ∙ ∙ ––
usw.
Ich mach's ihm vor,
er macht es mir nach, & ich verwende Ausdrücke,
Gebärden, der Zufriedenheit, der Unzufriedenheit, der
Erwartung usw..
| | |
| | | / \ | | |
Aber erklärst Du ihm wirklich alles, was Du selbst
verstehst? – Läßt Du ihn nicht
doch die Tendenz Deiner Erklärungen erraten?
Denn Du gibst ihm doch immer nur eine begrenzte
von
Beispielen[.|;][E|e]r aber soll erraten, wie Du sie
meinst, was Deine Absicht ist. – Eine Erklärung,
die ich 211 mir selbst geben kann, gebe ich auch
ihm. – “Er errät, was ich
meine”, hieße, ⌊:⌋ ihm
schweben mehrere Interpretationen vor, & er rät auf eine
von ihnen. Er könnte dann also fragen &
ich könnte & würde ihm antworten.
| | |
| | | / \ | | | Wie
immer Du ihn im Fortsetzen der Reihe
–– ∙ ∙ ∙ –– ∙ ∙ ∙ –– ∙ ∙ ∙ unterrichtest, wie
kann er wissen, wie er sie selbstständig
fortzusetzen hat?
Nun, wie weiß
ich's ˇselber? – Wenn das
heißt⌊:⌋, welche habe ich
Gründe⌊?⌋ kann ich für meine Handlung
angeben habe ich, – so kann ich vielleicht welche angeben, aber
bald werden sie mir ausgehen so ist die Antwort: sie
werden mir bald ausgehen. die Gründe werden mir bald
ausgehen. Und ich werde dann ohne
ˇweitere Gründe handeln.
| | |
| | | / \ | | | Wenn
mir jemand, den ich fürchte, den Befehl gibt, die Reihe die
Reihe –– ∙ –– ∙ ∙ –– ∙ ∙ ∙ –– fortzusetzen, so werde
ich schleunig & mit völliger Sicherheit
&, mit Sicherheit |
, handeln & das
Ausgehen 212 ˇFehlen von der
Gründe⌊n⌋ stört mich nicht.
| | |
| | | / \ | | |
Aber es ist doch klar, daß
Reihenanfang verschieden ˇ(algebraisch) gedeutet werden
konnte, & Du mußtest doch daher eine von diesen
Deutungen wählen! Durchaus nicht. Es war,
unter Umständen, ein (solcher)
Zweifel möglich, aber das heißt nicht, daß ich gezweifelt
habe, oder auch (nur), daß ich zweifeln
konnte.
| | |
| | | / \ | | |
Nur eine
Intuition konnte diesen Zweifel heben? – Wenn sie
eine Art innere Stimme ist
wie weiß ich wie ihr zu folgen ist. Und wie weiß ich,
daß sie mich nicht irreleitet.
| | |
| | | / \ | | |
So sagst Du also, daß die Übereinstimmung der
Menschen , was wahr
richtig & falsch unrichtig ist? –
Richtig & Unrichtig gibt es nur im Denken,
ˇalso im Ausdruck der Gedanken⌊;⌋ der
Menschen
213
& im der
Ausdruck der Gedanken, die Sprache, ist den
Menschen gemeinsam. Er ist eine Lebensform in der sie
übereinstimmen (nicht eine
Meinung).
| | |
| | | / \ | | |
es denn aber
nicht denkbar, daß jeder Mensch nur für sich selbst
dächte, nur zu sich selbst ? (In diesem Fall könnte dann
auch jeder ˇMensch ⌊s⌋eine andere
eigene
Sprache haben.)
Es ist klar:
man wir rede[t|n] mit den Andern,
& man wir rede[t|n] mit sich
uns selb[st|er]
| §
Es gibt Fälle, in welchen wir
sagen, ermahne sich selbst; befehle,
gehorche, bestrafe, tadle, frage & antworte sich
selb[st|er]. Dann es also Menschen geben, die nur
diese Sprachspiele
kennten, die
⌊jed⌋e[i|r]ner mit sich selbst spielt. Ja es wäre
denkbar, daß ein reiches Vokabular
hätten. Wir können uns denken, daß ein
Forscher in 214 das ihr Land
dieser Leute gekommen wäre käme &
beobachtet⌊e⌋, hätte wie wie jeder
ˇvon ihnen seine Tätigkeiten mit
wortähnlichenartigen ˇartikulierten
Laut[rei|en]hen begleitete, sich aber dabei
nicht an Andere we⌊n⌋dete. Der Forscher
k[a|om]m⌊t⌋ irgendwie auf den Gedanken daß diese
Leute Selbstgespräche führ⌊en⌋ten,
belauschte sie bei ihren Tätigkeiten & es
gel[a|i]ng⌊t⌋ ihm eine wahrscheinliche
Übersetzung dieserihrer Reden in unsere Sprache. Er
war ⌊ist⌋ durch das Lernen jener ihrer Sprache
auch ˇmanchmal im ⌊in den⌋ Stande
ˇgesetzt richtig ˇHandlungen vorauszusagen
was welche diese jene ˇdie Leute in
gewissen Fällen in der Zukunft für Handlungen
ˇspäter ausführen w[ü|e]erden,
denn manches was sie sag[t|e]n
sch[ie|ei]nt ˇist der Ausdruck von
ˇVorsätzen & [e|E]ntschlüssen,
zu sein so & so zu handeln oder Vorsätzen,
(wie diese Leute ihre Sprache haben lernen können ist hier
gleichgültig.)
| | |
| | | / \ | | |
Aber wenn nun so ein Mensch sich 215 selbst befielt auf
diesen Baum zu klettern & wenn anderseits ich es mir befehle,
der diesen Befehl nicht nur , sondern
auch Andern geben kann: ist der
Gedanke dieses Befehls in beiden Fällen der
gleiche?
Das kannst Du beantworten, wie Du
willst. Stell dir nur nicht vor, daß der Gedanke
ein Begleitung des Sprechens ist.
Stell Dir das Denken nicht vor wie die
Melodie, die den
Text
die in einem Lied das Sprechen |
den Text, der die Melodie des Lieds
begleitet, sondern eher wie den ‘Ausdruck’ mit
das Lied gesungen
wird.
| | |
| | | ∫ \ | | | Vom
Worte “denken” könnte man sagen, es sei nicht
ein Tätigkeitswort
| | |
| | | / \ | | |
Wenn wir reden oder schreiben (nämlich nicht
gedankenlos) so sind wir im allgemeinen 216 nicht zu sagen wir dächten schneller als wir
sprechen, sondern der Gedanke scheint mit dem Ausdruck zu gehen
solange zu dauern wie
sein Ausdruck |
. ⌊⌊ // sondern der Gedanke erscheint vom Ausdruck nicht
losgelöst abgelöst. // ⌋⌋
Anderseits aber hören wir von der
Blitzes[s|S]chnelle
ungeheuren des Gedankens, wie uns Gedanken
blitzartig durch den Kopf gehen ˇProbleme uns klar werden,
etc. & ähnliches.
Geschieht nun hier dasselbe mit großer
Geschwindigkeit
was beim gewöhnlichen Sprechen langsam
vo⌊r⌋sich geht, sodaß man beim
blitzartigen Denken etwa mit ungeheurer Geschwindigkeit zu
sich selbst ? Ich glaube, das wird man nicht
sagen wollen.
| | |
| | | ∫ | | |
Mozart in einem
berühmten Briefe schreibt, er sähe ein ganzes musikalisches
Werk mit einem Schlage vor seinem Geiste. – Wie ist
das möglich, er hörte ˇer es doch
nicht etwa in rasendem Tempo 217 gespielt seinem geist[i|e]gen Ohre; oder
gar so daß alle Töne gleichzeitig
erkl[i|a]ngen? Und mit welchem Rechte sagte er dann
er habe ein Musikstück im Geiste wahrgenommen?
Wie wußte er, daß ein Musikstück dem entsprach was
er wahrn[e|a]hm.
| | |
| | | / \ | | |
“Diese ganze Lösung sah ich in einem Augenblick vor
mir.” Wie weißt Du daß es das alles war,
was Du sahst? Denn Du sahst Du
es sie gleichsam in der Verkürzung,
ˇaber wie weißt Du, daß es
das war, was Dir in der Verkürzung erschien?
Kannst Du es mir, kannst Du es Dir selbst beweisen? – Aber dies bist Du zu sagen geneigt.
¥ •
| | |
| | | / \ | | |
“Jetzt weiß ich weiter!” ist ein
Ausruf. Ebenso auch (wie
ˇSo auch “Jetzt hab
ich's!, “Jetzt weiß 218 ich's.)
Er [e|E]ntspr[i|e]ch[t|end] einem
Naturlaut, ˇdem Ausdruck einer Art von
der angenehmen Überraschung, auf
welche⌊n⌋ (eine) Entspannung folgt ⌊⌊ˇeinem freudigen, erleichterten
Aufzucken⌋⌋.
| | |
| | | / ∕∕ | | | ↺
Ich kann in demselben Sinn blitzartig einen Gedankengang vor
mir sehen, oder verstehen, wie ich mit Worten, oder Strichen notieren kann.
Was macht diese Notiz zu einer
Zusammenfassung dieses Gedankens? Der Gebrauch, den
ich von ihr mache.
| | |
| | | ∫ | | | ↺ Das
‘erlösende Wort’ ist dieses nur,
kann nur
erlösen, |
weil es sozusagen, der
Schlußstein eines zu einem
Gebäudes ist das letzte noch fehlende Glied in der
Kette ist. [F|f]ür den,
[d|W]er diese Voraussetzungen nicht hat, ist es nicht das erlösende Wort.
| | |
| | | ∫ | | | Wie das Lachen
auf eine[n|m] Witz, so folgt dieser Ausdruck, auf ein
freudiges er-219 leichtertes
Aufzucken ˇ&
etwa die Worte ˇwie “jetzt hab
ich's!“ der ˇgewissen Situationen
de[s|m] Suchens nach einer Lösung. Manchmal ist die
Erscheinung dadurch hervorgerufen, daß wir plötzlich das
fehlende Glied einer Gedankenkette sehen, oder dergleichen.
| | |
| | | ∫ | | |
Daraus, daß es uns erscheint, als wüßten wir nun weiter
(oder dergl.) folgt aber nicht,
daß wir auch wirklich weiter können,
also also nicht wieder
steckenbleiben, wenn wir versuchen weiter zu gehen.
Und [h|H]ier könnte man
nun kann es Fälle unterscheiden
geben, in
denen wir sagen werden: “als ich sagte, ich wisse
weiter, da konnte ich fortsetzen, aber jetzt kann
ich's nicht”. Das werden wir
z.B. sagen wenn ˇwir
inzwischen etwas [u|U]nerwartetes geschehen ist, etwas
das eine Störung, die wir dafür verantwortlich
machen, daß unerwartete Weise gestört worden
sind wurden eine unvorhergesehene Störung
eingetreten ist Aber das
Unvorhergesehene
Unerwartete |
durfte
nicht einfach ˇdas das sein, daß wir
nicht stecken blieben. Es wäre wohl
denkbar, daß [e|E]iner immer 220 wieder solche Scheinerleuchtungen
hätte; also immer wieder ausriefe “Jetzt hab
ich's!” & dies nie durch die Tat rechtfertigen
könnte., weil es ihm scheint ˇEs
sch[ei|ie]n[t|e] ˇihm vielleicht als vergäße er sofort wieder die Bedeutung
des Bildes das ihm vorgeschwebt war hatte. | | |
| | | | | | ⌊⌊ [Alle
diese Sätze sind elend schlecht & ich weiß nicht, ob
ich recht tue, sie aufzuschreiben.] ⌋⌋
| | |
| | | / | | |
Was [u|U]ns interessiert
ist die Tatsache, daß wir unter
Umständen plötzlich die absolute
Sicherheit fühlen, wir könnten einen Gedanken
ausarbeiten ausspinnen // durchführen // ;
ebenso & daß wir
diese uns diese Sicherheit später ˇin schwierigen
Fällen durch die Tat rechtfertigen können. sehr
oft nicht trügt ⌊ // daß wir unter
Umständen sicher sind⌋⌊, wir können
einen Gedanken aus einem Keim desselben
entwickeln. // ⌋ ⌊ // , einen
Gedanken aus einem Keim entwickeln zu
können. // ⌋⌊ // daß wir
uns völlig sicher fühlen, wir werden einen Gedanken aus
einem Keim desselben entwickeln
können. // ⌋
Diese Sicherheit Sie ist ähnlich der, mit
welcher ich weiß daß ich eine werde die &
die Melodie werde fortsetzen können, wenn mir Einer nur
die ersten Takte angibt.
| | |
| | | / \ | | |
Man könnte hier sagen es handle sich eben um Induktion
& ich sei so sicher wie ich es bin, daß dieser Stein zu
[b|B]oden fallen wird, wenn ich ihn auslasse.
Darauf 221 kann man sagen daß man eben auch
zu dieser Sicherheit keine Rechtfertigung braucht. Was
könnte die Sicherheit mehr rechtfertigen als der
Erfolg, oder so sehr rechtfertigen, wie der Erfolg?
| | |
| | | ∫ | | |
Welchen Unterschied macht es, ob meine Sicherheit dem Andern
wohl begründet erscheint, oder nicht?
| | |
| | | ∫ | | | Diese
Betrachtungen werfen ein Licht auf die Grammatik des Wortes “[d|D]enken”, & zeigen daß diese
grundverschieden ist von der der Worte
“reden”, “schreiben”,
etc.
| | |
| | | ∫ | | |
Die Private
Sprache, die ich oben beschrieben habe ist eine
[S|s]olche,
wie sie etwa Robinson auf seiner
Insel hätte mit sich selbst sprechen können.
Hätte ihn jemand belauscht & beobachtet, er hätte
Ro diese Sprache
ˇRobinsons lernen
222 können.
Denn die Bedeutungen der Worte zeigten sich in dem was
Robinson tat
im Verhalten Robinsons.
| | |
| | | / \ | | |
Wäre es aber nicht eine Sprache denkbar in der
Einer für seinen eigenen Gebrauch seine privaten Empfindungen,
seine inneren Erlebnisse ausspricht oder aufschreibt?
Diese Sprache wäre dann natürlich nur für
ihn selbst verständlich, denn niemand als er könnte je
wissen worauf sich die Worte, Zeichen, der Sprache beziehen.
| | |
| | | / \ | | |
Die Frage ist: Wie beziehen sich Wörter
auf Empfindungen. Nun, das
[d|D]arin scheint kein Problem zu liegen; denn reden wir
nicht immer wieder von Empfindungen & benennen
sie? Z.B. Schmerzen aller Art,
Trauer, Freude etc
etc. – Aber wie wird hier die 223 Beziehung eines Namens mit
einer ⌊der⌋ ˇbenannten Beziehung
hergestellt. Denn wir können der Empfindung
jedenfalls keinen Namenszettel ankleben. Nun,
d[er|as] N Wort für die Empfindung wird
mit einem natürlichen Ausdruck der Empfindung verbunden an die
[s|S]telle dieses Ausdrucks gesetzt. Das Kind
hat sich [V|v]erletzt, es schreit, & nun lehren es
die Erwachsenen einen bestimmten Ausruf, Worte, – zuerst
etwa der Kindersprache, später der Sprache der
Erwachsenen.
| | |
| | | / \ | | |
“Sagst Du also, daß das Wort
ursprünglich
d[en|as] Schm Schreien des Schmerzes bedeutet? – Im Gegenteil.
Es ersetzt das Schreien, aber sagt nicht:
“ˇdaß ich ˇ[e|E]iner
schrei[e|t]“. Die Worte “ich
habe Schmerzen” werden zu einem Teil des
Schmerz-Beneh-224 mens; & sagen daher nicht,
daß jemand sich so benimmt. Und so sind alle
Worte sprachlichen Äußerungen der
Empfindungen mit den ursprünglichen
Empfindungsäußerungen verknüpft worden.
| | |
| | | / \ | | |
Inwiefern sind nun meine Empfindungen privat? Nun, nur
ich kann wissen ob ich wirklich Schmerzen
haben; der Andre kann es nur vermuten. –
Das ist einerse⌊i⌋ts falsch, andrerseits
unsinnig. Wenn wir “wissen”
gebrauchen wie es normalerweise gebraucht wird
(& wie, zum Teufel, sollen wir es denn
gebrauchen?) dann wissen es Andre sehr oft, wenn ich
Schmerzen habe. Ja, aber doch nicht mit der Sicherheit, mit
der Du es selbst weißt? – Von mir kann man
überhaupt (außer etwa im Spaß) nicht
sagen: ich wisse, daß ich Schmerzen 225 habe. Was soll es
heißen⌊?⌋ – außer etwa⌊:⌋
daß ich Schmerzen habe?.
Man kannc ˇnicht sagen:
Die die Anderen lernen meine
Empfindungen nur durch mein Benehmen, denn
ich lerne sie über von mir kann
man nicht sagen ich lernte sie. Ich habe
sie. Das ist richtig: es hat Sinn von Andern zu
sagen, sie seien im Zweifel darüber, ob ich Schmerzen habe,
aber nicht, es von mir selbst zu sagen.
| | |
| | | ∫ | | | Und das
ist auch von Bedeutung für die Grammatik der
ˇsprachlichen
Empfindungsaußerungen: Der
Arzt fragt die Schwester “Hat Schmerzen”. Die
Schwester sie antwortet “Er
stöhnt”. Der Patient aber sagt nicht
“Ich stöhne”, sondern er
stöhnt.
| | |
| | | / \\ | | |
Nun zurück zu jener ganz privaten Sprache.
Wie bezeichnet der, der 226 sie zu sich selbst spricht, seine
Empfindungen durch Worte? – So wie wir's
auch tun? Sind also seine Empfindungsworte mit den
natürlichen Empfindungsäußerungen verbunden? – Ja in diesem Falle ist seine Sprache nicht privat. – Aber wie, wenn er gar keine natürlichen
Äußerungen der Empfindung, sondern nur die Empfindung
besitzt? – Nehmen wir einen einfachen Fall
an. Er möge sich eine Art Tagebuch anlegen und seine
Empfindungen durch Zeichen in dieses Buch eintragen.
Und zwar setzt er sich vor eine bestimmte Empfindung durch
ein Kreuz zu vermerken. Wenn er sie also hat,
er zu dem entsprechenden Tag jenes
Zeichen.
| | |
| | | ∕∕ \ | | |
Zuerst muß ich sagen, daß er sich jenen Vorsatz,
also die Definition des Zeichens, weder durch Worte, noch durch
Gebärden, oder Schriftzeichen 227 ausdrücken konnte. – Aber wie ist es nun mit dem Wiedererkennen der
Empfindung? Das ist wohl auch eine Empfindung?
Und wie weiß er, daß sie ihn berechtigt, wieder ein
Kreuz hinzuschreiben? Wie erkennt er die Empfindung des
Wiederkennens?
Soll
ich sagen: er trägt ein Kreuz in's Tagebuch ein,
wenn er glaubt die gleiche Empfindung, wie damals als er ihr
den Namen gab, zu haben? Oder soll es heißen:
wenn er dies zu glauben glaubt? Und
[m|M]it
welchem Recht reden wir hier von ‘gleich’,
von ‘Empfindung’,
‘wiedererkennen’ &
‘glauben’? Denn das sind ja alles
Wörter unsrer allgemeinen Sprache.
| | |
| | | ∫ | | | Er hat ja eben
kein Kriterium der Gleichheit! – Aber wenn
er's nicht hat, dann haben wir's ja auch nicht
& doch reden wir von gleichen Empfindungen. –
Ja, 228 aber wir brauchen ˇhier kein
Kriterium⌊;⌋ sow der Gleichheit
sowenig wie eines dafür, daß wir
Schmerzen haben. Denn wir in unsrer Sprache benützen
die Äußerung des Schmerzes. Und wir
benutzen sie zu verschiedenen Zwecken.
Während ˇwir vorgaben, daß jener ˇMensch in
seiner privaten Sprache die Empfindungen benennt wie
Dinge benennt, die er in einem Guckkasten sieht
in den nur er alle⌊i⌋n schauen kann.
| | |
| | | | | | “Du sagst also, daß, wer
hofft, glaubt, fürchtet, erwartet, das & das sei der
Fall, werde eintreten, etc., ˇbewege,
ˇdaß sich der sich in ˇinnerhalb einer
Denktechnik bewegt, & daß
ˇes außerhalb einer solchen, & also
außerhalb einer Gepflogenheit, kein Denken gibt;
ˇebensoso wenig ˇkein Sprechen
außerhalb einer Sprache⌊.⌋ kein Sprechen.
(Plato nennt die Hoffnung eine
Rede.) Aber ich weiß es doch
unmittelbarcˇ, es ist mir doch unmittelbar
klar, daß ich (ˇz.B.) etwas
hoffen kann,
229 ganz unabhängig
davon, ob ich früher schon einmal etwas gehofft oder gedacht
habe. Es ist mir ganz klar, daß der Akt des
Hoffens einzeln, für sich, existieren kann, logisch
unabhängig von [f|F]rüheren oder
[s|S]päteren Akten.” – Wenn Du hier
(& noch in vielen andern Fällen) statt “es ist mir
klar” sag⌊t⌋est sagst: “ich bin geneigt,
das zu sagen ⌊ …⌋”, so
stimme⌊n⌋ ich wir überein[.|;]
[D|d]enn
auch ich bin oft geneigt ˇgerade zu sagen.
| | |
| | | / \ | | |
Wir sagen, der Hund fürchtet, er werde geschlagen werden, er
erwartet, daß ihm sein Futter gegeben wird.
sein Futter werde ihm gegeben werden. |
Aber wir
werden nicht sagen: er , sein Herr werde ihn morgen schlagen,
warum nicht? oder, sein Futter werde ihm
nicht schmecken⌊,⌋ ˇwie sonst. Warum
nicht?
| | |
| | | ∫ | | | Ich denke den
ganzen Tag an ihn. Was immer da in meiner Seele vorgeht
– was hat es mit 230 ihm zu tun? – Ich habe ein Bild von ihm vor meinem geistigen
Auge? Wie weiß ich, daß es sein Bild
ist? Und wenn dies [b|B]ild
einem Andern ähnlicher sieht als meinem Freund, denke ich da an
den Andern? Nein,
[s|S]o kann
es nicht sein. Die Frage “wie weiß
ich, daß es sein Bild ist, das mir
vorschwebte” hieß gar nichts, sowenig wie
die⌊:⌋ Frage “wie weiß ich daß er es ist
⌊an⌋ den ich denke?”. – Und wenn
ich seinen Namen ausspreche,
so könnte man auch nicht fragen: ‘wie weißt Du,
daß Du diesen Menschen meinst & nicht einen andern gleichen
Namens?” Und das kommt nicht daher, daß
zwischen dem Namen [den|wenn]
wenn ich ˇihn ausspreche & jener Person eine
seltsame ˇunsichtbare Verbindung
, die
ich dadurch mache nämlich, daß ich ihn
meine. Die wirkliche Verbindung 231 zwischen dem, was ich sage ˇoder
sonst tue & der Person von der ich rede ˇan die ich
denke, besteht in der Geschichte, in den Ereignissen die meinem Denken
vorangegangen sind.
| | |
| | | ∕∕ \ | | |
Ich denke in dem selben Sinne an ihn, wie ich von
ihm rede.
| | |
| | | ∫ / \ | | |
Ich habe gehofft er werde mich heute nachmittag besuchen ˇund
mir Geld bringen. Das hatte eine
Vorgeschichte. – Nachmittags ˇnun
blieb ich zu Hause; bereitete dies & das für ihn vor;
dachte oft an ihn; wenn ich die ⌊Haus⌋
[T|t]ür
gehn hörte horchte ich auf, fragte, wer gekommen sei,
u.s.w. Ich tat,
unterließ, dachte & sagte
verschiedenes meine
Stimmung wechselte dabei in bestimmter
Weise. Das ist das Bild, die Erscheinung, des Hoffens auf
dieses Ereignis. Der Zusammenhang ˇalles dessen
was ich tue, unterlasse, sage, denke, fühle mit diesem
Menschen ist ein 232 geschichtlicher. Reden,
Gedanken sind ein wichtiger Bestandteil meines Hoffens.
(Das Wort ‘Bestandteil’ könnte uns hier
leicht irreführen.)
| | |
| | | / \ | | |
Ich werde aber vielleicht, während ich so meinen Freund
erwarte, zu jemandem sagen: “ich hoffe
N.N. wird kommen”. Wenn ich
das sage, ist das nun eine Beschreibung der Gedanken & der
Handlungen, ich früher sprach die
Rede war? die ich vorhin erwähnt
habe? Nein; es ist ein Ausdruck des Hoffens.
⌊⌊ˇ Sage ich aber
“[i|I]ch
hoffe den ganzen Tag, er werde kommen”, so ist das eine
allgemeine Beschreibung meines Handelns &
Fühlens. ⌋⌋
| | |
| | | / \ | | |
Ein Beispiel, das die Grammatik Wörtern wie “hoffen”,
“glauben”, “meinen” klarer machen
kann: Der Ausdruck “Ich grüße
Dich” kann in einer Sprache ein Gruß sein;
“[i|I]ch
habe Dich gegrüßt” aber ein
Bericht.
| | |
| | | / \ | | |
Aber wenn ich nun in meinem Zimmer sitze & hoffe
N.N. werde kommen & mir 233 Geld bringen, & eine
Minute die Minute dieses Hoffens könnte isoliert,
aus ihrem Zusammenhang herausgeschnitten, werden:
wäre es dann // : wäre, was in dieser Minute geschieht
dann // kein Hoffen? – Aber nun
sind ja alle Verbindungen durchschnitten // & alle Zeichen, die in
dieser Minute gebraucht werden haben ihre Bedeutung
verloren. //
& was immer in
dieser Minute geschieht, hat seine Bedeutung
verloren. |
| | |
| | | ∕∕ \ | | |
Nur so ist die Frage zur Ruhe zu
bringen: “[w|W]ie weiß ich ˇwie kann ich wissen, was ich
erwarte oder wünsche ehe es eingetreten ist?”
Beziehung hat ein Zustand meiner Seele zu Dingen &
Ereignissen // Was für eine Beziehung
muß dazu zwischen einem Zustand
mein
Zuständen |
meiner Seele
& ⌊den⌋ Dingen & Ereignissen
bestehen? Ist es eine Erfahrungstatsache daß
der & der Zustand Geisteszustand dieser Zustand meiner Seele
eine Erwartung dieses Ereignisses ist?
| | |
| | | ∫ / | | |
Ja weiß ich denn, was ich wünsche, ehe
ich der Wunsch erfüllt ist? Wenn das
heißt 234 “Kann ich's
sagen?”, so ist die Antwort im allgemeinen
“ja”. Ist nun “Ich
möchte ein Glas Wein trinken” der Ausdruck
einer Meinung? Im
allgemeinen
nein! So wenig, wie die Worte “Wein
her!”, oder der Ruf “Hilfe”,
wenn ich in's Wasser falle. Wünschen
heißt nicht: glauben das & das werde
mi[c|r]h befriedigen, wohltun.
(ˇIch sage “mich“ im Gegensatz zu
nicht “meinen Wunsch“.)⌊.⌋
Auch wäre das ein
irreführender Vergleich: Was Das
ich ⌊[g|G]e⌋wünsch⌊t⌋e
paßt in irgendeinem Sinne zu⌊m⌋ meinem
Zustand des
W[ü|u]nsche[ns|es]. Und wie ich, eine
Schraube in eine Mutter drehe um zu sehen, ob sie
, so muß ich ˇzu dem
ähnlichen Zweck den Wunsch & die
Erfüllung zusammenhalten. Soll dieser Vergleich nicht
irreführend, sein so müßte man sagen: Wenn
ein kreisförmiges Loch von 2 cm
Durchmesser hat, so weiß ich damit schon, daß ein runder Bolzen
von 2 cm Durchmesser 235 hineinpassen wird.
| | |
| | | ∫ / \ ? | | |
Aber Deine Auffassung scheint dem geistigen
Vorgang, ⌊–⌋ der Hoffnung, dem
Wunsch etc – in der
[z|Z]eit in welcher er meinen Geist einnimmt Kraft & Bedeutung zu nehmen.
| | |
| | | / \ | | |
Worin liegt denn die Macht & Bedeutung des
Hoffens? Nicht in seinem
ihren
Äußerungen? – |
// Nicht darin,
wie es sich im Leben des Hoffenden
ausdrückt? // Die Hoffnung als
Leitstern.
| | |
| | | ∫ / | | | |
Hier könnte vom Gedankenstrom, die Rede sein von
dem James redet, gesprochen werden & man könnte darauf
hinweisen daß, so wie ein mir wohlbekannter Name genannt
wird, meine Gedanken sich gleich in eine Reihe von Kanäle
ergießen & in ihnen weiterlaufen & daß die
Bedeutung des Namens sich 236 gleich in diesen Strömen
offenbart.
| | |
| | | ∫ / | | |
Man
könnte das auch so sagen: Dieser Name
könnte freilich eine Menge Menschen bezeichnen, wen ich aber
meine, das zeigt sich in den Strömungen, die
von dem Namen ausgehen.
| | |
| | | ∫ | | |
Und hier haben
wir eine Erfahrungstatsache, während
James nur scheinbar von einer
solchen redet in Wirklichkeit aber um die Erfahrungstatsachen herum
geht & eine eine metaphysische Bemerkung
macht.
Es ist als wenn
[e|E]iner von den
Erfahrungen reden , aber immer
ausgleitet & nur eine Art Ausruf herausbringt statt
eines Satzes.
| | |
| | | / ∫ | | | Er
sollte uns sagen, was geschieht, & sagt statt dessen nur, was
geschehen muß. 237
| | |
| | | / ∫ | | | Er will
eine Erfahrungstatsache mitteilen, rutscht aber aus &
macht eine metaphysische
Bemerkung. // // ,
rutscht aber aus & sagt etwas
Metaphysisches. //
| | |
| | | ∫ | | | Die Worte
“ich meine den, der …” sind eine solche
Strömung, die von dem Namen ausgeht.
| | |
| | | ∫ | | | Es war, als ob
die Empfindungen Dinge in einem Guckkasten wären in welchen nur
ich im Stande bin allein schauen kann. –
Aber ist das nicht wirklich beinahe so im Falle der optischen
Nachbilder. Ist es denn nicht gleichgültig, ob ich die
Augen schließe um etwas zu sehen, oder ˇob ich dazu
in ein durch ein Loch in einen Kasten
schaue?
| | |
| | | ∫ | | | Wer sagt
“[e|E]s
hat jetzt aufgehört zu schneien”, dem man doch 238 nicht: Das ist nur leeres
Gerede”; wohl aber , der sagt
“Ich hoffe vom ganzen Herzen,
daß Du wirst gesund
bleib[st|en].” …” Am Ausdruck der Stimme ist
⌊es⌋ nicht zu erkennen, ob es wirklich nicht mehr
schneit.
| | |
| | | ∕∕ \ | | |
Unter welchen Umständen werde ich sagen ein Stamm habe einen
Häuptling? Und der Häuptling
muß doch Bewußtsein haben. Er darf doch
nicht ohne Bewußtsein sein!
| | |
| | | ∕∕ \ | | |
Aber kommt, was Du sagst, nicht doch darauf hinaus, daß es
kein ohne Schmerzbenehmen ˇauch keinen Schmerz
gibt? // , daß es keinen Schmerz ohne
Schmerzbenehmen? // –
Es kommt darauf hinaus, zu sagen, daß man
ˇkönne nur vom lebenden Menschen, oder dem, was ihm
ähnlich ist (sich ähnlich benimmt) sagen
kann es habe
Empfindungen, sehe, sei blind, höre, sei taub, sei bei Bewußtsein
oder bewußtlos.
wache,
oder sei bewußtlos, etc. |
239 // es habe Empfindungen;
sehe; sei blind; sei bei Bewußtsein, oder bewußtlos
etc. //
| | |
| | | / \ | | |
Aber im Märchen kann doch auch der Topf sehen &
hören! – ( aber er kann auch sprechen.)
Das Märchen erdichtet aber doch nur was
nicht der Fall ist [&| es] spricht ˇdoch
nicht Unsinn! // Aber das Märchen
spricht doch nur Unwahrheit; aber nicht
Unsinn! // Das ist so einfach
nicht. Ist es Unwahrheit, oder Unsinn zu sagen,
Topf rede? Macht man sich ein
klares Bild davon, unter welchen Umständen wir von einem Topf
sagen würden, er rede? (Auch ein Unsinngedicht
ist nicht Unsinn wie ˇz.B. das Lallen
eines Kindes.)
| | |
| | | ∫ | | | Ein Kind, im Spiel, kann ein
Stück Holz streicheln, verbinden, ihm zureden, oder sagen, es
habe Schmerzen.
240
| | |
| | | | | | Aber
es gibt doch auch Fälle in denen , & nicht im Spiel, etwa in
magischen, oder religiösen Verrichtungen, leblose Dinge
behandeln, als wären sie lebendige!
| | |
| | | ∕∕ \ | | |
Aber wie,
wenn ich, während ich der Schmerzen
hätte // habe // zu Stein erstarrte.
Könnte ich ni der Schmerzzustand nicht
weiter
bestehen?
fortfahren? |
Währen es nicht mehr
Schmerzen, wenn ich die Fähigkeit verloren hätte
sie auszudrücken? –
S Der Stein hat
diese Schmerzen nicht.
Du
müßtest eigentlich von Deinen Schmerzen sagen, es sei nur bis
jetzt immer so gewesen, daß ein Mensch sie hatte, oder
sogar, daß etwas sie hatte. (Und das
heißt eigentlich nur ihr
eigentlicher Ausdruck der
unartikulierte Laut ein Ausruf.)
| | |
| | | ∫ | | | Was ich gesagt
habe, könnte Einer 241 als den Beweis davon
, daß es Sinn hat zu sagen, ein
Stein habe Schmerzen; daß man nicht wissen könne, ob er
Schmerzen hat; ja das Schmerzen ohne einen Leib, oder überhaupt
ohne (einen) Träger existieren
können. Wenn man dumm genug ist, kann man
allerlei Schlüsse
ziehen.
| | |
| | | ? / | | | Nun ist
es aber sehr merkwürdig, daß ich sagen will, wenn ich zu
Stein geworden sei, können meine Schmerzen (die Schmerzen die
ich jetzt habe) fortdauern. // fortbestehen //
Woher nehme ich das nur?!
Nun,
daher, daß ich mir denken kann, ich öffne meine Augen
& finde daß mein Körper gegen die Berührung eines
Andern ganz unempfindlich ist; daß ein Andrer ein Stück von
meinem Bein abschlagen kann & ich es nur sehe, aber nicht
fühle, daß ich etwa fühle, ich mache Bewegungen, aber
242 keine Bewegung gewahre
usf.. Ja, ich könnte mir so
vorstellen, daß man meinen Körper (mitsamt dem Kopf)
wegtrüge & mein Gesichtsfeld sich nicht änderte,
außer daß ich ˇLeute meinen Körper wegtragen
sehe. // außer daß mein Körper aus ihm
entfernt wurde worden ist. // Und
wäre es nun nicht sogar möglich daß ich mich sprechen
fühlte & sprechen hörte?
Aber hat es Sinn, wenn ich
ann[ä|e]hm⌊e⌋, vor mir im Raum gebe es ein
unkörperliches Wesen, da[ß|s] mich ohne Augen
sieht, ohne Ohren hört etc;
& zwar so sieht, als wären seine Augen an einer
bestimmten Stelle des Raumes.
Es ist doch zu seltsam, daß ich legitimerweise zu solchen
Schlüssen soll gelangen können!
| | |
| | | ∕∕ \\ | | |
Schau auf einen Ziegelstein Stein
⌊an⌋ & denk Dir er alle Empfindungen. Man sagt
sich: wie konnte 243 man auch nur auf die Idee kommen
einem Ding eine Empfindung
zuzuschreiben? Man könnte sie ebensogut einer Zahl
zuschreiben. – Und nun schau auf eine zappelnde Fliege
& sofort ist diese Schwierigkeit verschwunden
& der Schmerz scheint (nun) einen Angriffspunkt zu
haben, wo früher alles gegen ihn glatt war & er nirgends
anhaften konnte. // & der Schmerz
scheint hier angreifen zu können, wo früher alles ˇgegen
ihn sozusagen glatt war. //
Und so scheint es auch, wenn wir von einem Leichnam sagten, er habe
Schmerzen, daß wir es absurderweise von einem Körper
sagten; aber nicht wenn wir's vom
[L|l]ebenden ˇWesen sagen⌊.⌋ weil
Denn es da scheint ⌊da⌋ als sagten wir
es von etwas Ungreifbarem, vom Leben selbst.
Unsre Einstellung zum Lebenden ist ganz
& gar verschieden von der zum Toten. // Unsere Einstellung 244 zum Lebenden & ˇunsre
Einstellung zum Toten sind verschieden. // ⌊⌊ // Unsere Einstellung zum Lebenden ist nicht
die zum Toten. // ⌋⌋
(Übergang von der Quantität zur
Qualität.) Das ist als ein Faktum
.
Alle unsere Reaktionen sind
. Wenn Du
sagst,: ⌊“⌋[d|D]as kann nicht einfach
daran liegen
darauf beruhen |
daß das Lebendige sich
so & so bewegt & das Tote nicht”, so will ich Dir bedeuten
so
könnte ich sagen |
,
◇◇◇ es sei hier ein Fall des Übergangs von der
Quantität zur Qualität.
| | |
| | | ∕∕ \ | | |
(Denke an das Erkennen des Gesichtsausdruckes, die
Beschreibung des Gesichtsausdruckes die nicht darin besteht
daß man die Maße des Gesichts angibt. Denke
auch daran wie man das Gesicht eines Andern ohne das eigene im Spiegel
zu sehen nachahmen kann.)
| | |
| | | ∕∕ \ | | |
Man kann wirklich sagen: der beseelte Körper
hat [s|S]chmerzen. Und 245 ob ein Körper beseelt ist,
das nimmt man durch die Sinne wahr. // ist, das
sieht man. //
| | |
| | | ∕∕ \ | | |
Ich erstarre zu einem Stein & meine Schmerzen dauern
an. –
Und wenn ich mich nun irrte
& es nicht mehr Schmerzen wären! – Aber ich kann mich doch hier nicht irren – es
heißt doch nichts, zu zweifeln, ob ich Schmerzen habe! – D.h., wenn Einer sagte
“Ich weiß nicht, ist das ein Schmerz, was ich habe;
oder ist es etwas anderes?”, so würden wir
uns etwa denken, er wisse nicht, was das Wort
“Schmerz” bedeutet & wir
würden's ihm nun erklären. –
Wie? – Vielleicht durch Gebärden, oder indem
wir ihn stechen & sagen “Siehst Du, das ist
Schmerz”. Er könnte diese Worterklärung,
wie jede andre, richtig, falsch, oder gar nicht
verstehen[; &|. Und] welches er tut, wird er im Gebrauch des
246 Wortes zeigen, wie
auch sonst auch. – Wenn er nun
z.B. sagte “Oh, ich weiß, was
‘Schmerz’ heißt, aber ob das Schmerzen
sind, was ich jetzt hier habe, das weiß ich nicht” –
da würden wir bloß die Köpfe schütteln &
müßten seine Worte für eine seltsame Reaktion ansehen,
mit der wir nichts anzufangen wissen.
| | |
| | | / \ | | |
(Ähnlich, wie wenn jemand im Enst sagte:
“Ich erinnere mich deutlich, drei Jahre vor meiner
Geburt geglaubt zu haben, …”.)
| | |
| | | ∕∕ \ | | |
Ein Ausdruck des Zweifels gehört hnicht zu
diesem Sprachspiel. – Aber wenn nun der Ausdruck des
Schmerzes, das Schmerzbenehmen, ausgeschlossen ist,
dann scheint es, ich dürfe wieder zweifeln.
Der Satz “Wenn ich mich nun irrte
& es gar nicht Schmerzen wären” ist Unsinn, weil
ein Kriterium der Identität der 247 Empfindung vorgespielt wird, das es
gar nicht gibt. (Ähnlich, wie im
Satz: “Ein Anderer kann nicht diese
identischen Schmerzen haben, die ich jetzt
habe”.) Aber daß ich hier versucht bin zu
sagen, man könne die Empfindungen für anderes halten, als was sie ist, kommt daher:
Wenn ich das Sprachspiel mit dem Ausdruck der Empfindung
abgeschafft denke, brauche ich nun ein Kriterium der Identität
für sie, & ˇhätte ich das dann besteht
(auch) die Möglichkeit des Irrtums.
[◇◇◇]
| | |
| | | | | | ⌊⌊ Es mußte doch da gerechnet werden,
& ist gerechnet worden. Denn er weiß,
daß, & wie, er gerechnet hat, & das richtige
Resultat wäre ohne Rechnung nicht erklärbar.⌋⌋
⌊⌊Wie aber, wenn ich sagte: Es kommt ihm
vor er habe gerechnet &⌋⌋ ⌊⌊ warum soll
ˇsich das richtige Resultat erklären
lassen?⌋⌋ ⌊⌊Ist es nicht
unverständlich⌋⌋⌊⌊ genug, daß er ohne ein Wort oder ein
Schriftzeichen rechnen konnte?⌋⌋
| | |
| | | ∫ \ | | |
Ist es in meiner
Macht, die philosophischen Schmerzen der Welt zu
heilen? Nein.
| | |
| | | | | |
Die Vielheit der philosophischen Fragen ist, in gewissem
Sinne, etwas beruhigendes(.
| | |
| | | ∕∕ / \ | | |
Du machst eine Berechnung im Kopf. Das
Resu Ergebnis verwendest Du im Bau einer
Brücke, oder Maschine. Du 248 willst doch nicht sagen, daß diese
Zahl nicht eigentlich durch Rechnen erhalten wurde! daß sie
[d|D]ir, ˇetwa
nach einer Art Träumerei, in den Schoß ! ⌊⌊Willst Du sagen, er habe die Zahl
eigentlich ohne Berechnung gefunden? Sie sei
ihm etwa, nach einer Art Träumerei, in den Schoß
gefallen?⌋⌋ Es mußte doch
doch da gerechnet werden! Wie anders wäre
die Richtigkeit der Zahl zu verstehen? –
“Es mußte da gerechnet werden” heißt
etwas ähnliches wie: es mußte ˇdoch da eine
Rechenmaschine am
Werke sein, (ob
ich sie wahrnehme, oder nicht), – weil ohne diese das
Ergebnis nicht verständlich wäre. –
ich nicht
antworten: “Was
macht es, wenn es nicht verständlich
ist?”
“Muß es denn
verständlich sein?” |
. (Wer sagt,
daß wir uns nicht angewöhnen sollen, anders zu
denken?)
Und wenn Du nun umgekehrt
sprächest: “Daß das Resultat das gleiche
ist, wie das einer Rechnung, läßt uns sagen, daß wir im
Kopf gerechnet haben”? ⌊ Nein; dies
könnte man eher sagen, wenn wir im
“Unbewußten” gerechnet hätten. ⌋
| | |
| | | / | | |
Statt etwas zu hypostasiren, stelle 249 Deine fest, zu tun
& erkläre sie. ⌊⌊ // Statt zu hypostasieren, stell fest,
daß Du die Neigung hast, es zu tun; // “stell fest, daß Du dazu die Neigung
hast; // & nun erkläre diese
Neigung. // ⌋⌋
| | |
| | | ∕∕ \ | | |
Ist das
Rechnen im Kopf in gewissem Sinne unwirklicher als das auf dem
Papier? Es ist das wirkliche – Rechnen im
Kopf. – Ist es ähnlich dem Rechnen auf dem
Papier? – Ist ein ˇweißes
Papier mit schwarzen Strichen darauf einem Menschen
ähnlich?
einem menschlichen
Kopf ähnlich? |
– im Kopfrechnen, etwas den einzelnen
Zeichen des Sc schriftlichen Rechnens
[e|E]ntsprechendes? – Manchmal ja. – Was ist dem entspricht
dem ˇin ihm im Kopfrechnen
einem Schriftzeichen? – Die Vorstellung
vo[n|m] ihm Zeichen, oder vielleicht vom entsprechenden
. –
Welches ist die Vorstellung vom Zeichen “2”,
z.B.? – Das ist keine
Frage. – Wie weiß ich denn, daß Einer
sich das Zeichen “2” vorstellt? – Diese Frage zu beantworten ist zu langwierig. – Wie weiß ichc, daß ich mir
das Zeichen vorstelle? – Von einem
[w|W]issen kann nicht die Rede
sein. 250
| | |
| | | ∕∕ \ | | |
Ist das Rechnen im Kopf irgen
unwirklicher, als das Rechnen auf dem Papier? –
Man ist vielleicht geneigt, so etwas zu sagen; (man)
kann sich aber auch dazu bringen, das Gegenteil zu
, indem man sich
sagt, ‘Papier’, ‘Tinte’,
etc. seien nur logische Konstruktionen. kann sich aber auch zur entgegengesetzten Ansicht bringen, indem
man … Es handelt sichc
da um eine falsche Auffassung von der Funktion der Sprache,
& ihrem Verhältnis zu einer
… entspricht.
–
dem Verhältnis der
Sprache zu einer Wirklichkeit, die ihr entspricht, & von der
Funktion der Sprache. – |
“Ich habe die Multiplikation … im
Kopfe ausgeführt”. Glaube ich
etwa Aussage nicht?! – Aber war es wirklich eine
Multiplikation? – Es war diese
Multiplikation – im Kopfe. – Dies ist der
Punkt, an dem ich irre gehe. Denn ich will jetzt
sagen: Es war eine
Multiplikation; ,
ˇirgendein dem
Multiplizieren auf dem Papier entsprechender Vorgang im
Geiste. Sodaß es also Sinn hätte zu sagen:
“Dieser Vorgang im Geiste entspricht
diesem Vorgang auf 251 dem Papier”. Und
es hätte dann Sinn von einer Projektionsmethode
einem Gesetz der Abbildung zu sprechen, nach
welcherm
die Vorstellung von “2” das Schriftzeichen selbst
. Und hier gerät man
(nun) in den Sumpf der Idee von den privaten
Erlebnissen & der privaten [b|B]edeutung
unsrer Worte.
| | |
| | | ∫ / | | | Ist das
Subjective, oder das Objektive wirklicher? – Unsinn! – Läßt sich nur
das Objektive durch die Sprache darstellen? , nicht das Subjektive? – Aber wir
reden ja vom Subjektiven! Und was wir
darüber im [ä|a]lltäglichen Leben
sagen ist in Ordnung, wie es ist & braucht sowenig einer
Richtigstellung durch den Philosophen, wie die Aussagen
über Stühle & Tische. Eines nur
ist zu betonen:
muß betont werden: |
daß die Grammatik der Sätze von den subjektiven
Gegenständen nicht die gleiche ist, wie die der
Sätze von den objektiven Gegenständen.
Oder, was 252 dasselbe heißt: die
Sprachspiele sind verschieden.
| | |
| | | ∕∕ \ | | |
Wäre es denkbar, daß Einer im Kopfe rechnen lernte, ohne je
schriftlich, oder
mündlich
sprechend, oder schreibend |
zu rechnen? Nun, warum
nicht? ‘Es lernen’, heißt doch
nur dazu gebracht werden, daß man's kann.
Und doch Aber könnte man dazu
abgerichtet werden? – Es könnte uns
doch einer Rechnungen schriftlich vormachen, &
& wir sie ˇaber würden nie
nachschreiben welcheˇ, oder
aussprechen: aber nach & nach dazu
[kommen|kämen] kämen wir dahin, einige Zeit
darauf nach [v|V]erlauf einer Denkpause
das richtige Resultat ˇohne Fehler hinzuschreiben.
auszusprechen, wenn wir einige Zeit nachgedacht haben
hätten.
| | |
| | | / \ | | |
Ist aber auch dies möglich, daß einem Volk nur das
Kopfrechnen bekannt ist & kein anderes? Wie wird
das aussehen?
| | |
| | | / | | | Könnte es
nicht ein merkwürdiges 253 Erinnerungsphänomen geben:
Einer sagt: “Ich habe die
gräßlichsten Schmerzen Tag & Nacht” –
dabei hat er immer die Empfindung als hätten sie jetzt soeben
nachgelassen. Er glaubt, sich immer daran
zu erinnern, daß er sie hatte.
| | |
| | | ? \ | | | Wenn
ich die Sprache beschreibe, so beschreibe ich die Handlungsweise
der Menschen –
sozusagen ethnologisch.
– ethnologisch gesehen. |
Das Wort
“I “ich” ist ein Wort
unter vielen & wird auch von jederman
gebraucht. Und ich schreibe für mich nicht
mehr, als für meinen Leser.
| | |
| | | ∫ | | | Das Sprachspiel
mit den Ausdrücken der Empfindung ‘in erster
Linie’ mit Lebendem gespielt; ‘in zweiter
Linie’ mit Leblosem.
| | |
| | | ∫ | | | Ich sage, ich
beschreibe den Gebrauch des Wortes “Schmerz”,
z.B.. 254 Das könnte man sich so
denken: ich beschreibe Scenen, in
denen das Wort “Schmerz” gebraucht wird.
Ich könnte mir diese Scenen auch
vorgeführt denken. (Etwa eine
Scene im Spital; ich höre, was der Kranke
sagt, was der Arzt ihm, & was er der Schwester
sagt,. etc. ˇAuch [e|E]ine
Scene auch, die zeigt, wie das Kind dies
Wort kennen & gebrauchen lernt; & wie
Wort dann im Spiel mit Puppen
etc. gebraucht wird.
Etc. etc..)
Auch der Philosoph müßte vorgeführt werden, der
über Begriff redet.
Aber solche Scenen
vorführen ist doch Beschreibung
geben. Wie wissen wir denn, worauf, in diesen
Scenen, wir zu achten
haben,⌊?⌋ was Was sollen wir aus ihnen
lernen? Wir könnten natürlich die Sprache
dieser Leute lernen. Aber die kennen wir so wie so.
Eines ist klar: Es hieße nichts,
ˇin diesen Scenen Leute vorzuführen,
die allem Anscheine 255 nach keine Schmerzen haben &
von denen auch sonst nicht irgendwie gezeigt wird, daß sie
Schmerzen verbeißen. D.h. der
Fall, der doch vorkommt, daß ich auf der Straße gehe &
Schmerzen habe & niemand es weiß, oder je erfährt, der
läßt sich so nicht zeigen. – Freilich
nicht[; a|. A]ber es werden ja Leute Menschen
vorgeführt, die sagen: “N.N.
zeigt es nicht, wenn er Schmerzen hat. Er lacht jetzt und
scherzt, aber man kann nie wissen, wie er sich
fühlt”. Und es wird auch gezeigt, von was
für Menschen wir so etwas sagen, & daß
wirs nicht von allen Leuten sagen.
| | |
| | | / \ | | |
Wie aber, wenn es ein Volk gäbe, das nicht sagt
“Es geht dem N.
ausgezeichnet“, sondern ˇstatt dessen
immer: “Man kann natürlich nicht wissen, ob
er ˇnicht fürchterliche Schmerzen hat
leidet – aber es scheint,
⌊es⌋ ˇgeht ihm ausgezeichnet⌊.⌋
⌊“⌋zu gehen“. aber allem Anschein nach
geht es ihm ausgezeichnet. Durch welches Verhalten
Wie |
würde dieser
Vordersatz Einleitung zur ‘bloßen 256 Redensart’?
| | |
| | | ∕∕ \ | | |
Wenn ich von mir selbst sage, ich wisse nur von meinem eigenen
Falle, was das Wort “Schmerz” bedeutet, muß ich
das nicht auch von Andern
sagen? Und wie kann ich Fall in so unverantwortlicher Weise
verallgemeinern? // den einen einzigen Fall
…
Noch dazu, wo
ich nicht die geringste habe, die mir zeigte Noch dazu ohne die geringste Führung, die mir
zeigte, wie ich ihn zu verallgemeinern
habe soll.
Nun, ein jeder
sagt es mir von sich, er wisse nur von sich selbst, was Schmerzen
seien! – Angenommen es hätte jeder eine
Schachtel, darin wäre etwas, was wir
“Käfer” nennen. Niemand kann
je in die Schachtel des Andern schauen, & jeder
sagte er wisse nur vom
Anblick seines Käfers, was ein Käfer ist.
Da könnte es ja sein, daß jeder ein anderes Ding in seiner
Schachtel hätte. Ja 257 man könnte sich vorstellen,
daß sich das Ding in einer Schachtel fortwährend
veränderte. – Aber wenn nun das Wort
“Käfer” dieser Leute doch einen Gebrauch
hätte, – so wäre wäre dieser ganz
verschieden von dem ˇGebrauch der Wörter, die
allgemein zugängliche Dinge bezeichnen. Ja das
Ding in der Schachtel gehört überhaupt nicht zum
Sprachspiel, auch nicht einmal, ganz allgemein, als
Ding, ⌊:⌋ denn die
Schachtel könnte ja ˇsogar auch leer sein.
Nein, durch dieses Ding in der Schachtel kann
‘gekürzt’ werden; es hebt sich weg, was immer
es ist.
| | |
| | | / \ | | |
Das heißt eigentlich (nur): Wenn man
die Grammatik des Ausdrucks der Empfindung nach dem Muster von
Bezeichnung & Gegenstand konstruieren will, dann
fällt der Gegenstand als irrelevant aus der
Betrachtung heraus.
258
| | |
| | | ∕∕ \ | | |
“Ich weiß nur vom eigenen Fall, was Schmerzen
sind”, kann nicht heißen, ich kenne die Bedeutung
des Wortes “Schmerz”
nur daher, daß ich ihm ein Etwas zuordne, wovon nur ich
weiß. – Und was soll “Ich weiß
nur vom eigenen Fall etc.
überhaupt für ein Satz sein? Ein
Erfahrungssatz? Nein. Ein
grammatischer? – Aber es ist merkwürdig, daß
wir ˇgerne jedem Menschen zugestehen, er
wisse nur vom eigenen Fall her, was Schmerzen seien. Das
ist eigentlich ein Zeichen von
Gutmütigkeit.
gutmütig von uns. |
Ich denke mir
also; ⌊:⌋
Jeder sage von sich selbst, er wisse nur von den eigenen
Schmerzen; was Schmerz⌊en⌋ sei⌊en⌋. Nicht, daß die
Menschen das wirklich sagen, oder auch nur bereit sind, zu
sagen. Aber wenn nun jeder es sagte – nun,
es könnte eine Art Ausruf sein. Und wenn der
Satz auch als Mitteilung nichtssagend ist, so ist er doch
ein Bild & warum sollten wir uns so ein
Bild nicht vor die Seele rufen 259 wollen! Denke Dir ein
gemaltes & alegorisches Bild, warum soll es uns
nicht Befriedigung gewähren? Nichts ist
gewöhnlicher. Ja, wenn wir in uns
sel sehen,
bekommen
schauen, so bekommen |
wir oft gerade so ein Bild zu sehen. Es ist
förmlich eine bildliche Darstellung unsrer
Grammatik. Nicht Fakten bekommen wir zu sehen, sondern die
Art & Weise, wie wir über sie reden. Gleichsam
illustrierte Redewendungen.
| | |
| | | / \ | | |
Ja aber es ist doch da ein Etwas, was meinen Ausruf des Schmerzes
begleitet! [Nämlich der Schmerz.]
Und um dessentwillen ich ihn mache. Und dieses Etwas
ist das Wichtige & das Schreckliche. // ist das, was wichtig ist, &
schrecklich. //
Könnte es
nicht sehr wichtig sein, daß wir das sagen
wollen?!
| | |
| | | ∕∕ \ | | |
Daß wir so gerne sagen 260 möchten:
“Das Wichtige ist das”, indem wir
für uns selbst auf die Empfindung deuten – zeigt schon, wie
sehr wir geneigt sind, etwas zu sagen, was keine Mitteilung
ist.
| | |
| | | | | | Wir kauen
fortwährend an der Sprache.
| | |
| | | ∕∕ \ | | |
In meinem “Ja aber es ist doch da ein Etwas
…” ist schon das falsche Bild. Denn
ich sagte “Etwas” um die Möglichkeit
offenzulassen daß es nicht immer das gleiche sein
müsse, sondern nur irgend etwas, woran sich der
Schmerzausruf lehnen kann.
| | |
| | | ∫ | | | Die Auffassung
könnte auch die sein: einer unserer Spielsteine trage ein
Ornament, um dessentwillen ich das Spiel spiele,
obschon das Ornament nicht ins Spiel eintritt; in den Regeln
z.B. nicht 261 erwähnt wird.
| | |
| | | ∫ | | | Es
kommt uns hier vor, als wäre der Schmerz gleichsam ein
Schein um den Ausdruck des Schmerzes. /
| | |
| | | ∫ ? / | | |
Denke Dir, Du hättest keine Sprache gelernt, hättest aber
Schmerzen & eine Reaktion (Hilfe, oder Mitleid) beim
Andern hervorzurufen. Du gäbest nun Zeichen,
zeigtest z.B. mit den einem
bestimmten Gesichtsausdruck auf die schmerzende Stelle. – Inwiefern kann man sagen, Du habest Deinen
Schmerz⌊en⌋ bezeichnet? sagen Deine Zeichen handelten von den Schmerzen?
Aber wenn diese Zeichen nur dazu dienen, den Andern
zur Hilfe, oder zum Mitleid zu bewegen, sagen sie ihm
da: ich habe Schmerzen // da: daß ich
Schmerzen habe // ? Nun, das nennt man eben
einem Andern dies . –
Aber das klingt ja nun gar, als müßte ich 262 ihm die Schmerzen
verschweigen! – Es klingt so, weil Du eine falsche
Auffassung davon hast, was es heißt jemand etwas
mitteilen.
| | |
| | | ∕∕ \\ | | |
Ich möchte sagen: Du siehst es für viel zu
selbstverständlich an, daß man dem Andern etwas mitteilen
kann.
Das heißt eigentlich: wir
sind so an die Mitteilung mittels gewöhnt, daß // : wir sind so sehr an die Mitteilung durch
Sprechen, im Gespräch, gewöhnt, daß … es uns
scheint, als läge der ganze Witz
Mitteilung darin; daß ein Anderer den Sinn der Worte
(ein ätherisches )
auffaßt ˇsozusagen im Gehirn aufnimmt. Wenn er
dann auch noch etwas damit anfängt so gehört das
nicht zum direkten Zweck der Sprache.
tut, so ist das eine Draufgabe, die
aber zur Mitteilung der Gedanken, dem direkten Zweck der
Sprache, nicht gehört. |
Man möchte da vielleicht 263 sagen: die Mitteilung bewirkt
nur, daß ich weiß, daß der Andre Schmerzen hat, sie
bewirkt dieses
geistige Phänomen; alles andere ist der Mitteilung
unwesentlich. Was dieses merkwürdige
Phänomen des Wissens ˇist, daß einer Schmerzen hat,
damit läßt man sich Zeit. Seelische Vorgänge
sind eben merkwürdig.
Etwas
[ä|Ä]hnlich
es, zu sagen:
“Die Uhr zeigt uns den Verfluß
d[er|ie] Zeit
an. Was die Zeit ist, das ist eine
weitere
andereˇnoch
nicht entschiedene |
Frage[;|.] &
wozu ˇUnd zu welchem Zweck wir die Uhr,
gebrauchen das Wissen um d[en|ie] der
Zeitverlauf gebrauchen, gehört nicht
hierher.”
| | |
| | | ∫ | | |
Das Gefühl der Kluft zwischen Geistigem &
Körperlichem. Zwischen Bewußtsein &
Nervenvorgang. Der stärkste Ausdruck dieser
Idee: die beiden sind verschiedene Aspekte desselben
Dings.
264
| | |
| | | ∕∕ \ | | |
Das Gefühl der Unüberbrückbarkeit der Kluft
zwischen Bewußtsein & Gehirnvorgang. Wie kommt
es, daß ins gewöhnliche
Leben nicht hineinspielt. Die Idee dieser
Artverschiedenheit ist mit einem leisen Schwindel
Schwindelgefühl verbunden, der
das auftritt, ˇwenn
wir stunts ˇlogische
Kunststücke mit
unserer der Sprache
(ein
ähnliches Gefühl bei gewissen Betrachtungen der
Mengenlehre).
Wann tritt dieses
Gefühl auf? Nun, wenn ich z.B.
meine Aufmerksamkeit in bestimmter Weise auf mein Bewußtsein
le⌊n⌋ke & mir dabei sage: dies solle
durch einen Gehirnvorgang erzeugt werden. – Aber
was kann das heißen
‘[s|m]eine die Aufmerksamkeit auf mein
Bewußtsein lenken’. Es ist doch nichts
merkwürdiger, als daß es so etwas gibt! Was ich
so nannte (denn diese Worte werden ja im gewöhnlichen Leben
nicht so gebraucht) war ein Akt des Schauens: ich schaute
steif vor mich hin, aber nicht auf irgend einen bestimmten
Punkt, oder Gegenstand 265 Ich schaute mit
weiten Augen,
Meine Augen waren
weitc offen, |
meine Brauen nicht
zusammengezogen, wie sie es meistens sind, wenn mich ein
bestimmtes Objekt vor ⌊mich⌋ meinen Blick fesselt.
mir interessiert. Kein solches Interesse war dem
Schauen vor[her|an]gegangen Mein Blick war
‘vacant’. Mein
Schauen
Er
& meine ganze Attitude |
(mein Aufmerksamkeitszustand) war
ähnlich dem,
Menschen, der ◇◇◇ die Beleuchtung des Himmels
bewundert & das Licht ‘eintrinkt’.
Bedenk' nun, daß in dem Satz, den ich
aussprach, – dies werde durch einen Gehirnvorgang
erzeugt – gar nichts paradoxes war.
Hätte [i|I]ch
ˇhätte den Satz während eines Experiments aussprechen
können, in
gezeigt wurde, dessen Zweck war, zu zeigen, daß
der besondere Beleuchtungseffekt
(z.B.), den ich sehe, durch die
Erregung einer bestimmten Gehirnpartie erzeugt
wurde wird. Aber ich sprach ihn nicht
in der Umgebung aus, in der er einen 266 alltäglichen &
nicht-paradoxen Sinn gehabt hätte. Und auch
nicht meine Aufmerksamkeit war nicht von der Art, die
zu⌊r⌋ ˇSituation des jenem
Experiment⌊s⌋ gehört
hätte. (Mein Blick wäre dann
‘intent’ & nicht
‘vacant’ gewesen.)
| | |
| | | ∕∕ \ | | |
Hier haben wir einen Fall von Introspektion. Sie
ist nicht unähnlich derjenigen durch welche
James herausbrachte,
das ‘’ bestehe hauptsächlich
’of the collection of …
ˇaus⌊’⌋peculiar motions in the
head & between the head &
throat’. Und was die Introspektion
James's
zeigte, war nicht die Bedeutung des Wortes
‘’
(insofern dies etwas ähnliches bedeutet wie
‘Person’, ‘der
⌊‘⌋Mensch’,
‘er selbst’, ‘ich selbst’) noch
eine Analyse eines solchen Wesens, sondern ˇdie
Attitude, den
Aufmerksamkeitszustand, eines Philosophen, der sich das Wort
‘’
vorspricht & seine Bedeutung analysieren . (Und daraus ließe sich
vieles 267 lernen.)
| | |
| | | ∕∕ \ | | |
Warum soll ich nicht sagen: der Schrei des Schmerzes (&) das
Lachen seien voll von Bedeutung?
| | |
| | | / \ | | |
Und was hieße das? – Es würde diese Laute
z.B. vom Reuspern unterscheiden.
Obwohl es auch ein bedeutungsvolles Reuspern gibt. – Aber kann der Schmerzensschrei auf der Bühne nicht
auch voll von Bedeutung sein? – Wenn ich nun sage,
diese Laute seien voll von Bedeutung, so meine ich so etwas wie,
sie kommen aus einem tief zerklüfteten Innern(hervor). // hervor & sind dessen
Bild. // Sie sind voll von
Bedeutung heißt: sie bedeuten viel,
i.e., es läßt sich
[V|v]ieles,
oder Wichtiges aus ihnen schließen.
| | |
| | | ∕∕ \ ∕∕ \ | | |
Wenn jemand in ängstlicher Erwartung sagt
“Wenn er nur schon käme!” so gibt
das Gefühl
Bedeu-268 tung es aber den
Wörtern ihre Bedeutung? //
Wenn der ängstlich Wartende sagt “Wenn er
doch nur käme!”, so gibt das Gefühl seinen
Worten Bedeutung. Gibt es aber den Wörtern des Satzes
ihre Bedeutung? // ⌊⌊Wenn die Sehnsucht
aus mir spricht “Wenn er doch nur
käme!”, so gibt das Gefühl den Worten
Bedeutung. Gibt es aber den Wörtern des
Satzes ihre Bedeutung? // ⌋⌋
| | |
| | | ∕∕ \ | | |
Wenn man aber sagt “Ich
hoffe, er wird kommen”, gibt das Gefühl nicht
dem Worte “hoffen” seine Bedeutung?
“Hoffen” ist der Träger eines
bestimmten Tonfalls, & man könnte es auch
den Träger einer Empfindung
eines Gefühls |
nennen.
Wenn das Gefühl dem Worte seine
Bedeutung gibt, so
“Bedeutung” hier: das, worauf es
ankommt. Warum aber kommt es auf's
Gefühl an?
| | |
| | | ∕∕ / | | |
Zweifelst Du, daß der Andre Sehnsucht empfindet?
Manchmal zweifelst Du, manchmal nicht. –
Versuch einmal in einem
Fall, die Angst, die
Schmerzen des Andern zu bezweifeln!
269 Aber ein guter Schauspieler kann
doch diese Zustände täuschend nachahmen. –
Versuch einmal ein guter Schauspieler zu sein!
| | |
| | | / \ | | |
Wenn die Andern Automaten sein könnten; dann ich auch. –
| | |
| | | ∕∕ \ | | | Ein Hund
zeigt Freude. Kann er auch Freude heucheln?
Und warum nicht? Weil er zu ehrlich ist?
| | |
| | | | | | Du hast schon
längst alles gesagt, nur siehst Du's nicht.
Es fehlt Dir nur der Schlußpunkt.
| | |
| | | / \ | | |
“Ich kann nur glauben, daß der Andre
Schmerzen hat, aber ich weiß es, wenn ich sie
habe.” – Ja:
– ⌊.⌋ Man kann sich dazu
entschließen, , zu sagen
… statt
…
& … statt … .
statt “Er hat Schmerzen”
zu sagen: “Ich glaube er hat
Schmerzen”; & statt “Ich habe
Schmerzen”: “Ich weiß, ich habe
Schmerzen”. |
Aber das ist
alles. – Was hier wie eine Erklärung, oder
Aussage über die seelischen 270 Vorgänge, ausschaut, ist in Wahrheit nur
ist
nur |
ein Vertauschen einer Redeweise
für eine and⌊e⌋re, die uns ˇwährend wir
philosophieren die treffendere
vorkommt.
Auf den treffenden
Ausdruck kommt es aber hier nur insofern an, als er unsere Tendenzen
klarer zeigt.
| | |
| | | | | |
Ich
will nun Einem erklären: “
Ich
will einem Philosophen erklären: “
Ich will Einem erklären: “ |
Ich versichere Dich, ich benehme mich nicht nur, als hätte
ich Schmerzen, ich fühle sie wirklich; ich weiß genau, was
‘Schmerzen’ heißt.” –
Warum soll er nicht sagen: Das ist alles auch
Schmerzbenehmen.
| | |
| | | ∫ | | | Wir müssen
unterscheiden zwischen dem, was wir in einem Sprachspiel sagen,
& dem, was wir, beim Philosophieren darüber, zu
sagen geneigt sind.
| | |
| | | | | | Wie kann ich denn mit der Sprache noch
zwischen die Schmerzäußerung & den Schmerz treten
wollen?
271
| | |
| | | ∕∕ \ | | |
Es zeigt ein fundamentales Mißverständnis an, wenn
ich meinen gegenwärtigen Zustand der Kopfschmerzen zu
betrachten geneigt bin, um über das philosophische Problem der
Empfindung ins klare zu kommen.
| | |
| | | ∕∕ \ ? | | |
Denke Dir einen Menschen, der es nicht im Gedächtnis behalten
könnte, was das Wort “Schmerz”
bedeutet, & der daher wieder
etwas anderes so nennt, ˇder aber das Wort immer in
Übereinstimmung mit den gewöhnlichen Zeichen &
Voraussetzungen des Schmerzes verwendete! – Das Rad
gehört nicht zur Maschine, das man drehen kann, ohne daß
sich
mitbewegt.
| | |
| | | ∫ | | | Ist es ebenso
sicher, daß der Andre traurig ist, wie, daß ich es
bin? Oder könnte der Andre nicht doch ein Automat
sein? – (Ist es so sicher, daß in des Nachbars
Zimmern Möbel stehen, wie, daß sie in meinen Zimmern
stehn? 272 Könnte ich kein
Automat sein? Bin ich keiner?
Gehören die Empfindungen mir?
| | |
| | | ∕∕ \ | | |
“Wenn ich sage ‘Ich habe
Schmerzen’, bin ich jedenfalls vor mir selbst
gerechtfertigt.” – Heißt das:
“Wenn der Andre , was ich ‘Schmerz’ nenne,
würde er zugeben, daß ich das Wort richtig
verwende”? –
| | |
| | | ∕∕ \ | | |
“Jeder kennt, aus erster Hand, nur seine
Empfindungen.” Was für eine Art von Satz ist
diese allgemeine Feststellung?
| | |
| | | ∕∕ \ | | |
“Aber warum traust Du Dir selbst so wenig?
Du weißt doch sonst immer, was –
(z.B.) –
“rechnen” heißt. Wenn Du also sagst,
Du habest in der Vorstellung gerechnet, so wird es eben so
sein. Hättest Du nicht gerechnet, so
würdest Du's nicht sagen. Ebenso, wenn Du
sagst, daß Du etwas Rotes in der Vorstellung siehst, so wird es
eben rot sein. Du weißt ja sonst, was
“rot” ist. – Und weiters: Du
verläßt Dich 273 ja nicht immer auf die
Übereinstimmung mit den Andern; denn oft berichtest Du, Du habest
das & das etwas gesehen, was niemand
anderer gesehen hat.”
Aber ich traue
mir ja. Ich sage ja ohne Bedenken, ich habe dies im Kopf
gerechnet, mir diese Farbe ˇmir vorgestellt,
⌊.⌋
Nicht das ist die Schwierigkeit, daß ich zweifle, ob ich mir
wirklich etwas Rotes vorgestellt habe. Sondern
dies: Wenn die Vorstellung ein Abbild der
Wirklichkeit ist kann ich da die Frage
stellen: “Wie muß eine richtige Vorstellung
dieser Farbe aussehen?” oder:
“Wie muß sie beschaffen
sein?”? Kann ich das lernen?
Der tiefe Aspekt entschlüpft
leicht. // Sondern dies:
Gefragt, welche Farbe ich mir vorgestellt habe, zeige ich auf
sie, oder beschreibe sie aber wie kommt es,
daß ich das ohne weiteres tun kann; daß mir das Abbilden der
Vorstellung in die Wirklichkeit so wenig Schwierigkeit
macht? Sehn sich denn Vorstellung 274 & Wirklichkeit zum
Verwechseln ähnlich? – Aber so kann ich
ja auch ohne weiteres einen Menschen nach einer Photographie
– Wenn
die Vorstellung ein Abbild der Wirklichkeit ist, – kann ich
fragen: “Wie
schaut eine richtige Vorstellung dieser Farbe aus”, oder
“Wie ist sie beschaffen”?
Kann ich das lernen? // // Sondern dies: Wie kommt es,
daß ich ohne weiteres zeigen, oder beschreiben kann, welche Farbe
ich mir vorgestellt habe; daß mir das Abbilden … //
| | |
| | | ∕∕ \ | | |
Um über die Bedeutung des Wortes “denken”
oder “hoffen” klar zu werden, sehen wir uns selbst
beim Denken, oder Hoffen zu: wir
da beobachten, werde das sein, was jene Worte bedeuten! – Aber so werden die Worte eben nicht gebraucht.
(Es wäre ähnlich, wenn ich, ohne Kenntnis des
Schachspiels, durch genauestes Beobachten des letzten Zuges einer
Schachpartie lernen wollte, 275 was das Wort
‘matsetzen’ bedeutet.)
| | |
| | | ∕∕ \ | | |
“Die Menschen stimmen mit einander
überein, daß
sie sehen, hören, fühlen, etc. (wenn auch
Mancher blind & Mancher taub
ist). Sie bezeugen also von sich, sie haben
Bewußtsein.” Aber wie merkwürdig!
wem mache ich eigentlich eine Mitteilung, wenn ich
sage: “Ich habe
Bewußtsein”? Was ist der Zweck, mir das zu
sagen, & wie kann der Andere mich verstehen? – Nun, Sätze, wie “Ich sehe”,
“Ich höre”, “Ich bin bei
Bewußtsein”, haben ja wirklich ihren Gebrauch.
Dem Arzt sage ich “Jetzt höre ich wieder auf
diesem Ohr”; wer mich ohnmächtig gesehen hat, dem sage
ich etwa “Ich bin wieder bei
Bewuß⌊t⌋sein”, usw.
| | |
| | | ∕∕ \ | | |
Beobachte ich mich also & nehme wahr, daß ich sehe, oder
bei Bewußtsein bin? Und wozu überhaupt von
Beobachtung reden! Warum nicht einfach sagen:
“Ich nehme wahr, daß ich bei Bewußtsein
bin”? – Aber wozu hier die Worte
“Ich nehme wahr”[?| .]
– 276 Warum nicht sagen:
Ich bin bei Bewußtsein”? –
Aber zeigen die Worte “Ich nehme wahr” hier
nicht an, daß ich auf mein Bewußtsein aufmerksam
bin, ? was doch gewöhnlich nicht
der Fall ist. (Denn ich habe ˇfür
gewöhnlich Besseres zu tun.) Wenn es so ist, dann
sagt der Satz “Ich nehme wahr, daß
…” also nicht, daß ich bei Bewußtsein bin,
sondern, daß meine Aufmerksamkeit so & so
eingestellt ist.
Aber ist es denn nicht eine
bestimmte Erfahrung, die mich veranlaßt zu sagen
“Ich bin wieder bei Bewußtsein”?
Welche Erfahrung?
[D|d]as ist zu
.
(Und zwar dem Andern verständlich. Denn
vom Andern habe ich die Sprache gelernt[;|.]
& ˇUnd was er nicht verstehen kann, kann ich auch
nicht verstehen.)
| | |
| | | ∫ ∕∕ \ | | |
“Aber ich habe doch Bewußtsein!”
– Aber es ist seltsam, daß ich weiß, daß das
“Bewußtsein” heißt!
277
| | |
| | | ∫ ∕∕ | | |
“Ich lebe doch; ich habe doch
Bewußtsein!” (Dabei öffne ich
die Augen weit & schaue um mich.) Wem sage ich
das, & wozu? Was die Worte wohl für eine
Beziehung zu dem Faktum haben; & warum ich es wohl mit Worten
begleite!
| | |
| | | ∕∕ \ | | |
Ist, daß ich Bewußtsein habe, eine
Erfahrungstatsache?
Aber sagt man nicht
vom Menschen er habe Bewußtsein; & vom Baum, oder Stein, er
habe keines? – Wie wäre es, wenn's
anders wäre? Wären die Menschen alle
bewußtlos? – Nein; nicht im gewöhnlichen
Sinne Worts; aber ich,
z.B., hätte nicht
Bewußtsein[:|,]⌊–⌋ wie ich's jetzt tatsächlich
habe.
| | |
| | | ∕∕ \ | | |
Aber kann ich mir nicht denken, daß die Menschen um mich
Automaten seien, kein Bewußtsein haben, wobei aber wenn
auch ihre Handlungsweise ˇaber ist genau die
gleiche ist, wie immer? – Wenn ich
mir's jetzt – allein in meinem Zimmer –
278 vorstelle, sehe ich die
Leute mit starrem Blick (etwa wie im trance) ihren Verrichtungen
nachgehen[;| ,] & die Idee ist ein wenig unheimlich. Aber nun
versuch einmal im gewöhnlichen Verkehr, ˇoder auf der
Straße, an dieser Idee festzuhalten! Sag Dir
“Diese Kinder dort sind bloße
Automaten. Alle ihre Lebendigkeit ist bloß
Schein.” – Und diese Worte werden Dir
entweder gänzlich nichtssagend werden; oder Du wirst in Dir
eine ˇArt
unheimliches Gefühl erzeugen.
erzeugen.hervorrufen. |
Einen
lebenden Menschen als Automaten sehen, ist äh⌊n⌋lich dem,
ein Fensterkreuz als Swastika sehen; oder irgend eine Figur als
Grenzfall, oder Variation einer andern.
| | |
| | | ∕∕ \ | | |
Der erste Fehler, den wir in einer philosophischen
Untersuchung machen, ist die philosophische Frage.
| | |
| | | ∕∕ \ | | |
Die gemeinsame menschliche Handlungsweise ist das
Bezugsystem, mittels welches wir uns eine fremde 279 Sprache
deuten.
| | |
| | | ∕∕ \ | | | Befehle
werden manchmal nicht befolgt. Aber wie würde es
aussehen, wenn Befehle nie befolgt würden.
| | |
| | | ∕∕ | | | Es ist nicht
leicht philosophische Schlüssel zu finden, die viele
Schlösser eröffnen. Aber die Schlösser zu
Schlüsseln finden, das
ist das Schwerste.
| | |
| | | ∕∕ \ | | | Wer uns die
Sprache eines Volkes beschreibt, beschreibt eine
Gleichförmigkeit ihres Benehmens. Und wer eine
Sprache beschreibt, die Einer mit sich allein spricht, der beschreibt
eine Gleichförmigkeit seines Benehmens & nicht etwas, was
sich einmal zugetragen hat.
Aber
“eine Sprache sprechen” werde ich nur ein Verhalten
nennen, das unserm, wenn wir
uns⌊(⌋e⌊)⌋re
Sprache sprechen, analog
ist.
| | |
| | | ∕∕ / | | |
Ein Schrei entringt sich ihm. Worte 278 entringen
sich ihm.
| | |
| | | ? ∫ | | | Ist der
Schrei wahr, oder falsch? Wie, wenn ich sagte, er sei
echt, oder nicht echt.
| | |
| | | ∫ | | | Nicht, natürlich, als sei
das Wort “echt” richtiger als
“wahr”! Es erinnert
ˇuns nur an einen grammatischen Unterschied, der
übersehen, oder nicht verstanden wird.
| | |
| | | ∕∕ \ | | |
“Wenn ich mir etwas vorstelle, so geschieht doch
wohl etwas!” Nun, es geschieht etwas
‒ ‒ ‒ ‒ ‒ ‒ & wozu mache ich dann einen
Lärm? Wohl dazu, was geschieht, mitzuteilen. – Aber wie teilt man denn überhaupt etwas
mit? Wann sagt man, etwas werde
mitgeteilt? Was ist das Sprachspiel des Mitteilens? Ist es das gleiche ob ich
nun einen physikalischen Vorgang mitteile, oder einen
seelischen?
| | |
| | | ∫ | | | Und das, was man
erlebt, davon sagt 281 man ja, daß es sich
nicht mitteilen lasse! Und wenn Du sagst:
“Ich sage es eben mir selbst”, so frage ich
wieder, was das heißt, & was
der Lärm mit dem zu tun hat, was
“geschieht”. Wie meint man denn mit den Worten, was
geschieht?
| | |
| | | ∕∕ \ | | |
Du gibst jemandem ein Signal, wenn Du Dir etwas
vorstellst & Du benützt verschiedene Signale für
verschiedene Vorstellungen. – Wie vereinbart
ihr, was jedes Signal bedeuten soll?
| | |
| | | ∕∕ \ | | |
Wie lehrt & lernt man, leise für sich selbst
lesen?
| | |
| | | ∕∕ \ | | |
Was ist das Kriterium der Gleichheit zweier
Vorstellungen? D.h.: wie
werden Vorstellungen verglichen? Ein Logiker denkt
: gleich ist
gleich – es ist eine psychologische Frage „keine logische: wie der Mensch
weiß ˇsich davon überzeugt,
daß zwei gleich
sind. Vergleiche ˇdamit: “Höhe
ist Höhe; es ist eine ˇgehört in die
[p|P]sychologi⌊e⌋sche Frage ob,
daß der 282 Mensch manchmal sieht, manchmal
hört.”
| | |
| | | | | | Ich stelle mir vor, daß der Baum
umfällt, ich sehe es deutlich vor mir. Ich habe ein
klares Bild vor meinem geistigen Auge. Warum ein
Bild? – Wenn ein Bild, warum nicht den
Baum?
| | |
| | | ∕∕ \ | | |
Gedankenlos, & gedankenvoll Musik machen.
‒ ‒ ‒
| | |
| | | ∕∕ \ | | |
Wenn Du Schmerzen hast // fühlst // & daraus auf
hohen Blutdruck schließt, wirst Du nicht sagen wollen, Du habest
aus nichts auf hohen Blutdruck
geschlossen.
Und wie ist das Experiment zu
beschreiben, ⌊:⌋ Du beobachtest
Deinen Blutdruck & siehst zu, wie er von Deinem Schmerzzustand
abhängt. Du rufts
nicht durch äußere Mittel die Schmerzen hervor, sondern
vergleichst nur ihren (natürlichen) 283 Verlauf mit dem des
Blutdrucks.
Denk dir, statt Zeichen in ein
Tagebuch einzutragen, wenn er Schmerzen hat, mache Einer so ein
Experiment! Ist es kein Experiment? Wird es
nur dadurch zu einem, daß er einen Ausdruck des Schmerzes
hat? Kann er nicht eben die
Veränderungen des Blutdrucks richtig, für Jeden
sichtbar, voraussagen?
| | |
| | | / \ | | |
Und hier spielt wieder das ‘richtige’
Wiedererkennen seiner ˇinnern Empfindung ⌊gar⌋ keine
Rolle. Denn es genügt, daß er sie wiederzuerkennen
glaubt, da, was uns interessiert, das richtige
Vorhersagen des Blutdrucks ist. – Und daher muß es
auch falsch sein, wenn ich sage, er glaube die Empfindung
wieder zu erkennen.
| | |
| | | ∕∕ \ | | |
Der Unsinn, gegen den ich angehe, ist der halbe Solipsismus, der
sagt, die Empfindung kenne ich unmittelbar daher, daß
ich sie habe & nun verallgemeinerte
284 ich meinen Fall // meinen eigenen Fall // .
| | |
| | | ∕∕ \ | | |
Den Begriff ‘Schmerz’ hast Du mit der
Sprache gelernt.
| | |
| | | ∕∕ \ | | |
Ich sitze in einem Sessel & habe die Augen
geschlossen. Ich fühle Schmerzen, ich fühle mich
athmen, ich fühle den Druck des Sessels
gegen meinen Körper. Nun,
[n|N]ennen wir das einmal eine
Erfahrung? Und nun sage ich ˇmir:
[w|W]ie weiß
ich, daß ich nicht zu einem Stein erstarrt bin?
(Oder auch: “daß mein Körper nicht
ganz verschwunden ist? Denn das eine ist doch eigentlich
so gut, wie das andre.) Die Erfahrung ist also da, auch
wenn mein Körper nicht mehr . ‘Die
Erfahrung’ – aber welche Erfahrung? –
Nun, [d|D]ie, die ich jetzt gerade habe. –
Aber damit das Sinn hat, brauche ich (doch) ein
Kriterium des Andauerns der gleichen
Empfindung. Es geht nicht an, zu sagen:
“Nun, eben diese!”
285
| | |
| | | / \ | | |
“Ich brauche ein Kriterium des Andauerns der
gleichen Empfindung”, sagte ich. – Warum
aber? Weil der Ausdruck für die Empfindung, so wie
er aus seinem Sprachspiel herausgelöst ist, in der Luft
hängt & nun einer neuen Unterstützung
bedarf.
| | |
| | | ∕∕ \ | | |
Es scheint paradox, daß wir in einem Bericht
Körper- &
Bewußtseinszustände kunterbunt durcheinander
mischen: “Er litt große Qualen & warf
sich unruhig umher; dann wurde er ruhiger &
verbiss seinen Schmerz.”
– Das ist ganz gewöhnlich; warum erscheint es
(mir) also paradox? Weil wir sagen
wollen, der Satz handle von Greifbarem & Ungreifbarem. – Aber findest Du etwas dabei, wenn ich sage:
“Diese 3 Stützen geben dem Hause
Festigkeit”? Sind 3 & Festigkeit
greifbar? – Sieh den Satz als Instrument an,
& seinen Sinn als seine Verwendung!
286
| | |
| | | / \ | | |
Ich identifiziere meine Empfindung freilich nicht, sondern ich
gebrauche den gleichen Ausdruck. Aber damit endet
ja das Sprachspiel nicht; damit fängt es (erst)
an.
Aber fängt es nicht mit der
Empfindung an – die ich beschreibe? – Das Wort
“beschreiben” hat uns vielleicht da zum
besten. Ich sage “Ich beschreibe meinen
Seelenzustand” & “Ich beschreibe
einen Wohnraum”. Hier muß man sich die
Verschiedenheiten der Sprachspiele ins
Gedachtnis rufen.
| | |
| | | ∕∕ \ | | |
Könnte der das Wort “Schmerz”
verstehen, der nie Schmerz gefühlt hat? –
Was ist das für eine Frage? Soll die Erfahrung
mich lehren, wie es sich verhält? Und wenn Du sagst
“Einer kann sich Schmerzen nicht vorstellen, außer
er hat sie einmal gefühlt” – woher weißt Du
das? Wie läßt sich entscheiden, ob das wahr
ist? 287
| | |
| | | ∕∕ \ | | |
“Aber Du wirst doch zugeben, daß ein Unterschied ist
zwischen Schmerzbenehmen mit Schmerzen & Schmerzbenehmen
ohne Schmerzen.” – Zugeben?
Welcher Unterschied könnte größer sein! – “Und doch gelangst Du immer wieder zum Ergebnis,
der Schmerz selbst sei ein Nichts.” – Nicht
doch! Er ist kein Etwas aber auch nicht ein
Nichts! Das Ergebnis war nur, daß ein Nichts die
gleichen Dienste täte, wie ein Etwas, worüber sich nichts
aussagen läßt. D.h., wir
verwarfen die Grammatik, die sich uns aufgedrängt
hatte. // uns
aufdrängte // aufdrängen will.
Und
das Paradox verschwindet nur dann, wenn wir ganz mit der
wir radikal mit
der |
Idee brechen, die Sprache
funktioniere immer auf eine Weise, diene immer dem
gleichen Zweck: Gedanken zu übertragen, – seien diese
nun Gedanken über Häuser, Schmerzen, Gut &
Böse, oder was immer. 288
| | |
| | | ∕∕ \ | | |
Ich sage jemandem, ich habe Schmerzen. Seine
Einstellung zu mir wird nun die des Glaubens sein; des
Unglaubens; des Mißtrauens; etc.
Nehmen wir an, er sagt: “Es wird
nicht so schlimm sein.” – Ist das nicht der
Beweis dafür, daß er an etwas glaubt,
hinter der Schmerzäußerung steht? – Seine
Einstellung ist (nur) ein Beweis seiner
Einstellung. Denke Dir nicht nur den Satz
“Ich habe Schmerzen”, sondern auch
den ,
“Es wird nicht so schlimm sein”, durch
Naturlaute & Gebärden ersetzt!
| | |
| | | / \ ∕∕ | | |
“Welcher Unterschied könnte größer
sein!” – Im Fall der Schmerzen glaube ich,
ich könnte mir diesen Unterschied privat vorführen.
Den Unterschied aber zwischen einem abgebrochenen & einem
nicht abgebrochenen Zahn kann ich Jedem vorführen.
Aber die private Vorführung ist eine Illusion & Du
brauchst Dir auch gar
nicht 289 Schmerzen hervorrufen, sondern es
genügt, z.B. wenn Du Dir
sie vorstellst,
z.B., ein wenig
das Gesicht verziehst. Und wie weißt Du, daß,
waß Du Dir so
vorstellstführst, Schmerzen sind & nicht ein
Gesichtsausdruck? – Diese Vorführung ist eine
Illusion.
Wie weißt Du auch, was Du Dir
vorführen sollst, ehe Du Dir's
vorführst? (Du mußt Dich an den Gedanken
gewöhnen, daß Sprachreaktionen, wie andere, oft
auftreten, sie keinen Zweck haben.
Und es wäre seltsam, wenn es nicht so
wäre.)
| | |
| | | ∕∕ | | |
“Häufe das Benehmen, wie Du willst, – es gibt
immer noch keine Schmerzen!”
| | |
| | | ∕∕ \ | | |
Aber sind die Fälle des Zahnes & der Schmerzen nicht
doch wieder ähnlich? Denn dem Gesichtsbild im einen
entspricht die Empfindung im andern. Die Gesichtsempfindung
kann ich mir so wenig vorführen, oder so gut, wie die
Schmerzempfin-290 dung.
Denk' Dir diesen Fall: Die Oberfläche
der Dinge die uns umgeben (Steine, Pflanzen, Knochen
etc) hätte bestimmte Flecken oder
Zonen die unseren Fingern der
Berührung Schmerzen verursachen; dies liege etwa in der
chemischen Beschaffenheit dieser Oberflächenteile, aber das
brauchen wir nicht zu wissen. Wi[e|r]
würden ˇnun, so wie heute von einem rotgefleckten Blatt,
von einem mit Schmerzflecken reden. Ich setze voraus,
daß die der
Schmerzflecken mannigfaltigen
verschiedenerlei |
Nutzen für uns
hat⌊.⌋, [d|D]aß wir etwaz.B.
eine Pflanzen nach ihnen
erkennenetc. ⌊;⌋
Schlüsse auf wichtige Eigenschaften der Gegenstände
ziehen,
etc. ⌊.⌋
| | |
| | | ∕∕ \ | | |
Ich kann Schmerzen vorführen, wie ich
Rrot vorführe, &
wie ich gerade & krumm, & Baum & Stein
vorführe. – Das nennen wir eben
“vorführen”.
| | |
| | | / \ | | |
Wie ist es nun mit dem Worte “rot” 291 z.B. –
soll ich sagen, dies bezeichne etwas, ⌊,⌋
“der Erkenntnis aller, oder der meisten Menschen, Gemeinsames
& Jeder sollte eigentlich außer diesem Wort noch
ein anderes haben zur Bezeichnung seiner eigenen
Empfindung von Rot? Oder ist es so: Das Wort
“Rrot”
bezeichnet für den Andern (& vielleicht
manchmal auch für mich) das Gemeinsame Rot, –
für mich // für den
Sprecher // aber bezeichnet es
außerdem etwas uns gemeinsam bekanntes,
& außerdem noch für jeden etwas nur ihm
bekanntes, etwas [p|P]rivates; oder vielleicht besser: es
bezieht sich auf etwas
[p|P]rivates?
| | |
| | | / \ | | |
Das Wesentliche am privaten Erlebnis
Privaten |
ist
eigentlich nicht, daß Jeder sein besonderes besitzt, sondern,
daß [K|k]einer weiß, ob der Andere auch
dies hat, oder etwas anderes. Es wären also
Annahmen möglich, wie die, daß der
Menschheit ˇhabe eine, eine andere Rotempfindung
haben – wenn
sie's auch nie wüßten.
| | |
| | | / \ | | |
Natürlich, wie & wozu man das
Private 292 bezeichnen soll, ist unklar. Sagt man
aber: das Wort bezieht sich auf die ˇeigene
Empfindung, so entspricht ist dies der psychologisch
richtigere Ausdruck für das Erlebnis beim
Philosophieren.
für ein Erlebnis, das ich beim
Philosophieren habe. |
⌊Es ist als werfe man bei dem Wort
einen Seitenblick auf den eigenen Eindruck.⌋
Schau auf das Blau des Himmels; sag ⌊zu⌋ Dir
selbst: “Wie blau der Himmel
ist!” – Wenn Du es spontan tust –
nicht mit erkenntnistheoretischen
philosophischen |
Absichten – so kommt es Dir nicht in den Sinn, dieser
Farbeneindruck gehöre nur Dir. Und Du
hast kein Bedenken diesen Ausruf an einen Andern zu richten.
Und wenn Du bei den Worten auf etwas zeigst, so ist es der
Himmel, ich meine: Du hast nicht das Gefühl des
in-sich-selber-Zeigens, das oft das
‘Benennen der Empfindung’ begleitet, wenn wir
über die ‘private Sprache’ nachdenken.
Du denkst auch nicht, Du solltest eigentlich nicht mit der
Hand, sondern nur mit der Aufmerksamkeit auf die Farbe zeigen.
| | |
| | | | | |
James ist eine Fundgrube für die Psychologie
des Philosophen.
| | |
1) See facsimile; line connecting this sentence with the following one.
2) See facsimile; line connecting this remark with the following one.
3) See facsimile; arrow pointing down in the left margin, probably to indicate the scope of the section mark.
4) See facsimile; line connecting this remark with the following one.
 ”
geschrieben
”
geschrieben 


