​

Handelt nur von Logik &      Mathematik.

​

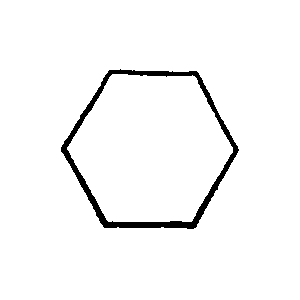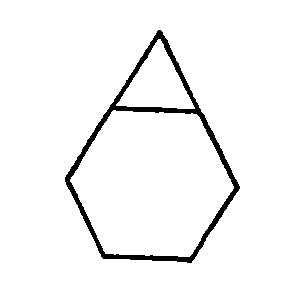
20.10.42.     Eine Addition von Formen in der gewisse Glieder verschmelzen spielt in unserm Leben eine sehr geringe Rolle. – Wie wenn und △ die Figur ergeben. Aber wäre dies eine wichtigere Operation, so hätten wir vielleicht ˇauch einen andern geläufigen Begriff von der arithm. Addition.

k

Daß man ein Boot, einen Hut, einen Katzenkopf etc aus einem Stück Papier falten ˇnach gewissen Regeln kann, betrachten wir als Sache Angelegenheit der Geometrie, nicht der Physik. Aber ist die Geometrie, so verstanden, nicht ein Teil der Physik? Nein[:W|; w]ir spalten die Geometrie von der Physik ab. Die geometrische Möglichkeit von der Physikalischen. Aber wie, wenn man sie beisammen ließe? Wenn man einfach sagte: ‘wenn Du das & das & das mit dem Stück Papier tust, wird dies herauskommen’? Was zu tun ist, könnte etwa durch einen Reim gegeben werden. Ist es denn nicht möglich, daß jemand zwischen den beiden Möglichkeiten gar nicht unterscheidet?

​

Wie wenn man sagte: ‘wenn Du gut ausgeruht bis & Du addierst die Zahlen ...... kommt meistens ..... heraus’? Hier, kann man sagen, heißt ‘addieren’ etwas anderes, als als in unserem Sprachgebrauch. Aber doch etwas Ähnliches.

​

Es heißt dann ungefähr, was wir “zu addieren versuchen” nennen. Und wir sagen, von einem Schüler z.B., er versucht die & die Zahlen zu addieren, & meinen damit etwas ganz bestimmtes, obwohl die Kriterien dafür, daß das es geschieht, nicht leicht aufzuzählen sind. (Es ist wie ‘zu lesen versuchen’.)

​

Wie ist es mit dem Satz “p ⊃ p ist eine Tautologie”? Er ist etwar vergleichbar mit: “318 ist durch 3 teilbar”.

​

Man könnte sich die Logik mit solchen Sätzen betrieben denken. Und dann natürlich, ebensogut auch mit Sätzen der Art “p ∙ ~p ist eine Contradiction”. Und daher auch einfach mit Contradictionen ˇwie bisher mit Tautologien. Daß ich in einer Beschreibung, oder einem Befehl Wiedersprüche nicht dulde, daraus folgt nicht, daß ich sie in der Logik nicht brauchen kannc. Die Reaktion auf ‘p ⊃ p’ ist: ‘Nun gut, – was weiter!’. Eine Art Bejahung, wie ˇdie einer gänzlich unverbindlichen Äußerung.

​

Denke Dir einen S[a|ä]tz⌊e⌋, wie 25 × 25 = 625, gewohnheitsmäßig immer so hingeschrieben: 25 × 25 ‒ 625 = 0, & endlich am Ende das ‘ = 0’ weggelassen, so daß einfach (diec) Sätze der Arithmetik die Form arithm. Ausdrücke annehmen, die gleich 0 sind, – obwohl dies das nicht gesagt wird ist . Wäre diese Situation nicht ähnlich der in unsrer Logik, die aus Tautologien besteht?

​

21.10.     Die Konstruktion einer (neuen) Schlußregel kann man als Einführung eines neuen Schlußregel Sprachspiels deuten. Ich denke mir eines, in welchem etwac eine Person ‘p ⊃ q’ aussagt, eine ˇandere ‘p’, & eine dritte den Schluß ‘q’ zieht. // Die Einführung einer neuen Schlußregel kann man als Übergang zu einem neuen Sprachspiel auffassen. Ich stelle mir eines vor, in welchem …

​

22.10.     Es handelt sich um die Beobachtung einer Fläche r b w g s o die in Stücke von verschiedener Farbe geteilt ist. Die Farben aller Stücke ändern sich zu gleicher Zeit immer nach einer Minute. ⌊⌊ Jeder beobachtet einen Aspekt der ihn aus bestimmten Gründen ◇◇◇ angeht. ⌋⌋ Jetzt sind die Farben            r, g, b, w, s, o. Es wird beobachtet, daß jedesmal immer            r ∙ b ⊃ w . ⊃ . s. Es wird auch beobachtet           ~g ⊃ ~ s. Und Einer zieht den Schluß           ~g ⊃ r ∙ b ∙ ~ w

​

⌊⌊ˇ Sind das echte Beobachtungen, so müssen sie einander widersprechen können. ⌋⌋ ⌊ These implications, by the way, are really ‘material’ implications. ⌋

​

Inwiefern hängt der Schluß von der Erfahrung ab?

​

Einer beobachtet ˇeine zweigeteilte Fläche & ruft aus “rot & blau”; ein Anderer macht von der Beobachtung Gebrauch & sagt: “Also rot”. Er zieht aus ‘p ∙ q’ den Schluß ‘p’.   Oder ihn interessiert es, ob die Flächen rot oder gelb zeigen, & er sagt: “Also: rot oder gelb”. Er hat von ‘p ∙ p’ auf ‘p ⌵ r’ geschlossen.

​

Ja, man kann sich ein Sprachspiel denken, in welchem dem der Eine immer den für seine Funktion Tätigkeit relevanten Schluß aus der Angabe des Andern zu ziehen hat, ⌊–⌋ etwa einen Schluß von ‘p ∙ q ∙ r’ auf ‘q’ – & daß er in dieser Tätigkeit ˇmanchmal ˇauch aus einer dieser Angabe ‘p’ den Schluß zieht: “also ‘p’”[;|,] daß er also nach der Formel ‘p ⊃ p’ schließt.

​

23.10. ‘So machen wir's’⌊.⌋,[d|D]ieser Regel folgen wir; & wenn dabei etwas schief geht, so schieben wir's nicht der Regel in die Schuhe.

​

Einer beobachtet eine Fläche, welche die in Quadranten g⌊e⌋teilt ist. Er ruft aus: “Ganz weiß”. Ein Arbeiter, den die Farbe des Quadranten No 4 angeht, sagt: “Also No 4 weiß”.   Wenn nun in dem Arbeitsprozess irgend etwas schief geht, so wird niemand sagen[;|:] aus ‘(x).f(x)’ habe hier nicht ‘f(a)’ gefolgt.

​

Wie aber, wenn wir Leute aus dem allgemeinen Satz auch entgegengesetzt schließen sähen?

​

Denke Dir Einen, der ein Patent auf eine Regel nimmt ˇum Regeln zu erzeugen nach denen Reihen von Kardinalzahlen erzeugt werden können (etwa zum Zweck von Numerierungen). Er sagt er habe eine Regel gefunden nach der alle möglichen endlosen Reihen erzeugt werden können & kein Konkur-rent könne eine Regel bilden die nicht in seinen enthalten wäre. Und nun zeigt ihm Cantor, daß das nicht möglich ist. Dieser Beweis ändert unzweifelhaft seinen Begriff von der endlosen Zahlenfolge.   Vorher hatte er etwa geglaubt, da er sich so große Mühe gegeben habe alle Regeln in sein System einzuschließen, so könne er keine ausgelassen haben. Nun denkt er ganz anders über die Sache.     Wie Einer, der nicht wußte, daß die Konstruktion einer Winkelteilung unmöglich sein könne. Er sieht es nun ganz anders an.

​

Wie, wenn man sagte: Wer die Folge 1 2 3 umgekehrt hat, lernt über sie, daß sie umgekehrt 3 2 1 ergibt? Und zwar ist, was er lernt, nicht eine Eigenschaft dieser Tintenstriche, sondern der Folge von Formen. Er lernt eine formale Eigenschaft von Formen. Der Satz, welcher diese formale Eigenschaft aussagt, wird durch die Erfahrung bewiesen, die ihm die Entstehung der einen Form aus der andern in dieser ˇauf diese Weise, zeigt.

​

Hat nun, wer das lernt, zwei Eindrücke? Einen davon daß die Reihenfolge umgekehrt wird, den andern davon daß 3 2 1 entsteht? Und könnte er die Erfahrung, den Eindruck, daß 1 2 3 umgekehrt wird nicht haben und doch nicht den daß 3 2 1 entsteht? Vielleicht wird man sagen: “nur durch eine seltsame Täuschung”. –

​

Warum man eigentlich nicht sagen kann, daß man jenen formalen Satz aus der Erfahrung lernt[:| –] weil man es erst nur dann diese Erfahrung nennt, wenn dieser Prozess zu diesem Resultat führt. Die Erfahrung, die man meint, besteht schon aus diesem Prozess mit diesem Resultat.

​

Darum sie mehr wie die Erfahrung: ein Bild zu sehen.

​

Kann eine Buchstabenreihe zwei Umkehrungen haben?           Etwa eine [A|a]kustische & eine ˇandere optische Umkehrung. Angenommen ich erkläre jemandem was die Umkehrung eines Wortes auf dem Papier ist, was man so nennt. Und nun stellt sich heraus daß er eine [A|a]kustische Umkehrung des Wortes hat, d.h., etwas was er so nennen möchte was aber nicht ganz mit der geschriebenen übereinstimmt. So daß man sagen kann: er hört das als Umkehrung des Wortes. Gleichsam als verzerrte sich ihm das Wort beim Umkehren. Und dies könnte etwa eintreten wenn er das Wort & die Umkehrung fließend schnell ausspricht im Gegensatz zum zu dem Fall wenn in welchem er es buchstabiert. Oder die Umkehrung könnte anders scheinen, wenn er das Wort in einem Zuge vor- & rückwärts spricht.

​

Es wäre möglich, daß man das genaue Spiegelbild eines Profils sogleich nach diesem gesehen nie für das gleiche & nur verkehrte in ˇdie anderer Richtung sehende gedrehte erklärte, sondern daß, um den Eindruck der genauen Umkehrung zu machen, das Profil in den Maßen ein wenig etwas geändert werden müßte.

​

​

Ich will doch sagen, man habe kein Recht zu könne nicht sagen: wir mögen zwar über die correcte Umkehrung, eines langen Wortes z.B., im Zweifel sein, aber wir wissen, daß das Wort nur eine Umkehrung hat.

​

‘Ja, aber wenn es eine Umkehrung in diesem Sinne sein soll, dann kann es nur eine geben!’   Heißt hier ‘in diesem Sinne’: nach diesen Regeln, oder: mit dieser Physiognomie. Im ersten Falle wäre der Satz tautologisch, im zweiten muß er nicht wahr sein.

​

24.10.           “Notwendige Wahrheit”            “necessary proposition” – ein schlechter Ausdruck ⌊p⌋ suggeriert Läßt uns an eine starre Verbindung gewisser Gegenstände, wie ⌊(⌋ Formen⌊,⌋ oder Zahlen ⌊, etc.)⌋ in der Natur ˇdenken; eine Art Naturwissenschaft dieser Fakten. D.h., wir bilden eine Art Superlativ der Starrheit einer Verbindung, wozu als Vorbild unsere Mechanismen dienen.

​

Ein Satz der Wahrscheinlichkeitsrechnung kann einen Begriff der Wahrscheinlichkeit des Eintreffens von Ereignissen bestimmen oder aber auch einen ˇgeometriechen Begriff. der Geometrie. Gibt es nun nun nicht eine reine Mathematik die bloß die Form aller solcher Anwendungen wäre, aber keine von ihnen andeutete?     Als solch eine reine Mathematik würde scheint sich uns das ein Zeichenspiel anzubieten das allen solchen Deutungen gemeinsam ist.

​

Und wozu nun dies Zeichenspiel mit Axiomen in den Formen der Axiomatik spielen & nicht gleich so, wie es ˇsich für gewöhnlich mit einer Deutung darstellt – , nur mit bedeutungslosen Zeichen gespielt? // Und wozu nun dies Spiel in den steifen ⌊⌊ 25.10. ⌋⌋ ˇaxiomatischen Formen der Axiomatik spielen statt gleich so wie es sich uns darstellt wenn es eine Deutung hat – nur eben mit bedeutungslosen Zeichengespielt. ⌊.⌋ //

​

Denke Dir also Menschen, welche addierten, multiplizierten, dividierten, wie wir, nur ohne jeden ˇnützlichen Zweck; etwa: weil es ihnen Spaß zu machen scheint. als ˇeine harmlose Unterhaltung⌊.⌋ wie es scheint. Die Jungen lernen es von den Alten durch [z|Z]uschauen. Übrigens ist die Bemerkung “ohne jeden nützlichen Zweck” ganz irrelevant denn ◇◇◇ warum soll Unterhaltung kein nützlicher Zweck sein, & es ließen sich leicht ganz andere nützliche Zwecke dieser Tätigkeit denken, welche die doch nicht ˇmathematische Anwendungen der Mathematik wären. Aber von einer solchen Tätigkeit ließen sich leicht Abbildungen denken, die niemand für Mathematik erklären würde, sondern etwa für einen Tanz oder für das Ornamentieren einer Wandfläche ◇◇◇

​

Ein Traum: Mir träumte neulich: Ich steige auf einen Sessel & kniehe mit einem Knie auf einen Tisch. Der Tisch war eine Art flacher Schreibtisch, ich glaube aus Mahagoniholz & hat in der mitte ein Loch, wie um eine Schreibmaschine aufzunehmen. In dem Loch liegen zwei Spachteln, eine stählerne & eine hölzerne, die sehr schön gearbeitet ist und eine aussieht wie wie ein grösser Brieföffner. Ich kniehe gerade auf den beiden Spachteln & breche die stählerne & die hölzerne. Habe d Fürchte mich dass mein Vorgesetzter sich darüber ärgern wird.

​

Heute nacht träumte ich: Ich steige eine Treppe hinauf. Auf dem obersten Absatz ist sind in einer Art Käfig ein Taubenpaar die b einander sehr lieben. Das Weibchen mag mich nicht, streubt die Federn & will auf mich los gehen so wie ich mich ihr nähere. Gedanke dass sie mir mit dem Schnabel in die Hand stossen würde wenn ich die Hand hin hielte. – Dann: Die Frau ist gest (die Taube) ist gestorben und ihr Mann (nfn ein Mann﹖1) zimmert ihr einen den Sarg: mehrere flache Kisten die um Bilder oder Schriften zu verwahren. Wann setzt er sich ermüdet, & wie um selbst zu sterben, nieder & seine Säge steckt vor ihm in einem Stüch Holz, einem Kasten     Entweder zwischen diesen beiden Szenen oder nach der zweiten (ich weiss es nicht mehr) eine andere: Francis & Drobil sind mit mit in einem Zimmer (einer Schenke?) & ich fange ein Argumet mit einem Dritten an der mir etwas gehagt hat das ich richtig stellen will (ich weiss nicht mehr was). Wahrend ich mit ihm spreche sind die beiden andern fort gegangen, wie ich mich umdrehe sind sie nicht mehr da. Ich gehe sie ◇ im Haus suchen, will erst ins obere dann ins untere Ssclf-zimmer◇ gehen um sie zu suchen, weiss aber dass sie ohne mich ausgegangen sind gahrscheinlich zum N Nachtmahl. Sie werden dann wohl wieder kommn. Bin sehr verstimmt daruber dass sie, & ohne auf mich zu warten, weggegangen sind & wache ˇtraurig auf. Das [h|H]aus in welchem ich in dieser Hzene die beiden suche ist dasselbe in welchem ich in der ersten Hzene die Treppe hinafgestiegen bin & in welchem auch der Mann mit den flacen Kisten die Taube einsargt. Wenn er sich dann zum sterben hinsetzt so ist es als sässe er auf dem Deck ˇim Hinterteil eines Schiffes.

​

26.10.     Ist ein Schachproblem ein Problem der angewandten Mathematik? Vergleiche es mit einem Problem der theoretischen Mechanik.

​

Wenn die Math. ein Spiel ist, so gibt es keinen Unterschied zwischen rein mathem. Axiomen & nicht rein mathematischen. Und man könnte ein Kapitel der M mathem. Physik ebensogut als (ein) Spiel spielen, wie eins aus der Zahlentheorie.

​

Denke Dir solche Schlußketten: dunkler als                     und dunkler als dunkler als daher: der Unterschied zwischen & größer als der zwischen & . Dies ist ein schlechtes Beispiel.

​

Denke Dir die Fünfeckskonstruktion gezeichnet & über sie einen ˇdurchsichtigen Kegel gestellt & in ihm solche Flächen gezogen (dreidimensionale Konstruktion) daß jeder ˇebene Schnitt parallel zur Basis ist offenbar wieder so eine ˇerfolgreiche Fünfeckskonstruktion ergibt ist . Dies wäre eine Konstruktion Beweis in einer anschaulichen Geometrie.

​

Die Augen & die Nase müssen nicht ‘irgendwie’ verwandt’ sein, um ein Gesicht zu ergeben.

​

Es ist natürlich klar, daß der Mathematiker, insofern er wirklich ‘ein Spiel spielt’ nicht keine Schlüsse zieht. Denn ‘[s|S]pielen’ muß hier heißen: nach ˇin Übereinstimmung mit gewissen Regeln handeln. Und schon das wäre ein Heraustreten aus dem bloßen Spiel; wenn er den Schluß zöge, daß er hier der allgemeinen Regel gemäß so handeln dürfe.

​

27.   Aber wie seltsam ist es, zu sagen, daß, wenn Einer die ganze mathem. Literatur Mathematik als Spiel hervorbrächte schriebe , dies daß es dann nicht Mathematik wäre!   Es kann, willst Du sagen, doch nicht auf gedankliche (psychologische) Prozesse ankommen. (Und soweit ist es richtig.)

​

‘Diese müssen unwesentlich sein. Gleichsam Abschweifungen vom Thema.’

​

Statt des obigen conventionellen & schlechten Beispiels wären farbengeometrische Beobachtungen am Farbenkreis zu setzen, die nicht mit der gemeinen Erwartung übereinst.. dem, was man etwa erwarten möchte übereinstimmen (Was man etwa Das also, was man farbengeometrische Paradoxe nennen könnte.)

​

28. Rechnet die Rechenmaschine?

​

Denk Dir, eine Rechenmaschine wäre durch Zufall entstanden; & nun drückt Einer durch Zufall auf ihre Knöpfe (oder eine Maus Tier läuft über sie) & sie rechnet das Produkt 25 × 20. –

​

Ich will sagen: Es ist der Mathematik wesentlich, daß ihre Zeichen auch im Zivil gebraucht werden.           Es ist der Gebrauch außerhalb der Mathematik, also die Bedeutung der Zeichen, was das Zeichenspiel zur Mathematik macht.

​

So wie es ja auch kein logischer Schluß ist, wenn ich von einnem Gebilde (einer Tonreihe in ein anderes transformiere (eine Anordnung ⌊von⌋ Stühle⌊n⌋ ˇetwa in eine andere) wenn diese Anordnungen nicht außerhalb dieser Transformation einen sprachlichen Gebrauch haben.

​

Aber ist nicht das wahr, daß Einer, der nichts von der Bed. der R'schen Zeichen wüsste, die R'schen Beweise … der keine Ahnung von der Bedeutung der Russellschen Zeichen hätte, R's Beweise nachrechnen könnte? Und also in einem wichtigen Sinne prüfen könnte ob sie richtig seien oder falsch?

​

G 1 2 3 S 4 5 6 a 7 8 9 b 10 11 12 c 13 14 15 W Wenn [d|D]as Feld G ⌊ist⌋ gleichmäßig gelb ist, S schwarz, W weiß, & a b c ˇdrei Töne von grau, die in gleichen Farbabständen von S zu W leiten führen . Ebenso leiten führen 1, 2, 3 von G nach S, 4, 5, 6 von G nach a u.s.w.. Dann wird man vielleicht sehen, daß die ˇlotrechten Reihen 1, 4, 7, 10, 13 & 2, 5, 8, 11, 14 & 3, 6, 9, 12, 15 nicht gleichabständig sind. ˇUnd [d|D]ies, ˇoder das Entgegengesetzte, wäre eine farbengeometrische Tatsache.

​

Ich meine: es könnte sein, daß man keine Gleichabständigkeit, der waagrechten &c der senkrechten Reihen ˇnicht zugleich erreichen kann. // Es könnte also sein, daß man gleiche Farbabstände Abstände in den waagrechten & in den senkrechten Reihen zugleich nicht erreichen kann. //

​

Architektur ist eine Geste. Nicht jede zweckmäßige Bewegung des menschlichen Körpers ist eine Geste. Sowenig, wie jedes zweckmäßige Gebäude Architektur.

​

29.   Man könnte eine mensch-liche Rechenmaschine so abrichten, daß sie, wenn ihr die Schlußregeln gezeigt & etwa an Beispielen vorgeführt wurden, die Beweise eines ˇmathem. Systems (etwa des R'schen) durchliest & nach jedem richtig gezogenen Schluß mit dem Kopf nickt bei einem Verstoß gegen die Regel bei einem Fehler aber den Kopf schüttelt, & zu rechnen aufhört. Dieses Wesen könnte man sich im übrigen vollkommen idiotisch vorstellen.

​

Einen Beweis nennen wir etwas, was sich nachrechnen, aber auch kopieren läßt.

​

Wenn die Math. ein Spiel ist, dann ist ein Spiel spielen Mathematik treiben, & warum dann nicht auch: Tanzen?

​

Man könnte sich den Fall denken, daß Einer seinem eignen Rechnen weniger traut, als dem einer Rechenmaschine.

​

Denke Dir, daß Rechenmaschinen Naturprodukte wären in der Natur vorkämen , ihre Gehäuse aber für die Menschen undurchdringlich (wären). Und diese Menschen benützten nun diese Maschine Vorrichtungen etwa wie wir das Rechnen, wovon sie aber gar nichts wissen. Sie machen also etwa Vorhersagen mit Hilfe der Rechenmaschinen, aber für sie ist das Benützen Handhaben dieser ˇseltsamen Gegenstände ein Experimentieren.

​

30.   Diesen Leuten fehlen Begriffe, die wir haben; aber wodurch ersetzen sie diese? // ; aber wodurch sind die diese bei ihnen ersetzt? – //

​

Denke an den Mechanismus dessen Bewegung wir als geometrischen (kinematischen) Beweis ansahen: Das ist klar, das normalerweise von Eeinem der das Rad umtreibt nicht gesagt würde, er beweist etwas.2     Ist es nicht ebenso mit dem, der zum Spiel Zeichen aneinander reiht & diese Reihen verändert; auch wenn, was er hervorbringt als Beweis angesehen werden könnte?

​

Zu sagen, die Math. sei ein Spiel, soll heißen: wir brauchen beim Beweisen nirgends an die Bedeutung der Zeichen appellieren, also an ihre außermathematische Anwendung. Aber was heißt es denn überhaupt : , an diese appellieren? Wie kann so ein Appell etwas fruchten?   Heißt das, aus der Mathematik heraustreten & wieder in sie zurückkehren, oder heißt es aus einer math. Schlußweise in eine andre treten?

​

Was heißt es, einen neuen Begriff von der Oberfläche einer Kugel gewinnen? In wiefern ist das dann ein Begriff von der Oberfläche einer Kugel? Doch nur insofern er sich auf wirkliche Kugeln anwenden läßt.

​

Wieweit muß man einen Begriff vom ‘Satz’ haben, um die R'sche mathem. Logik zu verstehen?

​

1.11.42.   Wenn die ˇintendierte Anwendung der Math. wesentlich ist, wie steht es da mit Teilen der Mathematik, deren Anwendung – , wenigstens oder doch d[ie|as], was Mathematiker für eine die Anwendung hielten halten, – gänzlich phantastisch ist. So daß man, wie in der Mengenlehre, einen Zweig der Math treibt, von dessen Anwendung man sich einen ganz falschen Begriff macht. Treibt man nun nicht doch Mathematik?

​

2.11.   Wenn die arithm. Operationen ˇlediglich zur Konstruktion einer Chiffre dienten wäre ihre Verwendung natürlich grundlegend von der unsern verschieden. Wären diese Operationen dann aber überhaupt mathematische Operationen?

​

Kann man von Dem, der eine Regel des Entzifferns anwendet, sagen, er vollziehe mathem. Operationen? Und doch lassen sich seine Umformungen Transformationen so auffassen. Denn er könnte doch sagen, er berechne, was bei der Entzifferung des Zeichens … ˇnach der und der Regel herauskommen müsse. // des Zeichens … gemäß dem & dem Schlüssel herauskommen müsse. // Und der Satz, ⌊:⌋ daß die Zeichen … dieser Regel gemäß entziffert … ergeben ist ein mathematischer. Sowie auch der Satz : , daß man beim Schachspiel von dieser Stellung constellation zu jener kommen kann.

​

Denke Dir die Geometrie des vierdimensionalen Raums zu dem Zweck betrieben, die Lebensbedingungen der Geister kennen zu lernen. Ist sie darum nicht Mathematik? Und kann ich nun sagen sie bestimme Begriffe?

​

Würde es nicht seltsam klingen Wäre es nicht seltsam von einem Kinde zu sagen, es könne ˇbereits tausende & tausende von Multiplikationen machen – womit man (nämlich) ⌊ge⌋meint ˇsein soll, es könne bereits im unbegrenzten Zahlenraum rechnen. Und zwar doch könnte das noch als eine ˇäußerst bescheidene Ausdrucksweise gelten, da er (ja) nur ‘tausende & tausende’ statt ‘unendlich viele’ sagt.

​

Könnte man sich Menschen denken, die im gewöhnlichen Leben etwa nur bis 1000 rechnen & die Rechnungen mit höheren Zahlen zu mathem. Untersuchungen über die Geisterwelt vorbehalten hat.3

​

‘Jedes Ding ist sich selbst gleich’. Betrachte: “Jedes Ding ist sich selbst sehr ähnlich”!

​

3.11.   Warum nun hat das ‘den Schein der Wahrheit’ & nicht einfach den der Unsinnigkeit?

​

Nehmen wir an, die Bahnen zweier Körper kreuzten sich, so daß die beiden sich zu einer in der Kreuzungsstelle zusammenfielen. Man könnte dann sagen: wo sie zusammenfallen sind sie einander gleich. Und das ist nicht notwendig der Fall: denke etwa an eine perspektivische Darstellung.

​

Wenn wir jemandem Einem zugeständen, daß ‘a = a’ nichts sagt, ihn aber fragten ob er sich nicht doch noch dennoch lieber mit einem der beiden Sätze             ‘a = a’     und ‘a ≠ a’, ˇals mit dem andern einverstanden erklärte; so ist kein Zweifel, er würde sich für ‘a = a’ entscheiden.

​

Er würde sagen: “Ein Ding ist jedenfallsc ˇsich selbst nicht ungleich mit sich selbst”.

​

Zu sagen “ein Ding fällt mit sich selbst zusammen” ist eigentlich eine Bestimmung dessen, was man ‘ein Ding’ nennt.

​

4.11.   Was für eine Art Satz ist eine Gleichung, wie           y = 3x² + 4? Es ist [j|J]edenfalls kein⌊er⌋ Satz der reinen Mathematik, obwohl er nur aus ‘mathematischen’ Zeichen zusammengesetzt ist. besteht.     Die Gleichung kann ein Satz der angewandten Math. sein. In der reinen Math. spielt ist sie die Rolle eines Satzteils (etwa des Satzes daß ihre Lösung für x = 1 y = 7 ist). (Und für “x = 1” gilt ähnliches.)

​

“Ob das nun von einer wirklichen Kugelfläche gilt – von der mathe-matischen gilt es” – das erweckt den Anschein, als unterschiede sich der mathem. Satz von einem Erfahrungssatz insbesondere besonders darin, daß wo die Wahrheit des Erfahrungssatzes schwankend & ungefähr ist, der mathem. Satz sein Objekt exact & unbedingt wahr beschreibt. Als wäre eben die ‘mathem. Kugel’ eine Kugel. Und man könnte sich etwa fragen ob es nur eine solche Kugel, oder ob es mehrere gebe (eine Fregesche Fragestellung).

​

Tut ein Mißverständnis, die denkbaren möglichen Anwendung ˇbetreffend, der Rechnung als ˇeinem Teil der Mathematik [e|E]intrag?

​

Und abgesehen von einem Mißverständnis, – wie ist es mit der bloßen Unklarheit?

​

Wer glaubt, die Mathematiker haben ein seltsames Wesen, die √‒1, entdeckt, das die quadriert nun doch ‒ 1 ergeäbe, kann der nicht doch ganz gut mit komplexen Zahlen [R|r]echnen & solche Rechnungen in der Physik anwenden? Und sind's darum weniger Rechnungen?     In einer Beziehung steht freilich sein Verständnis auf schwachen Füssen; aber aber er wird mit völliger Sicherheit seine Schlüsse ziehen, & sein, Kalkül wird auf festen Füßen stehen.

​

Wäre es nun nicht lächerlich, zu sagen, dieser triebe nicht Mathematik?

​

Es erweitert Einer die Math., & findet neue gibt neue Definitionen & findet neue Lehrsätze – – & in gewisser Beziehung kann man sagen, er wisse nicht, was er tut. – Er hat eine vague Vorstellung, etwas entdeckt zu haben wie einen Raum (wobei er an sein ein Zimmer denkt), ein Reich erschlossen zu haben, & würde, darüber gefragt, viel Unsinn reden.

​

Denken wir uns den primitiven Fall, daß Einer zu seinem Vergnügen ungeheure Multiplikationen ausführte um ˇwie er sagt: dadurch neue riesige Provinzen des Zahlenreichs zu gewinnen.

​

Denk Dir das Rechnen mit der √‒1 wäre von einem Narren erfunden worden, der bloß vom [p|P]aradoxen der Idee angezogen die Rechnung als eine Art Gottes- oder Tempelsdienst Gottesdienst des Absurden treibt. Er bildet sich ein das schlechthin Unmögliche Unmögliche aufzuschreiben & mit ihm zu operieren.

​

Mit andern Worten: Wer an die mathematischen Gegenstände glaubt & ihre seltsamen Eigenschaften, – kann der nicht doch Mathematik betreiben? Oder: – treibt der nicht auch Mathematik?

​

5.11.   ‘Idealer Gegenstand’. “Das Zeichen ‘a’ bezeichnet einen idealen Gegenstand” soll offenbar etwas über die Bedeutung, also den Gebrauch von ‘a’ aussagen. Und es heißt natürlich, daß dieser Gebrauch in gewisser Beziehung ähnlich ist dem eines Zeichens, d[en|as] ein⌊en⌋ Gegenstand ˇhat entspricht bezeichnet, & daß es ◇◇◇ (aber) keinen Gegenstand bezeichnet. Es ist aber interessant, was das Wort der Ausdruck ‘idealer Gegenstand’ aus dem diesem Factum macht.

​

Man könnte sich so ausdrücken: “Der Name ‘Regan’ im Lear bezeichnet eine ideale Person”.

​

Man könnte unter Umständen von einer endlosen Kugelreihe reden. – Denken wir uns eine solche gerade endlose Kugel[r|R]eihe von Kugeln in gleichen Abständen & wir berechnen die Kraft, die alle diese Kugeln nach einem bestimmten Attractionsgesetz auf einen bestimmten Körper ausüben. Die Zahl, die diese Rechnung liefert, betrachten wir als das Ideal der Genauigkeit für gewisse Messungen.

​

Das Gefühl des Seltsamen kommt hier von einem Missverständnis. Der Art von Mißverständnis, die ein Daumenfangen des Verstandes erzeugt⌊ –⌋ [, d|. ⌊–⌋ D]em ich Einhalt gebieten will.

​

Der Einwand, daß ‘das Endliche nicht das Unendliche erfassen kann’ richtet sich eigentlich gegen die Idee eines psychologischen Aktes des Erfassens oder Verstehens.

​

Oder denke Dir, wir sagen einfach: “Diese Kraft entspricht der Anziehung einer [E|e]ndlosen Kugelreihe die so & so angeordnet sind & den Körper nach diesem Attractionsgesetz anziehen”.   Oder wieder: “Berechne die Kraft die eine endlose Kugelreihe, von der & der Beschaffenheit, auf einen Körper ausübt!” – Dieser Befehl hat doch gewiß Sinn. Eine bestimmte Rechnung ist beschrieben.

​

Wie wäre es mit dieser Aufgabe: “Berechne das Gewicht einer Säule ˇvon sovielen aufeinander liegenden geschichteten Platten, als es Kardinalzahlen gibt; die unterste Platte wiegt 1 kg jede höhere immer die Hälfte der vorhergehenden.”

/

Die Schwierigkeit ist nicht die, daß wir uns keine Vorstellung machen können. Es ist leicht genug sich irgend welche eine Vorstellung einer unendlichen Reihe, (oder von dergl. z.B., zu machen. Es fragt sich: was nützt uns die Vorstellung.

/

Denke Dir unendliche Zahlen in⌊:⌋ einem Märchen gebraucht. Die Zwerge haben soviele Goldstücke aufeinander getürmt gelegt , als es Kardinahlzahlen gibt – , etc. Was in einem Märchen vorkommen kann, muß doch Sinn haben. –

/

Denke Dir die Mengenlehre wäre als eine Art Parodie auf die der Mathematik von einem Satiriker erfunden worden. – Später hätte man dann einen vernünftigen Sinn einen Nutzen in ihr gesehen & sie zur in die Mathematik gerechnet einbezogen. (Denn wenn der eine sie als das Paradies der Mathematiker ansehen kann, warum nicht ein andrer als einen Witz Scherz ?)

/

Die Frage ist: ist sie nun als Scherz nicht auch offenbar Mathematik? –

​

Und warum ist sie offenbar Mathematik? – Weil sie ein Zeichenspiel nach Regeln ist?

​

Werden hier nicht doch ˇoffenbar Begriffe gebildet[;| – ] auch wenn man sich über deren Anwendung nicht im Klaren ist?     Aber wie kann man einen Begriff haben & sich über seine Anwendung nicht im Klaren sein? // nicht klar sein? //

​

6.11. Nimm die Konstruktion des Kräfteparallelogrammspolygons: ist das nicht ein Stück angewandter Mathematik? & wo ist der Satz der reinen Mathematik der bei dieser graphischen Berechnung zu Hülfe genommen wird?   Ist dies nicht ein Fall wie der des Stammes, welcher eine rechnerische Technik zum Zweck gewisser Vorhersagungen hat, aber keine Sätze der reinen Mathematik?

​

Die Rechnung die zur Ausführung einer Zeremonie dient. Es werde z.B. nach einer bestimmten Technik aus dem Alter des Vaters & der Mutter & der Anzahl ihrer Kinder die Anzahl der Worte einer Segensformel abgeleitet die auf das Haus der Familie anzu-wenden ist. In einem Gesetz wie dem Mosaischen könnte man sich solche Rechenvorschriften niedergelegt denken Rechenvorgänge beschrieben denken . Und könnte man sich nicht denken, daß das Volk das diese siediese zeremoniellen Rechenvorschriften besitzt im praktischen Leben nie rechnet?

​

Dies wäre zwar ein angewandtes Rechnen, aber es würde nicht dem Zweck der einer Vorhersage dienen.

​

7.11.   Wäre es ein Wunder wenn die Technik des Rechnens eine Familie von Anwendungen hätte?!

​

8.11.   Wie seltsam die Frage ist ob in der unendlichen Entwicklung von π die Figur φ(eine gewisse Anordnung von Ziffern, z.B. ‘770’) vorkommen wird, sieht man erst wenn man die Frage in einer ganz hausbakkenen Weise zu stellen versucht: Menschen sind ˇdarauf abgerichtet worden nach einer gewissen Regel⌊n⌋ Zeichen zu setzen. Sie verfahren nun dieser Abrichtung gemäß & wir fragen sagen es sei ein Problem, ob sie der gegebenen Regel folgend jemals diese Figur φ anschreiben werden.

​

Was aber sagt der, welcher der , wie Weyl, sagt, eines sei klar: man werde oder werde nicht, in der endlosen Entwicklung auf φ kommen?

​

Mir scheint, wer dies sagt, stellt schon selbst eine Regel, ˇoder ein Postulat auf.

​

Wie, wenn man auf eine Frage hin erwiederte: ‘Auf diese Frage gibt es bis jetzt noch keine Antwort’?

​

So könnte etwa der Dichter antworten der gefragt wird ob der Held seiner Dichtung eine Schwester hat oder nicht – wenn er nämlich noch nichts darüber entschieden hat.

​

Die Frage – will ich sagen – verändert ihren Status, wenn sie entscheidbar wird. Denn ein Zusammenhang wird dann gemacht, der früher nicht da war.

​

Man kann von dem Abgerichteten fragen: ‘wie wird er die Regel für diesen Fall ◇◇◇ deuten?’, oder auch ‘wie soll er die Regeln ˇfür diesen Fall deuten’. Wie aber, wenn über diese Frage keine Entscheidung getroffen wurde? – Nun, dann ist die Antwort nicht: ‘er soll sie so deuten, daß φ in der Entwicklung vorkommt’ oder: od ‘er soll sie so deuten daß es nicht vorkommt’, sondern: ‘darüber ist noch nichts entschieden’.

​

Wir mathematisieren mit den Begriffen. – Und mit gewissen Begriffen mehr als mit andern.

​

10.11.   Ich will sagen: Es scheint, als ob ein Entscheidungsgrund bereits vorläge; & er muß erst erfunden werden.

​

Käme das darauf hinaus, zu sagen: Man benutzt beim Denken Reden über die gelernte Technik des Entwickelns das Falsche Bild einer vollendeten Entwicklung (dessen, was man für gewöhnlich ‘Reihe’ nennt) & wird dadurch gezwungen unbeantwortbare Fragen zu stellen.

​

Denn schließlich müßte sich doch jede Frage über die Entwicklung von √2 auf eine praktische Frage, die Technik des Entwickelns betreffend, bringen lassen // von √2 in Form einer praktischen Frage die Technik … stellen lassen // // von √2 als prak-tische Frage … stellen lassen // .

​

Und es handelt sich hier natürlich nicht nur um den Fall der Entwicklung einer Reellen Zahl oder überhaupt ◇◇◇ ein die Erzeugung mathematischer Zeichenspiel, sondern um jeden analogen Vorgang, er sei ein Spiel, oder ein Tanz, etc etc.

​

Wenn Einer den Satz vom ausgeschlossenen Dritten ˇuns als fundamentale größte Wahrheit uns vorhält, so ist klar, daß mit seiner Frage etwas nicht in Ordnung ist war . // uns als größte Wahrheit vorhält, der man nicht entgehen kann könne , – so ist … // // Wenn Einer uns den Satz vom Ausg. Dritten einhämmert, dem nicht zu entgehen sein, – so ist klar … //

​

Wenn einer den Satz vom Ausg Dritten aufstellt so legt er uns gleichsam zwei Bilder zur Auswahl vor & sagt eins müsse der Tatsache entsprechen. Wie aber, wenn es fraglich ist, ob ⌊sich die Bilder ˇhier anwenden lassen?⌋

​

Und wer von der endlosen Entwicklung sagt sie müsse entweder die Figur φ enthalten oder sie nicht enthalten zeigt uns sozusa-gen das Bild einer in die Ferne verlaufenden unübersehbaren Reihe.

​

Wie aber, wenn das Bild in weiter Ferne zu flimmern anfinge?

​

Von einer unendlichen Reihe zu sagen, sie enthielte eine bestimmte Figur nicht, hat nur unter ganz speziellen gewissen Bedingungen Sinn.

​

11.11.   D.h., ⌊:⌋ man hat diesem Satz nur für gewisse Fälle Sinn gegeben.

​

Ungefähr den: Es ist nicht im Gesetz dieser Reihe, keine Figur … zu enthalten. Ferner, man könnte sagen: Wie … Ferner: (So) wie ich die Entwicklung weiterrechne, errechne ich etwas neues über das Gesetz der Reihe. // errechne ich neue Gesetze, denen die Reihe folgt. // // weiterrechne, leite ich neue Gesetze ab, denen die Reihe folgt. //

​

“Nun gut, – so können wir sagen: ‘Es muß entweder im Gesetz der Reihe liegen, daß die Figur in der Entwicklung vorkommt, oder das Gegenteil’.” // , oder daß sie nicht vorkommt’.” Aber ist das so? – “Nun, determiniert das Entwicklungsgesetz die Reihe denn nicht vollkommen?” Und wenn sie es das tut, keine [z|Z]weideutigkeiten läßt, dann muß sie es, implicite, alle Eigenschaften der Reihe bestimmen.” // mitbestimmen.” // // es implicite alle Fragen die Struktur der Reihe betreffend entscheiden.” // – Du denkst da an die endlichen Reihen.

​

‘Aber es sind doch alle Glieder der Reihe bestimmt vom 1sten bis zum 1000sten, bis zum 10¹⁰-ten, etc. etc. u.s.f., bestimmt; also sind doch alle Glieder bestimmt.’ Das ist richtig, wenn es heißen soll es sei nicht (etwa) das so-&-so-vielte nicht bestimmt. Aber Du siehst ja, daß das Dir keinen Aufschluß darüber gibt, ob eine die Figur … (je) in der Reihe erscheinen wird (wenn sie ˇso weit nicht schon erschienen ist). ⌊⌊ˇ Wir sehen also, daß wir ein irreführendes Bild gebrauchen. ⌋⌋

​

Willst Du mehr über die Reihe wissen, so mußt Du, so zu sagen, in eine andere Dimension (gleichsam wie aus der Linie in eine sie umgebende Ebene in die Ebene ) gehen. – Aber ist denn die Ebene nicht eben da, so wie die Linie, ◇◇◇ nicht die Ebene da, wie die Linie, & nur zu erforschen, wenn man wissen will, wie es sich verhält?

​

Nein, die Mathematik dieser weiteren [d|D]imension muß so gut erfunden werden, wie jede Mathematik.

​

In einer Arithmetik, in der man nicht weiter als 5 zählt, hat die Frage, wieviel 4 + 3 ist noch keinen Sinn. Wohl aber kann die Aufgabe das Problem existieren, dieser Frage (einenc) Sinn zu geben. D.h.: die Frage hat so wenig Sinn, wie der Satz vom ausgeschlossenen Dritten, auf sie angewendet.

​

Man meint in dem Satz vom Ausg. Dritten ˇschon etwas Festes zu haben, was jedenfalls nicht in Zweifel zu ziehen ist. Während in Wahrheit der Sinn dieser Tautologie (wenn man so sagen darf) ebenso schwankend ist wie der der Frage, ob p oder ~p der Fall ist. // Während in Wahrheit diese Tautologie einen ebenso schwankenden Sinn (wenn ich so sagen darf) hat, wie die Frage ob p oder ~p der Fall ist.) // // wie die Frage, ob die eine, oder die andere Alternative wahr ist. //

​

12.11. Denke, ich fragte, ⌊:⌋ Was meint man damit “die Figur … kommt in dieser Entwickelung vor?”. So wird man antworten: “Du weißt doch was das heißt⌊.⌋ – [s|S]ie kommt vor, wie z.B. die Figur … in jeder Entwicklung … ˇtatsächlich vorkommt ◇◇◇.” – Wohl; – aber wie kann ich diese Analogie nun anwenden gebrauchen ? Denn ich verstehe wohl, wenn man mir nun sagt: “Kommt die Figur 159 in den ersten 100 Stellen von √2 vor; wie sie in den ersten 10 Stellen von π vorkommt?” // Sie kommt vor, wie die Figur … in der Entwickelung tatsächlich vorkommt” – Also so kommt sie vor? – Aber wie ist das? //           Denke Dir, man sagte: “Entweder sie kommt so vor, oder sie kommt nicht so vor”!

​

‘Aber verstehst Du denn wirklich nicht, was gemeint ist?!’ – Aber kann ich nicht glauben, ich verstehe es & mich irren? –

​

Wie weiß ich denn, was es heißt: die Figur … komme in der Entwicklung vor? Doch durch Beispiele ( – die mir zeigen, wie das ist, wenn … Diese Beispiele zeigen mir aber nicht, wie es ist, wenn die Figur in der Entwicklung nicht vorkommt!

​

Könnte man nicht sagen: wenn ich wirklich ein Recht hätte zu sagen, diese Beispiele lehren micht, wie es ist wenn die Figur in der Entw. vorkommt, so müßten sie mir auch zeigen, was das Gegenteil des Satzes bedeutet.

​

Der allgemeine Satz die Figur kommt in der Entw. nicht vor kann nur ein Gebot sein.

​

Wie wenn man die math. Sätze als Gebote ansieht & sie auch als solche ausspricht? “25² gebe 625!”   Nun, – ⌊–⌋ –, ein Gebot hat eine innere & eine äußere Verneinung.

​

Die Symbole “(x).φx” & “(∃x).φx” sind wohl nützlich in der Math., wenn man im übrigen die Technik der des Beweisees der Existenz oder [n|N]icht⌊-⌋Existenz kennt auf den sich die Russellschen Zeichen hier beziehen. Wird dies aber offen gelassen so sind diese Begriffe der alten Logik äußerst irreführend.

​

Wenn Einer sagt: “aber Du weißt doch was ‘die Figur kommt in der Entw. vor’ bedeutet, nämlich das” – & zeigt auf einen Fall des Vorkommens, – so kann ich nur erwidern, daß was er mir zeigt verschiedene Fakten illustrieren kann. Man kann daher nicht sagen ich wisse was der Satz heißt, weil ich weiß, daß er ihn in diesem Fall gewiß anwenden wird.

​

Das Gegenteil von “es besteht ein Gesetz, daß p” ist nicht: “es besteht ein Gesetz, daß ~p”. Drückt man aber das erste durch P, das andre zweite durch ~P aus, so wird man in [s|S]chwierigkeiten geraten.

​

13.11. Wie, wenn den Kindern beigebracht wird, die Erde Welt sei eine unendliche Ebene; oder Gott habe eine unendliche Reihe von Sternen geschaffen; oder ein Stern fliege in einer geraden Linie gleichförmig immer weiter & weiter ohne je aufzuhören.     Seltsam: wenn man so etwas als selbstverständlich, gleichsam ganz ruhig, aufnimmt, so verliert es alles paradoxe. Es ist als sagte mir uns jemand: Beruhige Dich, diese Reihe, oder Bewegung, läuft fort & fort ohne je aufzuhören. Wir sind sozusagen der Mühe überhaben (je) an ein Ende zu denken.

​

‘Wir werden ein Ende nicht in Betracht ziehen’. (We won't bother about an end.)

​

Man könnte auch sagen: ‘für uns ist die Reihe endlos’.

​

‘Wir werden uns um ein Ende der Reihe nicht bekümmern; für uns ist es immer unabsehbar.’

​

14.11.   Nicht ‘abzählbar’ sollte es heißen – von den rationalen Zahlen etwa – sondern ‘abzählfähig’. Man kann die rationalen Zahlen nicht abzählen, weil man sie nicht zählen kann – , aber man kann mittels der rationalen Zahlen zählen – , so nämlich, so, wie mit den Kardinalzahlen. Die schielende schiefe Ausdrucksweise gehört mit zu dem ganzen System der Vorspiegelung : , daß wir mit ˇdem neuen Apparat d[er|ie] unendlichen Mengen mit der gleichen selben Sicherheit behandeln, wie bis dahin nur die endlichen.

​

15.11.   Aber wo ist hier das Problem? Warum soll ich nicht sagen, [;|,] was wir Mathematik nennen sei eine Familie von Tätigkeiten zu einer Familie von Zwecken.     Die Menschen könnten z.B. Rechnungen zu⌊m⌋ ˇZweck einer Art ⌊von⌋ Wettrennen gebrauchen. Wie Kinder ja wirklich manchmal um die Wette rechnen; nur daß diese Verwendung bei uns eine ganz untergeordnete keine große Rolle spielt.

​

Oder das Multiplizieren könnte uns viel schwerer fallen, als es tut – wenn wir z.B. im Gedächtnis nur mündlich rechneten, & um uns eine Multiplikation zu merken, sie also zu erfassen, wäre es nötig sie in die Form eines gereimten Gedichts zu bringen. Wäre dies dann einem Menschen gelungen, so hätte er das Gefühl, eine große, wunderbare Wahrheit gefunden zu haben.     Es wäre sozusagen für jede neue Multiplikation eine neue individuelle Arbeit nötig.

​

Wenn diese Leute nun glaubten, die Zahlen wären Geister & durch ihre Rechnungen erforschten sie das Geisterreich, oder zwängen die Geister, sich zu offenbaren – wäre dies nun Arithmetik? Oder – wäre es auch dann Arithmetik, wenn diese Menschen die Rechnungen zu nichts anderm gebrauchten?

​

(Ich suche einen Abstieg.)

​

Der Vergleich mit der Alchemie liegt nahe. Man könnte von einer Alchemie in der Mathematik reden.

​

‘Man kennt sich nicht aus’ heißt nicht: man weiß nicht, wo man geht – sondern, man weiß nicht wohin diese Richtung führen wird & wohin jene andere führen wird. Ich meine: wer sich im Wald verloren hat, sieht wohl allerdings den Fleck um ihn herum klar vor sich, aber die Geographie des Waldes kennt er doch nicht. // Waldes ist ihm doch unbekannt⌊.⌋ // ,   D.h., er wird sich verloren fühlen, obwohl er seine Umgebung klar vor sich sieht.   So kennt man sich in den ‘Grundlagen’ der Math. nicht aus – nicht, weil man nicht weiß, was man tut; sondern weil die Geographie der ˇgroßen Zusammenhänge ˇuns unbekannt ist.

​

Charakterisiert schon das die mathem. Alchimie, daß Macht schon das die … aus, daßIst schon das die … die mathem. Sätze als Aussagen über mathem. Gegenstände betrachtet werden, – also die Math. als die Erforschung dieser Gegenstände?

​

In einem gewissen Sinn kann man in der Math. darum nicht an die Bedeutung der Zeichen appellieren, weil die Math. ihnen erst die Bedeutung gibt.

​

Es ist das typische der Erscheinung von welcher ich [R|r]ede, daß das mysteriöse an irgend einem mathem. Begriff nicht sofort als Fehler irrige Auffas-sung, als Fehlbegriff, gedeutet wird; sondern als etwas, was ˇjedenfalls nicht zu verachten, vielleicht sogar ˇeher zu respectieren ist.

​

Alles was ich tun machen kann ist einen leichten Weg aus dieser Unklarheit & dem Glitzern der Begriffe zeigen.

​

Man kann seltsamerweise sagen, daß an allen diesen glänzenden Begriffsbildungen ein sozusagen solider Kern ist. Und ich möchte sagen, daß der es ist der sie zu mathem. Produkten macht.

​

Man könnte sagen: Was Du siehst schaut freilich mehr wie eine glänzende Lufterscheinung aus; aber sieh sie von einem einer andern Winkel Seite an & [d|D]u siehst sie als den (einen) soliden Körper, der nur von aus jener Richtung aus gesehen schimmert glänzt & unkörperlich aussieht. // der nur aus von jener Richtung wie ein Glanz ohne körperliches Substrat aussieht. // // der nur aus jener Richtung wie ein Glanz aussieht der zu keinem Körper gehört. //

​

Ich fürchte sehr für die Gesundheit meiner Nerven. Sie sind sehr stark belastet.

​

16.11.   Ich habe die Tiefe nicht einfach durch Weite ersetzt.

​

‘Die Figur ist in der Reihe, oder sie ist nicht in der Reihe’ heißt: entweder schaut die Sache so aus oder sie schaut nicht so aus.

​

Wie weiß man, was das Gegenteil des Satzes “φ kommt in der Reihe vor”, oder auch des Satzes “φ kommt nicht in der Reihe vor” bedeutet? Diese Frage klingt unsinnig, hat aber doch einen Sinn.   Nämlich: wie weiß ich, daß ich den Satz, “φ kommt in der Reihe vor”, verstehe.   Es ist wahr : , ich kann Beispiele geben für das Vorkommen & Nicht-Vorkommen. // geben für den Gebrauch solcher Aussagen, & auch der gegenteiligen. // Und sie sind Beispiele dafür, daß es eine Regel gibt, die das Vorkommen in einer bestimmten Zone, oder einer Reihe von Zonen, vorschreibt, oder ˇbestimmt daß das dies Vorkommen ausgeschlossen ist.

​

Wenn “Du tust es” heißt: Du mußt es tun, & “Du tust es nicht” heißt: Du darfst es nicht tun – dann ist “Du tust es, oder Du tust es nicht” nicht der Satz vom ausgeschlossenen Dritten.

​

Jeder fühlt sich ungemütlich bei de[r|m] Idee Gedanken, ein Satz könne aussagen sage aus , in der endlosen Reihe komme das & das nicht vor[.| –] [d|D]dagegen hat es gar nichts befremdliches daß ein Befehl sage aussagt in dieser Reihe dürfe, soweit sie auch fortgesetzt werde, das nicht vorkommen.

​

Woher aber dieser Unterschied zwischen: “soweit Du auch gehst, wirst Du das nie finden” – & “soweit Du auch gehst darfst Du das nie tun”?

​

Auf jenen Satz kann man fragen: “wie kann man so etwas wissen”, aber nichts analoges gilt vom Befehl zweiten .

​

Die Aussage scheint sich zu übernehmen, der Befehl aber gar nicht.

​

Kann man sich denken, daß alle mathematischen Sätze im Imperativ ausgesprochen würden? Z.B.: “10 × 10 sei 100”

​

Und wer nun sagt: “Es sei so, oder es sei nicht so”, der spricht nicht den Satz vom ausgeschl. Dritten aus, – wohl aber sondern eine Regel. (Wie ich es schon auch weiter oben einmal gesagt habe.)

​

17.11.   Aber ist das wirklich ein Ausweg aus der Schwierigkeit? Denn wie verhält es sich dann mit allen anderen mathem. Sätzen, sagen wir 25² = 625, gilt für diese nicht der Satz vom ausg. Dritten innerhalb der Mathematik?

​

Wie wendet man denn den Satz vom ausg. Dritten an?

​

18.11.   “Es gibt entweder eine Regel die es geverbietet, oder eine, die es vergebietet”

​

Angenommen, es gibt keine Regel die das Vorkommen verbietet, – warum soll es dann eine [G|g]eben, die es gebietet?

​

Hat es Sinn zu sagen: “Es gibt zwar keine Regel die das Vorkommen verbietet, die Figur kommt aber tatsächlich doch nicht vor”? – Und wenn das nun keinen Sinn hat , – wie kann das Gegenteil davon Sinn haben, nämlich, die Figur komme vor?

​

Nun, wenn ich sage, sie kommt vor, schwebt mir das Bild der Reihe vor, von ihrem Anfang bis zu jener der Figur – wenn ich aber sage die Figur komme nicht vor, so nützt mir kein ˇsolches Bild der Reihec. // so nützt mir kein solches Bild, & die Bilder gehen mir aus. //

​

Wie, wenn die Regel sich beim Gebrauch unmerklich biegen würde? Ich meine so, daß ich von verschiedenen Räumen sprechen könnte, in denen ich sie gebrauche.

​

Das Gegenteil von “ φ es darf nicht vorkommen” heißt “ φ es darf vorkommen”. Für ein endliches Stück der Reihe aber scheint das Gegenteil von “ φ es darf in ihm nicht vorkommen” zu sein: “ φ es muß ˇdarin vorkommen”.

​

19.11.   Das Seltsame in der Alternative “φ kommt in der unendl. Reihe vor, oder es kommt nicht vor” ist, daß wir uns die beiden Möglichkeiten einzeln separat // ◇◇◇ // vorstellen müssen, daß wir nicht wie sonst nach einer Vorstellung für jedes ˇbesonders suchen, & daß nicht wie sonst eine zureicht für den negativen Fall & für den positiven zureicht.

​

Wie weiß ich, daß der allgemeine Satz “Es gibt …” hier Sinn hat? Nun, wenn er zu einer Mitteilung ˇüber die Technik des Entwickelns in einem Sprachspiel verwendet werden kann.

​

Eine Mitteilung heißt: “es darf nicht vorkommen” – d.h.: wenn es vorkommt, hast Du falsch gerechnet.   Eine heißt: “es darf vorkommen”, d.h., es existiert so ein Verbot nicht. Eine heißt: “es muß in de[n|r] & de[n|r] Inter Region (an diesen den & den Stellen, immer in diesen den & den Regionen) vorkommen”. Das Gegenteil ˇdavon aber scheint zu sein: “es darf – dort & dort – nicht vorkommen”, ⌊–⌋ statt “es muß dort nicht vorkommen”.     Wie aber, wenn man die Regel gäbe, daß, z.B., überall, wo die Bildungsregel von π 4 ergibt, statt der 4 auch eine beliebige andere Ziffer gesetzt werden kann.     Zieh auch die Regel in Betracht die an gewissen Stellen eine Ziffer verbietet, aber im übrigen die Wahl offen läßt.

​

20.11.   Ist es nicht so? [d|D]ie Begriffe in den mathematischen Sätzen von den unendlichen Dezimalbrüchen sind nicht Begriffe von Reihen, sondern von der unbegrenzten Technik des Entwickelns von Reihen.

​

Wir lernen eine endlose Technik: D.h., es wird uns etwas vorgemacht, wir machen es nach; es werden uns Regeln gesagt & wir machen Übungen in ihrer Befolgung; es wird dabei vielleicht auch ein der Ausdruck wie “u.s.f. ad inf.” gebraucht, aber damit ist nicht von ˇirgend einer riesenhaften riesigen Ausdehnung die Rede. // , aber es ist damit von keiner riesenhaften Ausdehnung die Rede. //

​

Das sind die Fa[c|k]ten. Und was heißt es nun: “φ kommt entweder in der Entwicklung vor, oder es kommt nicht vor”[!|?]

​

Aber heißt das nun, daß es kein Problem gibt: “Kommt die Figur φ in dieser Entwicklung vor?”? – Wer das fragt fragt & nach einer Regel das Vorkommen von φ betreffend. Und die Alternative des Existierens oder Nichtexistierens so einer Regel ist jedenfalls keine mathematische.

​

Erstc innerhalb einem, erst zu errichtenden, mathem. Gebäude wird die Frage zur mathematischen. // wird die Frage zur Forderung einer mathematischen Entscheidung. // // mathem. Gebäude läßt die Frage eine mathem Entscheidung zu & wird somit zur Forderung einer solchen Entscheidung. //

​

Ist denn das Unendliche nicht wirklich – kann ich nicht sagen: “diese zwei Kanten der Platte schneiden sich im Unendlichen”?

​

Nicht “der Kreis hat diese Eigenschaft weil er durch die beiden unendlich fernen Punkte … geht”; sondern: “die Eigenschaften des Kreises lassen sich aus dieser (merkwürdigen) Perspektive anschauen betrachten ”.

​

Es ist wesentlich eine Perspektive & eine weithergeholte. (Womit kein Tadel ausgesprochen ist.) Aber es muß immer ganz klar sein wie weit hergeholt diese Anschauungsart ist. Denn sonst ist ihre eigentliche Bedeutung im Dunkeln.

​

Was heißt das?: “der Mathematiker weiß nicht was er tut”, oder “er weiß was er tut”?

​

23.11.   Kann man unendliche Vorhersagungen machen? – Nun, warum soll man nicht z.B. das Trägheitsgesetz eine solche nennen? Oder den Satz, daß sich ein Komet eine Parabel beschreibt?     In gewissem Sinne wird freilich ihre [u|U]nendlichkeit nicht sehr ernst genommen.

​

Wie ist es nun mit einer Vorhersagung : , daß, wer π entwickelt, so weit er auch gehen mag geht , nie auf die Figur φ stoßen wird? – Nun, man könnte sagen, daß dies entweder eine unmathematische Vorhersagung ist, oder (aber) eine mathematische Regel.

​

Jemand, der das Entwickeln von √2 entwickeln gelernt hat geht zu einer ◇◇◇ ˇ◇◇◇ Wahrsagerin, & sie weissagt ihm, daß er sie, soweit er auch die √2 entwickeln mag, ˇer nie zur ˇeiner Figur … gelangen wird. Ist ihre Weissagung ein mathem. Satz Proposition? Nein[,|.] – [a|A]ußer sie sagt: “wenn Du immer richtig entwickel⌊s⌋t hast, wirst Du nie nicht dahin kommen”. entwickeln wirst, kommst Du nie …. Aber ist das noch eine Vorhersage?

​

Es scheint nun, daß so eine Vorhersage des richtig entwickelten denkbar wäre und sich von einem mathem. Gesetz, daß es sich so & so verhalten muß, unterschiede. So daß es in der ˇmathem. Entwicklung einen Unterschied gäbe zwischen dem, was tatsächlich so herauskommt – sozusagen gleichsam zufällig – & dem, was herauskommen muß.

​

24.11.     Wie soll man es entscheiden : , ob eine unendliche Voraussage Sinn hat?           So jedenfalls nicht, indem daß man sagt: “ich bin weiß doch offenbar, was ich sicher, ich meine etwas, wenn ich sage …”.

​

Auch ist wohl nicht so sehr die Frage, ob die Voraussage irgend einen Sinn hat, als: was für eine Art von Sinn sie hat. (Also, ˇin welchen Sprachspielen mit sie vorkommt.)

​

25.11.   Die Mathematiker lieben einen haut-goût an ihren Sätzen, der, wie überall, dadurch zustande kommt, daß etwas in Fäulnis übergegangen ist von der Fäulnis herrührt.

​

‘Übereinstimmung’ heißt zum Teil, ˇder Friede & ˇdie Eintracht.

​

Ein Traum: Ich lebte in einer Wohnung, wie in einem Wiener Mietshaus. Im gleichen Stock neben mir hatte Smythies eine Wohnung; im ersten Stockwerk unter ihm Timy Moore. Ich sehe diesen öfters & wir musizieren. – Ich trete einmal vor mir und ein Portier der aus S.'s Türe kommt sagt mir etwas in spaßhafter Weise (ich habe das Wort vergessen, welches er gebrauchte) woraus ich entnehme daß S. gestorben sei. Ich hatte ihn abwesend geglaubt, aber er muß ohne mein Wissen zurückgekommen, sein krank gewesen & gestorben sein. Ich bin sehr von der Nachricht betroffen, denke, daß er Moore & mich musizieren gehört hat & allein krank gewe-sen ist & mich nicht gerufen hat. – Ich gehe dann in S.'s Wohnung & treffe da seinen Vater, der komisch aussieht, mehr wie eine Frau. Ich frage ob S. eine Botschaft Nachricht für mich hinterlassen habe, oder etwas über mich gesagt habe. Es war auf einem großen Tisch ein Bild da mit andern Sachen aus dem Nachlaß das S. als Andenken für mich bestimmt hatte & eine Landkarte für einen Herrn in so & so (Namen vergessen) in Prag. Ich war ein wenig auf diesen, den S. kaum gekannt haben konnte, eifersüchtig, sagte mir aber dass ein Bild doch von mehr Zuneigung zeuge als eine Landkarte. – Wurde von großer Angst für Francis befallen, der irgendwo auf dem Lande sei & von dem ich lange nicht gehört hatte. Ich sagte mir, daß ich ihm gleich telegraphieren müsse und erfahren wie es ihm geht. – Ich wachte mit Angst und Besorgnis auf.

​

28.11. “Der unheilvolle Einbruch” der Logik in die Mathematik.

​

Denke Dir Menschen die keine Gelegenheit hätten je mehr als 1000 Dinge Gegenstände zu zählen, – die aber dennoch mit Zahlen über Tausend rechneten. [s|S]ie sagen z.B. 1000² = = 100² + 900² + 180000

​

1.12.   Was kann man eigentlich an der naiven Auffassung der ‘mathematischen Realität’ falsch nennen, ⌊ –⌋ abgesehen von dem Abstoßenden der Auffassung –?

​

In dem so vorbereiteten Feld ist das ein Existenzbeweis.

​

Das Verderbliche der logischen Technik ist, daß sie uns die spezielle mathem. Technik vergessen läßt // macht // . Während die logische Technik nur eine Hilfstechnik in der Math ist. ˇZ.B. gewisse Verbindungen zwischen anderen Techniken herstellt.

​

Es ist beinahe als wollte man sagen, daß das Tischlern im Leimen besteht.

​

So könnte man Dedekinds Theorem ableiten wenn, was wir irrationale Zahlen nennen ganz unbekannt wäre, wenn es aber eine Technik gäbe, die Stellen vor Dezimalzahlen zu würfeln. Und dieses Theorem hätte dann seine Anwendung auch wenn es die Mathematik der irrationalen Zahlen nicht gäbe. Es ist nicht, als sähen die Dedekindschen Entwicklungen die alle besonderen irrational reellen Zahlen schon voraus. Es scheint nur so, sobald man d[ie|en] D.sche⌊n⌋ Technik Kalkül mit den Kalkülen der besonderen reellen Zahlen vereinigt.

​

Der Beweis überzeugt Dich davon, daß es eine Wurzel der Gleichung gibt (ohne Dir eine Ahnung zu geben wo) – – wie weißt Du, daß Du den Satz verstehst, es gebe eine Wurzel? Wie weißt Du daß Du wirklich von etwas überzeugt bist? Du magst davon überzeugt sein, daß sich die Anwendung des bewiesenen Satzes finden lassen wird. Aber Du verstehst ihn nicht solange Du sie nicht gefunden hast.

​

Wenn ein Beweis allgemein beweist, es gebe eine Wurzel, so kommt alles darauf an, in welcher Form er das beweist. Was es ist, das hier zu diesem Wortausdruck führt, der ein bloßer Schein ist & die Hauptsache verschweigt. Während er den Logikern nur die Nebensache zu verschweigen scheint.

​

2.12.   Was hat die Beweismethode zu tun mit dem, was bewiesen ist?

​

Der eine Beweis ˇsagt Dir (als wäre er eine Person) sagt Dir daß dies vorkommt. Der andere ˇsagt Dir, wo es vorkommt. – So scheint es. Und es ist als käme es gar nicht mehr drauf an wie jener Satz bewiesen wurde. Genug, daß er bewiesen ist & wir nun wissen, daß es vorkommt ¤. Wir können es dann gleichsam unsern Kindern überliefern (hand down) ¤ … komme vor. Und sie werden so wenig wissen wie wir. Es klingt dann mehr wie eine Fabel. Und könnte vielleicht die Rolle einer Fabel spielen.

​

‘Wir müssen also müssen annehmen, daß … irgendwo 0 wird’. Dieser Satz ist nur darum nicht ein bloßer Mythus, weil sein Beweis der Anfang einer Ortsbestimmung ist. Oder vielmehr: Der Satz der als Existenzialsatz angesehen ein Mythus ist, ist es darum nicht in einer andern Beleuchtung.

​

Der Satz als Existenzsatz Existenzialsatz sagt uns, so zu sagen, ein Geheimnis.

​

3.12. Der Beweis zeigt dieses Bild der Sache. – Aber damit ist es noch nicht klar, was wir mit diesem Bild anfangen können.

​

Das Bewiesene sagt “es ˇder Ausdruck muß irgendwo 0 werden”: Aber nun kommt alles darauf an, auf welche Weise der an, wie der Beweis das sagt; ob das nun ein guter, oder ein, im Ganzen, irreführender Ausdruck des Bewiesenen war, wird sich auf diese Weise zeigen[,|.] Der Beweis kann Dich lehren, wie der Satz etwa anzuwenden wäre.

​

8.12. “Abzählbar” dürfte es nicht heißen, dagegen hätte es [s|S]inn zu sagen “numerierbar”. Und dieser Ausdruck läßt auch eine die Anwendung des Begriffs erkennen. Denn man kann zwar die R⌊r⌋nal⌊en⌋[z|Z]ahlen nicht abzählen wollen, wohl aber kann man ihnen Nummern zulegen wollen.

​

Das mathematisch Allgemeine steht zum mathematisch Besonderen nicht in dem Verhältnis wie sonst das Allgemeine zum Besondern.

​

Alles was ich sage kommt eigentlich darauf hinaus, daß man einen Beweis genau wohl kennen kann & ihm auch Schritt für Schritt folgen kann, & dabei doch, was bewiesen w[ü|u]rde, nicht ver-steht.

​

Und das hängt wieder damit zusammen, daß man einen ˇmathem. Satz richtig grammatisch richtig bilden kann ohne seinen Sinn zu verstehen.

​

Wann versteht man ihn nun? – Ich glaube: wenn man ihn anwenden kann.   Man könnte vielleicht // könnte auch // sagen: wenn man ein klares Bild von seiner Anwendung hat. Das heißt aber [d|D]azu aber genügt es nicht, daß man ein klares Bild mit ihm verbindet. Vielmehr wäre besser gewesen zu sagen: wenn man eine klare Übersicht von seiner Anwendung hat. Und auch das ist schlecht, denn es handelt sich nur darum daß man die Anwendung nicht dort vermutet wo sie nicht ist; daß man sich von der Wortform des Satzes nicht täuschen läßt.

​

Wie kommt es aber nun daß man einen Satz, oder Beweis, auf diese Weise nicht verstehen, oder mißverstehen kann? Und was ist dann nötig um dieses Verständnis herbeizuführen?

​

Es gibt da, glaube ich, Fälle in denen Einer man den Fall, daß Einer den Satz (oder Beweis) zwar anwenden kann, dar über die Art dieser der Anwendung aber keine nicht klar Rechenschaft zu geben im Stande ist. Und den Fall, daß er den Satz auch nicht anzuwenden weiß. (Mult. Ax.)

​

Wie ist es in der Beziehung mit 0 × 0 = 0?

​

9.12. Man möchte sagen, das Verständnis eines math. Satzes sei nicht durch seine Wortform guarantiert, wie im Fall der meisten nicht-mathematischen Sätze. Das heißt – so scheint es – daß der Wortlaut das Sprachspiel nicht bestimmt, in welchem der Satz funktioniert.

​

Die logische Notation verschluckt die Struktur.

​

Um zu sehen, wie man etwas ‘Existenzbeweis’ nennen kann, was keine Konstruktion des Existierenden zuläßt, denke an die verschiedenartigendenen Bedeutungen des Wortes “wo”., den (z.B. des topolo- gischen & des metrischen.)

​

10.12.   Es kann ja der Existenzbeweis nicht nur den Ort des ‘Existierenden’ unbestimmt offen lassen, sondern es braucht auf einen solchen Ort gar nicht anzukommen.           D.h.: wenn der bewiesene Satz lautet “es gibt eine Zahl, für die … ” so muß es keinen Sinn haben zu fragen “und welches ist diese Zahl”, oder zu sagen “und diese Zahl ist …”

​

11.12.   Vom Beweis durch reductio ad absurdum kann man sich immer vorstellen, daß er ˇwerde im Argument mit einem Opponenten jemand ge- braucht werde, der eine mathematisch unhaltbare Behauptung macht. Ich meine aber nicht eine mathematische Behauptung. // Ich meine aber nicht die Behauptung eines mathematischen Satzes. // Ich meine aber die Behauptung eines nicht-mathematischen Satzes. // Etwa, er habe gesehen, wie der A den B mit den & den Figuren matt gesetzt gemacht habe – wenn das ˇnach den Regeln nicht möglich ist. // er werde im Argument mit eine[m|r] Menschen Person gebraucht, die eine mathematisch widerlegbare nicht-mathematische Behauptung gemacht hat. Etwa: er habe gesehen … // // er werde im Argument mit jemandem verwendet, der eine nicht--mathematische Behauptung aufstellt, die sich mathematisch widerlegen läßt. Etwa: … // // er werde im Argument mit jemandem gebraucht, der eine nicht-mathematische Behauptung macht aufstellt (etwa: er habe gesehen, daß, A den B mit … matt gesetzt habe) die sich mathematisch widerlegen läßt. //

​

Die Schwierigkeit, die man beim Beweis durch reduc- tio ad absurdum in der Math. empfindet ist die: Was geht bei diesem Beweis vor? Etwas mathematisch Absurdes, also [u|U]nmathematisches? Wie kann man – möchte man fragen – das mathematisch Absurde überhaupt nur annehmen? Daß ich das physikalisch Falsche annehmen & ad absurdum führen kann macht mir keine Schwierigkeiten. Aber wie das ˇsozusagen Undenkbare denken?!

​

Der ˇindirekte Beweis sagt aber: “wenn Du es so willst, darfst Du das nicht annehmen: denn damit wäre ist nur das Gegenteil von dem dessen vereinbar wovon Du nicht abgehen willst”.

​

12.12.   Was mich in einer Darstellung, wie z.B. Hardy's, stört ist die scheinbar sinnlose Varietät von Beweisen ˇdesselben Satzes.   Ich möchte sagen: jeder dieser Beweise gehört zu einer bestimmten besonderen Gelegenheit bei der welcher gerade er anzwenden wäre.

​

Du glaubst daß ( 14142 10000 )² = 2

​

Ich sage: Nenne, zur Abkürzung 14142 ‘p’ & 10000 ‘q’. Dann folgt aus Deiner Aussage ‘ p² q² = 2’, daß auch (2q ‒ p)² (p ‒ q)² = 2 ist.

​

Aber p q mußte natürlich kleiner sein als 2, also ist p ‒ q ˂ q Da aber q ˂ p sein muß, ist 2q ‒ p ˂ q ˂ p Also ist p² q² = ( ˂ p)² ( ˂ q)² & das ganz abgesehen davon ob p² q² schon vollkommen gekürzt ist. Wenn immer Du also einen Bruch für die Wurzel aus zweier vollkommener Quadrate, der vollkommen gekürzt ist, für gleich 2 hieltest so kannst Du einen andern Bruch mit kleinerem Zähler & Nenner bilden, der dem ersten dann gleich sein müßte ([N|n]ämlich aus jedem p² q² , das gleich 2 ist, ein (2q ‒ p)² (p ‒ q)² ); der dem ersten gleich sein müßte, aber natürlich nicht ist.

​

Man kann den Beweis aber auch so anfangen: Wenn p q ein vollkommen gekürzter Bruch ist & p ˃ q q ˂ p ˂ 2q ist, so kann p² q² nicht gleich (2q ‒ p)² (p ‒ q)² sein, da p ‒ q ˂ q ist.     Wäre aber ein Bruch p² q² = 2 so müßte p² q² gerade gleich = (2q ‒ p)² (p ‒ q)² werden sein . Also kann ein Bruch p² q² nie gleich 2 sein.

​

Wohl aber kann p² q² sich (2q ‒ p)² (p ‒ q)² ‘beliebig nähern’ wenn p² q² sich der 2 nähert. [e|E]s wird dann (2q ‒ p)² (p ‒ q)² eine schlechtere Annäherung sein als p² q² , & wenn man den Prozess fortführt & aus (2q ‒ p)² (p ‒ q)² bildet (3p ‒ 4q)² (3q ‒ 2p)² , (10q ‒ 7p)² (5p ‒ 7q)² , etc. so kommt man, zu statt immer zu der gleichen Zahl, zu immer schlechteren Annäherungen.

​

Ich meine: man könnte die Umstände finden, unter welchen der Beweis gerade in der H.schen Form der richtige ist. // der richtige, der treffende, ist. //

​

13.12. Statt “Nehmen wir an ( p q )² = 2” wäre es besser zu sagen: “Prüfe ‘( p q )² = 2’”, oder “Prüfe: ( p q )² = 2”. – Denn nun kann man es ja auf verschiedene [w|W]eise prüfen.

​

Die Frage, ob p² q² je 2 wird, hängt mit einer großen Anzahl anderer mathematischer Verhältnisse zusammen, & die jener Beweise zeig[e|t]n diese solche Zusammenhänge & auch solche, daß wenn wir p² q² = 2 zulassen, welche Stellungen wir aufgeben müssen, wenn wir ( p q )² = 2 zulassen.

​

Dies ist eine bestimmte Beweis-Maschinerie, nicht die ewig-gültige Form eines Beweises. (Ich denke an Gödels einleitender beiläufiger Beweisführung.)

​

14.12.   Die ˇgeometrische Illustration der math Analysis ist allerdings unwesentlich, nicht aber die geometrische Anwendung. Ursprünglich waren die geometrischen Illustrationen Anwendungen der Analysis. Wo sie aufhören dies zu sein, können sie leicht gänzlich irreführen.   Hier haben wir dann die phantastische Anwendung. Die eingebildete Anwendung.

​

Die Idee des ‘Schnittes’ ist so eine gefährliche Illustration

​

Nur soweit, als die Illustrationen auch Anwendungen sind, erzeugen sie nicht d[ieses|as] jenes gewisse Schwindelgefühl, das die Illustration erzeugt im Moment, wo sie aufhört eine mögliche Anwendung zu sein; wo sie also dumm wi⌊r⌋d.

​

Ich habe wahrscheinlich zu wenig Ruhe & zu viel Unannehmlichkeit. Das Letztere ist in gewissem Sinne gut für mich, wenn ich noch im Stande bin daraus zu lernen, was ˇleider zweifelhaft scheint.

​

15.12. Wir kämpfen jetzt gegen eine Richtung. Aber diese Richtung wird sterben, durch andere Richtungen verdrängt,⌊.⌋ [un|Un]d dann wird man unsere Argumentation gegen sie nicht mehr verstehen; nicht begreifen, warum man all das hat sagen müssen.

​

So seltsam es klingt: [d|D]ie [w|W]eiterentwicklung einer irrationalen Zahl ist eine Weiterentwicklung der Mathematik.

​

Eine Beweisführung ist prüde, wenn die geringste kleinste logische // , wenn die lässigste logische // Zweideutigkeit ängstlich vermieden ˇwird, grober Unsinn aber geduldet⌊.⌋ wird. // vermieden wird, & grober Unsinn geduldet. //

​

Die Hauptunklarheit in der Mathematik ist die Unklarheit darüber, was entdeckt & was bestimmt wird.

​

16.12. Eine Beweisführung ist prüde: wenn man ängstlich die geringste logische Zweideutigkeit vermeidet, aber groben Unsinn duldet.

​

Wie, wenn ich sagte, die allgemeine Theorie der reellen Zahlen bereitet eine Phraseologie vor, die dann im besondern Fall von großem Nutzen ist. – Aber wenn indem sie diese Phraseologie vorbereitet kann ist sie entweder ein selbständiges Stück Mathematik⌊,⌋ sein oder sie kann könnte die reellen Zahlen in vager Allgemeinheit durch Beispiele behandeln. Dabei würde natürlich die Exactheit nichts einbüßen, denn die Anwendung dieser allgemeinen Fingerzeige auf jeden besonderen Fall würde immer wieder vollkommene Bestimmtheit herstellen.

​

17.12. Den Fehler in einem schiefen Raisonnement suchen & Fingerhut-Vestecken.

​

Man könnte fragen: Was könnte ein Kind von 10 Jahren am Beweis des Dedekindschen Satzes nicht verstehen? – Ist denn dieser Beweis nicht viel einfacher, als ˇalle die Rechnungen die so ⌊das⌋ ein Kind beherrschen muß? – Und wenn nun jemand sagte: den tieferen Inhalt des Satzes kann es nicht verstehen – dann frage ich: wie kommt dieser Satz dieses Gesetz zu einem tiefen Inhalt?

​

Es wird nirgends bei Hardy hervorgehoben, daß die irrationale Zahl nicht ˇin dem Sinne wie die rationale ein Zahl ein Zahlzeichen besitzt. Die Fiction ist wohl, daß sie ein unendlich langes hat. Am ehesten könnte natürlich noch das Zeichen der Entwicklungsregel als ⌊das⌋ Zahlzeichen gelten. – Aber dieses Fehlen des Zahlzeichens bedeutet einen unendlich fundamentalen Unter-schied. Und in gewissem Sinne sagt ja der Cantorsche Diagonalbeweis, daß sie kein Zahlzeichen haben kann.

​

Das Bild der Zahlengeraden ist ein absolut natürliches bis zu einem gewissen Punkt: nämlich, soweit man es nicht zu einer allgemeinen Theorie der reellen Zahlen gebraucht

​

23.12.   Ich will, daß alle Zeichnungen, Illustrationen die aus diskreten Punkten & Strichen bestehen, wie sie ˇin den Büchern die Lehre von den irrationalen Zahlen, des Limes, der Stätigkeitˇ der Funktionen, etc usw. begleiten, sich auf die Wahl diskreter Zahlen & Zahlenkombinationen beziehen, & – nicht auf Funktionen, irrationale Zahlen, etc!

​

Aber angenommen, Du hattest eine solche Lehre vom Wählen diskreter Zahlen, – würdest Du nicht dennoch eine allgemeine Lehre de über die Funktionen brauchen können

​

Ich brauche eine variable, die in gewissem Sinn Kurven als ihre Werte annimmt, aber nicht Gesetze, Gleichungen, son-dern Extensionen. Man könnte sich die Variable etwa durch eine Kombination einer gezeichneten Linie mit bezifferten Punkten & Tangenten vorstellen, etwa

​

D.h., die Zeichnung würde nur gewisse Züge (Eigenschaften) der Kurve aussprechen & nicht einer Gleichung der Kurve entsprechen.   Die Variable nimmt also, ˇz.B., nicht einen keinen Kreis als Wert an. Aber ein Kreis könnte z.B. dazu dienen diese die Werte zu begrenzen, ˇetwa auszudrücken zu zeigen daß die Kurve ganz innerhalb des Kreises liegen muß.

​

Und man braucht natürlich keine Zeichnung sondern kann eine Art Formel verwenden, die aber so einer Art Figur entspricht.

​

Alles kommt darauf an, daß man die Kurve, den Wert der Variablen, wählen kann, d.h. aus einem dazu vorbereiteten System beliebig wählen kann & sie nicht zu entdecken oder zu erfinden hat.

​

Die Kurven könnten sozusagen rationale Kurven sein, die man wählen kann wie rationale Zahlen.

​

Ich möchte also sagen daß die Continuität einer Kurve die sich aus ihrer Gleichung als secundäre Regel ergibt auch als primäre Regel soll funktionieren können.

​

Die Kontinuität eines Streifens scheint leicht zu definieren.

​

‘Ich stelle Dir alle Punkte dieses Streifens zur Verfügung.’

​

Aber wie soll man die kontinuierliche Teilung eines Streifens erklären?

​

Etwa durch eine Kette gerader Strecken?

​

29.12. Was an meinen Spekulationen über einen extensiven Kalkül, der sich mit dem der einzelnen Funktionen verbinden ließe, nicht in Ordnung ist: dash weil daß ich ˇbin ganz unklar darüber bin, was die Anwendung so eines Kalküls sein könnte. unabhängig von best den Funktionen sein könnte.

​

30.12. Die Variable, wie ich mir sie denke, ist sozusagen eine topologische Einheit.

​

Warum soll ein Punkt P(x,y) eine erlaubte Angabe sein, & nicht auch eine ‘Linie L(x1,y1 ❘ x2y2)’ was eine kontinuierliche Verbindung von P(x1 y1) & Q(x2 y2) bedeuten soll. L(P, Q) entspricht nicht einer bestimmten Kurve, oder Gleichung sondern nur, sozusagen, einem kontinuierlichen Faden zwischen P & Q über dessen Gestalt noch nichts gesagt ist; aber noch gesagt werden kann.

​

Nichts ist so schwierig in der Philosophie als den gegenwärtigen Stand der Dinge anzuerkennen.

​

‘Eine Kurve planen’

​

Ich will eine Kontinuität Stätigkeit des Fadens nicht der Kurve. Des Fadens, mit dem man stätige Kurven legen kann.

​

Die Kontinuität des Fadens soll gl so erklärt werden; daß er, gleichsam, nichts von der einen Seite auf die andere durchläßt.

​

31.12.42. Wäre es möglich Abschnitte auf der X & Y Achse einander zuzuordnen, & nicht bloß Punkte.                      x x1→x4 x4→x3 3→2 2→5 5 5→6 6         y y3→y4 y4→y5 5→4 4→2 2→1 1 2

​

1.1.43. Die Pfeile besag[t|en] eigentlich, daß, ⌊:⌋ wenn ich einem Punkt P einen Punkt Q zuordne & R ist rechts von P, ˇdaß dann φ(R)– , also S, über Q liegen soll muß , u. u.. Wenn ich dann die Erlaubnis habe jedem beliebigen Punkt (d.h. (Zahl) zwischen A & B einen Punkt zwischen C & D zuzuordnen, so kann mann dies, die Erlaubnis einer stetigen Zuordnung nennen.

​

2.1.43.     Die Rolle der Beispiele, das ist unser Problem. Und das zeigt von welcher Art die philosophischen Probleme in der Mathematik sind.

​

Wenn Du die reellen Zahlen in eine höhere & eine ni⌊e⌋dere Klasse Teilen willst, so tu's erst einmal roh durch zwei rationale Punkte P & Q. Dann halbiere P – Q & entscheide, in welcher Hälfte (wenn nicht im Teilungspunkt) der Schnitt liegen soll; wenn z.B. in der unteren, halbiere diese & mache eine genauere Entscheidung; u.s.f..   Hast Du ein Prinzip der [U|u]nbegrenzten [f|F]ortsetzung, so kannst Du von diesem Prinzip sagen, es führe einen Schnitt aus, da es von jeder Zahl entscheidet, ob sie rechts oder links liegt. – Nun ist die Frage, ob ich durch ein solches Prinzip der Teilung überall hin gelangen kann oder ˇob noch eine andere Art der Entscheidung nötig ist; & man könnte fragen, ob nach der vollendeten Entscheidung durch das Prinzip oder vor der Vollendung. Nun, jedenfalls nicht vor der Vollendung; denn solange noch die Frage ist in welchem endlichen Stück der Geraden der Punkt liegen soll, kann die weitere Teilung entscheiden. – Aber nach der Entscheidung durch ein Prinzip ist noch Raum für eine weitere Entscheidung?

​

Es ist mit dem Dedekindschen Satz wie mit dem Satz vom ausgeschlossenen Dritten: Er scheint ein Drittes auszuschließen, während von einem Dritten in ihm nicht die Rede ist.

​

Der Beweis des D.schen Satzes arbeitet mit einem Bild, da[ß|s] ihn nicht rechtfertigen kann, das eher vom Satz gerechtfertigt werden soll.

​

Ein Prinzip der Teilung siehst Du leicht für eine unendliche fortgesetzte Teilung an, denn es entspricht jedenfalls keiner endlichen Teilung & scheint Dich weiter & weiter zu führen.

​

Ist es aber nicht lächerlich, daß mir die Idee eines inten allgemeinen intentionalen Kalküls der Funktionen & Konstruktionen solche Schwierigkeiten zu bereiten scheint? Ist es nicht ein Vorurteil? Nun man müßte sich mit dem Begriff eines Kalküls vertraut machen der noch unvollendet, ergänzungsbedürftig, ist.   Er wird in mit der Begleitung von Beispielen betrieben, oder es wird vorausgesetzt, daß uns so viele Beispiele gegenwärtig sind, daß wir jeden Moment Anwendung auf ein bestimmtes machen können.

​

Ich will sagen: es muß ein Gesetz geben, möglich ein Befehl, gegeben werden können, der lautet: “[k|K]onstruiere eine Kurve deren y für x → ∞ sich ℓ nähern!” Es hängt alles davon ab ob so ein Befehl möglich ist. (Und er bezieht sich natürlich nicht auf das zufällige finden von gewissen Funktionen.     Was heißt aber “konstruiere eine Kurve”? Es kann doch nicht heißen ziehe eine unendlich lange Linie.

​

Man könnte auch so fragen: könnte man nicht die Lehre vom Limes, der Funktionen, der reellen Zahlen, mehr, als man es tut, extensional vorbereiten? auch wenn dieser vorbereitende Kalkül sehr trivial & an sich nutzlos erscheinen sollte?

​

Die Schwierigkeit der ◇◇◇ halb ˇbald [ex|in]tensionalen ˇbald wieder extensionalen Betrachtungsweisec Auffassung beginnt schon beim Begriff des ‘Schnittes’.   Daß man jede ration. Zahl ein Prinzip der Teilung der rat. Zahlen nennen kann ist wohl klar. Nun entdecken wir ein etwas anderes was wir Prinzip der Teilung ˇnennen können, etwas das, welches der √2 entspricht. Dann andere äh⌊n⌋liche Fälle – & nun sind wir mit der möglichkeit solcher Teilungen schon ganz wohlvertraut, & sehen sie unter dem Bild eines irgendwo entlang der Geraden ausgeführten Schnittes, also extensional. Denn wenn ich schneide, so kann ich ja wählen, wo ich schneiden will.     Ist der Schnitt aber ein Prinzip der Teilung ein Schnitt, so es dies doch nur weil man von beliebigen rat. Zahlen sagen kann sie seien oberhalb oder unterhalb des Schnitts. – Kann man nun sagen die Idee des Schnitts habe uns von den rat. Zahlen zu irrationalen Zahlen geführt? Sind wir denn z.B. zur √2 durch den Begriff des Schnitts gelangt. Oder nicht vielmehr umgekehrt   Was ist nun ein Schnitt der reellen Zahlen? Nun, ein Prinzip der Teilung in eine größere & eine untere & eine obere Klasse. So ein Prinzip gibt also jede rat. & irrat. Zahl ab. Denn wenn wir auch kein System der irrat. Zahlen haben so zerfallen doch die, die wir haben, in obere & untere in Bezug auf den Schnitt (soweit sie mit ihm nämlich vergleichbar sind).   Nun ist aber die Dedekindsche Idee, daß die Einteilung in eine obere & untere Klasse (mit den bekannten Bedingungen) die reelle Zahl ist.

​

Der Schnitt ist eine extensive Vorstellung.

​

Es ist freilich wahr daß wenn ich ein mathematisches Kriterium habe um für eine belie-bige rat. Zahl festzustellen ob sie zur oberen oder unteren Klasse gehört, es ein leichtes ist mich dem Ort beliebig systematisch zu nähern, wo die beiden Klassen sich treffen.

​

Wir machen bei Dedekind einen Schnitt nicht dadurch, daß wir schneiden ˇalso auf den Ort zeigen, sondern daß wir, – wie beim Finden der Quadratwurzel aus 2 √2 – uns den ˇeinander zugekehrten zweier oberen & unteren Klassen nähern.

​

Nun soll bewiesen werden, daß keine andere Art von Zahlen, als nur die reellen, so einen Schnitt ausführen können.

​

6.1.    Vergessen wir nicht Wir dürfen nicht vergessen , daß ursprünglich die Teilung der ration. Zahlen in zwei Klassen keinen Sinn hatte, bis wir auf gewisses aufmerksam machten, was man so beschreiben bezeichnen konnte. Der Begriff ist vom täglichen Leben // Sprachgebrauch // hergenommen & scheint darum auch für die Zahlen unmittelbar einen Sinn zu haben zu müssen.

​

Wenn man nun die eines Schnitts der reellen Zahlen einführt, indem man sagt, es sei jetzt einfach der Begriff des Schnitts von den rat. auf die reellen Z. auszudehnen; alles was wir brauchen ist eine Eigenschaft, die die reellen Z. in zwei Klassen einteilt (etc.) – so ist zunächst nicht klar was mit so einer Eigenschaft gemeint ist, die alle reellen Zahlen so einteilt. Nun kann man uns darauf aufmerksam machen, daß jede reelle Zahl so ein Prinzip ist dazu dienen kann. Aber das führt uns nur soweit & nicht weiter.

​

Denk' Dir, Du wolltest von Spielen in der Verallgemeinerung sprechen.

​

Haben wir zwei Reihen reeller Zahlen, deren eine ganz unterhalb der andern liegt & deren Glieder sich einander unbegrenzt nähern, dann kann man zwei Reihen rationaler Zahlen konstruieren, die dem gleichen Punkt zustreben: wie die Reihen den d.h.: die untere ˇrationale Reihe läuft nirgends der unteren reellen vor, noch die obere rationale der oberen reellen & die beiden rationalen Reihen nähern sich einander unbegrenzt.

Editorial notes

1) See facsimile; light deletion line with question mark over "nun ein Mann".

2) See facsimile; cancellation of new paragraph.

3) See facsimile; unclear sentence "... Rechnungen mit höheren Zahlen zu mathematischen Untersuchungen über die Geisterwelt vorbehalten hat".