1.
The experience of fright appears (when we philosophise) to be an amorphous experience behind the experience of starting. |
All I want to say is that it is
misleading to say that the word
“fright” signifies something which goes
along with the experience of expressing fright. |
There is here again the queer case of
a difference between
what we say, when we actually
try to see what happens, & what
we say when we think about it
(giving over the reins to
language). |
The ‘far away’ look, the dreamy voice
seem to be only means for conveying
the real inner feeling. |
“Therefore there must be something
else” means nothing unless it expresses
a resolution to use a certain
mode of expression. |
Suppose you tried to separate the feeling
which music
gives you from hearing music. 2. |
Say & mean “long, long
ago–”, “lang
ist es her–”& now put instead
of these words new ones with many
more syllables & try if you can
put the same meaning into the words.
Put instead of the copula a very
long word say “Kalamazoo”. |
Puella, Poeta
“‘masculine’ &
‘feminine’ feeling”
of || ‘attached’
to a. |
Aren't there two (or more) ways to
any event I might describe? |
We say “making this gesture isn't
all”.
The first answer is: We are talking about
the experience of making
the || this
gesture.
Secondly: it is true that different
experiences can be described by
the same gesture; but not in the
sense that one is the pure one
& the others consist …. |
Wie ist es wenn man einmal die
besondere Klangfarbe eines Tones
merkt || hört ein andermal nur den Klang als
solchen?
3. |
◇◇◇◇◇◇
“Ich nenne diesen Eindruck ‘blau’”. |
Wie kann man denn die genaue Erfahrung in
‘Poeta’ etc.
beschreiben? |
The philosophical problem is:
“What is it that
puzzles me
about || in this matter?” |
To give names is to label things;
but how does one label impressions. |
Das männliche a & das weibliche a. |
Es läßt sich über die besondere || bestimmte Erfahrung einiges sagen & außerdem
scheint es etwas, & zwar das
Wesentlichste, zu geben was sich nicht beschreiben
läßt. |
Man sagt hier, daß ein bestimmter
Eindruck benannt wird.
Und darin liegt etwas Seltsames &
Problematisches.
Denn es ist als wäre der Eindruck
4
etwas zu Ätherisches um ihn zu benennen.
(Den Reichtum einer Frau heiraten.) |
Du sagst Du hast einen ungreifbaren Eindruck.
Ich bezweifle nicht, was Du sagst aber ich
frage ob Du damit etwas gesagt hast.
D.h. wozu hast Du diese Worte geäußert, in welchem
Spiel. |
It is as though, if || although you can't tell me
exactly what happens inside you, you can nevertheless tell me something
general about it.
By saying e.g. that you are having an
impression which can't be further described. |
As it were: There is something further about it,
only you can't say it; you can only make the
general statement.
It is this idea || form of expression which plays hell with us. |
“There is not only the gesture but a
particular feeling which I can't describe”: instead
of that you might have said: “I am
trying to point out a feeling to you”
which || this would be a grammatical remark showing
how my information is meant to be used.
This is almost similar as though I said “This I call
‘A’ & I am pointing out a
colour to you not a
shape”. |
How can we point to the colour & not to the shape?
Or to the feeling of toothache & not to the tooth
etc.? |
What does one call “describing a feeling to
someone”? |
“Never mind the shape, – look at the
colour!” |
“Was there a feeling of pastness when you said you remembered
…?”
‘I know of none’. |
How does one point to a number, draw attention to a number, mean
a number? |
How do I call a taste
“lemon-taste”?
6
Is it by having that taste & saying the words: “I
call the taste …”? |
And can I give a name to any one
taste-experience without giving the
taste a common name which is to be used in common language? –
“I give my feeling a name, nobody else can know what the
name means.” |
A slave has to remind me of something
& isn't to know what he reminds me of. |
7 |
“I use the name for the impression
directly & not in such a way that anyone
else can understand it.” |
Buying something from oneself.
Going through the operations of buying. |
My right hand selling to my left hand. |
Gefühls- (Gedanken-) Übertragung. |
Eine gute Art eine Farbe zu benennen wäre, in einer
entsprechend gefärbten Tinte den Namen schreiben. |
“I name the feeling”– I
don't quite know how you do this, what use you are
making of the word || name. |
“I'm giving the feeling, which I
have || I'm having just now a
name”. –
I don't quite know what you are doing. |
One might say: “What is the use of talking of our
feeling at all.
Let
8 us devise a language which really
only says what can be understood.”
Thus I am not to say “I have a feeling of
pastness”: But |
“This pain I call ‘toothache’ & I can
never make him understand what it means”. |
We are under the impression that we can point to the pain, as it were
unseen by the other person, & name it. |
For what does it mean that this pain || feeling is the
meaning of this name? |
Or, that the pain is the bearer of the name?
It is the substantive ‘pain’ which puzzles us. This substantive seems to produce an illusion. What would things look like if we expressed pains by moaning & holding the painful spot? Or that we utter the word pain pointing to a spot. “But that the point is that we should 9 say ‘pain’ when there
really is pain.”
But how am I to know if there really is pain? if what I feel really is pain? Or, if I really have a feeling?‒ ‒ ‒ |
Es ist sehr nützlich zu bedenken: Wie würde ich in einer
Gebärdensprache ausdrücken: “ich hatte keine Schmerzen, aber
stellte mich, als ob ich welche hatte”? |
“He has pains, says he has pains & saying
‘pains’ he means his pains.”
How does he mean his pains by the word ‘pain’
or ‘toothache’? |
“He says ‘I see green’
& means the colour he sees.” –
If asked afterwards what did you mean by ‘green’ he
might answer ‘I meant the colour’, pointing to it.
10 |
“In my own case I know that when I say ‘I
have pain’ this utterance is accompanied by something;– but is it also accompanied by something in another man?”
In as much as his utterance needn't be accompanied by my pain. I may say that it isn't accompanied by anything. |
“I know what I mean by ‘toothache’ but
the other person can't know it.” |
Als negation: “The deuce he
is ….” |
Die Philosophie eines Stammes der als Negation nur den
Ausdruck benützt || kennt:
“I'll be damned
if …”. |
On a beau
dire …. |
“Man kann nie einen ganzen Körper sehen sondern nur
immer einen Teil seiner Oberfläche.” |
“Give the impression a name!”
that seems to have sense. “It seems to me that I can mean the impression”. It seems to me that I can will the table to approach. “Can one push air?” 3. |
We said that what we described as “numeral
equality”, “being 1-1 correlated”,
“having the number n” were widely differing
phenomena.
That therefore it was an illusion to think that to say
“the classes fall in pairs” is, generally speaking an
analysis of what we call numeric equality in simpler terms.
We can if we like put “being numerically equal” =
“falling into pairs” but the use of the one
expression just as of the other has got to be explained in the particular
case.
This we only forget.
Thinking about a very special class of examples.
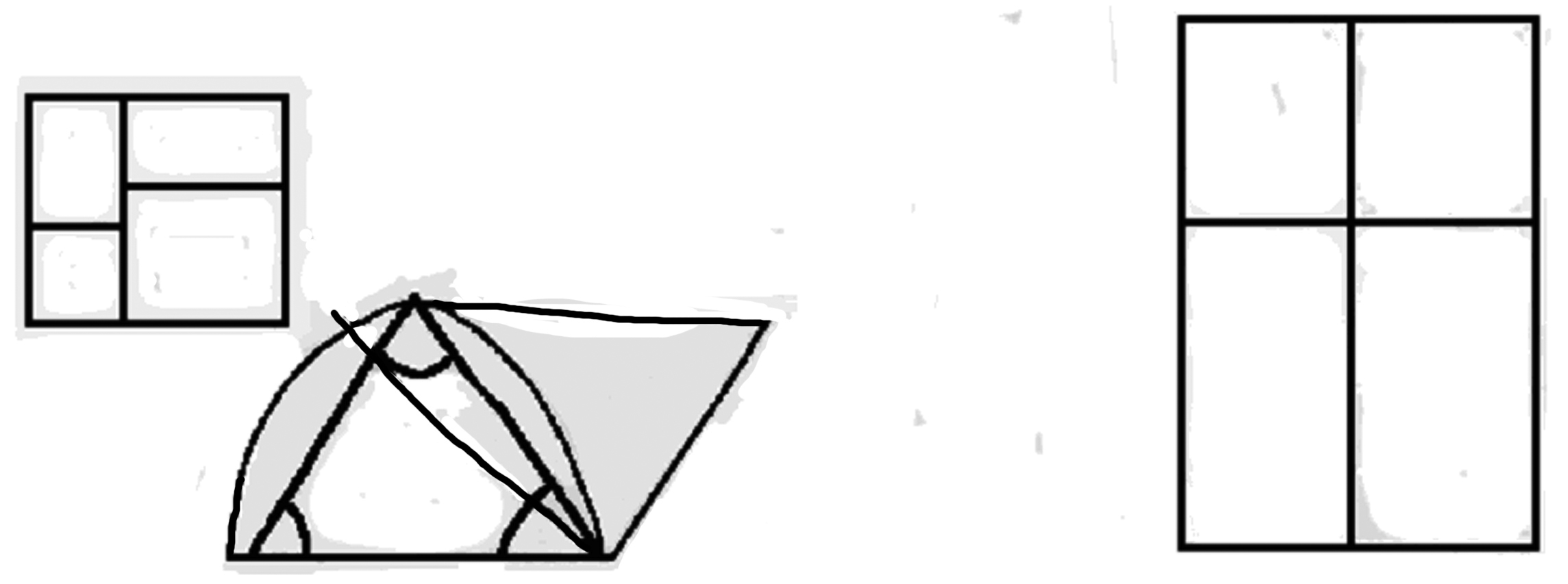
One could also say that a length a was twice another one b if two a superimposed gave b. Application for wavelengths. This brings me to the topic of 8 demonstration.
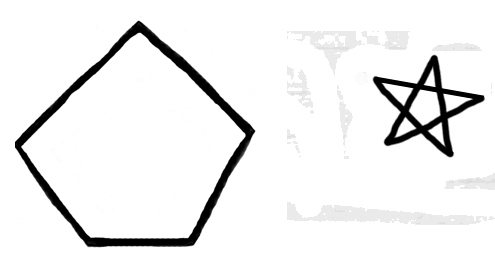
1)  number of outer
vertices =
5.
number of outer
vertices =
5.Compare with “the Hand has 5 Fingers.” Timelessness. The same holds of “The number of outer vertices = number of inner vertices”. Question which is answered by this proposition timeless. Apparent generality of demonstration The copula has no tenses. ◇◇◇ idea is that the idea of a pentagram is bound up with a cardinal number Now, we could make all sorts of connections. “It is the essence of these figures to be capable of being divided || connected in this way”. 9 |
Pythagoras Is the result of the process taken as a standard or not.  “These two
triangles by this nature give the
rectangle”. “These two
triangles by this nature give the
rectangle”.4 This aspect might never have struck you. 
10
a
+ (◇◇◇) = (◇◇◇ + b) + c
It seems you can't get out.
You must adopt a + (b + c) =
(a + b) + c if you adopt
a + (b + 1) = (a + b)
+ 1. a + (b + 1) = (a + b) + 1 a + (b + 2) = (a + b) + 2 |
But need we really say that a + (b + 2) =
(a + b) + 2 follows from
a + (b + 1) =
(a + b) + 1? |
The reasoning is:
a + (b + 2) = a + (b + (1 + 1)) = a + ((b + 1) + 1) = = (a + (b + 1)) + 1 = ((a + b) + 1) + 1 = (a + b) + (1 + 1) 5 + (6 + 1) = (5 + 6) + 1 5 + (6 + 2) = |
I show you a curve drawn in a pentagon which you had never
thought of & I say: I am showing you that
11. this curve can be
drawn, – or: that there is such a curve in the pentagon.
That there are two twos in four. |
Is there really no way out of saying, say, that a triangle which has
3 equal sides has also three equal angles. |
Does  consist of consist of
 & &
 ?
It depends what kind of dispute it is.
You could say it consisted of ?
It depends what kind of dispute it is.
You could say it consisted of Counting5 12
This
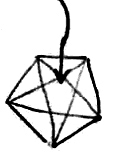
doesn't show that a + b fits butit shows that it looks like it does. “What kind of figure do you get if you draw the diagonals in a Pentagon?” What sort of body do you get if you draw the diagonals on a dodecaeder. What kind of number do you get if you draw 3s in 9. What kind of colour do you get if you mix red with yellow? “The figure shows him that a pentagram fits into a pentagon”. Is this an experimental result? 13. |
I am now talking always of a particular kind of
demonstration; what one might call a visual demonstration.
|
In what sense could I say that I didn't know that the
pentagram fitted the pentagon?
Could I have imagined the opposite?
Suppose I had imagined the opposite in some sense then in the same sense I could still hold the opposite after the demonstration. |
“I never knew that I could see the Pentagon
& its diagonals in this aspect.” 7 “Oh, that's how it fits!” Two tunes fitting together. 15 |
8 “I don't know whether the pentagram fits the pentagon. If so the diagonals of a pentagon must give a pentagram. Let's try it.” Is to see the figure 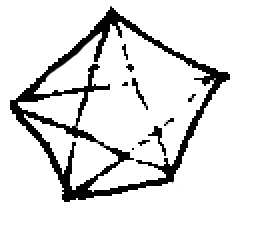 an experiment?
Or to see side by side the figures an experiment?
Or to see side by side the figures ? ?
But doesn't it teach us something? “It never struck me.” |
It seems we are learning by experience a timeless truth about the shape of
a Pentagon & of a Pentagram. |
“I never knew that one could look at it
16 that way.
I had never seen the pentagram in the pentagon.”
|
It is a new experience to me.
But is it the experience teaching me that the pentagram fits the
pentagon? |
“The visual image p fits
the visual image P.”
The importance of this proposition lies in this that
it seems a proposition of experience &
that on the other hand it also is used as a
proposition of geometry
i.e. of grammar. |
Problem: “Draw that Star which will fit the
Pentagon.”
This is a mathematical problem. |
“What do the diagonals of a P look
like?” |
We look at a puzzle picture & find a man in the foliage of a
tree.
Our visual impression changes.
But can't || mustn't we say that the new
experience would have been impossible if the old one
hadn't been what it was?
Such that we seem bound to say the new
experience was already preformed in the old
one.
Or that I found something new which was already in the essence of the
first picture. |
We seem to have demonstrated an internal property of the old
picture.
18 |
Die mathematische Frage. Could the Pythagorean theorem be assumed instead of being deduced? |
To see five figures as 3
figures + 2 figures.
If 5 is =
2 + 3 it
can't mean anything to see 5 as
2 +
3.
You could divide 5 into 2 + 3 but not into 3 + 3 as you could 6.
20
|
The whole question is really: “can it strike you
what a thing is?” 10 It seems you can find out something about the nature of a thing by experience. About its internal nature. Thus e.g. a similarity can strike you; the fact that a complex contains a constituent; even 21 identity of shape.
Two tunes fitting. |
“One can see immediately that 4 consists of
2 +
2”.
This is nonsense if 4 = 2
+ 2. |
~ [~p ∙ ~(~r ∙ ~s)] ∙ ~[~(~t ∙ ~~s ∙ ~t)) ∙ ~p] |
What do I do when I draw your attention to a fact about,
say, this formula?
It seems I make you see something about its essence.
You get a new experience; but this experience, ¤ it seems, teaches you
something about the essence the internal nature of the formula.
It seems to teach you a mathematical (or logical) truth
& this does not seem to be a rule of grammar but a truth about the
22
nature of things. |
If I made an experiment with a certain figure we can ◇◇◇
imagine this or that result.
But if I draw your attention to a feature … |
It consists of … appears to have 1) a grammatical meaning 2)
a physical meaning & 3) a meaning lying between these
two. |
We seem to learn something about the very
sense-datum. |
A certain symbolism will easily go with a certain aspect of looking at a
thing. |
“They regard the square as a double right
angle.” |
One couldn't call 0˙3̇
a shorthand for
0˙333 ….
Except insofar as 0˙33 … is also a shorthand for
0˙333 …. |
“Don't try to find a 4 in the development
it's hopeless!” –
“Don't multiply
25 × 25
24 again & again in the hope to find
600; it's hopeless!”
What's it like to try to find a 4 in the development of 1 : 3? And what is it like to find a 4. |
What is the importance ¤ of
the question: “What is it like?” or
“What is the verification?” |
Kein Kalkül ist im “Widerspruch mit der Logik”
d.h. mit gewissen Regeln die über allen andern
stehen.
Die Annahme einer obersten Logik ist es, die hier irreführt. |
What we should call finding a 4 in 1/3
obviously depends upon the operations in this case. |
What does it mean to imagine getting a result from a
calculation?
How far is this imagination to go? |
“There isn't a 4 in the first million
places”– “You've got a quick way of
calculating that!” |
Imagine this operation: A decimal
25 fraction constructed by multiplying again
& again 25 ×
25: 0˙625625625 … Look for an 8 in it!” “You know that you will never find an 8” means: “Don't try to divide 2476 without remainder by 3 it's hopeless”. |
In which case is it hopeless to find a particular result by a
calculation? |
Calculating is the process of imagining a calculation. |
“I can hope to find an 8 in the Product
284 × 379.” |
To say “it's hopeless to find a certain result
really means: our calculation has already shown it to
be wrong. |
Or: we have a calculation which we make have that
opposite result. |
What is the 65th || 56th
place of 1 : 7?
You can now say it seems what the 10¹⁰ place
‘will’ be. 26 |
How can one calculation anticipate the result of another? |
Or: Our
calculus || calculation
has already decided against it. |
What does it mean: to prophesy what one will correctly
find. |
|
Das Bild “Alle” angewandt auf die Unendlichkeit. |
To show mathematically that a 4 can be found is to describe what it is
like to find a 4.
And to find a 4 is here a process in space and time. |
“Find, as the result of a calculation” &
“Find, otherwise”. |
In 1 : 7 gibt es ein endliches
Problem & ein unendliches.
27 |
❘ ❘ ❘ ❘ ❘ ❘ ❘ ❘ ❘ ❘ ❘ ❘ ❘ 13 : 5 = 2 311 Two processes of calculation lead to the same result. |
“What if they at some stage did not lead to the same result”. – “That is impossible, we couldn't imagine their not leading to the same result.” But then the proof of their leading to the same result showed us what it was like to lead to the same result. |
The difficulty consists in this that it here seems impossible to
imagine anything but what really is the case: And
that of course means nothing!
We don't seem to be able to imagine finding a 4, because there is a three there. But then how are we capable of imagining to find a 3 as there is a 3 there? |
If I say I can't imagine a 4
29 to result it means that the calculation
shows me what it means to imagine a 3 to result & gives no sense
to the proposition “I imagine a 4 to
result”. |
x² +
ax + b = 0
“Solve this equation algebraically!”
|
“Do something that has an analogy to
….”
But we can't be sure that we shall not in the end give up the idea of something being analogous to …. |
The existence of a || something we call
the ‘solution’ seems to show clearly that there
was a clear & definite problem. |
Suppose we said that a solution is a solution only
so far as it could have been described
before it was found. |
“Solve x² + 2ab + b² = 0.” “Solve x² + 4x + 5 = 0.” 30 |
“We can't imagine that 1 : 7
should not repeat itself after the dividend has come
back.”
|
We have two ways of calculating the
10¹⁰th
place & we can't imagine that they lead to different
results. |
Ist es eine Bestätigung hierfür wenn die beiden
Bemerkungen in einem bestimmten Fall übereinstimmen?
|
Is it different to say “they lead to the same
result” & “they must lead
to the same result”? |
Does it mean anything to “prophesy” the result of a
calculation? |
We say we can't imagine that the two processes should not
lead to the same result.
What does it mean, we can't imagine it? 31 |
Must we recognise Periodicity as a proof that there will be no 6 in
the development of 1 : 7?
|
“How does it happen that
3 × 4 is
4 × 3?” |
“An dieser Stelle muß eine Primzahl kommen” –
“An dieser Stelle kommt || steht eine
Primzahl”. |
‘Gibt es einen Zufall in der Mathematik?’
|
How does the returning to the dividend show me the periodicity
of the quotient. |
Denke an den Fall wenn man mehrere Züge in einem Spiel zusammenzieht
& etwa im Schach gar nicht erst mit der ersten Position
anfängt. |
“Die Form ‘1 2 3 4 5’ paßt auf die Form Was für ein Faktum ist das, daß die Reihenfolge das Resultat nicht ändert. The process we are going through just does lead to the same result; – but so far as it “leads to the same result” we could imagine it to lead to a different 33 result.
And so far as we couldn't imagine it to lead to a
different result it doesn't lead to any result but shows
what it's like to lead to the same result.
I.e.: If we look at the Forms |
“How can you impose two rules on your
arithmetic unless you know that they must lead to the
same result?”
You wish to say: “These rules by their very nature, lead to the same result.” And you would therefore have recognised something about the very nature of them. |
Now it is time that you make a man look into the
case || working of these rules; that is, you can prove something
about them. |
“You go through this way of thinking & then you go
through another way of thinking which independently leads to the same
result.” |
123456 123456
2 2 2 |
After you have seen that 1000 : 3 must
lead to 333 is it a confirmation to calculate it & see what it
does?
Hadn't you calculated it by “seeing that it was
333”?
And what does it mean that one calculation confirms the result of the
other? 35
If you first see that the two calculations must lead to the same result is it a confirmation to find that they do?  |
“If this goes on this way & that goes on that way they
must meet there!” |
25 25 25 25 ‒ ‒ ‒ 16 times 16 16 16 16 25 times They must meet at the end. “Are you surprised that they meet? Didn't you know that they had to meet?” |
“I wasn't surprised I always followed the
25s while going on with the 16s.”
36 |
Can we try whether it does? |
Can we imagine the same calculation to lead twice || the
second time to a different result? |
The question is really whether there can be a “must” in
a proposition about the
37
nature of things. |
“In the sense in which they ‘must’
lead, we can't say
they do lead. |
Wir nehmen ein falsches Verhältnis von Prozeß
& Resultat an.
Denn es heißt nicht daß ein gewisser Prozeß zu einem bestimmten Resultat führen muß. |
Denn ein Prozeß muß nur dazu führen daß er
geschehen ist. |
Ich kann mir eine Blume auf gewisse Weise gewachsen
denken.
Und das Wachstum ist dann ein Prozeß dessen Ende der
Zustand der Blume ist. |
In welchem Sinne ist es möglich nicht zu wissen wohin ein
mathematischer Vorgang führt.
Man könnte antworten es ist möglich nicht zu wissen, wohin er führen
wird aber nicht, nicht zu wissen wohin er führt.
In one sense you can't know the process without knowing the result, as the result is the end of the process. In 39 the other you may know a process
& not know the result. |
In mathematics we object to say these processes have the
… |
A calculation leads to a result mathematically apart
from the fact whether I have actually performed it. |
‘If I say this calculation must lead to this result it
has already led to
it.’ |
If I say ‘this calculation must lead to the same result’
by “this calculation” I am referring to
whatever I call a method of calculating. |
Does calculating that there isn't a six … confirm
the result that there couldn't be? |
“You already see what happens, it must always go on like
this.”
Now suppose you actually went on would this confirm what you saw
before? |
A man says, “I see that the two calculations so far agree
but I don't know why they should go on agreeing”.
Shall we say that he doesn't see a truth
which the other sees? –
He tries always again & again.
We ask him: “But don't you see that you
must get to the same result again?”
Should we say that he must go the long way of experience, where we go the shorter one of seeing? 41 |
“If the multiplication led to this result once, it
must lead to it || the same result
again.” |
“What is the criterion of
periodicity?”
Here we are inclined to think that we have a criterion the reappearance of
the remainder & the actual periodicity
i.e., the repetition ad inf. of the period.
|
The infinite & the huge.
Absolute idea of large & small. |
“These people don't see a simple truth
….” |
But not “because it had to lead through to
the same result”. |
It is a remarkable fact that people almost always agree how to
count. |
Supposing I said this is the 100th house of this street, although
there are only 5 houses built. 43 |
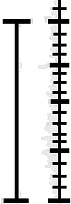 Am
I to be guided by this or by this?
And how do I know that they will guide me to the same result? Am
I to be guided by this or by this?
And how do I know that they will guide me to the same result?We have a general kind of idea of how it goes on; but can't this after all be contradicted by the actual detailed calculation? Isn't there a danger of it going wrong after all? What is the truth which we see (& which is ‘obvious’)? That This shows us that this was justified”. But then we leave behind us these justifications. At first imagination accompanies us a stretch & then we are left alone. |
If there are 777 in the first 100 places there are 777 in the infinite
development. 44 |
The process of calculation can || may be regarded as a
process where there is no compulsion or being guided & on the other
hand, as a process where we move under some strict
guidance. |
“If I follow this chain of steps it's bound
to lead me there.” |
“The question are there 777 in π is all right
because surely there either are 777 in π or
there aren't”.
Queer use of p ⌵ ~p.
Images characteristic for this statement.
It really means: “The question is all right because there is a method of verifying it although we can't use it.” |
“The third place of π is 4
whether I know it or not.” |
“What if we had proved it to be self-contradictory
that there should be no 777 in π,
mustn't we then say that there are 777?” |
Our prose expressions in mathematics are highly metaphorical.
|
“Every algebraic equivalent has a
root”.
Is this to be called a proposition?
46
The question corresponding to this proposition as answer is vague. But once the proposition this piece of mathematics has been done we are inclined to call it the proof that our question had to be answered is the positive. But, as one might say, there was much less in the question than there is now in the answer. – Compare this with: “Is 25 × 25 = 600?” |
Propositions which seem only to
have sense if their truth or falsehood is known. |
What kind of proposition will the
proposition be that there can't (or
must) be 777 in π. |
Will it be possible e.g. to calculate whether any
given proposition of digits occurs or how often
it does. |
Relation between proof showing that 777 must be between n &
m & proof that they are at the
vth place (v being between n
& m). 47 |
Negation of a mathematical proposition &
fault in a calculation. |
“Question” corresponds to
“investigation”. |
Heptagon must there have been an investigation. |
“Is 5. a cardinal
number?” |
There is a contradiction between the normal use of the word
“proposition”,
“question.” 11 |
“Wouldn't one like to know with real
certainty whether the other had || has
pains?” |
Feeling of pastness.
“The experiences bound up with the gesture etc.
aren't the experience of pastness, for they could be there without
the feeling of pastness”. –
But, on the other hand, would it be that experience
of pastness without those experiences bound up with the
gesture? –
Why should we say that the
characteristic || essential part is the
part outside those experiences?
Isn't the experience at least partially described if I have
described the gestures etc.? |
Auch so: Die Worte “lang ist es her –”
rufen in mir manchmal ein bestimmtes Gefühl
wach.
Manchmal nicht.
Aber wenn sie es wachrufen so sind sie, ihr ◇◇◇ Teil der
charakteristischen Erfahrung. |
Sprechen mit Andern & mit mir selbst: “Wenn
ich eine gewisse Erfahrung habe, gebe ich (nur) das Zeichen
✢ ….” 12. |
When one says “I talk to myself”
one generally means just that one speaks & is the only
person listening. |
If I look at something red & say, to myself, this is red, am I giving
myself an information?
Am I communicating a personal experience to myself.
Some philosophising people might be inclined to say that this
is the only real case of communication of personal experience because only I
know what I really mean by ‘red’. |
Remember in which special cases only it has sense to
inform a person || an other
person that the colour he sees now is red. |
One doesn't say to oneself “This
is a chair. –
Oh really?” |
Wie kann ich denn einer Erfahrung
(etwa einem Schmerz) einen
Namen geben?
Ist es nicht als wollte ich ihm, etwa, einen Hut aufsetzen?
|
Nehmen wir an man sagte: “Man kann
13 ihm nur indirekt einen Hut
aufsetzen” so würde ich fragen: Glaubst Du daß man je
auf die Idee gekommen wäre davon zu reden wenn man nicht daran gedacht hätte
daß man dem Menschen der Schmerzen hat einen Hut aufsetzen kann?
Zu sagen man könne dem Schmerz nur indirekt einen Hut aufsetze macht es
erscheinen als gäbe es dennoch einen direkten Weg der nur tatsächlich
nicht gangbar sei.
◇◇◇◇◇◇ |
The difficulty is that we feel that we have said something about the
nature of pain when we say that one person can't have
another person's pain.
Perhaps we shouldn't be inclined to say that we had anything
physiological or even psychological but something
metapsychological metaphysical.
Something about the essence, nature, of pain as opposed to its causal
connections to other phenomena. |
Es scheint uns etwa als wäre es zwar nicht falsch sondern unsinnig zu
sagen “ich fühle seine Schmerzen”, aber als wäre dies so
infolge der Natur
14 des Schmerzes, der Person
etc..
Als wäre also jene Aussage letzten Endes doch eine Aussage über die Natur
der Dinge.
Wir sprechen also etwa von einer Asymmetrie unserer Ausdrucksweise & fassen diese auf als ein Spiegelbild des Wesens der Dinge. |
Intangibility of impressions.
(Anguish)
Some we should say were more tangible than
others.
Seeing more tangible than a faint pain; & this more tangible
than a vague fear, longing etc.
In what way are these intangible experiences less easy to communicate to describe than the ‘simpler’ ones? In what way do we use the phrase: “This experience is difficult to describe.” And can an experience || And can it be even impossible to describe certain experiencesbe ever ? |
Was für einen Sinn hat es zu sagen diese Erfahrung ist nicht beschreibbar? Wir möchten sagen: sie ist zu komplex, zu subtil. |
“Diese Erfahrung ist nicht mitteilbar, aber ich kenne
sie, – weil ich sie habe.” 15 |
“Es gibt die Erfahrung, & die Beschreibung der
Erfahrung. –
Daher kann es nicht gleichgültig sein, ob der Andere die selbe Erfahrung
hat, wie ich, oder nicht; – & daher kann
es || muß es wenn ich mit mir selbst rede auf
diese || meine Erfahrung ankommen.
Es muß dabei eine entscheidende Rolle spielen daß
ich diese Erfahrung kenne (während ich mit der des Andern nicht direkt
vertraut bin).” |
Kann man sagen: “In dem || das was ich über die Erfahrung des Andern sage, spielt seine
Erfahrung (selbst) nicht hinein.
In dem || das was ich über meine Erfahrung sage spielt
sie || diese Erfahrung selbst
hinein.”?
“Ich spreche über meine Erfahrung, sozusagen, in ihrer Anwesenheit” || in ihrem Beisein. |
Wie wenn jemand sagen würde: “Es gibt nicht nur die
Beschreibung des Tisches sondern auch den Tisch.” |
“Es gibt nicht nur das Wort ‘Zahnschmerz’,
es gibt auch such a thing as || etwas wie den
Zahnschmerz selbst.” || … es gibt auch
Zahnschmerzen.” 16 |
Es scheint, daß, da ich etwa eine Erfahrung nicht beschreiben kann, sie
aber habe, daß ich sie daher genauer kennen kann, als irgend ein
Anderer.
Aber was heißt, die Erfahrung kennen, wenn es nicht heißt,
sie beschreiben & nicht heißt, sie haben.
Gibt es eine Kenntnis der Erfahrung, die wir nicht mitteilen können? |
Hat es Sinn zu sagen “ich kenne diese Erfahrung besser || genauer als irgend ein Anderer sie kennen
kann”?¤
Gibt es Erfahrungen die der Andere ebensogut kennen kann wie ich
& solche, die er nicht so gut kennen
kann?
Heißt das: er kann diese selbe komplizierte Erfahrung nicht
haben? –
Es heißt wohl: “Er kann sie haben, aber wir können
nie || nicht wissen, daß er gerade || genau
diese gehabt hat”.
Z.B. scheint es als könnten wir
sagen: “Wir können in einem Sinn wissen daß er gerade
diese einfärbige, glatte, rote Fläche sieht,
aber nicht, daß er genau dieses Flimmern sieht.
Weil sich das genaue Gesichtsbild beim Flimmern || des Flimmerns nicht beschreiben
läßt. |
Es gibt ja auch den Fall, in dem wir ein Gesichtsbild genauer durch
ein gemaltes Bild als durch
17 Worte
beschreiben können. |
Wie ist es damit: “Man kann eine Figur
genauer mit Hilfe von Maßzahlen als ohne diese
beschreiben”. |
Aber die Erfahrung, die ich habe scheint eine Beschreibung dieser Erfahrung, im gewissen
Sinne, zu ersetzen.
“Sie ist ihre eigene Beschreibung”. |
Vermischen wir hier nicht zwei Dinge: die Zusammengesetztheit
der Erfahrung &, was man ihren ursprünglichen
Geschmack || Ton || flavour nennen könnte?
Ihre eigentliche natürliche Farbe? |
Es ist die Auffassung, daß von der ursprünglichen Erfahrung
nur ein Teil bei || in der Mitteilung
erhalten bleibt, & etwas anderes von ihr verloren
geht.
Nämlich eben ‘ihr timbre’, oder wie
man es nennen möchte.
Es kommt einem hier so vor als könnte man,
sozusagen nur die farblose Zeichnung vermitteln & der
Andere setzte in sie seine Farben ein.
Aber das ist natürlich (eine) Täuschung. |
Aber können wir nicht wirklich sagen, wir hätten in dem Andern durch
unsere Beschreibung ein Bild hervorgebracht aber wir können nicht
wissen ob dieses Bild nun
18 genau das
gleiche ist, wie das unsere?
Denken wir hier an den Gebrauch des Wortes
“gleich” in solchen Sätzen
wie: “Diese Kreise sind dem Augenschein nach
ganz gleich.” |
Hierher gehört auch, daß wir gewöhnlich unser Gesichtsbild nicht als etwas
in uns empfinden wie etwa einen Schmerz im Auge daß wir aber wenn wir
philosophieren geneigt sind diesem Bild
gemäß zu denken. |
The
‘if-sensation’.
Compare with the ‘table-sensation’.
There is the question “What's the
table-sensation like” & the answer is a
picture of a table.
In what sense is the if-sensation analogous to the
table-sensation?
Is there a description of this sensation & what do we call a
description of it.
Putting the gestures instead of the sensation means
just giving the nearest rough
description there is of this || the
Experience. |
Example [“I have a peculiar feeling of pastness in my wrist.”] 19.
6) “We shall never know whether he meant this or
that”.
C died after the training in that room.
We say: “Perhaps he would have
reacted like B when taken into the
daylight.”
But we shall never know.
α) We should say this question was decided if he arose from his grave & we then made the experiment with him. Or his ghost appeared to us in a spiritualist séance & told us that he has a certain experience. β) We don't accept any evidence. But what if we didn't accept the evidence in 5) either & said (something like) “We can't be sure that he is the identical man who was trained in the room”, or: “he is the identical man but we can't know whether he would have behaved like this in the past time when he was trained”. 7) We introduce a new notation for the expression “If P happens then always (as a rule) Q happens. P didn't happen this time & Q didn't happen.” We say instead: “If P had happened Q would have happened”. E.g. “If the gunpowder is dry under these circumstances a spark of this strength explodes it. It wouldn't dry this time & under the same circumstances didn't explode.” We say instead “If the gunpowder had been dry this time it would have exploded”. The point of this notation is that it nears the form of this preposition very much to the form: “The gunpowder 20. was dry this time so it
exploded”.
I mean the new form doesn't stress the fact that
it did not explode but, we might say, paints a vivid picture of it exploding
this time.
We could imagine two forms of expression in a
picture language corresponding to the two kinds of
notations in the word language.
The second notation will be particularly appropriate
e.g. if we wish to give a person a shock by
making him vividly imagine what || that which
would have happened, stressing only slightly that it
hasn't
happened || didn't happen.
8) Someone might say to us: “But are you sure that the second sentence means just what the first one means & not just something similar or that & something else as well? (Moore) I should say: I'm talking of the case where it means just this, & this seems to me an important case (which you caused by saying what you have said). But of course I don't say that it isn't used in other ways as well & then we'll have to talk about these other cases separately. 9) Someone says –“lowering one's voice some 21
times means
that
what you say is less important than the rest
& in
other cases you lower your voice to show that you
wish to draw special attention to what you now say
.”We || It must be clear that our examples are not preparations to the analysis of the actual meaning of the expression so & so (Nicod) but giving them effects that “analysis”. 11) Have we now shown that to say in 5 “We can't know whether he would have behaved … ” makes no sense? We should say the sentence || to say this sentence under these circumstances has lost its || the point which it would have had under other circumstances but this doesn't mean that we can't give it another point. 10) We say “We don't || can't know whether this spark would have been sufficient to ignite that mixture; because we can't reproduce the exact mixture not having the exact ingredients or not having a balance to weigh them etc. etc.” But suppose we could reproduce all the circumstances & someone said “we can't know whether it would have exploded” as we can't know whether || & being asked why he said because under these circumstances it would have exploded then.” This answer would set our head whirling. We should feel he wasn't playing the same game with that expression as we do. We should be 22.
inclined to say “This makes no sense!”
And this means that we are at a loss not knowing what reasoning, what
actions go with this expression.
Moreover we believe that he made up a sentence analogous to sentences used
in certain language games not
noticing that he took the point away.
In which case do we say that a sentence has a point? That comes to asking in which case do we call something a language game. I can only answer. Look at the family of language games & that will show you whatever can be shown about the matter. |
12) (The private visual image.)
B is trained to describe his afterimage when he has looked say into
a bright red light.
He is made to look into the light, & then to shut his eyes
& he is then asked “What do you
see?”.
This question before was put to him only if he looked at physical
objects.
We suppose he reacts by a description of what he sees with closed
eyes. –
But halt!
This description of the training seems wrong for what if
23 I had had to describe my
own, not B's, training.
¤
Would I then also have said: “I reacted to the question by
… ” & not rather: “When I had
closed my eyes I saw an image & described
it”.
If I say “I saw an image & described it I say this as
opposed to the case where || in which I
gave a description without seeing an image.
(I might have lied or not.)
Now we could of course also distinguish these cases if B
describes an afterimage.
But we don't wish to consider now cases in which the mechanism of lying
plays any part.
For if you say “I always know whether I am lying
but not whether the other person is”, I
say: in the case I'm considering I can't be said
to know that I'm not lying, or let us say not saying the
untruth, because the dilemma saying the truth or the
untruth is in this case unknown to me.
Think of the fact || Remember that when
I'm asked “what do you see here” I
don't always ask myself: “Now shall I say the
truth or something else?”
If you say “but surely if you in fact speak the truth
then you did see something & you saw what you said you
saw”
I answer: How can I know that I see what I say I
see?
Do I have a criterion or use one
for the colour I see actually being
red? 24. |
13) We imagine that the expression
“I can't see what you see” has been given sense
by explaining it to mean: “I can't see what
you see being in a different position relative to the object we are looking
at”, or “ … having not as good eyes as
you”, or “ … having found as in … that
B sees something which we don't though we look at the same
Object.”
etc.
I can't see your afterimage might be explained to mean I
can't see what you see if I close my eyes meaning
you say you see a red circle, I see a yellow one.
14) Identity of physical objects, of shapes, colours, dreams, toothache. 15) (The thing || object we see) The physical Object & its appearance. Form of expression: different views of the same physical object are different objects seen. We ask “What do you see” & he can either answer “a chair”, or „this” (& draw the particular view of the chair). So we are now inclined to say that each man sees a different object & one which no other person sees, for even if they look at the same chair from the same spot it may appear different to them & the objects before the other mind's eye I can't look at. 16) (I can't know whether he sees anything 25
at all or
only behaves as I do when I see something.)
There seems to be an undoubted asymmetry in the use of the
word “I || to see” (&
all words relating to personal experience).
One can || is inclined to state this in the way that
“I know when I see something by just seeing it, without hearing
what I say or observing the rest of my behaviour whereas I know
that he sees & what he sees only by observing
his behaviour, i.e. indirectly”.
a) There is a mistake in this ◇◇◇: I know what I see because I see it”. What does it mean to know that. b) It is true to say that my reason for saying that I see is not the observation of my behaviour. But this is a grammatical proposition c) It seems to be an imperfection that I can only know ‒ ‒ ‒. But this is just the way we use the word ‒ ‒ ‒. – Could we then … if we could? Certainly. |
Does the person who has not learnt
language know || Should we say that the person who has not learnt the
language knows that he sees red but
can't express it? –
Or should we say: “he knows what he sees but
can't express it”? –
So besides seeing it he also knows what he
sees?
Imagine we described a totally different experiment; say this, that I sting someone with a needle & observe whether he cries out or not || makes a sound or not. Then surely it would interest us if the subject 26
whenever we || often when we
stung him saw, say, a red circle.
And we would distinguish the case when he cried out & saw a circle
from the case when he cried out & didn't see one.
This case is quite straightforward & there is no problem about it. || seems to be nothing problematic in it. |
If I say “I tell myself that I see red, I tell myself what I
see” it seems that after having told myself I now know better what
I see, am better acquainted with it, than before.
(Now in a sense this may be so …) |
“When he asked me what colours I saw,
I guessed what he meant || wished || wanted to know & told him.” |
“It is not enough to distinguish between the cases in which
B or I say that I see red & do see
red & the case in which I say this but don't
see red; but we must distinguish between the cases in which I see red, say I see red & mean to describe
what I see & the cases in which I don't mean
this. 27 |
Consider the case in which I don't say what I see
in words but by pointing to a sample.
Here again I distinguish now between the cases in which I ‘just
react by pointing’ & the case in which I see
& point. |
Now suppose I asked: “how do I know that I see
& that I see red?
“I.e. how do I know
that I do what you call seeing (& seeing
red)?”
For we use the word ‘seeing’ &
‘red’ between us. || in a game we play
with one another. |
Don't you say: “In
order to be a description of our personal experience
it || what we say must not just be
the || our reaction but must be
justified”?
But does the justification need another justification?
|
Suppose,
we play the game 2) & B calls out the
word “red”.
Suppose A now asks B: “do you only say
‘red’ or did you really see it?”. |
“Surely there are two phenomena: one, just speaking,
the other, seeing & speaking accordingly.”
Answer: Certainly we speak of these two cases but we shall
here have to show how
28 these expressions are used; or, in other
words, how they are taught.
For the mere fact that we possess a picture of them
does not help us as we must describe how || in what
way this picture is used.
More especially as we are inclined to assume a use different from the
actual one.
We have therefore to explain under what conditions we say: “I say ‘red’ but don't see red” or “I say ‘red’ & see red”, or “I said ‘red’ but didn't see red” etc. etc.. Imagine that saying red was often followed by some agreeable event. We found that the child enjoyed that event & often instead of ‘green’ said ‘red’. We would use this reaction to play another language game with the child. We would say “you cheat, it's red”. Now again we are dependent upon the subsequent reaction of the child. Such games are actually played with children: Telling a person the untruth & enjoying his surprise at finding out what really happened. |
But couldn't we imagine some kind of perversity in a child which
made it say red when it saw green & vice versa & at the 29
same time this not being discovered because
it happened to see red in those cases when we say green?
But if here we talk of perversity we could || might also
assume that we all were perverse.
For how are we or B ever to find out that he is perverse?
The idea is, that he ¤ finds out (& we do) when later on he learns how the word ‘perverse’ is used & now || then he remembers that he was that way all along. Imagine this case: The child looks at the lights: says the name of the right colour to himself in an aside & then loud the wrong word. It chuckles while doing so. This is, one may say, a rudimentary form of cheating. One might even say: “This child is going to be a liar”. But if it had not said the aside but only imagined itself pointing to one colour on the chart & then said the wrong word, – was this cheating too? Can a child cheat like a banker without the knowledge of the banker? |
“I can assure you that before when I said ‘I see
red’ I saw black.” 30 |
“He tells us his private experience, that experience which nobody
but he knows anything about”. |
“Surely his memory is worth more than our
direct criteria, as only he could know what he
saw.” |
¤ But let us see;– We sometimes say outside philosophy such things as “of course only he knows how he feels” or “I can't know what you feel”. Now how do we apply such a statement? Mostly it is an expression of helplessness like “I don't know what to do”. But this helplessness is not due to an unfortunate metaphysical fact, ‘the privacy of personal experience’, or it would worry us always || constantly. Our expression is comparable to this: “What's done can't be undone!”. |
We also say to the Doctor “Surely I must know
whether I have pains or not!”
How do we use this statement? |
“All right if we can't
talk in this way about someone else I can certainly say of myself that
I either saw red
31
at that time or didn't || had some other
experience.
I may not remember now, but at the time I saw one thing or the
other!”
This is like saying “one of these two pictures must have
fitted”.
And my answer is not that perhaps neither of them fits but that
I'm not yet clear about what ‘fitting’ in this
case means. |
Now is it the same case or are these different cases:
A blind man sees everything just as we do but he acts as a blind man
does & on the other hand he sees nothing & acts as a blind
man does.
At first sight we should say: here we have obviously two clearly
different cases although we admit that we
can't know which we have before us.
I should say: We obviously
use two different pictures which one || we could describe like
this: ….
But we use both || the pictures in
such same || a way that the two games
‘come to the same’. |
By the way, – would you say that he surely || certainly
knew that he was blind if he was so?
Why do you feel more reluctant about this statement? 32 |
“Surely he knew that he saw red but he
couldn't say so!” –
Does that mean “Surely he saw || knew that he saw
the colour which we call ‘red’ … ”
– or would you say it means “he
knew that he saw this colour” (pointing to a red
patch).
But did he while he knew it point to this patch? |
Use of: “He knows what colour he
sees”.
“I knew what colour I saw”
etc. |
“Nachdunkeln der Erinnerung” does
this expression make sense & in what cases. And isn't on the other hand the picture which we use quite clear in all cases? |
The case of old people usually having || getting memories of
the time in which they learnt to speak & understand speech:
a) They say or paint that such & such things have happened although other records always contradict them b) The memories agree with the records. Only in this case shall we say that they remember …. |
Suppose they paint the scenes they
33 say they remember & paint the faces
very dark;– shall we say that they saw them that dark or that the
colour had become darker in their memory? |
How do we know what colour a person sees?
By the sample he points to?
And how do we know what relation the sample is
meant to have to the original?
Now are we to say “we never know …”?
Or had we better cut these “we never know
… ” out of our language &
consider how as a matter of fact we are wont to use the word
“to know”? |
What if someone asked: “How do we || I know that what I call seeing red is not an
entirely different experience every
time & that I am not deluded
into thinking that it is the same or nearly the
same?”?
Here again the answer “I can't know & the
subsequent removal of the question”. |
Is it ever true that when I call a colour ‘red’ I
serve myself of memory?? || make use of
memory?? |
To use the memory of what happened
34 when we were taught language is
all right as long as we don't think
that this memory teaches us something essentially private. |
“Though he can't say what it is he sees
while he is learning № 1, he'll tell us afterwards what
he saw.
We mix this case up with the one: “When his
gag will have been removed he'll tell us what he
saw”. |
What does it mean ‘to tell someone what
one sees’?
Or (perhaps), ‘to show someone what one
sees’? |
When we say “he'll tell us what he
saw” we have an idea that then we'll know
what he really saw in a direct way
(“at least if he isn't
lying”). |
“He is in a better position to say what he sees than we
are.” –
That depends. – |
If we say “he'll tell us what he saw”, it is
as though he would now make a
35 use of
language which we had never taught him. |
It is as if now we got an insight into
something which before we had only seen from the outside. |
Inside & outside! |
“Our teaching || training connects the word
‘red’ (or is meant to connect it) with a
particular impression of his (a private impression an impression in
him).
He then communicates this impression– indirectly, of course–
through the medium of speech.” |
Where is the || our idea of “direct
& indirect communication” taken
from? |
How, if we said, as we sometimes might be inclined:
“We can only hope that this– indirect way of
communication really succeeds”.
|
We so long see the facts about the usage of our words crookedly
as || so long as we are still tempted
here to talk of direct & indirect. |
As long as you use the picture indirect-direct in this case you
can't trust yourself
36 about
judging the grammatical situation rightly otherwise.
|
Is telling what one sees something like turning one's
inside out?
And learning to say what one sees, learning to let others see inside
us? |
“We teach him to make us see what he sees”.
He seems in an indirect way to show us the object which he sees,
the object which is before his mind's eye.
“We can't look at it, it is in him.”
|
The idea of the private object of vision.
Appearance, sense-datum. |
The visual field.
(Not to be confused with visual space.) |
Telling someone what one sees seems like showing him, if indirectly, the
object which is before one's mind's
eye. |
The idea of the object before one's mind's eye is
absolutely bound || (firmly) tied up with
the idea of a comparison of such
objects in different persons compared to which the
comparison
37 really
used is an indirect one. |
Whence the idea of the privacy of sensedata? |
“But do you really wish to say that they are not
private that one person can see the picture before the
other person's eye?” |
Surely you wouldn't think that telling someone
what one sees is || could be a more direct way of
communicating than showing him by pointing to a sample! |
“He'll tell us later what it was he saw” means
that we'll get to know in a (comparatively) direct
& a sure way what he saw as opposed to the guesses we could
make before. |
We don't realize that the answer he gives us now is
only part of a game like № 1 only more complicated.
38 |
We don't deny that he can remember a dream || having dreamt so
& so before he was born.
Denying this to us would be like denying that he can say he remembers
having dreamt so & so before he was born.
I.e. we don't deny that he can make this move but we say that the move alone or together with all the sensations, feelings etc. he might have while he is making it does not tell us what game it is a move of. || to what game the move belongs. We might e.g. never try to connect up a statement of this sort with anything past (in an other sense). We might treat it as an interesting phenomenon & possibly connect it up with the persons writing in a Freudian way or on the other hand we may look for some phenomena in the brain of the embryo which might be called dreams etc. etc.. Or we may just say: “old people are liable to say such things” & leave it at that. |
Suppose now someone remembered that yesterday he called
red ‘green’ & vice versa but that this
didn't appear as he also saw green what today he
sees red & vice versa.
Now here is a case in which we might be inclined to say that we
39 learn from him today something about the
working of his mind yesterday, that yesterday we judged by the outside while
today we are allowed to look at the inside of what
happened.
It is as though we looked back but now got a glance at something that was
closed to us || covered up yesterday. |
If I say what it is I see how do I compare what I say with what I see in
order to know whether I say the truth?
Lying about what I see, you might say, is knowing what I see & saying something else. Supposing I said it just consists of saying to myself ‘this is red’ & aloud ‘this is green’. |
Compare lying & telling the truth in the case of telling what
colour you see with the case of describing a picture which you saw or
telling the right number of things you had to count. |
Collating what you say & what you see. |
Is there always a collating? 40 |
Or could you call it giving a picture of the colour I see if I say the
word “red”?
Unless it be a
picture by its connection with a sample. |
But isn't it giving a picture if I point to a
sample? |
“What I show reveals what I see”; – in
what sense does it do that?
The idea is that now you can so to speak look inside me.
Whereas I only reveal to you what I see in a game of revealing &
hiding which is altogether played with
signs of one category.
“Direct – indirect”.
|
We are thinking of a game in which there is an inside in the normal
sense. |
We must get clear about how the metaphor of revealing (outside
& inside) is actually applied by us; otherwise we shall be
tempted to look for an inside behind that which in our metaphor is the
inside. |
We are used to describing the case by means of a picture which say
41 contains 3 steps.
But when we think about language we forget how this
picture is actually applied in practical cases.
We then are often tempted to apply it as it wasn't
meant originally || originally meant & are puzzled about a third
step in the facts. |
“I see a particular sense-datum || image || thing & say a particular
thing”.
This is all right if I realise
the way in which I specify what I see & what I say. |
“If he had learnt to show me (or tell me) what he sees, he
could now show me.”
Certainly, – but what is it like to show me what he sees?
It is pointing to something under particular circumstances.
Or is it something else (don't be misled by the
idea of indirectness).
You compare it with such a statement as: “if he had learnt to open up he could now open up & show me what's inside || I could now see what's inside. I say yes, but remember what opening up in this case is like. |
But what about the criterion whether there
is anything inside or not?
Here we say “I know that there is something
42 inside in my case.
And this is how I know of the ‘inside’ at all first
hand”. || And this is how I have first
hand knowledge of the inside at all.” ||
This is how I know about an inside & am
led to suppose it in the other person too.”Further we are not inclined to say that only hitherto we have not known the mind of an other person but that the idea of this knowledge is bound up with the idea of myself. |
“So if I say ‘he has toothache’ I am supposing
that he has what I have if I have toothache.”
Suppose I said: “If I say ‘I
suppose’ he has toothache, I am supposing that he
has what I have if I have toothache”, – this
would be like saying “If I say ‘this cushion is
red’ I mean that it has the same colour which the sofa has if it is
red”.
But this wasn't what I intended to
say || was meant with the first sentence.
I wished to say that talking about his toothache at all was based
upon a supposition, a supposition which by its very
nature || essence could not be
verified. |
But if you look closer you will see that this is an entire
misrepresentation of the use of the word
“toothache”. 43 |
Can two people have the same afterimage? |
Language-game ‘Description of
imaginings || the picture before one's
mind's eye.’ |
Can two persons have the same picture before their
mind's eye. |
In which case would we say that they had two images exactly alike but not
identical? |
The fact that two ideas seem here inseparably bound up suggests to us that
we are dealing with one idea only & not with two & that by a
queer trick our language suggests a totally different
structure of grammar than the one actually
used.
For we have the sentence that only I can know directly my
experience & only indirectly the experience of the
other person.
This || Thus
language suggests 4 possible combinations but rules out
2.
It is as though I had used the 4 letters
44 a b c d to denote two objects only but
by my notation somehow suggesting that I am
talking of 4. |
I do this by spreading the use of the word I over all
human bodies as opposed to
L.W.
alone. |
I want to describe a situation in which I should
not be tempted to say that I assumed or believed that the other had what I
have.
Or, in other words a situation in which we would not speak of
my consciousness & his
consciousness.
And in which the idea would not 45 occur to
us that we could only be conscious of our own consciousness. |
The idea of the ego inhabiting a body to be abolished. |
If what any consciousness ¤ spreads over all human bodies then
there won't be any temptation to
use the word ‘ego’. |
Let's assume that hearing was done by no organ of the body we
know of. |
Let us imagine the following arrangement: If it is absurd to say that I only know that I see but not that the others do, – isn't this at any rate less absurd than to say the opposite? |
The idea of the constituent of a fact:
“Is my person (or a person) a constituent of the
fact that I see or not”.
This expresses a question concerning the symbolism just as if it were a
question about nature. |
“Es denkt”.
Ist dieser Satz wahr & “ich denke”
falsch? |
Language-game: I
paint, for myself, what I see.
The picture doesn't contain me.
|
A board game in which only one man is said to play
the other to ‘answer’.
|
What if the other person always correctly described what I
saw, & imagined, would I not say he knows what I
see? –
“But what if he describes …
13
|
Editorial notes
1) Ms-148, pages 4r-4v contain a number of figures and tables which are not included in the transcription.
2) Ms-148, page 7r contains a number of geometrical proof drawings which are not included in the transcription.
3) Ms-148, page 10r contains a number of technical figures as well as a multiplication formula which are not included in the transcription.
4) Ms-148, page 11v contains additional drawings and formulas which are not included in the transcription.
5) Ms-148, page 12v contains one additonal figure which doesn't seem related to the surrounding text and is not included in the transcription.
6) Ms-148, page 13r contains a number of figures which are not included in the transcription.
7) Ms-148, page 14r contains a number of figures which are not included in the transcription.
8) Ms-148, page 14v contains figures and calculations which are not included in the transcription.
9) Ms-148, page 16v contains a figure which doesn't seem related to the surrounding text and is not included in the transcription.
10) Ms-148, page 17r contains a figure which doesn't seem related to the surrounding text and is not included in the transcription.
11) Ms-148, page 20v contains further calculations which don't seem related to the surrounding text.
12) Ms-148, page 21r contains additional calculation and figure scribbles which are not included in the transcription.
13) Continuation in Ms-149,1r.