VIII.
Bemerkungen zur
philosophischen
Grammatik. |
5.10.31.
1 (Das Unaussprechbare (das, was mir
geheimnisvoll erscheint & ich nicht auszusprechen
vermag) gibt vielleicht den Hintergrund, auf dem das, was ich
aussprechen könnte, Bedeutung
bekommt.) |
Die Arithmetik ist kein
Spiel. Man kann doch in der Arithmetik nicht gewinnen
oder || und verlieren!2 |
Wohl aber
ist ein arithmetisches Spiel denkbar.
Zwei || Z.B. zwei
Leute operieren abwechselnd nach bestimmten Regeln (welche
die || die
Wahl der Operationen beschränken) mit Zahlen
welche etwa aus einer angenommenen Grundzahl
(Anfangsposition) durch diese Operationen
sukzessive entstanden sind. || entstehen. Wer zuerst auf diese Weise 0
erhält || erreicht hat gewonnen. (So
ein Spiel wäre dem Halma ähnlich.) |
Was spricht man der
Mathematik ab, wenn man sagt, sie sei nur ein Spiel (oder:
sie sei ein Spiel)? |
Ein Spiel im Gegensatz wozu? – Was spricht man ihr zu, wenn man sagt, ihre
Sätze hätten Sinn. || Was spricht man
ihr zu wenn man sagt (sie sei kein Spiel) ihre Sätze
hätten Sinn. |
Der Sinn
außerhalb des Satzes. |
Und was geht uns der an? Wo
zeigt er sich & was können wir mit ihm
anfangen? (Auf die Frage „was ist der Sinn
dieses Satzes?” antwortet ein Satz. || kommt ein Satz zur Antwort.) |
“Aber der mathem.
Satz drückt (doch) einen
Gedanken aus.” – Welchen Gedanken? – |
Kann er durch einen anderen Satz
ausgedrückt werden? oder nur durch
diesen Satz? – Oder überhaupt
nicht? In diesem Falle geht er uns nichts
an. |
Will man bloß die mathem.
Sätze von andern Gebilden, den Hypothesen
etc., || etwa, unterscheiden?
Daran tut man recht & daß dieser Unterschied
besteht unterliegt ja keinem Zweifel. |
Will man sagen,
die Mathematik werde gespielt wie das Schach oder eine
Patience & es gebe dabei ein Gewinnen oder
Ausgehen || & es laufe dabei auf ein
Gewinnen oder Ausgehen hinaus, |
Sagt man, daß die seelischen
Vorgänge die den Gebrauch der mathematischen Symbole
begleiten, andere sind, als die, die das Schachspiel || Schachspielen begleiten, so weiß ich darüber nichts
zu sagen. |
Es gibt auch beim Schach einige
Konfigurationen die
unmöglich sind, obwohl jeder Stein in einer ihm erlaubten
Stellung steht. (Z.B.
die wenn || Wenn z.B. die
Anfangsstellung der Bauern intakt ist & ein Läufer
schon auf dem Feld.) Aber man könnte sich ein Spiel
denken, worin || in welchem die Anzahl der Züge vom
Anfang der Partie notiert würde, & dann gäbe es
den Fall, daß nach n Zügen diese
Konfiguration nicht eintreten könnte
& man es der Konfiguration doch
nicht ohne weiters ansehen kann ob sie als n-te
möglich ist, oder nicht. |
Die Handlungen im Spiel
müssen den Handlungen im Rechnen entsprechen. (Ich
meine: darin muß die Entsprechung bestehen, oder, so
müssen die beiden einander zugeordnet sein.) |
Welche Gleichung, etwa,
von der Form abc… ×
cde… = ghi… ist richtig, welche
falsch? |
Ja, kann man von dem Schriftzeichen
(überhaupt) sagen, es sei richtig
(oder falsch)? Das nämlich hängt mit dem Sinn der Antwort zusammen: „richtig ist die Gleichung, die man nach den Regeln erzeugen kann” im Gegensatz zu der: „richtig ist die Gleichung, die man nach den Regeln erzeugt hat”. |
Das ist klar, daß die Position
(Gleichung) nur im System, in dem || worin sie
erzeugt werden kann, richtig oder falsch ist. |
„Man darf
ein System von Axiomen nicht benützen, ehe seine
Widerspruchsfreiheit nachgewiesen
ist.” „In den Spielregeln dürfen keine Widersprüche vorkommen”. Warum nicht? „Weil man dann nicht wüßte, wie man zu spielen hat”? |
Aber wie kommt es,
daß man auf den Widerspruch mit dem Zweifel reagiert?
|
Auf den Widerspruch reagiert man überhaupt nicht.
Man könnte nur sagen: Wenn das wirklich so gemeint
ist (wenn der Widerspruch hier stehen soll), so
versteh' ich es nicht. Oder: ich
hab' es nicht gelernt. Ich verstehe die Zeichen
nicht. Ich habe nicht gelernt, was ich darauf hin tun soll,
ob es überhaupt ein Befehl ist; etc..
|
Wie
wäre es etwa, wenn man in der Arithmetik zu den
üblichen Axiomen die Gleichung
2 × 2 =
5 hinzunehmen wollte? Das hieße
natürlich, daß das Gleichheitszeichen nun seine
Bedeutung geändert || gewechselt
hätte. || , d.h.,
daß nun andere Regeln für das Gleichheitszeichen
gälten. |
∣ Hilbert stellt Regeln eines bestimmten
Kalküls als Regeln einer || der
Metamathematik auf. ∣ |
Wenn ich nun sagte: „also
kann ich es nicht als Ersetzungszeichen gebrauchen; so hieße das,
daß seine Grammatik nun nicht mehr mit der des Wortes
„ersetzen”
(„Ersetzungszeichen”,
etc.)
übereinstimmt. |
„Die Regeln dürfen einander
nicht widersprechen”, das ist wie: „die
Negation darf nicht verdoppelt eine Negation
ergeben”. Es liegt nämlich in der
Grammatik des Wortes „Regel” daß
„p ∙ ~p”
(wenn „p” eine Regel ist)
keine Regel ist. || daß
„p ⌵ ~p”
keine Regel ist (wenn „p” eine Regel
ist). |
Das heißt, man könnte also
auch sagen: die Regeln können || dürfen einander
widersprechen, wenn andre Regeln für das Wort || für den Gebrauch des Wortes
„Regel” gelten – wenn das Wort
„Regel” eine andere Bedeutung hat. |
Wir können
eben auch hier nicht begründen (außer
(etwa) biologisch oder historisch)
& || sondern
(können) nur beschreiben, wie das
Wort „Regel” gebraucht
wird. || sondern nur die
Übereinstimmung oder || und den
Gegensatz der Regeln für gewisse Wörter
konstatieren, also sagen, daß diese Worte
mit diesen Regeln gebraucht
werden. |
Daß man die Gleichung A dem
Komplex B zuordnet, heißt,
|
Zwischen B &
A könnte man das Gleichheitszeichen setzen. |
Ist es so:
Der Satz A enthält nichts andres als
B; ja, ist eine Abkürzung |
Und
α,
β &
γ wurden eben
zusammengestellt. Sie wurden herausgegriffen
& etwas Neues aus ihnen konstruiert. |
Es
läßt sich nicht zeigen, beweisen, daß man gewisse || diese Regeln als Regeln dieser Handlung gebrauchen
kann. Außer, indem man zeigt, daß die Grammatik der Bezeichnung || Beschreibung der Handlung mit der jener Regeln übereinstimmt. |
Zu dem Problem vom
‚Haufen || Sandhaufen’: Man
könnte sich hier, wie in allen ähnlichen Fällen,
einen offiziellen || offiziell
festgesetzten Begriff denken ||
denken, daß es einen offiziellen Begriff wie den einer
Schrittlänge gäbe, etwa: Haufe ist
alles was über
|
(a + b) ∙ (a + b)
=
a ∙ (a + b) + b ∙ (a + b)
Dieser Übergang ist vermittels des Satzes .... gemacht worden &, wenn der Induktionsbeweis eine Rechtfertigung dieses Satzes ist, so ist er auch eine Rechtfertigung dieses || des Übergangs. || &, wenn der Induktionsbeweis eine Rechtfertigung dieses Satzes ist, auch vermittels dieses Beweises. || &, wenn der Induktionsbeweis ein Beweis dieses Satzes ist, dann ist er auch eine Rechtfertigung dieses Übergangs. |
(Punkt am Ende des
Satzes. Gefühl des Unabgeschlossenen, wenn er
fehlt.) |
Wie beweist man:
1 + (1 + (1 + 1))
= (1 + (1 + 1 + )) + 1?
Kann man es aus
1 + (1 + 1)
= (1 + 1) + 1 allein
beweisen? |
6.
Der Beweis B zeigt uns quasi || gleichsam
eine Eigenschaft der beiden Seiten der Gleichung A.
|
Ich möchte sagen, wenn ich
betrachte: es liegt alles in ihnen; kein weiterer Schritt gibt uns mehr, als schon da steht. Anderseits sieht man sie doch auf gewisse Weise an, wenn man sie als Induktionsbeweis auffaßt, aber das sagt nur, daß wir das in ihnen sehen, was wir z.B. || etwa durch Unterstreichen gewisser Ausdrücke anzeigen oder durch das Ziehen von Zuordnungslinien zwischen den Gleichungen. || oder durch Linien || Verbindungslinien, welche Teile der einen Gleichung Teilen der anderen zuordnen || zwischen den Gleichungen Teile der einen Teilen der anderen zuordnen. Und diese Linien sind nur neue Paßflächen || Paßstellen, welche den Gleichungskomplex in ein neues System einreihen. |
Man sagt
für gewöhnlich die
rekursiven Beweise beweisen || zeigen, daß die algebraischen Gleichungen
für alle Kardinalzahlen gelten; aber es kommt hier momentan nicht
darauf an ob dieser Ausdruck glücklich oder schlecht
|
∣ Die Ausdehnung eines Begriffes, der
Zahl, des Begriffs ‚alle’, etc.
erscheint uns (ganz) harmlos; aber sie
ist es nicht wenn || sobald wir vergessen,
daß wir unsern Begriff tatsächlich geändert
haben. ∣ |
Und ist es da nicht klar daß die
rekursiven Beweise tatsächlich dasselbe für
alle ‚bewiesenen’ Gleichungen
zeigen? |
Und das heißt doch, daß zwischen dem
rekursiven Beweis & dem von ihm bewiesenen Satz immer die
gleiche (interne) Beziehung besteht? |
Woher nun das
Widerstreben, dieses Verhältnis das eines Beweises zum
Bewiesenen || bewiesenen Satz zu nennen?
|
Ja es ist doch übrigens || Es ist ja
übrigens ganz klar daß es so einen rekursiven oder
richtiger iterativen ‚Beweis’ geben
muß. (Der uns die Einsicht vermittelt,
daß es ‚mit allen Zahlen so gehen muß’.)
( || [D.h. es scheint mir klar, & |
D.h.: Ich möchte Einem
zeigen daß das distributive Gesetz wirklich im Wesen der Anzahl
liegt; werde ich da nicht durch einen Prozeß
der Iteration zu zeigen versuchen daß das Gesetz gilt &
immer weiter gelten muß? |
Und in wiefern kann man
diesen Vorgang nicht den || einen Beweis des
distributiven Gesetzes nennen? |
Will ich nur konstatieren, || Sehe ich da nur auf die Tatsache hin, daß man durch die
|| Bin
ich da nur davon || von der Tatsache
impressioniert, daß man durch die
Prozedur der Iteration
nicht zu einem Resultat
„a + (b + c) =
(a + b) + c” kommen kann, weil die
Bestandteile dieses Satzes in jener Rechnung nicht
vorkommen? |
7.
Könnte ich nicht also in derselben Weise wie ich ihm
16 × 25 =
400 etwa durch aufschreiben || anschreiben von 16 Einsern in 25 Reihen || Reihen zu 25
Einsern begreiflich machen kann, ihm
a + (b + c) =
(a + b) + c durch eine Vorführung mit
Einsern |
Und dieser
Begriff des
‚Begreiflich-Machens’
kann uns hier wirklich helfen. || kann uns hier helfen || ist
hier ein Segen. || ist uns
hier ein Segen.
Denn man könnte sagen: das Kriterium dafür, ob etwas ein Beweis eines Satzes ist, ist ob man ihn dadurch begreiflich machen kann. (Freilich || Natürlich handelt es sich da wieder nur um eine Erweiterung der unserer grammatischen Betrachtung || Betrachtungen über das Wort || des Wortes ‚Beweis’; nicht um ein psychologisches Interesse an dem Vorgang des Begreiflich-Machens.) |
∣ „Dieser Satz ist
für alle Zahlen durch das rekursive
Verfahren bewiesen”. Das ist
der Ausdruck, der so
‚ganz’
irreführend ist. Es klingt so || Er
läßt es so erscheinen, als
würde hier ein Satz, der konstatiert daß das & das
für alle Kardinalzahlen gilt, auf einem
Während die Rekursion in Wahrheit nur sich selber zeigt, wie auch die Periodizität. || wie auch die Periodizität nur sich selbst zeigt. ∣ |
Ich will jemandem zeigen, daß das
(a + (b + c) =
(a + b) + c) stimmt. Was ich als
Methode || Weg || Gang das zu zeigen verwenden kann, ist ein
Beweis. (Z.B. die Methode der
Gruppierung einer Reihe von Strichen.) |
Ist die Frage
nicht
also || also nicht: Kann man
4 + (2 + 3)
= (4 + 2) + 3 ausrechnen? Wenn
ja, so konnte [nicht: könnte] man
also von diesem speziellen Zahlensatz einen Beweis geben & es
ist klar, daß sich dann, eine ‚Möglichkeit der
Weiterführung’ einer Reihe solcher Beweise zeigen
wird. |
Die Art der Ausrechnung nach dem Schema des
Rekursionsbeweises bestünde offenbar darin, daß
man zuerst von
4 + (2 + 1)
= (4 + 2) + 1 auf
4 + (2 + 2)
= (4 + 2) + 2 & dann auf
4 + (2 + 3)
= (4 + 2) + 3 übergeht.
|
Es muß die
Stellung des algebraisch |
(Und die größere Klarheit kommt
durch das || von dem Verschwinden jedes Scheins, als ob
es sich beim Rekursionsbeweis um einen algebraischen
Beweis der Art (a + b)² =
..... = a² + 2ab + b²
handelte.) |
(Der Übergang auf
4 + (2 + 2)
= (4 + 2) + 2 ginge nach dem
Skolemschen Schema so
(vor sich):
4 + (2 + 2)
=
4 + ((2 + 1) + 1) =
(4 + (2 + 1)) + 1 =
((4 + 2) + 1) + 1 =
(4 + 2) + 2.) |
Kann ich nicht sagen, der
Induktionsbeweis ist das Schema einer Rechnung || Zahlenrechnung? || .
– |
Das Problem der Unterscheidung von
1 + 1 + 1 + 1 + 1 + 1 + 1
und
1 + 1 + 1 + 1 + 1 + 1 + 1 + 1
ist viel wichtiger || fundamentaler, als es
zuerst || auf den ersten Blick
scheint. Es handelt sich um den Unterschied zwischen physikalischer & visueller Zahl. |
Es ist auch etwas Sonderbares
|
Wir haben es
(hier)
natürlich auch wieder damit zu tun, daß der Rekursionsbeweis
als eine Art von Beweisen aufgefaßt wird & man
nicht sieht, daß jetzt das Wort „Beweis” seine
Bedeutung (weil seine Grammatik) geändert
hat. |
Und könnte ich
nicht sagen, daß die Unreduzierbarkeit
der Grundgesetze || Grundregeln (kommutatives,
distributives, etc.) sich auch in den
Induktionen die ihnen entsprechen zeigen || wiederspiegeln muß?! |
Das
Verhältnis, was zwischen den algebraischen
Sätzen besteht, muß auch zwischen ihren
Induktionsbeweisen bestehen. || bestehen
bleiben. |
Wir haben also hier nicht
den Fall, in welchem eine Gruppe von Grundgesetzen
durch eine mit weniger Gliedern bewiesen wird, aber nun weiter in den
Beweisen alles im Gleichen bleibt. (Wie auch in einem
System von Grundbegriffen an || in der späteren
Entwickelung || Entwicklung dadurch nichts geändert wird daß man die
Anzahl der Grundbegriffe durch Definitionen reduziert.)
|
8.
(Übrigens, welche verdächtige Analogie zwischen
‚Grundgesetzen’ &
|
Es ist gleichsam || etwa so: der Beweis eines alten Grundgesetzes
setzt sonst das System der Beweise
(einfach) nach
rückwärts || hinten fort.
Die Rekursionsbeweise aber setzen das System von
algebraischen Beweisen (mit den alten Grundgesetzen)
nicht nach hinten fort, sondern bilden || sind ein neues System
das mit dem ersten nur parallel zu laufen scheint. |
Ich sprach
früher von Strichen || Verbindungsstrichen
Unterstreichungen etc. um die
korrespondierenden, homologen, Teile der
Gleichungen eines Rekursionsbeweises zu zeigen. Im
Beweis:
a + (b + 1) =
(a + b) + 1
entspricht
z.B. die Eins α nicht der
β sondern dem c der
nächsten Gleichung. β
aber entspricht nicht δ
sondern ε, &
γ nicht
δ sondern
c + δ.
etc. a + (b + (c + 1)) = a + ((b + c) + 1) = (a + (b + c)) + 1 (a + b) + (c + 1) = ((a + b) + c) + 1(Ƒ) Oder in:
(a + 1) + 1 = (a + 1) + 1
entspricht
1 + (a + 1) = (1 + a) + 1(Ƒ) |
Das ist eine seltsame Bemerkung, daß in den Induktionsbeweisen
der Grundregeln nach wie vor ihre Unreduzierbarkeit || (Unabhängigkeit) sich zeigen muß || zu Tage treten muß.
Was, wenn man das für
den Fall von || Was,
wenn man das in dem Fall ¤ von
gewöhnlichen Beweisen (oder Definitionen) sagte || Was,
wenn man das für || über Beweise || von
Beweisen sagte, also für
den Fall wo die Grundregeln eben weiter reduziert werden, eine neue
Verwandtschaft zwischen ihnen gefunden (oder
konstruiert) wird.
|
(Alles was die Philosophie tun
kann ist Götzen (zu)
zerstören. Und das heißt keinen neuen (etwa in
der Abwesenheit der Götzen || etwa: die Abwesenheit
von Götzen) zu schaffen.) |
Wenn ich darin recht habe daß durch die
Rekursionsbeweise die Unreduzierbarkeit || Unabhängigkeit
intakt bleibt dann ist damit (wohl)
alles gesagt was ich gegen den Begriff vom
Rekursions-„Beweis” sagen || vorbringen wollte || kann.
|
Ich möchte
sagen, || : wir haben
β &
γ durch || mit
α bewiesen aber nicht
B. Aber können wir denn nicht sagen,
B ist einfach das logische Produkt aus
α,
β &
γ?? Also
B =
α ∙ β ∙ γ? |
Dann hieße also
das distributive Gesetz – nur etwas ungeschickt angeschrieben
–: „a + (b + 1) =
(a + b) + 1 . & .
a + (b + (c + 1)) =
(a + (b + c + ))1 . & .
(a + b) + (c + 1) =
((a + b) + c) + 1”?
Aber warum dann nicht nur „a + (b + 1) = (a + b) + 1”, da doch die beiden andern Faktoren aus dieser Gleichung folgen? |
(Die Mathematiker wenn sie die
Grundlagen ihrer Wissenschaft sammeln || angeben sollen || angeben gleichen
einem Maurer der sagte zu einem Haus brauche ich:
Ziegel, Mörtel, Gewissenhaftigkeit, Kraft &
Festigkeit.) |
(Der
Stil meiner Sätze ist außerordentlich stark von
Frege
beeinflußt. Und wenn ich wollte so
könnte ich wohl diesen || den Einfluß
feststellen, wo ihn auf den ersten Blick keiner sähe.) |
Der Grund warum alle
Philosophien der Mathematik fehlgehen ist der, daß man
in der Logik nicht allgemeine Dikta durch
Beispiele begründen kann,
|
Wozu brauchen wir
denn das kommutative
Gesetz? Doch nicht um die Gleichung
4 + 6 =
6 + 4 anschreiben zu können, denn diese
Gleichung wird durch ihren besonderen Beweis
gerechtfertigt. Und es kann freilich auch der
Beweis des kommutativen Gesetzes als ihr Beweis
verwendet werden, aber dann ist er eben
(hier || jetzt)
ein spezieller (arithmetischer)
Beweis. Ich brauche das Gesetz also um danach mit
Buchstaben zu operieren.
¥ |
Habe ich mich aber
nicht doch geirrt? Ich dachte für den Satz
(a + b)² =
a² + 2ab + b² müsse es den
algebraischen & einen rekursiven Beweis geben.
Aber der Gang des algebraischen Beweises von
(a + b)² =
a² + 2ab + b²
entspricht ganz dem Beweis || Übergang von (b + 1) + a =
(b + a) + 1 im Induktionsbeweis
III. || entspricht ganz der Art
des Übergangs (b + 1) + a
=
(b + a) + 1 in III. |
Dieser
Übergang wird mit dem fertigen (bewiesenen) Satz
a + (b + c) =
(a + b) + c || mit dem fertigen
distributiven || assoziativen
Gesetz || mit dem fertig bewiesenen
assoziativen Gesetz gemacht.
|
Der rekursive
Beweis für (a + b)² =
a² + 2ab + b² besteht eben in der
gewöhnlichen Ableitung der Gleichung plus den
rekursiven Beweisen der Grundgesetze.
D.h., dem Beweis dieser Gleichung mittels der Reihe arithmetischer Beispiele entspricht eben die algebraische Ableitung der Gleichung zusammen mit den Induktionsbeweisen der algebraischen Grundregeln. |
(‚…
wir richten uns nach ihren Taten’ (bezieht
sich auf die Mathematiker).) |
Ich darf auch nicht vergessen, || Es darf auch nicht
vergessen werden, daß ja ein gewisser
Gang durch die Skolemschen Beweise führt, der dritte
vom ersten
& zweiten abhängig ist, sich
des ersten || dieser Beweise
bedient. (Also wesentlich nach
dem ersten || ihnen steht.)
u.s.w. |
Was soll es heißen daß
der Gleichungskomplex in I den || jenen
Übergang in III rechtfertigt.
Wie kann || macht er das? |
9.
Wie der Beweis I in III angewendet || verwendet ist, muß sich zeigen wenn wir die Beweise
als periodische
arithmetische Beweise führen. |
Aber eines
ist klar: Wenn uns der Rekursionsbeweis das Recht gibt
alle algebraisch zu rechnen, dann auch der
arithmetische Beweis. || dann gibt
uns auch der arithmetische Beweis dieses
Recht. |
Die Frage ist aber, rechne ich
(horizontal) anders algebraisch in III mit
I & II als in I mit der Definition
a + (b + 1) =
(a + b) + 1? Bediene ich mich des
Komplexes I nicht in derselben Weise in III wie der
rekursiven Definition in
I? |
[Es ist unglaublich, daß man
sich mit so einem || einem so einfachen Beweis so lange
soll beschäftigen können.] |
(Das Ganze ist
eine Auseinandersetzung zwischen dem
rekursiven & dem algebraischen Element
in diesen || den
Beweisen. || in dem Beweis.) |
Die rekursive
Definition scheint nämlich eine Doppelrolle zu
spielen. Und zwar als rekursive
Definition & als algebraische || die einer
rekursiven Definition & die einer algebraischen
Rechnungsregel (von der Art des
assoziativen Gesetzes.) |
∣
Kann man versuchen zu einer Melodie den falschen Takt zu
schlagen? Oder: Wie verhält sich
dieses Versuchen || dieser Versuch zu dem, ein
Gewicht zu heben das uns zu schwer ist? ∣ |
∣ Ich habe noch nie
eine Bemerkung darüber gelesen, daß, wenn man ein Auge
zumacht & „nur mit einem Aug sieht”, man die
Finsternis || (Schwärze) nicht zugleich mit dem andern
geschlossenen sieht! Das ist sehr
merkwürdig! ∣ |
Wie verhält sich
die Schachaufgabe || (das Schachproblem) zur
Schachpartie? Denn daß die Schachaufgabe der Rechenaufgabe entspricht, eine Rechenaufgabe ist, ist klar. |
Ein arithmetisches Spiel
wäre z.B. folgendes: Wir schreiben
|
Angenommen einem Menschen wäre
Arithmetik nur zum Gebrauch in einem arithmetischen Spiel gelehrt
worden. Hätte er etwas anders gelernt als der
welcher || der
Arithmetik zum normalen || gewöhnlichen
Gebrauch lernt? Und wenn er nun im Spiel 21 mit 8
multipliziert & 168 erhält tut er etwas Andres als
der, welcher herausfinden wollte wieviel
21 × 8
ist? |
Man wird sagen: Der Eine wollte doch eine Wahrheit
finden, während der Andre nichts dergleichen
wollte. |
Nun könnte man diesen Fall
|
Dieser Vergleich würde aber nicht
stimmen denn wir sehen im Schachzug kein Experiment (was wir
übrigens auch könnten), sondern eine
Handlung einer Rechnung. |
Es könnte Einer
vielleicht sagen: In dem arithmetischen Spiel werden wir zwar multiplizieren
|
Also kann man
nur einwenden daß in dem Spiel die Gleichung kein Satz ist.
Aber was heißt das? Wodurch wird sie dann zu einem
|
Man
könnte aber sagen daß der eigentliche Unterschied darin
bestehe, daß für Bejahung
& Verneinung im Spiel kein Platz sei. Es wird da
z.B. multipliziert &
21 × 8 =
148 wäre ein falscher Zug, aber
21 × 8 ≠
148, welches ein richtiger arithmetischer Satz ist,
hätte in unserm Spiel nichts zu suchen. |
Da kann || mag man sich daran erinnern daß in der Volksschule
nie mit Ungleichungen gearbeitet wird, vom Kind nur die richtige
Ausführung der Multiplikation verlangt wird
& nie oder höchst selten die
Konstatierung einer Ungleichung. |
Wenn ich im
Spiel || in unserm Spiel
Die Frage ist nun: kann man von dem Menschen der im Spiel die Stellung „21 × 8 = 168” erhalten hat sagen, er habe herausgefunden, daß 21 × 8 = 168 sei? Und was fehlt ihm dazu? Ich glaube es fehlt ihm nichts, es sei denn eine Anwendung der Rechnung. |
Die Arithmetik ein Spiel zu nennen ist
ebenso falsch, wie, das Schieben von Schachfiguren (den
Schachregeln gemäß) ein Spiel zu nennen, denn es kann auch
eine Rechnung sein. |
Man müßte also sagen:
Nein, das Wort „Arithmetik” ist
nicht der Name eines Spiels. (Natürlich || Das ist natürlich wieder eine
Trivialität.) – Aber die Bedeutung des Wortes
„Arithmetik” kann erklärt werden durch
die Beziehung der Arithmetik zu einem arithmetischen
Dabei aber ist es wesentlich zu erkennen, daß dieses Verhältnis nicht das ist einer Tennisaufgabe || Billardaufgabe zum Tennisspiel || Billardspiel. Mit „Tennisaufgabe || Billardaufgabe” meine ich etwa die Aufgabe einen Ball unter gegebenen Umständen in bestimmter Richtung zurückzuwerfen. (Klarer wäre der Fall, vielleicht, einer Billardaufgabe.) Die Billardaufgabe ist keine mathematische Aufgabe (obwohl zu ihrer Lösung Mathematik nötig sein || angewendet werden kann). Die Billardaufgabe ist eine physikalische Aufgabe & daher „Aufgabe” || ‚Aufgabe’ im Sinne der Physik; die Schachaufgabe ist eine mathematische Aufgabe & daher ‚Aufgabe’ in einem andern (im mathematischen) Sinn. |
In dem Kampf zwischen dem
‚Formalismus’ & der
‚inhaltlichen Mathematik’, was behauptet denn
jeder Teil? Dieser Streit ist so ähnlich dem
zwischen Realismus & Idealismus!
Z.B. || Auch darin, || Darin
z.B., daß er sehr bald
obsolet geworden sein wird & daß beide
Parteien entgegen ihrer täglichen Praxis
Ungerechtigkeiten behaupten. |
10.
|
Worin besteht denn
das Gewinnen & Verlieren in einem
Spiel (oder das Ausgehen in
der Patience)? Natürlich
nicht in der Konfiguration || Situation des
Spiels || Spielsituation die das Gewinnen
– z.B. – hervorbringt.
Wer gewinnt, muß durch eine eigene || besondere Regel festgesetzt werden. (Dame
& Schlagdame z.B. sind nur durch
diese Regel unterschieden.) |
Konstatiert nun die Regel etwas, die sagt, „wer zuerst
seine Steine im Feld des Andern hat, hat
gewonnen”? Wie ließe sich das
verifizieren? Wie weiß ich ob Einer
gewonnen hat? Etwa daraus daß er sich freut?
|
Diese
Regel sagt doch wohl: Du mußt versuchen, Deine Steine
so rasch als möglich etc.. |
Die Regel in dieser Form bringt das Spiel schon mit dem Leben in
Zusammenhang. Und man könnte sich denken daß
in einer Volksschule in der das Schachspielen ein
obligater Gegenstand || ein
Lehrgegenstand wäre die Reaktion des Lehrers
|
Ich möchte
beinahe sagen: Im Spiel gibt es
(zwar) kein ‚wahr’
& ‚falsch’, dafür gibt es aber in der
Arithmetik kein ‚gewinnen’ &
‚verlieren’. |
Ich sagte
einmal es wäre denkbar daß Kriege
zwischen Völkern auf einer Art großem Schachbrett nach den
Regeln des Schachspiels ausgefochten würden.
Aber: Wenn es wirklich bloß nach den Regeln des
Schachspiels ginge, dann brauchte man eben
kein Feld || Schlachtfeld für diesen Krieg
sondern er könnte auf einem gewöhnlichen Brett gespielt
werden. Und dann wäre er || es
(eben) im
gewöhnlichen || normalen Sinne
kein Krieg. Aber man könnte sich ja auch eine Schlacht
von den Regeln des Schachspiels geleitet denken. Etwa
so, daß der ‚Läufer’ mit der
‚Dame’ nur kämpfen sie angreifen
dürfte, wenn seine Stellung zu ihr es ihm im
Schachspiel erlaubte sie zu ‚nehmen’. |
Beispiele in
der Logik müssen immer ganz ausgeführt werden. |
(Es könnte dann so geregelt werden, daß etwa der Kampf zwischen Läufer & Dame in diesem Fall nur so geführt werden darf, daß der Läufer angreift & die Dame nur pariert. Tötet er sie so entspricht das dem „Nehmen” im Schach, gelingt ihm das nicht, so muß er einen andern Zug machen. etc..) |
Ich wollte eigentlich
sagen: Das was das Spiel zum Spiel macht ist seine
Stellung im Leben || im menschlichen
Leben. Aber ist das wahr? |
D.h.: könnte man sich eine
Schachpartie gespielt denken, d.h.,
sämtliche Spielhandlungen ausgeführt denken, aber in
einer andern Umgebung, so daß dieser Vorgang nun nicht die
Partie eines Spiels genannt würde? |
Gewiß, es
könnte sich ja um eine Aufgabe handeln die die
Beiden mit einander lösen. (Und einen
Fall für die Nützlichkeit einer solchen Aufgabe kann man
sich ja nach dem Oberen leicht konstruieren.) |
Die Regel
über das Gewinnen & Verlieren |
(Und ähnlich kommt es uns ja vor,
verhält es sich
(ja) mit dem ‚richtig’
& ‚falsch’ im Rechnen.) |
Könnte einer
nicht statt Patience zu legen am Abend ein paar Integrale
auszurechnen versuchen. Man könnte es sich so denken,
daß er sich die Aufgabe irgendwie vom Zufall stellen läßt
& nun versucht sie nach bestimmten Methoden zu
lösen. Gelingt es, so ist die
Patience ausgegangen. |
∣ Der Wirrwarr in Betreff des „wirklich
Unendlichen” || über das „wirklich
Unendliche” kommt von dem unklaren Begriff der
irrationalen Zahl her. D.h. davon
daß die logisch verschiedensten Gebilde, ohne klare
Begrenzung des Begriffs, „irrationale Zahlen”
genannt werden. Die Täuschung als hätte man einen
festen Begriff rührt daher || beruht
darauf, daß man in Zeichen von der Art
„0˙a b c
d … ad
inf.” einen
Standard || einen Ausdruck || einen Begriff || ein
Bild zu haben glaubt dem sie (die Irrationalzahlen)
jedenfalls entsprechen |
Aus
III: (b + 1) + a
d.h., hier gibt es einen arithmetischen periodischen Beweis.
|
Wenn wir den Komplex || Beweis „rekursiv
auffassen”, tun wir nämlich nichts
anderes, als ein Stück der arithmetischen Gleichungsreihe
überdenken || durchdenken. |
11.
In der Logik geschieht immer wieder, was in dem Streit über
das Wesen der Definition geschehen ist.
Wenn man sagt, die Definition habe es nur mit Zeichen zu tun
& ersetze bloß ein kompliziertes Zeichen durch ein
einfacheres, so wehren sich die Menschen dagegen & sagen die
Definition leiste nicht nur das, oder es gebe eben
verschiedene Arten von Definitionen || der
Definition & die interessante &
wichtige Sie glauben nämlich man nehme der Definition ihre Bedeutung, Wichtigkeit, wenn man sie als bloße Ersetzungsregel die von Zeichen handelt hinstellt. Während die Bedeutung der Definition in ihrer Anwendung liegt quasi in ihrer Lebenswichtigkeit. Und eben das geht heute in dem Streit zwischen Formalismus, Intuitionismus etc. vor sich. Es ist den Leuten unmöglich die Wichtigkeit einer Sache || Handlung || Tatsache, ihre Konsequenzen, ihre Anwendung, von ihr selbst zu unterscheiden; die Beschreibung einer Sache von der Beschreibung ihrer Wichtigkeit. |
Immer wieder
hören wir so daß der Mathematiker mit dem
Instinkt arbeitet (oder etwa daß er nicht mechanisch
nach der Art eines Schachspielers
(vorgehe) aber wir
erfahren nicht was das mit dem Wesen der Mathematik zu tun haben
soll. Und wenn ein solches psychisches Phänomen in der
Mathematik eine Rolle spielt, wie weit wir überhaupt
exakt über die Mathematik reden können, &
wieweit nur mit der Art von Unbestimmtheit, mit der wir
über Instinkte etc. reden
müssen. |
Immer wieder möchte ich sagen:
|
Die Menschen
sind im Netz der Sprache gefangen || verstrickt
& wissen es nicht. |
Auch so: Der Rekursionsbeweis hat es –
offenbar || natürlich – wesentlich mit Zahlen
zu tun. Aber was gehen mich die an, wenn ich rein
algebraisch operieren will. Oder: Der
Rekursionsbeweis ist nur dann zu gebrauchen || benützen, wenn ich
mit ihm || durch ihn den || einen
Übergang in einer Zahlenrechnung rechtfertigen
will. |
Man könnte nun aber fragen: Also brauchen wir
beide: sowohl den Induktionsbeweis
als auch das assoziative Gesetz, da ja
dieses Übergänge der Zahlenrechnung nicht begründen
kann & jener nicht Transformationen in der Algebra?
|
Ja hat man
(denn) vor den
|
Die Mathematiker verirren
sich nur dann wenn sie über Kalküle im
allgemeinen || Allgemeinen
reden wollen, & zwar darum weil sie dann die
besonderen || besondern
Grundlagen || Bestimmungen vergessen die
jedem besonderen Kalkül als
Grundlagen dienen || zu Grunde
liegen. |
Ich sollte sagen: Der
‚Beweis’ B steht für eine
Beweisreihe. Ist der Ausdruck (oder ein Teil des
Ausdrucks) eines Gesetzes wonach || nach
welchem Beweise gebildet werden können. –
Wenn ich sage „Teil des
Ausdrucks”, so ist das Übrige die Anleitung zum
Verständnis || Verstehen des
rekursiven Beweises (die im Bilden || in der Bildung einiger Glieder der
Beweisreihe besteht). |
Kann man sagen, daß diese
Beweisreihe ‚ein Beweis’ ist?
Kann man sie so nennen? |
Könnte man sagen a + (b + c) =
(a + b) + c stehe auch für eine
Gleichungsreihe? |
Man könnte sich natürlich ein
Stück so einer Gleichungsreihe (mit Pünktchen)
angeschrieben denken & als Korrelat
eines
(entsprechenden) Stücks der
Beweisreihe ansehen. Und dann in einem übertragenen Sinne sagen die eine Reihe sei der Beweis der andern. |
[Ich erscheine mir jetzt
außerordentlich ungeschickt.]
Ist denn nicht der Beweis B in
(eben) demselben Sinn ein Beweis
von A wie eine Reihe
(a + b)² =
‒ ‒ ‒
als Beweis
(a + b)³ = ‒ ‒ ‒ (a + b)⁴ = ‒ ‒ ‒ einer Formel (a + b)n = ‒ ‒ ‒ angesehen || betrachtet werden kann. Ich rechne die einzelnen Potenzen aus sehe ein Gesetz in diesen Rechnungen & drücke es allgemein in der Formel mit n || in der algebraischen Formel aus. Ich würde mich nie scheuen das einen Beweis der algebraischen Formel zu nennen. & || Und haben wir hier nicht denselben Fall wie zwischen A & B? |
Oder ist der für mich entscheidende
Unterschied daß wir hier keine Rekursion
|
Ich bringe die oben angedeutete Rechnung
nur into shape wenn ich sie, klarer, so
anschreibe (a + b)² = f(2) nach den Regeln der Multiplikation aber ist f(n) ∙ (a + b) = f(n + 1) also ist: ¤ f(n) = (a + b)n. Und hier haben wir den rekursiven Beweis. |
Denken wir der Fall wäre der: wir könnten
sagen: „nach den Regeln der Addition ist
a + (b + (c + 1)) =
(a + b) + (c + 1) außerdem aber
ist a + (b + 1) =
(a + b) + 1 also ......”.
|
Aber ist
denn das nicht wesentlich dasselbe wie: Nach den Regeln
der Addition (nämlich:
a + (b + 1) =
(a + b) + 1) ist
a + (b + (c + 1)) = (a + (b + c)) + 1 und (a + b) + (c + 1) = ((a + b) + c) + 1 also ...... |
Also scheine ich auf der ganzen Linie
geschlagen zu sein. Wenn ich nun den Rückzug antreten muß so fragt es sich: was ist der richtige Rückzugsweg? (Denn es gehört zur Methode der Philosophie daß ich nie die Flucht ergreifen darf. D.h. es darf keinen ungeordneten |
Zum
indirekten Beweis daß eine Gerade
über einen Punkt hinaus nur eine Fortsetzung hat:
Wir nahmen an es könne eine Gerade zwei Fortsetzungen
haben. – Wenn wir das annehmen so muß diese Annahme
einen Sinn haben –. Was heißt es aber: das
annehmen? Es heißt nicht eine
naturgeschichtlich falsche Annahme machen
wie etwa die, daß ein Löwe zwei
Schwänze hätte. – Es heißt nicht etwas
annehmen was gegen die Konstatierung einer Tatsache
spricht || verstößt.
Es heißt vielmehr, eine Regel annehmen & gegen die ist
weiter nichts zu sagen außer daß sie etwa einer anderen
widerspricht & ich sie darum fallen lasse.
Wenn4 im Beweis nun eine Gerade gezeichnet wird die sich gabelt, so darf das an & für sich nicht absurd sein & ich kann nur sagen das || so etwas nenne ich keine Gerade. || Wenn im Beweis gezeichnet wird  , & das
eine Gerade darstellen soll, die sich gabelt so ist darin nichts
Absurdes (Widersprechendes), es sei denn, daß
wir eine Festsetzung getroffen haben, der es
widerspricht. , & das
eine Gerade darstellen soll, die sich gabelt so ist darin nichts
Absurdes (Widersprechendes), es sei denn, daß
wir eine Festsetzung getroffen haben, der es
widerspricht. |
Wenn nachträglich ein Widerspruch
gefunden wird so waren vorher die Regeln noch nicht klar &
eindeutig. Der Widerspruch macht also nichts denn er ist
dann durch das Aussprechen einer Regel zu entfernen. |
In einem
völlig geklärten System [mit klarer
Grammatik] || In einem grammatisch geklärten
System gibt es keinen versteckten Widerspruch denn da
muß die Regel gegeben sein, nach welcher ein Widerspruch zu
finden ist. Versteckt kann der Widerspruch nur in dem
Sinne || Sinn sein, daß er
gleichsam in der Unordnung || dem Kraut &
Rüben der Regeln, in dem noch nicht geordneten Teil
der || in dem ungeordneten Teil der Grammatik, versteckt ist
dort aber macht er nichts || das aber macht
nichts, da er durch ein Ordnen der Grammatik zu
entfernen ist. |
Warum dürfen Regeln einander || sich Regeln
nicht widersprechen? Weil es sonst keine Regeln
wären. |
Zum mindesten muß ich sagen daß
welcher Einwand gegen den Beweis B
gilt auch z.B. gegen den der Formel
(a + b)n
= etc. gilt. |
12.
Ich würde aber doch fragen, wenn mir Einer
⇒die Formel
.) (a + b)n =
f(n) zeigt : wie ist man denn
dazu gekommen? Und als Antwort käme doch
C. Ist es || C also
nicht ein Beweis von ε? |
Oder antwortet C eher auf die Frage „was
heißt ε”? |
Wehre ich mich nicht gegen eine Analogie mit
einem Fall, in Ich meine einen (analogen) Fall, in dem das was der Induktion in unserem Fall entspricht wirklich weiter, zu der Konstatierung einer Tatsache, führt. Nämlich, daß nun sicher alle Gegenstände (um die es sich handelt) diese Eigenschaft haben. |
Das ist, glaube ich, einfach der Fall, wo || in dem || welchem
es sich um eine bestimmte Gruppe von Gegenständen handelt
& uns der Prozeß der Induktion von
einem zum andern & bis zum letzten führt,
& wir am Schluß sagen können:
|| also gilt dies von
allen diesen Gegenständen. Wenn ich sage der
Induktionsprozeß führt hier noch
weiter zur Konstatierung einer Tatsache, so heiß das daß
die bloße Möglichkeit der Induktion hier noch nicht
alles ist, sondern ich mit ihrer Hilfe auf etwas schließe
das nicht allein in ihr gegeben ist. |
Ich will
sagen: || , hier ist doch mit der
Induktion alles erledigt. |
Ich sagte ich bestimmte eine
algebraische Zeichenregel „in
Übereinstimmung” |
14.
Wie ich Philosophie betreibe, ist es ihre ganze Aufgabe, den
Ausdruck so zu gestalten, daß gewisse
Beunruhigungen || ¤
Probleme verschwinden. |
In dem Beweis des Satzes
muß (am Ende) der Satz vorkommen. |
Aber wo steht im
Induktionsbeweis der Satz A. Es sei denn, daß wir
ihn in den Beweis mit einbegreifen: Aber nach welchem Satz
wurde dann dieser letzte Übergang gemacht? |
Wenn ich sage, die periodische Zahlenrechnung
beweist den Satz der mich zu jenen Übergängen
berechtigt, wie hätte dieser Satz gelautet, wenn man ihn als
Axiom angenommen & nicht bewiesen hätte?5 |
Wie hätte der Satz
gelautet nach welchem ich
5 + (7 + 9)
= (5 + 7) + 9 gesetzt hätte, ohne es
beweisen zu können? |
Aber wenn der
Komplex kein Beweis ist, welche Rolle spielt er denn dann
überhaupt? Wie wird er verwendet? |
Ja, er ist ein Beweis, ein allgemeiner
Beweis – oder das
(allgemeine) Schema eines
Beweises || der Beweise für Zahlensätze
von der Form a + (b + c) =
(a + b) + c. |
Ja, als Rekursionsbeweis
aufgefaßt, ist der Komplex das allgemeine Schema von
Beweisen. |
Ich kann
(also) nur
dieses
nehmen & es als f(n) = (a + b)n auffassen. |
Wie wird
denn aber die Gleichung f(n) =
(a + b)n gebraucht?
Offenbar als Transformationsregel. (Wie,
wenn ich einmal f(x!) antreffe
& nun vermöge der Gleichung ε schreiben kann
f(x!)
= (a + b)x!.)
|
Könnte
mir denn aber da die Induktion allein den gleichen Dienst
tun? Müßte ich dann überhaupt einen
andern Symbolismus verwenden || benützen? |
Die Arbeit an der Philosophie ist
– wie vielfach die Arbeit in der Architektur
– eigentlich mehr die || eine Arbeit an Einem
selbst. An der eignen Auffassung. Daran,
wie man die Dinge sieht. (Und was man von ihnen
verlangt.) |
So blödsinnig es
klingt: ich möchte C eine Begründung von ε
nennen, nicht einen Beweis. |
Ein philosophisches
Problem ist immer von der Form: „Ich kenne mich
einfach nicht aus.” |
Gewiß, wenn ε als
Ersetzungsregel fungieren kann & ε aus C allein
hervorgeht, so muß C auch als Ersetzungsregel
i.e. Begründung der Ersetzung fungieren
können. |
C als
ε sehen. Das muß – meiner Meinung nach – möglich sein. |
Meine ich nicht
folgendes: Man könnte statt der ganzen
Algebra einen Kalkül || eine Rechnung
mit arithmetischen Induktionsreihen setzen.
Dann aber würde die || diese Rechnung
zerfallen, in das Rechnen mit Ziffern durch Transformieren von
Gleichungen etwa, und in ein Sehen |
Wenn ich,
übrigens, sage „das Sehen von Induktionen”
warum dann nicht lieber „das Bezeichnen von
Induktionen”? ist
denn die Induktion etwas wesentlich
Verstecktes? Und ist nicht
das Hervorheben der Induktion (dessen was ich in dem
Gleichungskomplex sehe) einfach das Bilden eines Zeichens || Symbols wie jedes andere? |
Ich sage,
z.B., ich muß die Periodizität in
1˙
|
Denn wenn jemand
(etwa) sagt
|
Wie verhält es sich aber mit
einer Rechnung wie
(5 + 3)² = (5 + 3) ∙ (5 + 3) = 5 ∙ (5 + 3) + 3 ∙ (5 + 3) = 5 ∙ 5 + 5 ∙ 3 + 3 ∙ 5 + 3 ∙ 3 = 5² + 2 ∙ 5 ∙ 3 + 3² ‒ ‒ ‒ R) in || aus welcher wir auch eine allgemeine Regel des Quadrierens (eines Binoms) sehen || herauslesen können? |
Wir können
diese Rechnung sozusagen arithmetisch & algebraisch
auffassen || ansehen. |
Und dieser
Unterschied in der Auffassung träte
z.B. zu Tage, wenn das Beispiel (5 + 2)² = + 5²
|
Nach der einen Auffassung
wäre z.B. die obige || vorige Rechnung ein Beweis von
(7 + 8)²
= 7² + 2 ∙ 7 ∙ 8 + 8²,
nach der anderen nicht. |
Übrigens ist die Rechnung R nur
insofern ein allgemeiner Beweis, als sie sich auf allgemeine
Regeln stützt, also auf die induktiven Beweise. || also doch auf
Induktionen. |
Kann ich sagen: Der induktive
Beweis besteht eben nicht bloß im Beweis von
α &
β &
γ sondern im Zusammenstellen
& richtigen Zusammensehen eben dieser
Gleichungen. |
Wenn man nämlich
sagt, B sei ein || der Beweis
von || für A, so
frage ich || so will ich fragen durch welche
Sätze || mit welchen
Sätzen ist A bewiesen? Und wenn man
mir sagt, „durch α”, so antworte
ich: β &
γ (oder
α, β &
γ) sind durch
α bewiesen, aber
α ∙ β ∙ γ
beweist A nicht & ist nicht A
(sowenig 1˙0 : =
0˙3 als bloße Division
Ich muß, um ‚A zu beweisen’, erst – wie man sagen würde – die Aufmerksamkeit auf etwas ganz bestimmtes || auf ganz bestimmte Züge in || von B lenken. || richten. || lenken oder richten. (Wie in der Division 1˙
|
(Und von dem, was
ich dann sehe, hatte das α sozusagen noch gar keine
Ahnung.) |
Das ist freilich noch
irreführend & schief
ausgedrückt || noch
irrend ausgedrückt. Die
Wahrheit ist, daß ich den Komplex B in ein bestimmtes System
einordne; bestimmtes || Bestimmtes in ihm
unterstreiche, verbinde || unterstreiche &
verbinde und das drücke ich eben dadurch aus,
daß ich ihn durch die Gleichung A ersetze die
(etwa) die Zusammenfassung, des
von unserm Standpunkt, Wesentlichen von || in B
ist. – Das sieht man, wenn man B als Weg der
Induktion auffaßt, ein paar Schritte a + (b + 2) =
(a + b) + 2, a + (b + 3) =
(a + b) + 3 rechnet, & darauf –
von diesen Schritten bestimmt – schreibt:
a + (b + n) =
(a + b) + n. – Das heißt
gleichsam: so will ich B verwenden.
|
(Ich
sollte mich übrigens vielleicht |
Meinen
Standpunkt könnte man so
ausdrücken: Wenn ich
frage, ist B ein Beweis von diesem Satz, so könnte
ich auch fragen: ist B ein Beweis davon, daß es sich so
verhält, wie A es sagt || wie A
sagt? || , &
„ist es gewiß so, wie A sagt?”
Aber wie denn? Was behauptet denn
A? Man würde sagen: „daß
diese Gleichung für alle Zahlen gilt”,
& der Beweis dafür soll die Induktion sein; das setzt
voraus, daß wir außer || außerhalb der || unabhängig von der Induktion einen
Begriff von der Gesamtheit der Werte || Zahlen haben. Als wäre – wie
ich oft gesagt habe – die Induktion nur ein
Vehikel um uns durch die Gesamtheit der Zahlen zu führen.
|
Es verhält sich
hier zwischen Allgemeinheit & Beweis der Allgemeinheit,
wie zwischen Existenz & Existenzbeweis. |
Können wir
aber nicht die falsche Analogie beiseite lassen &
sagen: A ist auf derselben Stufe wie
4 × 5 =
20 & sein Beweis auf der Stufe des Beweises von
4 × 5 =
20? |
Das heißt etwa: Wenn ich
frage „ist
4 × 5
wirklich 20”, so hat diese Frage Sinn, weil || ,
wenn & weil sie sich auf eine Methode der
Entscheidung bezieht. Die Antwort wäre:
„rechnen wir's aus! –”
Könnte nun nicht die Antwort im Falle
Oder:6 Auf die Frage „ist 5 × 4 = 20?” könnte man antworten: „sehen wir nach, ob es mit den Grundregeln der Arithmetik übereinstimmt”; und entsprechend könnte ich sagen: sehen wir nach ob A mit den Grundregeln übereinstimmt. Aber mit welchen? Nun, wohl mit α. |
Aber
zwischen α & A liegt eben die Notwendigkeit einer
Festsetzung darüber, was wir hier Übereinstimmung
nennen wollen. |
∣ „Hat die Prozession ein
Ende” könnte auch heißen: ist sie
eine in sich geschlossene Prozession.
Und nun könnte man sagen || Und nun
höre ich die Mathematiker sagen „da
siehst Du ja, daß Du Dir sehr wohl einen solchen Fall
vorstellen kannst, daß etwas kein Ende hat; warum soll es dann
nicht auch andere solche Fälle || einen andern
solchen Fall geben
können”. Aber die Antwort
ist: Die ‚Fälle’ in diesem Sinn des
Worts sind grammatische Fälle, & sie bestimmen erst den
Sinn der Frage. Die Frage „warum soll
|
D.h.
zwischen α & A liegt die Kluft von
Arithmetik & Algebra || von Arithmetik zur
Algebra, & wenn B als Beweis von A
gelten soll, so muß diese (Kluft)
durch eine Bestimmung überbrückt werden. |
Nun ist ganz
klar, daß wir Gebrauch von so einer Idee der
Übereinstimmung machen, wenn wir uns nur
z.B. rasch ein Zahlenbeispiel ausrechnen,
um dadurch die Richtigkeit eines algebraischen Satzes zu
kontrollieren. Und in diesem Sinne könnte ich z.B. rechnen
& sagen: „ja, ja, es stimmt, a ∙ b ist gleich b ∙ a” – wenn ich mir vorstelle daß ich das vergessen hätte. |
Man
müßte dann sagen: man kann allerdings von einer
Übereinstimmung zwischen α & A reden,
bezw., zwischen
α, β, γ & A, aber nicht
insofern als A die || eine Allgemeinheit
behauptet & B sie beweist, sondern nur insofern,
als α, β, γ diese & nicht,
etwa, die Allgemeinheit a + (b + c) =
(a + 2b) + c konstituiert
aufbaut || aufbaut. |
Mit dem Satz
α sind eben zwar
β &
γ, aber nicht die
Allgemeinheit, d.h. die Induktion
abgeleitet, die wir in B sehen. |
Wir könnten ein Beispiel rechnen um uns zu vergewissern daß
(a + b)²
gleich a² + b² + 2ab
& nicht a² + b² + 3ab
ist – wenn wir es etwa vergessen hätten; aber wir
könnten nicht in diesem Sinn kontrollieren, ob die Formel
allgemein gilt. Auch diese
Kontrolle gibt es natürlich & ich könnte in der
Rechnung
(5 + 3)²
= ‒ ‒ ‒ =
5² + 2 ∙ 5 ∙ 3 + 3²
nachsehen, ob die 2 im zweiten Glied ein allgemeiner Zug der Gleichung
ist, oder einer der von den speziellen Zahlen des Beispiels
abhängt. |
Da die Gebrauchsanweisung für α
in einer Reihe arithmetischer Sätze || Definitionen
besteht, so kann man diese Reihe auch als Symbol statt α setzen
& also Reihen statt α, β &
γ. |
Man könnte statt des
Satzes A auch sagen: ‚die Form der
Gleichungen, die die Induktion B
liefert’. |
Ist es nicht genug zu sagen, daß die
Algebra ganz mit arithmetischen Induktionsreihen &
Gleichungen betrieben werden kann || arbeiten
kann. Aber daß sich in der arithmetischen
Notation dennoch das Algebraische erhalten wird, daß die
arithmetischen Zeichen nun auf andere Art gebraucht
werden.‒ ‒ ‒ |
Unter die Induktionsreihen muß das
„und so weiter” geschrieben werden &
das ‚so’ konnte nur aus
α, β &
γ ersehen werden, wenn man sie alle
drei zusammen betrachtet & nicht aus
α allein, obwohl
β &
γ aus α hervorgeht; & das ist
|
In dem arithmetisch
geschriebenen Kalkül wird ein algebraisches Resultat kein
arithmetisches sein, sondern eine bestimmte Zusammenstellung
arithmetischer Gleichungen. |
(Die Philosophie
beruhigt sich in meiner Arbeit immer mehr
(& mehr.)) |
Und ich
möchte sagen, man wird nicht sagen können, daß ein
algebraisches Resultat durch die arithmetischen
Schritte bewiesen wird || sei, sondern mit ihrer
Hilfe konstruiert.
Bewiesen sind eben die arithmetischen Resultate & auch etwa ihr logisches Produkt aber nicht die Konstruktion die ich mit den arithmetischen Gleichungen als Bausteinen konstruiere || hervorbringe. |
Was tue ich aber
mit diesen Konstruktionen? Sind sie mir wieder
Bausteine für andre Konstruktionen? |
Daß diese
Konstruktionen (die Induktionsbeweise) nicht
bloß die arithmetischen |
Der
Prozeß durch den wir gehen
müssen um aus dem || vom Bild B zu
A zu gelangen, fehlt eben in
dem || den Zeichen.
|
Ich will
immer sagen daß B eine neue Einheit ist & nicht als
Induktionsbeweis aus α aufgebaut ist.
|
Ähnlich
wie das Spiralenstück
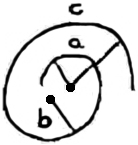 aus den 3
Halbkreisen a, b, c aufgebaut ist, aber das
Wesentliche der Spirale erst durch die besondere Art ihrer
Zusammenfügung entsteht & daher zum Halbkreis ein neues
Prinzip hinzukommen muß, damit die Spirale entsteht. aus den 3
Halbkreisen a, b, c aufgebaut ist, aber das
Wesentliche der Spirale erst durch die besondere Art ihrer
Zusammenfügung entsteht & daher zum Halbkreis ein neues
Prinzip hinzukommen muß, damit die Spirale entsteht.
Dieser Vergleich ist ein ziemlich verunglückter Versuch die richtige || klare Darstellung zu finden. |
Wenn
Einer fragt, „ist das ein Beweis des
allgemeinen Satzes A”, so könnte
man ihm drauf antworten || sagen: wenn
ein Beweis, so doch jedenfalls dieses Satzes
& keines andern. |
Aber das heißt natürlich nur:
Etwas hat die Induktion mit diesem allgemeinen Satz zu
tun. Die Frage ist nur, ob man die Induktion den
Beweis nennen kann. |
Das heißt, ich mache
(5 + 2)² = 5² + 2 ∙ 2 ∙ 5 + 2² zu einem andern Zeichen, indem ich schreibe: (
|
(Ich erkenne
(jetzt) die Wichtigkeit dieses Prozesses
der Zuordnung. Er ist der Ausdruck einer neuen
Betrachtung der Rechnung & daher die || der Betrachtung einer neuen
Rechnung.) |
„Du sagst
‚wo eine Frage ist, da ist auch ein Weg zu ihrer
Beantwortung’, aber in der Mathematik gibt es doch
Fragen, zu deren Beantwortung wir keinen Weg
sehen”. – Ganz richtig,
& daraus folgt nur, daß wir in diesem Fall das Wort
‚Frage’ in anderem Sinn Gebrauchen, als im oberen
Fall. Und ich hätte vielleicht sagen sollen
„es sind hier zwei verschiedene Formen
& nur für die erste möchte ich das
|
Alles was den
Charakter einer Behauptung trägt, schwindet mehr & mehr
in dieser || meiner Arbeit
& damit wird sie immer korrekter & anderseits immer
schwerer für die zu verstehen, die auf metaphysische
Theorien eingestellt sind. || die
metaphysische Theorien erwarten. |
D.h.,
einerseits wird, was ich sage, immer leichter verständlich,
anderseits seine Bedeutung immer schwerer
verständlich. || immer
schwerer zu verstehen. |
Könnte man auch so sagen:
In der Arithmetik wird das assoziative
Gesetz überhaupt nicht gebraucht, sondern da arbeiten wir
(nur) mit besonderen
Zahlenrechnungen. Und die Algebra, auch wenn sie sich der arithmetischen Notation bedient, ist ein ganz anderer Kalkül & nicht aus dem arithmetischen abzuleiten. |
Ist es
das nicht, was ich über die Skolemschen Beweise immer sagen will? |
Kann
ein algebraischer Satz nicht durch die arithmetischen Schritte
(im arithmetisch geschriebenen
Kalkül) bewiesen werden, dann auch nicht durch
Skolems Schritte, denn das
sind in Wirklichkeit arithmetische Schritte. |
15.
Der Philosoph notiert eigentlich
nur das was der Mathematiker so gelegentlich über seine
Tätigkeit hinwirft. |
Der Philosoph
kommt leicht in die Lage eines ungeschickten Direktors, der,
statt seine Arbeit zu tun & nur darauf zu
schaun || indem er darauf schaut daß seine Angestellten
ihre Arbeit richtig machen ihnen ihre Arbeit
abnimmt & sich so eines Tages mit fremder Arbeit
überladen sieht, während die Angestellten zuschauen und ihn
kritisieren.7 |
Besonders ist er geneigt sich die
Arbeit des Mathematikers aufzuhalsen. |
Eine logische
Fiktion gibt es nicht & darum kann man nicht mit
|
In der Mathematik kann es
nur mathematische Schwierigkeiten [troubles] geben,
nicht philosophische. |
20.
Wenn α, β, γ bewiesen sind, muß der
allgemeine Kalkül erst erfunden werden. |
Das
„u.s.w.” hat in der
reinen Arithmetik || in der reinen
Zahlenrechnung || Ziffernrechnung
noch gar keinen Sinn. |
AI,
AII, AIII etc.
begründen ein neues System; ein System zu dessen Grundlage man
freilich nicht gerade die A nehmen muß (dann
aber eben andere Gleichungen). |
Es kommt uns ganz
selbstverständlich vor, auf die Induktionsreihe hin
a + (b + c) =
(a + b) + c zu schreiben; weil wir nicht
sehen, daß wir damit einen ganz neuen Kalkül beginnen.
(Ein Kind das gerade rechnen lernt würde in dieser
Beziehung klarer sehen als wie wir.) |
Ich möchte
aber einwenden: ist nicht das allgemeine Prinzip dieses
algebraischen || allgemeinen Kalküls die
Grundlage (des Kalküls), &
A doch nur eine Folge aus dieser, zusammen mit
α, β, γ? |
Dann muß dieses
Prinzip in einem Satz des Kalküls ausgesprochen
sein. Und das ist es nicht. |
Muß ich sagen:
Der Fehler Skolems war,
nicht zu sehen daß A durch α, β, γ erst bewiesen wäre, wenn zu
α, β, γ noch ein anderes Prinzip
träte. Und ferner ist eben im Kalkül
Skolems ein solches
Prinzip nicht ausgesprochen & daher ist er nicht der,
welcher mit diesem Prinzip zustande käme, sondern ein
anderer. Und zwar wird in ihm ohne jede allgemeine
Betrachtung mit den „Beweisen” I,
II, III etc. wie mit Sätzen
operiert.
Ist es nicht wahr, daß ich aus B, A auf eine bestimmte Weise ableite? Ja, ich leite es auf eine bestimmte Weise ab. Es ist so, als hätte ich in B Röhren auf bestimmte Weise zusammengestellt || zusammengebaut & nun ließe ich einen bestimmten Strom (den Zahlenstrom) durchfahren || durchlaufen || durchfließen & der Vorgang der nun resultiert, der Lauf des Stroms || Wassers durch dieses System || Röhrensystem ist || wäre A. |
23.
Ich will nur
sagen: diese Weise, wie ich die Komplexe BI,
BII, etc. ansehe,
behandle, indem ich die algebraischen Sätze
|
Hier habe ich BI,
BII, BIII aufgerichtet; nun laß den
Zahlenstrom durch dieses laufen, & nun so
etc.. |
Aber ich sehe doch dann etwas ganz
bestimmtes, nämlich die
Allgemeinheit! |
[Solange mein Geist || Verstand so verkrampft ist wie jetzt, kann ich
überhaupt den Wurf nicht richtig
ausführen. Das macht
übrigens nichts, ich muß mich doch
für den Wurf üben.] |
Ich
will sagen: was Skolem
tut ist vollkommen damit beschrieben, daß || wenn man
sagt, er beweise etwas über die Formen der Gleichungen A,
indem er z.B. für die Gleichung
a + (b + c) =
(a + b) + c zeigt, daß
(a + (b + c) + 1
& ((a + b) + c) + 1
aus a + (b + (c + 1))
& (a + b) + (c + 1)
durch a + (b + 1) =
(a + b) + 1 ableitet, etc.
etc.. Von einem allgemeinen
Prinzip der Induktion ist hier || dabei gar keine Rede. || braucht in dieser Beschreibung gar keine
Rede zu sein. || Wir
brauchen in dieser Beschreibung nicht von einem allgemeinen Prinzip
der Induktion sprechen.* |
Wir sehen wohl die
Periodizität in der |
Es bleibt quasi uns
überlassen, daß wir die Analogie || Ähnlichkeit bemerken.
(Denn die
Worte die Skolem zur
Erläuterung sagt, gehen mich
offiziell || streng genommen
nichts an.) || gehen mich, wenn ich den
Kalkül überprüfe, nichts an.) |
(Ich
parodiere eine Auffassung, um einen Fehler in ihr zu zeigen.
Diese Methode läßt sich allgemein anwenden.
∣ Frege gegen
Cantor ∣ ) |
D.h. es ist nirgends,
klar, die Verbindung zwischen der Form von B &
A gemacht. |
Nirgends die Bedingung formuliert, unter
welcher wir A durch α, β, γ für bewiesen
ansehen. |
Es ist meine Privatangelegenheit, ob
ich die Analogie der Komplexe sehe || die Analogie … zu
sehen. (In der es doch liegen muß, daß
sie Beweise der algebraischen Sätze sind.) |
∣ „Die
rationalen Punkte liegen auf der Zahlengeraden nahe beisammen || beieinander”: |
Das strenge Kriterium
der Allgemeinheit ist nirgends ausgesprochen
(wodurch nämlich definiert wäre, was
hier unter ‚Allgemeinheit’ zu verstehen
ist). |
Nehmen wir nun an, es wäre
ausgesprochen, so wären damit nicht so sehr die A
bewiesen, als ersetzt. || dadurch
ersetzbar? ﹖ |
Das Kriterium der
Allgemeinheit würde das Wesen der algebraischen Rechnung
bestimmen || festlegen. |
Es wird dann
a + (b + n) =
(a + b) + n zu einer Rechnung wie jeder andern || eine
Rechnung wie jede andre || andere
(nur || allerdings
eine Rechnung von nur || bloß
einem Schritt) & das Paradigma
erhält die Form B. [R.] |
Wenn
nun die Paradigmen meines neuen Kalküls auch alle
die bestimmte Form R haben, so wäre es doch ein
verwirrender Ausdruck zu sagen, die Richtigkeit der Gleichung
AI, z.B., sei durch
α bewiesen. Sie
ist höchstens durch BI bewiesen, aber auch
nur so, wie etwa früher i + (k + l) =
(i + k) + l durch
a + (b + c) =
(a + b) + c. |
Als rechtmäßig
bewiesen ist er durch α nur dann, wenn ich
|
Dann kann ich sagen
„seine Rechtmäßigkeit ist durch
α bewiesen”.
Aber hier hat eben das Wort „Rechtmäßigkeit” eine andre Bedeutung, als wenn ich sage: die Rechtmäßigkeit des Übergangs von (a + b)² auf a² + 2ab + b² ist bewiesen & damit meine dieser Übergang lasse sich in lauter Stufen von zuvor bestimmten Formen zerlegen. |
Denn von
B nach A findet ja in diesem Sinn kein Übergang
statt, sondern B erlaubt den Übergang der in A
gemacht wird, wie in jeder andern Rechnung. |
Die
Ähnlichkeit der beiden Arten von Beweisen,
oder Rechtfertigungen, könnte man so darstellen:
„Ich habe die Gleichung (a + b)² =
a² + 2ab + b² auf bestimmte Weise mit
Hilfe der Grundgleichungen konstruiert || (aufgebaut) & die Gleichung A habe ich
auch mit Hilfe von Regeln konstruiert”.
|
Man hat den
Satz „daß für alle |
Ja, kann ich nicht für
beide Fälle || Arten von
Beweisen sagen: „Ein Übergang ist
gerechtfertigt, wenn sein Paradigma auf diese Weise konstruiert
werden kann”? |
Der Satz, daß A für alle
Kardinalzahlen gilt ist eigentlich der Komplex B.
Und sein Beweis, der Beweis von β &
γ. Aber das zeigt auch,
daß dieser Satz in einem andern Sinne Satz ist, als eine Gleichung,
& sein || dieser Beweis in anderm Sinne Beweis
eines Satzes. Vergiß hier nicht, daß wir nicht erst den Begriff des Satzes haben, dann wissen, daß die Gleichungen mathematische Sätze sind, & dann erkennen, daß es noch andere Arten von mathematischen Sätzen gibt! |
(Halte alle diese Dinge zusammen, dann wirst Du
die Sache || den Gegenstand verstehen. || dann wirst Du das Betrachtete || betrachtete
Gebiet verstehen.) |
Wenn man sagt, A sei
mit ρ & dem Prinzip
R bewiesen, welches ist die Art
der Allgemeinheit dieses allgemeinen Prinzips? |
Der
Übergang ist gerechtfertigt heißt im einen Falle, daß er
nach bestimmten gegebenen Formen vollzogen werden
kann. Im andern Fall wäre die Rechtfertigung, daß
der Übergang nach Paradigmen geschieht, die selbst
eine bestimmte Bedingung befriedigen.
|
Man
denke sich, daß für ein Brettspiel solche Regeln gegeben
würden, die aus lauter Wörtern ohne
‚r’ bestünden & daß ich eine
Regel gerechtfertigt nennte, wenn sie kein
‚r’ enthält. Wenn nun jemand
sagte, er habe für das & das Spiel nur
eine Regel aufgestellt, nämlich, daß die Züge
Regeln entsprechen müßten, die kein
‚r’ enthalten. – Ist denn das
eine Spielregel (im ersten Sinn)? Geht das Spiel
nicht doch nach den Regeln || nach den mehreren
Regeln vor sich, die |
Eine Regel zur Konstruktion
von Spielregeln ist keine Spielregel. |
Es macht mir
jemand die Konstruktion von B vor & sagt nun,
A ist bewiesen. Ich frage
„Wieso? – Ich
sehe nur daß Du um A eine Konstruktion mit Hilfe von
|
∫ In einem Sinn heißt
es, daß Du das Paradigma mittels ρ so & so konstruiert
hast, in dem andern, nach wie vor, daß eine Gleichung dem Paradigma
entspricht. |
[Ich suche nach der richtigen
Replik.] |
[„Ich habe nie daran
gedacht ihm das zu antworten”.]
|
In dem Sinne
V in welchem (a + b)² =
a² + b² + 2ab durch AI,
AII etc. beweisbar ist,
ist AI unbeweisbar || unbewiesen. |
Man
sagt ja daher auch wirklich die
Allgemeinheit || Allgemeingültigkeit
der Gleichung A || von A sei bewiesen, eben
um den Unterschied auszudrücken. |
Man erwartet sich unter einem
Beweis das eine & bekommt etwas anderes.
Und nun tröstet man sich damit, daß man nur eine
andere Art von Beweis erhalten habe. |
‚Gleichung’ & ‚Beweis
einer Gleichung’ haben eine bestimmte Grammatik.
Zu sagen
|
Er sagt, er habe A bewiesen &
zeigt mir den Komplex B. Ich frage „in
wiefern ist das ein Beweis von A?” Er
muß antworten: „Das ist die Form des
Paradigmas der erlaubten Übergänge. (Ist um die Enden des Übergangs diese Konstruktion
mittels ρ möglich, so ist der Übergang
erlaubt. |
Wenn wir fragen „ist das ein
Beweis oder nicht?” so bewegen wir uns in den
Formen der Wortsprache. || in der
Wortsprache. |
Nun ist natürlich gar nichts dagegen
zu sagen || einzuwenden, wenn Einer sagt:
Wenn die Glieder des Übergangs in einer Konstruktion
der & der Art stehen, so sage ich, die Rechtmäßigkeit
des Übergangs ist bewiesen. |
Was
wehrt sich in mir gegen die Auffassung von B als einen Beweis
von A? Zuerst entdecke ich, daß ich den Satz von
„allen Kardinalzahlen” in meiner Rechnung
nirgends brauche. Ich habe den Komplex B mit Hilfe
von ρ konstruiert und bin dann auf die
Gleichung A übergegangen; von „allen
Kardinalzahlen” war dabei keine Rede!
(Dieser Satz ist eine Begleitung der Rechnung in der
Wortsprache, die mich hier nur verwirren
kann.) Aber nicht nur fällt dieser
allgemeine Satz überhaupt fort, sondern kein anderer tritt an
seine Stelle.
(Außer etwa das logische
Produkt α ∙ β ∙ γ.
Aber auch das stimmt nicht, denn in diesem
Produkt müßte ich erst gewisse Züge
‚hervorheben’. Denn wenn man fragt,
was der Satz α ∙ β ∙ γ
sagt, so kann ich eigentlich nur den Satz
wiederholen,
Der Satz der die Allgemeinheit behauptet fällt also weg, „es ist nichts bewiesen”, „es folgt nichts”. „Ja aber die Gleichung A folgt, sie steht nun an der Stelle des allgemeinen Satzes”. – Ja, in wiefern folgt sie denn? Offenbar versende ich hier ‚folgt’ in einem ganz andern Sinn, als dem normalen, da das, woraus A folgt kein Satz ist. Darum fühlen wir auch, daß || Das ist es auch warum das Wort „folgen” nicht richtig angewandt ist. |
Wenn man sagt „aus dem
Komplex B folgt, daß a + (b + c) =
(a + b) + c”, schwindelt
Einem. Man fühlt, daß man da auf irgend
eine Weise einen Unsinn geredet hat, obwohl es äußerlich
richtig klingt. |
Daß eine Gleichung folgt, heißt
eben schon etwas (hat seine bestimmte Grammatik.) |
Aber wenn es heißt || ich
höre „aus B folgt A”, so
möchte man || ich fragen:
„was folgt?” Daß
a + (b + c) gleich
(a + b) + c ist, ist
ja eine Festsetzung, wenn es nicht auf normale Weise aus
einer Gleichung folgt. |
Wir können unsern
Begriff des Folgens mit A & B nicht zur Deckung
bringen. || Wir können unsern
Begriff des Folgens dem A & B
nicht aufpassen. || nicht aufsetzen,
er paßt hier nicht. |
Man
kann allerdings sagen, man rechtfertigt eine algebraische
Rechnung durch die Möglichkeit der Konstruktion der
Paradigmen durch ρ. Und das tut man auch
wirklich. Aber das sagt nicht, daß man
(a + b)² =
a² + 2ab + b² durch
α beweist. Im Gegenteil,
man beweist β &
γ mit α, kann aber A nicht damit
beweisen. Man zeigt jemand z.B. den Übergang von (x + y)² zu x² + 2xy + y² & er sagt: Ja, – aber warum machst Du diesen Übergang von (x + y) ∙ (x + y) zu x ∙ (x + y) + y ∙ (x + y)? Und ich zeige ihm nun den entsprechenden Komplex B, um ihn zu überzeugen. Aber heißt das, ich habe die Richtigkeit des Übergangs |
“Ich werde Dir beweisen, daß
a + (b + n)
=
(a + b) + n”. Niemand
erwartet sich nun den Komplex B zu sehen. Man
erwartet eine andere Regel über a, b
& n zu hören, die den Übergang von der einen
auf die andere Seite vermittelt. Wenn mir statt
dessen B & das Schema R gegeben wird, so kann ich
das keinen Beweis nennen, eben weil ich unter
‚Beweis’ etwas anderes
verstehe.8 |
Ja, ich werde dann etwa sagen:
„Ach so, das nennst Du ‚Beweis’, ich
habe mir vorgestellt …”. |
Der Beweis von
17 + (18 + 5)
= (17 + 18) + 5 wird allerdings nach dem
Schema B geführt & dieser Zahlensatz
ist von der Form A. Oder auch: B ist der
Beweis des Zahlensatzes; aber eben deshalb nicht von
A. |
„Ich werde Dir
AI, AII
AIII
aus dem einen || aus einem
Satz ableiten”. – Man denkt dabei
natürlich an eine Und da haben wir doch ein bestimmtes Bild; und es wird uns etwas ganz anderes geboten. Die Gleichung wird durch den induktiven Beweis quasi der Quere, statt der Länge nach zusammengesetzt. |
24.
Wenn wir nun die Ableitung
ausführen || ausrechnen, so kommen wir
endlich zu dem Punkt wo die Konstruktion von B vollendet
ist. Aber hier heißt es nun „also gilt
diese Gleichung”. Aber diese Worte
heißen ja nun etwas anders als, wo wir sonst
eine Gleichung aus Gleichungen folgern. Die Worte
„die Gleichung folgt daraus” haben ja schon
eine Bedeutung. Und hier wird eine Gleichung allerdings
konstruiert, aber nach einem andern Prinzip.
|
[Der Satz kommt mit lauter verrenkten
Gliedern zur Welt & ich muß ¤
sie ihm erst alle, so gut es geht,
einrenken. Kein Wunder wenn er dann keine
|
Wenn ich sage
„aus dem Komplex folgt die Gleichung”, so
‚folgt’ hier eine Gleichung aus etwas, was gar keine
Gleichung ist. |
In dem Sinne, daß ich auf dem
Papier das eine aus dem andern erhalte, das eine
nach dem andern hinschreibe, kann allerdings die Gleichung
A aus B folgen. In diesem Sinne könnte ich
sie aus B ableiten. |
Aber dadurch daß ich sie so
ableite, bleibt sie immer, was sie war, die Grundgleichung eines
Symbolismus. D.h. durch diese Ableitung wurde zwar, natürlich, ihr logischer Status ein anderer als er vor der Konstruktion dieser || der Ableitung war, aber er ändert sich nicht in der Weise wie, wenn die Gleichung bewiesen worden wäre. Es ist (ihr) etwas geschehen || widerfahren, aber nicht das. Ich mache eben wieder nur auf einen Unterschied aufmerksam. |
[Der Gedanke ist
schon vermudelt, & läßt sich
nicht mehr gebrauchen. (Eine ähnliche
Bemerkung hörte ich einmal von Labor,
musikalische |
Man kann nicht sagen:
die Gleichung wenn sie aus B folgt, folge doch aus einem Satz,
nämlich aus α ∙ β ∙ γ; denn
es kommt eben darauf an, wie ich aus diesem
Satz A erhalte; ob nach einer Regel des Folgens.
Welches die interne Relation || Verwandtschaft der
Gleichung zum Satz α ∙ β ∙ γ
ist. (Die Regel, die in diesem Falle zu A
führt, macht gleichsam einen Querschnitt durch
α ∙ β ∙ γ,
sie faßt den Satz anders auf, als eine Regel des
Folgens.) |
Wenn uns die Ableitung von A aus
α versprochen war & wir sehen nun den Übergang von
B auf A, so möchten wir sagen: „ach,
so war es nicht gemeint”. So, als hätte
jemand mir versprochen, mir etwas zu schenken || er wird mir etwas schenken & nun sagt
er: so, jetzt habe ich Dir meine Zeit
geschenkt. || & nun sagt er: so, jetzt
schenke ich Dir meine Zeit || mein
Vertrauen. (Eine Enttäuschung.) |
(Ich hätte natürlich nicht das
logische Produkt aus α, β & γ
bilden müssen, denn A konnte ja aus den drei
Sätzen folgen (wie z.B.
α ∙ β ∙ γ aus
seinen drei Faktoren). Aber das
|
Darin, daß
der Übergang von B auf A kein Folgen ist, liegt
auch, was ich damit meinte, || liegt auch was ich
damit meinte wenn ich sagte,
daß nicht das logische Produkt α ∙ β ∙ γ
die Allgemeinheit ausdrückt.
|
⍈
[Das Einschiebsel von diesem
* zum nächsten gehört nach ⋎.] Was heißt es, α ∙ β ∙ γ nicht als Satz ansehen? Dies sollte ja darauf ein Licht werfen, was es heißt, etwas als Satz ansehen. Und dabei denke ich wieder an ein Durchlaufen der Länge nach statt der Quere. |
⍈
Wie wenn man
eine Schiene die in Serpentinen läuft nicht als
 Schiene
(der Länge nach) benützte sondern als Leiter
(quer). Schiene
(der Länge nach) benützte sondern als Leiter
(quer). |
⍈
∣
Denken wir uns wir läsen die Sätze eines Buches verkehrt,
die Worte in umgekehrter Reihenfolge; könnten wir nicht dennoch
den Satz verstehen? Und klänge er jetzt nicht ganz
unsatzmäßig? ∣ |
⍈
Das Bild vom längs &
quer Durchlaufen ist natürlich wieder ein logisches
Bild & darum ein ganz |
Wenn ich sage, der Satz wird
hier nicht als Satz aufgefaßt, denke ich da nicht an einen Fall wie
den, wenn etwa eine Flasche nicht als Behälter, sondern als
Kerzenleuchter verwendet wird? Es ist dann so, daß nur
gewisse Züge der || Gewisses an der Struktur des
Gegenstandes zur Verwendung kommt, während die Erzeugung des
Gegenstandes auf eine andere Verwendung abgezielt hat.
Aber ist denn die Flasche, die als Kerzenleuchter dient (dadurch) eine andere (geworden) als die, die zum Aufbewahren einer Flüssigkeit dient? |
Die Ableitung
zweier Sätze aus einem
zeigt || erzeugt einen formellen
Zusammenhang zwischen den abgeleiteten.‒ ‒ ‒ |
Kann man
sagen: α, β, γ sind Gleichungen der Algebra,
aber weder fungiert die rekursive Definition
α |
Die
Hervorhebungen geschehen durch das Schema R &
könnten so ausschauen: a + (b + 1) = (a + b) + 1 a + (b + (c + 1)) = |a + ((b + c)| + 1 (a + b) + (c + 1) = |((a + b) + c)| + 1(Ƒ) |
Solche Hervorhebungen
könnte man ja aber an jedem Satz machen, aus dem man etwas nach
einer Regel schließt. Wenn ich nach der Regel
a + b = b + a schreibe:
¤ r ∙ s + s ∙ r =
s ∙ r + r ∙ s, so könnte ich die
Benützung der Regel durch
|
Es hätte aber
natürlich auch genügt (d.h.
wäre ein Symbol der selben Multiplizität gewesen) B
anzuschreiben & dazu: f1ξ =
a + (b + ξ), f2ξ =
(a + b) + ξ. (Und dabei ist
wieder zu bedenken || anzumerken, daß jedes
Symbol – wie explizit auch immer – mißdeutet werden
kann. –)
Und natürlich, um „f1ξ = … ” & „f2ξ = … ” bei || mit B zu verstehen, muß ich das B auf gewisse Weise sehen. |
Wer etwa zuerst
darauf aufmerksam macht daß B so gesehen werden
kann, der führt ein neues Zeichen ein; ob er nun die
Hervorhebungen mit B verbindet oder auch das Schema
R daneben schreibt. Denn dann ist eben
R das neue Zeichen. Oder wenn man will auch
B zusammen mit R. |
Wer entdeckt daß ein Satz
p aus einem von der Form
q ⊃ p ∙ q
folgt der konstruiert ein neues Zeichen, das Zeichen dieser
Regel. (Ich nehme dabei an, der || ein Kalkül mit p,
q,
⊃ ,
∙ , sei schon früher
gebraucht worden, & nun träte diese Regel hinzu &
schaffe damit einen neuen Kalkül.) |
Man könnte
etwa sagen: Hier wurde die untere Gleichung als
a + b =
b + a gebraucht; und analog: hier wurde B
als A gebraucht, wobei B aber gleichsam der Quere nach
gelesen wurde. Oder: B wurde als A
gebraucht, aber die neue Gleichung || das neue Zeichen || der
neue Satz wird aus α ∙ β ∙ γ
so zusammengestellt, daß, indem man
(nun) A aus B herausliest
man nicht α ∙ β ∙ γ
in jener verkürzten Form || Art von Verkürzung liest
in der man die Prämisse im Folgesatz vor sich
hat. || im Folgesatz liest.
|
Wenn ich sage: α ∙ β ∙ γ
entspricht noch nicht dem allgemeinen Satz der Wortsprache, so
will ich etwa sagen, daß man
„α ∙ β ∙ γ”
lesen kann, ohne daß einem das auffällt, was uns als Ausdruck
des allgemeinen Satzes gilt. Nur daß die Wortsprache
sagen möchte: Dieser Satz
α ∙ β ∙ γ
entspricht dem Schema R, also gilt …; während
wir sagen: || :
„dieser Satz entspricht dem Schema
R”; & kein „also”
hinzufügen. Wie ist nun aber dieser Satz im Symbolismus ausgedrückt? |
Ist denn das nicht der Fall
von „‚fa’ &
‚Fa’ haben den gleichen
Bestandteil”? Und ich sagte doch, das
müsse sich zeigen. Und wäre es denn
dadurch gesagt, daß ich schriebe
„f(a) &
F(a)”?
Dann brauchte ich ja einen weiteren Satz der sagte, daß
unter jedem der beiden ‚a’ ein Strich
ist. |
Was heißt es nun:
„Ich mache Dich darauf aufmerksam, daß hier in
beiden Funktionszeichen das gleiche Argument || Zeichen steht (vielleicht hast
Du es nicht bemerkt)”? Heißt das, daß
er den Satz nicht verstanden hatte? Und doch hat er etwas
nicht bemerkt, was wesentlich ⋎ * ‒ ‒ ‒ *
¥ |
Wenn ich sage, man sieht
α ∙ β ∙ γ
nicht als Satz an, so meine ich, ich benütze seine Zeichen nicht
in der Reihenfolge, in der ¤ ich sie beim Durchlesen
des Satzes berühre. Und das zeigt sich
darin, wenn ich die induktive Auffassung des
Satzes erkläre & dazu die Anwendung des Schemas B
zum Fortschreiben von einer Stufe zur andern in der Induktion
vorführe. Dann benütze ich
den Komplex eben der Quere nach. Und diese
Benützung zeigt mir eigentlich, wie ich den
Komplex || ihn auffasse. Die
Gleichungen α, β, γ sind der Länge nach
entstanden & ich benütze sie nun der
Quere nach. |
Ist der
Komplex B als logisches Produkt &
anderseits als |
Ich
sage, B gehört nun, als Zeichen der Induktion aufgefaßt,
einem neuen System an. (Bei || In der periodischen Division ist || wird das noch klarer. Die Unendlichkeit tritt in
die Betrachtung, die früher gar nichts mit || in der Rechnung zu tun hatte.) |
Wenn ich sagte, das neue Zeichen mit den Hervorhebungen müsse
ja doch aus dem alten ohne die Hervorhebungen abgeleitet
sein || entstehen, so heißt das nichts, weil ich
ja das Zeichen mit den Hervorhebungen abgesehen von seiner Entstehung
betrachten kann. Es stellt sich mir dann
[Frege] dar als drei
Gleichungen, d.h., als die Figur dreier
Gleichungen mit gewissen Unterstreichungen
etc.. Daß diese Figur ganz analog der der drei Gleichungen ohne den Unterstreichungen ist, ist allerdings bedeutsam, wie es ja auch bedeutsam ist, daß die Kardinalzahl 1 & die Rationalzahl 1 gleiche Regeln befolgen, || analogen Regeln unterworfen sind, aber es hindert nicht daß wir hier ein neues || anderes Zeichen haben. |
Aber
ist es denn auch bei der induktiven Benützung
von B den Gleichungen β &
γ nicht wesentlich, daß sie
„der Länge nach” abgeleitet
wurden? – Ich kann ja auch statt
β &
γ die ganze Ableitungskette
hinsetzen. |
Ich treibe jetzt etwas ganz Neues mit
diesen Zeichen. |
Verhält es sich hier nicht so, wie in
dem Fall, den ich einmal annahm, daß der Kalkül der
Wahrheitsfunktionen von Frege & Russell mit der Kombination ~p ∙ ~q
der Zeichen „~” &
„ ∙ ”
betrieben worden wäre, ohne daß man das gemerkt
hätte, & daß nun
Sheffer, statt eine
neue Definition zu geben, nur auf eine Eigentümlichkeit der
bereits benutzten Zeichen aufmerksam gemacht hätte. |
Übrigens sind ja alle mathematischen Entdeckungen von
dieser Art & das ist nur ein extremer Fall in dem
wir der Entdeckung (in gewissem Sinn)
im Symbolismus ganz nahe gebracht sind. |
Man hätte immer
dividieren können ohne je auf die Periodizität
aufmerksam zu werden. Hat man sie gesehen, so hat man
etwas Neues gesehen. |
Könnte man das
aber dann nicht ausdehnen & sagen: „ich
hätte Zahlen miteinander multiplizieren können, ohne
je auf den Spezialfall aufmerksam zu werden, daß ich eine Zahl mit
sich selbst multipliziere & also ist
x² nicht einfach
„x ∙ x.”
Die Schaffung des Zeichens „x²” könnte man den
Ausdruck dafür nennen, daß man auf diesen Spezialfall
aufmerksam geworden ist. Oder, man hätte
(immer) a mit b
multiplizieren und durch c dividieren können,
ohne darauf aufmerksam zu werden, daß man
„
|
∣ Die
Frage „können viele unter viele || einige unter einige
verteilt werden” || „können einige
Äpfel unter einige Menschen verteilt werden”
hat keinen Sinn. (Zum System 1, 2, 3, 4, 5, viele)
∣ |
∣
Ein Satz der auf einer falschen Rechnung beruht (wie etwa
„er teilte das 3 m lange Brett in 4 Teile zu je
1 m”) hat keinen Sinn || ist
unsinnig & das wirft ein Licht auf den Sinn
der Ausdrücke „Sinn haben” &
„etwas mit dem Satz meinen”. || & das beleuchtet was es heißt
„Sinn zu haben“ & „etwas mit dem Satz
meinen”. ∣ |
Es hat Sinn zu sagen: Ich
verteilte viele auf || unter viele. Aber der
Satz „ich konnte die vielen Nüsse nicht unter die vielen
Menschen verteilen” kann nicht heißen, daß es logisch
unmöglich war. Man kann auch nicht sagen:
„in manchen Fällen ist es möglich viele unter viele
zu verteilen, in manchen nicht”; denn darauf frage ich:
in welchen Fällen ist dies möglich &
in welchen unmöglich? Und darauf
könnte nicht mehr im Viele-System geantwortet werden.
|
In der
Notation „x²” verschwindet
ja wirklich die Möglichkeit das eine der x || den einen der Faktoren x durch eine andere
Zahl zu ersetzen. Ja, es wären zwei Stadien der
Entdeckung (oder
Konstruktion) von x² denkbar.
Daß man etwa zuerst statt
„x²”
„x⁼”
setzt, ehe es Einem nämlich auffällt, daß es das
System x ∙ x,
x ∙ x ∙ x,
etc. gibt & daß man dann erst hierauf
kommt. Ähnliches ist in der Mathematik unzählige
Male vorgekommen. (Liebig bezeichnete ein Oxyd noch nicht so, daß der
Sauerstoff darin als
gleichwertiges Element mit dem
Oxydierten || als Element wie das Oxydierte
auftrat. Und, so seltsam das klingt, so könnte
|
25.
Ich will also sagen: x² mußte man entdecken
wie den induktiven Zug in B (und wie die
Irrationalzahlen). Und damit hat man in
jedem der Fälle ein neues System konstruiert.
Aber ist denn nicht nach wie vor, x² =
x ∙ x? – Und wenn wir nun durch
Definition setzen: [a + (b + 1) = (a + b) + 1] & [a + (b + (c + 1)) = (a + (b + c) + 1] & [(a + b) + (c) + 1) = = ((a + b) + c) + 1] ≝ a + (b + c) .𝒥. (a + b) + c … U)(Ƒ) und allgemein: [f1(1) = f2(1)] & [f1(c + 1) = f1(c) + 1] & [f2(c + 1) = f2(c) + 1] .≝. .≝. f1(c) .𝒥. f2(c) … V)! – (Ƒ) |
∣ ﹖ Die 2 in
„x²” könnte
man wirklich noch durch ein beliebiges anderes Zeichen ersetzen,
solange man sie noch nicht mit den andern Potenzen in Verbindung
gebracht hat. |
Da muß man nun sagen, daß man die
Definition des ξ𝒥η
gar nicht verstehen kann || versteht, wenn man nicht
|
Wer aber z.B. so den
Potenzexponenten mißverstanden hätte, würde doch mit dem
Zeichen „x²” richtig
rechnen, solange er es nur als Abkürzung für
„x ∙ x”
gebrauchte. Daß wir aber hier über das
alte System hinausgehen zeigt die allgemeine Erklärung
des Exponenten, etwa x ∙ x ∙ x…n-mal
= xn[x¹ = x,
xⁿ⁺¹ = xn ∙ x]
weil diese Zeichen enthält
(„xn”) die in der
Algebra, die die Potenzen nicht kennt wenn auch die
Ausdrücke „x ∙ x”,
„x ∙ x ∙ x”
nicht vorhanden sind. Ich habe in dem Ausdruck des letzten Satzes „wenn auch die Ausdrücke ‚x ∙ x’, ‚x ∙ x ∙ x’” natürlich mit Absicht das ‚u.s.w.’ weggelassen, denn eben dieses ist es ja, welches die neue Konstruktion hinzufügt. (Das ‚u.s.w.’ wäre hier, wie schon so oft bemerkt, keine Abkürzung. Wenn ich sage „in dem Konzert waren alle meine Geschwister Paul, Gretl u.s.w.” so ist hier das |
Was ich
sagen will ist eigentlich nur: Mit den Definitionen
x ∙ x
= x², x ∙ x ∙ x =
x³, x ∙ x ∙ x ∙ x
= x⁴ kommen nur die Zeichen
x²,
x³, x⁴ zur Welt (und so weit war es noch
nicht nötig Ziffern als Exponenten zu
schreiben). ∣ Die rekursive Definition von
xn drückt nicht etwa
aus was im Kalkül mit x², x³, x⁴
schon war || schon vorhanden war
& nur hat gefunden werden müssen, sondern bedeutet eine
neue Konstruktion ∣ . (Die
keine frühere Lücke ausfüllt.) |
Es wäre eine
Frage, wie eine Algebra aussähe die ganz ohne Induktion
arbeiten würde || arbeitete.
Wie ist es in dieser Beziehung in der „Algebra der
Logik” wie sie Frege & Russell benützen? In dieser
werden
keine rekursiven Definitionen gegeben & keine
rekursiven Beweise gegeben || geführt. || keine rekursiven Definitionen
& keine rekursiven Beweise gegeben. |
Wenn ich
früher sagte, die Definition von ξ.𝒥.η kann
man nicht verstehen, Und dasselbe gilt, wenn es heißt „Fa, und a ≝ f(b) ist” oder „Fa, wo a ≝ f(b) ist”. Auch hier bilden Fa & die Definition wirklich ein Zeichen, – oder, richtiger & ohne Mythus: sie gehören zusammen & ich hätte ja auch schreiben können: F(a) ≝ F(f(b)). |
Aber auch das stellt die
Sache nicht richtig dar.
Die Definition U
hätte man sehr wohl als eine – gleichsam, willkürliche
– Abkürzung des Ausdrucks α ∙ β ∙ γ
auffassen können, also ohne das System zu sehen dem sie nach
unserer Auffassung angehört. Die Definition so
betrachtet ist eine andere als die von uns
gemeinte, die man durch Hervorhebungen von der ersten unterscheiden
könnte. Aber dadurch geben
wir dann in Wirklichkeit die
allgemeine Definition V. Und das
heißt: die erste Definition verstehen, wie ich sie gemeint
habe heißt sie als Gleichung verstehen die der Definition
V (der allgemeinen Definition) gemäß ist.
|
Ich
könnte es so ausdrücken:
man könnte die Definition U sehen ohne zu wissen
warum ich so definiere. || so abkürze.
Man könnte die Definition sehen ohne ihren Witz zu verstehen. – Aber dieser Witz ist eben etwas Neues, daß in ihr als spezieller Ersetzungsregel noch nicht liegt. |
Auch ist „I” natürlich kein
Gleichheitszeichen, in dem Sinn, wie sie in
α, β &
γ stehen. |
Aber man kann leicht zeigen,
daß „I” gewisse formale
Eigenschaften mit
= gemein hat. |
Nun habe
ich aber doch gesagt: wenn man aus
α ∙ β ∙ γ
A ableitet so betrachtet man α ∙ β ∙ γ
gar nicht als Satz! Heißt das nicht: in der Definition U ist die rechte Seite nicht in demselben Sinne ein Satz wie die linke, denn im System der Sätze der linken Seite kann die Funktion I nicht vorkommen? |
Das erste System
ist, gleichsam, in Bezug auf I unschuldig. Es
treibt seine Spiele mit a, b, c, +, = , und kann es selbst
nicht merken daß I entsteht. |
Was natürlich wieder
nichts anderes heißt, als daß U keine Definition von
I ist, sondern V.
|
∣ Der
Prozeß der Generalisation || Verallgemeinerung schafft ein neues
Zeichensystem. ∣ |
Daß man sagt „die
Richtigkeit der Gleichung ist bewiesen”, zeigt schon,
daß Beweis nicht jede Ableitung || Konstruktion
ist. || Konstruktion der
Gleichung ist. |
Die eigentliche Entdeckung ist die, die
mich fähig macht mit dem Philosophieren aufzuhören, wann ich
will. Die die Philosophie zur Ruhe bringt so daß sie nicht mehr von Fragen gepeitscht ist || wird die sie selbst in Frage stellen. Sondern es wird jetzt an Beispielen eine Methode gezeigt, & die Reihe dieser Beispiele kann man abbrechen. |
Richtiger
hieße es aber: Es werden Probleme gelöst || (Beunruhigungen || Schwierigkeiten
beseitigt) nicht ein Problem. |
Es ist
eine sehr wichtige Bemerkung daß das c in
A nicht dieselbe Variable ist wie das
c in β &
γ. Ich habe also den
Beweis nicht ganz richtig hingeschrieben, und
Es ist aber auch noch das zu fragen: kann ich nun aus A ableiten, daß i + (k + c) = (i + k) + c? und wenn ja, warum dann nicht gleich aus B? Also ist auch a & b in A nicht identisch mit a & b in α, β & γ? |
B tritt jetzt einfach
an Stelle von A. |
Diese Bemerkung ist so wichtig wie jede
über eine Verschiedenheit im Knochenbau zweier
Tiere. || Tierarten. |
Auf den ersten
Blick scheint es zwei Stadien der Allgemeinheit des Beweises zu
geben: Wir könnten zuerst in B statt a
& b zwei bestimmte Zahlen setzen 4 & 5 &
dann wäre also das Resultat
4 + (5 + n)
= (4 + 5) + n. Und nun
könnten wir einen weitern Schritt in der Allgemeinheit
machen & „allgemeine Zahlen” statt 4
& 5 setzen. |
Daß die Variable c in B
nicht identisch mit c in A ist sieht man klar wenn
man statt ihrer eine Zahl einsetzt. Dann lautet B
etwa:
|
Als Induktionsbeweis
betrachtet rechtfertigt W nicht gerade den Übergang
in AW. Nicht mehr als der Übergang
4 + (5 + 2)
= (4 + 5) + 2. |
Soll nun auf der
rechten Seite der Definition U ein ‚c’
stehen oder ein ‚n’? Ein c,
da ja die rechte Seite nichts weiter ist als eine Abkürzung
der rechten. (Auf den vorigen Fall angewendet wäre
also statt W zu schreiben
4 + (5 + 6)
.J.
(4 + 5) + 6. Aber das
wäre nicht die Gleichung
AW.) |
∣ Was die irrationalen
Zahlen betrifft so sagt meine Untersuchung nur, daß es falsch
(oder irreführend) ist, von
Irrationalzahlen zu sprechen indem man die || sie als Zahlenart den Kardinal- &
Rationalzahlen gegenüberstellt, weil
das was || die man
„Irrationalzahlen” nennt in Wirklichkeit
mehrere || verschiedene Zahlenarten umfassen die von einander
so verschieden sind || man „Irrationalzahlen” in
Wirklichkeit verschiedene Zahlenarten nennt, – von einander so
verschieden, wie die
Rationalzahlen von jeder von ihnen. ∣ |
[Zum vorletzten
Satz] Noch wäre es ihre besondere
Rechtfertigung. Will man also die Form der durch W gerechtfertigten Zahlengleichung |
Wenn ich so aber
in B statt a & b
bestimmte Zahlen einsetze so ändert der Beweis insofern
seinen Charakter, als nun β & γ nicht mehr aus
α hervorgehen sondern nur aus
dem früheren allgemeinen α. Und das gewährt
uns wieder einen Einblick in den Beweis. Denn
auch in seiner allgemeinen Form wird β &
γ nicht eigentlich mit Hilfe von
α konstruiert sondern mit Hilfe
eines algebraischen Paradigmas von der Form
α (daß
übrigens ganz andere Variable enthalten
kann). |
Vergessen wir nicht daß U
& W (wie alle Definitionen) nur Abkürzungen
einführen, die ebensogut wegbleiben könnten.
Durch diese Definitionen ist also kein entscheidender logischer
Schritt geschehen. Wohl aber durch die neue Auffassung
ihrer linken Seiten. Oder
richtiger durch deren Konstruktion die also fälschlicher Weise so
geschrieben wurde wie das alte Zeichen
α ∙ β ∙ γ.
Der richtige Ausdruck des logischen
Schrittes || unseres Schrittes ist nur die
Neueinführung eines || Einführung eines
neuen Zeichens. |
[Ich bin außerordentlich
ungeschickt, aber gerade darum
sehe ich die Schwierigkeiten, an denen ein
|
Ich fragte oben: ist
meine Behauptung, daß im induktiven Verfahren
α ∙ β ∙ γ
nicht als Satz aufgefaßt wird, nicht dadurch ausgedrückt
daß in U die rechte Seite nicht in dem
selben Sinne ein Satz ist wie || in einem andern Sinne ein Satz ist
als die linke. Aber der Ausdruck
dieser Behauptung ist, daß α ∙ β ∙ γ
mit den Hervorhebungen in anderem Sinne ein Satz ist als
α ∙ β ∙ γ
ohne die Hervorhebungen. |
Man könnte
sagen: was ich von B &
i + (k + l) =
(i + k) + l sage, bezieht sich auch auf den
Fall des Beweises (a + b)² =
a² + 2ab + b². Auch hier
könnte man vor der letzten Transformation stehen bleiben
& sie erst in einer Anwendung auf
(i + k)²
machen. |
[Meine Methode ist, mich immer wieder von
denselben Dingen
puzzlen zu lassen.] |
∣ Die Frage
nach der Verifikation ist nur eine andere Form der Frage „wie
meinst Du das?”. ∣ |
Darin daß das c in
B nicht identisch ist mit dem c in A oder:
darin daß man die beiden Stellen mit verschiedenen
|
∣ Es ist nicht nur
höchst bedeutsam daß man ❘ ❘ ❘ ❘ ❘
auf vielerlei Arten sehen kann (in vielerlei Gruppierungen)
sondern noch viel mehr bemerkenswert daß man es
willkürlich tun kann.
D.h., daß es einen ganz
bestimmten Vorgang gibt eine bestimmte
„Auffassung” auf Befehl zu bekommen; &
daß es – dem entsprechend – auch einen ganz
bestimmten Vorgang des vergeblichen Versuchens
gibt. So kann man auf Befehl die Figur
 so
sehen daß der eine oder der andere Vertikalstrich
die Nase, dieser oder jener Strich der Mund wird, und kann unter
Umständen das eine oder das andere vergeblich
versuchen. ∣ so
sehen daß der eine oder der andere Vertikalstrich
die Nase, dieser oder jener Strich der Mund wird, und kann unter
Umständen das eine oder das andere vergeblich
versuchen. ∣ |
∣ Das Wesentliche ist hier daß
dieser Versuch den Charakter des Versuchs hat, ein Gewicht mit der
Hand zu heben; nicht den Charakter des Versuchs in
welchem man verschiedenes tut verschiedene Mittel
ausprobiert um z.B. ein Gewicht zu
heben. In den zwei Fällen hat das
|
[Ich greife oft im
Schreiben meinem Denken vor!] |
Der Fluß der
Zahlen || Der
Zahlenstrom durch B zeigt das
assoziative Gesetz. |
Heißt
was ich oben geschrieben habe etwas anderes als das der Schein des
algebraischen Beweises von A dadurch entsteht, daß wir in den
Gleichungen A die
gleichen Variablen a, b, c wiederzufinden meinen wie in
α, β, γ & daher A für
ein Produkt || das Resultat einer
Transformation jener Gleichungen ansehen.
(Während ich ja in Wirklichkeit dem Schriftzeichen
α β γ eine ganz neue
Auffassung gebe, worin es liegt, daß das c in
β &
γ nicht in derselben Weise als Variable gebraucht wird, wie a &
b. So daß es also ein Ausdruck dieser andern
Auffassung von B ist, daß in A das c nicht
vorkommt.) |
Was ich von dem Wechsel in der Auffassung
von α β γ gesagt habe
könnte ich jetzt so sagen:
β &
γ entstehen mit
|
Man könnte das
auch (einfach) so sagen: die
rekursive || induktive Anwendung der
Buchstabengleichung ist eine andere als die nicht
induktive. Die Definition
a + (b + 1) =
(a + b) + 1 nicht induktiv auf 4 & 5
angewandt gibt für a = 4 &
b = 5
4 + (5 + 1)
= (4 + 5) + 1 & diese Gleichung ist
das Resultat der Anwendung von α. Die rekursive
Anwendung von α
auf 4 & 5 (a = 4, b = 5) besteht in der Erzeugung
einer Reihe von Gleichungen
4 + (5 + 1)
= (4 + 5) + 1 =
(4 + (4 + 1)) + 1 =
((4 + 4) + 1 ( + 1) =
((4 + (3 + 1)) + 1) + 1)
= etc. (hier ist
„etc.” eine
Abkürzung). Ebenso besteht die nicht induktive
Anwendung von B auf 4, 5, 7, in der Einsetzung
dieser Zahlen statt der Variablen. Dagegen die induktive
Anwendung im Erzeugen einer Reihe von Gleichungen die mit
4 + (5 + 1)
= (4 + 5) + 1 anfängt & mit
4 + (5 + 7)
= (4 + 5) + 7) endet. |
Man kann hier sagen:
die Anwendung der Variablen ist ihr Sinn. |
Oder: Die
Beschreibung der Anwendung des Zeichens ist eine Ergänzung
des Zeichens & ergibt eben in den
zwei Fällen etwas Verschiedenes. |
Die Beschreibung der
Anwendung des Zeichens ist ja ein Zeichen & statt des ersten
zu verwenden. Die Hervorhebungen könnte man ja sehr
wohl als Beschreibung || als Symbol zur
Beschreibung der induktiven Anwendung von B
auffassen. || ansehen. |
∣
Wenn auf die
Lösung – etwa – des
Fermatschen Problems Preise
gesetzt || angesetzt sind
so könnte man mir sagen || vorwerfen || vorhalten: wie kannst Du
behaupten || sagen, daß es dieses Problem nicht gebe, wenn
Preise auf die Lösung ausgesetzt sind
so muß es das Problem wohl geben. Ich müßte
sagen: Gewiß, nur mißverstehen die, die
darüber reden die Grammatik des Wortes
„mathematisches Problem” & des Wortes
„Lösung”.
Der Preis ist eigentlich
auf eine
naturwissenschaftliche || die Lösung einer
naturwissenschaftlichen Aufgabe gesetzt,
(gleichsam) auf das
Äußere der Lösung (darum spricht man
z.B. auch von einer
Riemannschen
Hypothese). Die Bedingungen der Aufgabe sind
äußerliche, und |
Wäre die Aufgabe eine
Konstruktion des regelmäßigen Fünfecks zu finden, so ist
die Konstruktion in dieser Aufgabestellung durch das
physikalische Merkmal charakterisiert, daß sie
tatsächlich ein durch Messung definiertes
regelmäßiges 5-Eck liefern
soll. Denn den Begriff der konstruktiven 5-Teilung (oder des konstruktiven
5-Ecks) haben wir ja noch gar
nicht [erhalten wir ja erst durch die Konstruktion.]
|
Ebenso
im Fermatschen Satz haben
wir ein empirisches Gebilde das wir als
Hypothese deuten also – natürlich –
nicht als Ende einer Konstruktion. Die
Aufgabe fragt also im gewissen Sinn nach etwas anderem als was
die Lösung gibt. ∣ |
Das Zeichen
B im Beweis wird also induktiv aufgefaßt das bewiesene
A aber nicht (sondern das ist wieder ein Zeichen wie
α in der
Anwendung || Ableitung von
β &
γ). Und darin, daß
man auf diesen logischen Unterschied nicht aufmerksam wird liegt die
Täuschung als sei A im alten Sinn des Wortes – also
|
∣
Natürlich steht auch der Beweis
des Gegenteils des Fermatschen Satzes z.B.,
im gleichen Verhältnis zur Aufgabe wie der Beweis
des Satzes. (Beweis der Unmöglichkeit einer
Konstruktion.) ∣ |
Wieweit hat sich der Philosoph in die
Mathematik zu mischen? |
26.
Der philosophische Witz. |
Ich
könnte algebraische Rechnungen || (Anwendungen) machen & mich dabei immer nur
auf die ‚Beweise I, II, III,
etc.’ beziehen, nie auf die ‚bewiesenen
Sätze’.
Wenn man aber so (a + b)² = etc. ausgerechnet & nun wieder eine Anwendung auf (s ∙ t + i ∙ k)² gemacht hätte, so käme man darauf, daß, so wie man hier (a + b)² = etc. verwendet hat, früher implizite von einer Gleichung || einem Vorbild a + (b + c) = (a + b) + c Gebrauch gemacht wurde. D.h., daß man, statt sich auf B zu beziehen, sich auf eine solche Gleichung hätte beziehen können. Man könnte aber jetzt nicht sagen, daß diese Gleichung aus || von B abgeleitet war, so wenig wie früher die Gleichung i + (k + l) = (i + k) + l. Und so wenig wie die Gleichung (i + k)² = etc. aus (a + b)² = etc.. |
Was heißt es denn, daß
alle Übergänge Wenn ich z.B. die Kette von Gleichungen des Beweises (a + b)² = … anschreibe, so ist jede dieser Gleichungen nach dem Modell eines der Grundgesetze geformt; und wir sagen dann, der Übergang geschieht nach diesem Grundgesetz. |
(Das
assoziative Gesetz ist das Vorbild des
assoziativen Übergangs.) |
Der Beweis B zeigt etwas um A. |
A ist die allgemeine
Form der Zahlengleichungen die B beweist.
((Und dieser Satz selbst bringt uns der Anwendung
von A nicht näher als A selbst &
ist nur eine Übersetzung von A
selbst.)) Und die algebraische
Notation wird verwendet um mir zu sagen, wie ich
z.B. im Falle (17 + 18)²
rechnen soll, indem mir gesagt wird || es
heißt „(a + b)²
= etc.”.
D.h., ich soll dieser Gleichung gemäß
rechnen. Und insofern könnte man unsere Induktion
einen Beweis der algebraischen Rechnung || Gleichung nennen. Denn ich könnte sagen:
Rechne nach || Rechne ruhig nach
dieser Gleichung, sie |
∣ („So
soll er sich kränken”, ist oft das
letzte Wort in einem philosophischen
Hin & Her; der Verstand wird so
lange von der Scheinfrage zurückgeworfen bis sie zwar nicht
gelöst wurde || nicht bis sie gelöst
wurde sondern seine Einstellung durch ihre
Rückstöße || Stöße
zurecht gerichtet hat.) ∣ |
Die kritische Stelle || Der Haken im vorigen
Satz liegt im Ausdruck || in in der
Bemerkung „wie ich z.B. im
Falle
(17 + 18)² …”.
Wenn ich jemandem im Falle
(17 + 18)²
die Rechnungsregel
(a + b)²
= etc. gebe, so kann
das || diese (hier) nicht
mehr leisten als unmittelbar die Regel
(17 + 18)²
=
17² + 2 ∙ 17 ∙ 18 + 18².
Ich könnte freilich der Bequemlichkeit halber, wenn
„(a + b)²
= etc.” schon
irgendwo aufgeschrieben ist darauf deuten aber was hier an dieser
Regel wirkt, || wirksam ist, ist nur, was in
der besonderen Ziffernregel || Zahlenregel auch
steht. Und das Gleiche gilt, natürlich, wenn ich
die Beispiele häufe. Nie komme ich
über die besonderen Zahlenregeln hinaus. Der
Haken liegt in dem Wort
„z.B.” der angeführten
Stelle. Dieses Wort macht die Rechnung
(17 + 18)²
zu einem Beispiel also bereits zum Ausdruck der
algebraischen Regel. Der Verstand rennt sich
hier immer || Wir rennen uns hier immer wieder
den Kopf an beim Versuch die Allgemeinheit in eine
Liste || Anzahl || Zahl von |
(Der Philosoph übertreibt, schreit gleichsam,
in seiner Ohnmacht, solange er den Kern der
Konfusion noch nicht entdeckt
hat.) |
…Rechne nach dieser Gleichung,
sie ist bewiesen worden. Und anderseits || andererseits, sie ist nur insofern bewiesen worden, als sie die Form der Zahlengleichung || Zahlengleichungen ist, die in der Induktion ihre Rechtfertigung haben. (Wieder irreführend! weil es klingt als hätten wir eine Gesamtheit von Zahlengleichungen die mit ihrer || deren Form äquivalent wäre. Denn die Zahlengleichung ist nichts als die Zahlengleichung, & die Auffassung der Form ist bereits Algebra. || Denn Zahlengleichungen sind nichts als Zahlengleichungen, & die Auffassung der Form ist bereits Algebra. Und hier darf es nicht heißen „die Zahlengleichungen”, denn das könnte nur heißen: die Zahlengleichungen die ich jetzt aufgeschrieben habe, oder dergleich.) |
Wie
verhalten sich: das Zahlenspiel
17 + (18 + 20)
= …, der Satz A & der Beweis
B? |
(Man muß sich zu einer
Ausdrucksweise hindurchringen || durchringen.) |
Drückt B weniger klar aus, wie im besonderen Fall
gerechnet werden soll als A? |
BI,
BII sind Beweise von
17 + (28 + 14)
= …,
17 + 1 =
1 + 17 etc.. Wenn das wahr ist,
so sind sie insofern auch Beweise von AI
AII etc., aber eben nur insofern
(als) A die Form des
Zahlenbeispiels ist, also nicht allgemein. Außer ihrer
Beweiskraft für das besondere Zahlenbeispiel besitzen sie
dann noch eine formelle Eigenschaft, die eben darin besteht,
daß B so & so gebaut ist (wie man es beschreiben
kann. Und mehr ist nicht da. |
R ist die allgemeine
Beschreibung von B
deren Notwendigkeit man immer fühlt. |
Ich sage
(a + b)²
= etc. ist mit Hilfe von
AI AII
etc. bewiesen, weil die
Übergänge von (a + b)² zu
a² + 2ab + b²
alle von der Form AI, oder AII,
etc. sind. In diesem Sinne ist
in III auch der Übergang von (b + 1) + a auf
(b + a) + 1 nach
AI gemacht, aber nicht der Übergang von
a + n
auf n + a! |
Wir
können einerseits sagen, daß BI
17 + (25 + 18)
= … beweist, anderseits BI
beschreiben oder BI, BII und
andere. Wir können auch hervorheben || sagen was diesen allen gemeinsam ist.
Aber das muß jedenfalls genügen. |
Wenn wir I, II & III ansehen so sehen
wir, daß die Gleichungen A immer || in
allen Fällen an einer bestimmten Stelle von B zu
finden sind; d.h., daß sie von einer
bestimmten Stelle von B herunter gelesen werden kann, &
ferner, daß auch im Übrigen zwischen den B eine gewisse
Analogie besteht; die man leicht völlig beschreiben
könnte. ((Und die durch die Hervorhebungen
völlig beschrieben ist.)) Es handelt sich eben
nur um diese (bestimmten)
Fälle. Eine Allgemeinheit in dieser
Beziehung die über die behandelten Fälle
hinausgeht kommt in unsern Kalkül nicht
hinein. ((Dies ist ein
Widerspruch; || : denn wenn ich
beschreibe was allen diesen Fällen
gemeinsam ist so gehe ich eben dadurch über diese
Fälle hinaus. Im Fall der primären Farben,
z.B., kann ich nicht beschreiben was
diesen gemeinsam ist & ihre Klasse ist
(zugleich) ihr Begriff. Kann
ich aber beschreiben was gewissen Zeichen
gemeinsam ist, so habe |
Man kann nicht
zugleich allgemein & besonders
beschreiben || sein. |
Es ist wohl ein
Unterschied zwischen den Fällen in denen einerseits
BI, BII, BIII für
AI, AII, AIII
konstruiert werden ohne daß dabei
gesehen (oder hervorgehoben) wird, daß eine Analogie zwischen
den B besteht, und anderseits die Analogie der B
hervorzuheben. Aber das ist wahr, daß das Hervorheben
dieser || der Analogien die B nicht zu Beweisen
macht. |
Ist es richtig zu sagen: Kein weiterer Schritt
kann B zu einem Beweis machen, wenn es nach dem
|
Es zeigt mir jemand die
Komplexe B & ich sage „das sind keine Beweise
der Gleichungen A”. Nun sagt
er: „Du siehst aber noch nicht das System, nach
dem diese Komplexe gebildet sind”, und zeigt es mir || & macht mich darauf aufmerksam.
Wie konnte das die B zu Beweisen
machen? – |
Durch diese Einsicht steige
ich in eine andere, sozusagen höhere, Ebene,
während der Beweis auf der tieferen hätte
geführt werden müssen || geführt werden
müßte. |
Ich schaue B zu || an
& sage: das ist kein Beweis von
A. Nun heißt es: ich werde Dir
zeigen, daß es doch ein Beweis ist. Aber wie kann man
das zeigen? wenn es nun einmal kein Beweis von A
ist. Nun macht er mir die rekursive
Verwendung || Anwendung von B vor. Aber
was hat das damit zu tun? |
Was ich richtig
gefühlt habe, ist die Unabhängigkeit der
Auffassung von B von der Frage ob B A beweisen
kann. |
Nur ein bestimmter Übergang von
Gleichungen zu einer Gleichung ist ein Beweis dieser
letzteren. Dieser ist hier nicht
gemacht || findet hier nicht statt
& alles Andere kann auf die Sache keinen
|
‒ ‒ ‒ Eine
Allgemeinheit in dieser Beziehung die über die
behandelten Fälle hinausgeht kommt in unsern Kalkül
nicht hinein. Daher beweisen wir auch nicht A durch B, sondern es ist ganz richtig, daß wir etwas über A beweisen. Natürlich, daß die linke Seite von A in β & die rechte in γ mit Hilfe von α so & so erhalten werden kann, während α selbst der Wert von A für n = 1 ist. |
Aber kann ich
eben nicht sagen, daß, wenn ich dies über A bewiesen
habe, ich damit A bewiesen habe? Und woher kam dann
überhaupt die Täuschung, daß ich es dadurch bewiesen
hätte? denn diese muß doch einen tieferen Grund
haben. |
Nun, wenn es eine Täuschung ist, so kam sie
jedenfalls von unserer Ausdrucksweise in der Wortsprache her
„dieser Satz gilt für alle
Zahlen”; denn der algebraische Satz war ja nach
dieser Auffassung nur eine andere Schreibweise dieses
Satzes || (der Wortsprache).
Und diese Ausdrucksweise ließ den Fall
|
27.
Wenn „den algebraischen Satz mittels der Sätze
p,
q,
r beweisen” heißt,
die Übergänge der Gleichungskette den
Sätzen p,
q,
r entsprechend machen,
dann ist B kein Beweis von A mittels α, noch
ein || der Beweis eines Satzes der mittels A
bewiesen ist. Denn den Übergang in A habe ich
nicht durch α vermittelt. |
Wenn ich mir die Funktionen
φ, ψ,
F exakt
definiert || bestimmt denke &
nun das Schema des Induktionsbeweises
|
Denn das Schema
des Übergangs |
Tatsächlich ist R nicht das Schema des
Induktionsbeweises BIII; dieses ist viel
komplizierter da es das Schema BI
enthalten muß. |
Es ist nur dann nicht ratsam etwas Beweis
zu nennen, wenn die übliche Grammatik des Wortes
„Beweis” mit der Grammatik des betrachteten
Gegenstandes nicht übereinstimmt. |
Was soll
es denn heißen, der Übergang sei durch R
gerechtfertigt? Der Übergang wird gemacht, oder
nicht gemacht, & ein Komplex von der Form R
läßt sich konstruieren oder nicht konstruieren. Das ist aber
alles. ((Auch das ist nur ein Ausdruck
dafür, daß ich in B nicht finde was ich eine
Rechtfertigung des Übergangs in A nenne,
nämlich, keine Vermittlung dieses
Übergangs.)) |
Die tiefgehende Beunruhigung
rührt am Schluß von einem kleinen aber offen zu Tage liegenden
Zug des überkommenen Ausdrucks her. |
Ich habe eine Klammer }
zwischen α, β, γ & A gemacht, als ob
es sich |
Man könnte
vermuten, die Klammer bedeute so viel, wie ein
Gleichheitszeichen. |
Diese Klammer könnte man
übrigens auch zwischen
„1˙
(Zwischen den ‚allgemeinen Satz’ & seine ‚Verifikation’.) Und wäre „}” hier nicht ein Gleichheitszeichen? |
Ich will
zeigen: Du hast geglaubt, Du gebrauchst einen Kalkül, in
dem das Wort „alle” in seiner gewöhnlichen
Bedeutung vorkommt (oder stehen könnte), aber das ist nicht
so: die Figur, die Du „alle”
nanntest || nennst, bewegst Du in diesem Spiel
tatsächlich gar nicht nach den Regeln, die von diesem Wort
in der Wortsprache gelten. (Sondern nach viel
einfacheren.) |
[Ich denke tatsächlich mit
der Feder, denn mein Kopf weiß oft nichts von dem, was meine
Hand schreibt.] |
(Die Philosophen sind oft
wie kleine Kinder die zuerst mit ihrem Bleistift beliebige
Striche auf ein Papier |
Es wäre
– nach den angenommenen Regeln – falsch das
Gleichheitszeichen so zu gebrauchen: ∆ … [(a + b)² = a ∙ (a + b) + b ∙ (a + b) = … = a² + 2ab + b²] = [(a + b)² = a² + 2ab + b²] wenn damit gemeint sein soll, daß die linke Seite der Beweis der rechten ist. Könnte man sich aber nicht diese Gleichung als Definition aufgefaßt denken? Wenn es z.B. immer Gebrauch gewesen wäre statt der rechten Seite die ganze Kette anzuschreiben || hinzuschreiben, und man nun die Abkürzung einführte. Freilich kann ∆ als Definition aufgefaßt werden! Denn das linke Zeichen wird tatsächlich gebraucht, & warum sollte man es nicht nach dieser Übereinkunft durch das rechte ersetzen. || abkürzen. Nur gebraucht man dann dieses oder jenes anders als es jetzt üblich ist. || & warum sollte man es dann nicht nach dieser Übereinkunft abkürzen. Nur gebraucht man dann das rechte oder linke Zeichen anders als es jetzt üblich ist. || als wir es jetzt gebrauchen. |
Hier scheint mir eine
Unklarheit zu entstehen (obwohl ich sie jetzt nicht klar vor
mir sehe || beschreiben kann) durch die Verwechslung
von || zwischen besonderer & allgemeiner
Definition (diese Bezeichnung selbst ist
natürlich irreführend).
Und es || Es ist nie
genügend hervorgehoben worden, daß
ganz verschiedene Arten von Zeichenregeln in der Form
der Gleichung geschrieben werden. |
Die
‚Definition’ x ∙ x = x²
kann || könnte so aufgefaßt
werden, daß sie nur erlaubt statt des Zeichens
„x ∙ x”
das Zeichen „x²” zu setzen
also analog der Definition
1 + 1 =
2; aber auch so (& so wird sie
tatsächlich aufgefaßt) daß sie
erlaubt a² statt
a ∙ a, &
(a + b)²
statt (a + b) ∙ (a + b)
zu setzen; auch so
daß das
x ‚jeden beliebigen Zahlenwert’ annehmen
kann. || daß für das x jede beliebige Zahl eintreten kann.
|
Was
heißt es also daß
R den Übergang
A || von der Form A
rechtfertigt? Es heißt wohl, daß ich mich
entschieden habe, nur solche Übergänge in meinem Kalkül
zuzulassen, denen ein Schema B entspricht, dessen Sätze
α, β, γ wieder aus || nach ρ ableitbar sein sollen.
(Und das hieße natürlich nichts anderes, als
daß ich nur die Übergänge AI,
AII, etc. zuließe & diesen
Schemata der Form R || B
entsprächen.) ((Richtiger wäre es zu
schreiben „& diesen Schemata der Form R
entsprechen”.))Auf diese allgemeine Regel kann man nachträglich aufmerksam werden. (Wird man nun dadurch aber (darauf) aufmerksam, daß die B in Wirklichkeit doch || doch in Wirklichkeit Beweise der A sind?) Man wird da auf eine Regel aufmerksam, mit der man hätte beginnen können & mittels der & α man AI, AII etc. hätte konstruieren || bauen können. Niemand aber würde sie in diesem Spiel einen Beweis genannt haben. |
Woher
dieser Konflikt: „Das ist doch kein
Beweis!” – „das ist doch ein
Beweis!”? |
Man könnte sagen: Es
ist wohl wahr, ich zeichne im Beweis von B, mittels α
die Konturen der Gleichung A nach, || die Konturen der
Gleichung A mittels α nach, aber nicht auf die
Weise, die ich nenne ‚A mittels α
beweisen’. |
Die Schwierigkeit, die in
dieser || durch diese Betrachtung
zu überwinden ist || überwunden werden
soll ist, den Induktionsbeweis als etwas
Neues, sozusagen, naiv zu betrachten. |
Ich scheine Argumente zu
benützen: 1.) Der allgemeine
Begriff der Induktion ist überflüssig, weil er nicht
gebraucht wird; 2.) wenn er auch gebraucht wird, ist
er kein Beweis. (Aber)
zwei Argumente sind zu viel || das ist zu
viel. In Wirklichkeit ist es so:
Ich kann wohl R brauchen || gebrauchen, um
die A zu konstruieren, sind sie aber konstruiert, so
entsteht der falsche Anschein, als wären sie auf eine andere
– beweisende Art konstruiert worden; & das soll
verneint werden. |
28.
Das Zahlenbeispiel an dem wir die Wirkungsweise des
Induktionsschemas zeigen, interessiert uns nur, so weit es eine
interne Eigenschaft des Schemas B darstellt.
Wie wir etwa eine gefärbte
Flüssigkeit durch ein System von Glasrohren
leiten um das System verstehen zu lernen. || Wie wir uns etwa die Wirkungsweise eines
Röhrensystems durch einen Strom darstellen der es
durchfließt. || Wie wir uns etwa
ein Röhrensystem klarmachen durch einen Strom, der
es durchfließt. |
Denn die allgemeine Form
R wird wirklich nicht dazu benutzt B zu
|
Wir müssen auch
bedenken, daß die || es eine
mathematische Aufgabe, ‚mittels ρ
einen Komplex von der Form R zu konstruieren’ nicht
gibt, da wir keine Methode haben sie zu lösen.
|
Wenn
wir also oben sagten, wir können mit R beginnen, so ist
dieses Beginnen mit R in gewisser Weise ein Humbug || Humbug. Es ist nicht so, wie wenn ich
eine Rechnung mit der Ausrechnung von
526 × 718
beginne. Denn hier ist diese Problemstellung der
Anfangspunkt eines Weges. Während ich dort das R
sofort wieder verlasse & woanders beginnen muß.
Und wenn es geschehen ist, daß ich einen Komplex von der
Form R konstruiert habe, dann ist es wieder gleichgültig,
ob ich mir das früher
(äußerlich)
vorgesetzt habe, weil mir dieser Vorsatz mathematisch
(gesprochen), d.h.
im Kalkül, doch nichts geholfen hat. Es bleibt
also bei der Tatsache, daß ich jetzt einen Komplex von der Form
R vor mir habe. |
Ja, kann ich nun nicht sagen, die
|
Und so könnten wir wirklich
anfangen & ein für allemal, ganz abgesehen
von der Möglichkeit eines Beweises, jedes algebraische
Vorbild in der Form R – konstruiert aus
A – schreiben. |
Wäre das nun geschehen, so würde
sich der induktive Beweis einfach darstellen, als algebraischer Beweis
von α, β &
γ. |
Wir könnten
uns denken, wir kennten nur den Beweis BI &
würden nun sagen: Alles was wir haben, ist diese
Konstruktion.
Von einer Analogie dieser mit anderen
Konstruktionen, von einem allgemeinen Prinzip bei
der Ausführung dieser Konstruktionen, ist gar keine
Rede. – Wenn ich nun so B & A sehe,
muß ich fragen: warum nennst Du das aber einen Beweis gerade
von AI? (ich frage noch nicht: warum
nennst Du es einen Beweis von A). Was
hat dieser |
„Die allgemeine Form R braucht man gar nicht im
Beweis von A”, darauf || dazu ist zu sagen: sie geht mich nichts an,
wenn ich nach dem Beweis von A in der
Konstruktion von B suche. Oder: ich sollte sie
nicht brauchen. Wenn ich die Form R in B
(oder die Beziehung V in A & B)
erkenne, so nützt sie mich nichts. Wird sie mir
gezeigt (in der Absicht mich auf die Beweisfähigkeit von
B für A aufmerksam zu machen), so möchte ich
sagen: „nun, & was weiter?”
|
Wenn ich
sage, das allgemeine Prinzip ist gleichgültig, denn es
kommt nur auf diesen einen Fall an (&
hic Rhodus, hic salta), so ist
das richtig, wenn mit der Allgemeinheit des Prinzips seine
Anwendbarkeit auf andere Fälle als diesen gemeint
ist. Dagegen kommt es darauf an, den Komplex B
mit diesen Hervorhebungen zu sehen. Ich
werde mich also um keine analogen Fälle bekümmern,
aber in B}A auf Bestimmtes aufmerksam machen.
|
Wenn ich
sage „R wird ja nie zur Konstruktion verwendet”,
so ist die |
Wir haben nur diesen
einen Fall, & die Aufzeigung eines allgemeinen
Prinzips, dem er angehört macht ihn nicht zum
Beweis. |
„Ich habe nur diesen einen Fall, ich weiß
nicht, ob ich je einen andern kennen werde, was soll da ein
allgemeines Prinzip?“ || “. Hier wäre wirklich
der Fall der primären Farben. |
Aber der Fall ist hier der,
des Beweises von B mittels α (oder
ρ). Für den
andern Fall, nämlich die Konstruktion von B aus
A gilt das nicht! Vielmehr sehe ich hier ein
allgemeines Prinzip in dem Augenblick, wo ich es
überhaupt in B & A entdecke. |
Es zeigt uns
jemand BI und erklärt uns den Zusammenhang mit
AI, d.i., daß die rechte
Seite von A so & so erhalten wurde etc.
etc.. Wir verstehen ihn; & er fragt
uns (nun): ist nun das ein Beweis
von A? Wir
würden || werden antworten: gewiß
nicht! [keine Zeile auslassen] Und wir könnten auch daraus schließen, daß man so aus jedem A ein B konstruieren kann & also auch umgekehrt A aus B. |
Dieser Beweis ist nach einem
bestimmten Plan gebaut (nach dem noch andre Beweise gebaut
sind). Aber dieser Plan kann den Beweis nicht zum
Beweis machen. Denn wir haben jetzt hier nur die eine
Verkörperung dieses Planes, & können von dem
Plan als allgemeinem Begriff
(ganz) absehen. Der Beweis
muß für sich sprechen & der Plan ist
nur in ihm verkörpert aber selbst kein Bestandteil || kein Instrument des Beweises.
(Das wollte ich immer sagen.) Daher nützt es
mich nichts, wenn man mich auf die Ähnlichkeiten zwischen
Beweisen aufmerksam macht, um mich davon zu überzeugen
daß sie Beweise sind. |
29.
Gewiß hilft es nichts zu dieser
Überzeugung, zu sehen, daß diese Beweise nach dem
selben Plan gebaut sind &, wie gesagt, ich könnte ja nur
einen einzigen Beweis vor mir haben. Anders ist es
aber wenn dieser Plan das Wesen des Beweisens
|
Ich muß sagen: Wenn A
aus B folgt, so folgt es, ob die Regel des Folgens || die Schlußregel allgemein formuliert
(d.h. aufgeschrieben)
wurde oder nicht. Alles, was die interne Relation von
B zu A betrifft sieht man aus diesen beiden
allein. |
Eine Regel des Folgens entspricht ganz || nur einem
Plan des Beweises. Sie kann die besondere Art des
Folgens registrieren, aber nicht die Folgerung
rechtfertigen; sondern das können nur die Glieder
des Schlusses || der Folgerung. |
Ich muß also auf B
& A allein zeigen können & fragen:
ist dies ein Beweis von dem? |
Aber dieses Argument
könnte man || Nun könnte man aber sagen:
dieses Argument könnte man || Nun könnte man aber
dieses Argument auch auf den Beweis
(a + b)²
= etc. anwenden
& sagen: ob der Übergang
(a + b) ∙ (a + b)
=
a ∙ (a + b) + b ∙ (a + b)
richtig ist oder nicht, kann man nur an ihm (seinen Gliedern)
selbst |
Die Schlußgesetze sind
Paradigmen. |
Wenn ich sagte: ‚ob
p aus
q folgt, muß aus
p &
q allein zu ersehen sein || hervorgehen’; so müßte es
heißen: daß p aus
q folgt ist eine Bestimmung die
den Sinn von p &
q bestimmt; nicht etwas, das,
von dem Sinn dieser beiden ausgesagt, wahr ist. Daher kann
man (sehr) wohl die
Schlußregeln
angeben, gibt damit aber Regeln
für die Benützung der
Schriftzeichen an die deren Sinn erst bestimmen was
nichts andres heißt als daß diese Regeln willkürlich
festzusetzen sind d.h. nicht
von der Wirklichkeit abzulesen wie eine
Beschreibung. – Denn wenn ich sage die
Regeln sind willkürlich so meine ich sie sind
nicht von der Wirklichkeit
bestimmt || festgelegt || determiniert, wie die Beschreibung dieser
Wirklichkeit. Und das heißt: Es
ist Unsinn von ihnen zu sagen, sie stimmen mit der Wirklichkeit
überein, |
Wenn Einer also auf B
& A zeigt & fragt „ist dies ein Beweis
von dem”, so könnte ich antworten: „ich
habe (gerade) die Regeln vergessen, ich
muß erst nachschauen”. |
Also kann ich nicht wissen
ob die Konstruktion von B ein Beweis von A
ist, auch wenn ich die Beziehung V in ihnen erkenne;
solange ich mich nicht davon überzeugt habe, daß
R im Regelverzeichnis steht? (Das
scheint die grundlegende Frage zu sein.) |
Wenn nun das
Regelverzeichnis nicht bei der Hand wäre & ich
sagte: „ich weiß nicht ob B ein Beweis
von A ist”! – |
Denn so müßte ich
dann sprechen. „Das kann man so
ohne weiteres
nicht sagen, ob
es ein Beweis von A ist.” |
Wenn ich nun früher
sagte „das ist doch kein Beweis”, so meinte ich
‚Beweis’ in einem bereits festgelegten Sinne, in
welchem es aus A & B allein zu ersehen
ist. Denn in diesem Sinne kann ich sagen: Ich
verstehe doch ganz genau, was B tut, & in
welchem Verhältnis es zu A steht. Jede
weitere Belehrung ist überflüssig &
das ist kein Beweis. || & das was da
ist, ist kein
Beweis. Dabei sehe ich das Verhältnis nach der Regel V sehr gut || wohl, aber es kommt für mich als Konstruktionsbehelf gar nicht in Frage. Sagte mir jemand, während meiner Betrachtung von B & A, daß man auch hätte B aus A (oder umgekehrt) nach einer Regel konstruieren können, so könnte ich ihm nur sagen „komm mir nicht mit unwesentlichen Sachen”. Denn das ist ja selbstverständlich & ich sehe sofort daß es B nicht zu einem Beweis von A macht. Denn daß es so eine allgemeine Regel gibt, könnte nur zeigen || Denn diese allgemeine Regel könnte nur zeigen, daß B der Beweis von A & keinem andern Satz || der Beweis gerade von A ist, wenn es überhaupt ein Beweis wäre. D.h., daß der Zusammenhang zwischen B & A einer Regel gemäß ist, kann nicht zeigen daß B ein Beweis von A ist. Und jeder solche Zusammenhang könnte zur Konstruktion von B aus A (und umgekehrt) benützt werden. |
Nun könnte
ich freilich || allerdings sagen: ob dieser
Zusammenhang der des Beweisens ist, hängt davon ab ob seine
allgemeine Beschreibung (sein Vorbild) auf
einer || meiner Liste der
Beweisregeln steht oder nicht. Aber dann
|
Wenn ich
also sagte „V || R wird ja gar
nicht zur Konstruktion benützt, also haben wir mit ihm nichts zu
tun”, so hätte es heißen müssen: Ich
habe es doch nur mit A & B allein zu
tun. Es genügt doch, wenn ich A &
B mit einander konfrontiere & nun frage „ist
B ein Beweis von A” & also brauche ich
A nicht aus B nach einer vorher festgelegten Regel zu
konstruieren, sondern es genügt, daß ich die einzelnen
A – wieviele es sind – den einzelnen B
gegenüberstelle (& frage „ist
dies ein Beweis von dem”).
Und das ist wahr: ich || Ich
brauche eine Konstruktionsregel nicht; & das ist
wahr. Ich brauche eine vorher aufgestellte
Konstruktionsregel nicht (aus der ich dann erst die A
gewonnen hätte). |
Dagegen muß ich wohl, wenn A
& B |
[Einige Sätze die ich
vor diesen9 geschrieben habe]:
Was ich sagen will ist also: Skolem nimmt nur die alten Grundgesetze der klassischen Algebra & ordnet ihnen gewisse Gleichungskomplexe zu, & zwar so, daß diese Zuordnungen eine gewisse Analogie aufweisen, die dem losen Gebrauch Allgemeinheitsbezeichnung in der Wortsprache entspricht. Er gebraucht aber diesen allgemeinen Begriff der Allgemeinheit selber nicht konstruktiv, d.h., gebraucht ihn nicht als allgemeinen Begriff. Seine Beweise verhalten sich zu seinem Begriff des Rekursionsbeweises, wie die einzelnen primären Farben zum Begriff der primären Farbe. D.h.: es liegt hier kein Begriff vor, sondern eine Liste. ((Daran ist nun wahr daß tatsächlich kein Begriff (d.h. kein System) des |
Und daß diese Liste
lauter Dinge || Gegenstände
umfaßt, die mit einander eine gewisse Ähnlichkeit haben,
hilft uns nichts; oder: daß die Dinge auf der Liste unter
einen gewissen Begriff fallen hilft uns nichts, wenn wir diesen
Begriff nicht konstruktiv verwenden
können. |
Ich meine: Im
Skolemschen Kalkül
brauchen wir diesen Begriff nicht || brauchen wir keinen solchen Begriff,
es genügt die Liste. Es geht uns nichts verloren, wenn wir nicht sagen „wir haben die Grundgesetze A bewiesen” || wir haben die Grundgesetze A auf diese Wiese bewiesen”, sondern bloß zeigen, daß sich ihnen – in gewisser Beziehung analoge – Konstruktionen zuordnen lassen. |
Wenn ich nämlich sage
„dieser Übergang ist nach BI
gemacht, dieser nach BII”, so ist
das Einzige, was daran ganz |
Der Begriff der
Allgemeinheit (& der Rekursion)
der in diesen Beweisen gebraucht wird, ist nicht allgemeiner, als er aus
diesen Beweisen unmittelbar herauszulesen ist. |
Die Klammer
} in R kann weiter nichts bedeuten, als daß wir den
Übergang in A (oder einen von der Form A) als
berechtigt ansehen, wenn die Glieder (Seiten) des Übergangs
in einer durch das Schema B charakterisierten Beziehung zu
einander stehen. Es nimmt dann B den Platz von
A. Und wie es früher hieß: der
Übergang ist in meinem Kalkül erlaubt,
wenn er einem der A entspricht, so kann es jetzt
heißen || so heißt es jetzt: er ist
erlaubt, wenn er einem der B entspricht.
Damit aber hätten wir noch keine Vereinfachung, keine Reduktion gewonnen. |
Der induktive Beweis
zerlegt den Übergang in A nicht. Ist es nicht
das, was macht, daß ich mich dagegen sträube ihn Beweis zu
nennen? Warum ich versucht bin zu sagen, er kann auf
keinen Fall ((nämlich auch wenn man A durch
R & α konstruiert)) mehr tun, als
etwas über den Übergang zu
zeigen. |
Es handelt sich darum, ob es gelingt, die
Gestalt || Form des Übergangs
aus der Gleichung ρ auf gewisse Weise zu
formen. – Aber hat man sie auf diese Weise
geformt, so muß man jetzt die ganze Form
anwenden. ((Und ich wollte sagen, daß mich darum
das Formen von B mittels ρ nichts nützt, den
Übergang in A nicht vermittelt. (Dazu
die weiteren Vergleiche.))) |
Wenn man sich einen
Mechanismus aus Zahnrädern & diese aus lauter gleichen
keilförmigen Stücken & je einem Ring der sie zu
einem Rad zusammen hält, zusammengesetzt denkt, so blieben in
einem gewissen Sinne die Einheiten des Mechanismus doch die
Zahnräder. |
Die Schritte des Beweises
von A sind nicht Schritte im Beweis mit Hilfe von
A. |
Es ist so: Wenn ein Faß
aus Dauben & Böden besteht, so halten doch nur alle diese
in dieser (bestimmten) Verbindung
(als Komplex) die Flüssigkeit und bilden als Behälter
neue Einheiten. |
¥
Ich würde dann sagen: die Regeln
des Überganges in meinem Kalkül sind alle auf eine
bestimmte Art & Weise (etwa alle mittels
ρ) geformt. Als wollte ich
sagen: diese Sessel sind alle aus Hölzern von
dieser Form aufgebaut. Aber die ganzen
Möbel sind die Einheiten der Einrichtung.
((Das würde noch einen Nachsatz
erfordern.)) |
⍈
Wie wäre es denn, wenn die B nach einer durch ihre Form
bestimmten Methode aus ρ abgeleitet (oder
ausgeschlossen) werden könnten? So daß man
also für jedes gegebene A die
entsprechende Rechnung ohne weiteres machen || ausführen könnte (wie für jede beliebige
Multiplikationsaufgabe ihre Kontrolle).
|
Ich will hier zwei Arten des Vorgehens von
einander unterscheiden; & das ist alles.
Und ich unterscheide sie dadurch, daß ich jede Form zerstöre, die eine Ähnlichkeit || die Gleichheit der beiden vortäuscht. || die eine Ähnlichkeit der beiden herstellen soll. |
Dadurch
ziehe ich dem einen den falschen Schein aus der es umgibt.
(Darum nämlich, weil || Weil
nämlich die Wortsprache diesen Schein um den
Gegenstand || Vorgang
webt.) |
Der Gleichungskalkül ist
gegeben. In diesem Kalkül
hat ‚Beweis’ eine
festgelegte || fixe Bedeutung.
Nenne ich nun auch die induktive Rechnung einen Beweis,
so erspart mir dieser Beweis doch nicht die Kontrolle, ob
die Übergänge der Gleichungskette, nach diesen
bestimmten Regeln (oder Paradigmen) gemacht sind.
Ist das der Fall, so sage ich die letzte Gleichung der Kette
sei bewiesen; oder auch, die Gleichungskette stimme. |
Denken wir uns eine
Kette, sie besteht aus Gliedern & es ist
möglich je ein solches Glied durch zwei
kleinere zu ersetzen. Die Verbindung die die Kette macht,
kann dann, statt durch die ¤
großen, ganz durch die kleineren || kleinen Glieder gemacht
werden. Man könnte sich aber auch denken, daß jedes
Glied der Kette aus – etwa – zwei halbringförmigen
Teilen bestünde, die zusammen das Glied bildeten, einzeln aber
nicht als Glieder verwendet werden könnten.
Es hätte nun ganz verschiedenen |
Der eine Beweis ersetzt eine
großgliedrige Kette durch eine kleingliedrige, der Andere
zeigt, wie man die (alten) großen Glieder aus
mehreren Bestandteilen zusammensetzten kann. |
Ähnlichkeit
& || sowie Verschiedenheit der beiden || zwei Fälle sind offenbar || augenfällig || klar zu Tage
liegend. |
Der Vergleich des Beweises mit der
Kette ist natürlich ein logischer Vergleich &
also ein vollkommen exakter Ausdruck dessen was
er zeigt || illustriert. |
Ich sage
z.B. „der Satz
(a + b)³ =
… ist bewiesen” & gebe nun die
Gleichungskette durch &
sage || er sagt
„ja es stimmt” Nun aber sage ich
(weiter): „& die
Gleichungen AI, AII,
etc. sind auch bewiesen”– und zeige ihm
die Komplexe BI, BII,
etc.. Im ersten Falle hieß „der
Satz ist bewiesen”: es wurde richtig gerechnet;
& er kontrollierte die Rechnung mit mir. – Im
zweiten Fall nun kontrolliere ich || kontrollieren wir auch Rechnungen,
aber sie führen nicht zu den Gleichungen A,
|
Denken wir uns, wir kontrollieren die
Rechnung (a + b)³ =
… auf die erste || in der ersten
Weise & beim ersten Übergang sagt er: „ja,
dieser Übergang geschieht (wohl || zwar) nach a ∙ (b + c) =
a ∙ b + a ∙ c, aber stimmt das
auch?” Und nun zeigten wir ihm die
Ableitung dieser Gleichung im induktiven
Sinne. – |
Die Frage „stimmt das
auch” hat, auf diese Gleichung bezogen, im ersten Kalkül
gar keinen Sinn. Und im andern hat sie einen dem ersten
Kalkül ganz fremden Sinn. |
((Besser gesagt:
Im einen Fall || In einer
Bedeutung heißt die Frage „stimmt das
auch || die Gleichung”: läßt
sie sich nach den Grundgleichungen || Paradigmen herleiten? Im andern
Fall heißt es: lassen sich die Gleichungen
α, β, γ nach dem Paradigma (oder
den Paradigmen) herleiten? – Und
hier haben wir die beiden Bedeutungen der Frage (oder
des Wortes ‚Beweis’) auf eine Ebene
gestellt (in einem System ausgedrückt)
& können sie nun vergleichen & sehen daß sie
nicht eines sind).)) |
Und zwar leistet dieser
neue Beweis nicht, was man annehmen könnte, daß er
nämlich den Kalkül auf eine kleinere || engere Grundlage setzte – wie es etwa
geschieht, wenn wir
p ∣ q durch
p ⌵ q &
~p ersetzen, oder
sonst die Zahl der Axiome vermindern. Denn
wenn man nun sagt, man habe alle die Grundgleichungen A aus
ρ allein abgeleitet, so
heißt hier das Wort „abgeleitet” etwas
(ganz) andres. (Was man
sich bei dieser Versprechung erwartet ist die Ersetzung der
großen Kettenglieder durch kleinere, nicht durch zwei halbe
Kettenglieder.) Und in einem Sinne hat man durch
diese Ableitungen alles beim alten gelassen. Denn es bleibt
im neuen Kalkül ein Kettenglied des alten wesentlich als ein
solches bestehen || bestehn. Die alte Struktur wird nicht
aufgelöst. So daß man sagen muß, der alte Gang
des Beweises bleibt bestehen. Und es bleibt im
alten Sinne auch die Unreduzierbarkeit. |
Man kann
daher auch nicht sagen |
„Ich weiß daß es da ein
Gesetz geben muß”. Ist dieses Wissen ein
amorphes das Aussprechen des Satzes begleitendes
Gefühl? Dann interessiert es uns nicht.
Und ist es ein symbolischer
Prozeß – nun, dann ist die Aufgabe ihn in
einem klaren || offenbaren
Symbolismus auszudrücken || darzustellen. |
Lichtenberg: „Unsere ganze
Philosophie ist Berichtigung des Sprachgebrauchs, also, die
Berichtigung einer Philosophie, & zwar der
allgemeinsten.” |
1.11.31.
(Ramsey
war ein bürgerlicher Denker.
D.h. seine Gedanken hatten den Zweck die
Dinge in einer gegebenen Gemeinde zu ordnen. Er dachte
nicht über das Wesen des Staates nach – oder doch nicht
gerne – sondern darüber |
Der Gebrauch des Wortes
„dieses↗”.
|
Onus
probandi (auf Seiten des Mathematikers
etc.) |
Wird ein Zusammenhang der
A durch die Induktionsbeweise
mittels α gezeigt & ist dies nicht
das Zeichen dafür daß wir es hier doch mit
Beweisen zu tun haben? – Es wird nicht
der Zusammenhang gezeigt, den ein Zerlegen der
Übergänge
A in
Übergänge ρ machen || herstellen würde.
Und ein Zusammenhang der A ist ja schon vor
jedem Beweis zu sehen. |
Was, wenn die Wörter „rot“, „blau“ die Wirkung
hätten || das Hören der Wörter „rot“,
„blau“ die Wirkung hätte uns farbige Kreise vor
das innere Auge treten zu lassen (wie etwa ein Druck auf
|
Aber so wirkt es ja zum Teil
wirklich, wenn auch nur dadurch daß wir das Wort
anfänglich immer mit dem Hinweisen auf einen blauen
Gegenstand verbanden (wie die spätere Wirkung des Wortes
‚blau’ entstanden ist, ist uns ja aber
gleichgültig). |
Die Unruhe in der Philosophie
entsteht dadurch || kommt daher, daß die
Philosophen die Philosophie falsch ansehen, oder falsch
sehen, nämlich gleichsam in (unendliche)
Längsstreifen zerlegt statt in (endliche)
Querstreifen.  Diese
Umstellung der Auffassung macht die größte
Schwierigkeit. Sie wollen also gleichsam den
unendlichen Streifen erfassen & klagen daß es || dies nicht Stück für Stück möglich
ist. Freilich nicht wenn man unter einem Stück einen
endlosen Längsstreifen versteht. Wohl aber wenn man
einen Querstreifen als Stück || ganzes definitives
Stück sieht. – Aber dann kommen wir ja mit
unserer Aufgabe || Arbeit nie zu
Ende! Gewiß || Freilich
nicht, denn sie hat Diese
Umstellung der Auffassung macht die größte
Schwierigkeit. Sie wollen also gleichsam den
unendlichen Streifen erfassen & klagen daß es || dies nicht Stück für Stück möglich
ist. Freilich nicht wenn man unter einem Stück einen
endlosen Längsstreifen versteht. Wohl aber wenn man
einen Querstreifen als Stück || ganzes definitives
Stück sieht. – Aber dann kommen wir ja mit
unserer Aufgabe || Arbeit nie zu
Ende! Gewiß || Freilich
nicht, denn sie hat |
(Der Philosoph ist nicht
Bürger einer Denkgemeinde. Das ist, was ihn zum
Philosophen macht.) |
2.
Ist das ‚dieses’ worauf ich zeige die Farbe,
oder, was die Farbe hat? Und könnte meine
Worterklärung nicht lauten „in diesem Falle
sage ich, daß ‚der Gegenstand rot
ist’” || „in diesem
Falle sage ich ‚der Gegenstand ist
rot’”? Oder
muß es heißen „diese Farbe nenne ich
‚rot’”? |
Aber wie wird es denn
entschieden, worauf gezeigt wird? ob auf die Farbe oder den
Ort? Doch wohl auf den Ort an dem die Farbe ist.
Aber weiter ist doch da nichts zu unterscheiden. |
Die
Worterklärung könnte auch lauten: die Farbe die
dieser Ort hat || dieses Orts nenne ich
‚rot’. |
Aber das hätte doch nur Sinn,
wenn Farbe im Gegensatz zu etwas Anderm stünde, also etwa
zu Form. Ich könnte also || so erklären: die Farbe dieses Flecks
ist || heißt ‚rot’ die
Form ‚Kreis’. Und hier stehen die Wörter ‚Farbe’ & ‚Form’ für Anwendungsarten (grammatische Regeln) & sind in Wirklichkeit (Bezeichnungen von) || bezeichnen in Wirklichkeit Wortarten wie „Eigenschaftswort”, „Hauptwort”. |
Wenn ich
sage: „die Farbe dieses Ding's nenne ich
‚blau’” so müssen die Worte
„die Farbe dieses Dings” bereits eine
Bezeichnung der Farbe sein & als solche dienen
können. Diese Worte präsentieren das Kind zur
Taufe. |
Auch angenommen wir wollten ¤ – in einem
übertragenen Sinn – einen blauen Kreis den „Träger des Namens ‚blau’” nennen¤
& führten diesen als Zeichen statt des
Wortes „blau” ein, so hätte nun
dieses Zeichen || dieser Fleck ebenso seine
Bedeutung, durch die Regeln seines Gebrauchs bestimmt, wie das
Wort. |
3.
Welches ist die ‚wirkliche
Lage’ des Körpers, den ich unter Wasser sehe,
was die ‚wirkliche Farbe’ des
Tisches. Hier macht eben die Frage nach der
Verifikation den Sinn der
Worte || dieser Ausdrücke
klar. |
Der falsche Ton in der Frage, ob es nicht primäre Zeichen
(hinweisende Gesten) geben müsse, während
|
(Statt der
turbulenten Mutmaßungen & Erklärungen wollen wir
ruhige Darlegungen || Konstatierungen
sprachlicher Tatsachen || von sprachlichen
Tatsachen geben.) || die ruhige
Feststellung sprachlicher Tatsachen.)
|
Nicht die Farbe Rot tritt an Stelle des Wortes
‚rot’,
sondern die Gebärde die auf einen roten Gegenstand hinweist, oder
das rote Täfelchen. |
9.
Nun sage ich aber: „Es gilt mit Recht als ein
Kriterium des Verstehens || Verständnisses des Wortes
„rot”, daß Einer einen roten Gegenstand auf
Befehl aus anders || anderen gefärbten
herausgreifen
[engl.:
pick] kann; dagegen ist das richtige
Übersetzen des Wortes ‚rot’ in's
Englische oder Französische kein Beweis
seines Verständnisses || kein
Beweis des Verstehens. Also ist das rote
Täfelchen ein primäres Zeichen für
‚rot’, dagegen jedes Wort ein
sekundäres || abgeleitetes
Zeichen.” ((Aber das zeigt nur, was ich
unter || mit dem „Verstehen des Wortes
‚rot’” verstehe || meine. Und was heißt „es gilt mit
|
10.
Welches ist denn das Kriterium unseres
Verständnisses: das Aufzeigen des roten Täfelchens,
wenn gefragt wurde „welches von diesen Täfelchen ist
rot”, oder das Wiederholen der hinweisenden Definition
„das↗ ist
‚rot’”? ((Ist denn das
Zweite nicht eine (Art) Probe zum
Ersten. Wie, wenn die erste Aufgabe gelautet
hätte: zeige auf das rote Täfelchen mit den Worten
„diese Farbe nenne ich
‚rot’”? – Vergleiche die
beiden Aufgaben: „welche Farbe nennen wir
‚rot’?” & „welches
ist das rote Täfelchen”. Die erste dieser
Aufgaben lautet || heißt nicht
„welche dieser Farben nennst Du
‚rot’?” denn sonst könnte er
nun auf irgend eine Farbe zeigen & was von ihm verlangt war,
war nicht die |
Das
Verstehen eines Satzes der Wortsprache ist dem Verstehen eines
musikalischen Themas (oder Musikstückes) viel verwandter als man glaubt.
Und zwar so, daß das Verstehen des sprachlichen Satzes
näher als man glaubt dem Ort liegt, an welchem man gewöhnlich das
Verständnis des musikalischen Ausdrucks sieht || dem liegt, was man gewöhnlich das Verständnis des
musikalischen Ausdrucks nennt. – Warum
pfeife ich das gerade so? warum bringe ich
den Rhythmus der Stärke & des Zeitmaßes
gerade auf dieses ganz bestimmte Ideal? Ich
möchte sagen: „weil ich weiß,
was das alles heißt” – aber
was heißt es denn? Ich wüßte es nicht zu
sagen, außer durch eine Übersetzung in einen Vorgang von
gleichem Rhythmus. Ich könnte nur
sagen: so wohnt |
Auch wenn wir verstehen, daß der
Ausdruck „das ist rot” zwei ganz verschiedene
Funktionen haben kann: als hinweisende Definition
|
Ich kann nicht auf die Bedeutung
eines Wortes zeigen. (Höchstens auf den Träger
eines Namens.) |
Das was in
der hinweisenden Definition auf der linken Seite des
Gleichheitszeichens steht (wenn auf der rechten das
Wort steht), ist nicht die Bedeutung des Worts (das hieße
nichts). |
„Dieses
Buch hat die Farbe die ‚rot’
heißt”. „Die Farbe die
dieses Buch hat heißt
‚rot’”. So klingen die
beiden Sätze am ähnlichsten; aber
wir könnten offenbar auch einem dieser Sätze den Sinn
des andern geben. Aber in einem Fall setzen wir den
Gebrauch eines Wortes fest, verkünden || enunciate also eine
grammatische Regel, im andern Fall machen wir eine
Behauptung, die durch die
Erfahrung |
Im einen Fall machen wir den Zug eines bestehenden
Spiels, im andern setzen wir eine Spielregel fest.
Man könnte auch das Ziehen mit einer Spielfigur auf diese
beiden Arten auffassen: als Paradigma
für künftige Züge & als Zug des
Spiels. || & als Zug einer Partie (des
Spiels). |
Es hat aber natürlich
etwas zu bedeuten, daß wir den Zug (dieselbe
Handlung) auf beide Arten meinen können.
((Es hat nicht mehr zu bedeuten || Nicht mehr, als was der Fall
❘ = 0 – = x
etc. zeigt. Was soll es denn
andres & mehr bedeuten
können, als was sich in den besonderen Fällen
zeigt. Denn wir müssen uns hier wieder
an die besonderen Fälle halten. Unklarheit
entsteht hier durch den Ausdruck „auf beide Arten
meinen können”.)) || Denn an die besonderen Fälle müssen wir uns hier
wieder halten & nicht trachten in
eine nebelhafte Allgemeinheit zu gelangen || nach einer nebelhaften Allgemeinheit trachten. Entsteht
die Unklarheit hier nicht durch die Worte „meinen
können”?)) |
11.
∣ (Es könnte sich
eine seltsame Analogie daraus ergeben, daß das Okular
|
In dem
einen Sinn des Satzes könnte ich sehr wohl auf ein grünes
Täfelchen zeigen & sagen „das heißt
‚rot’”, womit ich meine, daß das
grüne Täfelchen (oder die Geste die auf dasselbe
hinweist) als Zeichen für das Wort ‚rot’
gebraucht (eingesetzt) werden darf. |
Nun wird man
einwenden: „Aber so eine Erklärung
könnte doch nicht als Erklärung der Bedeutung des
Wortes ‚rot’ gebraucht werden”.
Darauf kann ich nur antworten: „das weiß
ich nicht; man müßte es versuchen & sehen, ob nach
dieser Zeichenerklärung der Andere verständnisvoll
reagiert”. |
Wie ist es aber, wenn ich für mich selbst eine
Bezeichnungsweise festsetze; wenn ich etwa || z.B. für den eigenen
Gebrauch gewissen Farbtönen Namen geben will: Ich
werde das etwa mittels einer Tabelle tun (es kommt
immer auf das || derlei
hinaus). Und nun werde ich doch nicht den Namen zur
falschen Farbe schreiben (zu der Farbe der ich ihn nicht geben
will). Aber warum nicht? Warum soll nicht
‚rot’ gegenüber dem grünen
|
Was ich hier
tue ist weiter nichts, als streng die Aussage „das
ist rot” von der Definition zu trennen.
Diese Trennung bereitet uns dieselbe Schwierigkeit, die immer zur Folge hätte || hatte, daß man der Definition eine andere Funktion vindizieren wollte als die, ein Zeichen für ein anderes zu setzen. || die Ersetzung eines Zeichens durch ein anderes zu erlauben. |
Man könnte sich denken,
daß das Hindeuten |
Kann nun aber nicht das grüne Zeichen auf
mehrere Arten statt des Wortes ‚rot’
treten? Einmal als Wort, ein andermal als
Komplementär gefärbtes
Zeichen? In dem letzteren Fall liegt natürlich eine
Ähnlichkeit mit dem des Kopierens der Farbe nach einer andern
Projektionsmethode vor (das farbige Zeichen ist
jetzt eine Art Muster). [Was
jetzt kommt ist sehr verworren; nicht im Sinn aber in der
Ordnung. Aber es ging nicht besser.] Es ist die Frage: Wenn sich diese Regel ihrem Wesen nach nur auf die Farben (oder Wörter) blau, rot, grün, gelb bezieht, ist sie dann nicht identisch mit der, welche das grüne Zeichen als Wort für ‚rot’ und umgekehrt etc. festsetzt? Denn eine Regel || Allgemeinheit die ihrem logischen Wesen nach einem logischen Produkt äquivalent ist, ist nichts anderes als  ; ein Querstrich in
der Grammatik der Farben gezogen. Anders wäre es, wenn die
Regel (ρ) hieße: das
Täfelchen bedeutet immer einen etwas dunkleren
Farbton als sein eigener || der seine
ist. Man muß nur wieder auf den
verschiedenen Sinn der Farb- &
der Gestaltprojektion achten (& bei
der letzteren wieder auf den Unterschied der
Abbildung nach visuellen Kriterien || im visuellen
Raum von || & der
Übertragung mit Meßinstrumenten.).
Das Kopieren nach der Regel
ρ
ist ‚kopieren’ in einem andern Sinne dieses
Wortes als dem in welchem das Hervorbringen des gleichen Farbtons
so genannt wird. Es handelt sich also nicht um zwei
Projektionsmethoden vergleichbar
etwa der Parallel- &
der Zentralprojektion durch
die ich eine geometrische Figur mit Zirkel & Lineal in eine
andere projizieren kann.
(Die Metrik der
Farbtöne). Wenn ich das berücksichtige, so
kann ich also in dem veränderten Sinn ; ein Querstrich in
der Grammatik der Farben gezogen. Anders wäre es, wenn die
Regel (ρ) hieße: das
Täfelchen bedeutet immer einen etwas dunkleren
Farbton als sein eigener || der seine
ist. Man muß nur wieder auf den
verschiedenen Sinn der Farb- &
der Gestaltprojektion achten (& bei
der letzteren wieder auf den Unterschied der
Abbildung nach visuellen Kriterien || im visuellen
Raum von || & der
Übertragung mit Meßinstrumenten.).
Das Kopieren nach der Regel
ρ
ist ‚kopieren’ in einem andern Sinne dieses
Wortes als dem in welchem das Hervorbringen des gleichen Farbtons
so genannt wird. Es handelt sich also nicht um zwei
Projektionsmethoden vergleichbar
etwa der Parallel- &
der Zentralprojektion durch
die ich eine geometrische Figur mit Zirkel & Lineal in eine
andere projizieren kann.
(Die Metrik der
Farbtöne). Wenn ich das berücksichtige, so
kann ich also in dem veränderten Sinn
Die ursprüngliche Frage war: Könnten wir nicht zur hinweisenden Erklärung von ‚rot’ ebensowohl auf ein grünes, wie auf ein rotes Täfelchen zeigen? denn, wenn diese Definition nur ein Zeichen statt des andern setzt so sollte dies doch gleichgültig sein || auf's gleiche hinauslaufen || keinen Unterschied machen. – Soweit || Wenn die Erklärung nur ein Wort für ein andres setzt ist es auch gleichgültig. || so macht es auch keinen. Bringt aber die Erklärung das Wort mit einem Muster in Zusammenhang, so ist es nun nicht unwesentlich mit welchem Täfelchen das Zeichen verbunden wird (denke auch wieder daran daß eine Farbe der andern nicht im gleichen Sinn zum Muster dienen kann, wie ihr selbst). „Aber dann gibt es also willkürliche Zeichen & solche die nicht willkürlich sind!” – Aber denken wir nur an die Verständigung durch Landkarten, Zeichnungen, & Sätze anderseits: die Sätze sind so wenig willkürlich wie die Zeichnungen. Aber die Worte sind willkürlich (vergl. ❘ = 0, – = x, ❘–❘ ❘–). Wird denn aber ein Wort eigentlich als Wort gebraucht, wenn ich es nur in Verbindung mit einer Tabelle gebrauche, die den Übergang zu Mustern macht? Ist es also nicht falsch, zu sagen ein Satz sei ein Bild, wenn ich doch nur ein Bild nach ihm
Die Frage war ursprünglich: muß ein rotes Täfelchen ‚rot’ vertreten oder macht dies nur den Übergang für uns leicht (natürlicher), wie es leichter ist, sich in einer Tabelle zurechtzufinden die nach dem gewöhnlichen Schema als in einer die nach einem verwickelteren Schema angeordnet ist. Und es ist klar daß ein grünes Täfelchen das Wort ‚rot’ so gut vertreten kann wie || als ein blaues. Auch, daß ein grünes nicht in dem Sinn als Muster eines roten Farbtons dienen kann, wie ein Täfelchen von diesem Farbton. (Ist übrigens das Täfelchen ein Muster des Farbtons, oder des Gegenstandes der etwa zu färben ist. Nun, das Täfelchen ersetzt jedenfalls das Farbwort & kein anderes. |
Das Wort in
Anführungszeichen ist ein Muster. |
∣ Die Schwierigkeit, die
uns das Sprechen über den Gesichtsraum ohne
Subjekt macht & über meine &
seine Zahnschmerzen, ist die, die Sprache einzurenken,
daß sie richtig in den Tatsachen sitzt. ∣ |
Vergiß
nicht: die Abmachung ist vergangen. |
Es besteht ja die
einfache Tatsache daß wir das Wort ‚rot’
anwenden, wie wir es anwenden & uns dabei nicht immer einen
roten Gegenstand vorstellen; & selbst wenn das geschähe,
so wäre damit die Möglichkeit der Ausführung des
Befehls „stelle Dir etwas Rotes vor” nicht
erklärt. |
»Aber wenn
ich, auf einen roten Gegenstand zeigend, sage „diese Farbe
nennt man ‚rot’”, gebe ich doch gewiß
nicht nur ein Zeichen statt des anderen! Und was
wäre der Nutzen dieser
Ersetzung?!«– Ich gebe
ihm ein Zeichen dessen Gebrauch er kennt, für eines dessen
Gebrauch er nicht kannte & lehre ihn damit
den Gebrauch des letzteren. ((Die Erklärung
daß ich den Gebrauch eines Zeichens
lehre indem ich es durch eins definiere dessen Gebrauch ich kenne
– oder durch eine bestimmte Verbindung solcher
|
Wenn ich sage „diese
Farbe nennt man ‚sepia’”, so habe ich in
diesem Satz das Wort ‚sepia’ noch nicht
gebraucht. (Auch nicht – wie jemand glauben || meinen könnte – zu sagen, daß die Farbe des
gezeigten Ortes sepia ist.) Gebrauche ich nun in
Hinkunft das Wort, so könnte ich immer statt seiner
die Geste
gebrauchen, durch die || den Hinweis gebrauchen, durch
den ich es damals erklärt habe.
|
Wäre diese Geste nun auf
jeden Fall || jedenfalls﹖
unmittelbarer (oder leichter) zu verstehen, als das
Wort? So daß man sich nun in der Bedeutung des
gebrauchten Zeichens nicht irren könnte (kein Zweifel
über die Bedeutung möglich wäre) während das
Wort erst einer Erklärung bedurfte?
So daß zwar „bring mir eine gelbe Blume” auf
eine Erklärung des Worts „gelb”
zurückgreifen müsse, aber der Befehl „bring mir
eine solche Blume” (wobei man auf ein gelbes
Täfelchen zeigt || deutet) eine weitere
Erklärung nicht zuließe.
Denken wir hier an die Befehle „bring mir 2
Äpfel” & „bring mir II
|
„Aber es hat doch gewiß
etwas zu bedeuten, daß ich bei der Erklärung eines Namens
gerade auf dessen Träger zeige”. Zeigen ist
doch wohl etwas, was geometrisch bestimmt ist || was
durch räumliche Verhältnisse definiert
ist.
Wenn ich dem Andern den Befehl gegeben hätte & ihm dabei zugenickt hätte mit den Worten „Du weißt schon was ich meine”, so hatten diese Worte offenbar nur als Erinnerung an die in der Abmachung gegebene Übersetzung des Befehls in die normale Sprache Sinn. Wenn ich jemand der deutsch versteht unter ganz gewöhnlichen Umständen den Befehl gebe „Geh zu Bett” so werde ich ihm nicht zunicken „Du weißt schon was ich meine” & täte ich's er würde nur – vielleicht in erstauntem Ton – den Wortlaut meines Befehls wiederholen & zwar um meine Bemerkung „Du weißt schon etc.” ad absurdum zu führen. Denn die richtige Antwort auf diese Bemerkung ist immer die Übersetzung des gegebenen Befehls in eine andere Sprache. Wenn nun eine Replik früher lautete: „dann mußte er eben meine Erklärung anders verstehen” so war das richtig auch wenn der Vorgang bei der Erklärung – auch |
Es liegt
in der menschlichen Natur das Zeigen mit dem Finger
so zu verstehen || so
aufzufassen. |
15.11.
Nun gebe ich aber natürlich zu daß ich, ohne
vorhergehende Abmachung einer Chiffre, ein
Mißverständnis hervorrufen würde wenn ich, auf den
Punkt A zeigend, |
Die Worte sind diskontinuierlich; die
Wortsprache eine Abbildung durch diskontinuierliche Zeichen.
Das ist einer der wichtigsten Gesichtspunkte von dem man sie
betrachten muß. Aber Ziffern sind ja auch Worte
& wir haben das Dezimalsystem. |
Wenn wir einen
geometrischen Beweis mit Zirkel & Lineal führen so
bedienen wir uns eines Symbolismus mit
kontinuierlichen Symbolen. |
Buchstaben als
Namen von Punkten in einer geometrischen Zeichnung.
|
Vergiß hier auch nicht, daß die
Wortsprache nur eine unter vielen möglichen Sprachen
ist & es |
Daß der Träger eines Namens tot ist, ist
eine Tatsache die wir mittels dieses Namens (der also
hier Bedeutung hat) beschreiben. Wie aber,
wenn wir sagen, daß der Träger niemals gelebt hat?10
|
Die
Bedeutung des Namens liegt darin, was wir von ihm mit Sinn (wahr
oder falsch) aussagen können.11 |
Ist die hypothetische
Existenz des Trägers involviert, wenn wir zur
Definition des Namens auf den Träger zeigen & sagen
„das ist N”?12 |
Es liegt
Alles darin, daß ich sagen kann
„Moses existiert
nicht” („hat nicht existiert”), aber
nicht „dieser Mensch (auf den ich zeige) existiert
nicht”.13 |
Und das führt wieder
dahin: daß wir sagen können „ich
sehe hier keinen roten Fleck” auch wenn überhaupt keiner
irgendwo zu finden ist (was immer das heißen mag).
Und warum soll dann jemals einer zu finden gewesen
sein? D.h. ich spiele vorläufig mein Spiel mit dem Namen allein, ohne ((Wenn man sagt „N existiert nicht”, so kann das verschiedenerlei bedeuten. Es kann heißen daß ein Mann der als er lebte diesen Namen trug nicht oder nicht zu einer gewissen Zeit in einem gewissen Land existiert hat; aber auch daß spätere Geschichteschreiber den Charakter den wir so (Moses) nennen erfunden haben, daß die & die Ereignisse nie stattgefunden haben & ein || ihr Held also nie gelebt hat. D.h. also: kein Mensch hat je || damals Moses geheißen & diese Taten vollbracht; oder: das Ding das Dir als Herr ‚N’ vorgestellt wurde war eine Puppe; etc. Denken wir uns jemand sagte uns er || es sagte uns einer er habe Moses auf der Straße gesehen. Wir würden ihn dann fragen: „wie meinst Du das, Du hast ihn gesehen? Wie wußtest Du denn daß es Moses war?” und nun könnte der Andre sagen: „er hat es mir gesagt” oder „er sah so aus wie ich mir Moses vorstelle”, oder „er hatte diese & diese Merkmale”, etc.. Ich will doch wohl das sagen was Russell dadurch ausdrückt daß der Name Moses durch verschiedene Beschreibungen definiert sein kann („der Mann welcher ‚Moses’ hieß & zu dieser Zeit an diesem Ort lebte”, oder „der Mann – wie immer er damals genannt wurde – welcher die Israeliten durch die Wüste führte”, oder „der Denn ich habe zur Feststellung des Regelverzeichnisses || der Regel nach der er handelt zwei Wege angegeben. Der eine, der hypothetische bestand in der Beobachtung seiner Handlungen & die Regel war dann von der Art eines naturwissenschaftlichen Satzes. Der andere war, den Andern zu fragen, nach welcher Regel er vorgehe. Wie aber, wenn der erste Weg kein klares Resultat liefert || ergibt & die Frage keine Regel zu Tage fördert wie es im Fall „N ist gestorben” geschieht. Denn, wenn wir den der das sagte fragen „was ist N?” so wird er zwar ‚N’ durch eine Beschreibung erklären, wird aber bereit sein diese Beschreibung zu widerrufen & abzuändern wenn wir ihm den einen oder andern Satz entziehen || widerlegen. Wie soll ich also die Regel bestimmen || auffassen nach der er spielt? er weiß sie selbst nicht. Ich könnte die || eine Regel für einen Fall nur danach || nach dem bestimmen, was er auf die Frage „wer ist N” in diesem Fall gerade antwortet. Steckt uns da nicht die Analogie der Sprache mit dem Spiel ein Licht auf? Wir können uns doch sehr wohl denken daß sich Menschen auf einer Wiese damit unterhielten mit einem Ball zu spielen & zwar so daß sie verschiedene bestehende Spiele der Reihe nach anfingen nicht |
16.
Wenn aber der Träger dem Namen abhanden kommen, oder nie
existiert haben, kann, so mußte man beim
Gebrauch des Namens von vornherein damit rechnen.
Das mußte in seiner Bedeutung liegen. ((Es sei
denn, daß wir diese Bedeutung Für uns ist es genügend daß es eine Frage gibt: „wie meinst Du das?” & daß als Antwort auf diese Frage das alte || zuerst gegebene Zeichen durch ein neues ersetzt wird. – Der Einwand dagegen ist, daß mir eine Erklärung ja nichts hilft wenn sie nicht die letzte ist, & daß sie nie die letzte ist: Ich kann zwar erklären: unter ‚Moses’ verstehe ich den Mann, wenn es einen solchen gegeben hat, der die Israeliten aus Ägypten geführt hat, wie immer er damals genannt worden sein mag & was immer er sonst getan oder nicht getan haben mag– ¤ aber ähnliche Fragen ergeben sich nun in Bezug auf die Wörter dieses Satzes || dieser Erklärung: „was nennst Du ‚Ägypten’?” wen, die Israeliten? etc. Ja, diese Fragen kommen auch nicht zu einem Ende wenn wir etwa bei Worten wie ‚rot’, ‚dunkel’, ‚süß’ angelangt wären. Unrichtig war es nur zu sagen, daß mir deshalb eine dieser Erklärungen |
Wenn man fragt „in
welchem Verhältnis stehen Namen & Sachen”,
so ist die Antwort: in dem Verhältnis der Hausnummer zum
Haus. |
Man könnte das Zeichen
„dieses↗”
„einen Namen’ nennen. Wenn man dann von
einem Träger dieses Namens spricht (dem Gegenstand,
auf den der Pfeil zeigt), so hat hier das Wort || der
Name ohne Träger keine Bedeutung. |
Ich erzähle
jemandem von einem Herrn N; er habe mit mir studiert,
|
Sage ich jemandem „bringe eine
rote Blume” & er bringt eine, & nun
frage ich „warum hast Du mir eine von dieser Farbe
gebracht”– & er: „das ist
doch rot” || „diese Farbe nenne ich
‚rot’”: so
ist dies letzte ein Satz der Grammatik. Er rechtfertigt
eine Anwendung des Worts. |
Fehlt dieser Satz || diese
Regel so ist die Grammatik des Worts (seine Bedeutung)
eine andere. |
Er hätte zweierlei sagen können: 1)
„ich bringe sie, weil sie rot ist (& Du
hast doch eine rote verlangt)”, 2) „ich bringe
sie, denn diese Farbe nenne ich || nennst Du
doch ‚rot’”. –
Sind diese beiden Verteidigungen
gleichwertig? ((Ich hätte einfach
fragen können: heißt es dasselbe: „dieses
Ding ist rot” & „die Farbe dieses Dings
heißt rot”?. Zuerst
könnte ich da fragen: auf welche Sprache heißt sie
so? Aber es ist doch gewiß eine eindeutige
Beschreibung wenn ich sage: bring mir eine Blume von der Farbe
die auf Deutsch ‚rot’ heißt. Die
Verteidigung hätte auch lauten || heißen
können: „ich bringe sie, weil sie rot ist,
denn diese Farbe nennst Du doch
‚rot’”.
„Die Farbe dieser Blume
heißt auf Deutsch ‚rot’” ist
derselbe Satz wie |
Die Wilden haben Spiele
(oder wir nennen es doch so), für die sie keine
geschriebenen Regeln, kein Regelverzeichnis, besitzen.
Denken wir uns nun die Tätigkeit eines
Forschers die Länder dieser Völker zu bereisen
& Regelverzeichnisse für ihre Spiele anzulegen.
Das ist das genaue Analogon zu dem, was der Philosoph tut.
|
Die
primären Definitionen (oder Definitionen mittels
primärer Zeichen) sind
wohl die Regeln der Anwendung der Zeichen auf die Dinge außerhalb
der Welt der geschriebenen oder gesprochenen Zeichen || sollen wohl
die Regeln der Anwendung der Zeichen auf die Dinge außerhalb der
Welt der geschriebenen oder gesprochenen Zeichen sein.
Denn es gibt, praktisch gesprochen, offenbar die Welt der
Bücher oder Rede, & anderseits die Welt außerhalb
dieser. Die primäre Regel soll quasi die „Verbindung der Zeichen mit dem Leben” herstellen. ((Dies bezieht sich offenbar nur auf die Welt der Wortsprache nicht auf die der Zeichnungen in den Büchern. Die Idee || Auffassung ist die: Wenn ich die Zeichnung  kopiere kann ich dies unmittelbar tun, wenn ich aber
❘–❘ ❘–❘ auf die seinerzeit beschriebene Art
kopieren will so geht das nur durch die Intervention einer
Tabelle. Aber ist es selbstverständlicher daß
ich die Zeichnung gerade in dieser (von
kopiere kann ich dies unmittelbar tun, wenn ich aber
❘–❘ ❘–❘ auf die seinerzeit beschriebene Art
kopieren will so geht das nur durch die Intervention einer
Tabelle. Aber ist es selbstverständlicher daß
ich die Zeichnung gerade in dieser (von
|
17.
∣ Man kann in gewissem Sinn mit philosophischen
Irrtümern nicht vorsichtig genug umgehn, sie enthalten so viel
Wahrheit. ∣ |
∣ Es geht nie einfach an zu sagen: Nein,
das ist falsch, heißt das muß aufgegeben werden. ∣ |
Wenn ich sage:
„die Farbe dieses Gegenstands
ist || heißt violett”, so
muß ich die Farbe mit den ersten Worten „die Farbe dieses
Gegenstands” schon benannt haben, sie schon zur Taufe
gehalten haben, damit der Akt der Namengebung das
sein kann, was er ist. Denn ich könnte
auch sagen „der Name dieser Farbe (der Farbe dieses
Dings) ist von Dir zu bestimmen”, & der den Namen gibt,
müßte nun schon wissen, wem er ihn gibt (an welchen Platz
der Sprache er ihn stellt). |
„Wenn ich nun auch sage || wir nun auch sagen, der Träger
des Namens ist nicht seine Bedeutung, so bestimmt doch der
Träger die Bedeutung, & wenn ich, auf ihn zeigend, sage
‚das ist
N’ so ist die Bedeutung von
‚N’ bestimmt.”
Aber es bestimmt hier schon das richtige Verstehen des Wortes ‚Träger’ in dem besondern Fall (Farbe, Gestalt, Ton, etc.) die Bedeutung bis auf eine letzte Bestimmung. |
„Aber ich habe ihn
gemeint”. Sonderbarer Vorgang dieses
Meinen! Kann man jemanden meinen auch wenn er in
Amerika & man in Europa ist?
Und || Oder gar, wenn er schon tot
ist? |
Die Bedeutung des Namens ist eine
Stellung (ich meine, seine Funktion) im
Spiel. |
„Ich will nicht verlangen,
daß in der erklärenden Tabelle das rote Täfelchen
horizontal gegenüber dem Wort ‚rot’ stehen
soll, aber irgend ein Gesetz des Lesens der Tabelle
muß es doch geben. Denn sonst verliert ja die Tabelle
ihren Sinn”. Ist es aber gesetzlos, wenn die
Tabelle so aufgefaßt wird
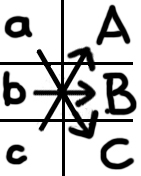 wie die Pfeile
andeuten. „Aber muß dann nicht eben das Schema wie die Pfeile
andeuten. „Aber muß dann nicht eben das Schema
 vorher
gegeben werden?”
Nur sofern auch das Schema vorher
gegeben werden?”
Nur sofern auch das Schema
 früher früher
|
Wird
aber dann nicht wenigstens eine gewisse
Regelmäßigkeit im Gebrauch gefordert! Würde
es angehen, wenn wir einmal eine Tabelle nach diesem, einmal
nach jenem Schema zu gebrauchen hätten? Wie
soll man denn wissen, wie man diese Tabelle zu gebrauchen
hat?!– Ja, wie weiß man es
denn heute? Die Zeichenerklärungen
haben doch irgend einmal || irgendwo ein
Ende. |
Es gibt eine Betrachtungsweise der elektrischen
Apparate & Maschinen || Maschinen &
Apparate (Dynamos, Radiostationen, etc.,
etc.), die sozusagen ohne vorgefaßtes
Verständnis diese Gegenstände als eine Verteilung
von Kupfer, Eisen, Gummi, Seide etc. im
Raum ansieht. Und diese Betrachtungsweise
könnte zu manchem interessanten Resultat führen.
Sie ist ganz analog || ähnlich der eines
mathematischen Satzes als Ornament. – Es ist
natürlich eine durchaus strenge &
korrekte Auffassung; & das
Charakteristische & Schwierige an ihr ist, daß sie den
Gegenstand ohne jede vorgefaßte Idee betrachtet
(sozusagen von einem Marsstandpunkt),
oder vielleicht richtiger: die normale vorgefaßte
Idee zerstört (durchkreuzt). |
Ist es denn wahr,
daß ich außer dem Satz „dieses Ding ist rot”
auf jeden Fall eine Regel von der
Form „diese Farbe heißt „rot’”
habe? – Aber hat nicht die
|
Das was mir
auffällt ist, daß die Regel für das Wort
‚rot’, unbedingt mit einem roten
Täfelchen sollte gegeben werden müssen.
((Siehe was früher über die verschiedenen
Arten gesagt wurde, wie ein färbiges Täfelchen
Farbmuster sein kann.)) |
Ist es ein
Widerspruch: dieses Ding ist
grün & seine Farbe heißt
‚rot’? – Nicht unbedingt, –
man kann ja auch sagen „dieses Ding ist grün &
seine Farbe heißt ‚Meerfarbe’” oder
„dieses Ding ist grün & seine Farbe heißt
‚vert’”. |
Der Satz „seine
Farbe heißt ‚rot’” bezieht sich aber auf
eine Tabelle. In dieser Tabelle steht also das
Täfelchen von dieser Farbe gegenüber dem Wort
‚rot’. |
Warum soll aber ein Zeichen für rot
rot sein? – Oder ist das Täfelchen in der
Tabelle dem Wort ‚rot’ gegenüber kein
Zeichen? ((Muster &
Wort)) |
„Es ist kein
Zeichen, es ist der Gegenstand selbst, – der den Namen
erhält.
Man ernennt ‚rot’ zum Namen der Farbe, wie man einen Menschen zum Stellvertreter eines andern ernennt.” Aber ist diese Namengebung nicht wieder der Deutung – der Anwendung – unterworfen? Ist die Namengebung etwas anderes als das Anhängen eines Namensschildes. Und der Zweck ist doch der, einen Übergang von (den) Operationen mit dem Namen zu Operationen mit dem Träger des Namens (Schildchens) zu machen. Aber die Träger der Namen, wenn auch nicht (selbst) Schrift- oder Lautzeichen sind doch, für unsern Standpunkt, von ihnen nicht wesentlich verschieden. Denn der Zweck & Nutzen der Operationen geht uns nichts an & auch nicht, ob wir mit Körpern oder Buchstaben operieren. |
Denn nun könnte ich ja sagen:
In jeder Definition wird einem Ding ein Name gegeben
& zwar wird eben einem Zeichen ein Name umgehangen.
Und wenn ich schreibe 1 + 1 ≝ 2 oder in der Tabelle
‚2’ dem ‚1 + 1’
gegenüberstelle, wie oben ‚rot’ dem
färbigen Täfelchen, so könnte ich
alle Fragen die ich über diese
Gegenüberstellung aufwarf auch
bezüglich jener stellen. |
Durch Russell, aber besonders durch
Whitehead, ist in die
Philosophie |
Ist das Zeigen mit dem Finger unserer
Sprache wesentlich? Es ist gewiß ein merkwürdiger
Zug unserer Sprache, daß wir
(ihre) Wörter hinweisend
erklären: das ist ein Baum, das ist ein Pferd, das
ist grün, etc.. ((Überall
auf der Erde || bei den Menschen finden sich
Brettspiele die mit kleinen Klötzchen auf Feldern
gespielt werden. Überall auf der Erde findet
sich eine Schrift || eine Zeichensprache die
aus geschriebenen Zeichen auf einer Fläche
besteht.)) |
Verhält es sich hier nicht
wieder, wie mit Papiergeld &
Waren? Ich kann
Geld kaufen und verkaufen, &
Waren kaufen &
verkaufen, etc.. Und solange nur von
kaufen & verkaufen die Rede ist, unterscheiden
sich Geld und Waren
nicht. Nur in ihrer
Nützlichkeit unterscheiden sie sich. Und so
könnte ich gesprochene & geschriebene Zeichen
‚Geld’ nennen, & die Träger der Namen
‚Waren’.
(Auch dieses Gleichnis ist wieder mehr als ein
Gleichnis.) |
Ich möchte sagen: Daß
das Hinweisen |
„Das Stück
Kuchen war für Dich gemeint”, wie äußert sich
das, was ist die Verifikation
dieses Satzes? So werden wir erfahren, was sein Sinn
ist. |
Denken wir an die Tafel der Farbmuster einer
Farbenhandlung. Hier haben wir unsre Tabelle der
Täfelchen || Farbmuster
& Farbnamen (oder
Nummern). Oder an den Katalog der Stoffmuster oder
Tapetenmuster. Der
Musterkatalog ist hier || Hier ist der Musterkatalog
ein notwendiges Requisit der Verständigung || Sprache. |
Eine Sprache ist, was sie ist, &
eine andere Sprache ist nicht diese
Sprache. Ich gebrauche also die Nummern des
Musterkatalogs anders, als die Wörter
„rot” „blau”
etc.. |
„Kommt das aber nicht nur daher,
daß ich die Erklärungen der einen im Kopfe habe,
die anderen nicht? Denn ein Angestellter der Weberei
könnte auch den ganzen Musterkatalog im Kopf haben &
würde dann dessen Nummern so gebrauchen, wie
wir die Namen der einfachen Farben”. ((Das
kommt darauf an, was man mit den Worten |
Was es also
mit den primären & sekundären Zeichen auf sich
hat, mußten wir ganz an dem
Musterkatalog & seiner Verwendung sehen
können, denn offenbar sind die Muster, was man primäre
Zeichen nennt || nennen möchte &
die Nummern die sekundären. |
Denken wir an das laute
Lesen nach der Schrift (oder das Schreiben nach dem
Gehör). Wir könnten uns natürlich eine
Art Tabelle denken (etwa Grammophonplatten mit den Buchstaben
als Aufschriften), nach der wir uns dabei richten
könnten. Aber wir richten uns nach keiner.
Kein Akt des Gedächtnisses, nichts vermittelt zwischen dem
geschriebenen Zeichen & dem Laut. |
18.
Es handelt sich doch darum, daß der Schritt des
Kalküls durch keine Vorbereitung ersetzt werden kann,
sondern immer frisch || von neuem
gemacht werden muß. Oder: die Tabelle ist die
Tabelle, aber nicht die Anwendung der Tabelle.
Das heißt ich muß den Schritt vom Buchstaben |
Ich mache
nach den Zeilen der Tabelle (oder nach den Strichen des
Gleichheitszeichens) den Sprung, den ich auch ohne die Hilfen
hätte machen können. ((Die Tabelle
ist daher allerdings sinnlos, wenn sie mir nicht hilft; wenn sie also
so angeordnet ist daß ich sie nicht verstehen kann (mich in ihr
nicht auskenne). Ob ich mich aber in ihr auskennen kann,
d.h. auskenne, || sie aber verstehen kann,
d.h. verstehe, ist etwas, was sich nur
durch Erfahrung entscheiden läßt || kann nur die Erfahrung
entscheiden. D.h.:
welches Schema uns den Sprung
tatsächlich erleichtert, ist Sache der
Erfahrung.)) |
Das
Definiendum ist der Name des
Definiens. ((Das ist nicht
wahr. Denn das Definiendum
vertritt das Definiens
d.h. es wird an dessen Stelle
eingesetzt. Kann man aber sagen daß Namen an der Stelle
ihrer Träger stehen & die Träger dann wieder
für sie eingesetzt werden? Nun, ein Name
kann so gebraucht werden; wenn etwa die Sitzordnung
eines Diners durch Tischkarten angegeben ist. Und
anderseits kann ich das
definierte Zeichen als Name des
In einem Sinn sind also die Namen stellvertretend, & die Definitionen setzen doch Stellvertreter für Zeichen || einen Stellvertreter für ein Zeichen ein. – Wenn es nun heißt: gib dem Weber das Muster 5 um es zu kopieren (& das ist doch der typische Gebrauch der Nummer & der Übergang von der Nummer zum Muster) so kann die Nummer hier gewiß als Name des Musters aufgefaßt werden & sie funktioniert jedenfalls genau so (oder kann so funktionieren) wie die Hausnummer wenn ich jemandem den Befehl gebe auf № 5 zu gehen. – Ist hier nicht die Quelle der Verwirrung || des Wirrwarrs die Mehrdeutigkeit des Wortes „stellvertreten”? Wenn in den Geschäftsbüchern eines Öbstlers || Obsthändlers von „100 Kisten Äpfel” die Rede ist so kann man doch in einem Sinn nicht sagen daß dieser Ausdruck die Kisten vertritt denn sonst müßten sie ja für ihren Vertreter eintreten können & was täten die 100 Kisten da? (sie sollten ja eben verschickt werden). ‚2’ ist der buchstäbliche Stellvertreter von ‚1 + 1’, & vertritt es in den verschiedenen Operationen in derselben Art wie der Finger die Schachfigur, wenn ich um mir die Folgen eines Schachzuges auszumalen |
Wenn man
mathematischen Ausdrücken oder Gleichungen
am Rande der Seite eine Nummer gibt um sich auf sie kurz
beziehen zu können, so gibt man damit gewiß dem Ausdruck
einen Namen; aber ist das wirklich eine
Definition? Wenn ja, müßte man die Definition
dann nicht so schreiben daß das Definierende in
Anführungszeichen steht? Sind die Buchstaben im Satz „a a c c c b d d”, der die Beschreibung des Linienzuges
Ich will natürlich sagen daß der Übergang vom definierten zum definierenden Zeichen einfach geschieht indem man das definierende an die Stelle im Satzzusammenhang stellt wo das definierte stand, daß aber das nicht der Übergang vom Satz in dem der Name steht zu dem ist was wir auf diesen Satz hin mit dem Träger des Namens tun. – Kann man aber sagen daß die Definition doch eine sehr spezielle Art der Namengebung ist? Da müßte man zuerst wissen, wem dieser Name gegeben wird. Doch nicht dem physikalischen Objekt des Zeichens. Denn zwei Gleichlautende Tabellen gelten Das Wichtigste ist wohl (zu bedenken, daß || Die wichtigste Überlegung ist wohl, daß wir ja auch außerhalb der Schrift || Sprache die || diejenige Stellvertretung brauchen, in der ein Zeichen für ein Anderes steht. Wäre nicht ein Fall dieser Stellvertretung auch der, wenn wir eine Schachpartie etwa auf dem Brett begönnen sie denn mit Schriftzeichen fortsetzten & ihre letzten Züge dann wieder auf dem Brett ausführten. – Und ist der Vertreter einer Figur hier was wir den Namen der Figur in der Zeichensprache nennen könnten? Das worauf ich hinaus will ist, klar zu sehen was die Ähnlichkeit || Analogie & Verschiedenheit zwischen dem Übergang vom definierten || stellvertretenden zum definierenden || vertretenen Zeichen & dem Übergang von der Überlegung zur Ausführung ist. || Worauf ich hinaus will, ist, die Analogie & Verschiedenheit zwischen dem Übergang vom stellvertretenden zum vertretenen Zeichen & dem Übergang von der Überlegung zur Ausführung klar zu sehen. Der Linienzug der nach a a b b b c gemacht wurde kann sehr wohl auch nur ein Zeichen sein & die Ausführung des Befehls in einer andern Bewegung bestehn die erst wieder von Die Definition & die Namengebung ordnet einer Sache ein Zeichen bei (im ersten Falle einem Zeichen ein Zeichen). – Aber ein Name wird dem Ding gegeben, daß ich von ihm sprechen kann. – Das klingt, als wäre der Name wie ein Fernglas & der vorige Satz analog dem Satz: ein Fernglas wird mir gegeben, daß ich ihn sehen kann. Aber das „von ihm reden” besteht nur darin, daß zuerst gesagt wurde „er↗ heißt ‚N’” & dann der Name ‚N’ in der Sprache gebraucht wird, & beim Übergang von der Sprache zu Handlungen, etc..– Immerhin ist von N reden verschieden von einer Operation, die ich mit N vornehme. Ja, auch verschieden davon, mit einem Gegenstand zu operieren, den N vertritt, für den aber auch N gebraucht || gesetzt werden könnte. – Wenn ich nun aber z.B. sehen möchte, an welcher Stelle des Zimmers ein Tisch am vorteilhaftesten stehen würde & ich verschiebe zu diesem Zweck eine etwa gleich große Kiste: kann ich nicht sagen, ich rede hier von dem |
Ich kann gewiß
auch das sagen, daß ich mich beim Einsetzen nach || im Einklang mit der Definition nach dem
Zeichen richte; & dasselbe, wenn ich einen Befehl
befolge (wenn ich einen Befehl in Übereinstimmung mit
Worterklärungen befolge). – Wenn ich zur
Abkürzung setze: Moore ≝ M – so ist nur
‚M’ der Name desselben
Gegenstandes wie ‚Moore’, aber doch nicht der Name des Namens
‚Moore’. Die beiden haben einen
Träger, aber der linke ist nicht der Träger des
rechten. – Gut, – was, wenn ich aber
dem linken Zeichen jetzt einen Namen gebe, –
kann der gebraucht werden, & kann er nicht gebraucht werden
wie ‚M’? Geben wir ihm den Namen
‚A’. Wenn ich dann also sage
„zeige auf A, so heißt das soviel wie
„Zeige auf das Wort ‚Moore’”, oder auch „zeige
auf ‚Moore’”. Also ist A =
„Moore”. Also ist A nicht dasselbe
wie M. Ich kann ja auch, so lächerlich das
klingen mag, definieren N = N, also N zum
Stellvertreter seiner selbst nehmen, aber wird es dadurch zu
seinem eigenen Namen? D.h.
eigentlich: Ich kann ein Ding statt seines Stellvertreters
setzen & den Stellvertreter überflüssig
machen; kann ich aber auch das Ding statt seines
Ist es denn also nicht einfach so: das Gleichheitszeichen zwischen zwei Ausdrücken bedeutet, daß die beiden die gleiche Bedeutung haben, d.h. daß die gleichen grammatischen Regeln von ihnen gelten. Aber dies kann man doch vom Namen & Benannten nicht sagen. Auch nicht, wenn beide Zeichen sind. Es ist ja auch die Relation der Bedeutungsgleichheit Wenn ich einem Ding einen Namen gebe, so gebrauche ich damit das Ding nicht als ein Zeichen. – Es gibt wohl Fälle, wo die Ausführung des Befehls, darin besteht, daß sich die Träger an Stelle der Namen setzen || die Träger an Stelle der Namen treten (in Fällen ähnlich dem der Sitzordnung); aber in einem Fall wird A für B eingesetzt, weil die beiden Zeichen gleicher Bedeutung sind, in anderen, weil das eine der Name des andern ist, & in diesem bestimmten Fall das der Übergang vom Satz zur Handlung ist. – Der Wesensunterschied zeigt sich in der Intransitivität der Namengebung. Denken wir uns eine Sprache in der eine Raute ◊ das bedeutet, was in der unsern „Quadrat”; & daß in jener Sprache ein Quadrat □ das Zeichen statt unseres Wortes „Rechteck” ist. Es handelt sich hier nicht um eine Projektion die von der Raute durch das Quadrat zum Rechteck führt. Sondern der Prozeß der Namengebung endet Wenn ich also einen Namen hinweisend definiere & einen zweiten durch ihn || den ersten, so steht dieser zu jenem in anderem Verhältnis || ist dieser zu jenem in anderer Beziehung, als zum Zeichen, das in der hinweisenden Definition gegeben wird || wurde. D.h., dieses letztere ist seinem Gebrauch nach wesentlich von dem Namen verschieden & daher die Verbaldefinition & die hinweisende Definition, ‚Definitionen’ in verschiedenem Sinne des Worts. |
22.
Wie wirkt nun die hinweisende Erklärung? Sie
lehrt den Gebrauch eines Zeichens; & das Merkwürdige ist
nur, daß sie ihn auch für die Fälle zu lehren scheint, in
denen ein Zurückgehen auf das hinweisende Zeichen nicht
möglich ist. Aber geschieht das nicht ,
indem wir, quasi, die in der hinweisenden Definition gelernten Regeln
in bestimmter Weise transformieren? (Wenn
z.B. der Mann, der mir vorgestellt wurde,
abwesend |
Behandle die deutlichen
Fälle in der Philosophie, nicht die undeutlichen.
Diese werden sich lösen, wenn jene gelöst sind.
Die Tendenz mit der Untersuchung eines Satzes da anzufangen, wo seine Anwendung ganz nebelhaft & unsicher ist (Satz der Identität z.B.) || (der Satz der Identität ist ein gutes Beispiel), anstatt diese Fälle vorläufig bei Seite zu lassen & den Satz dort anzugehen, wo wir mit gesundem Menschenverstand über ihn reden können, diese Tendenz ist für die aussichtslose Methode der meisten Menschen, die philosophieren bezeichnend. |
Es klingt wie
eine lächerliche Selbstverständlichkeit wenn ich sage,
daß der, welcher glaubt, die Gesten || Gebärden
seien die primären Zeichen, die allen andern zu Grunde
liegen, außerstande wäre, den gewöhnlichsten
Satz durch Gebärden zu ersetzen. |
Du
sagst, das Hinweisen auf einen roten Gegenstand ist das primäre
Zeichen für ‚rot’. Aber das
Hinweisen auf einen roten Gegenstand ist nicht mehr, als die
bestimmte Handbewegung gegen einen roten Gegenstand, &
ist vorläufig gar kein Zeichen. Wenn Du sagst, Du
|
∣
(Tolstoy: die
Bedeutung (Bedeutsamkeit) eines Gegenstandes liegt
in seiner allgemeinen Verständlichkeit. Das ist
wahr & falsch. Das, was den Gegenstand
|
‚Primär’ müßte
eigentlich heißen: unmißverstehlich. |
(Es gibt
keine Logik für den luftleeren Raum. Insofern es keine
Hypothese in der Logik gibt.) |
Der Zweck des guten
Ausdrucks & des guten Gleichnisses ist, daß es die
augenblickliche Übersicht erlaubt. |
Das Wesentliche
ist nicht, daß das Zeichen für ‚schwarz’
schwarz ist, oder nur dort wo es nicht wie dieses Wort als
Zeichen gebraucht wird. Wird es aber als Vorlage (zum
Nachmalen) gebraucht, dann ist es Unsinn zu sagen, es stehe nur
für ‚schwarz’, wenn es schwarz sei.
Denn in dem |
(Wer heute Philosophie
lehrt, gibt dem Andern Speisen, nicht, || lehrt, ist
wie ein Mensch, || Einer, der dem Andern nicht Speisen
gibt, weil sie ihm schmecken, sondern, um seinen Geschmack zu
ändern.) |
[Über die Einfachheit der
Differentialrechnung.] |
Wenn eine rote Blume da war; wozu brauchte
er das rote Täfelchen || Bildchen sie mit ihm
zu suchen? Denn wenn er die Farbe des Bildchens als
rot anerkannt hat, warum dann nicht gleich die Farbe der
Blume? – Nun wird man sagen: er erkennt ja die
Farbe des Bildes gar nicht als rot an, denn dieser Vorgang
ist nur mit dem farbigen Vorbild möglich. Denn es
heißt die Farbe dieser Blume als rot anerkennen nichts anderes,
als, sie als farbengleich anerkennen mit dem Täfelchen auf
dem das Wort ‚rot’ steht. –
Gewiß, in diesem Sinne kann Und das heißt: es ist ein anderes Spiel, mit einem Täfelchen herumgehen, es an die Gegenstände anzulegen & so die Farbengleichheit zu prüfen, & anderseits: ohne ein solches Muster nach Wörtern in einer Wortsprache handeln. Man denkt nun: Ja, das erste Spiel verstehe ich; das ist ja ganz einfach: Der erste Schritt ist der von einem geschriebenen Wort auf das gleiche geschriebene Wort des Musters; der zweite ist der Übergang von dem Wort auf dem Mustertäfelchen zu der Farbe auf dem gleichen Täfelchen; & der dritte, das Vergleichen von Farben. Jeden Schritt dieses Kalküls gehen wir also auf einer Brücke. (Wir sind geführt, der Schritt ist vorgezeichnet.) Aber wir sind doch hier nur insofern geführt, als wir uns führen lassen. Auf diese Weise kann ich alles, & muß ich nichts eine Führung nennen. – Und am Schluß tu ich, was ich tue & das ist Alles. Aber ein Unterschied bleibt doch: Wenn ich gefragt werde „warum sagst Du gerade von dieser Farbe, sie sei die Farbe rot” || nennst Du gerade diese Farbe ‚rot’”, so würde ich tatsächlich antworten: weil sie auf dem gleichen Täfelchen mit dem |
(Ein Grund läßt sich nur
innerhalb eines Spiels angeben.) |
Die Kette der Gründe
kommt zu einem Ende & zwar dem Ende in diesem Spiel || & zwar dem Ende des Spiels || & zwar (an) der Grenze
des Spiels*. |
(Ich
soll nur der Spiegel sein, in welchem mein Leser sein
eigenes Denken mit allen seinen Unförmigkeiten sieht
& mit dieser Hilfe zurechtrichten
kann.) |
Die einzig würdevolle Aufgabe der
Philosophie ist: den alten Götzen
(der) Philosophie zu
zerstören. D.h., ihre einzige
Verbindung mit Göttern.) |
Die Philosophie nimmt ihre
ganze Emphase von den Sätzen her, die sie
zerstört. || von der Auffassung her, die sie
zerstört. |
Man kann
sagen: die Regeln des Spiels sind die, die gelehrt werden, wenn
das Spiel gelehrt wird. – Nun wird z.B. dem Menschen
der lesen lernt tatsächlich gelehrt:
das ist ein a, das ein e etc.; also,
könnte man sagen, gehören diese Regeln, gehört diese
Tabelle mit zum Spiel. – Aber
erstens: lehrt man denn auch den Gebrauch dieser Tabelle?
& könnte man ihn, anderseits, nicht
lehren? Und, zweitens kann doch das Spiel
wirklich auf zwei verschiedene Arten gespielt
werden. Man kann nun fragen: ist es denn aber auch noch ein Spiel, wenn einer die Buchstaben a b b c sieht & irgend etwas macht? Und wo hört das Spiel auf, & wo fängt es an? Eine Regel kann ich nicht anders geben als durch ihren Ausdruck; denn auch Beispiele, wenn sie Beispiele sein sollen, sind ein Ausdruck für die Regel, wie jeder andre. Wenn ich also sage: Spiel nenne ich es nur, wenn es einer Regel gemäß geschieht & die Regel ist eine Tabelle, so kann ich nicht die Verwendungsart || die Art des Gebrauches Ich könnte auch sagen: Was ist das Schachspiel andres (oder was ist vom Schachspiel andres vorhanden) als Regelverzeichnisse (gesprochen, geschrieben, etc.) & die Beschreibung einer Anzahl von Schachpartien? Es steht mir (danach) natürlich frei, ‚Spielregel’ nur ein Ding von bestimmt festgelegter äußeren Erscheinung zu nennen. Und ich kann von primären & sekundären Zeichen sprechen – in einem bestimmten Spiel, einer bestimmten Sprache. – Im Musterkatalog kann ich diese || die Muster die primären Zeichen & die Nummern die sekundären nennen. Was soll man aber in einem Fall, wie dem, der gesprochenen & geschriebenen Buchstaben sagen? Welches sind hier die primären, welches sind die sekundären Zeichen? Die Idee ist doch die: Sekundär ist ein Zeichen dann, wenn, um mich danach zu richten, ich eine Tabelle brauche, die es mit einem anderen (primären) Zeichen verbindet über welches ich mich erst nach dem sekundären |
Aber ich richte mich ja nun doch nach dem sekundären Zeichen, wenn auch über die Tabelle. So braucht es also nur einen kleinen Trick um die sekundären Zeichen bedeutsam zu machen. Den Übergang mit Hilfe der Tabelle kann ich so darstellen: |
Da14
aber zeigt sich, daß ich ja den Übergang von 1 auf 0 in der
Tabelle mache wie ich ihn ohne Tabelle gemacht hätte;
& die Tabelle garantiert mir die Gleichheit aller
Übergänge nicht, denn sie zwingt mich ja nicht sie immer
gleich zu gebrauchen. Sie ist da, wie ein
Feld, durch das Wege führen, aber ich kann ja auch querfeldein
gehen. Ich mache den Übergang in der Tabelle bei jeder Anwendung Und also richte ich mich doch unmittelbar﹖ nach dem sekundären Zeichen, wenn ich in der Tabelle von diesem sekundären Zeichen gerade dorthin gehe. |
Nun
könnte man freilich die Tabelle durch die ersten
Anwendungen der sekundären Zeichen ersetzen
& man hätte sich in Zukunft nach dieser ersten
Anwendung zu richten. Und das geschieht bis zu einem
gewissen Maße, denn wir erinnern uns vielleicht daran den
Buchstaben a immer so gelesen
zu haben. |
Welcher Art ist denn meine Aussage
über die Tabelle: daß sie mich
nicht zwingt, sie so & so zu gebrauchen?
Und: daß die Anwendung durch die Regel (oder
Tabelle) nicht antizipiert wird? |
Woher nimmt die Betrachtung
ihre Wichtigkeit, da sie doch nur alles
Interessante, d.h. alles Große
& Wichtige, zu zerstören scheint?
(Gleichsam alle Bauwerke, indem sie nur Steinbrocken &
Schutt übrig läßt.) |
Woher nimmt die Betrachtung ihre
Wichtigkeit, || : die uns darauf aufmerksam macht,
daß man eine Tabelle auf mehr als eine Weise brauchen
kann, daß man sich eine Tabelle als Anleitung zum Gebrauch
einer Tabelle herstellen || ausdenken kann, daß man einen Pfeil auch als Zeiger der
Richtung von der Spitze zum Schwanzende auffassen kann, daß ich
eine Vorlage auf mancherlei Weise als Vorlage benützen
kann? |
Der Irrtum über die
primären Zeichen gehört zu denen, die die Philosophie wie
eine Art Physik behandeln; indem sie einfachen Gesetzen
nachspüren (wollen).
Gesetzen im Sinne der Newtonschen Bewegungsgesetze. |
„Verifying by
inspection” ist ein gänzlich irreführender
Ausdruck. Er sagt nämlich, daß zuerst ein
Vorgang, die Inspektion, geschieht, & die wäre mit
dem Schauen durch ein Mikroskop vergleichbar, oder mit dem Vorgang des
Umwendens des Kopfes um etwas zu sehen. Und
daß dann das Sehen notwendig erfolge || erfolgen müsse. Man
könnte von „sehen durch umwenden” oder
„sehen durch schauen” reden.
|
Die Sprache hat
für Alle die gleichen Fallen bereit; das ungeheure Netz
schon angelegter || gut erhaltener || gangbarer Irrwege. Und so sehen
wir also Einen nach dem Andern die gleichen Wege gehn & wissen
schon, wo er jetzt abbiegen wird, wo er geradeaus
fortgehen wird, ohne die Abzweigung zu bemerken, etc.,
etc.. Ich sollte also an allen den Stellen
wo falsche Wege abzweigen Tafeln aufstellen, die über die
gefährlichen Punkte hinweghelfen. |
Was
Eddington über
‚die Richtung der Zeit’ & den
Ent¤ropiesatz sagt, läuft darauf hinaus, daß die
Zeit ihre Richtung umkehren würde, wenn die Menschen eines Tages
anfingen rückwärts zu gehen. Wenn man will, kann
man das freilich so nennen; man muß dann nur darüber
klar sein, daß man damit nichts anderes sagt als, daß die
Menschen ihre Gehrichtung geändert haben. |
Untersuchen wir
die || unsere Sprache auf ihre Regeln
hin. |
Finden wir irgendwo keine
Regeln, nun so ist das das Resultat || Ergebnis. |
Einer teilt die
Menschen ein in Käufer & Verkäufer, &
vergißt, daß Käufer auch Verkäufer sind.
Wenn ich ihn daran erinnere || darauf aufmerksam
mache, wird seine Grammatik
geändert?? |
Wenn ich sagte „ich sah einen
Sessel”, so widerspricht dem (in einem
Sinne) nicht der Satz „es war keiner da”.
Denn den ersten Satz würde ich auch in der Beschreibung eines
Traums verwenden &
niemand würde mir dann mit den Worten des zweiten
widersprechen. Aber die Beschreibung des Traums mit
jenen Worten wirft ein Licht auf den Sinn der Worte
„ich sah”.
In dem Satz „es war ja keiner da” kann das „da” übrigens verschiedene Bedeutung haben. |
(Die meisten Menschen, wenn sie
eine philosophische Untersuchung anstellen sollen, machen es wie
Einer, der äußerst nervös einen Gegenstand in einer Lade
sucht. Er wirft Papiere aus der Lade heraus – das
Gesuchte mag darunter sein – |
Die philosophisch wichtigsten Aspekte
der Dinge || der Sprache sind durch ihre
Einfachheit & Alltäglichkeit verborgen.
(Man kann es nicht bemerken, weil man es immer (offen) vor Augen hat.) |
(Das
eigentliche Verdienst eines
Kopernikus oder Darwin
war nicht die Entdeckung einer wahren Theorie, sondern
eines fruchtbaren neuen Aspekts.) |
23.
Das philosophische Problem ist ein Bewußtsein der Unordnung in
unsern Begriffen, & durch ordnen derselben zu
heben. |
Also war es eine philosophische Frage die A.E.
an ihren Bruder stellte:
„Was ist eigentlich ein ‚Drittel’?
– ein Apfel hat doch vier Teile!”
– Sie konnte sich im Augen
|
Es hat Einer gehört, daß der
Anker eines Schiffes durch eine Dampfmaschine aufgezogen
werde. Er denkt nun || nur an die, welche das
Schiff treibt (& nach welcher es Dampfschiff heißt)
& kann sich, was er gehört hat, nicht
erklären. (Vielleicht fällt ihm die
Schwierigkeit auch erst später ein.) Nun sagen wir
ihm: Nein, es ist nicht diese Dampfmaschine,
sondern außer ihr gibt es noch eine Reihe anderer
auf dem Schiff || an Bord & eine von
diesen hebt den Anker. – War sein Problem ein
philosophisches? War es ein philosophisches, wenn
er von der Existenz anderer Dampfmaschinen auf dem Schiff
gehört hatte & nur daran erinnert werden
mußte? – Ich glaube, seine Unklarheit hat zwei
Teile: Was der Erklärende ihm als Tatsache mitteilt,
hätte der Fragende sehr wohl als Möglichkeit sich
selber ausdenken können, & seine Frage in bestimmter
Form, statt in der des bloßen Zugeständnisses der
Unklarheit vorlegen können. Diesen Teil des
Zweifels hätte er selber beheben können, dagegen konnte ihn
Nachdenken nicht über Die andere Beunruhigung & Unklarheit wird durch die Worte „hier stimmt mir etwas nicht” gekennzeichnet & die Lösung durch (die Worte) „Ach so, Du meinst nicht die Dampfmaschine” oder – für einen andern Fall – „… Du meinst mit Dampfmaschine nicht nur Kolbenmaschinen”. |
Die Arbeit des
Philosophen ist ein Zusammentragen von Erinnerungen zu einem
bestimmten Zweck. |
Eine philosophische Frage ist ähnlich
der, nach der Verfassung einer bestimmten Gesellschaft. –
Und es wäre etwa so, als ob eine Gesellschaft ohne klar
geschriebene Regeln zusammenkäme, aber mit einem Bedürfnis
nach solchen; ja, auch mit einem Instinkt durch welchen sie gewisse
Regeln in ihren Zusammenkünften beobachten || einhalten; nur, daß dies dadurch erschwert wird,
daß nichts hierüber klar ausgesprochen ist &
keine Einrichtung getroffen, die die Regeln deutlich macht || klar hervortreten läßt. So
betrachten sie tatsächlich Einen von ihnen als
den Präsidenten, aber er sitzt nicht oben
|
„Etwas habe ich aber doch
gemeint, als ich das sagte!” Gut, – aber
wie können wir, was es ist, herausbringen? doch wohl nur
dadurch daß er es uns sagt. Wenn wir nicht sein
übriges Verhalten zum Kriterium nehmen sollen, dann also das, was
er uns erklärt. |
24.
Wenn man die Philosophie fragt: „was
ist – z.B. –
Substanz?” so wird um eine Regel gebeten.
Eine allgemeine Regel, die für das Wort
„Substanz” gilt,
d.h.: nach welcher ich zu spielen
entschlossen bin. – Ich will sagen: die
Frage „was ist …” bezieht sich nicht auf
einen besonderen – praktischen – Fall, sondern wir fragen
sie von unserm Schreibtisch aus. Erinnere Dich nur an den
Fall des Gesetzes der Identität um zu sehen, daß es sich
bei der Erledigung einer philosophischen Schwierigkeit nicht um
das Aussprechen neuer Wahrheiten über den
Die Schwierigkeit besteht nur darin, zu verstehen, was uns die Festsetzung einer Regel hilft. Warum die uns beruhigt nachdem wir so schwer beunruhigt waren. Was uns beruhigt ist offenbar daß wir ein System sehen, das diejenigen Gebilde systematisch ausschließt die uns immer beunruhigt haben, mit denen wir nichts anzufangen wußten & die wir doch respektieren zu müssen glaubten. Ist die Festsetzung einer solchen grammatischen Regel in dieser Beziehung nicht wie die Entdeckung einer Erklärung in der Physik? z.B., des Kopernikanischen Systems? Eine Ähnlichkeit ist vorhanden. – Das Seltsame an der philosophischen Beunruhigung & ihrer Lösung möchte scheinen, daß sie ist wie die Qual des Asketen der eine schwere Kugel unter Stöhnen stemmend dastand & den ein Mann erlöste indem er ihm sagte: „laß sie fallen”. Man fragt sich: wenn Dich diese Sätze beunruhigen, Du nichts mit ihnen anzufangen wußtest warum ließest Du sie nicht schon früher fallen, was hat Dich daran gehindert? Nun, ich glaube es war das falsche System dem er sich anbequemen zu müssen glaubte; etc. |
»Ich sagte einmal, es gäbe keine extensionale
Unendlichkeit. Ramsey sagte darauf: „Kann man sich
nicht vorstellen, daß ein Mensch ewig lebt,
d.h. einfach, nie stirbt, & ist das
nicht extensionale Unendlichkeit?” – Ich
kann mir doch gewiß denken daß ein Rad sich dreht &
nie stehen bleibt.« Welches seltsame
Argument: „ich kann es mir denken”!
Überlegen wir (uns) welche
Erfahrung wir als Bestätigung oder Beweis dafür
betrachten würden daß das Rad nie
aufhört || aufhören wird sich zu
drehen. Vergleichen wir diese Erfahrung mit der
welche uns lehrt, daß das Rad einen Tag, ein Jahr, 10 Jahre lang
sich dreht & wir werden einfach den
Unterschied der Grammatik der Aussagen „etwas
… bleibt nie stehn” &
„bleibt in 100 Jahren stehn” erkennen.
Denken wir an die Art der Evidenz welche man für die
Behauptung anführen könnte daß zwei
Himmelskörper sich ohne aufzuhören um einander
drehen. Denken wir an das Gesetz der Trägheit
& daran wie es bestätigt wird. |
»Angenommen
wir wanderten auf einer Geraden in den
Euklidischen
Raum hinaus & begegneten alle 10 m einer
eisernen Kugel
ad inf.« Wieder:
Welcherlei Erfahrung würde ich als
Bestätigung |
»Die
bloß negative Beschreibung des
Nicht-Aufhörens kann keine
positive Unendlichkeit liefern.« Bei dem Ausdruck
„positive Unendlichkeit” dachte ich
natürlich an eine zählbare ( = endliche)
Menge von Dingen (Stühle in diesem Zimmer) &
wollte sagen, das Vorhandensein |
»Angenommen, mein
Gesichtsbild wären zwei gleichgroße rote Kreise auf blauem
Grund: was ist hier in zweifacher Zahl vorhanden
& was einmal? (Und was bedeutet diese Frage
überhaupt?) – Man könnte sagen:
wir haben hier eine Farbe aber zwei
Örtlichkeiten. Es wurde aber auch gesagt, rot
& kreisförmig seien Eigenschaften von zwei
Gegenständen die man Flecke nennen könnte & die in
gewissen räumlichen Beziehungen zu einander stehen.« Die
Erklärung „es sind hier zwei Gegenstände
– Flecke – die …” klingt wie eine
Erklärung der Physik. Wie wenn Einer
fragt „was sind das für rote Kreise die ich dort
sehe” & ich antworte „das sind
zwei rote Laternen,
etc.”. Eine
Erklärung wird aber hier nicht gefordert (unsere
Unbefriedigung durch eine Erklärung lösen zu wollen ist der
Fehler der Metaphysik). Was uns beunruhigt, ist die
Unklarheit über die Grammatik |
25.
Wir können in einem absoluten || in absolutem
Sinne von einem Ort im Gesichtsfeld reden. Denken wir
uns daß ein roter Fleck im Gesichtsfeld verschwindet & in
gänzlich neuer Umgebung wieder auftaucht, so hat es Sinn zu
sagen, er tauche am gleichen Ort oder an einem
andern |
Der
Gesichtsraum ist ein gerichteter Raum in dem es ein Oben &
Unten, Rechts & Links gibt. Und diese
Bestimmungen haben nichts mit der Schwerkraft oder der
rechten & linken Hand zu tun. Sie würden auch
dann ihren Sinn beibehalten, wenn wir unser ganzes Leben lang durch
ein Teleskop zu den Sternen sähen. – Dann
wäre unser Gesichtsfeld dunkel mit einem helleren Kreis
& in diesem Lichtpunkte. || ein hellerer Kreis vom
Dunkel begrenzt & im Kreis Lichtpunkte.
Hätten wir nie || Nehmen
wir an wir hätten nie unsern Körper gesehen,
sondern immer nur dieses Bild, wir könnten also die Lage eines
Sterns nicht mit der unseres Kopfes oder unserer Füße
vergleichen: was zeigt mir dann, daß mein Raum ein Oben
& Unten etc. hat, oder
einfach: daß er gerichtet ist? Es hat Sinn zu
sagen, daß sich das ganze Sternbild im Kreis dreht obwohl
es dadurch seine relative Lage zu nichts im Gesichtsraum
ändert. Oder richtiger ausgedrückt: ich
rede auch dann von einer Drehung im Gesichtsraum, wenn keine relative
Lageänderung in ihm stattfindet.
Dieser Sachverhalt ist nicht vielleicht dadurch wegerklärt, daß man sagt: die Retina hat eben ein Oben, Unten, etc., & so ist es leicht verständlich daß es das analoge im Gesichtsraum || Gesichtsfeld gibt. Vielmehr ist eben das nur eine Darstellung des Sachverhalts auf dem Umweg über die Verhältnisse in der Retina. |
Man könnte
meinen: es verhält sich im Gesichtsfeld immer so, als
sähen wir mit allem Übrigen ein gerichtetes
Koordinatenkreuz, wonach wir alle Richtungen fixieren
können. – Aber auch das ist keine richtige
Darstellung; denn sähen wir wirklich ein solches Kreuz (etwa
mit Pfeilen) so wären wir im Stande,
nicht nur die relativen Richtungen der Objekte dagegen zu
fixieren, sondern auch die Lage des Kreuzes selbst im
Raum anzugeben & zu sagen ob es stille steht, oder sich
dreht || Raum, gleichsam gegen ein ungesehenes im Wesen dieses
Raumes enthaltenes Koordinatensystem. |
Ich kann das Zeichen || die
Figur „V” als
Buchstaben, als Zeichen für „kleiner”,
oder für „größer” sehen auch ohne es mit meinem Körper
zusammen zu sehen.
Vielleicht wird man sagen, daß ich die Lage meines Körpers
fühle ohne ihn zu sehen. Gewiß, & ich sage
eben, daß ‚die gefühlte Lage’ nicht
‚die gesehene Lage’ ist; daher
Die Wörter „oben”, „unten”, „rechts”, „links” haben andere Bedeutung jenachdem sie im Gesichtsraum oder im Gefühlsraum angewandt werden. || im Gesichtsraum, andere im Gefühlsraum. Aber auch das Wort Gefühlsraum ist mehrdeutig. (Definitionen der Wörter „oben”, „unten” etc. durch die Spitze des Buchstaben „V” des Zeichens „kleiner” & „größer” einerseits, & durch Kopf- & Fußschmerzen; anderseits || anderseits durch Kopf- & Fußschmerzen; oder durch Gleichgewichtsgefühle.) |
„Ist ein Feld eines Schachbretts
einfacher als das ganze Schachbrett?” Das
kommt darauf an wie Du das Wort „einfacher”
gebrauchst. Meinst Du damit „aus einer
kleineren Anzahl von Teilen
bestehend”, so sage ich: „Wenn
diese Teile etwa die Atome des Schachbretts sind so ist also das
Feld einfacher als das Schachbrett, – wenn Du aber vom
visuellen Schachbrett sprichst so || von dem sprichst was wir am
Schachbrett sehen so bestehen ja die
Felder nicht aus Teilen, es sei denn daß die
Felder || sie wieder aus kleineren Flecken bestehen
& wenn Du dann den Fleck den einfacheren nennst der
weniger Flecken enthält so ist wieder das Feld
einfacher als das Schachbrett. „Ist aber die
gleichmäßig gefärbte Fläche
Aber können wir nicht sagen: einfach ist was sich nicht teilen läßt? – Wie teilen läßt? Mit dem Messer? Und mit welchem Messer? Beschreibe mir erst die Methode der Teilung die Du erfolglos anwendest, dann werde ich wissen was Du „unteilbar” nennst. Aber vielleicht willst Du sagen: ‚unteilbar’ nenne ich nicht das, was man erfolglos zu teilen versucht, sondern das wovon es sinnlos (unerlaubt) ist zu sagen es bestehe aus Teilen. – Dann ist ‚unteilbar’ eine grammatische Bestimmung. Eine Bestimmung also die Du selbst machen kannst & durch welche Du die Bedeutung, den Gebrauch andrer Wörter festsetzt. Wenn ich etwa sage: ein einfärbiger Fleck ist unteilbar (einfach), denn, wenn ich ihn – z.B. – durch einen Strich teile, so ist er nicht mehr einfärbig – so setze ich damit fest in welcher Bedeutung ich das Wort „teilen” gebrauchen will. Wenn nun gefragt wird: „besteht das Gesichtsbild aus minima visibilia”, so fragen wir zurück: Wie verwendest Du das Wort „aus … bestehen”? Wenn in dem Sinn in welchem ein Schachbrett aus schwarzen & weißen Feldern besteht – nein! – Denn Du willst || wolltest doch nicht leugnen, daß wir einfärbige Flecke sehen |
Wenn wir in der Geometrie sagen, das
regelmäßige Sechseck bestehe aus 6 gleichseitigen
Dreiecken so heißt das, daß es Sinn hat von einem
regelmäßigen Sechseck zu reden das aus 6 gleichseitigen
Dreiecken besteht. Wenn daraufhin gefragt würde
„ist also das Sechseck
einfach oder zusammengesetzt”, so müßte ich
antworten: Bestimme Du selbst wie Du die Wörter
„einfach” &
„zusammengesetzt” gebrauchen willst.
|
„Ist Distanz in der
Struktur des Gesichtsraums schon enthalten, oder scheint es uns
nur so, weil wir gewisse Erscheinungen des Gesichtsbildes mit
gewissen Erfahrungen des Tastsinnes assoziieren welche
letztere erst Distanzen betreffen?” Woher nehmen
wir diese Vermutung? Wir scheinen dergleichen
irgendwo angetroffen zu haben. Denken wir nicht an
folgenden Fall: diese Melodie mißfiele mir
nicht wenn ich sie nicht unter |
Zu sagen, der Punkt B ist
nicht zwischen A & C (die Strecke a nicht
kürzer als b)
Wenn Du sagst der Punkt B erscheint Dir nur zwischen A & C zu liegen so antworte ich: das ist es ja was ich sage, nur gebrauche ich dafür den Ausdruck „er liegt zwischen A & C”. Und wenn Du fragst „scheint es nicht nur so”, so antworte ich: Welche Methode würdest Du denn anwenden um die Antwort auf Deine Frage zu finden. Dann nämlich werde ich verstehen was Dein Verdacht eigentlich betrifft. Wenn Du sagst: ist auf diesem Tisch nicht doch vielleicht etwas was ich nicht sehe, so frage || antworte ich: Wie könnten wir denn das Betreffende finden? Versuche mir doch eine Erfahrung zu beschreiben die Dich sagen lassen würde: „es war doch noch etwas da”. Beschreibe mir die Erfahrung die Dich davon überzeugen würde daß B doch nicht zwischen A & C liegt & ich werde verstehen welcher Art der || dieser wirkliche Sachverhalt im Gegensatz zum scheinbaren ist. Aber Eines ist klar die Erfahrung die Dich das lehrt kann nicht diejenige ändern die ich mit den Worten beschrieb „B liegt zwischen A & C”. Dem Einwurf liegt aber eine falsche Auffassung der logischen Analyse zugrunde. Es handelt sich nicht um ein genaueres Hinsehen (etwa auf A, B & C) & die Entdeckung eines Vorgangs hinter dem gewöhnlich || oberflächlich beobachteten (dies wäre die Untersuchung eines physikalischen oder psychologischen Phänomens) sondern darum Klarheit in der Grammatik der Beschreibung des alten Phänomens zu schaffen || Was wir vermissen ist nicht ein genaueres Hinsehen (etwa auf A, B & C) & die Entdeckung eines Vorgangs hinter dem gewöhnlich || oberflächlich beobachteten (dies wäre die Untersuchung eines physikalischen oder psychologischen Phänomens) sondern die Klarheit in der Grammatik der Beschreibung des alten Phänomens. Denn sähen wir ¤genauer hin so sähen wir eben etwas anderes & hätten nichts für unser Problem gewonnen. Diese Erfahrung nicht eine andere sollte beschrieben werden. |
26.
Zu sagen daß diese Farbe jetzt an einem Ort ist, heißt, diesen
Ort vollständig beschreiben. – Zwei
Farben, Wenn also „f(x)” sagt, x sei jetzt an einem bestimmten Ort, so ist also ‚f(a) ∙ f(b)’ ein Widerspruch. Warum nenne ich wirklich aber ‚f(a) ∙ f(b)’ einen Widerspruch, da doch p ∙ ~p die Form des Widerspruchs ist? Bedeutet || Heißt es einfach, daß das Zeichen „fa ∙ fb” kein Satz ist wie etwa „ffaa” keiner ist? Unsere Schwierigkeit ist nur daß wir doch das Gefühl haben, daß hier ein Sinn vorliegt, wenn auch ein degenerierter (Ramsey). Daß, wenn ich „und” zwischen zwei Sätze || Aussagen setze, ein lebendes Wesen entstehen muß & nicht etwas Totes, wie wenn etwa „a ∙ f” geschrieben hätte. Das ist ein sehr merkwürdiges & sehr tief liegendes Gefühl. Man müßte sich darüber klar werden was die Worte „daß hier ein Sinn vorliegt” sagen wollen. Die Entscheidung darüber, ob „fa ∙ fb” Unsinn ist wie „a ∙ f” könnte man so fällen: Ist p ∙ ~(fa ∙ fb) = p, oder ist die linke Seite dieser Gleichung (& also die Gleichung) Unsinn? – Kann ich nicht entscheiden, wie ich will? Kann ich die Regel die dem allen fa = (fa ∙ ~fb)? d.i.: aus fa folgt ~fb. Ich glaubte, als ich die „Abhandlung” schrieb (& auch später noch), daß fa = fa ∙ ~fb nur möglich wäre, wenn fa das logische Produkt aus irgendeinem andern Satz & ~fb – also fa = p ∙ ~fb – wäre, & war der Meinung fa (z.B. eine Farbenangabe) werde sich in ein solches Produkt zerlegen lassen. Dabei hatte ich keine klare Idee || Vorstellung davon, wie ich mir die Auffindung einer solchen Zerlegung dachte. Oder vielmehr: ich dachte wohl an die Konstruktion eines Zeichens, daß die richtige grammatische Verwendung in jedem Zusammenhang durch seine Beschaffenheit zum Ausdruck brächte (d.h., seine Regeln ganz einfach gestaltete & in gewissem Sinne schon in sich trüge, wie jede übersichtliche Notation); aber ich übersah, daß, wenn diese Umgestaltung des Satzes f(a) in seiner Ersetzung durch ein logisches Produkt bestehen sollte, dann die Faktoren dieses Produkts einen unabhängigen & uns bereits bekannten Sinn haben mußten. |
Als ich dann eine
solche Analyse einer Farbangabe durchführen wollte kam zum
Vorschein || zeigte sich was es war, was ich mir unter der
Analyse vorgestellt hatte. Ich glaubte die Farbangabe als
ein logisches Produkt r ∙ s ∙ t ∙ …
auffassen zu |
Der Satz „an einem Ort hat
zu einer Zeit nur eine Farbe Platz” ist
natürlich ein verkappter Satz der Grammatik.
Seine Verneinung ist kein Widerspruch, widerspricht
aber einer Regel unserer angenommenen Grammatik.
|
Die meisten
Schwierigkeiten || Rätsel, die
das Wesen der Zeit betreffen || uns das Wesen der Zeit aufzugeben scheint, kann man durch die
Betrachtung einer Analogie verstehen die in einer oder der andern Form
den verschiedenen falschen Auffassungen zu Grunde liegt: Es ist der Vorgang im
Projektionsapparat durch den ||
welchen der Film läuft einerseits & auf der
Leinwand anderseits. Wenn man sagt die Zukunft sei bereits präformiert so heißt das offenbar: die Bilder des Filmstreifens welche den zukünftigen Vorgängen auf der Leinwand entsprechen sind bereits vorhanden. Aber für das was ich in einer Stunde tun werde gibt es ja keine |
Ich glaube, was
Goethe eigentlich
hat finden wollen, war keine physiologische sondern eine
psychologische Theorie der Farben. |
Es hat Sinn von einer Färbung zu sagen sie sei
nicht rein rot sondern enthalte einen gelblichen, oder
bläulichen, weißlichen oder schwärzlichen Stich;
es hat aber auch Sinn || und es hat Sinn zu
sagen sie enthalte keinen dieser Stiche sondern sei reines
Rot. Man kann in diesem Sinne von einem reinen blau, gelb,
|
Die
Farbenmischung von der hier die Rede ist bringt der Farbenkreisel
hervor aber auch er nicht, wenn ich ihn nur ruhend & dann in
rascher Drehung sehe. Denn es wäre ja denkbar daß
der Kreisel im ruhenden Zustand halb rot & halb gelb
aussieht || ist & daß er
dann in rascher Drehung (aus welchen
Ursachen immer) grün erscheint. Vielmehr bringt der
Farbenkreisel die Mischung nur insofern zustande, als wir sie optisch
als solche wahrnehmen können || kontrollieren
können. Wenn er sich nämlich nach &
nach schneller & schneller dreht & wir sehen
wie aus rot & gelb orange wird. Wir sind aber
|
Gibt es einen
kleinst sichtbaren Farbunterschied? – Welche
Farben sind hier gemeint? Nennen wir Farbe
das Ergebnis der Mischung von Farbstoffen: dann kann ich
das Experiment machen z.B. zu einer Menge eines
schwarzen || roten
Farbstoffes eine kleine Menge eines gelben beizumischen
& zu sehen || versuchen ob ich
einen Farbunterschied sehe; wenn ja,
so wiederhole ich
den Versuch mit einem kleineren Zusatz des gelben Farbstoffes
& immer so fort bis der Zusatz keinen sichtbaren
Unterschied mehr hervorbringt; das kleinste Quantum welches
noch einen sichtbaren Unterschied hervorbrachte nenne ich mit einem
gewissen Faktor von Ungenauigkeit den
|
Wenn man einen schwarzen
Streifen auf weißem Grund immer dünner & dünner
werden läßt, so kommt man endlich zu dem, was ich einen
visuellen Strich (im Gegensatz zu einer visuellen Linie der
Grenze zwischen zwei Farben || zweier Farben) nennen
will. Der Strich ist kein  einem andern Strich
durchkreuzt wird sehen wir nicht die 4 Eckpunkte in denen sich
die Grenzlinien zweier Streifen schneiden. Es ist
unsinnig von der optischen Unterteilung eines Strichs zu
reden. Ihm entspricht die Erscheinung eines
Fixsterns, die sich zum visuellen Punkt, dem Schnitt zweier
Farbgrenzen, ebenso verhält wie der Strich zur
Farbgrenze. Den optischen Fixstern könnte man also ein
minimum visibile nennen. Aber man kann nun nicht
vielleicht sagen, das Gesichtsfeld bestehe aus solchen
Teilen! Es bestünde nur daraus, wenn wir sie
sähen. Das Bild || visuelle Bild eines Fixsternnebels im Fernrohr besteht aus
ihnen, soweit wir sie unterscheiden können. Denn diese
beiden Ausdrücke heißen eben dasselbe. einem andern Strich
durchkreuzt wird sehen wir nicht die 4 Eckpunkte in denen sich
die Grenzlinien zweier Streifen schneiden. Es ist
unsinnig von der optischen Unterteilung eines Strichs zu
reden. Ihm entspricht die Erscheinung eines
Fixsterns, die sich zum visuellen Punkt, dem Schnitt zweier
Farbgrenzen, ebenso verhält wie der Strich zur
Farbgrenze. Den optischen Fixstern könnte man also ein
minimum visibile nennen. Aber man kann nun nicht
vielleicht sagen, das Gesichtsfeld bestehe aus solchen
Teilen! Es bestünde nur daraus, wenn wir sie
sähen. Das Bild || visuelle Bild eines Fixsternnebels im Fernrohr besteht aus
ihnen, soweit wir sie unterscheiden können. Denn diese
beiden Ausdrücke heißen eben dasselbe. |
Wenn gefragt wird „ist unser Gesichtsfeld
kontinuierlich oder diskontinuierlich”, so müßte man
erst wissen von welcher Kontinuität man redet. Einen
Farbübergang nennen wir
kontinuierlich wenn wir keine Diskontinuität in ihm
sehen. |
27.
«Wenn die Erinnerung kein Sehen in die Vergangenheit ist,
wie wissen wir dann überhaupt, daß sie mit Beziehung auf die
Vergangenheit zu deuten ist? Wir könnten uns dann
einer Begebenheit erinnern & zweifeln, ob wir in unserm
ErinnerungsbildIch kann natürlich sagen: Ich sehe nicht die Vergangenheit, sondern nur ein Bild der Vergangenheit. Aber woher weiß ich, daß es ein Bild der Vergangenheit ist, wenn dies nicht im Wesen des Erinnerungsbildes liegt. Haben wir etwa durch die Erfahrung gelernt, diese Bilder als Bilder der Vergangenheit zu deuten? Aber was hieße dies überhaupt „Vergangenheit”? »Die Daten unseres Gedächtnisses sind geordnet; diese Ordnung nennen wir Gedächtniszeit im Gegensatz zur physikalischen Zeit der Ordnung der Ereignisse in der physikalischen Welt. Gegen den Ausdruck „sehen in die Vergangenheit” sträubt sich unser Gefühl mit Recht; denn er gibt uns ein Bild davon || suggests, daß Einer einen Vorgang in der physikalischen Welt sieht der jetzt gar nicht geschieht sondern schon vorüber ist. Und die Vorgänge welche wir „Vorgänge in der physikalischen Welt”, & die welche wir „Vorgänge in unserer Erinnerung” nennen, sind einander wirklich nur zugeordnet. Denn wir reden von einem Fehlerinnern & das Gedächtnis ist nur eines von den Kriterien dafür, daß etwas in der physikalischen Welt geschehen ist. |
Die
Erinnerungszeit unterscheidet sich unter anderem dadurch von
|
(∃x) φx ∙
~(∃x,y) φx ∙ φy
(∃x,y) φx ∙ φy ∙ ~(∃x,y,z) φx ∙ φy ∙ φz (∃x,y,z) φx ∙ φy ∙ φz ∙ ~(∃x,y,z,u) φx ∙ φy ∙ φz ∙ φu »Wie müßte man es nun anfangen, die allgemeine Form solcher Sätze zu schreiben? Die Frage hat offenbar einen guten Sinn. Denn wenn ich nur einige solcher Sätze als Beispiele hinschreibe, so versteht man, was das Wesentliche dieser Sätze sein soll.« Nun dann ist also die Reihe der Beispiele schon eine Notation; denn das Verstehen dieser Reihe besteht doch in der Verwendung dieses Symbols & darin daß wir es von andern in demselben System unterscheiden z.B. von (∃x) φx (∃x,y,z) φx ∙ φy ∙ φz (∃x,y,z,u,v) φx ∙ φy ∙ φz ∙ φu ∙ φv Warum sollen wir aber nicht das allgemeine (∃ x1 … xn).Π
Ist diese Notation unexakt? Sie selbst soll uns ja nichts bildhaft machen, sondern nur auf die Regeln ihres Gebrauchs, das System in dem sie gebraucht wird, kommt es an. Die Skrupel die ihr anhaften schreiben sich von einem Gedankengang her, der sich mit der Zahl der Urzeichen in dem Kalkül der ‚Principia Mathematica’ beschäftigte. |
Hat die Anzahl wesentlich etwas mit einem
Begriff zu tun? Ich glaube, das kommt darauf hinaus, zu
fragen, ob es einen Sinn hat von einer Anzahl von Gegenständen zu
reden die nicht unter einen Begriff gebracht sind. Hat es
z.B. Sinn zu sagen:
„a, b, & c sind 3
Gegenstände”? – Es ist allerdings ein
Gefühl vorhanden, das uns sagt: Wozu von Begriffen
reden, die Zahl hängt ja nur vom Umfang des Begriffes
ab & wenn der einmal bestimmt ist, so kann der Begriff
sozusagen abtreten. Der Begriff ist
nur eine Methode || nur ein
Mittel || Hilfsmittel um einen
Umfang zu bestimmen, der Umfang aber ist selbständig
& in seinem Wesen unabhängig vom Begriff; denn es kommt
ja auch nicht darauf an, durch welchen Begriff wir den Umfang bestimmt
haben. Das ist das Argument Das Zeichen für den Umfang eines Begriffes ist eine Liste. Man könnte – beiläufig – sagen: die Zahl || Anzahl ist die externe Eigenschaft eines Begriffs & die interne seines Umfangs (der Liste der Gegenstände, die unter ihn fallen). Die Anzahl ist das Schema eines Begriffsumfangs. D.h.: Die Zahlangabe ist, wie Frege sagte, die Aussage über einen Begriff (ein Prädikat). Sie bezieht sich nicht auf einen Begriffsumfang, d.i. auf eine Liste die etwa der Umfang eines Begriffes sein kann. Aber die Zahlangabe über einen Begriff ist ähnlich dem Satz welcher aussagt daß eine bestimmte Liste der Umfang dieses Begriffs sei. Von so einer Liste wird Gebrauch gemacht wenn ich sage: „a, b, c, d fallen unter den Begriff F(x)”. „a, b, c, d” ist die Liste. Natürlich sagt der Satz nichts anderes als Fa ∙ Fb ∙ Fc ∙ Fd; aber er zeigt, mit Hilfe der Liste geschrieben, seine Verwandtschaft Die Arithmetik hat es mit dem Schema ❘ ❘ ❘ ❘ zu tun. – Aber redet denn die Arithmetik von Strichen die ich mit Bleistift auf Papier mache? – Die Arithmetik redet von gar nichts, sie operiert mit den Strichen || redet nicht von den Strichen, sie operiert mit ihnen. |
Ramsey schlug einst
vor, den Satz, daß unendlich viele Gegenstände eine
Funktion fξ befriedigen, durch die
Verneinung sämtlicher Sätze ~(∃x)fx (∃x)fx ∙ ~(∃x,y)fx ∙ fy (∃x,y)fx ∙ fy ∙ ~(∃x,y,z)fx ∙ fy ∙ fz u.s.w. auszudrücken. – Aber diese Verneinung ergäbe die Reihe (∃x)fx, (∃x,y)fx ∙ fy, (∃x,y,z) … etc.. Aber diese Reihe ist wieder ganz überflüssig: denn der zuletzt angeschriebene Satz enthält ja || denn erstens enthält ja der zuletzt angeschriebene Satz alle vorhergehenden & zweitens nützt uns dieser auch nichts da er ja nicht von einer unendlichen Anzahl von Gegenständen handelt. Die Reihe kommt also in Wirklichkeit auf einen Satz „(∃x,y,z
… ad
inf.)fx ∙ fy ∙ fz ∙ …
ad inf.”
hinaus. Und mit diesem Zeichen können wir gar nichts
anfangen, wenn wir nicht seine Grammatik
kennen. Eines aber ist klar: wir haben es nicht
mit einem Zeichen von der Form
„(∃x,y,z)fx ∙ fy ∙ fz”
zu tun; wohl aber mit einem Zeichen dessen Ähnlichkeit
|
»Die Zeit erscheint uns essentiell als
unendliche Möglichkeit. Und zwar, offenbar,
unendlich nach dem, was wir über ihre Struktur wissen. »
D.h. unendlich nach ihrer Grammatik.
|
28.
Wie kann ich wissen, daß
❘ ❘ ❘ ❘ ❘ ❘ ❘ ❘ und ❘ ❘ ❘ ❘ ❘ ❘ ❘ ❘ dasselbe Zeichen sind?
Es genügt doch nicht, daß sie
ähnlich ausschauen. Denn es ist nicht die
ungefähre Gleichheit der Gestalt, was die Identität der
Zeichen ausmachen darf, sondern gerade eben die
Zahlengleichheit. |
Ob es einen Sinn hat zu sagen
“dieser Teil einer roten Fläche (der durch keine
sichtbare Grenze abgegrenzt ist) ist rot” hängt davon
ab, ob es einen absoluten Ort gibt. Denn wenn im
Gesichtsraum von einem absoluten Ort die Rede sein
kann, dann kann ich auch diesem absoluten Ort eine Farbe zuschreiben,
wenn seine Umgebung gleichfärbig ist. |
Die Idee,
Elementarsätze zu konstruieren (wie
dies z.B. Carnap versucht hat) beruht auf einer falschen
Auffassung der logischen Analyse. Sie betrachtet das
Problem dieser Analyse als das, eine
Theorie der Elementarsätze zu finden. Sie
lehnt sich an das an was in der Mechanik || z.B. in der Mechanik
geschieht wenn eine Anzahl von Grundgesetzen gefunden wird aus
denen das ganze System von Sätzen || der
Mechanik folgt || hervorgeht. |
Meine eigene Auffassung war
falsch: teils, weil ich mir über den Sinn der Worte
„in einem Satz ist ein logisches Produkt
versteckt” (& ähnlicher) nicht
klar war, zweitens weil auch ich dachte die logische Analyse
müsse verborgene Dinge an den Tag bringen
¤ |
Wenn ich z.B. sage, ein Fleck ist zugleich
hellrot und dunkelrot, so denke ich dabei,
daß der eine Ton den andern deckt.
Hat es dann aber noch einen Sinn zu sagen, der Fleck habe den unsichtbaren, verdeckten Farbton? Hat es gar einen Sinn, zu sagen, eine vollkommen schwarze Fläche sei weiß, man sähe nur das Weiß nicht, weil es vom Schwarz gedeckt sei? Und warum deckt das Schwarz das Weiß und warum nicht Weiß das Schwarz? Wenn ein Fleck eine sichtbare und eine unsichtbare Farbe hat, so hat er diese Farben jedenfalls in ganz verschiedenem Sinne. |
Man kann den Satz
„dieser Ort ist jetzt rot” (oder „dieser
Kreis ist jetzt rot”,
etc.) einen Elementarsatz nennen,
wenn man damit sagen will
daß er weder eine Wahrheitsfunktion anderer
Sätze ist noch als solche definiert ist. (Ich sehe
hier von Verbindungen p ∙ (q ⌵ ~q)
& Analogem
ab.) Aus „a ist jetzt rot” folgt aber „a ist jetzt nicht grün” & diese || die Elementarsätze in diesem Sinn sind also nicht von einander unabhängig, wie die Elementarsätze in meinem seinerzeit beschriebenen Kalkül von dem ich annahm, der ganze Gebrauch der Sätze müsse sich auf ihn zurückführen lassen; – verleitet durch einen falschen Begriff von diesem ‚Zurückführen’. || von dieser Zurückführung. |
„Rot & grün
gehen nicht zugleich an denselben Ort” heißt nicht,
sie sind tatsächlich nie beisammen, sondern, es
hat keinen Sinn || ist Unsinn zu sagen, sie
seien zugleich |
Eine Mischfarbe,
oder besser Zwischenfarbe, von blau & rot ist dies durch
eine interne Relation zu den Strukturen von blau &
rot. Richtiger ausgedrückt: was wir
‚eine Zwischenfarbe von blau & rot’ (oder
‚blaurot’) nennen, heißt so, wegen einer
Verwandtschaft, die sich in der Grammatik der
Wörter || den Bestimmungen über die
Wörter ‚blau’,
‚rot’, & ‚blaurot’
zeigt. (Der Satz der von einer internen Relation der
Strukturen redet, entspringt schon aus einer
unrichtigen Auffassung || Vorstellung; aus
der, welche in den Begriffen rot, blau,
etc. komplizierte
Strukturen (Mechanismen || Gebäude) sieht; welche wir zunächst
von außen sehen & deren innere Konstruktion die
Analyse offenbaren wird. || zeigen
muß.) Die
Verwandtschaft aber zwischen den || der reinen
Farben & ihrer Zwischenfarbe ist elementarer Art,
d.h., sie besteht nicht darin, daß der Satz
welcher einem Gegenstand die Farbe blaurot zuschreibt
das logische Produkt der
Sätze ist || aus den Sätzen besteht, die ihm
die Farben rot & blau zuschreiben. Und ebenso
ist auch die Verwandtschaft verschiedener Grade
eines rötlichen Blau, z.B., eine
elementare Verwandtschaft. |
Worin liegt der Unterschied zwischen der Zahlangabe
über einen || die sich auf einen Begriff
Kann ich aber nicht eine Variable dadurch bestimmen, daß ich sage, ihre Werte sollen alle Gegenstände sein, die eine bestimmte Funktion befriedigen? – Dadurch bestimme ich ja die Variable nicht, außer wenn ich weiß welche Gegenstände die Funktion befriedigen, d.h., wenn mir diese Gegenstände auch auf andre Weise (etwa durch eine Liste) gegeben sind; & dann wird die Angabe der Funktion überflüssig. Wissen wir nicht, ob ein Gegenstand die Funktion befriedigt, so wissen wir nicht ob er ein Wert der Variablen sein soll & die Grammatik der Variablen ist dann in dieser Beziehung einfach nicht bestimmt. || ausgesprochen. |
Zahlangaben in der Mathematik
(z.B. „die Gleichung
x² = 1 hat 2
Wurzeln”) sind daher von ganz anderer Art als
Zahlangaben außerhalb der Mathematik („auf dem
Tisch liegen 2 Äpfel”). |
Nehmen wir an, es || Es
wäre unsere Aufgabe Figuren verschiedener
Gestalt die sich in einer Ebene I befänden in eine Ebene
II zu projizieren. Wir könnten dann eine
Projektionsmethode bestimmen (etwa die der orthogonalen
|
„Begriff & Gegenstand”
Freges, das ist nichts anderes
als Subjekt & Prädikat. |
Ich sagte: „Eine Schwierigkeit
der Fregeschen Theorie
ist die Allgemeinheit der Worte |
Die Arithmetik
aber kümmert sich aber (wie wir alle sehr wohl
wissen) überhaupt nicht um diese Anwendung. Ihre
Anwendbarkeit sorgt für sich selbst. |
Daher ist alles ängstliche Suchen
nach den Unterschieden
der || zwischen den
Subjekt-Prädikat-Formen, aber auch die Konstruktion von
Funktionen ‚in extension’
(Ramsey), zur
Begründung der Arithmetik Zeitverschwendung. |
Editorial notes
1) Continuation from Ms-111,200.
2) See facsimile; line connecting this remark with the following one.
3) See facsimile; line connecting this remark with the following one.
4) See facsimile; arrow pointing right, probably indicating that the indentation shall be increased.
5) See facsimile; line connecting this remark with the following one.
6) See facsimile; arrow pointing right, probably indicating that the indentation shall be increased.
7) See facsimile; line connecting this remark with the following one.
8) See facsimile; line connecting this remark with the following one.
9) See facsimile; "diesen" is followed by an arrow pointing up.
10) See facsimile; line connecting this remark with the following one.
11) See facsimile; line connecting this remark with the following one.
12) See facsimile; line connecting this remark with the following one.
13) See facsimile; line connecting this remark with the following one.
14) See facsimile; arrow pointing down in the right margin, probably to indicate the scope of the section mark.
15) Continuation in Ms-113,1v.