IV. Philosophische Bemerkungen. |
13.12.
1
Was
zum Wesen der Welt gehört kann die Sprache nicht
sagen || ausdrücken.
Daher kann sie nicht sagen, daß alles fließt. Nur was wir uns auch anders vorstellen könnten, kann die Sprache sagen. |
Daß alles
fließt muß in der Anwendung der Sprache
ausgedrückt sein, und zwar nicht in einer
Anwendungsart, im Gegensatz zu einer anderen, sondern in der
Anwendung. In dem was wir überhaupt die
Anwendung der Sprache nennen. |
Unter Anwendung meine ich
das was die Lautverbindungen oder Striche auf dem Papier
etc. überhaupt zu einer Sprache macht.
In dem Sinn in dem es die Anwendung ist die den Stab mit
Strichen zu einem Maßstab machen. Das
Anlegen der Sprache an die Wirklichkeit. |
Und dieses Anlegen
der Sprache ist die Verifikation der
Sätze. |
Wir sind in Versuchung zu
sagen: „Nur die Erfahrung
des gegenwärtigen Augenblicks hat
Realität”.
Und da muß die erste Antwort sein: „Im Gegensatz wozu?” Jener Satz, daß nur die gegenwärtige Erfahrung Realität hat scheint die letzte Konsequenz des Solipsismus zu enthalten. Und in einem Sinne ist das auch so; nur kann jener Satz || er ebensowenig sagen, wie der Solipsismus. – Denn was zum Wesen der Welt gehört läßt sich eben nicht sagen. Und die Philosophie wenn sie etwas sagen könnte müßte eben das sagen || das Wesen der Welt beschreiben. Das Wesen der Sprache aber ist ein Bild des Wesens der Welt & die Philosophie als Verwalterin der Grammatik kann tatsächlich das Wesen der Welt erfassen nur nicht in Sätzen der Sprache sondern in Regeln für diese Sprache die verhindern daß unsinnige Zeichenverbindungen gebildet werden. || unsinnige Zeichenverbindungen ausschließen. |
Wenn
man sagt die gegenwärtige Erfahrung nur
hat Realität so muß hier schon das Wort
„gegenwärtig” überflüssig sein wie Also etwas was die Sprache nicht mit Recht herausheben kann. |
Wenn jener Satz
einen guten Sinn hat so muß er dazu dienen leer
laufende Räder an unserem Symbolismus
auszuschalten. Er müßte dann sagen: wir
meinen eigentlich nur das, alles andere ist
überflüssiges Beiwerk.
Und dieses Bestreben hat Sinn denn es lassen sich aus unserer Sprache leer laufende Räder entfernen; aber nicht allzuviele. |
Die Gegenwart von der wir
hier reden ist nicht das Bild des Filmstreifens das gerade jetzt
in dem || im
Objektiv der Laterne steht, im Gegensatz
von || zu den Bildern vor & nach
diesem die noch nicht oder schon früher dort waren
sondern das Bild auf |
Es
gibt allerdings sehr interessante ganz allgemeine Sätze von
großer Wichtigkeit, wirkliche Sätze die
also auch eine wirkliche Erfahrung beschreiben, die also auch
hätte anders sein können aber nun einmal so
ist. Z.B. daß ich nur
einen Körper habe. Daß meine Empfindlichkeit nie über diesen Körper hinausreicht (außer in Fällen wo einem ein Glied z.B. ein Arm amputiert wurde & er doch Schmerzen in den Fingern spürt). Das sind merkwürdige & interessante Tatsachen. Nicht in diese Kategorie gehört es aber wenn man sagt daß ich die Zukunft nicht erinnern kann. Denn das heißt nichts & ist wie sein Gegenteil eine Undenkbarkeit. Daß ich immer, wenn ich wach bin, aus meinen Augen sehe ist auch || dagegen eine merkwürdige & interessante Tatsache. Ebenso ist es wichtig daß sich mein Gesichtsbild beinahe immer verändert || mein Gesichtsbild beinahe unausgesetzt in Veränderung begriffen ist. |
„Realismus”,
„Idealismus”, etc. sind schon von vornherein
metaphysische Namen.
D.h. sie deuten darauf hin daß ihre
Anhänger glauben etwas Bestimmtes über
das Wesen der Welt aussagen zu können. |
Wer den
Satz nur die gegenwärtige Erfahrung sei
real bestreiten will (was ebenso falsch ist wie ihn zu
behaupten) wird etwa sagen || fragen ob denn ein Satz wie „Julius Cäsar ging über die
Alpen” nur meinen
gegenwärtigen Geisteszustand der sich
mit dieser Sache beschäftigt, beschreibt. Und die
Antwort ist natürlich:
Nein! Er beschreibt ein Ereignis
das wie wir glauben vor
ca. 2000 Jahren geschehen ist. Wenn
nämlich das Wort „beschreibt” so
aufgefaßt wird wie in dem Satz „der
Satz ‚ich schreibe’ beschreibt was ich gegenwärtig
tue”. Der Name
Julius Cäsar
bezeichnet eine Person, klar! Aber was sagt denn
das alles? |
Alles was, wenn
es geschähe, einen Glauben mit Recht bestärken
würde bestimmt logisch die Natur dieses
Glaubens. D.h. es zeigt etwas
über das logische Wesen dieses Glaubens. |
Der Satz
über Julius Cäsar ist eben ein Gerüst (wie der über jede
andere Person) das die verschiedensten
Verifikationen zuläßt wenn
auch || allerdings nicht alle die es im Falle anderer
z.B. lebender Personen
zuläßt. |
Ist nicht
alles was ich meine daß es
außer zu || zwischen dem Satz &
seiner Verifikation nicht noch ein Mittelglied
gibt, das diese Verifikation
vermittelt? |
14.
Auch
unsere gewöhnliche Sprache muß ja für alle Fälle der
Unsicherheit vorsorgen (provide for) &
wenn wir gegen sie philosophisch etwas einzuwenden haben, so
kann es nur |
Eine der am meisten
irreführenden Darstellungsweisen unserer Sprache ist der Gebrauch
des Wortes „Ich” besonders dort wo sie damit das unmittelbare Erlebnis
darstellt wie in „Ich
sehe einen roten Fleck”. |
Es
wäre nun (philosophisch) lehrreich diese Ausdrucksweise durch eine andere
zu ersetzen in der das unmittelbare Erlebnis ohne ein
persönliches Fürwort || nicht mit Hilfe des
persönlichen Fürworts
dargestellt würde
weil man daraus sehen könnte daß jene Darstellung
der
Sache || den Tatsachen nicht
wesentlich ist. Nicht daß die neue
Darstellung in irgend einem Sinne richtiger wäre als die
alte sondern sie würde nur den Dienst tun klar zu zeigen was das
logisch Wesentliche der Darstellung ist. |
Man
könnte folgende Darstellung adoptieren || annehmen: Wenn ich L.
W. Zahnschmerzen habe
so wird das durch den Satz „Es
sind || gibt Zahnschmerzen” ausgedrückt. Ist aber das der Fall
was Nur die Anwendung unterscheidet wirklich zwischen den Sprachen, aber von ihr abgesehen sind alle Sprachen gleichwertig. – Alle diese Sprachen stellen doch nur ein Einziges Unvergleichliches dar & können nichts anderes darstellen. [Die beiden Betrachtungsweisen müssen zu demselben Ziel || Demselben führen: Die eine daß das Dargestellte nicht eines unter mehreren ist, daß es keines Gegensatzes fähig ist; die andere daß ich den Vorzug meiner Sprache nicht aussprechen kann.] |
15. Die mathematische Frage muß so
exakt sein wie der mathematische Satz.
|
16. Die Frage „Wie kann man das
wissen” ist eine logische
Frage, keine psychologische. |
Wenn ich wissen will was 1 : 3 =
0˙3̇
heißt so ist es eine
relevante Frage: „Wie kann ich das
wissen?” Denn auf dieses
„Wie” kommt der Beweis zur Antwort &
mehr als dieser zeigt weiß ich ja
nicht. |
Es ist klar daß jede
Multiplikation im Dezimalsystem eine Lösung
hat & daß man also jede arithmetische Gleichung von
der Form a × b = c beweisen
oder ihr Gegenteil beweisen kann. Wie sieht nun ein Beweis
dieser Beweisbarkeit aus? Er ist offenbar weiter nichts
als eine Klärung des Symbolismus & das Aufzeigen einer
Induktion die erkennen läßt, welcher Art die Sätze
sind zu denen die Leiter führt. |
Angenommen
nun ich habe zwei (klare) Systeme so kann man nicht nach
einem System fragen, das sie beide umfaßt. Denn
nicht nur kann ich dieses System jetzt nicht suchen,
sondern auch wenn || im Falle sich einmal eines
zeigt das zwei den ersten analoge Systeme umfaßt, sehe
ich daß ich es nie hätte suchen können. |
(Es gibt eben
in der Mathematik nur schwarz & weiß, & nicht das
grau woraus noch das eine oder das andere werden kann.)
|
Suchen kann
man nur in einem System: also gibt es unbedingt etwas
was man nicht suchen kann. |
Welcher Art
ist z.B. die Entdeckung
Sheffers daß man die Wahrheitsfunktionen |
Ich will sagen, daß das
Finden eines Systems zur Lösung von Problemen die man früher
nur einzeln durch
separate Methoden lösen konnte nicht
einfach || bloß die Auffindung
eines bequemeren || einfacheren Vehikels ist sondern
einer ganz neuen Sache die man früher überhaupt nicht
hatte. Die einheitliche Methode ist eben nicht nur
die Methode, der Herstellung eines Gegenstands, der der gleiche ist
wie || auf welche Art immer er
hergestellt wurde. Die Methode ist kein Vehikel das uns an
einen Ort führt der eigentlich
unser Ziel ist, wie immer wir ihn auch erreichen. |
Das heißt: ich glaube, man kann
|
Soll das nicht heißen
daß man in der Mathematik nichts Neues
über einen Gegenstand erfahren kann, weil es dann ein neuer
Gegenstand ist? |
Das kommt
auch darauf hinaus:
Wenn ich einen Satz z.B. der
Zahlentheorie höre aber seinen Beweis nicht kenne so
verstehe ich auch den Satz nicht. Das klingt sehr
paradox. Ich verstehe – heißt das – also den
Satz nicht daß es unendlich viele Primzahlen gibt, ehe ich seinen
sogenannten Beweis nicht kenne. Wenn ich den
Beweis kennenlerne so lerne ich also etwas
ganz Neues kennen nicht nur den Weg zu
einem mir schon bekannten Ziel. Dann ist es aber
unbegreiflich daß ich wenn der Beweis geliefert ist zugebe daß
es der Beweis eben dieses Satzes ist oder die
Induktion die mit diesem Satz gemeint
ist. |
17.
Heißt das nicht auch: Man kann denselben
mathematischen Satz nicht einmal so & einmal anders
beweisen? – Es kann nicht
zwei unabhängige Beweise eines mathematischen Satzes
geben. |
Das Knoten-Auflösen
in der Mathematik: Kann man versuchen einen Knoten
aufzulösen von dem einmal bewiesen wird daß er nicht
auflösbar ist? Die Auflösung der Gleichung
dritten Grades ist gelungen, die Dreiteilung des
Winkels mit Lineal & Zirkel konnte nicht
gelingen; an beiden hat man sich versucht lang ehe man
die Lösung der einen Aufgabe & die Unlösbarkeit der
anderen wußte. |
Denken wir
uns einen scheinbaren Knoten der in Wirklichkeit aus vielen in sich
zurücklaufenden Fadenstücken besteht
& etwa auch aus einigen nicht geschlossenen.
Ich stelle nun jemandem die Aufgabe den Knoten
aufzulösen. Sieht er den Verlauf der Schnurstücke
klar so wird er sagen das ist kein Knoten & man kann ihn
daher nicht auflösen || es gibt daher keine
Auflösung. Sieht er nur ein Gewirr von
Schnüren |
Ich
würde nun sagen von einem eigentlichen Versuch der Lösung
kann man nur insoweit sprechen, als die Struktur des Knotens
klar gesehen ist. Sofern sie nicht klar gesehen wird, ist
alles ein Tappen im Dunklen denn es kann ja sein daß was mir als
Knoten erscheint gar kein Knoten ist; der beste
Beweis dafür daß ich wirklich keine Methode
hatte nach einer Lösung zu suchen. Dieser
Prozeß ist nicht mit dem zu vergleichen
wenn ich z.B. in einem Zimmer methodisch nach
einem Gegenstand suche & eben dadurch herausfinde daß
er gar nicht im Zimmer ist. Denn hier suche ich nach einem
möglichen Sachverhalt & nicht nach einem
unmöglichen. |
Ich will aber nun sagen
daß das Gleichnis mit dem Knoten hinkt da
ich einen Knoten haben kann & ihn Ich sehe nicht ein wie die Zeichen die wir uns selbst gemacht haben um Gewisses auszudrücken uns Probleme aufgeben sollten. |
Es ist eher so als ob ein Knoten oder Knäuel uns nach
& nach gezeigt würde & wir uns (immer) fortlaufend Bilder von ihm machten soweit wir ihn
sehen. Was von dem Knoten uns
noch nicht geoffenbart ist davon haben wir keine Ahnung
& können darüber in keiner Weise
Konjekturen anstellen (indem wir etwa die
Bilder des bekannten Teils einer Untersuchung unterziehen).
|
Was hat man denn damals gefunden als man fand daß es unendlich
viele Primzahlen gibt? Was hat man denn gefunden wie man
eingesehen hat daß es unendlich viele Kardinalzahlen
gibt?! – Ist es nicht ganz analog der
Erkenntnis – wenn es eine ist – daß der
euklidische Raum unendlich ist,
nachdem wir schon längst Sätze über die
Gegenstände Was bedeutet denn eine Untersuchung des Raumes. – Denn jede mathematische Untersuchung ist quasi eine Untersuchung des Raumes. Daß man die Dinge im Raum untersuchen kann ist klar. Aber den Raum! (Geometrie & Grammatik entsprechen einander immer.) Erinnern wir uns daß in der Arithmetik || Mathematik die Zeichen selbst Mathematik machen nicht bloß || Mathematik beschreiben. Die mathematischen Zeichen sind ja wie die Kugeln einer Rechenmaschine. Und die Kugeln sind im Raum & die Ausführung || eine Untersuchung an der Rechenmaschine ist eine Untersuchung des Raumes. |
Ich habe mich
früher darüber gewundert daß unsere Zeichen uns
Probleme stellen sollten oder daß wir durch sie || mit ihnen Entdeckungen über etwas sollten machen
können was wir selbst mit ihnen bezeichnet
haben. Aber wir können an ihnen Entdeckungen machen
weil sie nicht bloße Zeichen sind sondern die Gegenstände
unserer Rechnung. |
Man kann Mathematik nicht
schreiben || beschreiben sondern nur
machen. |
(Eben
darum || daher kann man aber
in der Mathematik nicht mit diesen Zeichen „schmusen”.) |
Ich mache nicht an etwas
Anderem eine Entdeckung & drücke
es dann in ihnen aus (beschreibe es)
sondern ich mache die Entdeckung an ihnen. |
Was nicht vorhergesehen wurde war nicht vorhersehbar;
denn man hatte das System nicht in welchem es vorhergesehen
werden konnte. (Und
vorhergesehen worden wäre.) |
18.
Es
drängt sich immer wieder die Idee auf als wäre die
Mathematik || mathematische Untersuchung eine
Art naturwissenschaftlicher Untersuchung. |
Als könnte man sagen
„wir hatten diesen Zusammenhang
früher nicht, jetzt kennen wir ihn”,
oder „wir sehen hier noch keinen
Zusammenhang aber suchen einen”.
|
Angenommen ich wollte ein regelmäßiges
5-Eck konstruieren, wüßte
aber nicht, wie, & würde nun herumprobieren &
käme endlich, durch Zufall, auf die richtige Konstruktion:
haben wir hier nicht wirklich den Fall des
Knotens der durch Probieren aufgelöst wurde? |
Soll ich sagen:
Nein, denn wenn ich diese Konstruktion nicht verstehe so ist sie
für mich noch gar nicht die 5-Eck
Konstruktion. |
Ich kann auf dem Papier mit Strichen
& Buchstaben experimentieren aber nicht mit dem Sinn der
Zeichen. |
Ich kann schon
durch Zufall die Auflösung der Gleichungen
2ten Grades hinschreiben aber nicht sie
durch Zufall verstehen. |
In dem was
ich verstehe verschwindet dann die Art wie ich
dazugekommen bin. Ich verstehe dann was ich
verstehe. D.h., der Zufall kann
sich nur auf ein Äußerliches beziehen wie etwa wenn man
sagt: „das habe ich
herausgefunden nachdem ich starken Kaffee getrunken
hatte”. Der Kaffee ist
in meiner Entdeckung || dem
was ich entdeckt habe nicht mehr enthalten. |
Die Entdeckung des Zusammenhangs zweier Systeme war nicht in einem
Raum mit jenen beiden Systemen & wäre sie in
einem || demselben Raum gewesen, so wäre es
keine Entdeckung gewesen (sondern die Lösung einer
Schulaufgabe). |
Wo jetzt ein Zusammenhang
bekannt ist der früher nicht bekannt war dort war früher
nicht eine offene Stelle eine
Unvollständigkeit die jetzt ausgefüllt
ist. – (Man konnte damals nicht sagen „soweit kenne ich die Sache, von hier an ist sie
mir nicht mehr bekannt”). |
Ich habe also
gesagt: Die Mathematik hat keine offenen
Stellen. (Ich weiß daß das der gewöhnlichen
Auffassung widerspricht.) || Das widerspricht
der gewöhnlichen Auffassung. |
Es ist begreiflich,
daß ich die Entdeckung machen kann daß etwas im
Raume da steht wo ich es nicht erwartet habe; aber wie kann ich
Entdeckungen über den
Raum selbst machen? Und ein Beweis aus der
Zahlentheorie & die Konstruktion des
5-Ecks scheinen Entdeckungen über
den Raum zu sein. |
In der Mathematik gibt es
kein „noch nicht” und kein „bis auf
Weiteres”. (Außer in dem trivialen Sinne,
daß man noch nicht 1000-stellige Zahlen mit
einander multipliziert hat.) |
19.
Die
Induktion hat manches mit der
Multiplizität einer (natürlich
endlichen) Klasse gemeinsam. Anderseits ist sie doch
keine & nun |
Wenn ich, z.B., sage „wenn ich eine Windung kenne, so kenne ich die
ganze Spirale” so bedeutet das
eigentlich: Wenn ich das Gesetz der Spirale kenne so ist
das in vieler Beziehung analog dem Fall in dem ich eine
Gesamtheit von Windungen kenne –
natürlich aber eine „endliche” Gesamtheit denn etwas anderes gibt es ja nicht –.
Man kann nun nicht sagen: ja einer endlichen Gesamtheit ist
es || sie in vieler Hinsicht analog aber doch nicht ganz
analog dagegen einer unendlichen ganz, sondern daß die Induktion
einer endlichen Gesamtheit nicht
ganz analog ist || sich nicht ganz analog
benimmt, ist eben alles was wir sagen können.
|
Die Mathematik kann nicht unvollständig sein; wie ein
Sinn nicht unvollständig sein kann. Was ich
verstehen kann muß ich ganz verstehen. Das hängt
damit zusammen daß meine Sprache so wie sie ist in Ordnung ist
& daß die logische Analyse um zu vollkommener Klarheit zu
gelangen nichts zu dem vorhandenen Sinn meiner Sätze
dazufügen muß. So daß
der unklarst scheinende Satz bei || in || nach der Analyse seinen bisherigen Inhalt
unberührt behält |
Muß es aber denn nicht
eine Frage sein ob es eine endliche Zahl von || aller Primzahlen gibt oder nicht? Wenn man
einmal überhaupt zu diesem Begriff gekommen ist. Denn
es scheint doch daß ich wenn mir der Begriff der Primzahl
gegeben ist unmittelbar fragen kann „wie
viele Primzahlen gibt es?”. Wie ich wenn mir der Begriff Mensch in diesem
Zimmer gegeben ist ohne weiteres die Frage bilden kann
„wie viele Menschen sind in diesem
Zimmer?”. |
Wenn diese
Analogie mich irre leitet so kann es nur dadurch sein, daß der
„Begriff Primzahl” mir in ganz anderer Weise gegeben ist als ein eigentlicher
Begriff. Denn wie ist denn der
richtige || strenge Ausdruck
für den Satz „7 ist eine
Primzahl”? Offenbar ist es
nur der daß die Division der Zahl 7 durch kleinere
Zahlen einen Rest ergibt. Einen anderen (außer einen
analogen) Ausdruck kann es dafür nicht geben da wir
Mathematik nicht beschreiben sondern nur treiben können.
(Und schon das vernichtet jede „Mengenlehre”.) |
Das heißt,
Wenn ich also einmal die allgemeine
Form der Primzahl hinschreiben |
Denn da wir in der gewöhnlichen
Sprache das Wort Primzahl haben konnten noch ehe der strenge
Ausdruck vorhanden war der quasi eine Zahlangabe zuläßt so
konnte man auch vorher schon die Frage fälschlich bilden,
wie viele Primzahlen es gäbe.
Dadurch gewinnt es den Anschein als sei das Problem früher
schon vorhanden gewesen & jetzt gelöst
worden. Die Wortsprache schien diese Frage nach wie vor
zuzulassen & das erzeugte den Schein als sei ein
echtes Problem vorhanden gewesen & eine echte Lösung
((des
Problems)
erfolgt. In der exakten Sprache
dagegen hatte man ursprünglich nichts, wovon man nach der Anzahl
hätte fragen können & später einen Ausdruck an
dem man die Mannigfaltigkeit unmittelbar ablesen konnte.
|
Ich will also sagen: Nur in unserer Wortsprache
(die hier zu einem Mißverständnis der
logischen Form führt) gibt es in der
Mathematik |
Mein Leben ist sehr seltsam! Ich
weiß nicht wie hell oder wie finster es
ist. Es ist gleichsam halb hell, halb dunkel.
Respi
erklärte mir vor ein paar Tagen,
daß sie mich nicht mehr küssen werde
weil ihr
Gefühl zu mir || für mich nicht derart sei
daß es dieses Zeichen rechtfertige.
Ich bin nun davon schmerzlich getroffen und dabei
doch fröhlich. Denn es kommt doch eigentlich
darauf an daß mich der Geist
nicht verläßt.
Denn wenn der Geist mich nicht
verläßt, dann ist nichts was geschieht
schmutzig & kleinlich. Ich aber
muß viel auf den Zehenspitzen stehen wenn ich
mich || mein Herz ober Wasser halten
will. || nicht untergehen will. |
Es
scheint mir daß die Idee der
Widerspruchsfreiheit in den Axiomen der
Mathematik die jetzt so viel in den Köpfen der Mathematiker
herumspukt auf einem
Mißverständnis
beruht. |
Das
hängt (auch) damit zusammen daß
sie || die
Mathematiker die Axiome || sie
die mathematischen
Axiome || die
Mathematiker die
Axiome nicht für das |
Wenn in der Syntax ein
Widerspruch ist so
heißt das, daß wir unseren Zeichen keine feste
Bedeutung gegeben haben da eine
Zeichenverbindung sowohl erlaubt als auch
verboten ist.
|
20. Eine Frage nach der
Beweisbarkeit gibt es nicht und in sofern auch keinen Beweis
der Beweisbarkeit. Der sogenannte Beweis der Beweisbarkeit
ist eine Induktion deren Erkenntnis die Erkenntnis eines neuen
Systems ist. |
Ein Beweis der Widerspruchsfreiheit
kann nicht wesentlich sein für die Anwendung der Axiome.
|
Ein Postulat gibt es nur für die Ausdrucksweise.
Die „Axiome” sind Postulate der Ausdrucksweise. |
Wenn ich jemand die Anweisung
gebe „gehen Sie
geradeaus dann biegen Sie in die erste Gasse links
die N-Gasse ein” & die
N-Gasse ist die zweite Gasse & nicht die erste so ist
meine Anweisung widerspruchsvoll. Ein solcher Widerspruch
ist auch in den Postulaten der Geometrie denkbar wenn ich
z.B. zu den euklidischen Axiomen noch das weitere Axiom setze, daß
die Winkelsumme im ▵ 200˚ sein
soll. Der Russellsche Widerspruch & alle analogen sind
nicht von dieser Art. Was nun aber ein solcher
Widerspruch der ersten Art bedeutet müßte man am besten in der
Arithmetik sehen, denn hier macht es die Form der Gleichung klarer
daß wir es mit Zeichenregeln zu tun haben. |
21.
Wie kommt es
daß ich überhaupt sagen will, daß alles
fließt? Will ich damit nur sagen daß meine |
Was ich eigentlich zu meinen scheine ist
daß die Gegenwart unaufhörlich entschwindet &
gleichsam nicht zu fassen ist. (Aber das kann man
natürlich nicht sagen.)
Daß ich das sagen will,
muß auf irgend einem Mißverständnis beruhen.
Dieses die Gegenwart einfangen Wollen muß auf einem
Mißverständnis
beruhen. Und zwar darauf daß man auf
die unmittelbare Erfahrung eine Kategorie anwenden will
die nur in der Sprache der physikalischen Welt anzuwenden ist.
|
Was wir hier betrachten ist eigentlich die
Möglichkeit der Bewegung. Also die
logische Form der Bewegung. |
Dabei kommt es uns vor als
wäre die Erinnerung eine etwas
sekundäre Art der Erfahrung im
Vergleich zur Erfahrung des Gegenwärtigen. Wir sagen
„daran können wir uns nur
erinnern”! Als wäre in
einem primären Sinn die Erinnerung ein etwas schwaches
& unsicheres Bild dessen was wir
ursprünglich in |
In der physikalischen Sprache stimmt
das: ich sage „ich kann mich
nur undeutlich an dieses Haus
erinnern.“ |
Und warum es nicht dabei sein Bewenden haben
lassen? Denn diese Ausdrucksweise sagt ja doch
alles was wir sagen wollen & was sich sagen
läßt. Aber wir
wollen sagen daß es sich auch noch anders sagen
läßt; & das ist wichtig. |
Kann man
sagen, daß in dieser anderen Ausdrucksweise der Nachdruck gleichsam
auf etwas anderes gelegt wird. Die Worte „scheinen”, „Irrtum”,
etc. etc. haben
nämlich eine gewisse Gefühlsbetonung die den
Phänomenen nicht wesentlich sind || ist. Sie hängen || hängt irgendwie mit dem Willen
& nicht bloß mit der
Erkenntnis zusammen. |
Wir reden zum Beispiel von
einer Optischen Täuschung & verbinden mit diesem
Ausdruck die Idee eines Fehlers obwohl ja nicht wesentlich ein
Fehler vorliegt & wäre im Leben für
gewöhnlich das Aussehen wichtiger als die Resultate der
Messung so würde auch die Sprache zu diesen Phänomenen eine
andere Einstellung einnehmen || zeigen. Wenn es sich z.B.
meistens um |
Es gibt nicht wie ich
früher glaubte – eine primäre Sprache im
Gegensatz zu unserer
gewöhnlichen der „sekundären”. Aber in sofern könnte man im
Gegensatz zu unserer Sprache von einer
primären reden als in dieser keine
Bevorzugung gewisser Phänomene vor anderen ausgedrückt
sein dürfte; sie müßte so zu sagen absolut
sachlich sein. |
Wie funktioniert der indirekte Beweis
z.B. in der Geometrie. Das
Seltsamste an ihm ist daß man sich manchmal
bemüht für ihn eine ungeometrische Zeichnung zu
machen (was das exakte Analogon zu einem
unlogischen Satz ist).
Aber natürlich rührt das nur von einer falschen
Auffassung || Deutung des Beweises
her. Es ist z.B. komisch wenn man
sagt „angenommen eine || die Gerade g hatte vom Punkt P an zwei
Fortsetzungen”. Aber so etwas
braucht 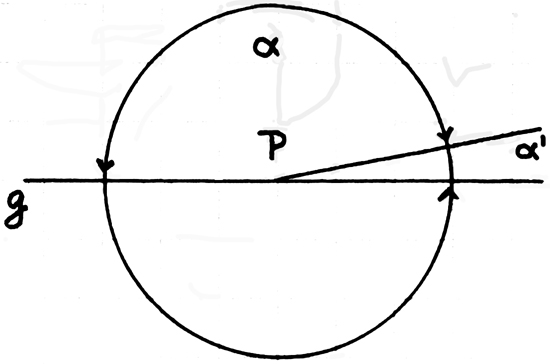 man ja gar nicht
annehmen. Die Beweise in der Geometrie, in der
Mathematik, können im eigentlichen Sinn nicht indirekt sein
weil man nicht das Gegenteil von einem geometrischen
Satz annehmen kann solange man nämlich an einer
bestimmten Geometrie festhält. Jener Beweis
zeigt einfach daß die Bogenstücke man ja gar nicht
annehmen. Die Beweise in der Geometrie, in der
Mathematik, können im eigentlichen Sinn nicht indirekt sein
weil man nicht das Gegenteil von einem geometrischen
Satz annehmen kann solange man nämlich an einer
bestimmten Geometrie festhält. Jener Beweis
zeigt einfach daß die Bogenstücke |
22.
Ist die Zeit in
der die Erlebnisse des Gesichtsraums vor sich gehen ohne Tonerlebnisse
denkbar? Es scheint ja! & doch wie seltsam
daß etwas eine Form sollte haben können die auch ohne eben
diesen Inhalt denkbar wäre. Oder lernt der
dem das Gehör geschenkt würde, damit auch eine
neue Zeit kennen? Die alten || hergebrachten Fragen taugen zur logischen Untersuchung der Phänomene nicht. Diese schaffen sich ihre eigenen Fragen oder vielmehr, geben ihre eigenen (Arten von) Antworten. |
Wie weit wird
die Logik von der || durch die Unsicherheit
über die Analyse der Elementarsätze
unsicher? – Was steht fest? |
Was ist der Unterschied zwischen der
logischen Multiplizität einer Erklärung der
Erscheinungen durch die Naturwissenschaft & der
logischen Multiplizität
einer Beschreibung? |
Wäre
z.B. ein gleichmäßig tickendes
Geräusch in der Physik darzustellen so würde dazu die
Multiplizität des Bildes
|–––|–––|–––|–––|–––|– →
genügen, aber hier handelt es sich nicht um die
logische Multiplizität des Tones sondern um die der
regelmäßig || Regelmäßigkeit
der beobachteten |
23.
Es
ist so: die grammatischen Regeln über „und”, „nicht”, „oder”
etc. sind eben nicht damit
erschöpft was ich in der Abhandlung
geschrieben || gesagt habe sondern es
gibt Regeln über die Wahrheitsfunktionen die auch von dem
elementaren Teil des Satzes handeln. |
Unserer Grammatik
fehlt es vor allem an Übersichtlichkeit. |
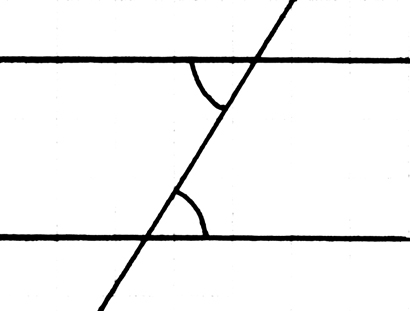
Wenn ich sage „die obere Strecke
|
Es ist merkwürdig,
daß wir das Gefühl daß das Phänomen uns
entschlüpft, den ständigen Fluß der Erscheinung, im
gewöhnlichen Leben nie spüren, sondern
erst dann wenn wir philosophieren.
Das deutet darauf hin daß es sich hier um einen Gedanken handelt
der uns durch eine falsche Verwendung unserer (gewöhnlichen) Sprache suggeriert wird. |
Das Gefühl ist
nämlich daß die Gegenwart in die Vergangenheit schwindet ohne
daß wir es hindern können. Und hier bedienen
wir uns doch offenbar des Bildes eines Streifens der sich
unaufhörlich an uns vorbei bewegt
& den wir nicht aufhalten können.
Aber es ist natürlich ebenso klar daß das Bild
mißbraucht ist. Daß man also
nicht sagen kann „die Zeit
fließt” wenn |
Vielleicht
⋎beruht diese ganze Schwierigkeit
¤ auf der Übertragung des Zeitbegriffs der
physikalischen Zeit auf den Verlauf der unmittelbaren
Erlebnisse. Es ist eine Verwechselung der Zeit
des Filmstreifens mit der Zeit des
Leinwandbildes. Denn „die Zeit” hat eine andere
Bedeutung wenn wir das Gedächtnis als die Quelle der Zeit
auffassen als || und wenn wir es als ein
aufbewahrtes Bild des vergangenen Ereignisses
auffassen. Wenn wir das Gedächtnis als ein Bild auffassen dann ist es ein Bild eines physikalischen Ereignisses. Das Bild verblaßt & ich merke sein Verblassen wenn ich es mit anderen Zeugnissen des Vergangenen vergleiche. Hier ist das Gedächtnis nicht Quelle der Zeit sondern mehr oder weniger gute Aufbewahrerin dessen was „wirklich” gewesen ist & dieses war eben etwas wovon wir auch andere Kunde haben können, ein physikalisches Ereignis. Ganz anders ist es wenn wir nun das Gedächtnis als Quelle der Zeit betrachten. Es ist hier kein Bild (mehr) & es kann auch nicht verblassen – in dem Sinne in dem || wie ein Bild verblaßt so daß es seinen Gegenstand immer weniger & weniger getreu darstellt. Die beiden || Beide Ausdrucksweisen sind in Ordnung || legitim & gleichberechtigt aber nicht mit einander vermischbar. Es ist ja klar |
24. Die neue Auffassung der
Elementarsätze bringt es mit sich daß ein Satz der
Wahrheit mehr oder weniger nahe sein kann. (Da
Rot näher an Orange als an Blau ist & 2 m
näher an 201 cm als an
3 m.) |
Die Sätze werden in
diesem Falle noch ähnlicher Maßstäben, als ich
früher geglaubt habe. – Das Stimmen
eines Maßes schließt automatisch alle anderen
aus. Ich sage automatisch: Wie
die || alle Teilstriche auf
einem Stab sind so gehören die Sätze die den
Teilstrichen entsprechen zusammen & man kann nicht mit einem
von ihnen messen ohne zugleich auch mit allen anderen von
ihnen zu messen. – Ich lege nicht den Satz
als Maßstab an die Wirklichkeit an sondern das System von
Sätzen. |
Man könnte nun die
Regel aufstellen daß derselbe Maßstab in einem Satz nur
einmal angelegt werden darf. Oder daß die
Teile die verschiedenen Applizierungen
des selben Maßstabs entsprechen
zusammengefaßt werden müssen. |
Hat nun
z.B. die Frage einen Sinn
„gibt es Sätze die einzeln, in
keinem System, stehen?”?
|
Ich
glaube die Frage kann keinen Sinn haben.
Angenommen es gäbe keinen solchen Satz wie könnte man
ihn dann auch nur denken? Also kann man auch nicht nach
ihm fragen, auch nicht wenn es ihn gibt. |
25.
Wenn ich etwas
über Verifikation & Grammatik sage
so bin ich mir so klar darüber wie über den Sinn des Satzes
„draußen regnet es”; nicht klarer. Aber klarer kann
ich auch über nichts sein. |
„Ich habe keine
Magenschmerzen” ist
vergleichbar dem Satz „diese Äpfel kosten
nichts”. Sie kosten
nämlich kein Geld aber nicht
keinen Schnee oder keine Mühe. Der Nullpunkt ist der
Nullpunkt auf einer Skala. Und da mir kein Punkt
des Maßstabes gegeben sein kann ohne den Maßstab, so
auch nicht sein Nullpunkt. „Ich habe keine Schmerzen” bezeichnet doch nicht einen Zustand in dem von
Schmerzen nicht die Rede ist. Sondern es ist von Schmerzen
die Rede. Der Satz setzt die Fähigkeit voraus
Schmerzen zu fühlen & das kann keine „physiologische Fähigkeit” sein – denn wie wüßte man sonst
wozu es die Fähigkeit ist – sondern eine logische
Möglichkeit. – Ich beschreibe
meinen gegenwärtigen Zustand durch die Allusion auf etwas
|
Ich beschreibe
eine Tatsache doch nicht dadurch daß ich
das erwähne was mit ihr nichts zu tun hat &
konstatiere daß es mit ihr || einen
Sachverhalt doch nicht dadurch daß ich das erwähne
was mit ihm nichts zu tun hat &
konstatiere daß es mit ihm nichts zu
tun hat. Das wäre keine negative Beschreibung.
|
„Der Sinn liegt
in der Wiedererkennbarkeit” aber dies ist
eine logische Möglichkeit. Ich muß mich
mit meinen Gedanken ﹖ in dem Raum
befinden in dem das zu Erwartende
liegt. |
Die Wahrheit hat einen Granitgrund, bis zu dem kann man kommen
& weiter |
Ich
bin ein Schwein & dabei bin ich doch nicht
unglücklich. Ich bin in der Gefahr noch seichter zu
werden. Möge Gott es
verhüten! |
26.
Wir können
von zwei verschiedenen unendlichen Möglichkeiten
sprechen aber hier hat das Wort verschieden einen
anderen Sinn als im Falle verschiedener endlicher
Möglichkeiten. Und das zeigt sich auch daran daß
diese Verschiedenheit eine andere Multiplizität hat.
|
Es hat einen
klaren & einfachen Sinn zu sagen
daß zwei (natürlich
endliche)
Dezimalbrüche sich von einander unterscheiden || verschieden sind. Es hat einen ganz
anderen (quasi abgeleiteten) Sinn zu sagen
die unendlichen Möglichkeiten der beiden seien
verschieden. & || Und diese Verschiedenheit hat eine andere
Multiplizität als jene. |
Was heißt der Satz „A ist mein Ahne”? D.h.: wie kann ich
wissen daß jemand mein Ahne ist? Wenn dadurch daß
ich ihn unter meinen Ahnen suche so heißt das unter einer endlichen
Anzahl. Oder die Verifikation
wäre daß er eine bestimmte Eigenschaft hat die man bei meinem
Vater, Großvater etc. wahrgenommen hat
dann sagt der Satz auch nicht mehr als:
A hat diese Eigenschaft.
Wie wäre es aber wenn unsre Ahnen |
Es ist z.B. wichtig daß
bei || in dem Satz
„ein roter Fleck
befindet sich nahe an der Grenze des
Gesichtsfeldes” das „nahe an” eine
andere Bedeutung hat als in einem Satz „der rote Fleck im Gesichtsfeld befindet sich
nahe an dem braunen Fleck”.
Das Wort Grenze in dem vorigen Satz hat ferners eine
andere Bedeutung – & ist eine andere
Wortart – als in dem Satz „die
Grenze zwischen Rot & Blau im
Gesichtsfeld ist ein Kreis”.
|
Welchen
Sinn hat es zu sagen: unser Gesichtsbild ist an den Rändern
undeutlicher als gegen die Mitte? Wenn
wir hier nämlich nicht davon reden Eines der klarsten Beispiele der Verwechslung zwischen physikalischer & phänomenologischer Sprache ist das Bild welches Mach von seinem Gesichtsfeld entworfen hat & worin die sogenannte Undeutlichkeit || Verschwommenheit der Gebilde gegen den Rand des Gesichtsfeldes durch eine Verschwommenheit (in ganz anderem Sinne) der Zeichnung wiedergegeben wurde. Nein, ein sichtbares Bild des Gesichtsbildes || Gesichtsbild des Gesichtsbildes kann man nicht machen. Kann ich also sagen, daß die Farbflecken in der Nähe des Randes des Gesichtsfeldes keine scharfen Konturen mehr haben: Sind denn Konturen dort denkbar? Wie aber ist so eine Frage überhaupt möglich? Ich glaube es ist klar daß die || jene Undeutlichkeit eine interne Eigenschaft des Gesichtsraumes ist. Hat, z.B., das Wort „Farbe” im Grunde eine andere Bedeutung wenn es sich auf Gebilde in der Randnähe bezieht? Was kann die Untersuchung über den Gesichtsraum zu Tage fördern? Die Grenzenlosigkeit des Gesichtsraums ist ohne jene „Verschwommenheit” nicht denkbar || vorstellbar. |
Es fragt sich: Welche Unterschiede gibt es im
Gesichtsraum? Kann man darüber aus der Koordination,
z.B., des Tastraums mit dem Gesichtsraum etwas
|
Die
Tatsache daß man ein physikalisches 100-Eck als Kreis
sieht, es nicht von einem physikalischen Kreis unterscheiden kann,
sagt gar nichts über die Möglichkeit ein
100-Eck zu sehen. |
Daß es mir nicht
gelingt einen physikalischen Körper zu finden, der das
Gesichtsbild eines Hundertecks gibt ist nicht von logischer
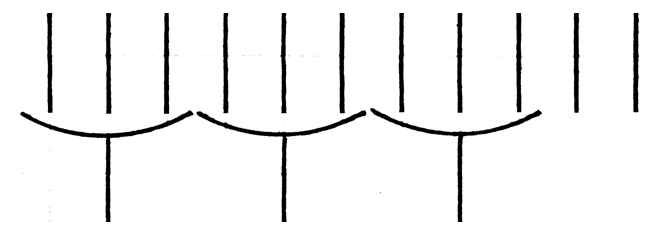
Bedeutung. Es fragt sich: Hat es Sinn
von einem Gesichtshunderteck zu reden. Oder:
Hat es Sinn von zugleich gesehenen dreißig
Strichen nebeneinander ❘ ❘ ❘ ❘ ❘ ❘ ❘ ❘ ❘ ❘ ❘ ❘ ❘ ❘ ❘ ❘ ❘ ❘ ❘ ❘ ❘ ❘ ❘ ❘ ❘ ❘ ❘ ❘ ❘ ❘
zu reden. Ich glaube,
nein! |
Der Vorgang ist gar nicht
so daß man zuerst ein 3-Eck, dann ein
4-Eck, 5-Eck
etc. bis etwa || z.B. zum 50-Eck sieht
& dann der Kreis kommt; sondern man sieht ein
3-Eck ein 4-Eck
etc. bis vielleicht zum
8-Eck dann sieht man nur mehr Viel-Ecke mit
mehr oder weniger langen Seiten.
(kann aber z.B. ein 20-Eck von einem
21-Eck nicht ¤ mehr
unterscheiden.) Die Seiten werden kleiner
dann beginnt ein Fluktuieren zum Kreis hin & dann kommt der
Kreis. |
Daß eine physikalische Gerade als Tangente
 das der
euklidischen Tangente entsprechende
Bild erzeugen. Tatsächlich aber ist
ein solches Bild undenkbar. das der
euklidischen Tangente entsprechende
Bild erzeugen. Tatsächlich aber ist
ein solches Bild undenkbar. |
27.
Was heißt der Satz: „wir
sehen nie einen genauen Kreis”? Was ist das Kriterium der Genauigkeit?
Könnte ich nicht auch sehr wohl sagen „ich sehe vielleicht einen genauen Kreis kann es
aber nie wissen”? Das alles
hat nur dann Sinn wenn man festgelegt hat in welchem Fall man eine
Messung genauer nennt als eine andere. Der Begriff des
Kreises setzt nun – glaube ich – einen Begriff der „größeren Genauigkeit” voraus der eine unendliche Möglichkeit der Steigerung
hat. Und man kann sagen der Begriff des Kreises
ist der Begriff der unendlichen
Steigerungsmöglichkeit der Genauigkeit.
Diese unendliche Steigerungsfähigkeit wäre
ein Postulat der Ausdrucksweise. Es muß
dann natürlich in jedem Fall klar sein was ich als
eine Vergrößerung der Genauigkeit auffassen
würde. |
Das heißt natürlich nichts, zu sagen, der Kreis sei nur
ein Ideal dem sich |
Es scheint mir der Applikation der
euklidischen Geometrie wesentlich
daß wir von einem ungenauen Kreis, einer
ungenauen Kugel etc. sprechen.
Und auch daß diese Ungenauigkeit einer Verkleinerung
logisch unbegrenzt fähig sein muß. Um also die
Anwendung der euklidischen
Geometrie zu verstehen muß man wissen was das Wort „ungenau”
heißt. – Denn etwas anderes ist uns nicht gegeben
als das Resultat unserer Messung & der Begriff der
Ungenauigkeit. Diese beiden zusammen
müssen der euklidischen
Geometrie entsprechen. |
Ist nun die
Ungenauigkeit der Messung der gleiche Begriff wie die Ungenauigkeit
des Gesichtsbildes? Ich glaube:
gewiß nicht. |
Wenn die Aussage, daß
wir nie einen Das Wort Gleichheit hat eine andere Bedeutung wenn wir es auf Strecken im physikalischen Sehraum anwenden als diejenige die es im || auf den physikalischen Raum angewendet hat. Die Gleichheit im Sehraum hat eine andere Multiplizität als die Gleichheit im physikalischen Raum, darum kann || können im Sehraum 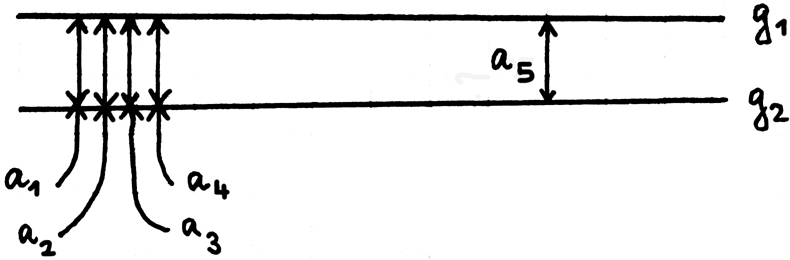 g1
& g2 Gerade (Sehgerade)
sein & die Strecken a1 = a2,
a2 = a3
etc. aber nicht
a1 = a5
sein. Ebenso hat der Kreis & die Gerade im
Gesichtsraum eine andere Multiplizität als Kreis
& Gerade im physikalischen Raum denn ein kurzes Stück
eines gesehenen Kreises kann gerade sein;
„Kreis”
& „Gerade” eben im Sinne der Gesichtsgeometrie angewandt. g1
& g2 Gerade (Sehgerade)
sein & die Strecken a1 = a2,
a2 = a3
etc. aber nicht
a1 = a5
sein. Ebenso hat der Kreis & die Gerade im
Gesichtsraum eine andere Multiplizität als Kreis
& Gerade im physikalischen Raum denn ein kurzes Stück
eines gesehenen Kreises kann gerade sein;
„Kreis”
& „Gerade” eben im Sinne der Gesichtsgeometrie angewandt.
Die Gewöhnliche Sprache hilft sich hier mit dem Worte „scheint” oder „erscheint”. Sie sagt a1 & a2 scheinen gleich zu sein während zwischen a1 & a5 dieser Schein schon nicht mehr besteht. Aber sie benutzt das Wort Schein |
28. Es ist jetzt an der Zeit
(einmal) Kritik am Worte „Sinnesdatum” zu
üben. Sinnesdatum ist die Erscheinung dieses Baumes ob nun „wirklich ein Baum dasteht” oder eine Attrappe, ein Spiegelbild, eine Halluzination etc.. Sinnesdatum ist die Erscheinung des Baumes und was wir sagen wollen ist, daß diese sprachliche Darstellung, diese || nur eine Beschreibung, aber nicht die wesentliche ist. Genau so, wie man von dem Ausdruck „mein Gesichtsbild” sagen kann daß es nur eine Form der Beschreibung aber nicht etwa die einzig mögliche & richtige ist. Die Ausdrucksform „die Erscheinung dieses Baumes” enthält nämlich die Anschauung als bestünde ein innerer || notwendiger Zusammenhang mit dem || dessen was wir diese Erscheinung nennen mit der „Existenz eines Baumes” & zwar entweder durch eine wahre Erkenntnis oder einen Irrtum. D.h. wenn von der „Erscheinung eines Baumes” die Rede ist so hielten wir entweder etwas für einen Baum was einer ist oder Manche (& insbesondere die Idealisten) möchten der Sprache vorwerfen daß sie das Sekundäre als primär & das Primäre als sekundär darstellt. Aber das ist nur in diesen unwesentlichen & mit der Erkenntnis nicht zusammenhängenden Wertungen der Fall („nur” die Erscheinung). Davon abgesehen enthält die gewöhnliche Sprache keine Entscheidung über primär & sekundär. Es ist nicht einzusehen in wiefern der Ausdruck „die Erscheinung eines Baumes” etwas dem Ausdruck „Baum” Sekundäres darstellt. Der Ausdruck „nur ein Bild” geht auf die Vorstellung zurück daß wir das Bild eines Apfels nicht essen können. |
Die Wahrheit
über sich selbst kann man in dem
verschiedensten Geiste schreiben. Im
anständigsten &
unanständigsten. Und danach
ist es sehr wünschenswert oder sehr
unrichtig daß sie geschrieben werde.
Ja es gibt unter den wahrhaften Autobiographien
die man schreiben könnte alle Stufen vom Höchsten
zum Niedrigen. Ich zum Beispiel kann meine
Biographie nicht höher schreiben als ich bin. Und
durch die bloße Tatsache
daß ich sie schreibe hebe ich mich
nicht notwendigerweise ich kann mich
dadurch sogar schmutziger Etwas in mir spricht dafür meine Biographie zu schreiben und zwar möchte ich mein Leben einmal klar ausbreiten um es klar vor mir zu haben & auch für andere. Nicht so sehr um darüber Gericht zu halten als um jedenfalls Klarheit & Wahrheit zu schaffen. Heute Nachmittag hörte ich Koder der mir vorspielte. Ich redete ihm ins Gewissen, er solle das Klavierspiel ernst nehmen, sein Spiel war mir nicht ernst genug. Dann ging ich zu Helene & pfiff mit ihrer Begleitung Schubertlieder & meine Gedanken waren nie wirklich konzentriert ich dachte immer an mich selbst & konnte mich nicht wirklich einfühlen oder der Sache hingeben. Es war nie wirklicher Ernst. Ich tat immer irgendetwas aber es war nie oder beinahe nie das Richtige. Ich sagte mir vor daß die Sache ernst sei aber es flog alles an mir vorüber. Ich fühlte daß ich ein Schwein bin weil ich auch Echtes mit Unechtem mische. Möchte mir Gott Reinheit & Wahrheit schicken. |
Daß uns nichts
auffällt wenn wir uns umsehen, im
Raum herumgehen, unseren eigenen Körper fühlen
etc. etc. das
zeigt wie natürlich uns |
Ich wollte sagen es ist
merkwürdig daß die, die nur den Dingen
nicht unseren Vorstellungen Realität
zuschreiben sich in der
Vorstellungswelt so
selbstverständlich bewegen und sich nie aus ihr
heraussehnen. |
D.h.
wie selbstverständlich ist doch das
Gegebene. Es müßte mit
allen Teufeln zugehen wenn das das kleine aus einem Winkel
aufgenommene Bildchen wäre. |
29.
Dieses selbstverständliche, das Leben, soll etwas
Zufälliges,
Nebensächliches sein; dagegen
etwas worüber ich mir normalerweise nie den Kopf zerbreche das
Eigentliche! |
D.h.
Das, worüber hinaus man nicht gehen kann,
noch gehen will, soll nicht die Welt sein || wäre nicht die Welt! |
30.
Immer wieder ist es der Versuch die Welt |
Denn da die
Sprache die Art ihres Bedeutens erst von ihrer Bedeutung, von
der Welt, erhält, so ist keine Sprache denkbar,
die nicht diese Welt darstellt. |
Wir können unser
altes Prinzip auf die Sätze, die eine Wahrscheinlichkeit
aussagen, anwenden & sagen daß wir ihren Sinn
erkennen werden wenn wir wissen || bedenken
wie sie
verifiziert werden || was sie
verifiziert. |
Wenn ich sage „das wird wahrscheinlich
eintreffen”; wird dieser Satz
durch das Eintreffen verifiziert oder durch das
Nichteintreffen falsifiziert? Ich glaube,
offenbar nein. Dann sagt er auch nichts darüber
aus. Denn wenn ein Streit darüber
entstünde ob es wahrscheinlich ist
oder nicht so würden immer nur Argumente aus der Vergangenheit
herangezogen werden. Und auch dann nur,
wenn es bereits bekannt wäre, was eingetroffen ist.
|
(Ich mache
damit keine Aussage über den Zustand der Erwartung in welchem ich
mich befinde denn sonst wäre die Aussage von der Art
der „ich habe
Kopfschmerzen” |
31. Um den Sinn einer Frage zu
verstehen, bedenken wir: Wie sieht denn die Antwort
auf diese Frage aus? |
Auf die Frage „ist A mein Ahne” kann ich mir nur die Antworten denken „A findet sich in meiner
Ahnengalerie” oder „A findet sich nicht in meiner
Ahnengalerie”.
(Wo ich unter Ahnengalerie die Gesamtheit aller
Arten von Nachrichten über meine Vorfahren
verstehe.) Dann konnte aber auch die Frage nur
dasselbe heißen wie die: „findet sich A in meiner
Ahnengalerie?”.
(Eine Ahnengalerie hat ein Ende: das ist ein
Satz der Syntax.) Wenn mir ein Gott
offenbarte, A sei mein Ahne, aber nicht welcher, so könnte
auch diese Offenbarung für mich nur den Sinn haben, ich werde
A unter meinen Ahnen finden wenn ich nur lang genug suche
da ich aber die || eine Zahl
N von Ahnen durchsuchen werde so muß die
Offenbarung bedeuten A sei unter jenen
N Ahnen. |
Frage ich wie viele
9er folgen unmittelbar
nacheinander auf
3˙1415
in der Entwicklung von π
& soll sich die Frage auf die Extension
beziehen, so lautet die Antwort entweder
Das ist aber freilich nicht die Frage die uns interessiert. |
Wenn ich nicht weiß wieviele
9er auf
3˙1415
folgen können so kann ich also keine Distanz angeben die kleiner
ist als der Unterschied zwischen π und
3˙1416
& das heißt, glaube ich, daß
π nicht einem Punkt
auf der Zahlengeraden entspricht denn entspricht es
einem Punkt dann muß sich eine Strecke angeben
lassen die kleiner ist als die Strecke von diesem
Punkt zum Punkt
3˙1416.
|
Wie seltsam
wenn sich die Logik mit einer „idealen” Sprache
befaßte & nicht mit unserer. Denn was
sollte diese ideale Sprache ausdrücken? Doch wohl
das was wir jetzt in unserer gewöhnlichen
Sprache ausdrücken dann muß die Logik also
diese untersuchen. Oder etwas anderes: aber wie soll
ich dann überhaupt wissen was das
ist. – Die logische Analyse ist die Analyse von etwas
was wir haben nicht von etwas was wir nicht haben. Sie ist
also die Analyse der Sätze wie sie sind.
(Es wäre seltsam wenn die menschliche |
1.1.30.
Der
Begriff des „Elementarsatzes”
verliert jetzt überhaupt seine
große Bedeutung. |
Die Regeln über
und, oder, nicht, etc.
die ich durch die W-F-W-Notation
dargestellt habe sind ein Teil der Grammatik über diese
Wörter, aber nicht die
ganze. |
Man kann, glaube ich, die
Sätze im Allgemeinen mit
den Sätzen vergleichen die eine färbige
Fläche beschreiben indem sie die Farbengrenzen vermittelst eines
Koordinatensystems beschreiben & dann nach irgend einer Art
die Farben zu beiden Seiten dieser Grenzen bezeichnen.
Vielleicht ist es richtiger nur ein bestimmtes
ebenes Flächenstück oder eine Kugelfläche als
Raum zu nehmen & auf dieser die
Farbenverteilung zu beschreiben. |
Der Begriff der unabhängigen Koordinaten der
Beschreibung! |
Die Sätze die
z.B. durch „und”
verbunden werden sind nicht von einander
unabhängig || mit einander
unzusammenhängend sondern sie bilden
Ein Bild & lassen sich auf ihre
Vereinbarkeit oder
Nicht-Vereinbarkeit || Unvereinbarkeit prüfen.
|
In meiner alten
Auffassung der Elementarsätze gab es keine Bestimmung des
Wertes einer Koordinate;
obwohl meine Bemerkung daß eine
Farbe || ein farbiger Körper in einem Farbenraum
ist etc. mich direkt hätte
dahin bringen können. |
Eine Koordinate der
Wirklichkeit darf nur einmal bestimmt
werden. |
2.1.
Wenn
ich den allgemeinen Standpunkt darstellen wollte, würde
ich sagen: „Man darf eben
über eine Sache nicht einmal das eine und
einmal das andere sagen”.
Diese Sache aber wäre die Koordinate der ich einen
Wert geben kann & nicht mehr. |
Es stellt
die Sache falsch dar wenn man sagt man dürfe
einer Sache || einem Gegenstand nicht zwei
Attribute beilegen die miteinander
unvereinbar seien || sind. Denn
so scheint es, als müsse man es in jedem Falle erst
untersuchen ob zwei Bestimmungen mit einander vereinbar
seien oder nicht. Die Wahrheit ist (eben) daß zwei Bestimmungen derselben
Koordinate || Art, [ich
sollte hier ein gebräuchliches Wort setzen]
unmöglich sind. |
Unsere Erkenntnis ist eben,
daß wir es mit Maßstäben & nicht quasi
mit isolierten Teilstrichen zu tun haben. |
Jede Aussage bestünde dann gleichsam im
Einrichten || Einstellen einer Anzahl von
Maßstäben und das |
Es
müssen übrigens nicht Maßstäbe sein denn eine
Scheibe mit den Signalen „frei” &
„besetzt”
kann man keinen Maßstab nennen. Es kann auch eine
Scheibe sein halb schwarz halb weiß. |
Was nicht
so sein kann, kann anders sein.
(﹖) |
Auch
Sätze die mit || durch „und” mit einander
verbunden sind schließen sich innerlich zusammen.
|
Daß alle Sätze die Zeit in irgend einer Weise
enthalten scheint uns zufällig im Vergleich dazu daß
auf alle Sätze die Wahrheitsfunktionen anwendbar
sind. Das scheint mit ihrem Wesen als Sätzen zusammenzuhängen das andere mit dem Wesen der vorgefundenen Realität. |
Wahr-Falsch
& die Wahrheitsfunktionen hängen mit der Darstellung der
Wirklichkeit durch Sätze zusammen. Wenn einer
sagte: |
Man
könnte sagen: Satz ist das worauf sich die
Wahrheitsfunktionen anwenden lassen. – Die
Wahrheitsfunktionen sind der Sprache wesentlich.
|
Aus „die Rose ist nicht gelb” folgt nicht daß sie rot ist, aber daraus daß sie rot ist
folgt daß sie nicht gelb ist: also kann man sagen daß der
positive Satz mehr sagt als der negative. (Wenn das
eben nichts weiteres bedeuten soll.)
|
Die Syntax verbietet
eine Bildung wie „A ist grün
und A ist rot” (das erste
Gefühl ist als geschähe damit diesem Satz
quasi ein Unrecht; als wäre er dadurch in den Rechten
des Satzes verkürzt.) Aber für
„A ist grün” ist der Satz „A ist
rot” sozusagen gar kein
anderer Satz – & das ist es eigentlich
was die Syntax festhält – sondern eine andere Form
desselben Satzes. |
Die Syntax zieht dadurch
Sätze zusammen |
3. Wenn ich sage ich habe heute
Nacht nicht geträumt, so weiß ich doch || muß ich doch
wissen wo nach dem Traum zu suchen
wäre. (d.h. der Satz „ich habe geträumt” darf auf die Situation angewendet nur falsch aber nicht
unsinnig sein.) |
Ich drücke die
gegenwärtige Situation durch eine Stellung
– die negative – der Signalscheibe „Träume – keine
Träume” aus.
Ich muß sie aber trotz ihrer negativen Stellung von anderen
Signalscheiben unterscheiden können. Ich muß
wissen daß ich diese Signalscheibe in der Hand
habe. |
Man könnte nun fragen: soll das heißen || heißt das, daß Du doch in der Nacht irgend etwas
gespürt hast sozusagen die Andeutung eines Traums die
Dir die Stelle zum Bewußtsein bringt an der ein
Traum gestanden wäre? Oder wenn ich sage „ich habe keine Schmerzen im
Arm” heißt das, daß ich eine
Art schattenhaftes Gefühl dort habe was die Stelle
andeutet in die der Schmerz eintreten würde?
Doch offenbar, nein! |
In wiefern
enthält der gegenwärtige schmerzlose
Zustand die Möglichkeit |
Es ist etwas
anderes ob auf die Frage „hast du im Arm
Schmerzen” die Antwort kommt
„nein” oder
„ich verstehe die Frage
nicht”. |
Wenn einer
sagt: „damit das Wort
Schmerzen Bedeutung habe, ist es notwendig, daß man
Schmerzen erkennt wenn sie auftreten”, so
kann man antworten: „es ist eben
so wesentlich daß man das Fehlen || nicht
notwendiger als daß man das Fehlen von Schmerzen
erkennt”. |
Man könnte
sagen: ja, aber der positive Sachverhalt ist der
primäre. Das Problem hängt damit zusammen daß
das Wort „Schmerzen” nur im Satz Bedeutung hat & daß
der Zustand der Schmerzen nicht durch das Wort „Schmerzen” sondern
durch den Satz „ich habe
Schmerzen” wiedergegeben
wird. |
„Schmerzen”
heißt so zu sagen der ganze Maßstab & nicht einer seiner
Teilstriche. Daß er auf einem bestimmten
Teilstrich steht ist nur durch einen Satz
auszudrücken. |
Wenn das Messer nicht auf dem Buch liegt so
liegt auch kein Schatten des Messers auf dem Buch, aber Es kann sich mit Magenschmerzen & Träumen etc. nicht anders verhalten als mit den Gegenständen || der Lage von Gegenständen im Raum. |
Was wäre das für
eine Frage: Könnte denn alles nicht der
Fall sein & nichts der Fall sein?
Könnte man sich einen Zustand einer Welt denken in dem
mit Wahrheit nur negative Sätze zu sagen
wären? Ist das
nicht offenbar alles Unsinn? Gibt es
denn wesentlich negative & positive
Zustände? |
Wenn man die
Sätze als Vorschriften auffaßt um Modelle zu bilden, wird ihre
Bildhaftigkeit noch deutlicher. |
Denn
damit das Wort meine Hand lenken kann muß es
die Mannigfaltigkeit der gewünschten
Tätigkeit haben. |
Und das muß auch das Wesen des negativen Satzes
erklären. So könnte einer
z.B. das Verständnis des Satzes „das Buch ist nicht rot” dadurch zeigen daß er bei der Anfertigung
des || eines Modells die rote Farbe
wegwirft. Das & Ähnliches würde dann auch zeigen wie der negative Satz die Mannigfaltigkeit des verneinten Satzes hat & nicht der Sätze |
Was heißt es zu sagen „ich sehe zwar kein Rot um mich, aber wenn Du mir
einen Farbenkasten gibst so kann ich es Dir darin
zeigen”? Wie kann man
wissen daß man es zeigen kann wenn …; daß man
es also erkennen kann wenn man es
sieht. |
Was hier gemeint
ist kann || könnte zweierlei Art
sein: Es könnte die Erwartung ausgesprochen sein
daß ich es erkennen werde wenn es mir gezeigt wird in dem Sinne wie
ich erwarte Kopfschmerzen zu bekommen wenn ich einen Schlag
auf den Kopf erhalte; das ist dann so zu sagen eine physikalische
Erwartung mit derselben Basis wie alle
Erwartungen die sich auf das Eintreffen physikalischer
Ereignisse beziehen. Oder aber es handelt
sich gar nicht um die Erwartung eines physikalischen
Ereignisses & daher kann dann auch mein Satz durch das
eventuelle Ausbleiben dieses Ereignisses nicht
falsifiziert werden. Sondern der Satz sagt gleichsam
daß ich ein Urbild besitze mit dem ich die Farbe jederzeit
vergleichen könnte (und diese
Möglichkeit ist eine logische
Möglichkeit). |
Nach der ersten
Auffassung: wenn ich nun |
In welcher Form aber kann ich denn das
Urbild der Farbe in mir tragen? Ich kann
z.B. sagen „nein
die Farbe ist es nicht, aber beinahe, die
Farbe, die ich meine ist noch etwas dunkler”. Ich kenne in irgend einem Sinne den Platz der
Farbe die ich meine & || denn ich erkenne eine
Näherung an diesen Platz als solche. |
Die
Sätze unserer Grammatik haben immer die Art physikalischer
Sätze & nicht || & nicht die
„primären” & vom Unmittelbaren
handelnden Sätze.
|
4. Der negative Satz zieht dieselbe
Grenze wie der positive, deutet sie nur anders. |
„Ist das Blatt blau”
„nein es ist nicht
blau”: Ich schalte also das
Blau aus. Aber wie kann ich durch Worte
Blau ausschalten? Es || Das ist dasselbe Problem wie: wie kann ich
durch diese Worte jemanden veranlassen eine bestimmte Farbe zu
wählen (oder auszuschließen)? |
Der Zusammenhang
des Wortes „blau” mit der blauen Farbe kann kein anderer sein als der
eines Wortes mit einem |
Man könnte sich ein zu dem Worte
„blau”
gehöriges blaues Täfelchen denken das ebensowenig immer an
Ort & Stelle ist wie || z.B. etwa die Negation eines Satzes wenn dieser Satz zur Stelle ist.
|
Zum
Verständnis des Satzes „das Blatt ist nicht blau” gehört es auch daß ich im Stande bin || wäre ein farbiges Bild des Blattes zu machen, wie es
nicht ist. |
Man könnte auf zwei verschiedene Weisen
darauf kommen daß ein Anderer nicht die selbe Sprache besitzt
wie man selbst. Entweder indem man ihn eine
Äußerung machen hörte die in meiner
Sprache ungrammatisch ist oder dadurch daß er einen Satz behauptet
der in meiner Sprache ein falscher wäre. Er
könnte im einen Fall etwa sagen „a & b sind im gleichen Grade
identisch” im anderen Fall „der Himmel ist wolkenlos &
rot”. |
Eine naive
Auffassung der Bedeutung eines Worts ist es daß man sich beim
Hören oder Lesen des
Wortes dessen Bedeutung „vorstellt”.
Und für dieses Vorstellen gilt auch wirklich die
gleiche Frage wie für das Bedeuten eines |
Wenn ich sage „diese Tischplatte ist
nicht blau” so muß ich
den Weg zum Blau sehen. Darin besteht
(eben) die Möglichkeit Blau wiederzuerkennen. Ich
habe auch gesagt: „Ich
muß wissen wie es wäre, wenn sie blau
wäre”. |
Was
heißt es aber: wissen wie es wäre? |
Kann das
heißen: Wiedererkennen, wenn es einem
begegnet? Aber wie weiß ich, daß ich Blau wiedererkennen werde, wenn ich es zu sehen
kriege. Vielleicht geschieht das erst nach
zehn Jahren & dann bin ich verrückt
geworden. Ist also dieses „Wissen wie es
wäre” eigentlich nur eine
Vermutung. Und ob der Satz einen Sinn hat läßt
sich dann auch nur vermuten. |
Kann man nicht zeigen daß man ein Wort versteht,
dadurch daß man die Regeln der Syntax angibt die sich darauf
beziehen oder – was auf dasselbe
hinausläuft – indem man
sinnvolle Sätze angibt, in denen das Wort
vorkommt (sie mögen wahr oder falsch
sein). |
Wenn ich den Satz „der Tisch ist blau”
verstehe, ob ich nun etwas Blaues vor mir
sehe oder nicht, so muß ich wissen ob, z.B.,
blau ein gewisser Grad von Helligkeit von rot ist
oder ob blau ein bestimmter süßer Geschmack ist,
etc. |
Ich will wissen was es heißt, einen Satz
zu verstehen: Wie verifiziert man denn diese
Aussage? |
5.
Doch nicht indem
man später wirklich einmal – etwa – blau
wiedererkennt! |
Weiß
ich, daß ich einen Satz verstehe, nicht durch
Introspektion? Ist hier
nachträgliche Verifikation
denkbar? |
Ganz falsch kann doch die
naive Theorie des sich eine Vorstellung
Machens nicht sein. |
Die Sackgasse ist die
(eigentliche) Gefahr |
Ich weiß
ich dokumentiere mein Verständnis des Satzes
„A ist blau” dadurch daß ich auf einen blauen Gegenstand
zeige oder || und auf einen bläulichen
& ihn bläulich nenne oder auf zwei
Gegenstände & sage „dieser ist bläulicher als der
andere”. Aber
besteht mein Verständnis eben darin? Ist
es hier auch so daß das „Verstehen”
gleichsam Facetten hat von denen im
besonderen Fall nur ein paar zur Anwendung
kommen? Und wäre es so auch mit der Grammatik,
d.h. mit den syntaktischen Regeln?
|
Ich sehe
Etwas & daß mir dabei
die Beschreibung „der Tisch
ist weiß” einfällt, ist nicht
weniger merkwürdig als daß mir die Beschreibung
einfällt || ich auf die Beschreibung
komme: der Tisch ist nicht blau. 2
|
16.2.30.
3 In wiefern hängt der Begriff der Kardinalzahl mit dem Begriff von Subjekt & Prädikat zusammen? |
Russell &
Frege fassen den Begriff
gleichsam als Eigenschaft eines Ding's auf.
Aber es ist sehr unnatürlich die Worte Mensch,
|
Das
principium individuationis muß die Eigenschaft
haben. Muß ihr Träger
sein. |
Wenn ein Tisch braun angestrichen ist
so ist es leicht sich das Holz als den Träger der
Eigenschaft braun zu denken & man kann sich das
vorstellen was bleibt wenn die Farbe wechselt. Ja
auch im Falle eines bestimmten Kreises der einmal
rot einmal blau erscheint. Es ist also leicht sich
vorzustellen was rot ist aber schwer, zu denken was
kreisförmig ist. Was bleibt hier wenn
Form & Farbe wechseln? Denn die
Lage ist ein Teil der Form & es ist willkürlich wenn ich
festsetze der Mittelpunkt soll fest bleiben & die Form
sich nur durch den Radius ändern. |
Wir werden
uns wieder an die gewöhnliche Sprache halten müssen und die
sagt daß ein Fleck kreisförmig
ist. Es ist klar daß hier das Wort Träger der Eigenschaft eine ganz falsche – unmögliche – Vorstellung gibt. – Wenn ich einen Klumpen Ton habe so kann ich mir den als Träger einer Form denken & daher, ungefähr, |
„Der Fleck ändert seine
Form” & „der Tonklumpen ändert seine
Form” sind eben grundverschiedene
Satzformen. |
Ziffern werden oft als Namen
gebraucht. |
Wenn ich mit der Hand auf
Etwas zeige & sage „das || dies ist
rot”, „dies
ist hart”, „dies ist Holz”, „dies ist ein
Sessel” so bedeutet „dies” offenbar
jedesmal etwas anderes. |
Man kann sagen „miß nach ob das ein Kreis
ist” oder „sieh nach ob das was dort liegt ein
Hut ist”.
Man kann auch sagen „miß nach ob das ein Kreis ist oder
eine Ellipse” aber nicht
„… ob das ein Kreis ist oder ein
Hut” auch nicht „sieh nach ob das ein Hut ist oder
rot.”. |
Wenn ich auf
eine Linie zeige & sage „das ist ein
Kreis” so kann man einwenden daß wenn
es kein Kreis wäre es nicht mehr das wäre.
Das heißt: Was ich mit dem Wort „das” meine muß
unabhängig von dem sein was davon ausgesagt wird. |
„War das
Donner oder ein Schuß?” Man kann aber in diesem Falle nicht fragen „war das ein Lärm”. |
Wie
aber wenn ich sage „ich sehe hier 3
Linien”? Das heißt doch
nicht 3 Dinge die Linien sind. |
„In diesem
Bild sind 5 verschiedene Farben.” Wie ist dieser Satz zu erklären? |
17.
Beiläufig gesprochen ist die Gleichung
eines Kreises das Zeichen für den Begriff Kreis wenn keine
bestimmten Werte für die
Mittelpunktskoordinaten & den Radius
eingesetzt sind oder auch wenn diese nur als in gewissen Intervallen
liegend gegeben sind. Der Gegenstand der unter den Begriff
fällt ist dann der nach Lage & Größe bestimmt
gegebene Kreis. |
In der Aussage in diesem Feld sind 3 Kreise
bezieht sich die 3 offenbar auf
„in diesem Feld sind ξ
Kreise” & der Begriff Kreis
muß da wie oben gegeben sein. Man könnte aber auch
sagen die 3 bezieht sich auf „Kreise in
diesem Feld”.
Es ist offenbar daß ich die Beschreibung so machen kann daß sie einer notwendigen Ergänzung durch eine Zahl bedarf. |
Das was ich zähle ist
das Vorkommen einer gewissen Charakteristik. |
18. Worin unterscheiden sich
zwei gleich große |
In der Darstellungsart
durch Gleichungen drückt sich das Gemeinsame durch die Form der
Gleichung aus & die Verschiedenheit durch die
Verschiedenheit der
Mittelpunktskoordinaten. |
So ist es
als ob hier die Mittelpunktskoordinaten das
wären was den unter den Begriff fallenden Gegenständen
entspräche. |
Könnte man denn nicht
statt „dies ist ein
Kreis” sagen „dieser Punkt ist Mittelpunkt
eines Kreises”? Denn
Mittelpunkt eines Kreises zu sein ist eine externe Eigenschaft des
Punktes. |
In Wahrheit ist ja das
Zahlenpaar das die Mittelpunktskoordinaten
darstellt nicht irgend ein Ding ebensowenig wie der Mittelpunkt
sondern das Zahlenpaar
charakterisiert eben dasjenige am
Symbol was die „Verschiedenheit”
der Kreise ausmacht. |
Drei Kreise werden dargestellt
durch die Kreisgleichung & drei Zahlenpaare (oder
Zahlentrippel). |
Ist es eine Zahlangabe von der Art „es sind 6 Menschen in diesem
Zimmer” wenn wir sagen 3 Elemente lassen
6 Permutationen zu? Gewiß
nicht. |
Schon das „sie lassen zu”
zeigt daß es sich hier um etwas anderes handelt.
Was heißt es „6
Permutationen sind möglich”? |
Wenn man wissen will was ein Satz
bedeutet so kann man immer fragen „wie weiß ich das”. Weiß ich daß es 6 Permutationen von 3
Elementen gibt auf die gleiche Weise wie, daß
es || daß 6 Personen im Zimmer sind?
Nein. Darum ist jener Satz von anderer
Art als dieser. |
Eine andere ebenso
nützliche Frage ist „wie
wird dieser Satz in der Praxis || in praxi wirklich
angewandt” & das wird
jener Satz der Kombinationslehre natürlich als
Schlußgesetz angewandt zum Übergang von einem Satz zum
anderen deren keiner eine
Möglichkeit || jeder eine Wirklichkeit keine
Möglichkeit, beschreibt. |
19. Man kann wohl überhaupt sagen daß
die Verwendung der scheinbaren Sätze über
Möglichkeiten, || – &
Unmöglichkeiten – immer der
Übergang von einem wirklichen Satz zum
anderen ist. |
So kann ich zum Beispiel aus dem
|
Wenn jemand mit
uns über die Anzahl der Menschen in diesem Zimmer nicht
übereinstimmt & behauptet es seien 7
während wir nur 6 sehen so können wir ihn verstehen, obwohl
wir nicht mit ihm übereinstimmen; behauptet er aber für ihn
gäbe es 5 reine Farben dann verstehen wir ihn nicht oder
wir müssen annehmen daß wir einander
gänzlich mißverstehen. Diese Zahl wird im
Wörterbuch & der Grammatik abgegrenzt &
so nicht innerhalb der Sprache. |
Was braucht
es zu einer Beschreibung daß – sagen wir – ein Buch an
einem
bestimmten Ort || einer bestimmten Stelle ist. Die
interne Beschreibung des Buches
d.i. des Begriffes & die Beschreibung
seiner Lage & das || die wäre
durch Angabe der Koordinaten dreier Punkte
möglich. Der Satz „ein solches Buch ist
hier” würde dann heißen
es hat diese 3 Paare || Trippel von
Bestimmungskoordinaten. Denn die
Angabe des hier darf eben nicht
präjudizieren was hier
ist. Ist es nun aber nicht dasselbe ob ich sage „dies ist ein Buch” & „hier ist ein Buch”? |
Man kann ähnlich auch sagen „dieser Kreis ist die
Projektion einer Kugel” oder „dies ist die
Erscheinung eines Menschen”. |
Wenn ich also den Satz „in diesem
Feld sind 3 Kreise” in der Form
(∃x,y,z)
φx ∙ φy ∙
φz schreibe so scheint es mir als
müssen || müßten die
x,
y,
z, Zahlentrippel sein von
denen φ( ) sagt daß
sie Mittelpunktskoordinaten & Radius
eines Kreises seien. |
Alles
was ich sage kommt darauf hinaus daß
φ(x) eine
externe Beschreibung von
x sein muß. |
Wenn ich nun in diesem Sinne im dreidimensionalen Raum sage
„hier ist ein Kreis” & ein andermal „hier
ist eine Kugel”,
sind die beiden hier von gleicher Art? Beide
könnten doch die beiden || drei
Koordinaten des betreffenden Mittelpunkts
sein. Aber die Lage des Kreises im
3-dimensionalen Raum ist ja durch seine
Mittelpunktskoordinaten nicht
bestimmt. |
Wenn ich recht habe so
gibt es keinen Begriff „reine
Farbe”; der Satz „A hat eine reine
Farbe” heißt einfach
„A ist Wenn ich nun nicht sagen kann „es gibt 4 reine Farben” so sind die reinen Farben & die Zahl 4 doch irgendwie mit einander verbunden & das muß sich auch irgendwie ausdrücken. – Z.B. wenn ich sage „auf dieser Fläche sehe ich vier Farben: gelb, blau, rot, grün.” |
Ganz analog muß es sich nun mit den Permutationen
verhalten. Die Permutationen (ohne
Wiederholung) von AB sind AB,
BA. Sie sind nicht die Extension eines Begriffs
sondern sie allein sind der Begriff. Dann kann man
aber von ihnen nicht sagen daß ihrer 2 sind. Und doch
tut man das scheinbar in der Kombinatorik. Es ist mir als
handle es sich da um eine ähnliche Zuordnung wie
die zwischen der Algebra & den Induktionen der
Arithmetik. Oder ist die Verbindung die von Geometrie
& Arithmetik?? Der Satz das es 2
Permutationen von AB gibt ist wirklich ganz analog dem,
daß die Gerade |
Wenn man sagt AB lasse 2 Permutationen
zu so klingt das als mache man eine
allgemeine Aussage analog der „in dem Zimmer sind 2 Menschen”, wobei über die Menschen noch nichts weiter gesagt
ist & bekannt sein braucht. Das ist aber im Fall
AB nicht so. Ich kann AB, BA nicht
allgemeiner beschreiben und daher kann der Satz es seien 2
Permutationen möglich nicht weniger sagen als es sind die
Permutationen AB & BA möglich. Zu
sagen es sind 6 Permutationen von 3 Elementen möglich kann
nicht weniger, d.h. etwas allgemeineres
sagen als das Schema a b c a c b b a c b c a c a b c b a zeigt. Denn es ist unmöglich die Zahl der möglichen Kombinationen || Permutationen zu kennen ohne sie || diese selbst zu kennen. Und wäre das nicht so, so könnte die Kombinatorik nicht zu ihren allgemeinen Formeln kommen. Das Gesetz welches wir in der Bildung der Permutationen erkennen ist durch den Ausdruck || die Gleichung p = n! dargestellt. Ich glaube, in dem selben Sinne wie der Kreis durch die Kreisgleichung. – Ich kann freilich die Zahl 2 den zwei Permutationen AB & || , BA zuordnen sowie die 6 den ausgeführten Permutationen von ABC, aber das gibt mir nicht den Satz der Kombinationslehre. – Das was ich in |
Ist nicht Harmonielehre
wenigstens teilweise Phänomenologie also
Grammatik? |
20.
Eine Kombinationsrechenmaschine ist denkbar ganz analog der
Russischen. |
Es ist klar
daß es eine Mathematische Frage gibt „wieviele Permutationen von –
etwa || z.B. – 4
Elementen gibt es”, eine Frage von genau
derselben Art wie die „wieviel ist
25 × 18?”. Denn es gibt eine allgemeine Methode zur
Lösung beider. Aber die Frage gibt es auch nur
in bezug || mit Bezug auf diese
Methode. |
Der Satz es gibt 6 Permutationen von 3 Elementen
ist identisch mit dem Permutationsschema & darum gibt es hier
keinen Satz „es gibt 7
Permutationen von 3 Elementen”,
denn dem entspricht kein Permutationsschema. || solches Schema. |
Man könnte die Zahl 6 in diesem Falle
auch als eine andere Art von Anzahl die Permutationszahl von a,
b, c auffassen. Das Permutieren als eine
andere Art des Zählens. |
Man kann auch sagen der
Satz „es gibt 6 Permutationen
von 3 Elementen” verhält sich
genau so zum Satz „es sind 6 Leute im
Zimmer” wie der Satz
3 + 3 = 6
den man auch in der Form „es gibt 6
Einheiten in
3 + 3” aussprechen könnte. Und wie ich in dem
einen Fall die Reihen im Permutationsschema zähle so
kann ich im anderen die Striche in
|
Wie ich
4 × 3 =
12 durch das Schema beweisen kann
|
In wiefern kann man sagen daß Grau im
selben Sinne eine Mischung von Schwarz & Weiß ist in
dem Orange eine Mischung von Rot & Gelb ist. Und
nicht in dem Sinne zwischen Schwarz &
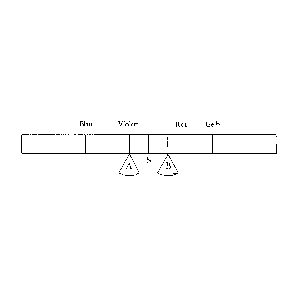
Weiß Stellt man die Farben mit einem || durch einen 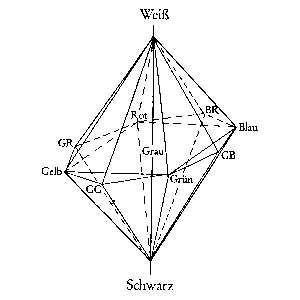 Doppelkegel dar
statt eines Oktaeders so
gibt es auf dem Farbenkreis nur ein zwischen & Rot
erscheint auf ihm in dem selben Sinne zwischen Purpur &
Orange in welchem Purpur zwischen Blau & Rot liegt.
Und wenn das wirklich alles ist was man sagen kann dann genügt
die Darstellung durch den Doppelkegel oder mindestens die durch
ein doppeltes || eine doppelte 8-seitige
Pyramide. Doppelkegel dar
statt eines Oktaeders so
gibt es auf dem Farbenkreis nur ein zwischen & Rot
erscheint auf ihm in dem selben Sinne zwischen Purpur &
Orange in welchem Purpur zwischen Blau & Rot liegt.
Und wenn das wirklich alles ist was man sagen kann dann genügt
die Darstellung durch den Doppelkegel oder mindestens die durch
ein doppeltes || eine doppelte 8-seitige
Pyramide. |
Nun scheint es
merkwürdigerweise von vornherein klar zu sein daß man nicht in
dem selben Sinne sagen kann Rot habe
einen orangen Stich wie Orange hat
einen rötlichen Stich. Das heißt es scheint klar zu
sein daß die Ausdrücke „ξ besteht aus x &
y || ξ ist ein Gemisch von x &
y” & „ξ ist das gemeinsame Bestandteil von x
& y” hier nicht
vertauschbar sind. Wären sie vertauschbar so
genügt die Relation „zwischen” zur Darstellung. |
Die
Ausdrücke „gemeinsamer Bestandteil von” & „Gemisch
von” haben überhaupt nur
dann verschiedene Bedeutung wenn der eine dort verwendet
werden kann wo der andere nicht verwendet werden
kann. |
Nun sagt es
nichts zu unserer Untersuchung daß wenn ich ein blaues
& grünes Pigment mische ich ein blaugrünes erhalte
wenn ich aber ein blaugrünes & blaurotes mische
kein blaues herauskommt. |
Gelbrot &
Blaurot enthalten einen gemeinsamen Bestandteil in einem Sinne
in welchem Rot & Blau keinen enthalten.
Oder kann ich sagen sie haben beide etwas vom Violett
ganz ebenso wie Orange & Violett beide
etwas vom Rot haben?! |
Hat das Grau etwas vom Schwarz in dem selben
Sinne wie das Schwarz vom Grau?! Offenbar nein
denn ich kann über Grau von Weiß nach Schwarz gelangen aber
nicht über Schwarz von Grau nach
Weiß. |
Man könnte auch so fragen: ist es ein sprachlicher
Zufall daß man Blau nicht
Orangeviolett || Orange-Violett
nennt? |
Ich möchte sagen, daß Blau nicht in
demselben Sinne eine Farbe ist wie Blaurot.
Wie drückt sich das aber aus? |
Könnte man etwa so
fragen: Wenn ich mir vier Farben A, B, C, D merke
oder Muster von ihnen mit mir herumtrüge, A wäre ein
Blaugrün, B ein Blaurot, C ein Gelbgrün
& D ein Gelbrot, – könnte ich nun nicht
|
Wenn ich
mit meiner Auffassung recht habe so ist es kein Satz zu sagen
„Rot ist eine reine
Farbe” & was damit
angezeigt werden soll keiner experimentellen Entscheidung
fähig. Es ist dann auch nicht denkbar daß mir
einmal Rot ein andermal Blaurot rein
erscheint. || erscheinen soll. || sollte. |
Die Frage ist ob für die interne
Relation zweier Farben nur die Wege maßgebend sind nach welchen sie
in einander übergeführt werden können.
|
Die Bemerkung
die ich oben über die Mischung von Pigmenten machte gibt einen
Fingerzeig wie || in welcher Weise die
reine || Reinheit einer Farbe definiert
werden könnte als eine externe Eigenschaft also so wie ich
sie nicht meine. |
21.
Es
scheint außer dem Übergang von Farbe zu Farbe auf dem
Farbenkreis noch einen bestimmten anderen zu geben den wir vor uns
haben wenn wir kleine Flecke der einen Farbe mit kleinen Flecken der
anderen untermischt sehen. Ich meine hier natürlich
einen gesehenen Übergang.
Und diese Art des Übergangs gibt |
Man könnte es so
beschreiben: Einen Orangefarbigen Fleck kann ich mir
entstanden denken durch Untermischen kleiner
roter & gelber Flecke dagegen einen Roten nicht durch
Untermischen von Violetten &
Orangefarbigen. – In diesem Sinn ist Grau eine
Mischung von Schwarz & Weiß & Rosa eine von Rot
& Weiß aber Weiß nicht eine Mischung von Rosa &
einem weißlichen Grün.
Nun meine ich aber nicht daß es durch ein Experiment der Mischung festgestellt wird daß gewisse Farben so aus anderen entstehen. Ich könnte das Experiment etwa mit einer rotierenden Farbenscheibe anstellen. Es kann dann gelingen oder nicht gelingen aber das zeigt nur ob der betreffende visuelle Vorgang auf diese physikalische Weise hervorzurufen ist oder nicht, es zeigt aber nicht, ob er möglich ist. Genau so wie die physikalische Unterteilung einer Fläche nicht die visuelle Teilbarkeit beweisen oder entkräften || widerlegen kann. Denn angenommen ich sehe eine physikalische Unterteilung nicht mehr als visuelle Unterteilung sehe aber die nicht geteilte Fläche im betrunkenen Zustande geteilt, war dann die visuelle Fläche nicht teilbar? |
Gesichtsraum & Retina. Es ist wie wenn man
eine Kugel orthogonal auf eine Ebene projiziert etwa in
der Art wie die beiden Halbkugeln der Erde in einem Atlas dargestellt
werden & nun könnte einer glauben daß was auf der
Ebene außerhalb der beiden Kugelprojektionen
vor sich geht immerhin noch einer möglichen Ausdehnung
dessen entspricht was sich auf der Kugel befindet. Hier
wird eben ein kompletter Raum auf einen Teil eines
anderen Raumes projiziert; und analog ist es mit den Grenzen der
Sprache im Wörterbuch. |
Man könnte sagen
Violett & Orange löschen einander bei der Mischung
teilweise aus nicht aber
z.B. Rot & Gelb.
|
Orange ist jedenfalls ein Gemisch von Rot
& Gelb in einem Sinne in dem Gelb kein Gemisch von
Rot & Grün ist obwohl ja Gelb im
Kreis zwischen Rot & Grün liegt.
Und wenn das offenbar Unsinn wäre so frägt es sich an welcher Stelle es anfängt Sinn zu werden; d.h. Wenn ich nun im Kreis von Rot & Grün aus dem Gelb näher rücke & Gelb ein Gemisch der betreffenden beiden Farben nenne. |
Ich
erkenne nämlich im Gelb wohl die Verwandtschaft
zu Rot & Grün –
nämlich die Möglichkeit zum
Rötlich-Gelb &
Grünlich- Oder auch Gelb liegt nicht in dem Sinne zwischen Grün & Rot wie Grau zwischen Schwarz & Weiß wohl aber liegt in diesem Sinn Orange zwischen Gelb & Rot. |
Ich will sagen daß Rot
nur in dem Sinn zwischen Violett & Orange ist wie Weiß
zwischen Rosa & Grünlichweiß. Aber ist in
diesem Sinn nicht jede Farbe zwischen jeden zwei anderen oder doch zwischen solchen zweien zu denen man
auf unabhängigen Wegen von der dritten
gelangen kann. Kann man sagen in diesem Sinne liegt eine Farbe || eine Farbe nur in einem gegebenen kontinuierlichen Übergang zwischen zwei anderen. Also etwa Blau zwischen Rot & Schwarz. |
Ist es also so: zu
sagen ein Fleck habe eine Mischfarbe von Orange & Violett
schreibt ihm eine andere Farbe zu als zu sagen der Fleck habe die
Farbe die Orange & Violett mit
einander gemein haben? Aber das geht auch nicht; denn in dem Sinn in welchem Orange eine Mischung von Rot & Gelb ist gibt es gar keine Mischung von Orange & Violett. |
In Blaugrün & Gelbgrün
sehe ich die unverträglichen Bestandteile nicht aber in Blau
& Grün. |
22.
Die
Grenzenlosigkeit des Gesichtsraumes ist am klarsten wenn wir nichts
sehen, bei vollständiger Dunkelheit. |
Die
Bedeutung des Ausdrucks Mischung der Farben A & B
muß mir allgemein bekannt sein da seine Anwendung nicht auf eine
endliche Anzahl von Paaren beschränkt ist. Zeigt
man mir also z.B. irgend ein Orange &
Weiß & sagt die Farbe eines Flecks sei eine Mischung dieser
beiden, so muß ich das verstehen & ich kann es
verstehen. Wenn man mir sagt die Farbe eines Flecks liege zwischen Violett & Rot so verstehe ich |
Der Induktionsbeweis wäre wenn er ein
Beweis wäre ein Beweis der Allgemeinheit
nicht ein Beweis einer gewissen Eigenschaft aller – Zahlen
z.B. |
Wenn ich im
gewöhnlichen Sinn sage Rot & Gelb geben Orange so ist
hier nicht von einer Quantität der Bestandteile die
Rede. Wenn mir daher ein Orange
gegeben ist so kann ich nicht sagen daß noch |
Der Vergleich den man
fälschlicherweise zu machen geneigt ist, ist der der
Farbenreihe mit einem System von zwei Gewichten an einem Maßstab
durch deren Vermehrung oder Verschiebung ich den Schwerpunkt
des Systems beliebig verschieben kann.
Es ist nun
Unsinn zu glauben daß wenn ich die Schale A
auf Violett halte & B in das Feld rot-gelb hinein
verschiebe S sich gegen rot hin bewegen
wird. Und wie ist es mit den Gewichten die ich auf die Schalen lege: heißt es denn etwas zu sagen mehr von diesem Rot? Wenn ich nicht von Pigmenten spreche. Das kann nur dann etwas heißen wenn ich unter reinem Rot eine bestimmte vorher angenommene Anzahl von Einheiten verstehe. Dann aber bedeutet die volle Anzahl |
Solange ich nun im Farbenkreis mit meinen beiden
Grenzfarben – z.B. – im Gebiete
Blau-Rot stehe & die rötere
Farbe gegen rot verschiebe so kann ich sagen daß die
Resultante auch gegen rot wandert.
Überschreite ich aber mit der einen Grenzfarbe das Rot
& bewege mich gegen Gelb, so wird die Resultierende nun nicht
röter! Die Mischung eines gelblichen Rot mit einem
Violett macht das Violett nicht röter als die Mischung von reinem
rot & dem Violett. Daß das eine Rot nun
gelber geworden ist nimmt ja vom Rot etwas weg & gibt nicht
Rot dazu. |
Man könnte das auch
so beschreiben: habe ich einen Farbtopf mit violettem Pigment
& einen mit Orange & nun vergrößere ich die
Menge des der Mischung zugesetzten
Orange so wird zwar die Farbe der Mischung nach & nach
aus dem Violett ins Orange übergehen aber nicht
über das reine Rot. |
Ich kann von zwei
verschiedenen Tönen von Orange sagen daß ich von keinem Grund
habe zu sagen er liege näher an
Orange || Rot als an |
Es ist freilich wahr
daß man von einem Orange sagen kann es sei
beinahe gelb, also es liege „näher am Gelb als am Rot” & Analoges von einem beinahe
roten Orange. Daraus folgt aber nicht – wie ich einmal
glaubte – daß es nun auch eine Mitte im Sinne eines Punktes
zwischen Rot & Gelb geben müsse.
Es ist eben hier ganz wie mit der
Geometrie des Gesichtsraums verglichen
mit der Euklidischen.
Es ist hier eine andere Art von
Quantitäten als die welche durch unsere rationalen
Zahlen dargestellt werden. Die Begriffe näher
& weiter sind eben hier überhaupt nicht zu brauchen oder
sind irreführend wenn wir diese Worte anwenden. |
Auch so: Von einer Farbe zu sagen sie liege zwischen
Rot & Blau definiert || bestimmt
sie nicht eindeutig || scharf. Die reinen Farben aber
müßte ich eindeutig durch die Angabe bestimmen sie
liegen zwischen gewissen Mischfarben. Also bedeutet hier
das Wort „zwischen || inzwischen
liegen” etwas |
Wir sagen eine
Farbe kann nicht zwischen Grüngelb & Blaurot
liegen in dem selben Sinne wie zwischen Rot & Gelb aber das
können wir nur sagen weil wir in diesem Falle den Winkel von
45˚ unterscheiden können; weil wir
Punkte Gelb, Rot sehen. Aber eben diese
Unterscheidung gibt es im anderen Fall – wo die
Mischfarben als das Primäre genommen werden –
nicht. Hier könnten wir also sozusagen nie
sicher sein ob die Mischung noch möglich ist oder nicht.
Freilich könnte ich beliebige Mischfarben
wählen & bestimmen daß sie einen Winkel von
45˚ einschließen das wäre aber ganz willkürlich
wogegen es nicht willkürlich ist wenn wir sagen daß es keine
Mischung von Blaurot & Grüngelb im ersten Sinne
gibt. |
23.
|
Man kann freilich auch
alle Farbtöne in einer Linie anordnen etwa mit den Grenzen
Schwarz & Weiß wie das geschehen ist aber
dann muß man eben durch Regeln gewisse Übergänge
ausschließen & endlich muß das Bild auf der Geraden die
gleiche Art des Topologischen Zusammenhangs
bekommen wie auf dem Oktaeder. Es ist
dies ganz analog wie das Verhältnis der
gewöhnlichen Sprache zu einer „logisch geklärten” Ausdrucksweise. Beide sind einander
vollkommen äquivalent nur drückt die eine die Regeln der
Grammatik schon durch die äußere Erscheinung aus.
|
Der Satz ist vollkommen logisch analysiert dessen Grammatik
vollkommen klargelegt ist. Er mag in welcher
Ausdrucksweise immer hingeschrieben oder |
Die
Oktaederdarstellung ist eine
übersichtliche Darstellung der
grammatischen Regeln. |
Zu sehen daß reine Farbe nicht
eine Eigenschaft – externe Eigenschaft – einer Farbe ist
heißt sehen daß ich mir nicht denken könnte
daß – etwa – Violett diese Eigenschaft hat oder daß das reine
Blau sie nicht hat. |
Ebendasselbe ist der Fall wenn wir sagen ein
Ton sei im Einklang mit einem anderen. Es ist Unsinn
(nicht
falsch) zu sagen die Terz von
C sei im Einklang mit C. |
Wenn ich die Regelmäßigkeit einer Figur
sehe die ich früher nicht bemerkt habe so
sähe || sehe ich jetzt eine andere
Figur. So kann ich
❘ ❘ ❘ ❘ ❘ ❘
als Spezialfall von ❘ ❘ ❘ ❘
❘ ❘ oder von ❘ ❘ ❘
❘ ❘ ❘ oder von ❘ ❘ ❘ ❘ ❘
❘ sehen etc. Das zeigt bloß
daß was wir sehen nicht so einfach ist als es scheint.
|
Wenn man frägt ob die Tonleiter eine
unendliche Möglichkeit der Fortsetzung in
sich trägt so ist die Antwort nicht
dadurch gegeben daß man Luftschwingungen die eine gewisse
Schwingungszahl überschreiten nicht So wie dünne Linien in unserem Gesichtsfeld interne Eigenschaften zeigen die die dickeren nicht haben so daß es eine Linie in unserem Gesichtsfeld gibt die keine Farbgrenze ist sondern selbst Farbe hat & doch in einem bestimmten Sinne keine Breite so daß bei ihrem Schnitt mit einer anderen ebensolchen nicht vier Punkte  A, B, C, D
gesehen werden. A, B, C, D
gesehen werden. |
Eine Kirchentonart
verstehen heißt nicht sich an die Tonfolge
gewöhnen in dem Sinne in dem ich mich an
einen Geruch gewöhnen kann & ihn nach einiger Zeit nicht
mehr unangenehm empfinde. Sondern es heißt etwas
Neues hören was ich früher noch nicht
gehört habe etwa in der Art – ja ganz analog
– wie es wäre Zehn Striche
❘ ❘ ❘ ❘ ❘ ❘ ❘ ❘ ❘ ❘
die ich früher |
24.
Wenn mir zwei nahe beieinander || aneinander liegende – etwa – rötliche
Farbtöne gegeben sind so ist es unmöglich darüber zu
zweifeln, ob beide zwischen rot &
blau, beide zwischen rot & gelb oder der eine zwischen rot
& blau der andere zwischen rot & gelb gelegen
ist. & || Und mit
dieser Entscheidung haben wir auch entschieden ob beide sich mit blau,
mit gelb oder der eine sich mit blau der andere mit gelb
mischen & das gilt wie nahe immer man
die Farbtöne einander bringt solange wir die Pigmente
überhaupt unterscheiden können.
|
Die Harmonielehre ist nicht Geschmacksache. |
Unterschiede einer || Vergleich zwischen
einer Mathematischen Expedition & einer
Polarexpedition. Diesen Vergleich anzustellen hat
Sinn & ist sehr nützlich. |
Wie seltsam
wäre es wenn eine geographische Expedition nicht sicher
wüßte ob sie ein Ziel also auch ob sie
überhaupt |
Es wäre wie eine Expedition die des
Raumes nicht sicher wäre! |
25.
Wie
kann es in der Mathematik Vermutungen geben? Oder
vielmehr: Welcher Natur ist das was in der Mathematik wie
eine Vermutung aussieht? Wenn ich also etwa
Vermutungen über die Verteilung der Primzahlen
anstelle. |
Ich könnte mir
z.B. denken daß jemand in meiner
Gegenwart die Primzahlen der Reihe nach
hinschriebe, ich wüßte nicht daß es die Primzahlen sind
– ich könnte etwa glauben, es seien Zahlen wie sie
ihm eben einfielen – & nun versuchte ich irgend ein
Gesetz in ihnen zu finden. Ich könnte nun geradezu
eine Hypothese über diese Zahlenfolge aufstellen wie über
jede andere die ¤ ein physikalisches Experiment
ergibt. In welchem Sinne habe
ich nun hiedurch eine Hypothese über die Verteilung der
Primzahlen aufgestellt? |
Man könnte sagen eine
Hypothese in der Mathematik hat den Wert daß sie die Gedanken an
einen bestimmten Gegenstand – ich meine ein bestimmtes
Gebiet – heftet & man könnte sagen „wir werden gewiß etwas
Interessantes über diese Dinge herausfinden
–”. |
Das Unglück ist daß man so
grundverschiedene Dinge mit den
Worten || unsere Sprache so
grundverschiedene Dinge mit
jedem der Worte „Frage”, „Problem”, „Untersuchung”,
„Entdeckung” bezeichnet. Ebenso mit den Worten „Schluß”,
„Satz”,
„Beweis”. |
Es fragt sich wieder
welche Art der Verifikation lasse ich für
meine Hypothese gelten? Oder kann ich vorläufig
– faute de mieux – die empirische gelten
lassen solange ich noch keinen „strengen
Beweis” hätte || habe? Nein. Solange ein solcher
Beweis nicht besteht besteht gar keine Verbindung zwischen meiner
Hypothese & dem „Begriff” der
Primzahl. |
Der Begriff der Primzahl
ist das allgemeine Gesetz wonach ich prüfe ob ein Satz || eine Zahl
eine Primzahl ist oder nicht. |
Erst
der sogenannte Beweis verbindet die Hypothese
überhaupt mit |
Was ist der
analytische Ausdruck für das Parallelenaxiom?
|
Wie
hängen die Gleichungen der Analysis mit den
Resultaten von Messungen im Raum
zusammen. Ich glaube so daß sie – die
Gleichungen – bestimmen was als genaue Messung, was als
Fehler gelten soll. |
26.
Jede Hypothese ist
eine heuristische Methode. Und in dieser Lage ist, glaube
ich, auch die euklidische oder eine
andere Geometrie auf den Raum der physikalischen Messungen
angewandt. Ganz anders verhält es sich mit dem was man
die Geometrie |
Man könnte beinahe von
einer externen & einer internen Geometrie
reden. Das was im Gesichtsraum angeordnet ist steht in
dieser Art von Ordnung a priori,
d.h. seiner logischen Natur nach & die
Geometrie ist hier einfach Grammatik. Was der Physiker in
der Geometrie des physikalischen Raumes in Beziehung zu einander setzt
sind Instrumentablesungen die ihrer internen Natur
nach nicht anders sind ob wir in einem geraden oder sphärischen
physikalischen Raum leben.
D.h. Nicht eine Untersuchung der
logischen Eigenschaften dieser Ablesungen führt den Physiker zu
einer Annahme über die Art des physikalischen Raumes sondern die
abgelesenen Tatsachen. |
Die Geometrie der Physik
hat es in diesem Sinne nicht mit der Möglichkeit sondern
mit den Tatsachen zu tun.
& || Sie wird von Tatsachen
bestätigt, in dem Sinne, nämlich, in
dem ein Teil einer Hypothese bestätigt
wird. |
Vergleich des Arbeitens an der
Rechenmaschine mit dem Messen geometrischer
Gebilde. |
Machen wir bei dieser Messung ein Experiment oder verhält es
sich |
Im Gesichtsraum gibt es
natürlich kein geometrisches Experiment. |
Ich glaube daß
hier einer der Hauptpunkte || der Hauptpunkt des
Mißverständnisses über das a priori &
a posteriori der Geometrie liegt. |
Die Frage ist die
in welchem Sinne die Resultate von Messungen uns etwas
über dasjenige sagen
können was wir auch sehen. |
27.
Es ist
merkwürdig daß all dies mit der Frage der unendlichen
Möglichkeit unmittelbar zusammenhängt. |
Das was die Physik
ihren Raum nennt ist eine Hypothese – zum
Unterschied von dem was wir unseren Gesichts- oder
unseren Bewegungsraum nennen. |
Was bedeutet das Axiom
Euklids || Euklidische
Axiom daß alle rechten Winkel
untereinander gleich sind? |
Das Paradox daß alles was
ich in der Logik tun kann ist, Vereinbarungen betreffs
der Zeichen zu machen. |
28.
Wie könnte
ein Satz einen Sachverhalt darstellen dem die bloße Form des
Gedankens widerspricht? |
Es ist außerordentlich
schwer in allen Unsinn einzudringen den Menschen annehmen
können. |
Um etwas über die Farben –
z.B. – sagen zu können muß ich
gewisse Regeln einhalten. Diese Regeln sind daher ein Bild des Zweckes || spiegeln daher den Zweck zu welchem sie genau aufgestellt
sind. || wurden. |
Die Regeln passen die Sprache
diesem Zweck an. |
Ich könnte die Grammatischen
Konventionen zuerst machen ohne daß
einer wüßte daß ich eine Sprache
konstruiere oder wie ich die
Sprache anzuwenden
gedenke. Wie ich sie dann
anwende kann ich ihm nur dadurch begreiflich machen daß ich
sie vor ihm anwende, wenn ich sie
nicht in eine ihm bekannte Sprache übersetze.
Oder ich kann die Untersuchung in einer ihm bekannten Sprache also
einer deren Anwendung er kennt anstellen & dann
werden die grammatischen Regeln nur das enthalten |
Indem ich die
Konventionen mache
portraitiere ich freilich gleichsam
die logische Form eines bestimmten
Anwendungsgebietes meiner Sprache aber dennoch sind es
Konventionen. Und ich könnte sie
anders machen, freilich könnte ich dann die Sprache nicht
so anwenden wie im ersten Fall. |
Könnte ich den Zweck dieser
Konventionen dadurch beschreiben daß ich
sagte ich mußte sie machen weil etwa die Farben gewisse
Eigenschaften haben so wären damit die
grammatischen Konventionen
überflüssig denn dann
könnte ich eben das sagen was die
Konventionen gerade
ausschließen. Umgekehrt wenn die
Konventionen nötig
wären also gewisse
Kombinationen der Wörter als unsinnig
ausgeschlossen werden mußten dann kann ich eben darum nicht
eine Eigenschaft der Farben angeben |
Daß es unsinnig ist von
einer Farbe zu sagen sie sei eine Terz höher als eine andere kann
nicht bewiesen werden. Ich kann nur sagen „wer diese Worte in der Bedeutung verwendet
in der || wie ich es tue der
kann mit dieser Kombination keinen Sinn
verbinden – || , verbindet
er || hat sie für ihn einen Sinn so versteht er etwas
anderes unter den Worten als ich.” |
Die Wörter „Farbe”, „Ton”,
„Zahl”,
etc. können in den
Kapitelüberschriften der || unserer
Grammatik erscheinen. In den Kapiteln
müssen sie nicht vorkommen sondern da wird die
Struktur gegeben. |
1.3.
Wenn es einen Sinn
hätte zu sagen „rot ist eine
Farbe” dann gäbe es einen Satz
„es gibt eine Farbe”. Und wie wenn es nun keine gäbe, wie
könnten wir dann sagen daß es keine gäbe?
Wer aber unter „Farbe” etwas ganz
anderes versteht als ich, kann das sagen dann aber besteht für
ihn die |
Die Möglichkeit
der Erklärung dieser Dinge beruht immer darauf daß der
Andere die Sprache so gebraucht wie ich. Behauptet er
daß eine Zusammenstellung von Wörtern für ihn Sinn
hat die für mich keinen besitzt so kann ich nur annehmen daß
er die Wörter hier in anderer Bedeutung gebraucht als ich
oder gedankenlos redet. |
2.
Kann
jemand glauben es habe Sinn zu sagen: „Das ist kein Lärm,
sondern eine Farbe”? |
Anderseits
kann man freilich sagen: „Was mich nervös macht ist nicht der
Lärm sondern die Farbe” &
hier könnte es scheinen als ob eine Variable eine Farbe &
einen Lärm als Wert
annehmen könnte. || annähme. |
„Laute & Farben können als
sprachliche Ausdrucksmittel dienen.” |
Im Gesichtsraum
gibt es absolute Lage & daher
auch absolute Bewegung. Man denke sich das Bild
zweier Sterne in stockfinsterer Nacht |
Es ist klar
daß jener Satz von der Art ist: „Wenn Du einen Schuß hörst oder
mich winken siehst laufe zurück. || davon.” Denn dieser
Art ist die Vereinbarung auf der die Funktion der gehörten oder
gesehenen Sprache beruht. |
Wenn das Kind lernt
„Blau ist eine Farbe Rot
ist eine Farbe, Grün, Gelb, Orange, das sind alles
Farben” so lernt es nichts
Neues über die Farben sondern es lernt die
Bedeutung einer Variablen in den Sätzen „das Bild hat schöne
Farben”
etc..
Dieser || Jener Satz gibt ihm
die Werte einer Variablen. |
Es gibt offenbar eine
Methode ein gerades Lineal anzufertigen. Diese Methode
schließt ein Ideal ein, ich meine ein Näherungsverfahren
mit unbegrenzter Möglichkeit, denn eben dieses
Verfahren ist das Ideal. Oder vielmehr: Nur wenn es ein Näherungsverfahren mit unbegrenzter Möglichkeit ist kann (nicht muß) die Geometrie dieses Verfahrens die euklidische sein. |
Unendliche
Teilbarkeit & Vergrößerung eines Teils durch die
Lupe. |
Die unendliche Teilbarkeit hat |
Russell,
Eddington etc. wollen alle
Hohe Priester der
Irreligiosität sein. |
Wie ist
eine „formally certified
proposition”
möglich? Es wäre ein Satz dem man ansieht ob er
wahr oder falsch ist. „Grün ist eine
Farbe” wäre so ein
Satz. Aber wie kann man durch Hinsehen
auf den Satz oder den Gedanken herausfinden daß er wahr
ist? Der Gedanke ist doch etwas ganz anderes als der
Sachverhalt den er || der Satz
behauptet. Durch
Hinsehen auf den Satz kann ich nur
eines über die Natur ersehen was er aber nicht behauptet
& das ist die Möglichkeit dessen was er
behauptet. |
Die Grammatik zeigt es nicht
selbst daß sie zu einem bestimmten
Zweck gemacht ist. Sie könnte
allein betrachtet eine bloße
Sammlung von Spielregeln sein. Ihre
Anwendung liegt außer ihr.
|
Eine
Erklärung wenn sie wirken soll darf das Problem nicht
verschmieren. |
Wenn ich einem Menschen die Bedeutung eines Wortes A
erklären
will || erkläre indem ich sage „dies ist A”
& auf etwas hinzeige so kann
der || dieser Ausdruck
in zweierlei Weise gemeint sein.
Entweder er ist selber schon ein Satz & kann dann
erst verstanden werden wenn die Bedeutung von A bereits
bekannt ist. D.h. ich kann
es nur dem Schicksal überlassen ob der Andere den Satz nun so
auffaßt wie ich ihn meine oder nicht. Oder der Satz ist
eine Definition. Ich
habe || hätte jemandem etwa gesagt
„A ist krank” er wüßte aber nicht wen ich mit A meine
& nun zeigte ich auf einen Menschen & sagte „dies ist A”. Nun ist der Ausdruck eine Definition aber diese
kann nur verstanden werden wenn die Art des Gegenstandes bereits
durch den grammatisch verstandenen Satz „A ist krank”
bekannt war. Das heißt aber daß jede Art
des Verständlichmachens einer Sprache
schon eine Sprache voraussetzt. Und die
Benützung der Sprache in einem gewissen
Sinne nicht zu lehren ist. D.h. nicht
durch die Sprache zu lehren wie man etwa Klavierspielen durch die
Sprache lernen kann. – Das heißt ja nichts anderes
als: Ich kann mit der Sprache |
3.
Die
Grammatik ist eine „Theory of logical
types || der logischen Typen”. |
4.
Ich
nenne die Regel der Darstellung keine
Konvention, die sich durch Sätze
rechtfertigen läßt, Sätze welche das Dargestellte
beschreiben & zeigen daß die Darstellung adäquat
ist. Die Konventionen der Grammatik
lassen sich nicht durch eine Beschreibung des
Dargestellten rechtfertigen. Jede solche
Beschreibung setzt schon die Regeln der Grammatik
voraus. D.h. was in der zu
rechtfertigenden Grammatik als Unsinn gilt kann in der Grammatik der
rechtfertigenden Sätze auch nicht als Sinn
gelten. || und umgekehrt. |
5.
Man
kann nicht die Möglichkeit der Evidenz mit der Sprache
überschreiten. |
6.
Man
ist in der Philosophie immer in der Gefahr eine Mythologie des
Symbolismus zu geben oder der Psychologie.
Statt einfach zu sagen was jeder weiß &
zugeben muß. |
7.
Was für eine Art Satz ist: „auf diesem Streifen sind alle Schattierungen von
Grau zwischen Schwarz & Weiß zu sehen”? Hier scheint es auf den ersten Blick Ja wir haben hier das scheinbare Paradox || scheinbar das Paradox daß wir zwar nur endlich viele Schattierungen von einander unterscheiden können & der Unterschied zwischen ihnen natürlich nicht ein unendlich kleiner ist & wir dennoch einen kontinuierlichen Übergang sehen. |
9.
Weyls Widerspruch „heterologisch”: ~Φ(„Φ”) ≝ „Φ” ist heterologisch ≝ F(„Φ”) = F(“F”) = ~ F(“F”) = ~ [ ~
|
Der
menschliche Bewegungsraum ist
unendlich wie die Zeit. |
Die Methode des Messens – || , z.B. des
räumlichen Messens
– || , verhält sich zu
einer bestimmten Messung genau so wie der Sinn eines Satzes zu seiner
Wahr- oder Falschheit. |
Die Geometrie in dem
einen Sinn ist eine Methodologie des Messens. |
„Alle Helligkeitsgrade unter diesem tun meinen
Augen nicht weh”. Das heißt
ich habe ein
Gesetz beobachtet || beobachtet daß die bisherigen
Erfahrungen einem formellen Gesetz entsprechen.
|
Auf die
Frage ob die Philosophen bis jetzt || bisher immer wirklichen Unsinn geredet haben
könnte man antworten nein, sie haben nur nicht gemerkt
daß sie das || ein Wort in ganz
verschiedenen Bedeutungen gebrauchen. In
diesem Sinne ist es nicht unbedingt
Unsinn zu sagen ein Ding sei so identisch wie das
andere denn wer das mit Überzeugung sagt meint in
diesem Augenblick etwas mit dem Wort „identisch”
(vielleicht „groß”)
aber er weiß nicht daß er hier das Wort in anderer
Bedeutung gebraucht als es in
2 + 2 = 4
gebraucht ist. |
10.
Welcher Art war Sheffers Entdeckung daß p ⌵ q & ~ p sich
durch p ∣ q ausdrücken
lassen? |
Man hatte keine Methode
nach p ∣ q zu suchen & wenn man
heute eine fände so könnte das keinen Unterschied
machen. |
Was war es was wir vor
der Entdeckung nicht wußten? Ich
glaube Es war nichts da was wir nicht
wußten sondern etwas was wir nicht
kannten. |
Das sieht man sehr
deutlich wenn man sich den Einspruch erhoben denkt Ist es ein Suchen, wenn ich das System Sheffers nicht kenne & sage ich möchte ein System mit nur einer logischen Konstanten konstruieren. Nein! Die Systeme sind ja gar nicht in einem Raum so daß ich sagen könnte: Es gibt Systeme mit 3 & 2 logischen Konstanten nun suche ich die Zahl der Konstanten in derselben Weise zu vermindern. Es gibt hier keine selbe Weise! |
Man kann nicht ein gegebenes Grau
als eines von den unendlich vielen grauen Tönen zwischen Schwarz
& Weiß auffassen. |
Aber den kontinuierlichen
Übergang – z.B. von
Weiß nach Schwarz – nimmt man ja tatsächlich
wahr. Handelt es sich auch hier nur um eine unendliche
Möglichkeit? Ist nicht die
Kontinuität selbst eine Art unendlicher
Wirklichkeit. Aber haben wir hier nicht denselben Fall wie
den des Kreises aufgefaßt als ein
∞-Eck? Hier ist der Kreis
ein Grenzwert. |
11. Man kann ein bestimmtes
Grau ebensowenig als eines der unendlich vielen Grau
etc. auffassen wie man eine
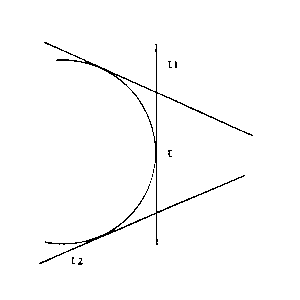 Tangente
t als eines der unendlich vielen
Übergangsstadien von t1 nach
t2 auffassen kann. Wenn ich etwa ein Lineal
sich von t1 nach t2 am Kreis abrollen
sehe so sehe ich ¤ – wenn es sich
kontinuierlich bewegt – keine
einzige der Zwischenlagen in dem Sinne in welchem
ich t sehe wenn die Tangente ruht; oder aber ich
sehe nur eine endliche Anzahl von
Zwischenlagen. Wenn ich aber
in so einem Fall scheinbar
vom einen || von
einem allgemeinen Satz auf einen Spezialfall schließe so
ist die Quelle dieses allgemeinen Satzes nie die Erfahrung &
der Satz wirklich kein Satz. Tangente
t als eines der unendlich vielen
Übergangsstadien von t1 nach
t2 auffassen kann. Wenn ich etwa ein Lineal
sich von t1 nach t2 am Kreis abrollen
sehe so sehe ich ¤ – wenn es sich
kontinuierlich bewegt – keine
einzige der Zwischenlagen in dem Sinne in welchem
ich t sehe wenn die Tangente ruht; oder aber ich
sehe nur eine endliche Anzahl von
Zwischenlagen. Wenn ich aber
in so einem Fall scheinbar
vom einen || von
einem allgemeinen Satz auf einen Spezialfall schließe so
ist die Quelle dieses allgemeinen Satzes nie die Erfahrung &
der Satz wirklich kein Satz. Wenn ich z.B. sage: „ich habe das Lineal sich von t1 nach t2 bewegen sehen also muß ich es auch in t gesehen haben” so haben wir hier keinen richtigen logischen Schluß: Wenn ich nämlich damit sagen will das Lineal muß mir in der Lage t erschienen |
Man kann einen Teil einer
Hypothese vergleichen mit der Bewegung eines Teils eines Getriebes einer
Bewegung die man festlegen kann ohne dadurch die bezweckte Bewegung
irgendwie zu bestimmen || zu
präjudizieren. Wohl aber hat man dann
das übrige Getriebe auf eine bestimmte Art einzurichten daß es
die gewünschte Bewegung hervorbringt. Ich denke an ein
Differentialgetriebe. 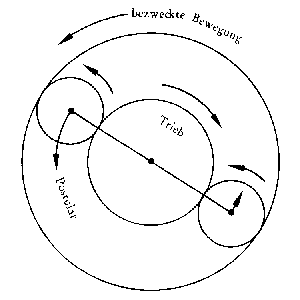 Habe ich die Entscheidung getroffen daß von einem gewissen Teil
meiner Hypothese nicht abgewichen werden soll was immer die zu
beschreibende Erfahrung sei so habe ich eine
Darstellungsweise festgelegt & jener Teil der Hypothese ist
nun ein Postulat. Ein Postulat muß von solcher
Art sein daß keine denkbare Erfahrung es widerlegen kann, wenn es
auch äußerst unbequem sein mag an dem
Habe ich die Entscheidung getroffen daß von einem gewissen Teil
meiner Hypothese nicht abgewichen werden soll was immer die zu
beschreibende Erfahrung sei so habe ich eine
Darstellungsweise festgelegt & jener Teil der Hypothese ist
nun ein Postulat. Ein Postulat muß von solcher
Art sein daß keine denkbare Erfahrung es widerlegen kann, wenn es
auch äußerst unbequem sein mag an dem |
12. Von einem Maß dieser
Wahrscheinlichkeit zu reden ist nun vorderhand
sinnlos. Es ist
ähnlich || verhält sich hier ähnlich wie im
Falle etwa zweier Zahlenarten wo wir mit einem gewissen Recht
sagen können die eine sei der anderen ähnlicher || stehe ihr näher als einer dritten ein
zahlenmäßiges Maß der Ähnlichkeit aber nicht
existiert. Man könnte sich natürlich auch in
solchen Fällen ein Maß konstruiert denken indem man etwa
die Postulate oder Axiome zählt die beide
Systeme gemeinsam haben etc.
etc.. |
Ich gebe jemandem die
Information & nur diese: Du wirst um
eine || diese & diese Zeit auf der Strecke AB
einen Lichtpunkt erscheinen sehen.
A|–––––––––
Ich kann freilich bestimmen daß die Wahrscheinlichkeit daß das Ereignis in CB eintritt sich zu der daß es in AC eintritt verhalten soll wie
Könnte ich nicht auch im Fall des Würfels etwa 5 Flächen zusammennehmen als eine Möglichkeit & sie der 6ten als der zweiten Möglichkeit gegenüberstellen? Und was außer der Erfahrung kann mich hindern diese zwei || beiden Möglichkeiten als gleich wahrscheinlich zu betrachten? |
Wenn man
glaubt sich einen |
Denken wir uns das Würfeln mit einer
Kugel (statt eines Würfels) deren Oberfläche in
gleiche oder ungleiche Teile verschiedener Färbung geteilt
ist. Kann ich hier a priori sagen daß
gleichen Teilen der Kugelfläche
gleiche Wahrscheinlichkeiten entsprechen? |
13. Denken wir uns etwa einen
roten Ball geworfen der nur eine ganz kleine grüne
Kalotte hat. Ist es in diesem Fall nicht viel
wahrscheinlicher daß er auf dem roten Teil auffällt als auf
den grünen? – Wie
würde man aber diesen Satz begründen?
Wohl dadurch daß der Ball wenn man ihn wirft viel öfter auf
die rote als auf die grüne Fläche
auffällt. Aber das hat nichts mit der Logik zu
tun. – Man könnte die rote & grüne
Fläche & die Ereignisse die auf ihnen stattfinden
immer auf solche Art auf eine Fläche
projizieren daß die
Projektion der grünen Fläche gleich
oder auch größer wäre als die der roten, so |
Dasjenige was der Spiegel nicht
verändern kann ist die Anzahl bestimmt umrissener
Möglichkeiten. Wenn ich also auf meinem Ball n
Farbflecke habe so zeigt der Spiegel auch n, und
habe ich bestimmt daß diese als gleich wahrscheinlich
gelten sollen so kann ich diese Bestimmung auch für das
Spiegelbild aufrecht erhalten. |
Um mich noch deutlicher
zu machen: wenn ich das Experiment im Hohlspiegel
ausführe d.h. die
Beobachtungen im Hohlspiegel mache so wird es
vielleicht scheinen als fiele der Ball
öfter auf die kleine Fläche als auf die viel größere
& es ist klar daß keinem der Experimente im Hohlspiegel
& unmittelbar gesehen || außerhalb ein Vorzug gebührt.
|
Was heißt es nun aber eigentlich zu
sagen || bestimmen zwei
Möglichkeiten hätten |
Heißt es nicht daß erstens die uns
bekannten Naturgesetze keine der beiden Möglichkeiten
bevorzugen & zweitens die
relative Häufigkeit || relativen
Häufigkeiten der Ereignisse sich unter
gewissen Umständen in beiden Fällen || in beiden
Fällen sich unter gewissen Umständen einander
nähern. |
20.
Manche Theorien der Russellschen &
Fregeschen
Logik machen || Die Theorie der Identität bei
Ramsey macht
den Fehler den man machen
würde wenn man sagte ein gemaltes Bild könne man auch als
Spiegel benutzen wenn auch nur für eine einzige Stellung wo dann
übersehen wird daß das Wesentliche beim Spiegel gerade das ist
daß man aus ihm auf der Stellung des Körpers vor dem Spiegel
schließen kann während man im Fall des gemalten Bildes erst
wissen muß daß die Stellungen übereinstimmen ehe man das
Bild als Spiegelbild auffassen kann. |
21.
Die Einführung der Kardinalzahl. Sind es
dieselben Zahlen mit denen ich die Pferde in einem Stall
& die verschiedenen Tierarten im Stall zähle?
Mit denen ich die Striche auf der Zeile & die Arten
von Gruppen (mit || nach den
verschiedenen Strichzahlen)
zähle? ❘ ❘ ❘ ❘ ❘ ❘ ❘ ❘ ❘ ❘ ❘ ❘ ❘ ❘ ❘ ❘ ❘ ❘ ❘ ❘ ❘ ❘ ❘ Ob es im gleichen Sinne Kardinalzahlen sind hängt doch davon ab ob die gleichen syntaktischen Regeln für beide || sie gelten. Daß auf || in einem Zimmer kein Mensch ist, ist denkbar aber nicht daß ein Mensch keiner Rasse darin ist. Wenn das ein wesentlicher Unterschied ist, muß er sich natürlich durch die ganze Arithmetik ziehen. |
Die
Arithmetik ist die Grammatik der Zahlen. Zahlenarten
können sich nur durch die sich auf sie beziehenden arithmetischen
Regeln unterscheiden. |
Man empfindet immer eine
Scheu die Arithmetik zu begründen indem man etwas über ihre
Anwendung ausspricht. Sie scheint uns
fest genug in sich selbst begründet zu sein. Und das
kommt natürlich alles daher daß die
Arithmetik ihre eigene Anwendung ist. |
Die Gefahr die darin liegt
Dinge einfacher sehen zu wollen als sie in Wirklichkeit sind
|
Die Kardinalzahl ist auf die
Subjekt-Prädikat-Form
anzuwenden, aber nicht auf jede Abart dieser Form.
Und soweit sie anwendbar ist charakterisiert sie eben die
Subjekt-Prädikat-Form. |
Einerseits
kommt es mir vor kann man die Arithmetik ganz
selbständig entwickeln & ihre Anwendung
sorgt für sich selbst, denn wo immer sie
anwendbar ist dort darf man sie auch anwenden.
Anderseits kann eine nebulose Einführung des
Zahlbegriffes mit Hilfe einer allgemeinen
Operationsform – wie ich es machte – nicht
nötig sein. |
Ich möchte die Arithmetik
zurechtlegen daß sie angewendet werden kann, wenn man sie
braucht. |
22. Das ist der Grund warum sich die Auffassung
der Arithmetik als eines Spiels so hartnäckig |
Man
könnte sagen: die Arithmetik ist eine Art Geometrie;
d.h. was in der Geometrie die
Konstruktionen auf dem Papier sind sind in der Arithmetik die
Rechnungen (auf dem Papier).
Man könnte sagen, sie ist eine allgemeinere Geometrie. |
Und kann ich nicht sagen daß in diesem Sinne auch das
Schachspiel (oder jedes andere) eine Art Geometrie
ist? Dann muß aber eine Anwendung des Schachspiels ganz analog der der Arithmetik ausgedacht werden können. |
Man könnte sagen: Wozu die Anwendung der
Arithmetik einschränken, sie sorgt für sich
selbst. |
Das wäre also so wie
man sagen könnte: Ich kann ein Messer herstellen ohne
Rücksicht darauf welche Klasse von Stoffen sich damit werden
schneiden lassen; das wird sich dann schon zeigen. |
Gegen die Abgrenzung des Anwendungsgebiets spricht
nämlich das Gefühl daß wir die Arithmetik
|
23.
Kritik der
Fregeschen Theorie der
Kardinalzahlen. Sie muß mit der Kritik
des Begriffes || der Begriffe „Begriff” &
„Gegenstand” anfangen. |
24.
Ich zähle
z.B. die Bäume im Garten.
Baum im Garten gilt als (eine) Eigenschaft. Aber was ist das Ding, das
diese Eigenschaft hat? Angenommen sie seien
irgendwelche Örter im Raum; dann zähle ich also die
Örter. Auch wenn ich Baum einen Stock nenne der im
Frühjahr ausschlägt so kann ich den Träger des
Prädikats als eine Art Ort
auffassen. |
Hier
könnte || kann es scheinen als ob die Zahlangabe
irgend eine Verallgemeinerung oder Unbestimmtheit
enthielte. Wie ist es aber mit einem Satz wie:
Die Strecke AB ist in 2 , (3, 4, 5
etc.) gleiche Teile
geteilt? Hier ist keine Unbestimmtheit
vorhanden. |
Es handelt sich immer darum ob &
wie es möglich ist die allgemeinste |
Es scheint nämlich die allgemeine
Form ihrer Anwendung dadurch dargestellt zu sein, daß
nichts über sie ausgesagt wird. (Und ist
das eine mögliche Darstellung so ist es auch die
richtige.) |
Das Charakteristische
an der Zahlangabe ist daß man für die eine || statt der einen Zahl jede andere einsetzen kann
und der Satz immer sinnvoll bleiben
muß. Das Charakteristische ist eben die
unendliche Reihe || Formenreihe von
Sätzen. |
Der Sinn der Bemerkung, daß die
Arithmetik eine Art Geometrie sei ist eben daß die
arithmetischen
Konstruktionen autonom sind wie die
geometrischen & daher sozusagen ihre Anwendbarkeit
selbst garantieren. Denn auch von der Geometrie muß man sagen können sie sei ihre eigene Anwendung. |
Was heißt es:
man kann eine |
Allgemeinheit der
Euklidischen Beweise. Man
sagt die Demonstration wird an einem Dreieck
ausgeführt || durchgeführt,
der Beweis gilt aber für alle Dreiecke –
oder für jedes beliebige Dreieck. Erstens ist es
sonderbar daß was für ein Dreieck gilt darum für alle
anderen gelten sollte. Es wäre doch nicht möglich
daß ein Arzt einen Menschen untersucht & nun
schließt, daß was er bei diesem konstatiert
& || auch für alle anderen
wahr ist || sein muß. Und
wenn ich nun die Winkel in einem Dreieck messe Die Konstruktion des Beweises ist aber wieder kein Experiment & wäre sie es so könnte das Resultat nichts über || für andere Fälle beweisen. Es ist darum auch gar nicht nötig die Konstruktion mit Papier & Bleistift wirklich auszuführen sondern die Beschreibung der Konstruktion muß genügen um aus ihr alles Wesentliche zu ersehen. (Die Beschreibung eines Experiments genügt nicht um aus ihr das Resultat des Experiments zu entnehmen sondern das Experiment muß wirklich ausgeführt werden.) Die Konstruktion im Euklidischen Beweis ist genau analog dem Beweise daß 2 + 2 = 4 mittels der russischen Rechenmaschine. |
Und ist dies nicht auch die Art der Allgemeinheit der Tautologien
der Logik die für p q r
etc. bewiesen || demonstriert werden? |
Das
Wesentliche ist in allen diesen Fällen, daß, was demonstriert
wird, nicht durch |
Die Euklidische Geometrie setzt
keine Meßmethode der Winkel & Strecken voraus sie
sagt ebensowenig unter welchen
Umständen zwei Winkel als gleich zu gelten haben wie die
Wahrscheinlichkeitsrechnung wann zwei Wahrscheinlichkeiten
als gleich gelten sollen. Ist dann eine bestimmte
Meßmethode angenommen etwa die || eine mit eisernen Maßstäben dann frägt es sich ob
die Resultate der so ausgeführten Messungen
euklidische Resultate
liefern. |
Die Geometrie sagt also etwa: Wenn diese beiden Winkel
als gleich gelten dann gelten auch jene als gleich. |
Unterscheidet sich die || der Fall des
allgemeinen Satzes der rote || ein roter Kreis befindet sich im
Quadrat wesentlich von einer allgemeinen Aussage der Zahlengleichheit
etwa „ich habe ebensoviele
Röcke als Hosen”? Und
ist dieser Satz nicht wieder ganz analog dem „in diesem Zimmer stehen eine Anzahl
Sessel”? Freilich im
gewöhnlichen Leben braucht man mit der Disjunktion der
Anzahlen überhaupt Auch wenn der erste Fall so verstanden wird daß wir die Lage & Größe des Kreises durch Messung feststellen können, auch dann kann der allgemeine Satz nie als Disjunktion verstanden werden (oder wenn, dann eben als endliche). Denn was ist denn das Kriterium dafür (für den allgemeinen Satz) daß der Kreis im Quadrat ist? Entweder überhaupt nichts, was mit einer Mehrheit von Lagen (bezw. Größen) zu tun hat oder aber (natürlich) etwas was mit einer endlichen Anzahl solcher Lagen zu tun hat. |
Zeichenregeln
z.B. Definitionen kann man zwar als Sätze
die von Zeichen handeln auffassen, aber man muß sie gar
nicht als Sätze auffassen. Sie sind Hilfsmittel
der Sprache. Hilfsmittel anderer Art als die
Sätze der Sprache. |
Die Frage „wieviele
Lösungen hat diese Gleichung” ist
das
In-Bereitschaft-Halten
der allgemeinen Methode zu ihrer Lösung. |
Angenommen mit dieser
Rechnung wollte ich folgende || folgende
Aufgabe lösen: Wenn ich 11 Äpfel habe
& Leute mit je 3 Äpfeln beteilen
will wieviel Leute kann ich beteilen? Die Rechnung liefert mir die Antwort || Lösung 3. Angenommen nun ich vollzöge alle Handlungen des Beteilens & am Ende hätten 4 Personen je 3 Äpfel in der Hand. Würde ich nun sagen die Ausrechnung hat ein falsches Resultat ergeben? Natürlich nicht. Und das heißt ja nur, daß die Ausrechnung kein Experiment war. |
Es könnte scheinen als berechtigte uns die
mathematische Ausrechnung zu einer Vorhersagung etwa
daß ich 3 Personen werde beteilen können & 2
Äpfel übrig bleiben werden. So ist es aber
nicht. Zu dieser Vorhersagung |
So verschieden Striche
& Gerichtsverhandlungen sind, so kann man doch
diese durch || Gerichtsverhandlungen
durch Striche in einem Kalender darstellen. Und kann
die einen statt den anderen
zählen. Seltsamerweise ist es nicht so wenn ich etwa Hutgrößen zählen will. Hier drei Hutgrößen durch drei Striche zu repräsentieren wäre nicht natürlich. Nicht ebenso wie wenn ich eine Maßzahl – 3 m – durch drei Striche darstellen wollte? Oder vielmehr: man kann das ja tun nur stellt dann „❘ ❘ ❘” auf eine andere Weise dar. |
Wenn drei
Striche auf dem Papier das Zeichen für die 3 sind dann kann man
sagen die 3 ist so anzuwenden wie sich 3 Striche anwenden
lassen. |
Der Buchstabe
π steht für ein
Gesetz. Das Zeichen
|
Der Begriff „Primzahl” ist die
allgemeine Form der Untersuchung einer Zahl auf die betreffende
Eigenschaft hin; der Begriff „teilbar” die
allgemeine Form der Untersuchung auf die Teilbarkeit
u.s.f. |
Ist es nicht klar daß es bestimmter
sein muß zu sagen 26 durch 5 geben den Rest 1 als zu sagen es
sei durch 5 nicht teilbar.
D.h. ist es damit nicht klar daß ich in
gewissem Sinne unbestimmte Sätze in der Arithmetik haben
kann? |
Daß 26 durch 5 nicht teilbar ist kann
man ja daraus erkennen daß 26 an der Einerstelle keine 5 hat
und hier haben wir wieder einen unbestimmten Satz. |
Aber haben wir
hier nicht was ich früher einmal sagte daß nämlich die
Negation oder die Ungleichungen in der Arithmetik nur in einer
gewissen Allgemeinheit |
Eine Gleichung wie eine Ungleichung || Ungleichung wie eine Gleichung muß entweder das Resultat
einer Ausrechnung oder eine Festsetzung sein. 5 ≠ 6 ist eine Festsetzung. |
So wie die Gleichungen
als Zeichenregeln im Gegensatze zu Sätzen aufgefaßt
werden können so muß es auch bei den Ungleichungen
geschehen können. |
Wie kann man
denn eine Ungleichung gebrauchen? Das
führt zu dem Gedanken daß es in der Logik auch die interne
Beziehung des nicht Folgens gibt
& es kann wichtig sein zu erkennen daß ein Satz aus einem
anderen nicht folgt. |
Die Verneinung der
Gleichung ist so ähnlich & so verschieden von der
Verneinung eines Satzes wie die Bejahung der Gleichung der Bejahung
eines Satzes. |
Es ist ganz klar daß die Negation in der
Mathematik || Arithmetik
gänzlich verschieden ist von der eigentlichen
Negation von Sätzen. |
Ich glaube sie entspricht
immer einer gewissen Disjunktion von Fällen.
Und es ist ja klar daß dort wo sie wesentlich – aus den logischen Verhältnissen heraus – einer Disjunktion entspricht oder einer Ausschließung eines Teils einer logischen Reihe zugunsten eines anderen – daß sie dort eine ganz andere Bedeutung haben muß. Sie muß ja eins sein mit jenen logischen Formen und also nur scheinbar eine Negation. |
Wenn „nicht-gleich”,
größer oder kleiner bedeutet so kann das für das „nicht” nicht, so zu
sagen, ein Zufall sein. |
Ein mathematischer Satz
kann nur, entweder eine Festsetzung sein, oder ein nach einer
bestimmten Methode aus
Festsetzungen errechnetes Resultat.
Und das muß für „7 || 9 ist durch 3 teilbar” oder „9 ist durch 3 nicht teilbar” gelten. |
Wie
errechnet man daß
2 × 2 ≠
5? Anders als
2 × 2 =
4? Wenn überhaupt dann über „2 × 2 =
4” und mit „4 ≠ 5”. |
Und wie errechnet man „9 ist durch 3 teilbar”? |
Man könnte
es als eine Disjunktion auffassen & dann erst
berechnen || rechnen
9 : 3 =
3 und dann statt dieses bestimmten Satzes die Disjunktion
nach einer Schlußregel einsetzen. || ableiten. |
Hilft uns hier nicht
die || meine Bemerkung daß die Negation
in der Arithmetik immer nur in Verbindung mit der
Allgemeinheit von Wichtigkeit ist: Die
Allgemeinheit wird aber durch eine
Induktion ausgedrückt. |
Es ist mir klar daß die Arithmetik nicht falsche
Gleichungen zu ihrem Aufbau braucht, aber es
scheint mir daß man wohl sagen kann
zwischen 10 & 20 || 11 &
17 liegt eine Primzahl ohne sich dabei auf falsche
Gleichungen zu beziehen. |
Zu dem
vorletzten Satz: Und dadurch wird es möglich daß Negation & Disjunktion die im Einzelfall (besonderen Fall) als überflüssige Unbestimmtheiten wirken im allgemeinen „Satz”, d.h. in der Induktion der Arithmetik wesentlich werden. |
Die Division liefert ein
Zahlenpaar. Ist ein Grund einer der beiden Zahlen den Vorzug zu geben? Das heißt in sofern nichts als man nicht statt 13/5 schreiben könnte (2,3) sondern nur 2 +
|
So wie
8 × 8 =
62 eine Vorhersage ist es werde bei der
Multiplikation 60 herauskommen, so ist „60 ist durch 8 teilbar” die Vorhersage es werde sich bei
der Division der Rest 0 ergeben. Beides kann man
unmittelbar prüfen, es gibt eine Methode, & also
sollte es hier auch Frage & Behauptung geben
können.
R
|
Eine Ungleichung kann so
gut auf ihre Richtigkeit geprüft werden, wie eine
Gleichung. |
Ist nicht eine Ungleichung eine völlig
verständliche
Zeichenregel, wie |
Ist es nun aber nicht so,
daß was nicht ausdrücklich erlaubt ist, verboten
ist? |
Es kann sicher von Bedeutung (im praktischen Leben) sein
daß
3 × 3 nicht
10 ist (etwa bei einer Verteilung) aber
warum schreiben wir nie
3 × 3 ≠
10. Wenn wir den Schluß im
gewöhnlichen || praktischen Leben wirklich
ausführen so sagen wir „3 × 3 ist
aber 9 & darum kann ich die Sachen nicht so
verteilen”. Zu sagen
„3 × 3 ist
aber nicht 10” wäre (beinahe) ironisch; aber warum sollte ich es nicht so
ausdrücken, wenn mir nämlich am Resultat von
3 × 3
nichts liegt sondern nur daran daß
ich die vorgeschlagene Verteilung nicht ausführen
kann. |
Wesentlich ist vielleicht nur daß man einsieht
daß, was sich durch Ungleichungen ausdrückt
wesentlich verschieden ist von dem durch Gleichungen
Ausgedrückten. Und so
kann man ein Gesetz das
Ziffern || die Stellen eines
Dezimalbruchs liefert & mit Ungleichungen arbeitet
gar nicht unmittelbar mit einem vergleichen welches
mit Gleichungen |
D.h. man kann nicht in der Arithmetik
Gleichungen & etwas Anderes (etwa Ungleichungen)
ohne weiteres auf eine Stufe stellen als wären
es etwa verschiedene Tiergattungen. Sondern
die beiden Methoden werden dann
kategorisch verschieden sein &, mit
einander unvergleichbare, Gebilde definieren || bestimmen. |
Die Negation in der
Arithmetik kann nicht das Gleiche sein wie die Negation von
Sätzen denn sonst müßte ich mir in
2 × 2 ≠
5 ein Bild machen wie es wäre wenn
2 × 2 =
5 wäre. |
„ = 5”, „durch 5
teilbar”, „nicht durch 5 teilbar”, „prim” könnte man arithmetische
Prädikate nennen & sagen:
Die arithmetischen Prädikate
entsprechen immer der Anwendung einer bestimmten allgemein
definierten Methode. Man kann ein Prädikat auch
so definieren (ξ × 3 =
25) ≝ F(ξ) „F”
ist das Prädikat. |
Arithmetische Prädikate, die im
besonderen Fall trivial || unwichtig sind –
weil die bestimmte Form die unbestimmte überflüssig macht
– werden im allgemeinen
Gesetz d.h. in der
Induktion bedeutungsvoll. |
3 × 3
= 9 ⌵ 3 × 3 = 10 Warum ist das
trivial? |
Man könnte
sagen „es sind wohl verschiedene
Hutgrößen aber ich stelle sie ja auch durch drei
verschiedene Striche dar”.
Aber hier hat das Wort „verschieden” zwei
verschiedene Bedeutungen. |
Wovon drei Striche ein
Bild sind, als dessen Bild können sie dienen. |
Das worauf sich die Reihe der
Kardinalzahlen bezieht sind nie
Gegenstände im Sinne von Elementen der
Erkenntnis, sondern Gebilde,
räumliche, || & zeitliche,
wie die Striche auf meinem Papier die sie vertreten. |
25.4. Nach den Osterferien wieder
in Cambridge
angekommen. In Wien oft mit der
Marguerite.
Ostersonntag mit ihr in Neuwaldegg.
Wir haben uns viel
geküßt drei
Stunden lang und es war sehr schön.
|
Die Methoden der
neueren mathematischen Logiker erinnern – glaube ich –
an die Methode der gegenwärtigen
Experimentalpsychologen. In beiden wird zwar etwas
Bestimmtes gearbeitet nur irren sich beide in
Bezug auf die Bedeutung & Tragweite ihrer
Arbeit. Die Tests der Intelligenz, Geistesgegenwart
etc. prüfen schon etwas aber nicht das
was wir Geistesgegenwart, Intelligenz
etc. nennen & die Beweise
der Widerspruchsfreiheit
beweisen || zeigen wohl etwas aber
nichts Wichtiges. So glaube ich wenigstens. Sie
krabbeln immer an der Oberfläche der Fragen herum
& sehen das eigentlich Wesentliche überhaupt
nicht. Ist die eigentliche Arbeit aber geleistet dann
werden viele jener äußerlichen Spiele
obsolet oder müssen doch erst gänzlich umgedeutet
werden. (Auch hier ist wieder viel Technik &
kein Geist.) |
27.4.
Wenn
ich sage || man
sagt der Fleck A ist irgendwo zwischen den
Grenzen B & C, ist es denn nicht
 offenbar
möglich eine Anzahl von Stellungen des A zwischen
D || B & C zu
beschreiben oder abzubilden, so daß ich die
Sukzession aller dieser Stellungen
für einen
kontinuierlichen Übergang nehme || als kontinuierlichen
Übergang sehe? Und ist dann nicht die offenbar
möglich eine Anzahl von Stellungen des A zwischen
D || B & C zu
beschreiben oder abzubilden, so daß ich die
Sukzession aller dieser Stellungen
für einen
kontinuierlichen Übergang nehme || als kontinuierlichen
Übergang sehe? Und ist dann nicht die
Aber wie verhält es sich mit diesen N Bildern? Es ist klar, daß ein Bild & das unmittelbar folgende visuell nicht unterscheidbar sein dürfen sonst ist der Übergang visuell diskontinuierlich. |
28.
In unserer
Notation oder Ausdrucksweise drückt sich auch aus
welche Ähnlichkeiten – & welche
Verschiedenheiten – wir besonders betont wissen wollen.
So nennt man einmal alles Räume was eine ähnliche
Struktur hat wie der Raum & will immer
darauf || auf diese Analogie
hinweisen. Und dann wieder will man nur diese
Analogie weil sie zu
Konfusionen führt fliehen
& die Verschiedenheit der „Räume” betonen
& nun bezeichnet man die frühere Ausdrucksweise als
irreführend & gebraucht selbst eine andere ebenso
irreführende – wenn man sie nämlich nicht
ganz versteht. |
Der kleinste sichtbare Unterschied wäre
einer der in sich selbst das
Kriterium des kleinsten trüge.
Denn im Fall des Flecks A zwischen B & C unterscheiden wir eben einige Lagen & andere unterscheiden wir nicht. Was wir aber brauchten wäre |
Zu jeder Wahrheit die mir jemand
entgegenhält muß ich immer sagen „ich habe nichts
dagegen! analysiere sie
nur gründlich dann muß ich mit dir
übereinstimmen”. |
Der Raum besteht
offenbar nicht aus
diskreten
﹖ || bestimmten ﹖ ⋎
Teilen. Denn sonst müßte man unmittelbar sagen können, aus welchen. Der Raum ist aber offenbar homogen. |
29.
Gehe geradeaus so
wirst Du, ehe Du zur anderen Wand kommst, mit der Hand an etwas
(Weiches) stoßen. Dieser Art sind jene
allgemeinen Sätze. Schau dem Tisch entlang so wirst Du
einen Strich sehen. Man gibt quasi eine Methode die ich
aber nicht „allgemein”
nennen möchte weil sie Ja im Falle man eine Bewegung macht ist es besonders klar. Wenn ich sage „Wischen Sie den Tisch ab” so meine ich nicht „Wischen Sie jeden Punkt || alle Punkte ab”. |
Es will einem vorkommen als
wäre es gar keine Allgemeinheit sondern etwas wie ein
spezielles Symptom einer Allgemeinheit.
Etwa wie wenn ich sage: „Wenn Du mein Fenster erleuchtet siehst, so
bin ich zu Hause”. Die || Eine
Allgemeinheit liegt dann darin daß ich irgendwo in meinem Zimmer
sein kann; das erleuchtete Fenster hat aber nicht die
Multiplizität einer Allgemeinheit & bezieht sich daher
auch nicht auf eine Gesamtheit sondern auf das
Substrat, welches als Substrat einer Gesamtheit dienen
kann. |
Die Möglichkeit welcher Art immer sie ist muß die Logik
voraussehen (d.h. es gibt keine
logische Überraschung).
Und im Raum besteht eben diese Möglichkeit nicht aus einer
Anzahl diskreter Möglichkeiten. |
30.
Der Raum ist
sozusagen eine Möglichkeit.
Er besteht nicht aus mehreren Möglichkeiten. |
Wenn ich also höre das Buch liegt – irgendwo – auf
dem Tisch & finde es nun in einer
bestimmten Stellung so kann ich nicht
überrascht sein & sagen „Ah, ich habe nicht gewußt daß es
diese Stellung gibt” & doch hatte
ich diese besondere Stellung nicht vorhergesehen
d.h. als besondere Möglichkeit vorher ins
Auge gefaßt. |
Was ist nun
aber der Unterschied zwischen dem Fall „das Buch liegt irgendwo auf dem
Tisch” & dem „das Ereignis wird irgend einmal in
Zukunft eintreten”?
Offenbar der daß wir in einem || im einen Fall eine sichere Methode kennen zu verifizieren ob das Buch auf dem Tisch liegt im anderen Fall eine analoge Methode nicht existiert. Wenn etwa ein bestimmtes Ereignis bei einer der unendlich vielen Bisektionen einer Strecke eintreten sollte oder besser wenn es eintreten sollte wenn wir die Strecke in einem (ohne nähere Bestimmung) Punkt || Punkt (ohne nähere Bestimmung) schneiden & an diesem Punkt eine Minute verweilen so ist diese Angabe ebenso sinnlos wie die über die unendliche Zukunft. |
(Nonsense is just
nonsense.) |
Wenn einer gegen eine
Euklidische
Demonstration |
Man möchte
hier immer sagen „es kommt
nicht auf die Buchstaben, oder die genaue Form des Dreiecks,
an”. Aber was
bedeutet das? |
1.5
Was heißt es
„von allem Unwesentlichen
absehen”? |
In der Demonstration –
z.B. – daß Scheitelwinkel gleich
sind 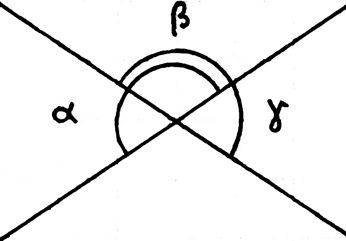 α + β =
β + γ :. α =
γ könnte man sich die Figur in
fortwährender Bewegung denken indem die beiden Geraden
sich
scherenartig auf & zu
bewegten || scherenartig auf
& zu machten || gingen
& man könnte die Demonstration an dieser bewegten Figur
geradesogut ausführen als an der ruhigen. Ich will
damit übrigens nicht sagen daß die so bewegte Figur
das allgemeinere Zeichen ist.
α + β =
β + γ :. α =
γ könnte man sich die Figur in
fortwährender Bewegung denken indem die beiden Geraden
sich
scherenartig auf & zu
bewegten || scherenartig auf
& zu machten || gingen
& man könnte die Demonstration an dieser bewegten Figur
geradesogut ausführen als an der ruhigen. Ich will
damit übrigens nicht sagen daß die so bewegte Figur
das allgemeinere Zeichen ist. |
Wenn man jemandem
der es noch nicht |
Angenommen es hätte einer den
pythagoräischen Lehrsatz zwar nicht bewiesen wäre aber
durch Messungen der Katheten & Hypotenusenquadrate auf
die || zur „Vermutung” dieses
Satzes geführt worden. Und nun fände (Ich sagte „aus der gleichen Quelle fließt nur Eines” & man könnte sagen es wäre doch zu verflucht sonderbar wenn aus so verschiedenen Quellen das selbe fließen sollte. Der Gedanke daß aus verschiedenen Quellen dasselbe fließen kann ist uns von der Physik d.h. von den Hypothesen her so geläufig. Dort schließen wir fortwährend von Symptomen auf die Krankheit & wissen daß die verschiedensten Symptome, Symptome desselben sein können.) |
Wie konnte man nach der Statistik
das vermuten was dann der Beweis zeigte?
|
Der Beweis des
pythagoräischen
Lehrsatzes ist ein allgemeiner Beweis |
Gäbe es
eine Vermutung daß der Satz für alle Fälle wahr
sein wird so könnte das so Vermutete
niemals bewiesen, sondern nur durch die
unendliche Erfahrung bestätigt werden. |
3.
Denken wir daran
was es heißt, etwas im Gedächtnis zu suchen.
Hier liegt gewiß etwas wie ein Suchen im eigentlichen Sinn vor. Versuchen eine Erscheinung hervorzurufen, aber, heißt nicht sie suchen. Angenommen ich taste meine Hand nach einer schmerzhaften Stelle ab so suche ich wohl im Tastraum aber nicht im Schmerzraum. D.h. was ich eventuell finde ist eigentlich eine Stelle & nicht der Schmerz. D.h. Wenn die Erfahrung auch ergeben hat daß Drücken einen Schmerz hervorruft so ist doch das Drücken kein Suchen nach einem Schmerz. Sowenig wie das Drehen einer Elektrisiermaschine das Suchen nach einem Funken ist. |
Woher || Wo soll aus dem Beweis dieselbe Allgemeinheit
hervorspringen die die früheren Versuche wahrscheinlich
machten? |
Ich hatte die Allgemeinheit
vermutet ohne den Beweis zu vermuten (nehme ich an) &
nun beweist der Beweis ja || gerade die Allgemeinheit die ich
vermutete!? |
Was
heißt das: jedes Dreieck
hat eine Basis & eine Spitze,
etc. man kann also in jedem Dreieck
durch die Spitze eine Parallele zur Basis ziehen
u.s.w.?
Hier ist die Allgemeinheit der Grammatik. |
Kann ich
sagen: die grammatische Regel hat
einfach eine andere Art der Allgemeinheit als ein Satz. |
4.
In irgend einem
Sinn liegt die Allgemeinheit einer Regel erst in
der Anwendung. Oder vielmehr: in ihrer
Anwendbarkeit. In der Möglichkeit ihrer
Anwendung, denn jede einzelne Anwendung ist
nicht-allgemein. |
Ja wir
sprechen, vom Kreis, seinem Durchmesser
etc. etc. wie von einem Begriff dessen
Eigenschaften wir beschreiben gleichgültig welche
Gegenstände unter diesen Begriff fallen.
– Dabei ist aber Kreis gar kein Prädikat im
ursprünglichen Sinne. Und
überhaupt ist dieses Gebiet || die Geometrie
der Ort wo die Begriffe der verschiedensten |
Ja Die
Allgemeinheit der Geometrie scheint immer wieder
die zu sein daß von einem Begriff die Rede ist und wir uns nicht um die
Gegenstände kümmern || man sich nicht um die
Gegenstände kümmert die unter diesen Begriff
fallen. Aber so kann es natürlich nicht sein,
sondern wir folgen hier – wie so oft – einer falschen
Analogie. |
Welcher Art ist eine allgemeine Anweisung
zu einer gewissen euklidischen
Konstruktion? Sie hat ihre Wirkung, erfüllt
ihren Zweck, erst wenn man sie anwendet & dann stellt sie sich
einem gleichsam zur Verfügung indem die Variablen in ihr
nun Werte annehmen. |
Man könnte so fragen: Ist
etwa ein allgemeiner geometrischer Satz unendlich komplex da
unendlich viele spezielle Anwendungen || Fälle aus ihm folgen? Nun, er ist es offenbar nicht. |
Ich möchte immer sagen: die
Allgemeinheit der Geometrie ist nur dadurch möglich, daß
sie nicht aus Sätzen besteht. [aber ich bin
mir jetzt über die Zusammenhänge nicht
klar.] |
Man kann ein Brotmesser nicht allgemein
nennen weil sich kleine |
¤Wenn Du eine Strecke
halbieren willst, so nimm sie in den Zirkel „etc.” Und nun zeichnet man eine Figur in der dies alles an
einer Strecke wirklich vollzogen ist || wird & nimmt an daß der Andere es nun danach an
jeder beliebigen Strecke wird
vollziehen können. Die Regel
setzt natürlich die unendliche Möglichkeit des Raumes
voraus, aber nicht „eine unendliche
Anzahl” von
Möglichkeiten. |
Stellen wir uns einen Menschen vor der so
eine allgemeine Vorschrift benützt er schaut auf die Vorschrift,
dann auf sein Papier: Ich soll die Strecke in den Zirkel
nehmen, – jetzt einen Kreis schlagen, –
etc., etc. Aber in der
Vorschrift steht ja gar nichts von dieser Strecke.
Aber so faßt der sie auf, der sie verwendet || anwendet. |
Die Vorschrift
zur Halbierung ist analog einer || Der
Vorschrift zur Halbierung entspricht eine
Vorrichtung zur Halbierung & in dieser wäre ein Teil etwa
ein verstellbarer Schlitten der sich der zu teilenden Strecke
anpassen würde. Und hier hätten wir das Analogon
zum Brotmesser || zur
Allgemeinheit des Brotmessers. |
(Kann man von einem dehnbaren Beweis
reden?) |
Kann man sagen die Figur dient nur
zur Demonstration einer gewissen
Multiplizität ‒ ‒ ‒ |
Könnte man sagen die Figur kann durch
bestimmte Arten von Zerrspiegeln betrachtet werden und
behält durch sie gesehen ihre beweisende Kraft.
Sie wird von vornherein so verstanden daß sie durch alle
diese Zerrspiegel betrachtet werden kann.
Nur das allen diesen Bildern
Gemeinsame welches sie verkörpert ist das
eigentliche Symbol. |
Man könnte nun freilich –
fälschlich – die Figur als den Begriff & ihre
verschiedenen Bilder die unter den Begriff fallenden
Gegenstände nennen. || als die unter ihn
fallenden Gegenstände
auffassen. |
6.
Der Beweis kann
nichts prophezeien. D.h. er kann
nichts Wirkliches prophezeien. |
Wir erkennen oft im
verzerrtesten Schatten die Figur die ihn wirft. |
Die Figur ist ein Zeichen & nicht
das Bezeichnete oder ein ungenaues Bild des
Bezeichneten. |
Es ist schwer in der Philosophie nicht zu
übertreiben. |
„Dies ist
hier” ist
Unsinn. |
Wir könnten sehr wohl
alle unsere gegenwärtigen Zahlen || die
Kardinalzahlen kennen aber nicht die Null & hätten
kein Mittel sie zu finden; ihr entspräche
keine Lücke in unserem System sondern wir hätten ein anderes
System. |
Man könnte glauben daß sich die
Allgemeingültigkeit der Figur
durch Sätze rechtfertigen läßt wie: Jedes
solche Dreieck muß |
(Dann
folgt immer wieder der Gedanke –
den ich freilich nie für eine Lösung sondern immer nur
für einen Schein gehalten habe – daß
der Beweis ja gar nicht von
diesem || einem
Zentriwinkel, einem Kreis
etc. handelt sondern von
Kreisförmigkeit, dem Begriff
Zentriwinkel etc.
etc.. Freilich ist auch an diesem Schein
etwas Wahres dran.) |
Ich würde
sagen die Alchimisten haben nicht die Goldmacherkunst
gesucht. |
Die fragliche Allgemeinheit tritt,
natürlich, schon in die Definition des Kreises als Ort aller
Punkte etc. auf || ein. |
Es muß sich da
natürlich um die Definition einer Variablen
handeln für die ein gewisses Gebiet von Werten bestimmt
wird aber freilich nicht als Klasse Wenn ich den Kreis etwa durch die Gleichung r = konstant definiere so muß die unendliche Möglichkeit der r nach der Lage des Radius natürlich in der Bedeutung dieser Definition beschlossen liegen; aber nicht in Form einer Klasse möglicher Werte sondern wenn es sich um eine zahlenmäßige Geometrie handelt, durch das Gesetz der Bildung rationaler Zahlen, und soweit es sich um eine Gesichtsgeometrie handelt, durch die jedem Radius anhaftende unendliche sichtbare Möglichkeit. |
Die irrationalen Werte kommen nur
so || dadurch in Betracht daß sie
sich durch Reihen rationaler Zahlen darstellen
lassen. |
Ich sagte früher einmal man
könnte sich die || eine
euklidische
Demonstration auch an einer bewegten Figur ausgeführt
denken. Es ist aber nicht wesentlich daß sie
bewegt sondern daß sie beweglich ist.
(d.h. variabel)
D.h. ich muß in ihr den Repräsentanten |
Wenn ich einen mathematischen Satz & einen Beweis
für ihn kenne & später lerne ich noch einen weiteren
Beweis desselben || dieses Satzes kennen so
habe ich damit ein neues System kennen gelernt.
|
Angenommen
jemand untersuchte gerade Zahlen auf das Stimmen des
Goldbachschen Satzes
hin. Er würde nun die Vermutung aussprechen –
& die läßt sich aussprechen, || – daß, wenn er mit dieser Untersuchung
fortfährt, er so lange er leben werde || lebt keinen
widersprechenden Fall treffen || antreffen
werde. Angenommen es werde nun ein Beweis des Satzes
gefunden, beweist der dann auch die Vermutung des
Mannes? Wie ist das möglich? |
7.
Kann man antworten: Alles was
der Beweis des Goldbachschen Satzes prophezeien wird ist, daß dies Resultat
richtig ist nicht || sein wird nicht
daß es sich ergeben || herauskommen || sich ergeben
wird. (Aber das erste ‚wird’ ist hier
unsinnig denn die Verben in der Mathematik haben keine
Zukunft.) |
Es sagt mir jemand „ich habe Ausdrücke von
der Form (a + b) + c
& || und
a + (b + c)
ausgerechnet & gefunden daß sie dasselbe
ergeben” 8.
jeden
Charakter einer
Prognose || Vorhersage. |
Kann man || jemand glauben daß
25 × 25 =
625 ist? Was heißt es das zu
glauben? |
Könnte man sagen, daß die
Arithmetischen oder Geometrischen Probleme immer so ausschauen, oder
oberflächlich || fälschlich so aufgefaßt werden
können als bezögen sie sich auf die
Gegenstände im Raum, während sie sich auf den Raum
selbst beziehen? |
So glaubt man, das
Problem der 3-Teilung des Winkels beziehe sich auf die
tatsächliche 3-Teilung eines bestimmten Winkels
oder gar aller Winkel. Während es
kein Problem ist & das was man als Lösung des
Problems anspricht eine Demonstration des Raumes
ist. |
Ist es nicht so: Glauben daß der
Goldbachsche Satz
immer ad inf. – stimmen
wird ist Unsinn; glauben daß er
1000000 mal stimmen wird ist auf der selben Stufe wie
zu glauben daß er einmal stimmen wird
& das ist auf derselben Stufe, wie zu glauben
daß
25 × 25 625
ergeben wird. |
So
seltsam es klingt so wäre es wohl || ist
es möglich die Primzahlen bis – sagen wir –
zur 7 zu kennen & daher ein endliches System von Primzahlen zu
besitzen. Das was wir die Erkenntnis nennen daß es
unendlich viele gibt ist in Wahrheit die Erkenntnis eines neuen
& mit dem anderen
gleichberechtigten Systems. |
(Was ich auch immer
schreibe, es sind Fragmente, aber der Verstehende wird daraus
ein geschlossenes Weltbild entnehmen || ersehen
﹖.) |
Glauben, daß
25 × 25 625 ist, kann man nur insofern
wie || als man auch glauben kann
daß 25 × 25 =
620 ist. Und es ist natürlich unmöglich
sich von diesem Sachverhalt – oder von jenem – ein Bild zu
machen. |
Wenn wilde
Völker ein Zahlensystem haben in dem auf 5 ein Ausdruck analog
unserem „viele” folgt & sie beim Angeben einer Zahl zuerst auf
Finger einer Hand dann auf ihre Haare zeigen so haben diese
Leute ein ebenso komplettes Zahlensystem wie wir. |
Zu fragen ob
es sich denken läßt || es
denkbar wäre daß andere Leute einen Raum
hätten der mit den Wänden dieses |
Ich kann diese Fragen in keiner
Sprache stellen weil jede schon eine bestimmte räumliche
Auffassung voraussetzt. |
9.
Der Bereich einer
Variablen muß durch die Grammatik bestimmt sein.
D.h. er muß völlig durch die
Zeichen & Zeichenregeln bestimmt sein. Mag
man auch noch so viel über die Anwendung des Zeichensystems offen
lassen, es muß in sich abgeschlossen sein. |
Man könnte
sagen der Bereich der Allgemeinheit muß in sofern bestimmt
sein als man in jedem Einzelfalle muß entscheiden
können ob er ein solcher Fall ist oder nicht.
Aber das heißt nicht daß ich dann durch eine besondere
Disposition meiner Seele oder besondere
äußere Umstände im Stande sein
muß die Entscheidung zu treffen, sondern das
Vermögen von dem wir hier reden ist ein logisches || eine logische Möglichkeit.
Es muß jetzt, wenn ich den allgemeinen Satz ausspreche, klar sein was als Spezialfall || besonderer Fall dieser Allgemeinheit zu gelten hat, der Raum |
Die Allgemeinheit die man
meint ist oft eine die der Unbestimmtheit der
Gestalt || Art – (etwa) – der Schachfiguren
entspricht. Wenn man die Regeln des Schachspiels
angibt so ist gar nicht gesagt mit welcher Art von Figuren
das Spiel ausgeführt wird & die aller verschiedensten
Arten sind hier denkbar von den hölzernen Figuren
auf einem Brett zu den geschriebenen Zeichen auf dem
Papier. Und es ist wichtig einzusehen daß keine von
beiden die primären sind. Denn das Schachspiel
hätte ebensogut gleich in den geschriebenen Zeichen erfunden
werden können. |
10.
Welcher Art ist
die Entdeckung, daß ~p ∙ ~p =
~p, daß
~p ein
Sonderfall von ~p ∙ ~q
ist? Gibt es nicht in demselben Sinne eine Entdeckung
daß ~~p = p,
~~~p
=
~p etc. ist?
Ich finde einen „Zusammenhang”
heraus. |
11.
Sheffers Entdeckung ist natürlich nicht die der Definition
~p ∙ ~q
= p ∣ q. Diese
Definition hätte Russell sehr wohl haben können ohne doch damit das
Sheffersche
System zu besitzen & andererseits hätte
Sheffer
auch ohne diese Definition sein System
begründen können. Sein System ist |
Raum nenne ich das,
dessen man beim Suchen gewiß sein
kann. |
Machen wir die Sache noch klarer durch die
Annahme der beiden Fregeschen
Urzeichen „~” und „ ∙ ” so bleibt hier die Entdeckung bestehen wenn auch die
Definitionen geschrieben werden ~p ∙ ~p =
~p und ~(~p ∙ ~p)
∙ ~(~q ∙ ~q) =
p ∙ q. Hier hat sich an
den Urzeichen scheinbar gar nichts
geändert. |
Man könnte sich jemand
vorstellen, dem diese Definitionen gezeigt würden & der
fragte „was ist denn damit
gewonnen”; weil er das neue System in
ihnen nicht sehen würde || sähe. Man könnte sich auch denken daß jemand die ganze Fregesche oder Russellsche Logik schon in diesem System hingeschrieben hätte & doch wie Frege „~” und „ ∙ ” seine |
Käme dann
Einer & gäbe die Definition
~p ∙ ~q =
p ∣ q so hätte er freilich nur
eine an sich unwesentliche Abkürzung
eingeführt aber sie wäre der Ausdruck einer Entdeckung in
dem Sinne daß sie einen bestimmten neuen Aspekt
betont.
(Russell hat
richtig darauf hingewiesen daß die Bedeutung von Definitionen
oft auf diesem Betonen beruht.)
|
(Beinahe
wie die Namengebung Mrs John
Robinson ein bestimmtes
Verhältnis von Mann & Frau betont.)
|
Es ist ein Unterschied ob man auf die Dampfmaschine
als die Maschine katexochen schaut
(wie man es einmal getan hat) oder als eine
Maschine, || – unter vielen
andern. – Und man sieht ein anderes System wenn man 12
Striche nur als das System  betrachten kann
(also kennt) oder dieses System als eins von
den vielen möglichen sieht. betrachten kann
(also kennt) oder dieses System als eins von
den vielen möglichen sieht. |
Die
Mathematik „abrunden” kann man so wenig wie man sagen kann „runden wir die 4 primären Farben auf 5 oder
10 ab” oder runden wir die
8 Töne einer Oktave auf 10 ab (oder
auf). |
Ich
gebrauche das Wort Raum als Möglichkeit der Bewegung.
|
Ich habe
einmal in der Diskussion gesagt zwei
Systeme || Zeichensysteme seien derselbe Raum wenn
sie in einander übersetzbar seien.
Aber wie ist es etwa mit zwei Systemen von Tautologien wovon das
eine in der Fregeschen Art
mit „~” und „ ∙ ” das andere im System ~ξ ∙ ~η
hingeschrieben ist. Diese beiden sind freilich in
einander übersetzbar aber erst wenn man in dem
ersten das zweite sieht. Man könnte das vielleicht auf die Lösung jeder algebraischen Aufgabe anwenden. Z.B. die Art & Weise der Lösung einer Gleichung x² + ax + b = 0 ist in ihr schon zu sehen – man könnte sich alle Transformationen in sie hineinprojiziert denken. – Aber das heißt die Lösung ist in ihr zu sehen – wenn man sie in ihr sieht dann sieht man aber etwas anderes als wenn man die Lösung nicht in ihr sieht. |
12.
Man könnte
meine Meinung auch in den Worten
ausdrücken, || : Man kann keine
Verbindung von Teilen der Mathematik oder Logik herausfinden die
schon vorhanden war ohne daß man es wußte. Sondern
kannte man die Verbindung noch nicht so war sie nicht |
Man könnte
so sagen: Wenn ich etwas suche – ich meine, den
Nordpol oder ein Haus in London – so kann
ich das was ich suche vollständig beschreiben ehe ich
es gefunden habe (oder gefunden habe daß es nicht
da ist) & diese Beschreibung wird
in jedem Fall logisch einwandfrei sein. Während ich im
Fall des „Suchens”
in der Mathematik wo es nicht in einem System geschieht, das
was ich suche nicht beschreiben kannoder || d.h. || ,
oder nur scheinbar, denn könnte ich es in
allen Einzelheiten beschreiben so hätte ich es eben schon
& ehe es vollständig beschrieben ist kann
ich nicht sicher sein ob das was ich suche logisch
einwandfrei ist, sich also überhaupt beschreiben
läßt; d.h. diese unvollkommene
Beschreibung läßt gerade das aus was notwendig wäre
damit etwas gesucht werden könnte. Sie ist also nur
eine Scheinbeschreibung des „Gesuchten”.
Irregeführt wird man hier leicht durch ¤ die Rechtmäßigkeit einer unvollkommenen Beschreibung im Falle des Suchens eines wirklichen Gegenstandes & hier spielt wieder eine Unklarheit über Beschreibung & Gegenstand hinein. Wenn man sagt ich gehe auf den Nordpol & erwarte mir dort eine Flagge zu finden |
13.
Die Frage ist kann
man sagen daß die Mathematik heute gleichsam ausgezackt
– oder ausgefranst – ist &
daß man sie deshalb wird abrunden
können. Ich glaube man kann das erstere nicht sagen,
ebensowenig wie man sagen kann die Realität sei
struppig weil es 4 Primäre Farben, 7 Töne in einer
Oktav, 3 Dimensionen im Sehraum etc.
gäbe. |
Die
Lösung der Gleichung x² + ax + b =
0 wird entdeckt indem man einen
bestimmten Aspekt dieser Gleichung |
Wenn man die
Lösbarkeit beweist so muß in diesem Beweis irgendwie der
Begriff Lösung vorhanden sein. (In dem
Mechanismus des Beweises muß irgend etwas diesem
Begriff entsprechen.) Aber dieser
Begriff ist nicht durch eine
äußere Beschreibung
darzustellen || zu
repräsentieren sondern nur
wirklich darzustellen. |
Wo der neue Zusammenhang gefunden
wurde dort sah man früher keine Lücke.
Und wo man doch eine zu sehen glaubte, war man im Irrtum. |
(Ich kämpfe immer wieder
– ob erfolgreich das weiß ich nicht – gegen die
Tendenz in meinem eigenen Geiste an, in der Philosophie Regeln
aufzustellen, (zu konstruieren), Annahmen (Hypothesen) zu
machen statt nur zu sehen was da
ist.) |
(Es ist
äußerst anstrengend den Blick anzuspannen & die
Physiognomie eines Gedankens in die Ferne, durch einen Nebel, zu
schauen || sehen.) |
Philosophie
könnte man auch das nennen was vor allen neuen
Entdeckungen & Erfindungen
möglich || da ist. |
Ich will immer wieder zeigen daß die
Logik is all right as it
is. |
Das muß sich auch darauf beziehen
daß ich keine Erklärung der Variablen „Satz” geben
kann. Es ist klar daß dieser logische
Begriff, diese Variable, von der Ordnung des
Begriffs „Realität” oder
„Welt” sein
muß. |
Die
Allgemeinheit der Variablen in der Logik ist die
Allgemeinheit der Demonstration. Sie besteht
darin, daß die Tatsache daß
p ⊃ p eine Tautologie
ist an jedem || einem beliebigen
speziellen Fall
allgemeingültig demonstriert
wird. D.h. aus
der Demonstration des besonderen Falles ersehe ich
tatsächlich ( || wie immer sie
gemeint war) alles was ich in der Logik brauche.
D.h. die Demonstration erhält
nicht dadurch ihre Demonstration || Allgemeinheit daß sie so gemeint ist sondern indem sie
tatsächlich allgemein (d.h. allgemein
gültig) demonstriert. D.h.
die Allgemeinheit besteht hier in der Allgemeinheit der
Anwendung. Und diese ist da so zu
sagen ob man es will oder nicht – einfach durch
die innere Relation des Einzelfalles zum Paradigma.
– Man könnte dann sagen eine Demonstration demonstriert
so allgemein als sie anwendbar ist.
D.h. sie demonstriert allgemein durch
den Raum in dem sie |
14.
Es ist klar daß die Entdeckung des
neuen || Shefferschen Systems in ~p ∙ ~p =
~p und
~(~p ∙ ~p)
∙ ~(~q ∙ ~q) =
p ∙ q der Entdeckung entspricht das
x² + ax +
|
Daß etwas so
angesehen werden kann sieht man erst, wenn es so angesehen
ist. Daß ein Aspekt möglich ist sieht man erst wenn er wirklich da || vorhanden ist. |
Man könnte eine Trigonometrie aufbauen nach dem Modell
der elementaren Trigonometrie aber
unabhängig von der Vorstellung der Dreiecke die aber nichts
von den trigonometrischen Reihen wüßte
sondern nur die Multiplizität der
elementaren hätte. |
Die
Dirichletsche
Auffassung der Funktion ist nur dort möglich wo sie nicht
ein unendliches Gesetz durch eine Liste
ausdrücken will, denn eine unendliche Liste gibt es
nicht. |
Wenn die
menschliche Kriegsführung dem Schachspiel
ähnlicher wäre als sie tatsächlich
ist so könnte man versuchen eine Schlacht auf dem
Schachbrett darzustellen & mathematische Probleme |
Es ist nichts
Allgemeines in der Demonstration, sie ist
durchaus besonders, aber
(sie strahlt ihre
Anwendungsmöglichkeit durch einen ganzen
Raum) || ihre
Anwendungsmöglichkeit enthält
die Allgemeinheit || ist
allgemein. |
Die
Anwendungsmöglichkeit strahlt durch den Raum & trifft
(&
erhellt) den
Körper den man in diesen Raum bringt. Man könnte
die Lichtstrahlen allgemein nennen, weil sie jeden beliebigen
Körper beleuchten der sich ihnen in den Weg
stellt. Aber die Lichtquelle allgemein zu nennen wäre
absurd. |
15. Wenn der Grund etwas zu glauben (Z.B. „warum nehmen wir das Gedächtnis als Grund für den Glauben, daß etwas in der Vergangenheit geschehen ist”.) |
Die Allgemeinheit der Interpretation
einer || der Demonstration besteht darin
– und nur darin – daß wir uns für
die internen Verhältnisse der Demonstration interessieren
& nicht für den physikalischen Vorgang (das
Experiment) in ihr. |
Die Zahlenart die man verwendet wo man
sinnvoll unendlich weiter
zählen kann & die man verwendet wo das nicht
möglich ist sind von einander verschieden.
|
Das sind 3 Kreise kann ich nur sagen wenn das „das” eine
Bedeutung hat die die 3 Kreise noch nicht
präjudiziert. |
Die Allgemeinheit einer
Demonstration ist die Ausdehnung || der
Bereich ihrer Wirkung. |
Eine Demonstration demonstriert
alles was sie demonstriert. Ihr Bereich |
Das ist der Unterschied zwischen der Demonstration &
einem Satz. In der Demonstration wird ja nichts
gesagt sondern etwas gezeigt. Und was der Bereich ihrer
Anwendung ist, hängt also von ihr und ihrem Raum ab aber nicht
von uns. |
Man könnte nämlich sagen:
Die Demonstration ist doch gar nicht allgemein sondern durchaus
besonders. Aber sie demonstriert ja eben etwas &
das gilt so allgemein als es gilt. (Das ist ja das Gute,
daß, wo immer auch Anspielungen & Andeutungen
etwas gelten mögen, in der Demonstration nur das zählt
was da ist. Sie ist in der Beziehung wie ein
Experiment.) |
Es gibt z.B.
Euklid die Anweisung zur Halbierung
einer Strecke indem er die Methode (an einem
Beispiel)
demonstriert. Nun, diese Anweisung gilt soweit man
sie anwenden kann. Und könnte man sie in einem Fall nicht anwenden so nützte es ihr nichts daß sie für diesen Fall gemeint war. |
Drei kann man nur durch das Modell der Drei
darstellen. |
17.
Die Allgemeinheit
der Demonstration ist nur der Raum um diese Demonstration.
Die Anwendung auf einen besonderen Fall ist ein neuer Körper
in diesem Raum. |
18.
Es ist ein
Unterschied ob ein System auf ersten Prinzipien
ruht oder ob es bloß
von ihnen ausgehend entwickelt wird. Es ist ein
Unterschied ob es wie ein Haus auf seinen
untersten Mauern ruht oder ob es wie etwa ein Himmelskörper
im Raum frei schwebt & wir
bloß unten zu bauen angefangen haben obwohl
wir es auch irgend wo anders hätten tun können.
|
Die Logik
& die Mathematik ruht nicht auf Axiomen;
sowenig eine Gruppe auf den sie definierenden Elementen &
Operationen beruht. Hierin liegt der Fehler das
Einleuchten die
self evidence || Evidenz der Grundgesetze als ein
Kriterium der
Richtigkeit in der Logik zu betrachten.
Ein Fundament das auf nichts steht ist ein schlechtes Fundament. |
Abgesehen von der Allgemeinheit der
Demonstration, welcher Art ist denn (Man könnte natürlich auch sagen „die Allgemeinheit des ganzen Systems”.) |
Diese Frage scheint
mir zur eigentlichen Verwendung der Geometrie
vorzudringen. |
Was für eine Art der Allgemeinheit ist
es, wenn wir sagen „zwischen je
zwei Punkten läßt sich eine Gerade
ziehen”? |
Die Allgemeinheit der
grammatischen Regel bezieht sich auf den Gebrauch von
Worten. |
Ich muß mir vorstellen können, was ein Punkt ist.
|
Es hat Sinn von zwei
Punkten zu sagen daß sie durch eine Gerade verbunden seien.
Aber heißt das „es hat
Sinn von zwei Dingen,
die Punkte sind zu sagen
etc.”?
(Natürlich nicht.) |
Wie weiß ich dann,
daß ein Zeichen A einen Punkt bezeichnet? Etwa
indem ich sehe daß a || A
in bestimmter Weise mit anderen Zeichen
verknüpft werden darf. Aber wie
weiß ich was || daß
diese anderen Geraden etc. bezeichnen || bezeichnen etc.? Dadurch daß sie
mit A so verknüpft werden dürfen? Sie
können doch nicht |
Das System wird aber
z.B. charakterisiert durch die Aussage,
daß keine Anzahl von Namen (für Punkte
z.B.) als komplett betrachtet werden
darf. |
Die Geometrie anders als als || wenn sie anders ist als reine Grammatik muß
angewendet sein & dann muß es wirkliche Punkte & Geraden
etc. geben, der Satz daß eine Gerade zwei
Punkte verbindet muß dann eben einen wirklichen Sinn
haben. |
Und es heißt der geometrische Satz dann auch nicht alle
Punktpaare sind durch eine Gerade verbunden sondern
können durch eine Gerade verbunden werden.
Und hier braucht man dann das Wort „je zwei Punkte” & nicht alle Punktpaare und deutet damit den
Unterschied von der || einer anderen
Art der Allgemeinheit an. |
Die Grammatik kann ihre
Regeln nicht auf gut Glück allgemein aussprechen
(d.h. sie offenlassen).
|
19. Denken wir uns ein Dame-Spiel
in dem es erlaubt wäre ein beliebig großes
Schachbrett || Brett zu verwenden ich
meine ein Brett mit einer beliebig großen Anzahl von
Feldern (also 64, 81, 100,
etc.). Das heißt
natürlich nicht „es ist erlaubt ein
Brett mit unendlich vielen Feldern zu verwenden” (das ist Stiefel).
Wir könnten dieses Spiel nicht gut ein unendliches nennen. |
Die Möglichkeit entspricht immer
einer Erlaubnis in den grammatischen Spielregeln.
Dem was man unendliche Möglichkeit nennt entspricht etwas, was man eine unendliche Erlaubnis nennen könnte. Und das ist natürlich nicht die Erlaubnis etwas Unendliches zu tun. |
Die
Unendliche Möglichkeit Namen zu bilden liegt nicht nur in der
unendlichen Möglichkeit von Zeichen der
Form x❘,
x❘ ❘,
x❘ ❘ ❘,
x❘ ❘ ❘ ❘
etc. sondern z.B. auch
in der Unendlichen Möglichkeit des Raumes die
Figur des Zeichens abzuändern. |
Verschiedene Arten von
Figuren wie Läufer, Rössel, etc.
entsprechen verschiedenen Wortarten. |
20.
Ich komme hier auf
jene Methode der Zeichenerklärung über die sich
Frege so lustig gemacht
hat. Man könnte nämlich die
Ausdrücke || Wörter „Rössel”,
„Läufer”, etc. dadurch erklären daß man die
Regeln angibt die von diesen Figuren handeln. |
Genau
dasselbe gilt in jeder Geometrie von den Ausdrücken „Punkt” und „Gerade”
etc. Was ein Punkt ist & was eine Gerade
sieht man nur daran welchen Platz || welche
Plätze das eine & das andere in dem
System von Regeln einnimmt. Denken wir uns etwa ein System
von Buchstaben von solcher Art daß alle erlaubten Zeichen
Gruppen von drei Buchstaben sind & zwar derart daß ein
Buchstabe der an einer Außenstelle stehen darf
auch nicht in der Mittelstelle stehen darf und
umgekehrt. Diese Regel würde zwischen zwei „Wortarten”
unterscheiden und wir könnten das dadurch zum Ausdruck
bringen daß wir für die Außenglieder große,
für die Innenglieder kleine Buchstaben
verwenden. – Andererseits aber hat die
Unterscheidung zweier Wortarten keinerlei Sinn wenn sie
nicht auf die obige Art syntaktisch unterschieden sind
d.h. wenn sie nicht auch ohne die verschiedene
Art der Bezeichnung
bloß durch die vor ihnen geltenden Regeln |
21.
Wenn ich eine
Klasse wirklicher Dinge gezählt habe & nun die 1 zu 1
Zuordnung einer anderen Klasse zu der ersten || ihr sehe, kann ich allerdings schließen daß
auch die andere die zuerst
erhaltene || gezählte Anzahl
haben wird; aber dies ist eine Hypothese wie das Resultat der
ersten Zählung. |
Ich kann in der Zuordnung die
Zahlengleichheit sehen, aber sie nicht aus (der
Zuordnung) || ihr schließen. |
Es gibt nicht zwei
Wortarten die ich grammatisch (ganz) gleich behandeln kann die aber doch
zwei || verschiedene || zwei Wortarten sind. Sondern die Regeln die von ihnen
handeln machen die Wortarten aus: Dieselben Regeln,
dieselbe Wortart. Das hängt damit
zusammen, |
22.
Die
Dirichletsche
Erklärung der Funktion ist der erste Schritt in der
Mengenlehre. Aber die Wahrheit ist eben daß eine
Funktion die man durch eine Tabelle definiert
& eine die man durch einen unendlichen
Prozeß definiert wesentlich
verschiedene Dinge gibt, denn eine unendliche Tabelle wie eine
unendliche Liste ist ein Unding. |
„Ist es denkbar daß 2 Dinge alle ihre
Eigenschaften mit einander gemein haben?” Wenn es nicht denkbar ist, so ist
auch
das Gegenteil nicht denkbar. |
„Unendlich” spielt
in Wirklichkeit
(unbewußt) die Rolle von
„sehr groß”! |
((1) + 1)
2 + 2
Dasjenige was 2 + 2 = 4 bedeutungsvoll macht das also was macht daß 2 + 2 = 4 richtig & 2 + 2 = 5 falsch ist und nicht zwei gleichberechtigte Festsetzungen, ist die Beweisbarkeit von 2 + 2 = 4 und nur sie. Daß also ((1) + 1) + ((1) + 1) = (((1) + 1) + 1) + 1 zu dem allgemeinen System a + (b + 1) = (a + b) + 1 gehört. |
Ohne
diese Beweisbarkeit wäre
2 + 2 = 4
eine willkürliche Zeichenregel & von richtig oder falsch
bei ihr nicht die Rede. Die Demonstrabilität macht die
Gleichung zu etwas was sich mit einem Satz vergleichen
läßt. |
23.
„a + (b + 1) =
(a + b) + 1” eine Definition zu nennen ist eigentlich schon
ein Fehler. Denn es ist eine Zeichenregel ganz
anderer Art als z.B.
(1) + 1 =
2. |
Man könnte nun fragen:
Welche Bedeutung hat
2 + 2 = 4
? ist es nicht eine Zeichenregel? Wenn
ja, so ist es willkürlich. Die Antwort ist,
daß die Bedeutung von
2 + 2 = 4
nicht in ihm selbst sondern in seiner Beweisbarkeit,
d.h. in seiner Beziehung zu
anderen Zeichenregeln liegt, also in
seiner || der Zugehörigkeit zu einem
System. Das heißt also daß jener Beweis ebenso
interne Beziehungen zwischen 2 & 4 aufzeigt wie der Beweis
daß p ⊃ q ∙ p
. ⊃ . q eine
Tautologie ist interne Beziehungen zwischen
p ⊃ q ∙ p
und q zeigt. |
Wenn „a + (b + 1)
=
(a + b) + 1” die allgemeine Regel ist, dann kann ich
2 + 2 durch 4
ersetzen; das liegt in der logischen Struktur der Welt. |
25.
Das Wort Zahl
ist || bedeutet nichts wenn dahinter nicht die variable
Zahlform (ausgedrückt in grammatischen Regeln
(Zeichenregeln)) steht. |
Eine Gleichung gewinnt erst
in einem Kalkül mathematische
Bedeutung. |
So ist „
Die Verbindung dieses Kalküls mit den induktiven Eigenschaften von
|
Dazu brauche ich die allgemeine Form eines Gliedes wie a und diese Form muß mit der des ersten solchen Gliedes so verbunden werden || zugeordnet werden daß man sieht wie das erste Glied ein Fall des allgemeinen Gliedes ist. Und es muß auch gezeigt werden wie der Nachfolger des allgemeinen Gliedes ein allgemeines
|
Beschreibung einer
solchen Bildungsregel durch die Wortsprache
‒ ‒ ‒ |
Man brauchte jedenfalls einen Ausdruck für:
Alle Permutationen mit n Wiederholungen von
0 und 1. |
Würde ich alle jene Induktionsregeln
nicht verstehen so könnte ich nicht mit Dezimalen
rechnen. Aber sie exakt auszusprechen
ist sehr schwer. – Oder es setzt eine
komplizierte Technik voraus. Welcher
Art diese Technik sein soll um strengen Anforderungen zu
genügen & ob es hier überhaupt ein
unstreng gibt weiß ich nicht. Ich vermute beinahe,
daß wenn man nur die Interne Relation der Glieder der
Formenreihe sieht alles in Ordnung ist & daß es gar keine
Methode geben kann || gibt einen
so zu sagen zu zwingen die interne Relation zu
sehen. Vielleicht ist es auch so daß man sie zuerst in
bestimmten Fällen sehen muß &
|
26.
Der Begriff
„irrationale Zahl” ist ein gefährlicher
Scheinbegriff. |
Ein Schnitt ist ein Prinzip der
Teilung in größer & kleiner. |
Und zwar braucht
die irrationale Zahl eine
andere Definition von größer & kleiner als
die rationale. Die ganzen Kunstgriffe
bei der Einführung der irrationalen Zahlen sollen dieses
Neue verhüllen. D.h. die
Einführung der √2 ist die Einführung
einer neuen mathematischen Welt & es soll immer
so ausschauen als wäre sie in der früheren doch
schon irgendwie enthalten gewesen. |
„~p” schließt einfach p aus. Was dann
statt p der Fall ist folgt aus dem
logischen Wesen der Welt || des
Ausgeschlossenen. |
12.6.
Zur Frage nach der
Existenz der Sinnesdaten. Man sagt wenn etwas rot
scheint so muß etwas rot gewesen sein, wenn
etwas kurze Zeit zu dauern schien so muß etwas
kurze Zeit gedauert haben¤ etc.
Man könnte nun || nämlich
fragen: Wenn Vor allem ist es möglich recht zu haben || Vor allem kann der Schein recht haben oder unrecht. – Er ist auch in einem Sinne erfahrungsgemäß mit der Wirklichkeit verbunden. Man sagt „das scheint Typhus zu sein” & das heißt diese Symptome sind erfahrungsgemäß mit jenen Erscheinungen verbunden. Wenn ich sage „das scheint rot zu sein” & dann „ja es ist wirklich rot” so habe ich für die zweite Aussage || Entscheidung einen Test angewandt der unabhängig von der ersten Erscheinung war. Wenn etwas rot schien so war dieser Schein. Und wenn in diesem Schein auch nichts in demselben Sinne rot ist in dem jenes Andere rot ist wenn der Schein recht hätte, so gab es doch in dem Schein etwas dem Rotsein Entsprechendes. – Wenn es scheint als wäre ein physikalischer ‒ ‒ ‒ |
„Satz” ist so
allgemein wie z.B. auch „Ereignis”.
Wie kann man „ein
Ereignis” von dem abgrenzen was kein
Ereignis ist? Ebenso allgemein ist aber auch „Experiment” das vielleicht zuerst || auf den ersten Blick spezieller zu sein scheint (und natürlich auch „Handlung” & „tun”). |
Man kann natürlich auch nicht sagen
Satz sei dasjenige wovon man wahr & falsch
aussagen könne denn das würde nur dann etwas bestimmen
wenn diese Worte in einer bestimmten Weise
gemeint sind das aber können sie nur im Zusammenhang
sein. Und eben im Zusammenhang mit einem Satz.
Alles was man machen kann ist hier wie in allen diesen Fällen
das grammatische Spiel bestimmen, seine Regeln angeben & es
dabei bewenden lassen. Hier handelt es sich um die Regeln |
„Da geschah
ein Ereignis …”: das heißt nicht „ein Ereignis” im
Gegensatz zu etwas anderem. |
In der Mengenlehre
müßte man das was Kalkül ist trennen von dem was
Lehre sein will (und natürlich nicht sein
kann). Man muß also die Spielregeln von
unwesentlichen Aussagen über die Schachfiguren
trennen. |
Es ist immer mit recht „höchst
verdächtig” wenn Beweise in
der Mathematik allgemeiner geführt werden als es der
bekannten Anwendung des Beweises entspricht. Es liegt hier immer der Fehler vor, der in der Mathematik allgemeine Begriffe & besondere Fälle sieht. In der Mengenlehre treffen wir auf Schritt & Tritt diese verdächtige Allgemeinheit. Man möchte immer sagen: „Kommen wir zur Sache!” Jene allgemeinen Betrachtungen haben stets nur Sinn wenn man einen bestimmten Anwendungsbereich im Auge hat. Es gibt eben in der Mathematik keine Allgemeinheit deren Anwendung auf spezielle Man empfindet darum die allgemeinen Betrachtungen der Mengenlehre (wenn man sie nicht als Kalkül ansieht) immer als Schmus & ist ganz erstaunt wenn einem eine Anwendung dieser Betrachtungen gezeigt wird. Man empfindet, es geht da etwas nicht ganz mit rechten Dinge zu. |
15.6.
Es mag nach dem
Vielen was ich schon darüber gesagt habe trivial klingen wenn ich
jetzt sage daß der ganze Fehler in der mengentheoretischen
Betrachtungsweise immer wieder darin liegt
Gesetze & Aufzählungen (Listen) als wesentlich
Eins zu betrachten & sie aneinander zu reihen; da, wo das
eine nicht ausreicht, das andere seinen Platz
ausfüllt. (So macht es die
Dirichletsche
Auffassung der Funktionen.) |
Wendet man meine
Betrachtung auf das Cantorsche
Diagonalverfahren an so ergibt sich: Eine unendliche Menge von Dezimalbrüchen 0˙a
0˙a
0˙a
– – – – – – – – kann nur ein Gesetz bedeuten nach dem Gesetze gebildet Und nun zeigt ein Induktionsbeweis daß F(x,x) + 1 eine andere Entwicklung hat als jedes beliebige F(x,y). Wo aber ist hier das höhere Unendliche? (oder gar das „eigentlich Unendliche”?) |
Die Schwierigkeit liegt auch hier wieder in der Bildung
mathematischer Scheinbegriffe. Wenn man
z.B. sagt man kann die Kardinalzahlen
ihrer Größe nach in eine Folge ordnen aber nicht die
rationalen Zahlen so ist darin unbewußt die
Voraussetzung enthalten als hätte der Begriff des
Ordnens der Größe nach für die rationalen
Zahlen doch einen Sinn & als erwiese sich dieses Ordnen
nun beim Versuch als unmöglich (was voraussetzt daß der
Versuch denkbar ist). – So denkt man ist
es möglich zu versuchen die reellen Zahlen (als
wäre es ein Begriff wie etwa Apfel auf diesem Tisch) in eine
Reihe zu ordnen & es erwiese sich nun als
undurchführbar. |
Wenn
der Mengenkalkül sich in seiner Ausdrucksweise so viel als
möglich an die Ausdrucksweise des
Kalküls der Kardinalzahlen anlehnt so ist das
wohl in mancher Hinsicht belehrend weil es auf gewisse formale
Ähnlichkeiten hinweist aber auch
irreführend wenn er, gleichsam, etwas noch ein
Messer nennt das weder Griff noch Klinge mehr hat.
(Lichtenberg) |
Es ist das
als wollte man Tarotkarten so viel als
möglich den Schachfiguren nachahmen wodurch
aber das Tarot dem Schach um kein Haar ähnlicher wird.
Es sind eben nur die Regeln die
hier „Bedeutung
haben”; nicht die Figuren. |
Dem periodischen
Dezimalbruch der ja ein Gesetz ist kann man nur nicht-periodische
Gesetze entgegenstellen & nicht nicht-periodische
Extensionen. |
Wie kommt es daß aus
~ (a ≧ b) folgt a ˂
b? |
Was heißt es: Er ist nicht
größer als ich. Daß der Satz nicht alle
Größen über der meinen verneint ist
selbstverständlich. |
16.
Wie beweist man
daß
2 × 2 nicht
5 ist? ist es ein anderer Beweis als der, daß
2 × 2 =
4? Denn da der Sinn des mathematischen
Satzes in seiner Beweisbarkeit liegt & der Art wie er zu
beweisen ist, so muß sich auch der Sinn des negativen Satzes
so finden. |
Wenn ich sage zeichne einen Strich
irgendwo zwischen diesen beiden
❘ ❘ so gebe ich damit keinen unendlich
komplizierten Befehl.
Andererseits muß der Befehl voraussehen was er als seine Erfüllung gelten lassen wird. |
Die rein
kausale Rechenschaft die man sich von der
Funktion der Sprache geben will – also ohne
Rücksicht auf die Intention – hat ihr
ganz Entsprechendes in einer Beschreibung – etwa –
des Funktionierens der Automobile. – Oder auch
bei der Betrachtung etwa der speziellen Sprache der
Werkzeichnung deren sich der Ingenieur bedient um sich dem
Arbeiter verständlich zu machen. |
17.
Die Intention
muß natürlich auch ein D.h. Wenn man alle Phänomene in Betracht zieht & die Intention würde sich in ihnen nicht zeigen so wäre sie auch nicht da. |
Angenommen das Anziehen des
Bremshebels bewirkt manchmal das Abbremsen der
Maschine & manchmal nicht. So ist
daraus allein nicht zu entnehmen || schließen
daß er als Bremshebel gedacht war. Wenn nun
eine bestimmte Person immer dann wenn der Hebel nicht als
Bremshebel wirkt, ärgerlich wird
–. So wäre damit auch nicht das gezeigt was ich
zeigen will. Ja man könnte dann sagen daß der Hebel
einmal die Bremse, einmal den Ärger betätigt.
– Wie drückt es sich nämlich
aus, daß die Person darüber
ärgerlich wird, daß der Hebel die Bremse nicht
betätigt hat? (Dieses über etwas ärgerlich sein ist nämlich scheinbar von ganz derselben Art wie etwas fürchten, etwas wünschen etwas erwarten etc.) Das „über etwas ärgerlich sein” verhält sich nämlich zu ¤ dem worüber man ärgerlich ist nicht wie die Wirkung zur Ursache also nicht wie das sich durch Die Intention ist nun aber von genau derselben Art wie – z.B. – der Ärger. Und da scheint es irgendwie als würde man die Intention von außen betrachtet nie als Intention erkennen; als müßte man sie selbst intendieren || meinen um sie als Meinung zu verstehen. Das hieße aber sie nicht als Phänomen, nicht als Tatsache, zu betrachten! Das ist natürlich wieder das vorige Problem denn der Witz ist daß man es dem Gedanken (als selbständige Tatsache betrachtet) ansehen muß daß er der Gedanke ist, daß so & so || das & das der Fall ist. Kann man es ihm nicht ansehen (sowenig wie den Magenschmerzen woher sie rühren) dann hat er kein logisches Interesse oder vielmehr, dann gibt es keine Logik. – Das kommt auch darauf hinaus daß man den Gedanken mit der Realität muß unmittelbar vergleichen können & es nicht erst einer Erfahrung bedürfen kann daß diesem Gedanken diese Realität entspricht. Meine Auffassung scheint unsinnig wenn man sie so ausdrückt: Man soll sehen können worüber Einer denkt wenn man ihm den Kopf aufmacht; wie ist denn das möglich, die Gegenstände über die er denkt sind ja gar nicht in seinem Kopf (oder || ebensowenig wie in seinen Gedanken)! Man muß – nach meiner Auffassung – nämlich die Gedanken, Intentionen (etc.) von außen betrachtet als solche verstehen ohne (noch) über die Bedeutung von etwas unterrichtet zu werden. Denn auch die Relation des Bedeutens wird ja dann als ein Phänomen gesehen & ich kann || darf dann nicht wieder auf eine Bedeutung des Phänomens hinweisen müssen da ja dieses Bedeuten wieder in den Phänomenen inbegriffen || mitbegriffen ist.) 18.
Wenn man den Gedanken betrachtet so kann also von einem Verstehen keine Rede mehr sein, denn, sieht man ihn, so muß man ihn als den Gedanken dieses Inhalts erkennen, es ist nichts zu deuten. – Aber so ist es ja wirklich, wenn wir denken; da wird nichts || nicht gedeutet. – Und man könnte sagen: der Denkende sieht den Gedanken tatsächlich von außen Man kann die Erwartung mit der Gegenwart unmittelbar vergleichen; – das gibt die Lösung. Und das kann man auch vom Wunsch ja auch vom Ärger sagen. Und das heißt, daß, wenn ich mich ärgere, daß jemand etwas in Paris getan hat, ich es damit vergleichen kann daß ich jetzt in Wien in meinem Zimmer sitze. Aber damit ist auch noch nicht alles gesagt. – Die Sprache wird verstanden der Gedanke nicht. (Das Verstehen der Sprache ist das Denken, das Verstehen der Sprache aber wird nicht noch einmal verstanden.) – Die kausale Erklärung des Bedeutens & Verstehens lautet insbesondere || im Wesentlichen so, daß || : einen Befehl verstehen heißt, man würde ihn ausführen wenn ein gewisser Riegel zurückgezogen [das Gegenteil von Vorschieben] würde. – Es würde jemandem befohlen den || einen Arm zu heben & man sagt: den Befehl verstehen heißt den Arm zu heben. Das ist klar wenn auch gegen unseren Sprachgebrauch (wir nennen das „den Befehl befolgen”). Nun sagt man aber: Den Befehl verstehen heißt entweder den Arm heben oder wenn das nicht etwas bestimmtes Anderes tun – etwa Das || Dieses Verstehen des Befehls kann nicht irgend eine Handlung sein (etwa den Fuß heben) sondern sie enthält das Wesen des Befehls selbst || muß das Wesen des Befehls selbst enthalten. |
18. [Kann man eine Farbe oder gar einen Ton
vergessen?] |
Sage ich jemandem „gehe 3 Schritte”
& er versteht den Befehl, so kann er ihn mir
etwa durch eine erklären. Er sagt etwa:
Wenn hier der Weg ist & A der Anfang, so
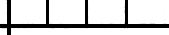 willst Du daß
ich nach B dann nach C & D kommen
soll; oder dergleichen. Und dabei ist es klar daß er in
gewissem Sinne nur einer Sache Ausdruck verliehen hat, die er
schon früher – als er den Befehl hörte &
verstand – wußte. Er könnte nun so
fortfahren & den Befehl noch näher erklären
etwa mit einem Diagramm willst Du daß
ich nach B dann nach C & D kommen
soll; oder dergleichen. Und dabei ist es klar daß er in
gewissem Sinne nur einer Sache Ausdruck verliehen hat, die er
schon früher – als er den Befehl hörte &
verstand – wußte. Er könnte nun so
fortfahren & den Befehl noch näher erklären
etwa mit einem Diagramm 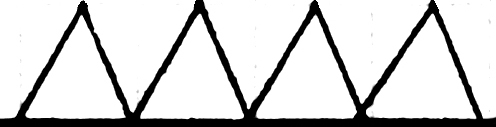 |
[Ich sehe undeutlich eine Verbindung
zwischen dem Problem des Solipsismus oder Idealismus & dem der
Bezeichnungsweise eines Satzes. Wird etwa das
Ich in diesen Fällen durch den Satz ersetzt
& das Verhältnis des Ich zur Wirklichkeit
durch das Verhältnis von Satz
& Wirklichkeit?] |
20.
Zwischen dem
Befehl & seiner Ausführung muß eine
Kontinuität bestehen. Die Ausführung
muß, sozusagen, nur die Endfläche des Befehls
(Befehlskörpers) sein. |
21. „Er hat den
Befehl nicht ganz ausgeführt”, daran
müßte man die kausale
Theorie der Bedeutung widerlegen können. |
Der Befehl muß
eine Art des Vergleichs eines Satzes mit der Realität
sein. |
Aber da
scheint es ja als
müsse man den Satz mit der Realität in einem bestimmten
Sinne vergleichen – ¤ also nicht nur vergleichen. Als
müßte also die Realität in gewissen
Fällen durch die Vergleichung einen Vorwurf empfinden oder
dergleichen. Wenn sich etwas einem Ziele nähert so liegt in dem Wort „Ziel” hier das was ich meine. (Die Intention.) |
Jeder
Mensch sieht daß
|
Das heißt, der Satz (Befehl) wird
nicht einfach mit der Wirklichkeit zusammengestellt, sondern er wird
mit || in einer bestimmten Tendenz
mit ihr verglichen. Aber worin liegt (Ist das so ähnlich wie wenn man Magenschmerzen beschriebe & es früge einer, „ich verstehe das aber woran liegt da das Unangenehme”.) |
Der Satz
– der Befehl – setzt die Wirklichkeit
gleichsam || quasi fort indem er an die
Realität anknüpft & eine Veränderung
darstellt. Es ist
als hätte man eine Puppe die meinen Körper in seiner
gegenwärtigen Lage vorstellt & mit der nun die
Veränderungen vorgenommen werden –
in effigie – die meinem Körper
zugedacht sind. |
Somit wäre das Problem wieder das
welcher Natur die stellvertretende Beziehung ist wenn
man etwa sagt „diese Puppe || Figur sollst Du sein
etc.”.
|
Ich
fühle daß ich auch hier wieder zur Antwort auf die Grenzen der
Sprache stoßen werde. Weiß aber noch nicht
wie. |
Was heißt es: Ich kann mir
vorstellen daß dieser(Ƒ) Punkt sich hier(Ƒ)
|
Es ist als ob im Befehl
bereits ein Schatten der Ausführung läge.
Aber ein Schatten eben dieser Ausführung.
Du gehst im Befehl dort & dort hin.
– Sonst wäre es aber eben ein anderer
Befehl. |
Ich weiß daß ich logisches Gift in
mich hineintrinken muß – um es überwinden
zu können. So sage ich mir jetzt eigentlich immer daß doch die Tatsache im Befehl im Satz schon liegen muß obwohl ich weiß daß sie nicht in ihm liegt aber dieser Schein muß angegangen werden. |
28.6.
Der Satz ist ein
Vergleichsobjekt – aber wie geht der
Vergleich vor sich? |
Irgendwie ist meine Schwierigkeit darin
gelöst daß ich mich andauernd in der
Sprache bewege. aus ihr nicht herauskann.
Wenn ich über das Vergleichen rede so rede ich über das Und hier kommt man auf etwas worin sich alles ausdrücken dürfte nämlich auf den Ausdruck „der Satz … ist wahr”. Darin wird alles beschlossen liegen daß „‚p’ ist wahr” nichts sagt als: p. |
Ich kann den
alten philosophischen Problemen keine Lösungen geben aber
ich kann ihnen Grenzen setzen. |
Zu Grunde liegt allen
meinen Betrachtungen (das
Gefühl) die
Einsicht, daß der Gedanke einen inneren Zusammenhang mit der Welt
hat & keinen äußeren. Daß man also das meint, was man sagt. Heißt das aber nicht nur, daß man sich in der Sprache nicht aus der Sprache, oder in den Gedanken nicht aus den Gedanken herausbewegen kann? |
Kann der Zusammenhang zwischen dem
„Meinen daß p der Fall
ist” & dem Geschehen |
In dem Worte
„etwas || das
& das meinen” liegt das ganze Problem
beschlossen || geschlossen.
|
Man
fühlt das Stellvertretende an dem
Gedanken. |
„Ich dachte,
Du würdest zu mir kommen”. An diesem Satz muß sich alles zeigen
lassen was man an exakteren Sätzen
zeigen will. |
In der Sprache wird alles
ausgetragen. |
Wenn man sagt „ich dachte Du würdest heute kommen
& habe schon die Vorbereitungen getroffen” so stehen diese Vorbereitungen mit dem Gedanken in
irgend einer Kontinuität. |
Wenn ich jemand einen Stuhl hinschiebe
damit er sich setzen
kann || setzt ist || bilden hier
auch der Gedanke & die Handlung eine Kette. |
Aber die
nächste Verwandtschaft von Sprache & Wirklichkeit ist
doch die daß wenn p eintritt |
Der Gedanke „daß es sich so
verhält” (p) wird durch die Tatsache
daß es sich so verhält (p) wahrgemacht.
Daß sich der Zusammenhang zwischen Gedanken & Welt so
nicht darstellen läßt (denn diese
Darstellung sagt gar nichts) muß die Antwort auf meine Probleme
sein. |
29. Es ist, natürlich, auch nicht so
daß das was den Gedanken „daß
p der Fall ist” verifiziert – befriedigt – eben
p genannt wird.
Wie wenn man sagen würde: ich habe Lust auf einen Apfel & was immer diese Lust befriedigt werde ich eben einen Apfel nennen. |
Denn ich rede ja
jetzt von der Befriedigung des Gedankens (der Erwartung)
noch ehe er befriedigt || der Gedanke
befriedigt ist. |
Man könnte nämlich
denken: Wie ist es: der Gedanke & die
Tatsache sind verschieden; aber wir nennen den Gedanken den
daß die Tatsache der Fall ist oder die Tatsache die die den
Gedanken wahrmacht. Ist da das eine ¤
Beschreibung mit Hilfe des Anderen? Wird |
Wenn man den Ausdruck „der Gedanke, daß … der Fall
ist” als Beschreibung
erklärt so ist damit wieder nichts erklärt, weil es
sich fragt: wie ist eine solche Beschreibung
möglich, sie setzt selber wieder das Wesen des
Gedankens voraus denn sie enthält
die Beziehung || den || den Hinweis auf eine Tatsache die nicht geschehen
ist also gerade das was problematisch war. |
Es ist – glaube
ich – offenbar daß unsere Schwierigkeit
eben darin beruht „über
das
Denken || den Gedanken || das Denken zu
denken” || :
daß wir „über das Denken
denken”
wollen. Hier stoßen wir auf eine
Unmöglichkeit & diesen Stoß klar zu machen || darzustellen das ist die Lösung. |
Meine Ansicht ist, daß
der Gedanke wesentlich das ist was durch den Satz
ausgedrückt ist wobei ausgedrückt nicht heißt
hervorgerufen Daß der Gedanke ganz Maß ist wie der Maßstab; d.h. daß || ich meine wie alles am Maßstab unwesentlich ist außer dem Längenmaß. |
Der Gedanke ist ein
Symbol. |
„Ich, der jetzt hier sitzt werde
morgen …”
Das Eintreten der
Realität (Ich, etc.) in das
Symbol, muß der eigentliche Zusammenhang des Satzes mit
der Wirklichkeit sein. |
Der (gegenwärtige) Gedanke enthält alle Realität die
gegenwärtig vorhanden ist. (Und mehr kann
er ja nicht haben.) |
Es ist sehr
merkwürdig – für den der
dafür Augen hat– daß in einem Buch
über Differentialrechnung in den Erklärungen
mengentheoretische Ausdrücke &
Symbole vorkommen, die in
dem || im Kalkül gänzlich
verschwinden. Das erinnert an die ersten Erklärungen
in den Lehrbüchern der Physik in denen vom
Kausalitätsgesetz &
Ähnlichem die Rede ist was, |
Das Symbol – ich meine
das, was als Symbol gebraucht wird – mit der Wirklichkeit zu
vergleichen ist einfach. Die Schwierigkeit
besteht darin es mit der symbolisierenden Beziehung
zusammen als Gedanke mit der Wirklichkeit zu
vergleichen. |
Kann das interpretierte Symbol
etwas anderes sein als das auf die
gegenwärtige Realität
angewandte? |
Die Kausalitäts-Erklärung
der Bedeutung nützt darum nichts
weil in ihr wieder hypothetisch von einem Sachverhalt
die Rede ist, was ja gerade das Problematische ist.
|
Der Wunsch,
die Erwartung, der Gedanke, der Glaube, die Befürchtung,
‒ ‒ ‒ etwa, daß er hereinkommen wird lassen mich
alle zur Türe schauen. – |
Ich erwarte daß die
Tür aufgehen wird: sie bleibt geschlossen. Nur
die geschlossene Tür ist Realität das Aufgehen |
Die vorige
Aufzählung ist etwas irreführend weil
sich Erwartung, Wunsch, etc. || Befürchtung
hauptsächlich auf die Zukunft beziehen
ich hätte dazusetzen müssen: der Gedanke
daß etwas so ist, die Beschreibung daß etwas so
ist (vielleicht) die Zufriedenheit damit daß etwas
so ist. Das Problem beginnt nicht erst, wo das angelegte Maß nicht mit dem Objekt stimmt sondern auch dort wo es stimmt mit der bloßen Anwendung des Bildes oder Satzes. |
Ich bin froh darüber daß Du
kommst heißt nicht ich bin froh weil Du kommst. (Im
letzteren Falle wäre es eine Vermutung daß ich
deshalb so guter Stimmung
bin.) |
Wenn ich sage: die
Worte „bedeuten” gar
nichts, ich will damit nur eine bestimmte Wirkung hervorbringen |
Es ist nämlich die Intention die man
erklären will & die kann man nicht
mit || mit sich selbst erklären.
|
Das Denken
ist das Gebrauchen von Symbolen. [Natürlich
nicht das Gebrauchen von Symbolen zum
Denken.] |
„Ein Satz
bedeutet, sagt, gar nichts; er bewirkt nur etwas; wie
z.B. ein Eisenbahnsignal, das man auch durch
eine automatische Vorrichtung ersetzen
könnte.” |
„Ich denke daß die Tür zu
ist” und „ich bin froh, daß die Tür zu
ist” sind auf einer
Stufe. (Und das letztere ist das viel bessere
Beispiel.) |
Ich schaue auf die geschlossene
Tür & stelle mir vor wie sie sich
öffnet. Wie kann ich mir
vorstellen daß sie sich
öffnet? Ist das analog
wie: „ich stelle mir vor daß
dort ein roter Fleck erscheint”? – Ich messe Wenn ich mir vorstelle daß dort ein roter Fleck erscheint, dann kommt der Ort „dort” wirklich in dem Vorgang vor (& nicht, etwa, nur ein Bild des Ortes). |
Man
würde etwa sagen: der Gedanke
knüpft an die Realität an. |
Ich sehe auf die geschlossene
Tür hin & stelle mir vor sie ginge auf. Meine
Phantasievorstellung (oder mein Gedanke) sind von
der Realität verschieden. Wenn ich aber nun an die
Tür eine andere etwa aus Papier anbrächte & die
öffnete während die eigentliche
geschlossen bliebe so könnte dieser Vorgang nicht den Vorgang in
der Phantasie ersetzen. Es sei || Es
sei denn daß ich nun wieder diese
papierene Tür als Stellvertreterin der
anderen interpretiere. Man sollte aber doch
glauben daß die papierene Tür &
die Phantasietür von außen betrachtet (also
überhaupt) auf der gleichen Stufe ständen.
Aber es ist nicht so. Und mit der Interpretation kommt
wieder jenes rätselhafte |
Es ist doch ein Unterschied,
ob ich daran denke was ich heute nachmittag machen werde
oder, was ein anderer im übrigen ganz gleich aussehender Mensch
machen wird. |
Man kann sich vorstellen es sei etwas der
Fall was nicht ist: sehr
merkwürdig!
Denn, daß die Vorstellung mit der
Wirklichkeit nicht übereinstimmt ist nicht
merkwürdig daß sie sie aber dann repräsentiert ist
merkwürdig. |
Ich bin seinerzeit auf die Bildtheorie
der Sprache durch eine Zeitungsnotiz gebracht worden worin gesagt war
daß ¤ in Paris bei einer
Gerichtsverhandlung über ein Straßenunglück dieses
Straßenunglück durch Puppen & kleine Omnibusse
vorgeführt wurde. Wie unterscheidet sich nun so
eine Vorführung von einem Spielen mit Puppen
etc.?
(Natürlich durch die Bedeutung)
|
Der Gedanke ist ein Stück
Wirklichkeit. Und wie kann ein Stück
Wirklichkeit einem anderen wesentlich vorzuziehen sein || in einer wesentlichen Ausnahmsstellung sein.
Außer in einer Beziehung zu sich selbst. Eben so
daß man über alles denken könnte aber über
das Denken nicht. |
Warum kommt mir mein
Gedanke ein so exzeptionelles Stück
Wirklichkeit vor? Doch nicht weil ich ihn „von innen” kenne,
das heißt ja nichts; sondern offenbar weil ich alles in
Gedanken ausmache &
über das Denken auch nur
wieder denken könnte. |
D.h. || Das hieße die Gedanken sind nur in Bezug auf
sich selbst in einer
exzeptionellen
Stellung. |
Das Gefühl über
den Gedanken ist etwa: Wenn ich das meine (meine, daß, das & das
der Fall ist) so meine ich wirklich daß das & das
der Fall ist. Ich meine die Tatsache & nichts
Anderes, Drittes. (Das scheint mir das
ganze Gefühl |
Am Vorgang
des Meinens daß diese Tür aufgehen wird kann nicht mehr sein
als der der das meint damit erlebt (es handelt sich ja
hier nicht darum etwa in den
Kopf eines Menschen während
eines psychischen Prozesses zu sehen). Aber
dieser Vorgang des Meinens hat keine Beschreibung durch
die Sprache als den Ausdruck dessen was man meint. |
Was geschieht wenn
ich den tatsächlichen Zustand
der Tür beschreibe „die Tür
ist jetzt zu”. Wenn ich
also Worte der gesehenen Wirklichkeit
zuordne? Man möchte sagen daß man die Worte
nach einer Regel der Wirklichkeit || der Wirklichkeit nach
einer Regel zuordnet aber das ist auch nicht
wahr denn die Regel würde lauten sag „p”
wenn p
der Fall ist. |
Wir wollen ja nicht beschreiben |
Warum beschäftigen wir uns denn gerade
mit dem Denken & nicht mit der Verdauung?
Es ist aber auch nicht so || Man kann aber auch nicht sagen daß wir nun einmal denken & eben über das Denken denken wollen; denn wir verdauen nun einmal, aber weiter geht es nicht analog. |
Aber auch das Interesse steht der Philosophie nicht frei
gegenüber, denn sie hat es auch mit dem Wesen des
Interesses zu tun. |
Vergessen wir auch nicht daß der
Unterschied zwischen einer Hypothese, einem Satz, einem mathematischen
Gesetz etc. in die Frage nach dem Wesen des
Gedankens & des Interesses
hineinspielt. |
Auch die Zusammengesetztheit des Satzes ist
problematisch. Diesem Gedanken der
wesentlichen Zusammengesetztheit liegt vielmehr die
Anknüpfung an eine bestimmte Realität
zu Grunde. Ich denke dabei daran daß ein
Wort, etwa „Löwe” nichts besagt. Wohl aber sagt
es etwas |
Wenn einer die
Lösung des Problems des Lebens gefunden zu haben glaubt &
sich sagen wollte jetzt ist alles ganz leicht so brauchte er
sich zu seiner Widerlegung nur sagen daß es eine Zeit
gegeben hat wo diese „Lösung”
nicht gefunden war; aber auch zu
der Zeit mußte man leben können & im
Hinblick auf sie scheint || erscheint die gefundene Lösung wie || als
ein Zufall. also irrelevant Und so geht es
uns in der Logik. Wenn es eine „Lösung der logischen
(philosophischen) Probleme”
gäbe so müßten wir uns nur
vorhalten daß sie ja einmal nicht
gelöst waren (und auch da mußte man leben & denken
können)
‒ ‒ ‒ |
Es ist ein
wesentlicher Unterschied zwischen Sätzen wie
„das ist ein Löwe”, „die Sonne ist
größer als die Erde” die alle ein
„dieser”,
„hier”,
„jetzt”
enthalten & also an die Realität unmittelbar
anknüpfen & Sätzen wie „Menschen haben zwei Hände” etc. Denn wenn
zufällig keine Menschen in meiner Umgebung
wären wie wollte ich diesen Satz
kontrollieren? |
Das Wesentliche am Gedanken ist daß er
nicht als Mittel zum Zweck als ein Instrument wirkt das man durch ein
anderes ersetzen könnte, sondern als
Unvergleichliches, Autonomes. |
Darum kann man sich keine
Gedankenprothese vorstellen || denken || ist eine Gedankenprothese nicht
denkbar. |
Aber heißt das was || etwas? Ich kann ja zwar den
Magen durch eine Prothese ersetzen aber nicht die
Magenschmerzen. Und kann man nicht vom Magenschmerz
dasselbe sagen wie vom Gedanken? |
Das Gefühl an das ich
jetzt alle meine Betrachtungen knüpfe ist das von der
Einzigkeit der Gedanken. |
Es wäre auch denkbar daß kein
|
Wer denkt läßt Bilder an seinem
Geist vorüberziehen. |
Wenn ich sage „ich freue mich, daß er lebt” & er aber in Wirklichkeit nicht lebt war dann mein
Satz falsch? Wie ist es mit dem Satz: „ich freue mich, daß ich keine Schmerzen
habe”? |
Wenn man sich
die Welt anders vorstellen will als sie ist so
muß man ein Gesetz der Ersetzung der
tatsächlichen || wirklichen || tatsächlichen
durch die vorgestellte annehmen, denn sonst würde die
wirkliche nicht durch die andere in der
Vorstellung ersetzt. |
„Nehmen wir an
Du wärst so hoch …” hier
muß die Bedeutung des Du im Symbol vorkommen. |
Auch die Verneinung enthält eine Art
Allgemeinheit. |
Aber freilich muß
auch die Bejahung sie enthalten,
und nur einen anderen Gebrauch von ihr
machen. |
Die dem
Satze zu Grunde liegende
Realität verstehen & die grammatischen
Regeln heißt bereits ihn verstehen. Es
heißt auch schon „Wissen was
der Fall ist, wenn er wahr ist”. – Insofern ist dieser Ausdruck
irreleitend da er glauben macht es sei noch eine
Synthese im Verständnis die das was der Satz
sagt in irgend einem Sinn zur Wirklichkeit machen
würde. |
[„Ist ein 6ter Sinn
denkbar?” Eindringen
des Totenkopfes in den Bienenstock.] |
Ich
kann einen Apparat beschreiben in dem ein Rad mit
einem bestimmten Einschnitt ist & wenn der Bolzen sich an
dieser Stelle befindet & das Rad in
diese Stellung kommt dann schnappt er ein. Kann man
aber das selbe auch || auch mit dem Satz
machen: Der Satz ist so gebaut
daß wenn nun die Realität so ist dann schnappt sie
ein. Ich müßte also den Gedanken beschreiben
können & dann die Realität die so gebaut ist daß
sie mit ihm übereinstimmt. Aber das heißt doch gar
nichts. |
8.7  Wenn ich mir
erwarte daß der weiße Kreis zu einer
gewissen Zeit auch grau wird wie der rechte Kreis so Wenn ich mir
erwarte daß der weiße Kreis zu einer
gewissen Zeit auch grau wird wie der rechte Kreis so Man sagt: „ich weiß genau, was ich mir erwarte”. Aber das gibt man doch zu, daß ein Unterschied ist zwischen der Erwartung & ihrer Erfüllung. Aber kann man sagen daß wenn dann die Erfüllung eintritt doch etwas eingetreten ist was sich nicht hat voraussehen lassen (oder, nicht vorausgesehen wurde)? Natürlich, nein! Was sich nicht hat voraussehen lassen von dem können wir eben nicht reden. |
Man kann auch nicht sagen „daß auch die lebhafteste
Vorstellung doch nicht an die Wirklichkeit
herankommt” denn damit wäre
es also doch denkbar daß sie herankäme – wenn es
auch nie einträte –. |
Es ist immer so als wäre
die Erwartung (der Gedanke) ein Maßstab der die
Höhe auf der || die es bei ihm einzig
ankommt mit dem zu messenden Objekt
gemein hat oder wenn man sagt:
Beschreibe einen Hohlzylinder & einen
Vollzylinder die genau zusammenpassen. Soweit sie
zusammenpassen haben sie eine Form mit einander
gemein. Und die Beschreibung beschreibt |
Man kann das erwarten woran man sich auch
erinnern kann. |
Man erwartet ja gerade das was im Zeichen in
der Erwartung nicht gegeben ist. |
Die Erwartung
& die Tatsache die die Erwartung befriedigt passen offenbar
irgendwie zusammen. Man soll nun eine Erwartung
beschreiben & eine Tatsache die zusammenpassen
damit man sieht worin diese Übereinstimmung besteht.
Da denkt man sofort an das Passen einer Vollform in eine
entsprechende Hohlform. Aber wenn man nun
hier die beiden beschreiben will so sieht man
daß soweit sie passen eine Beschreibung für beide
gilt. |
Angenommen
selbst, meine erwartende Vorstellung könnte den erwarteten Fleck
so auf die Fläche projizieren daß sich die
Erfüllung der Erwartung dadurch zeigte daß
das Ereignis sich gänzlich mit
der Erwartung deckte, auch dann wäre eben
gerade dieses in der Erwartung selbst
nicht vorhanden gewesen & käme bei der
Erfüllung neu hinzu. |
Die
Vollform unterscheidet sich ja auch nur durch einen Index,
durch etwas Amorphes, von der Hohlform.
|
‚Ich erwarte mir daß er kommt, & er
kommt.’ Man
möchte sagen: Mehr von ihm
konnte ja die Erwartung nicht wiedergeben als was sie dann an
(dem
Ereignis) || ihm befriedigt hat. Aber das ist
natürlich auch nicht richtig. Denn es ist
nicht so als bestünde das Ereignis gleichsam aus Qualitäten
die zum Teil schon die Erwartung des Ereignisses hatte
zum Teil noch nicht.
Man könnte sagen die einzige Qualität die der Erwartung noch abgeht ist die Wirklichkeit aber das wäre natürlich auch falsch. |
Das Merkwürdige ist ja
darin ausgedrückt daß wenn das der Fleck ist den ich erwartet
habe er sich nicht von dem unterscheidet den ich erwartet
habe. |
Erwartung & Erfüllung
verhalten sich wie Hohlform & Vollform. |
„Ich erwarte mir daß dieser Fleck gleich
diesem wird so daß man ihn gar nicht mehr von ihm
unterscheiden kann”; hier scheint doch
alles was die Erfüllung bringt vorausgesehen zu
sein. Aber natürlich nicht mehr als in jedem anderen
Falle. Und warum nicht gleich das Beispiel
nehmen: „Ich erwarte daß
dieser Fleck sich gleich bleiben wird”. |
Die Erwartung der Befriedigung der
Erwartung daß p eintreffen wird ist die
Erwartung daß p eintreffen
wird. Der Gedanke an den Inhalt des Gedankens p ist der Gedanke p. Und das enthält die Wahrheit über alle die Fragen die in dieser Sache aufgeworfen werden. |
Die Antwort
auf jede philosophische Frage ist eine
Selbstverständlichkeit. Es ist nur schwer
die Selbstverständlichkeit zu finden die gerade
das erledigt was mich jetzt
beunruhigt. |
Die Wahrheit eines Satzes kann man immer nur
behaupten; sie liegt nie in ihm so daß er nur das Zeichen wäre
das auf etwas Vorhandenes hinweist. |
Man denke sich den
Satz „in unserem Gesichtsfeld gibt es
keine Lücke”.
(Untersuche ihn auf das was damit gemeint sein kann.)
|
„Ich dachte, Du würdest kommen;
und du bist gekommen”; hier hat der Satz
„Du bist gekommen” durchaus keine einfachere, realere, Beziehung zur
Wirklichkeit als der Satz „Du
würdest kommen”.
Es ist nicht so als ob der erste doch der Name einer Tatsache wäre während der zweite nur eine probeweise Zusammenstellung der Begriffe ist. |
Es ist – glaube ich –
wichtig zu erkennen daß wenn ich etwa glaube daß jemand zu mir
kommen wird mein Dauerzustand nichts mit dem Betreffenden &
den übrigen Elementen des Gedankens |
Das Amorphe ist das was nicht Symbol
ist & wofür die Betrachtungen der
Kausalitätstheorie & des
Behaviourism gelten. |
Wenn ich beschreibe, so abkonterfeie
ich die Wirklichkeit; aber nicht nach Regeln. Es läßt
sich keine Regel geben nach der die || eine
Beschreibung die Wirklichkeit beschreibt denn diese Regel würde
sich selbst voraussetzen. |
19.7
Der Gedanke,
soweit man überhaupt von ihm reden kann, muß etwas ganz
Hausbackenes sein. |
(Man pflegt sich ihn als
etwas Ätherisches noch
Unerforschtes zu denken; als handle es sich um
|
Der Gedanke hat aber nur
eine Außenseite & kein Innen.
Und ihn analysieren heißt
nicht in ihn dringen. |
Ein amorpher Gedanke ist so
undenkbar, wie ein amorphes Schachspiel. |
Das was den Gedanken
für uns zum Gedanken macht kann nicht etwas
Menschliches sein, etwas das mit dem
Bau & Wesen des Menschen zu tun hätte, sondern
etwas – rein Logisches – was
unabhängig von der Naturgeschichte eines Lebewesens
besteht. |
Eine Gedankenprothese ist darum
nicht möglich weil der Gedanke
für uns nichts Menschliches
ist. Wir könnten die Rechenmaschine als eine Prothese statt der 10 Finger ansehen aber die Rechnung ist nichts spezifisch Menschliches & für sie gibt es keinen Ersatz || keine Prothese. |
Das Denken ist ein
Bilden von Bildern auf verschiedene Art &
Weisen. Ihre
Auffassung als Bilder aber die das Wesentliche ist, ist nicht
|
Es
ist sicher zwischen unseren Fantasien &
wirklichen Erlebnissen besteht eine
Ähnlichkeit. Aber Gedanken sind
sie erst wenn sie mit der Wirklichkeit verknüpft sind &
als Bilder von ihr aufgefaßt. Andrerseits braucht der
Gedanke gar nicht die || jene
Ähnlichkeit mit der Wirklichkeit zu haben („Er muß nur logisches Bild
sein”.) |
Wenn mir heute
geträumt hat daß A mich besucht hat || besucht & A besucht mich nun wirklich
so war deswegen jene Traumphantasie keine
Erwartung & die Tatsache daß A mich besuchte
keine Erfüllung der
Erwartung || des Traumes. Es fehlt die Intention. Kann aber die Intention eine externe Relation sein?! Da die Intention macht daß dieser Vorgang ein Bild ist & nun bewahrheitet oder nicht bewahrheitet wird & da das das eigentliche Wesen der Intention ausmacht |
Es drückt sich
jedenfalls in der Sprache keine Mehrdeutigkeit der Erwartung oder des
Wunsches etc. aus so daß also eine
Erwartung durch Verschiedenes befriedigt werden
könnte. Und das muß sich so rechtfertigen daß
das Seine Deutung schon enthalten kann aber nur heißen die Form der Wirklichkeit schon vorzuzeichnen. Aber auch dieses „Vorzeichnen” könnte falsch aufgefaßt werden, denn – könnte einer sagen – kann ich nicht das vorzeichnen und das meinen. Ja aber wenn ich sage „& das meinen” so ist doch dieses „das” selbst irgendwie gemeint. Und was, wenn ich sage: „ganz richtig, ich habe eben mit dem großen das kleine gemeint.” – Ich kann eben gar nicht reden ohne es schon irgendwie zu meinen. Darum muß sozusagen die Meinung aus der Betrachtung herausfallen. Denn wenn ich sagen will wie etwas gemeint ist so meine ich ja das selbst auch irgendwie. |
Kann ich also
festsetzen daß die Länge im Maßstab
1:1 gemeint
ist? |
Aber wenn sie auch nicht so
gemeint ist so gibt es doch immer eine Länge die dann im
Maßstab 1 : 1 |
|
Bedenken wir daß die
Erwartung in der Wirklichkeit von a & b gar nicht
vorhanden ist sondern nur in Symbolen existiert & zwar muß
hier ein Symbol für b & eines für a
vorhanden sein & sie müssen
beide schon irgendwie gemeint sein. Und
kann denn nicht durch eine Regel ausgedrückt sein daß sie
beide auf die gleiche Weise gemeint sind?
|
Aus dem Meinen kann ich nicht heraus
darum kann ich nicht sagen, wie etwas gemeint ist. Dann
aber muß eben das Wort meinen sinnlos
sein, so muß es sich herausstellen.
|
20. Es ist in der Erwartung alles
für das Eintreffen des Ereignisses hergerichtet. |
Von den
Teilstrichen des Maßstabes gelten nur die Punkte die sie mit dem zu
messenden Körper gemein haben. |
Es muß
alles hergerichtet sein, darin besteht die
Eindeutigkeit der Erwartung. |
Oder sie besteht eigentlich darin
daß man von ihr auch nicht reden kann. |
Es sagt einer „ich wünsche ein
rotes Stück Papier zu sehen”, man
zeigt ihm Stücke von verschiedener Farbe, Weiß, Grün,
endlich auch ein rotes; er sagt „das habe ich gemeint”. Wie konnte er denn rot || das
Rot meinen ohne es zu sehen? – Denn
wenn er auch eine Vorstellung hatte so war sie doch nicht das was er
dann zu sehen bekam (sonst hätte er ja nichts
erwartet) also mußte er diese Vorstellung auch erst irgendwie
meinen. – Ist es nun nicht so: daß
er die Vorstellung auch mit dem gegenwärtigen – nicht
erwarteten – Gesichtseindruck vergleichen kann &
vergleicht & dabei die Interpretation
dieser Vorstellung so zu sagen
festlegt. |
In dem selben Sinne in dem er jetzt
1 m groß || hoch ist wird er später
1˙5 m hoch sein. |
Ich denke
mir es würde jemand, etwa ein kleiner Bub gefeiert & man
stellt durch ein lebendes Bild dar was er einmal als Mann machen
wird. Sieht man die Vorstellung & den Buben so
weiß man noch nicht was das Ganze bedeutet. Man muß
wissen wie die Vorstellung gemeint ist. Das
weiß man aber wenn man sie mit dem gegenwärtigen Stand, dem
Knaben wie er jetzt ist, vergleichen kann.
Wenn ich sagen kann daß er jetzt noch nicht so groß ist so habe ich schon das Bild als Bild der || seiner Zukunft aufgefaßt. Wie aber bringt man dem der die Vorstellung sieht sie aber nicht versteht die Absicht bei? Indem man sie ihm sagt! |
Kann man
sagen: Von der Intention kann nur soweit die
Rede sein als man nach ihr fragen & sie
erklären kann. |
Also || also sie in Worten ausdrückt und also den
Zeichen noch weitere Zeichen hinzufügt. Man
könnte sich nun etwa
über dem lebenden Bild eine Schrift denken die es
erklärt. |
Die
Meinung des Zeichens kann man nur erklären indem man Zeichen
gebraucht also dem ersten Zeichen weitere hinzufügt.
Dieses Zeichen kann man wieder nur durch Zeichen erklären
etc. Also soweit das keine Erklärung der
Intention ist gibt's keine. (nämlich keine
Erklärung, aber auch keine Intention.) |
Gewiß, wenn man jemandem
erklären will wie etwas gemeint war so muß man Worte
gebrauchen, – die selbst irgendwie gemeint sind.
So setzt man zur Landkarte den Maßstab, aber nun ist eben das Ganze ein Zeichen … |
21. || 21.7. Das Charakteristische am Gedanken,
was ihn für uns so einzig macht ist, daß wir dabei nicht das
Gefühl einer Deutung haben. |
Ja, es ist offenbar daß
sich eben die Erwartung eben mit demselben, derselben
Wirklichkeit, abgibt wie die Tatsache die sie erfüllt.
Und das ist was sie uns wirklich macht. |
Wir schauen erwartend zu
derselben, wirklichen, Tür zu der die
erwartete Person eintreten soll. |
(Immer vergißt man, wie einfach
& natürlich alles ist.) |
Ich sage „schau dorthin, dort wird etwas
Schwarzes sichtbar werden wie ein
Vogelkopf”.
Er schaut hin & ich sage „siehst Du, da ist es”. Er sagt „ich
hätte || habe mir etwas Größeres
erwartet”. Wie hat er das
gemacht? Er war auf etwas Größeres eingestellt. Oder „ich habe mir etwas Dunkleres erwartet”. Er war auf etwas Dunkleres eingestellt. |
Ich erwarte mir
einen gelben Fleck zu sehen & nun sage ich „ja, so habe ich mir ihn vorgestellt, das habe
ich mir erwartet”. Und nun
fragte mich einer „woher weißt Du
daß Du Dir das erwartet hast, Du
hast es ja nicht gesehen?”. Es ist offenbar daß diese Frage nichts heißt
(& daß darin die Lösung meines
Problems liegt). |
Wenn das dasselbe Gelb sein
kann was || welches
ich mir vorgestellt habe (so daß es dafür nicht
noch ein äußeres Kriterium etwa eine
Reaktion gibt) dann mußte sich die
Erwartung auf das beziehen was der Vorstellung & der
Wirklichkeit gemeinsam ist denn die Vorstellung bleibt als Vorstellung
von der Wirklichkeit verschieden. |
Es beschäftigen uns
Fragen verschiedener Art etwa „wie
groß ist das spezifische Gewicht dieses
Körpers”, „wird es heute schön
bleiben” „wer wird als nächster zur Tür
hereinkommen” etc.
Aber unter unseren Fragen finden sich welche von
besonderer Art. Wir haben hier ein anderes
Erlebnis. Die Fragen scheinen fundamentaler zu sein
als die anderen. Und nun sage ich:
wenn wir dieses Erlebnis haben dann
sind wir an der Grenze |
Man könnte
sagen die Erwartung ist kein Bild sie bedient sich nur eines
Bildes. Ich erwarte etwa daß meine Uhr jetzt auf
 aus. Dieses
Bild kann ich nun mit der wirklichen
Zeigerstellung || Stellung vergleichen; die Erwartung aber nicht.
Die ist einfach eingetroffen oder nicht eingetroffen; während
man von der Zeichnung nicht sagen kann sie sei eingetroffen.
Denn dazu gehört erst die Deutung der
Zeichnung. aus. Dieses
Bild kann ich nun mit der wirklichen
Zeigerstellung || Stellung vergleichen; die Erwartung aber nicht.
Die ist einfach eingetroffen oder nicht eingetroffen; während
man von der Zeichnung nicht sagen kann sie sei eingetroffen.
Denn dazu gehört erst die Deutung der
Zeichnung. |
Ich habe etwas vorausgesagt, es tritt nun
erst ein & || und
ich sage nun einfach „es ist
eingetroffen” & das beschreibt
schon den Tatbestand vollkommen. Er ist also auch jetzt nur
insoweit || soweit
beschrieben als man ihn auch hat beschreiben
können bevor er (noch) eingetreten war. |
Wenn ich einfach sagen kann
„es ist eingetroffen || trifft ein”, so kann
ich andererseits nicht beschreiben wie ein
Tatbestand sein muß um eine bestimmte Erwartung zu
befriedigen. (Und hierin liegt wieder die ganze
Lösung, wenn ich sie auch noch immer nicht klar aussprechen
kann.) |
Die Erwartung verhält sich eben zu
ihrer Befriedigung nicht wie der Hunger zu seiner
Befriedigung. Ich kann sehr |
Die Erwartung ist keine
Phantasie, denn wenn ich erwarte daß dort ein lichter Punkt
erscheinen werde so muß das dort der Ort sein
wo der Punkt wirklich erscheinen wird wenn er erscheinen
wird. |
Sowohl vorschauend in der Erwartung als auch rückschauend
in der || bei der Erfüllung & in der
Erinnerung an die Erwartung sind Erwartung & Erfüllung im
selben Raum. Und die Erwartung ist auch ursprünglich schon die Erwartung der Erfüllung & die Erfüllung wird nur die Bejahung der Erwartung. |
Könnte man vielleicht sagen „rot” hat zwei
verschiedene Bedeutungen wenn man einen wirklichen Farbfleck rot nennt
& andrerseits einen vorgestellten Fleck?
Nein. Rot ist was beiden gemeinsam ist || sie beide gemeinsam hat. |
Die Erwartung kann
nur logisch auf das Erwartete weisen. Denn jedes
Bild bleibt immer deutungsbedürftig & die
Deutung kann nur eine logische Beziehung
herstellen. Denn jede materielle Beziehung die wir dem Bild
hinzufügen führt uns nicht zur Intention &
läßt das Bild weiterhin deutungsbedürftig. Denn nur da ist es auch möglich zu bezweifeln ob, & zu zeigen daß nicht, Übereinstimmung zwischen der Erwartung & einer Tatsache besteht. |
Das hängt auch damit zusammen daß
die Erwartung, der Gedanke der Beweis der Möglichkeit der
Tatsache sein muß. Wie eben der Meterstab an dieser
Stelle der „Beweis” dafür
ist || zeigt daß etwas 1 m lang
sein kann. |
„Wenn die Erwartung noch mehrdeutig ist, so
können wir jedenfalls von dieser Mehrdeutigkeit nicht
mehr reden.” Denn soweit die
Wirklichkeit zu beschreiben ist soweit beschreibt sie die Erwartung
& soweit die Wirklichkeit vorherzusehen ist sieht sie die
Erwartung voraus. |
Man kann nur
insoweit fragen, ob das wirklich die Erfahrung sei die die
frühere Erwartung befriedigt als man es kontrollieren
kann. Aber man kann es nur kontrollieren soweit die
logische Multiplizität in Frage ist.
Also ist auch nicht mehr notwendig als daß der Gedanke auf der Wirklichkeit fußt || fuße & auf ihr sein Gebäude errichte. |
22.7. Unterscheidet sich etwa ein
vorgestellter Ton von dem gleichen wirklich gehörten
durch die Klangfarbe? |
Die Schwierigkeit ist es, zu
verstehen daß der
Sachverhalt || die
Tatsache in der Erwartung ganz vorgebildet
ist. |
Im Maßstab der neben dem wachsenden Gegenstand steht ist
die Höhe auch vorgebildet aber nicht, daß dieser Gegenstand
sie erreichen wird. |
Es ist als ob der Gedanke ein Schatten des
Ereignisses wäre; aber so daß dann die Frage ob
dieses Ereignis wirklich das Ereignis || dasjenige ist dessen Schatten wir
vor uns hatten || haben unsinnig
ist. D.h. die Relation von Schatten & Tatsache kann keine äußere sein. |
Und muß das nicht eine falsche Darstellung sein?
Denn kann es denn in der Welt der
Tatsachen solche || eine Art geben die die Schatten der
anderen sind? Gewiß nicht. Aber ich sage ja
selbst, daß der „Schatten”
nicht etwas ist was auf eine äußere Art mit der
Tatsache zusammenhängt & das heißt, daß in diesem
Vergleich ein logischer Fehler ist. |
Wenn ich Einem
einen Befehl gebe & er hört ihn & handelt nun so
kann |
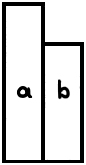 Wenn ich sage
„b ist nicht so lang wie
a” so scheint das jenen Schatten
voraus zu setzen der Tatsache daß b so lang wie
a ist. Wenn ich aber sage „b ist kleiner als
a” so scheint das diesen Schatten
nicht zu enthalten || vorauszusetzen
und doch sagte || sagt es auch
(wenn auch mehr als das) was der erste Satz
sagt. Wenn ich sage
„b ist nicht so lang wie
a” so scheint das jenen Schatten
voraus zu setzen der Tatsache daß b so lang wie
a ist. Wenn ich aber sage „b ist kleiner als
a” so scheint das diesen Schatten
nicht zu enthalten || vorauszusetzen
und doch sagte || sagt es auch
(wenn auch mehr als das) was der erste Satz
sagt. |
Man könnte also sagen:
„b ist so lang wie
a” hat Sinn, weil b
kürzer als a ist. (Oder „dieses Buch ist blau” hat Sinn weil es in Wirklichkeit rot
ist.) |
Etwas spricht in
mir für die Auffassung, daß die Interpretation des
Bildes nur im Gebrauch liegt den man vom Bild macht.
Nehmen wir an das Verstehen des Befehls bestünde darin daß man eine bestimmte Tätigkeit halluziniert & das Bild dieser Halluzination nun mit der wirklichen Handlung vergleicht indem man es gleichsam auf den Raum in dem diese vor sich geht auflegt. Der Befehl hätte etwa gelautet vom Punkt A aus nach rechts eine 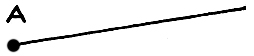 Gerade zu ziehen;
ich Gerade zu ziehen;
ich |
(Es ist eine
besondere Methode
der
Philosophie die in den Wissenschaften nicht erlaubt
ist, den günstigsten Fall anzunehmen.)
(Am ähnlichsten ist diese Methode noch der in der
Mathematik einen extremen Fall anzunehmen in welchem das & das
doch bestimmt || jedenfalls
eintrifft. (Argument a
fortiori?)) |
Nun dürfte man aber
nicht wieder fragen „ja woher weiß
man denn daß man dieser Halluzination zu folgen hat,
daß sie als Befehl aufzufassen ist es so zu
machen” denn das müßte jetzt
darin liegen daß man etwa ein bestimmtes Gefühl der
Befriedigung hat wenn man ihr folgt & nicht wenn man ihr nicht
folgt. |
Der Gedanke wäre also ein Bild das eine bestimmte Wirkung
hätte. |
Ich || Man könnte
fragen: woher weiß ich Es ist so wie wenn man einen Vorwurf spürt weil man es jemandem nicht gleichtut. Der Gedanke dient also der Wirklichkeit in einem gewissen Sinne als Vorbild || ist also in einem gewissen Sinne ein Vorbild der Wirklichkeit. |
23.7. Nehmen wir wieder den „günstigsten”
Fall an, nehmen wir an, ich
halluziniere bei der Erwartung
(zwar, wie kann ich
halluzinieren daß
er in 5 Minuten hereinkommen wird?) |
Was heißt
denn das Wort „dreiundzwanzig” zu
verstehen als seine Syntax zu verstehen, damit operieren
können? |
Erwartung, Befehl
etc. kann man sich immer an einer Landkarte
deutlich machen & an ihrem Gebrauch. Die
Landkarte ist das Bild das interpretiert wird. Denken
wir uns wir |
Man denke
sich man gebe jemandem den Befehl eine bestimmte Handlung
auszuführen etwa dieser Linie mit dem Bleistift
 nachzufahren. Die Sache wird
deutlicher wenn man sich den Befehl jemandem unserer Wortsprache
Unkundigen mit Zeichen gegeben
denkt. Man wird dann die Handlung
vormachen und nun ihm den Bleistift geben & ihn stupfen
& etwa seine Hand ein kleines Stückchen führen
(oder dergleichen). Das wird der Befehl
sein. Nun wird man freilich sagen: das ist bloß
der Ausdruck des Befehls & nicht was wir eigentlich meinen,
was wir meinen ist: … , & nun wird
man || er mir andere
Zeichen für das geben „was
gemeint ist”. – Aber wenn
man nun den Befehl ausführte & auf die Ausführung
als nachträgliche Erklärung des Befehls wiese?
Oder ist in dem Falle auch die Erfüllung nur ein
Zeichen?
nachzufahren. Die Sache wird
deutlicher wenn man sich den Befehl jemandem unserer Wortsprache
Unkundigen mit Zeichen gegeben
denkt. Man wird dann die Handlung
vormachen und nun ihm den Bleistift geben & ihn stupfen
& etwa seine Hand ein kleines Stückchen führen
(oder dergleichen). Das wird der Befehl
sein. Nun wird man freilich sagen: das ist bloß
der Ausdruck des Befehls & nicht was wir eigentlich meinen,
was wir meinen ist: … , & nun wird
man || er mir andere
Zeichen für das geben „was
gemeint ist”. – Aber wenn
man nun den Befehl ausführte & auf die Ausführung
als nachträgliche Erklärung des Befehls wiese?
Oder ist in dem Falle auch die Erfüllung nur ein
Zeichen? |
Man könnte sagen: Den
Befehl verstehen heißt ihn ausführen oder sich
ihm widersetzen. (Etwa ähnlich wie man sagen könnte die Schwerkraft äußert sich entweder darin, daß sie einen Körper beschleunigt |
Das
Zeichen der Widersetzlichkeit kann etwa ein Schütteln des Kopfes
sein; so daß, wenn er sich nach der Linie a
 bewegt &
den Kopf nicht schüttelt das bedeutet er habe den
Befehl so verstanden er solle sich auf a bewegen &
führe ihn aus. Wenn er a entlang geht &
dabei den Kopf schüttelt so hieße das er habe den Befehl
anders aufgefaßt & wolle sich ihm durch seine Handlung
widersetzen¤ etc.
etc. bewegt &
den Kopf nicht schüttelt das bedeutet er habe den
Befehl so verstanden er solle sich auf a bewegen &
führe ihn aus. Wenn er a entlang geht &
dabei den Kopf schüttelt so hieße das er habe den Befehl
anders aufgefaßt & wolle sich ihm durch seine Handlung
widersetzen¤ etc.
etc. |
Es habe
jemand Einem einen solchen Befehl durch Zeichen gegeben
& ich frage ihn „hast Du denn
diesen Befehl verstanden” &
er sagt mir darauf „ja, er wollte daß
ich …” & wiederholt mir
den Befehl in einer anderen Sprache. So komme ich aus den
Zeichen nicht heraus. |
24.7. Wenn man das Beispiel von dem durch
Gebärden mitgeteilten Befehl betrachtet möchte man
einerseits immer sagen ja dieses Beispiel ist eben
unvollkommen, die angenommene Gebärdensprache zu
roh darum kann sie den beabsichtigten Sinn nicht
vollständig ausdrücken – aber tatsächlich ist sie
so gut wie jede (Es ist eine der wichtigsten Einsichten daß es keine Verbesserung der Logik gibt.) |
Wenn ich
also jemandem einen Befehl gebe, so kann ich weiter
nichts tun als ihm ein Beispiel geben. Der
Befehl muß sich dann von dem Befehl jeder anderen Handlung
unterscheiden & das heißt der Befehl muß die gleiche
Multiplizität zulassen (die gleiche Geometrie) wie die
Handlungen. Mehr aber kann er nicht tun. |
Es ist sehr
trivial wenn ich sage, daß ich in der Erwartung eines Flecks die
Erwartung eines kreisförmigen von der eines
elliptischen muß unterscheiden können
& es überhaupt soviele
Unterschiede in der Erwartung geben muß wie in
den Erfüllungen der Erwartung.
(Der Hunger & der Apfel der ihn befriedigt
haben nicht die gleiche Multiplizität.)
|
Der
Befehl steht aber doch nicht selbständig da ich
will doch etwas mit dem Befehl. Ja was?
Nun, daß er || der Mensch das
& das tut. Ganz richtig aber hier habe ich eben den
Befehl nur in anderer Weise wiederholt.
|
Der Sinn
ist eben nicht etwas worauf man deuten kann wie etwa auf mich als
Bedeutung meines Namens sondern Eigentum des Satzes
der ihn hat. Der Satz hat ihn in sich. |
Angenommen
der Befehl würde darin bestehen einen Gegenstand nach einer
Werkzeichnung zu machen. Dann
projiziere ich bei der Ausführung des
Befehls diese Zeichnung – den Ausdruck des Befehls –
in die Wirklichkeit. Ich verwende also
die Zeichnung als Bild. |
Worin besteht aber
dieses „als Bild
verwenden”? Wenn ich
z.B. einer Vorlage nachzeichne, ist es da
dasselbe ob ich absichtlich oder unabsichtlich etwas der
Vorlage Ähnliches
zeichne? Und wenn ich mich nun verzeichne ist damit die
Absicht die Vorlage zu kopieren fallen gelassen || aufgehoben? – Und doch kann diese
Absicht nur darin bestehen daß sie mit der ausgeführten
Kopie || Zeichnung ein genaues Bild der
Vorlage oder eigentlich die Vorlage selbst ergibt.
Die Absicht muß die Ausführung zu der Vorlage ergänzen. Aber ist es dann nicht so daß Beflissenheit oder Widerwille die Ausführung oder Nicht-Ausführung zum Verständnis des Befehls ergänzen müssen? |
Eine
geometrische Figur zusammen mit ihrer
Projektionsmethode auf eine
bestimmte Ebene bestimmt nicht etwa erst
eine Figur in dieser Ebene sondern enthält
bereits diese Figur. |
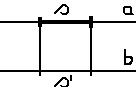 Die
orthogonale Projektion von s auf b
grenzt auf b schon das Stück s' ab.
Damit ist freilich nicht gesagt daß dieses Stück
nun auf b eine besondere Farbe hat also auch durch die Farbe
begrenzt ist. Besser mit
Kreisen auf Die
orthogonale Projektion von s auf b
grenzt auf b schon das Stück s' ab.
Damit ist freilich nicht gesagt daß dieses Stück
nun auf b eine besondere Farbe hat also auch durch die Farbe
begrenzt ist. Besser mit
Kreisen auf
 zwei parallelen
Ebenen vorzustellen. Die
Projektion des schwarzen Kreises auf die untere
Ebene begrenzt auf dieser schon einen Kreis, dadurch ist er aber noch
kein Farbenkreis || Farbkreis. (In diesem Satz liegt Richtiges
& Falsches.) zwei parallelen
Ebenen vorzustellen. Die
Projektion des schwarzen Kreises auf die untere
Ebene begrenzt auf dieser schon einen Kreis, dadurch ist er aber noch
kein Farbenkreis || Farbkreis. (In diesem Satz liegt Richtiges
& Falsches.) |
Wenn ich nun erwarte
daß auf der unteren Ebene ein Kreis erscheinen wird von dem gesagt
wird daß er die orthogonale Projektion des
oberen & von gleicher Farbe ist
–. |
(Die Philosophie wird am Schluß
aus äußerst trivialen Sätzen,
Bemerkungen, bestehen; es ist nur ungeheuer
schwer dazu zu gelangen sie zu verstehen.
D.h. sie als die Philosophie zu
verstehen.) |
(Die ganzen Anstrengungen die ich
jetzt mache, dienen nur dazu um gewisse triviale Sätze zu
verstehen d.h. sie in allen ihren
Konsequenzen zu verstehen.) |
[Zu dem oberen Satz] ‒ ‒ ‒ so gebe ich
weiter nichts als eine
Projektionsmethode. (Eine
Projektionsmethode ist eine allgemeine
Regel-Allgemeinheit.)
Die Projektionsmethode kann ich von anderen
Figurenpaaren || Gebilden kennen.
Ich kenne sie aber doch nur so daß eine Figur die
orthogonale
Projektion einer anderen ist aber doch nicht so
daß keine Figur die Projektion einer Figur
ist. – Ich nehme mir vor die
Erscheinungen auf der unteren Ebene in bestimmter Weise zu
beurteilen. Dann muß in diesem
Vorsatz schon die
Projektion stecken. |
Heißt das nicht: Die Erwartung muß die weiße
Ebene zu einem schwarzen Kreis ergänzen. |
Was heißt es, eine Strecke darauf hin untersuchen ob
sie die orthogonale
Projektion einer anderen sei? |
Es
kann nur heißen eben die Striche zu ziehen die man in
einem solchen Fall zieht. – Wie ist es aber mit der
Untersuchung ﹖ ob die untere Farbe die
gleiche ist wie die obere. Oder kann man sagen: auch
da stelle ich mich in bestimmter Weise ein so wie ich etwa
Das ist alles ein Einstellen, aber mehr kann ich nun nicht tun. Und dieses Einstellen ist nicht das Einstellen auf etwas anderes d.h. nicht mit Beziehung auf etwas was noch nicht da ist sondern es ist autonom, sozusagen das Aufrichten eines Maßstabes, was immer geschehen mag || geschieht. |
Des Rätsels
Lösung muß in der festgesetzten
Art & Weise || Festsetzung
über die Art & Weise liegen wie die Erscheinung dann
beschrieben wird wenn sie kommt.
|
25. Es ist ungemein schwer den eigentlichen
Punkt || Ort der Schwierigkeit mit Worten zu
erreichen. |
Denken wir uns die Einstellung durch
einen Zeiger wie den gelben Zeiger beim
Anäroidbarometer
und etwa ein solches Barometer & eine Uhr.
Auf beiden 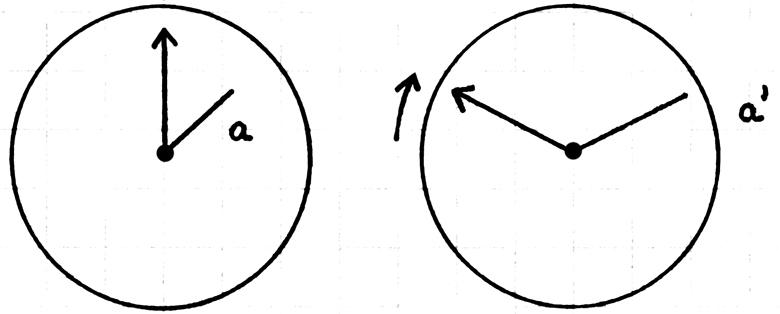 Zifferblättern stelle ich den freien Zeiger a
& a' ein & drücke dadurch
die Erwartung aus daß, wenn die Uhr || der Uhrzeiger bei
a' anlangt der andere auf a stehen wird.
(Es ist kein Zweifel daß das ein vollkommener
Ausdruck der Erwartung des Gedankens ist.)
Zifferblättern stelle ich den freien Zeiger a
& a' ein & drücke dadurch
die Erwartung aus daß, wenn die Uhr || der Uhrzeiger bei
a' anlangt der andere auf a stehen wird.
(Es ist kein Zweifel daß das ein vollkommener
Ausdruck der Erwartung des Gedankens ist.)
Bleibt nun die Uhr etwa stehen so |
Wo haben
wir aber in diesem Zeichen || Satzzeichen Worte oder etwas was den Worten entspricht?
Es „bedeutet” offenbar a' den Uhrzeiger & a den
Barometerzeiger. |
Ich bleibe in den Zeichen, bis ich
in ihrer Anwendung || Verwendung aus ihnen
heraus trete. Dann weist mein Benehmen meine Handlung die logische Verwandtschaft mit den Zeichen auf die ein solches Zeichen mit seiner Übersetzung aufweist. |
Was ich
immer sagen will ist daß der Gedanke nichts
Menschliches ist. Daß er auch nicht ein bestimmtes
Gefühl ist das man eben nur fühlen aber
nicht etwa auch sehen || ansehen
kann. Man kann z.B.
Zahnschmerzen nicht gleichsam herausstellen &
ansehen. |
Natürlich kann man nicht
sagen die Zahnschmerzen kenne man von innen indem man sie
fühlt & könne sie nicht von außen
betrachten. Denn die Zahnschmerzen |
Die heute
gewöhnliche Auffassung ist die, daß das Denken
– durch den Kopf oder die Seele besorgt –
ein
Privilegium eben des Kopfes oder der Seele ist (wie etwa die
natürliche Verdauung des Magens). Und das
ist sie auch als naturgeschichtlicher Akt betrachtet wie auch die
Verdauung in diesem Sinn dem Magen eigentümlich
ist, || – aber vom Standpunkt des
Chemikers betrachtet ist die Verdauung ein
Prozeß der dem Tierischen Magen nicht eignet
sondern || &ganz
unabhängig davon ist wo er tatsächlich
stattfindet. – So hat es der Logiker nicht mit einem
spezifisch menschlichen
Prozeß zu tun. |
Die Logik ist eine
Geometrie des Denkens. |
Was am
Denken menschlich ist, mit dem hat die Logik nichts zu
tun. |
Man könnte freilich sagen
daß die Uhr & das Barometer mit den verstellbaren Zeigern
nur der Ausdruck eines Gedankens aber nicht der Gedanke selbst sind,
aber dann sind sie doch Teile, Werkzeuge, eines
Gedankens & was immer der Gedanke selbst ist, so ist er
ein anderer Vorgang als der, welcher ihn
verifiziert & er hat mit diesem
Vorgang nur soviel gemein || kann mit diesem Vorgang nur soviel gemein
haben als jene Vorrichtungen der Uhr & des Barometers |
Man könnte nun (und
zwar in gewissem Sinne mit Recht) sagen, daß
jene Uhr & das Barometer noch gar nichts von der
genannten Erwartung enthalten,
daß man dazu ein weiteres Bild brauchte & zwar eine andere
Uhr & ein Barometer die den Vorgang den man von den
ersten erwartet sozusagen vormachten || vormachen. Aber nun brauchte man ⋎ ein weiteres
Paar Uhren etc. um nun die
Verbindung jener Uhren & Barometer vorzumachen
etc. |
Das Gleiche geschieht im Fall der
beiden Ebenen, wenn ich hier erwarte auf der unteren
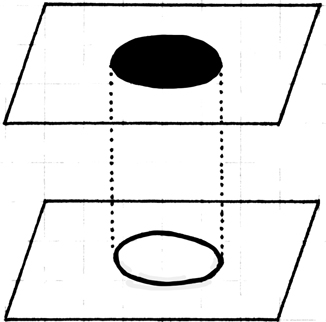 einen Fleck zu
sehen der die senkrechte
Projektion des Oberen ist.
Hier kann ich auch die
Projektionsmethode noch darstellen indem
ich etwa einen Glaszylinder zwischen die Ebenen
stelle. Dadurch bin ich aber der Erwartung oder dem
Gedanken nicht näher gekommen. einen Fleck zu
sehen der die senkrechte
Projektion des Oberen ist.
Hier kann ich auch die
Projektionsmethode noch darstellen indem
ich etwa einen Glaszylinder zwischen die Ebenen
stelle. Dadurch bin ich aber der Erwartung oder dem
Gedanken nicht näher gekommen. |
Der Gedanke ist das
wonach man die Tatsache müßte herstellen können, wie der
Befehl das ist, wonach man die Handlung tun || ausführen kann. Nehmen wir an der Befehl
wäre auf der unteren Ebene einen Kreis wie den oberen
hervorzubringen. Inwiefern Und soweit man es kann vergleicht man eben zwei verschiedene Vorgänge & kann höchstens aus der verschiedenen Mannigfaltigkeit einen Schluß auf einen begangenen Fehler ziehen; aber in keiner anderen Weise. |
Noch einmal:
was ist das Kriterium dafür daß der
Befehl richtig ausgeführt wurde? Was ist das
Kriterium, nämlich auch
für den Befehlenden? Wie kann er wissen daß der
Befehl nicht richtig ausgeführt wurde. Angenommen er
ist mit || von der Ausführung befriedigt
& sagt nun: „von dieser
Befriedigung lasse ich mich aber nicht täuschen denn ich
weiß daß doch nicht das geschehen ist was ich
wollte”. Er muß sich dann
in irgend einem Sinne daran erinnern wie er den Befehl gemeint hatte
‒ ‒ ‒ |
Angenommen die Erwartung
bestünde darin daß man den Fleck den man erwartet
halluziniert; man braucht
aber dazu in irgend einer Weise eine gewisse Kraft & an dem
Kraftaufwand merkt man – er ist sozusagen ein Maß dafür
– wie weit der wirkliche Zustand nach von dem erwarteten entfernt
ist; bis dann |
Wenn er
sagt daß er den Befehl nicht so gemeint
hatte so muß es in seiner Sprache eine Möglichkeit geben den
Vorgang zu beschreiben der tatsächlich
stattgefunden hatte & im Gegensatz dazu den Vorgang den
er gewünscht hatte. ‒ ‒ ‒
|
Ich
meine: Wenn er mit der Ausführung des Befehls nicht
einverstanden ist dann muß er sagen können
woran || worin der
Fehler liegt. Kann er das aber überhaupt sagen
d.h. mir verständlich
machen, so muß er sich in seiner Beschreibung auf
die Weise beziehen wie ich ihn
verstehe. ‒ ‒ ‒ Er muß mir eben wieder
Zeichen geben. ‒ ‒ ‒ |
Er
sagt || befiehlt mir „setze hier die gleiche Farbe hin wie
dort”, ich setze eine Farbe hin &
er sagt „ja das ist
gut” & ich |
Auf
„so hab ich's nicht
gemeint” folgt immer die Frage „wie denn?”
& darauf besteht die Antwort in weiteren || ist die Antwort
weitere Zeichen des alten Zeichensystems. |
Will ich
damit nicht sagen: || ? Man kann die
Auffassung der Sprache durch Zeichen nicht ändern
sondern nur wieder in der Sprache weiterreden. |
Darum darf man aber
von der Auffassung der Sprache
überhaupt nicht reden. ‒ ‒ ‒ Denn man kann
nicht von verschiedenen Auffassungen der Sprache reden. |
Das
führt zu der Frage: Was geschieht wenn ich
etwa eine Farbe die ich vor mir habe benenne, etwa sage
„das ist rot” oder „diese Farbe ist
rot”? |
Das
was ich meine muß das sein, was ich sagen
kann. |
Auf die
Frage „was meinst Du” muß zur Antwort kommen:
p; und nicht „ich meine das, was ich mit „p”
meine”. |
D.h. die Meinung, soweit sie nicht
erklärt werden kann ist ein Nichts. (Und die
Meinung ist der Sinn des Satzes.) |
Die
Vorstellung von dem erwarteten schwarzen Fleck ist
auch nur ein Zeichen, denn der erwartete schwarze Fleck ist sie
nicht. |
Und man kann nicht in
der Vorstellung die Vorstellung des schwarzen Flecks mit dem schwarzen
Fleck der nicht da ist vergleichen. |
Die
Ergebnisse der Philosophie sind die Entdeckung irgend eines schlichten
Unsinns und Beulen die sich der Verstand beim Anrennen an
die Grenze || das Ende der Sprache
geholt hat. Sie, die Beulen, lassen uns den Wert
jener Entdeckung verstehen || erkennen. |
26.
Man kann nicht
sagen die Bedeutung des Wortes „rot” hänge
davon ab daß es irgendwo etwas rotes
gebe || gäbe wenn ich es
auch jetzt nicht vor mir habe. Denn wenn ich also keine
Evidenz für das Existieren eines solchen roten Gegenstands habe
dann existiert er eben vielleicht nicht & in
diesem Falle hat das Wort auch keine Bedeutung || ist das Wort
auch bedeutungslos. |
Was sich nicht ausdrücken
läßt, darüber läßt sich auch nicht reden.
|
(Was ich mache ist nicht so sehr das Forschen
nach einer Entdeckung || der Entdeckung einer neuen
Wahrheit als vielmehr Denkübungen,
d.h. Übungen eine bestimmte Denkbewegung zu
machen, so wie man etwa Rumpfübungen macht um endlich eine
gewisse schwierige Bewegung ausführen zu
können.) |
Soweit sich nicht erklären läßt in wiefern ein
Befehl nicht richtig ausgeführt ist || wurde,
ist auch nichts zu erklären da. |
Ich habe gesagt, daß
in der Erwartung bereits die Tatsache irgendwie vorgebildet
sei, aber so schiene es als könnte man sagen
„siehst Du, nur diese Tatsache paßt
auf diese Erwartung”. „Ich weiß was der Fall ist, wenn die Erwartung
in Erfüllung geht”. Nun
– wenn Du es weißt – was ist denn der Fall?
Und die Antwort darauf ist ein neuerlicher Ausdruck der
Erwartung. |
Das heißt: Wissen
was der Fall ist wenn der Satz wahr ist heißt einen
anderen Ausdruck besitzen den man dem ersten
Satz gleichsetzt. |
Man sagt mir: „Du wirst hier einen hellen Kreis
sehen” & ich sage „oh, ich weiß Und kommt nun die Erfüllung endlich oder die Nichterfüllung so läßt sie sich sowenig vorausnehmen als die Zeit in der sie eintritt. |
Kann man aber nicht doch
sagen daß ein erwarteter Vorgang deren
Erwartung || den ich durch eine Zeichnung oder ein
farbiges Bild darstelle durch dieses Bild mehr
vorausgenommen wurde als durch den bloßen Satz durch den ich ihn
beschreibe? Wie aber wenn der Vorgang nicht
eintritt? ‒ ‒ ‒ |
Die Erwartung ist freilich nicht das
Bild, sondern die Attitude die ich zu dem Bild einnehme, &
diese macht den Unterschied zwischen Erwartung, Furcht,
Hoffnung, Glauben, Unglauben.
|
Wenn
ich dem Satz, dem Ausdruck der Erwartung, ein anderes Bild
zuordne als Erklärung seines Sinnes so kann ich es ihm
immer erst zuordnen bis es da ist. Wenn ich nun sage
„ ich weiß was das
heißt, ich kann es Dir aufzeichnen” so bedeutet dieses Vermögen etwas
aufzuzeichnen || darzustellen nichts anderes als
daß schon eine Darstellung „im Kopf” vorhanden
ist. Denn es würde sich fragen: Ist dieses
Können so aufzufassen daß es erst durch die
Ausführung |
Denn der Wunsch oder Wille etwas zu
tun ist ja von derselben Art wie Erwartung, Glaube,
etc. |
Im Fall des Wunsches ist es
besonders deutlich; denn daß,
wenn ich den Arm zu heben wünsche ich ihn dadurch in
keiner Weise gehoben habe, ist klar. Anderseits
müssen die Elemente des Gewünschten
im Wunsch vorhanden sein, wenn es dieser Wunsch sein soll.
Denn wenn es zweifelhaft ist ob ein Wunsch in
Erfüllung geht, so kann es nicht zweifelhaft sein
welcher Wunsch es ist d.h. was gewünscht
wird. |
Man könnte sagen der Satz liegt
auf der Lauer, & nun kann das
factum || Ereignis nur
entweder geschehen oder nicht geschehen. Wie4 ist es aber mit dem Nichtgeschehen, setzt das nicht doch in irgend einem Sinn das Geschehen voraus? |
Das ja
oder || und nein muß eine
Eigentümlichkeit unserer Welt sein die ich
daher nicht als Eigentümlichkeit darstellen
kann. Wenn ich nämlich sage „das Ereignis könne nun nur geschehen oder nicht geschehen” so sage ich ja gar nichts. |
„Ich
weiß wie das ist, wenn es geschieht & das soll nun
nicht der Fall sein, es soll gleichsam
ausgeschaltet || ausgeschlossen
sein.”
Aber wer den Satz versteht muß ja schon ja & nein verstehen denn er kann ja nicht wissen ob der Satz wahr ist oder nicht. Worin besteht denn die Möglichkeit daß der Zeiger sich in die Stellung || Lage || Stellung des Stabes a stellt? Darin daß a ja selbst diese Stellung hat daß a im gleichen Raum mit dem Zeiger ist. Ist aber dieser gleiche Raum unabhängig von einer Darstellung? || , von einem Bild? |
27. Überraschung,
Enttäuschung. ¤Man sagt „ich dachte mir der Zeiger würde schon da
sein, & nun ist er noch nicht da”. Man hatte sich ein Bild gemacht, das ist klar. ‒ ‒ ‒ Aber in wiefern ist dieses Bild ein Bild eben dieses Zeigers? Ein Porträt. Ein Porträt eines Menschen den es nicht gibt ist ein Unding. Zum Porträt gehört also der Mensch den es darstellt. „Das soll er sein” darin liegt das ganze Problem der Darstellung. |
Es ist
aber doch möglich eine allgemeine Regel der
Übersetzung zu geben ehe die
Übersetzung ausgeführt ist.
Und diese Regel scheint eine
Projektionsmethode darzustellen
d.h. die projizierende Relation zu geben
ehe noch beide Glieder
dieser Relation vorhanden sind. Wie ist das
möglich?! In der Kenntnis dieser Projektionsmethode besteht auch das Projizieren-Können das Aufzeichnen-Können etc. Wie kann man aber Jemanden eine Projektionsmethode lehren? doch nur indem man ihm Projektionen zeigt. Und wie ist denn die Anweisung eine Projektion zu machen, wenn man sagt „zieh die & die Striche etc.”? hier wird in der Sprache ein Bild gemacht von den Strichen daher aber auch von dem Projizierten. Wenn man z.B. jemandem durch ein Bild zeigen will wie er die Strecke a auf b senkrecht projizieren soll & man 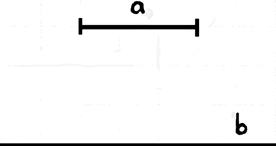 zeichnet nun
a' zeichnet nun
a' 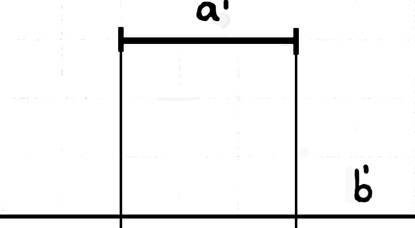 als Vertreter
von a & zieht die entsprechenden Striche so
zeichnet man damit auch die Projektion von
a' auf b'. als Vertreter
von a & zieht die entsprechenden Striche so
zeichnet man damit auch die Projektion von
a' auf b'. |
Ich rede aber doch von der Anwendung
dieser Projektionsmethode auf
a. Ist auch sie wieder nur ein Bild das
erst angewendet werden muß? – Gewiß, wenn
|
Aber wenn ich sie anwenden will, so weiß ich doch
schon was ich will! (Es ist da || hier immer so als ob etwas schon gemacht wäre, noch ehe es gemacht ist.) |
Man könnte ohne die Sache im
mindesten zu verändern sich alles sehr vereinfacht
denken. Der Befehl, die Erwartung
etc. wäre immer einen dünnen
Strich den der Befehl, die Erwartung, etc.,
zieht dicker nachzuziehen. Die Wirklichkeit des dünnen
Bildes ist (dann) die Möglichkeit des dicken Striches.
|
Wenn
ich aber so die Vorstellung die bei der Erwartung
etc. im Spiel ist durch ein wirklich
gesehenes Bild ersetzen will so geschieht etwa
folgendes: Ich sollte einen dicken schwarzen Strich ziehen
& habe als Bild einen dünnen gezogen. Aber die
Vorstellung geht noch weiter & sagt sie weiß auch schon
daß der Strich dick sein soll. So ziehe
ich einen dicken aber etwas blasseren Strich, aber
die Vorstellung sagt sie weiß auch schon daß er nicht grau
sondern schwarz gehört. (Ziehe ich
aber den dicken schwarzen Strich so ist das kein Bild mehr.)
|
Die
Vorstellung ist also nicht durch ein
wirkliches || gesehenes Bild
ersetzbar. – Oder soll ich sagen sie ist es nur dort
nicht wo man eben mit der Vorstellung denkt! – Ist
es so? das Bild ist das
Bild des Gedankens das auf eine bestimmte Art gebraucht
wird. – Von dem Bild kann man dann nicht sagen daß
ein andres Bild dem Gedanken („dem || oder was gemeint
ist”) näher kommt.
Das heißt: das auf bestimmte Weise verwendete Bild ist der Gedanke, die Erwartung ist das was gemeint ist. Durch ein anderes Bild ersetzen kann man dieses nicht & das andere wird uns quasi als fremd, außenstehend, erscheinen. – Dieses Bild das „Gedachte” kann ein „Vorstellungsbild” aber auch ein Schriftbild oder Lautbild sein. Das ist was geschieht wenn man jemand fragt „wie meinst Du diese Zeichnung” & er sagt „ich meine daß …” & nun sagt er es mit Worten & drückt damit was er meint für sich || ihn selbst besser aus als etwa durch die Zeichnung || das andere Bild. |
Ich glaube, auf die
Kausalitätstheorie der Bedeutung kann man einfach
antworten, daß wir wenn einer einen Stoß erhält &
umfliegtes nicht || , das Umfallen nicht die
Bedeutung des Stoßes nennen. |
Die
Beschäftigung mit dem Bild |
Könnte man nicht
so sagen: || ? die Vorbereitungen
können verschiedener Art sein: wenn
mir jemand etwa etwas in den Mund stecken möchte
so öffne ich den Mund entsprechend der Größe des
Stückes (das ist eine
Art) & außerdem sondert etwa mein
Mund Speichel ab (das ist die
andere Art). Die erste ist ein Bild
des Bissens den ich schlucken will, die andere keines. |
Das Denken
macht Pläne. Es zeichnet Pläne einfacher oder
auch sehr komplizierter Art.
Nun sagt man aber: das ist doch nicht alles, man will doch etwas mit diesen Plänen, sie bedeuten doch etwas d.h. sie sind doch mit einer Absicht gezeichnet. Wohl || Ja, aber hier gibt es zwei Möglichkeiten: entweder diese Absicht ist ein Gefühl oder dergleichen Die Logik ist immer sachlich. |
Wenn man bedenkt daß
jeder Gedanke – jeder Satz – einen
Plan entwirft dann sieht man klar wo die
Kausalitätstheorie das Wesentliche
übersieht. |
Wissen was das Zeichen
heißt, heißt es interpretieren. Es
auslegen. Das Auslegen heißt nach dem Zeichen handeln. Ehe die Handlung getan war konnte man nur ein Bild haben das ihr Bild wird || ist wenn sie getan ist. |
Ist es denn nicht so, daß, ehe die
Handlung getan ist, ehe das Bild interpretiert ist, nichts eine
andere Interpretation verhindert.
Ein Bild ist es erst wenn ich es interpretiere – oder interpretiert habe. (Das Typische am Gedanken ist nur daß ich ihn interpretiere so unterscheidet er sich von anderen Ursachen meiner Handlungen.) |
Wenn der Befehl z.B. darin besteht einen
gewissen Weg zu machen so kann ich ihn mit
Hilfe einer Karte (eines Plans)
ausdrücken. Daher kann der Befehl auch lauten einen
oder den anderen Weg zu gehen & etwa gewisse
Wege nicht zu gehen.  indem etwa
die ausgeschlossenen Wege durchstrichen
werden. Der Befehl könnte aber auch so aussehen indem etwa
die ausgeschlossenen Wege durchstrichen
werden. Der Befehl könnte aber auch so aussehen
 & das
würde etwa bedeuten man dürfe
überall zwischen den beiden Linien gehen außer
über das schraffierte Feld. & das
würde etwa bedeuten man dürfe
überall zwischen den beiden Linien gehen außer
über das schraffierte Feld. |
Wenn nun
tatsächlich ein Weg zwischen zwei Orten abgesperrt wird
& etliche andere offen gelassen werden ist in diesen Tatsachen
schon eine Verneinung & eine
Disjunktion enthalten? |
Wie ist es aber wenn ich einen
Befehl auf eine bestimmte Weise interpretiere & ihm
zuwiderhandle. Worin liegt es daß meine Handlung nicht
meine Interpretation des Befehls ist sondern ein
Entgegenhandeln? Wird dadurch nicht meine
frühere Auffassung über den Haufen
geworfen? Ich kann sagen wenn der Handelnde es nicht sagte so könnte man nie wissen daß es ein Entgegenhandeln ist. Und wenn er es nun sagt so verstehen wir es nur durch unsere Interpretation der Verneinung. |
Man würde glauben,
wenn ich dem Befehl so wie ich ihn
verstehe || auffasse zuwiderhandeln
kann, dann muß eben meine Handlung dem Ausdruck meiner
Auffassung (des
Befehls) unmittelbar
widerstreiten. – Oder |
Überhaupt, ich habe immer vom Bild oder sogar von der
Halluzination gesprochen, aber wie
kann man denn halluzinieren daß
einer entweder auf einem Weg oder auf den anderen geht oder daß er
auf irgend einem Weg innerhalb gewisser Grenzen
geht?? |
Disjunktion,
Negation etc. scheinen in der
Einstellung zu einem Bild zu liegen. Sie entspricht der
elektrischen Schaltung mit der || durch
die etwa eine Klingel mit Schaltern
verbunden sein kann. |
Denken wir uns folgende
Einstellungen:  1.) die Glocke läutet nur
dann wenn ich den Zeiger a dem Zeiger b gleichrichte
2.) die Glocke läutet nur dann
nicht wenn ich a dem b gleichrichte 3)
die Glocke läutet nur wenn a
entweder dem b oder auch dem c gleichgerichtet
ist. 4) die Glocke läutet in allen anderen
Zeigerstellungen von a außer wenn er mit b
oder c gleichgerichtet ist 5) die Glocke
läutet nur dann wenn sowohl b als c mit
a gleichlaufen || gleichgerichtet sind
6) die Glocke läutet nur wenn b mit a
gleichgerichtet, c mit a aber nicht gleichgerichtet
ist. etc. Das Glockenzeichen bedeutet
Annahme || Zustimmung
1.) die Glocke läutet nur
dann wenn ich den Zeiger a dem Zeiger b gleichrichte
2.) die Glocke läutet nur dann
nicht wenn ich a dem b gleichrichte 3)
die Glocke läutet nur wenn a
entweder dem b oder auch dem c gleichgerichtet
ist. 4) die Glocke läutet in allen anderen
Zeigerstellungen von a außer wenn er mit b
oder c gleichgerichtet ist 5) die Glocke
läutet nur dann wenn sowohl b als c mit
a gleichlaufen || gleichgerichtet sind
6) die Glocke läutet nur wenn b mit a
gleichgerichtet, c mit a aber nicht gleichgerichtet
ist. etc. Das Glockenzeichen bedeutet
Annahme || Zustimmung |
Eine
Meinung (d.h. ein Sinn) die man nicht
erklären kann geht uns nichts
an || interessiert uns nicht denn ihr kann man
auch nicht zuwiderhandeln. |
28.
Dem Kind lernt man
das „nicht”
durch Absperren, dadurch daß man es verhindert
etwas zu tun. |
Wie kann man denn gegen ein
Bild handeln? |
„In
dieses Gebiet gehe ich nicht” beschreibt eine bestimmte Tatsache.
Wenn die Aufschrift „Verbotener Weg” eine negative Aufschrift ist, läßt sie sich durch eine positive ersetzen? |
Wenn
eine || die Interpretation ein Bild ist so sind
zwei entgegengesetzte Interpretationen zwei
entgegengesetzte Bilder. |
In Wahrheit muß aber im
Verbot immer das beschrieben werden was verboten ist. Ist
eine Bewegung verboten so muß eben diese Bewegung
beschrieben werden, also eben das was ausgeschlossen werden
soll, & das || die Beschreibung
dessen was zugelassen ist wird nur dann das
Verbot ersetzen (können) wenn |
(Immer suche ich nach dem Punkt an dem
man sagen kann „ja, so ist einmal unsere
Welt”. – Die Philosophie
will das Wesen || Wesentliche der
Welt beschreiben, wenn sie aber danach sucht, nach Sätzen sucht die es beschreiben, so kommt
sie im entscheidenden Augenblick nicht zu
philosophischen Sätzen sondern an die Grenze der
Sprache.) |
(Man muß
sich in der Philosophie immer gleichsam dümmer stellen
als man ist, um an keiner Schwierigkeit
vorbeizugehen.) |
Gibt es einen
Beweis dafür daß einer einen Befehl verstanden hat &
ihm bewußt entgegenhandelt? – Ich
frage jemand „hast Du den Befehl
verstanden” er sagt ja & gibt mir
„Proben”
seines Verständnisses & handelt
nun dem Befehl entgegen. Können nun
die Proben (auch) || nicht so gedeutet werden daß der Befehl wie
er verstanden auch befolgt wurde? Schließt man hier
nicht nach Amorphem
z.B. dem Gesichtsausdruck
welche Deutung zu machen ist?
(In diesen Fragen ist irgendwo ein Behaviourism am Platz. Vielleicht || Wohl nur in sofern als man alles von außen betrachtet). |
In dem „Verstehen was jemand meint” muß man das spezifisch menschliche |
D.h. das Verstehen ist
für uns nicht wesentlich ein innerer
Prozeß, denn soweit er es wäre ginge er
uns nichts an. |
Fürchten daß etwas geschieht
heißt, wünschen daß es nicht
geschieht. Wenn also einer fürchtet daß
etwas geschieht, der andere wünscht daß es geschieht so
wünschen sie beide das Entgegengesetzte || liegt die Verneinung also nicht in der
Attitude. |
Was ist der Unterschied zwischen:
Wünschen, daß etwas geschieht & Wünschen daß
dasselbe nicht geschieht. Wollte man es bildlich darstellen man würde mit dem Bild der Handlung etwas vornehmen, es durchstreichen, in bestimmter Weise einrahmen & dergleichen. Aber das erscheint uns als eine rohe Methode des Ausdrucks, aber, || – ich glaube – daß jede wesentlich ebenso sein muß. In || ; in der Wortsprache setze ich das Zeichen „nicht” vor den Satz. Wie gesagt das scheint ein ungeschickter Behelf & man meint vielleicht im Denken geschieht es schon anders. Ich glaube aber, im Denken Erwarten, Wünschen, |
Nocheinmal:
der Ausdruck der Verneinung den wir gebrauchen wenn wir uns
irgendeiner Sprache || Schrift bedienen
erscheint uns primitiv; als gäbe es einen richtigeren
der mir nur in den rohen Verhältnissen dieser Sprache nicht zur
Verfügung steht. |
Man könnte sagen der verneinte Satz
stellt ein Hindernis dar das verhindert
daß das geschieht was er verneint. Ich meine
ein Hindernis welches ein Bild dessen ist was es
verhindert. Wenn ich jemanden
etwa || z.B. daran
verhindern will einen || seinen Arm in
eine bestimmte Lage zu bringen & tue das indem ich dort wo der
Arm nicht liegen darf einen Körper || ein
Stück Holz befestige so ist das
Stück Holz ein Bild der verbotenen Lage. Bewirke ich
aber dasselbe indem ich ihm einen lähmenden Trank eingebe so ist
der Trank kein Bild seiner Wirkung.
(Kausalitätstheorie) |
Ist nicht alles damit gesagt daß die
Erwartung, der Gedanke, daß hier ein roter Kreis erscheinen wird
anders ist als die, daß hier ein
grüner Kreis erscheinen wird &
anders als die, daß dort eine Ellipse erscheinen wird
& anders als die daß dort keine
Ellipse erscheinen wird? Wenn ich aber sage daß der Gedanke daß hier ein grüner Fleck erscheinen wird anders ist als der daß hier ein roter Fleck erscheinen wird so beschreibe ich damit nicht am Ende eine Erfahrungstatsache etwa wie daß der Magen eines Rehs anders ist als der eines Hirschen. – Denn die Erwartung ist gänzlich damit || damit intern beschrieben daß sie die Erwartung des Erscheinens ist || ist daß hier ein grüner Fleck erscheinen wird. „Intern beschrieben” ist aber hier gewiß irreführend. ‒ ‒ |
Jenes Primitive der
Ausdrucksform das uns bei der Verneinung aufgefallen ist haben wir
schon früher begegnet; wenn man nämlich etwa einem Menschen
begreiflich machen will daß er einen gewissen Weg
gehn soll so kann man ihm den Weg aufzeichnen & hierin
sehr genau || mit immer || beliebig weiter gehender Genauigkeit
verfahren. Die Andeutung jedoch
die ihm verständlich machen soll daß
Er || er den Weg gehen
soll ist wieder von der primitiven Art die man gerne verbessern
möchte. |
(Es ist die Art der Philosophie daß
sie das als merkwürdig hervorhebt was sonst als trivial
unbeachtet bleibt.) |
Was ist der Unterschied zwischen einem
unwillkürlichen Kopieren einer Zeichnung
– bei der ich etwa den kopierenden Bleistift
anschaue & immer wieder draufkomme daß er sich so bewegt
wie Wie ist es nun mit dem der sich von einem Befehl leiten läßt. Ist nicht das einem Befehl Nachhandeln oder auch ihm nachgehn indem man ihn interpretiert – ganz verschieden von dem Vergleichen eines Befehls mit einer fertigen Handlung oder einer fertigen Interpretation? |
29.
Ich verleibe beim
Denken sozusagen ein Bild meinem Leben ein. |
Das Bild was ich
meinem Leben einverleibe ist das Gedachte, jedes andere
erscheint uns als außenstehend. |
Ich möchte immer etwas
sagen wie: Es besteht von vornherein die Abmachung
daß die Sprache das was die Erwartung befriedigt mit
der Bejahung des Satzes der die Erwartung
ausdrückt beschreiben Ich möchte sagen: die Sprache drückt nur so || so, wie so das aus, was der Erwartung mit der Welt gemeinsam ist. – Oder vielmehr: ‒ ‒ |
Es ist meine
Stellungnahme zu dem Bild, die es zum
Repräsentanten macht. |
Ich erwarte mir
daß, wenn ich jetzt die Uhr aus der Tasche ziehen werde es 3 Uhr
sein wird. Diese Erwartung schließt
ein unbestimmtes Bild des Zifferblattes & der
Zeigerstellung ein; sie enthält eine Einstellung
zu meiner wirklichen || auf meine
wirkliche Uhr ‒ ‒
Und wenn ich nun die Uhr wirklich ansehe, – und die Zeiger stehen auf 3 Uhr so werde ich sagen die Zeiger stehen (wirklich) auf 3 – aber das heißt doch gar nichts, und diese Unmöglichkeit, die Bedingung der Übereinstimmung von sinnvollem Satz – Gedanken – & Wirklichkeit durch die Sprache auszudrücken ist des Rätsels Lösung. (obschon ich sie noch nicht durchschauen kann.) |
Bedenke, daß zwischen dem
Satz der die Erwartung ausdrückt & dem der sie
– etwa als einmal gewesen – beschreibt ein
Unterschied ist. |
Es könnte gesagt
werden: Wie kann man || ich denn das || ein Ereignis erwarten, es ist ja noch gar nicht da?
|
„Ja das habe ich mir
erwartet”. Wie konntest Du
Dir's denn erwarten, es war ja noch gar |
Und „das habe ich mir erwartet”, heißt wirklich, das habe ich mir erwartet
& nicht, etwas ganz gleiches (oder
ähnliches) habe ich mir erwartet. |
„Das habe ich mir erwartet” könnte man auch übersetzen durch:
darauf war ich eingestellt. |
Das Gefühl, das sich in
den oberen Sätzen ausspricht ist: ich kann doch keinen Dieb
ergreifen, wenn es ihn noch gar nicht gibt; wie kann
ich mich auf einen Sessel setzen der nicht vorhanden
ist. Und das zeigt, natürlich, nur daß wir hier
eine falsche Analogie sehen. d.h.
glauben eine Analogie zu sehen, wo keine da ist. |
Wie kann
man darauf vorbereitet sein daß Etwas geschehen wird?
Ich möchte sagen nur dadurch daß die Sprache auf jeden Fall
vorbereitet ist da entweder p geschehen wird oder nicht
geschehen wird. Das ist eine sachliche, logische,
Eigenschaft der Sprache. |
Man kann eine
Lehre auf das Maß eines Körpers einstellen,
vorbereiten. Dann liegt in dieser Einstellung zwar das
eingestellte Maß aber in keiner Weise, daß ein bestimmter
Körper es hat. Ja vor allem liegt darin keine Annahme
darüber ob der Körper dieses Maß hat, oder nicht
hat. |
Ich will sagen: Auch wenn die Erwartung
mit einem || dem Sehen eines
genauen optischen Bildes des Erwarteten verbunden ist,
wenn ich also bei der Erwartung, daß die Uhr auf
|
Wenn ich erwarte daß jemand zu mir
in's Zimmer kommen wird & ich richte einen Sessel zurecht
& zwei Teeschalen, ist dann ein Zweifel ob ich erwarte daß
er kommen oder daß er nicht kommen werde? |
30. (Es schadet gar nichts in der
Philosophie Unsinn zu reden, wenn man sich nur tief genug mit
dem Unsinn einläßt.) |
(Wenn ich vernagelt bin so bin ich
für viele vernagelt & wenn ich das Tor |
Wenn ich erwarte daß es
Nun schaue ich aber auf die Uhr & sehe es ist nicht
|
Meine ganzen
Überlegungen gehen immer dahin, zu zeigen, daß es
nichts nützt sich das Denken als ein
Halluzinieren vorzustellen.
D.h. daß es
überflüssig ist, die Schwierigkeit aber bestehen läßt || das
Problem aber bestehen bleibt. Denn auch die Halluzination, kein Bild, kann die Kluft zwischen dem Bild & der Wirklichkeit überbrücken, & das eine nicht eher als das andere. |
∣ In dem
normalen Gesichtsbild des Mondes sind die Krater
nicht zu klein als daß man sie sehen könnte, sondern nicht
vorhanden. ∣ |
Es
ist übrigens merkwürdig || zu beachten daß
wir uns bei dem Gedanken daß es jetzt
|
Ich möchte immer sagen:
Wenn ich glaube daß es
|
Kann man sagen: Das
Denken || Der Gedanke ist ein Instrument des
Handelns. |
Es ist so wie wenn ich mir im
Werkzeugkasten der Sprache Instrumente || Werkzeuge zum künftigen Gebrauch herrichtete.
Ein || Und ein Werkzeug ist ja auch
bis zu einem gewissen Grade das Abbild seines
Gebrauches || Zweckes. |
Ich suche immer
nach dieser || der Unmöglichkeit des
Ausdrückens die den eigentlichen Grund des Problems
macht. |
Wie kann ich
wissen daß ich mir das erwartet habe als
dadurch daß es meine Erwartung jetzt befriedigt,
meiner Erwartung jetzt entspricht. |
Es ist ein Schritt
nötig der dem der Relativitätstheorie ähnlich
ist. |
Kann man sagen die Erwartung ist eine vorbereitende,
erwartende, Handlung. – Es wirft mir jemand
einen Ball, ich strecke die Hände aus & richte sie zum
Erfassen des Balls. Aber sagen wir ich hätte mich
verstellt, ich hatte erwartet daß
er nicht werfen würde wollte aber so machen als würde ich es
erwarten. Worin besteht dann mein Erwarten daß
er nicht werfen wird, wenn meine Handlung die gegenteilige
Erwartung || das Gegenteilige ausdrückt?
Sie mußte doch auch in etwas
bestehen was ich tat. Ich war also doch
irgendwie nicht drauf vorbereitet daß der Ball
kam. |
Ich bin darauf vorbereitet einen roten Fleck zu sehen – diese
Vorbereitung ist sozusagen etwas Praktisches
ähnlich, wenn ich meine Muskeln zum
Heben || Halten eines Gewichts
vorbereite. (Und ich möchte sagen: ich kann
nicht mit || in der
Sprache die der Ausdruck jener Vorbereitung ist
über das hinaus || die
Möglichkeiten dieser Vorbereitung hinaus.)
|
Wenn
die Vorbereitung zum Essen eines |
Mein ganzer Gedanke ist immer daß
wenn einer die Erwartung sehen könnte er ersehen müßte
was erwartet wurde. |
[Meine
Gedanken schieben sich durcheinander, der eine verdrängt
den andern, schiebt sich vor etc. wie
viele Krebse in einer
Schüssel.] |
Die Vorbereitung ist quasi
selbst die Sprache & kann nicht über sich selbst
hinaus. (In dem nicht über sich selbst
Hinauskönnen liegt die
Ähnlichkeit meiner
Betrachtungen || Betrachtung & jener der
Relativitätstheorie.) |
Man könnte sagen, ob
eine Erwartung in Erfüllung gegangen ist
kontrolliere ich so: Wenn die
Erwartung || die Erwartung durch den Satz
ausgedrückt war daß
p der Fall sein werde &
der eingetretene Tatbestand wird durch den Satz „p” beschrieben dann ist die Erwartung in
Erfüllung gegangen. |
Wenn ich früher gesagt habe es kommt |
Die Sprache
als Ausdruck der Erwartung ist das
Vorbereitete. |
Die Sprache kann nur sagen:
Ich habe früher zur Vorbereitung den Satz
„p”
verwendet & verwende zur Beschreibung wieder den Satz
„p”. |
Das Merkwürdige
in || an diesem Fall ist ja, daß
in der Erwartung das Ereignis ganz vorgebildet ist so
daß, wenn es eintritt zu der Erwartung nur ja gesagt
werden braucht. Daß man sagen kann, das habe
ich mir erwartet, & am Wirklichen gar nichts
Überraschendes ist. –
Und die Erklärung scheint immer zu sein daß die
Sprache von der Wirklichkeit nicht mehr fassen könne || kann als sie schon in der Erwartung ausdrückt.
D.h. daß die Sprache von
der Wirklichkeit nicht mehr sieht als was sie
selbst versteht, & das hat sie schon in der
Erwartung gesagt. Denn die Sprache hat die Erwartung nicht
beschrieben, sie hat sie ausgedrückt. Sie hat
nicht zuerst die Erwartung beschrieben & dann eine
Tatsache die auf irgend eine Weise || irgend
wie zu der Erwartung paßt (wie wenn
man einen Tisch beschriebe & Sondern sie war die Erwartung (denn der Ausdruck des Gedankens ist der Gedanke; der Gedanke ist der Ausdruck des Gedankens) & ist jetzt erfüllt. |
Die Sprache
hat ja schon in der Erwartung alles gesagt was sie sagen
konnte. Sie hat ja nicht einen Zustand einer
Einstellung beschrieben sondern sich
eingestellt. Und dann beschreibt sie wieder nicht den
Zustand der Erfüllung sondern bejaht sich
selbst || ihre Einstellung. |
31.
„Davor hatte ich
mich gefürchtet || Das hatte ich
gefürchtet.”
– „Das hattest Du
gefürchtet?” –
„Ja, genau so hatte ich es mir
vorgestellt”. Man sagt aber
auch „Ja, das hatte ich
gemeint”. Und da hatte
man sich's gar nicht vorgestellt, & das Bild lag viel
weiter zurück (von der Wirklichkeit entfernt); und
doch hatte man es gemeint. |
Ich hatte mich vor etwas
gefürchtet etwa gefürchtet es werde ein bestimmter Mensch
zu mir
kommen || mir entgegenkommen mit einem bestimmten
Gesichtsausdruck. Er kommt nun; so kann ich Züge
wahrnehmen die ich in meiner || meine Furcht
vorausgesehen hatte, ferner Züge die ich mir etwas anders
gedacht hatte. Er kommt nicht in dem Anzug den ich
erwartet habe, kommt schneller als ich erwartet
hatte, sein Gesicht ist etwas milder als es meiner
Erwartung entspräche. (So sehr ist die Erwartung ein Bild.) |
Es fragt
sich || Die Frage ist: Liegt es
schon
im Wesen der Vorbereitung daß sie eine
Vorbereitung ist? eine Vorbereitung auf
Etwas? |
Ich habe das Gefühl:
nur die Stellungnahme zu dem Bild kann es uns zur
Wirklichkeit machen, d.h. kann es mit der
Wirklichkeit so verbinden, gleichsam wie eine
Lasche die die Überleitung von dem Bild zur Wirklichkeit
herstellt, die beiden in der  rechten Lage zueinander haltend dadurch daß beide für
sie das selbe bedeuten.
rechten Lage zueinander haltend dadurch daß beide für
sie das selbe bedeuten.
Die Furcht verbindet das Bild mit den Schrecken der Wirklichkeit. || mit der Wirklichkeit. |
An sich ist nichts eine Vorbereitung auf
etwas Anderes. |
„Ich dachte
mir, er würde jetzt kommen.” – „Ja, Du hast
gesagt, ‚er wird gleich
kommen’, aber woher weiß ich, daß
Du das damit gemeint hast?”. |
Das Porträt ist nur ein
dem N.
ähnliches Bild (oder auch das nicht) es hat aber nichts in
sich (wenn noch so ähnlich) was es
zum Bildnis dieses Menschen |
Als Porträt ist ein Bild
gemeint & wenn es & der || sein Gegenstand auch gänzlich unabhängig
von einem Menschen existieren könnten, als Bildnis
gemeint kann es nur von einem Menschen sein.
D.h. für das Bild & seine
Ähnlichkeit ist es ganz gleichgültig ob es jemand gemalt,
gesehen, es ähnlich gefunden
hat, wenn man es aber ein Porträt nennt so muß jemand da sein
der es als Porträt meint. Das hängt unmittelbar mit dem zusammen was ich früher über das einem Befehl nach Handeln & das Interpretieren eines Zeichens sagte. (Dieses Meinen ist die Stellungnahme von der ich oben geredet habe.) |
Nun kann man doch fragen: „Wie zeigt sich denn
das, daß er das Bild als Porträt des
N. meint?” – „Nun indem er's
sagt.” –
„Aber wie zeigt es sich denn daß er
das mit dem meint was er sagt?”
– „Gar
nicht!”. |
Das hängt mit der
Frage zusammen: Kann mir die Abweichung eines Bildes von
einem Gegenstand unangenehm sein so daß das unangenehme
Gefühl || die unangenehme Empfindung nicht
kausal, also
erfahrungsgemäß mit der Abweichung
zusammenhängt, Oder ist diese Empfindung sozusagen als Zeiger anzusehen dessen Ausschlag als Maß für die Spannung zwischen Bild & Gegenstand gedeutet wird? |
Keine
Untersuchung des Bildes kann je ergeben wessen Porträt es ist
(d.h. wen es darstellen
soll.). |
Der Meinende schweißt das Bild mit
seinem Gegenstand zusammen; nicht, indem er es ändert,
noch ähnlicher macht, – denn dadurch bliebe das
Bild das Bild, & immer noch vom
Gegenstand getrennt. |
Was ich also das „Meinen” nenne hat
also mit dem Bild nichts zu tun. |
Ich glaube es
verhält sich so: Die Frage, wie etwas gemeint
ist, || – das Reden von einer
Meinung, einem Sinn, || – hat nur
insofern Sinn als sie || sie || die Frage beantwortet werden kann.
Beantwortet aber kann sie nur durch die Sprache werden.
|
Kann ich
denn ohne Sprache erwarten? Wenn aber nicht, wie weiß
ich was der Satz für mich für einen Sinn
hat, wenn diese Frage überhaupt etwas heißt? |
Denken nenne ich das was sich durch eine
Sprache ausdrücken läßt. Dann muß es in
diese Sprache aus einer anderen übersetzt
werden. Ich will sagen: alles Denken muß dann in
Zeichen vorsichgehen. |
Wenn ich aber
sage || man aber sagt: „Wie soll ich wissen was er meint ich sehe
ja nur seine Zeichen” so sage
ich: „Wie soll er
wissen was er meint, er hat ja auch nur seine
Zeichen”. |
Die
Frage: „wie ist
das gemeint”, hat nur Sinn wenn es
heißt „es ist so
gemeint”. Dieses „so” ist ein
sprachlicher Ausdruck. |
Die Sprache || Gesprochenes kann man nur durch die Sprache
erklären, darum kann man die Sprache nicht
erklären. |
Das Ziel der Philosophie ist es eine Mauer
dort zu errichten wo die Sprache ohnehin aufhört. |
Man kann es auch so sagen: Wenn man sich
nur || immer in einem Sprachsystem ausdrückt
& also was ein Satz meint nur durch Sätze dieses Systems
erklärt, so fällt am Schluß die Meinung ganz aus der
Sprache, also aus der Betrachtung, heraus & es
bleibt die Sprache das einzige was wir betrachten
können. |
Wenn wir jemandem den Sinn eines Satzes
Wenn mir nun jemand einen Satz erklärt indem er etwa zeichnet, mit den Fingern deutet etc. & ich sage nun endlich: „ah, jetzt weiß ich, was er meint” was habe ich dann schließlich erfaßt als eine Zeichensprache die || einen Symbolismus der, in meinem Werkzeugkasten ist. |
Wenn mir jemand
einen komplizierten Befehl durch eine Zeichensprache gibt, – ich
verstehe ihn erst nicht, dann plötzlich verstehe ich „ah das will er”, was habe ich da erfaßt || (got
hold of) (got hold
of). Etwa die Vorstellung von einer Handlung; aber
sie wäre ja auch nur Zeichen, wenn ich sie nicht benützen
könnte. Oder, ich habe keine Vorstellung, sondern
Zeichen eines Systems die ich bereits
benützen kann. |
Man hat nicht den Gedanken, &
daneben die Sprache. – |
Es ist also nicht so, daß man für den Andern
die Zeichen, für sich selbst aber einen stummen Gedanken
hat. |
Der Gedanke
ist immer eine Konstruktion.
|
Die Verneinung muß mit zu der
Konstruktion gehören. Und zwar muß zum Beispiel in jedem Symbolismus ~~p = p sein. |
Man könnte so sagen,
am Gedanken ist nichts privat. – Er
kann von Jedem eingesehen werden || ((Es kann jeder in ihn Einsicht
nehmen)). |
Die Wahrheitsfunktionen gehören zum
Wesen des Satzes, & können darum nicht durch Sätze
erklärt werden. |
Man hat nicht den Zeichenausdruck
& daneben, für sich selbst, den (gleichsam
dunkeln) Gedanken. Dann wäre es doch auch zu
merkwürdig daß man den Gedanken durch den
Ausdruck || die Worte sollte
weitergeben || wiedergeben
können. |
D.h.:
wenn der Gedanke nicht schon artikuliert wäre, wie
könnte der Ausdruck durch die Sprache ihn
artikulieren. Der artikulierte Gedanke aber ist in allem
Wesentlichen ein Satz. |
1.8.
~p schließt
p aus; was es dann
zuläßt hängt von der Natur
von || des p ab. |
Nur einen
Satz kann man verneinen, – wenn man also ein Zeichen
mit den gleichen formellen Regeln wie das der Verneinung in
Verbindung mit Gleichungen verwendet, so wird zwar die
Versuchung naheliegen es Verneinung zu nennen aber es läßt sich
von Verneinung im ersten Sinn hier nicht
reden || von Verneinung im ersten Sinn ist
hier keine Rede. |
In der Mathematik ist alles
Algorithmus, nichts Bedeutung, auch dort wo es
so scheint weil wir mit Worten über
die mathematischen Dinge zu sprechen scheinen.
Vielmehr bilden wir dann eben mit diesen Worten
einen Algorithmus. |
Der einzige Beweis,
daß zwei Beweise dasselbe || das
gleiche beweisen, ist, daß sie in einander
überführbar sind. |
Ein Beweis beweist nur was er beweist; das heißt es ist durch
keine Auslegung mehr || etwas anderes
aus ihm
herauszukriegen als was in ihm selbst steht. |
Zwei Beweise die dasselbe
beweisen müssen sich ja begegnen.
Wie zwei Wege die zum selben Ort führen. Verfolgen
wir sie und sehen zu wie diese Begegnung geschieht. |
Kann man aus der Ungleichung
1 +
eine Zahl v konstruieren || ableiten, die jedenfalls in den Kombinationen der rechten
Seite noch fehlt?
Der Eulersche Beweis dafür daß es „unendlich viele Primzahlen
gibt” soll ja doch ein
Existenzbeweis sein & wie ist der ohne Konstruktion
möglich?
|
2.8. ~ 1 +
Das Argument läuft so: Das rechte
1 +
Wir haben nämlich hier wieder das
Merkwürdige, was man etwa einen
Indizienbeweis in der Mathematik nennen
könnte – der ewig unerlaubt ist. Oder, einen
Beweis durch Symptome. Das Ergebnis der Summation
ist ein Symptom dessen (oder wird als eines aufgefaßt),
daß rechts Glieder sind, die links fehlen. Die
Verbindung des Symptoms mit dem was man beweisen || bewiesen
haben möchte, ist eine lose.
D.h. es ist eine Brücke nicht
geschlagen, aber man gibt sich damit zufrieden, daß man das
andere Ufer sieht.
Alle Glieder der rechten Seite kommen in der linken Seite vor, aber die Summe links gibt ∞ & die rechte nur einen endlichen Wert – also müssen … aber in der Mathematik muß gar nichts, außer was ist. Die Brücke muß geschlagen werden. In der Mathematik gibt es kein Symptom; das kann es nur im psychologischen Sinne für den Mathematiker geben. Man könnte auch so sagen: Es kann sich in der Mathematik nicht auf etwas schließen lassen, was sich nicht sehen läßt. |
(Die Mathematiker haben von Strenge
überhaupt keinen Begriff.) |
Das ganze lose
Wesen jener Beweisführung Das sieht man eben || klar, wie weit immer man die rechte Reihe fortsetzt, immer kann man die linke auch soweit bringen, daß sie alle Glieder der rechten einschließt. (dabei bleibt noch offen ob die dann auch noch andre Glieder enthält.) |
Man könnte auch so
fragen: Wenn man
nur diesen Beweis hatte, was konnte man || Du nur diesen Beweis
hättest was könntest Du nun daraufhin
wagen? Wenn wir etwa die Primzahlen bis N gefunden
hätten, könnten wir nun daraufhin ins
Unendliche auf die Suche nach einer weiteren Primzahl gehen – da
uns der Beweis verbürgt, daß wir eine finden
werden? Das ist doch Unsinn. – Denn das
„wenn wir nur lange genug
suchen” heißt gar nichts.
(Bezieht sich auf Existenzbeweise im
allgemeinen.) |
Konnte ich auf
diesen || jenen Beweis hin weitere Primzahlen links
hinzufügen? Gewiß nicht, denn ich weiß ja gar
nicht, wie ich welche finden kann &
d.h.: ich habe ja gar keinen Begriff der
Primzahl, der Beweis hat mir keinen gegeben. Ich
könnte nur beliebige Zahlen
(bezw. Reihen)
hinzufügen. Es frägt sich ob durch Hinzufügung des Beweises von der eindeutigen Zerlegbarkeit jener Beweis beweiskräftig wird. |
2 & 3 tun's
nicht, || – welche Zahl soll ich als
nächste wählen? |
(Die Mathematik ist
angesogen von || mit falschen
Deutungen.) |
(Es muß noch eine
Primzahl || solche Zahl kommen,
heißt in der Mathematik nichts. Das hängt
unmittelbar damit zusammen, daß es „in der Logik nichts
Allgemeineres &
Spezielleres gibt”.) |
„Wenn die
Zahlen alle Kombinationen von 2 & 3 wären so
müßte
(
|
3.8. Es handelt sich
darum: Wie kommt es daß dieser scheinbare
Existenzbeweis keine Existenz aufzeigt?
Daß er uns scheinbar einen leeren |
1 +
Wieviel Glieder der Form
|
(1 +
|
Wie ist es nun, wenn ein Existenzbeweis
zeigt, daß eine Zahl der gewünschten Eigenschaft in
einem bestimmten Intervall vorkommt, ein anderer aber zeigt, daß
sich eine in einem kleineren Intervall finden muß?
Beweisen diese beiden nun dasselbe, nämlich die
Existenz? Nein. |
5.8
Es soll also werden:
Formen wir die linke Seite um in:
⇒
∴ 2nν + 2ν ‒ 2n² ‒ 2n + 2n + 2 ‒ n² ‒ nν + n + ν ≧ 0 nν + 3ν ‒ 3n² + 2 + n ≧ 0
ν ≧ 3n ‒ 1. Denke ich mir nun vom Anfang der Reihe 1 +
Die Reihe || Summe 1 +
1 +
Also muß unter den ersten 4m ganzen Zahlen mindestens eine sein, die durch keine der ersten m ganzen Zahlen teilbar ist. |
6. Wenn ich denke, so mache ich
fortwährend Pläne. Ich zeichne quasi
fortwährend Vorgänge auf
(d.h. ich mache Bilder von Vorgängen)
& ich könnte mir denken daß ich mit dem Bleistift
zeichnend, ¤ denke.
(Wenn man mit jemandem über eine Zeiteinteilung redet so
geschieht es oft daß man die Uhr zieht nicht um zu
sehen wieviel Uhr es ist sondern um sich
Bilder der überdachten Einteilung
machen zu können || zu
machen.) |
Wie kann man wissen daß, was der andere
sagt (schreibt,
etc.) so & so gemeint ist
doch nur daraus daß er es uns wieder sagt – also
andere Zeichen gibt – oder wir „schließen es aus seinem
Benehmen”. Wie weiß ich
aber wie das was ich sage gemeint ist? Heißt denn
diese Frage etwas? Diesem „wie es
gemeint ist” muß doch ein so
entsprechen & worin bestünde dieses
so. Denn durch andere Zeichen kann ich
mir es doch nicht deutlicher machen. Diese Frage
heißt also offenbar nichts. Es gibt keinen
Sinn losgelöst vom Satz auf den ich zeigen Das könnte einen nun fast zur Kausalitätstheorie bringen denn man könnte sagen: wenn es also nur das Arbeiten mit dem Satz ist das || was ihm Sinn gibt so ist es also seine Wirkung; – Hat er Wirkung so hat er Sinn & wenn nicht, so ist er unsinnig. Und doch ist das ganz falsch. Es wird dadurch der Satz etwa mit einer Säure verglichen & es wäre blödsinnig zu sagen „die Säure hat Sinn, wenn sie wirkt, etc.” Oder soll ich sagen: Der Satz hat Sinn wenn er wirkt aber sein Sinn ist nicht seine Wirkung; denn um seine Wirkung – so aufgefaßt – zu beschreiben, brauche ich ja eben ihn, den Satz. |
Man könnte
sagen: auf den Satz „dieser Satz hat Sinn” kann man nicht wesentlich fragen „welchen?” So wie man ja auch wirklich auf den
Satz „diese Worte sind ein
Satz” nicht sagen || fragen kann „welcher?”. |
Könnte man
sagen: || ? Ich deute den || diesen Satz heißt: ich ziehe ihn in irgend
einer Form (in
mir) nach.
Ich deute ihn wenn ich in irgend einer Form || Weise nach ihm handle. |
„Der Satz hat
Sinn” ist eine unglückliche
Redewendung. Und wenn man |
Ich glaube
es ist nicht richtig zu sagen „der Satz
ist
zusammengesetzt || muß zusammengesetzt
sein” sondern er kann auch || tatsächlich unzusammengesetzt sein
wenigstens im wörtlichen
Sinne; – seine „Zusammensetzung” besteht eigentlich darin, daß er ein besonderer
Fall einer allgemeinen Regel der Bildung von Zeichen ist.
Denn man kann zwar „ambulo” aus der Stammsilbe & der Endung
zusammengesetzt ansehen aber wie wäre es wenn der Sinn
dieses Satzes bloß || diese Form bloß durch die
Stammsilbe allein ausgedrückt || gebildet würde? |
Wie man von dem Sinn eines Satzes in
gewisser Weise nicht reden kann, so auch nicht von dem
Ausdruck des Gedankens, Wunsches, des Befehls
etc., denn auf die Frage „welcher Wunsch ist durch diesen Satz
ausgedrückt” muß
nur ein Ausdruck des Wunsches zur Antwort
kommen. |
Man möchte aber fragen, was ist nun der Mechanismus dieses
ausgedrückten |
Was ich oben gesagt habe gilt auch von dem
Wort „dieser Satz teilt mir etwas
(bestimmtes) mit”. Was
denn?! (darauf muß wieder ein Satz
kommen.) |
Ist es nicht klar, daß die einzige
Bedingung dessen, daß ein Satz Sinn hat, ist, daß seine Worte
Bedeutung haben, & das heißt wieder nichts anderes als
daß die äußeren Wortzeichen mit bestimmten Vorstellungen
oder anderen Vorgängen verbunden sind &
das wieder daß die Zeichen von bestimmter Natur
sind. Weiter können wir nicht kommen & nicht kommen wollen. – Ja, wir kommen über die || das Zeichen nicht hinaus & wollen aber nie über sie hinauskommen, – wenn man hier unter Zeichen das Ganze versteht, was beim Denken des Schrift- oder anderen Zeichens vor sich geht. |
Und hier muß man – glaube ich
– eben sagen, daß die Verneinung, Disjunktion
etc. im Gedanken ebenso „primitiv” ist, wie
in unserer Zeichensprache. Wie vermöchte man auch
in ihr die Verneinung zu denken wenn sie
nur wie ein schlecht passendes Kleid der Verneinung
wäre. Oder – würde man erwarten – man
müßte doch fühlen, wie einen der Ausdruck || die
Ausdrucksform überall drückt. |
Gibt es einen
Existenzbeweis für Primzahlen & einen der die Existenz
unendlich vieler Primzahlen beweist? und in welchem
Verhältnis stehen diese zu einander? |
7. Durch die Methode des
Multiplizierens (etwa im Dezimalsystem, aber gleichgültig
in welchem System) ist die Existenz von Produkten, von teilbaren
Zahlen bewiesen. |
8. Wenn n & m
relative Primzahlen || relativ
prim sind & n die größere &
n = a0 m +
r0, dann
können die Fälle
eintreten daß
|
Fügt
man nun n zusammen zu 1n,
2n,
3n
etc. so sieht man daß gegenüber
einem Vielfachen von m solange ein Rest bleibt bis man
zu m ∙ n
kommt, wo immer der euklidische
Algorithmus endet (d.h.
welche der Formeln immer für m anwendbar ist).
Im ersten Fall z.B. wenn m =
a1a2 + 1:
1n = a0m + a2 2n = 2a0m + 2a2 ‒ ‒ ‒ νn = νa0m + νa2 der Rest νa2 bleibt jedenfalls solange kleiner als m bis ν = a1 wird; dann ist a1n = a1a0m + a1a2. Noch immer ist der Rest ˂ m; aber nun wird
a2 ‒ 1 ist jedenfalls kleiner als m & der Rest verschwindet nur wenn a2 = 1 ist. Dann aber ist m = a1 + 1 also der Faktor a1 + 1 = m. Ist aber a2 ˃ 1 so geht die Sache weiter & es folgen nun (a1 + 2)n = ‒ ‒ ‒ + 2a2 ‒ 1 ‒ ‒ ‒ (a1 + ν)n = ‒ ‒ ‒ + νa2 ‒ 1. Dieser Rest ist gewiß kleiner als m bis (2a1)n = ‒ ‒ ‒ + a1a2 ‒ 1 & auch hier noch. Aber
der Prozeß wieder nur dann auf wenn a2 = 2, dann aber ist m = 2a1 + 1 also wieder gleich dem Faktor von n. – Ebenso geht es weiter bis (3a1)n = ‒ ‒ ‒ + a1a2 ‒ 2 und (3a1 + 1)n = ‒ ‒ ‒ + m + (a2 ‒ 3) solang bis (a2a1 + 1)n = ‒ ‒ ‒ + (a2 ‒ a2) = m ∙ n. |
Hat man
„intuitiv”
das Bildungsgesetz einer Reihe z.B. der Reihen
der m verstanden so daß man also im Stande
ist ein beliebiges m(v) zu bilden so
hat man das Bildungsgesetz ganz verstanden, also so gut wie
es etwa irgend eine algebraische Darstellung vermitteln
könnte. D.h. man kann es durch
eine solche Darstellung nicht mehr besser
verstehen. Und diese Darstellung ist daher
insofern auch nicht strenger. Obwohl
sie natürlich einprägsamer sein kann. |
Wenn man
bedenkt daß die Gleichung
2 × 2 =
4 ein Beweis des Satzes ist „es
gibt gerade Zahlen” so sieht man wie lose
hier das Wort Beweis gebraucht ist. Aus der Gleichung
2 + 2 = 4
soll der Satz „es gibt gerade
Zahlen”
hervorgehen?! – Und was ist der Beweis
der Existenz von Primzahlen? – Die
Methode der Zerlegung in Primfaktoren. Aber in dieser
Methode wird ja überhaupt nicht geredet, auch
nicht von „Primzahlen”. |
25 + 46 ≠
78 ist eine richtige Ungleichung, sie wird
bestätigt, wenn man die Summe
25 + 46 =
71 bildet. Man könnte die
Ungleichung || sie durch eine induktive Disjunktion
darstellen 25 + 46 = 1 . ⌵ .
25 + 46 = 2 . ⌵ . …
. ⌵ . 25 + 46 = 77 . ⌵ .
25 + 46 = 79 . ⌵ .
… |
Es ist ein korrekter Beweis für
3 + 4 =
7 wenn einmal die natürliche Ziffernreihe || Ziffernfolge aufgestellt ist:
|
Ein Beweis
in der Mathematik ist allgemein wenn er
allgemein anwendbar ist. Eine andere
Allgemeinheit kann nicht im Namen der Strenge gefordert
werden. Jeder Beweis stützt sich auf
bestimmte Zeichen, auf eine bestimmte Zeichengebung.
Es kann nur die eine Art der Allgemeinheit
eleganter erscheinen als die
andere. |
(Die Eleganz eines mathematischen
Beweises kann nur den einen Sinn haben gewisse Analogien besonders
stark zu Tage treten zu lassen, wenn das gerade
erwünscht ist, sonst
entspringt sie dem Stumpfsinn & hat nur die eine Wirkung das
zu verhüllen was klar & offenbar sein
sollte. Das stumpfsinnige Streben nach Eleganz ist eine
Hauptursache warum die Mathematiker ihre eigenen Operationen
nicht verstehen, oder entspringt die
Verständnislosigkeit & jenes Streben
einer gemeinsamen Quelle.) |
Das was die Gleichung (oder
Ungleichung) |
Nichts ist
verhängnisvoller für das
philosophische Verständnis als die
Auffassung von Beweis & Erfahrung als zweier
verschiedener, also doch vergleichbarer
Verifikationsmethoden. |
Eine Ungleichung ist
so wohl || so gut
eine syntaktische Regel wie eine Gleichung. Die
Analogie der Wahrheitsfunktionen in Verbindung mit
Gleichungen mit denen der
Sätze ist eine
vollständige –
d.h. die geltenden Regeln
sind in beiden Fällen dieselben – nur daß eben die
Gleichungen keine Sätze sind. (Wir haben ja in den Wahrheitsfunktionen auf Hypothesen angewendet ein weiteres Beispiel von Analogie.) |
Inwiefern kann man aber das Bild
Denn wenn ich die Gleichung 2 + 5 = 9 aufstelle so kann man sagen „wir werden gleich sehen ob das so ist” & nun stellt man den entsprechenden Kalkül an & sieht ob die Gleichung stimmt (und genau dasselbe gilt natürlich von den Ungleichungen). Aber der entsprechende Kalkül entspricht eben nur auf Grund einer allgemeinen || durch eine allgemeine Regel. |
Ist es
überhaupt denkbar daß diese Regel keine
allgemeine || nicht allgemein (ist), sondern nur für einen bestimmten Fall aufgestellt
ist? Ich glaube nicht. Was hätte es
für einen Sinn, d.h. was würde es
bedeuten, die Formel
3 + 4 = 7
mit dem Bild
|
In dem Additionsschema
|
Das Wort „Gasthaus” über
dem Tor eines Hauses zeigt an daß dort ein Gasthaus
ist. Es muß der besondere Fall einer allgemeinen Regel
vorliegen damit wir das Wort als Mitteilung, also als Satz,
verstehen. Das zeigt uns wie weit „Zusammensetzung || Zusammengesetztheit” ein
Charakteristikum des Satzes ist. |
„2 + 2 ≠
5” ist eine Zeichenregel
& daran sieht man schon wie hier die Verneinung etwas anderes
bedeutet da doch bei einer Festsetzung
jedenfalls von wahr &
falsch nicht die Rede ist. Ich sagte früher einmal daß die Verneinung in 2 + 2 ≠ 5 nicht die Bedeutung der Verneinung eines Satzes haben könne, weil das Verneinte 2 + 2 = 5 doch kein Bild eines nicht bestehenden logischen Sachverhalts sein könne. Aber Bejahung & Verneinung stehen auf einer Stufe, & könnte man 2 + 2 = 4 bejahen dann kann man es auch verneinen & dann kann man auch 2 + 2 = 5 bejahen. In Wahrheit– || , glaube ich, ist 2 + 2 = 5 eine Zeichenregel wie jede andere weder richtig noch falsch; & nur unverträglich mit unserer allgemeinen Regel der Darstellung || Bezeichnung &, wenn diese angenommen ist, nur in diesem Sinne falsch || unrichtig. – Darum ist sie auch kein Bild – davon wie es wäre wenn 2 + 2 = 5 wäre. Das Bild des Logischen Sachverhaltes – aber auch |
9.
Zum Beweis
eines mathematischen Satzes lenken wir die
Aufmerksamkeit auf ein Bild, aber der Beweis wird
noch nicht verstanden; plötzlich heißt es:
„jetzt sehe ich es
ein”. Man hat erst jetzt
das gesehen worauf es ankam. (siehe
p ∣ p. ∣ .q ∣ q
etc.) |
Ist es nicht
klar: || ? die Sätze der reinen
Mathematik können in ihrer Anwendung nur Zeichenregeln
sein. || nur als Zeichenregeln angewendet
werden. (Nur Bedingungen des
Sinn's.) |
Auch
3 + 4 ˂ 9
ist keine Mitteilung – wie etwa daß eine
gewisse Strecke länger ist als 9
Meter (ein Haus höher als
9 m). – Es ist nach dem was
wir unter 3, 4 & 9 verstehen
selbstverständlich (d.h.
beweisbar). Wir sehen es aber damit immer noch so
wie den Fall des Hauses an nur daß es sich
etwa dort um etwas weniger
Selbstverständliches
handelt. Aber er ist überhaupt mit dem des
Satzes unvergleichbar. – Wenn ich zuerst
sagte „es ist
selbstverständlich” so
heißt das, es ist hier nicht von einem Satz die Rede,
sondern von einer Zeichenregel, die übrigens aus einer
allgemeinen Regel folgt. Immer wieder drängt es uns zum Vergleich von 3 + 4 ˂ 9 mit einem Satz „wenn man diese beiden Stäbe aneinanderlegt so reicht es || reichen sie noch nicht bis dahinauf”.
Wäre 3 + 4 ˂ 9 nicht eine willkürliche Festsetzung oder die Folge aus einer Festsetzung so ginge es die Arithmetik nichts an. – Warum man es manchmal gern eine Tautologie nennen möchte (die es in meinem Sinne nicht ist) ist eben weil man sagen möchte „ja wenn Du das festsetzt, dann ist es ja selbstverständlich”. [Ich schreibe Paraphrasen auf || über logische Erkenntnisse.] |
Der arithmetische Satz
sagt nämlich nicht daß man in einer Ziffernreihe
durch Anlegen von 1 2 3 & 1 2 3 4 nicht
bis zum Zeichen „9” kommt, sondern es steht dafür daß es in der Reihe 1 2
3 4 5 6 7 8 9 nicht geschieht. Diese Reihe ist im
arithmetischen Satz präsupponiert & er ist daher
keine Beschreibung von außen dieser Reihe. – Man
könnte es auch so sagen: Es ist ein Satz:
„der Stab a & der Stab
b sind aneinandergereiht kürzer als der Stab c;
oder der Stab a ist 3 m lang, b
4 m & c 9 m.” (Aber von den Längen kann ich nicht
sagen, daß Oder: Die Angabe daß a 3 m, b 4 m, c 9 m lang ist, ist eben die durch welche ich zeige daß, c länger ist als a & b zusammen. Ein Satz der sagte daß 3 m + 4 m kleiner ist als 9 m entspräche einem Satz der sagte daß länger länger ist als kürzer. (oder „groß ˃ klein”.) Ein solcher Ausdruck entspräche vielmehr dem was festzusetzen ist ehe überhaupt etwas gesagt werden kann. 3 + 4 ˂ 9 gehört eben auch zum „Spiel” & ist eine Stellung der Figuren die nur mit den allgemeinen Regeln übereinstimmen kann oder nicht. Länger & kürzer sind eben eine externe Eigenschaft der Stäbe aber eine interne der Längen. (Sie durch einen Satz aussprechen zu wollen || auszudrücken hieße etwa die Bedeutung eines Wortes durch einen Satz in dem || worin das Wort vorkommt || steht aussprechen zu wollen.) ⇒XI 176f 5 |
Editorial notes
1) Continuation from Ms-107,229.
2) Continuation in Ms-107,229.
3) Continuation from Ms-107,300.
4) See facsimile; arrow pointing right, probably indicating that the line shall be indented.
5) Continuation in Ms-109,1.