Bemerkungen V. |
Ist
das Funktionieren || der Mechanismus
von „~p” damit erklärt, daß man sagt: ‚~p’ ist wahr wenn ‚p’
nicht wahr ist? |
12. Was sollte diese
„Erklärung” für ein Satz sein? Sie ist doch keine
grammatische Regel. Ist es nicht sehr charakteristisch
daß die Erklärung ausgedrückt (wie
in der WF-Notation) einfach zum Zeichen gehört &
nur eine Handhabe für den Angriff grammatischer Regeln –
Spielregeln – wird? Das „W” & „F” verfolgte eine Tendenz aber sie ist vereitelt, dadurch, daß nun doch wieder alles zum Zeichen gehört& WF nur mehr eine Anspielung bedeutet || . WF ist nur mehr eine Anspielung & nicht mehr. Und zwar nur eine Anspielung auf eine andere Notation nicht auf eine Erklärung. – Es ist ja selbstverständlich, || : es kann nicht eine Erklärung der Notation & die Notation geben. Denn die Erklärung wird sofort zur Notation & mehr als diese kann sie auch nicht enthalten. |
Denn wenn ich erkläre
„‚~p’ ist wahr wenn ‚p’
falsch || nicht wahr
ist”, so setzt
~p ≝ ‚p’ ist
nicht wahr und daran ändert sich natürlich nichts
wenn ich schreibe
~p ≝ ‚p’ ist
falsch. Es kommt nämlich wesentlich darauf
an daß es nicht möglich ist das Zeichen
p auf der rechten Seite der
Definition auszulassen bezw. durch
ein anderes zu ersetzen (es sei denn wieder durch eine
Definition). Solange das nicht möglich ist kann
& muß man auch die Rechte Seite als Funktion
auffassen von p, nämlich
‚( )’ ist falsch, oder wie Russell schreiben würde: ‚ξ̂’
ist falsch. Das hängt auch damit
zusammen daß ja der Tintenstrich nicht falsch
ist. (Wie auch das Bild nicht, es sei
denn, daß es als Porträt aufgefaßt wird.)
Das ‚p’ auf der rechten Seite muß nämlich eine Anspielung auf p, als Satz aufgefaßt, sein, & ist nicht der Name des Tintenstrichs „p”. Wenn ich also auch dem Schriftzug „p” den Namen A gebe & daher schreibe ~p ≝ A ist falsch
so hat das nur einen Sinn,
d.h. die rechte Seite kann nur
verstanden werden, wenn A für uns als
Satzzeichen |
Und dasselbe muß der
Fall sein wenn man erklärt,
„(x)fx” sei wahr wenn f( ) für alle
Substitutionen wahr ist. Man muß
auch dazu schon den logischen Mechanismus der Verallgemeinerung
verstehen. Es ist nicht so daß man erst
ahnungslos ist & die Verallgemeinerung nun durch die
Erklärung erst zum Funktionieren gebracht wird.
Wie wenn man in eine Maschine ein Rad einsetzt & sie dann
erst funktioniert (oder die Maschine erst in zwei getrennten Teilen
da ist & sie nun erst durch das Zusammensetzen als
diese Maschine
funktionieren). |
Man möchte also sagen: mit „der Kreis ist im Quadrat” ist, in einer Beziehung, alles gesagt; an
verschiedene mögliche Lagen im Quadrat braucht dabei
gar nicht gedacht zu werden. |
„Ich habe
(ja) nur
gesagt, daß der Kreis im Quadrat sein wird, ob er in der
Mitte oder weiter in einer Ecke sein werde || wird habe ich nicht gesagt”. ‒ ‒ ‒ |
„Er ist im Zimmer, ich höre ihn
auf & ab gehen.” Hier ist es deutlich, daß das im Zimmer sein eine,
komplette, Bestimmung für sich ist zu der die Angabe
des Orts im Zimmer nicht als eine nähere Bestimmung hinzutritt
sondern als eine neue fremde Bestimmung. || Angabe. |
In den grammatischen Regeln
für die Termini des allgemeinen Satzes muß es liegen
welche Mannigfaltigkeit er für
mögliche Spezialfälle
vorhersieht || voraussieht. Was in
den Regeln nicht liegt, ist nicht vorhergesehen.
|
Ist es
unmöglich, daß aus einem Satz unendlich viele Sätze
folgen, || – in dem Sinn nämlich, daß
nach einer Regel immer neue Sätze aus dem einen gebildet werden
könnten ad infinitum? |
Angenommen die ersten 1000
Sätze dieser Reihe schrieben wir in
Konjunktion an. Müßte
der Sinn dieses Produktes dem Sinne des
ursprünglichen Satzes nicht näher kommen als
das Produkt der ersten 100 Sätze? Müßte man
nicht eine immer bessere Annäherung an den ersten
Satz bekommen je mehr man das Produkt ausdehnte &
würde das nicht zeigen daß aus dem Satz nicht unendlich viele
andere folgen können da ich schon nicht mehr im Stande
wäre || bin das Produkt aus
10¹⁰
Gliedern zu verstehen & doch den Satz verstanden
habe dem das Produkt aus
10¹⁰⁰
Gliedern noch näher kommt als das mit || von
10¹⁰
Gliedern.? |
Man denkt sich
wohl, der allgemeine |
Denn im Satz müssen
die Sätze die aus ihm folgen || seine
Folgesätze mitgedacht sein; – also müssen in
jenem Satz jedenfalls die ersten 10000 Sätze mitgedacht
sein. (Hier ist noch eine Undeutlichkeit in der Theorie des Folgens.) |
14.
p folgt aus
q heißt offenbar || jedenfalls daß q ∙ ~p kein
möglicher Satz sein kann sondern eine
Kontradiktion ist.
– Ist q ∙ ~p ein
sinnvoller Satz dann folgt
p nicht aus
q. |
Wenn
p aus
q folgt so ist
q ∙
p = q. |
Wie verhält es sich nun mit dem Satz: die Fläche
ist von A bis B weiß?
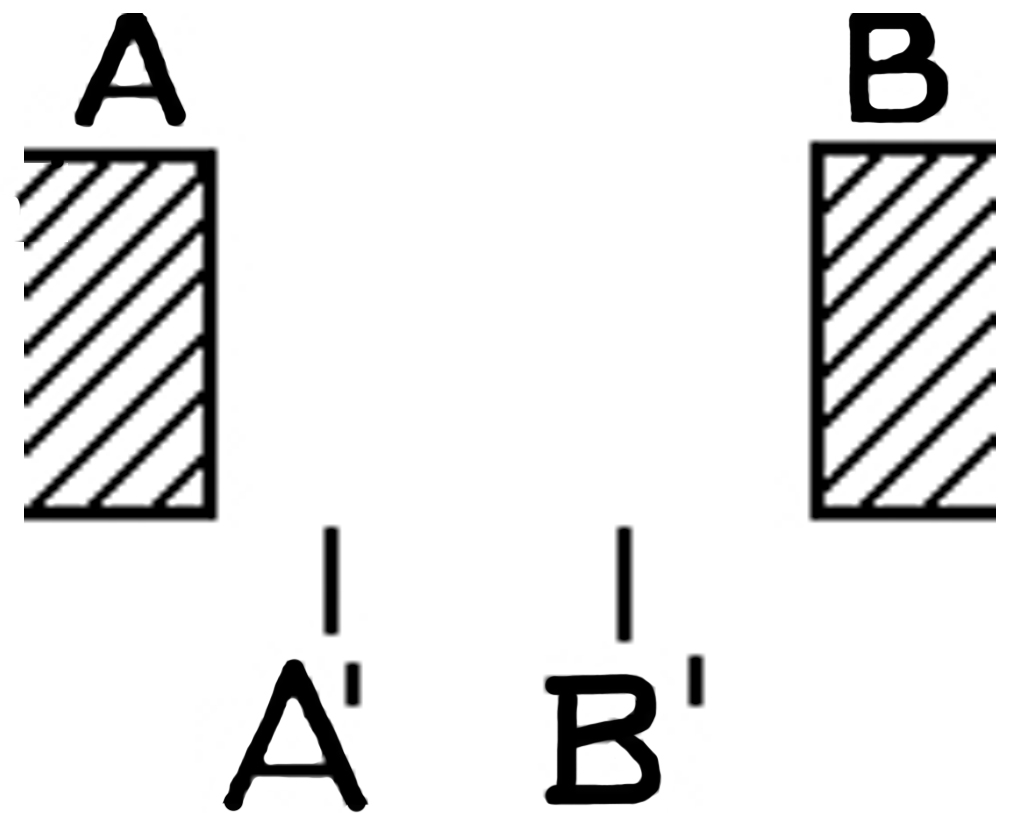 Aus ihm
folgt doch daß sie auch von A' bis
B' weiß ist.
Es braucht sich da ja nicht um sichtbares Weiß zu
handeln; und der Schluß von dem
ersten Satz auf den zweiten wird jedenfalls immer wieder
ausgeführt. Es sagt mir einer „ich habe die Fläche von A bis B
damit bestrichen” & ich sage
darauf „also ist sie jedenfalls von
A' bis
B' damit
angestrichen”. Aus ihm
folgt doch daß sie auch von A' bis
B' weiß ist.
Es braucht sich da ja nicht um sichtbares Weiß zu
handeln; und der Schluß von dem
ersten Satz auf den zweiten wird jedenfalls immer wieder
ausgeführt. Es sagt mir einer „ich habe die Fläche von A bis B
damit bestrichen” & ich sage
darauf „also ist sie jedenfalls von
A' bis
B' damit
angestrichen”. |
Wenn aber aus jenem
F(AB)
F(A'B') folgt dann
muß in F(AB) schon von
A' &
B' die Rede sein.
– „A'”, „B'” müssen also Symbole sein, die aus „A” &
„B”
konstruiert werden können wie etwa die Unterteilungen eines
Maßstabes aus seinen Endpunkten. |
Ist denn in
(x)fx von a die
Rede, da fa aus
(x)fx folgt?
In dem Sinne des allgemeinen Satzes, dessen Verifikation in einer Aufzählung besteht, ja. |
Was aus einem Gedanken folgt muß
in ihm mitgedacht werden. Denn an einem Gedanken ist nichts
dran was wir noch nicht wissen während wir ihn denken.
Er ist keine Maschine deren Untersuchung
Ungeahntes zu Tage fördern kann oder
eine Maschine die etwas leisten kann was man ihr
zuerst nicht ansieht. D.h.
er wirkt eben logisch überhaupt nicht als
Maschine. Wenn ich sage das Viereck  ist ganz weiß so
denke ich nicht an zehn kleinere in ihm enthaltene Rechtecke die
weiß sind & an alle in ihm enthaltenen Rechtecke
oder Flecken kann ich nicht denken weil das
(ein)
Unsinn ist. Ebenso denke ich im || beim Satz „er ist im
Zimmer” nicht an 100 mögliche
Stellungen die er einnehmen kann & gewiß nicht an
alle. ist ganz weiß so
denke ich nicht an zehn kleinere in ihm enthaltene Rechtecke die
weiß sind & an alle in ihm enthaltenen Rechtecke
oder Flecken kann ich nicht denken weil das
(ein)
Unsinn ist. Ebenso denke ich im || beim Satz „er ist im
Zimmer” nicht an 100 mögliche
Stellungen die er einnehmen kann & gewiß nicht an
alle. |
(Eine unendliche
Wirklichkeit wäre eine Kardinalzahl die alle anderen
Kardinalzahlen übersteigt.) |
Ein Gedanke aus dem unendlich viele andere folgen
ist || wäre ein Gedanke der mit
unendlich vielen anderen unverträglich
wäre || ist. Warum aber soll
ein Gedanke nicht seinem Wesen nach mit unendlich vielen anderen
unverträglich sein, d.h. daß sich nach
einer Regel ad¤ inf. Sätze
bilden ließen die ihrem Wesen nach mit jenem ersten
unverträglich wären. – Jener Gedanke
müßte also geradezu zum Inhalt haben daß alle nach einer
bestimmten Regel ad inf.
gebildeten Sätze wahr sind. Aber wie soll er das
denken? Denn er kann sich dann nur auf die Regel beziehen
da er |
„Wo immer, innerhalb dieses Kreises, Du die
Scheibe triffst, hast Du gewonnen”. „Ich denke, Du wirst die Scheibe irgendwo innerhalb dieses Kreises treffen.” Was den ersten Satz betrifft, könnte man fragen: woher weißt Du das, hast || ? Hast Du alle möglichen Orte ausprobiert? Und die Antwort müßte dann lauten: das ist ja kein Satz, sondern eine allgemeine Festsetzung. „Wo immer Du die Scheibe treffen wirst, wirst Du zufrieden sein”. „Woher weißt Du das?” – Das ist eine Hypothese. |
15. Auf den ersten Blick gibt es zwei Arten der
Deduktion: in der einen ist in der Prämisse von
dem || allem die Rede wovon die
Konklusion handelt
in der anderen nicht. Von der ersten Art ist der Schluß
von p ∙ q auf
q.
Von der anderen der Schluß: der ganze Stab
ist weiß also ist auch das mittlere Drittel weiß. In
dieser Konklusion wird von
Grenzen gesprochen von denen im ersten Satz nicht die Rede
war. (Das ist
verdächtig.) Oder wenn ich sage: „Wo immer in diesem Kreise Du die
Scheibe triffst, wirst Du den Preis gewinnen” & dann „Du hast sie
hier getroffen also …” so
war der || dieser Andererseits wird dem Satz „Wohin immer Du in diesem Kreis triffst …” nichts hinzugefügt wenn man sagt: „Wohin immer Du in diesem Kreis triffst & wenn Du insbesondere den schwarzen  Punkt
triffst …”.
Aber, war der schwarze Punkt schon da als man den ersten Satz
aussprach so war er natürlich mitgemeint; war er aber nicht da so
hat sich durch ihn eben der Sinn des Satzes
geändert. Punkt
triffst …”.
Aber, war der schwarze Punkt schon da als man den ersten Satz
aussprach so war er natürlich mitgemeint; war er aber nicht da so
hat sich durch ihn eben der Sinn des Satzes
geändert. |
Das folgt nicht denn vielleicht ist sie dann
innen schwarz, wenn wir sie hineinverlegen. |
„Das Ganze ist weiß, folglich ist auch ein
Teil davon der durch eine solche
Grenzlinie charakteristisch ist, weiß.” „Das Ganze war weiß,
also war auch jener Teil davon weiß, auch wenn
ich ihn damals nicht (durch eine
Linie) begrenzt darin
wahrgenommen habe.” Hatte denn das
Ganze || Rechteck keine rechte & linke
Hälfte ehe ich sie als solche wahrgenommen
hatte? Und doch
muß man das sagen. |
Der Schluß heißt auch
nicht so: „Wo immer auf der
Scheibe der Schuß hintrifft, hast Du den Preis gewonnen.
Du hast auf der Scheibe dahin
getroffen also hast Du den Preis gewonnen”. Denn wo ist dieses
da? Wie ist es außer dem Schuß
bezeichnet, etwa durch einen Kreis? Und war der auch
schon früher auf der Scheibe. Wenn nicht so
hat die Scheibe sich ja verändert, wenn aber ja, dann war
jener Kreis ohnehin ausdrücklich als eine Möglichkeit
des Treffens vorgesehen || wäre er aber schon dort gewesen
dann wäre er als eine Möglichkeit …
worden. Es muß vielmehr heißen „Du hast die Scheibe getroffen also
…”. |
Hat es nun nicht einen Sinn zu sagen:
Aber wenn man die Scheibe trifft, muß man
Oder auch: Wo immer er die Fläche trifft so wird es keine Überraschung sein so daß man sagen würde „das habe ich mir nicht erwartet, ich habe gar nicht gewußt daß es diesen Ort gibt”. Das heißt aber doch es kann keine geometrische Überraschung sein. |
Wenn p aus
q folgt, so muß
p in
q vorausgesehen
gewesen sein. |
Zu einem früheren Satz ist
noch zu sagen daß das da nicht notwendig
durch ein Zeichen auf der Scheibe angegeben sein muß &
daß es auf jeden Fall ein
Näher dem Mittelpunkt oder dem Rand, ein
Rechts oben oder Links unten gibt.
Wie immer die Scheibe getroffen wird stets muß so eine Beschreibung möglich sein. (Aber von diesen Beschreibungen gibt es auch nicht „unendlich viele”.) |
16. Wenn man ein
Beispiel braucht dafür daß unendlich viele Sätze aus
einem folgen so wäre vielleicht das einfachste das,
daß aus „a ist
rot” die Negation aller Sätze folgt
die dem a eine andere Farbe zuschreiben.
Diese negativen Sätze
werden gewiß in dem einen nicht mitgedacht. Man
könnte natürlich sagen: wir unterscheiden doch nicht
unendlich Müßte man nun nicht so sagen: Ein Satz folgt erst aus ihm, wenn er da ist. Erst wenn wir 10 Sätze gebildet haben die aus dem ersten folgen, folgen sie || 10 Sätze aus ihm. |
Statt
Farben hätte ich Längen nehmen
können. Aus „ich bin 170 cm hoch” folgt „ich bin nicht
171 cm hoch”, nicht 172, 173 etc. ad
inf. |
Was soll es aber dann heißen
zu sagen: wenn ein Satz aus dem anderen folgt, so muß der
erste im zweiten mitgedacht sein, da es doch nicht nötig ist im
Satz „ich bin 170 cm
hoch” auch nur einen einzigen der anderen
mitzudenken. Hier muß ein Unsinn vorliegen.
|
Ich möchte sagen ein Satz folgt erst dann aus dem
anderen wenn er mit ihm konfrontiert
wird. Jenes u.s.w. ad
inf. bezieht sich nur auf die Möglichkeit
der Bildung von Sätzen die aus dem ersten folgen, ergibt
aber keine Zahl solcher Sätze. |
Könnte ich
also einfach sagen: || ?
Unendlich |
Eines ist wohl
klar, es kann der Satz der aus p folgt der
Grammatik des p nicht fremd sein.
Der Satz könnte nicht überrascht sein daß der andere
aus ihm folgt. |
„Wenn aus
F1(a) [
=
a hat die Farbe F1] folgt
~F2(a) so
mußte in der Grammatik des ersten Satzes auch schon die
Möglichkeit des zweiten vorausgesehen sein (wie könnten
wir denn || auch sonst
F1 &
F2 Farben
nennen).” |
„Wenn der zweite Satz dem ersten
sozusagen unerwartet gekommen wäre so
könnte er nie aus ihm
folgen.”
|
„Der erste Satz
muß den anderen als seine Folge
erkennen. Oder vielmehr es muß dann beide eine Grammatik vereinigen & diese muß dieselbe sein wie ehe dem Schließen.” |
(Es ist sehr schwer
hier keine Märchen von den symbolischen
Vorgängen || von den Vorgängen im Symbolismus zu
erzählen, wie an anderer || der anderen Stelle keine Märchen
|
„Welchen Satz p nicht als
seine Folge erkennt, der ist nicht seine
Folge.”
|
D.h. aus der kompletten
Grammatik des Satzes p muß || müßte auch hervorgehen welcher Satz aus
p || ihm folgt, &
würde nun ein neuer Satz gefunden der
aus p folgt so würde damit
die Bedeutung || der Sinn von
p geändert werden.
|
Wenn z.B. aus „a ist grün” folgt „a ist
nicht rot” so muß „a ist
grün” den zweiten Satz || Ausdruck als seinen Verwandten
anerkennen.¤ |
Die Grammatik ist nicht
unendlich kompliziert, weil sie die endlose Bildung von Zahlzeichen
zuläßt. |
Ist es nicht einfach so:
Aus der Grammatik des Satzes – & aus ihr allein,
muß es folgen || erhellen || hervorgehen ob ein Satz aus ihm
folgt. Keine Einsicht in einen neuen Sinn kann das
ergeben; – sondern nur die Einsicht in
den alten Sinn. – Es ist nicht möglich
einen neuen Satz zu finden der aus |
Man überlege, welchen Grund hat
man ein neues Phänomen Farbe zu nennen wenn
es sich nicht in unser bisheriges Farbenschema
einfügt. |
Das was man
ursprünglich Satz nennt ist eine gewisse Leier die von
verschiedenster Art sein kann,
d.h. die
verschiedenartigsten Funktionen || verschiedenartigste Funktion || verschiedenen Arten sein
kann, d.h. verschiedene Funktionen
erfüllen kann.
2 + 2 = 4,
Ich sehe einen gelben Fleck in einer
blauen Umgebung, Vor mir liegt ein Buch auf dem Tisch,
Jedes Ding ist sich selbst gleich,
etc., gelten als Sätze. |
Hypothesen nenne ich solche Sätze für welche es
gilt daß man sich immer irren kann. |
17.
Was in
der Philosophie sagbar ist muß immer hausbackener werden; &
das einzige nicht Hausbackene ist die Grenze der
Sprache. |
Denn
immer wieder denkt man: ja wie soll ich dieses Letzte
aussprechen? Aber das Letzte soll ich eben nicht aussprechen, sondern das ist die Mauer an die wir stoßen. || das Ende an das wir kommen. |
Ich sage
jemandem: es liegt hier ein gelbes Buch vor
mir. Aber das kann ich nicht bestimmt wissen.
Was ich dagegen bestimmt wissen kann, kann ich das
mitteilen? – Sind nicht die
Sätze im engeren Sinne nur
Schnitte von Hypothesen & selbständig
existenzunfähig? |
Ich möchte sagen: die
alte Logik hat viel mehr
Konvention & Physik in
sich als man geglaubt hat. Wenn das
Substantiv der Name eines
Körpers ist das Verbum etwa
zur Bezeichnung einer Bewegung, das
Adjektiv der
Eigenschaft eines Körpers dient, dann sieht man wohl wie
voraussetzungsvoll diese Logik ist & kann annehmen
daß diese ursprünglichen Voraussetzungen
auch noch tiefer in die Anwendung dieser Worte, in
die Logik der Sätze reicht. |
Das Kreuzworträtsel wäre
die beste Illustration dafür, wie man eine Annahme aus
einem Grunde halten kann, der seinerseits wieder einen Grund
hat, der einen Grund hat etc.,
etc., daß es
unmöglich wird eine einzelne Entscheidung zu rechtfertigen
bis || ehe nicht alles beisammen ist. Denn
ich |
Angenommen ein
Kreuzworträtsel hätte zwei Lösungen die allen
Bedingungen entsprächen, wäre davon eine die
Lösung? Das hat eine Bedeutung in der Theorie der
Grammatik. |
Man könnte glauben daß es
günstig ist in der Logik recht || möglichst
„bestimmte”
Sätze zu Beispielen zu nehmen. In Wahrheit aber muß
ein Satz wie „dieser Anzug ist mir etwas
zu groß” oder „ich sehe meinem Vater
ähnlich” für uns ebensogut
taugen. – Beispiele taugen für uns nur dann
nicht, wenn sie einer anderen Art von Sätzen
angehören, als der die wir
betrachten wollen. Vage
Sätze würden uns also dann nicht
taugen wenn wir sie für eine eigene logische
Art von Sätzen hielten & sie augenblicklich
nicht betrachten wollten. (Aber dann
müßten wir sie ja doch einmal betrachten.) |
Die
Aristotelische Logik
ist ein Spiel, das sich auf Sätze
anwenden läßt. |
Alles
was man verlangen kann, ist, das Spiel komplett
kennen zu lernen. (Die Anwendung ist dann zu
tun || machen nicht zu
sagen || reden.) |
Immer ist hier das
Gleichnis gut von der Laterna
magica mit dem Film & den vereinzelten Bildern
auf der Leinwand; oder von dem Körper der sich dreht
& blitzartig hie & da beleuchtet
wird. Denn das ist ja eigentlich gar kein
Gleichnis sondern es verhält || es
verhält sich in der Logik der Hypothesen wirklich
so. |
18. Es werden immer
Facetten der Hypothese
verifiziert. |
Die Erlebnisse d.h.
die primären Ereignisse sind mit der Hypothese
vereinbar. (The hypothesis
accounts for them.) Man könnte etwa sagen: die Hypothese erklärt sie. |
Ist es nun nicht etwa so
daß das was die Hypothese erklärt selbst nur wieder
durch eine Hypothese ausdrückbar
ist. D.h. natürlich, gibt es
überhaupt primäre Sätze; die als
endgültig verifizierbar sind
& |
Am ehesten ließe sich das im
Verlauf eines Experiments sehen, wenn man die
unmittelbaren Erfahrungen beschreiben wollte,
die im Experiment den Ausschlag geben || die Entscheidung bringen || die im
Experiment für oder gegen die Hypothese
entscheiden. Denn es kommt doch am Ende darauf hinaus daß man einen Zeiger auf einem Teilstrich sieht( || , oder einen Lichtpunkt in einem Fernrohr) || , etc. Gibt es nun nicht Sätze die dieses rein „Subjektive” (was natürlich nicht subjektiv ist) beschreiben, – jene Haken woran alles endlich angehängt ist? Aber können solche Sätze zur || der Mitteilung dienen? Wären es nicht Sätze die dem Sprechenden als primäre, dem Angesprochenen || Anderen aber als Hypothesen gälten? |
19. Es kann jedenfalls kein
Unterschied sein zwischen einer Hypothese als Ausdruck einer
unmittelbaren Erfahrung gebraucht & einem Satz¤ im engeren
Sinne. |
Merkwürdig ist dann aber die Bedeutung der
Wahrheitsfunktionen angewandt Der Unterschied entspräche, natürlich, dem der Bedeutungen des Wortes Wahr (& Falsch) in jenen beiden Fällen. |
20. Es gibt
jedenfalls einen Unterschied zwischen Sätzen von denen man sagt
es ist wahrscheinlich der Fall & solchen von denen man
es nicht mit Sinn sagen kann. |
Es ist ein Unterschied zwischen einem Satz
wie „hier liegt eine Kugel vor
mir” & „es schaut so aus als läge eine Kugel vor
mir”. – Das zeigt sich
auch so: man kann sagen „es
scheint eine Kugel vor mir zu liegen”
aber es ist sinnlos: „es
scheint eine Kugel hier liegen zu scheinen”. Wie man auch sagen kann „hier liegt wahrscheinlich eine
Kugel” aber nicht „wahrscheinlich scheint mir hier eine Kugel
zu liegen”. Man würde in
so einem Fall sagen „ob es
scheint, mußt Du doch wissen”. |
Man möchte etwa auch
sagen: „Ich weiß schon
etwas, nämlich, was ich sehe; ich weiß nur
nicht, ob es eine Kugel ist”.
Hat es denn aber einen Sinn zu sagen „ich weiß, was Und nun ist es wohl auch Unsinn zu sagen, die Übereinstimmung |
Was
hat es nun mit der allgemeinen Regel auf sich die das Wort „Gemischtwarenhandlung” auf einem Haus zum Satz macht? Das
ist klar: wir verstehen dieses Wort wenn es in einem
(gewöhnlichen) Satz vorkommt; wenn ich es dagegen allein
auf einen Zettel auf meinem Schreibtisch schreibe, so sagt es nichts,
& man könnte etwa wenn man es so sieht,
fragen: nun, was ist's damit?
Es ist dann eben ein einzelnes Rad das wir zwar als Teil eines Mechanismus kennen, das aber hier, außerhalb jedes Verbandes, keinen Das Schiffssignal „Stop” ist auch ein einwörtiger Satz; wo ist hier der Satzzusammenhang? Oder soll man || ich so sagen: Das Wort „Stop” hat nur im Schiff Sinn nicht wenn ich es allein auf irgend einen Zettel schreibe; Wenn andrerseits das Wort an seinem Ort durch kein anderes zu ersetzen wäre, so wäre es wiederum sinnlos. Das Schild „Bass & Ale” zeichnet mir gewisse Häuser aus vor anderen welche es nicht tragen. Und selbst wenn es auf allen Häusern angebracht wäre als Zeichen daß tatsächlich überall diese Getränke zu haben sind so müßte es doch denkbar |
Hätte das Wort außer allem
Zusammenhang Sinn, dann genügte es daß es im
Wörterbuch steht; d.h. es brauchte
sonst nirgends erwähnt zu werden. Es würde so zu
sagen genügen daß man es ein für allemal
weiß. (Man könnte dann sagen „wozu steht das || dieses Wort
da? Ich weiß es ja ohnehin
schon.”) – Dieses Wort
sollte aber wahr & falsch sein können, dann nur ein
für allemal das eine oder das andere; es
müßte dann sozusagen von der Natur des
Satzes 2 + 2 =
4 sein. |
21. In dem, was
den Satz mit der gegebenen Tatsache verbindet ist nichts
Hypothetisches. |
Es ist doch
klar daß eine Hypothese von der Wirklichkeit – ich meine
von der unmittelbaren Erfahrung – einmal mit ja, einmal mit
nein beantwortet wird. Wobei || ¤ (wobei freilich
das „ja”
& „nein” hier nur Bestätigung & Fehler der
Bestätigung ausdrücken) & daß man
dieser Bejahung |
Die Hypothese wird, mit der Facette
an die Wirklichkeit || Realität
angelegt, zum Satz. |
Wie ist es mit den Sätzen die in
Dichtungen vorkommen. Hier kann doch
gewiß von einer
Verifikation nicht geredet werden & doch
haben diese Sätze Sinn. Sie verhalten sich zu den
Sätzen für die es Verifikation gibt wie
ein Genre-Bild zu einem Portrait. Und dieses Gleichnis
dürfte wirklich die Sache richtig || vollständig darstellen. |
Entsprechen diese Sätze etwa dem was Frege und Meinong Annahmen nannten? |
Denn in jenen erdichteten
Sätzen haben doch die Wörter Bedeutung wie in den
anderen, rot, blau, rechts, links, Kopf, Fuß, bedeuten dasselbe wie
sonst. D.h. es ist eine Verbindung
mit der Wirklichkeit vorhanden. In einem Sinne
wenigstens; – aber es fehlt die Verbindung mit dem Jetzt
& Hier. (Erinnern wir uns aber, wie die
Bedeutung eines Wortes fixiert ist.) |
Wenn ich ein Bild
anschaue so sagt es mir etwas auch wenn ich
keinen Augenblick glaube (mir
einbilde) die Menschen |
Meine Stellung gegen das Bild ist auch
keine hypothetische so daß ich mir etwa sagte „Wenn es solche Menschen gäbe, dann
…”. |
Und ist es nicht
unsinnig zu sagen „das Wort ‚Rot’
bedeutet in der Dichtung was es auch sonst bedeutet”? Was bedeutet es denn?
Kann || Darf man denn sagen
„es bedeutet
dieses” & auf einen roten
Gegenstand zeigen? Ist hier nicht nur eine Anwendung
dieses Wortes zu sehen. Läßt sich denn das
vergleichen mit dem Fall wenn jemand sagt „das ist der Ludwig || N”. Und doch kann ich jemandem der wüßte
daß „rot” eine Farbe bezeichnet aber nicht wüßte welche das Wort
auf jene Art erklären. „‚rot’ bedeutet hier
was es sonst bedeutet”
könnte nur heißen: es bedeutet dieselbe
Farbe. Denn ehe man nicht die Wortart des Wortes
„rot”
versteht, versteht man auch nicht die Erklärung „das ist rot”. |
Ist
der Satz || die Sprache ein Bild so kann ihn
nicht erst die Meinung dazu machen. Die Meinung macht ihn
nur zum Porträt. |
22.
Engelmann sagte
mir, wenn er zu Hause in seiner Lade voll von seinen
Manuskripten krame so kämen sie ihm so
wunderschön vor daß er denke sie wären es wert den
anderen Menschen gegeben zu werden.
(Das sei auch der Fall wenn er Briefe seiner verstorbenen
Verwandten durchsehe.) Wenn er sich aber
eine Auswahl davon herausgegeben denkt so verliere die Sache
jeden Reiz & Wert & werde
unmöglich. Ich sagte wir
hätten hier einen Fall ähnlich folgendem:
Es könnte nichts merkwürdiger sein als einen Menschen
bei irgend einer ganz einfachen alltäglichen
Tätigkeit wenn er sich unbeobachtet glaubt
zu sehen. Denken wir uns ein Theater, der Vorhang ginge auf
& wir sähen einen Menschen allein in seinem Zimmer auf
& ab gehen, sich eine Zigarette anzünden, sich
niedersetzen u.s.f. so daß wir
plötzlich von außen einen Menschen sähen wie man sich
sonst nie sehen kann; wenn wir gleichsam || quasi ein Kapitel einer Biographie mit eigenen Augen
sähen, – das müßte unheimlich &
wunderbar zugleich sein. Wunderbarer als
irgend etwas was ein Dichter auf der Bühne spielen oder sprechen
lassen könnte. Wir würden das
Nun scheint mir aber, gibt es |
Daß die Sprache ein Bild
hervorbringt zeigt sich schon darin, daß Bilder – im
gewöhnlichen Sinn des Wortes – sich ihr
natürlich einfügen.
Die Illustration in einem Buch ist dem Buch nichts Fremdes, sondern gesellt sich ihm zu wie ein verwandter Behelf einem anderen, – wie etwa eine Reibahle dem Bohrer. |
Wenn einen die
Häßlichkeit eines Menschen abstößt so
kann sie einen im Bild (im gemalten)
gleichfalls || ebenso abstoßen, aber auch
in der Beschreibung, durch
Worte || in den Worten. |
Wenn einer fragt was
bedeutet das Wort „rot” & ich
antworte „dieses” &
zeige auf einen roten Gegenstand so ist klar daß das Wort auch dann
seine Bedeutung gehabt hätte, wenn der rote Gegenstand nicht bei
der Hand gewesen
(wäre),
|
Das ist
selbstverständlich: wir können Namen von Personen
erdichten aber nicht Namen, etwa,
von Farben. |
Wir haben in der Dichtung || dem Erdichteten bloß das Spiel der Gedanken
& Vorstellungen. Soweit die Wirklichkeit in dieses
Spiel eingreift greift sie als Zeichen ein || wirkt sie als
Zeichen. |
Die Übereinstimmung der
Gedanken als solche mit der Wirklichkeit ist nicht
auszudrücken. Nimmt man das Wort
Übereinstimmung im Sinne der … eines wahren
Satzes mit der Wirklichkeit dann stimmt die Sache nicht weil es auch
falsche Gedanken gibt. Ein anderer Sinn aber ist durch die
Sprache nicht wiederzugeben. Wie alles
Metaphysische ist die
(prästabilierte)
Harmonie zwischen dem Gedanken & der
Wirklichkeit || Gedanken &
Wirklichkeit durch die Grenze der Sprache
uns gegeben. |
Das Alltäglichste, der Satz, ist Objekt unserer
Untersuchung. (Der Satz, wie ihn jeder
spricht.) |
Der Satz „Ich will nach Wien
fahren” hat Sinn auch wenn
Wien ohne daß ich davon erfahren hätte von einem
Erdbeben zerstört worden sein sollte. Der Satz
„ich freue mich den
N.N. zu sehen” hat
Sinn auch wenn dieser Mensch nicht mehr leben sollte,
ja selbst wenn er nie gelebt hätte. Hier handelt
es sich um Hypothesen. |
Die Grammatik
konstituiert einen Mechanismus; denn
indem sie gewisse Verbindungen erlaubt & andere
verbietet, tut sie dasselbe was die Lager, Führungen
(&
überhaupt alle
Teile) des Mechanismus tun:
sie lassen bestimmte || gewisse Bewegungen zu
& bestimmen so die Bewegung (der
Teile). |
Der Satz im engeren Sinne
verhält sich zur Hypothese wie eine
Projektion eines Körpers zum
Körper. |
Ob der Körper den ich sehe eine
Kugel ist kann zweifelhaft sein, aber daß er von hier
etwa eine Kugel zu sein scheint, kann doch nicht zweifelhaft
sein. – Der Mechanismus der Hypothese würde nicht
funktionieren, wenn der Schein auch noch
zweifelhaft wäre; Wenn auch diese Verbindung locker wäre so gäbe es auch nicht Bestätigung einer Hypothese, die Hypothese hinge dann gänzlich in der Luft & wäre zwecklos (& damit sinnlos). |
23. Ich habe
noch immer nicht die Maschinerie der Hypothese & des Satzes
erfaßt. |
Wenn ich von
Etwas sage „das
fühlt sich wie eine Schneide an” so
bilde ich damit unmittelbar mein Gefühl
ab. |
Es ist eine ungemein
wichtige Sache daß ich mich bei dem Gebrauch der Sprache
nicht erinnere wie ich sie gelernt habe.
Ich sage „hier sehe ich eine schwarze Kugel”. Ich weiß nicht wie ich „schwarz” & „Kugel” gelernt habe. Meine Anwendung der Wörter ist unabhängig von diesem Erlernen. Es ist so als hätte ich die Wörter selbst geprägt. Und nun kommt wieder die alte Frage: Wenn die Grammatik die von den Wörtern handelt für ihre Bedeutung wesentlich ist, muß ich die grammatikalischen |
[ || (Die Wahl der || unsrer Worte ist so wichtig weil es gilt die
Physiognomie der Sache genau zu treffen weil nur
der genau gerichtete Gedanke auf die richtige Bahn führen
kann. Der Wagen muß genau || haargenau auf die Schienen || Schiene gesetzt werden,
damit er richtig weiterrollen kann.)
|
Soll ich also sagen: Die
grammatischen Regeln wirken in der Zeit?
(Wie jene Führung) |
Also: Das Wort „Kugel” wirkt
nur durch die || in der Art seiner
Anwendung. Und es wäre die seltsame Frage
denkbar „wie kann ich denn dann
gleich wissen was ich mit ‚Kugel’ meine, ich
kann doch nicht die ganze Art der Anwendung auf einmal im
|
Und wenn mich jemand fragt „siehst Du dort eine schwarze
Kugel”, so muß ich doch diese
Anwendung des Wortes vor Augen haben um ihn verstehen
& ihm antworten zu können.
|
Nun
ist es seltsam, daß ich das Gefühl habe, als
trüge man die grammatischen Regeln auf irgend eine
Weise mit sich herum wenn man das Wort gebraucht || ich
die grammatischen Regeln auf irgend eine Weise mit mir herum
wenn ich das Wort gebrauche. Wie ich nicht
überrascht bin daß sich das Rad nur drehen kann & ich
seine Bewegungsfreiheit– || ,
gleichsam– || , mit
einem Blicke übersehe (&
kenne.) || , wie ich eine
Bewegungsfreiheit kenne. So, möchte ich sagen, weiß ich in irgend einem Sinn schon daß hinter der Halbkugel die ich sehe, eine zweite gleich große ist & nicht etwa eine Spitze, ich weiß daß die Kugel von der Seite gesehen auch als Kreis erscheint etc. etc.. Oder kann es mir doch durch das was ich in || mit mir herumtrage ableiten. |
Das Schließen in schwierigeren
Fällen geht tatsächlich so vor
sich, indem || in (der Zeit vor sich, daß) ich die
Regeln anschauen die Prämissen nachschlagen muß & so
den sprachlichen Apparat wie eine Maschine
|
Und ist es nicht ähnlich mit dem
Schachspiel; || : in irgend einem
Sinne kann man sagen, ich wisse die Regeln des Schachspiels (habe
sie im Kopf) die ganze Zeit während ich
spiele. Aber ist dieses „sie
im Kopf haben” nicht wirklich nur eine
Hypothese. Habe ich sie nicht nur in so fern im Kopf als
ich sie in jedem besonderen Falle anwende? –
Gewiß, dies Wissen ist nur das hypothetische Reservoir woraus das
wirklich gesehene Wasser fließt. |
Das Problem || Die Frage was unmittelbar mit
unserem in Beziehung steht ist: Was heißt es || ist die Frage nach dem Sinn der Aussage „ich kann Schach
spielen”?
Ist es nicht auf genau derselben Stufe wie „ich kann dieses Buch aufheben”? oder „ich kann lesen”? |
„Ich weiß, wie ein Bauer ziehen
darf” „Ich weiß, wie das Wort
‚Kugel’ gebraucht
werden darf.” |
Wenn ich sage „ich kann dieses Gewicht
aufheben || heben”
so kann man antworten „das wird sich
zeigen, wenn Du es versuchst” & geht es dann nicht so kann man sagen „siehst Du, Du |
Ist es nicht auch so
für den || beim Gebrauch des Wortes „Kugel”? Ich gebrauche das
|
„Siehst Du ein Reh dort?” „Oh ja,
deutlich!” Welch ein
komplizierter Gegenstand, wieviele Ansichten sind möglich
& doch verstehe ich augenblicklich. Oder kann doch
augenblicklich auf die Frage reagieren.
Denn ich habe die Sprache instinktiv gebraucht. Als Instrument, wie den Stock mit dem ich etwas beiseite schlage was mich am Gehen hindern will. |
Was ist aber
das Geschäft der logischen Untersuchung, ist es die
Wirkungsweise des Nervenmechanismus zu untersuchen, wie,
auf welchen Bahnen, der Reflex
zustande kommt?
Nein. Dann bleibt ihr aber nichts übrig als der Sprache eigene Gesetze zu erforschen denn die sind das Spiegelbild ( || – auf welchem Weg immer – von Gesetzen der Welt. |
Es droht in dieser
Untersuchung immer der psychologische Abgrund.
(Den || Dessen Gefahr
man aber nur dann überwinden kann, wenn man ihn klar ins Auge
gefaßt hat.) |
(Wenn ich die Logik paraphrasiere bin ich freilich auch in der
Gefahr wie die Katze um den heißen Brei zu gehen.) |
Könnte man sagen:
Es kommt nicht darauf an wieviele grammatische
Regeln der Anwendung er beim Gebrauch eines Wortes im Kopfe
habe || hat, sondern welche Regeln er dir
gefragt angibt || wenn befragt
nennt. |
Wenn ich sage „sieh dort ist eine
Kugel”, oder „dort ist ein Kegel”
so kann die Ansicht (ein Kreis) auf beides passen & wenn
ich sage „ja ich sehe
es”, so unterscheide ich doch
zwischen den beiden
(verschiedenen)
Hypothesen. Wie ich im Schachspiel zwischen einem Bauern & dem König unterscheide auch wenn der gegenwärtige Zug einer ist den beide machen könnten & wenn selbst eine Königsfigur als Bauer fungierte. Das Wort „Kugel” ist mir bekannt & steht in mir für etwas, das heißt, es bringt mich in eine |
„Siehst Du dort eine
Kugel?” „Nein – ach ja, aber man sieht nur ein
Stück, das Übrige ist bedeckt”. |
Dieses „Übersehen der
Wirkungsweise” eines
Rades ist es nicht darin vorhanden, wenn wir mit
einem Wort eine Vorstellung verbinden? Haftet der
Vorstellung die etwa das Wort rot in uns erweckt auch jene
Unbestimmtheit an, die erst, quasi, geschriebenen Regeln
bedarf um ihr einen bestimmten || den
richtigen Freiheitsgrad zu geben? |
Jedenfalls
aber machen geschriebene Regeln die Sprache nicht weniger
unmittelbar, denn sonst könnten sich geschriebene Regeln
– die langen Schlußketten der Mathematik
– nicht ohne Bruch in unsere Sprache
einfügen. || Jedenfalls aber ist die Sprache
ohne geschriebene Regel || geschriebener Regeln nicht
unmittelbarer, denn sonst könnten sich geschriebene Regeln
– die langen Schlußketten der Mathematik
– nicht ohne Bruch in unsere Sprache
einfügen. |
24.
Das ist klar: die Grammatik ist das
Leben des Satzzeichens. |
Ist es nun
nicht so: Würde man die Dinge sich selbst bezeichnen
Aber wenn die Vorstellungen Zeichen sind so geschieht eben dasselbe: Etwas Dunkleres als Schwarz kann ich mir nicht vorstellen & keine klingende Farbe etc. – Ich meine die grammatischen Regeln wirken sich erst mit der Zeit aus wenn das Wort in verschiedenen Verbindungen gebraucht wird aber die Grammatik der Vorstellung || Vorstellungen ist sozusagen zwangsläufig. Aber das ist auch eine schiefe Darstellung. Wenn ich sage „unsinnige Zeichenverbindungen wären nicht zu verbieten”, so meine ich es wäre unmöglich sie zu verbieten weil sie sich nicht beschreiben lassen. |
Wie weiß ich was der
Begriff Kugel alles beinhaltet, – wenn ich das Wort
„Kugel”
gebrauche, & doch wissen muß || weiß was
ich damit meine? Da geschieht doch folgendes: für manche der Konsequenzen muß ich mich an die Geometrie (also Grammatik) wenden & andere sind in der Vorstellung (schon || selbst) klar. |
Man könnte fragen: Wie mach ich's denn nur ein
Wort immer richtig anzuwenden, schau ich immer in der Grammatik
nach? Nein, daß ich etwas meine
– was ich meine, hindert mich einen Unsinn zu sagen;
– aber was meine ich denn?
¤ Die alte
Frage. Ich sage: ich rede vom Teilen eines Apfels
oder || aber nicht vom
Teilen der Farbe Rot weil ich beim Teilen eines Apfels mir etwas
denken kann, etwas vorstellen, etwas wollen kann beim
Ausdruck „Teilen einer
Farbe” nicht. Und ist es etwa
so daß man bei diesen Worten nur noch keine Wirkung auf andere
Menschen beobachtet hat?!
– Und auch das ist nicht so unsinnig, es muß
aber die Wirkung des Satzes || der Satz immer ein Bild
der Wirkung sein um die es sich hier handelt. |
Wenn das Reden ein Spiel mit Worten ist so
läßt sich der Unsinn so leicht spielen wie der
Sinn. Aber es geht eben noch etwas anderes
(dabei)
vor sich; so daß, wenn ich sage „rot ist in die Hälfte
geteilt” ich das Spiel
eigentlich gar nicht spiele. |
„Woher weiß ich daß ich Rot nicht teilen
kann?”
– Die Frage selbst heißt nichts. Ich möchte
sagen: Man || Ich muß mit der
Unterscheidung von Sinn & Unsinn |
[Ich bin jetzt in einer ungeheuren
Verwirrung.] |
Was ich sage
kommt || käme eigentlich immer darauf hinaus daß
Sprechen & Denken nicht einerlei sind.
Andererseits aber was ich hier unter denken verstehe
kein || nicht wesentlich ein menschlicher
(tierischer) Vorgang ist || sein
kann weil der mich hier || in der
Logik nicht interessiert. – Und doch muß
der Denkprozeß autonom sein denn er
muß alles in sich enthalten was den Gedanken
sinnvoll macht. Was dazugehört daß
der Satz sinnvoll werde, was zum Satz gehört damit das der Fall
ist muß alles innerhalb des Gedankens liegen.
Wenn ich sage „ich möchte hier
einen roten Kreis sehen” so
kann, ob das Sinn hat, nicht
(von einer
außerhalb des Gedankens liegenden
Existenz abhängen) || davon
abhängen ob es einen roten Gegenstand
irgendwo gibt & überhaupt kann der Sinn
eines Satzes nicht von einer
außerhalb des Gedankens liegenden Existenz
abhängen. Damit wäre der Sinn sofort |
Ich will
sagen: denk nicht daß das Denken im Kopf
vor sich gehen muß (wie die Verdauung im
Magen). Das Denken ist für mich
nicht ein menschlicher sondern ein sachlicher
Prozeß. |
Nein, was problematisch ist, ist
nicht der Gedanke (das ist etwas anderes, nicht der
Gedanke.) |
Aus der
Gedankenwelt komme ich in Gedanken nie heraus. |
Wenn man jemanden || jemand Naiven fragen würde,
was ein Gedanke ist || wie ein Gedanke vor sich
geht so würde er sagen es ist eine Kette von
Vorstellungen von Dingen, & Worten. |
25.
Immer in dem Versuch die Sprachgrenze zu finden, bis zu ihr
zu reden & sie so zu zeigen || weisen, stolpere ich über sie, in den Unsinn
hinein. |
Wodurch unterscheidet sich die Wirkungsweise des Wortes
‚Kugel’ von
der des Wortes ‚Kegel’, doch nicht durch die Verschiedenheit ihrer
Klangbilder || Klang- oder Schriftbilder, doch nur
durch |
(Fügt sich nicht auch eine
Rechnung unseren Gedanken ein?) |
Wie unterscheidet
sich Sinn & Unsinn? |
Da
scheint es als könnte man so etwas sagen wie: Die
Wortsprache läßt unsinnige
Ausdrücke zu, die
Sprache der Vorstellung aber nicht unsinnige
Vorstellungen. (Natürlich kann das, so wie es
da steht, nichts heißen.) Kann ich nicht antworten: oh doch, ich kann mir unsinnige Vorstellungen machen nämlich solche, mit denen ich nichts denke. |
Wenn ich mich
entschlösse (in meinen
Gedanken) „Abrakadabra || N” statt „rot” zu sagen, wie
würde es sich zeigen daß „Abrakadabra” an dem Platz des „rot”
steht. Wodurch ist der Platz || die Stelle
eines Wortes bestimmt? Angenommen etwa ich wollte auf
einmal alle Wörter meiner Sprache durch andere ersetzen wie
könnte ich wissen welches Wort an der Stelle
welches' steht. Sind es da die
Vorstellungen die bleiben & den Platz des Wortes
fixieren || halten. So daß an einer
Vorstellung |
Die
Naive Auffassung würde vielleicht sagen: dieses Wort
füllt denselben Platz aus wie jenes frühere wenn ich mit ihm
dasselbe meine wie mit dem ersten. Aber damit ich etwas
meinen kann, muß es da sein & ist es
so || da || vorhanden so gehört es zum Gedanken (denn es ist eine
Bedingung der Existenz dieses
Gedankens). |
Man kann
das Wort „existieren” so auffassen daß „rot
existiert” bedeutet es gibt
etwas || ein Ding das rot ist (dies ist ein
wirklicher Satz oder doch eine Hypothese) oder man
faßt ihn so auf daß damit gemeint ist, der Satz
„a ist rot” hat Sinn. |
Die Frage „habe ich diese Farbe schon
einmal gesehn” ist unsinnig wenn
ich in einem primären Sinne frage, & nicht das
Gedächtnis als einzigen Richter anerkenne.
(Das gehört unmittelbar
hierher.) |
Es hängt
damit zusammen: Wenn ich mir eine Farbe zu sehen erwarte
& es kommt eine & ich sage das ist die,
Im primären Sinn ist das Wiedererkennen nicht einfach das Kriterium || Symptom || Anzeichen der Gleichheit sondern der Ursprung des Begriffs der Gleichheit. Und zwar sowohl das Wiedererkennen der Erinnerung wie das des Erwartens. |
(In
gewissem Sinne verlieren alle Dinge ihre Farbe wenn sie
durch ¤ || in der
Sprache eingefangen werden.) |
Das Wiedererkennen
einer Erwartung in den Tatsachen ist keine || nicht die
Kontrolle der Ähnlichkeit oder Gleichheit
sondern das Gleichsein. |
Wie verträgt sich
das aber mit der gesonderten Betrachtung von Erwartung &
Ereignis || Erfüllung (Gedanken
& Tatsachen)? |
„Das ist die Farbe die ich mir erwartet
habe”: da gibt es keine
Täuschung. Es gibt keine Täuschung, weil es
auch keine Möglichkeit der Entdeckung einer
Täuschung gibt. || weil es kein
mögliches Daraufkommen auf eine Täuschung
gibt. |
Kann man
(denn) die
Erwartung mit der eingetroffenen Tatsache
vergleichen? Man sagt ja die Tatsachen stimmen
mit der Erwartung überein oder nicht überein; aber
dieses Übereinstimmen bezieht sich nicht auf
Eigenschaften der Erwartung (des Vorganges der
Erwartung) & Eigenschaften des Ereignisses,
vielmehr drückt sich die Übereinstimmung durch
eine Übereinstimmung der Zeichen aus. Ich nenne die Farbe eines Flecks „rot” wenn sie die
Erwartung er werde rot sein befriedigt. Wir sind hier an einer Grenze der Funktion der Sprache. Dort quasi wo die Sprache die Realität abstrahiert || verabstrahiert. |
Es ist aber nicht so als wenn || ob ich sagte: „ich habe
Lust auf einen Apfel, was immer also diese Lust beruhigen || stillen wird werde ich einen Apfel nennen”. (also etwa auch ein Schlafmittel)
|
Der Zusammenhang zwischen Wiedererkennen &
Namengebung erzeugt jene Funktion der Sprache & ihre
Grenzen. |
26.
Ich sehe ein Buch & sage, es ist
rot so drücke ich in dieser || durch diese
Namengebung das Wiedererkennen in der Sprache aus, es ist
also nicht durch |
Es ist irgendwo ein
Mißverständnis über die Funktion der Sprache das es uns
so schwer macht hier richtig zu sehen.
Es dürfte das Mißverständnis sein das || welches uns dazu führt zu glauben daß die Bedeutung des Wortes „rot” erklärt ist wenn || indem wir auf einen roten Gegenstand zeigen & sagen „das ist rot”. (oder auch: „‚rot’ bedeutet das”) |
Es ist falsch den
Gedanken ein Bild einer Realität zu nennen denn so ist
es als vergliche man den Gedanken mit einer Realität auf ihre
Ähnlichkeit. Während eine
Ähnlichkeit überhaupt keine Rolle
spielt wohl aber eine Identität,
die eben durch die || jene Art der Namengebung
angezeigt || gezeigt wird.
|
Was ich
erwarte ist nicht dem ähnlich was die Erwartung erfüllt
sondern es ist das was die Erwartung
erfüllt. |
Ich
erwarte nicht etwas Ähnliches wie das
was dann eintritt sondern dasselbe was eintritt.
|
Es hat auch einen Sinn zu sagen es sei nicht das geschehen was ich
erwartet habe sondern etwas Ähnliches im
Gegensatze aber zu dem Fall wo das geschieht was erwartet
wurde. Und das zeigt
(zu)
welchem Mißbrauch der Sprache || welcher Art der Mißbrauch der Sprache ist zu
welchem wir hier verleitet werden.
|
27.
Es ist
jenes Mißverständnis – glaube ich – das ich oben
erwähnt habe. |
Es ist
hier ein ähnliches
Mißdeuten der Funktion
eines Satzes wie im Falle „ich habe er hat Zahnschmerzen” || der Sätze „ich
habe Zahnschmerzen” & „er hat Zahnschmerzen”. |
Wie Wenn man
nun sagt: Das Rot das Du Dir
vorstellst ist doch gewiß nicht dasselbe (die selbe
Sache) wie, das, was Du wirklich vor Dir siehst,
– wie kannst Du dann sagen ‚das ist das selbe was ich mir vorgestellt
habe’? – Zeigt denn das
nicht nur, daß was ich ‚dieses
Rot’ nenne eben das ist, was meiner
Vorstellung & der Wirklichkeit gemein ist? Denn
das Vorstellen des Rot ist natürlich
anders Ist es denn nicht dasselbe in den Sätzen „hier ist ein roter Fleck” & „hier ist kein roter Fleck”. In beiden kommt das Wort „rot” vor, also kann dieses Wort nicht das Vorhandensein eines roten Gegenstandes || von etwas Rotem bedeuten. – (Der Satz „das ist rot” ist nur eine Anwendung des Wortes „rot” gleichberechtigt mit allen anderen, wie mit dem Satz „das ist nicht rot”.) (Das Wort „rot” hat eben – wie jedes Wort – nur im Satzzusammenhang eine Funktion. Und ist das Mißverständnis das, in dem Wort allein schon den Sinn eines Satzes zu sehen glauben?) |
[Das Nachdenken über
philosophische Fragen liefert sozusagen || in
gewissem Sinne das Material, – der Einfall, die
Synopsis.] |
Wenn man sagt, ich
könne das Wort „rot” nicht sinnvoll
gebrauchen wenn ich nie etwas Rotes
gesehen hätte so ist das Unsinn || falsch wenn es sich |
Der Vergleich des Satzes mit
einem Maßstab kommt uns wieder näher & scheint
nun ja weiter nichts darzustellen als das Verhältnis von Gedanken
& Wirklichkeit || Realität das sich im Satz
dadurch || so darstellt daß der Ausdruck der
Erwartung lautet „ich erwarte
daß p
eintritt” & der Ausdruck
der Erfüllung „p ist
eingetreten”.
p ist – im
strengsten Sinne – das Gemeinsame zwischen Maßstab
& Gemessenem. |
Das Gemeinsame zwischen Gedanken & Realität, das sich
sprachlich |
Man kann nicht in der Sprache das Wesen der Sprache
beschreiben. |
Wenn
das was wir „denken” nennen in
einer Art Krabbeln im Kopfe bestünde so könnten wir das
natürlich mit der Sprache darstellen wie jeden anderen Vorgang;
nur was am Denken unmittelbar durch die Sprache
seinen Ausdruck findet || ausgedrückt wird,
kann die Sprache nicht von außen betrachten. |
Wie komisch wäre es zu
sagen: ein Vorgang sieht anders aus, wenn er geschieht als, wenn
er nicht geschieht. Oder: „ein roter Fleck sieht anders aus wenn er da ist,
als wenn er nicht da ist, aber die Sprache abstrahiert von
diesem Unterschied, denn sie spricht von einem roten Fleck
ob er da ist oder nicht”. |
Wie unterscheidet sich das
Rot eines Flecks den wir vor uns sehen von dem
des || dieses Flecks wenn wir ihn uns bloß
vorstellen? – Aber wie wissen wir denn
|
Wie ist es möglich daß ich erwarte,
& das was ich erwarte
kommt?! Wie konnt' ich es erwarten,
da es nicht da war? |
Die Realität ist
keine Eigenschaft die dem Erwarteten noch fehlt & die
nun hinzutritt wenn es eintritt. – Sie ist auch nicht
wie das Tageslicht das den Dingen erst ihre Farbe gibt wenn sie
¤ im Dunkeln schon gleichsam farblos vorhanden
sind. Alle diese grammatischen Formen stellen den Gegensatz Erwartung & Erfüllung nicht dar. Die Sprache stellt ihn nur so dar, wie sie ihn immer darstellt durch den Gegensatz der Sätze „ich erwarte p” & „p ist eingetroffen”. |
Wie konnte ich es
erwarten, & es kommt dann wirklich; –
als ob die Erwartung ein dunkles Transparent wäre &
mit der Erfüllung (Es ist das im Grunde derselbe Unsinn, wie der, der die vorgestellte Farbe als matt im Vergleich zur wirklichen darstellt.) |
Du
siehst also, möchte ich sagen, an diesen Beispielen, wie die
Sprache tatsächlich funktioniert. – Aber auch das
stellt die Sache falsch dar, denn es scheint dann daß man sich die
Funktion der Sprache anders vorgestellt hat (sie
sich anders vorstellen konnte) & nun resignieren
muß. Aber es ist richtig zu sagen: Du siehst
also, wie die Worte wirklich gebraucht werden. |
Die ganze Antwort auf mein Problem
liegt darin, daß ich nicht fragen kann: „woher weißt Du daß das wirklich
das ist, was Du Dir erwartet hast”. – Denn weder kann man es an einem
Dritten (einem Gefühl der Befriedigung)
erkennen. (sonst müßte zum
Voraus durch eine Regel bestimmt sein die sagt
daß, immer wenn dieses Gefühl eintritt
…. Aber das setzt wieder die Möglichkeit einer
Annahme voraus.) Noch
erklärt es etwas wenn ich sage, ich erkenne das
Erwartete wieder. Das ist nur ein
hinzugesetztes || ein hinzugefügtes Wort,
|
Denn
könnte man diese Frage beantworten (hätte die Frage
einen Sinn), so enthielte die Antwort eine Beschreibung von
Gedanken & Wirklichkeit, & der
Bedingung ihrer Übereinstimmung. |
Man könnte das auch so
auffassen || ansehen: Es ist
möglich den Gedanken zu beschreiben & die Tatsache die
ihm entspricht; dann zeigt es sich daß der Gedanke in
der Sprache (denn nur in ihr kann ich ja ﹖
darstellen) p lautet & die
Tatsache: daß p der Fall ist.
Wenn Du willst kannst Du das als || Das kannst Du
wenn Du willst als die Funktion der Sprache
charakterisierend auffassen. |
Gibt es noch eine andre
Art den Gedanken zu beschreiben, als das Zeichen zu
geben wodurch gedacht wurde?
Nein! – Gäbe es || es noch eine andere Art wie würden sich die
beiden vertragen? Sie dürften sich ja nicht
widersprechen was aber jene gibt müßte diese auch
geben. |
Ist zwischen der Vorstellung eines Erinnerungsbildes
& der eines Erwartungsbildes ein Unterschied?
Ich kann |
Ich habe
gesagt es hat keinen Sinn zu fragen „woher || wie weißt Du daß Du
Dir gerade das erwartet hast”. (Man würde
das || da wohl antworten:
„ich muß doch wissen was ich mir
erwartet habe”.
Könnte man aber auch so
antworten: Ja, ich habe die Erwartung || Vorstellung noch vor mir & sie & die Farbe
hier sind ganz gleich? |
Kann man nun
sagen: Man kann in Sätzen der Wortsprache
oder || aber auch in Vorstellungen
denken. Die Worte sind willkürlich dagegen die
Vorstellungen nicht also bedient sich hier das
Denken zweier radikal verschiedener Mittel? –
Wie aber wenn sich das Denken gemalter
Bilder bedient || das Denken gemalte Bilder
benützt? Ist das nicht noch ein krasserer
Fall als der der |
Also muß jede Deutung
angenommen werden wenn sie kommt solange || wenn sie
eine Deutung d.h. eine Übersetzung
ist. |
28.
Die Intention ist nur dadurch
auszudrücken indem gezeigt wird
was intendiert ist. |
Das
Verhältnis, die Beziehung zwischen Gedanken &
Wirklichkeit gibt die Sprache durch die Gemeinsamkeit
des Ausdrucks wieder. Anders kann sie dies
Verhältnis nicht darstellen. Wir haben hier eine Art Relativitätstheorie der Sprache (vor uns). (¤Und die Analogie ist keine zufällige || nicht zufällig. –) |
(Ein Irrtum schadet nichts, er
nützt, wenn er nur tief genug gefaßt ist.)
(Drum scheue Dich nicht einen Irrtum immer
wieder zu wiederholen &
|
Ich wollte mir die Erwartung
& das Ereignis von außen betrachten || ansehen um zu sehen worin ihre
Ähnlichkeit, ihre
Gemeinsamkeit || ihr Gemeinsames, ihre
wesentliche || merkwürdige Beziehung liegt.
Und wenn ich sie nun wirklich betrachte (& die Erwartung als Erwartung nicht nur als Vorstellung) so kann ich nur sagen daß das Ereignis die Erfüllung der Erwartung ist. || die Erwartung erfüllt. Aber ich will diese Antwort nicht gelten lassen. Sehe ich die Erwartung als Bild nur, nicht als Portrait an, so ergibt die Betrachtung nur Ähnlichkeit oder Unähnlichkeit & nichts über das Wesen der Erwartung; sehe ich sie aber als Erwartung – und nicht nur als selbständige Vorstellung – an– || , dann ergibt die Betrachtung nur daß die Erwartung die Erwartung & das Ereignis die Antwort auf die Erwartung || Erfüllung – oder Nichterfüllung – ist. |
Die Erwartung wartet bis
zum Moment der Entscheidung. Dann aber berührt sie die
Entscheidung. ‒ ‒ ‒ Wie die Rechnung ihr
Resultat. |
Das
Zusammenpassen der Erwartung |
Das „ja”
(oder „nein”) oder die Beschreibung des
Ereignisses deutet das Ereignis || es als
Erfüllung der || Antwort auf die Erwartung.
|
In der Sprache berühren
sich Erwartung & Ereignis. |
Es ist als brächte die
Beschreibung am Ereignis die || jene Teilstriche || Striche || Marken an die
sich dann mit denen der Erwartung berühren. |
„Ich
erwarte mir einen Schuß”; er kommt nun. || der Schuß fällt. Wie das hast Du Dir
erwartet, war also dieser Krach irgendwie schon in Deiner
Erwartung? Oder stimmt Deine
Erwartung nur in anderer Beziehung mit dem
Eingetretenen überein, war der || dieser
Lärm nicht in Deiner Erwartung enthalten
& kam nur als accidens hinzu als die Erwartung
erfüllt wurde? Aber nein, wenn der
Lärm nicht eingetreten wäre so wäre meine
Erwartung nicht erfüllt worden, der Lärm hat sie
erfüllt, er kam nicht zu der Erfüllung hinzu
wie ein zweiter Gast |
War das am Ereignis was nicht auch in der Erwartung war ein
accidens eine Beigabe der Schickung || des Schicksals? Aber was war denn
dann nicht Beigabe, kam denn irgend
etwas vom Schuß schon in meiner Erwartung vor? Und was
war denn Beigabe, denn hatte ich mir nicht den ganzen
Schuß erwartet? |
Die Auffassung der Realität als Beigabe zur Erwartung ist der
Unsinn, gegen den ich mich unmittelbar wenden
darf. || kann. |
Wäre nur das am Ereignis
Erfüllung der Erwartung, was schon in der Erwartung war, dann
brauchte die Erwartung keine
Erfüllung mehr, dann wäre sie ihre eigene
Erfüllung. (Ich dränge jetzt das Gleichnis vom Maßstab zurück, obwohl es sich immer wieder als das beste zeigt.) |
Die Verwechselung
die hier vor sich geht
vermengt den Fall „ich habe das erwartet und
das ist auch geschehen” mit dem
„das || hält den Fall „ich habe
es erwartet und es ist geschehen” für den „es stand
früher draußen & jetzt
|
Wenn man
sagt, daß die Erwartung durch den selben Satz || mittels des selben
Satzes ausgedrückt wird wie die Tatsache die sie
erfüllt, so scheint es als beschriebe man eine
Eigentümlichkeit der Sprache die
(sich wohl auch anders
denken ließe) || man sich
auch anders denken könnte. Es ist als gäbe
man ein Charakteristikum
unserer Sprache wie sie nun einmal ist, sich aber auch anders denken
ließe. Die Betrachtung macht dann einen psychologischen Eindruck statt eines grundsächlichen || grundsätzlichen. |
29.
Man kann beim Wiedererkennen des
Erwarteten quasi nur beschreiben was geschieht ohne einen Grund
anzugeben. – Man befindet sich im Zustand der
Erwartung & macht Bilder bis das Ereignis eintritt welches man
als Entscheidung anerkennt. Daß man es als
entscheidend anerkennt zeigt
sich, indem man es mit dem || durch den
Satz beschreibt der die Erwartung ausdrückte.
– Hier tritt die Frage auf:
Welche Beziehung besteht zwischen einer || der Beschreibung & der Tatsache?
Welche Beziehung der Beschreibung stelle ich zur Tatsache
her? Welche Beziehung zur Tatsache stelle ich her, wenn
ich die Beschreibung mache? |
Ich lenke meine Worte
(offenbar)
nach den Tatsachen. D.h.
ich porträtiere die Tatsachen. |
Ich schaue in ein Fernrohr
& es fragt mich jemand „was
siehst Du?”, und ich
antworte: „ich sehe vier Sterne
die ein Quadrat bilden”.
– Wie kam ich zu diesen Worten? – Wie
drückt sich aus, daß diese Beschreibung der Tatsache
paßt? |
Nehmen wir den
krassesten Fall an: es sei
diese Beschreibung in einem Buch – etwa einer Art Fibel – zu
lesen neben einem Bild das die vier Sterne in
der gleichen Anordnung zeigt wie sie im Fernrohr zu sehen
sind. Könnte man sich nun einfach auf die
Fibel berufen um zu zeigen daß die
Beschreibung stimmt? – Es könnte dann
freilich die Beschreibung in der Fibel nicht als
Beschreibung aufgefaßt werden, denn sonst
wiederholte sich unser Problem dort, sondern die Regel
müßte einfach lauten: eine Beschreibung ist
richtig wenn der Wortlaut in diesem Buch neben dem entsprechenden Bild
gefunden wird || steht. – Ist nun die
Schwierigkeit die, daß diese Regel selbst auf diese Art nicht
darstellbar ist? Wie weiß ich daß das die richtige Beschreibung ist? Weil sie hier steht. |
Mir hätte jene
Beschreibung auch englisch einfallen können; wenn mir aber durch
Zufall die chinesischen Worte für
diese Tatsache || dafür eingefallen wären,
ohne daß ich weiß daß diese Lautverbindungen die
chinesischen Zeichen für diesen Fall sind, so wären sie mir
unsinnig erschienen; aber nicht mehr, sobald mich jemand soviel
Chinesisch gelehrt hätte um in dieser
Sprache diesen Satz bilden zu können. |
Aber um in dieser Sprache || in Chinesisch diesen
Satz bilden zu können dazu genügt es nicht die
Lautverbindung || Lautreihe zu lernen & zu wissen daß sie in der
(chinesischen Fibel)
neben jenem Bild steht. Denn das befähigt mich nicht
die Tatsache auf Chinesisch zu
porträtieren. |
Ja wenn es mir im Deutschen so
geschehen würde daß ich die ganze Sprache
vergäße mir aber bei einer bestimmten Gelegenheit
plötzlich die Lautverbindung einfiele die man in diesem
Falle gebraucht, so würde ich diese Lautverbindung
|
Das Porträtieren || Nachzeichnen der Tatsache durch die Sprache ist in
dem Ausdruck || Worte
be-schreiben
vollständig wiedergegeben.
Beschreiben heißt nachschreiben, nachzeichnen. |
Gibt es nun – im
Primären – ein Kriterium
dafür daß richtig nachgezeichnet wurde? (Es
scheint mir nämlich, als könnte es das
nicht geben.) „Wie weißt Du, daß diese Worte, das wiedergeben, was Du siehst?”. – Könnte man denn diese Worte daraufhin rechtfertigen? Und wie, durch eine Beschreibung in Worten? – Ist es nicht klar daß diese Rechtfertigung selbst eine Beschreibung des Sachverhalts in irgend einer Sprache (in der Sprache der Rechtfertigung) sein müßte? Denn sie müßte doch sagen: da sich die Sachen so & so verhalten & die Vereinbarungen so getroffen sind, so war die Beschreibung richtig. |
Es ist,
übrigens, das Gleiche ob ich einen Sachverhalt beschreibe
oder einen Wortlaut als Beschreibung deute. |
Wenn sich die Beschreibung nicht
rechtfertigen Es wäre also die Konsequenz zu ziehen: Eine Rechtfertigung schien Dir denkbar, also schaust Du die ganze Sache falsch an. |
Wenn man jemanden fragt „wie weißt Du daß diese Beschreibung
wiedergibt was Du siehst” so könnte er etwa antworten „ich meine das mit diesen
Worten”. Aber was ist das
„das”, wenn es nicht selbst wieder
artikuliert also schon Sprache
ist? Also ist „ich meine
das” gar keine Antwort.
Die Antwort ist eine Erklärung der Bedeutung der
Wörter || Worte. |
Wenn ich die
Beschreibung nach Regeln bilde, was auch möglich ist, dann
übersetze ich sie als eine Sprache aus einer anderen.
Und das kann ich natürlich mit Grammatik &
Wörterbuch tun & so
rechtfertigen. – Aber dann
ist die Übertragung von Artikuliertem
in Artikuliertes.
Und wenn ich sie durch Berufung auf die
Grammatik & das Wörterbuch
rechtfertige so tue ich nichts als eine Beziehung
zwischen Wirklichkeit & Beschreibung |
(Alles liegt jetzt in dem
„deuten”
beschlossen. Wie das Problem sein Haus
wechselt!) |
Ich sehe
diesen Sinn in diese Worte hinein. Ich sehe diesen
Sachverhalt in diese Worte hinein. |
„Sie sagte mir daß sie um
3 Uhr von der Hochreith
weggehn || fortgehn wolle; sie wird den kürzesten Steig
gehn, das dauert 40 Minuten, also || so ist sie um
ca.
|
30. Wenn ich einen vorliegenden
Sachverhalt mit den Worten beschreibe: „hier ist ein roter Kreis” geben diese Worte die Tatsache etwa besser wieder
als die Worte || der Satz „hier ist ein grünes
Viereck”? Gewiß nicht;
aber der Klang der Worte ist es auch nicht der abbildet,
nachzeichnet, sondern das Wort in seinen Beziehungen durch die
Grammatik ist ein Werkzeug der Abbildung. || des Abbildens. |
Die Deutung des Satzes
liegt in der Namengebung. Die Namengebung ist unabhängig davon || von der Hypothese daß wir – etwa in unserer Jugend diesen Namen in dieser Anwendung gelernt haben. Das Historische (das immer hypothetisch ist) kann hier nicht hineinspielen. Wir geben den Namen als gäben wir ihn zum ersten mal. – Überhaupt aber liegt in der Idee der Namengebung ein Unsinn, sie ist von der Namengebung an Personen – & etwa manche Dinge – genommen, führt aber zu Unsinn wenn man sie auf Wörter wie „rot”, „grün” etc. anwenden will. Wo ist das, was mit dem Wort „grün” bezeichnet wird? Wie schon oft gesagt wird das Wort „grün” auch dort im Satz gebraucht, wo kein grünes Ding vorhanden ist. |
Das
Artikuliert-Sehen der
Tatsache – – Der Wortausdruck verdoppelt das artikulierte Bild. |
Wie kann man durch
Denken die Wahrheit lernen?
Wie man ein Gesicht besser sehen lernt wenn man es zeichnet. |
Was ist
das Geschäft des Denkens? |
Sieht man es nicht an jenem
Fall wo |
Man kann sich nach Gedanken
richten. – Das kann ihnen nicht
zufällig anhaften. Es muß – glaube ich –
ihnen wesentlich sein, ja ihr Geschäft sein.
|
Der Satz ist eine
Vorrichtung, die ihren Zweck erfüllt hat wenn sie sich
mit der Wirklichkeit gemessen hat. |
Denken ist das
Benützen von Sätzen. |
Am Satz mißt man
unmittelbar die Wirklichkeit. |
Die Wirklichkeit die man an
ihm || am Satz mißt ist seine Bedeutung, die
Entscheidung über seine Wahr-
& Falschheit. |
Das Denken kann ja keine Spielerei
sein kein Spiel menschlicher Kräfte || kein
Spiel menschlicher Kräfte sein. Und ist es
das, so wäre es für uns |
Nehmen wir an,
ich erwarte jemand: ich sehe auf die Uhr, dann zum
Fenster hinaus, richte etwas in meinem Zimmer zurecht, schaue wieder
hinaus etc. Diese Tätigkeit könnte ich
das Erwarten nennen. Denke ich nun die ganze Zeit
dabei? (d.h. ist diese
Tätigkeit wesentlich eine Denktätigkeit oder von
ihr begleitet?) Letzteres
bestimmt nicht. Und wenn ich jene
Tätigkeiten Denken nennte, welches wären
die Worte durch die dieser Gedanke ausgedrückt
würde? – Wohl aber werden auch Gedanken
während diesem Warten sich einfinden. Ich werde mir
sagen: „Vielleicht ist er zuhause
aufgehalten worden” &
dergleichen mehr; vielleicht auch die
artikulierte Erwartung „wenn er nur käme”. In allen jenen erwartenden Handlungen ist nichts was uns interessiert (die Erfüllung der Erwartung in diesem Sinn ist nichts anderes als die Stillung des || eines Hungers). Uns interessiert nur das zu einem Zweck gemachte Bild – der artikulierte Gedanke. |
Ich mache mir das Bild anläßlich einer
Sachlage. || eines
Ereignisses. Ich gebe ihm aber die Beziehung zu seinem || zum Gegenstand wie jedem Ist es nicht dieselbe die entsteht wenn ich etwa die Reihen || Reihe der Zahlen 3, 7, 2, 5, 1 durch eine Reihe von Quadraten des entsprechenden Flächeninhaltes darstellen will & nun nach einer Regel (Wurzelziehen, Auftragen der Seite, etc.) vorgehe? Wenn ich eine Linie abzeichne, so heißt || lautet die Regel etwa ziehe immer parallel zu diesem Linienzug von links nach rechts. |
Besteht also das Abbilden darin,
nach einer solchen Regel vorzugehen? Wie ist aber diese
Regel gegeben? – Wie ist mir die Regel
bewußt?! Was ist ihr Ausdruck?
|
Ich meine hier die Regel als etwas
Vorgesetztes (quasi als
allgemeines Programm). |
Nun ist ja
der Vorgang des Abbildens tatsächlich || wirklich
damit beschrieben, daß man das Abzubildende & die
Regel gibt (also etwa 3, 7, 5 || 2, 5, 1
& die allgemeine Vorschrift der
Abbildung).
Wenn ich sage er || der Vorgang des Abbildens sei damit beschrieben so meine ich aber nur, seine Multiplizität sei dann gegeben. (die „Intention” der Beschreibung bleibt |
Ich wollte
den Vorgang des Nachbildens so beschreiben: daß ich
meine Hand von dem Abzubildenden || Vorbild führen
lasse. Aber dieses Führen ist eben in der Regel der
Abbildung ausgedrückt. |
Das hieße also wir übersetzen die
Wirklichkeit mit Hilfe von Regeln in die Sprache. Und das
ist, wenn man sich einfache Fälle, sozusagen eine
einfachere Welt,
konstruiert leicht zu denken. Wenn
etwa die Welt aus einem Quadratnetz bestünde worin in
gleichmäßigen Zeitabständen verschiedene
Gitterpunkte aufleuchteten so wäre dieser Vorgang sehr einfach
durch eine Sprache darzustellen die etwa in einer Klammer die
Koordinatenpaare der jeweils
aufleuchtenden Punkte vereinigt etwa (7, 3; 5, 4; 8,
6) u.s.w.. |
Wäre dann aber die Abbildung
nicht, durch diese Regeln, rechtfertigbar? Ja
& nein; die Abbildung ist mit den Regeln
in || im Einklang
aber nicht durch sie beschrieben. |
31.
Wozu denken wir denn, denn dadurch
wird es sich auch zeigen, ob das Denken eine wichtige
AngelegenheitDa ist es ganz klar, wir denken zu einem Zweck. Der Zweck des Denkens besteht offenbar darin, meine Handlungen danach einzurichten & zwar genau so wie ich sie nach der Berechnung eines Dampfkessels einrichte. (Diese Berechnung ist ja auch ein Denkakt.) |
Ich mache z.B. einen Plan, einen Kampfplan,
Fluchtplan. |
Der Gedanke ist der angewandte Plan. |
Und zwar
mache || zeichne ich einen Plan || Ich mache einen Plan nicht nur um mich anderen
verständlich zu machen sondern auch um selbst über die
Sache klar zu werden.
(D.h. die Sprache ist
nicht nur Mittel zur Mitteilung.) |
Die
Verwendung des Plans ist eine
Rückübersetzung || Übersetzung in unsere
Handlungen. Eine Übertragung in unsere
Handlungen. (Es ist klar daß da kausale Zusammenhänge gesehen werden, aber es wäre komisch die als das Wesen eines Planes anzugeben.) |
Dagegen
liegt vielleicht der Kausalitätstheorie der Bedeutung
|
Daß
etwas ein Portrait des A ist besteht ja nicht darin daß es
ähnlich ist sondern darin daß es ähnlich sein
soll. Also nicht darin daß eine bestimmte Übersetzungsregel aus der Betrachtung von Bild & Gegenstand abzulesen ist, sondern daß zu dem Bild eine Regel gegeben ist nach der es zu kontrollieren ist. |
Nehmen wir
für einen Augenblick an die Übersetzung aus einer
Sprache in eine andere etwa aus dem Englischen ins
Deutsche ginge so vor sich daß man mit dem Wörterbuch
immer ein englisches in ein ihm eindeutig
entsprechendes deutsches Wort übertrüge. Wenn ich
nun sage diese Schrift ist die deutsche
Übersetzung von jener englischen || soll die
deutsche Übersetzung von jener englischen sein, so gebe ich
dem Andern eigentlich damit die deutsche Schrift
& das englisch-deutsche Wörterbuch (den Ausdruck
der Regel) zur möglichen Kontrolle. |
Die Kontrolle einer Übersetzung
|
Das Kontrollieren einer
Übersetzung nach dem Wörterbuch ist genau
analog dem Kontrollieren einer Rechnung nach den
Rechnungsregeln. |
Ist also nicht ein Satz der Art
„dieses Bild soll
jenen || den Gegenstand A
vorstellen” von der Art der
mathematischen Sätze? Etwa der Gleichung
25 × 24 =
230 ‒ ‒ ‒? |
Ich
glaube, daß dies kein Satz ist sieht man schon daraus, daß darin
die Abbildungsregel abgetrennt von den beiden Komplexen gegeben
ist || wird die in der internen
Beziehung stehen. |
„Diese Linie soll ein Abbild jener
sein” ist eine Bestimmung
& kein Satz. Es || Sie händigt einem quasi, Bild, Abgebildetes & Abbildungsregel ein. Hier ist aber die Schwierigkeit daß sie diese Dinge uns stumm einzuhändigen |
Und doch
scheint der Vorgang keine Worte zuzulassen; denn, was immer dazu
gesagt würde, woher wüßten wir was es
bedeuten soll || bedeutet?
|
Kein Zusatz würde die
Multiplizität der Sache ändern, weil statt
dieses Zusatzes kein anderer mit anderem Sinn eingesetzt werden
kann. Er ist also so überflüssig (also
bedeutungslos) wie etwa das Fregesche „⊢”. |
Könnte ich nicht sogar zwischen ¤ die beiden Linien das Zeichen „ = ”, im mathematischen Sinn, setzen?
Kann ich es nicht offenbar eben mit dem Recht hier setzen wie
zwischen den englischen & deutschen Satz.
Und hier wird die Gleichung buchstäblich nach Regeln
aufgelöst, wie jede mathematische. |
Kann ich
nicht sagen: die Definition ist ein Ausdruck der
Intention? Und der einzig mögliche –?
|
Wenn ich sage „der Sinn eines Satzes ist dadurch bestimmt, wie
er zu verifizieren ist”, was muß ich
dann von dem Sinn des Satzes, daß |
1.9. Was zum Wesen
des Satzes gehört kann die Sprache schon darum nicht
ausdrücken weil es für jeden Satz das gleiche wäre; und
ein Zeichen das in jedem Satz vorkommen muß logisch eine bloße
Spielerei wäre. Die Zeichen des Satzes sind ja nicht
Talismane oder magische Zeichen die auf den Betrachter einen
bestimmten Eindruck hervorrufen sollen. Gäbe es philosophische Zeichen im Satz so müßte ihre Wirkung || Funktion eine solche unmittelbare sein. |
Darum kann die Sprache nur den
Plan ausdrücken nicht seine Anwendung. Und die
Logik nur den Plan untersuchen. |
Denken heißt einen Plan machen
& mit ihm arbeiten. Aber was macht den Plan zum
Plan? Was unterscheidet ihn von einem
beliebigen Gekritzel? Was ich mit ihm
vorhabe. Aber was hast Du mit ihm vor?
– Es folgt ein weiterer Plan. – Nein, zu
dem Plan gehört noch die Regel der
Anwendung || Übersetzung,
|
Die Sprache duldet keine
Verzierungen, keine psychologischen Hilfen. |
Ihre Anwendung kann die
Sprache nicht vorwegnehmen. |
„Wissen was der Fall ist, wenn der Satz wahr
ist” kann nur heißen, die Regel kennen
nach der er zu kontrollieren ist. – Aber wie ist es
ausgedrückt daß er nach dieser Regel zu
kontrollieren ist? Die Regel ist ja dem Satz nur
beigegeben, aber wo ist ihre Anwendung auf den Satz
dargestellt? Wo aber immer sie dargestellt
wäre, da durch ein anderes || weiteres Bild,
& so kämen wir in einen endlosen
Regreß
(hinein).
Aber wie kann man da von Darstellung reden, & wozu diese Darstellung? Wir müssen doch endlich zur Anwendung kommen! |
Ich mache mir einen Plan um nach
ihm || danach zu gehen. Der Punkt
 (ist meine gegenwärtige
Stellung) || bin ich, wo ich jetzt
stehe. So ein Plan ist offenbar ein nützliches
Instrument. Und das rechtfertigt eine
Untersuchung seiner
(ist meine gegenwärtige
Stellung) || bin ich, wo ich jetzt
stehe. So ein Plan ist offenbar ein nützliches
Instrument. Und das rechtfertigt eine
Untersuchung seiner
|
Insofern jeder Satz ein Plan ist
& man mit einem Plan einen Plan nicht erklären
kann, kann man keinen Plan mit einem Satz erklären.
Jede Erklärung durch einen Satz liefert – wie gesagt – einen neuen Plan & nie das Wesen des Planes. |
Man könnte auch so
sagen: Der Satz ist ein Instrument des Gedankens,
darum kann ich in den Satz nicht den Gedanken fassen. |
Die Sache
ist solange nicht völlig geklärt als noch eine Unbefriedigung über die Grenze des
Ausdrucks vorhanden ist. || &
diese nicht vielmehr die Befriedigung bringt. – Denn
es |
Einem Plan
folgen ist wesentlich dieselbe Tätigkeit wie eine
Projektion (Übersetzung) nach
einer bestimmten Regel zu kontrollieren. |
Ich kontrolliere den Plan
nach der Regel. Ich verbinde durch meine
Tätigkeit die Regel mit dem Plan. Wenn ich also sagte,
die Regel werde dem Plan sozusagen ohne ein verbindendes Wort
beigegeben, so soll es in Wirklichkeit
heißen: die Verbindung der Regel mit dem Plan wird durch die
Anwendung der Regel auf den Plan gemacht. || hervorgebracht. || kommt durch die Anwendung
der Regel auf den Plan zu Stande. |
„Kontrolliere
die rechte Zahlenreihe, die Zahlen sollen immer die Quadrate der
Zahlen der linken Reihe sein”.
Oder: „bilde eine Reihe von
Zahlen die die Quadrate der linken Zahlenreihe sind”. Das Wesentliche ist hier, daß die
Regel unabhängig von den beiden Reihen gegeben
ist. Und genau so kann ich sagen: „sieh nach ob diese Reihe von Figuren die
orthogonalen Projektionen jener
Figuren sind”.
Wenn ich einen Plan mache, oder |
Das ist auch das Wesen der Vorlage (Zeichenvorlage) &
man kann den Satz || Befehl als Vorlage
auffassen. |
Der Satz ist als Richter hingestellt
& wir fühlen uns vor ihm verantwortlich. |
2.
Auf die Frage „was ist mit diesem Plan
gemeint” durfte nicht ein anderer Plan
zur Antwort kommen sondern etwas was die Beziehung
zu dem Anderen offen läßt wie sie ja sein
muß da es ja fraglich ist ob sie befriedigt
wird oder nicht. Dies was die Beziehung offen
läßt ist die Regel der Übersetzung. |
Und es
ist klar daß der Plan zusammen mit der Regel der
Übersetzung die nötige Multiplizität
gibt || hat; das zeigt sich einfach dadurch, daß ich
jemandem zur Kontrolle nur diese beiden Sachen geben
brauche. |
Nun könnte man sagen:
Es ist Damit aber würde wieder ein neuer Plan erzeugt, der der Erklärung so bedürftig wäre wie der erste. |
Die Antwort aber scheint zu sein: Du
kannst die Sprache (als solche) dem Anderen nicht
erklären, d.h. ihn durch einen Satz
zwingen sie in einer bestimmten Weise zu gebrauchen.
Hier ist quasi die Funktion der Erklärung
mißverstanden. |
Denn, wenn
ich den Plan verstehe, so geht das || es nicht
so vor sich daß ich über ihn einen Gedanken
denke. |
(Das Wesen der Erklärung
erklären wollen, geht nicht.) |
Sondern daß || indem ich
die Wirklichkeit durch den Plan ansehe. |
Ich möchte sagen: einen Plan
verstehen muß schon heißen ihn anwenden.
D.h. ihn als Plan verstehen heißt schon nach ihm handeln, ihm nachhandeln. |
Der Plan den ich gezeichnet habe, um später nach
ihm zu gehen ist für mich nicht irgend eine Zeichnung auf
einem Stück Papier. Wie unterscheidet er sich für
mich von irgend einem Fetzen
(Papier)?
|
Durch seine Beziehung auf etwas anderes. Aber da das
Ereignis dessen Plan er ist nicht stattgefunden haben muß
so kann er darauf nicht zeigen, sondern nur auf Gegenstände die
vorhanden sind ob dieses Ereignis stattfindet oder nicht.
Gegenstände die ihm seinen Sinn gestatten nicht
die ihn wahr machen. Aber diese Gegenstände
zusammen mit dem Plan || der Zeichnung machen auch
nicht einen Plan, denn die Beziehung nach außen die für
ihn wesentlich ist richtet sich gerade auf das Eventuelle, das
Unbestimmte. |
Der Plan kann
(also) nur
seine Fühler ausstrecken bis dorthin wo das Ereignis eintrifft
oder nicht eintrifft. Und das verlangende
Ausstrecken ist es was wir im Plan als Plan verstehen.
|
Dieses || Das Verlangende besteht darin daß
der Plan nicht abgeschlossen ist (keine
Tatsache); denn |
Der Plan
ist als Plan daher nicht zu beschreiben.
|
[Das muß sich alles
hausbacken darstellen lassen.] |
Der Plan ist als Plan etwas
Unbefriedigtes.
(Wie der Wunsch, die Erwartung, die Vermutung u.s.f.) |
Ich möchte manchmal mein Gefühl dem Plan gegenüber
als eine Innervation bezeichnen. Aber auch die
Innervation an sich ist nicht
unbefriedigt, ergänzungsbedürftig. |
Ich sollte glauben das
wird || würde sich so zeigen daß, wenn
ich vom Plan rede, ich die Ergänzung irgendwie vornehmen
muß. |
Es ist eben etwas anderes, einen
Plan haben & von einem Plan reden. |
(Die Methode zu
philosophieren ist sich wahnsinnig zu machen, &
den Wahnsinn wieder zu heilen.) |
Wenn ich die beiden Gegenbilder
& die Regel der Übersetzung gebe
|
Ein deutscher Text, ein englischer Text, das
englisch-deutsche Wörterbuch.
Freilich wenn ich will daß jemand die Texte mittels des
Wörterbuches vergleicht so drücke ich
ihm die drei Dinge nicht wortlos in die Hand sondern sage etwas dazu
aber alles was er zu seiner Tätigkeit
braucht, die einzigen Utensilien sind die Texte & das
Wörterbuch; was ich dazu sage mag ihn veranlassen es zu tun aber
es hilft ihm dabei nicht. Wenn er den Vergleich
ausführt so macht er von jenen „verbindenden”
Worten keinen Gebrauch. |
Auch so: Wenn man nach einer
Regel einen Tatbestand abbildet so ist dieser
dabei die Vorlage. Ich brauche keine weitere
Vorlage die mir zeigt wie die Abbildung vor sich zu gehen hat, wie
also die erste Vorlage zu benutzen ist, denn sonst
brauchte ich auch eine Vorlage um mir die Verwendung || Anwendung der zweiten zu zeigen u.s.f.
ad infinitum. D.h. eine
weitere Vorlage nutzt mich nichts, ich muß ja doch einmal ohne
Vorlage handeln. |
Ich kann meine Tätigkeit dahin verschieben daß ich statt
von der einen Vorlage von einer anderen abzeichne,
aber das ist auch alles. |
Ich kann
also den Gebrauch der Vorlage an
sich an einer Vorlage nicht zeigen. Nicht einen
Plan machen der nur zeigen soll wie ein Plan
(im allgemeinen || allgemein) zu gebrauchen sei.
|
Auch verbindet die zweite Vorlage die erste
Vorlage mit der Regel nicht, denn es fehlt immer das letzte
Glied. Das nur die Anwendung geben kann.
|
Man könnte auch so sagen:
Eine Zeichnung ist nicht darum ein Plan weil einer einmal –
durch Zufall – so gegangen ist
daß sein Weg dem Plan entsprochen hat, sondern weil er
dem Plan nach einer bestimmten Regel nachgegangen
ist. Übrigens entspräche ja
sonst jeder Weg dem Plan (nach irgendeiner
Regel).
D.h.: Der Plan ist nur Plan nach einer bestimmten Regel. Erst Zeichnung & Regel machen einen Plan. |
Der Symbolismus kann nichts
Das aber ist die Schwierigkeit beim Verständnis des Zeichens || der Bezeichnungsweise für die Negation. Der Symbolismus darf für nichts wesentliches (bloß) einen hint geben darf nichts wesentliches bloß andeuten, wie man jemand stupft || anstößt um ihn an etwas zu erinnern. Aber dieses Stupfen || Anstoßen kann doch nur dann verstanden werden wenn die Sache vorher schon ausführlich besprochen wurde. Und so darf uns der Symbolismus nur stupfen wenn uns das nur etwas ins Gedächtnis rufen soll was er uns schon vorher dargestellt hat. (Eine Definition ist so ein Stupfer.) |
3.
Wir können den Plan
von seiner Negation unterscheiden.
Ich meine: Wir haben was den Plan & seine
Negation anbelangt sozusagen absolutes
Gehör. Sie erscheinen
uns nicht nur als entgegengesetzt wenn wir sie mit einander
konfrontieren. |
Heißt das nicht
folgendes: Der Satz wird nicht gebildet aus dem Bild, der
Projektionsregel & einem vorgesetzten
+ oder
‒ (ja oder nein) denn
sonst könnte man +
& ‒ nicht
absolut von einander unterscheiden.
Ist das aber wahr? Es gelten doch andere Regeln von + als von ‒ ( ‒ ‒ = + aber + + ≠ ‒ ). D.h. Ja und nein sind nicht einfach entgegengesetzt wie rechts & links, absolut genommen aber dasselbe. Der Satz besteht also nicht aus Bild, Projektionsregel & einer daran angebrachten Scheibe mit einem Pfeil die man entweder nach rechts oder nach links stellen || drehen kann. |
Analoges wie von „ja”
& „nein” gilt von „wahr” & „falsch”.
Ja & Nein verhalten sich nicht wie rechts & links sondern wie Umkehren zu Lassen-wie-es-ist. D.h. wie Wenden zu Nicht-Wenden || Stehenbleiben, nicht wie Rechtswenden zu Linkswenden. |
‚p’
ist wahr = p. Man
gebraucht das Wort „wahr” in
Zusammenhängen wie „was er sagt ist
wahr” das aber sagt das selbe wie
„er sagt ‚p’,
& p”. |
Da das
„ja”
anzeigt daß alles so bleibt wie es ist, so kann man es ganz
weglassen. Man kann also „ja p”
durch „p”
erstatten || ersetzen; dagegen kann man nicht „~p” durch „p”
ersetzen & „p”
durch „~p” ersetzen, denn wie wollte man dann die Verneinung wieder
verneinen & die Bejahung
erhalten? |
Das Wesen der Verneinung erklären ist so
unmöglich als das Wesen des Satzes erklären. |
Die
Erklärung ‚~p’ ist wahr für den Fall wenn || in welchem ‚p’
falsch ist, wäre identisch mit der
Erklärung daß, ‚p ⌵ ~p’ kein sinnvoller Satz sondern eine Tautologie
ist. |
Denken heißt
Pläne machen. |
Ist die Verneinung ein
Zusatz zum Plan? d.h. besteht
der neue Plan jetzt aus dem Bild, der
Projektionsregel und der
Verneinung? Oder hat die Verneinung
(etwa)
die Projektionsregel
geändert? |
Die Verneinung
verbindet sich mit dem verneinten Plan & der
verneinte kommt als Plan nicht im neuen Plan
vor, || :
d.h., wenn ich
~p glaube so glaube
ich dabei nicht zugleich p weil
p in
~p vorkommt.
|
Es wäre charakteristisch für eine bestimmte irrige
Auffassung, wenn ein Philosoph glaubte einen Satz mit roter Farbe
drucken lassen zu müssen da er erst so ganz das
ausdrücke was der Autor sagen wolle.
(Hier hätten wir die magische Auffassung
der Zeichen statt der logischen.)
(Das magische Zeichen würde wirken wie eine Droge, & für sie wäre die Kausalitätstheorie richtig. || völlig zureichend.) |
Das worauf es ankommt ist die
interne Beziehung der Pläne „~p” und „p”. Es2 ist klar, wenn ich den Plan ~p habe so habe ich nicht auch den Plan p insofern also kommt der Plan p im Plan ~p nicht vor. Anderseits zeigt das Vorkommen von ‚p’ in ‚~p’ & noch klarer ~(~p) = p den Zusammenhang. |
p kommt in
~p in
(genau)
demselben Sinne vor wie ~p in
p. |
Die Worte „vorkommen”
etc. sind eben ambig || unbestimmt wie alle solche Prosa.
Exakt & unzweideutig &
unbestreitbar sind nur die grammatischen
Regeln die am Schluß zeigen müssen worum
es sich handelt. || was gemeint ist. |
Sie sind der letzte & einzige
Ausdruck dafür wie es sich wirklich verhält
(d.h. was es logisch || in der
Logik für eine Bewandtnis hat.) |
Ich zeichne einen Plan (wie ich gehen
will) & schreibe das Verneinungszeichen dazu;
aber das nützt nichts solange man nicht weiß, daß es das
Verneinungszeichen ist. Aber wie kann man
|
„Wie ich einen Körper durch seine
verschiedenen Ansichten geben kann
& er mit diesen ⋎ äquivalent ist, so
offenbart sich die Natur der Negation in den verschiedenen
grammatisch erlaubten Anwendungen des
Negationszeichens.” |
„Was
hilft es daß als Negationszeichen nur ein Haken vor dem Satz
p steht, ich muß ja
doch die ganze Negation denken.” |
Eine Projektionsmethode mag einen Punkt in einen Kreis projizieren aber die Komplikation dieser Projektionsmethode wird sich offenbaren wenn man nun alle die || die Gebilde durchgeht die sie in einander verwandelt. |
Wenn ich z.B. sage ich gehe nicht diesen Weg so stimmt damit überein daß ich jenen anderen Weg || alle jene anderen Wege gehe (& daß ich einen Weg gehe verträgt sich nicht damit daß ich einen anderen gehe) & so zeigt es sich was das ‚nicht’ bedeutet. |
Aber eines ist doch klar daß
|
Und zeigt sich auch diese
Verschiedenheit endgültig nur in der
Grammatik? |
Das
„nein”
wäre ein Stoß um uns zu erinnern „Du, das ist eine Negation”. |
Das Zeichen „~” deutet an, Du sollst das was folgt negativ
auffassen. |
Es deutet
an heißt, daß das nicht der letzte sprachliche Ausdruck
ist. Daß das nicht das Bild des Gedankens ist.
Daß mehr in der Negation ist als das. |
Die
Erklärung eines Zeichens ist
sofort ein Zeichen. Denn sie
könnte doch nur darin bestehen, daß sie
den Gedanken genauer darstellt … || als
jenes Zeichen. |
Was ist
der Unterschied zwischen dem Schachbrett & einer
Schachfigur? Es ist die Anwendung gänzlich anderer Art. (Denke an das einander Aufheben der Operationszeichen ~, ⌵ etc. was sonst nie vorkommt.¤ |
4. |
Das Zeichen hat nur
einen Zweck uns etwas mitzuteilen. Eine || ; eine Erklärung
des Zeichens kann also nur diese Mitteilung
verdeutlichen, (die
Erklärung) ist also selbst nur ein
Zeichen statt des ersten. Eine Erklärung des Zeichens der Negation muß also selbst nur eine grammatische Auseinanderlegung der Negation sein. |
Ich will sagen, man kann ein
Zeichen in gewissem Sinne nicht erklären. Es
muß in den Regeln seiner Anwendung für sich selbst
sprechen. Und alles sagen was sich
überhaupt
(Erklärendes)
|| Verdeutlichendes sagen
läßt. |
Könnte eine Erklärung die
nicht zur Grammatik gehört etwas Wesentliches über die
Negation etwa sagen so müßten wir gerade dieses
Wesentliche im Gebrauch des Zeichens entbehren.
– Es würde dann das Sachliche nicht genügen
& das Unsachliche enthielte
|
Die Sprache hat nur einen Zweck, ihre
Anwendung; – ist diese durch die Grammatik fixiert,
so kann es nichts mehr Wesentliches über sie
zu sagen geben. |
Eine
Sprache muß dafür sorgen, daß sie verstanden werde;
die || eine Erklärung ist ja auch nur
Sprache & kann sie besser verstanden
werden als die erste dann ist sie eben der bessere Ausdruck.
für das erste. || und
kann sie sich besser verständlich machen als die erste,
so ist sie eben die bessere Sprache. |
So ist es auch zu begreifen daß die
Fregesche Erklärung der
Wahrheitsfunktionen von mir nur auf ein Schema
gebracht eine neue Notation der
Wahrheitsfunktionen ergeben. |
Vergleich der verschiedenen Arten von Linien || der Linien mit verschiedenen Funktionen auf der
Landkarte mit den Wortarten im Satz. Der Unbelehrte sieht
eine Menge Linien & weiß nicht, daß sie sehr
verschiedene Bedeutungen haben. |
Das Negationszeichen
veranlaßt uns zu etwas. Aber wozu? und
wie? Sie veranlaßt uns nur zu etwas, |
Man
hat das Gefühl, die Negation veranlasse || veranlaßt uns
nur zu etwas, was aber viel komplexer ist als das Signal. Und das ist (ja) wahr, der Haken ~ vor dem Satz ist es nicht, der uns die Negation erklärt. Der uns erklärt was wir machen sollen. (Er hat eben nicht die nötige Multiplizität.) |
Denn der
Symbolismus muß sich selbst erklären. |
Auf die
Frage „was bedeutet
das”, muß es eine Antwort geben, oder
die Frage ist unsinnig. Da aber zur
Antwort immer wieder ein Zeichen kommt so ist sie immer eine || hat sie die Form einer Definition & gehört also
zur Grammatik. |
Ich sage, die Verneinung ist nur eine
Veranlassung, um etwas viel Komplexeres zu
tun; aber was? Läßt sich die Frage nicht
beantworten (und die eine Negation durch eine andere zu
ersetzen || das eine Symbol der Negation durch ein anderes
zu ersetzen ist keine Antwort) so ist sie
unsinnig & dann ist
es auch jener erste Satz. || auch jener erste Satz
unsinnig. |
Es ist als veranlaßte uns das „~” zu
etwas, aber was, das wird scheinbar nicht
gesagt. Es ist, als brauchte es nur angedeutet werden, als
wüßten wir es schon. Als
wäre eine Erklärung jetzt unnötig, da wir die Sache
ohnehin schon kennen. Nun könnte man sagen || sogar sagen, die Erklärung liegt in extenso in allen Anwendungen, in den grammatischen Regeln (die übrigens – was das „alle” erklärt – eine induktive Regel enthalten). |
Das ist
doch ganz klar, daß die Regeln das Wesen der Negation
wiederspiegeln (da sie für ein Zeichen anderer
Bedeutung nicht gelten). Die Frage ist nur,
spiegeln sie es ganz wieder, oder lassen sie
auch || noch einen
Spielraum, so daß das Zeichen wovon diese Regeln gelten zwar
manches andere nicht, aber doch noch manches andere darstellen
könnte, daß zum mindesten nicht alles gesagt
ist. Denn, wohlgemerkt, gesagt muß es werden können, denn sonst ist alles gesagt. Hat die Sprache alles gesagt, was zu sagen war, so hat sie alles gesagt. |
Gäbe es
eine explizitere Ausdrucksweise der Negation, so
müßte sie sich doch in die andere abbilden lassen &
|
Die Grenze der Sprache kann ich
eben in der Sprache nicht ziehen. |
Ich
kann eben nicht die ganze Sprache in meine Untersuchung einbegreifen;
& dann dennoch außerhalb ihr || dieser in der
Sprache stehen.
|
Wenn ich die ganze Sprache in meine Untersuchung einbegreife so kann ich nicht außerhalb der Untersuchung in der Sprache Fuß fassen. |
Wenn unser Symbolismus die ganze
Sprache einbegreift dann ist kein Raum mehr in ihr für
die || eine Erklärung des
Symbolismus. Hier haben wir die Grenze der Sprache erreicht. |
5. Erinnern
wir uns, daß in der Sprache nur die logische Multiplizität
|
D.h. Es darf nichts geben
was die Sprache nur andeutet, der Gedanke aber ausführt.
Denn der Gedanke ist selbst nur eine angewandte
Sprache. |
Gedanke & Sprache || Sprache &
Gedanke verhalten sich nicht wie Signal & Ausführung
des signalisierten Befehls. Denn in diesem Falle
gibt es ja noch eine ausführlichere Erklärung auf die sich
das Signal (gleichsam durch Definition) bezieht.
Während im Fall Sprache & Gedanke die
ausführliche Erklärung ja
selbst zur Sprache gehört. So daß, wo es
überhaupt eine
Auseinanderlegung || Ausbreitung gibt die selbst zur Sprache gehört &
wo es in der Sprache keine gibt überhaupt von keiner die Rede
sein kann & also auch nicht von einem
Signal. |
Nun kommt
es aber vor daß die Wortsprache zur Mitteilung nicht
genügt. Wenn ich z.B.
jemand eine Farbe wie ich sie mir denke mitteilen will so muß ich
ihm wenn es ein bestimmter Farbton ist ein Muster dieser
|
Der Gedanke ist kein geheimer –
& verschwommener – Prozeß
von dem wir nur Andeutungen in der Sprache sehen, als wäre
die Negation ein Stoß & der Gedanke darauf wie
ein unbestimmter Schmerz, von diesem Stoß hervorgerufen aber
gänzlich von ihm verschieden. |
(Nichts ist wichtiger als die falschen Gedanken ganz ans Licht
zu ziehen & absolut richtig || getreu
& handgreiflich darzustellen || wiederzugeben.) |
Nun
wäre aber die Frage: wie zeigt sich das uns bekannte
Spezifische der Negation in den Regeln die
vom Negationszeichen gelten. Daß
z.B. ein gezeichneter Plan eines Weges ein Bild
des Weges ist verstehn wir ohne
weiteres, wo sich der gezeichnete Strich nach links biegt, biegt
sich auch der Weg nach links etc.
etc. Daß aber das Zeichen „nicht” den Plan
ausschließt sehen wir nicht. Eher noch wenn wir etwas
Ausgeschlossenes |
Man denkt
da leicht an die Regel daß
~p ∙ p keinen
sinnvollen Satz ergibt. Und in der
W-F-Notation ist die Sonderstellung dieser
Zeichenkombination besonders klar. |
Wie ist es aber damit: || mit diesem Gedanken: Wenn
~p ein Bild sein soll,
wäre, was es bedeutet da nicht am besten dadurch
darzustellen daß das nicht der Fall ist was
symbolisch p || , daß
p der Fall ist,
darstellt. Es ist aber klar daß so ein Symbolismus
nicht arbeitet || funktioniert. (Das
scheint mit eine wichtige Sache zu sein.)
Nicht sagen, daß p der Fall ist, heißt nicht, || : sagen, daß p nicht der Fall ist. |
Ist es nicht aber doch manchmal so,
wenn man zum Beispiel sagt „keine Antwort ist auch eine
Antwort”? Oder wenn der Arzt
nicht sagt daß die Krankheit gefährlich ist &
man daraus schließt er habe gemeint sie
sei nicht gefährlich. – Oder
wenn man keine Tafel „verbotener Weg” sieht & sagt, das heißt, daß der Weg nicht
verboten ist. („Was nicht
verboten ist, ist erlaubt.”) |
Es ist keine
Erklärung zu sagen (was ich einmal sagte) ein solcher
negativer Symbolismus ginge schon er sei nur darum nicht zu
brauchen weil man durch ihn nicht wissen könne
was verneint sei. Dann ist er eben kein
Symbolismus der Negation wenn er uns nicht das
Nötige mitteilt. Und dann fehlt
es ihm an etwas Wesentlichem. Es hat ja (auch) seinen Grund warum in gewissen Fällen der negative Symbolismus geht, & keine Antwort auch eine Antwort ist. In diesen Fällen ist eben die Bedeutung || der Sinn des Schweigens eindeutig festgelegt || bestimmt. |
Das hängt
(natürlich)
damit zusammen, daß die Wörter unserer Sprache die
Worttypen, nicht die Schriftzüge,
individueller Wortexemplare, sind. So
entspricht ¤ der
Zeichenverbindung aRb nicht als Gegensatz eine
Tatsache daß „a”
& „b”
nicht zu beiden Seiten von „R”
stehen. |
Im negativen Satz wird das Bild
(der Plan) anders gebraucht als im positiven,
dadurch daß es ausschließend, hindernd
gebraucht wird. |
Es wird eine
andere Art Portrait entworfen, durch ein Bild, was zeigen soll, wie es
sich nicht verhält, |
Es wäre
nun die Frage, kann je ein Porträt der negativen Art das Gleiche
porträtieren, wie eins der positiven;
d.h., von dem gleichen Sachverhalt wahr
bzw. || oder falsch
gemacht werden? |
Die
Farbangabe daß etwas nicht rot ist, ist von anderer Art als die,
daß etwas rot (oder blau) ist.
D.h. sie ist nicht in demselben || dem gleichen Sinn eine Farbangabe. |
Dagegen kann die Negation eines Satzes eine
Angabe gleicher Art sein wie der negierte Satz. |
Der negative Satz schließt etwas aus
& nun kommt es auf das Gebiet an, in dem die Ausschließung
geschieht, ob das
Nicht-Ausgeschlossene von der
gleichen Art ist, wie das Ausgeschlossene. |
(Meine
Methode besteht darin immer neue Worte, wie frische
Keime || Kräfte in die
Untersuchung zu werfen.) |
Ich kann ein Bild davon zeichnen, wie zwei
einander küssen; aber doch nicht davon, wie
zwei einander nicht küssen.
(d.h. nicht ein Bild, das
bloß dies darstellt.)
|
Man kann nicht das kontradiktorische
Negative sondern nur das
Konträre zeichnen
(d.h. positiv
darstellen). |
„Sie küssen einander nicht” heißt nicht, daß davon keine || nicht
die Rede ist, sondern es ist eben davon die Rede
& wird
(nur)
ausgeschlossen. |
Das Küssen wird hier quasi
weggeworfen. Aber könnte man den Zustand dann nicht
eben so darstellen, daß eben das Küssen weggeworfen ist, also
nicht da ist. Wohl, aber dann muß man den
tatsächlichen Zustand etwa in einer allgemeinen Weise darstellen
(wenn man nämlich einen bestimmten positiven nicht darstellen
will) daß dadurch das Küssen & nur dieses
ausgeschlossen ist, & dann ist es eben durch das
Dargestellte doch wieder bestimmt. |
Wenn ich
sagen will „er ist nicht in diesem Kreis
◯”
so kann ich das freilich so darstellen, daß er irgendwo
außerhalb ist, aber dann tritt der Kreis doch wieder in der
Darstellung auf. |
Es ist also klar daß ich im
negativen Satz das intakte Bild des positiven Satzes
brauche. Wie aber bestimmt
mich das „~”, den Es müßte sich ja also zeigen, daß p und ~p Gegensätze sind. |
6.
Wenn ich die ganze Sprache in meine
Untersuchung einbeziehe, dann muß in ihr alles
erklärt sein wonach man überhaupt fragen kann, &
keine Frage nach einer Erklärung mehr
übrigbleiben. |
In dem
Zeichen ~ kann
sich die Verneinung nicht zeigen || die Verneinung nicht
liegen. „nicht” ist eben nur
eine Andeutung für die Art, wie der Satz aufzufassen ist.
Und die Natur des angedeuteten || Angedeuteten kann sich nur im
Gebrauch der Verneinung || des
Zeichens zeigen. || des andeutenden
Zeichens zeigen. || im Gebrauch der Verneinung, des andeutenden Zeichens, zeigen. |
(Denke daran daß p ∙ ~p
kontradiktorisch,
p ⌵ ~p tautologisch
ist. ~(~p) =
p, ~(~(~p))
= ~p etc.
etc.) |
„Ich habe das Stück von A bis B
bestrichen
Es trägt allerdings diese Folgerung den Charakter von etwas Konstruiertem. Als handle es sich nicht eigentlich |
Wir fragen uns nämlich:
Wenn wir denken daß wir das ganze Stück von A bis
B bestrichen haben so scheinen wir etwas
Einfaches zu denken & gar nicht
etwas, woraus dann etwa 1000 Sätze folgen könnten. – Nicht etwas was 1000 Sätze in sich
enthielte. – Wir
fühlen, wenn diese Sätze aus dem ersten folgen
dann durch eine || mittels einer
Hypothese & nicht dadurch daß sie wirklich in ihm
liegen. Ja der erste Satz als Satz genommen hat etwas Einfaches. Und wenn ich recht habe darf auch nicht ein Satz jener Art aus ihm folgen. Und so ist es auch wenn z.B. vom Gesichtsraum die Rede ist. Eine ohne Teilung gesehene weiße Fläche besteht nicht aus zwei Hälften. Denn beschriebe man sie auf die Art || in der Weise zwei Teile || Hälften zu beschreiben, so hätte man nicht die ungeteilte Fläche beschrieben. |
„Eine ungeteilt gesehene Fläche
besitzt || hat keine Teile.” |
Ich kann nun aber doch
vorhersagen: die eine || linke
Hälfte dieser weißen
(Denken wir uns eine Fläche halb weiß halb schwarz & die schwarze Hälfte wird weiß, dann verschwindet die Teilung.) |
Die normale
Auffassung vom Beispiel des Anstrichs ist dadurch
charakterisiert, daß es gleichgültig ist ob wir uns die
Striche A' &
B' schon vorhanden denken
wenn der Stab gestrichen wird oder ob wir das Stück
A'B' erst später
auf ihm abmessen. || abtragen. –
Denken wir uns || Sind die
Striche A' &
B' schon ursprünglich
vorhanden || hier dann folgt
allerdings jener zweite Satz aus dem ersten (dann ist die
Komplexität schon in dem ersten Satz
offenbar vorhanden) dann folgen aber aus dem
ersten Satz |
Wenn ich sage
„in dem Quadrat ist ein schwarzer
Fleck” so ist es mir immer als habe ich
hier wieder etwas Einfaches vor mir.
Als müsse ich nicht an verschiedene mögliche Stellungen
& Größen denken. Und doch kann man
sagen: wenn ein Fleck in dem Quadrat ist so muß er irgendwo
& von irgend einer Gestalt sein. Nun kann aber doch
auf keinen Fall davon die Rede sein, daß ich mir alle
möglichen Lagen
(etc.)
eines Flecks zum voraus denke. – In dem ersten Satz
scheine ich sie vielmehr sozusagen durch ein Sieb zu fassen so daß
„Fleck innerhalb des
Quadrats” einem Eindruck zu
entsprechen scheint für den das
Wo
etc. überhaupt noch nicht in Betracht
kommt als sei es (gegen allen Anschein) etwas was mit
jenem ersten Sachverhalt nur physikalisch nicht
logisch verbunden sei. |
(Je roher die
Bilder sind die ich mir mache, desto besser.)
|
Der Ausdruck „Sieb” kommt daher: || so in
die Untersuchung: Wenn ich etwa eine Landschaft
ansehe, durch ein Glas das nur die Unterschiede von Dunkelheit
& Helligkeit durchläßt, Die Frage ist, ist so ein Sieb denkbar? |
Von einem Sieb aber
kann hier, glaube ich, tatsächlich nicht die Rede
sein. |
7.
Wir müssen wissen was
Erklärung heißt. Es ist die ständige
Gefahr, dieses Wort in der Logik in einem Sinn verwenden zu
wollen, der von der Physik hergenommen ist. |
Es ist eine Hauptgefahr der
Philosophie dieses Wort falsch zu verstehen. |
Wenn ich sage, der Fleck liegt im
Quadrat, so weiß ich – und muß wissen – daß
es verschiedene mögliche Lagen für ihn gibt. Aber
auch, daß ich nicht eine bestimmte Zahl aller solcher
Lagen nennen könnte. Ich weiß von vornherein nicht,
wieviele Lagen „ich unterscheiden
könnte”. – Und ein
|
Das Dunkel welches
über den Möglichkeiten der Lage
etc. herrscht, ist die
gegenwärtige logische Situation. Sowie
trübe Beleuchtung auch eine bestimmte Beleuchtung
ist. |
Es kann doch nicht darauf
hinauslaufen, daß zwar nicht unendlich viele Sätze aus einem
folgen können, aber wohl einer aus unendlich
vielen. |
Es ist wichtig, daß ich den
Sachverhalt: der Kreis ist irgendwo im Quadrat, nicht
malen könnte, ohne einen bestimmten Fall zu malen, den ich aber
hier nicht meine. |
Ich möchte den Sachverhalt am
liebsten durch einen || mit einem lockeren Kreis
im Quadrat darstellen, oder dadurch, daß ich den
Kreis sozusagen ins Quadrat werfe, ohne zu zeigen wo er
hineinfällt. |
Es ist da
immer so als könnte man eine logische Form nicht ganz
übersehen, da man nicht weiß, wieviel, oder welche,
mögliche Lagen es für den Fleck im Viereck gibt.
Anderseits weiß man es doch, denn man ist von
keiner überrascht, wenn sie
auftritt. |
Aber so wäre es ja mit allem
Gesehenen. Wenn ich eine seltsame
Blume sehe, wie ich nie eine gesehen habe, so bin ich nicht über
ihre Möglichkeit überrascht, & doch
überrascht, weil ich mir dergleichen nie vorgestellt
hatte. |
Es ist als
sähe man im Speziellen das Allgemeine
& vergleiche das mit dem allgemeinen Satz, ohne auf
das Spezielle
(viel)
zu achten (das Spezielle läßt man links
liegen). Und doch ist das Allgemeine an ein
Spezielles gebunden. |
Es ist so
als artikulierte der allgemeine
Satz || Gedanke die Wirklichkeit
anders. |
Man könnte
sagen, der Satz ist immer ein Sieb (das sondert, das eine
durchläßt, das andre
zurückhält). Und dann ist eben auch
der allgemeine Satz eins. |
Es ist hier auch etwas falsch an || nicht in Ordnung
mit dem Begriff der bestimmten Lage.
|
Bestimmt ist eine Lage, wenn sie bestimmbar ist;
durch eine Angabe bestimmt ist. |
Die bestimmte Lage
im Gesichtsraum kann man nur durch graphische Bilder
angeben. Und hier kommen wir in das Gebiet der
Darstellung durch Nachahmung statt
durch eine Zeichensprache. Und
hier harren richtige Probleme.
Was ist das Wesentliche dessen, was wir nicht durch Worte darstellen können? – Aber fängt denn das nicht schon dort an, wo wir überhaupt die Vorstellung zu Hilfe nehmen müssen? Also überhaupt, wo z.B. von rot & blau gesprochen wird, auch wenn es sich gar nicht um ganz bestimmte Töne dieser Farben handelt. |
Denn die ganz entsprechenden
Fälle liegen ja auch bei dem Kreis im Quadrat vor. Ich
brauche z.B. keine Zeichnung um zu verstehen,
was es heißt, daß der Fleck in dem linken oberen Viertel des
Quadrats liegt. (Man kann auch auf eine bestimmte
Erinnerung in der Beschreibung anspielen. „Es schaut aus wie ein …”) |
„Wenn der Fleck da liegt, so liegt er
in dem Viereck”.
‒ ‒ ‒ ‒ ‒ ‒ ‒ ‒ ‒ ‒ ‒ ‒ |
In
wiefern sieht der allgemeine Gedanke hier jeden besonderen
Fall voraus? Ich sage: ich kann keine neue
Möglichkeit durch die Erfahrung lernen. |
(Das Schwere ist, das
System der Grammatik zu sehen.) |
Wir sehen auf das Bild & sehen
von den Abständen des Kreises von den Seiten ab. Sie
gelten nicht. „Auf die Lage schaue ich nicht; es kommt auf sie nicht an.” Ich möchte sie förmlich verschwimmen machen. Ja, kann denn nicht der Fleck sich wirklich im Viereck bewegen? Ist das nicht nur ein spezieller Fall vom || von dem im Viereck zu sein? Dann wäre es also doch nicht so daß der Fleck an einer bestimmten Stelle im Viereck sein muß wenn er |
Wenn einer nicht verstünde was der Satz „der || ein Kreis ist im
Quadrat” sagt, so würde man es ihm
vielleicht || etwa so
erklären: es ist entweder
so
 oder so oder so
 oder so oder so
 etc., & würde so ein paar
Stellungen des Kreises zeigen. Aber natürlich darf
diese Erklärung nur als das Geben || das Zeigen || das Aufzeigen einer
Regel aufgefaßt || angesehen werden,
ähnlich den ersten Gliedern einer formalen
Reihe.
etc., & würde so ein paar
Stellungen des Kreises zeigen. Aber natürlich darf
diese Erklärung nur als das Geben || das Zeigen || das Aufzeigen einer
Regel aufgefaßt || angesehen werden,
ähnlich den ersten Gliedern einer formalen
Reihe. |
(Ich glaube aber daß in
meiner ganzen Auffassung von der Allgemeinheit noch etwas falsch
ist.) |
Der Satz „der Fleck ist im Quadrat” hält gleichsam selbst den Fleck
bloß im Quadrat, das heißt, beschränkt
die Freiheit des Flecks nur auf diese Weise &
gibt ihm sonst || innerhalb des
Quadrats || in dem Quadrat
Freiheit. Der Satz bildet
dann einen Rahmen der die Freiheit des Flecks begrenzt & ihn
innerhalb frei läßt, |
Kann man aber nun sagen, daß
der Satz aus unendlich vielen Sätzen
folgt? – D.h. daß quasi unendlich viele um ihn herum wären || stünden || stehen deren gemeinsamer Bestandteil er ist? |
8.
(Von dem Sehen || ersten Aufscheinen eines Gedankens in der Ferne bis zum
völlig klaren Erkennen dieses Gedankens ist
es meist nicht so weit als es zuerst
scheint.) || (Von dem ersten Sehen eines Gedankens in weiter Ferne bis daß er in unserer unmittelbaren Nähe steht ) |
Daß der Satz die Wirklichkeit in einer
Beziehung frei läßt, heißt, daß er auf sie in
dieser Beziehung (d.h. sie auf seine
Wahrheit) keinen Einfluß nimmt.
Er von ihr in dieser Beziehung nichts weiß. Der
Satz hält die Wirklichkeit an einer Leine & solange diese
nicht beansprucht wird da die |
Es scheint mir alles gesagt zu
sein damit, daß der Satz „der Fleck befindet sich im
Viereck” verstanden wird. Und
damit, daß was aus ihm folgt (& das
woraus er folgt) dadurch bestimmt ist daß || wie er verstanden werde || wird || ist; nicht
dadurch || durch den Umstand ob er wahr oder
falsch ist. |
D.h. daraus
daß er verstanden wird einen bestimmten Sinn hat schöpfe ich
die Zuversicht, daß es für ihn bestimmte eben seinen Sinn
bestimmende Regeln der Grammatik gibt &
daß die Unbestimmtheit die in ihm liegt
doch einen bestimmten (seiner Natur nach bestimmten)
Spielraum definiert. – Daß seine
Folgesätze, & die aus denen er folgt, durch was
er bedeutet, nicht durch die Tatsachen bestimmt sind, das ist es
eigentlich was ich meinte || meine wenn ich
sage || auseinander setze es
gäbe darin keine Überraschungen.
Denn, wo es keine Überraschungen gibt, das ist die Grammatik, || – (das Spiel) – & ein Bild  das ich etwa von
einer zu erwartenden Situation mache gehört zu den
Zeichen, steht also unter der Herrschaft der
Grammatik. das ich etwa von
einer zu erwartenden Situation mache gehört zu den
Zeichen, steht also unter der Herrschaft der
Grammatik. |
Das hängt nun mit der
Bedeutung der „bestimmten
Lage” des Flecks im
|
Man kann dieses Bild nicht anders bestimmen
als durch sich selbst. Darum ist es nicht vielleicht eine
ungenaue Bestimmung sondern eine
exakte. |
Es ist
natürlich nicht „Stellung des
Kreises in diesem Quadrat” ein Begriff
& die besondere Stellung ein Gegenstand der unter
ihn fällt. |
(Ein Gedanke nähert sich erstaunlich schnell
von der großen Entfernung in der er zuerst auftaucht zur
unmittelbaren Nähe in der wir ihn deutlich
gewahren. || in der er deutlich vor uns
steht.) |
So daß
Gegenstände gefunden werden || würden von
denen man sich überzeugt, daß sie auch Stellungen
des Kreises im Quadrat sind von denen man aber
früher nichts gewußt hat. |
D.h. ‚Stellung des Kreises im
Quadrat’ kann kein amorpher Begriff
sein. Ich weiß auch daß, wenn zwei Stellungen verschieden sind die |
Die Mittelstellung des Kreises & andere
ausgezeichnete Stellungen sind übrigens ganz analog den
primären Farben in der Farbenskala. (Dieses
Gleichnis könnte man mit Vorteil fortsetzen.) |
Wie ist es aber mit diesem
Schluß: „Wenn ein diesem
Kreis gleichgroßer in das Dreieck hineingeht dann geht auch
jeder kleinere hinein.”? Ich kann  nämlich
noch nicht einsehn warum es nicht möglich sein sollte daß
unendlich viele Sätze nach einer Regel aus einem folgen sollten
in dem selben Sinne nämlich in dem ein Satz aus
unendlich vielen folgen
kann? || . Obwohl etwas
sagt daß es so ist, aber die
Formulierung ist nicht richtig || kann nicht richtig
sein. nämlich
noch nicht einsehn warum es nicht möglich sein sollte daß
unendlich viele Sätze nach einer Regel aus einem folgen sollten
in dem selben Sinne nämlich in dem ein Satz aus
unendlich vielen folgen
kann? || . Obwohl etwas
sagt daß es so ist, aber die
Formulierung ist nicht richtig || kann nicht richtig
sein. |
Denn wenn
daraus daß der Kreis sich im Quadrat da befindet, folgt
daß er im Quadrat ist; |
„Er folgt aus
unendlich vielen Sätzen” würde
heißen: man kann die Reihe der Sätze aus denen er folgt
ins Unendliche fortsetzen. Statt „ins unendliche” müßte man aber doch sagen „man kann sie unendlich
fortsetzen”. Aber auch das
trifft nicht ganz meine Schwierigkeit. Denn in mir wehrt
sich nicht bloß etwas dagegen daß unendlich viele Sätze aus
einem folgen sondern ebenso auch daß 1000
Sätze aus einem so einfachen Satz folgen. Ich habe es
hier überhaupt nicht mit der
Schwierigkeit der Auffassung des Unendlichen zu tun die
wie ich glaube leicht zu
überwinden ist sondern, mit einer ganz
anderen. |
Und da ist
nun allerdings klar daß aus 1000 Sätzen von der Form
Und andrerseits: Folgt aus „dieser Kreis hat im Quadrat Platz” auch nur ein Satz der Art „dieser kleinere Kreis hat darin Platz” so ist nicht einzusehen warum nicht 1000 solcher Sätze aus dem einen folgen sollen. Und somit ist die Schwierigkeit || das Problem an eine andere Stelle gerückt. |
9.
Frägt es sich nicht, ob ich
den Sinn eines Satzes ins Unendliche verdünnen kann?
Das heißt beliebig verdünnen kann.
Man kann von Verdünnung & Konzentration des Sinnes reden. |
Freilich kann man unendlich
verdünnen (das geht ja schon mit
der Disjunktion etc.) aber || Aber eben nur auf diese Weise folgen
beliebig viele Sätze aus einem, & durch die
bloße Verdünnung erfahren wir nichts
Neues. – – – |
Können wir uns eine Sprache denken, die nur mit primären
Sätzen arbeitet, und nicht mit Hypothesen?
(Könnte man sich etwa menschliche Wesen denken, die Hypothesen nicht |
Aber heißt denn das etwas, wir bilden
doch die Hypothesen nicht aus einem neuen Erkenntnismaterial, sondern
aus den Sätzen & die Sätze ohne die
Möglichkeit der Hypothesen ¤ || sind so undenkbar wie
¤ das Multiplizieren ohne
die Möglichkeit des Wurzelziehens. |
Hängt das Wesen der Hypothese
vom Zeitbegriff ab? || mit dem
Zeitbegriff zusammen? D.h.
gäbe es ohne Zeit keine Hypothesen & was heißt diese
Frage überhaupt? |
Wie drückt es sich aus, daß die Zeit zur
Phänomenologie gehört nicht aber die
Wahrheitsfunktionen? Und wie drückt es sich aus was
wir fühlen, daß nämlich die Wahrheitsfunktionen
fundamentaler sind als das Phänomenologische?
Denn, ich glaube, nur in der Grammatik muß sich
auch das ausdrücken. |
10.
Daß die
Hypothese dem Satz kein neues Material hinzufügt, sieht man auch
daraus daß eine Hypothese durch den Ausdruck
„es scheint” (oder einen ihm entsprechenden) zum Satz wird.
|
Die Grammatik wenn sie in der Form
Und in dieser müßte man – wenn ich recht habe – auch den Unterschied zwischen Phänomenologischem & Nicht-Phänomenologischem sehen. Es wäre da etwa ein Kapitel über die || von den Farben worin der Gebrauch der Farbwörter geregelt wäre; aber dem vergleichbar wäre nicht was über die Wörter nicht, oder etc. (die „logischen Konstanten”) in der Grammatik gesagt würde. Es würde z.B. aus den Regeln hervorgehen daß diese letzteren Wörter in || ⌇ bei || zu ⌇ jedem Satz anzuwenden seien (nicht aber die Farbwörter). Und dieses „jedem” hätte nicht den Charakter einer erfahrungsmäßigen Allgemeinheit; sondern der inappellablen Allgemeinheit einer obersten Spielregel. Es scheint mir ähnlich wie das Schachspiel wohl ohne gewisse Figuren zu spielen (oder doch fortzusetzen) ist aber nie ohne das Schachbrett. |
Die wichtigste Frage hier ist nur:
Kann sich der Wesensunterschied zwischen „logischen & phänomenologischen
Konstanten” auch
allein in der Grammatik zeigen? Ist hier nicht doch
Und bedenke: die Theorie sollte über die Negation & die Farbe Rot etwas sagen das ihren Unterschied klar machte? Oder soll sie bloß sagen daß hier verschiedene Arten der Interpretation von Zeichen vorlägen? Das wäre dann etwas, was mit Hilfe von verschiedenen Indexen auszudrücken wäre & wir kämen || kommen hier nur zu einer || haben hier nur eine Fortführung der Grammatik. |
Ich
will immer zeigen daß alles was in || an der Logik business ist, in
der Grammatik gesagt werden muß. |
Wie etwa der Fortgang eines Geschäftes
aus den Geschäftsbüchern muß ganz
& gar || vollständig
herausgelesen werden können. So daß
man auf die Geschäftsbücher deutend muß sagen
können: Hier! hier muß sich alles zeigen;
und was sich hier nicht zeigt gilt nicht. Denn am Ende
muß hier alles herauskommen || sich
hier alles auswirken || abspielen || sich hier alles Wesentliche
ereignen || abspielen. |
Alles wirklich
Geschäftliche – heißt das – muß sich in der
Grammatik abwickeln. |
(Eine
Modedummheit der heutigen populären Physik ist es zu
sagen daß der Raum etwa || – sagen wir –
eines Eisenwürfels nicht wie der Laie glaubt ganz oder
beinahe ganz von Materie erfüllt sei sondern daß er vielmehr
beinahe leer sei da die Elektronen im Vergleich zu ihren
Abständen
von einander winzig klein seien. In Wahrheit aber wäre
die Ansicht des Laien natürlich gerechtfertigt
wie klein immer man die Elektronen annimmt denn
dem Erfülltsein des Raumes mit Materie im
gewöhnlichen Sinn, dem erfahrungsmäßigen
Erfülltsein, entspricht in der physikalischen
Hypothese gar nicht das Erfülltsein mit
Elektronenmasse sondern die Häufigkeit der
Elektronen.) |
Was ich die ‚Ansicht dieses Gegenstandes von
hier’ nenne gehört auch noch
zur Hypothese d.h. zur
Darstellung. D.h. der Körper mit seinen verschiedenen Ansichten von den verschiedenen Stellen des Raumes oder mit der Regel wie diese zu konstruieren sind ist alles die Hypothese. D.h. die Hypothese ist ein System  um das Polygon
liegen & deren richtiges oder falsches Abbild das Polygon
ist. um das Polygon
liegen & deren richtiges oder falsches Abbild das Polygon
ist. Das beste Gleichnis für jede Hypothese & selbst ein Beispiel ist ein Körper mit seinen, nach einer bestimmten Regel konstruierten Ansichten aus den verschiedenen Punkten des Raumes.  Die Punkte A muß man sich durch ein
Koordinatensystem bestimmt denken.
Die Punkte A muß man sich durch ein
Koordinatensystem bestimmt denken.
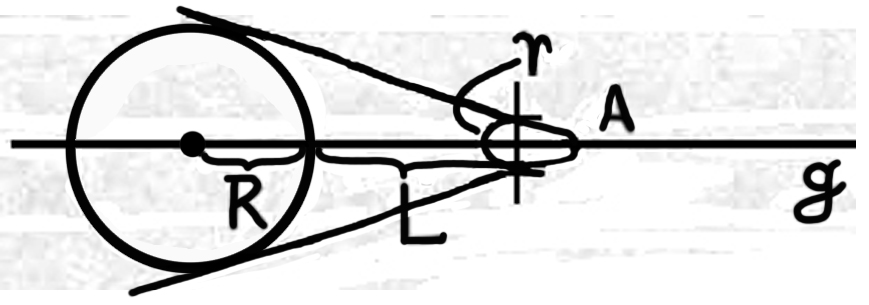 p =
p =
a = 1, 2 R = D p =
|
11.
Man weiß || denkt gar nicht, wie
merkwürdig das 3-dimensionale Sehen ist. Wie
sonderbar || seltsam etwa ein Bild, eine
Photographie, aussähe, wenn wir im Stande wären,
sie als Verteilung grauer, weißer & schwarzer Flecken in
einer ebenen Fläche zu sehen. Was wir sehen, würde dann ganz sinnlos wirken. Ebenso wenn wir mit einem Auge flächenhaft sehen könnten. Es ist z.B. gar nicht klar, was geschieht, wenn wir mit zwei Augen die Gegenstände || Welt plastischer sehen als mit einem. Denn sie wirken auch mit einem gesehen schon plastisch. Und der Unterschied zwischen Relief & Rundplastik ist auch keine richtige Analogie. |
Es
scheint mir daß die Hypothese nicht notwendigerweise
etwas mit der Zeit zu tun haben muß, außer insofern
als alle Sätze etwa Zeitliches
behandeln. |
Aber ist das wahr? Und wenn, was ist das für eine
Allgemeinheit? Warum ist dann die Zeit in der Logik nicht
fundamental wie die Wahrheitsfunktionen? – Ist
es denn wahr daß die Zeit in alle Sätze
eintritt? – Da
Das heißt: jeder || Jeder Sachverhalt ist ein Ereignis. |
Nun scheint aber doch,
wenn ich etwa sage, „der Himmel
ist blau” & von allem
Hypothetischen darin || daran absehe,
die Zeit hier wenigstens nicht explizit
vorzukommen. |
„Wahr” & „Falsch” || „wahr”
& „falsch” sind tatsächlich nur Wörter einer bestimmten
Notation der Wahrheitsfunktionen. |
(Wenn ein Problem lebhaft
auftritt || auftaucht, so ist immer schon viel
gewonnen.) |
Ich sage
„wenn ich von allem Hypothetischen
absehe” denn daß die Zeit in der
Hypothese eine Rolle |
Ich
glaube, ich könnte auch so
fragen: Kann man tatsächlich jeden Satz sinnvoll ins
Futurum & Perfektum
setzen? (Die mathematischen
Sätze natürlich
nicht.) |
Und wenn das der
Fall ist, wie kommt es, daß es uns beinahe wie eine
Zufälligkeit erscheint, verglichen mit den Regeln
über die Negation & Disjunktion? |
Negation & Disjunktion möchten wir sagen hat mit
dem Wesen des Satzes zu tun die Zeit aber nicht sondern mit seinem
Inhalt. Wie aber kann es sich in der Grammatik zeigen daß Etwas mit dem Wesen des Satzes zusammenhängt & etwas anderes nicht, wenn sie beide gleich allgemein sind? Oder sollte ich sagen die geringere Allgemeinheit wäre auf seiten der Zeit da die mathematischen Sätze negiert & disjungiert werden können aber nicht zeitlich sind. Ein Zusammenhang ist wohl da wenn auch diese Form die Sache darzustellen irreführend ist. |
Aber es ist merkwürdig daß es
in der Grammatik eine wesentliche & eine
unwesentliche Allgemeinheit geben sollte.
Eine phänomenologische & eine logische. Aber wie || worin unterscheiden sich die von einander. |
Wie unterscheidet die Grammatik zwischen
Form || Satzform &
Inhalt? Denn dies sollen ja grammatikalische Unterschiede
sein. Wie sollte man sie beschreiben können,
wenn sie die Grammatik nicht zeigt?
Was hat es mit dem Schema „Es verhält sich so & so” für eine Bewandtnis? – Hier deutet „Es verhält sich” die Satzform an & „so & so” steht für den Inhalt. – Man könnte auch sagen daß „es verhält sich” ist die Handhabe für den Angriff der Wahrheitsfunktionen. |
Meine Theorie kommt darauf hinaus, daß man die Sprache
|
„Es
verhält sich” ist also nur
ein Ausdruck aus einer Notation der
Wahrheitsfunktionen. Ein
Ausdruck, der uns zeigt welcher Teil der Grammatik hier in
Funktion tritt. |
Die Grammatik
ist das Geschäftsbuch || die
Geschäftsbücher der Sprache; woraus || aus
denen alles zu ersehen sein muß, was nicht Gefühle
sondern harte Tatsachen || Fakten
(betrifft) || betrifft sondern harte
Tatsachen || Fakten. |
Ich will also
eigentlich sagen: Es gibt nicht Grammatik &
Interpretation der Zeichen. Sondern soweit von einer
Interpretation, also von einer Erklärung der Zeichen, die Rede
sein kann, soweit muß sie die Grammatik selbst besorgen.
Denn ich brauchte nur zu fragen: Soll die Interpretation durch Sätze erfolgen? Und in welchem Verhältnis sollen diese Sätze zu der Sprache stehen die sie schaffen? |
Jene
zweifache Art der Allgemeinheit wäre so seltsam,
wie wenn von zwei Regeln eines Spiels die beide gleich
ausnahmslos gelten die eine als die fundamentalere
angesprochen würde. |
Man könnte auch so
fragen: Ist ein nicht negierbarer Satz schwerer zu denken
als ein zeitloser? – Ist es leichter das
Phänomenologische anders zu denken als das
Logische? Oder ist das Hindernis das eine zu denken ein andres als das Hindernis das andre zu denken? Aber gibt es denn einen für uns zählenden Unterschied zwischen Unsinn & Unsinn? |
12.
Wie ist das richtig in Worten
wiederzugeben was ich deutlich als den Unterschied zwischen
inhaltlicher & formaler Logik im Satz
empfinde. (das sind noch
immer nicht die richtigen Ausdrücke || ist noch immer nicht der
richtige¤ Ausdruck.) Der
Unterschied zwischen der Logik des Inhalts & der Logik der
Satzform überhaupt. Das Eine erscheint gleichsam bunt
das Andre || andre matt. Das eine handelt von dem was
das Bild darstellt das andre ist wie der Rahmen des Bildes ein
Charakteristikum der Bildform. |
Es ist nämlich als könnte
man sagen, die Zeit habe zwar mit dem Wesen des Satzes
nichts zu tun, |
Nun
ist es allerdings || aber merkwürdig,
daß die Zeit von der ich hier rede nicht die im physikalischen
Sinne ist. Es handelt sich hier nicht um eine
Zeitmessung. Und es ist verdächtig daß etwas was
mit einer solchen Messung nichts zu tun hat, in den
Sätzen eine ähnliche Rolle spielen
soll, wie die physikalische Zeit in den Hypothesen der Physik.
|
Auch unbegreiflich ist es, daß die Zeit wenn sie zum Wesen der Wirklichkeit gehört, || im Wesen der Wirklichkeit liegen soll, nicht offenbar
zum Wesen des Satzes gehören soll || , wenn das
Wesen der Wirklichkeit in ihr liegt, nicht offenbar
zum Wesen des Satzes gehören soll
. |
Das schaut
so aus als könnten wir doch aus unserer Welt heraus, wenn auch
nicht aus der Logik der Satzform so doch aus der
phänomenologischen
Begrenzung. |
Zum
mindesten scheint eine Frage |
Es ist
offenbar, daß der Charakter des Zeitlichen in
der Bedeutung der Wörter „früher”
& „später”
etc. liegt. In der Reihe
die so gebildet wird. Und es frägt sich ob wir jedes
Erlebnis als Glied der Reihe erleben. – Auch die Dauer
scheint mir nicht in jedes Erlebnis unmittelbar
hineinzuspielen. |
Man könnte
sagen, es handelt || handle sich um die Wörter „früher”
& „später” einerseits & „nicht” &
„oder”
andrerseits. Und was wir sehen wäre, daß
nicht notwendigerweise überall wo diese
|
Denn wie || Wie offenbart sich die
Zeitlichkeit der Tatsachen, wie drückt sie sich aus, als dadurch,
daß gewisse Ausdrücke || Wendungen || Ausdrücke in
den || unsern Sätzen vorkommen
müssen. D.h.:
Wie drückt sich die Zeitlichkeit der Tatsachen
aus, als grammatisch?! |
Die Sprache
kann nicht durch eine Erklärung gelehrt werden. |
Da Zeit
& Wahrheitsfunktionen so verschieden schmecken &
da sie ihr Wesen allein & ganz in der Grammatik
offenbaren, so muß die Grammatik den verschiedenen Geschmack
erklären. |
Das eine schmeckt nach Inhalt, das
andre nach Darstellungsform. |
Sie schmecken so verschieden, wie der
Plan & der Strich durch den Plan. |
Ich glaube daß das gegenseitige sich || gegenseitig sich Aufheben von
Wahrheitsfunktionen ihr wesentliches
Merkmal ist. |
Aber noch eines: Es
spielt doch die Wirklichkeit außerhalb des Zeichens in dem
Symbol mit & denken wir daran ob nicht
|
Wenn man
sagt, ein Satz sei alles was wahr oder
falsch sein könne so heißt das dasselbe wie:
Satz ist alles was sich verneinen läßt. |
Die Möglichkeit
der Wahrheitsfunktion ist dasjenige was wir als Wesen des Satzes
auffassen. Die Wahrheitsfunktion ist der
Repräsentant der Satzform.
‒ ‒ ‒ Ich will sagen, wenn wir von dem sprechen was der Satzform als solcher wesentlich ist, so meinen wir die Wahrheitsfunktion. |
13.
Wenn ich sage „ich gehe jetzt dort hin”, so kommt in dem Symbol manches vor was
in dem Zeichen allein nicht
liegt. Der Satz, wenn ich ihn etwa, von unbekannter
Hand auf einen Zettel geschrieben
irgendwo vorfinde, sagt gar nichts; das Wort „ich”, das Wort
„jetzt”
& „dorthin” sind allein ohne die Gegenwart der sprechenden Person, der
gegenwärtigen Situation & der im Raum gezeigten Richtung
bedeutungslos. |
„Jetzt”,
„früher”, „hier”, „dort”,
„ich”,
„du”,
„dieses” sind solche Wörter zur Anknüpfung an
die Wirklichkeit. |
Wenn ich sage daß ein
Satz der Mengenlehre – etwa
– || Satz, der Mengenlehre etwa,
in Ordnung ist aber eine neue Interpretation erhalten muß, so
heißt das nur dieser Teil der Mengenlehre bleibt in sich
unangetastet, muß aber in eine andere grammatische Umgebung
gerückt werden. |
Ich sage jemandem ohne ihn
anzuschauen „geh dort
hin”, er hört die Worte, versteht
sie aber nicht, da ich ihn nicht beim
Sprechen angeschaut habe. Das
gleicht einem Plan ohne Orientierungsregel. |
Nun könnte man fragen:
Gehört die Windrose noch zum Plan? Oder vielmehr: Gehört die Regel nach der die Windrose angewandt wird, noch zum Plan? Und es ist klar daß ich diese Regel durch eine andere Orientierungsregel ersetzen kann in der von der Windrose nicht die Rede ist sondern statt dessen etwa von einem Weg auf dem Plan & was ihm in der Gegend entspricht. |
Statt den Worten „Geh dorthin”
könnte es ja auch heißen „Ludwig, geh |
Statt dem Worte „dieses” kann also
in meinen Sätzen ein Name fungieren statt „jetzt” eine
Zeitangabe, statt „dort” der Name einer Richtung. Und es ist dann dieser
Name ebenso sehr und so wenig dem Mißverstehen ausgesetzt wie etwa
das Zeigen mit dem Finger, was || welches ja auch gedeutet werden muß und seine eigene
Deutung nicht schon in sich trägt.
(D.h. auch nur ein Zeichen
ist.) Und andrerseits muß sich die Zeitangabe um Bedeutung zu haben auf eine vorhandene Uhr beziehen, der Personenname auf eine vorhandene Person; oder es muß doch die Methode gegeben sein herauszufinden ob diese Person vorhanden ist & dazu muß wieder an die wirkliche Welt angeknüpft sein. |
Aber ich
sagte ja schon daß der Plan mit der Wirklichkeit durch eine
Übersetzungsregel verbunden sein
muß || müsse. |
Wie ein Zeichen eben jetzt
angewendet wird, |
Ich will sagen man kann zwar, z.B. durch
Deuten, einen Gegenstand, etwa eine Uhr, in den
Plan einbeziehen & damit gehört er nun
etwa als wesentlicher Bestandteil zum Plan, aber damit
gehört er jetzt zum Bild, die Deutung dieses || des
Bildes ist aber damit nicht vollzogen. |
Ich
sage „ich kann
das || dieses Thema so & so
singen”, ich versuche es & bleibe
stecken. Konnte ich's dann singen als ich sagte ich
könne es singen, so daß ich also auf
jeden Fall recht hatte das zu sagen, oder hat mein Stocken
bewiesen, daß ich unrecht hatte? Das kommt drauf
an.
etc.… || etc.
|
Denken wir uns nun
z.B. daß ich so durch
Deuten eine Person in einen Plan einbeziehe indem
ich etwa sage „Du wirst diesen Weg
gehen” & ihm einen
Plan || eine Zeichnung einhändige. Dann
spielt jedenfalls die
betreffende || der Betreffende eine ganz andre
Rolle in dem Plan als die Striche, Punkte
etc. des Plans. || der
Zeichnung. |
Wenn (in einem
Satz „ich will, daß Du dorthin
gehst”) der Sprechende, der
Angesprochene & der Pfeil der die Richtung weist zum
Symbolismus gehören, so spielen |
Wenn aber die Grammatik den ganzen
Symbolismus umfassen soll, wie zeigt sich in ihm || ihr die
Ergänzungsbedürftigkeit der Wörter
„ich”,
„du”,
„dieses”
etc. durch Gegenstände der
Realität? |
Denn, daß jener Satz ohne eine solche
Ergänzung nichts sagt, muß die
Grammatik sagen. Wenn sie das vollständige
Geschäftsbuch der Sprache sein soll (wie ich es
nenne.) |
„Die Kinder müßten, um das Rechnen der
Volksschule zu verstehen große || bedeutende Philosophen sein, in Ermanglung dessen brauchen
sie die Übung.” |
Könnte ich so
sagen: Das Zeichen hat
verschiedenerlei mit der Wirklichkeit gemein, unter anderem,
räumliche Eigenschaften, Richtungen, Farben, aber
|
Wie
erklärt die Grammatik das Wort
„jetzt”? Doch wohl durch die Regeln, die
sie für seinen Gebrauch angibt. Das gleiche für das Wort „ich”. |
Besteht
hier eine Analogie mit dem über das Wort „nicht”
Gesagten? Und wie unterscheiden sich
die beiden Fälle? |
Die Sprache ist nicht durch
Erklärung lehrbar, – wohl aber wird sie durch das Beispiel
gelehrt & das ist wichtig.
Erinnern wir uns immer daran, wie das Wesen einer Formenreihe durch die Angabe || Vorlegen einiger ihrer Glieder gezeigt wird. |
14. Die Grammatik
erklärt die Bedeutung der Wörter soweit sie zu erklären
ist. Und zu erklären ist sie soweit, als nach ihr zu fragen ist, & nach ihr fragen kann man soweit, als sie zu erklären ist. |
Welches ist die Bedeutung eines
Wortes? Der Ausdruck „das Wort hat Bedeutung” ist verständlich. Die Einheit des Ausdrucks
ist dann „Bedeutung
haben” & die Frage „Was bedeutet
es”, „welche Bedeutung hat es”, muß dann keinen Sinn haben. |
Wie erklärt man die Bedeutung || den Sinn des
Wortes „jetzt”, || ? – dann das ist
doch was die Philosophie tun will. |
Die Bedeutung (eines
Wortes)
könnte || kann nur das sein was
wir in der Erklärung eines Wortes
erklären. |
Man hat immer die
falsche Vorstellung als wäre die Bedeutung
eines Wortes ein || handelte es sich bei der Bedeutung
eines Wortes um einen Gegenstand d.h. ein
Ding, in dem Sinn in dem das Schwert Nothung die Bedeutung
des Wortes „Nothung”
war. Aber auch hier stimmt etwas nicht, denn ich kann doch
sagen „das Schwert
Nothung || „Nothung existiert nicht
mehr” & ist etwa hier ‚Nothung’
bedeutungslos eben weil das Schwert nicht mehr existiert?
‒ ‒ ‒ |
Ich könnte mir denken
daß einer um das Wort „jetzt” zu
erklären auf den gegenwärtigen Stand der
Zeiger || Zeigerstand einer Uhr zeigt. Sowie er
zur Erklärung des Ausdrucks „in fünf Minuten” auf die Ziffern || Ziffer der Uhr zeigen kann wo der Zeiger sich in 5
Minuten befinden wird. Es ist klar daß dadurch nur die Uhr in unsere Zeichensprache hineinbezogen || einbezogen wird. |
Das Wort „jetzt” wirkt
ja ganz anders als
irgend ein anderes da es gleichsam
der Schlag eines Zeitmessers ist || gleichsam als Schlag eines Zeitmessers || gleichsam als Schlag eines Zeitmessers.
Es gibt durch sein Ertönen
eine Zeit an. Man kann es ja auch wirklich durch ein anderes Zeitzeichen ersetzen. Wenn man z.B. sagt: tu das wenn ich in die Hände klatsche. Das Klatschen ist dann ein Zeitzeichen wie der Pfeil ein Richtungszeichen ist wenn ich sage „ich gehe dort → hin”. |
Wenn
mir z.B. die Rede die ein anderer gestern || den Satz den ein anderer gestern || die Rede die ein
Anderer gestern gesprochen hat mitgeteilt
wird: „es geschieht jetzt || heute das & das”, so muß ich verstehen daß der Satz im
Augenblick wenn ich ihn höre nicht dadurch || so verifiziert werden kann wie
(er zu verifizieren
wäre) || er zu verifizieren
war wenn ihn der || sein Sprecher
jetzt gesprochen hätte || sprechen
würde. || damals als er ursprünglich
ausgesprochen wurde.
Ähnlich, || Die Grammatik sagt
mir: wenn ich gestern sagte „heute geschieht es”, so heißt das soviel wie wenn ich heute sage „gestern ist das || es
geschehen”. |
Ich muß aber zwischen dem
strengen Teil der Erklärung eines Worts
unterscheiden und dem Schwefel der auf eine
unbestimmte || ungeklärte Art
erläuternd wirkt. |
Wenn ich etwa von zwei
kreisförmigen Flecken auf diesem Papier reden wollte etwa
über die Veränderung in ihrer Farbe, dann könnte ich
die beiden  wenn ich sage der Name
bezeichnet den Kreis der unter ihm steht? Es ist eine
Erklärung, denn man könnte in gewissen Fällen
zweifelhaft sein ob der Name zu dem unter ihm befindlichen oder zu
einem ober ihm befindlichen || anderen Kreis
gehört. Aber ist damit erklärt, was es heißt
daß ein Name zu einem Kreis
gehört? wenn ich sage der Name
bezeichnet den Kreis der unter ihm steht? Es ist eine
Erklärung, denn man könnte in gewissen Fällen
zweifelhaft sein ob der Name zu dem unter ihm befindlichen oder zu
einem ober ihm befindlichen || anderen Kreis
gehört. Aber ist damit erklärt, was es heißt
daß ein Name zu einem Kreis
gehört? |
15. Zur
Grammatik gehört nur das nicht, was die Wahrheit &
Falschheit eines Satzes ausmacht. Nur darum
kümmert sich die Grammatik nicht.
Zur Grammatik || Zu ihr gehören alle Bedingungen des Vergleichs des Satzes mit den Tatsachen || der Wirklichkeit. Das heißt, alle Bedingungen des Verständnisses. (Alle Bedingungen des Sinnes.) |
Statt die Namen A & B über ihre Kreise zu
schreiben hätten wir auch auf die Kreise deuten und sagen
können „das ist
a || A,
das ist B” & dieser Satz
lautet richtiger „das heißt ‚A’, das
heißt ‚B’”. |
Wenn man nun sagt „der heißt Ludwig || N”, so muß uns die Grammatik sagen
Die Formel „darf ich Ihnen Herrn N. vorstellen” sagt nichts wenn man nicht wirklich jemanden vorstellt. |
Gehört das Vorstellen
(in diesem
Sinne) der Dinge wirklich zur
Grammatik? |
Wenn ich in
einer Gesellschaft von einem Herrn N. reden höre den
ich nicht kenne, er sei mit seiner Frau auf Reisen
etc. etc., so sind doch diese
Sätze für mich nicht völliger
Unsinn wenn mir N auch nie vorgestellt wurde. |
Wenn der Kreis A
schon verschwunden ist so kann man noch
immer von ihm reden. |
Ist nicht auch dies ein Satz: ich
zeige zuerst auf den einen || einen Kreis dann auf den anderen & sage dabei
„‒ ‒ ‒ größer als
‒ ‒ ‒”? Und fungieren
da nicht eben jene Dinge || Gegenstände als
Zeichen, die ich bei dem Vorstellen || der Vorstellung in
die Namen übersetze? Oder wenn ich auf zwei Menschen deute & sage: „↖ gescheiter als ↗”. In diesem Sinn könnte ich auch auf die gegenwärtige Zeigerstellung einer Uhr zeigen und sagen || Punkte des Zifferblattes einer Uhr zeigen auf die jetzt die Zeiger zeigen: „er kommt ↗” & meinen „er kommt jetzt”. |
Von den Kreisen A & B kann ich noch reden wenn
sie schon nicht mehr existieren – dagegen muß das Zeichen
(alles was zum Zeichen gehört) des Satzes den ich
ausspreche existieren. Ich glaube daß die Zeichen „A” & „B” eine andere Bedeutung haben wenn die Kreise zu denen sie gehörten nicht mehr existieren, sie stehen dann für Beschreibungen & wenn dann jemand fragt was bedeutet A? so kann ich nicht antworten „diesen Kreis” sondern muß sagen: „hier war einmal ein Kreis der war der Kreis A”. D.h. die Bedeutung von „A” & „B” ist dann eine andere als wenn || da ich statt „A ist größer als B” sagen konnte „↑ ist größer als ↑”. Da habe ich offenbar die Kreise als Teil des Symbolismus gebraucht. Denn der Satz „↑ größer als ↑” ist nicht nur sinnlos wenn ich dabei nicht wirklich zeige, sondern auch wenn nichts || nicht etwas da ist worauf ich zeige. |
Wie schaut die
Erklärung eines Zeichens aus? Das müßte doch
eine für die Sprache außerordentlich wichtige Form sein,
sei dieser Behelf
nun ein Satz oder nicht. |
Denke an das
Kollationieren des Satzes mittels der
Wirklichkeit. Hier wird sie Schritt für Schritt mit
dem Satz verglichen, in ihn übersetzt. |
Denken wir uns
aber eine Sprache in der „A ist größer als
B” nicht nur so
ausgedrückt ist || ich „A ist größer als
B” nicht nur so
ausdrücke „↑ ist größer als
↑”
sondern in der ich auch statt des Wortes ‚größer’
eine Geste mache die die Bedeutung des Wortes zeigt. –
Wie könnte ich nun so eine Sprache erklären?
(Wie könnte ich die Zeichen so einer Sprache
erklären?) |
Ich
glaube: Wenn es eine Erklärung für die Bedeutung
eines Wortes gibt, so muß diese Erklärung statt des Wortes
treten können. Man könnte sich ja die Wörter
des Satzes „A ißt zwei
Äpfel” durch
Zeigen erklärt denken; auf die Frage
„wer ist A” zeige
ich || zeigt man auf einen Menschen &
sagt „dieser ist || heißt A”; auf die Frage
„was ist
essen” macht man es vor & sagt
„das ist || heißt essen” & das
Analoge für ‚zwei’ &
‚Äpfel’. & || Und nun
könnte man den Satz durch eine
Bilder- & Gebärdensprache
aussprechen. Aber hätten wir nun die Dinge statt der
Zeichen gesetzt? Mit Menschen deren Sprache man nicht
versteht, verständigt man sich ja manchmal durch eine solche
Gebärdensprache. |
Vergessen wir nicht: der Satz „das heißt A” zusamt der zeigenden Gebärde, muß auch
gedeutet || verstanden werden.
Die bloße Frage worauf || auf welche || worauf dieser Satz zur Antwort kommt kann nicht gestellt werden, wenn man das Wesen, die Methode, der Sprache nicht schon versteht. |
„Das läßt sich nicht
beschreiben” – – – – |
Ich sage „das ist
rot” || „das heißt ‚rot’” um die Bedeutung
des Wortes || das Wort ‚rot’ zu
erklären, aber wer erklärt mir diesen Satz mit der ihn
begleitenden Gebärde? |
Die
Erklärungen müßten eigentlich
lauten: „diese Farbe
heißt ‚rot’”, „dieser Mensch heißt ‚Paul’”, „diese Tätigkeit heißt ‚essen’” (statt „das heißt ‚rot’”, „das heißt ‚Mensch’”
etc.); und wenn diese
Sätze einen Sinn haben sollen so muß
der Ausdruck || müssen die Ausdrücke
‚diese Farbe’, ‚diese
Tätigkeit’,
etc. bereits verstanden werden und
könnten wie gesagt (mit der zeigenden Hand) statt || anstatt der Namen verwendet werden. |
Ich
möchte sagen: wenn das
Verstehen der Sprache ohne
fortwährendes gleichzeitiges
Verstehen von Erklärungen möglich
ist. So || ,
so ist die Erklärung am verstehen der
Sprache nur historisch |
Müßte man aber nicht
eigentlich sagen: „‚rot’
↗” denn wir müssen ja schon wissen
was für eine || welche Wortart
‚rot’
ist. |
Wenn aber diese Erklärung
dem Verständnis wesentlich ist, wie kann ich dann in
Abwesenheit der Erklärung, in Abwesenheit von etwas
Rotem das Wort ‚rot’ gebrauchen
& verstehen. Denn das Verständnis muß in
sich komplett sein & unabhängig davon wie es einmal
erreicht wurde. Denn ‚rot’ kommt ebenso im Satz vor „das ist nicht rot”, wie „das ist rot” & warum kann man was das Wort ‚rot’ bedeutet, nur dort zeigen, wo etwas die Farbe hat & nicht, wo etwas die Farbe nicht hat? |
Das würde dafür sprechen daß jene
Erklärung des Wortes nur eine
besondere Anwendung desselben || des
Wortes ist. (Aber auch das scheint nicht
zu stimmen.) Oder nur eine Übersetzung aus einer
besonderen Sprache. |
16.
Nehmen wir aber an ich sage Einem || Jemandem „diese
Mischung || Farbenmischung von rot & gelb heißt ‚orange’” (wobei ich ihm die Farbe
zeige) erhält er dann nicht durch diese Erklärung
eine Bedeutung || ein Wissen um eine
Bedeutung mit [sozusagen auf den Weg] die nun die
Bedeutung des Wortes ‚orange’ ist wann
immer er es || das Wort
braucht? Ja, – aber dem steht entgegen daß
nun alle Fälle || (Instances) des
Auftretens von ‚orange’
verschwinden können & das Wort für ihn doch seine
Bedeutung behält – es muß also an der Verbindung
(zwischen Gegenstand & Wort) die durch
die || bei der Erklärung gemacht || geschlagen wurde nur das wesentlich sein, was
auch, wenn wir
Orangefarbenes || etwas
Orangefarbenes nicht wirklich
sehen, bestehen bleibt. – Das was bestehen
bleibt ist, beiläufig gesprochen, eine Vorstellung.
Dasjenige was es ermöglicht, daß ich eine
wirklich gesehene Farbe, welche immer, mit
orange vergleichen kann – sagen kann, daß
sie gelblicher, rötlicher etc. ist als
orange. Es wäre auch möglich daß ich die
Bedeutung des Wortes wiederum vergäße (und das
geschieht ja tatsächlich).
Andererseits gehört aber, was immer von der || jener Verbindung wesentlich ist zum Bestand des
Symbols. |
Ich meine
also: Die Vorstellung |
Es gibt offenbar eine Wirklichkeit die vom
Zeichen unabhängig ist das ist die vom Satz zu beurteilende die
ihn wahr oder falsch macht. Dann aber gibt es
eine
(Wirklichkeit)
ohne die der Satz nicht wahr oder falsch sein
(also)
nicht Sinn haben kann. Diese gehört zum Satz und die
Grammatik muß von ihr reden. Wenn die Erklärung des Zeichens (was sie doch tut) uns die Bedingung gibt, das Zeichen sinnvoll zu gebrauchen, (und tut sie das nicht so ist sie irrelevant) so gibt sie uns erst das Symbol. |
(Die gänzliche Unklarheit
schaut oft so aus wie der Zustand als wären alle Probleme
gelöst || wenn alle Probleme gelöst sind, da beiden
die Möglichkeit einer klaren Frage fehlt.) |
Es ist sehr
interessant die
Allgemeinheitsnotation Russells (& Freges) mit der gewöhnlichen
Sprache zu vergleichen. Denn dabei zeigt es sich,
daß diese es ist die der
Vernunft || dem
Common sense entspricht. |
Unsere || Die gewöhnliche Sprache sagt „es gibt einen roten || ist ein
roter Kreis in diesem Viereck” die Russellsche
Notation sagt: „es gibt
ein Ding das || einen Gegenstand der ein
roter Kreis Wenn man also in größter || größt möglicher Annäherung an die Russellsche Ausdrucksweise sagt „es gibt einen Ort in diesem Viereck an dem || wo ein roter Kreis ist”, so heißt das eigentlich, unter diesen Orten gibt es einen wo etc. |
17. Der
Ausdruck „in diesem Viereck
ist || (oder gibt es) einen
Ort” hieße allein natürlich
nichts, & daß ein Kreis im Viereck sich an einem
Ort befindet sagt ebensowenig. || natürlich auch nichts.
|
Zu sagen „Es gibt einen
Ort im Viereck an dem sich ein Kreis befindet” hat nur dann einen Sinn wenn es
heißt: unter den Orten im Viereck gibt
es einen, an dem sich der Kreis befindet. Und das
setzt voraus daß man sich diese Orte als eine Klasse
(Gesamtheit) gegeben denkt. Das
entspricht aber nicht der Daß man aber diese Freiheit einfach so beschreiben kann, durch den Ausdruck „frei in der Kiste”, daß man also nicht erst die verschiedenen Möglichkeiten der Lage in der Kiste angeben muß um die Freiheit die der Kreis hat zu beschreiben, das drückt schon || selber aus was mit der „Einfachheit der Relation” gemeint ist. |
(Der
schwierigste || schwerste Standpunkt in der
Logik ist der des gesunden
Menschenverstandes. Denn er verlangt
zur Rechtfertigung seiner Meinung die volle Wahrheit & hilft
uns nicht durch die geringste Konzession (oder
Konstruktion).)
|
Der (richtige)
Ausdruck dieser Art Allgemeinheit ist also der der
gewöhnlichen („unentschieden” ist ein richtiger Ausdruck, weil die Entscheidung einfach fehlt). Aber nun frägt es sich: Wie verhalten sich die Wahrheitsfunktionen zu dieser logischen Allgemeinheit. Denn eine Verbindung muß durch das logische Folgen hergestellt sein || werden. || … bestehen. D.h. es nützt uns nicht daß wir einfach eine neue Art der Allgemeinheit annehmen, diese muß sich jetzt vor den Wahrheitsfunktionen rechtfertigen. |
Denn
aus der Angabe der Kreis befinde sich an einer bestimmten Stelle
im Viereck muß folgen daß er im Quadrat
ist. – Das heißt aber daß –
z.B. – das logische Produkt des
ersten Satzes & der Negation des zweiten eine
Kontradiktion sein
muß. Oder (was auf dasselbe hinausläuft)
I
. ⊃ . II muß eine Tautologie
sein. Das muß so zu Stande kommen indem die Ortsangabe es in sich enthält ob der Ort außerhalb oder innerhalb des Vierecks liegt. Also liegt es in der Geometrie des betreffenden Raumes. |
Die Vorschrift
daß diese beiden Angaben einander
widersprechen sollen, jene
Implikation eine Tautologie ergibt liefert eben
die hier entsprechende Geometrie. |
Daß die Tautologie &
Kontradiktion nichts sagen,
geht nicht etwa aus dem W-F-Schema hervor
sondern muß festgesetzt werden. Und die
Schemata machen nur die Form der allgemeinen Festsetzung
leicht || einfach. || machen nur
die Festsetzung der Form leicht. || einfach. |
Und
so muß – meine ich – || – will ich
sagen – welche
Satzverbindungen || Verbindungen unserer
allgemeinen Sätze nichts sagen auch von uns
einfach festgesetzt werden. Aber da ergibt sich eine Schwierigkeit. Denn wie unterscheiden wir hier Tautologie & Kontradiktion? |
Ist
fa der besondere &
fξ der allgemeine Satz so
verhält es sich mit den Wahrheitsmöglichkeiten
so:
|
Wenn die Negation
eine aus dem |
Kann
man nun nicht sagen: „A ist
rot”
gehört zum Feld der durch „A ist nicht
grün”
ausgeschlossenen || zugelassenen
Möglichkeiten. „A ist grün” ist ausgeschlossen & damit alles übrige
freigegeben. In diesem ganzen
übrigen Feld befindet sich auch „A ist rot”. |
Wie
aber soll sich das symbolisch ausdrücken? –
daß nämlich ‚A ist
rot’ außerhalb von ‚A ist grün’ liegt. Wie zeigt es sich daß „A ist grün || rot” in dem Gebiete von „A ist nicht grün” liegt? Wie anders, als daß eine Wahrheitskombination ausgeschlossen wird? |
„A ist nicht
grün” schließt „A ist rot”
als eine || seine Möglichkeit
ein. |
Daß „A ist
grün” & „A ist rot”
konträre Sätze sind muß sich in einer ähnlichen
(analogen) Weise zeigen, wie, daß
„A ist grün” & „A ist nicht
grün” kontradiktorische
Gegenteile sind. |
Wie
zeigt es sich denn daß „p”
und „~p” komplementär sind?
– Nämlich so muß es sich auch zeigen, daß „A ist rot” im
Komplement von „A ist grün” liegt. |
Das
erste zeigt sich doch offenbar darin, daß
p ⌵ ~p tautologisch
ist. Und das wieder wird dadurch klargemacht, daß q ∙ (p ⌵ ~p) = q ist. (Und (durch) andre ähnliche Beziehungen.) |
Wenn man freilich an dieser
Erklärung bemängelt, daß ja eben der Sinn des „ ∙ ” noch nicht erklärt ist & wieder einer
Erklärung bedarf, so ist – glaube ich – die Antwort,
daß es eine andere Erklärung als das vollständige
Aufstellen der Regeln nicht gibt. Und gewiß ist der Begriff des „und” nicht weniger erklärungsbedürftig als || ebenso erklärungsbedürftig wie der der Tautologie. Und sie werden nur alle zusammen |
Wer
übrigens die Negation erklären will, der merkt bald, daß
er nur wieder eine Negation in anderer Form vorbringt (er verwendet
etwa den „Ausschluß” oder anderen Ausdruck.) |
q ∙ (a ist rot
. ⊃ . ~(a ist grün))
= q |
Die Erklärung die man erhält
wenn man nach dem Wesen des Satzes fragt: Satz sei alles was
wahr oder falsch sein könne, ist so unrichtig
nicht || nicht so ganz unrichtig. Es
ist die Form der Wahrheitsfunktion (in welcher Form immer
der Zeichengebung || der Zeichengebung immer
ausgedrückt || dargestellt) die das logische
Wesen des Satzes ausmacht. |
Ich
sagte daß in dem Satz „in dem Viereck
ist ein roter Kreis” von keiner
Gesamtheit der Orte an denen ein Kreis sich befinden
kann, die Rede sei, so daß es zu diesem „es gibt …”
kein „für alle
…” gäbe. –
Muß ich denn aber nicht sagen, daß aus jedem Satz der
eine bestimmte Lage des Flecks im Viereck beschreibt der Satz „in dem Viereck ist ein roter
Kreis” folgt? Ist
diese || jene Allgemeinheit
nicht das Korrelat des || dieses Existentialsatzes? |
In Wahrheit gibt es zu dem
„in dem Viereck ist
…” ein „wo immer im Viereck ein roter Kreis ist
…”. „Wenn im Viereck ein roter
Kreis ist, dann …”
kann man immer auch so ausdrücken „Wo immer im Viereck ein roter Kreis ist,
…”. |
(∃x) ∙ φx
. ⊃ . p = (x):φx
. ⊃ . p Aber das zeigt uns auch, wie wir das „wo immer …” aufzufassen haben. Denn auch das „wo immer …” enthält keine Beziehung || Anspielung auf eine Gesamtheit. |
Die
Erklärung über das Zeichen „in
dem Viereck ist || gibt es
…”, es folge aus jedem Satz, der
aussage, der Fleck befinde sich an einer || der
& der bestimmten Stelle des Vierecks, ist nicht besser,
als die, der Satz „in dem Viereck
ist || gibt es …” folge aus einem Satz, wenn || sobald der
aussage der Fleck finde || befinde sich an der & der bestimmten Stelle
etc. |
Wie
verhält sich dazu die Erklärung
~p folge immer daraus
daß p nicht der Fall ist?
|
Ist es seltsam oder
unrichtig, daß in der grammatischen Regel für die uns
interessierende Allgemeinheit, diese selbst angewendet werden
muß? Ist das nicht vielmehr sogar
selbstverständlich? |
19.
Jedenfalls ist es unbillig zu verlangen die Allgemeinheit
deren Symbolismus erklärt werden soll, solle nicht in dieser
Erklärung selbst vorkommen denn erklären laßt
sie sich ja ohnehin nicht & irgendwelche
Begriffe müssen ja in den
Syntaktischen Regeln gebraucht werden. |
„Wo immer der Fleck im Viereck ist
…” heißt „wenn er || solange er im Viereck
ist …” & hier ist nur
(wieder)
die Freiheit (Ungebundenheit) im Viereck
gemeint || gedacht, aber keine Menge von
Lagen. |
Es besteht freilich eine logische
Ähnlichkeit (formelle
Analogie) zwischen dieser Freiheit & der
Gesamtheit von Möglichkeiten daher gebraucht
man oft in beiden Fällen die selben
Wörter || Worte („alle”,
„jeder”
etc.). |
„Wo immer er ist
…” heißt, „er
ist an keinen Ort gebunden”. Aber hier ist
wieder das „keinen” zweideutig (da es bedeuten könnte: keinen von
diesen …) & man sollte etwa sagen „er ist örtlich nicht
gebunden”. – Die
Multiplizität ist die richtige die der
gewöhnliche Satz „in dem Viereck ist …” hat. Hätte er in Wirklichkeit
eine größere || andere als die
scheinbare, so müßte
sich das in seiner Anwendung zeigen. |
Wenn ich sagte,
der Satz sei zusammengesetzt |
Wäre er einfach
d.h. ein für allemal unveränderlich
vorhanden, so brauchte man ihn überhaupt nicht.
|
Und
zwar genau so wie ein Zeichen, das in allen Sätzen
vorkäme, überflüssig ist. || wäre. |
Die
Methode der Philosophie ist, auf alle Stimmen zu hören
& sie alle miteinander zu versöhnen
(reconcile). |
Das Zeichen hat nur
einen Zweck, wenn ich mit ihm operieren kann.
Und dann muß es in verschiedenen Zusammenhängen vorkommen können. |
Das
Wesentliche, der Sinn (d.h. Zweck), des
Satzes ist ja, daß ich die einzelnen
Zeichen durch eine Übersetzungsregel erklären
kann, aber der Satz sich selbst
erklärt. |
Die Bildung von Wortzeichen ist ja nur
präliminar.
|
D.h. sie ist an sich wertlos
& ihr Zweck ist erst die Bildung einer
Kombination aus ihnen.
|
Wie gesagt: das Satzzeichen
repräsentiert nicht. – Es
stellt dar. |
Wäre der Satz einfach, was soll ich
mit ihm anfangen? Nehmen wir an ich wollte jemandem die
Mitteilung machen: a. Aber
um sie zu verstehen || damit er sie versteht,
müßte ich ihm die die Bedeutung
von a || das Zeichen a
erklären; dann wüßte er aber auch schon alles, was
ich ihm mit „a” sagen
könnte. Es muß Eines || ein
Anderes sein die Sprache zu lernen, & ein Anderes
eine Mitteilung in der Sprache zu erhalten. Hier aber, wenn
der Satz einfach wäre, wäre es
(nur)
eines. || wäre es eins. || ein & dasselbe. Dann
bedürfte es aber doch der Sprache gar nicht. |
Denn sage || gebe
ich jemandem ein neues Zeichen, so versteht er
es nicht. || Variante:
Denn gebe ich jemandem ein neues Zeichen, so versteht er
es nicht.
Es muß ihm erklärt werden.
Wozu es ihm aber dann überhaupt geben? (Anders
ist es, wenn man es zum zukünftigen Gebrauch
erklärt.) |
7.10.
Es gibt keine
Metamathematik. |
Der
Unterschied zwischen etwas Allgemeinem, das man wissen könne,
& dem Besonderen das man aber nicht
wisse, oder zwischen der Beschreibung des Gegenstands die man
kenne & dem Gegenstand den man nicht gesehen hat ist auch ein
Stück das man von der physikalischen Beschreibung der Welt
in die Logik hinüber genommen hat.
Daß unsere Vernunft Fragen erkennen kann, aber
deren Antworten nicht, gehört auch hierher. |
Zu
Erklärung der Bedeutung:
Bemerkung „lies
…”.
Erklärung der Aussprache dieser Zeichen durch die
Aussprache jener || anderer.
Aber nicht eine Erklärung der
Aussprache || des Aussprechens von Zeichen
überhaupt, also der Beziehung zwischen Zeichen
& Aussprache überhaupt. |
Hypothese, daß alle Menschen eigentlich nach
N. gehen & nur früher oder später;
& einige (die meisten) sterben ehe sie
hinkommen. Muster einer wissenschaftlichen
Hypothese. |
„The room is 12 foot
(oder 12 feet) high.” Bedeutung von
Singular & Plural
|
13.
Wenn wir sagen „es hat sehr lang gebraucht
…” so ziehen wir oft die
Worte in die Länge um die Länge abzubilden &
umgekehrt wenn wir sagen „es war ein
kurzer Augenblick” so sprechen wir
die Wörter kurz & bestimmt
aus. Es würde eine sehr komische Wirkung tun wenn wir
in diesem Ausdruck die Worte nach der ersten Art ziehen
wollten. |
16.
Wenn ich sage „A hat einen
grauen Hut” & ich gefragt werde
„wer ist A” & antworte „dieser ist
der A”, so mache ich damit den
Menschen A zu einem Symbol in meinem Satz oder es ist
doch möglich, daß ich ihn zu einem Bestandteil
meines Satzes mache; aber das muß nicht
Tritt dieses Problem auch auf wenn es sich z.B. um eine Farbe handelt? Wenn ich etwa sage „dieses || das Tuch ist mauve” & auf die Frage „was ist || bedeutet ‚mauve’” auf einen Gegenstand von dieser Farbe zeige. Man könnte dabei sagen „merke dir, das ist mauve” & hat dabei eine ganz bestimmte Art der Wirkung dieses Zeichens || Zeigens im Sinn. |
Wenn nun der
Betreffende (wie es tatsächlich oft
geschieht) vergißt welche Farbe man so bezeichnet hat aber
nicht vergißt daß bei einer bestimmten
Gelegenheit ihm die Bedeutung des Wortes „mauve”
erklärt würde || wurde & nun fällt dieses
Wort wieder & er weiß nur es ist die Farbe von
der bei einer || jener || dieser
Gelegenheit die Rede war, hat nun das Wort für ihn
eine andere Bedeutung als damals wie er wußte wie
|
Das verhält
sich aber doch ebenso wenn ich Herrn A kennen lerne
& vergesse wie er ausschaut & später von ihm
reden höre. Und es lassen sich Sätze angeben die
für mich sinnlos sind wenn dem Namen a kein visuelles
Erinnerungsbild entspricht. |
18 || 17.
In
einem Sinn ist das Schwert Nothung die Bedeutung
des Namens „Nothung”. So zwar daß der Name seine Bedeutung verliert
wenn dieses Schwert aufhört zu existieren. In dem
anderen Sinn in welchem das Wort || der Name seine
Bedeutung nicht verliert, wenn auch das Ding
zerstört wird, hat seine Bedeutung nie von der Existenz
des Dinges abgehangen, auch nicht in dem Moment da die
Erklärung gegeben wurde: „dieses Schwert ist
Nothung” denn
diese || die Erklärung behält ihren
Sinn auch wenn es sich um eine Illusion handelte & in
Wirklichkeit gar kein Schwert vorhanden war.
Wenn man andrerseits das Wort „rot” durch Hinweisen auf etwas Rotes erklärt, ‒ ‒ ‒ |
Ich könnte die Bedeutung
von „rot”
so erklären daß ich sagte: drücke auf
die || deine
Augenlider, was du dann siehst ist rot. |
Aber könnte ich nicht auch
die falsche Erinnerung in jemandem wachrufen daß er etwas
Rotes gesehen habe oder überhaupt die
Vorstellung von rot ohne daß er je rot gesehen
hat. Kann ich nicht jedenfalls durch eine Beschreibung – sagen wir – ein Blaugrün in seine Vorstellung bringen wenn er auch noch nie eines wirklich gesehen hat & nur etwa blau & grün? |
Ich will sagen:
Wenn es nicht wesentlich ist daß es etwas
Rotes gibt damit das Wort rot
Bedeutung habe dann kann es nie wesentlich gewesen
sein. Die Geschichte des Erlernens einer
Bedeutung kann nie wesentlich sein. |
22.
Die Sprache kann
nicht durch Unterrichtsbriefe gelernt werden.
(Was wir also so lernen können steht im Gegensatz zur Sprache.) |
Wir müssen
wissen daß jedes Stück altes Eisen das
wir auf der Straße finden ein Schlüssel ist
& daß es sich sozusagen |
Was heißt es,
einen Satz verstehen? Ich glaube das Verständnis was
da ist muß sich zeigen lassen & nur so weit es sich zeigen
läßt ist || existiert es.
Die Frage ist eigentlich nicht „was heißt es einen Satz so verstehen wie ihn ein anderer gemeint hat” sondern „was heißt es einen Satz irgendwie zu verstehen” also besser: zu deuten. Wie würde ich zeigen daß ich das Wörterbuch als Übersetzungsregel deute? Doch dadurch daß ich danach eine Übersetzung ausführe. Es ist etwa dies mein Wörterbuch:
und ich übersetze danach den Satz bdca in fhge. Nun habe ich – im gewöhnlichen Sinne – gezeigt, daß ich den Gebrauch des Wörterbuchs verstehe & kann sagen daß ich auf gleiche Weise den Satz cdab übersetzen kann wenn ich will. – Wenn also der Satz cdab ein Befehl ist den entsprechenden Satz in der Man kann geradezu sagen: Ich habe dir jetzt gezeigt was f(❘), f(❘ ❘), f(❘ ❘ ❘) & f(❘ ❘ ❘ ❘) heißt, jetzt wirst du verstehen was f(❘ ❘ ❘ ❘ ❘ ❘) bedeutet. D.h. man rechnet damit daß ihm von dem Demonstrieren der Ausführung von f(❘), f(❘ ❘), etc. etwas – quasi ein Eindruck – geblieben ist was er nun auf f(❘ ❘ ❘ ❘ ❘ ❘) anwenden wird. |
Aber natürlich kann
das nicht anders sein als wenn ich, z.B. sage
„ich will diesen Fleck rot
anstreichen”, eine Vorstellung von der
Farbe habe & nun „weiß”
wie diese Vorstellung in diese Vorstellung || in die
Wirklichkeit zu übersetzen ist.
Es ist das Verhältnis der || meiner Vorstellung zu der gegenwärtig gesehenen Farbe was das Verstehen der Vorstellung als eines Zeichens möglich macht. Ja dieses Verhältnis muß das Verständnis ausmachen nicht nur möglich machen. |
Ja
das ganze Problem ist schon darin enthalten: Was
heißt es zu wissen wie der Fleck aussähe, wenn er meiner
Vorstellung entspräche? |
Dieses Wissen
muß ganz & gar in dem liegen was wirklich gegeben
ist. |
Wäre die Vorstellung
allein so könnte aus ihr keine Wirklichkeit konstruiert
werden. |
Es handelt sich darum
daß ich die Distanz meiner || der
Vorstellung von dem sehe was ist. |
Ich
muß, scheint es, eine allgemeine
Übersetzungsregel in ihrer Allgemeinheit verstehen. |
Wenn wir einen
einfachen Fall vor uns haben so ist es gut zu trachten den
einmal zu verstehen; ob er sich nun als das
Prototypische aller Fälle erweisen
sollte oder nicht. |
23.
Was heißt
es, eine allgemeine Regel zu verstehen? Man kann die Zahlen ❘ ❘, ❘ ❘ ❘ ❘, ❘ ❘ ❘ ❘ ❘ ❘, sehen ohne eine allgemeine Regel ihrer Bildung zu verstehen & man kann eine allgemeine Regel aus ihnen entnehmen. Der Befehl kann ja wirklich so lauten: ❘ ❘, ❘ ❘ ❘ ❘, ❘ ❘ ❘ ❘ ❘ ❘, – setze diese Reihe fort. |
Die Regel
der Interpretation kann nicht ausgedrückt werden, weil jeder
Ausdruck einer Interpretation bedarf. |
Das Wörterbuch
ist || gibt die allgemeine Regel der
Übersetzung. Aber auch das Wörterbuch muß ja
so erst verstanden werden. Gibt es ein
Verstehen einer allgemeinen Regel als solcher außer
durch ihre Anwendung? |
Wenn man
sagt daß das Übersetzen von einer
Zeichensprache in die andere alles ist wodurch ich mein Verstehen
dokumentieren kann ja alles worin es besteht so muß man
sich – glaube ich
– nur gegen einen Vorwurf schützen, den, daß dann die
letzte Übersetzung in die Wirklichkeit & damit der
Sinn des Satzes unbestimmt bleibt. Dasjenige
was man gegen diese Auffassung einwenden möchte ist:
Du sagst also daß ich solange nicht wissen kann welche Tat
den Befehl befriedigt bis sie nicht getan ist.
Aber das sage ich gerade nicht.
Eine Erwartung ist nicht mehrdeutig weil das was sie erwartet || die Entscheidung tatsächlich noch nicht eingetroffen ist. |
Aber wenn ich denkend Zeichen gebrauche so rede ich doch
nicht nur sondern meine etwas ganz
Bestimmtes! Freilich
etwas ganz Bestimmtes im Gegensatz zu dem Fall wo
einer redet & nur unbestimmt weiß was die Worte
bedeuten. Für beide Fälle kann man
Beispiele angeben aber beide treten aus der Sprache nicht
heraus. |
Wenn ich sage ich erwarte mir
hier einen roten Kreis so stelle ich mir doch etwas ganz Bestimmtes
vor || erwarte ich doch etwas ganz bestimmtes, es
kann dann doch nicht etwa ebensogut dieser blaue Kreis meine Erwartung
befriedigen. Freilich nicht, aber das sagte ich auch nicht
& wir sind ja damit doch nicht bis zur Entscheidung
unserer Erwartung
vorgeschritten || vorgedrungen sondern haben nur eine
Übersetzung abgelehnt. |
Wenn man nun fragt: Ist also
die Tatsache durch die Erwartung auf ja & nein bestimmt oder
nicht d.h. ist es bestimmt in welchem
|
Wenn ich voraussehe
wie es kommen wird, sehe ich da etwa doch nicht voraus wie es kommen
wird, weil ich die Voraussicht nicht in die Wirklichkeit
projizieren kann die noch nicht vorhanden
ist? Im Gegenteil die Möglichkeit meiner
Voraussicht beruht gerade darauf daß die zu dieser
Voraussicht gehörige Realität nicht auch die
Erfüllung (oder ihr Gegenteil) der Voraussicht
beinhaltet. |
Die scheinbare Unbestimmtheit
von der ich sprach, ist ebensowenig vorhanden wie die,
von der manche Leute reden die daher kommen soll
daß wir nicht wissen können ob wir die gleiche Farbe sehen wenn wir || zwei
Leute || Menschen die gleiche Farbe sehen wenn
sie einen Gegenstand betrachten. Das
ist Unsinn denn unter dem Sehen verschiedener Farben meinen || verstehen wir etwas ganz anderes & es gibt in
diesem Sinne Kriterien dafür ob die Beiden die gleiche oder verschiedene Farben
sehen. |
24.
Könnte ich einen Farbfleck
|
Ist es nur eine
Art der Beschreibung eines seelischen Vorgangs zu sagen er sei
die Erwartung daß hier ein roter Fleck auftreten wird oder
ist es die interne Beschreibung dieses Vorgangs in dem
Sinn in welchem der Satz „ein roter Fleck tritt dort auf” die interne Beschreibung der
Erfüllung jener Erwartung ist? Ich
glaube, – offenbar das Letztere. |
Der
Ausdruck der Erwartung ist die Erwartung. |
„Meine Erwartung ist so gemacht, daß, was
immer kommt mit ihr übereinstimmen muß
oder nicht.” |
25.
Zum Beweis dessen daß
man wirklich weiß was man mit dem Satz „ich erwarte mir hier einen roten
Fleck” meint, sagt man etwa:
freilich weiß ich was ich mir erwarte, ich sehe den Fleck jetzt
deutlich vor mir! |
Wenn ich gehe
so enthält der einzelne Schritt nicht das Ziel wohin mich
das Gehen bringen wird. |
Ich mache Versuche mich, oder
meinen Hörer, in's Wasser fallen zu
lassen & ihn dann herauszuziehn um so eine Rettung zu
demonstrieren. Aber es geht nicht sehr elegant:
einmal gelingt es mir nicht recht ihn ins Wasser zu werfen &
ich wälze ihn auf der Erde herum ohne ihn ins Wasser zu bringen,
& dann wieder habe ich ihn ins Wasser geworfen aber ich bringe
ihn nicht mehr heraus & er ist in der Gefahr zu
ertrinken. |
Komme ich an's Ziel so war
jeder || der Schritt ein Schritt zum || zu diesem Ziel. |
Wie kann man etwas abbilden was
nicht da ist!? (Offenbar liegt hier eine Zweideutigkeit in den Worten „etwas” & „da ist || sein”.) |
In dem Faktum
des Verstehens muß das Verstehen (was immer es ist) seinen
Ausdruck finden. In dem Vorgang des Verstehens (welcher immer der sei) muß das Verstehen ausgedrückt sein. |
Man ist (durch falsche Grammatik)
|
Der
falsche Vergleich besteht hier darin daß wir uns die
Sache wie einen Mechanismus denken || vorstellen
¤
dessen Äußeres wir kennen
dessen inneres Arbeiten uns aber noch
verborgen ist. |
Es ist eine Haupttätigkeit der Philosophie vor falschen
Vergleichen zu warnen. Vor
(den) falschen Vergleichen || Gleichnissen zu warnen
die unserer Ausdrucksweise – ohne daß wir uns dessen
ganz bewußt sind – zu Grunde liegen.
Ich glaube unsere Methode ähnelt hier der der Psychoanalyse die auch Unbewußtes bewußt & dadurch unschädlich machen will & ich glaube daß diese Ähnlichkeit keine rein äußerliche ist. |
Das Etwas was
wir erwarten scheint uns immer wie || erscheint uns immer als der
Mensch der etwa zur Tür herein kommen soll nicht wie
die Tatsache || der Umstand || das
Ereignis daß er kommen soll. |
Die
Bedeutung eines Zeichens |
In irgend einem Sinne kann man
sagen: Ein Satz || Satzzeichen hat nur im System einer Sprache Sinn.
|
Wenn ich einen Befehl gebe so
muß ich in der selben Sprache auch die || eine Tat beschreiben können, die
dem
Befehl zuwiderläuft. |
D.h. Ein Satz kann nur als Teil
eines Systems verstanden werden. |
Kann man sagen:
Verstehen was der Satz heißt || sagt: „hier wird ein
roter Kreis erscheinen”, heißt, den
gegenwärtigen Zustand in die selbe Sprache
übersetzen können (den gegenwärtigen Zustand in der
gleichen Sprache beschreiben
können)? |
Man
kann einen Satz nicht losgelöst von einer Sprache
verstehen. |
„In der gleichen Sprache
ausdrücken” heißt mit dem
gleichen Maßstab messen. |
Wir
können nur innerhalb der Sprache vergleichen.
|
Ist es so:
denken heißt Anwenden des
Planes || Denken ist eine
Anwendung des Planes. Aber die
Anwendung kann nicht im Plan liegen. |
Gedankenlesen kann nur darin bestehen daß
wir Zeichen interpretieren also einfach lesen
(nur vielleicht andere Zeichen).
Oder aber es besteht darin daß einem wenn man des
Anderen Hand hält (oder in andrer Art mit ihm in
Kontakt steht) Gedanken
kommen die durch nachträgliches Fragen
als die Gedanken auch des Anderen erkannt werden.
Aber da handelt es sich überhaupt um kein Lesen sondern
es wäre nur die Hypothese erlaubt daß zwei Leute
unter gewissen Umständen das gleiche dächten. |
Da das Denken ein symbolischer Vorgang ist so kann es uns
ganz gleich sein wo sich dieser Vorgang abspielt wenn seine symbolischen Eigenschaften, wenn also
das was seinen Zweck ausmacht, gewahrt bleibt. (Wenn wir
uns nicht für die psychologische Seite gewisser dieser
Vorgänge interessieren.) |
Ist das Denken ein
augenblicklicher Vorgang oder etwa || vielleicht ein andauernder Zustand wovon die
Worte, der Satz, nur eine ungeschickte Wiedergabe sind
(so daß man etwa sagen könnte, wie von dem Eindruck
etwa einer Landschaft: Worte können das gar nicht
wiedergeben)? Der Gedanke braucht so lange wie sein
Ausdruck. Weil der Ausdruck der Gedanke ist. |
27.
Ein Symbol verstehen heißt
seine Multiplizität verstehen. Die
Multiplizität seiner Anwendung verstehen.
(﹖) |
28.
Ich habe
einmal gelesen daß ein Franzose || französischer Politiker –
ich glaube M.
Briand – gesagt
habe, die französische Sprache sei dadurch
ausgezeichnet, daß in ihr die Wörter
(im Satz)
in der Reihenfolge stehen, || in der Ordnung
folgen, wie man wirklich denkt. – Das ist ein
sehr bedeutungsvoller Ausspruch, |
Wenn Bauern darüber || mit
einander streiten weil
der eine dem anderen für die Kühe die er von ihm gekauft hat
zuwenig Geld gegeben hat & dieser Streit kommt vor den Richter
& wird entschieden, so kann es offenbar dabei nicht
drauf ankommen was für eine Vorstellung der
Eine oder der Andere beim
Hören des Worts Kuh
(gehabt)
hat. Sondern es wird dabei sozusagen mit Worten
gerechnet & auch﹖
die Anwendung des Resultats ist
eine exakte Übersetzung der Sprache
in eine Handlung (etwa das
Aufzählen von
Geldstücken.) |
Wenn die Logiker die psychologischen
Operationen beschreiben die sie für das Denken & die
Interpretation von
Sätzen halten so ist es immer ein Wunder
daß || wie bei so
vagen Vorgängen etwas so
Bestimmtes wie ein Urteil soll herauskommen
können. |
Eine allgemeine Regel verstehen
heißt sie in irgend einem Fall anwenden.
(nicht „anwenden
Wenn ich z.B. mein Verständnis für einen erwartenden Satz dadurch ausdrücke, daß ich den gegenwärtigen Zustand in der gleichen Sprache beschreibe so ist das die Anwendung der allgemeinen Regel in einem Fall. |
Aber hier
möchte ich immer sagen: die Anwendung der allgemeinen Regel
ist nicht genügend sondern diese Regel muß darin
irgendwie betont werden. – Aber das ist
falsch. |
Ist nicht das Verstehen also
Anwenden-können eines Satzes auf einer Stufe mit dem
Schachspielen-können. In dem Sinne in dem ich
auch nicht irren kann wenn ich gefragt werde „kannst du Schach spielen” & ich antworte „ja”, in diesem
Sinne muß ich die Regeln im Geiste durchfliegen & sie also
irgendwie anwenden; denn in jedem anderen Sinne kann ich
mich doch irren & plötzlich daraufkommen daß ich die
Regeln für eine Figur vergessen habe & dann nicht
sagen kann „ich habe
Schachspielen gekonnt || konnte Schachspielen als
ich sagte daß ich es könne
etc.”.
|
Ist aber nicht dadurch der Sinn des Satzes wieder problematisch
geworden? |
Oder darf ich sagen:
Der Sinn des Satzes ist ebensowenig
problematisch wie die Regeln der Grammatik. |
Man würde sagen: Ich verstehe die
Übersetzungsregel meint: ich kann sie anwenden,
wenn keine äußeren Hindernisse entgegenstehen.
„Ich verstehe die Übersetzungsregel
scheint mir auf genau derselben Stufe zu stehen wie die Aussage „ich kann Schachspielen”. Könnte ich ohne bei dieser Aussage an die Regeln über die Bewegung des Turmes gedacht zu haben, & wenn ich nun (beim Versuch) fände daß ich sie vergessen habe, könnte ich nun sagen „ich konnte Schachspielen wie du mich gefragt hast & nur jetzt kann ich es nicht”? |
Kann ich wissen
daß ich die Regeln weiß, wenn ich sie nicht
durchfliege? Kann ich wissen daß
ich eine Regel wußte als ich
gefragt wurde ob ich sie wisse, wenn ich sie mir damals
|
Kann ich
mich darin nicht irren, wenn ich sage „ich kann
multiplizieren”
wenn ich mir dabei nicht die
Multiplikation irgendwie
vorführe || vor den Geist
stelle &
wie verhält es sich dann mit dem Wurzelziehen
worüber ich nicht sicher bin & vielleicht, wenn
ich es versuche finde daß ich es noch kann oder auch
nicht? |
29. Niemand
würde fragen ob die Multiplikation zweier
Zahlen (etwa nach der gewöhnlichen Art
durchgeführt) gleichläuft
mit dem Gedanken. Weil jeder die
Multiplikation als ein Instrument
ansieht. Während man den Gedanken nicht als
ein Instrument ansieht. |
Man
unterscheidet zwischen dem bloßen Lesen eines Befehls & dem
Lesen des Befehls mit Verständnis.
Bei diesem Lesen oder Sehen des Planes geht also noch etwas anderes vor sich. Und zwar wird es – so scheint es mir – von einer Übersetzung begleitet. Oder ist das falsch & soll ich sagen, || : |
Die Auffassung des Satzes also des Verstehens &
des Gedankens muß gewiß die
Möglichkeit des Kalküls
rechtfertigen. Und der Kalkül vollzieht sich in
der Zeit &
ist – sozusagen – ausgebreitet. |
Ist das Verstehen eines
Satzes dem Verstehen eines Zuges im
Schachspiel || Schachzuges als solchen nicht
analog. Wer das Schachspiel gar nicht kennt &
sieht jemand einen Zug machen, der wird ihn nicht verstehen
d.h. nicht als Zug eines Spieles
verstehen. Und es ist etwas anderes dem Zug mit
Verständnis zu folgen,
als ihn || Spiel mit
Verständnis zu folgen,
als es || den Zug mit
Verständnis zu sehen,
als ihn || das Spiel mit
Verständnis zu sehen,
als es bloß zu
sehen. |
Kann man sagen ich sehe
den Zug im Schachraum? |
Was ist es aber dann was uns immer
das Gefühl gibt, daß das Verstehen eines Satzes das
Verstehen von etwas außerhalb ihm
Liegendem ist & nicht
von der Welt außerhalb des Zeichens wie sie eben ist,
|
Von der Welt als Teil des
ganzen Spieles (von dem wir nur einen Zug
sehen) |
Wie kann ich mir vornehmen einer allgemeinen Regel
zu folgen. |
Nicht nur soweit als ich die
Regel ausdrücken kann? |
Das
hängt
(alles)
damit zusammen, daß man nicht fragen
kann, || : „ist das wirklich die Farbe die Du sonst rot
genannt hast.” Es sei denn
man fragt „ist das die
Farbe die Du erwartet hast & nicht
vielmehr das”. Jeder
Unterschied muß sich als Unterschied in einer
Sprache ausdrücken. |
Ich kann
mir vornehmen einer Regel zu folgen & nicht einer
anderen. Dann müssen beide
ausgedrückt sein. |
Nur was
kontrollierbar ist kann sich in der Sprache
ausdrücken. |
Man kann freilich dem
Gedächtnis durch eine Notiz nachhelfen
|
Von Verschiedenheit kann man
nur (dann)
reden, wenn ein Vergleich möglich ist.
Und der ist nur in einer Sprache möglich &
zwei Sprachen müssen erst in einander übersetzt sein,
(auf gleichen Nenner gebracht) ehe ein Vergleich von
Ausdrücken möglich ist, dann findet er aber eben
in einer Sprache statt. |
30. In
der Sprache kann man von einem reden nur im Gegensatz
zu etwas anderem. |
Die Regeln des
Schachspiels unterscheiden das Schachspiel von einem
Spiel das in der selben Sprache andere Regeln hat || von
einem || jedem Spiel mit anderen
Regeln in derselben Sprache. |
Jeder Satz einer
Sprache hat nur Sinn im Gegensatz zu anderen
Wortzusammenstellungen derselben Sprache. |
Wir
könnten uns zwei Schachspieler denken die, da sie kein
Gedächtnis haben, die Regeln des Spiels
|
Um einen Plan zu verstehen
muß man in gewissem Sinne erst das allgemeine Prinzip der
Plandarstellung verstehen & man versteht den Plan im
Gegensatz zu anderen die nicht gelten.
Wenn ich das nun sage bezieht es sich auf den momentanen Geisteszustand des Betreffenden, der den Plan auffaßt? Doch gewiß nicht – er geht doch nicht alle anderen Möglichkeiten des Planes || der Darstellung durch so wenig wie der Schachspieler etwa fortwährend die Regeln des Schachspiels rekapituliert (und täte er's so müßte er einmal die eine dann die andre sich vorsagen nicht aber alle auf einmal). |
Man könnte so fragen:
Ist Schachspielenkönnen ein andauernder – quasi
amorpher – Geisteszustand, etwa wie
Zahnschmerzen? |
Das Verständnis der Sprache
– quasi des Spiels – scheint wie ein Hintergrund auf
|
Die allgemeine Regel erst
enthält den Freiheitsgrad, die
Beweglichkeit des Mechanismus. Das Bild des Mechanismus in
einer seiner Stellungen enthält
hievon nichts. |
Soll ich nun sagen der Freiheitsgrad
des Mechanismus kann sich nur mit der Zeit enthüllen?
Aber wie kann ich dann je wissen daß er gewisse Bewegungen
nicht machen kann, (und daß er gewisse
Bewegungen machen kann die er gerade noch nicht gemacht
hat). Darauf ist doch die Antwort: Der Freiheitsgrad des Mechanismus kann doch beschrieben werden. Wohl, aber dann ist eben nichts mehr gegeben als was diese Beschreibung gibt. (Die doch selber nur eine Stellung eines Mechanismus ist!) |
Das Verständnis als eine
Disposition der Seele oder des Gehirns geht
uns nichts an. |
Der Ausdruck des Verständnisses
der Schachregeln ist doch gewiß |
Aber man könnte || kann fragen: ist
denn das Verständnis nicht etwas anderes als der
Ausdruck des Verständnisses? Ist es
nicht so, daß der Ausdruck des Verständnisses eben
ein unvollkommener Ausdruck ist? Das heißt doch wohl
ein Ausdruck der wesentlich etwas ausläßt was
unausdrückbar ist. Denn sonst könnte
ich ja eben einen besseren finden. Also wäre der
Ausdruck ein vollkommener Ausdruck.
‒ ‒ ‒ |
Ein Mechanismus offenbart
seinen Zweck nach & nach, so wie er ein um das andere
mal gebraucht wird. Und so
muß es auch mit einem Satz, mit dem Ausdruck eines
Gedankens gehen. |
Wozu
denn überhaupt diese ganze Untersuchung, was interessiert mich
denn der Gedanke, das Denken etc.,
warum ist mir |
Wenn
man übrigens das Wort seelisch, wie ich soeben, gebraucht so
darum weil man sich das Denken notwendig als eine Reihe
von Fantasiebildern vorstellt.
Wie aber wenn man diese Fantasiebilder durch
Wahrnehmungen ersetzt (das Wort „rot”, wo es
notwendig ist durch das Vorzeigen eines roten
Fleckes || Gegenstandes begleitet).
Fantasiebilder sind unserem Denken nicht wesentlich || unwesentlich. |
Welche
Beziehung hat die Vorstellung von einer Photographie die ich heute
gesehen habe zu der Photographie (dem Gesichtsbild der
Photographie)? Ist sie ihr
ähnlich?
Vorausgesetzt daß sie genau mit der Wirklichkeit
übereinstimmt (was eben bei einer Vorstellung „übereinstimmen mit der
Wirklichkeit” heißt)
–. Ich sage:
Genau so habe ich mir's vorgestellt. Und jemand
antwortet etwa „das ist
unmöglich denn das eine war eine Vorstellung
& das andere ist keine & hast Du etwa deine
Vorstellung für Wirklichkeit
gehalten?” |
„Das ist das Rot das ich meinte”. „Wie konntest Du
es meinen, es war ja
(früher)
gar nicht da.”
„Ja, ich wollte daß Du das tust”. Wie konntest Du es wollen da es ja noch gar nicht getan war. |
(Der Ausdruck „Nicht- … ische
‒ ‒ ‒” bezeichnet
eine || steht für eine Denkbewegung die mit der
Konstruktion einer Nicht-Euklidischen Geometrie anfing & damals eine Tat war,
verdienstlich & bedeutend || folgenreich, heute aber noch immer Mode ist bei den Mathematikern || bei den
Mathematikern noch immer Mode & beliebt ist obwohl
die Arbeit die diese Bewegung || Denkbewegung leisten sollte, längst getan ist.)
|
Kann man den Vorgang des Vorbeiziehenlassens von
Vorstellungen beim Denken durch einen anderen etwa das Schreiben von
Zeichen (oder sonst einen) ersetzen der den gleichen
Dienst tut, so ist der Zug der Vorstellungen für uns damit
gleichgültig geworden. Uns
interessiert am Gedanken nur die Anwendung || der Gebrauch. |
Wenn wir sagen meine
Vorstellung von diesem Bild war der Wirklichkeit
ähnlich, so meinen wir daß sie in gewisser Beziehung
mit der
Wirklichkeit übereingestimmt |
Heißt das nun daß ich mir
z.B. diese Farbe vorgestellt habe, indem
ich eine ganz bestimmte Übersetzungsregel
angewendet habe? Und kann ich diese
Übersetzungsregel die Projektionsart
ändern wenn ich will? |
Kann
man sagen daß die Vorstellung, das was etwa beim
Aussprechen eines Satzes vor sich geht,
nur dann ein Gedanke ist wenn es || sie angewandt wird || nur ein Gedanke ist
insofern es || sie angewandt
wird? Wie ein
Mechanismus nur wenn er arbeitet als solcher || Mechanismus auftritt || funktioniert. Aber wir nennen auch eine stehende Uhr, eine Uhr. |
31.
Bei einem
onomatopoetischen Wort gehört der Klang mit
zum Symbol. Es ist als schriebe man das Wort „rot” mit roter
Tinte das Wort „grün” mit
grüner Tinte. |
Wie wird ein Plan
gebraucht, || ? denn das ist die
einzige Frage die uns hier angeht & deren Beantwortung zeigen
kann worin das Verständnis || Verstehen des Planes besteht, soweit es für uns
Interesse hat. |
1.11.
Man kann manchen Satz nur im
Zusammenhang mit anderen verstehen. Wenn ich
z.B. etwa in einer Novelle lese:
„Nachdem er das gesagt hatte,
verließ er sie, wie am vorigen Tag”. Wenn man mich fragt ob ich diesen
Satz verstehe, wäre es nicht leicht darauf zu antworten.
Es ist ein deutscher Satz & insofern verstehe ich
ihn. Ich wüßte wie man diesen Satz etwa gebrauchen
könnte, ich könnte selbst einen Zusammenhang
für ihn erfinden. Und doch verstehe ich ihn nicht
so wie ich ihn verstünde wenn ich das Buch
bis dorthin gelesen
hätte. |
Die
Philosophischen Probleme sind wie die Kassenschlösser die durch
Einstellen eines bestimmten Wortes oder einer
bestimmten Zahl geöffnet werden so daß keine Gewalt das Tor
öffnen kann ehe gerade dieses Wort
getroffen ist & ist es getroffen, jedes Kind
sie öffnen kann. || – – – & ist es getroffen,
keinerlei Anstrengung nötig ist es zu öffnen.
|
Wenn ich gefragt würde
„kannst Du das Alphabet
hersagen”, so würde ich antworten,
ja. „Bist
Du sicher”, „ja”.
Wenn ich nun aber im Hersagen stecken bliebe & nicht weiter
wüßte, so könnte Etwas tun können hat ja eben jenen schattenhaften Charakter, d.h. es erscheint Er ist in sich abgeschlossen & weist nicht weiter als er selbst reicht. |
Die Idee daß eine Sprache
eine Wortfolge haben kann, die der Reihenfolge des Denkens
entspricht, im Gegensatz zu einer anderen Sprache, rührt von der
Auffassung her daß das Denken vom Ausdruck des Gedankens
getrennt vorgeht. Also ein wesentlich anderer Vorgang
ist. Nach dieser Auffassung könnte man
nun freilich sagen: Die
wesentlichen Eigenschaften des Negationszeichens offenbaren sich
freilich erst nach & nach im Gebrauch, aber ich
denke die Negation auf einmal. Das Zeichen
‚nicht’ ist
ja nur ein Hinweis auf den Gedanken ‚nicht’.
Es stößt mich nur daß ich das rechte denke.
(Es ist nur |
Ja, wenn man
einem Philosophie lehrt so kommt man sich genau so vor wie einer der
an den Stellgriffen eines Kassenschlosses,
herumprobiert, bis vielleicht endlich alle
Bedingungen beisammen sind, daß die Tür aufgeht. |
Was ich oben
gesagt habe kommt aber so heraus wie: Etwas können, heißt etwas
anderes tun || Eine Sache können, heißt eine
andere tun. Aber welche Beziehung muß zwischen
den beiden bestehen? |
Was
heißt es ‚einen Satz
p verstehen’, ist die gleiche Frage wie: Was macht den
Gedanken daß p der Fall ist zu dem Gedanken
der gerade dadurch befriedigt wird daß
p der Fall ist. Das
heißt: was ist die Beziehung ‒ ‒ ‒? |
Wenn man fragt: was macht den Schatten dieses
Ereignisses gerade zum Schatten dieses Ereignisses oder was
macht diesen Schatten zum Schatten dieses Ereignisses so
könnte || kann man etwa
Ähnlichkeiten des Schattens & des Ereignisses angeben die
die beiden verbinden. Aber im Fall Gedanken &
Tatsache geht das nicht. Denn die Tatsache macht
nur das zur Verifikation
|
Und
übersetzt man den Gedanken oder vielmehr den Ausdruck des
Gedankens in die Tat dann reicht der Ausdruck plus
die Übersetzungsmethode || Projektionsmethode
d.i. der Gedanke allerdings bis zur
Tatsache heran und berührt sie wie der Maßstab den zu
messenden Gegenstand. |
Understanding a symbol means
to know || knowing how it works. |
Das Denken scheint in
gewissem || einem Sinne weiter zu
reichen als jeder beschreibbare Vorgang der nicht die Wahrheit des
Gedankens beinhaltet. Aber das was eben
weiterreicht ist der Vorgang des
Projizierens || das
Projizieren.
|
Wahr & falsch verhalten sich nicht wie
rechts &
links. |
Man könnte sich ein
negatives Portrait denken d.i. ein Bild
was || das darstellen soll wie Herr
N. || A.
nicht ausschaut. (das also ein
schlechtes |
2.
Eine
Sprache die ich nicht verstehe ist keine Sprache.
Angenommen nun ich hörte einen chinesischen Satz der mir also nichts sagt & ich wollte ihm Sinn geben (irgend einen). Ich wollte ihn etwa sagen lassen daß ich einen gewissen Weg gehn soll. Könnte ich nun erstens einfach so verfahren daß ich sage, diese Lautfolge soll nun das sagen? Nein, denn die Frage wäre gleich: wie drückt diese Lautfolge das aus. Und die Antwort darauf muß nicht sein daß ich ein chinesisches Wort in ein deutsches übersetzte sondern ich muß nur den Bereich der Möglichkeiten der deutschen Satzbildung in den der anderen Satzbildung übersetzen. |
„Wie
weißt Du, daß Du rot erwartest || einen
roten Fleck erwartest?”
– aber ebensogut könnte man fragen: „wie weißt Du daß das ein roter
Fleck ist?” |
Wie weißt Du daß was Du
getan hast wirklich war das Alphabet im Geist hersagen? – Aber wie weißt Du
daß was Du hersagst nun wirklich das Alphabet
ist? |
Von
einem Wiedererkennen sollte man eigentlich nur reden, wo es außer
dem Wiedererkennen noch ein Kriterium
dafür gibt daß ich es richtig wiedererkannt habe.
|
Ein
Mensch || Einer dem man eine
Photographie des A zeigt & den man fragt findest
Du nicht daß ihm die Photographie sehr ähnlich sieht
könnte sagen „Keine Spur, sie
ist gar nicht ähnlich: das Papier ist viereckig &
ganz dünn & er nicht
…”. |
Zu dem Vorigen:
„Wie weißt Du daß was Du
jetzt hersagst das ist was Du früher im Geist hergesagt
hast?” –
„Es ist
das”, heißt
einfach: ich projiziere es in
das was || das
Symbol das ich früher hervorgebracht
habe. |
(Ich glaube Bergson hat
auf etwas Ähnliches
hingewiesen.) |
Vergleichst Du es etwa & sagst: „ja das ist es, das hat die richtige
Ähnlichkeit mit dem Symbol”? Aber welches ist die richtige
Ähnlichkeit? |
Das ist auch der Punkt wo Russells Kausale Theorie des Symbols abzutun
ist. Denn wenn || Wenn ich sage das Symbol ist das was
diesen Effekt hervorruft so
fragt es sich eben wie ich von diesem
Effekt reden kann wenn er
(noch) gar
nicht da ist. Und wie ich weiß daß es der
ist den ich gemeint habe, wenn er kommt || eintritt. |
Es ist darum keine Erklärung zu
sagen: sehr einfach wir vergleichen die
Tatsache mit unserem Erinnerungsbild, weil
vergleichen eine bestimmte Vergleichsmethode voraussetzt die nicht
gegeben ist. |
Es
wäre richtiger von einem Erkennen oder Anerkennen der
Tatsache als der erwarteten statt von einem Wiedererkennen
zu reden. |
Für das Wiedererkennen nämlich kann man
Gründe angeben, für das Anerkennen aber
nicht. |
Wir sagen „ein langer, langer Weg” aber nicht „ein kurzer, kurzer
Weg”. |
3.
Hat mir je jemand die Vorstellung der
blauen Farbe gezeigt & gesagt daß sie das ist?
|
Das
Fregesche Behauptungszeichen
ist am Platze wenn es nichts weiteres || weiter
bezeichnen soll als den Anfang des
Satzes. Man könnte allerdings auch sagen
„den Anfang der
Behauptung”, im Gegensatz zu den
Sätzen die in der Behauptung vorkommen können.
Das Behauptungszeichen dient dann
(genau)
demselben Zweck wie der Schlußpunkt des vorhergehenden
Satzes, oder etwa der große Anfangsbuchstabe. |
„Ich denke p”
hat dann mit „⊢p” eben nur „p”
gemein. |
4. Die
Denkbewegung die hier nötig ist, ist wieder die typische
Denkbewegung || Bewegung der
Relativitätstheorie. – Wenn ich sage: So arbeitet die Sprache eben, ‒ ‒ ‒ |
Mechanismus ist wesentlich das was || dessen Funktionieren man beschreiben kann,
das man erklären kann. Also kann man die Sprache
nicht mit einem Mechanismus
vergleichen. |
Im gewöhnlichen Leben, wenn ich
jemandem einen Befehl gebe so ist es mir ganz
genug ihm Zeichen zu geben. Und ich
würde nie sagen: das sind ja nur Worte,
& ich muß hinter die Worte dringen ebenso wenn ich jemanden
etwas gefragt hätte & er gibt mir eine Antwort
(also Zeichen) bin ich zufrieden – das war gerade was ich
erwartete – & sage nicht || wende nicht ein: das ist ja eine bloße
Antwort. Es ist klar daß nichts anderes erwartet werden
konnte & daß die Antwort den Gebrauch der Sprache
voraussetze, wie alles was zu sagen ist. |
5.
Ich lese in Renan Peuple
d'Israel:
„La naissance, la
maladie, la mort, le délire, la catalepsie, le sommeil, les rêves
frappaient infiniment, et, même aujourd'hui, il n'est donné
qu'à un petit nombre de voir clairement que
ces phénomènes ont leurs causes dans notre
organisation.” Im
Gegenteil es besteht gar kein Grund sich über diese Dinge zu
wundern; weil sie so alltäglich sind. Wenn
sich der primitive Als ob der Blitz heute alltäglicher oder weniger staunenswert wäre als vor 2000 Jahren. Zum Staunen muß der Mensch – und vielleicht Völker – aufwachen. Die Wissenschaft ist ein Mittel um ihn wieder einzuschläfern. |
D.h. einfach es ist falsch zu sagen:
Natürlich, diese primitiven Völker
mußten alle Phänomene |
Wenn
Renan vom bon sens
précoce der semitischen Rassen spricht (eine Idee die mir vor
langer Zeit schon vorgeschwebt ist || hat) so ist das das
Undichterische, unmittelbar auf's Konkrete
Gehende. Das was meine Philosophie
charakterisiert || bezeichnet.
Die Dinge liegen unmittelbar da vor unsern Augen || uns, kein Schleier über ihnen. – Hier trennen sich Religion & Kunst. |
Die Analyse eines Satzes ist nur
durch Definitionen möglich
|
Was
immer ich über die Erfüllung der Erwartung sagen mag, was
sie zur Erfüllung dieser Erwartung machen soll, zählt
sich zur Erwartung, ändert den
Ausdruck der Erwartung.
D.h. der Ausdruck der Erwartung ist der
vollständige Ausdruck |
Ich kann
nichts von einem Gedanken aussagen was ihn genauer beschreibt als sein
Ausdruck. |
6. Zu sagen „ja die Demonstration dieses
euklidischen Satzes mit Zirkel
& Lineal überzeugt mich schon in diesem Fall, aber wie
weiß ich daß er auch in allen anderen Fällen
stimmt” ist ganz ebenso als wollte man
sagen: Ja, jetzt um 4 Uhr stimmt der Satz aber wie weiß
ich ob er zu jeder anderen Zeit stimmt. Wer das sagte
zeigte damit daß er die Demonstration, ihr Wesen,
ganz falsch verstanden hat. Er hat sie etwa als Experiment verstanden & dann ist allerdings der zweite Einwand (so) gültig, wie der erste. |
Zu
einem Vorwort: Dieses Buch ist für diejenigen || die geschrieben, welche || die dem Geist || seinem Geist in dem es geschrieben ist freundlich gegenüberstehn. Dieser Geist ist, Zur Zeit der Unkultur aber zersplittern sich die Kräfte und die Kraft des Einzelnen wird durch entgegengesetzte Kräfte & Reibungswiderstände verbraucht Ist es mir so klar daß das Verschwinden einer Kultur nicht das Verschwinden menschlichen Wertes bedeutet sondern bloß gewisser Ausdrucksmittel dieses Werts so bleibt dennoch die Tatsache bestehen daß ich dieser || dem Strom der europäischen Zivilisation ohne Sympathie zusehe, ohne Verständnis der || für die Ziele wenn sie welche hat. Ich schreibe also eigentlich für Freunde welche in Winkeln der Welt verstreut sind. |
Ob ich von
dem typischen westlichen Wissenschaftler verstanden oder
geschätzt werde ist mir gleichgültig
weil er den Geist in dem ich schreibe doch nicht versteht.
|
Unsere Zivilisation ist durch
das Wort Fortschritt charakterisiert. Der Fortschritt
ist ihre Form nicht eine ihrer
Eigenschaften daß sie fortschreitet.
Sie ist typisch aufbauend. Ihre
⋎ Tätigkeit ist es ein immer
komplizierteres Gebilde zu konstruieren. Und auch die
Klarheit dient doch nur wieder diesem Zweck & ist
nicht Selbstzweck. Mir dagegen ist die Klarheit die Durchsichtigkeit Selbstzweck. Es interessiert mich nicht ein Gebäude aufzuführen sondern die Grundlagen der möglichen Gebäude durchsichtig vor mir zu haben. Mein Ziel ist also ein anderes als das der Wissenschaftler & meine Denkbewegung von der ihrigen verschieden. |
Jeder Satz den ich schreibe meint immer schon das Ganze also
immer wieder dasselbe & es sind
quasi || gleichsam nur Ansichten eines
Gegenstandes von || unter verschiedenen
Winkeln betrachtet. |
Ich
könnte sagen: Wenn der Ort zu dem ich gelangen will
nur auf einer Leiter zu ersteigen wäre, ich gäbe es auf
dahin zu gelangen. Denn dort wo ich wirklich hin muß,
dort muß ich eigentlich schon sein. Was auf einer Leiter erreichbar |
Die eine Bewegung reiht
einen Gedanken an den andern, die andere zielt immer nach
demselben Ort. |
Die eine Bewegung baut & nimmt Stein auf Stein
(in die
Hand) || ergreift einen Stein um den
andern, die andere greift immer wieder nach
demselben || dem
Selben. |
7. Die Gefahr
eines langen Vorworts ist die daß der Geist eines Buches sich in
diesem zeigen muß & nicht beschrieben werden kann.
Denn ist ein Buch nur für wenige geschrieben so wird
sich das eben dadurch zeigen daß nur wenige es
verstehen. Das Buch muß automatisch die Scheidung
derer bewirken die es verstehen & die es nicht
verstehen. Auch das Vorwort ist eben
für solche || die
geschrieben, die das Buch verstehen.
Es hat keinen Sinn jemandem etwas zu sagen was er nicht versteht, auch wenn man hinzusetzt daß er es nicht verstehen kann. (Das geschieht so oft mit einem Menschen den man liebt.) Willst Du nicht daß gewisse Menschen in ein Zimmer gehen so Anständigerweise hänge ein Schloß vor die Türe das nur die anzieht || nur denen auffällt die es öffnen können & denen nicht auffällt die es nicht öffnen können. || den andern nicht auffällt. Aber es ist richtig zu sagen daß das Buch meiner Meinung nach mit der fortschreitenden europäischen & amerikanischen Zivilisation nichts zu tun hat. Daß diese Zivilisation vielleicht die notwendige Umgebung dieses Geistes ist aber daß sie verschiedene Ziele haben. Alles Rituelle (quasi Hohepriesterliche) ist streng zu vermeiden weil es sofort fault || weil es unmittelbar || gleich in Fäulnis übergeht. Ein Kuß ist freilich auch ein Ritus & er fault nicht; aber eben nur soviel Ritus ist erlaubt als eben so echt ist wie ein Kuß. |
Es ist eine große Versuchung
den Geist explizit machen zu wollen.
|
Ausdruck &
Beschreibung des Gedankens. |
Der Gedanke ist durch seinen Ausdruck vollständig
beschrieben. Eine Beschreibung die nicht im
Ausdruck || außerhalb des Ausdrucks des
Gedankens enthalten ist || liegt geht uns nichts an da sie den
Gedanken psychologisch oder physiologisch
beschreibt || zur Psychologie oder Physiologie
gehört. |
Denken
heißt Sätze gebrauchen aber der Gebrauch der Sätze ist in
jeder Erklärung vorausgesetzt. Das Einzige was man an
der Sprache erklären kann ist ihre Struktur (die
Grammatik). Denn die Anwendung entzieht sich unserer
Erklärung. Es sei denn ihre Anwendung zum
Hervorbringen gewisser Wirkungen also ihre kausalen
Beziehungen. Aber diese interessieren den
Psychologen, uns nicht.
Insofern haben
Ogden &
Richards mit ihrer
kausalen Theorie || Ansicht recht nur daß sie
den anderen Aspekt nicht sehen. |
8.
Der
Sündenbock auf den man seine Sünde legt & der damit
in die Wüste hinausläuft ist ein falsches Bild wie
alle, die philosophische Irrtümer verursachen. || wie die falschen Bilder der Philosophie.
Man
könnte sagen |
Dieses Buch ist für die
geschrieben die dem Geist in dem es geschrieben || erzeugt || gemeint ist freundlich
gegenüberstehen. Dieser Geist ist ein anderer als der
des großen Stromes der europäischen &
amerikanischen Zivilisation. Dieser äußert sich in
einem Fortschritt, im Bauen immer größerer &
komplizierterer Strukturen jener andere in einem Streben
nach Klarheit & Durchsichtigkeit jeder
möglichen Struktur || welcher Struktur
immer. Dieser will die Peripherie jener das
Zentrum der Kugel erfassen || Dieser will die Welt an
der || ihrer Peripherie jener an ihrem Zentrum
erfassen. Daher reiht dieser einen
Stein an den anderen oder steigt von einer Stufe zur anderen
während jener bleibt wo er ist & immer wieder dasselbe zu
erfassen trachtet. |
Dieses Buch ist
für solche geschrieben die seinem Geist freundlich
gegenüberstehen. Dieser Geist ist ein anderer
als der des großen Stromes der
europäischen & amerikanischen Kultur || Zivilisation in dem wir alle stehen. |
Dieser will die Welt durch ihre Peripherie –
in ihrer Mannigfaltigkeit – erfassen, jener in ihrem Zentrum
– ihrem Wesen. Daher reiht dieser ein Gebilde an das
andere, steigt quasi von Stufe zu Stufe immer weiter,
|
Ich möchte sagen „dies Buch sei zur Ehre Gottes geschrieben”, aber das
wäre heute eine Schmockerei d.h. es
würde nicht richtig verstanden werden.
Das || Es heißt es ist in gutem
Willen geschrieben & soweit es nicht mit gutem
Willen also aus Eitelkeit etc.
geschrieben ist, soweit möchte der Verfasser es
verurteilt wissen. Er kann es nicht weiter von
diesen Ingredienzien reinigen als er selbst davon
rein ist. |
Wo man
an die Grenze seiner eigenen Anständigkeit stößt dort
entsteht quasi ein Wirbel der Gedanken (&) || , ein endloser
Regreß: man mag
sagen was man will, es führt einen nicht
weiter. |
Dies Buch übergebe
ich allen denen, die dem Geist in dem es gemeint ist
freundlich gegenüberstehen. |
In meinem
früheren Buch ist die Lösung der Probleme noch viel zu wenig
hausbacken dargestellt es hat noch zu sehr den
Anschein als wären Entdeckungen notwendig um unsere
Probleme zu lösen & es ist alles noch zu wenig die Form
von grammatischen Selbstverständlichkeiten |
9. Wir
verwechseln das Wort „grün” mit dem
Satz „a ist
grün”. (Daher auch
unsere Schwierigkeit es im Satz „a
ist nicht grün” zu
erklären.) [Das
ist auch eine jener
Selbstverständlichkeiten.]
Wie wir auch in den Schwierigkeiten die
‚Zahnschmerzen’
betreffend das Wort „Zahnschmerzen”
verwechseln mit dem Satz „ich habe
Zahnschmerzen”. Das heißt
wir glauben daß was erst in diesem Satz ausgedrückt ist schon
in dem Wort liegt. |
Wir fragen: Was ist
ein Gedanke, welcher Art muß etwas sein um die Funktion
des Gedankens verrichten zu können. Und diese Frage
ist ganz analog der: Was ist, oder wie
funktioniert, eine Nähmaschine.
„Wie macht sie
das?” Aber die Antwort könnte sein: Schau den Stich an; alles was der Nähmaschine wesentlich ist, ist in ihm zu sehen; alles andere kann so oder anders sein. |
Wir
fragen wie muß der Gedanke beschaffen sein um seine
Funktion zu verrichten || Bestimmung zu
erfüllen; aber was ist denn seine Funktion?
Wenn sie nicht in ihm selbst liegt |
Welcher Art muß die
Bewegung der nähenden Hand & Nadel sein damit dieser
Stich herauskommt? – Alles kann man
ändern – d.h. ist unwesentlich
– außer das was dem Stich selbst wesentlich
ist. Das was der Stich mit jener ganzen Vorrichtung gemein
haben muß. |
Die logische
Erklärung der Nähmaschine könnte also
nichts tun als den Stich beschreiben.
Und zwar das Geometrische an
ihm, während alles andere als unwesentlich dargestellt
wird. |
10. Von
der Sprache kann man kein Gleichnis machen, nur ein Beispiel
geben. |
Ehe das
Kombinationsschloß nicht auf die richtige
Kombination eingestellt ist kann keine Kraft
es || die Türe öffnen &
ist die richtige Kombination eingestellt so braucht es keine
Kraft sie zu öffnen. Es ist
schwer für solche Menschen sich daran zu gewöhnen die
es immer mit Türen zu tun
|| die sich durch Kraftanstrengung öffnen lassen & im Verhältnis zur angewandten Kraft. |
„Wie arbeitet der Gedanke, wie
bedient er sich seines Ausdrucks?”, das ist || klingt analog der
Frage: „wie arbeitet der
Webstuhl, wie bedient er sich der Karten?”. |
Daraus daß wir das Eine
mit den Worten beschreiben „ich glaube, daß
p”
das Andere mit den Worten „p” || „es ist wahr daß
p” sollen wir eben lernen wie die Worte im Satz
p gebraucht sind. Es
ist klar daß die beiden Sätze || Behauptungen
ganz verschiedene Tatsachen beschreiben. Die Frage
ist werden in beiden Fällen diese Worte in einer
anderen Weise gebraucht? So als
wäre etwa im zweiten Fall nur von den Worten die Rede &
gehörte der Satz p in
Anführungszeichen. Aber das ist offenbar nicht
der Fall. Das Gefühl ist daß mit dem Satz „ich glaube daß p der Fall ist” der Vorgang des Glaubens nicht beschrieben sei. (daß vom Webstuhl nur die Karten gegeben seien & das || alles Übrige bloß |
Man hat
vielleicht das Gefühl: es kann doch nicht im Satz „ich glaube daß
p”
das ‚p’
dasselbe bedeuten wie in der Behauptung „p”
weil ja in der Tatsache des Glaubens daß
p die Tatsache daß
p nicht enthalten ist.
Aber ‚p’
ist ja auch im ersten Satz
zusammengesetzt & nicht ein Name.
|
Was heißt der Satz: „N
hat nie gelebt”. |
Man hat das
Gefühl daß ich mich im Satz „ich erwarte daß er kommt” der Worte „er
kommt” in anderer Weise bediene als in
der Behauptung „er
kommt”. – Aber wäre
es so so könnte ich nie wissen ob |
Nun könnte man aber
fragen: Wie schaut das aus wenn er kommt?
– „Es geht die Tür auf
& ein Mann tritt herein der …”. Und wie schaut das
aus, wenn ich erwarte daß er kommt?
– „Ich gehe auf & ab,
sehe auf die Uhr …”.
– Aber der eine Vorgang hat ja mit dem anderen nicht die
geringste Ähnlichkeit! Wie kann man dann die
selben Worte zu ihrer Beschreibung
gebrauchen? Aber
auf & ab gehen
konnte ich ja auch ohne zu erwarten daß er kommen werde, auf
die Uhr sehen auch etc. das ist also nicht das
Charakteristische des Erwartens daß er
kommt. Das Charakteristische aber ist
nur eben durch diese Worte gegeben. Und „er” heißt
dasselbe wie in der Behauptung „er
kommt” & „kommt” heißt
dasselbe wie in der Behauptung & ihre Zusammenstellung
heißt || bedeutet nichts anderes.
Natürlich muß die Erwartung mit der Tatsache etwas gemein haben. Aber das ist ja auch dadurch ausgedrückt daß die Sprache beide mit den |
Die Worte sind die Eckpunkte
bestimmter Strukturen. |
11. „Die Vorstellung die mit dem Wort
rot verbunden ist, ist gewiß die welche der Tatsache entspricht
daß etwas rot ist, nicht die die der Tatsache entspricht daß
etwas blau also nicht rot ist.
Statt der Worterklärung „das↗ ist
rot” sollte
ich sagen „so sieht es aus
wenn etwas rot ist”. Ja, die Vorstellung rot ist die Vorstellung daß etwas rot ist. Und darauf beruht jene Verwechslung von Wort & Satz von der ich früher sprach.” |
Ich nehme oft die Gräben der Philosophie im Anlauf &
Sprung. Wenn dann aber jemand kommt
& sagt: wir haben diesen
Sprung || Übergang nicht
verstanden, mach uns ihn noch |
Der Vorgang des Denkens zeichnet die Wirklichkeit
nach. || Der Vorgang des Denkens ist ein
Nachzeichnen der Wirklichkeit. |
Die Kopie aber die der
Vorgang des Denkens von der Wirklichkeit macht, hat nur Bedeutung
d.h. ist nur dadurch keine
unmaßgebliche Zuordnung || maßgeblich, daß sie ein Teil eines Systems
ist. Ich will sagen: nur dadurch
verpflichtet sie zu etwas. Hat sie weitere
Konsequenzen. |
Die Zuordnung des Satzes zur
Wirklichkeit (Beschreibung) hört nur dann auf
willkürlich zu sein
(ist nur dann eine Beschreibung) wenn || wenn der Satz einem
Sprachsystem angehört. |
Daß das Wort kein Satz ist,
daß der Satz – wie ich sagte – zusammengesetzt sein
muß, heißt nichts anderes als daß der Satz Teil eines
grammatischen Systems (Mechanismus) sein muß. |
Ich
kann einen Zustand, eine Tatsache, wohl in einer ganz neuen von mir
erfundenen Sprache beschreiben, d.h. ihm
eine von mir |
„Mit welchem Recht nenne ich die
Farbe dieses Flecks ‚rot’?” |
Man
könnte sagen daß die Beweglichkeit, die
Bewegungsfreiheit, eines Mechanismus, wie des obigen,
durch eine allgemeine Gleichung ausgedrückt wird
x =
f(y), die einzusetzenden Werte sind Zahlen (und
es genügt anzunehmen daß es Kardinalzahlen sind) &
die Zahlen sind uns durch ihr Bildungsgesetz gegeben.
Aber sind wir dadurch weitergekommen? Warum sollte der
Begriff des „Und-so-weiter” nicht auch || gleich auf die Zeichnung
des Mechanismus angewandt werden?
Etwa auf die möglichen
Stellungen des 
Ja habe ich nicht wirklich nur die Zeichnung des Mechanismus in die Gleichung übersetzt? |
12.
Was heißt es ein Gesetz in
einer Reihe von Erscheinungen wahrnehmen? |
Das
Zeichen || Der Ausdruck einer allgemeinen Regel
ist auch ein Zeichen das in einem Kalkül
gebraucht werden muß (nur anders als andere
Zeichen). |
Die Grammatik besteht aus
solchen allgemeinen Regeln. Und es ist nichts zwischen dem
Ausdruck einer solchen Regel || dieser Regeln &
dem Resultat ihrer Anwendung. |
Was geschieht
wenn wir die allgemeine Regel die eine
Reihe von Fällen beherrscht herausfinden &
ausdrücken || anschreiben? Wenn ich etwa die
Fälle
Wenn ich aber nun von einer || der allgemeinen Regel Gebrauch mache, wie kommt sie in diesem Gebrauch vor? Wenn ich z.B. a a c b nach der Regel
In welcher Weise mache ich von dem Zeichen der allgemeinen
Das muß sich auch zeigen wenn ich mir z.B. etwas notiere & mit Zeichen die gewöhnlich nicht in Gebrauch sind. Ich wollte mir etwa rasch die Zahl der männlichen & weiblichen Hörer im Zimmer notieren & machte dazu für jeden Mann ein Kreuz für jede Frau einen Strich ins Notizbuch; auch diese Notiz ist eine solche nur in einem System, das ich mir geschwind für mich zurechtgelegt habe. |
Auch
jede Erklärung die ich gebe (welcher Art
immer) ist eben eine Erklärung die sagt daß es so ist
im Gegensatz zu einem anderen Fall, daß es so ist (und
nicht anders). Dieses so muß eben in einem Raum von
anderen Möglichkeiten sein. || gesehen werden. Es ist der Fall des
Zeigens an einen Ort, wenn man etwa sagt „hier ist ein roter Fleck”. Dieses Zeigen zeigt an einen Ort im
Gegensatz zu anderen Orten oder richtiger im
Gegensatz zum übrigen Raum. Der Hinweis durch
das Zeigen muß als ein Fall in einem System von
Aber kann ich ein System als solches verstehen ohne mich in ihm zu bewegen? Andrerseits aber erschöpft doch keine Bewegung ¤ die Möglichkeiten des Systems? Brauche ich also wirklich eine Bewegung um das System zu verstehen. Es ist der analoge Fall der Erklärung eines formalen Gesetzes durch eine || die Aufzählung einiger Glieder einer Reihe etwa 1, 8, 27, 64, |
Natürlich
das Zeichen eins Satzsystems bezeichnet es nur
im Gegensatz zu anderen Systemen & setzt selbst ein System
voraus. (Interne Relation die nur besteht wenn ihre
Glieder da sind.) |
13.
Ich überlege mir, der
wievielte heute ist & sage mir in
Gedanken vor: „Montag der
10te Dienstag der 11te Mittwoch der 12te
Donnerstag der 13te”; & || . Und
schreibe die ‚13’. Bei Montag der 10te
schwebte || schwebt mir vor eine Einladung die ich
für diesen Tag hatte, weswegen || & derentwegen ich mir dieses Datum
gemerkt hatte. |
Das Denken als Ganzes
& seine Anwendung geht sozusagen automatisch vor
sich. – Wieviele Zwischenstufen ich auch
zwischen den Gedanken & die Anwendung setze,
|
Die Verbindung unseres
Hauptproblems mit dem epistemologischen Problem des Wollens ist mir
schon früher einmal
aufgefallen.
Wenn in der Psychologie ein solches
hartnäckiges Problem auftritt so ist es nie eine Frage
nach der tatsächlichen Erfahrung (eine solche ist immer
viel gutmütiger) sondern ein logisches, also eigentlich
grammatisches Problem. |
Warum die grammatischen Probleme so hart
& scheinbar unausrottbar sind – weil sie mit den
ältesten Denkgewohnheiten d.h. mit den
ältesten Bildern, die in unsere Sprache selbst geprägt sind,
zusammenhängen. |
Ich habe eine bestimmte
Vorstellung, & dann kommt jemand zur Tür
herein. Aber warum nenne ich nun die Vorstellung die
ich hatte „die Vorstellung daß dieser Mensch zur Tür
hereinkommen werde”?
Aber so verwenden wir die Sprache eben. |
Jede für uns relevante
Beschreibung der Erwartung ist
zugleich eine Beschreibung des
Erwarteten. |
Aber, wird
man sagen, daß ich die Sprache so verwende ist doch nicht
genug sondern ich muß berechtigt sein, sie so zu
verwenden. – Aber die
Sprache || Verwendung der
Sprache läßt sich nicht rechtfertigen. Denn
rechtfertigen, hieße sie durch Sätze rechtfertigen.
|
Woher dann aber das Bedürfnis nach
Rechtfertigung? die Unbefriedigung?
Es ist jedenfalls das selbe Mißverständnis unserer Sprachlogik, das uns fühlen macht || das Gefühl gibt, daß p ⌵ ~p doch noch etwas sagt daß es nicht den ganzen logischen Raum erfüllt, oder wenn, daß man doch diesen Raum abgrenzen kann gegen etwas außer ihm. Ja das Wort „den ganzen” im vorigen Satz enthält schon dasselbe Mißverständnis. |
Ich nenne es nicht so || So weil es gewisse Eigenschaften
hat, || .
Außer wenn man statt dem So diese
Eigenschaften nennen kann (wenn das So
durch sie definiert ist). Ja wie ich Etwas nenne
ich ganz gleichgültig
|
Und hier ist glaube ich ein
Hauptanlaß || Hauptanstoß zum
Mißverständnis daß das „Vorkommen von rot” in zwei Tatbeständen
zwei ganz verschiedene Bedeutungen || als
„gemeinsamen
Bestandteil” einen doppelten Sinn
hat || zweierlei ganz Verschiedenes bedeuten
kann. In dem einen Fall heißt es daß sowohl da
wie dort etwas rot ist – d.h. die
Eigenschaft rot hat. In dem andern
Fall handelt es sich nicht um eine Gemeinsamkeit der Farbe
(die ja durch eine Farbangabe ausgedrückt
würde). |
Diese Gemeinsamkeit
ist eben die Harmonie zwischen Welt || Wirklichkeit & Gedanken die nicht zu beschreiben
ist. |
Kann man sagen:
Der Mechanismus muß funktionieren, wenn man ihn
braucht. Der Freiheitsgrad muß sich erst dann
äußern, & natürlich
äußert er sich dann nur in einem bestimmten || besondern Falle. So aber muß sich der Freiheitsgrad einer
grammatischen Konstruktion nur in dem Falle der Anwendung
zeigen. |
Könnte man auch
sagen: Wir verwenden |
Wenn man
einen Satz braucht, so muß er schon irgendwie
funktionieren. Das heißt man
gebraucht ihn nicht um einer Tatsache einen Lärm
beizuordnen. |
D.h. der
Gedanke muß schon eine Bewegung des
Mechanismus darstellen, nicht einfach eine seiner
Lagen. |
Der Gedanke kann kein
beliebiger Vorgang sein. Wie könnte sonst
über eine Beschreibung ein Streit entbrennen? |
Jemand
sagt „diese Blume hat vier
Blätter”; ich sehe hin &
sage „ja”. Um die Angabe mit der Wirklichkeit zu vergleichen,
mußte ich die Blätter zählen, meine Aufmerksamkeit
in bestimmter Weise auf sie
richten. Und darin bestand das Deuten des Satzes
entsprechend den grammatischen Regeln. Ich mußte die
Wirklichkeit artikulieren um sie mit dem Satz zu vergleichen.
Dieses Artikulieren kommt im Kollationieren der
Wirklichkeit |
14. Das
was Einen sagen macht daß reden nicht denken sein
kann, ist, daß das Reden als etwas
Willkürliches empfunden ist, das Denken
nicht. Und darin ist natürlich eine
Wahrheit. Nur daß das Reden auf keiner anderen
Stufe steht als irgend ein anderer Vorgang der als Symbol
verwendet wird. |
Solange
eine Zuordnung zu nichts verpflichtet (commit)
ist sie nicht symbolisch. |
Sind nicht die Worte wie
Papiergeld, das nur zwischen zwei wirklichen Werten
vermittelt? |
Aber, I feel I have
committed myself, wenn ich sage „ich wünsche hier etwas
Braunes”. |
Ist es
so? Indem ich die Wirklichkeit beschreibe mache ich
bereits von den Regeln der Grammatik Gebrauch (oder
handle gemäß diesen || solchen
Regeln). Eben weil ich die Wirklichkeit um sie zu
beschreiben bereits artikuliert sehen muß. –
Ich habe Die Wirklichkeit bereits in
gewisser Weise in den Satz übersetzt & also den
Gebrauch der Sprache bereits fixiert & bin so
also, gleichsam, eine Verpflichtung eingegangen. |
Aber auch wenn mich jemand
fragt „ist dort ein brauner
Fleck” & ich antworte „nein, ein blauer Fleck” so war ich bereits verpflichtet so zu sagen. Es war
keine willkürliche Zuordnung von Worten zu dem was ich
sah. |
Es wäre doch nicht einen
Tatbestand porträtieren wenn ich etwa beliebige Striche
auf das Papier kritzelte & sagte „es gibt gewiß eine
Projektionsmethode die diesen
Tatbestand in diese Striche || Zeichnung
projiziert”.
|
Ja auch hier (beim Porträtieren || Abbilden) fühle ich mich schon beim ersten Strich
verpflichtet – d.h. er ist nicht
willkürlich. Jedenfalls aber fängt das
Bild erst dort an wo die Verpflichtung
anfängt. |
Heißt, einer Regel
folgen, einer ausgedrückten
(ausgesprochenen) Regel folgen? |
Wenn ich
absichtlich eine gewisse Form nachzeichne so hat der Vorgang des Kopierens –
ich meine der ganze seelische Vorgang – mit der Wirklichkeit
|
Ich kann wenn ich die Figur
 kopiere
& etwa bei der oberen horizontalen Linie anfange
meinen Bleistift von ihr in verschiedener Weise leiten lassen.
Ich kann etwa trachten diese Linie ihrer Länge nach
wiederzugeben – oder nicht. Dann wird im einen
Falle mein Bleistift plötzlich angehalten werden (von dem
Modell) & wenn ich übers Ziel schieße so wird eine
andere bestimmte Reaktion eintreten die dem
tatsächlichen Anhalten hier äquivalent ist.
Im andern Fall wenn der Maßstab der Wiedergabe
gleichgültig ist wird mein
Bleistift auch anhalten aber die begleitenden seelischen
Erscheinungen werden verschieden sein. Ich könnte
sagen der Körper des gesamten Vorgangs des Kopierens
liegt mit einer bestimmten seiner
Facetten an der Vorlage an. kopiere
& etwa bei der oberen horizontalen Linie anfange
meinen Bleistift von ihr in verschiedener Weise leiten lassen.
Ich kann etwa trachten diese Linie ihrer Länge nach
wiederzugeben – oder nicht. Dann wird im einen
Falle mein Bleistift plötzlich angehalten werden (von dem
Modell) & wenn ich übers Ziel schieße so wird eine
andere bestimmte Reaktion eintreten die dem
tatsächlichen Anhalten hier äquivalent ist.
Im andern Fall wenn der Maßstab der Wiedergabe
gleichgültig ist wird mein
Bleistift auch anhalten aber die begleitenden seelischen
Erscheinungen werden verschieden sein. Ich könnte
sagen der Körper des gesamten Vorgangs des Kopierens
liegt mit einer bestimmten seiner
Facetten an der Vorlage an.
|
Und
es hat ja auch der Satz der das Kopieren beschreibt eine
Facette gemeinsam mit dem
|
Man könnte dann
sagen: Wenn auch mein Bleistift die Vorlage nicht trifft,
die Absicht trifft sie immer. |
So könnte ich sagen der
Körper des Beschreibens wenn ich
z.B. || etwa sage
„hier ist ein brauner || roter Kreis” liegt mit
einer seiner Facetten an dem Beschriebenen
an. Dadurch daß ich mit diesen Worten die
Tatsache porträtiert, nachgezeichnet,
habe. D.h. die Handlung dieses
Nachzeichnens liegt mit einer ganz
bestimmten ihrer Facetten an der
Vorlage. (Hat diese Facette mit
der Vorlage gemein – oder auch die Vorlage bildet
eine || diese
Facette.) |
Die Regel nach der
ich die Vorlage projiziert habe wäre in gewissem
Sinne eine Beschreibung des Körpers dieses Kopierens.
Denn sie würde beschreiben wie ich meinen
Bleistift von der Vorlage habe leiten lassen. Sie
wäre gleichsam eine nachträgliche Beschreibung des
Mechanismus der zwischen Vorlage & Bild eingeschaltet
ist. Und würde die weiteren
Bewegungsmöglichkeiten dieses Mechanismus
beschreiben. |
Porträtiert man aber auch etwas || Bildet man aber auch etwas nach wenn man eine Erwartung
ausdrückt? |
15. Der Satz „ich erwarte mir hier einen roten
Fleck” bildet offenbar etwas von dem
gegenwärtigen Zustand & noch etwas anderes ab.
|
Wie wenn ich eine Erinnerung
beschreibe? – Ist es nicht
wesentlich anders als wenn ich eine Erwartung
beschreibe? |
Die
Beschreibung der Erwartung ist in
gewissem || einem Sinne eine
negative Beschreibung der Gegenwart.
Denn wenn ich mir erwarte daß hier ein roter Fleck erscheinen wird || werde so heißt das jedenfalls, daß jetzt keiner da ist. Ich könnte sagen: was an dieser Beschreibung die Zukunft beschreibt ist ihr Verhältnis zu der Beschreibung der Gegenwart in derselben Sprache. Oder: ist ihr besonderes Verhältnis zur Gegenwart. |
Wie aber wenn ich sage: „Stell' Dir ein Zimmer vor
…” & nun beschreibe ich
ein Zimmer & einen Vorgang darin. Ein solcher Satz
hat zu einer Behauptung dasselbe Verhältnis wie ein Bild im
allgemeinen |
Ein
Vexierbild ist ein
ausgezeichnetes Beispiel dafür || für die
verschiedenen Weisen wie wir ein uns vorliegendes
Bild sehen können. |
Heißt „sich rot
vorstellen” „sich vorstellen daß
etwas (etwa ein Teil meines Gesichtsfeldes) rot
ist”?
Und || Oder gibt es zwei
verschiedene Vorstellungen & die eine daß ein Teil
des Gesichtsfelds (oder
das Ganze) rot ist; die andre: die
Vorstellung der Farbe rot; also die Vorstellung dessen was dem
Wort rot entspricht nicht dessen was einem Satz entspricht,
der das Wort
(rot)
enthält? Und wenn es so etwas gäbe, wie verhielte sich die eine dieser Vorstellungen zur anderen? |
Ich kann die || jene Beschreibung eines
Zimmers in eine Zeichnung übersetzen. Und das ist ihr
wesentlich. |
Von Noten spielen.
|
Das Signal gibt im Gegensatz zu seiner Erklärung
nicht die volle Multiplizität der
Tatsache. Die Erklärung aber kann
nicht mehr geben als diese Multiplizität. |
Ich
zeige Jemandem die Noten eines Musikstückes & sage
„kannst Du das lesen”. Er durchfliegt es & sagt
„ja”. Er hat beim Durchfliegen irgend
etwas getan, vielleicht
Bewegungen seines Kehlkopfs gemacht oder
gewisse Muskeln innerviert & zwar hat er die
Notenschrift in ein anderes System von
Innervierungen oder Bewegungen
übersetzt. |
Die
Regel nach welcher ich übersetze zeigt sich in meiner || im Resultat meiner Übersetzung plus || zusammen mit || und den Reaktionen der
Unbefriedigung |
In wiefern setzt das Verständnis einer Sprache, soweit es
durch das Übersetzen in eine andere Sprache (durch das
Nachzeichnen dieser Sprache) gezeigt ist,
andere Sätze derselben Sprache also grammatische
Regeln voraus. || hat das
Verständnis einer Sprache, soweit es durch das
Übersetzen in eine andere Sprache (durch das Nachzeichnen
dieser Sprache) gezeigt ist, andere Sätze
derselben Sprache also grammatische Regeln zur
Voraussetzung. |
Man könnte das auch so sagen: Ist in dem Vorgang der Übersetzung
eines Satzes schon die allgemeine Regel der
Übersetzung der Sprache dieses Satzes unzweideutig
enthalten. (Ist das nicht so als
würde man fragen: ist in dieser Bewegung des
Mechanismus schon seine ganze Wirkungsweise unzweideutig
ausgedrückt?) |
Denken wir uns den
einfachen Fall daß jemand die Strecke
|––––––––| absichtlich im
Maßstab 1 : 1 kopiert. Ist dann in dem Vorgang
des Kopierens
(nicht)
schon das Verständnis des Nachzeichnens irgend einer
Strecke im Maßstab 1 : 1 enthalten?
D.h. ist die Weise in der mein Bleistift von
der Strecke geführt wird
(nicht)
eben dieses allgemeine Gesetz? Mein Stift wurde
|
Ich würde dann sagen: Wäre die Vorlage
länger gewesen so wäre ich mit meinem Bleistift
noch weiter gefahren & wenn kürzer weniger weit.
Aber war quasi der Geist der sich hierin ausspricht schon im
Nachziehen des einen Strichs enthalten. |
Ich
kann mir vornehmen: Ich gehe solange bis ich ihn finde
(ich will etwa einen Menschen auf einer Straße
treffen.) Und nun gehe ich etwa die
Straße entlang & treffe ihn an einem bestimmten Punkt
& bleibe stehen. War in dem Vorgang des Gehens,
oder irgend einem anderen gleichzeitigen, die Befolgung der
allgemeinen Regel die ich mir vorgesetzt hatte
enthalten. Oder war der Vorgang nur in
Übereinstimmung mit dieser Regel aber auch mit
anderen entgegengesetzten Regeln? Aber wenn ich mir die allgemeine Regel vorgenommen hatte, || vornehmen konnte, so war schon in dem Festhalten dieses Vorsatzes dasjenige enthalten was das Gehen zu einer Befolgung In dem Vorsatz wird die Länge der Strecke absichtlich offen gelassen. Das wollte ich früher mit dem Wort „voraussetzungslos” andeuten. |
Das kann aber nur heißen: Es ist ein Unterschied
zwischen einem Vorsatz & einem anderen. Ich
hätte mir auch vornehmen können einen km zu gehen
& das war zufällig der Weg den || die
Weglänge die ich gehen mußte um jenen Menschen zu
treffen. (Hier erklärt sich auch das Wort
„Grund”.) |
Muß nun dieses Vornehmen
darin bestehen daß ich vor der Ausführung
meiner Handlung einen Satz, den Vorsatz,
ausspreche? |
Ich könnte
z.B. eine Linie so ziehen wollen daß sie
parallel mit der Linie a wird die etwa übrigens
eine  Parabel ist.
Aber ich will keine Parabel ziehen sondern ziehe sie nur
inzidentell wenn ich parallel zu a
fahre. Parabel ist.
Aber ich will keine Parabel ziehen sondern ziehe sie nur
inzidentell wenn ich parallel zu a
fahre. Ich hätte aber auch können eine Parabel ziehen wollen die dann zufällig mit a parallel geworden wäre. Der gesamte Vorgang wäre aber in jedem der beiden Fälle ein andrer gewesen. |
16. Unsere
Sprache macht immer wieder neue Knoten in's Denken. Und
die Philosophie wird nicht fertig damit, sie
aufzulösen. |
Beabsichtigen ist ein menschlicher psychischer
Vorgang. |
 Ich gebe
jemandem den Befehl von A eine Linie parallel zu a zu
ziehen. Ich gebe
jemandem den Befehl von A eine Linie parallel zu a zu
ziehen. Er versucht (beabsichtigt) es zu tun, aber mit dem Erfolg daß die Linie parallel zu b wird. War nun der Vorgang des Kopierens derselbe als hätte er beabsichtigt parallel zu b zu ziehen & seine Absicht ausgeführt? Ich glaube offenbar, nein. Er hat sich von der Linie a führen lassen. |
Wenn das allgemeine
Gesetz der Abbildung sich in der Tätigkeit || dem
Vorgang des Abbildens ausdrückt dann muß es in einem Zug
dieser Tätigkeit liegen & das allgemeine Gesetz ein
notwendiger Teil der Beschreibung des Vorgangs sein.
|
D.h. Das allgemeine Gesetz der
Abbildung muß ein Teil der besonderen Beschreibung
dieses Vorgangs der Abbildung sein. |
Wenn ich
meinen Bleistift von dieser |
Die Allgemeinheit
muß darin bestehen daß man etwas offen
läßt. Und dieses Offenlassen ist darin
ausgedrückt daß ich sage: Ich
lasse meinen Bleistift nur von der Linie leiten,
wie immer sie geht, gebe ich ihr nach. |
Die
Frage ist nun: wenn ich
(nun) auf
diese Weise eine Vorlage nachgezeichnet habe ist es dann
möglich den Vorgang des Nachzeichnens
wie er war auch nach einer anderen allgemeinen Regel richtig zu
beschreiben. Oder könnte || kann ich so eine Beschreibung
zurückweisen || ablehnen mit den
Worten: „nein, ich habe mich
wirklich nur von dieser (allgemeinen)
Regel leiten lassen (und nicht von jener anderen die in diesem
Falle allerdings auch dasselbe Resultat ergeben
hätte)”. |
Denken wir uns wir schalteten
tatsächlich zwischen Vorlage & Stift eine
Kopiermaschine ein (denn
schließlich sind wir ja auch eine
Kopiermaschine). Hier könnte nun von
Absicht nicht die |
Ich sagte:
Wenn ich mich von einer Vorlage || Linie leiten
lasse so ist das wie wenn ich einen Mechanismus zwischen
mich & die Vorlage || Linie
einschaltete. Aber wie, wenn dieser Mechanismus nicht
funktioniert? Ja, das heißt hier nichts; denn
funktioniert er nicht so wird der Fehler des Funktionierens als
Korrektur zu dem Erzeugnis || Resultat
gerechnet. |
Nein ein
wirklicher Mechanismus ist nicht der
Ausdruck einer allgemeinen Regel, auch dann nicht wenn seine
Bewegungen erfahrungsgemäß mit einer bestimmten Regel
übereinstimmen. Es sei denn daß ich den Fall des
Nicht-Funktionierens dadurch ausschalte, daß ich
bestimme: wie immer er sich bewegt
ist, der Definition nach, der Regel gemäß. |
Nehmen wir in unserem
psychischen Apparat einen Zeiger an dessen Ausschlag die
Abweichung der Tätigkeit von der Intention anzeigt,
dann ist eben zum Feststellen der Intention nicht
nur auf das Resultat || den Erfolg zu sehen sondern
zugleich auf den Zeiger (der die Korrektur
angibt). Befolgt etwa das Resultat eine Regel
so ist noch zu schauen ob der Zeiger dabei nicht ausgeschlagen hat
& nur dann ist diese Regel ein Ausdruck der
Intention. |
 Kopiermaschine.
Kopiermaschine. Wieder: Worin besteht es ein Gesetz zu erkennen. Es gibt doch tatsächlich diesen Vorgang. Ich zeige jemand die Reihe 2x, 4x², 6x⁴, 8x⁸, und er sagt „ja, jetzt weiß ich weiter, ich sehe das Gesetz”. (Vielleicht hat er nach den zwei ersten Gliedern ein anderes Gesetz vermutet & war erstaunt, Ein allgemeines Gesetz sehen heißt, daß in dem was man sieht in irgend einem Sinne etwas offen gelassen ist. |
Unsere Frage kann dann so
gestellt werden: Ist ein Unterschied zwischen zwei || den Fällen wenn ich die Glieder
2x, 4x² einmal
als Glieder der Reihe 2nxn ein andermal als
Glieder der Reihe
2n ∙ x(2n ‒ 1)
hinschreibe?
Offenbar ist hier || da ein
Unterschied. |
Muß nicht die
geschriebene allgemeine Regel ein Bild des Vorgangs
sein wenn ich etwas nach dieser Regel tue?! |
17.
Wie kann mich das Wort
„rot” im
Satz führen, oder ich zu diesem Wort geführt
werden? |
Ich
glaube, es war der Hauptgedanke (oder doch
einer) meines Buches daß man auch durch das Wort
„rot” oder
das was an ihnen drum & dran ist
geführt werden muß. |
Erklärung der Vorzeichen in der
Notenschrift. Muß nicht in ihr jene Multiplizität
nachgeholt (So sind die musikalischen Vorzeichen Signale.) |
Man könnte sich denken
daß die Bedeutung von ‚rot’ in einem
Archiv gleich dem Urmeter in Form eines
Täfelchens von den betreffenden Farben festgelegt
wäre. (Auch im Fall des Urmeters muß
Etwas 1 m lang sein.) |
Wie
könnte man ein Signal je verstehen, ja, wie sich etwas
selbst darunter denken & wie sollte es in
exakter Weise gebraucht werden der Gegenstand
eines Streites sein können wenn es keine Erklärung
dafür gebe, kein Kriterium daß es das
meint. Soweit darüber geredet
(gestritten) werden kann, soweit muß es sich auch
entscheiden lassen. |
Kann man sich auch ein
Ur-Nicht denken, wie man sich ein Ur-Rot denken
kann? Hätten Russell & Frege die Farbe Rot behandelt, sie hätten |
18.
Andrerseits kann doch dieses
Urrot || Ur-Rot nicht nötig sein da wir
tatsächlich einen Satz worin das Wort ‚rot’ vorkommt
ohne das Muster verstehen. Es wäre das etwa dem Fall
vergleichbar wenn man unter einem Meter das Meter des
Augenmaßes verstünde.
(Wohlgemerkt: das Meter des Augenmaßes ist nicht ein
ungenaues Meter sondern etwas anderes als das physikalische
Meter.) |
Angenommen nun aber die Sprache
gebrauchte tatsächlich statt des Wortes ‚Rot’ ein rotes
Täfelchen auf das man zeigt; diese Ausdrucksweise wäre
jedenfalls möglich. Und auch das
bedeutet etwas. – Die Frage ist aber: hilft
diese Ausdrucksweise uns mehr im Verständnis dessen
was gemeint ist & wenn, in wiefern || wodurch. Denn da wir auch die
Wortausdrucksweise verstehen so muß dann außer
dem Wort noch das vorhanden sein was
die Ausdrucksweise mit Hilfe des
Musters || das Muster vor dem Wort allein voraus
hatte. Denn: Mehr als verständlich kann eine Ausdrucksweise |
Wenn ich nun mein rotes
Täfelchen nicht bei der Hand hätte & zeigte statt
darauf auf etwas anderes Rotes; & wie
wenn ich nun gerade das Rote dazu nähme wovon ich sagen
will daß es rot ist? Wenn ich also etwa auf einen
Apfel zeigte & sagte „Das ist
so”? Oder:
„Hier ist
diese Farbe”? Warum sagt das nun nichts? Weil es stimmt was immer der Fall ist. Weil ich nicht fragen kann: „im Gegensatz zu ‒ ‒ ‒?” Das ist natürlich der gleiche Fall wie die Antwort „Ich bin's” auf die Frage „Wer ist da?”. |
Aber es hat Sinn
zu sagen: Hier ist die Farbe die ich meine. |
Ebensowenig Sinn aber wie zu sagen „hier ist diese Farbe” hat es zu sagen „ich nenne diese
Farbe hier ‚rot’ & hier ist rot”.
|
Auf die Aussage || Angabe „diese Farbe ist hier” wäre die Antwort: „würdest du |
23. Wenn ich vergessen habe welche Farbe
„rot”
bedeutet so kann ich nicht wissen ob „rötlich grün” einen Sinn hat. |
Wenn die Philosophen ein Wort
gebrauchen & nach seiner Bedeutung
fragen || forschen muß man sich
immer fragen wird denn dieses Wort in der Sprache die es
geschaffen hat || für die es geschaffen ist je
tatsächlich so gebraucht? Man wird dann meistens finden daß es nicht so ist & das Wort gegen seine normale || entgegen seiner normalen Grammatik gebraucht wird. („Wissen”, „sein”, „Ding”) |
„Ich würde diese Farbe
(jederzeit)
wiedererkennen, ich erinnere mich noch genau an
sie.” Also wird hier
das sich an sie erinnern als Bürgschaft für die
Möglichkeit des Erkennens
genommen. Und das scheint ja auch nur natürlich,
ja selbstverständlich.
Merkwürdigerweise sträubt sich jetzt
etwas in mir gegen die althergebrachte Ansicht.
Und zwar ist es das Erinnerungsbild was mir
Schwierigkeiten „Würdest Du Deinen Bruder wiedererkennen wenn er jetzt zur Tür hereinträte?” – „Gewiß”. Aber wie kann ich dessen gewiß sein? Und wenn ich ihn nun nicht erkenne wenn er wirklich eintritt, kann ich dann sagen: Ja, als ich es sagte, hätte ich ihn auch erkannt? Der Fall des Nichtwiedererkennens den ich hier meine wäre der, daß einer zur Türe hereinkäme & ich sagen müßte „ich weiß nicht ob das mein Bruder ist” (denn wenn ich sagte „nein, so schaut er nicht aus” so wäre das ja auch ein Wiedererkennen). Es hätte im Fall des Nichtwiedererkennens das Wort gleichsam seine Bedeutung verloren. |
„Ich weiß wie dieses Wort zu
gebrauchen ist”.
Was heißt das? Wie kann es niedergelegt
werden, wie ein Wort zu gebrauchen ist? Etwa
das Wort „rot”. – |
Vielleicht ist die eigentliche
Schwierigkeit die (die zwar Manchem beinahe närrisch
erscheinen mag): daß ich das Wort „rot” erkläre
indem ich auf etwas Rotes zeige &
sage „das |
„Also so wird dieses Wort
gebraucht!” Aber wie bewahre
ich denn dieses so in der Erinnerung? |
Das
Wort „rot”
wird via das Erinnerungsbild gebraucht. |
24.
Die Erklärung eines Zeichens
muß natürlich jede Meinungsverschiedenheit im Bezug auf
seine Bedeutung beseitigen können.
D.h. sie muß alle Gegensätze der
Bedeutung zum Ausdruck bringen. Und nun ist die Frage ist
dann noch eine Frage zu entscheiden? |
Jede Erklärung
eines Zeichens kann für das Zeichen (an seiner Statt)
substituiert werden. |
Die Erklärung
des Symbols muß die ganze Verantwortung
|
Jede Streitfrage
kann entschieden werden, – aber mehr ist auch nicht
nötig. |
Wo eine Meinungsverschiedenheit
über die Bedeutung eines Wortes möglich ist muß die
Erklärung sie
beseitigen || (settle) || entscheiden. |
Man könnte das
Wesen der Sprache an einem System von
Signalen erklären. |
Z.B.
a, b, c,
d bedeuten Bewegungen und zwar a = ↑,
b = ↓,
c = →,
d = ←, also
z.B. bccbda heißt
|
Ist nur die Wahl
zwischen vier Bewegungen so genügen 4 Signale.
|
Wenn die Erklärung nur Zeichen für Zeichen setzt,
wozu ist sie dann überhaupt
nötig? – Sie ist nur nötig wo sie
die Multiplizität erhöht. |
25. |
Kann man etwas in einem
wesentlich anderen Sinne
„offen
lassen” als man eine Klammer leer
läßt? |
Ich lasse mich von der Sprache
(der
Vorlage) führen aber dazu
muß ich ihr die Zügel in gewisser Weise in
die Hand geben. Und dann erst kann sie mich
führen. |
Die gedruckte Note zwingt auch
nicht den Finger auf die Taste zu
drücken. Das Notenbild zwingt mich nicht mich in
dieser (oder irgend || überhaupt einer) Weise
von ihm führen zu lassen. Habe ich mich
entschlossen mich auf diese Weise von ihm führen zu lassen,
dann führt es mich nun zu diesen & diesen
Bewegungen. |
Aber das sieht so aus als
müsse dem
Vorgang || Akt der
Übersetzung, der Abbildung ein
besonderer allgemeiner Entschluß
vorhergehen (der Entschluß, mich auf diese
Weise leiten zu lassen). |
Ich übergebe mich
der Regel. || der
Vorlage. |
Ich lasse
meine Handlung von der Vorlage bestimmen. Wenn ich
z.B. nach Noten spiele. |
26.
Wir werden nicht durch
die Noten || das Notenbild
dazu geführt überhaupt
Klavier zu spielen sondern
so zu spielen (wie wir es tun).
|
D.h. wir werden
nicht durch das System von Signalen dazu gebracht uns ihm zu
übergeben sondern wir übergeben || überlassen uns ihm & werden dann ihm
entsprechend geführt. |
So übergeben wir uns auch der
Sprache. |
„Welchen Ton wirst Du
spielen?” – „Ich werde mich danach richten, welche
Note dort steht”. |
Mein Gedanke ist daß
aus dem einzelnen Fall des
Sich-nach-etwas-Richtens
die sogenannte allgemeine Regel muß abgelesen werden
können. Diese allgemeine Regel ist also nicht etwa eine Hypothese die durch mehr Einzelfälle mit größerer Sicherheit zu bestimmen ist, sondern im Gegenteil muß man schon von einem zweiten Einzelfall |
Wie man
sich bei dem Orakel durch Abzählen der Knöpfe des Rockes
oder der Blätter eines
Gänseblümchens von der Zahl dieser
Blätter leiten läßt. |
Ich sagte schon
früher, wenn dies so ist, so muß in dem
Prozeß etwas offen gelassen
werden. So muß ich in der Absicht mich nach dem
Blumenorakel zu richten es offen lassen wie viele
Blätter die Blume tatsächlich haben wird.
¤ Der
Ausdruck dieser Absicht lautet auch:
„Wieviel Blätter immer die
Blume haben mag, … || etc.”. |
Kann nun dieses
Offen-Lassen von anderer Art sein
als das welches wir vor uns haben wenn wir etwa einen Ball
gegen eine Wand werfen & dieser Wurf es offen läßt
wann der Ball zurückkommen wird weil das von
der Entfernung der Wand abhängt die in dem Wurf nicht
präjudiziert || gegeben
ist? Oder, ist es nicht dasselbe Offenlassen das uns vorliegt |
Es handelt sich in allen
diesen Fällen darum einen vorbestimmten
Bestandteil des Satzes als Argument & daher alles
Übrige als Funktion zu
betrachten. |
Denn das Hypothetische
„wenn¤ die Wand weiter weg
gewesen wäre, so …”
nützt || hilft uns
nicht. „Wenn die Note
in || auf der nächsten Linie gestanden
hätte, so …”. Ich
könnte antworten: „Was dann geschehen wäre weiß ich
nicht, oder, wenn ich es weiß dann eben nur durch das, was mir
jetzt vorliegt”.
Denn dieses „wenn die Note auf der
anderen Linie gestanden hätte”
kann ja nichts ausdrücken als eben
die allgemeine || ist ja nur der Ausdruck der allgemeinen
Regel die ich aber aus dem gegenwärtigen Fall
ersehen muß, wenn ich sie ersehen kann. –
Anders ist es, natürlich,
wenn dieses „wenn
…” der Ausdruck einer
Hypothese ist & dann eben durch die Erfahrung erst
bestätigt oder widerlegt werden soll. |
Ist ein Blatt Papier auf dem nichts
geschrieben steht || leeres Blatt
Papier in irgend einem Sinne allgemein –
weil es uns Gelegenheit bietet was immer wir wollen darauf zu
schreiben? || Ist ein Blatt Papier auf dem nichts
geschrieben steht in irgend einem Sinne
Ist eine leere Schachtel allgemein? – |
Aber wenn
ich die allgemeine Regel aus diesem || dem besonderen Fall || diesem Fall ablesen || herauslesen kann, kann ich mehr als den Ausdruck
der allgemeinen Regel herauslesen? |
Wenn ich eine Anzahl
Striche auf einem Blatt Papier – etwa –
abzähle, so lasse ich mich von der || ihrer Anzahl leiten. Und hier haben wir – im Dezimalsystem – || , im Dezimalsystem, & wo etwa weniger als 10 Striche vorhanden sind noch dazu den Fall daß wir zu strukturell unzusammenhängenden Zeichen, den Wörtern 1, 2, 3, 4, 5, etc. geleitet werden. Aber haben wir es da nicht mit einer falschen Verwendung der Analogie des Führens zu tun? |
Daß ich einen Vorsatz
fassen kann, wissen wir. Ich kann sagen: „ich werde diese Striche
zählen”. Und das ist ein allgemeiner Vorsatz weil in ihm
offen gelassen ist wieviele Ich könnte sagen dieser Vorsatz – welcher Art er immer sein mag – beherrscht in irgend einem Sinn die Handlung. |
Wie aber wenn ein
mechanischer Zähler (eine Maschine) etwas zählt
– || (etwa die Anzahl der
km die ein Wagen zurücklegt || etwa die
Touren einer
Maschine– || )?
Er läßt sich dann auch leiten & wo ist
hier die allgemeine Regel? Wenn sie im
Mechanismus zum Ausdruck kommt so ist es nur die Allgemeinheit
der leeren Schachtel. Wenn wir das so
genau wissen, was immer die Maschine sein mag, wie kann dann die
Allgemeinheit eines Denkprozesses eine andre sein?
|
In der || einer Maschine gibt es das was man
einen verstellbaren Anschlag nennt; nach ihm richtet sich die
Länge der Bewegung eines Maschinenteiles.
Da ist es immer wieder, Und wieder nicht in der Auffassung durch einen Menschen, (einer Tätigkeit eines Menschen) sondern in einem Zeichensystem. Als ob die Auffassung nur niedergelegt sein könnte in der Grammatik eines Zeichensystems. |
Ich singe
oder spiele ein Stück nach Noten; plötzlich komme
ich an ein # und nun interpretiere ich das als den Befehl
(oder was auf dasselbe hinausläuft – erinnere mich daß
das der Befehl ist) einen Halbton höher zu
singen. Es ist nicht, daß das # || der Anblick des # mich dazu bringt einen Halbton höher
zu singen, in magischer Weise oder wie eine Droge. Was
geschieht kann man vielmehr so ausdrücken
daß ich handle als richte ich mich nach einer allgemeinen
Regel die bestimmt einen Halbton höher zu singen wo
immer ein # vor einer Note steht. Und zwar auch dann wenn mir diese allgemeine Regel nicht von
Anfang an bekannt war & |
27.
Es
ist ja auch so: Wenn ich den Befehl – etwa das
Notenbild – als Bild der Ausführung auffasse
so ist das Auftreten des # natürlich || jedenfalls kein Bild der Tätigkeit
die ich in Befolgung des # ausführe, sondern bildhaft
wird das Auftreten des # erst dadurch
daß, wo immer es auftritt ich diese selbe
Tätigkeit wiederhole. |
Aber natürlich ist auch diese Wiederholung selbst nicht
wesentlich, denn es könnte ja das # nur
einmal vorkommen & müßte dann doch ebenso
wirken wie wenn es zwei- oder 1000 mal
vorkäme. Es ist hier
wieder die Möglichkeit nicht die Wirklichkeit des
Vorkommens um die es sich handelt.
|
Man
könnte auch so sagen: In einer Sprache kommt keine
Willkürlichkeit vor. Jedes Gesetz ist ein
allgemeines Gesetz. Wäre das Wesentliche an den
Zeichen daß sie mich durch irgendwelche Kräfte zu diesem
& jenem veranlassen so brauchte es gar kein System zu
geben. Man könnte darauf freilich antworten: Die Sprache ist eben eine bestimmte Art von Drogen die durch Verabredung (Vereinbarung) wirken. Wir aber interessieren uns nur für das Wesen der Verabredung || Vereinbarung, nicht für ihre erfahrungsmäßigen Folgen. Wir interessieren uns für nichts, was auch anders sein könnte. |
Wer sich nach einem Zeichen
richtet, handelt in Befolgung einer allgemeinen Regel.
Und das kann nicht heißen daß er handelt wie er handelt & die || eine allgemeine Regel (quasi) |
Und hier droht wieder ein
Mißverständnis: Es scheint als wäre jetzt
wieder ein Mechanismus zu erforschen wie man eine Nähmaschine
erforscht wenn || indem man sie öffnet
(& das Ineinander Greifen
der Teile) untersucht. Aber darum kann es sich natürlich nicht handeln, denn sonst hätte man ja nur wieder etwas Hypothetisches || eine Hypothese gewonnen. |
Es müßte also
das allgemeine Gesetz in meiner Handlung
bewußt ausgesprochen liegen. Es ist aber doch gar kein Zweifel, daß wir auf Zeichen sehr oft rein automatisch reagieren. Etwa wenn ein geübter Notenleser etwas vom Blatt spielt. Er reagiert dann auf die Zeichen wie eine Maschine (Wir sind hier offenbar in einem Gebiet das uns eigentlich nichts angeht). Wie aber wenn der Klavierspieler danebengreift? – |
Es ist nur die
Absicht die an das Modell heranreicht. Und
das ist dadurch ausgedrückt, daß der Ausdruck der Absicht die
Beschreibung des Modells & den Ausdruck der
Projektionsregel |
Von der Vorlage geführt werden
heißt nichts anderes als die Absicht haben die Vorlage auf diese
Weise abzubilden. Die einzige
Beschreibung dieser Absicht ist ihr Ausdruck.
|
Das allgemeine Gesetz von dem ich hier rede, darf
keine Hypothese || nicht hypothetisch sein weil
feststehen muß & ein hypothetisches Gesetz durch
keine Reihe von Erfahrungen endgültig festgestellt werden
kann || könnte. |
28. Wenn ich
einen Apparat machte der nach Noten spielen könnte der
also auf das Notenbild (die zurückgeworfenen Lichtstrahlen)
in der Weise reagierte, daß er – etwa – die
Kein Mechanismus, welcher Art immer, kann eine solche Regel etablieren. Man kann nur sagen: dieser || der Mechanismus arbeitet bis jetzt dieser Regel gemäß (was natürlich heißt daß er auch anderen Regeln gemäß arbeitet). Das Funktionieren des Apparates bis zum gegenwärtigen Zeitpunkt würde gewisse Regeln zu seiner Beschreibung ausschließen aber nie eine Regel eindeutig bestimmen. |
Das Wort „geistiger || seelischer
(psychischer) Vorgang”,
„mental
process” ist an vieler Verwirrung
schuld. Wenn wir sagen der Gedanke, die Intention
sind psychische Vorgänge so stellen wir uns
dabei || darunter etwas
Ähnliches oder
Analoges vor wie unter dem Wort
chemischer Vorgang oder physiologischer Vorgang.
– Und soweit das richtig |
Gebrauchen
wir das Wort „Gedanke”, „Intention” nicht in
ähnlicher Weise wie man das Wort „geometrische Gerade”, „geometrischer
Körper” gebraucht
was zum Mißverständnis führt
als gäbe es außer der wirklichen Geraden (etwa der Kante
eines festen Körpers) noch eine andere quasi
ätherische Gerade. Im übrigen ist
aber die Ausdrucksweise „geometrische Gerade” oft vorteilhaft, wenn man nur ihre Grammatik
kennt & so wäre es auch mit dem
Wort „Gedanke” etc. |
Die Intention, wie
ich das Wort verstehe, ist nicht etwa eine psychische
Maschine die das leisten kann, was eine aus Holz und Eisen
nicht leisten kann. Sondern ich brauche das Wort
überhaupt nicht zur Bezeichnung einer Art von
Mechanismus. Ist es die Form eines
Mechanismus? Das Verhältnis eines bestimmten
Vorgangs zur Sprache. |
Wenn ich in
Wirklichkeit eine Form nachzeichne, so werde ich sie
vielleicht |
Die Intention setzt einen
Maßstab || stellt einen Maßstab auf, (sets a
standard) wonach nun die Tatsache beurteilt werden
kann. |
„So soll diese Maschine
funktionieren.”
|
„Wenn man kopiert
d.h. überhaupt abbildet, sich von einer
Vorlage leiten läßt so ist das Charakteristische daran daß
nur die Vorlage mir bewußt wird dagegen nicht die
Projektionsart. Ich bin mir bewußt daß mich die
Vorlage einmal so einmal so lenkt aber das
Wie dieser Übertragung
nehme ich sozusagen hin; ich bemerke es weiter nicht.
Und zwar weil ich es nicht mit einem Anderen
vergleiche. Ich befolge die Projektionsregel aber ich
drücke sie nicht |
„Ja in
gewissem Sinne ist alles was beim
Nachbilden der Vorlage geschieht daß diese
Vorlage an uns vorüberzieht und wir sie besser oder weniger gut
treffen. D.h. es ist das Ende der
Kopiermaschine das unserer Vorlage
entlangläuft was wir beobachten, die ganze übrige
Maschine nehmen wir als gegeben hin. Wir merken sozusagen
nur was sich ändert nicht was sich gleichbleibt.
Der
Abbildungsweise haben wir durch eine Einstellung die
gleichbleibt (ein für alle mal) Rechnung
getragen. – Und was wir spüren ist nur das
Modell.”
|
„Darum, wenn wir falsch nach Noten
singen oder spielen – so verschieden diese Abbildung der Art nach
von ihrem Vorbild ist – fühlen wir es als einen Verstoß
gegen das Modell.” |
„Die ganze Verbindung
zwischen Ton & Note muß gegeben sein.
|
Wie, wenn ich die Richtigkeit einer Abbildung
kontrollieren will, etwa die Reihe 1, 4, 9, 16 nach
der Regel y
= x². Hier verwende ich
natürlich auch eine Interpretation der
allgemeinen Regel aber diese Interpretation fällt aus meiner
Kontrolle heraus. |
29. „Wenn ich mich bei der
Konstruktion der Reihe 1, 2,
5, 26, 677, nach der Regel an =
a²n ‒ 1 + 1 richte so muß ich
natürlich dabei diese Regel deuten. Man könnte glauben daß es das Entstehungsgesetz der Reihe ausdrückt daß ich 677 tatsächlich dadurch erhalten habe, daß ich |
Man || Ich könnte sagen das erste Glied 1 macht das
nächste auf eine Weise zu 2, & 2 macht das
nächste Glied auf die selbe Weise zu
5. Das was von 2 zu 5 reicht ist die Regel. |
„Nach der Regel sollte dieser Punkt hier
sein.” –
„Aber wie weißt Du daß, nach der
Regel dieser Punkt hier sein sollte?” Dies Frage heißt irgendwie nichts. –
|
„Es ist unendlich
wichtig daß ich eine || die
Projektionsregel verstehen (sehen)
kann, ohne sie in einer allgemeinen Notation vor mir zu haben.
Ich kann aus der Reihe
 nichts darüber
aussagt wie der Mechanismus
tatsächlich funktionieren
wird. Wenn wir in dieser Zeichnung bereits die Angabe des
Freiheitsgrades sehen so geschieht es darum weil wir sie als
Ausdruck einer bestimmten Regel auffassen. Aber das
Schema nichts darüber
aussagt wie der Mechanismus
tatsächlich funktionieren
wird. Wenn wir in dieser Zeichnung bereits die Angabe des
Freiheitsgrades sehen so geschieht es darum weil wir sie als
Ausdruck einer bestimmten Regel auffassen. Aber das
Schema
|
Es ist übrigens klar, daß man nicht versucht wäre die
Regel durch
|
Das was ich
bezeichnen will, ist doch etwas was
|
Der Ausdruck der Regel,
obwohl er natürlich ein Bild der Anwendung der
Regel sein muß, kann doch in der Anwendung selbst nicht
vorkommen oder vielmehr wenn er
vorkommt || in der Anwendung der Regel
enthalten ist so ist eben die Art wie er enthalten
ist bezeichnend & der Ausdruck isoliert kann die Art
dieses Vorkommens nicht || zeigen. |
Kann ich sagen: die Absicht
sieht in der Abbildung diese Regel befolgt oder nicht
befolgt. |
Es ist || wäre dann so als unterstriche die Intention eine
gewisse Funktion, einen gewissen Zug der Beschreibung.
Etwa als schriebe man jedes Subjekt eines
Satzes mit roter Tinte um dadurch das
Prädikat als Funktion hervorzuheben.
|
Die
Intention ist nichts als ein Maßstab den wir an das was
geschieht anlegen & nach dem wir es
beschreiben. |
Wenn wir z.B. ein Musikstück von Noten
lesen so beurteilen wir das Ergebnis nach der Intention die Noten in
bestimmter Weise zu übersetzen. Dieses Urteil
reagiert in gewisser Weise auf das was sich in
der Beschreibung des Ergebnisses als
Übereinstimmung oder
Abweichung von der beabsichtigten
Übertragung darstellt. |
Wenn es etwa meine Absicht
wäre die Ziffern 1, 2, 3, 4, 5 durch ihre Quadrate abzubilden
& das Resultat wäre 1, 5, 9, 15, 27 so könnte ich dieses Resultat zunächst schreiben 1, 4 + 1, 9, 16 ‒ 1, 25 + 2 & meine Reaktion auf das Ergebnis wäre etwa: 0, + 1, 0, ‒ 1, + 2. |
Wir können wohl eine Maschine zur
Illustration der Koordination zweier Vorgänge, der
Abbildung des einen in den andern verwenden, aber nur die Maschine
wie sie funktionieren soll, also die Maschine
in ganz bestimmter Weise als Ausdruck
aufgefaßt, also als Teil der
Sprache. |
Nur in diesem Sinne bildet
z.B. das Pianola die
Schrift || Loch-Schrift auf dem Streifen in das
Musikstück ab. || den Verlauf des Musikstückes
ab. Oder der Musterwebstuhl die Sprache der
|
30. Unter dem
Verstehen verstehe ich ein Korrelat
zur || der Erklärung, nicht zu einer
– etwa medizinischen –
Beeinflussung. Unter Mißverständnis meine ich also wesentlich etwas was sich durch Erklärung beseitigen läßt. Eine andere Nichtübereinstimmung nenne ich nicht Mißverständnis. |
Die
Absicht, der Vorlage
zu folgen hat die Vorlage im Auge. |
2.12.
Es ist unsinnig zu sagen „ich sehe
die Dinge || diesen Gegenstand im
Gesichtsraum”. Im Gegensatz
wozu? Ist es denkbar daß ich sie höre
oder daß ein anderer sie || ihn höre oder daß ein anderer
ihn sieht? |
Darum kann ich auch nicht sagen daß der
Gegenstand in meinem Gesichtsraum die Ursache
dessen ist, daß ich ihn sehe.
Darum ist es auch Unsinn zu sagen aus dem Urnebel haben sich die Sonnen, Planeten, die einfachsten Lebewesen & endlich ein Wesen entwickelt was so organisiert ist daß es all diese Dinge sehen & über sie Betrachtungen anstellen |
Im Gesichtsraum
ist || gibt es nichts das || was wesentlich Subjekt wäre. Und
ebenso in meinen Zahnschmerzen nichts was man den
Besitzer dieser Schmerzen nennen könnte. |
Wenn man
gefragt würde: was ist der Unterschied zwischen einem Ton
& einer Farbe &
die Antwort wäre „Töne
hören wir dagegen Farben sehen wir”
so ist das nur eine durch Erfahrung gerechtfertigte Hypothese,
wenn es überhaupt einen Sinn haben soll das zu sagen.
Und dann || in diesem Sinn ist es
denkbar, daß ich einmal Töne mit den Augen
wahrnehmen also sehen werde, & Farben hören.
Das Wesentliche der Töne & Farben ist offenbar in der
Grammatik der Wörter für Töne & Farben
gezeigt. |
29.1.31 4 Und wenn ich sagte, daß er die
Wahrheit auf ja & nein festlegt, so heißt
das, daß er nichts festlegt,
(oder)
nichts was sich sagen läßt. |
Ich sagte, der Satz
wäre wie ein Maßstab an die Wirklichkeit angelegt:
Aber der Maßstab ist, wie alle richtigen Gleichnisse des
Satzes, ein spezieller Fall des Satzes.
Und auch er bestimmt nichts, solange man nicht mit ihm
mißt. Aber Messen ist Vergleichen (und muß
heißen Übersetzen). |
Der Maßstab ist
auch ein Bild, aber er muß als Bild aufgefaßt werden.
|
Man
möchte sagen: Lege den Maßstab an
einen Körper an; er sagt nichts || nicht, daß der Körper so lang
ist. Vielmehr ist er an sich gleichsam
tot & leistet nichts von dem was der
Gedanke leistet. Es ist, als hätten wir uns
eingebildet, das Wesentliche am lebenden Menschen sei || ist die äußere Gestalt || Form
& hätten nun eine Holzpuppe || einen
Holzblock von dieser Gestalt hergestellt & sähen
mit Enttäuschung den toten Klotz, der auch keine Ähnlichkeit
mit dem Leben hat. |
Ich sage jemandem: „Geh ruf den Peter”. – Wie soll er wissen was ich meine? Es muß ihm erklärt worden sein. Aber doch nur wieder mit Zeichen. Er folgt nun dieser Erklärung. |
Wenn das Verstehen eine
notwendige Vorbereitung des Folgens war, so muß es dem Zeichen
etwas hinzugefügt haben; aber etwas was jedenfalls
nicht die Ausführung war. |
Kann man denn, und in
welchem Sinne kann man, aus dem Zeichen plus dem Verständnis
(also der Interpretation) die Ausführung ableiten,
ehe sie geschieht? Alles was man ableitet ist
doch nur eine Beschreibung der Ausführung & auch diese
Beschreibung war erst da, nachdem man sie
abgeleitet hatte. |
Die Ausführung des Befehls
leiten wir von diesem erst ab, wenn wir den
Befehl || ihn ausführen.
|
Nun
könnte man aber fragen: Warum nenne
ich gerade die eine Übertragung des
Symbols die Ausführung &
|
Alles was man im voraus
weiß, ist, daß, was immer man von diesem Befehl
ableiten wird, von ihm abgeleitet sein
wird. |
„Aber ich
verstehe doch schon vor der Ausführung, was ich zu machen
habe”. –
Gewiß. Und zwar was ist
es denn? |
Wenn ich sage
„der Satz bestimmt doch schon
im vorhinein || im voraus was ihn
wahr machen wird”, || :
Gewiß der Satz ‚p’
bestimmt, daß p der Fall sein muß, um ihn
wahr zu machen das ist aber auch alles, was man darüber sagen
kann. |
Wenn gesagt würde, daß der, Es ist damit auch gezeigt, daß das Vorkommen von Phantasiebildern, || sogenannten Vorstellungen für den Gedanken ganz unwesentlich ist. || Es ist damit auch das Unwesentliche der Phantasiebilder für den Gedanken gezeigt. |
(Man muß mit
manchem Problem erst vertraut werden, dadurch daß man zu
unzähligen Malen daran anläuft. Man lernt dann
den Geschmack des Problems kennen.) |
Ich stoße hier an die
Einmaligkeit einer Tatsache & das hängt mit dem Sinn
des Satzes „alles
fließt” zusammen. |
Wenn einer den
Befehl mißversteht & eine Übertragung die wir
nur als Bild der Ausführung auffassen für die
Ausführung selbst hält so entspräche
doch seine Übertragung auch einem Befehl unserer Sprache
& zwar einem der dem Unseren sehr ähnlich
sähe. Der Befehl etwa eine bestimmte Bewegung
auszuführen & der Befehl diese Bewegung nur zu
zeichnen haben eben die Beschreibung dieser
Bewegung mit
einander gemein. Aber sie unterscheiden
sich auch von einander & nur dadurch kann der eine das
eine der andere das andere befehlen. |
Der Befehl kann die
Ausführung nur insofern bestimmen als man sie von ihm ableiten
kann. – |
Nur das kann es
heißen ‚daß er sie
bestimmt’, daß man sie von ihm
ableiten kann. |
Der Befehl
|
Angedeutet aber ist etwas nur
insofern als ein System nicht ausdrücklich oder
unvollkommen festgelegt ist.
Wir möchten sagen, es sei uns unvollkommen angedeutet was wir zu tun hätten || haben || oder das Zeichen suggeriere nur undeutlich, was wir zu machen || tun hätten. Es sei etwa in dem Sinn undeutlich wie eine Tafel mit der Aufschrift „Links gehen” deutlicher wird wenn zugleich ein Pfeil die Richtung zeigt || Es sei etwa in dem Sinn undeutlich || undeutlich in dem Sinn in welchem wir der Deutlichkeit halber Zeichen ausführlicher geben. |
Aber für uns ist der Befehl
|
Eindeutig
aber kann er nur werden, daß in dadurch daß in dem
System || Befehlssystem || System von Befehlen eine Unterscheidung gemacht
wird die wenn sie fehlt eben die Zweideutigkeit
hervorruft. (Wenn also das System die richtige
Multiplizität || Mannigfaltigkeit
erhält.) |
Ich könnte auch sagen: Es
scheint uns als ob, wenn wir den Befehl
(
|
Nun
müßte man allerdings darauf sagen: Aber was
veranlaßt Dich denn zu gerade der Deutung?
Ist es der Befehl, dann war er ja schon eindeutig, da er nur diese
Deutung befahl. Oder hast Du die Deutung
willkürlich hinzugefügt –, dann hast Du ja auch
den Befehl nicht verstanden sondern erst das was Du aus ihm (auf
eigene Faust) gemacht hast. |
(Meine Methode ist in gewissem Sinne eine
psychologische.) |
Was heißt es die Handlung aus dem Befehl
ableiten außer eben sie ausführen; denn wie kann mir die
Handlung sonst gegeben sein es sei denn durch eine
Beschreibung. Dann aber leite ich nur eine Beschreibung
von einer anderen ab. |
Wissen was der Satz besagt kann
nur heißen: die Frage beantworten
können „was besagt
er?”. |
Den Sinn eines Satzes
verstehen || kennen kann nur heißen: die Frage
„was ist sein Sinn” beantworten können. |
Denn ist hier „Sinn-Haben” intransitiv gebraucht so daß man also nicht
den Sinn eines Satzes von dem eines anderen Satzes
unterscheiden kann, dann ist das Sinnhaben eine den Gebrauch des
Satzes begleitende Angelegenheit die uns nicht
interessiert. |
Wenn ich
aber sage: Ich leite |
Wie aber kommt die Regel in dem Handeln
nach der Regel vor? |
Nicht unbedingt so, daß meine Handlung
der Regel entspricht. Aber ein Teil des ganzen
Vorgangs der Ableitung muß der Regel entsprechen: es muß
unsere Absicht sein der Regel zu folgen. – Und man
könnte sagen daß das eben darin
besteht daß unsere Absicht der Regel folgt. |
Wie ist aber der
Zusammenhang des Gebrauchs der Sprache & der Regeln der
Grammatik || grammatischen Regeln? Soll ich
sagen die Regeln der Grammatik seien die Regeln nach
denen (d.h. in
Übereinstimmung mit welchen) das Sprechen
der || einer Gruppe von Menschen
tatsächlich || erfahrungsgemäß
|
30.1.31.
Heißt ‚den Regeln der Grammatik
folgen’, in irgend einem Sinne
während des Sprechens an diese Regeln denken?
Nein. – Heißt es bestimmten Regeln immer
gemäß reden || sprechen?
Nein. – Es heißt Regeln folgen.
– Aber das tut doch jeder der irgend etwas
macht; || : denn eine Regel wird es schon
geben der das entspricht was er tut. |
Man möchte sagen: „man muß nur etwas mit dem meinen
was man sagt, dann ist alles Wesentliche
gegeben”. Und ich betrachte
also ‚etwas meinen’ & ‚einer Regel
folgen’ als gleichbedeutend || synonym. |
Kann ich sagen: Wenn ich etwas
meine so habe ich meine Worte nach einer gewissen Regel
gewählt? |
Oder so? Wenn ich etwas meine
so habe ich Etwas porträtiert, also || d.i. nach einer Regel
dargestellt. |
Ist die
Grammatik nur die Beschreibung der tatsächlichen Handhabung
der Sprache? So daß ihre
Sätze eigentlich wie
|
Es könnten ja auch die Regeln
des Schachspiels als Sätze aus der Naturgeschichte des
Menschen aufgefaßt werden. (Wie die Spiele
der Tiere in naturgeschichtlichen Büchern beschrieben
werden.) |
„Ich meine aber doch mit diesen Worten
etwas”. Gewiß: im
Gegensatz zu dem Falle wo ich nichts meine, wo ich etwa Silben ihres
(angenehmen
oder) komischen Klangs wegen
aneinanderreihe. |
D.h. Einen Satz
sinnvoll aussprechen ist ein anderer Vorgang als etwa zu
singen lalala. |
Ich will
eigentlich sagen, daß „ich meine etwas mit dem Wort” nur heißt: ich unterscheide doch diesen Fall von
dem des sinnlosen Plapperns etc. Und
das ist zugegeben. Aber es ist damit noch keine besondere
Theorie des Meinens gegeben. |
Und so geht es in allen solchen
|
Der Vorgang ‚einer Regel
folgen’ muß durch eine Regel beschrieben
werden. Man könnte sagen, er heißt so, weil er durch eine Regel beschrieben werden muß. |
Oder auch so:
Man könnte aus jedem sinnvollen Satz eine Grammatik
ableiten. |
Aus dem Vorgang der
Übertragung von 1, 2, 3, 4, in 1, 4, 9, 16 muß ich
eine Regel entnehmen können. – Was heißt
das? Doch, daß ich einen Ausdruck einer Regel aus dem
Vorgang muß ableiten können;
d.h. einen Ausdruck
im Gegensatz zu einem anderen. |
D.h. daß ich in
einem System von Regeln eine als die passende
werde || muß auswählen
können. |
Wenn
ich z.B. sage: „ich glaube, daß er kommen
wird” – woher nehme ich diese
Worte. Warum wähle ich sie. Ist
etwas vor diesem Ausdruck || diesen Worten da,
das ich abbilde. |
Ich bin mir zwar nicht grammatischer
Regeln explizite bewußt, wenn ich die Sprache
gebrauche aber ich bin mir bewußt, die Sprache nicht ad
hoc zu erfinden. Und erfände ich sie so wäre
sie nichts nütze, wenn ich mich nach den erfundenen
Regeln nicht wieder richten wollte. |
D.h.
die Sprache funktioniert als Sprache nur durch die Regeln nach denen
wir uns in ihrem Gebrauch richten. (Wie das
Spiel nur durch Regeln als Spiel funktioniert.) |
Und zwar, ob ich
zu mir oder Andern rede. Denn auch mir teile ich nichts
mit, wenn ich Lautgruppen ad hoc mit irgend welchen
Fakten assoziiere.
|
Ich muß,
wenn ich zu mir rede,
|
Wenn ich ein Wort
in der Sprache gebrauche, so ist es entweder, weil ich es als einen
bereits bekannten Ton anschlagen will, oder indem ich
festsetzen will, daß ich das Wort in Hinkunft so gebrauchen
werde ||
anschlagen, oder aber festsetzen will, daß ich
das Wort in Hinkunft so gebrauchen
werde
|| anschlagen, oder: festsetzen will, daß ich das Wort in Hinkunft so gebrauchen
werde
. |
31. ‚Ich verstehe diese Worte’ (die ich etwa zu mir selbst sage) ‚ich meine etwas damit’, ‚sie haben einen
Sinn’ muß immer dasselbe heißen,
wie: ‚sie sind nicht ad
hoc erfundene Laute sondern Zeichen aus einem
System’. |
Etwa,
wie die Teilstriche auf einem Maßstab nur solche sind, wenn sie ein
System bilden. |
Wir verwenden die Sprache nur ihrer
Konsequenz wegen. |
Man kann sagen: „so wie ich das Wort
‚lieben || Liebe’ hier
gebrauche, kann ich nicht davon sagen …”
|
Das
Verstehen dessen was der Andere sagt kann nur
als das Befolgen einer von
vornherein || im vorhinein gegebenen
Regel beschrieben werden. |
Denn wenn wir einen Befehl befolgen
so deuten wir die Worte nicht willkürlich.
D.h. wieder, wir müssen die Unterscheidung anerkennen zwischen dem „Befolgen des || eines Befehls” & einem „willkürlichen Zuordnen einer Handlung”. |
Und die
Rechtfertigung einer Handlungsweise als Befolgung eines
Befehls wäre immer: „so habe ich's
gelernt” || „so habe ich die Sprache
gelernt”.
|
Wie aber
funktioniert so eine Rechtfertigung: „Man hat mir gesagt, das sei ein
Sessel” oder „… das sei rot” etc. Oder auch man hat mir gesagt,
wenn es heißt ‚tu p &
q’
so soll ich's so machen (wobei ich die
Tätigkeit vormache).
|
Das sind aufklärbare
Mißverständnisse. „Ist das eine Orange? ich dachte
das sei eine.” |
Kann man sagen: „Ist das rot? ich dachte das sei ein
Sessel.” |
Aber kann man sich nicht einbilden
(wenn man etwa nicht deutsch kann) ‚rot’ heiße laut
(d.h. werde so gebraucht wie in
Wirklichkeit ‚laut’ gebraucht wird). Wie wäre aber die
Aufklärung dieses
Mißverständnisses?
Etwa so? || : „rot ist eine Farbe, keine
Tonstärke”? – Eine
solche Erklärung könnte man natürlich geben, aber sie
wäre nur dem verständlich der sich bereits ganz in der
Grammatik auskennt. |
Der Satz „Ist das rot? ich dachte
das sei ein Sessel” hat nur Sinn wenn das
Wort „das”
beide Male im gleichen Sinn gebraucht wird & dann
kann || muß ich entweder ‚rot’ als Substantiv oder „ein Sessel”
als Adjektiv auffassen. |
Die
Rechtfertigung kann nur verstanden werden wenn sie in einer Sprache
gegeben wird, die unabhängig von dem
Mißverständnis
besteht. |
Man kann ein
Mißverständnis |
In der Erklärung „das
ist ein Sessel nicht das”
müssen die beiden Wörter „das” & die
dazugehörigen Gebärden verstanden werden &
sind dann vollwertige Zeichen. Die Erklärung
kann dann auch so gegeben werden: „das heißt ‚Sessel’, nicht
das” & dies ist ein
Satz, wie etwa „der Sessel ist blau,
nicht rot”. – Aber
freilich wird hier nicht die Sprache erklärt sondern
eine Sprache (mit Hilfe einer vorhandenen
andern). |
[Ich könnte als Motto meines Buches
wählen: Ein Narr kann mehr
fragen, als zehn Weise beantworten können.
Eigentlich müßte es hier heißen „zehn Gescheite”.] |
Ist es so: Grammatik hat nur die
Sprache als in der Zeit ausgedehntes Phänomen. |
Aber der Satz ist
doch etwas in Raum oder Zeit, oder in Raum & Zeit,
Ausgedehntes. |
Das
Aussprechen eines Satzes wäre kein
Porträtieren wenn ich meine Worte nicht aus einem System
wählte, so daß man sagen kann, ich wähle sie im
Gegensatz zu anderen. Aber die Worte wenn sie nicht in einem grammatischen System stehen sind ja alle gleichwertig & also wäre es dann ganz gleichgültig welche ich wählte ja – man könnte sagen – als Worte würden sie sich (dann) voneinander gar nicht unterscheiden. Man muß die Worte wählen [in demselben Sinne wie] man die Striche wählt mit denen man einen Körper abbildet. |
1.2. Wer die
Notenschrift lernt, lernt nicht alle Musikstücke, sondern die
Noten & Regeln & nur dadurch ist ihm die Notenschrift
nütze. |
Aber nicht vielleicht weil sie nur dann
ökonomisch ist, sondern weil sie sonst keine Schrift ist.
|
(Die Regel
hat die selbe Allgemeinheit wie eine
Hypothese.) |
Wenn man
den || einen Hund gelehrt hat, den Zeichenverbindungen
von a, b,
c, d  laufen zu lassen,
so muß ich das Zeichen von dem Linienzug nach der Regel
ableiten. laufen zu lassen,
so muß ich das Zeichen von dem Linienzug nach der Regel
ableiten. |
Die Aufschreibung der Regel nützt mir
nur, insofern sie mich an diese Regel im Gegensatz zu anderen erinnert,
– verhindert, daß ich etwa denke a
heiße || bedeute
↓, etc.
|
Wenn ich
sage, ich folge einer Regel, so muß darauf die Frage Sinn
haben: Welcher || Was für
einer Regel? Und die Antwort ist der Ausdruck
einer Regel (wie der
obige). Mehr aber kann
darauf nicht || unmöglich zur Antwort kommen
& also kann auch die Frage nach weiter nichts fragen, als
dieser Ausdruck beantwortet. |
Woher
aber die Unbefriedigung? Was ist es
das wir sagen möchten was || und sich nicht sagen läßt? |
Wenn ich, den
Regeln folgend statt „→” „a” schreibe, so ist es als wäre hier eine Kausalität im
Spiel die nicht hypothetisch, sondern
unmittelbar |
Eines ist klar, daß, wenn ich der Regel
(richtig)
gefolgt bin das Resultat zu der Vorlage & dem
Ausdruck der Regel || & der Regel
¤ in einer internen
Beziehung || Relation || Beziehung stehen wird, die ich nicht anders ausdrücken
kann, als durch die Wiedergabe jener drei Komplexe, weil
(so sonderbar das klingt) durch diese || in dieser
Wiedergabe allein schon alles bestimmt ist. |
„Die interne Relation sehen” kann natürlich auch nichts anderes
heißen, als die Komplexe sehen, die in ihr stehen.
Vielleicht wendet man ein, daß man die Komplexe auch sehen kann
ohne daß einem die interne Relation
auffällt || die interne Relation zu
bemerken. Aber dann sieht man eben etwas Anderes als
was man sieht ‚wenn sie einem
auffällt || man sie bemerkt’. Aber sie, die einem auffällt, kann nur etwas sein was sich beschreiben läßt, & die interne Relation läßt sich nur durch die Beschreibung der Komplexe zeigen || beschreiben. |
(Immer wieder die
Gedankenbewegung die z.B.
Freud macht wenn er
|
Wenn ich sage
beim Nachbilden || Abbilden einer Vorlage richte ich
mich nach ihr gemäß einer Regel, so will ich
sagen: im Gegensatz zu dem Fall, wenn ich mich nicht nach einer
Vorlage einer Regel gemäß richte. Dann kann dieses
Merkmal des Abbildens nur ein äußeres sein wie jedes
andere, was einen Vorgang von einem anderen
unterscheidet. |
Eigentlich sind die Worte „gemäß einer Regel” überflüssig. Alles liegt in den Worten
„sich nach der || einer
Vorlage richten”. Die Regel beschreibt nur eine Art des
Sich-Richtens im Gegensatz zu einer andern. – Die
Worte sind überflüssig, weil man sich nur einer Regel
gemäß nach etwas richten kann. |
Das heißt,
das Abbilden kann sich von einem andern Vorgang auch nur so
unterscheiden wie eben |
So wie ich früher einmal gesagt
habe: Die Intention kann auch nur ein Phänomen wie
jedes andere sein, wenn ich überhaupt von ihr reden
darf. |
Das Wählen der Striche beim Abbilden einer Vorlage ist
also allerdings ein anderer Vorgang als etwa das
bloße Zeichnen dieser Striche, wenn ich mich „nicht nach der Vorlage richte”, aber der Unterschied ist ein äußerer,
beschreibbarer wie der Unterschied zwischen den
Zeichengruppen
|
Und so steht es also auch mit dem
Wählen der Worte, wenn ich etwas mit Worten
beschreibe: dieser Vorgang unterscheidet sich von dem des
willkürlichen Zuordnens von Worten, aber eben nur
äußerlich wie sich die beiden Zeichen im vorigen
Satze unterscheiden. |
Nicht nur sind wir uns beim
Sprechen || Gebrauch der Sprache der
grammatischen Regeln nicht bewußt, sondern wären wir
es so würde es nicht helfen, nichts deutlicher machen.
|
Sich der
Regeln bewußt sein kann doch nur heißen einen
Ausdruck der Regel vor uns
haben. |
Was, in der Logik, nicht nötig ist,
hilft auch nicht || ist
auch nicht hilfreich || von
Nutzen. Was nicht nötig ist, ist überflüssig. |
Ja, wären wir uns
immer der grammatischen Regeln beim Sprechen bewußt so
würde das meinem Fall nicht auf die Beine helfen.
|
Die
gesamte Sprache kann nicht mißverstanden werden.
Denn sonst gäbe es zu diesem Mißverständnis wesentlich keine Erklärung || Aufklärung. |
Das heißt eben die
ganze Sprache muß für sich selbst sprechen. |
Warum wir ein
Wort – & nicht ein anderes – an dieser
Stelle gebrauchen, erfahren Und das ist eine Regel der Grammatik die die Position des Wortes in der Sprache bestimmt. Und (zum Zeichen daß es sich hier wirklich um Grammatik handelt) wenn A das Wort „und” gewesen wäre so könnte man weiter nichts tun als die Regeln für „und” angeben. |
Eine
Erklärung „das ist
rot” oder „das ist süß” gehören || gehört auch zur Grammatik (denn sie erklären
nur Zeichen durch Zeichen.) Und was uns außer dem
Wort „rot”
durch diese Erklärung noch bleibt ist nicht in dem Sinne
willkürlich wie das Laut- oder Schriftbild
„rot”. Denn die Vorstellung eines roten & eines
grünen Flecks bilden ein System,
während die bloßen Wörter rot & grün keines
bilden. (﹖) |
Was hat die Vorstellung
meines Spaziergangs mit diesem || dem
(Spaziergang)
gemein? Eben das was dadurch ausgedrückt ist daß
ich das eine meinen Spaziergang das andere die
Vorstellung von ihm nenne. |
cf. PU 251
Was heißt es wenn man sagt: „ich kann mir das Gegenteil davon nicht
vorstellen” oder „wie wäre es denn,
wenn es || wenn's anders wäre”;
z.B. wenn jemand gesagt hat daß meine
Vorstellungen privat seien oder daß nur ich selbst
wissen kann ob ich Schmerz empfinde und
dergl.. |
Wenn ich mir nicht vorstellen kann wie es
anders wäre || sein könnte so kann
ich mir auch nicht vorstellen wie es so sein kann.
„Ich kann mir nicht vorstellen” heißt nämlich hier nicht was es im Satz „ich kann mir keinen Totenkopf vorstellen” heißt. Ich will damit nicht auf eine mangelnde Vorstellungskraft deuten. |
Die Vorstellung liefert uns hier die
Sprache die jedenfalls die richtige Multiplizität hat.
Die Sprache mit der einfacheren
Grammatik. |
Die Rechtfertigung auf die Frage, warum
gebrauchst Du hier das Wort blau?: „Weil diese Farbe „blau”
heißt”, entspricht genau der Antwort
auf die Frage „warum liest Du hier
(den Laut) ‚a’”: „weil das Zeichen
‚a’ || als a-Laut gelesen wird”. In beiden Fällen berufe ich mich auf eine
Regel. |
2.2. Wozu
beschreibe ich denn etwas? (denn daraus soll ja das Wesen
der Sprache hervorgehen). Und das scheint sich
ja in dem Fall des Hundes, den ich
durch Zeichen lenken will, leicht zeigen zu lassen. |
Worin besteht das Vorgehn nach einer Regel? – kann man
das fragen? – Es heißt doch wohl, daß man den
allgemeinen Befehl der in der Regel liegt befolgt. |
Ich gehe nach
einer Regel vor heißt: ich gehe so vor, daß das, was
herauskommt … Daß das was herauskommt dieser Regel
genügt. |
Nach der Regel vorgehn heißt
so vorgehn, & das muß die Regel
enthalten. |
Die allgemeine Regel ist selbst ein Befehl;
wie kann sie dann dazu dienen das Wesen des Befehls zu
erklären? |
Ich kann natürlich in dem
Fall des Hundes den ich oben erwähnt habe, ganz
leicht ¤ beschreiben was ich zu tun habe &
warum. |
3.2. Wenn die Regel
heißt „wo Du ein
↑ siehst, schreib ein ‚c’”, so ist damit gegeben, was ich
tun soll, soweit es überhaupt gegeben sein kann.
|
Denn mehr
bestimmt, als durch eine genaue Beschreibung, kann etwas nicht
sein. Denn bestimmen kann nur heißen, es
beschreiben. Und das ist sehr
wichtig. |
Denn dies scheint
die einfache Antwort auf unsere langen
Schwierigkeiten zu sein. |
Alle
Schwierigkeiten || Schwierigkeit der Philosophie kann nur auf
Mißverständnissen beruhen. Eine Entdeckung
ist nie nötig, kann nie nötig sein sie
aufzulösen. Es ist ein
Mißverständnis & kann nur als solches aufgelöst
werden. D.h. ohne
Gewalt. Denn die Türe geht auf & es ist alles
an ihr in Ordnung, Du mußt nur das Schloß
verstehen & in der richtigen Weise
bewegen. |
Dann ist eine Handlung nicht
bestimmt, wenn die Beschreibung |
(Erinnern wir uns an die
Argumentation über „Zahnschmerzen”.) |
Hier ist auch der Zusammenhang mit der
Frage: „sieht der Andere
wirklich dieselbe Farbe, wenn er blau sieht, wie
ich?” Freilich, er sieht
blau! Das ist ja eben dieselbe Farbe. –
D.h. die Frage ob er als blau
dieselbe Farbe sieht ist unsinnig, wenn angenommen ist,
daß wir das Recht haben, was er sieht & ich sehe
als blau zu bezeichnen. Läßt sich im
gewöhnlichen Sinne – d.h. nach der
gewöhnlichen Methode – konstatieren, daß er nicht die
selbe Farbe sieht, so kann ich nicht sagen, daß wir beide
blau sehen. Und läßt es sich
konstatieren, daß wir beide blau sehen, dann „sehen wir beide die gleiche
Farbe” denn dieser Satz hat ja nur auf
diese Proben |
Und
so || analog verhält es sich mit der
Farbe || Frage:
„ist das was ich jetzt ‚gelb’ nenne
gewiß die gleiche Farbe, die ich früher ‚gelb’ genannt
habe?” – Gewiß, denn
es ist ja gelb. – Aber woher weißt Du
das? – Weil ich mich dran erinnere.
– Aber kann die Erinnerung nicht täuschen? –
Nein. Nicht, wenn ihr Datum gerade das ist
wonach ich mich richte.
(Übrigens weiß ich nicht ob
es noch Sinn hat zu sagen „weil ich mich
dran erinnere”; könnte ich nicht
eben so gut || ebensogut antworten „weil
ich's weiß”?)
Es gibt keinen Test dafür daß das blau ist. (d.h. daß ich diese Farbe blau nenne) |
Wir fragen: „Wie kann der Satz einen Sachverhalt
bestimmen?” Aber hat es denn
Sinn zu sagen: „Der Satz
bestimmt einen Sachverhalt”? |
Ist das nicht der Sinn des
Gleichnisses von der Nähmaschine: Wenn es sich
um die kausale Erklärung des Mechanismus handelt, hat die
Frage „Wie macht die
Nähmaschine das” einen Sinn.
Ist das aber nicht was gemeint ist, dann liegt die Antwort … |
Editorial notes
1) Continuation from Ms-108,300.
2) See facsimile; arrow pointing right, probably indicating that the indentation shall be increased.
3) Continuation in Ms-110,1.
4) Continuation from Ms-110,31.
5) Continuation in Ms-110,31.