VII.
Bemerkungen zur Philosophie. |
7. 1 Historisches
Drama; kann man es falsch nennen? „Nein, es ist
ja nicht als Geschichtsschreibung gemeint”.
Worin liegt diese Meinung? |
Denken wir uns den Fall, daß Einer ein
Geschichtswerk in aller Form geschrieben
hätte || schriebe, es aber dennoch nicht als
Geschichtswerk, sondern als die Erdichtung eines
Geschichtswerkes meinte. Was würde es
heißen, dieses Werk einmal so, einmal so
aufzufassen? Worin besteht diese Auffassung?
Doch offenbar in etwas außer dem Werk.
Quasi in einem Zusatz zu dem Werk. Oder nicht
vielmehr in einer bestimmten Verwendung, Wirkung des Werks, in einem
Eindruck, den es mir macht? Denn ein Zusatz von
Zeichen || Symbolen kann doch wieder einer
Auffassung unterliegen. || unterliegt doch wieder
einer Auffassung. |
Wir neigen dazu jede Erscheinung nur als ein Symptom der
Auffassung, Meinung, gelten zu lassen, aber nicht als diese
selbst. |
Wie sich die Sprache
von der Beschreibung der
Verifikation entfernt. Man muß
wieder entdecken, daß man die Zeit mit der Uhr mißt. – Und erkennt |
(Labor ist,
wo er gute Musik schreibt absolut unromantisch. Das ist ein
sehr merkwürdiges & bedeutsames
Zeichen.) |
Auffassung ist eine im Gegensatz zu einer
anderen. |
„p ist der
Fall”. „Es ist wahr daß
p der Fall
ist”. „Es ist wirklich wahr
daß p der Fall
ist.” Wenn der Multiplizität nichts
hinzugesetzt wird, ist das Hinzugefügte
bedeutungs-, zwecklos.
Der Zusatz der eine Auffassung ausdrückt, darf also nicht von
dieser Art sein. |
Was ist der
Unterschied zwischen der wirklichen Anwendung eines Satzes
& der nachgemachten || nachgeahmten,
gespielten? |
Kann man von
‚Beschreibung’ &
‚Ausdruck’ der Auffassung reden?
|
Das
erdachte || fingierte
Porträt. In einem Buch eine Illustration mit der
Überschrift: Baron
Münchhausen. |
„Doch solcherlei Verdrüsse pflegen die
Denkungskräfte anzuregen.” Wie
|
„Hast Du das im Ernst oder im Spaß
gemeint?” Das „im Ernst meinen” besteht nicht darin, daß zu dem ausgesprochenen Satz im Stillen noch etwas dazugedacht || hinzugesetzt wird, etwa die Worte „ich meine das im Ernst”. Von dem ganzen Satz, dem ausgesprochenen mit den dazugedachten Worten, könnte man wieder fragen: wie war er gemeint. Von Ernst oder Spaß kann man das aber nicht fragen. Also ist die Meinung (Auffassung) in diesem Sinne ein bestimmtes Erlebnis, das mit den Zeichen || dem Aussprechen des Satzes Hand in Hand geht, aber an dem Sinn des Satzes nichts ändert, ob es nun so oder anders ist. |
Wäre der Sinn nicht durch die Zeichen
& Regeln bestimmt, so gäbe es keine Verständigung
& nichts, was wir Sprache nennen könnten. |
Wie unterscheidet
sich: das (zu) glauben was man
sagt, davon daß man es sagt ohne es zu glauben? |
„Ich habe gesagt, ‚sie
ist nicht zuhause’ habe aber dabei
gewußt, daß sie zuhause war”.
Wie geht dieses Wissen zeitlich mit dem Sagen des Satzes
Hast Du es in jedem Augenblick gewußt, & braucht das Wissen keine Zeit? Ein falsches Bild verführt uns. |
Diese Art der
Betrachtung die immer wiederkehrt, nimmt ihre Wichtigkeit daher,
daß sie uns über einen falschen Begriff aufklärt den wir
vom Unmittelbaren haben. |
Es
hat freilich Sinn, zu sagen: „Während ich
ihm das erzählte wußte ich (die ganze
Zeit), daß es nicht wahr war”, sowie auch
„während ich es erzählte, glaubte ich es
auch”. Nur sind die beiden Vorgänge sehr
kompliziert & sehen sehr einfach aus;
d.h., jeder der beiden Sätze
beschreibt viele verschiedene
Prozesse || kann viele verschiedene Prozesse
beschreiben. Etwa wie wenn ich
sage „ich habe mich eine halbe Stunde lang
umgezogen”, diesem Satz die mannigfachsten
Tätigkeiten nacheinander
entsprechen. |
Wir laborieren nämlich unter || an
dem Irrtum, daß Glauben,
Meinen, Wissen,
Wünschen, Suchen,
Denken etc.
Zustände sind & daß daher hinter den
symbolischen Prozessen im Denken etwas von anderer Art |
Es ist nämlich die Anschauung
aufzugeben, daß, um vom
Unmittelbaren zu reden wir von dem Zustand in einem Zeitmoment
reden müßten. Diese Anschauung ist darin
ausgedrückt, wenn man sagt: „alles, was uns
gegeben ist, ist das Gesichtsbild &
die Daten der übrigen Sinne, sowie die Erinnerung, in dem
gegenwärtigen Augenblick”. Das
ist Unsinn; denn was meint man mit dem
„gegenwärtigen Augenblick”?
Dieser Vorstellung liegt vielmehr schon ein physikalisches
Bild zu Grunde, nämlich das, vom Strom der Erlebnisse, den
ich nun in einem Punkt || an einer
Stelle quer durchschneide. Es liegt hier eine
ähnliche Tendenz & ein ähnlicher Fehler , wie beim Idealismus (oder
Solipsismus). vor. || vor, wie beim Idealismus
(oder Solipsismus). Woher aber diese Tendenz, „zum Unmittelbaren” kommen zu wollen? Entspringt sie nicht aus dem Bedürfnis, die Verifikation des Satzes verstehen zu wollen, die |
Intuitives Denken, das wäre so, wie
eine Schachpartie auf die Form eines dauernden, gleichbleibenden
Zustandes gebracht (ebenso undenkbar). |
Auch jene Tendenz muß durch
das Verstehen der Grammatik unserer || der
Sprache deren wir uns in unserem Ausdruck bedienen &
der Ursachen unserer Mißverständnisse aufgehoben
werden. |
Auf die Frage
„wie hast Du das
gemeint”, können eben mehrerlei Antworten
kommen: „Ich hab's im Ernst (Spaß) gemeint” „Ich wollte damit sagen; daß … (folgt ein Satz)” „Ich wollte dich nur aufsitzen lassen.” |
Wie geht das vor sich, wenn man einen Satz ausspricht &
dabei den Andern nur aufsitzen lassen will? Man
spricht, lächelt, sieht zu || beobachtet was der
Andre macht, fühlt eine Spannung. Aber nirgends ist die amorphe Meinung. Diese stellt man sich gleichsam vor, wie den Inhalt eines Tiegels, dessen Aufschrift der Satz ist. |
„Inhalt des Satzes”.
|
Es stört uns quasi, daß der
Gedanke eines Satzes in keinem Moment ganz vorhanden
ist. Hier sehen wir, daß wir den Gedanken mit einem Ding
vergleichen, welches wir erzeugen & das wir nie als Ganzes
besitzen; sondern kaum entsteht ein Teil, so verschwindet ein
andrer. Das hat gewissermaßen etwas
Unbefriedigendes, weil wir – wieder
durch eine Erklärung || ein Gleichnis verführt
– uns etwas Anderes erwarten. |
Im lebendigen Gebrauch der Sprache fühlen
wir ja eine solche Unbefriedigung nicht, sondern erst, wenn wir
ein bestimmtes Bild auf die Vorgänge || Welt anwenden wollen. Aber es ist schwer
zu sagen, welches das ist. |
Der
Zeitmoment von dem ich sage, er sei die Gegenwart, die alles
enthält, was mir gegeben ist,
gehört selbst zur physikalischen Zeit. |
Denn wie ist
(denn) so ein Moment bestimmt?
Etwa durch einen Glockenschlag? Und kann ich
denn nun die ganze, mit diesem Schlag gleichzeitige Erfahrung
wirklich beschreiben? Wenn man daran denkt, es zu
versuchen, wird man sofort gewahr, daß es eine Fiktion
ist, wovon wir reden. |
Wir
stellen uns das Erleben wie einen
Filmstreifen vor, so daß man sagen kann:
dieses Bild, & kein anderes, ist in diesem Augenblick
vor der Linse. |
Aber nur
im Film kann man von einem in diesem Moment
gegenwärtigen Bild reden; nicht, wenn man aus dem
physikalischen Raum & seiner Zeit in den
|
Es ist viel seltsamer als man
gewöhnlich || wohl glaubt, daß man
im Bereich der gewöhnlichen Sprache auf den Begriff des
Lichtstrahls gekommen ist. |
Schwerlich wäre es geschehen, wenn man nicht
manchmal „Lichtstrahlen” im Staub der Luft
sähe. |
Und die Annahme
einer Lichtgeschwindigkeit hängt damit
zusammen. |
„“Das was ein cm3
Wasser wiegt, hat man ‚1 Gramm’ genannt”
– „Ja, was wiegt er denn?”
(„Bedeutung eines Wortes”)
|
8.
Wenn das Bild die Krönung
Napoleons darstellen
soll, so müßte man das nicht darunter schreiben, wenn es in
dem Bild enthalten wäre. Wenn es also auch in der
bloßen Beschreibung des Bildes mitbeschrieben
wäre. Und da könnte man nun den Unterschied || Gegensatz zwischen Gedanken & Bild scharf fassen, indem man sagt, daß die Beschreibung des Gedankens im Gegensatz zu der, des |
Liegt denn der Grund der
Verschiedenheit nicht darin, daß das gemalte Bild an
sich nicht ein Teil eines viel umfassenderen Bildes – einer
Sprache – ist? Durch die Überschrift
gliedern wir das Bild in das umfassendere ein. Könnten
wir es nicht auch so tun, daß wir es in eine Serie von gemalten
Bildern mit demselben Erfolg eingliederten? |
Das Charakteristische an der Sprache ist, daß alle
Erklärungen von vornherein || zum Voraus gegeben
werden können. D.h., daß man
sie alle mußte voraussehen können & keine erst
ad hoc gegeben werden muß. (Und das
ist es, was die Bildhaftigkeit auszumachen scheint.) |
Ich könnte mein Problem so
darstellen: Wenn ich untersuchen wollte, ob die
Krönung Napoléons
wirklich so & so stattgefunden hat, so könnte ich mich
dabei als einer Urkunde des Bildes bedienen, statt einer
Beschreibung. Und es frägt sich nun, ist die
|
Aber womit soll man die Wirklichkeit
vergleichen, || : als mit dem Satz? Und was
soll man andres tun, || : als sie mit ihm zu
vergleichen? |
Oder soll ich
sagen: Solange man das Bild mit nichts vergleicht,
kann man es mit Allem vergleichen. Wenn wir
aber denken, so vergleichen wir das Bild schon mit der
Wirklichkeit, denn wir wissen z.B.
daß Napoléon jetzt nicht hier ist, wohl aber Herr
N.N.. |
Das
hängt mit dem Problem von hier &
jetzt zusammen. |
(Die Fähigkeit zur Philosophie besteht in der
Fähigkeit von einer Tatsache der Grammatik einen
starken (nachhaltigen) || & nachhaltigen Eindruck zu
empfangen.) |
In gewissem
Sinne ist die Bedeutung der Wörter „hier”,
„jetzt” (etc.) die
einzige die ich nicht von vornherein festlegen kann.
Aber das ist natürlich |
Die Wörter
„hier”, „jetzt”,
etc. bezeichnen den Ursprung || Anfangspunkt eines
Koordinatensystems:
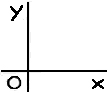 . Wie der
Buchstabe „O” aber sie beschreiben nicht seine
Lage gegenüber den Gegenständen im Raum. || sie stehen nicht für Beschreibungen der Lage des
Punktes 0 im Verhältnis zu räumlichen
Gegenständen. Sie stehen nicht für die
Beschreibung einer räumlichen Situation. . Wie der
Buchstabe „O” aber sie beschreiben nicht seine
Lage gegenüber den Gegenständen im Raum. || sie stehen nicht für Beschreibungen der Lage des
Punktes 0 im Verhältnis zu räumlichen
Gegenständen. Sie stehen nicht für die
Beschreibung einer räumlichen Situation. |
Die Bedeutung eines Worts verstehen,
heißt, seinen Gebrauch kennen, verstehen. |
Kann ein logisches Produkt in
einem Satz verborgen sein? Und wenn,
wie erfährt man das, & was für Methoden haben
wir das in ihm || im Satz
verborgene || Verborgene ans Tageslicht zu ziehen. Haben wir
noch keine sicheren Methoden es zu finden, dann können
wir auch nicht davon reden daß etwas
verborgen ist, oder verborgen sein könnte. Und haben wir eine Methode des Suchens so kann, das logische Produkt etwa, im Satz nur so verborgen sein, wie es etwa die Teilbarkeit durch 3 in der Zahl 753 ist, solange ich das Kriterium noch nicht angewandt habe, oder aber auch die √7 solange ich sie noch nicht ausgerechnet habe. Denn, das verborgene logische Produkt (in einem Satz) finden ist eine mathematische Aufgabe. |
Also ist Elementarsatz ein solcher, der sich
in dem Kalkül wie ich es
jetzt || heute benütze nicht als
Wahrheitsfunktion andrer Sätze darstellt. |
14.
Unsre Weise von den
Wörtern zu reden können wir durch den
Gegensatz || das beleuchten was
Sokrates im
„Kratylos” sagt.
Kratylos:
„Bei weitem & ohne Frage ist es
vorzüglicher, Sokrates,
durch ein ähnliches darzustellen, was jemand darstellen
will, als durch das erste beste.” –
Sokrates:
„Wohlgesprochen, …”. |
Verbindung von Wort & Sache
durch die Erklärung || das Lehren der
Sprache hergestellt. Was ist das für eine
Verbindung, welche Art? Was für Arten von
Verbindungen gibt es? |
Sokrates zu
Theaitetos:
„Und wer vorstellt, sollte nicht etwas
vorstellen?” Theaitetos: „Notwendig.” Sokrates: „Und wer etwas vorstellt, nichts Wirkliches?” Theaitetos: „So scheint es.” |
Was heißt
es: Sich eine Vorstellung machen, die der Wirklichkeit
nicht entspricht? |
Wie
unendlich einfach dieses Problem! Und wie seltsam, daß
man es überhaupt als Problem kann || konnte
ansehen wollen. |
Ich
versuche etwas, kann es aber nicht. – Was heißt es
aber: „etwas nicht versuchen
können”? |
„Wir können auch nicht einmal
versuchen, uns ein rundes Viereck
vorzustellen.” |
Man vergleiche das Vorstellen mit dem Malen eines Bildes.
Er malt also ein Bild des Menschen |
Sehr einfach. Aber warum nennen
wir es das Bild dieses Menschen? Denn, wenn es das
nicht ist, ist es (ja) nicht
falsch. – Wir nennen es so, weil er selbst es
drübergeschrieben hat. |
Also hat er nichts weiter getan, als jenes Bild zu malen &
jenen Namen drüber zu schreiben. Und das tat er
wohl auch in der Vorstellung. |
Augustinus
über das Lernen der Sprache. |
15.
Plato nennt die Hoffnung eine
Rede. (Philebos) |
Augustinus,
wenn er vom Lernen der Sprache redet, redet ausschließlich
davon wie wir den Dingen Namen beilegen, oder die Namen der Dinge
verstehen. Hier scheint also das Benennen Fundament & Um-und-Auf der Sprache zu sein. (Und was Augustinus sagt ist für uns wichtig weil es die Auffassung eines natürlich-klar denkenden Mannes ist, der von Gewiß aber denkt er zunächst an Hauptwörter & an die übrigen als ◇◇◇ etwas, was sich finden wird. (Und Plato sagt, daß der Satz aus Haupt- & Zeitwörtern besteht.) Sie beschreiben eben || also das Spiel einfacher, als es ist. Dieses Spiel gibt es aber wohl in der Wirklichkeit || kommt aber wohl in der Wirklichkeit vor. Nehmen wir etwa an ich wolle aus Bausteinen ein Haus bauen, die mir ein Andrer zureichen soll, so könnten wir erst ein Übereinkommen dadurch treffen, daß ich auf einen Stein zeigend sagte „das ist eine Säule”, auf einen andern zeigend „das ist ein Würfel”, – „das ist eine Platte” u.s.w. Und nun bestünde die Anwendung im Ausrufen jener Wörter „Säule”, „Platte” etc. in der Ordnung || Reihenfolge wie ich sie brauche. Und ganz ähnlich ist ja das Übereinkommen
|
Ich will damit sagen:
Augustinus beschreibt
wirklich einen Kalkül; nur ist nicht alles was wir Sprache
nennen dieser Kalkül. |
(Und das muß man in einer großen
Anzahl von Fällen sagen wo es sich frägt: ist diese
Darstellung brauchbar oder unbrauchbar. Die Antwort
ist dann: „ja, brauchbar; aber nur dafür, nicht für das ganze Gebiet das Du darzustellen
vorgabst”.) |
Es
ist also so, wie wenn jemand erklärte:
„Spielen || spielen besteht darin, indem || daß man Dinge gewissen Regeln gemäß auf einer
Fläche verschiebt.....” und wir ihm antworten:
Du denkst da gewiß an die Brettspiele, & auf sie ist Deine
Beschreibung auch anwendbar. Aber das sind nicht die
einzigen Spiele. Du kannst also deine Erklärung
richtigstellen indem Du nur behauptest die
Brettspiele gingen so vor sich. || sie ausdrücklich auf
diese Spiele einschränkst. |
(Man könnte
also sagen Augustinus stelle das Lernen der Sprache || die
Sache zu einfach dar; aber
auch, || : er stelle eine einfachere
Sache dar.) |
(Wer das
Schachspiel einfacher beschreibt (mit einfacheren Regeln)
als es ist, beschreibt damit dennoch ein Spiel,
aber ein anderes.) |
Ich wollte eigentlich || ursprünglich
sagen: Wie Augustinus das Lernen der Sprache beschreibt, kann uns zeigen,
woher sich diese Auffassung überhaupt schreibt.
(Von welcher primitiven
Anschauung || welchem primitiven Bild,
Weltbild.)
Man könnte den Fall mit dem einer Schrift vergleichen in der Buchstaben zum Bezeichnen von Lauten benützt würden aber auch etwa zur Bezeichnung der Stärke & Schwäche der Aussprache und als Interpunktionszeichen. Fassen wir dann diese Schrift als eine Sprache zur Beschreibung des Lautbildes auf so könnte man sich denken daß einer diese Schrift beschriebe als entspräche einfach jedem Buchstaben ein Laut & als hätten die Buchstaben nicht auch ganz andere Funktionen. – Und so einer – zu einfachen – Beschreibung der Schrift |
Man kann
z.B. – für andre verständlich
– von Kombination || Kombinationen von Farben mit Formen sprechen
(etwa der Farben rot & blau mit den Formen
Quadrat & Kreis) ebenso wie von Kombinationen
verschiedener Formen oder Körper. Und hier haben wir
die Wurzel des irreleitenden Ausdrucks,
die Tatsache sei ein Komplex von Gegenständen.
Es wird also hier, daß ein Mensch krank ist verglichen
mit der Zusammenstellung zweier Dinge
wovon das eine der Mensch ist, das andere die Krankheit
repräsentiert. Und ich kann nur
sagen: hüten wir uns vor diesem Gleichnis, oder davor zu
vergessen daß es ein Gleichnis ist. Oder man muß sagen, es verhält sich hier mit dem Wort „Kombination”, oder „Komplex”, wie mit dem Wort „Zahl” das auch in verschiedenen – mehr oder weniger logisch ähnlichen – Weisen (oder wenn man will Bedeutungen) gebraucht wird. |
Philosophieren ist, || :
falsche Argumente zurückweisen. |
Sokrates: Wer also vorstellt, was nicht
ist, der stellt nichts vor? Theaitetos: So scheint es. Sokrates: Wer aber nichts vorstellt, der wird gewiß überhaupt gar nicht vorstellen? Theaitetos: Offenbar, wie wir sehen. Setzen wir in diesem Argument [& dem ihm vorhergehenden] statt „vorstellen” etwa „zerschneiden” || „töten” so läuft es auf eine richtige Regel-Beschreibung || Regel der Verwendung dieses Wortes hinaus. Man dürfe nicht sagen || Es hat keinen Sinn zu sagen: „ich zerschneide || töten etwas was nicht existiert”. |
Ich kann
mir einen Hirsch auf dieser Wiese vorstellen der nicht da ist, aber
keinen töten der nicht da ist. – Und sich einen
Hirsch vorstellen der nicht da ist heißt, sich vorstellen,
daß ein Hirsch da ist obwohl keiner da ist. Einen Hirsch
töten aber heißt nicht: töten, daß ein Hirsch da
ist (also: verschiedene grammatische
Regeln). Wenn aber jemand sagt: „um mir
einen Hirsch vorzustellen muß es ihn doch in
einem gewissen Sinne geben”, so ist
die Antwort: nein, es muß ihn dazu in keinem Sinne
geben. Und wenn darauf gesagt würde:
Aber z.B. die braune Farbe muß es doch
geben, damit ich mir sie vorstellen kann, so ist zu sagen:
„‚Es gibt die braune Farbe’ |
„Der Klang scheint mir von dort zu
kommen.” – „Genau aus welcher
Richtung?” |
Euklidischer Haufe &
Haufe im Gesichtsfeld. |
„Er kam ungefähr von dort
→.” „Ungefähr da ist der hellste Punkt des Horizontes.” „Mach das Brett ungefähr 2 m lang.” „Das Brett ist ungefähr 2 m lang.” Muß ich, um das sagen zu können, Grenzen wissen die den Spielraum dieser Länge bestimmen? Offenbar nicht. Genügt es nicht z.B. zu sagen: „der Spielraum ± 1 cm ist ohne weiteres erlaubt; ± 2 cm wäre schon zuviel”? – Es ist doch dem Sinn meines Satzes auch wesentlich, daß ich nicht im Stande bin dem Spielraum „genaue” Grenzen zu geben. Kommt das nicht offenbar daher daß der Raum in dem ich hier arbeite eine andre Metrik hat als der Euklidische? Wenn man nämlich den Spielraum |
Ist es denn nicht so
wie man etwa beim Fleischhauer das Fleisch nur auf
Deka genau abwiegt obwohl das anderseits
eben willkürlich ist und nur bestimmt durch die
herkömmlichen Messinggewichte. Es genügt
hier zu wissen: mehr als P1 wiegt es nicht
& weniger als P2 auch nicht.
Man könnte sagen: die Gewichtsangabe besteht hier
prinzipiell nicht aus einer Zahlangabe sondern aus der Angabe eines
Intervalls, & die Intervalle bilden eine
diskontinuierliche Reihe. |
Man könnte doch sagen:
„Halte Dich jedenfalls
innerhalb
± 1 cm”
|
Träte nun auch bei dem Experiment zur
Grenzbestimmung || Bestimmung der Grenzen
kein Schwanken ein, solange wir tatsächlich das
Experiment weiterführen, so müssen wir doch damit einmal
aufhören & das Ergebnis wird immer nur sein daß
eine gewisse Länge noch erlaubt, eine andere schon unerlaubt
ist. Hier führt uns wieder die || eine
falsche Vorstellung vom Unendlichen irre, wenn wir
den
unendlichen || endlosen Prozeß dieser Untersuchung || die
unendliche || endlose Möglichkeit dieser
Untersuchung || dieses Prozesses
als || uns
abgeschlossen denken & nun von einem Grenzpunkte reden
als gäbe es hier ein Gesetz, eine geometrische Konstruktion der
der Grenzpunkt entspräche. |
„Mach mir hier einen Haufen Sand” –
„Gut, das nennt er gewiß noch einen
Haufen”. Ich konnte dem Befehl
Folge leisten also war er in Ordnung. Wie aber ist es mit
diesem Befehl: Aber auch das trifft nicht genau wie es sich wirklich verhält. Vielmehr scheint die Unsicherheit meistens von der Art wie die der Angabe des höchsten Punktes dieser Kurve 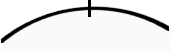 . Wir
sind eben nicht im
Euklidischen Raum & es gibt
nicht im Euklidischen Sinne einen
höchsten Punkt. Die Antwort wird heißen:
„der höchste Punkt ist ungefähr
da”, & die Grammatik des Wortes
ungefähr – in diesem Zusammenhang – gehört
dann zur Geometrie unseres Raumes. . Wir
sind eben nicht im
Euklidischen Raum & es gibt
nicht im Euklidischen Sinne einen
höchsten Punkt. Die Antwort wird heißen:
„der höchste Punkt ist ungefähr
da”, & die Grammatik des Wortes
ungefähr – in diesem Zusammenhang – gehört
dann zur Geometrie unseres Raumes. |
„Ich war der Meinung
Napoléon sei
1805 gekrönt
worden”. – „Warst Du die ganze Zeit
ununterbrochen dieser Meinung?” |
Was hat aber Deine Meinung mit
Napoléon zu tun?
Welcher Zusammenhang
besteht zwischen Deiner Meinung &
Napoléon?
Es kann, z.B., der || Welche Verbindung besteht zwischen Deiner Meinung &
Napoléon?
Es kann, z.B.,
die sein, daß das Wort
„Napoléon” in dem Ausdruck meiner Meinung
vorkommt, & der || plus dem Zusammenhang
den dieses Wort mit |
„Aber mit dem Wort
Napoléon bezeichnest
Du doch, während Du es aussprichst, eben diesen
Menschen”. – Wie geht denn, Deiner Meinung
nach, dieser Akt des Bezeichnens vor sich?
Momentan? oder braucht er Zeit? –
„Ja, aber, wenn man Dich fragt ‚hast Du
jetzt (eben) den Mann gemeint der die
Schlacht bei Austerlitz gewonnen hat?’
wirst Du doch sagen ‚ja’. Also hast Du
diesen Mann gemeint als Du den Satz in dem sein Name vorkommt
aussprachst!” – Wohl, aber nur etwa in
dem Sinne, in welchem ich auch damals || damals auch
wußte, daß 2 + 2
= 4 ist || sei. Nämlich
nicht so, als ob zu dieser Zeit ein besonderer Vorgang
stattgefunden hätte, den wir dieses
‚Meinen’ nennen könnten; auch wenn vielleicht
gewisse Bilder das Aussprechen begleitet haben, die für diese
Meinung charakteristisch sind & bei andrer
Bedeutung des Wortes Napoléon vielleicht andre gewesen wären.
Vielmehr ist die Antwort „ja, ich habe den Sieger von
Austerlitz gemeint” ein weiterer Schritt im
Kalkül. Täuschend ist an |
Wie sich der Gedanke zur
Rede verhält, kann man am besten verstehen, wenn man bedenkt, ob
etwa das Verständnis (der Gedanke), einer Rechnung
(etwa || z.B. einer
Multiplikation) als gesonderter
Prozeß neben dem Rechnungsvorgang
einherläuft. |
Wenn man
das Verstehen, Wissen, etc. als Zustand
auffaßt, dann nur hypothetisch im Sinne einer psychischen
Disposition, welche auf der selben Stufe steht, wie eine
physiologische Disposition. |
„Dachtest Du denn, als Du den Satz sagtest, daran, daß
Napoléon
…” – „Ich dachte nur, was ich
sagte”. |
Ich finde
bei Plato auf eine Frage wie
etwa „was ist Erkenntnis” nicht die
vorläufige Antwort: „ Sehen wir
einmal nach, wie |
Etwas wissen, ist von der Art dessen, einen Zettel in
einer Lade meines Schreibtisches zu haben, auf dem es
aufgeschrieben steht || ist. |
16.
Wenn ich sage: „in meine Gedanken tritt
die gegenwärtige Situation ein”, so heißt das
nicht: die Situation, soweit ich sie beschreiben kann.
Denn soweit ich sie beschreiben kann, kann ich sie malen.
|
Hier & Jetzt sind
geometrische Begriffe, wie etwa der Mittelpunkt meines
Gesichtsfeldes. |
Hier & Jetzt haben nicht eine größere
Multiplizität, als sie zu haben scheinen. Das
anzunehmen ist die große Gefahr.
Ersetze sie, durch welchen Ausdruck Du willst, immer ist es
nur ein Wort – & daher eins so gut wie das
andere. |
„Ich bin
jetzt hier.” In welcher Situation hat dies Sinn,
in welcher nicht? |
Denken
wir uns einen Brief datiert: „Hier,
Jetzt”. Aber ich glaubte, das zeigt, was diese
Wörter bedeuten; sie stehen für das vorgedruckte
„Ort … , Datum …”. Unterschied zwischen Sage & Märchen, Märchen (& andere Dichtungen) vom Jetzt & Hier abgeschnitten. |
Es ist aber ein wichtiger Satz in der
Grammatik des Wortes „hier”, daß es keinen
Sinn hat „hier” zu schreiben, wo eine
Ortsangabe stehen soll; daß ich also auf meinem Sessel kein
Täfelchen befestigen soll, mit der Aufschrift
„Dieser Stuhl ist immer nur hier zu
benützen”. |
„Dieses ist jetzt
hier”. |
Ich kann
natürlich in Bezug auf die Wörter „jetzt”
& „hier” etc. nur das
tun was ich sonst tue, nämlich ihren Gebrauch
beschreiben. Und || Aber diese
Beschreibung muß allgemein sein. D.h.
im Vorhinein, vor jedem
Gebrauch. |
Ist ein Raum
denkbar, der nur alle rationalen Punkte, aber nicht die
irrationalen enthält? Wäre etwa diese
Struktur für
unseren || unsern
Raum zu ungenau || grob? Weil wir
zu den irrationalen Punkten dann
(immer) nur
näherungsweise gelangen könnten? || Weil wir die irrationalen Punkte dann nur
näherungsweise erreichen könnten?
Unser Netz wäre also nicht fein genug? |
Ist ein Raum denkbar, der nur alle rationalen aber nicht die
irrationalen Punkte enthält? Und das heißt nur: Sind die irrationalen Zahlen nicht in den rationalen bereits präjudiziert? Sowenig wie das Schachspiel im Damespiel. Die irrationalen Zahlen füllen keine Lücke aus die die rationalen offen lassen. |
Der einfärbige Fleck in der
färbigen || farbigen Ebene ist nicht aus kleineren
Teilen zusammengesetzt außer so wie die 10 etwa aus
hundert Hundertsteln.
|
Das kleinste
sichtbare Stück ist ein Stück der physikalischen Fläche
nicht des Gesichtsfeldes. Der Versuch, der das kleinste
noch Sichtbare ermittelt, zeigt || untersucht eine Relation || stellt eine Relation fest zwischen zwei
Erscheinungen. |
Der || Dieser Versuch untersucht nicht den Gesichtsraum
& man kann den Gesichtsraum nicht untersuchen.
Nicht in ihn tiefer eindringen. |
(Wenn man
beschreiben wollte, was auf der Hand liegt, könnte man nicht
„untersuchen was auf der Hand liegt”. || „untersuchen wollen was auf der Hand
liegt”.) |
Man könnte glauben das Gesichtsfeld sei aus den minima
visibilia zusammengesetzt, etwa aus lauter kleinen
Quadraten, die man als unteilbare
Fläche || Flecke sieht. Unsinn.
Das Gesichtsfeld ist nicht zusammengesetzt wenn wir die Zusammensetzung nicht sehen. Denn bei dem Wort „Zusammensetzung” denken wir doch an die Zusammensetzung eines größeren Flecks aus kleineren. Von kleinsten sichtbaren Teilen des Gesichtsfeldes zu reden ist irreführend; gibt es denn auch Teile des Gesichtsfeldes die wir nicht mehr sehen? Und wenn wir etwa das Bild || Gesichtsbild eines Fixsterns so nennen so könnte das nur heißen daß es keinen Sinn habe hier von ‚kleiner’ zu reden, & nicht, daß tatsächlich kein Fleck im Gesichtsfeld kleiner ist. Also ist der Superlativ „das kleinste …” falsch angewendet. |
Es scheint, man kann einen einfärbigen
Fleck nicht zusammengesetzt sehen, außer, wenn man ihn
|
„Ein
Gegenstand läßt sich, in gewissem Sinne, nicht
beschreiben” (auch bei
Plato): „er
kann nicht beschrieben (erklärt) werden, sondern nur
benannt”). Unter || Mit „Gegenstand” meint man hier
„Bedeutung eines nicht weiter definierbaren
Wortes”, & mit „Beschreibung”
oder
„Erklärung” eigentlich „Definition”.
Denn daß der Gegenstand ‚von außen beschrieben
werden’ kann, daß ihm etwa Eigenschaften beigelegt || zugeschrieben werden können, wird natürlich nicht
geleugnet. |
Wir denken also
bei einem Satz wie dem oberen an einen Kalkül mit undefinierbaren
– aber richtig gesagt undefinierten – Zeichen, den
Namen, & sagen von ihnen, daß sie nicht
definiert || erklärt werden
können. |
Folgt der Satz,
daß der Kreis zwischen den beiden Geraden liegt, aus dem Satz
daß er gerade hier liegt? – Aber wie
ist dieses Hier bestimmt? Aus den
Worten „der Kreis liegt hier” folgt |
p ∙ q = p heißt
„q folgt aus
p” |
Aber es ist nicht klar, daß
es sich in dem oberen Fall um dieses Folgen handelt. |
Wie ist der Umfang des Begriffs
„dazwischenliegen”
bestimmt? Denn es soll doch im
Vorhinein festgelegt werden, welche
Möglichkeiten zu diesem Begriff gehören. Es kann,
wie ich sage, keine Überraschung sein daß ich auch
das „dazwischenliegen”
nenne. Oder: Wie können die Regeln
für das Wort „dazwischenliegen” angegeben
werden, da ich doch nicht die Fälle des Dazwischenliegens
aufzählen kann? Natürlich |
Wir würden das Wort ja auch
nicht durch Hinweisen auf alle besonderen
Fälle jemandem zu erklären suchen,
sondern || aber wohl indem wir auf einen solchen
Fall (oder mehrere) || (oder
einige) zeigten & in irgendeiner
Weise andeuteten, daß der besondere Fall nichts
ausmache || es auf den besonderen Fall nicht ankomme.
|
Das Aufzählen von Lagen ist
nicht nur nicht nötig sondern es kann hier wesentlich von
so was keine Rede sein.
|
Wie aber fügt sich dann das
Folgen in die Regeln von den Wahrheitsfunktionen ein?
Oder geschieht das durch eine festgesetzte Regel der Art
p ∙ q
= p? |
Ich
werde also ein allgemeines Zeichen der Art
„❘ •❘” haben das sich zu dem früher gebrauchten so verhält wie
x² + x zu
4˙3² +
4˙3. Und diese beiden Zeichen
müssen äußerlich unterscheidbar sein &
verschiedene Regeln von ihnen gelten (wie von
„x” und
„4”). – Eine Regel aber muß
sagen || besagen, daß 4 aber auch irgend eine andre
Zahl Und nun könnte man fragen: wie soll man es ausdrücken daß jede beliebige Zahl für „x” stehen darf, da doch dazu auch schon eine solche Variable nötig wäre. |
p ⌵ q = q heißt
„q folgt aus
p”.
Das folgt aus p ∙ q = p, denn p ⌵ q ist im allgemeinen = (p ∙ q) ⌵ (p ∙ ~q) ⌵ (~p ∙ q). Wenn aber q aus p folgt, so wird dies = p ⌵ Cont ⌵ (~p ∙ q) = p ⌵ (~p ∙ q) = q. |
Zu sagen „der Kreis liegt
entweder zwischen den beiden Geraden oder hier”
(wo dieses || das ‚hier’ ein Ort
zwischen den Geraden ist) heißt offenbar nur zu
sagen: „der Kreis liegt zwischen den beiden
Geraden” & der Zusatz „oder hier”
erscheint überflüssig. Man wird sagen: in
dem ‚irgendwo’ ist das ‚hier’
schon mitinbegriffen. Das ist aber merkwürdig weil es
nicht darin genannt ist. |
Eine
gewisse || bestimmte Schwierigkeit besteht
darin, daß || wenn die Wörter || Zeichen das nicht zu sagen scheinen, was der Gedanke
|
So, wenn wir sagen „dieser Satz gilt von allen
Zahlen” & glauben in dem Gedanken alle Zahlen wie die
Äpfel in einer Kiste gefaßt || aufgefaßt zu
haben. |
Man kann für den
Gebrauch der Variablen wohl eine Regel aufstellen & es
ist kein Pleonasmus, daß wir dabei diese
Art der Variablen gebrauchen. Denn
brauchten wir sie nicht, so wäre ja durch die Regeln
die Variable definiert. Und wir nehmen ja nicht an daß
sie sich definieren lasse, oder: daß sie definiert werden
müsse (denn einmal nehmen die Definitionen doch ein || ihr Ende). |
Das
heißt (nur), daß –
z.B. – die Variable
„x²” keine
Abkürzung ist (etwa für eine logische Summe) &
daß in unseren Gedanken auch nur ein Zeichen
dieser Multiplizität vorhanden ist. |
Nun könnte man aber fragen:
Wie kann ich nun im Voraus wissen aus welchen
Sätzen dieser allgemeine Satz folgt? |
Wenn wir
eine Erklärung etwa Kann man aber sagen:
„man kann nicht sagen, aus welchen Sätzen dieser Satz
folgt”? Das klingt so wie: man weiß es
nicht. Aber so ist es natürlich nicht. Und
ich kann ja Sätze sagen, & im vorhinein sagen, aus denen
er folgt. – „Nur nicht
alle”. – Aber das heißt ja eben
nichts. |
Es ist eben nur der
allgemeine Satz & besondere Sätze (nicht: die
besonderen Sätze). Aber der allgemeine
Satz zählt besondere Sätze nicht auf. Aber was
charakterisiert ihn denn dann als allgemein & was zeigt,
daß er nicht einfach diejenigen || die
besonderen Sätze umschließt, von denen wir in diesem
bestimmten Falle sprechen? |
Er kann nicht durch seine Spezialfälle
charakterisiert werden; denn wieviele man auch
aufzählt, so könnte er immer mit dem Produkt der
angeführten Fälle || Spezialfälle verwechselt werden.
Seine Allgemeinheit liegt also in einer
Eigenschaft || grammatischen
Eigenschaft der Variablen. |
Wie man die Zeichnung
❘ ⚬❘ als eine
Darstellung des „allgemeinen |
Worin
besteht aber – z.B.
– die unendliche Möglichkeit der Besetzung
einer || der Variablen? Wie kann
man sich etwa nach der Regel
richten: „an diese Stelle darf
keine Zahl gesetzt werden”? Die
Allgemeinheit so einer || dieser Vorschrift muß
von der Art der hypothetischen Allgemeinheit (alle Menschen
müssen sterben) sein. |
Es scheint nämlich als könnte eine Allgemeinheit
über eine bestimmte Aufzählung mit einer Art schattenhafter
Aufzählung hinausgehen. |
Denn nehmen wir an ich
hätte 7 Fälle || Spezialfälle
aufgezählt & sagte „ihre logische Summe ist aber
nicht der allgemeine Satz”, so ist das nicht genug &
ich will noch sagen, daß auch keine andere Zahl
von Fällen || Spezialfällen den
allgemeinen Satz ergibt.
Aber in diesem Zusatz scheine ich nun wiederum eine
Aufzählung, wenn auch nicht wirklich,
so doch quasi schattenhaft
auszuführen.
Aber so ist es nicht denn in dem Zusatz kommen ganz
andre Wörter als die Zahlwörter vor. |
„Wie aber soll ich es verbieten,
daß ein Zahlwort dort & dort
eingesetzt wird? Ich kann doch nicht vorhersehen
welches Zahlwort einer wird einsetzen wollen um es zu
verbieten”. – Du kannst es ja
verbieten, wenn es kommt. – Aber da || hier sprechen wir ja schon, allgemein, vom
Zahlbegriff! |
Ich
müßte sagen: Die Zahlvariable ist ein dem
Zahlzeichen verwandtes Zeichen (durch die Regeln die
von ihm gelten – wie etwa der Läufer der Königin
verwandter ist als dem Rössel). Und in der
Verwandtschaft der Regeln |
Aber es gibt nicht etwas, was eine Aufzählung
ist & doch keine Aufzählung. Eine
Allgemeinheit die quasi nur nebelhaft aufzählt aber
nicht wirklich & bis zu einer bestimmten
Grenze. |
Die Punkte
im in
„1 + 1 + 1 + 1
....” sind eben auch nur die vier
Punkte. Ein Zeichen für das sich gewisse Regeln
angeben lassen müssen. (Nämlich dieselben wie
für das Zeichen „u.s.w.
ad inf.”.) Dieses Zeichen ahmt zwar die Aufzählung in gewisser Weise nach, ist aber keine Aufzählung. Und das heißt wohl daß die Regeln, die von ihm gelten bis zu einem Punkt mit denen die von einer Aufzählung gelten übereinstimmen aber nicht ganz übereinstimmen. |
Es
gibt kein Mittelding zwischen einer || der bestimmten Aufzählung & der
Variablen || dem allgemeinen Zeichen. |
Ich habe einmal gesagt, es könne nicht Zahlen
geben und den Begriff der Zahl.
Und das ist
richtig wenn es heißt Anderseits ist die Zahlvariable kein Zahlzeichen. |
Ich wollte aber auch sagen daß der Zahlbegriff
nicht unabhängig von den Zahlen gegeben sein
könnte & das ist nicht nicht wahr.
Sondern die Zahlvariable ist in dem Sinne von einzelnen
Zahlen unabhängig als es einen Kalkül mit der
einer Klasse unsrer Zahlzeichen & ohne die allgemeine
Zahlvariable wohl gibt. Freilich gelten dann eben
nicht alle Regeln von diesen Zahlen die von unsern gelten aber doch
entsprechen sie unseren wie die Damesteine im Damespiel denen im
Schlagdamespiel. |
Was
aber macht ein Zeichen zum Ausdruck der
Unendlichkeit? Was gibt ihm den
eigentümlichen Charakter dessen was wir unendlich
nennen? Ich glaube, daß es sich ähnlich
verhält wie das Zeichen einer enormen Zahl.
Denn das |
Wenn man etwa fragt „ist das nun die letzte Regel in der
Reihe”, so wäre die Antwort: natürlich
nicht. – Auch kann man
sagen; || : keine wird die letzte
sein. – Aber hier bedient man sich schon einer Variablen,
denn dem ‚keine’ entspricht nicht ein logisches
Produkt. |
Soll ich nun
sagen: keine ist die letzte, – oder: Es ist
sinnlos von einer ‚letzten’ zu sprechen, &
auch das Wort ‚keine’ ist in diesem
Zusammenhang nicht erlaubt? |
Die Grammatik des
Ausdrucks || Wortes
„u.s.w., ad inf.” |
Wenn wir etwa die Regeln für Division
oder Multiplikation geben, so enthalten
die schon die ‚unendliche Allgemeinheit’.
Nämlich die Unbeschränktheit & das
‚u.s.w.’.
(Und so kann man sich überzeugen, daß alles mit rechten
Dingen zugeht.) |
Schon das
Kind in der Schule lernt die Rechenregeln mit || in dieser Wir zeigen ihm einige Multiplikationen & verlangen, daß es dann andere mit größeren Zahlen als denen im Paradigma selbst ausführe. |
„Wieviel Punkte muß man nach der
Reihe setzen um das
‚u.s.w.’
anzudeuten?”
Tat || Tut es nicht
einer? |
Kann man von der
Zahlenreihe sagen, sie habe kein Ende?
„Aber wie wäre es wenn es anders
wäre?” Aber kann ich nicht vom Schachspiel
sagen: die Reihe der Schachfiguren habe ein Ende & in
einem andern Spiel, sie habe kein Ende,
wenn man die Erlaubnis hätte beliebig viele Felder,
einer Regel gemäß, mit Steinen zu besetzen.
|
D.h. also: ist es
überhaupt ein erlaubter Ausdruck, zu
sagen; || , etwas habe ein Ende, oder
keines. |
Zu sagen
„diese Reihe hat kein Ende” heißt || sagt natürlich dasselbe wie: „So
geht es weiter”. |
Man hat natürlich nur die Zahlen bis zu einer gewissen
höchsten |
Hier ist die Schwierigkeit sich zu wehren gegen den Gedanken, die
Möglichkeit sei eine Art schattenhafter Existenz || Wirklichkeit. |
Mit Gewalt
drängt sich hier der Gedanke auf die
Allgemeinheit antizipiere die ◇◇◇ besonderen
Fälle doch in schattenhafter Weise. Die Variable
sei nur eine Abkürzung || abgekürzte
Schreibweise für besondere Fälle || für eine Gesamtheit || ein
Ganzes von besonderen
Fällen. |
In den Regeln für die Variable
a kann eine
Variable b vorkommen
& auch besondere Zahlzeichen; aber
auch keine Gesamtheit von Zahlen.
|
Nun scheint es aber als |
Würde uns
aber nun nach der Erklärung einer Rechnungsart jemand
fragen: „und ist nun 103 das letzte
Zeichen der Reihe welches ich benützen kann”, was
sollen wir antworten? „Nein es ist nicht das
letzte” oder „es gibt kein letztes”? – Aber muß ich ihn nicht zurückfragen:
„Und wenn es nicht das letzte ist, was käme dann
noch?” Und sagte er nun „104”,
so müßte ich sagen: Ganz richtig, Du
kannst die Reihe selber fortsetzen. |
Von einem Ende der Möglichkeit kann ich
überhaupt nicht reden. |
(Nur vor dem Geschwätz muß Eine Regel aber die praktisch anwendbar ist, ist immer in Ordnung.) |
Es ist klar daß man einer Regel von der Art
❘a, ξ, ξ + 1❘
folgen kann; ich meine ohne schon von vornherein die
Reihe hinschreiben zu können sondern indem man
sich wirklich nach der
Bildungsregel richtet || wirklich der
Bildungsregel folgt || sich wirklich nach der
Bildungsregel richtet. Es ist ja dann dasselbe wie
wenn ich eine Reihe etwa mit der Zahl 1 anfinge &
sagte: „nun gib 7 dazu, multipliziere mit 5 &
zieh die Wurzel, & diese zusammengesetzte Operation wende
immer wieder auf das Resultat an”. (Das
wäre ja die Regel
❘1, ξ, √(ξ + 7) ∙ 5 ❘.) |
Aber was tut der,
der || welcher diese Regel
versteht? Wendet er sie etwa schon in schattenhafter
Weise auf alle Zahlen an? – |
Um nun die Regel etwa 3 mal nach einander anzuwenden, braucht es keine
weitere Regel die diese Anwendung regelt (die Verbindung der ersten
Regel mit der Zahl 3 herstellt). Sondern, daß wir den
Raum für die Anwendung offenlassen ist gerade unser |
Schließlich ist ja das Wort
„u.s.w.”
nichts anderes als das Wort
„u.s.w.”
(d.h. wieder als ein Zeichen des
Kalküls das nicht mehr tun kann als durch die Regeln zu
bedeuten, die von ihm gelten. Das nicht mehr
sagen kann als es zeigt.)2
|
D.h. es wohnt dem Wort
„u.s.w.” keine geheime
Kraft inne, durch die nun die Reihe fortgesetzt wird, ohne fortgesetzt
zu werden. |
Das wohl nicht,
wird man sagen, aber eben die Bedeutung der unendlichen
Fortsetzung. |
„Kann man sich einen leeren Raum
vorstellen?” (Diese Frage gehört
merkwürdigerweise
hierher.) |
Es ist einer der tiefstwurzelnden Fehler der
Philosophie: die Möglichkeit als ein Schatten
der Wirklichkeit. || einen Schatten der Wirklichkeit zu
sehen. Anderseits aber kann es kein Irrtum sein & ist es auch nicht wenn man den Satz als diesen Schatten nennt. |
Es muß um
die unendliche
Und wenn wir die „unendliche Möglichkeit der Fortsetzung sehen” so können wir doch nichts sehen was nicht beschrieben ist, wenn |
Die Gefahr ist natürlich hier wieder in einen
Positivismus zu verfallen, nämlich
einen, der einen eigenen Namen
verdient & daher natürlich ein Irrtum sein
muß. Denn wir dürfen überhaupt keine Tendenz
haben keine besondere Auffassung der Dinge sondern
(wir) müssen alles anerkennen, was
jeder Mensch darüber je gesagt hat außer soweit er selbst eine
besondere Auffassung oder Theorie hatte. |
Denn das Zeichen
„u.s.w.”, oder ein ihm
entsprechendes, ist wohl für die Bezeichnung der
Endlosigkeit wesentlich. Natürlich durch die
Regeln die von einem solchen Zeichen gelten.
D.h. wir
können wohl das Reihenstück
„1, 1 + 1,
1 + 1 + 1” unterscheiden von der Reihe
„1, 1 + 1, 1 + 1 + 1,
u.s.w.” Und das
letzte Zeichen & sein Gebrauch ist so wesentlich für den
Kalkül als eines der
vorhergehenden. || irgend ein andres. |
Das was
mich nun bedrückt ist, daß das
„u.s.w.” scheinbar auch
in den Regeln für das Zeichen
„u.s.w.” vorkommen
muß. |
Aber haben wir denn hier nicht die
alte Erkenntnis || Einsicht daß
wir die Sprache nur von außen beschreiben können.
Daß wir also nicht erwarten dürfen durch eine
Beschreibung der Sprache wesentlich tiefer || in andere
Tiefen zu dringen als die Sprache selbst
offenbart: Denn die Sprache beschreiben wir
mittels der Sprache. |
Wir
könnten sagen: Es ist ja gar kein Anlaß zu
fürchten daß wir das Wort
„u.s.w.” in einer das
Endliche übersteigenden Weise gebrauchen. |
Übrigens kann der für das
„u.s.w.”
charakteristische Teil seiner Grammatik nicht in Regeln über die
Verbindung von „u.s.w.”
mit einzelnen Zahlzeichen (nicht: „den
einzelnen Zahlzeichen”) bestehen – denn diese
Regeln geben ja wieder ein beliebiges Stück einer Reihe
– sondern in Regeln der Verbindung des Zeichens || von „u.s.w.”
mit sich selbst || „u.s.w.”.
|
Aber hier habe ich schon das
Wort „beliebig” gebraucht, & wie drückt
es sich aus, daß ein |
Das Zeichen „1, 1 + 1, 1 + 1 + 1,
…” kann im Wesentlichen nicht
deutlicher sein als „❘1, ξ, ξ + 1❘”.
(Das ist sehr wichtig.)
|
Was sieht der, der in
„1˙
|
Von dem Zeichen
„0˙3̇
”
kann man sagen: es ist keine Abkürzung.
|
Ich hatte einmal von der
Division gesagt: „ich sehe eben etwas Bestimmtes
in ihr, wenn ich die Periodizität
erkenne.” – Muß ich nun nicht sagen, sie
gehört in diesem Fall zu
einem andern System als im Falle, wenn ich die
Periodizität nicht erkenne? |
Man könnte fragen
„fällt Dir an dieser Division nichts
auf?” (die
Periodizität.)¤
„Ja, es fällt mir auf, daß das immer so weiter gehen muß”. Wenn ich nun fragen würde: |
Es ist übrigens
klar daß es keinen exakteren Beweis
der Periodizität dieser Division gibt als das oben
ausgeführte Stück. |
Das was ich an || in dieser Division sehe
befähigt mich z.B. das vierstellige
Resultat 0˙3333 auf Verlangen ohne
weitere Rechnung anzuschreiben. Und hierin liegt die
andere Art der Benützung dieser Division || dieses Zeichens. |
Es ist als entdeckten wir an gewissen Körpern die vor
uns liegen Flächen mit denen sie aneinander gereiht
werden können. Oder vielmehr als entdeckten wir daß
sie mit den & den Flächen die wir auch schon früher
|
Der, welcher || der die
Periodizität entdeckt, erfindet einen neuen
Kalkül. Die Frage ist, wie unterscheidet sich
der Kalkül mit der periodischen Division von dem
Kalkül der die
Periodizität nicht kennt? |
(Wir
hätten einen Kalkül mit Würfeln betreiben
können ohne je auf die Idee zu kommen sie zu Prismen
aneinanderzureihen.) |
Was macht es, daß ich
weiß, daß die Definition „a + ((b) + 1) =
(a + b) + 1 Def” rekursiv
auf alle Zahlen angewandt werden kann?
Oder: Wie zeigt sich die Periodizität dieser Definition? |
Ich könnte übrigens
sagen, daß sich das Zeichen
„1, 1 + 1,
1 + 1 + 1” || „1, 1 + 1, 1 + 1 + 1,
u.s.w.” vom Zeichen
„1, 1 + 1,
1 + 1 + 1” durch die Anwendung
unterscheidet. Daß sie verschiedenen Kalkülen
angehören. |
Die Schwierigkeit fängt
schon da an, |
Diese Aufzählung muß
sich durch „❘1, ξ, (ξ) + 1❘”
ersetzen lassen. |
Anderseits
aber muß es auch klar sein, daß „1, (1) + 1,
((1) + 1) + 1,
u.s.w.” keine
Abkürzung ist. |
Vielmehr muß es auch das
vollständige Zeichen sein eines Kalküls.
D.h., man muß mit ihm ebenso
exakt arbeiten können, wie mit jedem
anderem. |
30.7.
Man könnte nun aber fragen:
Wie kommt es, daß der, welcher die allgemeine Regel nun auf
eine weitere Zahl anwendet, nur dieser Regel
folgt. Daß keine weitere Regel
nötig war die ihm erlaubt die allgemeine Regel auch
auf diesen Fall anzuwenden; & daß doch
dieser Fall in der allgemeinen Regel nicht genannt
war. |
Es wundert uns
also daß wir diesen Abgrund zwischen den |
Woher || Wie weißt Du daß er im Zimmer
ist? – Weil ich ihn hineingesteckt
habe, & er nirgends herauskann. – So ist
also Dein Wissen der allgemeinen Tatsache, daß er
irgendwo im Zimmer ist, auch von der
Multiplizität dieses Grundes: Gezeichnet etwa
so: 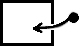 Das Bild des allgemeinen Sachverhalts wäre
also auch ❘ •❘. Und dieses
Zeichen würde nur anders benützt als dann, wenn es eine
spezielle Lage angibt. Das Bild des allgemeinen Sachverhalts wäre
also auch ❘ •❘. Und dieses
Zeichen würde nur anders benützt als dann, wenn es eine
spezielle Lage angibt. Übrigens haben wir ja dasselbe, wenn wir in der Geometrie einen Beweis durch Zeichnung führen & ein (allgemeines) Dreieck hinzeichnen. Von dem Gebrauch des allgemeinen Dreiecks gelten dann andere Regeln als von dem des speziellen. |
Man sagt:
„auf die Größe dieses Dreiecks kommt
es hier nicht an”. |
Wenn die Intuitionisten von der „Grundintuition”
sprechen, – ist diese ein psychologischer
Prozeß? Und wie kommt er dann in
die Mathematik? |
Es
ist wohl charakteristisch für das allgemeine
❘ ⚬❘, daß
❘ ⚬❘ = ❘ ⚬ ❘, aber man kann das
allgemeine Zeichen nicht durch eine Aufzählung solcher
Gleichungen erklären || bestimmen, da
man ja wieder nicht alle aufzählen kann.
(Darum sagte ich früher das „u.s.w.” müsse durch die möglichen || erlaubten Verbindungen mit sich selbst, nicht mit diesen || seinen besonderen Fällen charakterisiert || erklärt werden.) |
(Wenn man die
Sokratischen Dialoge liest, so hat
man das Gefühl: welche fürchterliche
Zeitvergeudung! Wozu diese Argumente die nichts beweisen
& nichts klären.) |
Es ist als gäbe es eine allgemeine
Auffassung des Zeichens, (etwa eines Dreiecks
in der geometrischen Konstruktion
etc.). |
Es gibt ein „zwischen” bei
dem man nicht von einem besonderen Ort reden
kann. Das also quasi alle Züge des räumlichen
„Zwischen” hat Das heißt es gibt einen Kalkül mit einer Relation die man „zwischen” nennen könnte bei der aber von (einer) Allgemeinheit nicht die Rede wäre. Anderseits aber ist dieser Kalkül derjenige der Allgemeinheitsbezeichnung für die räumliche Lage. Wie kriegt er aber den Charakter der Allgemeinheit, wenn er ihn doch nicht durch die Beziehungen zu speziellen Fällen bekommt? – Aber worin besteht denn dieser Charakter der Allgemeinheit? Handelt es sich nicht hier wieder um einen falschen Vergleich? |
Die Allgemeinheit ist so vieldeutig,
wie die
Subjekt-Prädikat
Form. |
„Außer diesem, diesem, diesem & diesem
Stuhl sind keine || ist keiner im Zimmer
& sie alle sind braun.”
„Zähl die Stühle in diesem Zimmer”. |
Alles was
man eigentlich in der Philosophie wissen muß, ist, daß jeder
Unterschied des Gebrauchs || im Gebrauch
eines Worts ein logischer Unterschied ist, & daß es
|
D.h. man darf nur nicht an einem Unterschied
der Formen vorbeigehen – wie man wohl an einem Unterschied
zwischen Sesseln vorbeigehen kann wenn er etwa sehr gering
ist. In gewissem Sinne gibt es für uns – nämlich in der Grammatik – nicht geringe Unterschiede. Und überhaupt bedeutet ja das Wort Unterschied etwas ganz anderes als dort wo es sich um einen Unterschied zweier Dinge || Sachen handelt. |
Denn Worin besteht der
Charakter der Allgemeinheit des allgemeinen
Kalküls? Denn ich möchte daß er die
besonderen Fälle allgemein behandelt & nicht quasi
etwas von den besonderen Fällen ganz
Losgelöstes ist. (Wie es
auch in der Bezeichnung
„1, 1 + 1, 1 + 1 + 1
u.s.w.” angedeutet
ist.) Wo ist die Verwandtschaft zwischen der Allgemeinheit & dem Besonderen? Die muß offenbar in der Bezeichnung zum Ausdruck kommen. |
Ich möchte sagen: das allgemeine
Bild ❘ ⚬ ❘ hat eine andre
Metrik als das besondere. |
Die Möglichkeit noch weitere Zahlen anzuführen.
Die Schwierigkeit scheint uns die zu sein daß die Zahlen die ich
tatsächlich angeführt habe ja gar nicht
wesentlich sind || keine wesentliche Gruppe sind &
nichts dies andeutet, daß sie eine beliebige
Kollektion sind:
die zufällig aufgeschriebenen unter allen
Zahlen. (So als hätte ich in einer Schachtel alle Karten || Steine eines Spiels & auf dem Tisch daneben eine zufällige Auswahl aus dieser Schachtel.) Oder als wären die einen Ziffern in Tinte nachgezogen während sie alle schon gleichsam blaß vorgezeichnet sind || seien.) Daß wir aber außer diesen zufällig benützten nur die allgemeine Form haben. Haben wir hier übrigens nicht – so komisch das klingt – den Unterschied zwischen Zahlzeichen & Zahlen? |
Ist es nicht
klar daß wir bei unseren Schwierigkeiten eben an einem falschen
Bilde laborieren? |
Im allgemeinen Zeichen
❘ ⚬ ❘ spielen die
Distanzen so wenig eine Rolle wie im Zeichen
aRb (die der
Buchstaben). |
Bedenke, daß aus dem allgemeinen Satz eine logische Summe
mit || von, sagen wir, 100 Summanden folgen
könnte, an die wir doch bestimmt nicht gedacht haben als wir den
allgemeinen Satz aussprachen. Können wir dennoch
sagen, daß sie aus ihm folgt? |
31.
„Hast Du es ohne Unterbrechung
die ganze Zeit verstanden?” |
Die Allgemeinheitsbezeichnung
unserer gewöhnlichen Sprache faßt die logische Form noch
viel oberflächlicher als ich früher geglaubt
habe. Sie ist eben in dieser Beziehung mit der
Subjekt-Prädikat
Form vergleichbar. |
Nehmen wir die besonderen Fälle des
allgemeinen Sachverhalts daß das Kreuz sich zwischen den
Grenzstrichen befindet
|
„Das Kreuz
liegt so auf der Geraden:
„Es hat hier 16
|
Wenn man sich übrigens wundert,
daß dieser Satz || ein Satz aus jenem || aus
dem anderen folgt obwohl man doch bei jenem gar
nicht an ihn dachte || bei diesem gar nicht an jenen dachte,
so denke man nur daran daß p ⌵ q aus
p, & ich denke doch
gewiß nicht (an) alle
Sätze p ⌵ ξ wenn
ich p denke. |
Die ganze Idee daß man bei dem Satz aus dem ein
anderer folgt an diesen denken muß beruht auf
einer falschen, & psychologisierenden,
Auffassung. Wir haben uns ja nur um das zu
kümmern, was in den Zeichen &
(ihren) Regeln liegt. |
Dagegen ist es eine
wirkliche Schwierigkeit || ein ernst zu nehmender
Gedanke || ein wirklicher Gedanke daß
das Folgen immer
verbunden scheint mit dem || gebunden scheint an den
Kalkül der
Wahrheitsfunktionen. |
Will ich sagen
daß sich das Folgen immer aus der Übereinstimmung der || von Wahrheitsmöglichkeiten ergeben muß?
|
|
(∃x)fx ⌵ fa =
(∃x)fx,
(∃x)fx ∙ fa =
fa Wie weiß ich das?
(denn das obere habe ich sozusagen
bewiesen). Man möchte etwa sagen:
„ich verstehe (∃x)fx
eben”. (Ein herrliches Beispiel dessen, was
‚verstehen’ heißt.)
Ich könnte aber ebensogut fragen „wie weiß ich daß (∃x)fx auf || aus fa folgt” & antworten: „weil ich (∃x)fx verstehe”. Wie weiß ich aber wirklich, daß es folgt? – weil ich so kalkuliere. Wie weiß ich daß aus (∃x)fx (x)fx ∙ fa folgt || aus (x)fx fa folgt? || (∃x)fx aus fa folgt? Sehe ich quasi hinter das Zeichen (∃x)fx, & sehe den Sinn der hinter ihm steht & daraus || aus ihm, daß er aus fa folgt? ist das das Verstehen? Nein, jene Gleichung ist ein Teil des Verstehens || Verständnisses || drückt einen Teil des Verstehens aus (das so ausgebreitet Denn die Annahme eines Verstehens das ursprünglich mit einem Schlag erfaßbar || ein Erfassen mit einem Schlag erst so ausgebreitet werden kann, ist ja unrichtig. Wenn ich sage „ich weiß, daß es || (∃x)fx folgt, weil ich es verstehe”, so heißt || hieße das, daß ich, es verstehend, etwas anderes sehe als das gegebene Zeichen gleichsam eine Definition des Zeichens, aus der das Folgen hervorgeht. |
Die
Mathematik besteht aus Rechnungen. || Die
Mathematik besteht ganz aus Rechnungen. |
1.8.
Meine Auffassung des allgemeinen Satzes war doch, daß
(∃x)fx eine
logische Summe ist & daß nur ihre Summanden hier
nicht aufgezählt seien, sich aber aufzählen ließen
(& zwar aus dem Wörterbuch & der Grammatik der
Sprache). Denn ließen sie sich nicht aufzählen, so handelt es sich ja doch nicht um eine || um keine || haben wir ja doch keine logische Summe. (Vielleicht ein Gesetz, logische Summen zu bilden.) |
Die Zahl ist
durchaus kein „grundlegender mathematischer
Begriff”. Es gibt so viele Kalküle || Rechnungen in denen von Zahlen nicht die Rede ist.
Und was die Arithmetik betrifft, so ist es mehr oder weniger willkürlich was wir noch Zahlen nennen wollen. Und im übrigen ist der Kalkül – z.B. – der Kardinalzahlen zu beschreiben, d.h. seine Regeln sind anzugeben, & damit sind die Grundlagen der Arithmetik gegeben || & damit ist die Arithmetik begründet || grundgelegt. |
Lehre sie uns, dann hast Du sie
begründet. |
|
Ja sagt denn eben (∃x)fx ⌵ fa =
(∃x)fx nicht, daß
fa schon in
(∃x)fx
enthalten ist? Zeigt es eben nicht die
Abhängigkeit des fa von
(∃x)fx?
Nein, außer wenn (∃x)fx als
logische Summe definiert ist (mit einem Summanden
fa). – Ist
das der Fall, so ist (∃x)fx
weiter nichts als || nur eine Abkürzung. |
Einen verborgenen Zusammenhang gibt es
nicht in der
Logik || in der Logik nicht. |
Eines der größten Hindernisse |
Wird nicht vielmehr die Abhängigkeit
durch die Gleichung hergestellt & festgesetzt?
Denn eine verborgene Abhängigkeit gibt es eben nicht.
|
(∃x)fx ∙ ~fa,
(∃x)fx ∙ ~fa ∙ ~fb ∙ ~fc. „Das Kreuz befindet sich irgendwo zwischen den Strichen, außer in der Lage a.” Man könnte nun fragen: wird durch solche fortgesetzte Subtraktion von Möglichkeiten endlich eine Kontradiktion erzeugt? |
Angenommen ich gäbe ein
Disjunktion von so vielen Stellungen an, daß
es mir unmöglich wäre eine Stellung von
allen angegebenen als verschieden zu erkennen || sehen;
wäre nun die Disjunktion der allgemeine Satz
(∃x)fx?
Wäre es nicht sozusagen Pedanterie die
Disjunktion noch immer nicht als den allgemeinen Satz
anzuerkennen? Oder besteht ein wesentlicher
Unterschied, & ist die Disjunktion vielleicht dem
allgemeinen Satz gar nicht ähnlich? |
Das, was uns
auffällt ist, daß der eine Satz so kompliziert, der andere so
einfach ist. Oder ist der einfache nur eine kurze
Schreibweise des komplizierten? |
Es scheint uns aber, das ‚zwischen
den Strichen, oder Wänden, liegen’ etwas
Einfaches, wovon die verschiedenen Lagen (ob
damit die Gesichtserscheinungen oder die durch
Messen festgestellten Lagen) ganz unabhängig
sind. D.h. wenn wir von den einzelnen (gesehenen) Lagen reden, so scheinen wir von etwas ganz anderem zu sprechen || reden, als von dem, wovon im allgemeinen Satz die Rede ist. |
Es ist ein anderer
Kalkül zu dem unsere Allgemeinheitsbestimmung gehört
& ein anderer der || in dem es jene
Disjunktion gibt. Wenn wir sagen, das Kreuz liegt
zwischen diesen Strichen, so haben wir keine
Disjunktion bereit, die den Platz des || dieses allgemeinen Satzes nehmen könnte. |
Ist aber gegen eine Allgemeinheit etwas
prinzipiell einzuwenden, die als Allgemeinheit
auftritt || fungiert, für die also
(∃x)fx ∙ fa =
fa ist & die doch |
Oder: Ist es
möglich daß (∃x)fx ∙ fa =
fa ist, ohne daß (∃x)fx eine
Wahrheitsfunktion von fa ist? |
(Er || Es kann keine
Wahrheitsfunktion von fa sein, ohne daß man es
weiß.) |
(Was ich mit
den Zeichen tue ist für den Mathematiker ein
Herumsch … (& war es
z.B. für Ramsey), & mit Recht, denn er will
vorwärtskommen, während ich mich
ungestört || unbeirrt || unbeirrbar
bei einigen wenigen Zeichen & zwei Schritten des Kalküls
aufhalte.) |
Ich kann doch
einen Kalkül haben, in dem es nur ein
a b
a, ein b a a & ein
a a
b gibt,
|
Kann ich denn aber die Regeln des Folgens in diesem Fall
angeben? Denn wie weiß ich, daß gerade aus
fa
Die gebraucht werden, werden gebraucht, & für sie kann ich immer in der Grammatik vorsorgen. |
Ich
sage „es war möglich vor jeder Erfahrung zu
wissen, daß (∃x)fx aus
fa folgt & es in der
Grammatik anzugeben”. Es sollte aber
heißen: ‚(∃x)fx folgt
aus fa’ ist kein Satz
(Erfahrungssatz) der Sprache der
‚(∃x)fx’
& ‚fa’ angehören,
sondern eine in ihrer Grammatik festgesetzte Regel.
|
Ich betrachte die Sprache &
Grammatik unter dem Gesichtspunkt des Kalküls || als Kalkül || unter der Form des
Kalküls, d.h. der
Operationen || des Operierens nach festgelegten
Regeln. || d.h. als Vorgang || des Operierens nach
festgesetzten Regeln. |
Es ist nur wesentlich, daß wir
(hier) nicht sagen können, wir sind
durch |
Es ist die alte Frage: in
wiefern kann man jetzt von einer Erfahrung
sprechen, die man jetzt nicht hat. Was ich nicht voraussehen kann, kann ich nicht voraussehen. – Und wovon ich jetzt sprechen kann, davon kann ich sprechen, unabhängig von dem, wovon ich jetzt nicht sprechen kann. Die Logik ist eben immer komplett. |
„Wie kann
ich wissen, was alles folgen wird.” – Was ich
dann wissen kann, kann ich auch jetzt wissen. |
Eine allgemeine Regel des
Folgens insofern sie nicht ein logisches Produkt
besonderer Regeln ist, ist von ganz anderer Art, als eine besondere
Regel des Folgens. |
Aber gibt es denn auch allgemeine Regeln, oder nicht
nur Regeln über allgemeine Zeichen? |
Was
wäre etwa eine allgemeine & eine besondere Regel im
Schachspiel (oder einem andern)? Jede Regel ist ja
allgemein. |
Doch ist eine
andere Art der Allgemeinheit in der Regel daß
p ⌵ q aus
p folgt, als in der, daß
jeder Satz der Form, p, ~~p,
~~~~p, …
aus p ∙ q folgt.
Ist aber nicht die Allgemeinheit der Regel für den
Rösselsprung eine andere als die einer Regel für den
Anfang einer Partie? |
Ist
das Wort „Regel” überhaupt
vieldeutig? Und sollen wir also nicht von Regeln im
Allgemeinen reden, wie auch nicht von Sprachen im
Allgemeinen? Sondern nur von Regeln in besonderen
Fällen. |
Sokrates stellt
z.B. die Frage, was Erkenntnis sei, und
ist nicht mit der Aufzählung von Erkenntnissen
zufrieden. Wir aber kümmern uns nicht viel um diesen
allgemeinen Begriff & sind froh, wenn wir
Schuhmacherei, Geometrie etc. verstehen. |
Gilt diese Überlegung aber nicht auch
für den Begriff des Folgens? || das
Folgen? |
Wir glauben nicht, daß
nur der ein Spiel versteht, der eine Definition des Begriffs
‚Spiel’ geben kann. |
Ich mache es mir in der Philosophie immer
leichter & leichter. Aber die Schwierigkeit ist, es
sich leichter zu machen & doch
exakt zu bleiben. |
„In's Inn're der Natur dringt kein
erschaff'ner Geist”. Wie kann er dann
von dem Innern reden? Oder vielmehr, wir haben hier ein
unzutreffendes Bild. |
Hinter die Regeln kann man
nicht dringen, weil es ein Dahinter nicht gibt. |
fE ∙ fa = fa
Kann man sagen: das ist nur möglich, wenn
fE aus
fa folgt; oder muß man
sagen: das bestimmt, daß fE aus
fa folgt || folgen
soll? |
Wenn das
erste, so muß es vermöge der Struktur folgen, etwa indem
fE durch eine Definition so
bestimmt ist, daß es die entsprechende Struktur
hat. Aber kann denn wirklich das Folgen, gleichsam aus der
sichtbaren Struktur der Zeichen hervorgehen wie ein
physikalisches Verhalten aus einer physikalischen |
Und warum sollte auch die Regel
fE ∙ fa = fa aus
einer andern Regel hervorgehen & nicht die primäre Regel
sein? |
Denn was soll es
heißen „fE muß doch
fa in irgendeiner Weise
enthalten”? Es enthält es
eben nicht, insofern wir mit fE arbeiten können,
ohne fa zu erwähnen.
Wohl aber insofern eben die Regel
fE ∙ fa = fa
gilt. |
Die Meinung || Idee ist nämlich, daß
fE ∙ fa =
fa nur vermöge der Definition von
fE gelten kann. |
Und zwar – glaube ich
– darum, weil es sonst den falschen Anschein hat, als
würde nachträglich noch eine Bestimmung über
fE getroffen, nachdem es
schon in die Sprache eingeführt sei. Es wird
aber tatsächlich keine Bestimmung einer künftigen Erfahrung
überlassen. |
Und die
Definition des fE aus ‚allen
Einzelfällen’ ist ja ebenso
unmöglich, wie die Aufzählung aller Regeln
von der Form fE ∙ fx = fx.
|
Ja die
Einzelgleichungen fE ∙ fx =
fx sind eben gerade ein Ausdruck dieser
Unmöglichkeit. |
Wie
äußert es sich aber in unsern Regeln, daß die
behandelten Fälle fx keine
wesentlich abgeschlossene Klasse
sind? – Doch wohl nur durch die
Allgemeinheit der allgemeinen Regel.
– [kein Absatz] Daß sie nicht die Bedeutung für den Kalkül haben, wie eine abgeschlossene Gruppe von Grundzeichen (etwa den Namen der 6 Grundfarben). Wie anders, als durch die Regeln die von ihnen ausgesagt sind. – Wenn ich etwa in einem Spiel die Erlaubnis habe eine gewisse Art von Steinen in beliebiger Anzahl zu borgen, andere aber in festgesetzter Anzahl vorhanden sind; oder das Spiel zwar zeitlich unbegrenzt, aber räumlich begrenzt ist, haben wir ja wohl den selben Fall. Und der Unterschied zwischen den einen & den |
Das heißt, daß der Ausdruck für
die Unbegrenztheit der behandelten Einzelfälle
(eben) ein allgemeiner Ausdruck sein
wird , & kein andrer sein kann, kein Ausdruck, in dem
die anderen nicht behandelten Einzelfälle in schattenhafter Weise
vorkämen. |
Es ist
ja klar, daß ich keine logische Summe als
Definition des Satzes „das Kreuz liegt zwischen den
Strichen” anerkenne. Und damit ist doch
alles gesagt. |
Wenn man
gefragt wird: ist es aber nun auch sicher,
daß ein anderer Kalkül als dieser nicht gebraucht wird, so
muß man sagen: Wenn das heißt
„gebrauchen wir nicht in unserer
tatsächlichen Sprache noch andere
Kalküle” so kann ich nur antworten,
„ich weiß jetzt keine anderen (so,
wie wenn |
Ein
Kalkül ist ja da, indem man ihn beschreibt. |
Kann man sagen:
‚Kalkül’ ist kein mathematischer
Begriff? |
11.
„–
Wie? sagte er, die sollte nicht nutzen? Denn wenn
doch einmal die Besonnenheit die Erkenntnis der
Erkenntnisse ist & den andern Erkenntnissen vorsteht, so
muß sie ja auch dieser sich auf das Gute beziehenden Erkenntnis
vorstehen & uns so doch nutzen. – Macht auch
sie uns, sprach ich, etwa gesund & nicht die
Heilkunde? so auch mit den andern
Künsten; verrichtet sie die Geschäfte derselben &
nicht vielmehr jede von ihnen das
Ihrige? Oder haben wir nicht lange
schon eingestanden, daß sie nur der Erkenntnisse &
Unkenntnisse Erkenntnis wäre & keiner anderen
|
Das ist klar, daß die Frage
„was ist ein Kalkül?” von
genau der gleichen Art ist wie die:
„was ist ein Spiel” oder
wie die: „was ist eine
Regel”. |
Daß wir
nun jemanden das Schachspiel beibringen || erklären können ist klar. Und es fragt
sich: Versteht er es (nun
doch) weniger weil er nicht gelernt hat ‚was
ein Spiel ist’? Oder macht das gar nichts
aus? |
Was bedeutet
„undefinierbar”? Dieses Wort ist
offenbar irreführend denn es erweckt
den Anschein als könnten wir hier etwas versuchen
was sich dann als unausführbar erwiese. Als
wäre also das Undefinierbare etwas was sich
|
Nun könnte man freilich sagen: die Definition
ist ja etwas Willkürliches d.h. wie
ich ein Wort definiere, so ist es definiert. Aber
darauf kann geantwortet werden: Es kommt darauf
an es so zu definieren wie wir das Wort meinen. Also so
daß wir zur Definition des Wortes
„Tisch”; || ,
z.B., sagen: ja, das ist es was ich
unter || mit dem Wort meine. Ja
hat Dich nun aber die Definition dahingebracht das mit dem Wort zu
meinen oder willst Du sagen daß Du das schon immer gemeint
hast? Und wenn das letztere, so hast Du also immer
das gemeint, was die Definition sagt (im Gegensatz
zu etwas anderem, was sie auch sagen
könnte.)
D.h., || : die Definition ist auch eine Beschreibung dessen, was Du schon früher gemeint hast. Du warst also auch früher schon im Besitz einer Übersetzung dieser Definition; sie hat sozusagen nur laut gesagt was Du schon im Stillen wußtest. Sie hat also auch |
[Die
Geschichte des Peter Schlemihl sollte, wie mir scheint, so gehen || lauten: Er verschreibt seine Seele um Geld dem
Teufel. Dann reut es ihn & nun verlangt der Teufel
den Schatten als Lösegeld.
Peter Schlemihl aber bleibt die Wahl seine Seele
dem Teufel zu schenken, oder mit dem Schatten auf das
allgemeine Leben in der Gemeinschaft der Menschen || schöne
Gemeinschaftsleben unter den || der Menschen zu verzichten.]
|
Der, welcher darauf
aufmerksam macht, daß ein Wort in zwei verschiedenen
Bedeutungen gebraucht wurde, oder daß bei dem Gebrauch dieses || eines Ausdrucks uns dieses Bild
vorschwebt, & der überhaupt die Regeln
feststellt (tabuliert) nach welchen Worte gebraucht werden,
hat gar keine Pflicht || ist gar nicht
verpflichtet || hat gar nicht die Pflicht übernommen, eine
Erklärung (Definition) des Wortes „Regel”
(oder „Wort”, „Sprache”,
„Satz” etc.) zu
geben. |
Ich sagte oben
„Kalkül ist kein mathematischer
Begriff”; das heißt, das Wort ‚Kalkül’ ist kein Schachstein der
Mathematik. Es brauchte in der Mathematik nicht vorzukommen. – Und wenn es doch in einem Kalkül gebraucht |
So ist es mir erlaubt das Wort Regel zu verwenden
ohne notwendig erst die Regeln über dieses Wort zu
tabulieren. Und diese Regeln sind nicht
Über-Regeln. |
Das
Wort „Regel” muß in der Erklärung
eines Spiels nicht gebraucht werden (natürlich auch kein
äquivalentes). |
Wie
gebrauchen wir denn auch das Wort Regel (wenn wir etwa
von Spielen reden)? Im Gegensatz wozu?
Wir sagen z.B. „das folgt aus dieser
Regel” aber dann könnten wir ja die Regel des Spiels
zitieren & so das Wort „Regel”
ersetzen? Oder wir sprechen von „allen Regeln
des Spiels” & müssen sie dann entweder
aufgezählt haben (& dann liegt wieder der
erste Fall vor), oder wir sprechen von
den Regeln als einer Gruppe – die auf bestimmte Art aus
bestimmten || gegebenen Grundpositionen
erzeugt werden & dann steht das Wort Regel für den
Ausdruck dieser Grundpositionen &
Operationen. Oder wir sagen:
„Das ist eine Regel, das
nicht”, wenn etwa das Zweite |
Ebenso verhält
es sich nun auch mit dem Begriff der Regel. Nur in ganz
besonderen || speziellen
Fällen handelt es sich uns darum die Regeln von etwas
abzugrenzen was nicht Regel ist, & in allen diesen
Fällen ist es leicht ein unterscheidendes
Kriterium zu geben.
Das heißt, wir brauchen das Wort „Regel” im
Gegensatz zu „Wort”,
„Konfiguration der
Steine” und einigem Andern, & diese Grenzen sind klar
gezogen. Dagegen ist es
müßig Grenzen dort zu ziehen wo wir sie nicht
brauchen. Verhält es sich hier nicht ebenso wie etwa
mit dem Begriff ‚Pflanze’? Wir
gebrauchen |
Was heißt es, zu wissen was eine Pflanze ist?
Was heißt es, es zu wissen & es nicht sagen zu können? „Du weißt es & kannst hellenisch reden, also mußt Du es doch sagen können.” |
[Eine Art
von Wahnsinn ist ein In Ohnmacht fallen des Verstandes,
weil er einen Schmerz nicht länger |
Müßigkeit
der || einer Definition, || etwa der des Begriffs Pflanze. Aber ist die
Definition kein Erfordernis der
Exaktheit? „Der Boden
war ganz von Pflanzen bedeckt”: damit meinen
wir nicht Bazillen. Ja wir
denken uns dabei vielleicht auch || an
grüne Pflanzen einer gewissen || bestimmten Größenordnung.
Wer uns sagen würde wir wissen nicht, was wir
reden ehe wir keine Definition der Pflanze gegeben haben, würden
wir mit Recht für verrückt
halten. Ja wir könnten auch mit einer solchen
Definition uns in den
gewöhnlichen Fällen nicht besser
verständigen. Ja es scheint sogar in
gewissem Sinne überhaupt nicht || schlechter weil es gerade das Undefinierte in diesem
Fall zu unserer Sprache zu gehören scheint. |
12.
Denken wir uns in dem Satz einer Erzählung „der Boden war ganz mit Gräsern & Kräutern bedeckt” die Wörter „Gräser” & „Kräuter” durch Definitionen ersetzt. Es ist klar daß diese Definitionen lange & komplizierte Ausdrücke sein müssen || werden; & nun ist die Frage ob wir denn wirklich mit dem Satz das gemeint haben was jetzt in dem ungleich viel komplizierteren steht. |
Kann man nun aber auf eine
solche Sprache die Idee des Kalküls anwenden?
Und ist das nicht so als sollte man in || bei einem Bild in welchem || worin alle Farbflecken ineinander verlaufen von
Farbgrenzen reden? |
Oder
liegt die Sache so: Denken wir uns ein Spiel etwa das Tennis in
dessen Regeln nichts über die Höhe gesagt ist, die ein Ball
im Flug nicht übersteigen darf. Und nun sagte
einer: Das Spiel ist ja gar nicht klar
geregelt denn wenn einer nun den Ball so hoch wirft daß
er nicht wieder auf die Erde zurückfällt oder so weit,
daß er um die Erde herumfliegt so wissen wir nicht ob dieser
Ball als ‚out’ oder
‚in’ gelten soll. Man
würde ihm – glaube ich – antworten, wenn ein solcher
Fall eintrete so werde man Regeln für ihn geben, jetzt sei
es nicht nötig. |
Könnten wir uns nicht überhaupt ein Spiel mit
unvollständigem Regelverzeichnis denken & wir
hätten ausgemacht die Regeln nach Bedarf später zu
ergänzen, allerdings so, |
So können doch
grammatische Regeln über den Gebrauch des Wortes
„Pflanze” angegeben werden & wir können
also auf Fragen von der Art || Form
„folgt aus diesem Sachverhalt, daß dort eine
Pflanze steht” Bescheid geben. Auf
andere solche Fragen aber sind wir nicht gerüstet
& können antworten: Ein solcher Fall
ist noch nie vorgekommen & es wäre für uns
müßig jetzt für ihn vorzusorgen.
(Wenn es etwa gelänge ein Lebewesen halb maschinell
& halb auf organischem Weg || organisch zu erzeugen & nun gefragt
würde: ist das nun noch ein Tier oder eine
Pflanze.) |
Wenn etwa beim
Preisschießen für gewisse Grenzfälle keine
Bestimmungen getroffen sind || wären
ob dieser Schuß als in's Schwarze getroffen gelten
soll (oder
nicht). || diese Schüsse noch als Zentrumsschüsse
gelten sollen. Nehmen wir nun aber an ein solcher
Schuß komme bei unserem Preisschießen gar nicht vor;
könnte man dann dennoch sagen, die |
Denken wir uns nun das
Verzeichnis der Statuten für dieses Schießen & es sei
in ihm von jenen Grenzfällen gar nicht die Rede.
(Das wäre etwa ähnlich, wie wenn einer bei den
Berechnungen von Längenausmaßen nur nach den
Regeln der Kardinalarithmetik
verführe.) Kann man nun sagen das Regelverzeichnis
sei wesentlich unvollständig? Denn
wenn ein Schuß auf die Grenze zwischen Schwarz & Weiß
trifft wird sich doch der Richter irgendwie entscheiden
müssen: er wird dann entweder sagen
können, dieser Schuß gilt nicht, oder er wird ihn zum
Schwarzen rechnen, etc. || u.s.w.¤ Wenn er das
gegebene Schema anwenden will so wird er es
irgendwie anwenden müssen. Ich
meine: Er wird sie || die Regeln
nur entweder anwenden können wie sie sind, oder andere.
Man könnte es auch so sagen: Diese Regeln sind eigentlich für ein anderes Spiel gemacht nämlich für eines bei dem es || wo es || in dem es wirklich nur die zwei Möglichkeiten gibt ganz innerhalb & ganz außerhalb dem Kreis || des Kreises zu treffen. Wende ich die gleichen Regeln also auf das Scheibenschießen an so muß ich seine |
(D.h. wir haben nur die Ungerechtigkeiten
der Philosophie aufzuzeigen &
zu
lösen || haben richtigzustellen || aufzuheben aber nicht neue Parteien (&
Glaubensbekenntnisse) zu schaffen || aufzustellen.) |
Was versteckt ist muß
gefunden werden können. (Versteckter
Widerspruch) |
Was
versteckt ist muß sich auch ehe es gefunden wurde ganz
beschreiben lassen als wäre es schon
gefunden. |
Wenn man sagt der Gegenstand
ist so versteckt, daß es unmöglich ist ihn zu finden, so
hat das guten Sinn & die Unmöglichkeit ist hier
natürlich keine logische; d.h., es hat
Sinn von dem Finden des Gegenstandes zu reden &
auch, es zu Beschreiben || beschreiben; und wir leugnen
nur, daß das || es geschehen wird. |
Ich mache mich
doch anheischig das Regelverzeichnis unserer Sprache
aufzustellen: Was Soll ich sagen, daß es für diesen & diesen Fall keine Regel aufgestellt ist? Gewiß, wenn es sich so verhält. Soll ich aber also sagen es gibt kein Regelverzeichnis unserer Sprache & das ganze Unternehmen eins aufzustellen ist Unsinn? – Aber es ist ja klar daß es nicht Unsinn || unsinnig ist, denn wir stellen es ja mit Erfolg Regeln auf, & wir müssen uns nur enthalten Dogmen aufzustellen. (Was ist das Wesen eines Dogmas?) Besteht es nicht darin Sätze || naturnotwendige Sätze über alle möglichen Regeln zu behaupten? || Ist es nicht die Behauptung eines naturnotwendigen Satzes über alle möglichen Regeln?) |
„Ich weiß was
eine Pflanze ist, kann es aber nicht sagen”. Hat
dieses Wissen die Multiplizität eines Satzes, der nur nicht
ausgesprochen wurde? So
daß, wenn der Satz ausgesprochen würde ich ihn als
den Ausdruck meines Wissens anerkennen würde? –
Ist es nicht vielmehr wahr daß jede
exakte Definition als Ausdruck unseres
Verstehens abgelehnt werden müßte?
D.h. würden wir nicht von so einer sagen
müssen sie bestimme zwar einen dem unseren verwandten
Begriff aber nicht diesen selbst. Und die
Verwandtschaft sei etwa die zweier Bilder (Gemaltes Bild & Gobelin.) Die Verwandtschaft wäre dann ebenso unleugbar wie die Verschiedenheit. |
Die Frage ist nun:
kannst Du bei dem ersten Bild auch von Flecken
reden? Gewiß, nur in einem
andern, aber verwandtem, Sinn. |
Das heißt:
die unscharfen Grenzen gehören zu meinem Begriff der
Pflanze so wie er jetzt ist, d.h. so wie ich
dieses Wort jetzt gebrauche & es charakterisiert diesen
Begriff, daß ich z.B. sage: ich habe
darüber keine Bestimmung getroffen, ob dieses eine
Pflanze heißen soll oder nicht. |
Es scheint mir hier aber
auch eine falsche Verwendung des Wortes „unscharf”
vorzuliegen, in einem Fall nämlich wo kein
„scharf” denkbar ist. – So als
wendete man diesen Begriff aus der farbigen
euklidischen
Ebene genommen, auf den Gesichtsraum an. –
{Ich weiß aber die Anwendung dieser
Bemerkung noch nicht recht.} |
Die Erfahrung (der Begriff der
Erfahrung) scheint (uns) von
völligem Dunkel begrenzt. Aber auch Schwarz ist eine Farbe, & wenn eine Farbe gegen Schwarz abgegrenzt ist so durch eine Farbgrenze wie jede andre. |
Es
verhält sich doch mit dem Begriff Pflanze ähnlich
wie mit dem der Eiförmigkeit wie wir sie im gewöhnlichen
Leben meinen. Die Grenzen dieses Begriffs sind nicht scharf
bestimmt & wir würden z.B. ein
Osterei von dieser Form  nicht als
solches gelten lassen & doch nicht sagen können bei
welchem Verhältnis der Länge & Breite etwas
anfängt ein Osterei zu sein. Ja, wenn einer nun ein
solches Verhältnis angäbe, was es auch sei, so
könnten wir es nicht als die richtige Begrenzung unseres
Begriffs anerkennen. Sondern wir müßten entweder
sagen nein, das nenne ich kein Osterei, es ist zu
schlank oder dick etc., oder: ja, das ist
auch ein Osterei aber die Grenze || der
Grenzfall ist es nicht gerade. Diesen gibt es eben
nicht in unserm Kalkül & wer einen Grenzfall
einführt, führt einen andern Kalkül ein. nicht als
solches gelten lassen & doch nicht sagen können bei
welchem Verhältnis der Länge & Breite etwas
anfängt ein Osterei zu sein. Ja, wenn einer nun ein
solches Verhältnis angäbe, was es auch sei, so
könnten wir es nicht als die richtige Begrenzung unseres
Begriffs anerkennen. Sondern wir müßten entweder
sagen nein, das nenne ich kein Osterei, es ist zu
schlank oder dick etc., oder: ja, das ist
auch ein Osterei aber die Grenze || der
Grenzfall ist es nicht gerade. Diesen gibt es eben
nicht in unserm Kalkül & wer einen Grenzfall
einführt, führt einen andern Kalkül ein. |
Ist nun aber etwa eine
Verschwommenheit in den Regeln dieses Kalküls?
Oder ist das || diese || dies schon wieder eine der unsinnige || sinnlosen Fragen über alle möglichen Kalküle? |
Denken wir uns die Erklärung des
Begriffs der Pflanze. Wir zeigen jemand mehrere
Gegenstände & sagen das sind Pflanzen. Dann
zeigt auch er auf einen weiteren || andern Gegenstand
& sagt „ist auch das eine
Pflanze” & wir antworten „ja, das
auch” u.s.w..
Ich hätte nun einmal gesagt, er habe nun in dem Gezeigten den Begriff Pflanze – das gewisse Gemeinsame – gesehen & er sähe die Beispiele der Erklärung anders wenn er in ihnen eben diesen Begriff sähe || sieht als, wenn er sie etwa als Repräsentanten dieser bestimmten Form || Gestalt & Farbe allein auffasse. (So wie ich auch sagte er sähe in der Variablen, wenn er sie als solche versteht, etwas was er im Zeichen für den besonderen Fall nicht sieht.) Aber die Idee || der Gedanke des ‚darin Sehens’ ist von dem Fall hergenommen wo ich die Figur ❘ ❘ ❘ ❘ verschieden ‚phrasiert’ sehe. Aber dann sehe ich eben in einem anderen Sinn wirklich verschiedene Figuren & was diese gemein haben ist außer ihrer Ähnlichkeit die Verursachung durch das gleiche physikalische Bild. Aber diese Erklärung ist doch nicht ohne weiteres auf den Fall des Verstehens der Variablen oder der Erklärung des Begriffs || Beispiele für den Begriff Pflanze anzuwenden. Denn angenommen wir hätten wirklich etwas anderes in ihnen gesehen als Beispiele || in Pflanzen die nur um ihrer selbst willen gezeigt wurden, so ist die Frage, kann denn (dieses oder) irgendein (anderes Bild uns zu der Anwendung als Variablen berechtigen? Ich hätte einem also die Pflanzen zur Erklärung zeigen können & ihm dazu einen Trank gegeben durch den es verursacht wird, daß er die Beispiele in der bestimmten Weise sieht. (Wie es möglich wäre daß ein Alkoholisierter eine Gruppe ❘ ❘ ❘ ❘ immer als ❘ ❘ ❘ + ❘ sieht) & damit wäre die Erklärung des Begriffs in eindeutiger Weise gegeben & wer sie verstanden hat hätte die || von den vorgezeigten Spezimina || Specimina & die || den begleitenden Gesten dieses Bild empfangen. So ist es aber doch nicht. – Es ist nämlich wohl möglich daß der welcher, z.B., das Zeichen ❘ ❘ ❘ ❘ ❘ ❘ als Zahlzeichen für die Zahl 6 sieht in ihm || darin etwas anders sieht || es anders sieht (etwas anderes darin sieht) als der, welcher es nur als Zeichen für „einige” auffaßt, weil er seine Aufmerksamkeit nicht auf das gleiche lenken || richten wird; aber es kommt dann auf |
13.
Es wäre also möglich zu sagen: „jetzt sehe ich das nicht mehr als Rose, sondern nur noch als Pflanze”! Oder: „Jetzt sehe ich es nur als Rose, nicht mehr als diese Rose.” |
„Ich sehe
den Fleck nur noch im Quadrat, aber nicht mehr in einer
bestimmten Lage.” |
Der seelische Vorgang des
Verstehens interessiert uns eben gar nicht. (So
wenig wie der einer Intuition.) |
„Es ist doch gar
kein Zweifel, daß der, welcher die Beispiele als beliebige
Fälle zur Veranschaulichung des Begriffs versteht, etwas
anderes || andres versteht,
als der, welcher sie als bestimmt begrenzte Aufzählung
auffaßt”. Sehr richtig, aber was
versteht der erste also, was der zweite nicht versteht?
Nun er sieht eben nur Beispiele in den vorgezeigten
Dingen, die nur gewisse Züge aufzeigen || aufweisen sollen, aber er meint nicht daß ich
ihm im übrigen diese Dinge um ihrer selbst willen zeige. – |
Man || Ich möchte die
eine Aufzählung || Klasse
‚logisch begrenzt’ die
andere ‚logisch nicht begrenzt’ nennen.
|
Ja aber ist
es denn so, daß er nun tatsächlich nur diese Züge an den
Dingen sieht? Etwa am Blatt nur das, was allen
Blättern gemeinsam ist? Das wäre so, als
sähe er alles übrige „in
blanko”. Also gleichsam ein
unausgefülltes Formular, in dem die wesentlichen Züge
vorgedruckt sind. (Aber die Funktion
„f( …)” ist ja
so ein Formular.) |
Aber was ist denn das
für ein Prozeß, wenn mir Einer mehrere
verschiedene Dinge als Beispiele eines Begriffes || für
einen Begriff zeigt, um mich darauf zu führen das
Gemeinsame in ihnen zu sehen; & wenn ich es nun
suche & wirklich sehe? || suche & nun
wirklich sehe? Er kann mich auch auf das
Gemeinsame aufmerksam machen. –
Bringt er aber dadurch hervor, daß ich den Gegenstand anders
sehe? Vielleicht auch, denn ich kann jedenfalls
besonders auf einen seiner Teile schauen, während ich sonst alle
gleichmäßig deutlich gesehen hätte. Aber
dieses Sehen ist nicht das Verstehen des Begriffs. Denn wir
sehen nicht etwas mit einer leeren Argumentstelle.
|
„Such aus diesen Federstielen die
so geformten heraus”. ‒ ‒
„Ich wüßte || wußte nicht, ob Du diesen auch
noch dazu rechnest”. |
Man könnte auch
fragen: Sieht der, welcher das Zeichen
„❘ ❘ ❘ …” als
Zeichen des Zahlbegriffs (im Gegensatz zu
„❘ ❘ ❘” welches 3
bezeichnen soll) auffaßt, jene erste Gruppe von Strichen anders,
als die zweite. Aber auch wenn er sie anders –
gleichsam vielleicht, verschwommener – sieht,
sieht er da etwa das Wesentliche des
Zahlbegriffs? Hieße das nicht, daß er dann
„❘ ❘ ❘ …” und
„❘ ❘ ❘ ❘ …”
tatsächlich nicht voneinander müßte unterscheiden
können (wenn ich ihm nämlich etwa
den Trank eingegeben hätte, der ihn den Begriff sehen
macht)? |
Denn wenn
ich sage: Er bewirkt dadurch, daß er uns mehrere
Beispiele zeigt, daß wir das Gemeinsame in ihnen sehen &
von dem Übrigen absehen, so heißt das eigentlich, daß das
Übrige || übrige in den Hintergrund
tritt, also gleichsam blasser wird (& warum
sollte || soll es dann
nicht ganz verschwinden) & „das
Gemeinsame”, etwa die Eiförmigkeit, allein im
Vordergrund bleibt. Aber so ist es nicht. Übrigens wären die mehreren Beispiele nur ein technisches Hilfsmittel, & wenn ich einmal das Gewünschte gesehen hätte, so könnte ich's auch in einem Beispiel sehen. (Wie ja |
Es sind
also die Regeln, die von dem Beispiel gelten, die es zum Beispiel
machen. – |
Nun
genügt aber doch heute jedenfalls das bloße Begriffswort ohne
eine Illustration, um sich mit mir verständlich
zu machen || mit mir zu verständigen (und die
Geschichte des Verständnisses interessiert uns ja nicht)
z.B. wenn mir Einer sagt „forme ein
Osterei”.
Und || ; und ich will doch nicht sagen, daß ich
etwa dabei den Begriff des Ostereies vor meinem inneren
Auge || Aug sehe, wenn
ich diesen Befehl (& das Wort
„Osterei”) verstehe. |
Wenn wir eine Anwendung des Begriffes Osterei oder
Pflanze machen, so schwebt uns gewiß nicht vorerst ein allgemeines
Bild vor, oder bei dem Hören des Wortes
„Pflanze” das Bild des unbestimmten Gegenstandes,
den ich dann als eine Pflanze bezeichne. Sondern ich mache
die Anwendung sozusagen
(ganz) spontan.
Dennoch gibt es eine Anwendung von der ich sagen würde:
nein, das habe ich unter ‚Pflanze’ nicht gemeint;
oder anderseits „ja, das habe ich auch
gemeint”. Aber heißt das, daß mir diese
Bilder vorgeschwebt haben || vorschwebten
& ich sie in meinem Geist ausdrücklich abgewiesen
& zugelassen habe? – |
14.
∣ Wer aufgefordert würde
das Gesichtsfeld zu malen & es im Ernst
versuchte würde bald sehen, daß es unmöglich
ist. ∣ |
Eines möchte
ich immer sagen um den Unterschied der Fälle die
als Beispiele für einen Begriff beigebracht werden von denen zu
erklären die in der Grammatik eine bestimmte abgeschlossene
Im ersten Fall handelt der der Regel nicht zuwider der einen anderen Gegenstand bringt als die in der Regel genannten, im zweiten Fall würde er dadurch der Regel zuwiderhandeln. Wenn Du aber auch nur A B C D im Befehl nanntest aber die Handlung f(E) als Befolgung des Befehls ansahst, heißt das nicht daß Du mit F(A,B,C,D …) doch F(A,B,C,D,E) meintest? Oder wie unterscheiden sich diese Befehle, wenn sie doch von dem Selben befolgt werden? – Ja, aber es hätte ja auch f(G) mit dem Befehl übereingestimmt & nicht nur f(E). – Gut, dann meintest Du eben mit dem ersten Befehl F(A,B,C,D,E,G).(u.s.f.). Was immer Du mir bringst, ich hätte es doch in einer Disjunktion einschließen können. Wenn wir also eine Disjunktion aller von uns tatsächlich gebrauchten Fälle konstruierten, wie würde sich die F(A,B,C,D,E) ist die Disjunktion aller tatsächlich von uns gebrauchten Fälle aber auch andere Fälle (es wird natürlich keiner erwähnt) machen den allgemeinen Satz „F(A,B,C,D …)” wahr. Während man hierin natürlich nicht den allgemeinen Satz für F(A,B,C,D,E) einsetzen kann. |
15.
Es ist übrigens hier gerade wichtig daß die
Parenthese im vorigen Satz „und also ist auch jede andere
ähnliche Antwort unmöglich” ein
Unsinn || unsinnig ist weil man zwar verschiedene
besondere Fälle als Beispiel einer Allgemeinheit
geben || angeben kann, aber nicht verschiedene
Variable da die Variablen R, S, T sich ihrer
Bedeutung nach nicht unterscheiden. |
Darf || Kann ich
nicht sagen: Wer sich auf den
Befehl „F(A B C …)”
f(D) tut, richtet sich
anders || auf andere Weise nach dem Befehl, als
wer f(D) auf
„F(A,B,C,D)”
16. Der Prozeß wäre dann der, daß statt des allgemeinen Satzes F(∃) zuerst F(∃) ⌵ f(A) dann F(∃) ⌵ f(A) ⌵ f(B) dann F(∃) ⌵ f(A) ⌵ f(B) ⌵ f(C) gesetzt würde u.s.w. bis endlich das F(∃) überflüssig wäre. Wir weigern uns daß aber || Nun weigern wir uns aber eine Disjunktion als Ersatz des allgemeinen Satzes anzuerkennen. (Es gibt freilich eine empirisch bestimmte Disjunktion physikalischer Gegenstände deren Unterschied wir nicht mehr wahrnehmen können.) Also kommen wir nie dazu das F(∃) aus der Disjunktion weglassen zu können. Man könnte dann freilich nicht sagen wir befolgen F(∃) anders wenn wir f(D) tun als eine Disjunktion worin f(D) vorkommt, denn f(∃) = F(∃) ⌵ f(D)? Wem der Befehl gegeben wird 17.
Ist es also so, daß der Befehl „bringe mir eine Blume” nie durch den Befehl ersetzt werden kann von der Form „bringe Aber warum tut der allgemeine Satz so unbestimmt, wenn ich ja doch jeden Fall der wirklich eintritt auch im voraus hätte voraussehen können? || voraus beschreiben können? Aber eine Aufzählung ist ja wohl die größte || längste || (& vollständigste die ich geben kann – in irgend einem Sinne vollständig, etwa die Aufzählung aller besonderen Fälle die mir vorgekommen sind – & auch nach || mit ihr wird das „oder eine andere” seinen Sinn behalten. Aber auch das scheint mir noch nicht den wichtigsten Punkt dieser Sache zu treffen. Weil es, wie ich glaube, nicht eigentlich auf die Unendlichkeit der Möglichkeiten ankommt, sondern auf eine Art von Unbestimmtheit. Ja, gefragt, wieviele Möglichkeiten es denn gäbe für einen Kreis im Gesichtsfeld || für einen Kreis im Gesichtsfeld gäbe innerhalb eines bestimmten Vierecks zu liegen, könnte ich weder eine endliche Anzahl nennen, noch sagen es gäbe unendlich viele (wie in der Euklidischen Ebene). Sondern wir kommen hier zwar nie zu einem Ende, aber die Reihe ist nicht endlos im Sinne von ❘1, ξ, ξ + 1❘. Sondern kein Ende zu dem wir kommen, ist wesentlich das Ende. Das heißt, ich könnte immer sagen: ich seh' Der Begriff ‚Pflanze’ & ‚Osterei’ wird also von der Aufzählung gar nicht angetastet. Würde f(a) darum im f(∃) untergehn, weil dieses schon eine Disjunktion wäre, so würde eine Disjunktion der Art f(∃) ⌵ f(a) ⌵ f(b) ⌵ f(c) gleich sein f(a) ⌵ f(b) ⌵ f(c). Wirklich aber liegt es in der Natur || Bedeutung des f(∃), daß das nicht eintritt. Wenn wir auch sagen, wir hätten die besondere Befolgung f(a) immer als möglich voraussehen können, so haben wir dies doch in Wirklichkeit nicht getan. – Aber selbst wenn ich diese || die Möglichkeit f(a) vorhersehe & ausdrücklich in meinen Befehl aufnehme, so verliert sie sich neben dem allgemeinen Satz & zwar, weil ich eben aus dem allgemeinen Satz ersehe, daß dieser besondere Fall erlaubt ist & nicht einfach daraus daß er im Befehl als erlaubt festgesetzt ist. Denn steht der allgemeine Satz da, so nützt mir das Hinzusetzen des besonderen Falles nichts mehr (d.h. es macht den Befehl nicht expliziter). Denn nur aus dem allgemeinen Satz leite ich ja die Rechtfertigung her diesen besonderen Fall neben ihn zu setzen. Man könnte nämlich glauben & darauf geht ja meine ganze Argumentation |
18.
Ich befehle zuerst f(∃); er
befolgt den Befehl & tut f(a). Nun denke
ich, ich hätte ihm ja gleich den Befehl
f(∃)
⌵ f(a) geben können.
(Denn daß f(a) den Befehl
f(∃) befolgt
wußte ich ja früher & es kam
|
[Nur neuer Absatz] Ich möchte auch sagen: In der Grammatik ist nichts nachträglich, keine Bestimmung nach einer andern, sondern alles ist zugleich da. || zugleich. Insofern kann ich also (auch) nicht sagen, ich habe zuerst den Befehl f(∃) gegeben & bin dann erst drauf gekommen, daß f(a) ein Fall von f(∃) ist; jedenfalls aber war & blieb mein Befehl f(∃), & f(a) setzte ich dazu wissend || in der Erkenntnis daß f(a) mit f(∃) übereinstimmt. Und diese Bestimmung, daß f(a) mit f(∃) übereinstimmt setzt doch eben den || diesen Sinn des Satzes f(∃) voraus wenn er überhaupt selbständig festgehalten wird, & nicht erklärt wird er sei (ganz) durch eine Disjunktion zu ersetzen. Und mein Satz „jedenfalls war & blieb aber mein Befehl f(∃) u.s.w.” hieß nur daß ich den allgemeinen Befehl nicht durch eine Disjunktion ersetzt hatte. Man kann sich nun denken daß ich einen Befehl p ⌵ f(a) gebe & der |
Auf keinem
Umweg kann, was über eine Aufzählung von
Einzelfällen gesagt ist || wird, die Erklärung
der Allgemeinheit ergeben || sein. |
[Nachtrag]
Statt „Bildnis des Herrn
N.N.” könnte die Aufschrift des
Bildes auch sein: „Ein solcher Mensch ist jetzt
dort & dort zu sehen”. |
Und hier würde man klarer sehen, wie
|
Das Gemälde, die Krönung
Napoléons darstellend,
ohne die Überschrift entspräche ganz einer
fiktiven Beschreibung. |
Die Landkarte & ihre
Orientierung. |
„Ich
stelle mir die Sonne vor” ist Bild &
Überschrift. |
Ich richte
mich nach seinen Worten &
Gebärden. |
Die
Gebärden müssen als Grundlage des Kalküls dienen, wie
immer dieser Kalkül auch ausgeführt werden
mag. |
Ist nun nicht mein
Ausdruck, daß der Satz ein Bild ist, ein schiefer Ausdruck,
der eine gewisse Analogie zu weit treibt?? |
Nicht das ist wahr, daß, was ich
sage || wir sagen, nur für eine „ideale
Sprache” gilt oder Geltung hätte; wohl aber kann man
sagen, daß wir eine ideale Sprache konstruieren, in die aber dann
alles übersetzbar ist, was in unidealen Sprachen gesagt werden
kann. |
Was ist denn die
„gegenwärtige Situation”?
Nun, daß das & das der Fall ist. |
„Jetzt”
ist ein Wort. Wozu brauche ich dieses Wort?
‚Jetzt’ – im Gegensatz wozu? – Im Gegensatz zu ‚in einer Stunde’,
‚vor 5 Minuten’, etc.,
etc. „Jetzt” bezeichnet kein System sondern gehört zu einem System. Es wirkt nicht magisch; wie kein Wort. – |
Müßte
ich nicht sagen: Die Sätze die ich brauche
um die Wirklichkeit zu beschreiben, sind genau dieselben, wie die,
welche in der Dichtung geraucht werden, etwa im
King Lear: aber ich gebrauche sie anders.
Aber wenn ich das sagen kann, „anders”, so
müßte ich doch auch den Unterschied angeben
können. |
Wenn die
Sprache sich mit dem Gelde vergleichen läßt, an dem
an und für sich nichts
liegt, sondern das nur indirekt von Bedeutung ist, weil man
mit ihm Gegenstände kaufen kann, die für uns Bedeutung
haben; so kann man sagen, daß hier beim Gebrauch
der Wörter „Ich”,
„hier”, „jetzt”
etc. der Tauschhandel in den Geldhandel eintritt.
(?) |
Es ist klar, daß, wer einen Plan macht, ein Bild macht.
|
Aber es gibt doch
etwas anderes: Wenn er nämlich auf den Plan &
die Wirklichkeit Orientierungszeichen macht. |
Erklärung der Sprache z.B. des
Planes durch Vormachen der Benutzung || des
Gebrauches in einem bestimmten Fall: aber dieses
Vormachen interessiert uns nicht, so weit es Ursache des
richtigen Nachahmens ist, sondern, soweit es
(nachträglich) als Erklärung gedeutet
werden kann. |
Das was
„particular” ist, ist das
Ereignis. Das Ereignis das durch die Worte
beschrieben wird „heute hat es geregnet” &
den nächsten Tag durch „gestern hat
es geregnet”. |
Scheinbare
Konsequenz, wenn einer heute verspricht
„morgen werde ich Dich besuchen” & dieses
Versprechen am nächsten Tag wörtlich
wiederholt. || Wort für Wort
wiederholt. |
Bild & Wirklichkeit müssen
ein System geben. Sowie das Resultat der Rechnung
& die ganze übrige Rechnung. |
Wenn wir eine
Abbildung vormachen, so geht es uns nichts an,
ob dies |
Was uns interessiert ist nur die
exakte Beziehung des Beispiels zum
Nachmachen || Folgen. || zu der Nachfolge || zu dem
Danachhandeln. |
∣ ∣ Die Philosophie hat es
in dem selben Sinn mit Kalkülen zu tun wie sie es mit
Gedanken zu tun hat (oder mit Sätzen &
Sprachen). Hätte sie's aber wesentlich
mit dem Begriff des Kalküls zu tun also mit dem Begriff des
Kalküls vor allen Kalkülen so gäbe es eine
Metaphilosophie. Und die gibt es nicht.
¤ (¤ Man könnte alles was wir zu sagen
haben so darstellen, daß das als ein leitender Gedanke
erschiene.) ∣ ∣ |
Es wird aus dem Beispiel heraus wieder
kalkuliert. |
Beispiele
sind ordentliche Zeichen, nicht Abfall, nicht Beeinflussung.
|
Denn uns interessiert nur die
Geometrie des Mechanismus. (Das heißt
doch, die Grammatik seiner Beschreibung.) |
Die Bedeutung ist eine Festsetzung, nicht
Erfahrung. Und damit nicht Kausalität. |
Das Exakte ist die
interne Beziehung. |
Das Zeichen, soweit es suggeriert, also soweit es
wirkt interessiert uns garnicht.
Es interessiert uns nur als Zug [hier ist das Satzzeichen gemeint?] in einem Spiel: Glied in einem System das selbständig ist || , das seine Bedeutung in sich selbst hat || , das selbstbedeutend ist. |
Die Differenz, der || Der Unterschied der Wortarten ist immer wie der
Unterschied der Spielfiguren, oder, wie der noch
größere, einer Spielfigur & des
Schachbrettes. |
Der Name
„Napoléon” hat nur Sinn als Zeichen eines
Kalküls (wie jeder Name). Das System ist hier z.B. das, daß dieser Name über verschiedenen Bildern stehen könnte & über einem steht. |
Was das Zeichen
suggeriert, findet man durch Erfahrung. Es ist die
Erfahrung, die uns lehrt, welche Zeichen am
wenigsten leicht || am seltensten
mißverstanden werden. |
Es muß uns klar sein, daß der Zusammenhang
unseres Gedankens |
„Aber
der Gedanke an Napoléon
muß doch mit Napoléon
etwas zu tun haben”. Gewiß, & er muß
das enthalten, dessen Existenz nicht zweifelhaft
ist. |
Und das
muß den Wörtern entsprechen, dessen Existenz nicht zweifelhaft
ist. |
[Nachtrag & Zusätze]
19.
Wer Grün einen Gegenstand nennt, muß sagen, daß
dieser Gegenstand im Symbolismus vorkommt.
Denn sonst wäre der Sinn des Symbolismus, also daß es ein
Symbolismus ist, nicht gewährleistet.
Das stößt natürlich den ganzen Begriff vom Gegenstand um! Und mit Recht. Gegenstand darf nicht Rot, links , & viel sein, sondern nur der rote Fleck, der Tisch, etc.. Will man sich mit diesen Dingen nicht abgeben, so ist es wohl besser, man gebraucht das Wort „Gegenstand” nicht. |
Die Unbeholfenheit mit der das Zeichen
|
Denken ist
Pläne machen. Wenn Du Pläne machst, so machst Du einen Plan zum Unterschied von || im Gegensatz zu andern Plänen. |
Du machst diesen zum Unterschied von
anderen. [kein
Absatz] Und so charakterisiert das Zeichen, das Vorstellungsbild, den Plan. [kein Absatz] Im Gegensatz nämlich zu anderen Zeichen & Vorstellungsbildern. |
Der Gedanke kann für uns
nur das sein, was gebraucht wird. |
Wir sind nicht im Bereiche der Erklärungen
& jede Erklärung klingt für uns
trivial. |
Aber dieser
Verzicht auf die || jede Erklärung macht
es so schwer zu fassen || sagen, was der Gedanke
eigentlich leistet. |
Man kann
sagen: Er rechnet auf Grund von Gegebenem
& endet in einer Handlung. |
Die Berechnung der Wandstärke eines Kessels & der || [﹖]dieser[﹖] entsprechenden Verfertigung || Die Berechnung der Wandstärke eines Kessels &, der entsprechenden, Verfertigung ist ein sicheres Beispiel des Denkens || muß ein Beispiel des Denkens sein. |
Der Schritt, der von der Berechnung auf dem Papier
zur Handlung führt, ist noch ein Schritt der Rechnung.
|
Wenn man sagt: „es
muß der Mathematik wesentlich sein, daß sie angewandt
werden kann”, so meint man, daß diese
Anwendbarkeit nicht die eines Stückes Holz ist, von dem
ich sage „das werde ich zu dem & dem anwenden
können”. |
Wenn
das Denken nicht in gewissem Sinne mechanisch – zwangsläufig
– wäre, so wäre es nichts nütze. |
„Der Plan besteht darin, daß
ich mich das & das tun sehe.” Aber
woher || wie weiß ich, daß ich
es bin. – Nun ich bin es ja nicht, was ich sehe,
sondern etwa ein Bild. Warum aber nenne ich es
mein Bild? Nicht etwa, weil es mir ähnlich
sieht. [Hier kein Fragezeichen]
¥
|
[Im Christentum sagt der liebe
Gott gleichsam zu den Menschen:
Spielt nicht Tragödie, das heißt Himmel &
Hölle auf Erden, Himmel & Hölle habe ich
mir vorbehalten.] |
Es ist wahr: Namen können Dinge vertreten; aber
sie vertreten nicht ihre Bedeutungen; & die Dinge
(etwa räumliche Gegenstände) die Bedeutungen der
Wörter zu nennen, ist absurd. |
⍈
[Zum drittletzten Satz]
„Woher weiß ich daß ich es
bin?” Das ist
ein gutes Beispiel einer falsch angebrachten
Frage: Die Frage hat nämlich Sinn wenn es
etwa heißt: Woher weiß ich daß
was ich da im Spiegel sehe, ich bin || ich
es bin, den ich da im Spiegel sehe. Und
die Antwort gibt dann Merkmale nach denen || durch die
dies zu erkennen ist || ich zu erkennen bin! – |
Hieße das nicht: Der Träger des
Namens ist nicht seine Bedeutung? |
Aber ist nicht L.
W. der Träger
des Namens „L.W.”? Und ist nicht
L.W. die Bedeutung von
„L.W.”? |
Ist nicht „L.W. ist tot” der
selbe Satz wie „der Träger des
Namens ‚L.W.’ ist tot”?
|
Ist es aber nicht Unsinn zu sagen,
L.W. sei die Bedeutung des Namens
„L.W.”?! Das hieße doch wohl,
daß |
Man kann sagen, daß die Worte „der
Träger des Namens ‚L.
W.’” dieselbe Bedeutung haben wie
der Name „L.W.” – also füreinander
eingesetzt werden können. |
Aber heißt es nicht dasselbe, zu sagen „zwei Namen
haben einen Träger” & „zwei
Namen haben ein & dieselbe Bedeutung”?
(Morgenstern, Abendstern, Venus) |
Wenn mit dem Satz
„‚a’ &
‚b’ haben denselben
Träger” gemeint ist: „der Träger von
‚a’” bedeutet dasselbe wie
„der Träger von ‚b’”,
so ist alles in Ordnung, weil das dasselbe heißt wie
a = b. Ist aber mit
dem Träger von ‚a’ etwa der Mensch
gemeint, von dem es sich feststellen läßt, daß er auf den
Namen ‚a’ getauft ist; oder der Mensch, der
das Täfelchen mit dem Namen ‚a’ um den Hals
trägt; etc., so ist es gar nicht gesagt, daß
ich mit ‚a’ diesen Menschen meine, &
daß die Namen, die den gleichen Träger haben, dasselbe
bedeuten. |
Die Frage
„Woher weiß ich, daß |
Wohl aber könnte man fragen „was hat denn der Name
‚a’ mit diesem Menschen zu
tun”. Und die Antwort
wäre: Nun, das ist a. |
Aber zeigen wir nicht zur Erklärung
der Bedeutung auf den Gegenstand den der Name vertritt?
Ja; aber dieser Gegenstand ist nicht die Bedeutung, obwohl sie
durch das Zeigen auf diesen Gegenstand bestimmt wird. |
„Diese Figur des Bildes bin
ich” ist ein Übereinkommen. |
Ja, aber worin kommen wir
überein? Welche Beziehung zwischen Zeichen &
mir stellen wir her? Nun, nur die, die etwa
durch das Zeigen mit der Hand, oder das Umhängen eines
Täfelchens besteht, denn diese Relation ist nur durch das System
bedeutungsvoll, dem sie angehört. |
Es ist von der größten Bedeutung, daß wir
uns zu einem Kalkül der Logik immer ein Beispiel denken auf
das || welches der Kalkül wirklich angewandt wird
& nicht Beispiele von denen wir sagen sie seien
eigentlich nicht die idealen diese aber hätten
wir noch nicht. Das ist das Zeichen einer ganz falschen
Auffassung. Kann ich den Kalkül überhaupt
verwenden dann ist das || dies auch die
ideale Verwendung & die Verwendung
um die es sich handelt. Man geniert sich
nämlich einerseits das Beispiel als das eigentliche
anzuerkennen weil man in ihm noch eine
Komplikation
erkennt auf die der Kalkül sich nicht bezieht; anderseits ist es
doch das Urbild des Kalküls & er davon hergenommen
& auf eine geträumte die Anwendung kann man
nicht warten. Man muß sich also eingestehen welches das
eigentliche Urbild des Kalküls ist.
|
Das ist aber kein Eingeständnis
– als habe man damit einen Fehler gemacht || begangen, den Kalkül von daher
genommen zu haben–, sondern der Fehler liegt darin ihn
jetzt in nebelhafter Weise anzuwenden oder eine
Anwendung zu versprechen. || oder eine Anwendung in
nebuloser Ferne zu versprechen. |
(So könnte
Spengler besser verstanden
werden wenn er sagte: ich vergleiche verschiedene
Kulturperioden dem Leben von Familien; innerhalb der Familie gibt es
eine Familienähnlichkeit, während es auch zwischen
Mitgliedern verschiedener Familien eine Ähnlichkeit gibt;
die Familienähnlichkeit unterscheidet sich von der andern
Ähnlichkeit so & so etc.. Ich
meine: das
Vergleichsobjekt, der Gegenstand von
welchem diese Betrachtungsweise abgezogen ist, muß uns
angegeben werden, damit nicht in die Diskussion
immer Ungerechtigkeiten einfließen. Denn
da wird dann alles, was für das Urbild der
Betrachtung || des Vergleichs wahr
ist || stimmt nolens volens auch
für von dem Objekt worauf wir die
Betrachtung anwenden behauptet; & behauptet „es
müsse, immer …”.
Das kommt nun daher, daß man den Merkmalen des Urbilds einen Halt in der Betrachtung geben will. Da man aber Urbild & Objekt vermischt dem Objekt dogmatisch beilegen muß, was nur das Urbild charakterisieren muß. Anderseits glaubt man die Betrachtung ermangle ja der || habe nicht die Allgemeinheit die man ihr geben will, wenn sie nur für den einen Fall wirklich stimmt. Aber das Urbild soll ja eben als solches hingestellt werden; daß Man möchte so bei allen übertriebenen dogmatisierenden Behauptungen immer fragen: Was ist denn nun daran wirklich wahr. Oder auch: In welchem Fall stimmt denn das nun wirklich.) |
Wenn ich also auf
einen Fleck zeige & als Worterklärung sage „das
ist rot”, so hätte ich nicht sagen dürfen
„das ist die Bedeutung des Wortes
‚rot’”. |
Wer so dogmatisiert weiß seinem Satz nicht den
richtigen Platz zu geben (das ist so, als wollte ich daß einer
Präsident bei einer Versammlung || Sitzung ist, wüßte aber nicht, wie ich ihm die
richtige Stellung das richtige Ansehen geben kann || solle. Denn er kann nicht etwa statt jedes der
Mitglieder sprechen, er kann nicht auf allen Stühlen sitzen;
sondern nur auf einem, aber auf dem einen an der
Spitze.)
Was ich hier sage, ist eigentlich, was
Boltzmann
über die Stellung des mechanischen Modells, etwa in der Theorie
der Elektrizität, sagt. |
Die Zuordnung von Gegenstand & Name ist
keine andere, als die durch die Worte „das ist
…” oder eine Tabelle erzeugte
|
Das Denken
ist eine fortlaufende Kalkulation. |
Daß mich das Feuer brennen wird, wenn
ich die Hand hineinstecke: das ist Sicherheit.
|
D.h.,
da sehe¤ ich was Sicherheit bedeutet.
(Nicht nur was das Wort „Sicherheit”
bedeutet, sondern auch was es mit ihr an || auf sich
hat.) |
20.
Was heißt: die Zahlenreihe ist unendlich? |
Das muß doch eine
Bestimmung sein, nicht die Konstatierung einer
Tatsache. |
Darin hatte ich
freilich recht, daß die unendliche Möglichkeit
(z.B. unendliche Teilbarkeit) einer ganz
anderen grammatischen Kategorie angehört, als die
endliche (Möglichkeit in 3 Teile zu
teilen). Aber damit ist noch nicht die
Grammatik |
Wenn ich z.B. sage
„‚Kardinalzahlen’
nenne ich alles, was aus 1 durch fortgesetztes Addieren von 1
entsteht”, so vertritt das Wort
„fortgesetzt” nicht eine nebelhafte
Fortsetzung von 1,
1 + 1, 1 + 1 + 1, vielmehr ist auch
das Zeichen „1, 1 + 1,
1 + 1 + 1, …” ganz exakt zu
nehmen, als verschieden von
„1, 1 + 1,
1 + 1 + 1” anderen bestimmten Regeln
unterworfen & nicht ein Ersatz || Vertreter
einer Reihe „die sich nicht hinschreiben
läßt”. |
Das
heißt: mit dem Zeichen
„1, 1 + 1, 1 + 1 + 1
…” wird auch gerechnet wie mit
(den) Zahlzeichen, nur
anders. |
Was bildet man sich denn aber ein? Welchen
Fehler macht man ¤ denn || denn? Wofür hält man
dann das Zeichen
„1, 1 + 1, …?
D.h.: wo kommt denn das
wirklich vor, was man in diesem Zeichen zu sehen
meint? Etwa, wenn ich sage „er zählte 1, 2,
3, 4, 5, 6 und so weiter bis tausend”? wo es auch
möglich wäre wirklich alle Zahlen
hinzuschreiben. |
Als
was sieht man denn „1, 1 + 1, 1 + 1 + 1
…” an? Als eine ungenaue Ausdrucksweise. Die Pünktchen || Punkte sind so wie weitere Zahlzeichen |
Es frägt sich auch, wo denn der
Zahlbegriff (oder Begriff der Kardinalzahl)
unbedingt gebraucht wird. Zahl im Gegensatz
wozu? [1, ξ, ξ + 1] wohl im
Gegensatz zu [5, ξ, √ ξ]
u.s.w. – Denn wenn ich so ein
Zeichen (wie „[1, ξ, ξ + 1]”)
wirklich einführe – & nicht nur als Luxus
mitschleppe – so muß ich auch etwas mit ihm tun,
d.h., es in einem Kalkül verwenden,
& dann verliert es seine Alleinherrlichkeit & kommt in
ein System ihm koordinierter Zeichen. |
Man wird vielleicht sagen: aber
‚Kardinalzahl’ steht doch im
Gegensatz zu ‚Rationalzahl’,
‚reeller Zahl’ etc. Aber
dieser Unterschied ist ein Unterschied der Regeln (der von
ihnen geltenden Spielregeln) – nicht |
Wir sagen nicht, daß der Satz
f(x), wenn
f(1) gilt & aus
f(c) f(c + 1)
folgt, also für alle Kardinalzahlen gilt || wahr ist, sondern „der Satz
f(x) gilt für alle
Kardinalzahlen” heißt „er gilt
für x = 1 &
f(c + 1) folgt aus
f(c)”.
¥ |
Wie aber weiß ich
28 + (45 + 17)
= (28 + 45) + 17 ohne es bewiesen zu
haben? Wie kann mir ein allgemeiner Beweis einen
besonderen Beweis schenken. Denn ich könnte doch den
besonderen Beweis führen & wie treffen sich da die
beiden Beweise & wie, wenn sie nicht
übereinstimmen. |
⍈
Und hier ist ja der Zusammenhang mit der
Allgemeinheit in endlichen Bereichen ganz klar, denn eben das
wäre in einem endlichen Bereich allerdings der Beweis dafür,
daß f(x) für alle Werte
von x gilt & eben
das ist der Grund, warum wir auch im arithmetischen Falle sagen,
f(x) gelte für alle
Zahlen. |
Und wenn man nun fragt: ja kann denn etwas anderes
bei dem besondern Beweis herauskommen, als
28 + (45 + 17)
= (28 + 45) + 17, so müßte ich
antworten: freilich kann etwas |
21.
Aber ich würde doch sagen:
Der || der
allgemeine Beweis zeigt schon, daß nichts anderes
herauskommen kann. |
Hier
kommen wir wieder auf den Fall
 der Spirale von der wir sagen sie
schneidet auf der Geraden, wenn sie so
weiterläuft, immer das gleiche Stück a ab
& kommt daher in weiteren drei Windungen nach A.
Diesen Punkt könnte ich konstruieren indem ich die
Spirale bis A verlängere aber auch, indem ich
einfach a dreimal auf der Geraden abtrage. –
der Spirale von der wir sagen sie
schneidet auf der Geraden, wenn sie so
weiterläuft, immer das gleiche Stück a ab
& kommt daher in weiteren drei Windungen nach A.
Diesen Punkt könnte ich konstruieren indem ich die
Spirale bis A verlängere aber auch, indem ich
einfach a dreimal auf der Geraden abtrage. – |
Zuerst ist es nötig klar zu
sehen, daß wir keine Tatsache beweisen. Denn, weil es
sich in dem einen Fall so verhält, wie kann ich wissen,
daß es sich in dem andern so verhält?
Und ein ‚Sich verhalten müssen’ gibt
es nicht. Ist es nicht so, so kann man auch nichts
machen. Nur was von uns abhängt können wir im
Voraus bestimmen. |
Der Beweis kann also nichts
prophezeien. |
Ist der Beweis
für A ausgeführt auch der Beweis für B, so
daß es ganz gleichgültig ist, in welchem Dreieck er
gezeichnet ist. Und wenn er also in beiden
Dreiecken gezeichnet ist || wäre nur
derselbe Beweis wiederholt wäre? Daß
also das Zeichen des Beweises – der Beweis als Zeichen || Symbol – ebensogut aus der Konstruktion in A
& dem Dreieck B bestehen könnte, wie aus
diesem Dreieck & in einer Konstruktion in ihm.
|
|
Der Beweis || Das
Zeichen des Beweises daß (3 + 4)² =
3² + 2 ∙ 3 ∙ 4 + 4²
bestünde dann in einer Sprache in:
(x + y)² = … = x² + 2xy + y² ¥ |
Man möchte
vielleicht || wohl sagen: Die
selbe Konstruktion ist ein Beweis des geometrischen Satzes
für das bestimmte Dreieck; wir können sie aber
auch allgemein meinen || auffassen; oder: wir
können an ihr auch einsehen, daß das, was für
dieses Dreieck gilt, für jedes andre auch gelten
muß. – Aber worin besteht dieses
„meinen” || „auffassen” & das
„einsehen”? Die psychologischen
Prozesse sind uns ja ganz gleich. || kümmern uns ja nicht. „Das Dreieck
steht eben hier für irgend ein
Dreieck”. Aber worin besteht dieses
„für etwas stehen”? Es handelt
sich für uns eben wieder nur um den
Ausdruck jener ‚Auffassung’,
d.h. den Ausdruck dessen was wir
auffassen oder einsehen & den Ausdruck dafür
daß das Dreieck nur für sich selbst oder für alle
Dreiecke steht. Der Kalkül muß
(wieder) festgestellt werden.
|
Nicht seelische Vorgänge
interessieren uns sondern symbolische. |
Wie
macht mich der allgemeine
Induktionsbeweis || Beweis
sicher || gewiß, daß der
besondere das ergeben wird? |
(Verachte nur nicht die simplen Kalküle wie sie jedes Kind
& jede Kaufmannsfrau benützt.) |
|
Und hier kann
man die beiden Fälle deutlich unterscheiden, von denen wir
im geometrischen Beweis sprachen. Denn die Figur
|
Ein
Kalkül ist nicht strenger als ein anderer! Man
muß nur die Grenzen eines jeden kennen.
Nur insofern kann man einen Kalkül unstreng nennen, als seine Regeln nicht klar formuliert sind. |
Man sagt: „dieser
Satz ist für alle Kardinalzahlen
bewiesen”. Aber sehen wir doch nur hin, wie der
Begriff der Kardinalzahl in den Beweis eintritt. Doch
nur, indem im Beweis nur von 1 &
der Operation ξ + 1 die Rede ist – aber
nicht im Gegensatz zu Etwas, was den Rationalzahlen
entspräche. Wenn man also den Beweis in Prosa
mit Hilfe des Begriffsworts ‚Kardinalzahl’
beschreibt, so sehen wir wohl, daß diesem Wort kein
Begriff entspricht. || , daß dieses
Wort nicht die Bezeichnung eines Begriffes
ist. || , daß kein
Begriff diesem Wort
entspricht. |
Genügt aber das als Beweis?! Ja, denn der Beweis besteht nun in der Beschreibung dessen was ich zeichnen könnte. Und die Beschreibung eines Beweises ist ja (auch) der Beweis. – Und nun muß ich ja das Zeichen „
|
Muß ich hier nicht auch von einem System von Beweisen
reden? |
Wie verhält sich der
‚ausgeführte’ Beweis zum allgemeinen,
scheinbar nur angedeuteten? ◇◇◇
Oder: Gehören sie verschiedenen Symbolsystemen an? Sonst aber muß doch, was der erste mehr enthält als der zweite, überflüssig sein. |
Es ist || wird eben in dem Zeichen „
|
22.
Man kann übrigens das Übereinkommen treffen einen
Ausdruck der Form
((((1) + 1) + 1) + 1) (der
Kardinalzahlform) nur durch die Zahl der ersten Klammern
((((
anzudeuten da durch sie alles weitere gegeben ist.
Und nun kann man ihn ❘ ❘ ❘ ❘
schreiben. (Ein Umweg.) |
(Man muß sich in die Fehler
hineindenken. „Laß ihn Dir den rechten Eindruck
machen … (Rückert)). |
(Zeitdauer eines Tones & Zeitdauer einer
akustischen Schwingung.) |
Kritik meiner früher
dargelegten || auseinandergesetzten Auffassung des
induktiven Beweises. Ein Beweis ist Beweis eines (bestimmten) Also ist auch der Satz „jede Gleichung n-ten Grades hat n Lösungen” nur ein Satz der Mathematik sofern er einem System von Sätzen & sein Beweis einem korrespondierenden System von Beweisen entspricht. Denn welchen guten Grund habe ich dieser Kette von Gleichungen etc. (dem sogenannten Beweis) diesen Prosasatz zuzuordnen. Es muß doch aus dem Beweis – nach einer Regel – hervorgehen von welchem Satz er der Beweis ist. |
Nun liegt es aber im Wesen dessen,
was wir als Satz bezeichnen, daß es sich verneinen lassen
muß. Und auch die Verneinung des bewiesenen Satzes
muß mit dem Beweis zusammenhängen; so nämlich daß sich
zeigen läßt unter welchen anderen entgegengesetzten
Bedingungen sie herausgekommen wäre. |
Man |
(Mit „sweeping
statements” ist in der Philosophie nichts
gemacht; sondern es muß alles so dargestellt werden wie es
ist.) |
23.
(Aus dem
Simplicissimus: „Rätsel der Technik.
(Bild: Zwei Professoren vor
einer im Bau befindlichen Brücke) Stimme von
oben:
„Laß abi – –
hüah – – laß abi
sag' i – – nacha drah'n
mer'n anders um!” – – – –
„Es ist doch unfaßbar Herr Kollega,
daß eine so komplizierte & exakte Arbeit
in dieser Sprache zustande kommen
kann”.) |
Alle
Überlegungen können viel hausbackener || grober angestellt werden, als ich sie in
früheren || frühen Zeiten angestellt
habe. Und darum brauchen in der
Philosophie auch keine neuen Wörter angewendet
werden, sondern die alten, |
„Ist das ein Beweis dieses
Satzes?” Wird er als Beweis
gebraucht? Wenn ja, warum soll ich ihn nicht
einen Beweis nennen? |
Jede
Multiplikation ist ein Beweis. Sie
entscheidet, daß
16 × 25 400
ist & nichts anderes, || & keine andere
Zahl, & wird wirklich als Beweis
dafür gebraucht. |
∣ Beim || Im
Euklidischen
Beweis ist nicht die Figur allein maßgebend, sondern auch
die Reihenfolge der konstruktiven Operationen & man
könnte sich den Beweis durch eine Serie von Figuren geführt
denken (die den Gang des Beweises
geben || den Gang des Beweises).
| |
24.
Man hört immer wieder die Bemerkung daß die Philosophie eigentlich keinen Fortschritt mache, daß die gleichen philosophischen Probleme die schon die Griechen beschäftigten uns noch beschäftigen (u.s.w.). Die das aber sagen verstehen nicht den Grund dessen warum es so ist. || sein muß. Der ist aber, daß unsere Sprache seit diesen Zeiten sich gleich geblieben ist & uns immer wieder zu jenen || denselben Fragen verführt. Solange es ein Verbum ‚sein’ geben wird das zu funktionieren scheint wie ‚essen’ & ‚trinken’, solange es Und dies kommt || befriedigt im übrigen ein Verlangen nach dem Überirdischen || Transzendenten denn indem sie die „Grenze des menschlichen Verstandes” zu sehen glauben, glauben sie natürlich über ihn hinaussehen zu können. |
Ich lese
„… philosophers are no nearer to the meaning of
‚Reality’ than
Plato
got; …”. Welche
sonderbare || seltsame Sachlage.
Wie sonderbar daß Plato dann
überhaupt doch so weit hat kommen können || kommen
konnte!
Oder, wenn daß wir dann nicht weiter kommen konnten!
War es, weil
Plato so gescheit
war? |
Ist nicht die
Hauptgefahr die, daß uns der Prosa-Ausdruck des Ergebnisses
einer mathematischen Operation einen Kalkül
vortäuscht der gar nicht vorhanden ist. Indem er
seiner äußeren Form nach einem System anzugehören scheint
das es hier gar nicht gibt. |
Ist der Induktionsbeweis ein Beweis von
a + (b + c) =
(a + b) + c, so muß man sagen
können: die Rechnung liefert daß
a + (b + c) =
(a + b) + c ist (& kein
anderes Resultat). Denn dann muß erst die Methode der Berechnung (allgemein) bekannt sein, &, wie wir darauf || in diesem Fall || nur 25 × 16 ausrechnen können, so auch a + (b + c). Es wird also dann erst eine allgemeine Regel zur Ausrechnung aller solcher Aufgaben gelehrt & danach die besondere gerechnet. – Welches ist aber hier die allgemeine Methode der Ausrechnung? Sie muß auf allgemeinen Zeichenregeln beruhen (– etwa, wie dem assoziativen Gesetz –). |
Ist nun etwa dieser Beweis des
assoziativen Gesetzes der, daß
a + (b + c) =
(a + b) + c ist & nicht
(a + 2b) + c?
|
∣ Wenn man die irrationalen
Zahlen einführt, so tut man immer so, als hätte man
nun etwas Neues entdeckt (etwa neue Punkte zwischen den
alten). Während es sich nicht um eine neue
Entdeckung sondern um eine neue Konstruktion handelt (die man dann
auch „Zahl” nennen kann, oder
nicht). ∣ |
Angenommen wir nennten den Satz daß 7 durch keine kleinere Zahl
außer der 1 teilbar ist „das Gesetz der heiligen
Zahl” & es würde lauten
„7 ist die heilige Zahl” || würden es in den
Worten „7 ist die heilige Zahl”
aussprechen. |
Nur für einen solchen
‚Satz der Mathematik’
gibt es verschiedene unabhängige Beweise.
Die voneinander unabhängigen Rechnungen enthalten nämlich willkürlich den gleichen Namen. |
Ich brauche nicht zu
behaupten, man müsse die n Wurzeln der Gleichung
n-ten Grades konstruieren können, sondern der
Satz ich sage nur, daß der Satz „diese Gleichung hat
n Wurzeln” etwas anderes heißt,
wenn ich ihn durch Abzählen der konstruierten Wurzeln &
wenn ich ihn anderswie bewiesen habe. Finde ich aber eine
Formel für die Wurzeln einer Gleichung, so habe ich einen neuen
Kalkül konstruiert & keine Lücke eines
alten ausgefüllt. |
Es
ist daher Unsinn zu sagen, der Satz ist erst erst
bewiesen, wenn man eine solche Konstruktion
aufzeigt. Denn dann haben wir eben etwas Neues konstruiert
& was wir jetzt unter dem Hauptsatz der Algebra verstehen ist
|
Zu fürchten, es
könne also der Algebra diese Stütze entrissen werden, ist
Blödsinn. |
25.
[Nachtrag] „Ich habe das
vorausgesehen.” – Wie ist das möglich, da es
doch damals nicht (& vielleicht niemals)
geschehen ist?! |
Wozu denkt der Mensch? Wozu ist es
nütze? Wozu berechnet er Dampfkessel
& überläßt es nicht dem Zufall, wie stark
die Wand des Kessels wird || er die Wand
des Kessels macht? Es ist doch nur
Erfahrungstatsache, daß Kessel die so berechnet wurden nicht so oft
explodieren || explodierten. Aber so, wie er
alles eher täte, als die Hand in's Feuer stecken, das ihn
früher gebrannt hat, so wird er alles eher tun als den Kessel
nicht berechnen. Da uns aber Ursachen nicht interessieren,
so können wir nur sagen: die Menschen denken
tatsächlich: sie gehen, z.B.,
auf diese Weise vor wenn sie einen Dampfkessel machen. Kann
nun ein so erzeugter Kessel nicht explodieren? Oh
ja. – |
Augustinus: Wann messe ich einen
Zeitraum. Ähnlich meiner Frage: Wann
kann ich Schach spielen. |
Sich
etwas überlegen. Ich überlege, ob ich jetzt
in's Kino gehn soll. Ich mache mir ein Bild der
Zeiteinteilung des Abends. Ich könnte es auch sehr
wohl graphisch darstellen. Aber wozu tue ich
das?? Ich mache ja kein
‚Gedankenexperiment’! |
∣
Falsche Ideen über das Funktionieren der Sprache:
Dr. Broad, der sagte, eine || die
Aussage die sagt ‚etwas werde
eintreten’, sei kein Satz. Was spricht man dieser
Aussage damit ab? Etwas anderes, als, daß sie
ein Gegenwärtiges oder Vergangenes
beschreibt? – Die Magie mit
Wörtern. Ein solcher Satz, wie der
Broads, kommt mir so
vor, wie ein Versuch eine chemische Änderung magisch zu
bewirken; indem man den Substanzen, quasi, zu verstehen gibt,
was sie tun sollen (wenn man etwa Eisen in Gold
überführen wollte indem man ein Stück Eisen mit der
rechten Hand faßte & zugleich ein
Stück Gold mit der linken Hand
faßte.) ∣ |
Hier kommen wir
auch zur Frage: „inwieweit hilft
Denken die Wahrheit finden?
(Johnson) |
„Ich male mir das aus.” |
Das Denken faßt
in gewissem Sinne |
„Der Satz ist ein Bild”. Ein Bild
wovon? Kann man sagen: „von der Tatsache,
die ihn wahr macht, wenn er wahr ist & von der
Tatsache die ihn falsch macht, wenn er
falsch? || . Im ersten Fall ist
er ein korrektes Bild, im zweiten Fall ein
unkorrektes.”? |
Denn er ist nicht
ein Bild davon, wie es wäre wenn..... Das heißt
nichts. Dann wäre er höchstens ein Bild des
Satzes oder eines andern Bildes davon, wie es wäre
wenn..... |
Wenn man mit Bild
meint: die richtige, oder falsche Darstellung der Realität,
dann muß man wissen, welcher Realität, oder welches Teils der
Realität; d.h., man muß ein
Mittel haben, den Satz in bestimmter Weise mit der
Wirklichkeit zu vergleichen. Ich kann dieses Zimmer
richtig oder falsch darstellen, aber um herauszufinden ob richtig oder
nicht, muß ich wissen, daß dieses Zimmer gemeint ist.
|
Denken
wir an eine Chiffre: Ein Satz sei uns in der Chiffre
gegeben & auch der Schlüssel, dann ist uns
natürlich, in gewisser Beziehung, alles zum
Verständnis der Chiffre gegeben. Und doch
|
Wenn man
hier die Frage stellte: „In welchem Augenblick
der Übertragung (aus der Chiffre in's
Deutsche) verstehe ich den Satz”, würde man einen
Einblick in das Wesen des Verstehens erhalten.
|
Wir
verstehen alle, was es heißt, in einem Kalender nachschlagen, an
welchem Tag der Woche wir frei sind. Das Bild, das wir
sehen ist etwa
| / | / | / | / | | / | / |
& wir sagen
nun, wir seien nur Donnerstag frei, & handeln dem
gemäß. Nun ist es aber dabei schwer zu sagen, was hier eigentlich geschieht & mit welcher Berechtigung wir nach dem Bild handeln. |
Was geschieht, wenn
ich mir einen Schachzug überlege? In diesem Falle
kann ich die Züge im vorhinein machen & also das
direkteste Bild dessen entwerfen was geschehen wird. |
I
a + (b + (c + 1)) ≝
a + ((b + c) + 1) ≝
(a + (b + c)) + 1
II
a + (b + c) =
(a + b) + c Wenn wir
I den Beweis von II nennen, was ist das allgemeine Prinzip
dieses Beweises? Denn es nützt ja nichts zu sagen,
I beweise II, da mir dadurch doch
nicht mehr als nur I & II gegeben wird;
es sei denn, daß ich nun noch eine allgemeine Regel
erfahre, von der der Schluß von I auf II nur ein
Beispiel ist. |
Ein merkwürdiges Wort: „Es ist mir
gelungen, das zu beweisen”.
(Das ist es, was im Falle 25 × 16 = 400 niemand sagen würde.) |
Das System des oberen Beweises ist
dies: F1(c) =
F2(c) ..... S ist zu beweisen.
F1(1) =
F2(1) ist eine anerkannte Regel.
Wenn aus dieser & den andern bereits anerkannten Regeln
hervorgeht daß einerseits
F1(c + 1) =
f(F1(c)) andrerseits
F2(c + 1) =
f(F2(c)), dann gilt S als
bewiesen. |
Ist nun I
ein Beweis für
5 + (2 + 7)
= (5 + 2) + 7? Es ist ein Beweis
für ❘ ❘ ❘ ❘ ❘ +
(❘ ❘ + ❘ ❘ ❘ ❘ ❘ ❘ ❘) =
(❘ ❘ ❘ ❘ ❘ + ❘ ❘) +
❘ ❘ ❘ ❘ ❘ ❘ ❘. Denn
begännen wir den linken Ausdruck nach der Definition
a + (b + 1) =
(a + b) + 1 zu transformieren wie im Beweis,
so sähen wir bald, daß uns jede Transformation der
rechten Seite näherbrächte (Ist es nicht so wie ich fünf Männer durch      darstellen kann, aber
auch durch darstellen kann, aber
auch durch  (❘ ❘ ❘ ❘ ❘)?) (❘ ❘ ❘ ❘ ❘)?) |
Insofern der Beweis also für || auf Zahlen mit denen wir rechnen angewandt werden kann,
können wir ihn allgemein nennen (wie etwa einen Hut den jedes
Familienmitglied benutzen kann). |
(In dem Sinne von möglichen &
wirklich gezogenen Geraden könnten || können
wir auch von möglichen & wirklich
dargestellten Zahlen reden.) |
Wie ist es aber mit dem andern Beweis von
25 + (8 + 17)
= (25 + 8) + 17 der nach den Regeln des
1 + 1 die
rechte & linke Seite ausrechnet
|
Wenn man die rekursiven Beweise
Skolems gleichsam von
oben ansieht, so stellen sie sich uns dar als
Gleichungsketten deren Übergänge nach gewissen Regeln
erlaubt sind & die eine besondere strukturelle
Eigentümlichkeit haben, || haben: gewisse Höhepunkte, durch
welche sie besonderen Gleichungen zugeordnet werden
können. |
Man könnte
auch so sagen: Der Beweis aller dieser
Sätze gelingt Skolem; aber er gibt uns nicht ein System
in welchem wir mittels einer Regel alle zu beweisenden
Sätze ableiten können. Sondern wir müssen
immer von neuem lernen, wie ein weiterer Satz abzuleiten ist –
also nicht, |
(Daß
das Bewiesene nicht am Ende der Gleichungskette
steht macht gar nichts. Der Beweis könnte dem zu
vergleichen sein daß
25 × 16 =
400 ist: Wir nehmen das an & dividieren
dann 4000 durch 16 dann durch 25, & wenn 10 herauskommt, war
die Annahme richtig.) |
Die
Frage ist, wie geht denn der Kalkül weiter, nachdem die
Grundgesetze durch Induktion bewiesen sind? |
Am Schluß mache ich immer nur auf
etwas aufmerksam. (Und stelle solches Auffallende || solche Bemerkungen
zusammen.) |
Arithmetik, Algebra. |
26.
„Streng” heißt:
klar. |
Zwei Beweise
„desselben Satzes” können nur unabhängig
von einander sein, wenn sie
den || diesen Satz niemals erreichen.
(Denn sonst kommunizieren sie ja
miteinander.) Wenn sie also im strengen Sinn
keine Beweise dieses Satzes sind. |
Es gibt eben in der Mathematik sehr
Verschiedenes was |
Man nennt es eine Aufgabe wenn gefragt wird „wieviel ist
25 × 16”
aber auch eine Aufgabe: „Was ist das
∫ sin²xdx?
Die erste hält man zwar für viel leichter als die zweite,
sieht aber nicht daß sie in verschiedenem Sinn Aufgaben
sind. Der Unterschied ist natürlich kein
psychologischer, und || denn es handelt sich nicht drum
ob der Schüler die Aufgabe lösen kann sondern ob der
Kalkül sie lösen kann, oder, welcher Kalkül sie
lösen kann. |
Die
Unterschiede auf die ich aufmerksam machen kann sind solche wie
sie jeder Bub in der Schule wohl kennt. Aber man verachtet
diese Unterschiede später, wie die Russische
Rechenmaschine (& andere Behelfe des
ersten Unterrichts || & den geometrischen
Beweis mit Lineal & Zirkel) & sieht sie
nicht als unwesentlich an wie den Unterschied zwischen
endlich & unendlich statt als wesentlich
& fundamental. |
Es
ist gleichgültig ob man eine Regel weiß
nach der man || der Schüler eine Regel
weiß nach der er
∫ sin²xdx
gewiß Nicht ob der Schüler es kann sondern ob der || dieser Kalkül es kann & wie er es tut interessiert uns. |
Im Falle
25 × 16 =
370 nun, schreibt der Kalkül den wir
benützen jeden Schritt zur Prüfung dieser
Gleichung vor. ¤ |
Wenn Frege
gegen die formale Auffassung der Arithmetik spricht so sagt er
gleichsam immer: diese kleinlichen Erklärungen
die Symbole betreffend sind unnötig wenn wir sie || diese verstehen & das Verstehen besteht quasi im || ist quasi
das Sehen eines Bildes aus dem dann alle Regeln folgen
(wodurch || durch daß sie verständlich
werden). Frege sieht aber nicht daß dieses Bild nur wieder ein
Zeichen ist, oder ein Kalkül der uns den mit
geschriebenen Schriftzeichen erklärt.
Aber das Verständnis gleicht überhaupt immer [sehr] dem welches wir für einen Kalkül kriegen wenn wir seine Entstehung, oder praktische Anwendung, kennenlernen. Und natürlich lernen wir auch da wieder nur einen andern & uns übersichtlicheren Symbolismus statt des uns fremden kennen. (Verstehen heißt hier übersehen.) |
a + (b + 1) = (a + b) + 1 (R)
a ∙ 1 = a ‒ ‒ ‒ (D) a ∙ (b + 1) = a ∙ b + a (M)
|
(Eine Untersuchung Schritt für
Schritt dieser Beweise wäre sehr lehrreich.)
Der erste Übergang in I a + (b + (c + 1) =
a + ((b + c) + 1) wenn er nach
R vor sich gehn soll zeigt,
daß die Variablen in R anders gemeint sind als die in
den Gleichungen von I denn sonst erlaubte
R nur
a + (b + 1) durch
(a + b) + 1 zu
ersetzen aber nicht b + (c + 1) durch
(b + c) + 1.
Dasselbe zeigen
natürlich || auch alle || die
andern Übergänge dieses Beweises.
Wenn ich nun sagte, die beiden Zeilen des Beweises berechtigen || der Vergleich der beiden Zeilen des Beweises berechtigt mich
|
An dieser Regel sieht man aber etwas
Merkwürdiges: || scheint aber eines
merkwürdig: daß es nämlich möglich ist
sie als Vorschrift zu verstehen, auch ohne zu sehen, daß
aus ihr die Reihe F1((1) + 1) =
F2((1) + 1),
F1(((1) + 1) + 1) =
F2(((1) + 1) + 1),
u.s.w. hervorgeht || sie die Reihe
F1((1) + 1) =
F2((1) + 1),
F1(((1) + 1) + 1) =
F2(((1) + 1) + 1),
u.s.w. erzeugt. |
Die allgemeine Regel für den
Induktionsbeweis kann ich natürlich nur dann anwenden,
wenn ich die Substitution entdecke, durch die sie anwendbar
wird. So wäre es möglich, daß einer die
Gleichungen (a + 1) + 1 = (a + 1) + 1 1 + (a + 1) = (1 + a) + 1 sähe ohne auf die Substitution a = x, F1(x) = x + 1, F1(x + 1) = (x + 1) + 1, F2(x + 1) = 1 + (x + 1), F2(x) = 1 + x(Ƒ) zu kommen. |
Wenn ich
übrigens sage ich verstehe
die Gleichungen als besondern Fall jener Regel so muß doch das
Verständnis das sein was sich in der Erklärung der
Beziehung zwischen der Regel & den Gleichungen zeigt also,
Ja das Sehen der internen Beziehung kann nur wieder das Sehen von etwas sein das sich beschreiben läßt wovon man sagen kann „ich sehe daß es sich so verhält” also wirklich etwas von der Natur der Zeichen der Zuordnung (wie Striche || Verbindungsstriche, Klammern, Substitutionen etc.). Und alles andere kann nur in der Anwendung des Zeichens der allgemeinen Regel in einem besonderen Fall liegen. |
Kann man nun
sagen, wir haben I, II & III aus
R errechnet?
Nein. – Aber aus R und
ρ? |
27.
Wir könnten nun die obigen
Beweise auch anders hinschreiben, nämlich als Gleichungen
zwischen besonderen Zahlen, die als Beispiele wirken || symbolisieren. So ein || Ein solcher Beweis ist dann von ähnlicher Art
wie der eines geometrischen Satzes über das Dreieck
durch eine Konstruktion in einem Dreieck.
(Aber doch
|
Das ist einerseits der
Beweis von
5 + (4 + 3)
= (5 + 4) + 3, anderseits kann man es als
Beweis von
5 + (4 + 4)
= (5 + 4) + 4 etc.
etc. gelten lassen d.h.
benützen. Wenn ich nun sagte, was ich tun könnte¤: A ist der Beweis des Satzes a + (b + c) = (a + b) + c so würde das Eigentümliche am Übergang vom Beweis zum Satz viel auffälliger. Und was wäre die Regel nach der dieser Übergang erlaubt || berechtigt ist? |
| Ein Satz
(wie) „es gibt keine letzte
Kardinalzahl” schockiert den naiven –
& rechten – Sinn mit Recht. Wenn ich frage
„wer war der letzte Mann der Prozession” &
nun die Antwort lautet „es gibt keinen
letzten” so verwirrt sich mir das Denken; was heißt
das „es gibt keinen letzten”? ja wenn die Frage
geheißen hätte „wer war der
Fahnenträger” so hätte ich die Antwort verstanden
„es gibt |
Ist nicht unser
Prinzip, || : keinen Begriff zu
verwenden, wo keiner nötig ist? –
D.h. die Fälle zu zeigen in denen
das Begriffswort in Wirklichkeit für eine Liste || Aufzählung steht. || D.h. in den Fällen in denen
das Begriffswort für eine Liste steht dies klar zu
machen. || D.h. die
Fälle in denen das Begriffswort in Wirklichkeit für eine
Liste || Aufzählung steht, als solche zu
erklären. |
Was ich über das Verstehen
eines Satzes sage kommt darauf hinaus daß wenn
wir aus den Wirkungen || dem
Wirkungsbereich der Sprache etwa
eine Folge eines || das
Phänomen eines Befehls & seiner Befolgung
(an & für
sich) betrachten & auch mit allen psychischen
Phänomenen die es begleiten & die
wir das Verstehen des Befehls nennen möchten, das Wesen der
Sprache in diesem ganzen Phänomen || diesen
Phänomenen nicht zum Ausdruck käme. | |
Muß ich sagen daß
der Gang || die Übergänge des
Beweises A nach der Regel a + (b + 1) =
(a + b) + 1 geschehen? – Und
inwieweit gehen sie nach einer solchen
Buchstabenregel vor sich? |
Der erste Übergang
geschieht nach der Regel 3
= 2 + 1 der zweite nach der Regel
4 + (2 + 1)
= (4 + 2) + 1, der dritte nach der Regel
5 + ((4 + 2) + 1)
= (5 + (4 + 2)) + 1
u.s.w. Diese Regeln haben allerdings
einen gemeinsamen Zug & der ist in
a + (b + 1) =
(a + b) + 1 zusammengefaßt.
Da wir aber jetzt || hier nicht mit Buchstaben
arbeiten wollen, sondern mit Zahlenbeispielen, so
möchten wir (vielleicht)
sagen, die Regel nach der wir vorgehen ist
5 + (3 + 1)
= (5 + 3) + 1. Aber hier ist uns (5 + 3) unverständlich da wir alles auf die Addition von Einsen zurückführen wollen. Und das Beispiel der Regel muß also lauten: 5 + 3 = 5 + (2 + 1) = (5 + 2) + 1 = (5 + ((1) + 1)) + 1 = (((5 + 1) + 1) + 1) oder: 5 + (((1) + 1) + 1) = (5 + ((1) + 1)) + 1 = ((5 + 1) + 1) + 1 .... P. Diese Regel erklärt das Zuzählen einer Zahl als das sukzessive Zuzählen so vieler Einser als die Zahl enthält. Nach dieser Regel P gehen alle Übergänge in A vor sich & man könnte sie alle auf die Form von P bringen indem man etwa statt 4 + (2 + 1) = (4 + 2) + 1 schriebe: 4 + (2 + 1)
Daraus sieht man übrigens daß „5 + (((1) + 1) + 1) = (5 + ((1) + 1)) + 1) = etc.” sondern unmittelbar: 5 + (((1) + 1) + 1) = ((5 + 1) + 1) + 1 denn die Zwischenschaltung des zweiten Gliedes geschähe ja wieder nur gemäß einer Regel die doch erst durch das letzte Resultat der Gleichungskette gerechtfertigt wird. |
Wenn übrigens 3,
z.B., als
((1) + 1) + 1
definiert ist wie unterscheidet sich dieses Zeichen von
2 + 1?
Denn wenn kein Unterschied da ist, so ist in
diesem Symbolismus auch keiner zwischen
((5 + 1) + 1) + 1
und 8. Ich möchte aber doch zeigen, daß die 8 dann aus 5
& 3 besteht. ‒ ‒ ‒ |
Definitionen führen nur praktische
Abkürzungen ein, aber wir könnten auch ohne sie
auskommen. Aber wie ist es mit den rekursiven
Definitionen? |
Anwendung der Regel
a + (b + 1)
= (a + b) + 1 kann man zweierlei
nennen: 4 + (2 + 1) = (4 + 2) + 1 ist eine Anwendung in einem Sinne, im andern: 4 + (2 + 1) = ((4 + 1) + 1) + 1 = (4 + 2) + 1 |
Das Resultat der Rechnung
A ist
5 + (4 + 3)
= (5 + 4) + 3 außerdem aber hat sie auch
in einem andern Sinne ein Ergebnis. Kann man dieses nun
durch die Gleichung a + (b + c) =
(a + b) + c ausdrücken, wie das erste
durch
5 + (4 + 3)
= (5 + 4) + 3? |
Könnte ich bestimmen
daß „((1) + 1) + 1”
2 + 1 bedeuten
solle dagegen „(((1) + 1) + 1)”
3? Und etwa ([((1) + 1) + 1] + 1) + 1 = ((((1) + 1) + 1) + 1) + 1 etc. etc.? |
Richtiger ist die Bestimmung
daß „[(1) + 1] + 1”
2 + 1 bedeutet
&
„[((1) + 1) + 1]”
3. Und man braucht dann die Regel daß
[((1) + 1) + 1] + 1
Dann heißt es z.B.
[(1) + 1] + [((1) + 1) + 1]
|
28.
(Es ist beinahe unglaublich, daß die Analyse
einer so einfachen Sache so schwer sein sollte.) |
Das
Charakteristische an einem Beweis wie dem von
(a + b) ∙ (a + b)
= a ∙ a + b ∙ b +
2 ∙ a ∙ b ist daß die Buchstaben
nicht abgebrochen werden wie die Ziffern in einer Rechnung (in der
das Zeichen 5 verschwindet & statt dessen eine
4 & 1
auftaucht.) |
(Die unendliche
Schwierigkeit ist die „allseitige Betrachtung”
des Kalküls.) |
Wenn ich sage daß beim
Beweis A a + (b + c) =
(a + b) + c herauskommt, habe ich da schon
vorher einen Begriff dessen, was ich als den Beweis dieser
Formel ansehen würde. |
„Jeder
Existenzbeweis muß eine Konstruktion dessen enthalten
dessen Existenz er beweist.” Man kann nur sagen
„ich nenne Existenzbeweis nur einen der eine
solche Konstruktion enthält”. Der
Fehler ist || liegt darin daß man glaubt || vorgibt einen klaren Begriff des Existenzbeweises || der
Existenz zu besitzen. Man glaubt ein Etwas, die Existenz, beweisen zu können, sodaß man nun unabhängig vom Beweis von ihr überzeugt ist. (Die Idee der voneinander – und daher wohl auch vom Bewiesenen – unabhängigen Beweise!) In Wirklichkeit ist Existenz das was man mit dem beweist, was man „Existenzbeweis” nennt. Wenn die Intuitionisten & Andere darüber reden so sagen sie: „Diesen Sachverhalt, die Existenz, kann man nur so & nicht so beweisen.” Und sehen nicht, daß sie damit einfach das definiert haben was sie Existenz nennen. Denn die Sache verhält sich eben nicht so wie wenn man sagt: „daß er || ein Mann in dem Zimmer ist kann man nur dadurch beweisen daß man hineinschaut aber nicht, indem man an der Türe horcht”. |
Wir haben keinen Begriff der
Existenz unabhängig von unserem Begriff des
Existenzbeweises. |
17 + 28
kann ich mir nach Regeln ausrechnen ich brauche
17 + 28 =
45(α) nicht als Regel zu geben. Kommt
also in einem Beweis der Übergang von
f(17 + 28)
auf f(45)
vor so brauche ich nicht sagen er geschähe nach der Regel
α,
sondern nach andern Regeln des
1 + 1.
|
Wie ist es
hiermit aber in der
(((1) + 1) + 1)
Notation? Kann ich sagen ich könne mir in ihr
z.B.
2 + 3
ausrechnen? Und nach welcher Regel? Es
geschähe so:
Als die Zahlen im Dezimalsystem hingeschrieben waren gab es Regeln, nämlich die der Addition für je zwei Zahlen von 0 bis 9 & die reichten mir nicht, entsprechend angewandt, für alle Additionen aller Zahlen aus. Welche Regel entspricht nun diesen Elementarregeln? Es ist offenbar daß wir uns in einer Rechnung wie σ weniger oder keine Regeln merken brauchen als in 17 + 28. Ja, wohl nur eine allgemeine & gar keine der Art 3 + 2 = 5. Im Gegenteil, wieviel 3 + 2 ist scheinen wir jetzt ableiten || ausrechnen zu können. |
Es hat hier übrigens
mit den Zahlzeichen
(1),
((1) + 1),
(((1) + 1) + 1), etc.
eine gewisse Schwierigkeit: Nämlich die, daß wir
|
Haben wir 45 in
α so in demselben
Sinne ausgerechnet wie das Ergebnis in
σ? |
In einem andern Symbolismus ließe es sich
vielleicht eher sehen. Ich schreibe [ohne weitere
Erklärung]: 1, 2, 3, 4, 5, 6, 7,
8, etc.
[(1) + 2] + [((1) + 2) + 3]
=
((([(1) + 2] + 1) + 1) + 1)
=
[((((1) + 2) + 3) + 4) + 5].
Die Rechnung hätte man dann auch so durchführen
können:Die Aufgabe ist 2 + 3 = ? & man schreibt 1, 2, 3, 4, 5, 6, 7 1, 2; 1, 2, 3 So rechnen Kinder tatsächlich, wenn sie „abzählen”. (Und dieser Kalkül muß so gut sein wie ein andrer.) |
Denken wir uns den Fall, Einer
gäbe uns || es gäbe uns Einer eine Rechenaufgabe in
der Strichnotation, etwa ❘ ❘ ❘ ❘ ❘ ❘ ❘ ❘ ❘ ❘ ❘ ❘ ❘ ❘
+
❘ ❘ ❘ ❘ ❘ ❘ ❘ ❘ ❘ ❘ ❘ ❘,
& während wir rechneten machte er sich den Spaß,
Striche, ohne daß wir es bemerkten |
Hier könnte man nun
die Fragen aufwerfen, wie die: Ist es nun nur
sehr wahrscheinlich, daß
3641 + 7986 =
11627? Und ist also nicht auch
2 + 3 = 5
nur sehr wahrscheinlich? Und was || wo ist
denn die objektive Wahrheit der sich diese
Wahrscheinlichkeit nähert?
D.h., wie bekommen wir denn einen Begriff
davon daß
2 + 3 eine
bestimmte || gewisse Zahl wirklich
ist abgesehen von dem was sie || es
uns zu sein scheint? – |
Wenn man nämlich fragen
würde: was ist das Kriterium in der
Strichnotation, daß wir zweimal das gleiche
Zahlzeichen haben? – Die Antwort könnte
sein: „Wenn es beide
Male gleich aussieht”, oder „wenn es
beide Male die gleiche Anzahl von
Strichen enthält”. Oder soll es
heißen: Wenn eine 1→1 Zuordnung
etc. möglich ist? |
Oder sollen wir das
Additionstheorem so lauten lassen:
a + (b + 1) = (a + 1) + b … (β, also so addieren: ((1) + 1) + (((1) + 1) + 1) = (((1) + 1) + 1) + ((1) + 1) = ((((1) + 1) + 1) + 1) + (1) = (((((1) + 1) + 1) + 1) + 1)? |
Wenn ich die Zahl nach ihrem letzten Buchstaben nenne so beweist das daß (E + D) + C = E + (D + C) = M. |
Diese Form des Beweises ist
gut, weil sie deutlich zeigt daß das Ergebnis wirklich errechnet
ist & weil man aus ihr doch auch wieder den allgemeinen
Beweis herauslesen kann. |
Es ist hier eine gute
Mahnung – so seltsam sie klingt –: treibe
hier nicht Philosophie sondern Mathematik. |
7.9.
Was ein geometrischer Satz bedeutet
welche || was für eine Art der
Allgemeinheit er hat, das muß sich alles zeigen wenn wir sehen, wie
er angewendet wird. Denn wenn einer auch
etwas Unfaßbares || Unerreichbares
mit ihm meinte, || meinen
könnte, so hilft ihm das nicht, da er ihn ja
doch nur ganz offenbar || offen & jedem
verständlich anwenden kann.14
|
Wenn sich etwa jemand unter
dem Schachkönig auch etwas Mystisches vorstellt, so
kümmert uns das nicht, weil er ja doch mit ihm nur
auf den 8 ×
8 Feldern des Schachbretts ziehen kann. |
a + (b + 1) =
(a + b) + 1 kann doch nur eine
Abkürzung des Induktionsbeweises sein.
|
Denn wir
müßten ja im Notfall |
Was || Welche Operationen immer die
Regel a + (b + c) =
(a + b) + c
rechtfertigen kann || rechtfertigt, kann auch der Induktionsbeweis
rechtfertigen. |
Man kann
nicht eine Rechnung als den
Beweis eines Satzes bestimmen. || zum Beweis eines Satzes
ernennen. |
(Ich möchte
sagen): Muß man diese
Rechnung || die Induktionsrechnung den Beweis
des Satzes a + (b + c) =
(a + b) + c nennen?
D.h. tut's keine andere
Beziehung? |
Auch in || nach der herkömmlichen Auffassung || Interpretation gibt der Induktionsbeweis nicht vor
a + (b + c) =
(a + b) + c zu beweisen, sondern nur zu
beweisen, daß dieser Satz für alle Zahlen gilt.
|
Der
Induktionsbeweis scheint eine Einheit zu sein &
nicht aus den || seinen einzelnen Übergängen
als seinen Einheiten zu bestehen. |
So ist
z.B. das Resultat der Division
1 : 3 auf 2 Stellen
berechnet 0˙33, aber außerdem
sieht man in dieser Division die Periodizität, |
Wir könnten ja den Induktionsbeweis
sehr wohl eine periodische Rechnung nennen. |
Und ihr Resultat a + (b + c)
= (a + b) + c wäre dann mit
0˙3̇
analog, dagegen die Enden || das Ende
der Schlußkette || das Ergebnis der
Gleichungstransformation mit
0˙33. |
Ich möchte sagen: Ich
konnte doch nicht darauf ausgehen, die Periodizität in der
Rechnung zu finden. – Außer, wenn ich schon
eine habe & eine Methode mit ihrer
Hilfe andere zu erzeugen. || und eine Methode mittels ihrer andere zu
erzeugen. |
Man
kann die Rechnung als Ornament betrachten. Eine Figur in
der Ebene kann an eine andere passen oder nicht,
mit anderen in verschiedener Weise
zusammengepaßt || aneinander gepaßt
werden. Wenn die Figur noch gefärbt ist, so gibt es
dann noch ein Passen in Bezug auf die Farbe. || der Farbe nach. (Die Farbe ist nur
eine weitere Dimension.) |
Die Rechnung als Ornament zu betrachten, das
ist auch Formalismus, aber einer guten Art. |
Wenn ich den Satz mit einem Maßstab verglichen
habe, so habe ich strenggenommen, nur einen Satz, der mit Hilfe
eines Maßstabes die Länge eines
Gegenstandes || eine Länge beschreibt || aussagt, als Beispiel für alle Sätze
herangezogen. || als Beispiel eines Satzes
herangezogen. |
8.
Der bewiesene Satz wird planmäßig
erzeugt; die Periodizität wurde nicht
planmäßig erzeugt. || Die
Periodizität wurde nicht planmäßig
erzeugt. (Der bewiesene Satz wird planmäßig
erzeugt.) |
Bei der Division 1 : 3 kommt
nicht 0˙3̇
heraus
im Gegensatz, etwa, etwa zu 0˙3
sondern im Gegensatz zu einer andern Periode. |
Unter welchen Umständen wäre es
denn wahr daß a + (b + c) =
(a + 2b) + c statt
(a + b) + c
wäre?– Es müßte 1) a + (b + 1) = (a + 2b) + 1 2) a + (b + (c + 1)) = [a + (b + c)] + 1 [etwa] 3) (a + 2b) + (c + 1) = [a + (2b + c)] + 1 Aber warum soll 1) nicht gelten? darf ich es nicht willkürlich bestimmen? |
Liegt die Hauptsache darin, daß nicht
a + (b + (c + 1)) = [a + (b + c)] + 1 & (a + b) + (c + 1) = [(a + b) + c] + 1 allein den Beweis ausmachen, sondern erst zusammen mit a + (b + 1) = (a + b) + 1? |
So daß man schon deshalb nicht sagen kann es gehe
nun a + (b + c)
=
(a + b) + c
(bloß) aus
a + (b + 1) =
(a + b) + 1 hervor. |
12.
[Nachtrag] Ist es nicht so, daß alles Denken
über die Wirklichkeit auf der Induktion fußt?
|
Von der Erwartung zur Erfüllung ist
ein Schritt einer Kalkulation || Rechnung. Ja die Rechnung:
|
Und soweit – & nur soweit – als
diese Rechnung ein Bild des Resultats ist, ist auch die
Erwartung ein Bild der Erfüllung. |
Und soweit das Resultat von
der Rechnung, soweit ist die Erfüllung durch die Erwartung
bestimmt. || von der Rechnung
bestimmt ist, soweit ist die Erfüllung durch die Erwartung
bestimmt. |
Wir
erwarten etwas & handeln nach der || dieser
Erwartung. Muß die Erwartung eintreffen?
Nein. Warum aber handeln wir nach der
Erwartung? Weil wir dazu getrieben werden, wie dazu,
einem Automobil auszuweichen, uns niederzusetzen, wenn wir müde
sind & aufzuspringen, wenn wir uns auf einen Dorn
gesetzt haben. |
Ich lege
meine Hand auf eine Platte || die Herdplatte, fühle
unerträgliche Hitze & ziehe die Hand schnell
zurück: War es nicht möglich, daß die Hitze
der Platte im nächsten Augenblick aufgehört
hätte? konnte ich es wissen? Und war es
nicht möglich, daß ich gerade durch meine
Bewegung mich einem Schmerz Es ist also in gewissem Sinne keine gute Begründung zu sagen: „Ich zog die Hand zurück || Ich mußte die Hand zurückziehen, weil die Platte zu heiß war”! |
13.
[Nachtrag etc.]
Und wenn man nun
fragte: Bist Du sicher, daß Du es deswegen
getan hast? Würde man da nicht schwören, daß
man es nur deswegen getan hat? Und ist es nicht doch Erfahrung? |
„Ich hab es nicht mehr
(länger)
ausgehalten”. „Ich halte es nicht mehr aus; ich muß die Hand zurückziehen”. Aber worin besteht dieses Zurückziehen, als zu wünschen, || als in dem Wunsch, die Hand würde sich zurückziehen, während sie sich wirklich zurückzieht? Zieht sie sich nicht zurück, so können wir auch nichts machen. Jedenfalls ist ‚sie zurückziehen wollen’ eine Erfahrung, die wir zwar wünschen können aber nicht herbeiführen. Denke an die Erfahrung beim Zeichnen der Figur  durch den
Spiegel. durch den
Spiegel. |
Wenn ich sage die
Erfahrung des Wollens könne ich zwar |
Was ist ein Satz? wodurch ist dieser Begriff
bestimmt? – Wie |
Ich kenne einen Satz, wenn ich ihn sehe.
|
Diese Frage ist fundamental:
Wie, wenn wir eine neue Erfahrung machen, etwa einen neuen
Geschmack oder einen neuen Hautreiz kennen lernen; woher weiß ich, daß, was diese Erfahrung
beschreibt, ein Satz ist? Oder, warum soll ich das einen
Satz nennen? Nun, ||
Wohl mit dem selben Recht, womit || mit
welchem ich von einer neuen Erfahrung gesprochen
habe. Denn Erfahrung & Satz sind
äquivalent. Aber warum habe ich das Wort Erfahrung
gebraucht, im Gegensatz wozu? |
Habe ich denn, was geschehen ist, schon etwas || bis zu einem (gewissen) Grade
damit charakterisiert, daß ich gesagt habe || sagte,
es sei eine Erfahrung? Doch offenbar
garnicht. Aber es
scheint doch als hätte ich es schon getan, als
hätte ich davon schon etwas ausgesagt: |
Das Wort
„Satz” & das Wort
„Erfahrung” haben schon eine bestimmte
Grammatik. |
Das heißt, ihre Grammatik
muß im vorhinein bestimmt sein & hängt nicht von
irgendeinem künftigen Ereignis ab. |
Hier ist auch der Unsinn in
der „experimentellen Theorie der Bedeutung”
ausgesprochen. Denn die Bedeutung ist in der
Grammatik festgelegt. |
Wie verhält sich die
Grammatik des Wortes „Satz” zur Grammatik der
Sätze? |
„Satz” ist offenbar die Überschrift
der Grammatik der Sätze. In einem Sinne aber auch die
Überschrift der Grammatik überhaupt, also äquivalent
den Worten „Grammatik” &
„Sprache”. |
∣ ∣
Der Denker gleicht sehr dem Zeichner. Der alle
Zusammenhänge nachzeichnen will || möchte. ∣ ∣ |
Das ist es auch, was damit gemeint ist, daß es in
der Welt zwar Überraschungen gibt, aber nicht in der
Grammatik. |
∣ ∣
Grenze, die die Grammatik sichtbar in der
Sprache zieht, & Darstellung einer Reise auf dem Globus
einerseits, & auf seiner Projektion in zwei Kreisen
⚬⚬ in der Ebene
anderseits. ∣ ∣ |
Es scheint unsere Frage noch zu erschweren, daß auch die
Worte „Welt” &
„Wirklichkeit” Äquivalente des Wortes
„Satz” sind. |
Aber es ist doch lächerlich die Welt, oder die Wirklichkeit,
abgrenzen zu wollen. Wem soll man sie denn
entgegenstellen. Und so ist es mit der Bedeutung des
Wortes „Tatsache”.
Aber man gebraucht ja diese Wörter auch nicht als Begriffswörter. |
We are only concerned
with what Das heißt: Zum Glück müssen wir keine Enttäuschungen eingestehen; es gibt nichts, was wir versuchen, aber nicht ausführen können. |
Etwas ist ein Satz
nur in einer Sprache. |
Wenn ich nun sage:
aber die Sprache kann sich doch ausdehnen, so ist die Antwort:
Gewiß, aber wenn dieses Wort „ausdehnen”
hier einen Sinn hat, so muß ich jetzt schon wissen, was
ich damit meine, muß angeben können, wie ich mir so eine
Ausdehnung vorstelle. Und was ich jetzt nicht denken kann,
das kann ich jetzt auch nicht ausdrücken & auch nicht
andeuten. |
Hierher gehört die alte Frage:
„wie bin ich dann aber überhaupt zu diesem Begriff
gekommen” (etwa zu dem der außer mir liegenden
Gegenstände). (Es |
⍈
⍈
[Ursprünglich] Hier haben wir dieses bohrende Problem: wie es möglich ist auch nur an die Existenz von Dingen auch nur zu denken, wenn wir immer nur Vorstellungen – ihre Abbilder – sehen. || : wie es denn möglich ist, auch nur auf den Gedanken der Existenz von Dingen zu kommen, wenn wir immer nur Vorstellungen (nie die Dinge selbst) erhalten. |
Wir haben es
natürlich wieder mit einer falschen Analogie zu
tun: Es hat guten Sinn zu sagen „ich
weiß, daß er in diesem Zimmer ist, weil ich ihn höre, wenn
ich auch nicht hineingehen & ihn sehen kann”.
|
Wenn ich
„es verhält sich so & so” als
|
Ist es quasi eine Verunreinigung des Sinnes,
daß wir ihn in einer bestimmten Sprache mit ihren
Zufälligkeiten ausdrücken & nicht gleichsam
körperlos & pur || rein? Nein, denn es ist wesentlich,
daß ich die Idee der Übersetzung von einer
Sprache in die andere verstehe. |
(Kleist schrieb
einmal, es wäre dem Dichter am liebsten, er könnte
die Gedanken an sich || selbst ohne Worte
übertragen. (Welch seltsames
Eingeständnis.)) |
Spiele ich eigentlich doch
nicht das Schachspiel selbst, da die Figuren ja auch anders
sein könnten?! |
Da der Sinn eines Satzes
ganz in der Sprache fixiert ist & es auf den Sinn ankommt, so
ist jede Sprache gleich gut. Der |
Was heißt es nun, die
Idee der Übersetzung oder Übersetzbarkeit
verstehen? |
∣ ∣ Hier liegt
übrigens der Unterschied zwischen der philologischen &
der philosophischen Betrachtung. ∣ ∣ |
Es kann doch nicht
heißen: jede mögliche Übersetzung, also alle
möglichen äquivalenten Sprachen kennen! |
Sondern die
Übersetzungen verhalten sich zur Sprache, wie die
verschiedenen Ansichten oder Projektionen zu
einem Körper, dessen Projektionen es
sind. Ist der Körper gegeben – etwa durch eine
Gleichung bezüglich eines Koordinatensystems || mit Bezug auf ein Koordinatensystem, so sind auch seine
Gleichungen bezüglich |
‚2 × 2 =
4’, ‚die Rose ist rot’
etc. Warum soll ich nicht schreiben:
‚2 × 2 = 4’
& ‚die Rose =
rot’. Wenn es mit ‚ist’ geht,
dann auch mit ‚ = ’. Gewiß, aber was
die logische Form charakterisiert, ist gerade die
Bestimmung, daß das Zeichen ‚ = ’ in
der zweiten Verbindung nicht gebraucht werden darf.
|
Die
Bedeutung des Zeichens ‚ist’ auch ohne diese
Übertragung richtig auffassen, heißt, im besonderen Fall
keine falschen Operationen machen; also z.B.
nicht die Worte ‚die Rose’ für
‚rot’ substituieren. |
Ein ernster Einwand gegen
das, was ich sage ist nicht die Frage nach der Erweiterung der
Grammatik, denn was ich Soll das heißen, daß ich in jedem bestimmten Fall weiß oder wissen kann ob das Wort der Regel gemäß, oder nicht, angewendet ist. |
Das ist eine der vielen
Stellen, wo man (immer) versucht ist,
mehr zu sagen, als klar, & nötig, ist. Das
heißt, daß man versucht ist eine Annahme zu
machen. |
Die Logik „normativ”. |
„Der Satz hat Sinn,
wenn ich etwas mit ihm meine”. |
Kann man sagen:
‚Ich meine etwas mit diesen Worten’, das
heißt, sie sind ein Teil einer || meiner |
Wenn ich jemand mit dem Finger
zu mir winke, ist das eine Operation in einer Rechnung, ein
Gedanke? |
Ist dieses Winken nun nicht auf
derselben Stufe, wie, den Knopf einer Klingel drücken, damit mein
Diener komme? |
Suchen & || zu || zum
Finden verhält sich nicht wie Hunger & || zur Stillung des Hungers. |
Soll || Kann ich sagen: Mich interessiert die
Sprache nur soweit als sie ein Kalkül ist. |
Laß
die Grammatik, wie sie ist. |
Aber wie ist
es: Ich gehe diesen Weg, um um dorthin zu
kommen, ich drehe den Hahn auf, um Wasser zu erhalten, ich winke,
damit jemand zu mir kommt & endlich teile ich ihm meinen
Wunsch mit, damit er ihn erfüllt! |
Aber was geht vor
sich, wenn ich den Hahn aufdrehe damit Wasser
herausfließt? Was geschieht ist, daß ich den Hahn
aufdrehe & daß dann Wasser herauskommt, |
Ich suche meinen
Bleistift; dann ist in den Bewegungen des Suchens die Absicht des
Suchens nicht ausgedrückt. |
Es gibt
jedenfalls eine bestimmte Erfahrung: jemandem etwas
mitteilen wollen. Beschränkt man die Bedeutung
des Worts „Sprache” auf diese Mitteilung,
so ist es vielleicht klar abgegrenzt, sonst || anderseits aber sieht man hier die Unbestimmtheit im Begriff
der ‚Sprache’? |
Wenn
ich etwas suche, so ist es wesentlich, daß ich das Finden ebenso
ausführlich muß beschreiben können (ob es
(je so) eintritt oder nicht),
ehe der Gegenstand gefunden ist. Nun wende das auf
das Suchen der Lösung einer mathematischen Aufgabe |
Eine der
gefährlichsten Ideen ist, merkwürdigerweise, daß
wir mit dem Kopf, oder im Kopf, denken. |
Aber auch Papier
& Bleistift ist nicht das Wichtige, denn ich kann mir alles
Aufgeschriebene (wie alles Ausgesprochene) vorstellen.
|
Die Idee von einem Vorgang im Kopf, in dem gänzlich
abgeschlossenen Raum, gibt dem Denken etwas
Okkultes. |
Die
grammatischen Regeln gelten nicht „nur für den
luftleeren Raum”. |
Die Philosophie rein deskriptiv, & zwar beschreibt sie die
Sprache. D.h.: sie gibt keine
Gründe. |
Das
schwierigste Problem scheint der Gegensatz, das
Verhältnis, zu sein zwischen dem Operieren mit der Sprache
in der Zeit || im Lauf der Zeit & dem
momentanen Erfassen des Satzes. |
Aber wann erfassen oder verstehen wir den
Satz?! Nachdem wir ihn ausgesprochen
haben? – |
Man könnte
fragen: Wie lange braucht es || man, um
einen Satz zu verstehen. Und wenn man ihn eine Stunde lang
versteht, beginnt man da immer von frischem? |
∣ ∣ Das
Läuten der Glocke; das Zeichen, daß etwas gefunden
wurde. ∣ ∣ |
The bridge can only be
crossed when we get there, not before.
(Gemeint ist die Brücke zwischen Zeichen &
Realität.) |
[Es
wird oft gesagt, daß die neue Religion die Götter der alten zu
Teufeln stempelt. Aber in Wirklichkeit sind diese
dann wohl schon zu Teufeln geworden.]
|
Ist das Verstehen nicht das
Erfassen |
Das Verstehen ist, wie es meistens
aufgefaßt wird, ein vager
Vorgang – uns interessiert nur, was exakt
ist. Aber nicht, weil uns nur das
„Ideal” einer Sprache interessiert,
„der || dem sich die
Wirklichkeit nur nähert”, sondern weil wir nur so
das fassen können, was in jeder Sprache ausgedrückt
ist. |
Aber was sage ich damit
„daß mich nur Exaktes
interessiert”? Was ist denn das Unexakte? Was ist das Vage, das ich ausschließe? |
Ist es nicht, daß ich das,
was ich nicht genau kenne, ausschalten muß.
D.h. will ich nicht sagen, daß
‒ ‒ ‒ |
Warum sage ich:
die Gefühle, die Stimmungen, etc., die einen Satz
begleiten, oder ihm folgen, oder vorhergehen, interessieren mich
nicht! Weil es nur die symbolische Struktur ist, die mich interessiert. |
Besteht das Vage
nicht darin, daß es nicht zum Symbol
gehört, so & anders sein kann, auch wenn das Symbol
das gleiche ist? |
Nein es
ist noch etwas anderes: Quasi, daß es nur meine
Aufgabe ist, etwas klar zu sagen & nichts
anzudeuten. |
Es ist beinahe, als wollte ich
sagen, ich webe einen Gobelin & da kann ich keine
unklaren || verschwommenen Farbübergänge
brauchen. Aber das ist in Wirklichkeit kein gutes
Gleichnis. |
Soll ich
sagen: || , die
Exaktheit besteht darin, daß uns, was
zweifelhaft ist, nicht angeht? |
Worin besteht unsere Exaktheit?
|
Frege
über die psychologische Logik. Seine Bemerkungen
beziehen sich alle auf die Inexaktheit
der psychologischen Betrachtung im Gegensatz zur
logischen. |
Kann ich sagen,
mich || uns interessiert nur der Inhalt des
Satzes? Und der Inhalt des Satzes ist in ihm.
|
Seinen Inhalt hat der Satz als Glied des
Kalküls. |
Ist also
„einen Satz verstehen” von der gleichen Art, wie
„einen Kalkül
können || beherrschen”?
Also wie: multiplizieren können? Das glaube
ich. |
Denn ist nicht die
Probe auf das Verstehen immer ein Weitergehen von dem Satz
aus?! |
Und es muß
heißen auf die Frage „was heißt ‚einen
Satz verstehen’?”:
Was ist die Probe des Verstehens? |
Bei der Frage nach der
allgemeinen Satzform bedenken wir, daß die gewöhnliche
Sprache zwar einen bestimmten Satzrhythmus hat, aber nicht
alles, was diesen Rhythmus hat, ein Satz ist.
D.h. wie ein Satz klingt & keiner ist. – Daher die Idee vom sinnvollen & unsinnigen ‚Satz’. |
Anderseits ist dieser
Rhythmus aber natürlich nicht wesentlich.
Der Ausdruck „Zucker Tisch” klingt
nicht wie ein Satz, kann |
Es fragt sich
also, ob wir außer diesem irreführenden Satzklang noch einen
allgemeinen Begriff vom Satz haben. (Ich rede
jetzt von dem, was durch ∙ , ⌵ , ~
zusammengehalten wird.) |
Wovon unterscheide ich denn
einen Satz? Oder, wovon will ich ihn denn
unterscheiden? Von Satzteilen in seinem grammatischen
System (z.B. || wie die Gleichung vom Gleichheitszeichen), oder von
allem was wir nicht Satz nennen, also diesem Sessel, meiner
Uhr etc., etc.? Denn,
daß es Schrift- oder Lautbilder gibt
die Sätzen besonders ähnlich sind, braucht uns eigentlich
nicht zu kümmern. |
Oder wir müssen
sagen: Vom Satzbegriff || Satz kann nur in einem grammatischen
System || innerhalb eines grammatischen Systems gesprochen
werden. || kann nur in der
Erklärung |
Es geht mit dem
Wort „Satz” wie mit dem Wort
„Gegenstand” & andern: Nur auf
eine beschränkte Sphäre angewandt sind sie
zulässig & dort sind sie natürlich.
Soll die Sphäre ausgedehnt werden,
damit der Begriff ein philosophischer wird, so verflüchtigt sich
die Bedeutung der Worte & es sind leere Schatten.
Wir müssen sie dort aufgeben & wieder in den engen
Grenzen benützen. |
Nun möchte man aber
sagen: „Satz ist alles, womit ich etwas
meine”. Und gefragt „was heißt das
‚etwas’ meinen”, müßte || würde ich Beispiele anführen. Nun haben
diese Beispiele zwar ihren Bereich, auf den sie ausgedehnt
werden können, aber weiter führen sie mich doch
nicht. Wie ich ja in der Logik nicht ins Blaue
verallgemeinern kann. Hier handelt es sich aber nicht
um Typen, sondern, darum, daß die Verallgemeinerung selbst
etwas bestimmtes ist; nämlich ein Zeichen mit
vorausbestimmten grammatischen |
Also nicht nur
Bewegungsfreiheit sondern eine
Unbestimmtheit der Geometrie. |
Über sich selbst
führt uns kein Zeichen hinaus; & auch kein
Argument. |
Wenn wir sagen, Satz ist
jedes Zeichen, womit wir etwas meinen, so könnte man
fragen: was meinen wir & wann meinen
wir es? Während wir das Zeichen geben,
etc., etc. || u.s.w.,
u.s.w.?
Und damit wird es wieder klar daß dieses Meinen, wenn es relevant sein soll, zum Vorgang des Symbols gehören muß. Es sei denn, daß unter dem ‚Meinen’ ein Vorgang verstanden würde, der durch seine psychologische oder physiologische Art für uns besondere Bedeutung hätte. Es könnte z.B. sein, daß wir erst dann von einem Befehl sagen, er habe für uns Sinn, wenn Es wäre, als würde man sagen: Der Satz hat Sinn, wenn er Bedeutung für's Leben gewinnt. |
Wenn ich frage „was
ist die allgemeine Form des Satzes”, so kann die
Gegenfrage lauten: „haben wir denn einen
allgemeinen Begriff vom Satz, den wir nun? || nur? exakt fassen
wollen?” – So wie: haben wir einen
allgemeinen Begriff von der Wirklichkeit? Die
„Wirklichkeit”– im Gegensatz wozu?
|
Oder
kann || soll man || ich
sagen: Wir haben einen Begriff von der ganzen
Wirklichkeit im Gegensatz zu einem Teil der
Wirklichkeit? |
Die Frage kann auch
lauten: Was geschieht, wenn ein neuer Satz in die Sprache
aufgenommen wird: Was ist das
Kriterium dafür, daß er ein Satz
ist? oder, wenn das Aufnehmen in die Sprache ihn zum Satz
macht, stempelt, worin besteht diese Aufnahme?
Oder: was ist Sprache? |
Da scheint es nun offenbar,
daß man das Zeichengeben von anderen |
Zeichen geben =
sich einer Sprache bedienen. |
Wie vergleicht sich
das „sich einer Sprache bedienen” mit dem
„ein Spiel spielen”. Denn auch das ist
eine von den Tätigkeiten, & eine, die mit dem
Zeichengeben Ähnlichkeit hat. |
Es wäre also so, daß,
was ‚Sprache’ heißt, ebenso schwer zu sagen
wäre wie, was „Sport”,
„Spiel”, „Reinigung”
heißt. |
In der Grammatik wird also
das Wort „Sprache” nicht vorkommen. |
‚Sprache’ im Gegensatz zu Sport,
ja, – aber damit hat ja die Grammatik nichts zu
tun. |
Aber warum
zerbreche ich mir über den Begriff ‚Sprache’
den Kopf, statt Sprache zu gebrauchen?
Dieses Kopfzerbrechen ist nur dann berechtigt, wenn wir einen allgemeinen Begriff haben. |
Wenn man sagte: Sprache ist alles, womit man
sich verständigen kann, so muß || müßte
man fragen: Aber worin besteht Ich könnte als Antwort darauf einen realen oder fiktiven Fall einer Verständigung von Menschen oder andern Lebewesen beschreiben. In dieser Beschreibung werden dann fingierte kausale Verbindungen eine Rolle spielen. Aber wenn der Begriff Sprache durch solche bestimmt ist, so interessiert er uns nicht. Aber abgesehen von jenen empirischen Regelmäßigkeiten der Ereignisse haben wir dann nur noch einen willkürlichen || beliebigen Kalkül. – Aber worin besteht denn das Wesentliche eines Kalküls? |
‚Sprache’ &
‚Lebewesen’. Der Begriff des Lebewesens
ist so unbestimmt || hat die gleiche Unbestimmtheit wie
der der Sprache. |
„Ist dieser Satz nicht vielleicht
ein logisches Produkt mehrerer Sätze?”
Wie würde sich denn das ergeben? |
Wir halten uns an die Worte. |
Wenn wir eine Erklärung, etwa des logischen
Folgens, lesen, so halten wir uns an das, was er || Er schreibt. Wir halten uns an die
Worte; an die Zeichen. |
Die Unendlichkeit ist keine Größe, schaut
aber aus wie eine Größe. (Das ist unsere
Schwierigkeit.) |
„Diese
Gegend macht mich melancholisch”. Woher
weißt Du, daß es die Gegend ist? Ist das eine
Hypothese; – wie Du auch nur glaubst, daß es
jene Speise war, die die Magenschmerzen verursachte,
oder gehört es zur unmittelbaren Erfahrung.
Wäre es also widerlegt, wenn Du, in eine andere Gegend
versetzt, melancholisch bliebest; oder ist es nicht
durch eine künftige Erfahrung zu widerlegen, da es die
Beschreibung der gegenwärtigen ist?
Ja, wie bist Du auf den Gedanken gekommen, daß es die Gegend ist, die diese Stimmung hervorruft? Oder handelt es sich eben gar nicht um einen durch sie hervorgerufenen Zustand meiner Person, sondern, etwa, darum, daß das Bild der Gegend melancholisch ist? (Dies hängt unmittelbar zusammen mit dem Problem: Motiv & Ursache.) „Das ist ein furchtbarer Anblick”. – „Wie weißt Du daß er furchtbar ist?” „Ich zittere, weil ich ihn sehe”. Das kannst Du nicht wissen. Vielleicht hättest Du auch sonst Wie hängt die Furcht mit dem Anblick zusammen? oder mit der furchtbaren Vorstellung? Oder soll ich etwa sagen: „sich vor dieser Vorstellung fürchten” heißt, sie haben & sich fürchten? Wenn man nun aber mehrere Vorstellungen hat, während man sich fürchtet (mehreres sieht oder hört), ist da ein Zweifel darüber, was das Furchtbare ist? Oder weiß man es eben aus Erfahrung, wovor (von allen diesen Sachen) man sich fürchtet? Kann man anderseits nicht Anblick & Furcht trennen, also sagen, daß der „Anblick an sich” nicht furchtbar ist? – Ich möchte auch sagen „das Fürchten ist eine Beschäftigung mit dem Anblick”. Kann ich sagen: es sei ein sehr komplizierter Vorgang, in welchen die Vorstellung an ganz bestimmten || an charakteristischen Stellen eintritt? |
Denken wir an ein
furchtbares Antlitz.
Welche Rolle spielt der Anblick im Vorgang der
Furcht. |
Ich will
sagen: die Furcht begleitet nicht den Anblick.
(Sondern) das Furchtbare &
die Furcht haben || hat die Struktur des
Gesichtes. Denken wir daß wir den Zügen
eines Gesichts |
Denke Dir Du
gingest mit jemand spazieren & zwar in einem
Gespräch. Du würdest dann, wie das
Gespräch vor sich geht, bald langsamer, bald
schneller gehen & da & dort immer wieder
stehnbleiben. Der welcher das Gespräch mit
anhört wird diese Pausen im Gehn ganz natürlich
finden, da sie ja auch unmittelbar aus dem Leben des
Gespräches || Gesprächs hervorgehen. Nehmen wir nun an das
Gespräch würde nur dem Sinn nach von jemandem wiedergegeben
(etwa in eine andere Sprache übersetzt) & man
müßte dazu auch wieder den gleichen Weg gehen &
es wären die Stellen bezeichnet an denen damals geruht wurde, so
würden diese erzwungenen Pausen im Gehen jetzt als
äußerst störend wirken, die doch früher
dem Gespräch geholfen haben. So verhält es sich
mit der Übersetzung der
Platonischen Dialoge in
Dialogform. Nur in dem ursprünglichen einzigen
|
Buchstaben in gleichem
Abstand: „Ich glaube, dieser Buchstabe ist in der
Mitte zwischen diesen zweien”. |
„Wenn das Buch auf dem Tisch |
„Du hast in die
rechte obere Ecke getroffen”. Wovon?
(„Fahren Sie mich auf
№ 47, die Gasse sag' ich
Ihnen später”.)
„Habe ich ins Schwarze getroffen?”
– „Ja, und zwar in die obere
Hälfte”. |
„Ist
der Schuß im Schwarzen?” –
„Ja” – „Wo liegt
er?” – „Das weiß ich nicht, ich
hab' nur gesehen, daß er im Schwarzen liegt, aber nicht,
wo”. – Das entspricht nicht der Erfahrung die
wir meinen. |
[Die
Werke der großen Meister sind Sterne || Sonnen, die
um uns her auf- & untergehen. So wird die Zeit
für jedes große Werk wiederkommen, das jetzt
untergegangen ist.] |
„Außer diesem Kreis ist keiner mehr im
Quadrat”. |
(Mendelssohns Musik, wo sie vollkommen ist, sind musikalische
Arabesken. Daher empfinden wir bei ihm jeden
Mangel an Strenge peinlich.) |
Der Jude wird in
der westlichen Zivilisation immer mit Maßen gemessen, die auf ihn
nicht passen. Daß die griechischen Denker weder im
westlichen Sinne || Sinn
Philosophen, noch im westlichen Sinn Wissenschaftler waren,
daß die Teilnehmer der Olympischen Spiele nicht Sportler
waren & in kein westliches Fach passen,
ist vielen klar. Aber so geht es auch den Juden || Aber Und indem uns die Wörter unserer Sprache als die Maße schlechtweg || schlechthin erscheinen, tun wir ihm || ihnen immer Unrecht. Und er wird || sie werden bald überschätzt bald unterschätzt. Richtig reiht daher Spengler Weininger nicht unter die westlichen Philosophen || Denker. |
Nichts was man tut läßt sich endgültig
verteidigen. Sondern nur in Bezug auf etwas anderes
Festgesetztes. D.h., es läßt sich kein ¤ Grund angeben, warum man so handeln soll (oder hat handeln sollen), als der sagt, daß dadurch dieser Sachverhalt hervorgerufen werden, den man wieder als Ziel hinnehmen muß. |
(Zu
Engelmanns Orpheus:
Ich glaube: Wenn
Orpheus aus der Unterwelt
zurückgekehrt ist, nachdem er
Euridice nun verloren hat, darf er
im Stück nichts mehr reden; denn, was immer er sagt, ist
Geschwätz. Nur Genien
können noch etwas sagen, nämlich, daß das das
Los der Sterblichen ist & daß er erst in einer andern Welt
sich wieder mit Euridice
vereinigen |
Wenn ich übrigens sage „den Vorgang des Umwendens mit ihren Reden begleitend”, so denke ich mir das nicht so, wie etwa eine Schlacht im Theaterstück von einem gespannten Beobachter geschildert wird. Denn die Horen sind nicht gespannt, sondern vollkommen gefaßt. Und sie begleiten den Vorgang mit ihren Reden und umspringen || umschreien ihn nicht. Das Drama hat dann allerdings nicht eigentlich 5 Akte. Aber – es scheint mir – der fünfte „Orpheus” ist freilich || eben auch keine Tragödie & Orpheus kein Held. Denn der Held siegt (ja) indem er umkommt. D.h. er wird nicht innen, sondern nur äußerlich bezwungen. (Würde er innerlich bezwungen, so würde er nach dem Augenblick des Untergangs unser Interesse verlieren. Der 5te Akt ist || kann dann nur ein Nachspiel sein.) |
Ja, der
5te Akt im
Orpheus kann nur noch ein Epilog
sein. |
Editorial notes
1) Continuation from Ms-110,300.
2) See facsimile; drawing between this remark and the following one.
3) See facsimile; line connecting this remark with the following one.
4) See facsimile; line connecting this remark with the following one.
5) See facsimile; arrow pointing upwards, connecting this remark with the first text block on the page.
6) This rendering of the figure follows its representation in Ts-211.
7) This rendering of the figure follows its representation in Ts-211.
8) This rendering of the figure follows its representation in Ts-211.
9) This rendering of the figure follows its representation in Ts-211.
10) This rendering of the figure follows its representation in Ts-211.
11) This rendering of the figure follows its representation in Ts-211.
12) This rendering of the figure follows its representation in Ts-211.
13) This rendering of the figure follows its representation in Ts-211.
14) See facsimile; line connecting this remark with the following one.
15) See facsimile; arrow pointing right.
16) Continuation in Ms-112,1v.