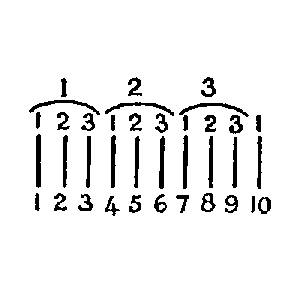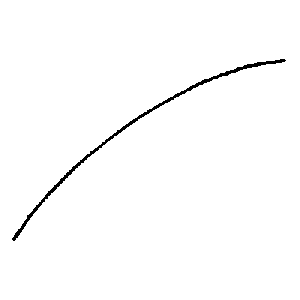​

⌊⌊ Philosophische Bemerkungen XIV. ⌋⌋

​

Mjömna 13.8.37. Einiges gearbeitet. Und doch ist mein Geist nicht ‘wholeheartedly’ [yv|be]i der Arbeit. Dahinter steht doch ein vages Gefühl vom Problem dieses meines Lebens.

​

16.8. ⌊ Auf dem Schiff nach Skjolden. ⌋ Schreibe mehr oder weniger aus langer weile. Ich fühle: ich treibe. Eitel, gedankenlos, ängstlich. Ich wunsche jet[a|z]t durchaus nicht, allein zu leben. Fürchte, ich werde bedrückt sein & nicht arbeiten können. Ich o möchte jetzt bei jemanden wohnen. In der Früh ein menschliches Gesicht sehen. – Anderseits bin ich jetzt ˇwieder so verweichlicht, daß es vielleicht gut wäre allein sein zu müssen. Bin jetzt außerordentlich verächtlich. Darin daß ich das schreibe liegt natürlich eine [F|U]nwahr[s|h]eit. – Haltlos.    Ich habe das Gefühl, daß ich jetzt nicht ganz ohne Ideen wäre, aber daß mich die Einsamkeit bedrücken wird, daß ich nicht arbeiten werde können. Ich fürchte mich, daß in meinem Haus alle meinen Gedanken werden getötet werden. Daß mich doch ein Geist der Niedergeschlagenheit von mir ganz Besitz ergreifen wird. Es ist denn vielleicht, daß ich finde, daß ich dort leben muß, weil kein andrer Platz für mich ist. Es ist nun seltsam. daß ich mich doch auch beinahe fürchte in Skjolden & nicht in meinem Haus zu wohnen, ich fürchte mich davor, daß mein Haus wie ein drohender Gedanke hinter mir stehen wird, wie ein Vorwurf.    Denn ich wünsche mir jetzt eine gewisse Fröhlichkeit bei der Arbeit. Und gibt es die für mich? Gibt es sie für mich hier? Oder wo anders? Ist mein Arbeitsgeist schon gebrochen[?|,] oder werde ich noch arbeiten können? In Cambridge könnte ich lehren, aber schreiben auch nicht.

​

17.8. In Skjolden. Fühle mich übel.         Unglücklich, rastlos & gedankenlos.       Kari Klingenberg hat sich verlobt & ich verstand was das für ihre Eltern bedeuten muß die an ihr eine Dienerin gehabt haben, die sich in keiner Weise kann ersetzen lassen. Und da kam mir wieder zum Bewußtsein, wie einzig Francis ist & unersätzlich. Und wie wenig ich doch das weiß wenn ich mit ihm bin.       Bin ganz in Kleinlichkeit verstrickt. Bin [ri|ir]itiert, denke nur an mich & fühle daß mein Leben elend ist, und dabei habe ich auch gar keine Ahnung, wie elend es ist. – Was ich alles in meinem Haus brauche! Welcher Apparat, & wie wenig dabei herauskommt! Mein Zimmer, das mich f⌊r⌋üher entzückt hat, sieht mich ist mir jetzt fremd, es sieht mich unfreundlich an, oder doch ohne jede Freundlichkeit. Ich bin ungut, & unfromm.     Ich schähme mich dieses Haus zu haben & nicht darin zu wohnen. Es ist aber sonderbar, daß diese Schahm ein so mächtiges Gefühl sein soll. Ich habe nämlich jetzt das Gefühl, daß ich nicht in meinem Haus werde arbeiten können. Die Einschicht bedrückt mich. Dage[t|g]en habe ich einige Hoffnung bei Anna Rebni arbeiten zu können. Aber der Gedanke ist mir unheimlich daß ich dort wohnen soll & mein Haus leer stehen lasse. B[r|i]n wieder furchtbar ungeduldig.       Bin zu Anna Rebni übersiedelt. Bin sehr müde, obwohl ich eigentlich nicht gearbeitet habe. Werde ich hier arbeiten können? Wenn Gott will, so werde ich wieder genesen & arbeiten können, & auch in meinem Haus arbeiten können. –

​

Wie weiß ich, daß ich im Verfolg der Reihe + 2 200004, 200006 schreiben muß & nicht 200004, 200008?    Die Frage ist ähnlich der: wie weiß ich, daß diese Farbe ‘rot’ ist?

​

“Aber Du weißt doch, daß Du immer die gleiche Zahlenfolge ˇin den Einern schreiben mußt: 2, 4, 6, 8, 0, 2, 4, u.s.w.!” – Ganz richtig[,|!] das Problem muß auch schon in dieser Zahlenfolge, ja also auch schon in der             2, 2, 2, 2, 2, 2 u.s.w. ad inf. auftreten. – Denn wie weiß ich, daß ich nach der 500sten 2 wieder “2” schreiben soll? Daß nämlich dann “2” ‘die gleiche Zahl’ ist? Ja weiß ich es denn? Und wenn ich es jetzt weiß, was hilft mir dieses Wissen für später? Ich meine: wie weiß ich später was ich mit diesem Wissen anzufangen habe?

​

Wenn zur Fortsetzung der Reihe + 1 eine Intuition nötig ist, dann auch zur ˇFortsetzung der Reihe + 0 (ich meine etwa die Reihe 1, 1, 1, 1, 1, ad inf.).

​

Was ist denn der Fehler, vor dem ich warnen will?

​

“Aber Du weißt doch ganz genau, daß nach “64” “66” kommt, Du bist doch nicht einen Moment darüber in Zweifel!” – Es ist wahr, ich bin nicht einen Moment darüber i[n|m] Zweifel.    Aber überlege: welchen Grund gebe ich dafür an? Was sage ich, wenn ich gefragt werde: warum?

​

Erinnere ich nicht nur daran : , daß die Kette der Gründe zu einem Ende kommt? Und woran erinnert der, der was bringt der in Erinnerung, der dies tut?

​

Es ist ganz richtig: Ich zweifle nicht einen Augenblick, welche Zahl in der Reihe + 2 nach 64 kommt, & ich bin sicher, daß ich morgen das Gleiche schreiben werde, wie heute & ˇvielleicht, daß alle normalen Menschen es ebenso machen werden; u.a.m.. Aber sind das Tatsachen, mit denen es die die Logik zu tun hat? konstatiert konstatieren soll? – Anderseits sind es aber sehr interessante Tatsachen!

​

“Du wirst doch nicht sagen, daß Du zweifelst, daß das Grün ist!” Nein. Aber daß ich nicht zweifle, heißt das, daß Gründe mich dazu zwingen es zu sagen?!

​

“Wie kann ich es wissen, wenn mich die Gründe nicht ⌊(⌋dazu⌊)⌋ zwingen? – Es gibt nur eins: ich weiß es durch Intuition!” Muß ich denn immer ein Geistiges Reservoir annehmen, aus dem jede meiner Denkhandlungen (d.i. was ich sage, schreibe, etc.) fließt?

​

Ist dies nicht so, wie wenn ich sage: “Muß denn jeder Körper Einrichtung⌊s⌋gegenstand mit einem Gesims abschließen?”

​

Oder denk Dir, ich sagte: “Das Gesims schließt ja doch auch mit einem Prisma ab!” Oder gar: “Das Gesims kommt ja doch auch zu einem Ende!” – Mußte ich ihn daran erinnern; konnte er gla⌊u⌋ben sich einbilden, daß das Gesims nicht zu einem Ende käme? – Es muß anders zugehen.

​

19.8. ⌊Ich fuhle mich sehr seltsam;⌋ ich weiß nicht ob ich ein Recht oder einen gu[g|t]en Grund habe, jetzt hier zu leben. Ich habe kein wirkliches Bedürfnis nach Einsamkeit, noch einen überwältigenden Trieb zu arbeiten. Eine Stimme sagt: warte noch, dann wird es sich zeigen. ⌊–⌋ Eine Stimme sagt: Du wirst es hier unmöglich aushalten können; Du gehörst nicht mehr hierher! – Aber was soll ich machen? Nach Cambridge? [d|D]ort werde ich nicht schreiben können. Ich sehne mich nach F[.|r]. Oder, ich fürchte, daß er sich nach mir sehnt & möchte sein, wo er ist. – [u|U]nd ich möchte sein, wo ich gebraucht werde. Freilich, – vielleicht sehe ich es alles falsch an. Ich will nicht leiden. – So närrisch es scheint, so kommt es mir fast vor, als sollte ich sofort meine Sachen packen & nach Cambridge zurück fahren. – Anderseits ist auch das möglich: Ich sage mir (& meinen Freunden): ich werde hier 4-6, höchstens aber 8 Wochen bleiben, & dann nach England zu (bezw. Dublin) zurückkommen[.| (]D.v.). Ich kann mir vornehmen, es 4-6 Wochen hier auszuhalten & zu arbeiten & ich kann von F. verlangen, daß er es solange aushält! Dagegen kommt mir vor, als hätte ich kein Recht, bis Weihnachten hier zu bleiben; ganz abgesehen davon, daß ich mir nicht denken kann, wie ich es hier so lange würde treiben können. Eines ist klar: ich bin jetzt hier – wie ˇ& warum immer ich hierher gekommen bin. So laß mich mein Hiersein benützen, soweit es geht.      Ich kann mir nicht vornehmen, bis Weihnachten hier zu bleiben. (Wie ich es voriges Jahr getan habe.) Denn ich habe keinerlei Aussicht, eine solche Zeit mit Arbeit & Denken ausfüllen zu können! – Ich befinde mich jetzt ganz anders. – Wohl aber kann ˇ& soll ich mein Hiersein jetzt benützen, & denken & arbeiten: Aber nicht auf unbestimmte Zeit! Denn davor graut mir, & ich glaube, mit Recht. D.h. ich kann etwa 6 Wochen dableiben, wie immer meine Arbeit gehen sollte, habe ich aber nach dieser Zeit keinen klaren Grund zur A anzunehmen, daß ich hier besser arbeite als anderswo, dann wird es Zeit zu gehen. Möge Gott geben, daß ich die Zeit, welche ich hier bin, gut benütze! Es ist [h|s]ehr seltsam, daß ich mich – scheinbar vor lauter Panik – in den Beinen schwach fühle. Ist es das Klima?? – Es ist fürchterlich, wie leicht mich die Sorge übermannt! –

​

‘Die Kette der Gründe hat ein Ende’ 20.8. “Ja, das ist wahr! –” sagen wir; “daran hab' ich nicht gedacht”. Das ändert den Aspekt. –

​

“Das Gesims kommt ja doch auch zu einem Ende”: das lenkt seine Aufmerksamkeit auf das obere Ende des Gesimses. Das [O|o]berste abschließende prisma des Gesimses hatte er früher nie mit einem Prisma von größerer Höhe verglichen. “Denke an so einen Satz wie: “Die Platte ist ja doch auch ein Prisma”. Es wird auf eine Analogie aufmerksam gemacht & so ‘der Aspekt geändert’.

​

“Wie weiß ich, daß ich im Verfolg der Reihe + 2 … 200004, 200006 schreiben muß, …?” – ja muß ich denn?    “Doch, ⌊!⌋ wenn ich sie so verstehe[!|.]” – Wie verstehe? Wenn ich sie wie verstehe? Was ist der Ausdruck desieses Verständnisses, dieser Auffassung? Etwa “ + 2”, oder ein anderer algebraischer Ausdruck? oder etwa die Glieder “200004, 200006”?        “Aber – ohne Sophisterei – hast Du denn als Du den Befehl gabst ‘ + 2’ nicht doch gemeint, er solle, wenn er bis dorthin kommt jene Zahlen schreiben?” Erstens: ich habe, als ich den Befehl gab, gar nicht an diese beiden Zahlen gedacht; zweitens: wenn ich an sie gedacht hätte, so hätte ich sicher diesen Übergang als den erklärt, welchen ‘ich meine’. Überlege Dir die Gründe für diese Sicherheit. – Und man sagt in so einem Falle ˇetwa, wenn der Andre z.B. zu von nach ‘264’ ‘267’ schreibt: “Ich habe gemeint Du sollst schreiben ‘264, 266’” oder sogar: “Als ich den Befehl gab … meinte ich …”. Und so kann man sagen: “Als wir uns zum Schachbrett setzten, mein⌊t⌋e ich, wir sollten Schach spielen & der soll sollte gewinnen, der dem Andern den seinen König nimmt”, obwohl Du in keiner Weise an diese Konsequenz dies letztere gedacht hast. // , obwohl Du man weit entfernt warst war, an diese Konse- quenz zu denken. // Und warum kann man denn dennoch so etwas sagen? Man sagt in so einem Falle auch: “[a|A]ls wir uns zum Schachbrett setzten, habe ich natürlich gemeint, …”.    Wenn man nun an jene Konsequenz ebensowenig gedacht hat, wie etwa an ihr Gegenteil, mit welchem Recht wieso kann man dann sagen, man habe damals dies gemeint. Dies Das hat doch wohl mit der Gepflogenheit zu tun, das Spiel so zu spielen.

​

21.8.    Ich denke immer wieder dran, in mein Haus zu übersiedeln, wo ich mehr Freiheit habe; aber ich fürchte mich vor der Traurigkeit, [wrv|die] mich dort überwältigen kann. –     Es ist schwer, bergauf zu gehen, & man tut es ungern.     Bin außerordentlich matt. Mein Körper ist offenbar nicht recht in der Ordnung. Es ist mir, als ob ich ausgezeichnete Gedanken in mir hätte, die aber nicht an die Oberfläche kommen können höchstens einen Augenblick hervorschauen ⌊(⌋können⌊)⌋ & sich wieder zurückziehen. & wieder verschwinden. Anderseits fühle ich auch, daß mir zum Ausdrücken dieser großen Gedanken eine Kraft nötig wäre, die ich weit entfernt bin zu besitzen. Ich habe ˇtatsächlich nicht die Kraft, sie zu gebären. Sie herauszupressen. Oder sie zerbröckeln beim Austritt.

​

Was nennen wir ‘logische Konsequenz’ aus einer Regel? In welchem Fall sagen wir, wir richteten uns nur nach der einmal gegebenen Regel – & in welchem, wir stellten Regeln auf ‘as we go along’? D.h., in welchem Fall gebrauchen wir das Praeteritum “ich habe gemeint, …”?

​

“Wenn Du mit derc die Aussage “kein Mensch lebt länger als 200 Jahr Jahre“ dasselbec so meinst wie ich, nämlich keiner, kein einziger, dann folgt aus ihr, daß so & so, den Du als Menschen anerkennst, auch nicht länger als 200 Jahre leben kann” – “Ja ich meine: keiner, kein einziger (hierzu der entsprechende Ton & die eine Geste der Allgemeinheit); aber dieser ⌊(⌋Mensch⌊)⌋ lebt länger als 200 Jahre.”

​

Die Meinung, daß die logischen Gesetze Ausdruck von ‘Denkgewohn- heiten’ sind, ist nicht so absurd, als sie ausschaut.

​

22.8. Bin jetzt wirklich krank. Unterleibschmerzen & Temperatur.

​

23.8 Heute Temperatur (nach dem Puls beurteilt) beinahe normal[.| (]vormittag). Bin ganz matt. Weiß nicht, was ich tun werde. Gleich nach England zurück, scheint, so seltsam das klingt, das vernünftigste. Das will tue ich aber nicht gern: teils weil ich mich damit ˇvor den Leuten lächerlich mache, wenn ich gleich wieder abreise, teils aber, weil ich damit in Ungeduld eine Chance wegzuwerfen scheine; die, vomn meinem Aufenthalt hier gebrauch zu machen. zu profitieren. Und anderseits wieder ist es mir, als könnte ich, wie ich lebe, gar keinen Gebrauch von diesem Aufent- halt machen, weil ich, irgendwie, in einer Unwahrheit lebe.     Abends, Tempe⌊r⌋atur normal. Ich, übrigens so öde, wie zuvor.

​

24.8. Unwohl. War nicht freundlich zu Anna Rebni. Sagte ihr, daß ich morgen in mein Haus übersiedle. Das ist übrigens recht; denn hier bin ich den andern mehr oder weniger zur Last & hab es darum in mancher Beziehung noch schlechter als allein bei mir. Und im Übrigen ist es wohl auch besser für mich. –     Habe in den letzten Tagen oft in Mcaulay's Essays gelesen. Und was ich aus ihnen ziehe ist immer wieder: Was ist der Mensch?!

​

25.8.      ⌊Fühlte mich vormittags furcht⌋bar müde; übersiedelte in meine Hütte & dachte: wie wird es werden? Als ich aber endlich mit Sack & Pack dort war, fühlte war ich mich auf einmal frischer! sowohl körperlich als geistig. Bin jetzt müde aber nicht mehr so trübe. Kann wieder die Gegend mit Freude betrachten. Gott sei Dank. – Fühle mich innerlich mehr aufgelockert & freilich auch allem [S|s]chrecklichen näher, aber lebendiger. Gott weiß, was mit mir werden wird. Möge mir Ruhe gegeben werden! – Temperatur normal, obwohl ich viel Bewegung gemacht habe & ziemlich viel gegessen. Möge es mir [e|v]ergönnt sein [e|v]ernünftig zu sein! denn ich fühle mich allerdings in etwas labilem unsicherem Gleichgewicht. Teils auch wegen einer gewissen Sehnsucht nach Fr., die zuhinterst in meinem Geist liegt & ˇmich von dort aus beunruhigt. “Gott, in Deine Hände gebe ich mich!” so sollte ich sprechen.      Als ich vor einer Woche nach Skjolden kam & mir vornahm nicht oder nicht gleich in mein Haus zu ziehen, da sagte mir eine innere Stimme, daß ich gleich dahin ziehen sollte; aber ich tat es nicht. – Heute als ich hier auspackte, da sagte mir eine innere Stimme, daß ich nicht für lange auspacke. – ‒ ‒

​

“Hacke alle diese Bäume um!” ‒ ‒ “Ja, verstehst Du nicht, was ‘alle’ heißt?” (Er hatte einen stehen gelassen.) Wie hat er gelernt, was “alle” heißt? Doch wohl durch Übung[!|.] –

​

Das Wort hätte ja auch bedeuten können: alle außer [e|E]inem. Dieser Begriff könnte als grundlegend gelten.

​

Das Bild, w ( [w|d]as man sich von ‘alle’ macht wird dann wohl ein andres sein, oder die Geste, die man macht.

​

Desgleichen: “schreibe alle Zahlen von 1 bis 10 an!” Oder: aus – “Alle Zahlen von 1-10 haben diese Eigenschaft” folgt nicht: “5 hat diese Eigenschaft”. (Wohl aber, “5 oder 6 hat diese Eig.”.)

​

Wenn ich nun sage: “Alle Zahlen haben diese Eigenschaft”; ich finde dann daß die Zahl z 777 sie nicht hat: Nun sage ich einfach: “Ja 777 hat sie nicht!”. Nun sagt man mir: “Ja, hast Du denn, als Du sagtest, alle Zahlen hätten die Eigenschaft, gemeint, daß 777 sie nicht hat?” – Ich antworte: “Ich habe damals gar nicht an 777 gedacht. Aber jetzt nehme ich eben 777 aus!” // . Jetzt nehme ich 777 aus. –” //        Man wird in diesem Fall von mir sagen: “Man kann sich auf ihn nicht verlassen”. –

​

Der Witz des Wortes “alle” sei ist ja, daß ich mich gebunden fühle.           Und man kann das auch so sagen: Die Übungen , womit ich … , mit welchen ich den Gebrauch des Wortes “alle” // einübec // lehre, zielen gehen alle darauf hin, daß keine Ausnahme gemacht werden darf.

​

Immer wieder will ich mich den Größten gleichsetzen. – Und was für Grund habe ich denn dazu?? – Es ist also wie ein Wahnsinn; & doch geschieht es immer wieder & wieder. Und nicht nur Großen gleich – und welchen Grund habe ich denn dazu – son- dern ˇzu den Größten möchte ich gehören. Das [g|t]u[g|t] man doch!

​

“Aus ‘[a|A]lle …’ folgt ‘[d|D]ieses …’ – Das heißt nicht: “wenn Du ‘Alle’ mit dieser Meinung gesagt hast, kannst Du nicht, ohne daß eine Art geistige Explosion ( der ein Widerspruch) die Folge ist geschieht , // erfolgt, // nun diesen besonder⌊e⌋n Fall negieren.” Sondern es heißt: ‘Alle’ gebraucht man so so .

​

‘Alle’ gebraucht man so, daß der besondere Fall Satz aus der allgemeinen Feststellung Behauptung folgt

​

Wie erscheint denn nun das Folgen // Folgern // im Sprachspiel? –            In einem Reglement heißt es [A. Gide]: “Alle, die über 1 m 80 hoch sind, sind in die & die N-Abteilung aufzunehmen.” Einer ˇKanzlist verließt die Namen der Leute & gibt ihre Höhe dazu an; ein [a|A]ndrer teilt sie auf.     “N.N., 1⌊˙⌋9˙0 m” – “Also ˇN.N. in die U-cAbteilung.”

​

26.8. Wenig geschlafen, sehr schlechtes Bett. Im übrigen aber geht mir's besser, obwohl ich nicht weiß, wie ich's aushalten werde mit schlechten Nächten! Bin übrigens mißgünstig & ungeduldig.

​

Man sagt[;|,] “di⌊e⌋ser Satz folgt aus diesem” & dabei ist es nicht klar, was denn da vor sich geht, wenn der eine aus dem andern folgt ˇoder gefolgert wird. (Russell dachte sich durch die Konstatierung der Implication helfen zu können.) Was geht denn beim Folgern vor sich? – “Wenn ich die Wahrheit der Sätze … erkannt habe, so bin ich nun berechtigt … hinzuschreiben.” – Inwiefern berechtigt? Hatte ich früher kein Recht es ihn hinzuschreiben? “Jene Sätze überzeugen mich von der Wahrheit dieses Satzes.” – Aber darum handelt sich's natürlich auch nicht.        “Nach diesen Gesetzen vollzieht der Geist die Übergänge, die den Übergang, den man ‘logischen Schluß’ nennt.” – Das ist gewiß interessant & wichtig; // “Nach diesen Gesetzen vollführt vollzieht der Geist die besondere Tätigkeit des ˇlogischen Schließens.” … ; // aber ist es denn auch wahr ? , ⌊?⌋ schließt er immer nach diesen Gesetzen? und Und worin besteht die besondere Tätigkeit des Schließens?         Darum ist es notwendig zu schauen, wie wir denn in der Praxis der Sprache Schlüsse vollziehen – was . Was denn das S⌊c⌋hließen im Sprachspiel für eine Tätigkeit ist.

​

Was nennen wir, z.B., Schlüsse bei Russell (Princ. Math.), oder bei Euclid? Soll ich sagen: die Übergänge von einem Satz zum nächsten? Aber wo steht der Übergang? – Nun ich sage bei Russell folge dieser Satz aus jenem, wenn sie in seinen ’Beweisen’ in der & der Ordnung stehen, & wenn ich den einen aus dem andern mittels seiner Schlußregeln gewinnen kann. – Wird das letztere experimentell festgestellt? Ja! [d|D]enn ich schreibe gewisse Zeichenfolgen hin, richte mich dabei nach gewissen Schemen – dabei ist freilich wesentlich, daß ich keines Zeichen übersehe, oder daß es sonst wie abhanden kommt – kommt bei diesem Vorgang dann das & das heraus, so sage ich, es folge. Ich kann aber auch sagen, ich habe damit kein Experiment gemacht. Denn, wenn 2 & 2 Äpfel nur mehr 3 Äpfel geben, d.h. wenn 3 Äpfel da liegen nachdem ich 2 und 2 hingelegt 2 & dann wieder 2 hingelegt habe, sage ich nun nicht: 2 & 2 ist also doch nicht immer 4; sondern: einer muß irgendwie weggekommen sein.

​

Auch ist wichtig, daß ein Beweis in einem Buch niedergeschrieben sein kann. – Aber worin besteht dann das Experiment des Beweises? – Wohl darin, daß ich dem Beweis ‘folge’? – Denn hat nicht der eins gemacht, der den Beweis hingeschrieben hat? – Aber wie kann inwiefern mache dann ich es, indem ich ihn durchsehe? – Man könnte nun freilich sagen: Wenn Du diese Kette von Übergangen durch ansiehst, kommt es Dir nicht auch so vor, als stimmten sie mit den Paradigmen?        Wenn das also ein Experiment genannt werden soll, dann wohl ein psychologisches. – Denn der Anschein des Stimmens kann ja auf ˇeiner Sinnestäuschung beruhen. Und dies geschieht ja auch ˇmanchmal, wenn wir uns einen Rechenfehler machen. // wenn wir uns verrechnen. //         Man sagt auch: “Das kommt mirc heraus”. Und es ist doch wohl ein Experiment, was welches zeigt[.|,] daß das mir herauskommt.        Man könnte sagen: Das Resultat des Experiments ist dies, daß ich am [e|E]nde, beim Resultat des Beweises angelangt, sage: mit Überzeugung sage: “Ja, es stimmt.”

​

Was ist die ˇcharakteristische Verwendung des Vorgangs als einer B Berechnung Rechnung ? ⌊(⌋[i|I]m Gegensatz zu der ˇVerwendung als Experiment.⌊)⌋           Wir betrachten die Berechnung als Demonstration einer internen Eigenschaft (einer Eigenheit des Wesens) der Strukturen.        Aber was heißt das?

​

Es geht mir viel besser als gestern, spüre nur noch ganz leichte Schmerzen. Ich kann auch die Natur wieder mit Genuß ansehen, & bin mit Gaben uberschüttet. Aber ich benehme mich schlecht & habe gemeine ˇ& schäbige Genüsse & Gedanken. Zwei Briefe von Drury & Francis. Beide rührend lieb. Wie wenig verddient. Ein schäbiger Mensch.     Lade Fr. ein zu kommen. Möge es gut werden! Und moge es mir gegeben werden halbwegs anständig zu sein.      Ich will immer Gott betrügen.

​

Urbild der ‘internen Eigenschaft’ 3 × 3 + 1 = 10    Wenn ich nun sage: 10 Striche bestehen notwendig aus 3 mal 3 Strichen & einem Strich – das he⌊i⌋ßt doch nicht: wenn ich zehn [s|S]triche dastehen so stehen immer alle die Ziffern & Bogen rundherum! – Setze ich sie aber zu den Strichen hinzu, so sage ich, ich demonstrierte nur das Wesen jener Reihe Gruppe von Strichen.             “Aber bist Du sicher, daß sich die Gruppe beim dDazuschreiben jener andern Zeichen nicht geändert verändert hat?” – “Ich weiß nicht; aber eine bestimmte Zahl von Strichen stand da, & wenn nicht 10 so eine andre & dann hatte die eben andre Eigenschaften. –”

​

Die Rechnung ‘entfaltet’ die Eigenschaften der Hundert

​

‘Hundert besteht aus 50 und 50’.      Was heißt es eigentlich 100 bestehe aus 50 & 50? Man sagt der Inhalt der Kiste besteht aus 50 Äpfeln & 50 B[e|i]rnen. Aber wie, wenn Einer sagte: “der Inhalt dieser Kiste besteht aus 50 Äpfeln & 50 Äpfeln”?, –, wir wüßten zun- nächst nicht, was er meinte. – Wenn Einer sagt: “[d|D]er Inhalt der Kiste besteht aus 2 mal 50 Äpfeln”, – so denken wir heißt das entweder, es seien ˇda zwei Abteilungen zu 50 Äpfeln in der Kiste; oder es handelt sich etwa um eine Verteilung in der [j|J]eder 50 Äpfel erhält kriegen soll & ich höre nun, daß man aus der Kiste 2 Leute beteilen kann.

​

27.8.    Etwas besser geschlafen. Lebendige Träume. Et[d|w]as niedergedrückt; Wetter & Befinden.    Die Lösung des Problems, das Du im Leben siehst, ist eine Art zu leben, die das Problemhafte zum V[r|e]rschwinden bringt.    Daß da[ß|s] Leben problematisch ist, heißt, daß Dein Leben nicht in die Form des Lebens paßt. Du mußt dann Dein Leben verändern, & paßt es in die Form, dann verschwindet das Problematische.      Aber haben wir nicht das Gefühl, daß der, welcher es nicht darin ein Problem sieht fur etwas Wichtiges, ja das Wichtig⌊s⌋te, blind ist? Möchte ich nicht sagen, der lebe so dahin, ⌊ –⌋ eben blind, gleichsam wie ein Maulwurf[?|,] & wenn er bloß aufschauen sehen könnte, so sähe er das Problem?    Oder soll ich nicht sagen, ⌊:⌋ daß wer richtig lebt, das Problem nicht als Traurigkeit, also doch nicht problematisch, empfindet, sondern vielmehr als eine Freude; also gleichsam als einen lichten Aether um sein Leben, nicht als einen fraglichen Hintergrund.

​

Wenn man sagt: “die 100 Äpfel in der Kiste bestehen aus 50 und 50”, so ist wichtig hier der das Wichtige hier der unzeitliche Charakter von “bestehen”. Denn es heißt nicht, sie bestünden jetzt …, oder für einige Zeit … aus 50 + 50. .

​

Was ist denn das Charakteristicum der ‘internen Eigenschaften’? Daß sie immer, unveränderlich in dem Ganzen, das sie ausmachen, bestehen; – gleichsam unabhängig von allen äußeren Geschehnissen allen Geschehnissen . Wie die Konstruktion einer Maschine auf dem Papier nicht bricht, wenn die Maschinenteile selbst sich verbiegen biegen , oder brechen. // , wenn die Maschine selbst den äußern Kräften untererliegt. //

​

‒ ‒ ‒ Daß sie immer, unver- änderlich in dem Ganzen bestehen, das sie ausmachen // bilden herstellen // . Daß sie nicht Wind & Wetter unterworfen sind, wie das Physikalische der Dinge , ;c sondern unangreifbar unveränderlich wie Schemen.

​

Statt “100 bestehen besteht aus 50 & 50”, könnte man sagen: “ ich Ich lasse 100 aus 50 & 50 bestehen”.

​

“Aber bin ich also in einer Schlußkette nicht gezwungen zu gehen, wie ich gehe?” – Gezwungen? Ich kann doch wohl gehen, wie ich will! – “Aber wenn Du im Einklang mit den Regeln bleiben willst, mußt Du so gehen vorgehen .” – Durchaus nicht, ich nenne ⌊(⌋eben⌊)⌋ etwas anderes ‘Einklang’.” – “Ja, aber dann veränderst Du ⌊(⌋eben⌊)⌋ den Sinn des Wortes ‘Einklang’, oder den Sinn der Regel.” – Nein[;|, –] denn wer sagt was hier ‘verändern’ & was ‘gleichbleiben’ ist heißt ?     Wieviele Regeln immer Du ˇmir angiebst, ich gebe Dir eine Regel, die meine Verwendung Deiner Regeln rechtfertigt.

​

“Du darfst doch das Gesetz jetzt nicht auf einmal anders anwenden!” – Wenn ich nun darauf antworte: “Ach ja, ich hatte es ja so angewandt!” oder auch ⌊(⌋etwa⌊)⌋ : “Ach, so sollte ich es anwenden –!” es angewendet werden – !” , dann spiele ich mit ( I'm playing I play the game); sage entgegne antworte ich aber einfach: “Anders! ⌊?⌋ – Das ist doch nicht anders!”, was willst Du machen?

​

Inwiefern ist das Argument ein Zwang? – “Du gibst doch das zu, – & das zu – – ; dann mußt Du auch das zugeben!” Das ist die Art jemanden zu zwingen – – – d.h., man kann so, (tatsächlich)⌊,⌋ Menschen zwingen, etwas zuzugeben. – Nicht anders, wie Wie man [e|E]inen etwa dazu zwingen kann dorthin zu gehen, indem man gebietend mit dem Finger dorthin zeigt.     Denke, ich zeige in diesem Fall mit drei zwei Fingern in drei zwei verschiedene Richtungen & laße stelle es dem ⌊(⌋aAndern⌊)⌋ offen frei , in welcher der beiden er gehn will, ein andermal aber zeige ich nur in einer Richtung; so kann man das auch so ausdrücken: ich mein erster Befehl habe hätte ihn nicht gezwungen in einer Richtung zu gehen, wohl aber mein Zweiter der zweite ⌊(⌋Befehl⌊)⌋. Das ist aberc eine Aussage, die sagt, welcher Art jene diese Befehle sind ; , aber nicht, was sie ausrichten. // welcher Art etwa ihre Wirkung ist // // aber nicht, etwa & was sie bewirken , wie sie wirken . //

​

Ist eine Berechnung ein Experi⌊⌋menment? – Ist es ein Experiment wenn ich am Morgen aus dem Bette steige? Aber könnte dies nicht ein Experiment sein? welches zeigten soll ob ich nach so & so viel Stunden Schlaf die Kraft habe mich zu erheben. – [&|U]⌊nd⌋ was fehlt ihm dem Vorgang jenemr Handlung dazu, dies Experiment zu sein? Bloß, daß er sie nicht zu diesem Zwecke , d.h., , in der Verbindung mit einer solchen Untersuchung stattfindet ausgeführt wird. Experiment ist etwas durch den Gebrauch, der davon gemacht wird.

​

Beinahe ähnlich, wie man sagt, daß die alten Physiker plötzlich gefunden haben, daß sie zu wenig Mathematik verstehen, um die Physik bewältigen zu können, kann man sagen, daß die jungen Menschen heutzutage plötzlich in der Lage sind, daß der normale, gute Verstand für die seltsamen Ansprüche des Lebens nicht mehr ausreicht. Es ist alles so verzwickt geworden, daß , es zu bewältigen, zu seiner Bewältigung ein ausnahmsweiser Verstand gehört⌊e⌋. Denn es genügt nicht mehr, das Spiel gut spielen zu können[;|,] sondern die Frage ist immer wieder: was für ein Spiel ˇist jetzt überhaupt zu spielen ist? sondern immer wieder ist die Frage: ist dieses Spiel jetzt überhaupt zu spielen & welches ist das rechte Spiel?

​

Wäre es möglich, daß Leute heute eine unsrer Berechnungen durchgingen & von den Schlüssen befriedigt wären sind , morgen aber ganz andre Schlüsse ziehen wollen, ziehen, & einen andern Tag wieder andere?

​

Ja kann man sich nicht denken, daß dies gesetzmäßig so geschieht stattfindet , daß wenn er einmal diesen Übergang macht, er ‘eben darum’ das nächste Mal einen andern macht, & eben darum etwa wieder das nächste Mal wieder den ersten?

​

(Äh⌊n⌋lich, wie etwa die Farbe, die einmal “rot” genannt wird, darum beim nächsten Mal anders genannt wirü⌊r⌋d⌊e⌋ & dann wieder “rot”, u.s.f.. Dies könnte den Menschen so natürlich sein. Man könnte es ein Bedürfnis nach Abwechslung nennen.)

?

Ist es nicht so: Solange man denkt, es kann könne nicht anders sein, zieht man logische Schlüsse.

​

Das heißt wohl: solange das & das – gar nicht in Frage gestellt gezogen wird[﹖|.]

​

∣ In Macauley's Essays ist vieles ausgezeichnet; nur seine Werturteile über große Menschen sind lästig, & überflüssig. Man möchte ihm sagen: laß die Gestikulation! & sag nur, was Du zu sagen hast. ∣

​

[Denke daran, dieses Schreibbuch einmal meiner Schwester Grete zu schenken & dieser Gedanke & Eitelkeit stören mich daher beim Schreiben.] Bin voller Eitelkeit.]

​

Die Schritte, welche man nicht in Frage zieht, sind logische Schlüsse. Aber man zieht sie nicht darum nicht in Frage, weil sie ‘sicher der Wahrheit entsprechen’ – oder g dergl.; – sondern, dies ist eben was man ‘Denken’, ‘Sprechen’, ⌊(⌋etc.⌊)⌋ ˇ‘Schließen’, ‘Argumentieren’ nennt. Es handelt sich hier gar nicht um irgend eine Entsprechung ˇdes Gesagten mit der Realität Wahrheit ; vielmehr ist die Logik vor einer solchen Entsprechung; nämlich in dem Sinne, in welchem die Festlegung der Meßmethode vor der Richtigkeit oder Falschheit einer Längenangabe.

​

“Wenn wir nicht in Gewissem übereinstimmen, können wir nicht argumentieren” – Vielmehr: ohne die diese Übereinstimmung nennen wir ˇwohl es nicht “[a|A]rgumentieren”.

​

“Nach Dir könnte also jeder die Reihe fortsetzen, wie er will; & also auch auf irgend eine Weise schließen!” Wir werden es dann wohl nicht “ˇdie Reihe fortsetzen” nennen & auch wohl nicht “schließen”.

​

Denn daß ihn Schlußgesetze u. dergl. nicht zwingen das & das zu reden (oder zu schreiben), darüber sind wir ja einig. Und wenn Du sagst, er könne es zwar reden, aber er kann es nicht denken, so sage ich nur, das heiße nicht: er könne es, quasi trotz aller Anstrengung, nicht denken, sondern es heißt: zum ‘Denken’ gehört für uns wesentlich, daß er (beim Reden, Schreiben, etc.) solche Übergänge macht.        Und ferner sage ich, daß die Grenze zwischen dem was wir noch ‘[D|d]enken’ & ˇdem was wir nicht mehr so ‘denken’ nennen so wenig scharf gezogen ˇist, wie die Grenze zwischen dem was noch “Gesetzmäßigkeit” he genannt wird & dem was wir nicht mehr so nennen.

​

Wenn man eine Rechnung einen Rechnungsgang Beweisgang als Experiment auffaßt // ‘Experiment’ nennt // , so ist das Resultat des Experiments jedenfalls nicht das, was man das Resultat des Beweises nennt. Das Resultat der Rechnung ist der Satz mit welchem sie abschließt; das Resultat des Experiments ist: daß ich von diesen Sätzen mit durch diesen Regeln zu diesem Satz geführt worden bin. // geführt wurde. //

​

Aber nicht darauf richtet daran heftet sich ⌊(⌋nun⌊)⌋ unser Interesse, daß die & die ˇ(oder alle) Menschen ⌊(⌋oder⌊)⌋ von diesen Regeln so geleitet worden sind, so geführt worden sind (oder so gegangen sind); es gilt uns als selbstverständlich daß die Menschen – ‘wenn sie richtig denken können’ – so gehen. Wir haben jetzt aber einen Weg ˇerhalten, sozusagen durch die Fußtapfen derer, die so gegangen sind. Und auf diesem Weg geht nun der Verkehr ⌊(⌋vor sich⌊)⌋, – zu verschiedenen Zwecken. // , für verschiedene Zwecke. //

​

Wenn wir sagen: “dieser Satz folgt aus jenem”, so ist hier “folgen” wieder unzeitlich gebraucht. (Und das zeigt, daß dieser Satz nicht das Resultat eines Experiments ausspricht beschreibt .)

​

28.8.     Vergleiche damit; “Weiß ist heller als [s|S]chwarz”. Auch dieser Ausdruck ist zeitlos & auch er spricht sagt das Bestehen einer internen Relation aus.

​

Mit Gaben überhäut, die ich nicht verdiene.

​

“Diese Relation besteht aber eben.” möchte man sagen – –. Aber die Frage ist: hat dieser Satz einen Gebrauch? Denn einstweilen weiß ich nur, daß mir dabei ein Bild vorschwebt – aber dies garantiert mir die Verwendung nicht – & daß die Worte einen deutschen Satz geben. Aber es fällt Dir auf, daß die Worte hier anders gebraucht werden, als im normalen Fall einer nützlichen Aussage. – Wie etwa der Radmacher bemerken kann, daß die Aussagen die er über Kreisförmiges & gerades kreisförmig & gerade macht andrer Art sind, als die, die ⌊im⌋ Euklid macht stehen. – Denn wir sagen: dieser Gegenstand ist heller als jener, – & dann ist er etwa jetzt heller & kann später dunkler sein.    Woher die Empfindung “Weiß ist heller als Schwarz” sage etwas über das Wesen der ˇbeiden Farben aus? –        Aber ist die diese Frage überhaupt rich- tig gestellt? Was meinen wir denn mit “dem “Wesen” von Weiß oder Schwarz? Wir denken etwa an ‘das ‘Innere’, ‘die ‘Konstitution’; aber das ergibt hier doch keinen Sinn. Wir sagen ˇetwa auch: “Es liegt im Weiß, daß es heller ist …”      Ist es nicht so: das Bild eines schwarzen & eines weißen Flecks dient uns zugleich als Paradigma dessen, was wir unter “heller” & “dunkler” verstehen & als Paradigma von für “Wweiß“ & von für “Sschwarz“. In so fern ‘liegt’ nun die Dunkelheit ‘imc’ Schwarz, als sie beide von diesem Fleck dargestellt werden. Er ist dunkel dadurch daß er schwarz ist : – aber richtiger ⌊(⌋gesagt⌊)⌋: er heißt ‘dunkel’ er heißt “schwarz” & damit, in unserer Sprache, auch “dunkel”.      ⌊⌊ Man kann Mißverständnisse vermeiden, dadurch daß man erklärt es sei Unsinn zu sagen: “[D|d]ie Farbe dieses Körpers ist heller als die Farbe jenes”, es müsse ⌊(⌋statt dessen immer⌊)⌋ heißen: “dieser Körper ist heller als jener”. D.h., man schließt jene Ausdrucksform aus unsrer Sprache aus. ⌋⌋ Jene Verbindung, eine Verbindung der Paradigmen & Namen, ist in der unserer Sprache hergestellt. Und unser jener Satz ist unzeitlich, weil er nur die Verbindung der Worte “weiß”, “schwarz” & , “heller” mit einem dem Paradigma ausspricht.

​

Wir könnten auch sagen: Wenn wir den Schlußgesetzen (Schlußregeln) folgen, so liegt darin immer auch ein Deuten dieser Regeln Gesetze . // , so liegt in einem Folgen immer auch ein Deuten. //

​

“Aber wir folgern doch diesen Satz aus jenem, weil er tatsächlich folgt!” Wir überzeugen uns doch, daß er folgt.” Wir überzeugen uns, daß, was hier steht, aus dem folgt, was dort steht. Und dieser Satz ist zeitlich gebraucht.

​

Wie ist es aber, wenn ich mich davon überzeuge, daß das Schema    dieser Striche gleichzahlig ist dem Schema dieser     Eckpunkte (I⌊i⌋ch habe ˇsie absichtlich unmittelbar übersehbar einprägsam gemacht gewählt .⌊)⌋, indem ich zuordne ?   Nun, wovon überzeuge ich mich denn, wenn ich diese Figur ansehe?! Ich sehe ein Fünfeck mit Fortsätzen ⌊(⌋an den Ecken⌊)⌋, die wie Staubgefäße aussehen. –

​

Aber ich kann von der Figur so Gebrauch machen: fünf Kinder stehen im Fünfeck aufgestellt, & an der Wand stehen Stäbe nach dem ersten Schema // nach dem Schema | | | | | // ; [I|i]ch sehe auf die Figur & sage: ⌊“⌋ich kann jedem der Kinder einen Stock geben”.             Ich könnte die Figur etwa als schematisches // primitives // Bild davon auffassen, daß ich fünf Kindern fünf Stäbe gebe.

​

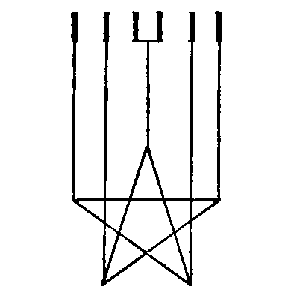
Wenn ich nämlich erst ein b⌊e⌋liebiges Vieleck zeichne – & dann eine beliebige irgend eine Reihe von Strichen – ❘ ❘ ❘ ❘ ❘ ❘ ❘ ❘ ❘ ❘ ❘ ❘ ❘ ❘ ❘ ❘ ❘ ❘ ❘ ❘ ❘, so kann ich nun durch Zuordnung herausfinden, ob ich oben so viele gleichviel Ecken habe, wie unten Striche. – Ich weiß nicht was herauskommen würde wird . – Und so kann ich auch sagen, ich habe mich durch das ziehen der Projektionslinienstriche davon überzeugt, daß am ober⌊e⌋n Ende der Figur ( ) so viele [s|S]triche stehen, wie das Vieleck unten am untern Ecken hat. ([z|Z]eitlich⌊!⌋). In Nach dieser Auffassung gleicht die Figur ( ) diese Figur nicht einem mathematischen Beweise (sowenig wie es ein mathematischer Beweis ist, wenn ich einer Gruppe Kindern je einen Apfel gebe & sehe daß jedes gerade einen kriegen kann).        Ich kann die Figur aber als mathematischen Beweis auffassen. Geben wir dem Schema ( ) einen Namen! Ich werde es das Handschema E-Schema nennen. [i|I]ch nehme an daß etwa auch andere solche die Schemen etwa | , | | , | | | , | |  | | Namen haben hätten . Und die Figur □ ⌊⬠⌋ heißet Drudenfuß S-Figur . Ich beweise den Satz: Ich habe den Satz bewiesen: “das S E-Schema Handschema hat so vielee Striche, wie die S Drudenfuß -Figur Ecken” Dies ; und dies . ⌊(⌋Und⌊)⌋ dies ist wieder unzeitlich.

​

Der Beweis – kann ich sagen – ist eine Figur, an deren einem Ende gewisse Sätze stehen, & an dere[m|n] anderm Ende ein Satz steht (den wir den ‘bewiesenen’ nennen).        Man kann als Beschreibung so einer dieser Figur sagen: in ihr folge der Satz … aus … & …. (Wie man zur Beschreibung eines Hauses sagen kann ein Mansardendach ruhe auf drei Stockwerken in ihm liege ein Giebeldach auf drei Stockwerken & einem gewölbten Unterbau⌊.)⌋ aus Quadern) Wie man zur Beschr. eines Ornaments sagen kann, es liege … .) Ich kann also ˇz.B. sagen: “[i|I]n dem Beweise, den welchen ich hier hingeschrieben habe, folgt der [s|S]atz p aus den Sätzen q … & r …”, & dies ist eine Beschreibung dessen, Angabe über das, was ich hingeschrieben habe. Eine Beschreibung einer bestimmten Beweisfigur[ …| ] Es ist aber nicht der mathematische Satz, daß p aus q & r folgt. Dieser hat eine ganz andere Anwendung.

​

Denken wir uns, wir hätten das Paradigma für “heller” & “dunkler” in Form eines weißen & schwarzen Fleckes gegeben[;|,] & nun leiten wir mit seiner Hilfe – sozusagen – ab: daß rot dunkler ist als weiß. – – – – [Kann man etwas ausführen.]

⌇

29.8.     Und überlegen wir uns noch das dies : Wir wollen sagen: ein Polygon ⌊p⌋ ‘folge’ aus einem andern ⌊q⌋, wenn es ⌊p⌋ aus ihm dadurch gewonnen wird daß man jede zweite Seite des ersten verlängert & das Polygon ist, das von allen geraden, oder ungeraden, [s|S]eiten des Polygons q gebildet wird. So folgt also das Viereck in Quadrat in der Figur aus dem Achteck.

​

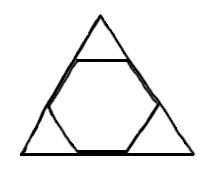
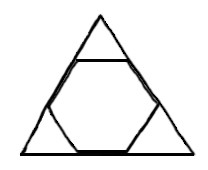
Was ist das nun ⌊(⌋z.B.⌊)⌋ für ein Satz: “Aus dem regelmäßigen Sechseck folgt “[d|D]as gleichseitige Dreieck” folgt aus dem regelmäßigen Sechseck”?

​

Ich kann mir sehr gut wohl vorstellen, daß [j|J]emand überrascht ist, zu sehen finden , daß man ein gleichseitiges Dreieck erhält, wenn man jede zweite Seite eines des Sechsecks verlängert. (Krystalle.).

​

Beweis daß Hand & Drudenfuß gleichzahlig sind:    Andere Form des Beweises:

​

Der bewiesene Satz dient nun als neue Vorschrift zum Konstatieren der Gleichzahligkeit: Wenn man eine Menge Klasse von Gegenständen als Hand angeordnet hat & eine andre als Drudenfuß, so sagen wir nun sie sind gleichzahlig.

​

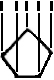
“Aber ist das nicht bloß, weil wir Hand & Drudenfuß schon einmal zugeordnet gezah haben hatten & gesehen daß sie gleichzahlig sind?” – Ja aber, wenn sie es in einem Fall waren, wie weiß ich daß sie es jetzt wieder sein werden? – “Weil es eben im Wesen der H. und des D. liegt, daß sie gleichzahlig sind.” – Aber wie konntest Du das bei der // durch die // Zuordnung Zählung herausbringen? (Ich dachte die Zählung oder Zuordnung ergibt nur, daß diese beiden Gruppen, die ich jetzt vor mir habe, gleichzahlig sind⌊,⌋ ⌊–⌋ oder nicht gleichzahlig ⌊–⌋ sind.)

​

– “Aber wenn er nun eine H. Dinge Hand von Dingen hat & einen Dr. Dinge von Dingen ˇhat & sie nun tatsächlich eins zu eins zuordnet & er ordnet macht nun wirklich die [z|Z]. O. // // ordnet sie nun tatsächl. einander zu // , so ist es doch nicht möglich, daß er etwas andres erhält, als daß sie gleichzahlig sind!” – Und daß es nicht möglich ist, das sehe ich doch aus dem Beweis.” – Aber ist es denn nicht möglich? Wenn er ˇz.B. – wie wir sagen würden – eine der Zuordnu⌊n⌋gslinien zu ziehen übersieht[?|.] Aber ich gebe zu, daß er in der ungeheuren unendlichen Mehrzahl der Fälle das gleiche Resultat erhalten wird; & wäre es nicht so, so würde dem ⌊(⌋ganzenc⌊)⌋ Beweis ˇ damit dadurch der Boden entzogen. Wir entscheiden uns ˇnun // nämlich // , das Beweisbild statt einer Zuordnung zu gebrauchen; wir ordnen sie nicht zu ; , sondern vergleichen statt dessen die Gruppenbilder mit denen des ‘Beweises’ (in welchem allerdings zwei Gruppen einander zugeordnet sind).

​

Ich könnte als Resultat des Beweises auch sagen: “Eine H. & ein D. heißen ‘gleichzahlig’”. // heißen von nun an ‘gleichzahlig’”. //

​

Ich könnte sagen: Der Beweis erforscht nicht das Wesen der beiden Figuren, aber er spricht aus, was ich von nun an zum Wesen der Figuren rechnen werde. –– Was zum Wesen gehört, lege ich unter den Paradigmen der Sprache nieder.

​

Wenn ich sage “Dieser Satz folgt aus jenem”, so ist das die Anerkennung einer Regel. Sie geschieht auf Grund des Beweises. D.h. : , ich lasse mir diese Kette (ˇdiese Figur) als Beweis gefallen. – “Aber könnte ich denn anders? Muß ich mir sie nicht gefallen lassen?” – Warum sagst Du, Du müssest? Doch darum, weil Du am Schlusse des Beweises ⌊(⌋etwa⌊)⌋ sagst: “Ja, ⌊–⌋ ich muß diesen Schluß anerkennen.” – aber Aber das ist doch nur der Ausdruck Deiner unbedingten Anerkennung. –    Das heißt, glaube ich, ⌊:⌋ die Worte “[d|D]as muß ich zugeben” werden in zweierlei Fall Fällen gebraucht: wenn wir einen Beweis erhalten haben – aber auch, im Bezug auf die ⌊(⌋einzelnen⌊)⌋ Schritte des Beweises. // – aber auch in Bezug auf den einzelnen Schritt selber Schritt selber des Beweises. //

​

Und worin äußert es sich denn, daß der Beweis mich zwingt? Doch darin, Doch, daß ich so & so darauf vorgehe, daß ich mich 1 ¤

​

Das Treuherzige Gemütvolle & das Treuherzige in der Religion der Germanen, oder Abendländer, ist mir zuwider. Das heißt, das ist kein Zugang zur Religion für mich. Dies ist, natürlich, keine Kritik der Andern, aber es heißt: mein Weg ist nicht dieser – & mit allem, was so aussieht, habe ich nichts zu tun. Das ist eine Landestracht, ⌊–⌋ aber nicht die meine.   Wenn also [e|E]iner, quasi gleichsam , sagt: “[n|N]ur die Treuherzigen kommen in den Himmel”, so kann ich sagen: Nein, das ist meine Religion nicht. – Deshalb bin ich, wenn ich Religion von einem “Treuherzigen” lernen will scheinbar , gewissermaßen, inm einem Nachteil, aber doch wirklich in keinem Nachteil. Das heißt, ich bin dann geneigt zu sagen: “Hätte ich nur den richtigen Religionslehrer …!” was ein Unsinn ist. Die [g|G]egen den Strom schwimmen müssen ist kein Nachteil, wenn Schwimmen das Ziel ist.

​

¤ 2 weigere einen andern Weg zu gehen. Als letztes Argument, gegen [e|E]inen, der so nicht gehen wollte, würde könnte ich nur noch sagen: “Ja siehst Du denn nicht! …!” – & das ist doch kein Argument.

​

“Aber, wenn Du recht hast, wie kommt es dann, daß sich alle Menschen (oder doch alle normalen Menschen) diese Figuren als Beweise dieser Sätze gefallen lassen?” – Ja, es besteht eine große, ⌊–⌋ & interessante, ⌊–⌋ Übereinstimmung. // Ja, es besteht tatsächlich eine große Übereinstimmung. //

​

Denk Dir Du hättest eine Reihe von 100 Kugeln, sie sind numˇmeriert seien mit römischen Ziffern nummeriert. Du nummerierst sie nun erst mit arabischen Ziffern; dann von Kugeln vor Dir; Du numerierst sie nun mit arabischen Ziffern, sie lassen sich gerade von 1 bis 100 numerieren; dann … machst Du nach je zehn (die sich in dieser Nummerierung nun deutlich hervorheben) einen größern Abstand; in jedem Reihenstück von je 10 machst Du einen etwas kleineren Abstand zwischen zwei gleichen [h|H]älften von je 5 (so werden die 10 übersichtlich); nun nimmst Du das zweite [z|Z]ehnerstück & legst es unter das erste, das dritte unter das zweite & so fort bis zum Ende; nun machst Du einen ˇetwas größern ˇvertikalen Abstand zwischen der ersten ˇ& der zweiten Hälfte der ˇZehenReihen & & nummerierst die⌊se⌋ Reihen von 1 bis 10. Ich kann sagen, ich habe Eigenschaften der hundert Kugeln entfaltet. – Nun aber denke Dir daß dieser ganze Vorgang, dies Experiment mit den hundert Kugeln, gefilmt wurde. Ich sehe nun auf der Leinwand dem Film doch nicht ein Experiment, denn der Film eines Experiments ist doch nicht selbst ein Experiment. – Aber das ‘mathematisch wesentliche’ sehe ich nun auch in der Projek- tion jenes Films! Denn es erscheinen da zuerst 100 Flecke römisch nummeriert, dann werden sie in Zehnerstücke eingeteilt, usw. usw..

​

Ich könnte also sagen: der Der Beweis dient mir nicht als Experiment, wohl aber sondern als Bild eines Experiments.

​

Ich bin noch sehr ünklar.

​

Lege 2 Äpfel auf die ˇleere Tischplatte, schau daß niemand in die Nähe kommt & der Tisch nicht erschüttert wird; nun lege noch 2 Äpfel auf die Tischplatte; nun zähle die Äpfel die da liegen[;|.] Du wirst so hast ein Experiment gemacht; das Ergebnis Res der Zählung ist wahrscheinlich 4. (Wir würden das Ergebnis Resultat des Experiments so beschreiben, daß wir sagen: Wenn man unter den & den Umständen erst 2 & dann noch 2 Äpfel auf einen Tisch legt verschwindet zumeist von keiner, noch kommt einer dazu.) Und ganz ähnliche Experimente kann man, mit dem gleichen Ergebnis, mit allerlei festen Körpern, ⌊–⌋ Bohnen, Erbsen, Büchern, Stäben etc. – ausführen. – So lernen ja unsre Kinder rechnen, denn man läßt sie drei Bohnen hinlegen & noch drei Bohnen & dann zählen. Käme dabei einmal 5 einmal 7 heraus[,| (]weil wie wir jetzt sagen würden einmal von selbst eine dazu einmal eine weg käme) so würden wir zunächst Bohnen a⌊l⌋s für den Rechenunterricht ungeeignet erklären. Geschähe das gleiche aber mit Stäbchen, Fingern ˇStrichen & den meisten andern Dingen, so hätte das Rechnen damit ein Ende.       “Aber wäre dann nicht doch noch 2 + 2 = 4?” – Dieses Sätzchen wäre damit unbrauchbar geworden. –

​

Wenn wir Geld in eine Lade legen & später finden wir es nicht mehr dort, so sagen wir: “Von selbst ist es nicht verschwunden.” Dies ist eine wichtige Lehre // ein wichtiger Satz // der Physik.

​

29.8.    “Du brauchst ja nur auf die Figur zu sehen, um zu sehen, daß 2 + 2 4 ist.” – Dann brauche ich nur auf die Figur zu schauen, um zu sehen, daß 2 + 2 + 2 4 ist.

​

Multiplizieren mit musikalischen Themen Melodien : Multipliziere die Tonreihe des ersten eines Taktes des Kaiserliedes eines gleichförmig fortschreitenden Themas mit der Tonreihe der ersten zwei⌊er⌋ Takte⌊.⌋ ⌊(⌋also 4 × 9⌊)⌋. Pfeife dases ˇdie ersten zwei Takte Thema⌊s⌋ langsam & bei nach jedem Ton den einen Takt des Themas & sieh wie weit Du in ihm kommst.

​

Wir lehren jemand eine Methode Nüsse unter Leute Menschen zu verteilen; ein Teil dieser Methode ist das Multiplizieren zweiter Zahlen im Dezimalsystem.    Wir lehren jemand ein Haus bau errichten; dazu dabei auch, wie er sich genügende die genügenden Mengen von Material, etwa Brettern Holz anschaffen soll, hiezu dazu eine Technik des Rechnens. Die Technik des Rechnens ist ein Teil der Technik des Hausbaues.

​

Leute verkaufen & kaufen Scheitholz für Geld; die Stöße werden mit einem S Maßstab gemessen die Maßzahlen von Länge, Breite, Höhe multipliziert; was dabei herauskommt ist die Zahl der Groschen die sie fordern & zu geben haben. Sie wissen nicht, ‘warum’ dies so geschieht, sondern sie machen es einfach so, so wir es gemacht. – Rechnen diese Leute nicht?

​

Wer so rechnet, muß er einen ‘ arithmetischen mathematischen Satz’ aussprechen? Wir lehren freilich die Kinder das Einmaleins in Form von Sätzchen, aber ist das wesentlich? Warum sollten sie nicht einfach – Rrechnen lernen. Und wenn sie es können, haben sie nicht Arithmetik gelernt?

​

Aber in welchem Verhältnis steht dann die Begründ[ü|u]ng einers Rechnunenvorgangs // einer Rechenart // zu dem Rechenvorgang ˇselbst? zu der Rechnung selbst? //

​

Arbeite weiter & sieh, was wird! –

​

“Ja ich verstehe , daß dieser … folgt.” , dieser Satz folgt aus diesem.” – Verstehe ich warum er folgt, oder verstehe ich nur daß er folgt?

​

Werde ich je damit zu Rande kommen? Arbeite weiter & überlaß es der Schickung!

​

Wie, wenn ich gesagt hätte: [j|J]ene Leute zahlen für's für das Holz auf Grund der Rechnung; sie lassen sich die jene Rechnung als Beweis dafür gefallen, daß sie so viel zu zahlen haben. – Nun das es ist einfach eine Beschreibung ihres Vorgehens (Benehmens).

​

Wer uns erinnert sagt : “die Kette der Gründe hat ein Ende”, stellt den ihren Anfang Ursprung Anfang der Kette // ihren Ursprung // mit ihrer Mitte zusammen, daß wir den Unterschied wahrnehmen gewahr werden . ‘Schau das an – & schau das an!’ ‘Präg' [d|D]ir diese beiden Formen ein!’

​

Die Logik – kann man sagen – zeigt, was wir unter “Satz” & unter “Sprache” verstehen. –

​

Gedan Auch Gedanken fallen manchmal unreif vom Baum.

​

Trenne die Gefühle ( Gebärden Gesten ) der Übereinstimmung von dem, was Du mit dem Beweise machst!

​

Jene Leute – würden wir sagen – verkau- fen das Holz nach dem Kubikmaß – – aber haben sie darin recht? Wäre es nicht richtiger es nach dem Gewicht zu verkaufen – oder nach der Arbeitszeit des Fällens die das Fällen gekostet hat – oder nach der Mühe des Fällens, gemessen am Alter & an der Stärke des Holzfällers? Und warum sollten sie es nicht für einen Preis hergeben, der von all dem unabhängig ist: jeder Käufer zahlt ein & denselben einen bestimmten Betrag, wieviel ˇHolz immer er nimmt (denn man hat gefunden, daß man so befriedigend leben kann). Und ist etwas dagegen zu sagen, daß man das Holz einfach verschenkt?

​

Gut! Wie aber, wenn sie das Holz in Stöße von beliebigen beliebigen, verschiedenen Höhen schlichteten & es dann ˇzu einem Preis genau proportional der Grundfläche der dieser Stöße verkauften bezahlten ?

​

Und wie, wenn sie dies sogar mit den Worten begründeten: “Ja, wer mehr Holz kauft, muß auch mehr zahlen[!|.]”

​

Wie könnte ich ihnen nun zeigen, daß – wie ich sagen würde – der nicht wirklich mehr Holz kauft, der einen Stoß von größerer Grundfläche kauft? – Ich würde z.B. einen nach ihren Begriffen, kleinen Stoß nehmen & ihn durch Umlegen der Scheiter in einen ‘großen’ verwandeln. Das könnte sie überzeugen – vielleicht aber würden sie sagen: “ja, jetzt ist es viel Holz & kostet mehr” – & damit wäre es Schluß. – Wir würden in diesem Falle ˇwohl sagen: sie meinen mit “viel Holz” & “wenig Holz” einfach nicht das Gleiche wie wir; & sie haben ein ganz anderes System der Bezahlung, als wir.

​

Frege sagt: [‒ ‒ ‒| Zitat aus dem Vorwort der “Grundgesetze d. Arithm.”] – aber er hat nie angegeben, wie dieser ‘Wahnsinn’ wirklich aussehen würde.

?

Denken wir uns nun, ich gehe einen Beweis durch & sage bei jedem Schritt: “ja, das folgt.” – Was sag' ich damit? – Ich konstatiere doch wohl , daß da etwas steht, was aus jenem folgt. Das ist nicht das, ⌊:⌋ ‘was nicht anders sein kann’, sondern ⌊(⌋etwas⌊)⌋, was sehr wohl anders sein kann, nämlich, daß hier etwas geschrieben steht, was folgt & nicht etwas, was nicht folgt. Wie, wenn ich auf das Resultat am [e|E][i|n]de einer Multiplikation schaue & sage: “ja, das ist das Produkt⌊”,⌋ von … + … ” ich nicht den arithmetischen Satz ausspreche “… x … = …”, sondern, daß hier jetzt das Produkt der beiden Zahlen steht, daß wirklich (oder richtig) multipliziert worden ist.

​

Ich komme heute nicht recht weiter. Bin irgendwie gleich ermüdet & meine Gedanken brechen ab ab, kaum daß sie unterwegs sind. Ich bin eben in der Hand der Schickung & muß mich irgendwie fügen.       Lieber hundert mal von frischem anfangen, als sich im [v|V]erfolg eines Gedankens ermüden!    Und ich muß jetzt fortwährend frisch anfangen, denn ich kann, was ich schreibe, kaum ˇgar nicht ruhig festhalten & nicht lebendig fortsetzen. – Nur die Gedanken nicht vor Erschöp[u|f]ung verenden sterben lassen!    Es ist hart, zu denken, daß es mit meinem Arbeiten wieder zu Ende gehen sollte, daß der Atem der Ideen Gedanken schon ˇwieder zu ende sein soll. Ist es aber so, so muß man es hinnehmen.

​

30.8.    Worin besteht die Übereinstimmung der Menschen bezüglich der Anerken- nung einer Struktur als Beweises?   Darin, daß ˇsie Worte als Sprache gebrauchen? ⌊ Als das, was wir “Sprache” nennen. ⌋        Denke Dir Menschen, die Geld im Verkehr gebrauchten, nämlich Münzen, die ganz so aussehen, wie unsre Münzen, aus Gold oder Silber & geprägt, & sie geben sie es auch für Waaren her – aber anderseits gibt jeder was ihm gerade gefällt & dieer Kaufleutemann dem Kunden nicht nach dem er bezahlt, kurz, was ˇso aussieht wie Geld ˇ // dies Geld oder // diese Münzen, oder was so aussieht wie Münzen, spielt bei ihnen eine ganz andere Rolle ˇals bei uns. Wir würden uns diesen Leuten viel weniger verwandt fühlen, als solchen, die zwar ˇnoch kein Geld kennen & irgend eine primitive Art des Tauschhandels trieben. – “Aber die ‘Münzen’ dieser Leute werden doch auch irgend einen Zweck haben!” – Hat denn alles, was Menschen tun man tut , einen Zweck? Etwa religiöse Handlungen –.

​

Es ist schon möglich, daß wir geneigt wären, Menschen, die sich so benehmen wahnsin vVerrückt⌊e⌋ verruckt zu nennen. Und Aber doch nennen wir nicht Alle alle die Verrückte, die in den Formen unserer Kultur in unseren Kulturen ähnlich handeln, & ˇauch Worte ‘zwecklos’ verwenden.

​

Wir können es einen Beweis der für die ⌊’die⌋ Gleichung“⌊:⌋ 274 + 181 + 693 = 1148 ⌊beweisen’⌋ nennen, wenn wir addieren   274   181   693 1148;         Vielleicht besser noch: 10⁶ × 10⁷ = 1013 (Ƒ) aber heißt auch das ein Beweis sie beweisen : nimm 274 Sandkörner, gib dazu 181 & dann noch 693 Sandkörner & zähle dann den Haufen?       Ich will sagen: Zum Beweis gehört Übersichtlichkeit.

​

Würde der Prozess durch den ich das Resultat gewinne⌊⌇⌋ unübersehbar⌊⌇⌋, so könnte ich zwar die Tatsache, daß diese Zahl herauskommt vermerken, aber ich wüßte nicht, zur Bestätigung welcher Tatsache ich dies Resultat verwenden sollte, denn ich könnte nicht sagen: ‘was hera⌊u⌋skommen soll’.

​

Habe ich jene drei Zahlen addiert & 1148 gefunden erhalten , so sage ich nun: Wenn Du so viel & so viel & so viel Sandkörner hast & ˇzusammenschüttest sie zusammen & kein⌊e⌋s keins keines kommt ˇdabei weg, so mußt Du im ganzen 1148 Körner habe.

​

Aber ist es denn unmöglich, daß ich mich in der Rechnung geirrt habe? Und denk Dir, ich nehme an, daß mich ein Teufelchen irrt, so daß ich irgend etwas übersehe immer wieder übersehe, so oft & langsam bedächtig ich auch ˇSchritt für Schritt nachrechne. Sodaß, wenn ich aus der Verzauberung // Behexung // erwachte, ich mir e⌊t⌋wa sagen müßte würde : “ja war ich denn blind!” [‒ ‒ ‒| ] Unterschied macht es, wenn ich das ‘annehme’? Ich könnte dann sagen: ”Ja, ja, die Rechnung ist gewiss falsch – –; aber so rechne ich. Und das nenne ich nun addieren & diese Zahl die Summe dieser drei.”

​

Denke Dir, jemand würde ˇso behext, so daß er rechnete: “         also: (4 × 3) + 2 = 10”   Nun soll er seine Rechnung anwenden. Er nimmt viermal 3 Nüsse & noch 2 Nüsse & verteilt sie unter 10 Leute; & jeder erhält eine [n|N]uß: Er teilt sie nämlich, den Bögen in der Rech⌊n⌋ung Figur entsprechend, aus & wenn er dem 3ten, 5ten, 7ten, 9ten die zweite Nuß gibt, verschmilzt sie mit der ersten zu einer.

​

Man könnte auch sagen: Du schreitest gehst in dem Beweis von Satz zu Satz: aber laßt Du Dir denn auch eine Kontrolle dafür gefallen, daß Du richtig gegangen bist? – Oder sagst Du bloß, “Es muß stimmen” und mißt ⌊(⌋nur⌊)⌋ alles andre nach Deinem Satz? // mit dem Satz, den Du erhälst? //

​

Denn, wenn es so ist, dann schreitest Du nur von Bild zu Bild

​

Es könnte praktisch sein, mit einem Maßstab zu messen, der die Eigenschaft hat sich unter gewissen Umstanden um ein Zehntel seiner Länge zusammenzuziehen ; , – was ihn aber, unter andern Verhältnissen zum Maßstab untauglich machen würde.        Es könnte praktisch sein, wenn wir beim Abzählen einer Menge unter gewissen Umständen vergäßen, daß nach “7” “8” kommt und ein zählten “7”, 9, 10”.

​

Wovon überzeuge ich Einen, der jene Abbildung im Film des Versuchs mit den 100 Kugeln verfolgt?     Man könnte natürlich sagen: davon, daß sich dies so zugetragen hat. – Aber das wäre keine [m|M]athematische Überzeugung. ‒ ‒ Aber kann ich den[m|n] nicht sagen: ich präge ihm einen Vorgang ein? Dieser Vorgang ist die Umgruppierung einer Reihe von 100 Dingen in 10 Reihen zu 10. Und dieser Vorgang ist tatsächlich immer wieder leicht durchzuführen. Und davon kann er mit Recht überzeugt sein.       Und so prägt auch der Beweis 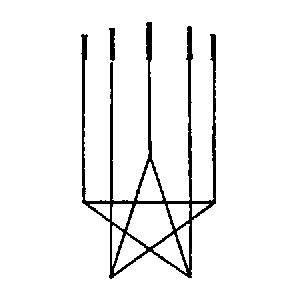durch [z|Z]iehen der Projektionslinien einen Vorgang ein, den der 1 → 1 Zuordnung der H. & des D.. – Aber überzeugt er mich nicht auch davon, daß diese Zuordnung möglich ist? – Wenn das heißen soll, dDaß Du sie immer ausführen kannst, so muß da[ß|s] durchaus nicht wahr sein. Aber er überzeugt mich, daß in dieser Figur oben soviele Striche sind, wie unten Ecken; & er ist eine Vorlage, um danach eine H. & einen D. 1 → 1 zuzuordnen. – “Aber zeigt er dadurch nicht, daß es geht?” – Doch höchstens, daß es hier gegangen ist! – “Aber er zeigt doch, daß es geht, in dem Sinne, in welchem es nicht ginge, wenn oben statt | | | | | stünde | | | | | |.” Wieso; geht es denn da nicht? S    So z.B.: “Ja so hab ich's ja nicht gemeint!” – Dann zeig mir, wie Du's meinst, & ich werde es machen.    “Aber kann ich denn nicht sagen, die Figur zeige, wie eine solche Zuordnung möglich ist sei – & muß sie darum also nicht auch zeigen, daß sie möglich ist?” –

​

31.8.       Was war denn damals der Sinn davon, daß wir ˇvorschlugen den Formen | | | | | , ˇder 5 parallelen Striche, des Fünfecksterns und andern Namen beiˇzulegten? Was ist denn damit geschehen, daß man ihnen Namen gegeben hat? // , daß sie Namen gekriegt haben? // Es wird dadurch wohl etwas über den Gebrauch eine Art des Gebrauchs dieser Figuren angedeutet. Und zwar wohl da[ß|s], daß man sie auf einen Blick ˇals die & die erkennt; man denkt nicht dran ihre Striche ˇoder Ecken zu zählen, etc., sondern erkennt sie als Gestalttypen, wie man Messer, ⌊&⌋ Gabel, Löffel ¤↻erkennt & die Form Buchstaben & Ziffern ¤. // , sondern sie sind für uns Gestalttypen, wie Messer,& Gabel⌊,⌋, Löffel, ˇwie die Buchstaben & Ziffern. //       Ich kann also auf den Befehl “[z|Z]eichne eine H!” ˇ(z.B.) diese Form unmittelbar hin reproduzieren wiedergeben ⌊(⌋& das Gleiche mit der Form D.). – Nun lehrt mich der Beweis die Figur ( ), wie ich die beiden einander ˇ1 → 1 zuordnen kann. (Ich möchte sagen, es seien sind in dem Beweis nicht einfach diese individuellen Striche, etc. zugeordnet, sondern die Formen selbst. Aber das heißt doch nur, daß ich mir jene Formen gut als Paradigmen einpräge.;) als Paradigmen einpräge.) Kann ich nun, wenn ich die Formen H. & D. einander so zuordnen will, nicht in Schwierigkeiten geraten, so daß etwa eine Ecke unten zu viel, oder oben ein Strich zu viel ist? – “Aber doch nicht, wenn Du wirklich wieder H. & D. hingezeichnet hast!” Und das läßt sich ja beweisen – ; sieh diese Figur an:” –

​

Diese Figur lehrt mich eine neue Art der Kontrolle, daß ich wirklich die gleichen Figuren hingezeichnet habe hatte ; aber kann ich, wenn ich mich nun nach dieser Vorlage richten will, nicht trotzdem in Schwierigkeiten geraten? Ich sage aber, ich bin sicher, daß ich normalerweise in keine Schwierigkeiten kommen werde.         Was

​

Was tut nun diese Überlegung? –

​

1.9.﹖    “Dieser Beweis zeigt mir, daß diese Figur, die ich so gut kenne & diese Figur, die ich so gut kenne, so mit einander verbunden werden können.” ‒ ‒

​

“Ich habe nicht gewußt, daß man und so   zusammenlegen kann.”                 Kann man auch sagen: “Ich habe ich habe gedacht, man könne sie nicht so zusammenlegen”?

​

Aber man kann sagen: ich habe gedacht, man könne sie nicht Seite an Seite (oder: ‘gut passend’) zusammenlegen. Ich kann mir z.B. denken daß Einer dreht & dreht & auf diese Stellung nicht verfällt.

​

“Ich habe nicht gedacht, daß man sie so zusammenlegen kann: Wenn mich jemand gefragt hätte, ⌊:⌋ “kann man sie passend zusammenlegen”, hätte ich “nein“ geantwortet.: “nein.“: Ich habe versucht sie ˇpassend zusammenzulegen & es nach einigem Probieren aufgegeben. (Geduldspiele)

​

Was findet der, der das Geduldspiel zusammenbringt?         Er findet: eine Lage – an welche er früher nicht gedacht hat. – Gut; aber kann man also nicht sagen: er überzeugt sich davon, daß man ein Dreieck & ein Sechseck so zusammenlegen kann? – Aber sag mir: – dieses Dreieck & das Sechseck, welche man so zusammenlegen kann: sollen sie schon, so ineinander liegen oder noch nicht, & erst so zusammengelegt werden?

​

Wer sagt: “Ich hätte nicht geglaubt, daß man diese Figuren so zusammensetzen kann”, dem kann man doch nicht, auf das zusammengesetzte Geduldspiel zeigend, sagen: “So, Du hast nicht geglaubt, daß man die Stücke so zusammensetzen kann?” – Er würde antworten: “Ich meinte: ich habe an diese Art der Zusammensetzung gar nicht gedacht⌊.⌋“.

​

Denken wir uns die physikalischen Eigenschaften der Teile des Geduldspiels so, daß sie in die gesuchte Lage nicht kommen können. Ich meine aber nicht, daß man einen Widerstand empfindet, wenn man sie in diese Lage bringen will, sondern man macht einfach alle Versuche, nur den nicht & sie die Stücke kommen auch du⌊r⌋ch Zufall nicht nie in diese Lage. Es ist gleichsam diese Lage aus dem Raum der Geometrie ausgeschlossen. Als wäre hier Sozusagen ein B “blinder Fleck” in unserm Gehirn. – Und ist es denn nicht so, wenn ich glaube, alle möglichen Stellungen versucht zu haben & an dieser, wie durch Verhexung, immer vorbeigegangen bin.

​

Kann man nicht sagen: die Figur, die Dir uns die Lösung zeigt beseitigt eine Blindheit; oder auch, sie ändert Deine Geometrie. Sie zeigt Dir gleichsam eine neue Dimension des Raumes. (Wie wenn man einer Fliege den Weg aus dem Fliegenglas zeigte.)

​

Irgend ˇEin eEin Wesen hat diese Stellung Lage mit einem Bann umzogen belegt & aus unserm Raum ausgeschlossen.

​

Die neue Lage ist wie aus dem Nichts entstanden. Dort wo früher nNichts war, dort ist jetzt auf einmal etwas.

​

Inwiefern hat Dich denn die Lösung davon überzeugt, daß man … kann? – Du konntest es ja früher nicht, ⌊–⌋ & jetzt kannst Du es etwa. –

​

Es ist ˇfür mich wichtig beim Philosophieren immer smeine Lage zu verändern, nicht zu lange auf einem Bein zu stehen, um nicht steif zu werden.   Wie, wer ˇlange bergauf geht, ein Stückchen rückwärts geht, um sich zu erfrischen[.|,] andre Muskeln anzuspannen.

∫

Es ist eben mehrdeutig, wenn man sagt: “Ich glaube nicht, daß man diese Stücke so zusammensetzen kann.”.

∫

Einfacher Beweis[;| ,] indem man die fünf Finger der Hand erst auseinanderstreckt, dann zu krumm zusammenkrümmt & mit den fünf Fingespitzen ein ˇregelmäßiges Fünfeck bildet. // daß die fünf Fingespitzen im Fünfeck stehen. //

∫

“Ja, Du hast mich überzeugt, daß man es machen kann.”

​

2.9.   Ich bin eine Memme, das merke ich immer wieder, bei jedem Anlaß.

f ? /

Du hast mir einen Weg gezeigt den ich bisher nicht gesehen hatte. – Aber war dieser Weg nicht immer schon im Raum? – Das heißt nichts. Der Weg, von dem ich rede, ist ein materieller Weg, – der mir nun als Vorlage dient. – Aber Du hast doch früher geglaubt, daß es diesen Weg nicht gibt! – Das heißt: ich bin war nicht im Stande gewesen, mir diesen den Weg vorzustellen. – Aber Du hast also versucht Dir ihn vorzustellen – wie hast Du das gemacht? – Ich habe verschiedenes getan, was man in diesem Fall “versuchen …” nennt. Was tue ich denn, wenn ich versuche, das Geduldspiel richtig zusammenzustellen & es nicht treffe? Nun ich mache verschiedene Zusammenstellungen dieser Figuren. Ist an diesen Zusammenstellungen etwas falsch? – Ich bin unbefriedigt, ich zerstöre sie wieder; ich sage auch: das muß herauskommen & zeige dabei auf den Umriss der fertigen Figur. – Wenn es mir gelingt diesen Umriss zu treffen, so bin ich befriedigt, sage, es sei mir gelungen. – Nein, das ist nicht genug: ich bin befriedigt, wenn es mir gelingt, dies, diese Zusammenstellung dieser Figuren, zu legen. Das heißt also: ⌊–⌋ wenn ich sie lege.

f /

Worauf mache ich aufmerksam? – Darauf, daß der Wunsch ˇdie Figur zu legen in diesem Falle anders aussieht, als, in dem Falle, in welchem ich wünsche, diese Zusammenstellung, auf welche ich zeigen kann, zu legen. Der Wunsch sieht anders aus, das Versuchen Probieren sieht anders aus, aber die Lösung sieht in beiden Fällen gleich aus.

f /

Und der mich ‘überzeugt hat, daß man es machen kann’, hat mir i[n|m] einen Fall eine Vorlage gegeben: & das heißt hier: ‘mich in Stand setzen, es zu machen’. Im andern Fall hätte er mir etwa gezeigt, daß er die Kraft hat etwas zu tun, wozu ich nicht die Kraft habe.

∫

“Ja, Du hast mich überzeugt, daß die H & der D gleichzahlig sind.” – Wie hat er mich überzeugt? Er hat mir ein Bild gezeigt, da[ß|s] ich bis dahin nicht gesehen hatte. – Ja, aber er hat Dich dadurch von der Möglichkeit dieses Bildes überzeugt, an welche Du früher nicht geglaubt hattest. – Aber hier muß man sich darüber klar werden, worin es bestand : , ‘nicht an diese Möglichkeit zu glauben’. Ich hatte etwa ‘versucht’ sie zu sehen (siehe oben), aber sie nicht gesehen. Und das heißt doch: ich hatte das Bild nicht gesehen.        Besser wäre es gewesen zu sagen: er hatte mir eine Möglichkeit gezeigt, die ich nicht gekannt hatte. – Aber warum bin ich hier geneigt, zu sagen, er hat habe mir eine Möglichkeit gezeigt, & nicht einfach ‘ein Bild’? Denn ich könnte ja immer, wenn man mir ˇirgend ein Bild zeigt, das ich noch bisher nicht gesehen hatte, sagen: Ja, Du hast mir gezeigt, daß dies möglich ist. Und doch fiele das niemandem ein. – Obwohl das auch einfach die Formel sein könnte, mit der man ausdrückt, man habe das bisher noch noch nicht gesehen.    Nun, die Möglichkeit ist doch wohl eine, die früher beschrieben wurde: z.B., “die Figuren 1 → 1 zuzuordnen”. Und diese Aufgabe ist von der Art der des Geduld- spiels. Frage Dich: in welchem Verhältnis steht die Aufgabestellung zur Lösung. Ja, man kann wohl sagen: die Aufgabe ‘beschreibt’ die Lösung. Verschiedene Anwendungen des Wortes “beschreiben”.

∫

“Ich weiß nun, daß eine H. immer gleichzahlig einem D. ist ˇ& dieser Beweis überzeugt mich davon.” – Warum soll ich das nicht sagen? Aber könnte man nicht, ohne den Sprachgebrauch zu vergewaltigen, statt dieser Worte, & in gleicher Weise, die gebrauchen: “Eine H. & ein D. werden mir nun immer als gleichzahlig gelten & der Beweis wird mir als Vorlage dienen um die Figuren nötigenfalls ˇeinander zuzuordnen, oder ˇauch zu prüfen, ob ich hier wirklich eine H & einen D. vor mir habe. ist.”

∫ / ?

Renne Kämpfe nicht gegen den Ausdruck Ausdrücke . Das ist, gegen Windmühlen kämpfen. Son- dern prüfe seine die Verwendungen ˇdes Ausdrucks & vergleiche sie mit einander.

/ /

Es schien zuerst, als sollten diese Überlegungen zeigen, … Diese Überlegungen schienen zuerst zeigen zu sollen, daß ‘was ein logischer Zwang zu sein scheint, in Wirklichkeit nur ein psychologischer ist’ – und da fragte es sich doch: kenne ich also beide Arten des Zwanges?! –         Denke Dir, es würde der Ausdruck gebraucht: “Das Gesetz ⌊§ …⌋ bestraft den Mörder mit dem Tode”. Das könnte doch nur heißen[;|,] das dieses jenes Gesetz laute: u.s.w.. Diese Jene Form des Ausdrucks ⌊(⌋aber⌊)⌋ könnte sich uns aufdrängen, weil das Gesetz es ⌊(⌋ein⌊)⌋ Mittel ist // als Mittel fungiert // wenn der Schuldige der seiner Bestrafung Strafe zugeführt wird. – Nun reden wir von der von ’Unerbittlichkeit’ derer, bei denen, die jemand bestrafen. Da könnte es uns einfallen, von der ‘Unerbitt- lichkeit des Gesetzes’ zu sprechen. zu sagen : , das Gesetz ist unerbittlicher als alle Menschen, denn sie können den Schuldigen laufen lassen, das Gesetz aber richtet ihn hin. // das Gesetz ist absolut unerbittlich: ˇdie Menschen können den Schuldigen laufen lassen, … // ([J|j]a man könnte sogar sagen: das Menschen “das Gesetz richtet ihn immer hin”.). – Wozu ist so eine Ausdrucksform zu gebrauchen? – Zunächst sagt dieser Satz sie ja nur, das im Gesetz sage stehe das & das, & Menschen richten sich manchmal nicht danach. Dann aber zeigt sie ⌊er⌋ uns doch das Bild des einen unerbittlichen ˇRichters, & vieler laxer Richter. Er dient darum als ist also ein Ausdruck des Respekts vor dem Gesetz. Endlich aber kann man denie Ausdruck⌊s⌋ˇform auch so gebrauchen, indem daß man ein Gesetz ‘unerbittlich’ nennt, wenn es nicht die Möglichkeit der Begnadigung & etwa ‘milde’ im andern entgegengesetzten Fall.         Aber wir reden ja auch von der [u|U]nerbittlichkeit der Logik& ⌊.⌋ ˇUnd wir denken uns die logischen Gesetze unerbittlicher, als ⌊(⌋die⌊)⌋ Naturgesetze. Wir ⌊(⌋aber⌊)⌋ machen nun drauf aufmerksam, daß das Wort “unerbittlich” ⌊(⌋hier⌊)⌋ auf mehrerlei zweierlei Weise angewendet werden kan wird. Einerseits entsprechen unsern logischen Gesetzen sehr besonders unerbittliche d.h. allgemein bestätigte, Naturgesetze Erfahrungsgesetzesätze, welche es welches was es ˇuns möglich macht diese Gesetze immer wieder auf sehr einfache Weise zu demonstrieren (“von selbst kommt nichts weg” usw.). [d|D]as legt den Gebrauch ˇgerade dieser Schlußregelngesetze nahe, & nun deshalb sind wir unerbittlich in der ˇgleichförmigen Anwendung dieser Gesetze; weil wir ‘messen’ ⌊(⌋& es gehört zum Messen, daß [a|A]lle das gleiche Maaß haben). Nu[m|n] kann man aber außerdem noch unerbittliche⌊,⌋ ˇd.h. eindeutige⌊,⌋ von nicht eindeutigen Schlußgesetzen unerbittlichen Gesetzen unterscheiden, sol diese sind etwa Schlußgesetze nach welchen auf eine Alternative geschlossen wird. dc.i. von solchen, die eine Alternative freistellen.

/ /

Ich sagte, ‘ich lasse mir das & das als Beweis dieses Satzes gefallen’ – aber kann ich mir die Figur, die die Stücke meines Geduldspiels zusammengesetztfügt zeigt, nicht als Beweis dafür gefallen lassen, daß man jene Stücke zu diesem Umriss zusammensetzen kann?

/ /

Aber denk Dir eines seiner Stücke liege so, daß sein Umriss das Spiegelbild des entsprechenden Umrisses in der Vorlage ist. Er versucht nun die Figur nach der Vorlage (dem Beweis) zusammenzusetzen, denkt aber nicht daran jenes das Stück umzudrehen & er findet sieht , daß es ihm nicht gelingt das Zusammensetzen nicht gelingt.

​

3.9.        Wie schätzt man, wie viel Uhr es ist, ich meine ohne sich nach äußeren AnzZeichen zu richten, wo die Sonne steht, wie hell es im Zimmer ist, etc. ich meine aber nicht nach außeren Anhaltspunkten wie der Stand der Sonne die Helligkeit im Zimmer u. dergl.? – Man fragt sich: “wie viel Uhr kann es sein?”, überlegt einen Augenblick; d.h. hier: man hält sich still ruhig , stellt sich etwa das Zifferblatt der Uhr vor; & endlich dann sagt man mit einer gewissen Sicherheit Ruhe, ich meine, ohne Zweifel , die & die eine Zeit. – Oder man überlegt sich verschiedene ein paar Möglichkeiten: d.h., man denkt sagt sich zur Probe eine Zeit, dann eine andere & endlich bleibt man bei einer zwischen ˇden beiden stehen. So & ähnlich geht es vorsich. – Aber ist nicht das Einfallen der Zeit von einem Gefühl der Überzeugung begleitet? & heißt das nicht, daß der Einfall mit einer inneren Uhr übereinstimmt? – Nein, ich lese den Ein die Zeit von keiner ‘inneren Uhr’ ab; & ein Gefühl der Übe⌊r⌋zeugung ist in so fern da, als ich mir ohne Zweifels ˇeine Empfindung des sage “es ist … Uhr”. – Aber schnappt also nicht doch etwas bei dieser Zeitangabe ein? – Nichts, das ich wüßte, außer wenn Du die Beruhigung, das Stehenbleiben auf einer Zahl so nennst. Offen gestanden, ich hätte hier nie von einem ‘Gefühl der Überzeugung’ geredet, sondern etwa gesagt: ich habe eine Weile überlegt & mich dann dafür entschieden, daß es … Uhr ist. Und Wonach aber hab ich mich entschie- den? Ich hätte gesagt: bloß ‘nach dem Gefühl’. Das heißt aber nur: [m|M]ein Einfall ist, etwa nach einigem Schwanken, bei dieser Zeitangabe stehengeblieben. – Aber Du mußtest Dich doch wenigstens in einen bestimmten Zustand versetzen; & Du würdest doch nimmst doch nicht jede Vorstellung irgend einer Zeitangabe, als Angabe der gegenwärtigen Stunde! – Wie gesagt: ich hatte mich gefragt “wie viel Uhr mag es sein?”, d.h. ich habe diese Worte nicht⌊,⌋ ˇz.B.⌊,⌋ in einem Buch gelesen, noch sie als Ausspruch eines Andern zitiert, noch mich im Aussprechen dieser Wörter geübt, u.s.f., nicht unter diesen Umständen habe ich die Worte gesagt. Fragst Du aber: “unter welchen also?” – Nun ich stand da & da, dachte an mein Frühstück, & ob es schon heute spät würde. Solcherlei waren die Umstände. Und nur dies kann ich über den ‘Zustand’ aussagen, in welchen ich mich zur bei der Schätzung der Zeit versetzen mußte. – Aber siehst Du denn wirklich nicht, daß Du ˇDich doch in einem, wenn auch quasi ungreifbaren, für das Schä⌊t⌋zen der Zeit charakteristischen Zustand, gleichsam in einer spezifischen bestimmten Atmosphäre warst? – Ja, das spezifische war, das ich mich fragte: “[w|W]ie viel Uhr mag es sein?”, ⌊–⌋ & hat dieser Satz eine bestimmte Atmosphäre, wie soll ich sie von ihm selbst trennen können? – Auch wäre es mir nie eingefallen, zu denken, dieser Satz hatte einen solchen Dunstkreis eine solche Atmosphäre , wenn ich nicht dran gedacht hätte⌊,⌋ // wenn mir nicht eingefallen wäre, // wie man ihn auch anders – als Zitat, im Scherz, als Sprechübung zur Übung , etc. etc. – sagen kann. Und da wollte ich auf einmal sagen, da erschien es mir auf einmal, ⌊:⌋ ich mußte als ich den Satz dies⌊e⌋ Wort⌊e⌋ als richtige Frage meinte, sie doch irgendwie besonders gemeint haben, eben anders, als in jenen andern Fällen. Und wollte ich ⌊(⌋nun⌊)⌋ näher hinschauen, um zu sehen, wie denn, ⌊ –⌋ so konnte ich wieder nichts ⌊(⌋besondres⌊)⌋ entdecken. Es hatte sich mir das Bild von ‘der besonderen Atmosphäre’ aufgedrängt; ich sehe sie förmlich vor mir, solange ich nämlich nicht auf das sehe was meiner Erinnerung nach wirklich geschehen gewesen ist, sondern mir etwa sage: “[i|I]ch habe doch die Zeit geschätzt.”       Und was das Gefühl der Überzeugung, oder vielleicht besser, der Sicherheit, anbelangt : , so sage ich mir manchmal: “ich bin sicher, es ist … Uhr”, & in mehr oder weniger sicherem Tonfall, etc. Wenn Du mich nach dem Grund für diese Sicherheit fragst, so habe ich keinen. Wenn ich sage: ich lese es auf meiner inneren Uhr ab, so ist das ein Bild, dem doch wieder nur entspricht, daß ich diese Zeitangabe gemacht habe. Und der Zweck des Bildes ist diesen den Fall dem ˇandern anzugleichen[,|.]◇◇◇ Ich weiger streube mich die beiden verschiedenen Fälle anzuerkennen.

/ /

Man kann ein Rechteck aus zwei Parallelogrammen & zwei Dreiecken zusammensetzen. Beweis:        Ein Kind würde die Zusammensetzung [des| ein⌊es⌋] Rechtecks aus diesen Bestandteilen schwer treffen & davon überrascht sein, daß zwei [s|S]eiten der Parallelogramme in eine grade Linie fallen, wo doch die Parallelogramme schief sind. ⌊–⌋ Es könnte ihm vorkommen, daß das Rechteck gleichsam wie durch Zauberei aus diesen Figuren wird. Ja, es muß zugeben, daß sie nun ein Rechteck bilden, aber durch einen Trick, durch eine vertrackte Stellung, nicht auf naturliche in natürlicher [w|W]eise.           Ich kann mir denken, daß das Kind, wenn es ˇdurch Zufall die beiden Parallelogramme in der Weise zusammengelegt hat, seinen Augen nicht traut, wenn es sieht, daß sie so zusammenpassen. ‘Sie sehen nicht aus, als ob sie so zusammenpaßten⌊.⌋’. Und ich könnte mir denken, daß man sagt: Es erscheint scheint nur durch ein Blendwerk, als gäben sie das Rechteck, – in [w|W]irklichkeit haben sie ihre Natur verändert, sie sind nicht mehr die Parallelogramme, die wir hatten ich hatte . // , sie sind nicht mehr die Parallelogramme. //

/ /

Aber kann ich den Satz der Geometrie nicht auch ohne Beweis glauben, z.B. auf die Versicherung eines Andern hinnehmen? – Und was verliert der Satz, wenn er seinen Beweis verliert? –     Ich soll hier wohl fragen: “Was kann ich mit ihm machen?”, denn darauf kommt es an. Den Satz auf die Versicherung des Andern annehmen, – wie zeigt sich das? Ich kann ihn z.B. in weiteren Operationen verwenden, oder ihn bei der Beurteilung eines physikalischen Sachverhalts verwenden. Versichert mich jemand z.B., 13 mal 13 wäre sei 396 ˇ& ich glaube es, so werde ich mich nun wundern, daß bei einer Verteilung von 396 Nüssen unter 13 Kinder jedes 15 kriegt & noch eine Nuß übrig übrig bleibt überbleibt & etwa annehmen die Nüsse hätten sich von selbst vermehrt.           Oder soll ich sagen: man könne nicht glauben, daß 13 × 13 396 ist, man könne diese Zahl nur mechanisch vom Andern annehmen? Aber warum soll ich nicht sagen, ich glaubte es? Es Dies glauben, ist ja kein geheimnisvoller Akt, der sozusagen unterirdisch mit der richtigen Rechnung in Verbindung wäre ist . Ich kann doch jedenfalls sagen: “ich glaube es”, & nun danach handeln.             Man möchte hier fragen: “Was tut der, der glaubt⌊,⌋ ˇdaß 13 × 13 396 ist?” Und man kann antworten: Nun, das wird davon abhängen : , ob er z.B. die Rechnung selber gemacht & sich dabei verschrieben hat, ⌊–⌋ oder ob sie ein Andrer für ihn gemacht hat, er aber ˇdoch weiß, wie man so eine Rechnung macht – oder ob er nicht multiplizieren kann, aber weiß, daß man das Resultat erhält, wenn man 13 Reihen zu je 13 Punkten macht & sie dann alle zählt , – u.s.f..

/ /

Denkt man nämlich an die arithmetische Gleichung als den Ausdruck einer internen Relation, so möchte man sagen: “Er kann ja gar nicht glauben, daß 13 × 13 dies ergibt, weil das ja keine Multiplikation, oder kein ‘Ergeben’ ist, wenn 396 am Ende steht. herauskommkommt. ” Das heißt aber nur, daß man das Wort “glauben” für den Fall einer Rechnung & ihres Resultats nicht anwenden will, – oder nur dann, wenn man die richtige Rechnung vor sich hat.

/ / / /

“Was glaubt der, der glaubt, 13 × 13 ist 396?” – Wie tief dringt er – könnte man sagen – mit seinem Glauben in das Verhältnis dieser Zahlen ein? Denn bis zum Ende – will man sagen – kann er nicht dringen, sonst könnte er es das nicht glauben.        Aber wann dringt er in die Verhältnisse der Zahlen ein? Gerade während Während er sagt, daß er glaubt …? Darauf wirst Du nicht bestehen, ⌊–⌋ denn es ist leicht zu sehen daß dieser Schein nur durch die Oberflächenform Oberfläche unsrer Grammatik – wie man es nennen könnte – erwecktzeugt wird.         Denn ich will sagen: “Man kann nur sehen, daß 13 × 13 369 ist, & man kann auch das nicht glauben’. Man kann nur ˇnoch, mehr oder weniger blindlings, eine Regel annehmen.” Und was tue ich, wenn ich dies sage? Ich mache einen Schnitt ; – zwischen Rechnung ⌊(⌋d.i. einem bestimmten Bild, einer bestimmten Vorlage⌊)⌋ & ihrem dem Resultat ˇeiner der Rechnung einerseits & dem Vorgang ˇ& Resultat eines Experiments Versuchs anderseits. // & einem Versuch & seinem Ergebnis anderseits.

​

Jener Satz über die Zusammensetzbarkeit des Rechtecks aus den Parallelogrammen & Dreiecken ist ja ganz ähnlich einem Ar arithmetischen, wie etwa: 3 + 3 + 2 + 2 = = 10 // 3 + 4 = 7. //

​

4.9. Etwas verkühlt & denkunfähig. Grausliches Wetter. –    Das Christentum ist keine Lehre, ich meine, keine Theorie darüber, was mit der Seele des Menschen gesche- hen ist & geschehen wird, sondern eine Beschreibung eines tatsächlichen Vorgangs im Leben des Menschen. Denn die ‘Erkenntnis der Sünde’ ist ein tatsächlicher Vorgang & die Verzweiflung desgleichen & die Erlösung durch den Glauben desgleichen. Die, die davon sagen, ˇ⌊(⌋wie Bunyan⌊)⌋⌊,⌋ beschreiben einfach, was ihnen geschehen ist; was immer einer dazu sagen will!

? ∫ / / /

5.9.    “Du gibst das zu – dann mußt Du das zugeben.” – Er muß es zugeben – & dabei ist es möglich, daß er es nicht zugibt. Oder willst Du sagen: “er kann es sagen, daß er es nicht zugibt, aber er kann es nicht denken”. Nimmst Du hier da nicht einen okulten Vorgang des Denkens an? Oder es heißt, daß ein solcher Gebrauch der Worte kein Denken ist.           “Ich werde Dir zeigen, warum Du es zugeben mußt. ⌊–⌋” Ich werde Dir einen Fall vor Augen führen, welcher, wen[m|n] Du ihn bedenkst, Dich bestimmen wird, so zu urteilen.

/

Wie können kann ihn denn die Manipulationen Manipulation des Beweises dazu bringen, daß er etwas zuzugeben?

/ /

“Du wirst doch zugeben, daß 5 aus 3 + 2 besteht!” Ich will es nur zugeben, wenn ich damit nichts zugebe. Außer, – ⌊–⌋ daß ich dieses Bild verwenden will.

/ /

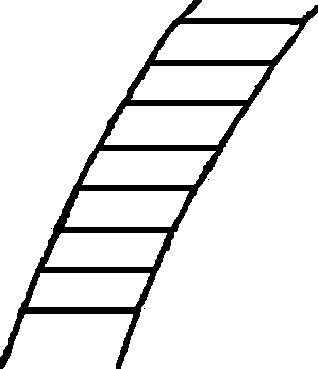Man könnte z.B. die Figur als Beweis dafür nehmen, daß 100 Parallelogramme, so zusammengesetzt einen geraden Streifen ein Parallelogramm geben müssen. Wenn man dann wirklich 100 zusammenfügt erhält man nun etwa einen gebogenen Streifen. – Jener Beweis hat uns bestimmt, das Bild & die Ausdrucksweise zu gebrauchen: Wenn sie keinen geraden Streifen geben, waren sind sie ungenau hergestellt.

/ /

Denke nur, wie kann micht das Bild, das Du mir zeigst (oder diese die Tatsache) dazu verpflichten, nun so & so ˇimmer zu urteilen!    Ja, liegt hier ein Experiment vor, so ist eines ja doch zu wenig, mich zu irgend einem Urteil zu verbinden.

/ /

Der Beweisende sagt: “[s|S]chau diese Figur an. – [w|W]as wollen wir dazu sagen? – Nicht, daß …? –” // Nicht, daß ein Rechteck aus … besteht? –” //

/ /

Oder auch: “Das nennst Du doch zwei gleiche ‘Parallelogramme’ & das ‘Dreiecke’ & so sieht es doch aus wenn eine Figur aus andern zusammengesetzt ist // besteht // . –”

/ /

Ja, Du hast mich überzeugt: ein Rechteck besteht immer aus ….” – Würde ich auch sagen: “Ja Du hast mich überzeugt: dies dieses Rechteck ( das des des Beweises) besteht aus …” – und dies wäre ja doch der bescheidenere Satz!; den auch der zugeben sollte, der etwa den allgemeinen Satz ˇnoch nicht zugibt. Seltsamerweise aber scheint der, der das zugibt nicht den bescheideneren geometrischen Satz zuzugeben, sondern gar keinen ge Satz der Geometrie. Freilich, – denn bezüglich des Rechtecks des Beweises hat er mich ja von nichts überzeugt. (Über diese Figur, wenn ich sie früher gesehen hätte, wäre ich ja in keinem Zweifel gewesen.) Ich habe ja, aus freien Stücken, was diese Figur anbelangt, alles zugestanden. Und er hat mich nur mittels ihrer überzeugt. – Aber anderseits, Aber wenn er micht nicht einmal bezüglich dieses Rechtecks dieser Figur von etwas überzeugt hat, wie dann erst von einer Eigenschaft andrer Rechtecke[!|?]

f

“Du hast mich überzeugt, daß jedes Rechteck alle Rechtecke aus … bestehen .” – dieser Satz ist offenbar gleichgebildet einem, nachgebildet dem, // ist offenbar analog einem konstruiert, // den man gebraucht wenn ein Gegenstand den man für ein Ganzes: “Ich dachte diese Kugeln seien aus einem Stück, Du hast mich überzeugt, daß sie aus zwei ˇsolchen Teilen bestehen // zusammengesetzt sind // .”

/ /

6.9.    Wir halten absichtlich gefließentlich an der kindischen Schwierigkeit fest.

/ ∫

Wer philosophiert, leidet unter einem Sprachkrampf Sprachkrämpfen ; & ich suche nach dem sprachlichen Übergang in die krampflosefreie Stellung.

∫

Der Krampf löst sich durch einen sprachlichen Übergang. Und dieser Übergang ist zu finden.

∫

Ich suche nach den Worten, die den Weg bilden aus der Stellung, in die ich gebannt scheine.

/ ∫

Ich suche den sprachlichen Ausweg aus dem Krampf.

/ /

Wenn ich ein Rechteck ˇals auf diese Weise zusammengefügt sehe, so vergleiche ich dies dem Fall Vorgang ⌊:⌋ daß meine Blicke in das Innere dringen meine Blicke ˇdringen in das Innere & dort diese Zusammensetzung sehen. Man kann ja auch sagen: “Ich könnte es nicht so zusammengesetzt sehen wenn es nicht so zusammengesetzt wäre.”

∫

Wie der experte Kassenschloßöffner versuche ich alle Lagen des Sperrhakens, mache hundertmal die gleiche Bewegung mit ihm und es kommt alles auf das feine Gefühl der Finger an, die die Bewegung machen. Drum hat es auch gar keinen Sinn diese Bewegung zu machen, es sei denn mit Gefühl.

/ /

“Ich habe nicht gewußt, daß die Rechtecksform aus diesen Formen besteht.”       Es ist als wäre die Form aus diesen Formen gemacht, geschweißt.

/ /

“Ich wußte nicht, daß die Form aus diesen Formen besteht.” – So hat's Dich das Bild gelehrt.         Du hast etwas Neues gesehen . – Und – & willst sagen, Du habest gesehen erkannt , daß das Alte so & so zusammengesetzt sei. ist.

/ /

Du vergleichst also Dein Erstau[h|n]en, dem: Du siehst ein Brett & rechteckiges Brett & findest, daß es auf diese seltsame Weise zusammengefügtsetzt ist.

/ /

‘ˇJa [D|d]ie Form sieht nicht so aus, als könnte sie aus zwei windschiefen Teilen bestehen.        Was überrascht Dich? Doch nicht, daß Du jetzt diese Figur vor [d|D]ir siehst! Mich überrascht etwas in dieser Figur. – Aber in dieser Figur geht ja nichts vor!       Mich überrascht die Zusammenstellung des Schiefen mit dem Graden. Mir wird – gleichsam – schwindelig. Das ist vergleichbar damit, daß mir schwindelig wird, wenn ich eine Spirale sehe.

/ ∫

‘Mich überrascht, daß die windschiefen Stücke ein Gerades geben. (Ich hätte es nicht gedacht.)’ – Ja, das ist so, als hätte ich sie zusammengesetzt. Sie haben nicht ausgesehen als würden sie zu etwas Geradem zusammenpassen, ich hatte mir etwas Winkeliges erwartet. – Aber kann ich mir denn beim Anblick der geteil ten Rechtecksfigur etwas Winkeliges erwarten?!           Eher könnte ich sagen: “Es will mir nicht recht ein, daß diese Stücke das ergeben“. Das ist aber gleichsam ein Gefühl des Schwindels

/ ∫

“Du hast mich überzeugt, daß ein Rechteck aus … besteht”. “Zusammengesetzt werden kann” könnte ich auch sagen. Und dabei Dabei schaue ich nicht auf ein Rechteck, das tatsächlich so geteilt ist, sondern auf ein [ü|u]ngeteiltes; & stelle mir Teilungslinien vor.

/ ∫

Ich sehe ein Bild & umgebe es in den Gedanken der Vorstellung hartnäckig mit einem Vorgang von welchem ich meine Ausdrucksformen hernehme. Ich habe ein geteiltes Dre Rechteck vor mir; ich gebe vor, ich habe es aus diesen Teilen zusammengesetzt & sei durch das Ergebnis überrascht. Ich gebe vor, ich sei davon überzeugt worden, man habe mich davon überzeugt, daß Teile, ⌊–⌋ die nicht so danach ausgesehen haben, ⌊–⌋ sich zu dieser Figur zusammenfügen.

∫ ∫

“Ja, Du hast mich überzeugt: zwei P. geben ein R..” Es ist wesentlich daß ich das R. als das Ergebnis davon betrachte, daß ich zwei ein P. auf eindasandere stelle.

/

⌊⌊andre Version⌋⌋  Ich sage aber doch ˇwirklich: “Ich habe mich überzeugt, daß man die diese Figur aus diesen Teilen legen kann” : , wenn ich nämlich die Zeichnung etwa die Abbildung das Bild der Lösung gesehen habe.        Wenn ich Einem das sage, so will ich doch sagen: “Versuch nur; diese Stücke richtig geschoben gelegt geben die Figur.” Ich meine, ich will doch ihm also etwas Physikalisches sagen mitteilen. Es ist wesentlich, daß die Abbildung der Lösung mich in Stand setzt, die Figur ohne weiteres zusammenzusetzen. Dazu gehört doch das Faktum, daß man die einzelnen Stücke in beliebige Lagen bringen kann, ohne daß sie, z.B., verschwinden.

∫ ∫

Wie kann mich denn ein Bild davon überzeugen, daß etwas möglich ist? Z.B. daß ich genug Steine habe diese eine Figur damit zu legen? –  Hier genügt also, scheint es, das Bild des eines Experiments, statt des Experiments!        Aber mußte ich nicht doch auch ein Experiment machen : , nämlich das des Vergleichs (welches analog ist dem einer Ausmessung)?

​

7.9. Unwetter. Sturm & Regen. Schlecht geschlafen. Wenig wohl. Bin irreligiös, aber mit Angst.

/ /

‘Du sagst, Du bist erstaunt über das, was Dir der Beweis zeigt. Aber bist Du erstaunt darüber, daß sich diese Striche haben ziehen lassen? Nein. Du bist erstaunt, nur wenn Du Dir sagst, daß zwei solche Stücke diese Form geben. Wenn Du Dich also in die Situation hineindenkst: Du habest Dir etwas anderes erwartet & nun sähest Du das Ergebnis.

​

Warum sollte mir Wind & Regen unheimlich sein?! Aber es ist mir ˇhier unheimlich; ⌊–⌋ und und das ist schlecht.”

/ /

“Aus dem folgt unerbittlich das.” Ja, in dieser Demonstration geht es aus ihm daraus hervor.    Und eine Demonstration ist dies für den, der sie als Demonstration anerkennt. Wer sie nicht anerkennt, [W|w]er ihr nicht als Demonstration folgt, der trennt sich von uns, noch ehe es zur Sprache kommt. // , der trennt sich von uns eben, ehe es zu einer zur Sprache kommt. //

​

Es ist hier, wenn es draußen stürmt nicht gemütlich, so daß man sich etwa drinnen um so gemütlicher fühlt, je, häßlicher draußen das Wetter ist. Sondern das Toben des Sturmes macht mich drinnen aufgeregt, laßt mich nicht arbeiten. Es ist, als seien die Wände zu dünn; man hat nicht das Gefühl des Schutzes & der Geborgenheit. Es ist als wäre die Schutzmauer nur dünn & könnte jederzeit durchbrochen werden. Macht das auch die Einsamkeit? Mein Gefuhl wird gewiß durch den leisen M Zug hervorgerufen, der durch die Hütte geht, & durch das Zittern der Wände, die im übrigen stark genug sind.         In dem Sturm & Unwetter war ich versucht Gott zu verfluchen, was doch nur böse & abergläubisch ist. Später war mir's gegeben zu denken: Preg' dir doch ein Sturm recht ein, dass du etwas lernst; & da wurde mir besser. – (Die Eitelkeit verläßt mich nie.)

∫

Wie kann mich denn das Bild zu etwas verpflichten?

∫ / ∫

Wir sagen z.B. wir haben gleichviel Leute hier & dort, wenn wir bei der Zählung hier ‘6’ & hier ‘6’ herausbringen. Und wenn das so ist – & man nicht sieht daß einer dazukommt oder wegkommt – so laßen sich die Mengen Gruppen auch zu normalerweise 1 → 1 räumlich zuordnen, oder wiegen ungefähr das Gleiche, u.s.f.. Man kommt selten in die Lage zu sagen: “Ich weiß nicht was geschehen ist! Habe ich beim Zählen eine Zahl ausgelassen[?|,] oder habe ich mich verschaut, oder eine Haluzination gehabt?!

∫ / ∫

8.9. “Aus diesem folgt unerbittlich das, – solange nämlich die Wörter das bedeuten.” – Aber erhalten sie nicht eben ihre Bedeutung durch diese Regel?

∫

Dieses Schema, kann als Beweis gelten, dafür, daß 3 + 4 7 ist. Aber was würde es dem zeigen, der jene Haken – die Ziffern – nicht kennte? Und worin besteht unsre Bekanntschaft mit ihnen?

∫

Wenn ich mir aber das Aussehen einer Dreier- & einer Vierergruppe einpräge, so kann der Beweis auch so aussehen:

∫

‘Wenn Du eine Dreier- & eine Vierer-Gruppe hast, so folgt unerbittlich, daß Du 7 hast.’

∫

“Ich lasse mir dies als Beweis dieses Satzes gefallen” – heißt, ich nehme es als Beweis an, nicht anders als ich die Regel selbst als Regel annehme.

∫

D.h., es ist alles ein Spiel. Wie ich zugleich dies als Maßeinheit ansehen betrachten , & so messen lehr lerne.     Oder dies als Beweis von 3 + 2 = 5

​

(Oder kinematographisch vorgeführt.)

​

Ich habe eine schwehre Zeit! Innere & äußere Störung. –

/ / /

Hier haben wir etwas, was unerbittlich ausschaut. Und doch: ‘unerbittlich’ kann es nur in seinen Folgen sein. ⌊!⌋ Denn sonst ist es nur ein Bild.                     Worin besteht denn die Fern- wirkung – wie man's nennen könnte – dieses Diagramms?

/ /

Ich habe einen Beweis gelesen – nun bin ich überzeugt. – Wie, wenn ich diese Überzeugtheit sofort vergäße!       Denn es ist ein eigentümliches Vorgehen : , daß ich den Beweis durchlaufe & dann sein Ergebnis annehme. – Ich meine: so machen wir es eben. Das ist so bei uns der Brauch& [;| ,] oder eine Tatsache unsrer Naturgeschichte.

/ / /

‘Wenn ich fünf habe, so habe ich drei, und & zwei.’ – Aber woher weiß ich, daß ich fünf habe? – Nun wenn es so | | | | |         ausschaut. –     Und ist es auch gewiss, daß, wenn es so ausschaut, ich es immer in solche Gruppen zerlegen kann?         Es ist einec Tatsache, daß wir dies Spiel spielen können: Ich lehre [e|E]inen wie eine Zweier-, Dreier-, Vierer- & Fünfergruppe aussieht[;|,] & ich lehre ihn Striche einander (etwa durch Striche) zuordnen; dann lasse ich ihn je immer je zweimal den Befehl ausführen: “zeichne eine Fünfergruppe” – & dann den Befehl: “ordne die beiden Gruppen einander zu”; und es zeigt sich, da zeigt es sich, daß er, so gut wie immer, die Striche Gruppen Restlos einander zuordnet.           Oder auch: [E|e]s ist Tatsache, daß ich bei der 1 → 1 Zuordnung dessen, was ich als Fünfergruppen hinschreibe, so gut wie nie in Schwierigkeiten komme.

/ /

Ich soll jenes das Geduldspiel zu- sammenlegen, ich versuche hin & her, bin zweifelhaft, ob ich es zustande bringen werde. Nun zeigt mir jemand das Bild der Lösung Auflösung : – – nun sage ich – ohne irgend einen Zweifel – “jetzt kann ich's!” – Ist es denn sicher, daß ich es nun zusammen bringen werde? – Aber die Tatsache ist , : ich zweifle nicht daran.              Wenn nun jemand fragte: “Worin besteht die Fernwirkung jenes Bildes⌊?⌋” – Doch in seiner Anwendung wo immer es sei.

/ / /

⌊⌊2te Version⌋⌋         Ich sagte einmal, es sei keine Erfahrungstatsache, daß die Tangente einer visuellen Kurve ein Stück mit dieser gemeinsam hätte; & wenn es diese Figur zeige, so nicht als ˇdas Resultat eines Experiments.     Man könnte auch sagen,⌊:⌋ dDu siehst hier, daß Stücke einer kontinuierlichen visuellen Kurve gerade sind. – Aber sollte ich nicht sagen: – “Das nennst Du doch eine ‘Kurve’[?| .] ⌊–⌋ Und nennst Du dieses Stückchen nun– ‘krumm’ oder ‘gerade’? – Das nennst Du doch eine ‘Gerade’, – & sie enthält dieses Stück.” Aber warum sollte man nicht für visuelle Strecken, die sowohl in einer Kurve als auch in einer Geraden liegen ˇkönnen, einen ganz andern Namen brauchen verwenden ?        “Aber das Experiment des Ziehens dieser Linien hat doch gezeigt, daß sie sich nicht in einem Punkt berühren!” – Wie sind “sie” definiert? Oder: kannst Du mir ein Bild davon zeigen, wie es ist, wenn sie sich in einem Punkt berühren? Denn warum soll ich nicht einfach sagen: das Experiment hat ergeben, daß sie – nämlich Linien einer Art, wie ich sie schon anderswo gezeichnet hatte habe – einander berühren. Denn ist dies nicht, was ich die “Berührung” solcher Linien nenne?

​

Aber wie ist es nun, wenn ich das Stück, das sie gemeinsam haben nachträglich messe? Die Länge dieses Stückes konnte ich doch nicht voraussehen! Wenn ich also messe – ungefähr – ein wie großes Stück einer bestimmten Kurve mir noch als grade erscheint _. Dies ist offenbar ein Experiment; & man könnte es sich so ausgeführt denken, daß eine Reihe paralleler Kurven gezeichnet wären, & zwar in schwarzen & weißen Stücken. Diese Stücke sind etwa in der ersten Kurve 1 mm lang, in der zweiten 2 mm, u.s.f.. Das Subject des Ex- periments geht nun diese Kurven ˇder Reihe nach durch, indem es von jeder ein sch schwarzes Stück anschaut & sagt, ob es gerade oder gekrümmt ist.     Das Ergebnis des Experiments ist nun, daß er das Stück der n-ten Kurve, der so konstruierten Reihe, als gerade & das Stück der n + 1ten als gekrümmt sieht.       Aber braucht es denn die nach dem Maß konstruierte Reihe von Kurven? Kann man nicht einfach sagen: (z.B.) ‘In einer solchen dieser Kurve sieht er ein so |––| langes Stück schon als krumm’? Und ist das nicht gerade das, was ich auch sähe, wenn ich das Bild so einer Kurve in so langen Stücken gezeichnet vor mir sähe? Oder denken zeichnen wir uns einen Kreis aus Stücken die abwechselnd lang (gekrümmt) & kurz (grade) sind! Oder aus Stücken, die nach & nach läger werden, so daß man auf das weisen kann, welches als das erste zuerst krumm erscheint. Und dies ist wieder eine offenbare Experimentfrage: “Welches dieser Stücke ⌊(⌋von rechts nach links⌊)⌋ ist das erste das [d|D]u gekrümmt siehst.

/ / /

Wie, wenn jemand sagte: “Die Erfahrung lehrt Dich, daß diese Linie krumm ist.” – Da wäre zu sagen, daß hier die Worte “diese Linie”, die auf dem Papier gezogene physikalische Linie bedeuten. Man kann ja tatsächlich den Versuch anstellen & diese Lienie verschiedenen Menschen (oder einem, aber unter verschiedenen Umständen) zu zeigen & zu fragen: “Was siehst Du; eine gerade, oder eine krumme Linie?” –       Wenn aber jemand sagte: “ich stelle mir jetzt eine krumme Linie vor” & Du wir ihm sag⌊t⌋en: “Da siehst Du also, daß diese Linie eine krumme ist”; was für einen Sinn hätte das?        Nun kann man aber doch auch sagen: Ich stelle mir einen Kreis vor aus schwarzen & weißen Stücken, – einige teils großen, &⌊,⌋ gekrümmten, teils kleinen graden. einem großen⌊,⌋ gekrümmten, , eines ist, die folgenden werden immer kleiner, das sechste ist schon gerade. Wo liegt hier das Experiment?

/ /

In der Vorstellung kann ich rechnen, aber nicht experimentieren.

? /

Die Grundlage der Mathematik ist das Rechnen.          Gib uns ein Gift, was das Rechnen unmöglich macht, & es gibt keine Mathematik mehr.

/ /

“Du siehst doch – es kann doch keinem Zweifel unterliegen– ⌊,⌋ daß eine solche Gruppe Gruppe A wie A wesent (Ƒ) lilich aus einer solchen wie B & einer solchen wie C besteht!” – Ich sage auch – d.h., ich drücke mich auch so aus – daß die ˇganze Gruppe A, die Du hingezeichnet hast aus B und C den beiden kleineren besteht; aber ich weiß nicht, ob jede Gruppe, die ich eine von der Art (oder Gestalt) der ersten ersteren nennen würde, unbedingt aus zwei Gruppen von der Art B und C der jener kleineren zusammengesetzt sein wird. –– ‒ ‒ Ich glaube aber, es wird wohl immer so sein (meine Erfahrung hat mich dies vielleicht gelehrt)[;|,] & darum will ich als Regel annehmen: Ich will eine Gruppe nur dann & nur dann eine von der Art Gestalt A nennen, wenn sie in zwei Gruppen der Arten wie B & C zerlegt werden kann.

/ /

Und so wirkt auch die Zeichnung: als Beweis “Ja bei Gott wirklich ! zwei Parallelogramme stellen sich zu dieser Form zusammen!” (Das ist sehr ähnlich, wie wenn ich sagte: “Ja wirklich! eine Kurve kann aus graden Stücken bestehen.”⌊)⌋ – Ich hätte es nicht gedacht. – Ja : – nicht, daß die Teile dieser Figur ˇoben diese Figur ergeben! Das heißt ja nichts! – Sondern ich erstaune nur, wenn ich denke ich hätte das obere P. auf das … ahnungslos auf das untere gesetzt & sähe nun dieses Ergebnis.

/ /

Und man könnte sagen: der Beweis beweist eben das, was Dich überrascht. // [ Er ] der Beweis hat mich von dem überzeugt, ⌊–⌋ ⌊–⌋ was mich überrascht. //

/ /

Denn warum sage ich jene Figur überzeuge mich von etwas, & nicht geradeso auch diese: [S|s]ie zeigt doch auch daß zwei solche Stücke ein Rechteck geben. ‘Aber das ist uninteressant’ – will man sagen. Und warum ist es uninteressant?

/ ∫

“Ja, es sieht nicht so aus, aber es paßt”, sagt man auch manchmal beim Zusammenlegen eines Jig-saw puzzles.

/ /

Wenn man sagt: “Diese Form besteht aus diesen Formen” – so denkt man sich die Form als eine feine Zeichnung, ein feines Gestell von dieser Form auf das gleichsam die Dinge gespannt sind, die diese Form haben.

/ /

Hiermit ist in Zusammenhang, daß ich oben schrieb: “… daß eine Gruppe wie A wesentlich aus … besteht”.

/ ∫

Was ist Dein Ziel in der Philosophiephie? – Ich zeige der Fliege den Ausgang aus dem Fliegenglas.         Dieser Weg ist, in einem Sinne, unmöglich zu finden;, & in einem andern Sinne, ganz leicht.

​

9.9. Wenn ich mir Musik vorstelle, was ich ja täglich & oft tue so reibe ich dabei – ich glaube immer – meine oberen & unteren Vorderzähne rythmisch aneinander. Es ist mir schon früher aufgefallen geschieht aber für gewöhnlich ganz unbewußt. Und zwar ist es als würden die Töne ˇmeiner Vorstellung durch diese Bewegung erzeugt. Ich glaube, daß diese Art, im Innern Musik zu hören, vielleicht sehr allgemein ist. Ich kann mir naturlich auch ohne die Bewegung meiner Zähne musik vorstellen, die Töne sind aber dann viel Schemenhafter, viel undeutlicher, weniger prägnant.

/

Wann besteht denn eine Gruppe ‘wesentlich’ aus …? Das hängt natürlich von der Art der Verwendung der Bezeichnung ab, die wir der Gruppe geben. Eine Hand hat Wir haben zwar 5 Finger, aber ich hätte nicht gesagt: die Finger einer Hand ⌊be⌋kanstehen wesentlich aus 3 und 2 Fingern.    Nun, wesentlich ist es, ‘wenn es nicht anders sein kann’; & es kann nicht anders sein, wenn die Gruppe mit ihrer Teilung als Paradigma dient. // dienen soll. //    Der wesentliche Zug ist ein Zug der Darstellungsart.

/ /

“Diese Form besteht aus diesen Formen. Du hast mir eine wesentliche Eigenschaft dieser Form gezeigt.” – Du hast mir ein neues Bild gezeigt.        Es ist, als hätte Gott sie so zusammengesetzt. – Wir bedienen uns also eines Gleichnisses. Die Form wird zum ätherischen Wesen, welches diese Form hat; es ist als wäre sie ein für allemal so zusammengesetzt worden (von … hat.). , von dem, der die wesentlichen Eigenschaften in die Dinge gelegt hat. (Man sagt ja etwa auch , : gebraucht ja auch den Ausdruck: “[I|i]ch wußte nicht, daß es so etwas gibt”, wenn einem die überraschendec Teilung gezeigt wird : , so, als wäre uns ein Naturding gezeigt worden, dessen Existenz wir nicht vermutet hätten.)       Denn machen wir die Form zum Ding, so machen wir den Werkmeister der Form zu demjenigen, der nicht ⌊(⌋nur⌊)⌋ die Dinge aus ihren Bestandteilen ˇnur zusammensetzt, wie der Mensch, der etwas hervorbringt, sondern, der auch Härte, Farbe, Licht & Dunkelheit schafft. geschaffen hat. – Man hat, bekanntlich, das Wort “Sein“ gebraucht, um eine ätherische Art des Existierens “Sein“ gebraucht als Wort für eine sublimierte der von Existenz zu bezeichnen. Denke nun an einen Satz wie Betrachte z.B. den : … “Rot ist.” Freilich, niemand gebraucht ihn je. Wenn ich mir aber doch einen Gebrauch für ihn erfinden sollte zu ihm erfände , so wäre es der, daß ich diese Art Satz ausspräche, während ich ein Muster der Farbe vor mir habe : , als Einleitung zu irgend etwas welchen Aussagen, die welche dann die ⌊von den⌋ Wörter⌊n⌋ “rot“, und ander[e|n], Gebrauch etc., machen. ⌊(⌋Ähnlich ist vielleicht diese Einleitung ˇso eine ˇwie: “Angenommen, eine Strecke sei ist L & eine andere lx –”, wo ja noch nichts angenommen wird.⌊)⌋           Einen Satz, wie “Rot ist”, ist man versucht zu sagen, wenn man diese Farbe mit Aufmerksamkeit betrachtet: also in der gleichen Lage Situation , in der man die Existenz einer Sache feststellt. (eines blattähnlichen Insekts etwa).           Und ich will sagen, ⌊:⌋ wenn man den Ausdruck gebraucht “der Beweis hat mich gelehrt – hat mich davon überzeugt, ⌊–⌋ daß es sich so verhält”, ⌊(⌋so⌊)⌋ ist man noch immer in jenem Gleichnis.

/ /

Der Philosoph sagt: “Sieh' es doch so an –”.

? / /

“Wundert es Dich jetzt auch noch?” – Wie kommt es, daß etwas aufhört Dich zu wundern, wenn Du es anders ansiehst? – Eine Überlegung gibt ein überraschendes Resultat. ⌊(⌋Aber eine Uberlegung ist ja ein Bild⌊)⌋⌊,⌋ warum überrascht es Dich?⌊)⌋ Oder sollte ich sagen: “Mmich überrascht nicht das Bild, sondern der Ausgang des Gedankenexperiments”? Ist es also ähnlich, wie wenn mich Einer aufforderte eine Assotiationskette mit dem Wort … zu beginnen & durch ˇeine Reihe von 20 Wörter⌊n⌋ zu verfolgen. So gelange ich zum Wort … & bin erstaunt daß man da dorthin kommen kann? – Denn man sagt auch am Ende einer Schlußkette: “Ja, ja, ich werde dorthin geführt!” – Aber wenn Du einmal dorthin geführt wirst, – so vielleicht ein anders mal andermal wo anders hin. – Aber Du bleibst bei der überraschenden Schlußfolgerung. – Du überprüfst sie ⌊(⌋zwar⌊)⌋ vielleicht & sagst: “ja, es kommt immer das Gleiche heraus!”, aber wenn Du ein psychologisches Experiment machst um ein psychologisches Gesetz festzustellen, so machst Du es doch mit möglichst vielen Sub- jekten! Und wenn Du hier ˇin der Mathem. das Experiment gemacht & seinen Gang notiert hast, so gehst Du nun dieses Bild Deines Experiments immer von neuem durch & es überrascht Dich; aber nicht: daß Du einmal so gegangen bist; sondern das Bild, – welches Du, in irgend einem gewissem Sinne, anerkennst. Hättest Du z.B. bei der Überprüfung einen ‘Fehler’ in Deinen Schlüssen entdeckt, so würde Dich das Resultat nun nicht mehr wundern, obwohl ˇes doch da[ß|s] ⌊(⌋tatsächliche⌊)⌋ Resultat des Experiments // Denkexperiments // war. (Das Experiment, in welchem Du einen Schlußfehler machtest war ja als Experiment nicht fehlerhaft.    Überrascht mich das Resultat eines Experiments, so werde ich meine Überraschung los, indem ich die Ursachen des überraschenden Ausgangs auffinde. – Hier verhält es sich anders.           Wenn das Gedankenexperiment – mit allen Vorkehrungen – so verläuft ausgeht , dann nehmen wir seinen Gang zur Regel.

/

Ist er bei dem Gedankenexperiment erst einen Weg gegangen, so kann es sein, daß er beim ‘Überprüfen’ einen andern Weg geht, & erklärt, der ers er habe sich beim ersten geirrt.

/

10.9.    Wie lernen wir denn Schließen? Oder lernen wir es nicht –?    Weiß daß Kind, daß aus der doppelten Verneinung die Bejahung folgt? – Und wie überzeugt man es davon? Wohl dadurch, daß man ihm einen Vorgang zeigt, (etwa diesen da ), den es nun als Bild der Verneinung annimmt.    Und man macht die Bedeu den Sinn von ‘(x) ∙ fx’ klar, indem man darauf dringt, daß daraus ‘fa’ folgt.

/ /

Ist ein Experiment, in welchem wir die Beschleunigung beim freien Fall beobachten ein physikalisches Experiment oder ein psychologisches, das zeigt, w[as|ie] Menschen, unter solchen Umständen, sehen? – Kann es nicht beides sein? Und kommt das nicht drauf an, wie die Reihe der Experimente aussieht deren eines dieses Experiment ist; & darauf, wie wir über die Experimente reden?           Was ich aus einem Experiment lerne, ist selber ein Teil des Spiels, das ich spiele.       Man könnte auch sagen: [E|e]in Experiment ist dies ˇerst als Teil einer Theorie.

/ / /

“Das ist ein überraschendes Resultat!” – Wenn es Dich überrascht, dann hast Du es noch nicht verstanden. Denn die Überraschung ist hier nicht legitim, wie beim Ausgang eines Experiments. Da – möchte ich sagen – darfst Du Dich ihrem Reiz hingeben; aber nicht wenn sie ˇsich Dir am Ende einer Kette Schlußkette Deiner Schlüsse [wie eine Aussicht] kommt. ergibt. ˇzuteil wird // sie sich Dir … darbietet. // Denn da ist sie nur ein das Zeichen Zeiger dessen dafür , daß noch Unklarheit, oder ein Mißverständnis herrscht.           “Aber warum soll ich nicht überrascht sein, daß ich dahin geleitet worden bin?” – Denk' Dir Du hättest einen langen algebraischen Ausdruck vor Dir; es sieht zuerst aus, als ließe er sich nicht sonderlich wesentlich kürzen; dann aber siehst Du eine Möglichkeit ⌊(⌋der Kürzung⌊)⌋ & nun geht sie die Kürzung weiter, bis der Ausdruck zu einer äußerst kompakten Form zusammengeschrumpft ˇist. zusammenschrumpft. Können wir hier nicht über dies Resultat überrascht sein? (Beim Patience-Legen geschieht etwas ähnliches.) ˇGewiß, [U|u]nd es ist eine angenehme Überraschung; & sie ist von psychologischem Interesse, denn sie zeigt ein Phänomen des Nicht-Überblickens & der Änderung des Aspekts eines ˇgesehenen Komplexes. Es ist interessant ˇ& vielleicht sehr wichtig, daß man es diesem Komplex nicht ˇimmer ansieht, daß er sich so kürzen läßt; ist aber der Weg der Kürzung übersichtlich vor unsern Augen, so verschwindet die Überraschung       Wenn man nun sagt, man sei eben überrascht, daß man dahin geführt worden sei, so ist dies keine ˇganz richtige Darstellung des Sachverhaltes. Denn diese Überraschung hat man doch nur dann, wenn man den Weg noch nicht kennt. Nicht, wenn man ihn ganz vor sich sieht. Daß dieser Weg, de[m|n] ich ganz vor mir habe, da anfängt, wo er anfängt, & da aufhört, wo er aufhört, das ist keine Überraschung. Die Überraschung & das Interesse kommen dann sozusagen gleichsam von außen. Ich meine – : man kann sagen: ⌊,⌋ : “Diese mathematische Untersuchung hat großes psychologisches Interesse”, oder “großes physikalisches Interesse”.

/ ∫

Ich nähere mich einer Frage meistens nicht so: x ⟶ •         sondern so: Ich schieße immer wieder an ihr vorbei, aber in immer näherem Abstand.

? ∫ /

“Sieh' es so an, & Du wirst nicht mehr erstaunt sein.” Dich nicht mehr wundern.” Man staunt eben nicht nur, weil wenn das Niedagewesene geschieht; ⌊[⌋– “sondern auch aus Unklarheit”, wollte ich sagen. Aber kann man es immer ‘Unklarheit’ ∕∕ nennen? –⌊[⌋ Ich staune immer wieder bei dieser Wendung des Themas; obwohl ich es unzählige Male gehört habe, & es auswendig weiß.    Es ist vielleicht sein Sinn Witz , Staunen zu erwecken.

/ /

Was soll es dann heißen bedeuten , wenn ich sage: ‘Du darfst nicht staunen!’?    Denke an mathematische Rätselfragen. Sie werden gestellt, um zu weil sie überraschen ; das . Das ist ihr ganzer Sinn.    Ich will also sagen: Du sollst nicht glauben, es sei hier etwas verborgen, in das man nicht Einsicht nehmen kann, – – als seien wir durch einen einen unterirdischen Gang gegangen & kämen nun irgendwo ans Licht, ohne aber wissen zu können, wie wir dahin gekommen sind, oder welches die Lage des Anfangspunkts Anfangs zum Ausgangs des Tunnels ist sei       Wie aber konnte man denn überhaupt in dieser Einbildung sein? Was gleicht denn in der Rechnung ◇◇◇ einer Bewegung unter der Erde im unterirdischen Gang ? – Was konnte uns denn dieses Bild nahe legen? Daß Ich glaube : , daß kein Tageslicht auf diese Schritte fällt.⌊;⌋ daß wir den Anfangs- & Endpunkt der Rechnung in einem Sinne verstehen, in dem wir den übrigen Gang der Rechnung nicht verstehen.    “Hier ist kein Geheimnis!” – Aaber wie konnten wir den glauben, daß eines sei? – Nun, ich bin immer wieder den Weg gegangen & war immer wieder überrascht, & auf den Gedanken, daß man hier etwas verstehen kann, bin ich nicht gekommen. “Hier ist kein Geheimnis”, heißt also: Schau Dich doch um!

∕∕ ∕∕

Ist es nicht, als sähe man in einer Rechnung eine Art Kartenaufschlagen? Man hat die Karten gemischt– ⌊;⌋ man weiß nicht, was dabei vorsich ging : ; aber am Ende lag obenauf der Zehner, & das bedeutet das schlechtes Wetter wird. … …

∫ / /

“Denk Dir eine Zahl – – zähl 3 dazu – multipliziere mit 2 – subtrahiere das doppelte der Zahl; ⌊–⌋ nun hast Du 6 erhalten.”

/ /

Unterschied zwischen dem Werfen des Loses & einem Auszählspiel Abzählspiel & dem Auszählen vor einem Spiel. Könnten aber nicht naive Menschen auch im Ernstfalle statt einen Mann auszulosen ein Auszahlspiel Abzählspiel gebrauchen? // ein Auszählen⌊s⌋ sich des … bedienen? //

/ / /

Was tut der, der uns mich d⌊a⌋rauf aufmerksam macht, daß beim Auszählen Abzählspiel das Ergebnis abgekartet ist?

/ / /

Ich will sagen: “Wir haben keinen Überblick über das, was wir gemacht haben, & deshalb kommt es uns geheimnisvoll vor.”. Denn nun steht ein Resultat vor uns, & wir wissen nicht mehr, wie wir dazu gekommen sind, aber wir sagen (wir haben gelernt, zu sagen): “ also muß es so sein so muß es sein ”; & wir nehmen es hin, & staunen darüber.         Könnten wir uns nicht denken, daß ein Mensch verschiedene Befehle von in der Form “Du mußt jetzt das & das tun” ˇeinzeln auf Karten geschrieben hätte, die Karten dann mischte, & die, welche obenauf zu liegen kommt liest, & sagt: Also, ich muß das tun! – Denn das Lesen eines geschriebenen Befehls macht nun einmal einen bestimmten Eindruck. ˇhat eine bestimmte Wirkung. Und ebenso auch das Anlangen bei einer Schlußfolgerung. – Man könnte aber vielleicht den Bann ˇeines solchen Befehls brechen, indem man ˇnochmals // noch einmal // klar vor Augen führt, wie man zu diesen Worten gelangt ist, & mit diesen Vorgang mit anderen Vorgängen vergleicht – indem man z.B. sagt: “Es hat Dir doch niemand den Befehl gegeben!”       Und ist es nicht auch so, wenn ich sage: “Hier ist kein Geheimnis!”? – Er hatte ja, in gewissem [s|S]inne, nicht geglaubt, daß ein Geheimnis vorliegt. Aber er war unter dem Eindruck des Geheimnisses (wie der Andere unter dem Eindruck eines Befehles). In einem Sinne kannte er ja die Situation, aber er verhielt sich zu ihr (im Gefühl & im Handeln), ‘als verhielte es sich so & so’ // , ‘als läge der & der ein andrer Sachverhalt vor’[.| (]wie wir ˇdann sagen würden). .

/ / /

Die logischen Gesetze sind allerdings der Ausdruck von ‘Denkgewohnheiten’, aber auch von der Gewohnheit des Denkens zu denken . D.h., man kann sagen, sie zeigten: wie Menschen denken & auch, was Menschen “denken” nennen.

/ /

Frege nennt ‘ein Gesetz des menschlichen Fürwahrhaltens’: “Es ist den Menschen … unmöglich einen Gegenstand als von ihm selbst verschieden anzuerkennen”. – Wenn ich denke, daß mir das unmöglich ist, so denke ich ⌊(⌋mir⌊)⌋, daß ich es versuche, es zu tun. Ich schaue also z.B. auf meine Lampe & sage: “diese Lampe ist verschieden von ihr selbst”⌊. (⌋(aAber es rührt sich nichts). ⌊.)⌋ Ich ich sehe nicht, etwa, daß es falsch ist, sondern ich kann damit gar nichts anfangen. Außer, wenn die Lampe im Sonnenlicht flimmert, dann kann ich das ganz gut durch diesen Satz ausdrücken. – Man kann sich auch in eine Art Krampf Denkkrampf versetzen, in dem welchem man tut, als versuchte man das unmögliche etwas ‘unmögliches’ zu denken & es gelänge nicht. & als gelä⌊n⌋ge es einem nicht. Ähnlich wie man auch tun kann kann man auch tun , als versuchte man ⌊(⌋vergeblich⌊)⌋ einen Gegenstand durch aus der Ferne durch bloße[n|s] W[i|o]llen an zu an sich zu ziehen. (Dabei schneidet man gewisse Gesichter, so ähnlich , als gäbe man dem Ding wollte man durch Mienen Zeichen, zu verstehen geben, es solle herkommen.

/ / /

“Wie ist es möglich, die Zeit zu schätzen? ⌊,⌋ Wie kann man die Zeit schätzen, da man ganz das Leben gleichsam fern von jeder Uhr weilt weilt? – Daß uns die Zeiten übereinstimmend in Übereinstimmung mit der Uhr einfallen, daß wir die Zeit schätzen können, ist ein Grund, warum ⌊(⌋das⌊)⌋, was die Uhr mißt, die Zeit, so wichtig ist. // Wie kann man die Zeit schätzen messen , ⌊–⌋ da das Leben doch fern von der einer Uhr ist? – Daß uns … //

/ / /

11.9. [Nachgetragen] / Denk Dir ein Material härter & fester als irgend ein anderes. Aber wenn man einen Stab aus diesem Stoff aus der horizontalen in die vertikale Lage bringt, so zieht er sich zusammen; oder denk' Dir er biegt sich, wenn man ihn aufrichtet & ist dabei so hart, daß man ihn auf keine andre Weise biegen kann. – Ein◇ Mechanismus aus diesem Stoff, etwa eine Kurbel Pleuelstange & Kreuzkopf. Andere Bewegungsweise des Kreuzkopfs.        Oder: eine Stange biegt sich, wenn man ihr eine gewisse Masse nähert, gegen alle Kräfte aber, die wir auf sie wirken lassen, ist sie vollkommen starr. Denk D⌊i⌋r die Führungsschienen des biegen sich & strecken sich wieder, wenn die Kurbel sich ihnen nähert & sich wieder entfernt. Ich nehme aber an, daß keinerlei besondere ⌊(⌋äußere⌊)⌋ Kraft dazu nötig ist dies hervorzurufen. Dieses Benehmen der Schienen würde wie das eines lebenden Wesens anmuten.           Wenn wir sagen: “Wenn die Glieder des Mechanismus ganz starr wären, würden sie sich so & so bewegen”, was ist das Kriterium dafür, daß sie ganz starr sind? Ist es, daß sie gewissen Kräften widerstehen? oder, daß sie sich so & so bewegen?           Denke, ich sage: “das ist das Bewegungsgesetz des Kreuzkopfes (die Zuordnung seiner Lage zur Lage der Kurbel etwa), wenn sich die Länge der Kurbel & der Pleuelstange nicht ändern”. Das heißt wohl, : [w|W]enn sich die Lagen der Kurbel & des Kreuzkopfes so zu einander verhalten, so dann sage ich, daß die Länge der Pleuelstange gleichbleibt.

∕∕ ∕∕

“Wenn die Teile ganz starr wären, würden sie sich so bewegen”: ist das eine Hypothese? Es scheint, nein. Denn wenn wir sagen: “die Kinematik be- schreibt die Bewegungen des Mechanismus unter der Voraussetzung, daß seine Teile vollkommen starr sind”, so geben wir einerseits zu, daß diese Vorau⌊s⌋setzung in der Wirklichkeit nie zutrifft, anderseits soll es keinem Zweifel unterliegen, daß vollkommen starre Teile sich so bewegen würden. Aber woher diese Sicherheit? Es handelt sich hier wohl nicht um Sicherheit, sondern um eine Bestimmung, die wir getroffen haben. Wir wissen nicht, daß Körper, wenn sie (nach den & den Kriterien) starr wären, sich so bewegen würden; wohl aber würden wir (unter Umständen) Teile ‘starr’ nennen, die sich so bewegen.3        ﹖ Denke in so einem Fall immer daran, daß ja die Geometrie (oder Kinematik) keine Meßmethode angibt // spezifiziert // , wenn sie von gleichen Längen, oder vom Gleichbleiben einer Länge spricht.           Wenn wir also die Kinematik etwa die Lehre von der Bewegung vollkommen starrer Maschinenteile nennen, so liegt hierin einerseits eine Andeutung über die (mathematische) Methode: wir bestimmen gewisse Distanzen als die Längen von der Maschinenteilen e, die sich nicht ändern; anderseits eine Andeutung über die Anwendung des Kalküls.

? ∫

Bestimmt die Operation // die Regel // ‘ + 2’ den Übergang, der von 200 aus zu machen ist, oder nicht? Bestimmt die Funktion x3 + x2 + 1 die Zahl, die wir für x = 5 erhalten? – Wie ist diese Frage zu erledigen beantworten ? – Prüfen wir ⌊(⌋dazu⌊)⌋, ob die Resultate, welche die Menschen durch diese Substitution erhalten immer die gleichen sind? Nein. Und doch ist das Factum, daß von der größten Bedeutung, daß das erhaltene Resultat, gegeben mathematisch erzogene Rechner in der ungeheuern Mehrzahl der Fälle das gleiche selbe ist.       Wir würden diese Rechenmethode⌊n⌋ nicht gebrauchen, wenn sie nicht, normalerweise, tatsächlich ständig zu dem gleichen Resultat führen würden.       Die Frage hat, mathematisch, gar keinen Sinn, – wenn wir nicht den Fall der Funktion x3 + x2 + 1 von bestimmten andern Funktionen unterscheiden wollten, etwa von Funktionen von mehr als einer Variablen. Und dann ist die Frage die gleiche, wie die: ist die Funktion x3 + x2 + 1 eine Funktion nur einer Variablen. Und was man mit dieser Frage in diesem Falle anfangen könnte, ist wieder nicht klar , ; es sei denn etwa, da[s|ß] eine – in diesem Falle sehr primitive – Methode der Ausrechnung der Anzahl der Variablen anzuwenden sei. Unter bestimmten Verhältnissen könnte die Frage z.B. durch eine Untersuchung zu beantworten sein : , ob alle Variablen eines des Ausdrucks sich bis auf eine ˇnach bestimmten Regeln wegheben.

s ∫ ? / /

Aber willst Du sagen, daß der Ausdruck ‘ + 2’ es für Dich zweifelhaft läßt, was Du, nach 234 z.B., schreiben sollst? Nein; ich sage unbedenklich: ohne mich zu besinnen, ˇBedenken: “236”; aber darum ist ist es auch überflüssig ja unnötig, daß darunter schon früher etwas bestimmt wurde wird .          Daß ich keinen Zweifel habe, wenn die Frage an mich herantritt, heißt das, daß sie ⌊(⌋früher⌊)⌋ schon ˇvorher beantwortet worden ist? ⌊⌊ // früher bereits beantwortet worden ist? // ⌋⌋ // … heißt eben nicht, daß sie ˇfrüher schon // ˇunbedingt schon früher // beantwortet worden war. //             Aber ich weiß doch auch, daß, welche Zahl immer man mir geben wird, gibt, ich die folgende gleich mit Sicherheit werde angeben können. – Ausgenommen ist doch gewiß der Fall, daß ich sterbe, ehe ich dazukomme die nächste Zahl zu nennen , – & natürlich auch viele andere Fälle. Daß ich aber so sicher bin, daß ich fortsetzen kann, werde fortsetzen können, ist natürlich sehr wichtig. – freilich von der größten Bedeutung.

​

“Eine Definition führt Dich doch nur wieder einen Schritt zurück, zu etwas anderem nicht dDefiniertem.” Was sagt uns das? Wußte das irgend jemand nicht? – Nein; aber konnte er es nicht aus dem Auge verlieren?

/

Oder: “Wenn Du schreibst ‘1, 4, 9, 16, .....’, so hast Du nur vier Zahlen angeschrieben, & fünf Pünktchen” – worauf machst Du da aufmerksam? konnte jemand etwas anderes glauben?    Man sagt Einem in so einem Falle auch: “Damit hast Du weiter nichts hingeschrieben als vier Zahlzeichen & noch ein fünftes Zeichen, die Pünktchen”. das hier aus einigen Pünktchen besteht”. Ja, wußte er das nicht? Aber kann er man nicht doch sagen: Ja wirklich, ich habe die Pünktchen nie als ein weiteres fünftes Zeichen ˇin der dieser Reihe // als ein Zeichen nach den Zahlzeichen // aufgefaßt, – das hier allerdings ⌊(⌋etwa⌊)⌋ so aus- sieht, wie weitere, flüchtig geschriebene, Zahlzeichen Ziffern , – daß – aber auch anders geschrieben werden könnte, ˇso etwa, daß es etwa selbst den Charakter eines Buchstabens oder Zahlzeichens hätte. hat (sagen wir ‘’).

/

Oder wie ist es, wenn man darauf aufmerksam macht, daß eine Linie im Sinne Euklids eine Farbengrenze ist & nicht ein Strich, & ein Punkt der Schnitt solcher Farbengrenzen & kein Tupfen (dot)? (Wie oft ist ⌊⌊(⌋es⌊)⌋⌋ gesagt worden, daß man sich einen Punkt nicht vorstellen kann.)

/

11.9. Ja, es genügt nicht, daß man Einen uns auf das aufmerksam macht, was er wir schon weiß wissen, man muß ihn uns sogar gerade im rechten Moment drauf auf[f|m]erksam machen!

/

Man kann in der Einbildung leben, ˇdenken, daß es sich so & so verhält, oh⌊n⌋e es zu glauben; d.h: wenn man gefragt wird, so weiß man es, wird hat man aber nicht auf die Frage zu antworten, so weiß man es nicht, sondern d.h., man handelt & denkt dann als glaubte man das Gegenteil. nach einer andern Ansicht.

/

Denn eine ⌊(⌋gewisse⌊)⌋ Ausdrucksform läßt uns so & so handeln. Wenn sie unser Denken beherrscht, so möchten wir auf jed alle Einwendungen sagen: trotz aller Einwendungen sagen: “in gewissem Sinne verhält es sich doch so.” Obwohl es ja gerade auf den ‘gewissen Sinn’ ankommt. ⌊(⌋Ähnlich ˇbeinahe, wie es ˇuns die Unehrlichkeit eines Menschen bedeutet, wenn wir sagen: er sei kein Dieb.)

∫ ∫

Wenn man z.B. ˇgewisse bildhafte Sätze als Dogmen des Denkens ˇfür die Menschen festlegt, so zwar, daß man damit nicht Meinungen bestimmt, aber den Ausdruck aller der Meinungen völlig beherrscht, so wird dies eine sehr eigentümliche Wirkung haben. Die Menschen werden unter einer unbedingten, ˇfühlbaren Tyrannei leben, ohne doch sagen zu können, sie seien nicht frei daß sie nicht frei sind . Ich meine, daß ⌊die⌋ Katholische Kirche es irgendwie ähnlich macht. Denn das Dogma hat die Form des Ausdrucks einer Behauptung, & es ist an ihm nicht zu rütteln, & dabei kann man jede praktische Meinung mit ihm in Einklang bringen; freilich manche leichter, manche schwerer. Es ist keine Wand um die Bewegung Meinung zu beschränken, sondern ein Gewicht daß man wie eine Art Bremse, die aber [P|p]raktisch den gleichen Dienst tut die gleiche Wirkung hat eine Hemmung, die durch Reibung die Bewegung vernichtet; ˇetwa als hängte man, um [d|D]eine Bewegungsfreiheit zu beschränken, ein Gewicht an Deinen Fuß. ⌊⌊ // aber ein Gewicht, uns an den Fuß gehängt, das uns nicht weit gehen lassen wird. // ⌋⌋ Dadurch nämlich wird das Dogma unwiderlegbar! . & dem Angriff entzogen.

/ / /

Die Sätze der Logik sind ‘Denkgesetze’, ‘weil sie das Wesen des menschlichen Denkens zum Ausdruck bringen’ – richtiger aber: weil sie das Wesenˇ, die Technik, (Watson) des Denkens zum Ausdruck bringen, oder zeigen. Sie zeigen, was das Denken ist, & auch Arten des Denkens.

​

Auch im Denken gibt es eine Zeit des Pflügens & eine Zeit der Ernte.    Es ist mir eine Befriedigung, jeden Tag viel zu schreiben. Dies ist kindlich, aber so ist es.

s / /

Denke daran, wie man Sätze gebraucht der Art: “Ich bin nun einmal so.”, oder “Da kann man nichts machen.” Sätze, als Gedankenstriche verwendet, oder als Abschlußformel. Aber sind sie deswegen unwichtig?

/ /

Das Überraschende kann in der Mathematik // in der Behandlung der Mathematik // zweierlei völlig verschiedene Rollen spielen.     Man kann den Wert einer mathematischen Gedankenreihe darin erblicken, sehen, daß, sie etwas ˇuns überraschendes zu Tage fördert: weil es von großem Interesse, ˇvon großer Wichtigkeit ist, zu sehen, wie ein Sachverhalt durch die & die Art seiner Darstellung überraschend, oder ⌊(⌋auch⌊)⌋ paradox, wird // überraschend, erstaunlich, oder auch paradox, wird. //       Hiervon ganz verschieden ist ˇaber die gegenwärtig gepflogene gebrauchte Darstellungsartweise in der Mathematik : , // heute herrschende Auffassung der … – // die ⌊der⌋ das Überraschende & , das Erstaunliche, darum als Wert gilt, weil es zeigt zeige in welche Tiefe Tiefen die mathematische Untersuchung dringt; so wie wir den Wert eines Teleskops daran ermessen können könnten , daß es uns Dinge zeigt, die wir ohne dieses dies Instrument nicht hätten ahnen können. Der Mathematiker sagt gleichsam also : “Siehst Du, das ist doch wichtig, das hättest Du ohne mich nicht gewußt⌊.⌋” – als hätte er durch eine Art von Experiment Erstaunliches an den Tag gefördert . So als als wären durch diese Überlegungen, als durch wie durch eine Art höheren Experimentes ⌊(⌋von⌊)⌋ Experiment, erstaunliche, ja die erstaunlichsten, Tatsachen ans Licht gefördert worden. gekommen.

/

Der Mathematiker ist kein Entdecker, sondern ein Erfinder.

ø

Es gibt ⌊es⌋ im Religiösen, wWie im bürgerlichen Leben eine Ehre & sie ist bei verschiedenen Menschen von sehr versch ungleicher Empfindlichkeit. Wie [d|D]er [e|E]ine ˇempfindet einen Schimpf als Ver[n|ni]chtung seiner moralischen Persönlichkeit empfindet den e & nichts als Blut ⌊kann⌋ ihn abwaschen kann, während der Andere ihn ˇnur oberflächlich fühlt & schnell vergißt[,|.] Der Eine sagt: “Wie kann ich leben, wenn ich beschimpft bin?” & der Andere kann dennoch weiterleben.

∫

“Aber sind die Übergänge also durch die algebraische Formel nicht bestimmt?” – In der Frage liegt ein Fehler.       Oder ich kann sagen: sie ist zweideutig. Wie verwende ich denn die Fragen, ob Übergänge durch eine Formel bestimmt sind? Ich könnte einmal verschiedene Arten von Formeln einander entgegenstellen entgegensetzen z.B. Formeln der Art y = 2n, y = n + 5, y = n2 (wo n die Reihe der Kardinalzahlen durchläuft) Formeln, wie       y = n2K (wo n die Reihe der Kardinalzahlen durchläuft & K eine der K = 2 . ⌵ . K = 3 . ⌵ . K = 5)        y = n2. ⌵ . n3

∫

Wir verwenden den Satz Ausdruck : “die Übergänge sind durch die Formel … bestimmt”. Wie verwenden wir ihn?     Wir können etwa davon reden, daß Menschen durch Abrichtung & Erziehung dahin gebracht werden diese Formeln so anzuwenden, daß m alle, wenn sie eine Zahl für die Variable substituieren das gleiche Resultat herausbringenrechnen.    Wir können anderseits verschiedene Arten der Formeln, & ihnen entsprechend verschiedene Arten der Abrichtung zu ihrem Gebrauch, einander entgegensetzen. Z.B. Formeln von der Art – – – – solchen wie – – – – & sagen, die ersten bestimmten die Übergänge – – – – die andern nicht.

​

Habe heute angefangen an dem gr[ö|o]ssen Manuskript weiterzuschreiben. Moge es gehen! Geht es aber nicht, so soll ich nicht unglücklich werden. Ich fürchte mich davor in meinem Buch in einem geschraubten & schlechten Stil zu schreiben.

s / /

12.9.    “Die denknotwendige Folge.” Das ist die Folge, die nicht in Frage ge- zogen wird. (Ich sage nicht: “werden kann”.)

​

Ich schreibe jetzt an meinem Buch, oder versuche zu schreiben, & schreibe tropfenweise & ohne jeden Zug; [V|v]on der Hand in den Mund. Es ist unmöglich, daß so etwas Gutes herauskommt. Ich bin vor allem viel zu ängstlich, viel zu unfrei im Schreiben. Wenn ich so schreiben muß, da ist es besser, kein Buch zu schreiben, sondern mich darauf zu beschränken Bemerkungen tant bien que mal zu schreiben, die nach meinem Tode vielleicht veröffentlicht werden.       Die Bemerkungen, die ich schreibe befähligen mich wohl Philosophie zu lehren, aber nicht ein Buch zu schreiben.        Bin geneigt über mein Un- geschick unmutig zu sein.

⁎ /

13.9.     “Ich kann doch nur folgern, was wirklich folgt⌊!⌋” – ˇD.h.⌊:⌋ Was folgt denn? die logische Maschine wirklich hervorbringt. ⌊ Die logische Maschine, das wäre eine Art Weltäther; eine alles durchdringende⌊r⌋ ätherische⌊r⌋ Maschine. Mechanismus. Und vor diesem Bild muß man warnen. ⌋

s @ ∫ / /

Wenn wir ein Experiment machen & dabei, sagen wir, ein Galvanometer gebrauchen – ist es ein Experiment : über über das Verhalten des Galvanometers? // ist es ein Experiment zur Bestimmung⌊,⌋ ˇzur Untersuchung⌊,⌋ des Verhaltens des Galvanometers? //        Wie drückt es sich im Messen aus, ob ich den Maßstab messe, oder den Tisch? – Ich sehe auch manchmal nach, ob der Maßstab stimmt, indem ich den Tisch mit ihm messe (oder ihn mit dem Tisch).

/ ? / ∫ /

Gibt es soetwas wie einen logischen Schluß in der Verwendung eines Meßinstruments? Ein Umschalten Eine Transformation des Maßstabes. [E|I]st es nicht, wie wenn auf der einen Kante eines Maßstabs cm auf der andern Zoll aufgetragen sind, & wir messen nun etwas i[m|n] Zoll & gehen auf dem Maßstab zu ˇden cm über? ⌊ (Ich suche aber nach einem andern Beispiel.) ⌋

∫

Könnte man sich denken, daß mit den Zeigern verschiedener Meßinstrumente eine Rechenmaschine verbunden wäre, so daß, sagen wir, die Ablesungen zweier Instrumente durch sie multipliziert würden. ⌊ Und die Rechenmaschine hätte auch Zifferblatt & Zeiger wie die andern Instrumente. ⌋

s /

Warum schauen wir auf die Uhr, wenn wir einen Zug nach … erreichen wollen? Ist es sicher bestimmt , daß der Zug nach der Uhr abfährt? Muß es diesmal geschehen, weil es meistens in meinem Leben so geschehen ist? Ist der Induktionsschluß gültig? – Aber ich schaue auf die Uhr; ja ich ängstige mich wenn ich keine bei mir habe; zeigt sie schon so & so viel, so laufe ich, bis zur Erschöpfung; bin in größter Aufregung; … laufe ich, was ich kann & bin in äußerster Hast; etc., etc., etc.. So geht es tatsächlich vor sich.

s ? / /

Du kannst jemanden zählen lassen, um zu sehen, wieviel Äpfel da liegen – aber auch, um zu sehen, ob er sie richtig zählt. Wie unterscheiden sich die Vorgänge Fälle ? Wenn nun Zählen ein Experiment ist, was zeigt es? Denn ein Experiment ist etwas im Bezug auf ein bestimmtes Resultat. in Bezug auf etwas als sein Resultat. //

∫ /

Denk' Dir es ginge Einer durch die Handlungen eines Experiments & sagte, auf das & das was geschieht zeigend ˇeinfachc: “[s|S]iehst Du!” – da könnte man doch fragen: “Was soll ich sehen? Was ist hier das Resultat?”

s ? /

Man möchte sagen: Es e muß doch einen Grund haben, warum auf dieses Thema gerade dieses Thema zweite ˇThema folgt. Und was denkt man sich als Grund? – Irgend eine Verwandtschaft⌊,⌋ ˇBeziehung⌊,⌋ ein Gegensatz. Aber irgend eine Beziehung haben die Themen ja immer! – Aber es ist wahr: manchmal können wir sagen: [D|d]ieses Thema folgt auf das, weil es so & so damit verwandt ist.       Es ist also als müßte die Folge dieser Theman einem schon in uns vorhandenen Paradigma entsprechen.        Wie aber, wenn ich sagte: Er wollte eben dieses Ornament, – bestehend aus diesen beiden Themen – machen[?| .] – Nach dem Grund gefragt, hätte er keinen geben können. Und wir können auch keinen sehen geben . wissen auch keinen. – Hat es dann einen Grund?       Oder wie wenn ich fragte: sagen würde: “Nun, gefällt es Dir nicht? [f|F]indest Du es nicht natürlich? – Was braucht es dann einen Grund?” Und wenn wir [f|v]on einem Paradigma reden – warum soll das nicht das Paradigma, etwa für andere Kompositionen werden sein ? Es ist eben … Dann ist es eben vielleicht ein neues Paradigma!         Und Aber doch hat die Suche nach einem Vorbild Paradigma eine Berechtigung. ⌇ Es ist vielleicht wahr, daß uns diese Folge einen so tiefen Eindruck nicht machen würde, wenn ihr nicht schon etwas wie ein Paradigma in unsern Erlebnissen entspräche. Ich sage: es ist vielleicht wahr.             Es drängt sich uns das Bild auf …. Es ist sehr interessant, daß sich uns Bilder aufdrängen können.

v / /

Denke Dir den analogen Fall in einem Gemälde: Es zeigt zwei Menschen; & wir sagen ˇuns: “Es muß natürlich schon einen Grund haben, warum uns gerade diese zwei Gesichter ˇzusammen ˇuns einen solchen Eindruck machen.” Wir möchten – heißt das – diesen Eindruck der beiden Gesichter wo anders wiederfinden, in einem andern Gebiet. Aber ob er wiederzufinden ist? –

v /

Man könnte auch fragen: Welche Zusammenstellung von Themen Gesichtern hat eine [p|P]ointe, welche keine? Oder: warum hat diese Zusammenstellung eine [p|P]ointe, & die andere keine? Das mag nicht leicht zu sagen sein! Oft können wir sagen: diese entspricht einer Geste, diese nicht.

​

14.9. Es ist grauenhaft, daß ich die Arbeitsfähigkeit, d.h. die philosophische Sehkraft, von einem Tag auf den andern verliere. Teils verursacht vielleicht durch sehr schlechten Schlaf. Woher der, das weiß ich nicht. Aber was ist doch das für ein Leben! Denn kann ich nicht schreiben, so kann ich nicht schreiben: es nützt nichts, daß ich alles schon gedacht habe.     Ich hatte gestern Hoffnung, daß es mit dem Schreiben gehn wird. Heute aber ist meine Hoffnung wieder gesunken.     Und leider brauche ich die Arbeit, denn ich bin noch nicht resigniert, sie aufzugeben. So muß ich also, wie eine ‘vom Wind gepeitschte Wolke’ hin & her ziehen.

​

Das Leben stellt uns Bilder vor Augen als Ziele & macht uns danach laufen & dann verlieren wir die Kraft.        Dann ist es also richtig – kann man sagen – sich nicht verlocken zu lassen & nichts als Ziel zu nehmen.

​

“Fang etwas Anderes an!” Aber ich will nicht! Wie soll ich die Kraft haben jetzt, etwas anderes anzufangen? Es sei denn, daß ich gezwungen werde, wie durch einen Krieg.

​

15.9.     Wenn ich für mich denke ohne ein Buch schreiben zu wollen, so springe ich um das Thema herum; das ist die einzige mir natürliche Denkweise. In einer Reihe for gezwungen fortzudenken ist mir eine Qual. Soll ich es nun überhaupt probieren??       Ich verschwende unsägliche Mühe auf ein Anordnen der Gedanken, das vielleicht gar keinen Wert hat.

∫

Worin besteht es, wenn man einen Menschen nachmacht? Ich mache dieses Gesicht, versetze mich in ihn, & rede mit seiner Stimme & [i|I]ntonation.     Dies deu hat wahrscheinlich ˇirgend eine Bedeutung für das ˇVerständnis des Wesen⌊s⌋ der Wahrnehmung. Obwohl ich den Zusammenhang jetzt nicht sehe.

v / /

16.9.    “Doch, – er kann es nicht denken!” D.h. etwa: er kann es nicht mit Denkinhalt erfüllen: [E|e]r kann nicht wirklich mitgehen, // er kann ˇdenm Worten Gesagten mit seinem Verstand, mit seiner Person. Es ist ähnlich als sagte man: Diese Tonfolgen geben keinen Sinn, ich kann sie nicht mit Ausdruck singen. Ich kann nicht mitschwingen. Oder, was hier auf dasselbe hinauskommt: ich schwinge nicht mit.

​

Vorwort: Dieses Buch besteht aus Bemerkungen die ich im Lauf von 8 Jahren über den Gegenstand der Philosophie niedergeschrieben geschrieben habe. Ich habe oft vergebens versucht sie in eine [B|b]efriedigende Ordnung zu bringen oder am Faden eines Gedankenganges aufzureihen. Das Ergebnis war künstlich & unbefriedigend, & meine Kraft ˇerwies sich als viel zu gering es zu Ende zu führen. Die einzige Darstellung, deren ich ˇnoch fähig bin, ist die, diese Bemerkungen durch ein Netz von Zahlen so zu verbinden, daß ihrˇ, äußerst komplizierter, Zusammenhang sichtbar wird. Möge dies statt eines Besseren hingenommen werden – , was ich gerne g⌊e⌋liefert hätte.

/

“Ich habe gemeint …” heißt hier: ich habe dies in petto gehabt. Aber dies ist doch ein Bild.          “Die Maschine hat es ‘in sich’, sich so zu bewegen.” Der Fall wird also verglichen dem, daß wir etwas aus einem Behälter holen, was in ihm dort lag. (Dieses Bild liegt in den verschiedensten Formen in einer Menge von Wendungen unsrer Sprache wird immer wieder von uns … wieder & wieder von uns verwendet angewandt // ausgesprochen // ; kein Wunder wenn es große Gewalt über uns hat.)

/ /

Es singt [e|E]iner eine ihm wohlbekannte Melodie; wir Wenn jemand eine ihm … singt, wir … unterbrechen ihn an irgend einer Stelle & fragen dann: “ Hast Du gewußt … Wußtest Du wie es weitergeht?”, oder “: “[wW|]olltest Du so ˇfortsetzen oder so ⌊?⌋ weitersingen ” (indem wir ihm die richtige & eine fal⌊s⌋che Fo⌊r⌋tsetzung angeben) – er . Er wird selbstverständlich antworte[n|t]: “Freilich wußte ich, wie es weitergeht & ich wollte natürlich for so fortsetzen: …”. Es Hier drängt sich ˇuns ⌊(⌋sehr stark⌊)⌋ das Bild auf, // Und es drängt sich das Bild auf, // die ˇFortsetzung der Melodie habe schon existiert, sei schon da gewesen, & zwar in uns, gleichsam hinter der Mundöffnung. Dies Bild wird verstärkt dadurch, daß wir etwa nach der Unterbrechung noch ein Stückchen der Melodie mit dem innern Ohr hören & es nun ist, als sähen wir noch ein Stück der Reihe jener der Töne entlang, die bereit liegen lagen ans Licht zu kommen gesungen zu werden . Und dies ist wieder ganz ähnlich wie dem, was beim Zählen vorsich geht oder beim Anschreiben einer Reihe mit ‘Pünktchen’, die ‘u.s.w. ad inf’ bedeuten.

/ / /

“Es ist aber doch ein entscheidender Unterschied zwischen einem Reihenstück wovon wir welches ein bestimmtes Ende haben soll, & jenen Anfängen einer Reihe die endlos ist, ich meine ein wesenhafter wesentlicher Unterschied in un- serer Auffassung von dem hingeschriebenen Reihenstück. Endlos – möchte ich sagen – ist eben wirklich endlos. Und hier kann doch die Bedeutung nicht im Gebrauch bestehen, denn der Gebrauch ist ja endlich & wenn man auf ihn schaut, so kommt man ⌊(⌋ebenc⌊)⌋ auf finitistische Gedanken! Sieht man aber auf die Bedeutung, das was wir uns bei dem Wort denken, so sieht man, wovon hier die Mathematik redet.” – Erstens, wenn Du sagst, der Gebrauch des Wortes ist ein endlicher, was heißt das? Wie sieht denn ein unendlicher Gebrauch aus? – Also kann man wohl ‘endlich’ & ‘unendlich’ gar nicht auf die Verwendung den Gebrauch eines Wortes anwenden. – Ist nun aber der Gebrauch, den wir von “u.s.w. ad inf” machen der Gleiche, wie der, den wir von “u⌊.⌋s.w. ad 734” machen? Offenbar nein. Nur ist der Unterschied der Verwendung von “u⌊.⌋s.w. ad 734 & “u⌊.⌋s⌊.⌋w. ad 176” nicht von der gleichen Art, wie der zwischen der Verwendung eines dieser Zeichen & des Zeichens “u⌊.⌋s⌊.⌋w. ad inf.”

/ / /

Wie z.B. auch die Verwendung der Befehle “zeichne ein Krei[ß|ss]tück vom Radius 25 cm”, “zeichne ein Kreisstück vom Radius 6 cm” nicht die von gleiche⌊r⌋ ˇArt ist, wie die des Befehles: “Zeichne ein Kreisstück vom Radius ∞”. In den beiden ersten Fällen benützen wir einen Zirkel, im dritten ein Lineal.

/ /

An der Verwendung des Wortes “endlos”, oder “unendlich”, ist weiter nichts zu beanstanden, als der Geist⌊,⌋ in dem sie verwendet werden. Der hocus pocus, der, bei aller scheinbarer Nüchternheit, in den Worten liegt, mit denen die Mathematiker ihre Kalküle begleiten. Zeige uns statt der Bilder, Assoziationen, die dieses Wort & diese Sätze hervorrufen – , ihre Verwendung!

/ / /

Wenn man sich nun nach dem Gebrauch des eines Zeichens “ … wie “usw ad inf ” umschaut, so fällt einem freilich ⌊(⌋mit [r|R]echt⌊)⌋ auf, daß das [e|E]igentümliche dieses Gebrauches ja nicht darin bestehen kann, daß er, in irgend einem Sinne, ausgedehnter ist, als der, jener andern Zeichen // als der, der Zeichen “usw. ad n” // . Er unterscheidet sich eben nicht durch die Ausgedehntheit // ‘Länge’ Ausdehnung // von dem des begrenzten endlichen ‘u.s.w.’.

? //

Das [b|B]ild, das wir uns von der logischen Notwendigkeit, vom logi- schen Zwang machen, ist etwa das : , daß der logische Mechanismus die Maschine ˇsei aus ˇeinemc unendlich hartem harten Material ⌊(⌋gemachtc⌊)⌋ ist besteht // daß es eine logische Maschine gibt deren Teile aus einem unendlich harten Material bestehen gemacht sindc // daß seine Teile nicht brechen, noch sich biegen können; & wenn … daß seine Teile daß sie weder nicht brechen, noch sich biegen können. Und wenn in diesem Mechanismus dies ein Rad so gedreht wird, dann muß das andere sich so drehen.

​

17.9.     Aber inwie was für Eigenschaften der 100 Kugeln hast Du entfaltet, oder gezeigt? – Nun, daß man diese Dinge mit ihnen tun kann. – Aber welche Dinge? Meinst Du: daß Du sie hast so bewegen können, daß sie nicht an der Tischfläche festgeleimt waren? – Dies auch, aber hauptsächlich : , daß keine von ihnen verschwand, daß man sie verschieben & der Verschiebung mit den Augen folgen konnte, daß sie dabei ihre Form beibehielten. – Aber warum hast Du das den Ausdruck “entfalten” gebraucht? Du hättest doch nicht gesagt, Du entfaltest die Eigenschaften einer Eisenstange, indem Du zeigst, daß sie bei so & so viel Grad schmilzt? Und nimm einen einfachern Fall: ‘entfalte die Eigenschaften ˇeiner Reihe’ von 4 Äpfeln, indem Du sie erst so: ⚬ ⚬ ⚬ ⚬ dann so: ⚬ ⚬     ⚬ ⚬ legst! Könntest Du nicht ebensogut sagen, Du entfaltest die Eigenschaften unseres Zahlengedächtnisses (z.B.)? Was Du eigentlich entfaltest, ist ja wohl die Reihe der Kugeln. – Und Du zeigst daß, wenn eine Reihe so & so aus- schaut, z.B. so & so römisch numeriert ist, daß sie dann auf einfache Weise sehr einfach , & ohne daß eine dazu- oder wegkommt, in jene andere einprägsame Form gebracht werden kann. Aber ebensogut konnte das doch ein psychologisches Experiment sein, das zeigt, daß Du jetzt gewisse die Formen einprägsam findest, in die 100 Flecke durch ˇbloßes Verschieben gebracht werden.        “Ich habe gezeigt, was sich mit 100 Kugeln machen läßt.” Du hast gezeigt, daß sich diese 100 Kugeln so entfalten ließen. Das Experiment war eines des Entfaltens[.| (]im Gegensatz z.B. zu einem des Verbrennens).           Und das psychologische Experiment konnte z.B. zeigen, wie leicht man Dich betrügen kann; daß Du es nämlich nicht merkst, wenn man Kugeln zu der Reihe dazuschmuggelt, oder wegschmuggelt.    Man könnte ja auch so sagen: Ich habe gezeigt was sich mit ˇeiner Reihe von 100 Flecken durch scheinbares Verschieben machen läßt, welche Figuren man durch scheinbares Ver⌊s⌋chieben aus ih[n|r]en erzeugen lassen. – Was aber habe ich in diesem Fall entfaltet?       Es kann doch z.B. nicht gut ein Entfalten der Eigenschaften von 100 römisch numerierten Kugeln genannt werden, daß sie sich arabisch bis zur [z|Z]ahl ‘100’ numerieren lassen!           Wie⌊,⌋ wenn ich sagte: “Ich habe die Eigenschaften dieser Formation (von Leuten) entfaltet”?

​

Ich bin sehr hin. Ermüdbar, ohne rechtes Leben. Kann zwar arbeiten, aber ohne Lust. Es ist, wie wenn meiner Arbeit der Saft entzo- gen wäre. Das einzige menschliche Gefühl, was ich noch habe ist das, daß ich von dem allem über mich etwas lernen soll. Uber den Wert meiner Arbeit & über das, was ich machen soll. – Es ist mir aber manchmal, als wäre ich sehr reich, & manchmal als wäre ich ganz arm.

⌇ /

Denk Dir, man sagte: ich wir entfalte⌊n⌋ die Eigenschaften eines Polygons indem ich wir je immer j[3|e] & 3 Ecken Seiten durch eine Diagonale zusammennehme[.|n]. Es zeigt sich dann etwa als 15 Eck. Habe Will ich sagen : , ich habe eine Eigenschaft des 15 Ecks entfaltet? Nein. Ich will sagen ich habe eine Eigenschaft dieses (hier gezeichneten) Vielecks entfaltet.      Ist dies ein [e|E]xperiment? Gewiß. Ich weiß wußte ja nicht was herauskommen wird würde, noch weiß ich, ob das Gleiche bei⌊m⌋ de nächsten Versuch herauskommen wird.     Ja; wie aber, wenn ich so einen diesen Versuch an einem Fünfeck anstelle, das ich ja schon übersehen kann? – Nun, nehmen wir für einen Augenblick an ich könnte es nicht übersehen, was z.B. geschehen kann, wenn es zu groß ist & ich zu nahe. Dann wäre das Ziehen der Diagonalen ein Mittel, um mich davon zu überzeugen, daß da ein Fünfeck steht. Ich könnte wieder sagen, ich habe die Eigenschaften des Polygons das da gezeichnet ist entfaltet. – Kann ich es nun übersehen, dann kann sich doch daran nichts ändern. Es war etwa überflüssig diese Eigenschaft zu entfalten, wie es überflüssig ist zwei Äpfel die vor mir auf dem Tisch liegen zu zählen.      Soll ich nun sagen: “es war wieder ein Experiment, aber ich war des Ausgangs sicher”[!|?] Aber bin ich des Ausgangs in der Weise sicher, wie des Ausgangs der einer Elektrolyse einer Wassermenge? Nein, – sonderndern anders! Ergäbe die Elektrolyse der Flüssigkeit nicht H2O so würde ich mich nicht für närrisch halten oder sagen, ich wisse jetzt überhaupt nicht mehr was ich sagen soll.         Denk' Dir ich sagte: “Ja, hier steht ein Quadrat, ⌊–⌋ aber schauen wir noch nach, ob es durch eine Diagonale in zwei Dreiecke zerlegt wird!” Ich ziehe sie dann nun & sage: “Ja, hier haben wir zwei Dreiecke.” Da würde könnte man mich fragen: Hast Du denn nicht gesehen daß es in zwei 3-Ecke zerlegt werden kann? Bist Du erst jetzt überzeugt, daß hier ein Viereck steht; & warum traust Du jetzt Deinen Augen mehr als wie früher?       Aber dann ist es ja auch ein Experiment, wenn ich die Linien gar nicht ziehe, sondern nur ‘[i|m]it dem Auge’ immer so & so viele Seiten zusammennehme. Freilich, auch es so prüfen ist ein Experiment. – Und so ist es auch ein Experiment, wenn ich Analoges mit einem dem am an einem Quadrat tue mache .; Ees zeigt, daß ich dies ⌊(⌋jetzt⌊)⌋ an der Figur die hier steht ausführen kann – was immer dies zeigen mag.        Man könnte es ja auch “die Eigenschaften einer Reihe von Kugeln entfalten” nennen, wenn ich sie einfach zähle; & anderseits könn- te man das mehrmalige Umgruppieren einer Reihe auch ‘ein mehrmaliges zählen auf verschiedene Arten’ nennen.          Aber dann ist das Umgruppieren der Bilder im Film auch nur ein [z|Z]ählen der Kreise Flecke . Dann muß es ja aber auch ein Experiment sein. Denk Dir es würde im Film gezählt indem die ⌊das⌋ Nummerieren der Reihe nach gefilmt würde; dann zählt hier also der Film selbst die Reihe der Kreise Flecke – aber damit es mich überzeugt muß ich mitzählen, d.h., das gefilmte [z|Z]ählen kontrollieren, denn wenn im Film falsch gezählt würde, so wäre kämen wir zwar ⌊(⌋dennoch⌊)⌋ zu der & der Zahl, aber ich dürfte sie nicht als Resultat Ergebnis der Zählung anerkennen. Mein Zählen besteht hier darin, die Reihenfolge der auftauchenden Ziffern zu prüfen.

/ /

Aufgaben: Zahl ˇder Töne, die innere Eigenschaft einer Melodie; die äußere Zahl der Blätter, äußere Eigenschaften eines Baumes. Wie hängt das es mit der Identität des Begriffes zusammen.

/ /

Wir sagen: “Es paßt, ich habe es probiert” nicht nur: “es hat gepaßt, ich habe es probiert”. Und ebenso: “er ist 1 m lang ich habe ihn gemessen” “Er wiegt 50 kg, ich habe ihn gewogen” , & auch: “Ich kann es, ich habe es probiert.”         Wir sagen⌊:⌋ von einem “der Schuh er paßt⌊“⌋, auch wenn wir ihn nicht anhaben.

s

Das Bild zeigt: Das nennen wir eine Umgruppierung von … den Vorgang einer Umgruppierung von 100 auf 10 × 10. Das Expe- riment zeigt: eine solche Umgruppierung hat sich hier vollziehen lassen. (Ist das richtig?)

/ /

Was für einen Sinn hätte es anzunehmen, daß ein Stück Stahl wenn wann immer man seine Festigkeit Härte auf keine Weise beansprucht ⌊gerade⌋ nicht prüft , sie verliert, oder verändert ändert . Hängt mit der Idee zusammen, daß die Körper um uns nur solange existieren als sie wahrgenommen werden. Das ist wirklich: das Zifferblatt mit dem Zeiger kuppeln; denn hier kuppelt man ˇin der Grammatik die Aussage eines Tatbestandes mit der Bedingung der Nichtkontrollierbarkeit. Man hat die Annahme dadurch zu einem leerlaufenden Rad der Sprache gemacht ; und . Und sie stört nun den Mechanismus der Sprache jedenfalls nicht.

​

18.9.    Reise heute nach Bergen Francis entgegen. Bin wieder sehr sinnlich; in der Nacht wenn ich nicht schlafen kann, sinnliche Phantasien. Vor einem Jahr wahr ich viel anständiger, ich meine[;|:] mein Sinn viel mehr auf Besserung gerichtet, ernster.

/ /

Hat es einen Sinn, zu fragen: Ist Hat dieses Stück Eisen nur dann diese Festigkeit, oder Elastizität,, wenn wir etwas dran hängen, oder auch wenn niemand sie prüft?” // , wenn sie geprüft wird, oder auch sonst?” // Dies ist doch eine gut deutsche Fr⌊a⌋ge! Und, daß wir empfinden, ⌊:⌋ “das heißt ja nichts!”, – weist uns auf den eigentlichen eigentümlichen Gebrauch des Ausdrucks, “eine Festigkeit haben hin”, auf seine Beziehung zu den einzelnen Erfahrungen, die die Festigkeit prüfen. darauf hin, den … aufzusuchen , seinen & den Zusammenhang mit den Erfahrungen, die uns die Festigkeit zeigen.     (Von so einer Frage sagen wir: ‘sie treibe das Problem auf die Spitze’.)

? / /

Vergleiche den ‘Zustand’ der diese Festigkeit zu haben mit dem ‘Zustand’ diese Farbe zu haben, & ⌊.⌋ ⌊Und⌋ wieder mit dem ˇZustand, diese Länge zu haben⌊:⌋ a) die gesehene, b) die gemessene. Und nun mit dem ‘Zustand’ einer bestimmten Fähigkeit: Z.B., der Fähigkeit dieser Feder diesen Druck auszuüben, meiner Fähigkeit dies Gewicht zu stemmen, meiner Fähigkeit dies Gedicht aufzusagen, meiner Fähigkeit, diese Reihe fortzusetzen.

? / /

Unter welchen Umständen sagt man: “x ist in diesem Zustande”. D.h. wie, unter welchen Umständen, gebraucht man hier die Gegenwart des Verbums; unter welchen, die andern Zeitformen?

/

Es gibt [f|F]älle, in denen Umstände unter denen man sagt: “ich kann es”, während man es nicht gerade tut. – Andere unter denen in denen man in so einem Fall sagt: “ich glaube, ich kann es”. Es gibt auch Fälle, in welchen man nur dann sagt: “ich kann es”, wenn man es gerade tut.

​

Was sind unsere die Kriterien dafür, ‘daß wir etwas können’? Daß wir es früher getan haben; daß wir etwas anderes (etwa ‘schwereres’) früher getan haben; daß wir es jetzt tun; daß wir jetzt gerade etwas getan haben, was als Probe der Fähigkeit gilt (sich das Gedicht leiße vorsagen ˇals Probe dafür daß man es laut aufsagen kann).

​

Meine Darstellungsform, wie ich sie begonnen habe, ist zu wenig elastisch.         Die ˇzufälligen Zusammenˇhänge der Darstellung zu zäh, & geben nicht Raum für die vielen unzähligen andern, die auch vorhanden sind. Kein Mittel um rasch diese Zusammenhänge anzudeuten.

​

22.9. Francis von Bergen geholt. Auf der [h|H]infahrt viel geschrieben, voller Gedanken. Dann mit F. sinnlich, reizbar, unanständig. Zwei oder d dreimal mit ihm gelegen. Immer zuerst mit dem Gefühl, es sei nichts schlechtes, dann mit Scham. Bin auch ungerecht, auffahrend & auch falsch gegen ihn gewesen & quälerisch.

/ /

Man kann sich leicht eine Sprachen denken, in der es keine Frage- & keine Befehlsform gibt, sondern in der alles in Frage & Befehl in Formen in der Form der Behauptung ausgedrückt wird in Formen z.B. denen in unserer Sprache “Ich möchte wissen, ob …” & “Ich wünsche daß …” entsprechen. Dies mag uns kann ⌊(⌋uns⌊)⌋ zeigen, wie mannigfach die Verwendung der Form der Behauptung ist.        Niemand würde doch von einer Frage (etwa: ob es draußen regnet) sagen, sie sei wahr oder falsch. Es ist freilich deutsch, dies von einem Satz, “ich wünsche zu wissen, ob …”, zu sagen. Wenn nun aber diese Form immer durchgängig ˇanstatt der unserer Frage verwendet wird? –

/

23.9.    Die ˇgroße Mehrzahl der von uns Sätze, die wir ˇaussprechen, schreiben & lesen sind Behauptungssätze.    Und – sagst Du – diese Sätze sind entweder wahr, oder falsch. Oder, wie ich auch sagen könnte, mit ihnen wird das Spiel der Wahrheitsfunktionen ~, ⌵ , etc. gespielt. Denn die Behauptung ist nicht etwas, was zu dem Satz hinzutritt, sondern ⌊(⌋ein⌊)⌋ wesentlicher Zug des Spiels, das was wir mit ihm spielen. Etwa [V|v]ergleichbar dem Charakteristicum des Schachspiels daß ˇes ein Gewinnen & Verlieren dabei gibt & daß der [G|g]ewinnt, der welcher dem [a|A]ndern den König nimmt. Freilich es könnte eine dem Schach sehr verwandtes Spiel geben, das darin besteht daß man die Schachzüge macht, aber ohne daß es dabei ein Gewinnen ˇ& Verlieren gibt, oder daß aber die Bedingungen des Gewinnens sind ganz andere.

/

Denke man sagte: Ein Befehl besteht aus dem einem Vorschlag (‘Annahme’) & dem Befehlen des Vorgeschlagenen.

/

Könnte man nicht Arithmetik treiben ohne auf den Gedan- ken zu kommen arithmetische Sätze auszusprechen & ohne daß un[d|s] die Ähnlichkeit einer Multipli[c|k]ation mit einem Satz je auffiele?           Aber würden wir nicht den Kopf schütteln, wenn [e|E]iner uns eine falsche gerechnete Multiplikation zeigte : , wie wir es tun wenn [e|E]iner er uns sagt, es regnet, ⌊–⌋ wenn es nicht regnet? – Doch; & hier liegt die Ähnlichkeit // ein Punkt der Anknüpfung // . Wir machen aber auch abwehrende Gesten, wenn ein unser Hund sich nicht ˇso benimmtc, wie wir es wollen wünschen . Wir sind gewohnt, zu sagen “2 mal 2 ist 4” & das [W|V]erbum ‘ist’ macht dies zum Satz & stellt eine scheinbar nahe scheinbar eine nahe Verwandtschaft her mit allem übrigen, was wir ‘Satz’ nennen während es sich nur um eine sehr oberflächliche Bekanntschaft äußerliche Beziehung handelt.

s ? / /

Wo es [B|b]ei Euklid heißt: das & das sei zu konstruieren & am Schluß, “q.e.c.” könnte es man auch setzen: Es e sei zu beweisen, daß das & das die Konstruktion dieser Figur sei & am Schluß schreiben “q.e.d.”, also das Resultat auf die Form des bewiesenen Satzes des Satzes bringen.

s / /

Denk an die Verwendung der Behauptungsform, wenn es in den Regeln eines Spiels heißt: “Man stellt die Steine in der & der Ordnung auf”. Denk Dir, es fragte [e|E]iner: “[i|I]st das wahr, oder falsch⌊?⌋“.    Ich höre, daß es von dieser Stadt zu⌊r⌋ der jener andern 100 km sind ist , & sage: “100 km, ⌊–⌋ das ist weit lang . –” (Ein Satz der sich nur mathematischer Begriffe bedient.)

/ /

Gibt es wahre Sätze in Russells System, die nicht in seinem System zu beweisen sind? – Was nennt man denn einen wahren Satz in Russells seinem System?

/ /

Was heißt denn, ein Satz ‘ist wahr’? p ist wahr = p. ⌊(⌋ Dies Das ist die Antwort.⌊)⌋        Man will also etwa fragen: unter welchen Umständen [B|b]ehauptet man einen Satz? oder: Wie wird die Behauptung also das Aussprechen des Satzes im Sprachspiel gebraucht. Und die “Behauptung des Satzes” ist hier ⌊(⌋nur⌊)⌋ entgegengesetzt: dem Aussprechen des Satzes etwa als Sprachübung, oder als Teil eines andern Satzes, u. dergl.         Fragt Sagt man also in diesem Sinne: “Unter welchen Umständen behauptet man in Russells Spiel einen Satz”, so ist die Antwort: Am [e|E]nde eines ˇseiner Beweises oder als ‘Grundgesetz’ (p.p.). Anders werden in diesem System Behauptungssätze in den R.schen Symbolen nicht verwendet.

/ /

“Kann es aber nicht ˇwahre Sätze geben, die in diesem Symbolismus angeschrieben sind, aber in dem System R's nicht beweisbar?” – ‘Wahre Sätze’, das sind also Sätze, die in einem andern System Spiel wahr sind, d.h. in einem andern Spiel mit Recht behauptet werden können. Gewiß; warum soll es keine solchen Sätze geben; oder vielmehr: warum soll man nicht Sätze, – der Physik, z.B., – in R's Symbolen anschreiben? Die Frage ist ganz analog der: Kann es wahre Sätze in Euklids Sprache geben, die in seinem System nicht beweisbar, aber wahr sind? – Aber es gibt ja sogar Sätze die in Euklids System zw beweisbar, aber in einem andern falsch sind. Können nicht Dreiecke – in einem andern System – ähnlich (sehr ähnlich) sein, die nicht die gleichen gleiche Winkel haben? – “Aber das ist doch ein Witz – ⌊!⌋ sie sind ja dann nicht im selben Sinne ˇeinander ‘ähnlich’!” – Freilich ˇnicht; & ein Satz der nicht in Russells System zu beweisen ist, ist in anderm Sinne “wahr” oder “falsch”, als ein Satz der ‘Principia Math.’

/ /

Nun teilt mir Nimm an Ich stelle mir vor,, es fragte mich ⌊(⌋nun⌊)⌋ Einer um Rat er & sagt: “Ich habe einen Satz ˇ(ich will ihn mit P nennen bezeichnen) in R.'s Symbolen konstruiert, hergestellt, & den kann man durch gewisse entsprechende Definitionen & Transformationen so deuten, daß er sagt“ ⌊:⌋ ⌊‘⌋P ist nicht in R's System beweisbar” ⌊’⌋. // auch in der Form aussprechen: “ ⌊‘⌋P ist ˇ(in R's System) nicht beweisbar” ⌊’⌋ // Muß ich nun von diesem Satz nicht sagen: einerseits, er sei [W|w]ahr, anderseits er sei unbeweisbar? denn angenommen, er wäre sei falsch, so ist es also wahr, daß er beweisbar ist⌊!⌋ & das kann doch nicht sein. Und ist er unbeweisbar bewiesen, so ist damit bewiesen, daß er nicht beweisbar ist! So kann er also nur wahr aber unbeweisbar sein.”         Wenn wir von beweisbar & unbeweisbar in R's System reden, dann müssen wir auch von wahr & falsch in diesem System       So wie wir fragen: “in welchem System ‘beweisbar’?”, so müssen wir auch fragen: “in welchem System ‘wahr’?”. ‘In R's System wahr’ heißt in R, wie gesagt, ⌊:⌋ in R's System bewiesen; & ‘in R.'s System falsch’ heißt: das Gegenteil sei in R's System bewiesen. – Was heißt nun Dein: “angenommen er sei falsch”? In R.'s Sinne heißt es: “angenommen das Gegenteil sei ˇin R's System bewiesen”; ist das Deine Annahme, so wirst Du jetzt die Deutung, er sei unbeweisbar, wohl aufgeben. Und unter dieser Deutung verstehe ich die Übersetzung in diesen deutschen Satz. – Nimmst Du an, der Satz sei in R's Sinne b⌊e⌋weis- bar, so ist er damit in R's Sinne wahr & die Deutung “P ist nicht beweisbar ist wieder aufzugeben. Nimmst Du an der Satz sei in R's Sinne wahr, so folgt das gleiche. Ferner: Soll der Satz in einem andern als R's Sinne falsch sein: so widerspricht dem nicht, daß er in R's System bewiesen ist. ⌊(⌋Was im Schach “verlieren” heißt, kann darin kann doch in einem andern Spiel das gGewinnen ausmachen. bestehen.⌊)⌋

/

Die ganze Frage wäre ohne jedes Interesse, wenn sie nicht an einen Aberglauben der Mathematiker anknüpfte. Und diesen wieder lohn⌊t⌋en es sich nicht zu widerlegen // Und mit diesem wieder lohnte es sich nicht zu streiten, // wenn er nicht eine Symptom einer allgemein verbreiteten Denkkrankheit wäre.

/ /

Was heißt es denn: “P” & “P ist unbeweisbar” seien der gleiche Satz? Es heißt daß diese zwei deutschen Sätze in der & der Notation den einen Ausdruck haben.

∫

Haben sie aber Denk nun Einer fragte mich: “Ist ‘P’ beweisbar?” – [n|N]un antworte ich: “P.” Das ist n[ä|a]türlich keine Antwort.; Aauf Deutsch hätte ich antworten müssen: “‘P’ ist unbeweisbar”. Denke aber es fragte mich Einer in jener andern Notation: “P?” – Was soll ich antworten?

/ /

“Aber P kann doch nicht beweisbar sein, denn ˇangenommen es wäre es beweiies⌊en⌋bar so wäre der Satz bewiesen, er sei nicht beweisbar.” Aber wenn dies nun bewiesen wäre, oder wenn ich glaubte – vielleicht irrtümlich – durch ˇeinen Irrtum – ich hätte es bewiesen, warum sollte ich den [b|B]eweis nicht als solchen anerkennen & erkl sagen, gelten lassen & sagen, ˇich habe meine Deutung⌊:⌋ der “Uunbeweisbarkeit” zu sehr weit ausgedehnt? // sagen, ich müsse meine Deutung … zurückziehen //

/ /

Nehmen wir an, ich beweise die Unbeweisbarkeit (in R's System) von P; so habe ich mit diesem Beweis P bewiesen. Wenn nun dieser Beweis einer in R.'s System wäre, – dann hätte ich also zugleicherzeit seine Zugehörigkeit & Unzugehörigkeit zum R'schen System bewiesen. – Das kommt davon, wenn man solche Sätze bildet. – Aber hier wäre ist ja ein Widerspruch! – Nu[m|n] so ist hier ein Wiederspruch. Schadet er hier etwas?

/ /

Schadet der Widerspruch der ents[f|t]eht, wenn [e|E]iner sagt: “Ich lüge. – Also lüge ich nicht. – Also lüge ich. etc.” Ich meine: ist unsere Sprache dadurch weniger brauchbar, daß man in diesem Fall aus einem nach den gewöhnlichen Regeln sein Gegenteil & daraus wieder ihn folgern kann? – Der Satz ⌊(⌋selbst⌊)⌋ ist unbrauchbar, & ebenso dieses Schlüsseziehen; aber warum soll man es nicht tun? im übrigen kann man es tun, wenn man will. Ich würde sagen: [e|E]s ist ˇim eigentlichen Sinne eine brotlose Kunst⌊.⌋, aber Es ist ⌊(⌋nur⌊)⌋ eine brotlose Kunst ! . – Es ist ein Sprachspiel das welches eine Ähnlichkeit hat ˇmit dem Spiel des Daumenfangens. ⌊(⌋ Dieses Dies wird so gespielt: Man Hahälte den Daumen der Deiner rechten Hand mit Deiner der linken, so daß seine Spitze noch oben aus der linken Hand hervorschaut. Nun ⌊ent⌋ziehet den Daumen man die rechte Hand rasch aus derm ˇGriff der linken Handc & trachte⌊t⌋ seine die ˇrechte ⌊Daumen⌋Sspitze noch mit der rechten Hand zu fangen, ehe sie sich zurückzieht.⌊)⌋

/ /

Interesse erhält so ein jener Widerspruch nur dadurch, daß er Menschen gequält hat gequält hat; & so dadurch zeigt, wie die Sprache zu ˇquälenden Problemen führen kann. // was für Dinge uns quälen können. // ⌊ // [W|w]ie aus der Sprache quälende Probleme w[ä|a]chsen können. // ⌋ ⌊⌊ˇ // wie aus der Sprache quälende Probleme wachsen können; & was für Dinge uns quälen können. // ⌋⌋ // zeigt, was Menschen quälen kann. //

/ / /

24.9.    Ein Beweis der Unbeweisbarkeit ist quasi ein geometrischer Beweis; ein Beweis die Geometrie der Beweise betreffend. Ganz analog einem Beweise etwa daß man die & die Konstruktion nicht mit Zirkel & Lineal ausführbar ist. Nun enthält so ein Beweis ein Element der Vorhersage, ein physikalisches Element. Denn als Folge dieses Beweises sagen wir ja einem Menschen: “Bemüh Dich nicht, eine Konstruktion (der 3-Teilung des Winkels, etwa) zu finden, – man kann beweisen, daß es nicht geht.”     Das heißt: [e|E]s ist wesentlich daß sich der Beweis der unbeweisbarkeit in dieser Weise soll anwenden lassen. Er muß – könnte man sagen – für uns ein triftiger Grund sein, die Suche nach einem Beweis a (ˇalso eine⌊r⌋ ˇsolchen Konstruktion ˇder & der Art) aufzugeben.

/ /

Leute Menschen sagen gelegentlich haben mir manchmal gesagt , sie könnten das & das nicht beurteilen, sie hätten nicht Philosophie gelernt. Ich war dann immer etwas un- willig, da dies Unsinn ist: als wäre ⌊⌊Dies ist ein irritierender Unsinn;, es wird ;: denn es wird vorgegeben,⌋⌋ die Philosoph⌊i⌋e eine ˇsein irgend eine Wissenschaft– wie die Medizin. ⌊.⌋ ˇUnd man redet von ihr etwa wie von der Medizin. – – Das aber kann man sagen, daß Leute, die nie eine philosophische Untersuchung ˇphilosophischer Art angestellt haben, wie die meisten Mathematiker z.B., nicht mit den richtigen Sehwerkzeugen ˇfür so einec derlei Untersuchung oder Prüfung ausgerüsstet sind,⌊.⌋ eine solche Untersuchung zu machen. So, Beinahe, wie [e|E]iner der nicht gewohnt ist ˇim Wald nach Blumen oder Beeren Blumen, Beeren, oder Kräutern zu suchen, keine findet, weil sein Auge für sie nicht geschärft ist & er nicht weiß, wo insbesondere man nach ihnen ausschauen muß. So geht der in der Philosophie ungeübte an allen Stellen vorbei, wo Schwierigkeiten ˇunter dem Graß verborgen liegen, während der Geübte dort stehenbleibt & fühlt, hier sei eine Schwierigkeit, obgleich obwohl er sie noch nicht sieht. – Und das ist ⌊,⌋ kein Wunder, wenn man weiß wie lange Du weißt, daß auch der sehr Geübte Sucher, der wohl merkt, hier liege eine Schwierigkeit, sie oft dessen genauesten Suchens ˇlange nicht finden kann. // sie oft, dem genauesten Suchen zum Trotz, ˇlange nicht finden kann. // suchen muß, um sie zu finden.    Wenn etwas gut versteckt ist, ist es schwer zu finden.

/ /

Ob etwas mit Recht der Satz genannt wird: “ξ ist unbeweisbar”, hängt davon ab, wie wir diesen Satz beweisen. Nur der Beweis zeigt, was als das Kriterium der Unbeweisbarkeit gilt. Der Beweis ist ein Teil des Systems ˇvon Operationen, des Spiels, in dem welchem // worin // der Satz gebraucht wird & zeigt uns seinen ‘Sinn’.

/ /

Der Satz “p ist unbeweisbar” hat einen andern Sinn, nachdem, ⌊–⌋ als ehe er bewiesen ist.     Ist er bewiesen, so ist er die Schlußfigur des U⌊n⌋beweisbarkeitsbeweises. – Ist er unbewiesen, so ist ja noch nicht klar, was als Kriterium seiner Wahrheit zu gelten hat, & sein Sinn ist – kann man sagen – noch verschleiert. vag & unbestimmt.

/ /

Wie, soll ich nun annehmen, ist P bewiesen? Durch einen U⌊n⌋beweisbarkeitsbeweis[.| ?] ? oder auf ˇeine andere Weise? Nimm an, durch einen Unbeweisbarkeitsbeweis: Nun, um zu sehen, was bewiesen i⌊s⌋t, schau auf den Beweis! Vielleicht ist hier bewiesen, daß die & die Form des [b|B]eweises nicht zu P führt. – Oder, es sei P auf eine direkte Art bewiesen – wie ich einmal sagen will –, dann folgt also der Satz “P ist unbeweisbar” & es muß sich nun zeigen, wie warum diese Deutung der Symbole von P mit der Tatsache des Beweises kollidiert & warum sie hier aufzugeben sei.    Angenommen aber, ~ P sei bewiesen. – Wie bewiesen? Etwa dadurch, daß P ˇdirekt bewiesen ist – denn daraus folgt, daß es beweisbar ist : , also ~P.   Was soll ich nun aussagen: “P”, oder “~P”? Warum nicht beides? Wenn mich jemand fragt: “Was ist der Fall: P, oder ~ nicht -P?” so antworte ich in dies : “⊢ P” steht am [e|E]nde eines R'schen Beweises, insofern kannst Du also schreibst Du … ˇschreibst also im R'schen System schreiben⌊:⌋ “⊢ P”; anderseits ist es aber eben beweisbar & dies drückt man durch ⊢ ~P aus. ˇdieser Satz aber steht nicht am Ende eines R'schen Beweises gehört also nicht zum R'schen System. – Als die Deutung “P ist unbeweisbar” für P gegeben wurde, da kannte man ja den einen diesen den Beweis für P nicht & man muß kann also nicht sagen “P” sage: dieser Beweis existierte nicht. – Ist der Beweis hergestellt konstruiert , so ist damit eine [N|n]eue Lage geschaffen: Und wir haben ˇuns nun zu entscheiden, ob wir dies einen Beweis (noch einen Beweis) oder ob wir dies noch die Aussage der Unbeweisbarkeit nennen wollen.        Angenommen ~[p|P] sei direkt bewiesen; es ist also bewiesen, daß sich P direkt beweisen läßt? ⌊!⌋ Das ist also wieder eine Frage der Deutung – es sei denn, daß wir nun auch einen direkten Beweis von P haben. Wäre es nun so, nun, so wäre es so. –

/ /

⌊(⌋ˇSehr komisch ist Ddie abergläubische Angst & Verehrung, die der Mathematiker vor dem Widerspruch ˇempfinden.⌊)⌋

/ /

“Aber angenommen, der Satz wäre nun falsch – & daher beweisbar! –” – Warum nennst Du ihn ‘falsch’? Weil Du einen Beweis siehst? – Oder aus andern Gründen? Dann macht es ja nichts. Man kann ja den Satz des Wide⌊r⌋spruchs sehr wohl falsch nennen, mit der Begründung z.B., daß wir sehr oft mit gutem Sinn auf eine Frage antworten: “Ja – & nein.” Und desgleichen ebenso den Satz daß “p ≡ ~~p”, ⌊:⌋ weil wir sehr gut die Verdoppelung der Verneinung als eine Verstärkung der Verneinung verwenden können& ⌊,⌋ & ˇauch verwenden. // können, & nicht bloß als ihre Aufhebung. //

/ /

Du sagst: “… also ist P wahr & unbeweisbar.” Das heißt wohl: “Also ⊢ P.” Von mir aus, ⌊ –⌋ aber zu welchem Zweck schreibst Du diese ‘Behauptung’ hin? ( Das Es ist, als hätte jemand man au[f|s] irgend welchen Gründen auf eine Weiseaus ˇgewissen Prinzipien über Naturformen & Baustil abgeleitet, auf den Mount Everest, wo niemand wohnen kann, gehörte ein Schlösschen Haus ˇim Barockstile mit 20 Zimmern, etc. etc.) Und wie könntest Du mir die ihre Wahrheit ˇder Behauptung plausibel machen, da Du sie ja zu nichts weiter verwenden brauchen kannst, als zu jenen Kunststückchen?

s ? / /

[Nachtrag]  “Entfalte die Eigenschaften der Hundert!” Auf diesen Befehl hat er 100 Dinge in 50 & 50 zu zerlegen – nämlich ⌇sichtbar⌇ // // Er hat diese & diese einprägbare Veranderung mit dem Gesicht der 100 vorzunehmen. Und die Veränderungen dieses Gesichts sind nur zeitliche Fortsetzungen des Gesichts. Wir er- halten einfach ein raum-zeitliches Gesicht. Oder Du kannst auch sagen: ein Gesicht mit von einer Dimension mehr. Die Veränderung muß so einprägbar sein, wie das ˇstationäre Gesicht selbst.

s / /

Aber mit welchem Recht spricht man von einem “Entfalten der Eigenschaften” der Hundert? Ist es nicht ein Entfalten der Merkmale des Begriffes? ([i|I]n Freges Ausdrucksweise.)        Kann ich sagen: ich entfalte die Eigenschaften einer Gruppe von Kugeln – & nehme nun, was hier geschieht (was hier tatsächlich geschieht) zum Paradigma für die Erklärung (Definition) eines Begriffes. Und ich tue dies, weil, was hier geschieht sich immer wieder & wieder geschieht & weil ˇalso dieser Be- griff also dadurch sehr brauchbar wird. (Wie eine Maßeinheit, wenn viele der zu messenden Längen ganze Vielfache von ihr sind.)

s ? / /

Die Rechnung ist das Bild eines Experiments Vorgangs das wir als Paradigma niederlegen zum Maß – Vergleichsobjekt – für die Beschreibung von Vorgängen

​

Man kann von religiösen Gleichnissen sagen, sie bewegen sich am Randes des Abgrundes. Z.B. von der Alegorie B's. Denn wie, wenn wir bloß dazusetzen: “und alle diese F[ä|a]llen, Sümpfe, Abwege, sind vom Herrn des Weges angelegt, die Ungeheuer, Diebe, Räuber von ihm geschaffen worden”?     Gewiß, das ist nicht der Sinn des Gleichnisses! aber diese Fortsetzung liegt zu nahe! Sie nimmt dem Gleichnis, für Viele & für mich, seine Kraft.     Dann aber besonders, wenn dies – sozusagen – verschwiegen wird. Anders wäre es, wenn auf Schritt & Tritt offen gesagt würde: ‘Ich brauche dies als Gleichnis, aber schau: hier stimmt es nicht’. Dann hätte man nicht das Gefühl, daß man hintergangen wird, daß jemand versucht auch auf Schleichwegen zu überzeugen. Man kann Einem z.B. sagen: “Danke Gott für das Gute, was Du empfängst, aber beklage Dich nicht über das Übel : , wie Du es natürlich tätest, wenn ein Mensch Dir abwechselnd Gutes & Übles widerfahren ließe”. Es werden Lebensregeln in Bilder gekleidet. Und diese Bilder können mir dienen, zu beschreiben, was wir tun sollen, aber nicht dazu, es zu begründen. Denn um begründen zu können, dazu müßten sie auch weiter stimmen. Ich kann sagen: “Danke diesen Bienen für ihren Honig, als wären sie es gute Menschen, die ihn für Dich bereitet haben”.; Ddas ist verständlich & beschreibt, wie ich wünsche, Du sollest Dich benehmen. Aber nicht: Danke ihnen, denn sieh', wie gut sie sind!” – denn sie können Dich im nächsten Augenblick stechen.          Die Religion sagt: Tu dies! – Denk so! – aber sie kann es nicht begründen, & versucht sie es auch nur, so stößt sie ab; denn zu jedem Grund, den sie gibt, gibt es einen stichhältigen Gegengrund.       Überzeugender ist es, zu sagen: “Tu dies “Denke so! – so seltsam dies scheinen mag. –” Oder: “Möchtest Du das nicht tun? – so abstoßend es ist. –”

​

Gnadenwahl: So darf ˇman nur schreiben unter den fürchterlichsten [l|L]eiden – & dann heißt es etwas ganz anderes. – Aber darum darf dies auch niemand als Wahrheit zitieren, es sei denn, er selbst sage es unter Qualen. – Es ist eben keine Theorie. – Oder auch: Ist dies Wahrheit, so ist es nicht die, die damit auf den ersten Blick ausgesprochen zu sein scheint. Eher als eine Theorie, ist es ein Seufzer, oder ein Schrei.

Editorial notes

1) Arrow indicating continuation on page 31r.

2) Arrow indicating continuation from page 30r.

3) See facsimile; line connecting this sentence with the following one.