28.12.41.      Habe nichts zu schreiben fühle mich aber so leer & deprimiert, daß es eine Erleichterung ist irgend etwas aufzuschreiben. Bin sehr schwermütig. Denke viel an Francis, aber immer nur mit Reue wegen meiner Lieblosigkeit; nicht mit Dankbarkeit. Sein Leben & Tod scheint mich nur anzuklagen, denn ich war in den letzten 2 Jahren seines Lebens sehr oft sehr lieblos & im Herzen untreu gegen ihn. Wäre er nicht so unendlich sanftmütig & treu gewesen, so wäre ich gänzlich lieblos gegen ihn geworden. An meine Freunde in Wien denke ich beinahe gar nicht. Koder hat geheiratet & ich kann daher nicht mehr an ihn denken, oder: im Geiste sehen, da eine Wand vor ihn getreten ist. Wäre er gestorben so wäre die Erinnerung an ihn nicht ausgelöscht; so aber scheint auch sie entwertet.      Keith sehe ich oft, und was das eigentlich heißt, weiß ich nicht. – Verdiente Enttäuschung, Bangen, Sorge. Unfähigkeit, mich in einer Lebensweise niederzulassen. Nur wenige, kurze Stunden des Glücks in langen Strecken von Traurigkeit: Traurigkeit der schlimmen Art.      Ich habe kein positives Leben, oder einen Zweck oder Ziel. Ich fahre fort zu leben, ohne eigentliche Hoffnung. Bei der Arbeit – die manuell ist – ist mir am wohlsten. Ich denke da oft mit Trauer an Fr., aber die Trauer ist ruhig & nicht schlecht.

Manchmal, wie heute, scheint mir mein Leben kaum erträglich. Es scheint durch verschiedene Umstände zu einem Schluß gekommen zu sein, während ich noch bei guter Gesundheit & gar nicht alt bin.

3.1.42      Jedes Wort steht in einem Feld von Beziehungen, an einem bestimmten Punkt des Sprachfeldes: Wer also geneigt ist dies Wort zu wählen & nicht jenes, wählt einen Ort des Feldes statt eines anderen, eine Gruppe von Beziehungen statt einer anderen.

4.1.      Warum sind die Menschen viel mehr geneigt für als || für das Charakteristische des Gedächtnisses ein Gesichtsbild anzusehen || zu halten, als ‘eine Rede’. Man ist geneigt von “bloßen Worten” zu reden, aber nicht von einem “bloßen Gesichtsbild”. Die Weise, wie dies || ein Bild anzuwenden ist scheint viel selbstverständlicher als die Weise wie Sätze anzuwenden sind.

Der Mathematiker (Pascal) der die Schönheit eines Theorems der Zahlentheorie || von den Zahlen bewundert; er bewundert gleichsam eine Naturschönheit. Es ist wunderbar, sagt er, welch herrliche Eigenschaften die Zahlen haben. Es ist als bewunderte er die Gesetzmäßigkeiten eines Kristalls || die Regelmäßigkeiten einer Art von Kristall.

Man könnte sagen: welch herrliche Gesetze hat der Schöpfer in die Zahlen gelegt!

Wolken kann man nicht bauen. Und darum wird die erträumte Zukunft nie wahr.

Ehe man ein Flugzeug hatte hat man Flugzeuge erträumt & wie die Welt mit ihnen aussehen würde. Aber, wie die Wirklichkeit nichts weniger als diesem Traume glich, so hat man überhaupt keinen Grund zu glauben, die Wirklichkeit werde sich zu dem entwickeln, was man träumt. Denn unsere Träume sind voll Tand, gleichsam Papiermützen & Kostüme.

Beweis, daß zwei so aussehende Figuren das regelmäßige 5-Eck geben.

Wenn ich die (2) ringsherum getreu kopiere so ist das erste || letzte Zeichen dasselbe wie das letzte || erste.

Betrachte den mathematischen Satz als eine Bildbeschreibung; also so wie man etwa den Satz betrachten kann: “Der Engel führt Petrus aus dem Gefängnis”. (Beachte das Präsens.) Man könnte statt des Satzes eine Partizipialkonstruktion setzen: “Petrus vom Engel aus dem Gefängnis geführt”

Der Beweis zeigt 50 + 25 75 gebend.

Man kann das || ein Sprachspiel, im allgemeinen, nicht rechtfertigen. So tun wir's.

“Die Axiome eines mathematischen Axiomsystems sollen einleuchtend sein.” Wie leuchten sie denn ein?

Wie wenn ich sagte: so || So kann ich mir's am leichtesten vorstellen.      Und hier hat || ist Vorstellen nicht ein bestimmter seelischer Vorgang bei dem man zumeist die Augen schließt, oder mit den Händen bedeckt.

Was sagen wir, wenn uns so ein Axiom dargeboten wird, z.B. das Parallelenaxiom? Hat Erfahrung uns gezeigt, daß es sich so verhält? Nun vielleicht; aber welche Erfahrung? Ich meine: Erfahrung spielt eine Rolle; aber nicht die, die || welche man unmittelbar erwarten würde. Denn man hat ja doch nicht Versuche gemacht & gefunden, daß wirklich nur eine Gerade aus dem Strahlenbüschel durch den Punkt die andere Gerade nicht schneidet. Und doch leuchtet der Satz ein. – Wenn ich nun sagte: es ist ganz gleichgültig, warum er einleuchtet. Genug: wir nehmen ihn an. Wichtig ist nur, wie wir ihn gebrauchen.

Der Satz beschreibt ein || steht für ein Bild. Nämlich dieses:

Dies Bild ist uns annehmbar. Wie es uns annehmbar ist, die ungenaue || beiläufige Kenntnis einer Zahl durch Abrunden auf ein Vielfaches von 10 anzudeuten.

‘Wir nehmen diesen Satz an.’ Aber als was nehmen wir ihn an?

Ich will sagen: Wenn der Wortlaut des Parallelen-Axioms, z.B., gegeben ist (& wir die Sprache verstehen) so ist die Art der Verwendung dieses Satzes & also sein Sinn, noch gar nicht bestimmt. Und wenn wir sagen, es leuchtet uns ein, so haben wir damit, ohne es zu wissen, uns für schon auf eine ganz bestimmte Art der Anwendung festgelegt || Verwendung des Satzes gewählt. Der Satz ist kein mathematisches Axiom, wenn wir ihn nicht gerade dazu verwenden.

Daß wir nämlich hier nicht Versuche machen, sondern das Einleuchten gelten lassen || anerkennen legt schon die Verwendung fest. Denn wir sind ja nicht so naiv, das Einleuchten statt des Versuchs gelten zu lassen.

Nicht, || Ich will sagen: Nicht … daß er uns als wahr einleuchtet, sondern daß wir das Einleuchten gelten lassen, macht ihn zum mathem. Satz.

Lehrt uns die Erfahrung, daß zwischen je 2 Punkten eine Gerade möglich ist? Oder, daß zwei verschiedene Farben nicht an einem Orte sein können?      Man könnte sagen: die Vorstellung lehrt es uns. Und darin liegt die Wahrheit; man muß es nur recht verstehen || auffassen.

Vor dem Satz ist der Begriff noch geschmeidig.

Aber könnten nicht (Wahrheiten), Erfahrungen uns bestimmen das Axiom zu verwerfen?! Ja. Und dennoch spielt es nicht die Rolle des Erfahrungssatzes.

Warum ist || sind die Newtonschen Gesetze keine Axiome der Mathematik? Weil man sich sehr || ganz wohl vorstellen könnte, daß alles || es sich anders verhielte. Aber – will ich sagen – dies || dieses schreibt || weist jenen Sätzen nur eine gewisse Rolle im Gegensatz zu einer anderen zu. D.h.: von einem Satz zu sagen, || : ‘man könnte sich das auch anders vorstellen’ oder ‘man kann sich auch das Gegenteil davon vorstellen’ || man soll sich das auch anders vorstellen, schreibt ihm die Rolle des Erfahrungssatzes zu.

Der Satz den man sich nicht anders als wahr soll vorstellen können hat eine andere Funktion als der für den es sich nicht so verhält.

Die mathem. Axiome funktionieren dergestalt, daß, wenn Erfahrung uns dazu brächte || bewegte, ein Axiom aufzugeben, sein || das Gegenteil darin nicht zum Axiom würde. ‘2 × 2 ≠ 5’ heißt nicht, ‘2 × 2 = 5’ habe sich nicht bewährt.

Man könnte den Axiomen, sozusagen, ein spezielles Behauptungszeichen vorsetzen.

Axiom ist etwas nicht dadurch, daß wir es als äußerst wahrscheinlich, ja als gewiß anerkennen, sondern dadurch, daß wir ihm eine bestimmte Funktion zuerkennen & eine, die der des Erfahrungssatzes widerstreitet.

Wir geben dem Axiom eine andere Art der Anerkennung als dem Erfahrungssatz. Und damit meine ich nicht daß der ‘seelische Akt des Anerkennens’ ein anderer ist.

Das Axiom ist, möchte ich sagen, ein andrer Redeteil.

Man nimmt, wenn man das math. Axiom, das & das sei möglich, hört, ohne weiteres an, man wisse, was hier ‘möglich sein’ bedeutet; weil uns die Satzform gebräuchlich ist. || diese Satzform uns natürlich geläufig ist.

Man wird nicht gewahr, wie verschiedenerlei die Verwendung der Aussage, etwas || dies sei möglich || ‘… ist möglich’, ist & kommt nicht auf den Gedanken, nach der besondern Verwendung in diesem Fall zu fragen. || & kommt darum nicht auf den Gedanken nach der besondern Verwendung in diesem Fall, zu fragen.

Ohne die Verwendung im geringsten zu übersehen, können wir hier gar nicht zweifeln, daß wir den Satz verstehen.

Ist der Satz, daß es keine Wirkung in die Ferne gibt von dem Geschlecht der math. Sätze? Man möchte so auch sagen: der Satz ist nicht dazu bestimmt eine Erfahrung auszudrücken, sondern daß man sich etwas nicht anders vorstellen könne.

Zu sagen zwischen zwei Punkten sei – geometrisch – immer eine Gerade möglich, heißt: Von mehr als zwei Punkten auszu sagen, sie lägen auf einer Geraden ist eine Aussage sagt etwas; es von zweien zu sagen ist keine. || heißt: ein Satz “die Punkte .... liegen auf einer Geraden” sagt etwas über die Lage der Punkte nur, wenn er von mehr als 2 Punkten handelt. || heißt: der Satz “ … ” ist eine Aussage über die Lage von Punkten nur, wenn ‒ ‒ ‒.

So wie man sich auch nicht fragt, was ein Satz der Form “Es gibt kein …” (z.B.) “Es gibt keinen Beweis den Satz || dieses Satzes”) im besonderen Fall bedeutet. Auf die Frage was er bedeutet antwortet man dem Anderen & sich selbst mit einem Beispiel des Nicht-existierens

Der math. Satz steht auf vier Füßen, nicht auf dreien; er ist überbestimmt.

Wenn wir das Tun eines Menschen, z.B., durch eine Regel beschreiben, so wollen wir, daß der, dem wir die Beschreibung geben, durch Anwendung der Regel wisse, was im besonderen Fall geschieht. Gebe ich ihm nun durch die Regel eine indirekte Beschreibung?

Es gibt natürlich einen Satz, der sagt,: wenn Einer die Zahlen nach den & den Regeln zu multiplizieren trachtet so erhält er …

Eine Anwendung des math. Satzes muß immer das Rechnen selber sein. Das ist || bestimmt das Verhältnis der Rechentätigkeit zum Sinn der math. Sätze.

Wir beurteilen Gleichheit & Übereinstimmung nach den Resultaten unseres Rechnens, darum können wir nicht das Rechnen mit Hilfe der Übereinstimmung erklären.

Seit zehn Tagen schreibe ich wieder, trotz körperlicher Arbeit & schwacher Gesundheit. Das zeigt wie unabhängig Ideen (wenn auch schwache) von äußeren Umständen sind. Bin körperlich sehr matt.

Wir beschreiben mit Hilfe der Regel: wozu? Warum? das ist eine andre Frage. || Die Frage steht auf einem andern Blatt.

‘Die Regel, auf diese Zahlen angewandt, gibt jene’, könnte heißen: der Regelausdruck auf den Menschen angewendet macht ihn diese Zahlen erzeugen. || läßt ihn aus diesen Zahlen jene erzeugen.

Man fühlt ganz richtig daß dies kein math. Satz wäre.

Der math. Satz setzt einen gewissen Weg fest. || steckt einen bestimmten Weg aus || Der math. Satz bestimmt (für uns) einen Weg; legt (für uns) einen Weg fest!

Es ist kein Widerspruch daß er eine Regel ist und nicht einfach festgesetzt, sondern durch || nach Regeln erzeugt wird.

Wer mit einer || durch eine Regel beschreibt, weiß selbst auch nicht mehr als er sagt. D.h., er sieht auch nicht die Anwendung voraus, die er im besondern Fall von der Regel machen wird. Wer “u.s.w.” sagt, weiß selbst auch nicht mehr als “u.s.w.”.

Wie könnte man Einem erklären, was der zu tun hat, der einer Regel folgen soll?

Man ist versucht zu erklären: vor allem einmal muß er || tu das Einfachste (wenn die Regel z.B. ist immer das gleiche zu wiederholen. Und daran ist natürlich etwas. Es ist von Bedeutung, daß wir sagen können, es sei einfacher eine Ziffernreihe || Zahlenreihe anzuschreiben, in der jede Zahl gleich der vorhergehenden ist, als eine Reihe, in der jede Zahl um 1 größer ist als die vorhergehende. Und wieder, daß dies ein einfacheres Gesetz ist als das, abwechselnd 1 und 2 zu addieren.

Ist es denn nicht übereilt, einen Satz, den man an Stäbchen & Bohnen erprobt hat, auf Wellenlängen des Lichts anzuwenden? Ich meine: daß 2 × 5000 = 10000 ist.      Rechnet man wirklich damit, daß, was sich in so viel || vielen Fällen bewahrheitet hat, auch für diese stimmen muß? Oder ist es nicht vielmehr, daß wir uns mit der arithmetischen Annahme noch gar nicht binden?

Die Arithmetik als die Naturgeschichte (Mineralogie) der Zahlen. Wer spricht aber so von ihr? Unser ganzes Denken ist von dieser Idee durchsetzt.

Die Zahlen sind Gestalten (ich meine nicht die Zahlzeichen) & die Arithmetik teilt uns die Eigenschaften dieser Gestalten mit. Aber die Schwierigkeit ist da, daß die || diese Eigenschaften der Gestalten Möglichkeiten sind; || – nicht die gestaltlichen Eigenschaften der Dinge, die die Gestalt haben. || der Dinge solcher Gestalt. Und diese Möglichkeiten wieder entpuppen sich als physikalische, oder psychologische, Möglichkeiten (der Zerlegung, Zusammensetzung, etc.). Die Gestalten aber spielen (nur) die Rolle der Bilder, die man so & so verwendet. Nicht Eigenschaften von Gestalten ist es, was wir geben, sondern Transformationen von Gestalten, als irgendwelche Paradigmen aufgestellt.

Wir beurteilen nicht die Bilder, sondern mittels der Bilder.

Wir erforschen sie nicht sondern mittels ihrer etwas anderes.

Du bringst ihn zu der || zur Entscheidung dies Bild aufzunehmen. Und zwar durch Beweis, d.i., durch Vorführung einer Bilderreihe, oder einfach dadurch, daß Du ihm das Bild zeigst. Was zu dieser Entscheidung bewegt ist hier || hierbei gleichgültig. Die Hauptsache ist, daß es sich um das Annehmen eines Bildes handelt.

Das Bild einer Zusammensetzung; || des Zusammensetzens; ist keine Zusammensetzung || kein Zusammensetzen; das Bild einer Zerlegung keine Zerlegung; || des Zerlegens kein Zerlegen; das Bild des || keines Passens kein Passen. Aber diese Bilder sind von der || Aber || Und doch sind diese Bilder von der größten Bedeutung; So sieht es aus, wenn zusammengesetzt wird; wenn zerlegt wird; usw.

Wie wäre es, wenn Tiere oder Kristalle so schöne Eigenschaften hätten wie die Zahlen || Anzahlen. Es gäbe also z.B. eine Reihe von Gestalten, eine immer um eine Einheit größer als die andere. || Gegenständen, einer immer um eine Einheit größer als der andere.

Ich möchte darstellen können, wie es kommt, daß die Math. uns jetzt || jetzt uns als Naturgeschichte des Zahlenreiches, jetzt wieder als eine Sammlung von Regeln erscheint. || jetzt uns als die Beschreibung eines Naturreiches (des Zahlenreiches etwa), jetzt als ein System von Konstruktionen erscheint.

Könnte man aber nicht Transformationen von Tiergestalten (z.B.) studieren? Aber wie ‘studieren’? Ich meine: könnte es nicht nützlich sein, sich Transformationen von Tiergestalten vorzuführen? Und doch wäre dies kein Zweig der Zoologie. –

Ein math. Satz wäre es dann (z.B.), daß diese Transformation diese Gestalt in diese überleitet. (Die Gestalten & die Transformation wiedererkennbar.)

Wir müssen uns aber dessen || daran erinnern, daß der math. Beweis durch seine Transformationen || Umformung nicht bloß || nur zeichengeometrische Sätze, sondern Sätze des verschiedenartigsten Inhalts beweist. als wahr erweist

So beweist || beweisen die Umformungen || Transformationen eines Russellschen Beweises, daß dieser Tautologie || logische Satz sich mit Hilfe dieser Regeln || mit Hilfe dieser Regeln sich aus den Grundgesetzen bilden lasse.

Aber der Beweis wird als Beweis der Wahrheit des Schlußsatzes angesehen, oder als Beweis dafür, daß der Schlußsatz nichts sagt.      Das ist nun nur durch eine Beziehung des Satzes nach außen möglich; d.h. durch seine Beziehung zu andern Sätzen, z.B., & deren Anwendung.

‘Die Tautologie (‘p ⌵ ~p’, z.B.) sagt nichts’ ist ein Satz der sich auf das Sprachspiel bezieht, worin die ein der Satz der Satz wie p angewendet || verwendet wird. (Z.B.: “Es regnet, oder regnet nicht” ist keine Mitteilung über das Wetter.)

Die R.sche Logik sagt nichts darüber, welcher Art & Verwendung Sätze, ich meine nicht logische Sätze, sind: Und doch erhält die || diese Logik ihren ganzen Sinn (nur) von der supponierten Anwendung auf die Sätze.

Man kann aber den R.schen Beweis auch z.B. als Beweis dafür ansehen daß der bewiesene Satz in bestimmter Weise || in eine bestimmte andere Notation übersetzt || übertragen, die & die Struktur haben werde. Das ist wie wenn man beweist, es werde sich eine Zahl durch die & die Zahl teilen lassen.

Bewiesen wird durch Reden oder Schreiben, || – ein Beweis fungiert im Gebiete der Sprache.      Ein Beweis geht in der Sprache vor sich. Im Geschriebenen oder Gesprochenen.

Aber, sagst Du, durch einen Beweis sagen wir auch die Zukunft voraus. Aber wie können sie durch einen math. richtigen Beweis wahr & falsch vorhersagen.

Wenn sich ein Körper einer Parabel entlang bewegt, so kann ich für einen Satz der sagt auf welcher Abszisse er steht einen Satz konstruieren, der sagt, wie hoch auf || nach der Ordinate ich ihn zu suchen habe. || wie hoch ich ihn, der Ordinate nach, zu suchen habe.

Was ist z.B. an einem Russellschen P.p. mathematisch?!

Als Erfahrungssatz ist so ein Satz nicht aufzufassen. –

Wir nehmen dieses Bild 1 1 ÷ 3 = 0˙ 3 dafür an.

Der Math. ist nichts weniger charakteristisch als die || eine axiomatische Methode.

Die math. Sätze werden in einem Gedankenzug wie die nicht-mathematischen verwendet; ich meine: es werden aus beiden zusammen Schlüsse gezogen; || es werden Schlüsse aus beiden zusammen gezogen; sie spielen in der Rede die || eine ähnliche || gleichartige Rolle. (Das erinnert an die Rolle des Satzes “der Winkel α ist sich selbst gleich”)

Es ist Erfahrungstatsache, daß, z.B., bei einer Multiplikation immer oder so gut wie immer dasselbe Resultat sich ergibt, und wenn einmal etwas anderes herauskommt, daß wir dann immer, oder so gut wie immer einen Fehler entdecken können. Übrigens bezieht sich das nur auf kleine || nicht zu große Multiplikationen. Der mathematische Satz aber sagt nicht dies nicht. Und doch kann man sagen, daß diese Tatsache ihm zu Grunde liegt.

Ich meine, diese Tatsache bestimmt unsere Einstellung || Stellungnahme || [Attitude] zu dem Rechenvorgang || zu der Rechnung.

Die populärwissenschaftlichen Schriften unserer Wissenschaftler sind nicht der Ausdruck der harten Arbeit, sondern des Ruhens || der Ruhe auf ihren Lorbeeren. || … Wissenschaftler drücken nicht (harte) Arbeit aus, sondern das Ruhn auf den Lorbeeren. || … Wissenschaftler drücken nicht harte Arbeit aus, sondern sie sind der Ausdruck des Ruhens auf den Lorbeeren.

Wenn Du die Liebe eines Menschen hast, so kannst Du die Liebe || sie mit keinem Opfer zu teuer bezahlen; || überzahlen aber jedes Opfer ist zu groß || viel, um Dir die Liebe || sie zu erkaufen.

Denken wir uns Leute die z.B. zwei Gedichte auswendig lernen || gelernt haben als z.B. den Feuerreiter & Schön-Rohtraut, diese aus irgendeinem Grunde einander Wort für Wort zuordnen & nun sagen, die Erfahrung lehre, daß das zweite || eine immer bis zum Wort … des andern reiche. Das klingt || klänge seltsam. Warum? –

Ist diese Erfahrung eine ihr Gedächtnis betreffend, oder ihre Neigung so & nicht anders zuzuordnen, oder betrifft sie Eigenschaften des niedergeschriebenen Gedichts? || der Niederschriften der Gedichte?

Ich könnte sagen: Erfahrung lehrt, daß diese Leute (oder Leute in diesem || dem & dem Zustand) gemeinhin Worte in Gedichten auslassen, oder solche dazusetzen & daß daher jene Zuordnung nicht immer zum gleichen Resultat führt. (Oder, umgekehrt, daß sie es bei Leuten in dem & dem Zustande tut.)

Daß das Gedicht A auf diese Weise bis zum Wort … so & so des Gedichtes B reicht, kann ein mathematischer Satz sein, & hat die mathematische Gewißheit, wenn das als wesentliche Eigenschaft dieser || der Gedichte aufgefaßt wird. || Daß das Gedicht A bis zu dem Wort so & so des Gedichtes B reicht, ist ein mathematischer Satz, & hat mathematische Gewißheit, wenn das als wesentliche Eigenschaft der Gedichte aufgefaßt wird.

Was wirklich absurd wäre, || Wirklich absurd wäre – zu sagen, das Gedicht A reiche immer bis zu diesem Wort des Gedichts von B. Oder zum mindesten ließe dieser Satz eine Menge verschiedener Interpretationen zu.

Wäre das ein mathematischer Satz, || : zu sagen, daß die & die Regel an jedem zweiten Tag, die andere an den übrigen Tagen gelten solle?

Wir haben, z.B., das kommutative Gesetz für das Multiplizieren im Dezimalsystem rekursiv bewiesen: & nun finden wir eine Multiplikation (etwa eine sehr lange), für die a × b nicht dasselbe wie b × a ergibt. – (Der Raum, in dem die Rechnungen vor sich gehen – könnten wir annehmen – wäre gleichsam kein gerader.)      Was sollten wir nun tun? Nun die Anwendung der Rechnung würde sich ändern.

‘Es muß || muß ja so herauskommen!’ – das Auge des Geistes eilt scheinbar dem körperlichen Auge || den besonderen Rechnungen voran, & sieht, schon, was das körperliche Auge noch nicht sieht || gesehen hat: || & sieht, was das körperliche Auge noch nicht sieht. || & sieht, was wir mit unseren leiblichen Augen noch nicht gesehen haben.

1.4.42 Es geht mir außerordentlich schlecht: Ich habe keine Hoffnung mehr für die Zukunft in meinem Leben. Es ist als hätte ich nur mehr eine lange Strecke lebendigen Todes vor mir. Ich kann mir nur mich keine Zukunft als eine gräßliche vorstellen. Freundlos & freudlos.

Daß an der Stelle der periodischen Division, die mir die fünfzigste scheinen wird ‘5’ stehen werde, ist eine echte Voraussage.

Stell' ich mir etwa die ganze Reihe vor; habe ich so ein Bild? Das Rechnungsstück, das ich etwa hinschreibe ist meine ganze Vorstellung. Und das zeigt, welche Rolle die Vorstellung spielt. || Und das zeigt, was die Vorstellung ist. Ich will sagen: Die Vorstellung fliegt der Rechnung nicht voraus – wie man manchmal glauben möchte. Es ist die Anwendung, die den Sprung macht.

Ist es nun Erfahrung, die uns erlaubt, so etwas richtig vorherzusagen? Ist dies nicht ganz gleichgültig? Genug, wir machen eine richtige Vorhersage.

Man könnte wohl sagen, daß die Math. eine Leistung der Vorstellung ist.

Der math. Satz sagt nicht vorher, daß es herauskommen wird, sondern sagt, daß es so richtig ist.

‘Ein Pfund Käse kostet so & so viel’: damit das überhaupt || dies möglich ist, muß Käse allerlei Eigenschaften haben. Er muß sich z.B. wägen lassen, sein Gewicht nicht regellos verändern. Aber sagt jener Satz das? Wäre das Gegenteil des Satzes wahr, wenn es sich anders verhielte?

Beim Denken verwenden wir die Vorstellung.

Nur (auf dem Weg) über die Sprachspiele kann man die Mathematik verstehen.

Man kann sich denken daß Leute eine angewandte Mathematik haben ohne eine reine Mathematik. Sie können z.B. – nehmen wir an , || – die Bahn berechnen, die || welche gewisse sich bewegende Körper beschreiben werden & deren Ort zu einer gegebenen Zeit vorhersagen. Dazu benutzen sie ein Koordinatensystem, die Gleichung || Gleichungen von Kurven, als (eine Form der Beschreibung wirklicher Bewegung) & die Technik des Rechnens im Dezimalsystem. Die Idee eines Satzes der reinen Mathematik kann ihnen ganz fremd sein.      Diese Leute haben also Regeln denen gemäß sie die betreffenden Zeichen insbesondere z.B. Zahlzeichen handhaben transformieren zum Zweck der Voraussage des Eintreffens gewisser Ereignisse.

Aber wenn sie nun z.B. multiplizieren, werden sie da nicht einen Satz gewinnen, der sagt || des Inhalts, daß das Resultat der Multiplikation das gleiche ist, wie immer man die || dasselbe ist, wenn man die Faktoren vertauscht? Das wird eine primäre Zeichenregel sein, aber auch kein Satz ihrer Physik.      Nun, sie brauchen so einen Satz nicht zu erhalten – selbst wenn sie das Vertauschen der Faktoren erlauben.

Ich denke mir die Sache so, daß diese Mathematik ganz in Form von Geboten betrieben wird. “Du mußt das & das tun” – um nämlich die Antwort darauf zu erhalten, || – ‘wo wird sich dieser Körper zu der & der Zeit befinden’ (Wie die || diese Menschen zu dieser Methode der Vorhersagung gekommen sind, ist ganz gleichgültig).

Der Schwerpunkt der || ihrer Mathem. liegt für diese Menschen ganz im Tun.

Ist das aber möglich? Ist es möglich, daß sie das kommutative Gesetz (z.B.) nicht als Satz ansprechen?

Ich will doch sagen: Diese Leute sollen nicht zu der Auffassung kommen, daß sie mathem. Entdeckungen machen – sondern nur physikalische Entdeckungen. [Wie sehr ich doch bei meinem Denken von Spengler beeinflußt bin!]

Frage: Müssen sie mathem. Entdeckungen als Entdeckungen machen? Was geht ihnen ab wenn sie keine machen? Könnten sie (z.B.) den Beweis des kommutativen Gesetzes gebrauchen, aber ohne sein Resultat des Satzes auszusprechen zu betrachten die Auffassung, er gipfle in einem Satz, er habe also ein Resultat das ihren || den physikalischen Sätzen irgendwie vergleichbar sei?

Das bloße Bild       ⚬ ⚬ ⚬ ⚬ ⚬ ⚬ ⚬ ⚬ ⚬ ⚬ ⚬ ⚬ ⚬ ⚬ ⚬ ⚬ ⚬ ⚬ ⚬ ⚬ einmal als 4 Reihen zu 5 Punkten, einmal als 5 Kolumnen zu 4 Punkten betrachtet könnte jemand vom kommutativen Gesetz überzeugen. Und er könnte daraufhin Multiplikationen einmal in der einen, einmal in der andern Richtung ausführen.

6.4.42.      Ein Blick auf die Vorlage & die Steine überzeugt ihn, daß er mit ihnen die Figur wird legen können, d.h., er unternimmt darauf, || daraufhin, sie zu legen.

Ich fühle mich fürchterlich unglücklich.

‘Ja, aber nur, wenn die Steine sich nicht ändern? – Wenn sie sich nicht ändern & wenn wir keinen unbegreiflichen Fehler machen, oder Steine unbemerkt verschwinden oder dazukommen.

‘Aber es ist doch wesentlich, daß sich die Figur tatsächlich allemal aus den Steinen legen läßt! Was geschähe wenn sie sich nicht legen ließe?’ – Vielleicht würden wir uns dann für geistesgestört || irgendwie gestört halten. Aber – what of it || was weiter? – Vielleicht würden wir die Sache auch hinnehmen, wie sie ist.      Und dann würde || könnte Frege sagen: “Hier haben wir eine neue Art der Verrücktheit || , wie sie ist. Und Frege könnte dann sagen: Hier haben wir eine neue Art der Verrücktheit.

Es ist klar, daß die Mathematik als Technik des Transformierens || Umwandelns von Zeichen zum Zweck von Vorhersagungen || der Vorhersagung || des Vorhersagens mit (der) Grammatik nichts zu tun hat.

(Jene) Leute, deren Mathematik nur eine solche Technik ist, sollen nun auch Beweise anerkennen, die sie von der Brauchbarkeit || Zulässigkeit einer Zeichentechnik überzeugen. || anerkennen || , die sie von der Ersetzbarkeit einer Zeichentechnik durch eine andere überzeugen. D.h., sie finden Transformationen, Bilderreihen, auf die || welche hin sie es wagen || wagen können statt einer Technik eine andere zu verwenden.

Ein Bild überzeugt uns von etwas Wenn uns das Rechnen als maschinelle Tätigkeit erscheint, so ist der Mensch, der die Rechnung ausführt, die Maschine.

Die Rechnung wäre dann gleichsam ein Diagramm, von || das ein Teil der Maschine hinschreibt || aufzeichnet.

Und das bringt mich darauf daß ein Bild uns sehr wohl davon überzeugen kann daß ein bestimmter Teil eines Mechanismus sich so & so bewegen werde wenn man den Mechanismus in Gang setzt.

So ein Bild (oder eine Bilderreihe) wirkt wie ein Beweis. So könnte ich z.B. konstruieren, wie der Punkt x des Mechanismus sich bewegen werde.

Ist es nicht seltsam, daß es nicht augenblicklich klar ist, wie uns das Bild der Periode im || beim Dividieren von der Wiederkehr der Ziffernreihe überzeugt?

The mathematical proof makes him change his tune. It convinces him that the || a new tune will in a certain way agree with the old tune.

Er nimmt eine Regel statt der andern an.

(Es ist so schwer für mich, die innere Beziehung von der äußeren zu scheiden; || – das Bild von der Vorhersage.)

Du tust etwas auf den Beweis hin.

Der Beweis sagt nicht voraus daß wir an der … ten Stelle die Zahl so & so schreiben werden – das könnte durch Experimente gefunden werden. Sondern er macht es unvorstellbar, daß etwas anderes geschrieben wird, wenn den Regeln nach gerechnet wird.

Das Experiment macht nichts unvorstellbar, es macht nicht den Ausgang, den es nicht nimmt, unvorstellbar. Ja, im Gegenteil, wer das Experiment mit ansieht || sieht erhält eine Vorstellung davon, wie es anders hätte kommen || gehen können.      Der Beweis zwingt die || leitet die Vorstellung.

Der Doppelcharakter des math. Satzes : || – als Gesetz & als Regel.

‘Es ist eben eine Leistung unseres Vorstellungsvermögens, daß wir uns vorstellen, wie es weiter gehen wird.’ Ja wie kann denn (das) Vorstellen (die) Erfahrung || die Vorstellung die Erfahrung ersetzen? Wer sagt denn der Vorstellung daß sie dem tatsächlichen Geschehen || der Natur nachgeht? || daß sie sich der Erfahrung nachbewegt.

‘Die Rechnung lehrt uns etwas Neues!’ Ist denn ein neuer Entschluß nichts?

Wie, wenn man statt “Intuition” sagen würde “richtiges Erraten || Raten? Das würde den Wert einer Intuition in einem ganz andern Lichte zeigen. Denn das Phänomen des Ratens ist ein psychologisches, aber nicht das des richtig Ratens || des Erratens.

Daß wir die Technik gelernt haben, macht, daß wir sie nun, auf den Anblick dieses Bildes hin, so & so abändern. 9.2.

Ich leide sehr unter Furcht vor der gänzlichen Vereinsamung, die mir jetzt droht. Ich kann nicht sehen, wie ich dieses Leben ertragen kann. Ich sehe es als ein Leben in dem ich mich jeden Tag werde vor dem Abend fürchten müssen der mir nur dumpfe Traurigkeit bringt.

“Er schreibt, wie 25 × 5 125 gibt.”      Wie, wenn man sagte: “Der Beweis zeigt, wie 25 × 5 125 gibt.”?

Es ist hier so ungeheuer schwer, eine Sache nicht zweimal in Anschlag zu bringen!

Was ist das für ein Satz: ‘wenn ich diese beiden Zahlen richtig miteinander multipliziere muß immer das gleiche herauskommen’?      “Es wird immer so herauskommen; Du wirst es immer für richtig anerkennen, wenn es so herauskommt” – das ist eines – – “wenn das richtig war, wenn ich mich bei dieser Rechnung nicht geirrt habe, so soll es immer so herauskommen – das ist etwas andres.

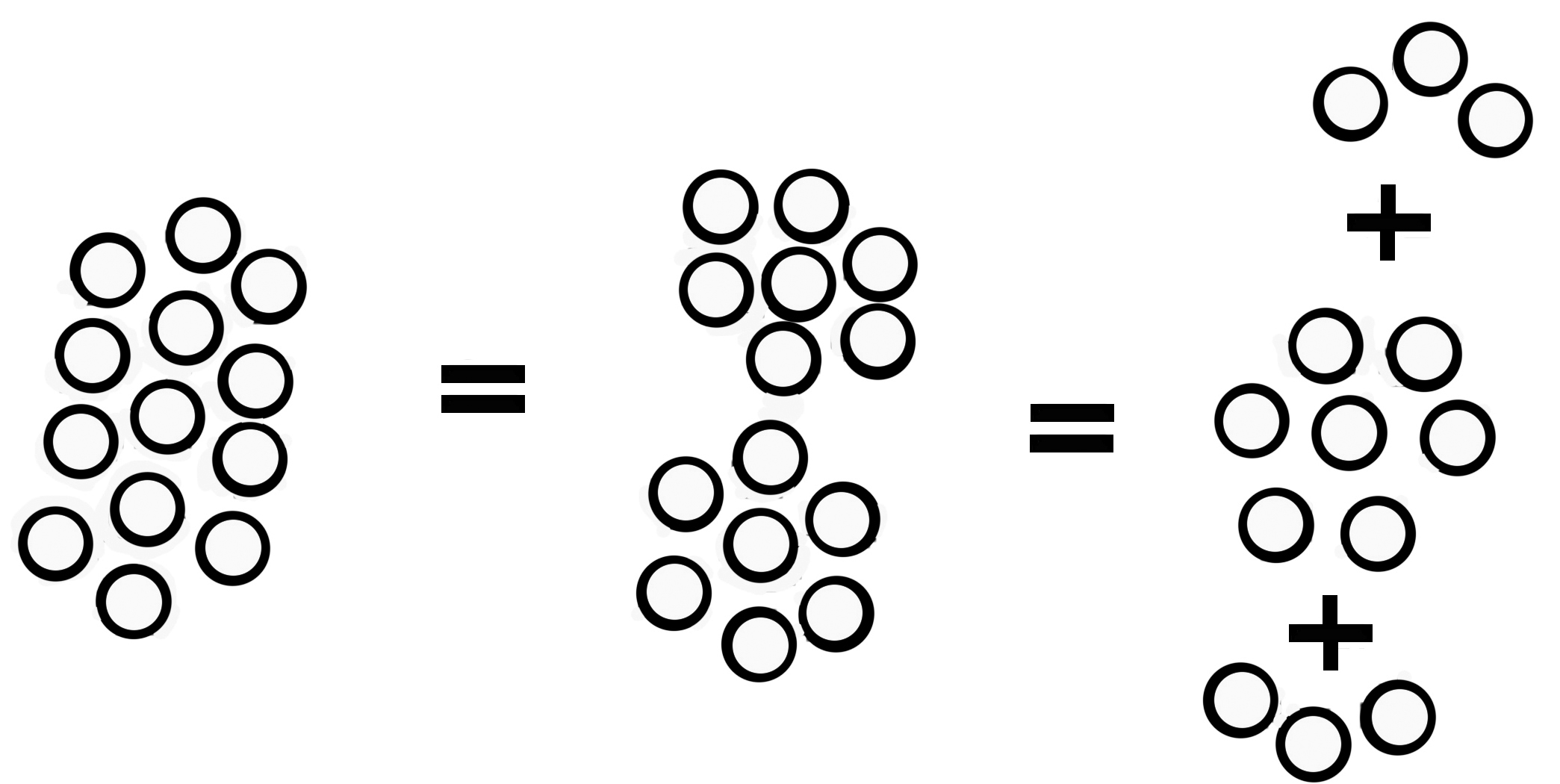
Wenn ich (wie in der vorigen Figur) immer von einer Semmel eine Linie ziehe & so alle in einer Reihe von parallelen Strichen verbinde & diese in 2 gleiche Gruppen teile, so kann ich auf diese Weise zwei Gruppen von Semmeln bilden die zu verschiedenen Zwecken sich als gleichzahlig erweisen werden. Das ist eine große physikalische Sicherheit.

Zu dem Beweis gehört, daß man ihn mit Sicherheit kopieren kann.

Wie, wenn Einer sagte: die Sicherheit des Kopierens sei nicht geringer als mathematische Sicherheit, ja sei die mathematische Sicherheit selbst?

Wie verhält es sich mit dem Satz, daß alle richtigen Kopien eines Beweises richtige Kopien von einander sein müssen? –

Was ist das für ein Satz: ‘Wenn ich ein das gleiche ein Gedicht zweimal hintereinander aus dem Gedächtnis aufschreibe, & mein Gedächtnis trügt mich nicht, & die Niederschriften bleiben unverändert, dann muß ich die beiden Kopien || sie einander auf dem Papier Wort für Wort durch Striche zuordnen können”?!

Oder das: “wenn ich zwei Zeichenreihen einander mit grünen Strichen ‘zu’ zuordnen kann, dann kann ich es auch mit blauen Strichen, wenn ich nicht physikalisch || physisch daran gehindert werde”?

“Daß es mit grünen Strichen geht, beweist daß es auch mit blauen Strichen geht.” Und zwar beweist es das im mathematischen, aber nicht im physikalischen Sinn.

‘Wir entschließen uns zu einem neuen Sprachspiel.’      ‘Wir entschließen uns spontan (möchte ich sagen) zu einem andern || neuen Sprachspiel.’

Ja – || ; es scheint: wenn unser Gedächtnis anders funktionierte, daß wir dann nicht so, wie wir es tun || wie wir's tun,, rechnen könnten. Könnten wir aber dann Definitionen geben, wie wir es tun; so reden & schreiben, wie wir es tun?      Wie aber können wir die Grundlage unsrer Sprache durch Erfahrungssätze ausdrücken || beschreiben?!

Angenommen, eine Division wenn wir sie ganz ausführen würde nicht zu demselben Resultat führen wie das Kopieren der Periode. Das könnte z.B. daher kommen, daß wir die Rechengesetzchen ohne uns dessen bewußt zu sein veränderten. (Es könnte aber auch daher kommen, daß wir anders kopieren.)

Was ist der Unterschied zwischen nicht rechnen & falsch rechnen. – Oder: ist eine scharfe Grenze zwischen dem, die Zeit nicht zu messen & sie falsch messen? Keine Zeitmessung zu kennen & eine falsche?

Gib auf das Geschwätz acht, wodurch wir jemand von der Wahrheit eines math. Satzes überzeugen. Es gibt einen Aufschluß über die Rolle || Funktion dieser Überzeugung. || die diese Überzeugung spielt. Ich meine das Geschwätz womit die Intuition wachgerufen || geweckt wird.      Womit also die Maschine einer Technik || Rechentechnik in Gang gesetzt wird.

Kann man sagen, daß, wer eine Technik lernt, sich dadurch von der Gleichförmigkeit || Gleichheit der Resultate überzeugt??

Die Grenze der Empirie – ist die Begriffsbildung.

Welchen Übergang mache ich von “es wird so sein” zu “es muß so sein”? Ich bilde einen andern Begriff. Einen, in dem inbegriffen ist was es früher nicht war.      Wenn ich sage: “Wenn diese Ableitungen gleich sind, dann || so muß … ”, || dann mache ich etwas zu einem Kriterium der Gleichheit. Bilde also meinen Begriff der Gleichheit um.

Wie aber, wenn Einer nun sagt: “Ich bin mir nicht dieser zwei Vorgänge bewußt, ich bin mir nur der Empirie bewußt, nicht einer von ihr unabhängigen Begriffsbildung & Begriffsumbildung”. “Alles || ; alles scheint mir im Dienste der Empirie zu stehen”?      Mit andern Worten: wir scheinen nicht bald mehr, bald weniger rational zu werden, oder die Form unseres Denkens zu verändern, so daß damit sich das ändert, was wir “Denken” nennen. Wir scheinen es nur immer der || nur immer unser Denken der Erfahrung anzupassen.

Das ist klar, || : daß, wenn Einer sagt: “wenn Du der Regel folgst so muß es so sein”, (daß) er keinen klaren Begriff von Erfahrungen hat die dem Gegenteil entsprächen.

Oder auch so: Er hat keinen klaren Begriff davon, wie es aussähe, wenn es anders wäre. Und das ist sehr wichtig.

Förmlich wie es einen tiefen & einen seichten Schlaf gibt, so gibt es Gedanken die tief im Innern vor sich gehen & Gedanken die sich an der Oberfläche herumtummeln.

Was zwingt uns den Begriff der Gleichheit so zu formen, daß wir etwa sagen:      “wenn Du beide Male wirklich das Gleiche tust, muß auch dasselbe herauskommen”? – Was zwingt uns, nach einer Regel vorzugehen, etwas als Regel aufzufassen? Was zwingt uns mit uns selbst in den Formen der von uns gelernten Sprache zu reden || sprechen?

Denn das Wort “muß” drückt doch aus, daß wir von diesem Begriff nicht abgehen können. (Oder soll ich sagen “wollen”?)

Ja, auch wenn ich von einer Begriffsbildung zu einer andern übergegangen bin, so bleibt der alte Begriff noch (immer) im Hintergrund.

Kann ich sagen: “Ein Beweis bringt uns zu einer gewissen Entscheidung, & zwar zu der, eine bestimmte Begriffsbildung anzunehmen,”??

Aber was ist mit einer neuen Begriffsbildung getan? Denn auf den ersten Blick erscheint sie höchstens als eine bequeme Zusammenziehung.

Du kannst den Keim nicht aus dem Boden ziehen. Du kannst ihm nur Wärme, Feuchtigkeit & etwa Licht geben || gibst ihm Wärme … & dann muß er wachsen. (Nur mit Vorsicht darfst Du ihn selbst berühren. || angreifen)

Sieh den Beweis nicht als einen Vorgang an der Dich zwingt, sondern der Dich führt. – Und zwar führt er Deine Auffassung eines (gewissen) Sachverhalts.

Aber wie kommt es, daß er jeden von uns so führt, daß wir übereinstimmend von ihm beeinflußt werden. Nun, wie kommt es daß wir übereinstimmend zählen? ‘Wir sind eben so abgerichtet’, kann man sagen., ‘und die Übereinstimmung die so erzeugt wird setzt sich durch die Beweise fort’.

Während dieses Beweises haben wir eine Anschauungsweise von der Dreiteilung des Winkels gebildet, die eine Konstruktion mit Lineal & Zirkel ausschließt.

Während des Beweises ist dies die herrschende Anschauungsweise geworden. || Wie der Beweis sich entwickelte, ist dies die …

Dadurch, daß wir einen Satz als selbstverständlich anerkennen, sprechen wir ihn auch von jeder Verantwortung gegenüber der || irgendwelcher Erfahrung frei.

Während des Beweises wird unsere Anschauung geändert – & daß das mit Erfahrungen zusammenhängt tut dem keinen Eintrag.

Unsre Anschauung wird umgemodelt.

Es muß so sein, heißt nicht, es wird so sein. Im Gegenteil: ‘Es wird so sein, wählt zwischen einer & einer andern Möglichkeit. || eine aus anderen Möglichkeiten. ‘Es muß so sein’ sieht nur eine Möglichkeit.

Der Beweis leitet unsere Erfahrungen sozusagen in bestimmte Kanäle. Wer das & das immer wieder versucht hat gibt den Versuch auf den Beweis hin auf || nach dem Beweis auf. || läßt auf den Beweis hin vom Versuch ab.

Es versucht Einer ein gewisses Bild aus Steinen zusammenzulegen. Er sieht nun || aber eine Vorlage in welcher ein Teil jenes Bilds aus allen seinen Steinen zusammengelegt erscheint, & gibt nun den || seinen Versuch auf.      Die Vorlage war der Beweis dafür, daß sein Vorhaben unmöglich ist.

Auch die Vorlage, sowie die, die ihm zeigt daß er wird ein Bild aus diesen Steinen zusammensetzen können, ändert seinen Begriff. Denn er hat, könnte man sagen, das Zusammensetzen dieses Bildes aus diesen Steinen noch nie so angesehen. || Denn er hat, könnte man sagen, er hat habe die Aufgabe des Zusammensetzens des Bildes aus diesen || den Steinen noch nie so angesehen.

Ist es gesagt, daß Einer, der sieht, daß man mit diesen Steinen einen Teil des Bildes legen kann, einsieht, daß man also auf keine Weise das ganze Bild aus ihnen wird legen können? Ist es nicht möglich, daß er versucht & versucht, ob nicht doch eine Stellung der Steine dies das Ziel erreicht? || und ist es nicht möglich, daß er sein Ziel erreicht? (Doppelte Verwendung eines Steins z.B.)

Muß man hier nicht zwischen (dem) Denken & dem praktischen Erfolg || success des Denkens unterscheiden?

“… die nicht, wie wir, eine || gewisse Wahrheiten unmittelbar einsehen, sondern vielleicht auf den langwierigen Weg der Induktion angewiesen sind”, so sagt Frege. Aber ich möchte sagen was mich interessiert ist das unmittelbare || dieses sogenannte unmittelbare Einsehen, ob es nun das einer Wahrheit ist, oder einer Falschheit. Ich frage: was ist das charakteristische Benehmen || Gebahren von Menschen, die etwas ‘unmittelbar einsehen’? – was immer der praktische Erfolg dieses Einsehens ist?

Mich interessiert nicht das unmittelbare Einsehen einer Wahrheit, sondern das Phänomen des unmittelbaren Einsehens. Nicht (zwar) als das einer besondern seelischen Phänomens || Erscheinung sondern als einer Erscheinung im Handeln der Menschen.

Ja; es ist, als ob die Begriffsbildung unsre || die Erfahrung in bestimmte Kanäle leitete so daß man nun die eine Erfahrung mit der andern auf neue || andere Weise zusammensieht. (Wie ein optisches Instrument Licht von verschiedenen Quellen auf bestimmte Art in einem Bild zusammenkommen läßt.)

Denke Dir, der Beweis wäre eine Dichtung ja ein Theaterstück. Kann mich das Ansehen eines solchen zu nichts bringen? || nicht zu etwas bringen?

Ich wußte nicht wie es gehen werde, – aber ich sah ein Bild, & nun wurde ich überzeugt, daß es so gehen werde, wie im Bilde.      Das Bild verhalf mir zur Vorhersage. Nicht als ein Experiment– –es war nur der Geburtshelfer der Vorhersage.

Erst wenn Du Dir nicht so viel aus Deinen eigenen Leiden machen wirst, wirst Du leben können!

Denn, was immer meine Erfahrungen sind || waren, oder waren, ich muß doch noch die Vorhersage machen. (Die Erfahrungen machen sie nicht für mich.)

[Sei nicht undankbar. Sieh Dein Leben nicht immer als eine fürchterliche Tragödie an. Hast Du nicht Dummheiten gemacht? Willst Du nicht auch für sie leiden? – Denk nicht immer ans Zusammenbrechen!]

Dann ist es ja kein so großes Wunder, daß der Beweis uns zur Vorhersage hilft. Ohne dieses Bild hätte ich nicht sagen können, wie es werden wird, aber wenn ich es sehe so ergreife ich es zur Vorhersage.

Welche Farbe eine chemische Verbindung haben wird kann ich nicht mit Hilfe eines Bildes vorhersagen, das mir die Substanzen in der Proberöhre & die || ihre Reaktion veranschaulicht. Zeigt das Bild ein Aufschäumen & am Ende eine rote Substanz || Kristalle, so könnte ich nicht sagen: “Ja, so muß es sein”, oder auch “Nein, so kann es nicht sein”. Anders aber ist es wenn ich das Bild eines Mechanismus in Bewegung setze; dieses kann mich lehren wie ein Teil sich wirklich bewegen wird. Würden sich aber Stellte aber das Bild einen Mechanismus dar dessen Teile aus einem sehr weichen Material (etwa Teig) bestünde & sich daher im Bild auf alle mögliche || verschiedenste Art verbögen, so würde mir das Bild vielleicht wieder nicht zu einer Vorhersage verhelfen.

Kann man sagen: “E || ein Begriff wird || werde so gebildet || geformt daß er einer gewissen Vorhersage angepaßt ist, d.h., sie in den einfachsten Termini ermöglicht –?

Das philosophische Problem ist: wie können wir die Wahrheit sagen, & dabei diese starken Vorurteile beruhigen?

Es ist ein Unterschied: ob ich etwas als ein Versehen von mir deute || eine Täuschung meiner Sinne oder als ein äußeres Ereignis deute, ob ich diesen Gegenstand zum Maß jenes nehmen oder umgekehrt, ob ich mich entschließe, zwei Kriterien entscheiden zu lassen, oder nur eins.

Wenn richtig gerechnet wurde, so muß das herauskommen. Muß es dann auch so herauskommen? Natürlich.

Indem wir in || zu einer Technik erzogen sind, sind wir auch zu einer Betrachtungsweise abgerichtet, die || wir es auch zu einer Betrachtungsweise, die … ebenso fest sitzt als jene Technik.

Sei dankbar für das, was Du genossen hast!!

Der math. Satz scheint weder von den Zeichen, noch von den Menschen zu handeln, & er tut es daher auch nicht.

Er zeigt die Verbindungen die wir als starr betrachten. Wir schauen aber sozusagen || gewissermaßen, von diesen Verbindungen weg & auf etwas anderes. Wir drehen ihnen sozusagen den Rücken. Oder, || : wir lehnen uns an sie oder fußen auf ihnen.

Nochmals: wir sehen den math. Satz nicht als einen Satz, der von Zeichen handelt an, & er ist es daher auch nicht.

Wir erkennen ihn an, indem wir ihn den Rücken drehen.

Wie ist es, z.B., mit den Grundgesetzen der Mechanik? Wer sie versteht, muß wissen, auf welche Erfahrungen sie sich stützen. Anders verhält es sich mit den Sätzen der reinen Mathematik.

Ein Satz kann ein Bild beschreiben & dieses Bild mannigfach in unserer Betrachtungsweise der Dinge, also in unserer Lebensart Handlungsweise verankert sein.

“Jeder Körper hat eine bestimmte Größe & Form. D.h.,, z.B., wir || Das, z.B., heißt, wir … können immer fragen welche Form hat dieser Körper?” wir können immer dieses Sprachspiel spielen. Der Satz steht sozusagen für die Beschreibung eines Sprachspiels.

Ist nicht dieser || der Beweis ein flimsy || zu dünner Grund die Suche nach einer Konstruktion der Dreiteilung ganz aufzugeben? Du bist nur ein oder zweimal diese Zeichenreihe durchgegangen & daraufhin willst Du Dich schon entschließen? Nur weil Du diese eine Transformation gesehen hast willst Du die Suche aufgeben?

… Der Effekt des Beweises sei, daß er || sei, (so meine ich), daß … || der Mensch sich in die neue Regel hineinstürzt.

Er hatte bisher nach der & der Regel gerechnet || die Bahn berechnet; nun zeigt ihm Einer den Beweis, man könne auch anders rechnen, & er schaltet nun (auf die andre Technik) um – nicht weil er sich sagt, es werde so auch gehen, sondern weil er die neue Technik mit der alten als identisch empfindet, weil er ihr denselben Sinn geben muß weil er sie als gleich anerkennt wie er diese Farbe als grün anerkennt.      D.h.: das Einsehen der math. Relationen spielt eine ähnliche Rolle wie das Einsehen der Identität. Man könnte beinahe sagen, es ist eine kompliziertere Art der || von Identität.

‘Wenn Du das Glück nicht in der Ruhe finden kannst, finde es im Laufen!’ Wenn ich aber zu müde werde zu laufen? ‘Sprich nicht vom Zusammenbrechen ehe Du zusammenbrichst.’      Wie ein Radfahrer muß ich nun beständig treten, mich beständig bewegen um nicht umzufallen.

Man könnte sagen: Die Gründe warum er nun von einer Technik auf eine andere || auf eine andere Technik umschaltet, sind von gleicher Art wie die, die ihn eine genaue || die Multiplikation so ausführen lassen, wie er sie ausführt; indem er die Technik als die gleiche anerkennt, wie die, die er bei andern Multiplikationen angewandt hatte.

[Was hübsch ist, kann nicht schön sein. ‒ ‒ ‒ ‒ ‒ ‒ ‒ ‒ ‒]

26.4. Im Krankensaal, warte auf die morgige Operation. Es scheint ein echt abscheulicher Ort. Außer Männern sind auch ein paar kranke Kinder da, eines wimmert unaufhörlich. Es ist zugig unbequem & ungemütlich. Ungemütlich auch die Pflegerinnen.

18.5.      Ein Mensch ist in einem Zimmer gefangen, wenn die Türe || Tür nicht unversperrt ist, aber sich nach innen öffnet; während er || er aber nicht auf die Idee kommt an ihr zu ziehen, statt gegen sie zu drücken.

Bring den Menschen in die unrichtige Atmosphäre & nichts wird funktionieren wie es soll. Er wird an allen Teilen krank || ungesund erscheinen. Bring ihn wieder in das richtige Element, & alles wird sich entfalten & gesund erscheinen. Wenn er nun aber im unrechten Element ist? Dann muß er sich also damit abfinden, als Krüppel zu erscheinen.

Wenn Weiß zu Schwarz wird, sagen manche Menschen: “Es ist im wesentlichen noch immer dasselbe”. Und andere, wenn die Farbe um einen Grad dunkler wird || wurde, sagen “Es hat sich ganz verändert”.

26.5.42      Mein Unglück ist so komplex, daß es schwer zu beschreiben ist. Aber wahrscheinlich ist doch Vereinsamung die Hauptsache.

27.5. Höre seit 10 Tagen nichts mehr von K. obwohl ich ihn vor einer Woche um dringende Nachricht gebeten habe. Ich denke, daß er vielleicht mit mir gebrochen hat. Ein trauriger Gedanke! Und in ein paar Tagen soll ich nach Cambridge gehen um mich zu erholen! Wie werde ich es dort aushalten? Ich kann es mir nicht vorstellen. Ich kann mir nicht vorstellen, wie ein Mensch in meiner Lage leben kann || soll. Wie entschließt man sich dazu, oder ergibt sich drein, den Rest seiner Tage unglücklich zu verbringen || sein? Was für ein Gesicht macht man dazu?

Ich habe viel gelitten, aber ich bin scheinbar unfähig aus meinem Leiden zu lernen. Ich leide noch immer so wie vor vielen Jahren. Ich bin nicht stärker & nicht weiser geworden. Mein Lebenselement scheint noch immer das gleiche zu sein; ich war ein Fisch & bin ein Fisch geblieben.

Die Sätze “a = a”, “p ⊃ p” “Das Wort ‘Bismarck’ hat 8 Buchstaben, “Es gibt kein rötlichgrün”, sind alle einleuchtend & Sätze über das Wesen: was haben sie gemeinsam? Sie sind offenbar jeder von anderer Art & anderem Gebrauch. Der vorletzte ist einem Erfahrungssatz am ähnlichsten. Und es ist verständlich daß man ihn einen synthetischen Satz a priori nennen kann.      Man kann sagen: wenn einer die Zahlenreihe & die || mit der Buchstabenreihe nicht zusammenhält, kann er nicht wissen, wieviel Buchstaben das Wort hat.

15.9.42      Eine Figur aus der andern nach einer Regel abgeleitet. (Etwa die Umkehrung vom Thema.)

Dann das Resultat als Äquivalent der Operation gesetzt.

Wenn ich schrieb “der Beweis muß übersichtlich sein” so hieß das: Kausalität spielt im Beweis keine Rolle.      Oder auch: der Beweis muß sich durch bloßes Kopieren reproduzieren lassen.

Daß bei der Fortsetzung der Division von 1 ÷ 3 immer wieder 3 herauskommen muß ist || wird ebenso wenig durch Intuition erkannt, wie, daß die Multiplikation 25 × 25 wenn man sie wiederholt immer wieder dasselbe Produkt liefert.

Man könnte vielleicht sagen daß der synthetische Charakter der Sätze der Math. sich am klarsten in der unregelmäßigen Verteilung der Primzahlen zeigt. || daß das synthetische a priori der mathem. Sätze am klarsten || sehr klar sich im unregelmäßigen Auftreten der Primzahlen zeigt. || daß der synthetische Charakter der mathem. Sätze sich am augenfälligsten || sehr augenfällig im unvorhersehbaren Auftreten der Primzahlen zeigt.

Aber weil sie synthetisch sind (in diesem Sinne), sind sie darum nicht weniger a priori. Man könnte sagen, will ich sagen, daß sie nicht aus den || ihren Begriffen durch einen Vorgang der Analyse abgeleitet || erhalten werden können dennoch aber einen Begriff definierend || nach der Hand bestimmen. || daß sie nicht aus ihren Begriffen durch eine Art von Analyse erhalten werden können wohl aber einen Begriff durch Zusammensetzung || Synthese bestimmen, etwa wie man durch die Durchdringung von Prismen einen Körper bestimmen kann.

Könnte man nicht wirklich von Intuition in der Math. reden? Nicht so aber, daß eine mathem. Wahrheit intuitiv erfaßt würde wohl aber eine physikalische, oder psychologische. So weiß ich mit größter Sicherheit, daß ich jedesmal 625 errechnen werde, wenn ich zehnmal 25 × || mit 25 multipliziere. D.h. ich weiß die psychologische Tatsache, daß mir immer wieder diese Rechnung als richtig erscheinen wird; so wie ich weiß, wenn ich die Zahlenreihe von 1 bis 20 zehnmal nacheinander aus dem Gedächtnis aufschreibe, die Aufschreibungen sich beim Kollationieren als gleich erweisen werden. – Ist das nun eine Erfahrungstatsache? Freilich – und doch wäre es schwer die Erfahrungen || Experimente anzugeben die mich von ihr überzeugen würden. Man könnte so etwas eine intuitiv erkannte Erfahrungstatsache nennen.

Ist ein versteckter Widerspruch ähnlich wie ein verstecktes perpetuum mobile?

Du willst sagen, daß jeder Beweis || jeder neue Beweis in einer oder der anderen Weise den Begriff des Beweises ändert || verändert.

Aber nach welchem Prinzip wird denn etwas als neuer Beweis anerkannt? Oder vielmehr gibt es da gewiß || natürlich kein ‘Prinzip’.

Wenn Rechenmaschinen in der Natur vorkämen & von den Menschen gefunden & benützt würden, so hätten wir z.B. eine Arithmetik ohne Sätze & ohne Beweise.

Es gibt also etwas, was man wird Mathematik nennen müssen, eine Technik ohne Sätze & ohne Beweise.       y = x². Dazu eine Technik des Multiplizierens im Dezimalsystem.

23.9.42      Wenn ich mir aber das Resultat von 25 × 25 anmerke statt es wieder zu rechnen, habe ich schon eine Gabe der Math. benützt. – Oder ich habe auch nur meine Technik geändert.

Man könnte hier sagen, der Gebrauch mathem. Sätze & Beweise fange da an, wo eine Rechnung, die früher schon einmal || einmal gemacht wurde, nicht wiederholt, wird & || & ihr Resultat einfach aber || einfach übernommen wird. Wo gesagt wird: “das haben wir ja schon gerechnet.”

Soll ich nun sagen: “ich bin || wir sind überzeugt, daß immer wieder dasselbe Resultat herauskommen wird”? Nein, das ist nicht genug. Wir sind überzeugt, daß immer dieselbe Rechnung herauskommen, gerechnet werden, wird. Ist das nun eine mathematische Überzeugung? Nein – denn würde nicht immer dasselbe gerechnet so könnten wir nicht folgern, daß die Rechnung zu versal || einmal ein Resultat einmal ein andermal || das andre mal ein andres || anderes ergibt.

Wir sind freilich auch überzeugt, daß wir beim wiederholten Rechnen das Bild der || die Rechnung reproduzieren || wiederholen werden. –

Ich will sagen, daß die Beschreibung “Er hat 25 × 24 den Regeln gemäß multipliziert” & die “Er hat die & die Rechnung hingeschrieben” äquivalent sind.

Unsre Rechenmaschine in der wir die Operationen verfolgen können – & eine Rechenmaschine, die durch einen chemischen Prozeß, den wir das richtige Resultat auf einem besonderen Papier, worauf wir die Angabe schreiben, durch einen chemischen Vorgang das richtige Ergebnis erscheinen läßt. –

So könnte man den Kubus einer Zahl finden indem man einen Eiswürfel von der betreffenden Kantenlänge abwägt. Und man könnte natürlich unser Rechnen auch als so einen Vorgang betrachten. In diesem Fall wäre die Rechnung ein Nebenprodukt bei der Erzeugung des Resultats. (Wie das Schnurren der || einer Maschine.)

Denke Dir den Fall, in welchem Menschen zwar immer gleiche Endresultate bei einer Rechnung erzeugten aber, sozusagen, unerforschliche Wege zu diesen gingen, d.h. Rechnungen hinschrieben, die wir nicht nachrechnen können & die sie selbst nicht erklären könnten. (Wie es bei schwierigen Problemen oft geschieht.) (Kunstrechnen)

Warum sollte man den Russellschen Widerspruch nicht als etwas Überpropositionales auffassen, etwas das über den Sätzen thront & nach beiden Seiten (wie ein Januskopf) || zugleich schaut. || nach beiden Richtungen schaut. N.B.: der Satz F(F) – in welchem F(ξ) = ~ξ(ξ) – enthält keine Variablen & könnte daher || also als ein überlogischer Satz || etwas Überlogisches, als etwas Unangreifbares, dessen Verneinung a es nur wieder α es selber aussagt, gelten || dastehen. Ja könnte man nicht sogar die Logik mit diesem Widerspruch auffangen? Und von ihm gleichsam zu den Sätzen niedersteigen. ‘Das wäre sozusagen ein Januskopf.

Der sich selbst widersprechende Satz stünde wie ein Denkmal (mit einem Januskopf) über den Sätzen der Logik.

‘Das Wort … lautet umgekehrt … ’ – muß es für uns unbedingt etwas heißen vom umgekehrten Klang eines Wortes zu reden?

Daß eine Fünffigur & ..... & eine Dreifigur ... eine Achtfigur ........ ergibt kannst Du nur finden, indem Du die Synthese machst (nicht durch Analyse der Begriffe). Hast Du sie aber gemacht, so dient der Vorgang zur Aufstellung eines Begriffes || neuen Begriffes.

Das bloße Bild der Rotation der beiden Figuren kann mich davon überzeugen, daß zwei so geformte Körper sich ungefähr so bewegen können || werden. Aber so überzeugt mich auch die || eine Multiplikation davon daß ich wirklich so viele || 322 Leute haben werde, wenn ich 14 mal 23 erhalte. || wenn man mir 14-mal 23 Leute zuweist.

Könnte ich nicht sagen: wer die Multiplikation macht findet jedenfalls nicht das math. Faktum, aber den math. Satz? Denn, was er findet ist das nicht-math. Faktum, & so den math. Satz. Denn der math. Satz ist eine Begriffsbestimmung die auf eine Entdeckung folgt.

Du findest eine neue Physiognomie. Du kannst Dir sie z.B. jetzt merken oder sie kopieren.

Es ist eine neue Form gefunden, konstruiert worden. Aber sie wird dazu benützt mit der alten einen neuen Begriff zu geben:      Man ändert den Begriff so, daß das hat herauskommen müssen.

Es ist z.B. ein Unterschied: ob ich die Figur mit einem Blick übersehe nachdem sie gezeichnet ist, oder etwa jeden Strich verdecke & vergesse, sobald er gezeichnet ist.

Ich finde nicht das Resultat; sondern ich finde, daß ich dahin gelange.

Und nicht das ist eine Erfahrungstatsache, daß dieser Weg da anfängt & da endet, || ; sondern, daß ich diesen Weg, oder einen Weg zu diesem Ende, gegangen bin.

Aber könnte man nicht sagen, daß die Regeln diesen Weg führen, auch wenn niemand ihn ginge?

Denn das ist es ja, was man sagen möchte – und hier ist die Vorstellung von einem math. Mechanismus, einem, der nicht den Gesetzen der Physik, sondern nur denen der Math. gehorcht. || und hier denkt man an einen math. Mechanismus … || und hier denkt man || stellt man sich eine math. Maschine vor, die sozusagen vo von Regeln getrieben wird. || und hier sehen wir die math. Maschine, die von den Regeln selbst getrieben wird. || – und hier sehen wir die math. Maschine, die von den Regeln selbst getrieben wird & nur math. Gesetzen, & nicht physikalischen, gehorcht || , die, von den Regeln selbst getrieben, nur math. Gesetzen gehorcht & nicht physikalischen.

Ich will sagen: das Arbeiten der math. Maschine ist nur das Bild des Arbeitens einer Maschine.

Die Regel arbeitet nicht, denn, was immer der Regel nach geschieht ist eine Interpretation || Deutung der Regel.

Nehmen wir an, ich habe die Zeichnungen der || Stadien der Bewegung von im Bilde vor mir, so verhilft mir das zu einem Satz, den ich von diesem Bild gleichsam ablese. Der Satz enthält das Wort “ungefähr”, & ist ein Satz der Geometrie.

Es ist seltsam, daß ich einen Satz von einem Bild soll ablesen können.

Der Satz aber handelt nicht von dem Bild das ich sehe. Er sagt nicht, daß auf diesem Bild das & das zu sehen ist. Er sagt aber auch nicht, was der wirkliche Mechanismus tun wird, obwohl er dies andeutet.

Aber könnte ich von der Bewegung des Mechanismus wenn ihre Teile sich nicht ändern, auch andere Zeichnungen anfertigen? D.h., bin ich nicht gezwungen eben dies als Bild der Bewegung, unter diesen Bedingungen, anzunehmen.

Denken wir uns die Konstruktion der Stadien des Mechanismus mit Strichen von wechselnder Farbe ausgeführt. Die Striche seien zum Teil schwarz auf weißem Grund, zum Teil weiß auf schwarzem Grund. Denke Dir die Konstruktionen im Euklid so ausgeführt; sie werden allen Augenschein verlieren.

Das umgekehrte Wort hat ein neues Gesicht.

Und der Erfahrungssatz ist, daß wir dieses Gesicht erhalten wenn wir das Wort umkehren. – Aber was heißt es: ‘es umkehren’? Es darf natürlich nicht heißen: dies Gesicht erzeugen. Es ist also ein Prozeß, der nicht schon ‘notwendig’ mit diesem Resultat verbunden ist. Wir aber nennen freilich || allerdings ‘umkehren’ schon etwas was durch das Ergebnis des Umkehrens bestimmt ist. Was nicht so bestimmt ist würden wir etwa ‘umzukehren versuchen’ nennen.

“Wenn ich es umzukehren versuche, erhalte ich das” – das ist natürlich ein Erfahrungssatz.

Wenn ich aber dies als das Bild des Umkehrens & der Umkehrung ansehe || annehme, so kann ich mir freilich keine andere Umkehrung der Reihe denken. – Aber kann ich überhaupt etwas anderes als Bild der Umkehrung ansehen? Kann ich z.B. zwei Bilder als Umkehrungen eines desselben Wortes annehmen? Bei sehr langen Worten gewiß; aber wie ist es mit solchen, die man übersehen kann?

Es ist natürlich denkbar, daß man beim Versuch ein kurzes Wort umzukehren zwei verschiedene Resultate erhält. Normalerweise aber stellt sich das eine gleich als irgend ein Versehen heraus.

Denk Dir eine Maschine, die ‘so konstruiert ist’, daß sie eine Buchstabenreihe umkehrt. Und nun den Satz, daß das Resultat im Falle ABER REBA ist. –

16.10. Ein Traum: Mir träumte heute nacht, meine Schwester Gretl gebe der L. Pollitzer ein Geschenk: eine Tasche. Ich sah die Tasche im Traum oder vielmehr nur den stählernen Verschluß der sehr groß & viereckig war und sehr fein gearbeitet. Er sah aus wie eines von den komplizierten alten Schlössern, die man manchmal in Museen sieht. In diesem Verschluß war unter anderem ein Mechanismus durch den beim Öffnen die Worte “deiner Gretl” oder etwas ähnliches, gesprochen wurden. Ich dachte darüber nach wie fein der Mechanismus dieser Vorrichtung sein müsse & ob er eine Art Grammophon sei & aus welchem Material die Platte könnt sein möglicherweise aus Stahl sei.

Die Regel, wie sie wirklich gemeint ist, scheint eine treibende Kraft zu sein, die eine ideale Reihe so umkehrt, – was immer ein Mensch mit einer wirklichen Reihe tun mag.      Sie ist also || Dieser ist also der Mechanismus, der für den wirklichen als Maßstab, als Ideal zu gelten hat. || der für den wirklichen der Maßstab, das Ideal ist.

Und das ist verständlich. Denn wird das Resultat der Umkehrung zum Kriterium dafür genommen, ob || daß die Reihe wirklich umgekehrt worden ist || wurde, & übersetzen || drücken wir dies so aus, daß wir es einer idealen Maschine nachtun müssen, so muß diese Maschine unfehlbar dies Resultat erzeugen

Kann man nun sagen: daß die Begriffe, die die Math. schafft, eine Bequemlichkeit sind, daß es, wesentlich auch, ohne sie ginge?

Zuvörderst drückt die Annahme dieser Begriffe die sichere Erwartung gewisser Erfahrungen aus.

Wir nehmen es, z.B. nicht hin, daß eine Multiplikation zweimal einmal nicht jedesmal || immer das gleiche || dasselbe Resultat ergibt. || einmal dies, einmal ein anderes Resultat ergibt.

Und was wir mit Sicherheit erwarten, ist für unser ganzes Leben wesentlich.

Warum soll ich aber dann nicht sagen, daß die math. Sätze eben jene bestimmten Erwartungen, d.h. also Erfahrungen ausdrücken? Nur weil sie es eben nicht tun. Die Annahme eines Maßes || Begriffes ist eine Maßregel die ich vielleicht nicht ergreifen würde, wenn ich nicht das Eintreten gewisser Tatsachen mit Bestimmtheit erwartete; aber darum ist die Festsetzung dieses Maßes nicht äquivalent mit dem Aussprechen der Erwartungen.

Es ist schwer den Tatsachenkörper auf die richtige Fläche zu stellen: das Gegebene als gegeben zu betrachten. Es ist schwer den Körper anders aufzustellen als man gewohnt ist, ihn zu sehen. Ein Tisch in einer Rumpelkammer mag immer auf der Tischplatte stehen || liegen, aus Gründen der Raumersparnis, etwa || z.B.¤ So habe ich den Tatsachenkörper immer so aufgestellt gesehen, aus mancherlei Gründen; & nun soll ich etwas anderes als seinen Anfang & etwas anderes als sein Ende ansehen. Das ist schwer. Er will gleichsam nicht so stehen, es sei denn daß man ihn in der Lage durch andere Vorrichtungen unterstützt.

Was Einen von einem synthetischen Satz reden macht, ist die neue Form.