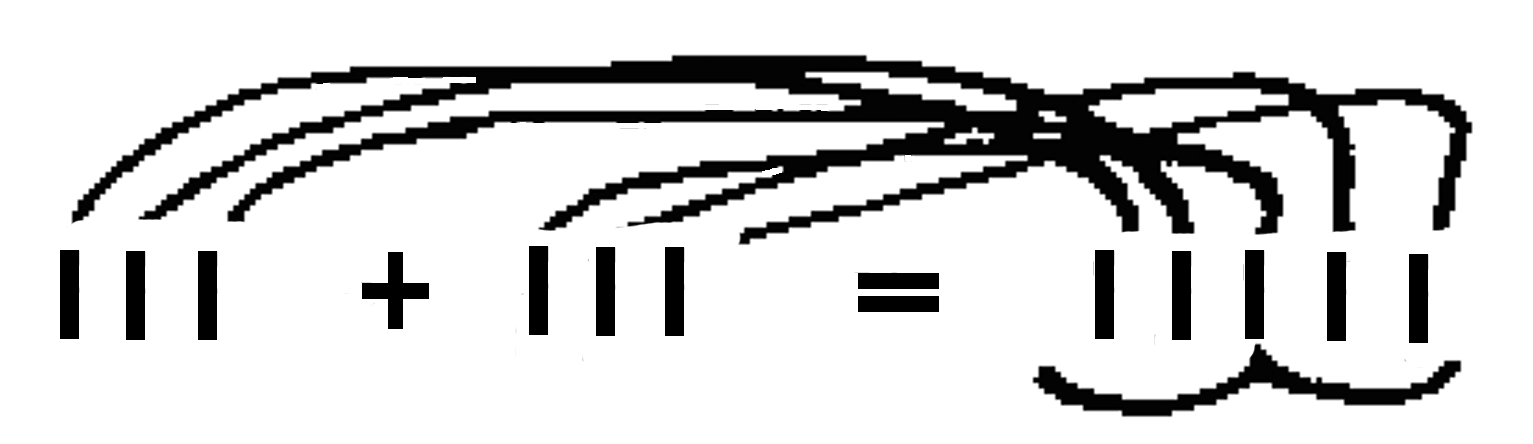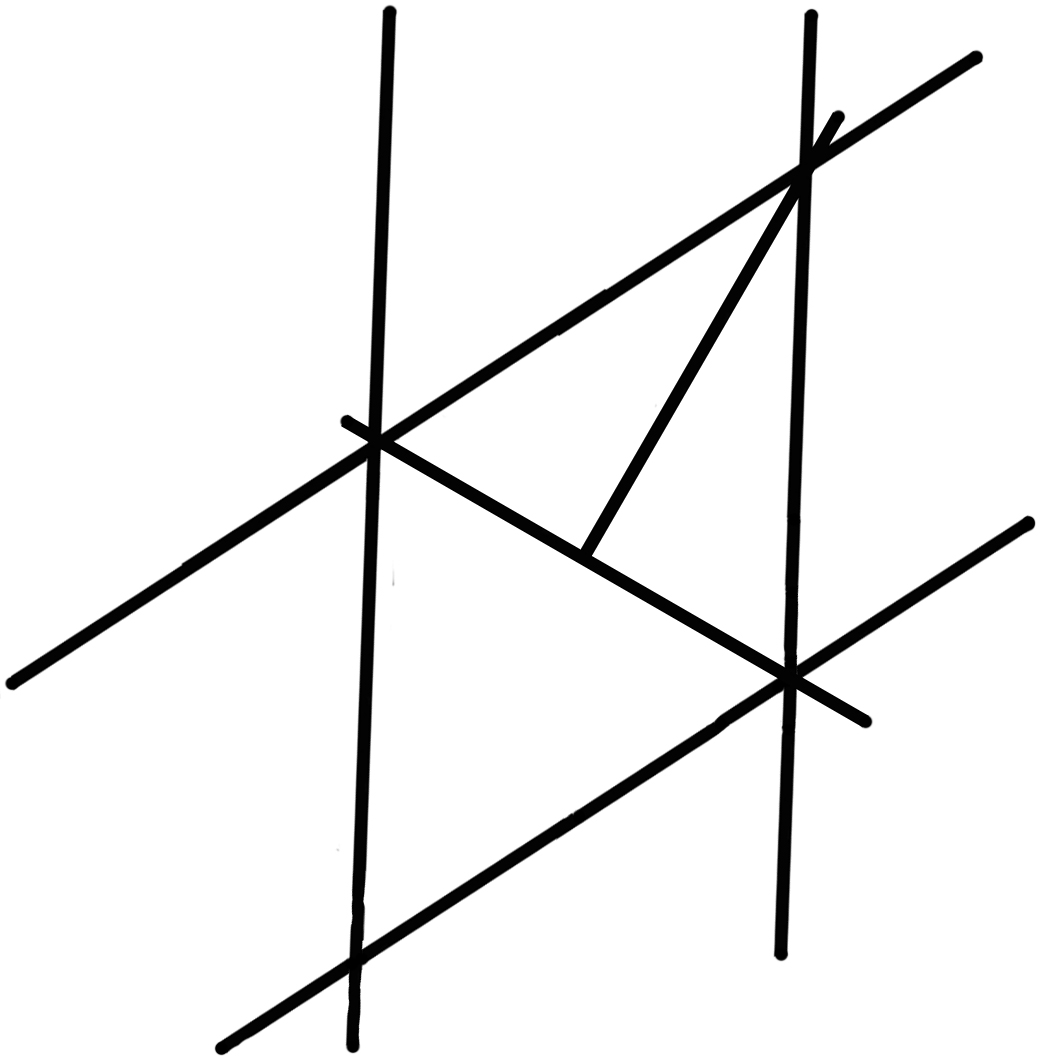27.2.37.

… ¹ “Welt” hatte.

Denk' es würde gefragt: “Was ist das Wesen eines Tisches?”; so könnte der Eine sagen: “Schauen wir uns an, was wir alles einen Tisch nennen”; der Andre aber würde sagen: “Du verstehst doch das Wort “Tisch” – (oder nicht?) – dann mußt Du auch ohne auf besondere Beispiele zu schauen, sagen können, was Du unter dem Wort verstehst.

Die ‘Ordnung der Dinge’, die Idee der

Formen || Form der Vorstellung, also des a priori ist selber eine grammatische Täuschung.

Man sagt: “Es sind ja nicht die Worte,– sondern der Geist der Worte.” Aber was ist das für ein Geist?

Das Mißverständnis, welches zu der Idee führt, der Satz, der eigentliche Satz, müsse ein reineres Wesen sein, als, was wir für gewöhnlich das “Satzzeichen” nennen, ist ein sehr zusammengesetztes.

Betrachte die Aussprache

eines Worts durch das Medium || durch das Darstellungsmittel || die Darstellungsform || die Form seiner Schreibung! Wie leicht glaubt man, ¤ zwei Worte klingen doch verschieden, nur weil man sie verschieden schreibt. Und freilich, wenn man sie sich || vorsagt, während man || indem man ¤ || gerade an ihre verschiedene Schreibung denkt, spricht man sie auch wohl etwas verschieden aus. Daraus aber ist gar kein Schluß zu ziehen auf die Aussprache im normalen Gebrauch. (Vergl. auch eis & f.)

So wird man durch das Darstellungsmittel irregeführt zu suchen, was

nicht da ist.

So kann das Darstellungsmittel eine Einbildung erzeugen.

Die Strenge der Logik || Ihre Strenge scheint hier aus dem Leim zu gehen.

Denn, wie kann die Logik ihre Strenge verlieren?! Natürlich nicht dadurch daß man etwas von ihr abhandelt sondern nur durch eine Umgruppierung in der die Idee der Strenge einen andern Platz erhält.
So nämlich,

indem das Ideal der Ordnung als ein Teil der Darstellungsart erkannt wird.
Indem man aufhört krampfhaft in der Welt nach dem || das zu suchen, was auf unsrer Brille gezeichnet ist. Dann aber muß sich die Brille abnehmen lassen & mit andern Brillen vertauschen. Eine Brille, ohne die || welche das Sehen undenkbar ist, ist keine Brille. Das Gleichnis von der Brille ist dann || hier falsch || schlecht angewandt & irreführend.

Die Idee, daß die Logik in irgendeiner Weise das “Wesen der Welt” zeigt || zeige, muß verschwinden.

(Das a priori muß zu einer Form der Darstellung || Betrachtung werden. D.h. es muß diesem Begriff auch sein Nymbus genommen werden.
Ein Satz a priori entsteht dadurch, daß ein Satz der von der Darstellungsart handelt eingekleidet wird in die Form einer Aussage über die dargestellten Gegenstände.

Betrachte Sätze wie diesen: “Die Farbe, die ich sehe mag || kann unrein sein, verwaschen: aber ich sehe doch immer [fett zu drucken] eine bestimmte Farbe!”

“Der Sinn des Satzes kann freilich das || dies oder jenes offen lassen, aber der Satz muß doch einen bestimmten Sinn haben!.”

Was heißt es: “Eine Vagheit in der Logik kann es nicht geben””? (Vor allem kann es dann auch keine Bestimmtheit geben.)

“Ein ‘unbestimmter Sinn’, das wäre eigentlich gar

kein Sinn”: das ist wie wenn man sagt: “eine unscharfe Begrenzung, das ist eigentlich gar keine Begrenzung”. Man denkt da etwa so: Wenn ich sage: “ich habe diesen Mann fest im Zimmer eingeschlossen, (nur eine Tür ist offen)”– so habe ich ihn eben gar nicht eingeschlossen; er ist nur zum Schein eingeschlossen. Hier vergißt man, daß ja die verschlossenen Türen doch etwas ausrichten. Man wäre geneigt hier zu sagen: also hast Du damit gar nichts getan. Und doch hat er etwas getan. Eine Grenze die ein Loch hat – möchte man sagen – ist so gut wie gar keine. Aber ist denn das wahr?

“Wenn Du den Satz verstehst, – meinst, so mußt Du doch etwas meinen!” (Es gibt doch nicht ein halbes Ding!)

Es scheint ja, als ob die Logik ihr Wesentliches verlöre,: ihre Strenge. Als hätte || habe man sie ihr schon abgehandelt.
Aber sie spielt jetzt nur eine andere Rolle. Sie ist, aus einem Vorurteil über die Wirklichkeit, zu einer Form der Darstellung geworden.

Wo ist die Kristallklarheit hingekommen? Sie ist eine Form der Darstellung geworden, sonst nichts.

Das Verstehen kein pneumatischer Vorgang.
Der Begriff der Familie
Zwei Axthiebe gegen die ‒ ‒ ‒

Es zeigte sich nämlich

daß ich nicht einen allgemeinen Begriff vom Satz & der Sprache hatte.
     Ich mußte das & das als Zeichen anerkennen (Sraffa) & konnte doch keine Grammatik dafür angeben. Verstehen & Wissen der Regeln.
     Das Pneumatische am Verstehen verschwand ganz & damit das Pneumatische des Sinnes.
     Zuerst erschienen die strengen Regeln als etwas, im Hintergrund, || noch im Hintergrund, im Medium || im nebulosen Medium des Verstehens versteckt; & man konnte sagen: sie müssen da sein, – oder

ich sehe sie, sozusagen durch ein dickes Medium hindurch, aber ich sehe sie. Sie waren also konkret. Ich hatte ein Gleichnis gebraucht (von der Projektionsmethode, etc.) aber durch die grammatische Täuschung des einheitlichen Begriffes erschien es nicht als Gleichnis. Das Wort ‘eigentlich’.
Wenn || Je offenbarer diese Täuschung wird, je klarer es wird daß Sprache eine Familie ist, desto klarer wird es daß jenes scheinbar Konkrete, eine Abstraktion, eine Form war & daß wenn wir vorgeben sie seien nun überall

zur Stelle, unsere Aussagen leer & sinnlos werden. Daß wir nur mehr logische Possen treiben.
Wir sehen, || – daß wir uns an die Beispiele klammern müssen, um nicht haltlos herumzutreiben.
Unsere Betrachtungen aber verlieren nun nicht etwa ihre Bedeutung, sondern diese liegt nun ganz auf den Mißverständnissen die uns irreführen.

‒ ‒ ‒ Diese Idee nun verband sich mit der der Strenge.

Der Fatalismus ist keine wissenschaftliche Wahrheit; sondern eine Betrachtungsweise, die uns liegt, oder nicht liegt.

/ Denk Dir in einem Kalender stände statt “3. Februar”, “4. Februar”, etc., immer, “heute ist der 3. Februar”, “heute ist der 4.” etc..– Wäre || Was wäre damit mehr gesagt?! /

‒ ‒ ‒ Diesem Mißverständnis (nun) kommen eine Reihe andrer || von andern Mißverständnissen entgegen. Besonders aber

zwei: ‒ ‒ ‒‒ ‒ ‒.

Die Mißverständnisse aber werden beseitigt indem wir gewisse Ausdrucksformen durch andere ersetzen & dies kann man wohl eine “Analyse” unsrer Ausdrucksformen nennen. – Nun aber gewinnt es den Anschein, als sei unsre || als gäbe es so etwas wie eine Aufgabe die, eine letzte Analyse unsrer Sprachformen vorzunehmen. Als gäbe es eine (bestimmte) vollkommen zerlegte Art || analysierte Form des Ausdrucks. D.h., als

sei unser gewöhnlicher Ausdruck wesentlich noch unanalysiert; als sei in ihm || seien unsere gewöhnlichen Ausdrucksformen wesentlich noch unanalysiert; als sei in ihnen etwas verborgen, was ans Tageslicht zu befördern ist. Ist dies geschehen, so ist || sei der Ausdruck vollkommen geklärt & unsre Aufgabe gelöst.
Dieses Mißverständnis drückt sich aus in der Frage nach dem Wesen, der Sprache, des Satzes (&) des Denkens. Denn wenn wir auch, in einem (hausbackenen) Sinn, das Wesen der Sprache, etc., in unseren Untersuchungen kennen lernen, so ist es doch nicht das, was diese

Frage anstrebt. – Denn sie sieht in dem ‘Wesen’ nicht etwas was schon offen zu Tage liegt || offen da liegt & was man durch Ordnen ◇◇◇, sondern etwas, was unter der Oberfläche liegt. Etwas, was man sieht wenn man die Sprache durchschaut & was die Analyse hervorgräbt.

Und diesen Mißverständnissen kommen von verschiedenen Seiten eine Reihe anderer Mißverständnisse entgegen.

‒ ‒ ‒ Es scheint wir können nicht in das Innere dieser Dinge

dringen. Darin läge || liege unser Problem. Einer könnte sagen: “ein Satz, das ist … ‒ ‒ ‒”

Die Antwort aber ¤ ist ein für alle mal zu geben unabhängig von zukünftiger Erfahrung.

“Logischer Bau der Welt”.

Sein Wesen stellt eine Ordnung dar.

‒ ‒ ‒ Zurück auf den rauhen Boden.
Und nun sieht man daß die Darstellungsweise verfehlt war, die gleichsam ins Blaue

schaute, statt nur auf die konkreten Beispiele. Der Ursprung des Ideals?

– Es ist wie eine Forderung an die Realität.

Die Idee sitzt als Brille auf unserer Nase & wir denken gar nicht dran sie abzunehmen || & wir kommen gar nicht auf die Idee, sie abzunehmen.

“Ja so ist es,”, sagst Du, “denn so muß es sein!”

(Schopenhauer: der Mensch lebt eigentlich 100 Jahre lang.)
“Natürlich, so muß es sein!” Es ist da, als habe man die Absicht eines Schöpfers verstanden. Man hat das System verstanden.
Man fragt sich nicht: ‘Wie lange leben denn Menschen wirklich’, sondern das erscheint jetzt als etwas Oberflächliches; sondern man hat etwas tiefer liegendes verstanden.

Wir haben eine Form der Darstellung gefunden || sind auf eine Form der Darstellung gekommen,

¤die uns einleuchtet. Aber es ist, als haben wir nun etwas gesehen, was tiefer liegt als die Erscheinungen. || was unter der Oberfläche liegt.

Diese Tendenz aber scheint in der Logik ihre strenge Berechtigung zu haben man scheint hier mit voller Berechtigung zu schreiben: “Wenn ein Satz ein Bild ist ‒ ‒ ‒” Als sei hier, konkret was in den Wissenschaften nur Abstraktion ist || Abstraktionen sind.

Je länger || näher wir aber die wirkliche Sprache betrachten desto stärker wird der Widerstreit zwischen dieser || der Forderung & der Wahrheit || tatsächlichen Sprache. Das Aufrechterhalten der Forderung erscheint nun immer leerer & leerer, immer mehr als eine Selbsttäuschung wird als || zu etwas Leerem || Die Forderung erscheint mehr & mehr || zeigt sich uns klarer & klarer als etwas Leeres || Wollen wir sie aufrechterhalten so wird sie nun zu etwas Leerem.

“Phänomenologische Sprache”

Aber das Ideal ist Deine Ausdrucksweise

& Du mißverstehst sie & wendest sie hier falsch an. || & || Aber Du mißverstehst ihre Grammatik & wendest sie hier falsch an. [Wie bei manchem Fehlschlag || Trugschluß den man macht.]

|| Aber das Ideal sitzt in Deiner Ausdrucksform || Ausdrucksweise & Du wendest sie hier falsch an. || & Du mißverstehst seine Funktion (seine Grammatik) & wendest es hier falsch an.

[Ich will doch sagen: Es ist doch ein Spiel, & auch Du würdest || wirst es Spiel nennen,]

nur wirst || bist Du vom Ideal geblendet & || nur blendet Dich jetzt das Ideal & || nur bist Du vom Ideal jetzt geblendet & siehst daher || also nicht deutlich die wirkliche Anwendung des Wortes ‘Spiel’.

Ich will sagen: Das Ideal liegt in Deiner Ausdrucksform, aber || & Du mißverstehst die Rolle, die es || in Deinem Ausdruck spielt.

– – – Aber ich will sagen, Du mißverstehst die Rolle die das Ideal in Deiner Ausdrucksweise spielt. D.h., auch Du würdest es ein Spiel nennen, nur ….

Wir sind in der Idee gefangen, das Ideal müsse … Wir leben nun in der Idee ….
Wir leben nun mit unsern Gedanken in der Idee ….

Denn die Idee sitzt gleichsam als Brille auf unsrer Nase.
Denn wir glauben es schon in ihr zu sehen.

Wir glauben es muß in ihr stecken: d.h. || D.h. wir glauben es schon in ihr zu sehen.
Und das Ideal sitzt nun ….

Wir sehen sie schon jetzt (wenn auch durch ein Medium hindurch), da wir ja …

Wie bist Du zu diesem¤ Ideal gekommen? Aus welchem Material hast Du es geformt? Welche konkrete Vorstellung war sein Urbild || ist sein eigentliches Urbild¤ || ist dazu Modell gestanden?
Das mußt Du Dich fragen; sonst kannst Du die Faszination des Ideals nicht los werden.

Zentren der Variation.

Rolle in der Ästhetik.

1
2
3
0
4
0
0
0

⇒S. 409
⇒S. 410
⇒S. 411
⇒S. 412
⇒S. 413
⇒S. 415
⇒S. 416
⇒S. 417
⇒S. 418
⇒S. 419
⇒S. 420
⇒S. 421
⇒S. 422
⇒S. 424
⇒S. 425
⇒S. 430
⇒S. 431 Ende

Das Ideal muß seinen Ursprung || sich bezüglich seines Ursprungs ausweisen.

“Ach so –!” sagen wir wenn uns die philosophische Erklärung gegeben wird & atmen auf.

Die Lösung der Probleme besteht im Eliminieren des beunruhigenden Aspekts den gewisse Analogien in unsrer Grammatik auslösen.

Die Philosophie verändert den Aspekt. Indem sie andere Analogien aufzeigt. Zwischenglieder einschiebt. etc.

‘Da muß doch etwas sein (Zeit)!’ ‘Aber da ist doch nichts!’

Merke, wie verschieden Du das Zeichen “❘❘❘” ansiehst wenn Du es einmal als römische Drei, einmal als hundertelf liest. Was ist der Unterschied. Ist wirklich ein Unterschied?

Zu “Idealer Name” & Ursprung des Ideals gehört die Bemerkung daß wir die Wörter die der Philosoph in metaphysischer Weise verwendet ihrer gewöhnlichen

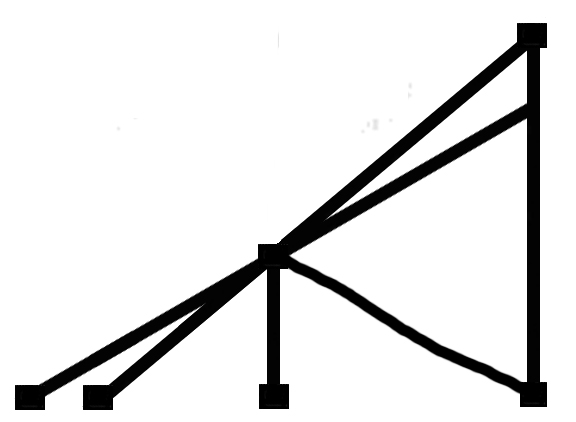
Verwendung wieder zuführen. ⇒Siehe Typescript

Man könnte sich denken daß jemand Rutenbündel zählt & sagt: Die eigentlichen Bündel || daß jemand sagt: Wenn ich Rutenbündel zähle: die eigentlichen Bündel können ¤ja || doch nicht ‘die Stäbe’ sein. Denn Stäbe können abbrechen, herausfallen, & doch bleibt das Bündel das Bündel. Die Stäbe sind etwas unreinliches & ich könnte sie nicht mit den reinlichen Zahlen 1 2 3 … zählen. ||

Man könnte sich denken daß jemand Rutenbündel zählt & sagt: Das eigentliche Bündel können doch nicht die Stäbe sein. Denn die Stäbe können abbrechen & herausfallen, – & doch bleibt das Bündel das Bündel. Die Stäbe, || : das ist eine unreinliche Angelegenheit & ich könnte dieses Unsichere || Unklare nicht mit meinen reinen, klaren Zahlen 1, 2, 3, … zählen.

‒ ‒ ‒ die er gleichsam übersieht.

Nur so nämlich || dadurch können wir || unsere Behauptungen der Ungerechtigkeit – oder Leere

unserer Behauptungen entgehen, indem wir das Ideal als das was es ist, nämlich als Vergleichsobjekt – sozusagen als Maßstab – an die Spitze || in unsrer Betrachtung hinstellen || ansehen, & nicht || statt als das Vorurteil, dem Alles konformieren muß || müsse. Dies nämlich ist || Hierin nämlich liegt der Dogmatismus. indem wir das Ideal als das hinstellen / was

Was ist denn aber das Verhältnis einer Betrachtung wie der

Spenglers

& der meinen?
… in dem die || unsre Philosophie so leicht verfällt. || verfallen kann.

Die Ungerechtigkeit bei Spengler: Das Ideal verliert nichts von seiner Würde, wenn es als Prinzip der Betrachtungsform hingestellt wird. Ein guter Maßstab || Eine gute Maßeinheit. –

Russell – Nicod

‒ ‒ ‒ Denn diese Antworten machen sich gleichsam über die Frager lustig.

Wenn die Philosophen das Wesen des “Seins”, der Realität, des Wissens

u.s.w. zu erfassen trachten || suchen, so muß man sich immer fragen, – wird denn dieses Wort in der Sprache, in der es seine Heimat hat d.i. in der Sprache des Alltags, je tatsächlich so gebraucht?

Aber es waren nur Luftgebäude die wir zerstörten; & wir legen den Grund der Sprache frei auf dem sie standen.

Auch sind unsere Sprachspiele nicht (etwa) Vorstudien für eine zukünftige

vollständige Beschreibung ‒ ‒ ‒

‒ ‒ ‒ die durch Ähnlichkeit & Unähnlichkeit ein Licht auf die Funktion unserer Sprache werfen sollen || in die Verhältnisse unsrer Sprache hineinleuchten sollen.

‒ ‒ ‒ & damit das Sprachspiel in dem wir das Wort “lesen” verwenden, wäre für den der sie nicht kennte beinahe nicht zu beschreiben.

Denk Dir || Stell Dir vor, Menschen,

oder andere Wesen, würden von uns als Lesemaschinen benützt. Sie werden zu diesem Zweck abgerichtet:
Überlege Dir folgenden || diesen Fall: Denke Dir es würden von uns Menschen, oder andere Wesen von uns, als Lesemaschinen benützt ….

Verwenden wir aber “lesen” für ein gewisses Erlebnis || Erleben des Übergangs von Zeichen zum gesprochenen Laut, ‒ ‒ ‒.

“Aber ein Mensch || der Mensch selbst muß doch wissen, ob er wirklich liest, oder nur vorgibt zu lesen)!”

Die philosophischen Probleme unlösbar – bis sie verschwinden
Das Problem rührt sich nicht vom Fleck – & dann geht es ganz leicht.
Kassenschloß.

Der Mathematiker ist kein Entdecker, sondern ein Erfinder.

Denk Dir ein Material härter & fester als irgendein anderes. Aber wenn man einen Stab aus diesem Stoff aus der horizontalen in die vertikale Lage bringt, so zieht er sich zusammen, oder denk Dir er biege sich, wenn man ihn aufrichtet während er so hart ist, || & ist dabei so hart, daß man ihn auf keine andre Weise biegen kann. Denk Dir Ein Mechanismus aus diesem

Stoff, etwa eine Kurbel Pleuelstange & Kreuzkopf. Andere Bewegungsweise des Kreuzkopfs.

Oder: eine Stange biegt sich, wenn man ihr eine gewisse Masse nähert, gegen alle Kräfte aber die wir auf sie wirken lassen, ist sie ganz || vollkommen starr. Denk Dir die Führungsschienen biegen sich & strecken sich wieder wenn die Kurbel sich ihnen nähert & sich wieder entfernt. Ich nehme aber an daß keinerlei besondere äußere Kraft dazu nötig ist dies hervorzurufen.

Das || Dieses Benehmen der Schienen würde einen || uns (in so einem Fall) wie das eines lebenden Wesens anmuten.
Wenn wir sagen “wenn die Glieder des Mechanismus ganz starr wären, würden sie sich so & so bewegen”, was ist das Kriterium dafür daß sie ganz starr sind? Ist es, daß sie gewissen Kräften widerstehen? Oder, daß sie sich so & so bewegen?
Denke, ich sage: “das ist das Bewegungsgesetz des Kreuzkopfes (die

Zuordnung seiner Lage zur Lage der Kurbel etwa, wenn sich die Länge der Kurbel & der Pleuelstange nicht ändern”. Das heißt wohl wenn sich die Lagen der Kurbel & des Kreuzkopfes so zueinander verhalten, dann || so sage ich, daß die Länge der Pleuelstange gleichbleibt.
“Wenn die Teile ganz starr wären, würden sie sich so bewegen”: ist das eine Hypothese? Es scheint, nein. Denn wenn wir sagen: “die Kinematik beschreibt

die Bewegungen des Mechanismus unter der Voraussetzung daß seine Teile vollkommen starr sind”, so geben wir einerseits zu, daß diese Voraussetzung in der Wirklichkeit nie zutrifft, anderseits soll es keinem Zweifel unterliegen, daß vollkommen starre Teile sich so bewegen würden. Aber woher diese Sicherheit? Es handelt sich hier wohl nicht um Sicherheit sondern um eine Bestimmung, die wir getroffen haben. Wir wissen nicht, daß

Körper, wenn sie ( (nach den & den Kriterien) starr wären sich so bewegen würden; wohl aber würden wir (unter Umständen) Teile “starr” nennen die sich so bewegen.

Denke in so einem Fall immer daran daß ja die Geometrie (oder Kinematik) keine Meßmethode angibt || spezifiziert, wenn sie von gleicher Länge oder vom Gleichbleiben einer Länge spricht.
Wenn wir also die Kinematik etwa die Lehre von der Bewegung vollkommen starrer Maschinenteile nennen, so liegt

hierin einerseits eine Andeutung über die (mathematische) Methode, wir bestimmen gewisse Distanzen als die Längen von Maschinenteilen, die sich nicht ändern; anderseits eine Andeutung über die Anwendung des Kalküls.

Bestimmt die Operation || die Regel + 2 den Übergang, der von 200 aus zu machen ist, oder nicht? Bestimmt die Funktion x³ + x² + 1 die Zahl, die wir durch für x = 5 erhalten? Wie ist diese Frage zu beantworten?

Sehen wir || Prüfen wirdazu, ob die Resultate, die die Menschen durch diese || die Substitution erhalten übereinstimmen || immer die gleichen sind? Nein. Und doch ist das Faktum, daß || das erhaltene Resultate für || gegeben den Fall mathematisch erzogene Menschen || Rechner in der überwiegenden || ungeheuern Mehrzahl der Fälle das gleiche || selbe ist, hier von der größten Bedeutung.
Wir würden diese Rechenmethode nicht gebrauchen wenn sie nicht – normalerweise – tatsächlich zu dem gleichen Resultat führen würde.
Die Frage hat, für uns mathematisch,

gar keinen Sinn, – wenn wir nicht den Fall die der Funktion x³ + x² + 1 von bestimmten anderen Funktionen unterscheiden wollen etwa von Funktionen von mehr als einer Variablen. Und dann ist die Frage die gleiche wie die: ist die Funktion x³ + x² + 1 eine Funktion nur einer Variablen. Und was man mit dieser Frage in diesem Fall anfangen könnte ist wieder nicht klar, es sei denn etwa daß eine – in diesem Fall sehr primitive – Methode der Ausrechnung der Anzahl der Variablen anzuwenden wäre || sei.

Unter bestimmten Verhältnissen könnte die Frage z.B. durch eine Untersuchung zu beantworten sein, ob alle Variablen eines Ausdrucks sich bis auf eine wegheben.

Aber willst Du sagen, daß der Ausdruck + 2 es für Dich zweifelhaft läßt, was Du, nach 234 z.B., schreiben sollst? Nein; ich sage unbedenklich 236; aber darum

ist es ja || auch ganz unnötig || überflüssig daß über diesen Übergang || darüber schon im Voraus || früher etwas bestimmt worden wäre. || ist || wird. || Nein, aber ich sage unbedenklich 236; aber darum ist es auch überflüssig daß darüber schon früher etwas bestimmt wird || wurde.
Daß ich keinen Zweifel habe, wenn die Frage an mich herantritt, heißt das, daß sie früher schon beantwortet worden ist?
Aber ich weiß doch auch, daß, welche Zahl immer man mir gibt ich die folgende

gleich mit Bestimmtheit werde angeben können || angeben werde können.
Ausgenommen ist doch gewiß der Fall, daß ich sterbe ehe ich die nächste Zahl nennen kann, & natürlich auch viele andere Fälle. Daß ich aber so sicher bin, daß ich werde fortsetzen können ist freilich von der größten Bedeutung.

“Eine Definition führt Dich doch nur wieder einen Schritt zurück zu etwas anderem nicht definiertem.” Was sagt uns das? Wußte das irgend jemand

nicht? – Nein; aber konnte er es nicht aus dem Auge verlieren?

Oder: “Wenn Du schreibst
‘1, 4, 9, 16 . . . .’,
so hast Du nur vier Zahlen angeschrieben, & ein paar || vier Punkte”. Worauf machst Du da aufmerksam? Konnte denn jemand etwas anderes glauben?
Man sagt Einem in so einem Falle auch: “Damit hast Du weiter nichts hingeschrieben als vier Zahlzeichen & noch ein fünftes Zeichen, das hier aus ein paar || einigen Punkten besteht”. Ja

wußte er das nicht? Aber kann man nicht doch sagen: Ja wirklich, ich habe die Pünktchen nie als ein fünftes Zeichen in der || dieser Reihe aufgefaßt, – das hier (freilich || allerdings) so aussieht, wie weitere flüchtig geschriebene Ziffern, dem ich aber auch eine Form geben kann die etwas selbst || das ich aber auch anders schreiben könnte, so etwa daß es selbst den Charakter eines Buchstabens oder Zahlzeichens hat, sagen wir

Oder wie ist es, wenn man darauf aufmerksam macht, daß

eine Linie im Sinne Euklids eine Farbengrenze ist & kein || nicht ein Strich, & ein Punkt der Schnitt zweier Farbengrenzen & kein Tupfen. (Wie oft ist (es) gesagt worden, daß man sich keinen Punkt vorstellen kann!.)

“3 Äpfel + 3 Äpfel = 5 Äpfel, aber in praxi kommt dann meistens || beinahe immer noch einer dazu.”

Beweis:

“Ich habe nicht gewußt, daß man

△

zusammenlegen kann.”

Kann man auch sagen: “Ich habe gedacht man könne sie nicht

zusammenlegen”?

Aber man kann sagen: ich habe gedacht, man könne sie nicht Seite an Seite (oder: so gut passend) zusammenlegen. Ich kann mir z.B. denken daß einer dreht & dreht & auf diese Stellung nicht verfällt.
Ich habe nicht gedacht daß man sie so zusammenlegen kann. Wenn mich

jemand gefragt hätte kann man sie passend zusammenlegen hätte ich geantwortet: ‘Nein¤. Ich habe den Versuch sie zusammenzulegen nach einigem Probieren aufgegeben.’

(Geduldspiele.)

Was findet der der das Geduldspiel zusammenbringt?
Er findet: eine Lage – an die er früher nicht gedacht hat. – Gut – aber kann man also nicht sagen: er überzeugt sich davon, daß man ein Dreieck

& ein Sechseck so zusammenlegen kann? – Aber sag mir: dieses Dreieck & das Sechseck welches man so zusammenlegen kann, sollen sie schon so in einander liegen, oder noch nicht – & sie sollen erst so zusammengelegt werden?

Aber ich hatte keine Möglichkeit angezweifelt, sondern nur eine Möglichkeit nicht gesehen.

Du hast mir einen Weg von da dorthin gezeigt.

Wenn ich sage: ich habe nicht geglaubt, daß es so einen Weg gibt, so müssen wir uns doch fragen wie man eine solche Aussage gebraucht, wie man zu ihr kommt. Ich habe versucht so einen Weg zu finden habe aber keinen

gefunden. Wie habe ich versucht? Worin bestand dieses Versuchen & worin das nicht Gelingen?

“Du gibst das zu, – dann mußt Du das zugeben.” Er muß dies zugeben – & doch ist es möglich daß er es nicht zugibt. Und wenn ich keinen okkulten Vorgang des Denkens annehme so kann ich auch nicht sagen: “ja er kann sagen daß er es nicht zugibt, aber er kann es nicht denken.” Es sei denn ich will damit

sagen, daß ich einen solchen Gebrauch der Worte nicht “denken” nenne.
“Ich werde Dir zeigen, warum Du es zugeben mußt. –”

Wie kann ihn denn die Manipulation || können ihn denn die Manipulationen des Beweises dazu bringen etwas zuzugeben?

“Du wirst doch zugeben daß 5 aus 3 + 2 besteht!” – Ich gebe Dir zu daß ich “2”, “3”, “5” + “bestehen” in dieser Weise gebrauchen will.”
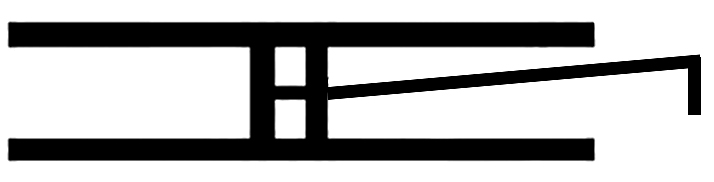
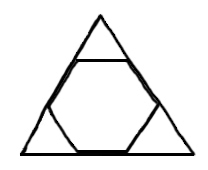
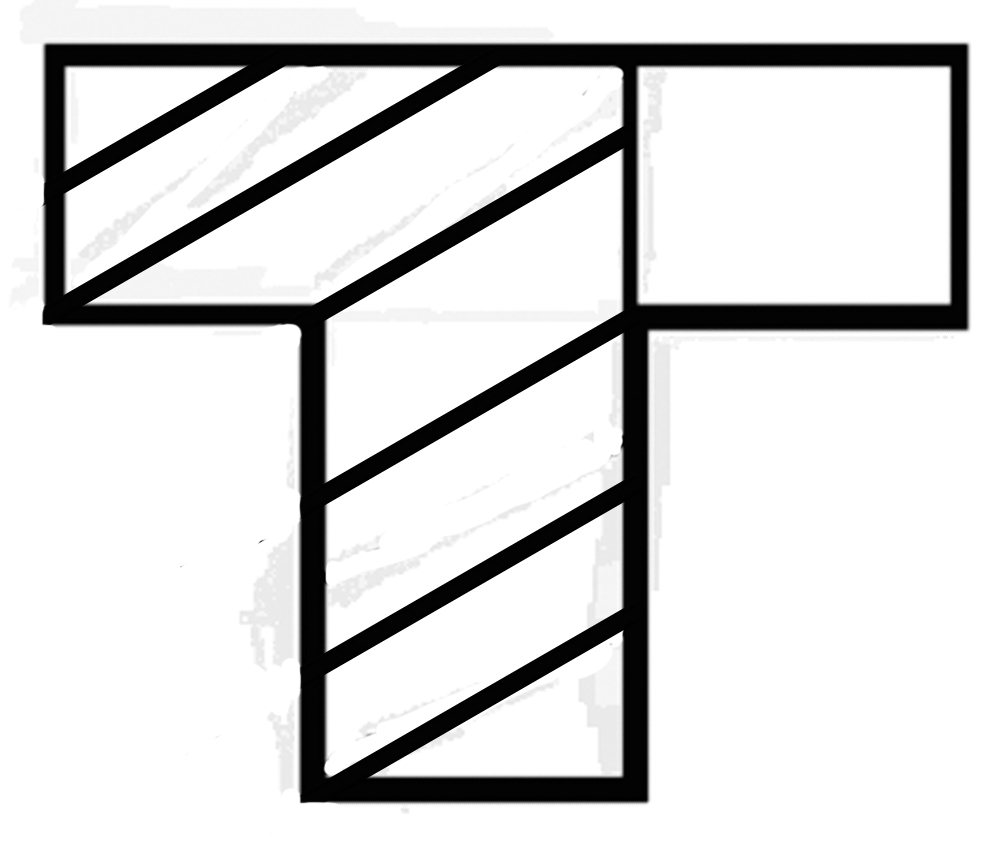
Und ich kann sagen:

– Ja bei Gott, sie sieht nicht so aus, aber sie besteht aus 2 Parallelen …!”
Was überrascht Dich? Daß die Figur, die Du jetzt siehst aus den || diesen Teilen besteht? Nein das heißt ja nichts! Daß sich das Rechteck in diese Figur hat umformen lassen? Nein, auch nicht. – “Daß sich ein Rechteck so teilen läßt”– will ich sagen. (Wie teilen läßt?) Aber mich überrascht, was ich in dieser Figur || der geteilten Figur sehe. Das ist ein neuer & befremdender Aspekt || Anblick eines Rechtecks & zweier Parallelogramme.

‘Ich hatte nicht gedacht, daß ein Rechteck das in sich haben kann oder ‘das in sich hat’.

Ich hatte nicht geglaubt daß man von einem Rechteck sagen könne es bestehe aus zwei Parallelogrammen & ….

I am trying to hold the puzzlement as long as possible; whereas you – the mathematician – get rid of it as quickly as possible.

Mein Talent für die || der Philosophie besteht darin daß ich im Stande bin über etwas noch puzzled zu sein wenn für Andere das puzzlement längst abgleitet.
My talent consists in being capable of being puzzled when the puzzlement has glided off your mind. I'm able to hold the puzzlement when it has slipped through your hands¤ (& you therefore think, you are clear¤).
The art of the philosopher is not to be cheated out of your || his puzzlement before it's really cleared up.

Mich überrascht es ein Rechteck so geteilt zu sehen.
“Ja bei Gott, das ist ein Rechteck! & das sind zwei Parallelogramme!”

‘Ich wäre nicht auf die Idee gekommen zwei Parallelogramme so in ein Rechteck zu legen!’

‘Das sind vor allem einmal Worte. Aber nun ihr Gebrauch! –’

Ich bin überrascht, daß, was ein Rechteck ist, (dann) so zusammengesetzt ist.

Ich bin – so zu sagen – überrascht, daß es das gibt.

Vergleiche: Ich bin überrascht, daß so viel so große || solche Teile aus diesem Kuchen gehen.

“Du mußt ja nicht zugeben, daß das noch ein Rechteck ist.”

Ich bin überrascht, daß es eine Figur gibt die den Umriß des Rechtecks hat & aus solchen Teilen zusammengesetzt ist.

“Ich bin überrascht zu sehen, daß so ein Rechteck entsteht” – Ja, was hättest Du geglaubt, daß so entsteht?

Ich bin überrascht einen Rhombus als Raute zu sehen.

Ich bin überrascht daß ein Rhombus eine Raute ist.

“Ja, Du hast mich überzeugt, daß jedes Rechteck aus … besteht.” – ‘Aber das ist ja ein Aberglaube || ja Täuschung; es besteht ja gar nicht aus diesen Teilen, sondern Du stellst es Dir jetzt nur immer so vor.’
Ja ich habe ja gemeint: daß ich mir jetzt jedes Rechteck so geteilt || zusammengesetzt vorstellen kann. – Wohl – aber wovon bist Du denn dann ‘überzeugt’?

Aber was meinst Du denn – ‘jedes ist so zusammengesetzt’?! Es besteht doch nicht jedes aus diesen || solchen Teilen. Du

stellst sie Dir jetzt nur so zusammengesetzt vor! Das ist doch keine Überzeugung über ihre Zusammensetzung!

Du meinst: Du siehst jetzt jedes (Rechteck) so an. Aber wovon habe ich Dich da überzeugt? – Nun, ich wußte nicht, daß dieses Rechteck z.B.– aus zwei solchen Parallelogrammen … besteht. – Aber dieses Rechteck

besteht ja gar nicht aus solchen Teilen & daß dieses

aus ihnen besteht,

hast Du doch nie bezweifelt! Der Satz – Du wußtest nicht daß … ist offenbar nachgebildet diesem: ‘Ich wußte nicht, daß dieses Werkstück aus diesen beiden Teilen bestand’. Denn Du denkst Dir nun das Rechteck so zerteilt.

Ich habe Dich gelehrt die Figur in Teile von dieser Physiognomie zu zerlegen. Du wußtest nicht daß sie aus Teilen von solcher

Physiognomie besteht.

Ich habe nicht gewußt daß die Figur aus 2 Teilen von dieser wohlbekannten Physiognomie besteht.
Ich konnte dies auch dann noch nicht wissen als die Linien schon gezogen waren. – Ich sage dann etwa: ‘Ja, richtig das sind ja Parallelogramme!”
Man würde jetzt nicht

sagen: “Du hast mich überzeugt, … ”, sondern: “Du hast mich drauf aufmerksam gemacht.”

Ich wußte nicht daß diese Form aus den || diesen, mir so gut bekannten, Formen zusammengesetzt ist. ¥
“Wie eigentümlich dieses Brett zusammengesetzt ist!”

⍈ “Wer hat sie denn so zusammengesetzt?” Der das Rechteck geschaffen hat.

“Ich habe nicht gewußt daß das Rechteck so zusammengesetzt ist”– hier

ist es als habe der ◇◇◇ Werkmeister es so zusammengefügt || zusammengesetzt.

“Ich habe nicht gewußt daß ein Rechteck aus diesen Formen besteht.” Es ist als hättest Du einen neuen Einblick in sein Wesen erhalten.

Aus dem folgt unerbittlich das.

Wir sagen z.B. wir haben gleichviel Leute || Nüsse hier & dort wenn wir bei der Zählung hier 6 + hier 6 herausbringen.

3 + 4 = 7

3 + 4 reicht bis 7.

d
a

e
b

f
c

g
d

a + b = c

     Unterschied der Rolle des Überraschenden

     “Denkgesetze”

     Denkgewohnheiten
     Denkarten

… als wären also durch seine Manipulationen erstaunliche || die erstaunlichsten Tatsachen ans Licht gekommen.

Russell über “Ursache”. Das Bild eines Experimentes, welches zeigt was wir unter Ursache verstehen.

     Wir sagen: ich fürchte mich weil er so schaut & hier haben wir scheinbar eine Ursache, die man unmittelbar ohne wiederholtes Experiment als solche erkennt.
     Russell sagte, man müsse, ehe man etwas als Ursache durch Experiment || wiederholte Erfahrung erkenne, etwas || irgendetwas durch Intuition als Ursache erkennen.
     Ist das nicht als sagte man: Man muß ehe man etwas als 2 m durch Messung anerkennt, etwas durch Intuition als 1 m erkennen?

     Wie nämlich, wenn jener Intuition durch wiederholtes Experiment widersprochen wird? Wer hat dann recht?
     Und was ist es denn was uns die Intuition über die Erfahrung sagt die wir ‘als Ursache erkennen’?
     Handelt sich's da um etwas andres, als eine Reaktion unsererseits gegen den Gegenstand: die Ursache?

Aber erkennen wir nicht unmittelbar, daß der Schmerz von dem Schlag herrührt, den wir erhielten || erhalten?

Ist er nicht die Ursache & kann ein Zweifel sein, daß er es ist. Aber läßt es sich nicht ganz gut denken, daß wir in gewissen Fällen hierüber getäuscht werden? und später die Täuschung erkennen: Es scheint uns etwas zu schlagen & zugleich wird ein Schmerz in uns hervorgerufen. (Man glaubt manchmal einen Lärm durch eine Bewegung hervorzurufen.)
Und freilich es ist hier eine echte Erfahrung die man ja Erfahrung der Ursache nennen kann: Aber nicht

weil sie uns unfehlbar die Ursache zeigt, sondern weil in ihr der Anfang des Ursache-Wirkung-Schemas liegt.

Wir reagieren auf die Ursache.
Etwas “Ursache” nennen ist ähnlich, wie, zeigen & sagen: “Der ist schuld!”

Wir stellen intuitiv die Ursache ab, wenn wir die Wirkung nicht wollen. Wir schauen intuitiv vom Gestoßenen auf das Stoßende.

Wie nun wenn ich sagte, wir vergleichen, wenn wir von Ursache & Wirkung reden alles mit dem Fall des Stoßes; der ist das Urbild der Ursache einer Wirkung. Hätten wir da den Stoß als Ursache erkannt? Denk eine Sprache in der statt “Ursache” immer “Anstoß” gesagt wird.

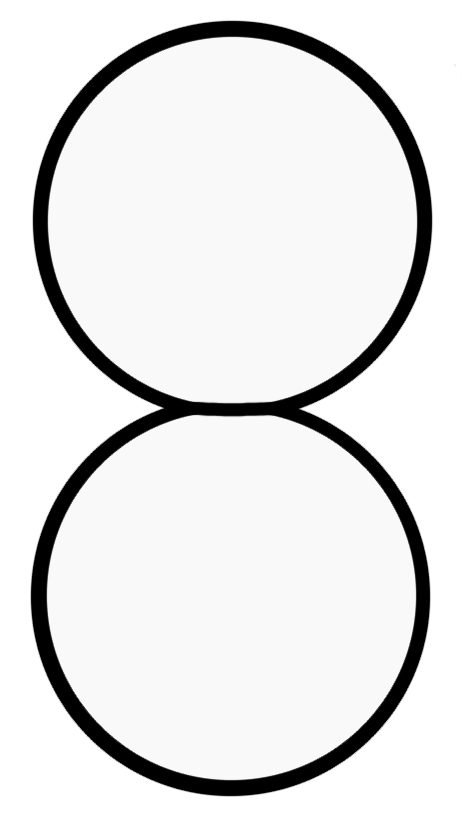
Was zeigt uns der der 4 Kugeln in 2 und 2 zerlegt || trennt, (sie) wieder zusammenschiebt, wieder trennt & so einige Male?
Er prägt uns eine typische Änderung der Physiognomie ein.

Warum soll man

statt des Sätzchens 3 + 2 = 5 nicht lernen den Befehl ausführen: “Trenn 5 || eine Anzahl in 3 + 2.” oder: zeig mir was sich in 3 + 2 trennen läßt. Zeichne in welcherlei Gruppen Du ❘ ❘ ❘ ❘ ❘ trennen kannst. Und die Antwort sollte sein: in ❘ ❘ + ❘ ❘ ❘, in ❘ + ❘ ❘ ❘ ❘ etc.

Was wir liefern sind eigentlich Bemerkungen zur Naturgeschichte des Menschen; aber nicht kuriose Beiträge, sondern solche die vor aller Augen liegen || Feststellungen an denen niemand gezweifelt hat & nur darum die Augen nie auf sich

ziehen. Wie ein Dieb der sich der Aufmerksamkeit entzieht nicht indem er sich versteckt sondern dadurch daß er vor aller Augen || von allen sichtbar handelt || etwas einsteckt,als könnte es nicht anders sein.

… & die nur darum dem Bemerktwerden entgehen weil sie uns ständig vor den Augen sind

… nicht dadurch daß er versteckt || heimlich, sondern || aber dadurch daß er vor aller Augen etwas einsteckt || mitnimmt.

… & die dem Bemerktwerden nur dadurch entgehen, weil sie ständig vor unsern Augen sind || weil sie sich ständig vor unsern Augen herumtreiben. ¤

290

Editorial notes

1) Continuation from Ms-157a,BCr.

2) See facsimile; connecting line between "417" and "419".

Editorial notes

(2015–) Wittgenstein Source Bergen Nachlass Edition (WS-BNE). Edited by the Wittgenstein Archives at the University of Bergen under the direction of Alois Pichler. In: Wittgenstein Source, curated by Alois Pichler (2009–) and Joseph Wang-Kathrein (2020–). (N) Bergen: WAB.