Ms-162b,FCr

Ms-162b,FCv

Ms-162b,1r

“Ich kann Einem nicht alle Techniken durch eine Technik beibringen.”

Man kann wohl die Namen aller Systeme in eine Reihe ordnen, aber sie nicht alle den Systemen der Reihe nach zuteilen || aber nicht die Namen allen

Ms-162b,1v

Systemen der Reihe nach zuordnen.

     D.h. man hat, wenn man eine endlose Reihe von Namen hat, nicht zu wenig Namen; wenn man sie (nur) nicht so aufteilt, daß dem System von Namen ein System von Systemen entspricht. Verwendet man diese besondere Art der Zuteilung, dann hat man zu wenig Namen; und das kann man

Ms-162b,2r

so ausdrücken: “man kann nicht alle Namen allen Systemen zuteilen” – weil man unter dem Zuteilen || Verteilen aller Namen an Systeme das Verteilen aller Namen an ein System von Systemen versteht.

Die Verwirrung entsteht hier durch den Ausdruck “man kann … in eine Reihe ordnen”.

Ms-162b,2v

Es gibt Reihen, welche man “Reihen aller Brüche” nennt.
     Es gibt Reihen, von welchen man sagt, sie enthielten alle Brüche.

‘Wir wollen nicht || unter keinen Umständen sagen: eine Reihe von Funktionen enthielte alle Funktionen weil || denn, wenn sie alle Funktionen f_n(x) enthält || f₁(x), f₂(x), f₃(x), … enthielte alle Funktionen, da sie f_x(x) nicht enthält.’ ||

Ms-162b,3r

3

‘Wir wollen unter keinen Umständen von einer Reihe von Funktionen f₁(x), f₂(x), … sagen sie enthielte alle Funktionen, weil f_x(x), (z.B.) nicht in ihr enthalten ist.’ || weil f_x(x) (z.B.) keines ihrer Glieder ist.’

‘Wir wollen unter keinen Umständen von einer Reihe aller Reihen sprechen.’
     ‘Wir wollen unter keinen Umständen von einer Kiste sagen, sie enthielte alle Kisten.’

Ms-162b,3v

     “Wieviele Multiplikationen hast Du zu machen || auszuführen gelernt?” – – ℵ₀ – (d.h. ein || immer neue, & ein unbegrenztes System von Multiplikationen || ihnen). – “Und wieviele Funktionen hast Du zu bilden gelernt?” – “Viel mehr || Oh viel mehr als ℵ₀, 2^(ℵ₁)!” (d.h. ich habe gelernt, aus irgend einem unbegrenzten || dem Ausdruck für ein unbegrenztes System von ihnen, neue Systeme || Funktionen zu erzeugen). – “Aber Du hast doch auch gelernt, aus irgend einem unbegrenzten System der Größe nach geordneter Brüche

Ms-162b,4r

weitere || neue solche Systeme zu erzeugen.”

Bestimmen wir, daß alle Systeme || Funktionen φ(ξ) mit Brüchen benannt werden sollen! Man kann alle Brüche in eine Reihe ordnen – hat man damit nun alle Systeme || Funktionen || φ(ξ) in eine Reihe geordnet? ‘Systeme || Funktionen in eine Reihe ordnen’ heißt: aus einer Reihe von Reihen in gewisser Weise eine Reihe abzuleiten. || aus einem Begriff der uns durch eine Reihe || ein System von

Ms-162b,4v

Reihen || Systemen gegeben ist, einen Begriff von gleichem Umfang || von Systemform zu machen || Begriff von Systemform || Reihenform zu machen || konstruieren, der mit jenem den gleichen Umfang hat.

     Wenn ich jemand die Reihe der Reihen πⁿ erklärt habe, so muß er nun im Stande sein z.B. π⁵²⁰ Schritt für Schritt || Ziffer für Ziffer zu berechnen. Ich habe ihm also die Technik von π⁵²⁰ erklärt.

Ms-162b,5r

     Was heißt es denn eigentlich die f_v(x) seien Funktionen von x? Genügt es dazu, daß ich einerseits die Zeichen f_v(x) – d.h. ‘f₁(x)’, ‘f₂(x)’ … || etc. etc. f₁(1), f₂(1) … || etc. etc. anschreiben kann & anderseits einige von diesen || dieser Zeichen als Namen gewisser || von Techniken der Reihenentwicklung benütze? So ist es doch offenbar nicht, denn es muß vielmehr mit dem System f_v(x) eine bestimmte Technik verbunden sein, Techniken der Entwicklung zu bilden.

Ms-162b,5v

Dies ist aber nicht damit erreicht || gegeben, daß ich eine Technik zur Bildung der Zeichen f_v(x) besitze.

     Man kann alle Funktionsnamen in eine Reihe || ein System ordnen; aber man kann sie nicht alle systematisch erklären.

‘Ein System von Funktionsnamen systematisch erklären’ heißt: eine Erklärung an den Kopf zu stellen.

Ms-162b,6r

‘Den Gebrauch eines Systems von Zeichen || der Zeichen eines Systems systematisch erklären’ heißt: eine Erklärung an den Kopf des Systems stellen, die die richtige Verwendung der Zeichen des Systems bewirkt || verbürgt.

Kann diese Erklärung selbst ein Zeichen des Systems sein?

Die Erklärung der Funktionszeichen geschieht systemweise.

Ms-162b,6v

‘Habe ich Dich gelehrt || geübt, ein System von Funktionen zu beherrschen, so habe ich Dich damit auch abgerichtet, eine weitere || außerhalb des Systems stehende Funktion zu beherrschen.’

Meine Aufgabe ist es Euch die Geographie eines Labyrinths zu lehren, so zwar, daß Ihr Euch vollkommen darin auskennt.

Ms-162b,7r

Wie bewegt man Menschen dazu¤, mit Überzeugung eine bestimmte Behauptung zu machen?

Ms-162b,7v

     “Sei || Aber sei nicht lächerlich! Freilich bedienen wir uns zum Erkennen der Anzahl gewisser Mittel, die Anzahl übersichtlich zu machen; z.B. des Dezimalsystems.” – Aber was ist hier Zweck, & was Mittel?

     Wir würden also nicht erkennen, daß 10.000 Variable in dieser Klammer stehen. Ist das nicht, als sagte man: “wir würden nicht erkennen,

Ms-162b,8r

wieviele || wieviel Jahre ein || der Elefant || Mensch lebt, wenn die Erde nicht um die Sonne ginge”?

Ist denn das nicht eben, was wir Zahlbestimmung nennen, diese Technik, das Zählen im Dezimalsystem anzuwenden? – Nein; denn wir hätten ebensowohl in einem andern System zählen können. – Aber liegt dies nicht daran, daß wir verschiedene solche Techniken lernen

Ms-162b,8v

können & so gut wie immer übereinstimmende Resultate erhalten? – Aber wir erkennen doch die Zahlen ∣, ∣∣, ∣∣∣, ∣∣∣∣ auf den ersten Blick & wir könnten uns doch Wesen denken, die auch 10.000 Striche als 10.000 Striche auf den ersten Blick erkennen würden. – 10.000 Striche als 10.000 Striche? Wie wüßten wir denn, daß es wirklich 10.000 Striche sind die sie als 10.000 Striche erkennen?

Ms-162b,9r

Doch nur durch eine von unseren Zählmethoden. Also durch die Übereinstimmung unsrer Resultate. Aber kann man denn sagen, daß diese Übereinstimmung zeige, daß jene Leute das Richtige erkennen. (Dann könnte die Übereinstimmung ja ebensogut zeigen, daß wir richtig zählen!)

Ms-162b,9v

     So hatte Frank Ramsey (also) völlig recht damit, daß || als er schrieb || zu schreiben (Last papers): … Nur, glaube ich, sah er || Er sah aber – – || (so glaube ich– || ) das Problem nicht || nicht das Problem, welches || das darin liegt || lag, die Beziehung dieser || der logischen Exaktheit & dieser Vagheit anzugeben. || das || welches darin lag || liegt, anzugeben || zu zeigen welche Beziehung zwischen der Exaktheit der Logik & jener Vagheit, von der er spricht, besteht. || das darin liegt, anzugeben, welches

Ms-162b,10r

10

¤ die Beziehung ist zwischen der logischen Exaktheit & jener Vagheit. || welches darin liegt, anzugeben, in welcher Beziehung die logische Exaktheit & jene Vagheit stehen. || Er sah aber || Nur sah er (glaube ich) das Problem nicht, das || welches darin liegt, anzugeben, in welcher Beziehung die logische Exaktheit & jene Vagheit stehen. || , das darin liegt, die Beziehung anzugeben zwischen jener Vagheit & der logischen Exaktheit.

Ms-162b,10v

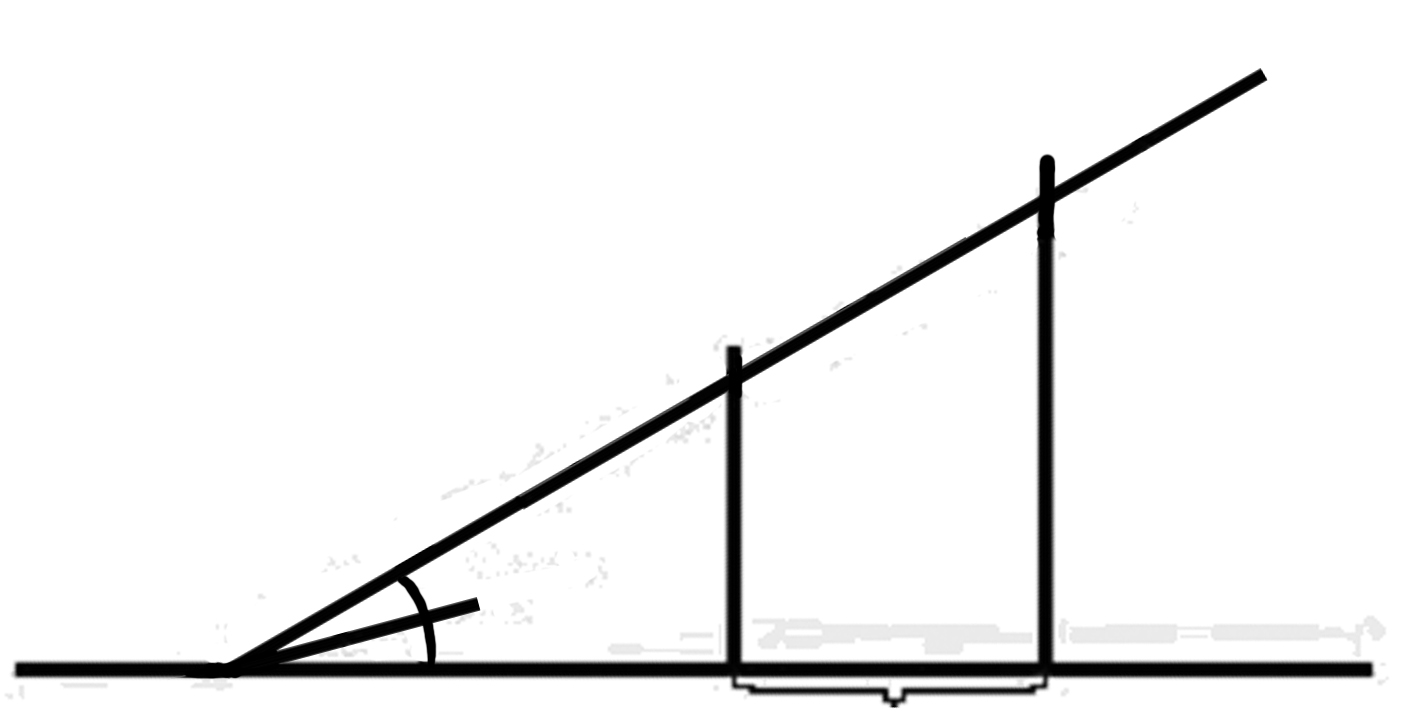
We can't describe with words the relation between

a | & b |.

|| Worte können das Verhältnis der Längen

a | & b |.

nicht ausdrücken. An welche Art von Beschreibung denken wir denn, wenn wir sagen Worte könnten das nicht beschreiben?

Für diese Relation könnten wir nur einen Namen haben; beschreiben können wir sie nicht.

Wann wäre sie aber beschrieben?

Ms-162b,11v

     Nun es ist doch hier ein bestimmter Grad des Größenunterschieds, & der läßt sich mit Worten nicht ausdrücken.

     Kann ich diesen Winkel nicht beschreiben? Doch, z.B. als das Doppelte eines andern für den ich einen Namen habe.

Warum aber nicht

Ms-162b,12r

als das 27-fache eines andern Winkels?

Was ist das für ein Satz: “Wir können uns das 27-fache eines Winkels nicht vorstellen”?
     Vor allem einmal heißt es nicht: das physikalisch 27-fache.

Verwandtes Beispiel: Wir können uns 27 Stücke nicht vorstellen.
     (Absolutes Gehör.)

Ist es nur behaviouristisch bestimmt?

Ms-162b,12v

Wann würde ich von einem Andern sagen er könne sich 27 Striche vorstellen – – – wann würde ich es von mir selber sagen?

Statt ‘vorstellen’ nehmen wir besser Bilder auswählen.

     Wie wäre es, wenn ich 27 Stücke als ‘bestimmte Figur’ sehen könnte?

Wie wäre es wenn ‘27’ etwas analoges für mich bedeutete

Ms-162b,13r

wie ‘4’? Wenn z.B. ein ‘27-Eck’ etwas analoges für mich bedeutete wie ein ‘4-Eck’?

Ich würde z.B. verschiedene Eigenschaften des 27-Ecks zeigen können. Die Mitte etc. “Es paßt hierher & nicht daher”. Ich könnte es mit einem Stern 1-1 verbinden etc.

“Diese Farbe liegt in der Mitte zwischen … & …” Wir sind nicht geneigt das zu

Ms-162b,13v

sagen, obwohl wir sagen diese Farbe ist näher dieser als jener. Wir können eine Farbe malen auf den Befehl: male eine Farbe näher dieser als jener, aber nicht auf den Befehl male die Farbe in der Mitte.

“Es ist logisch unmöglich, eine Farbe exakt zu beschreiben.”

Beschreibung eines Farbtons durch den

Ms-162b,14r

Sprechton.

Warum sagt man ein Ton & seine Oktav seien derselbe Ton? “Was haben die beiden mit einander gemein?” –

---

     Kann ich mir vorstellen daß ∣∣∣∣∣∣∣∣∣∣∣∣ als charakteristische Gestalt gesehen wird?

D.h.: Kann ich mir vorstellen, daß es gesehen wird wie

Kann ich ∣∣∣∣∣ sehen wie ich ∣∣∣ sehe? Oder wie ∣∣, oder wie ∣ Man möchte sagen:

Ms-162b,14v

“Nein” & dies Nein scheint mir erfahrungsmäßiger & zugleich auch wieder logisch zu sein; ein synthetisches Apriori.

     Was sagt der Satz: ‘Ich sehe ∣∣∣∣∣∣∣∣∣∣∣∣ jetzt nicht als Gestalt’?

Man möchte sagen || antworten: die beiden S.D. ∣∣∣∣∣∣∣∣∣∣∣∣ & ∣∣∣∣ sind von verschiedener Art. Und das ist sozusagen der logische Grund weshalb man sich ∣∣∣∣∣∣∣∣∣∣∣

Ms-162b,15r

nicht vorstellen kann man könne ∣∣∣∣∣∣∣∣∣∣∣∣ als Gestalt sehen. Nämlich: dies S.D. ist keine Gestalt.
     Die Frage kann man sich … vorstellen hieße also: kann man sich ein S.D. einer andern Art vorstellen, das das S.D. von 12 Strichen wäre?

Der Satz: “ich sehe jetzt ∣∣∣∣∣∣∣∣∣∣∣∣∣∣ nicht als Gestalt” hat keinen klaren Sinn.
     Man kann ihn so erklären: ‘ich

Ms-162b,15v

sehe jetzt ∣∣∣∣∣∣∣∣∣∣∣∣∣ nicht so, wie ich ∣∣∣∣∣ sehe’. Aber ist nun die Anwendung des Satzes klar gemacht? (Erinnern wir uns: Wir dürfen nicht beliebige Kriterien anwenden.) Vergleiche ‘Ich bin hier’.

‘Die Zahl 131 ist mit bloßen Strichen unbeschreibbar’ – wie: ‘rot ist durch eine Zeichnung nicht wiederzugeben’.

“Der Rhythmus ist

Ms-162b,16r

nicht beschreibbar”.
     Das könnte z.B. heißen: daß er nicht ein gemessener Rhythmus ist.
     Sowie – “die Farbe ist nicht mit Worten zu beschreiben”, daß sie keine derjenigen ist, die Namen haben.

“Der Eindruck ist nicht mit Worten zu beschreiben.” “Ich kann nur eine Geste machen.” Die Ohnmacht der Worte sagt natürlich auch etwas. Kein Wort kommt mir, kein Vers, nur eine Geste.

Ms-162b,16v

     Du mußt Dich || Wir müssen uns immer fragen: “arbeitet dieser Satz (z.B. ‘ich bin hier || sehe dies’) & wie arbeitet er?”

Das alte Testament gesehen als der Körper ohne Kopf; das neue Testament, || : der Kopf; die Briefe der Apostel, || : die Krone auf dem Haupt.
     Wenn ich an die Judenbibel denke, das alte Testament allein, möchte ich sagen: diesem Körper

Ms-162b,17r

fehlt (noch) der Kopf. Diesen Problemen fehlt die Lösung. Diesen Hoffnungen die Erfüllung. Aber ich denke mir nicht notwendigerweise einen Kopf mit einer Krone. Ja, im Gegenteil.

---

‘Kann ich mir vorstellen ∣∣∣∣∣∣∣∣∣∣∣ als charakteristische Gestalt zu sehen?’ Kann ich mir vorstellen, daß sich ∣∣∣∣∣∣∣∣∣∣∣∣ klärt & mir irgendwie in der Klarheit von ∣∣∣∣ erscheint?
     Ich scheine es mir halb vorstellen, halb nicht vorstellen zu können. Und mancher

Ms-162b,17v

wäre geneigt hier zu sagen: “Ich glaube ich kann mir es vorstellen.”

Nun, was er sich vorstellen kann, kann er sich vorstellen. –

Rufen diese Worte eine Vorstellung hervor? Ja, sie rufen eine Vorstellung hervor. Aber wozu ist sie nütze?

‘Diese Worte geben einen Sinn; denn ich weiß genau, wie das wäre, wenn ich

Ms-162b,18r

die Strichreihe als Gestalt sähe.’

‘Ich weiß es, wie ich weiß, wie es wäre, wenn dieser Sessel dort stünde.’

‘Ich weiß wie es wäre wenn wir in einem 4-dimensionalen Raum lebten.’

‘Ich weiß, wie es wäre, wenn einer ein 7-Eck konstruierte.’

Wir haben gleichsam den Text || das Wort & eine Illustration – – – aber sollen

Ms-162b,18v

wir hier sagen, es sei eine Illustration?

Hat es Sinn, zu sagen: “die || diese Leute sehen ∣∣∣∣∣∣∣∣∣∣ als charakteristische Gestalt”? Denke Dir eine Film-geschichte. Wie würde dies dargestellt?

Beweisen, daß man das regelmäßige 7-Eck nicht konstruieren kann, heißt eigentlich, zeigen daß keine Vorstellung in gewisser Art zu ihm führt.

Denken wir uns ein psychologisches Experiment:

Ms-162b,19r

jemand zeigt mir Tafeln mit Strichreihen und fragt mich ob ich sie jetzt als Gestalten sehe. Denke bei 1000 Strichen sagte ich plötzlich: “die sehe ich als Gestalt!” – – – Du willst sagen: das kann man sich gar nicht || darunter kann man sich gar nichts vorstellen. Man will mich fragen: sind es wirklich die 1000 Striche die Du siehst || erfaßt?
     Eine Beschreibung des Phänomens ist möglich, die mich befriedigt!

Frage: “Sieht er dieselbe

Ms-162b,19v

Zahl, die wir sehen?”

Wieder: “1000 läßt sich nicht durch eine Strichreihe darstellen.”

‘Diese Takte geben eine unbeschreibbare Empfindung.’

Kommt sie uns immer unbeschreibbar vor? Womit vergleichen wir sie, wenn sie uns so erscheint? (Unstillbare Sehnsucht)

     Kannst Du

Ms-162b,20r

die Empfindung beschreiben, die Dir diese Takte geben?

‘Ich kann die Zahl der Diagonalen eines 8-Ecks nicht durch eine Strichreihe beschreiben.’

Wann ist es mir geglückt eine Empfindung zu beschreiben? Wenn ich selbst befriedigt bin?

Zu sagen: “Diese Takte geben mir eine unbeschreibliche Empfindung” –

Ms-162b,20v

drückt die Tatsache aus, daß ich intrigiert bin, daß ich nach einer Beschreibung oder Erklärung suche.

     ‘∣∣∣∣∣∣∣∣∣∣∣∣∣ ist keine Beschreibung der Zahl 13.’ – Aber wie ist man denn überhaupt auf die Idee gekommen, es könnte eine sein?! Warum soll es denn eine sein?!

‘Es ist unmöglich dies mit Worten zu beschreiben, weil

Ms-162b,21r

Worte nicht die dazu erforderlichen logischen Eigenschaften haben.’

‘Man kann 1000 nicht als die & die Strichgestalt beschreiben.’

‘Ich kann es mir nicht vorstellen.’

     Eine Ähnlichkeit zwischen diesen Gesichtern die sich nicht beschreiben läßt.

Ich kann mir 1000

Ms-162b,21v

Striche nicht als Gestalt vorstellen kann heißen: ich verliere immer wieder den Faden, wenn ich es so & so versuche.

Der Neid ist etwas oberflächliches – d.h.: die typische Farbe des Neides reicht nicht tief, – weiter unten hat die Leidenschaft eine andere Färbung. (Das macht den Neid, natürlich, nicht weniger real.)

Ich habe

Ms-162b,22r

22

Imagination, & das unterscheidet mich von allen Lehrern der Philosophie hier, aber darum bin ich noch kein || das macht mich noch nicht zum Genie.

Das Maß des Genies ist der Charakter, – wenn auch der Charakter an sich nicht das Genie ausmacht.
     Genie ist nicht ‘Talent und Charakter’, sondern Charakter der sich in der Form eines speziellen Talents kundgibt. Wie ein Mensch aus Mut

Ms-162b,22v

einem ins Wasser nachspringt, so schreibt ein anderer aus Mut eine Symphonie. (Dies ist ein schwaches Beispiel.)

Die ‘logische Unmöglichkeit der Beschreibung durch ein bestimmtes Beschreibungsmittel’. Das Mittel ‘paßt logisch nicht’ für den Zweck der Beschreibung.

Warum sollen Zahlen das Mischungsverhältnis

Ms-162b,23r

von Farben beschreiben können!? Es ist uns, als könnten wir versuchen & würden zurückgestoßen.

     Worauf beruht es, daß es nicht geht? “Aber das meine ich nicht!”

     Kannst Du Dir absolutes Gehör vorstellen, wenn Du es nicht hast? Kannst Du es Dir vorstellen, wenn Du es hast? – Kann ein Blinder sich das Sehen von rot vorstellen? Kann ich mir es vorstellen?

Ms-162b,23v

     Kann ich mir vorstellen daß ich so & so spontan reagiere, wenn ich's nicht tue? Kann ich mir's besser vorstellen, wenn ich's tue?

     Kann ich aber das Sprachspiel spielen, wenn ich nicht so reagiere?

     Beide Überlegungen führen zu dem gleichen Resultat. D.h.: auf beide Arten siehst Du, daß das herankommen muß.

Ms-162b,24r

Du hast z.B. die römischen Ziffern von I bis C arabisch numeriert.

∣ Compare chairs, materials, lengths, numbers ∣

Das Genie hat nicht mehr Licht als ein andrer, guter || rechtschaffener Mensch, – aber es sammelt dieses || dies Licht durch eine bestimmte Art von Linse in einem Brennpunkt.

Wann || Worin wird die

Ms-162b,24v

Seele von eiteln Gedanken bewegt, – wenn sie doch eitel sind? Nun sie wird von ihnen bewegt.
     (Wie kann der Wind den Baum bewegen, wo er doch nur Wind || Luft ist? Nun er bewegt ihn; & vergiß es nicht.)

Die Antwort zu manchen Problemen kannst Du nicht einfach durch Denken, sondern nur durch Üben erhalten.

Ms-162b,25r

Ich muß mir eine lange Zeit die Wange streicheln, ehe ich wieder bereit bin ein wenig zu arbeiten.

Wir sagen nicht: “Also || also so gehen wir!” sondern: “Also || also so geht es!”.

Wenn Einer sagt: “das Resultat der Rechnung findet man experimentell”, so müßte man antworten: “ja, wie soll er es denn_﹖ finden?”

Ist der Ausdruck der || einer Entscheidung ein

Ms-162b,25v

Satz, der sagt, daß ich mich so entscheide?
     Der bewiesene Satz als Ausdruck einer Entscheidung.

     Diese Dinge sind feiner gesponnen, als grobe Hände ahnen.

Ich lasse mich ablaufen & das Ende des Ablaufs ist der bewiesene Satz. Aber sagt dann der Satz etwas über diesen Ablauf?
     Wir haben ein Experiment

Ms-162b,26r

gemacht – aber im Experiment wurde ein Satz erzeugt (wie sonst etwa eine chemische Verbindung). Und nun gibt es einen andern Satz, der sagt, daß jener Satz erzeugt wurde. – Aber wie, wenn ich als zum Ausdruck hiefür eben jenen Satz gebrauchte? Sodaß also “25 × 25 = 625” mir sagen soll, daß die Menschen, so & so abgerichtet, in allgemeinem || allgemein dies herausbringen. Nun so eine Aussage gibt es doch, hat doch einen guten

Ms-162b,26v

Sinn. Und wenn das so ist – könnte man fragen –, soll es dann wirklich zwei Sätze geben: einen, der dieses anthropologische Faktum ausspricht, das doch offenbar für den Sinn || Nutzen der Arithmetik wesentlich ist, & einen andern, der sagt, daß 25 × 25 625 ist? || andern, der ein davon unabhängiges arithmetisches Faktum 25 × 25 = 625 aussprechen soll?
     Hier liegt der gewisse Unsinn nahe: “es || Es kommt drauf an,

Ms-162b,27r

wie wir den Satz meinen.” Man kann aber sagen: es kommt drauf an wie wir den Satz verwenden, was wir mit ihm tun.

“Aber daß 25 × 25 = 625 ist etwas, was wir vor dem Ausführen der Multiplikation nicht wußten.” – Könnte ich nicht auch sagen: dieser Satz ist einer, dessen Beweis wir vorher nicht kannten.

‘Der Beweis schafft einen Begriff.’ || schafft uns einen Begriff.’

Ms-162b,27v

Wir sind alle || Alle gleich gestimmt, wir laufen alle gleich ab; || – – – aber heißt das, daß wir diese Gleichheit des Ablaufs unbedingt || nun immer dazu verwenden, den Ablauf des Einen aus dem Ablauf des Andern vorherzusagen || vorauszusagen?

Wer sagt, er sei neugierig zu wissen, was die Multiplikation … × … ergeben wird, könnte sagen, er sei neugierig zu sehen, womit er am Schluß übereinstimmen werde. || welcher Rechnung er zustimmen werde. – Das

Ms-162b,28r

könnte aber ganz mißverstanden werden.

Unsre Zustimmung läuft gleich ab, – aber wir bedienen uns dieses gleichen || dieser Gleichheit des Ablaufs nicht einfach, um Zustimmungsabläufe vorauszusagen. Wie wir uns des Satzes “dies Heft ist rot” nicht nur dazu bedienen um vorherzusagen, daß die meisten Menschen es ‘rot’ nennen werden.

---

Worte & Erfahrung inkommensurabel.

Ms-162b,28v

Prüfe: “Das Wort ‘absolutes Gehör’ hat für mich nicht den Sinn, den es für den hat der das absolutes Gehör besitzt.”
     “‘Sehen || Rot’ hat für mich einen andern Sinn als für den Blinden.” Soll ich auch sagen: “‘Blindheit’ hat für einen blinden einen andern Sinn als für mich.”?

Man ist geneigt zu sagen daß für den Menschen mit absolutem Gehör gewisse Ausdrücke

Ms-162b,29r

Sinn haben, die für einen anderen Menschen keinen Sinn haben.

‘Das Multiplizieren lehrt Dich, daß dieses Zeichen herauskommt. Und das hast Du nicht gewußt. – Sie lehrt Dich also ein Dir neues empirisches Faktum.’ Aber halt – lehrt sie mich, daß dieses Zeichen am Ende dieses Beweises steht? Lehrt sie mich daß ich mit dieser Zeichenreihe übereinstimme?

Ms-162b,29v

Habe ich nicht gewußt was diese lange Multiplikation ergibt, so habe ich auch nicht gewußt was 50+1 ergibt.

Es ist absolut wesentlich für's Rechnen, daß ich immer wieder auf die gleiche Weise rechne & also immer wieder das gleiche Resultat kriege. Daß ich also voraussagen kann, ich werde wieder zu dieser Zahl gelangen. Aber das heißt natürlich auch: immer

Ms-162b,30r

auf dem gleichen Weg zu dieser Zahl gelangen! D.h. immer wieder den gleichen Weg gehen. (Und das klingt schon ganz anders). Aber das Resultat der Rechnung kann diese Prophezeiung nicht sein.
     Aber warum nannte ich dann die Übereinstimmung ‘wesentlich für's Rechnen’? Für mich während ich rechne, ist sie nicht wesentlich; wohl aber für das anthropologische Phänomen Rechnen.

Ms-162b,30v

Wenn ich sage: ein bestimmter Farbton sei unbeschreibbar, so habe ich natürlich eine bestimmte Art der Beschreibung im Sinn. Ich sage mir z.B.: nicht so, wie ein einfaches Ornament mit einfachen

Ms-162b,31v

Farben beschreibbar ist. “Der Farbton ist nicht weiter zerlegbar”. – Nun, ich verlange nicht daß Dir seine Zerlegung gelingt, wenn es Dir nur gelingt, die Zerlegung zu versuchen.

Ich denke an eine bestimmte Methode der Beschreibung & sage: “sie paßt nicht”.

Wir denken dann || Dann denken wir an Beschreibungen, die der gewünschten Beschreibung noch am nächsten kommen, z.B. die Beschreibung von Farbenmischungen || Farbstoff in verschiedenen Verhältnissen. Oder an Mischungen durch den Farbenkreisel.

Von allen diesen Beschreibungsmethoden fühlen wir daß sie in die Nähe dessen kommen,

Ms-162b,32r

wovon wir reden, es aber doch nicht treffen.

‘Wir könnten uns denken, daß Engel solche Farbtöne beschreiben könnten.’
     Aber wie stellen wir uns das vor? Sie würden, denken wir etwa in Hauchen die Farbe messen & sagen 3000 Hauche von Rot 450 von Gelb oder dergleichen.
     Gut; aber || Aber || Und was hindert uns daran, dies || dasselbe zu tun? Daß uns dies feine Verständnis mangelt || fehlt. || Daß wir dies feine Verständnis nicht besitzen. Können wir's uns aber vorstellen?

Ms-162b,32v

Nun, – man möchte sagen: “in einer Beziehung nicht.” || nein.”

     Und das heißt doch: daß wir es uns nicht vorstellen können in dem Sinn, in welchem wir uns vorstellen können, was wir selber erleben.

Wir sagen, daß, wer gewisse Erlebnisse gehabt hat, sie sich vorstellen kann, während es der Andre || ein Andrer nicht kann.

Das ist nun ähnlich, aber auch wieder ganz

Ms-162b,33r

unähnlich dem Fall: wer dieses Muster besitzt, kann sich die Farbe vorstellen, der Andre nicht.

Ist es Erfahrungstatsache || Soll es Erfahrungstatsache sein, daß, wer ein Erlebnis hatte, es sich vorstellen kann, & daß es der Andre || ein Andrer nicht kann? (Wie weiß ich, daß der Blinde sich die Farben nicht vorstellen kann.) Aber: er kann ein Sprachspiel nicht spielen. Aber wie: erfahrungsgemäß, oder eo ipso? Das Letztere.

Ms-162b,33v

     Zu dem Sprachspiel mit “er hat Schmerzen” gehört – möchte etwa man sagen – nicht nur das Bild des Benehmens, sondern auch das Bild der Schmerzen. – Aber hier muß man sich in Acht nehmen: Denke an mein Beispiel von den privaten Tabellen, die nicht zum Spiel gehören. – Im Spiel zeigt sich die ‘private || entsteht der Eindruck der ‘privaten Tabelle’ einerseits durch die Abwesenheit einer Tabelle bei gleichzeitiger Ähnlichkeit

Ms-162b,34r

des Spiels mit einem, welches mit einer Tabelle gespielt wird.

“Aber können die Spielenden nicht in Bezug auf ihre Erlebnisse lügen?” – Das Lügen ist ein sehr spezielles Sprachspiel – das gelernt wird. || sein will. Betrachte andre Fälle, die nicht Lügen sind & in welchen wir doch nicht sagen würden, er habe das Erlebnis.

Zu sagen “das Bild des Schmerzes tritt

Ms-162b,34v

in's Sprachspiel mit dem Worte ‘Schmerz’ ein”, ist ein Mißverständnis. Die Vorstellung des Schmerzes ist kein Bild & diese Vorstellung ist auch nicht durch etwas ersetzbar, was wir ein Bild nennen würden. Wohl aber tritt die Vorstellung in einem Sinn ins Spiel ein; nur nicht als Bild.

     Was lerne ich aus dem Induktionsbeweis des Distributionsgesetzes, wenn

Ms-162b,35r

ich dieses schon annehme? Wie, wenn ich sagte: Ich lerne einen beliebigen Satz von der Form ‘a+(b+c) = (a+b)+c’ aus Satz ‘a+(b+1) = (a+b)+1’ erzeugen & zwar entsprechend gewissen Regeln || Transformationsregeln?
     Wäre, ihn so zu erzeugen, analog einer euklidischen Konstruktionsaufgabe?
     Was ist aber davon der grammatische Nutzen? (Hier ist mir noch etwas gänzlich unklar.)

Der Philosoph braucht Geduld in dem Leiden der

Ms-162b,35v

Unsicherheit. Wenn Mathematiker sich an philosophische Probleme heranmachen || machen, sind sie zu ungeduldig im Ertragen der Unklarheit; wollen auf dem schnellsten Weg davon || (von ihr) befreit werden, & können daher das Problem nicht lösen, sondern nur oberflächlich zudecken. || , sondern es nur zudecken.

     ∣∣∣∣∣∣∣∣∣∣∣∣∣∣∣∣
‘Wir können uns nicht vorstellen, wie es ist, wenn

Ms-162b,36r

Einer diese Striche als Gestalt sieht.’ – Wir können uns jede Reaktion des Menschen vorstellen, von dem wir sagen würden, er tut es.
     ‘Wir können uns aber sein Erlebnis nicht vorstellen.’

Wer nun aber sagt, er habe dies Erlebnis, – ist er auch berechtigt, es zu sagen? Sollen wir nicht sagen: das könnten wir nicht wissen, es hinge ja eben vom || von seinem Erlebnis, von der Natur ab? || Sollen wir nicht

Ms-162b,36v

sagen: “das können wir nicht wissen; es hängt ja eben von seinem Erlebnis ab.”?
     Das ist falsch: Ob er berechtigt ist, diesen Ausdruck zu gebrauchen, können wir wohl wissen, so gut wie er selbst. Die Rechtfertigung des Gebrauches ist nicht ‘das Erlebnis’. Nicht im grammatischen Sinn nämlich.

     Ich habe in meinem Alter von hervorragenden Menschen gute Manieren gelernt; sozusagen

Ms-162b,37r

37

Kinderstube; aber auch das höchst unvollkommen.

Man kann nicht die Wahrheit sagen, wenn man sich noch nicht selber bezwungen hat. Man kann sie nicht sagen; – aber nicht, weil man noch nicht gescheit genug ist.

Nur der kann sie sagen der schon in ihr ruht; nicht der, der noch in der Unwahrheit ruht, & nur einmal aus der Unwahrheit heraus nach

Ms-162b,37v

ihr langt.

Wie weiß ich, daß ich mir Purpur vorstellen kann und nicht eine Gestalt ∣∣∣∣∣∣∣∣∣∣∣∣∣ || ∣∣∣∣∣∣∣∣∣∣∣∣∣ als Gestalt gesehen? Wie weiß ich, daß, was ich mir vorstelle, Purpur ist, & daß, was ich mir schon manchmal vorgestellt habe, nicht die Gestalt ∣∣∣∣∣∣∣∣∣∣∣∣∣ ist || war?

Die Vorstellung ist keine Rechtfertigung aber das (materielle) Bild ist eine Rechtfertigung.

Es gibt auch eine

Ms-162b,38r

Rechtfertigung für den Gebrauch der Worte: “das kann ich mir vorstellen”. Angenommen, Einer sagte: “Ich kann mir vorstellen, wie es der Pavlova bei diesem Tanz zu Mute war || was die Pavlova bei diesem Tanz erlebt hat¤”, so könnte man fragen: “Wie kannst Du Dir das vorstellen; was hast Du ähnliches erlebt?” – Wenn er nun antwortete: “Das ähnlichste Erlebnis, das ich hatte, war, mir vorzustellen, wie es Mozart beim Komponieren zu Mute war”. –

Ms-162b,38v

Helmholtz sagte, er hätte sich in seltenen Momenten den 4-dimensionalen Raum vorstellen können. – Was ist dazu zu sagen?

“Nichts leichter als Dir einen 4-dimensionalen Würfel vorstellen! er schaut so aus: …” – Aber das meine ich nicht, ich meine etwas wie nur mit 4 Ausdehnungen! – “Aber ist nicht, was ich Dir gezeigt habe eben etwas wie nur

Ms-162b,39r

mit 4 Ausdehnungen?” – Nein; – das meine ich nicht! – – – Was aber meine ich || meinst Du? Was ist mein Bild? Nun der 4-dimensionale Würfel … || wie Du ihn gezeichnet hast, ist es nicht! Ich habe jetzt als Bild nur die Worte & die Ablehnung alles dessen, was Du mir zeigen kannst. || & die Ablehnung eines Bildes der Art, wie Du's mir gezeigt hast.

     “Ich kann es mir insofern vorstellen, als ich auch schon …”.

Bin ich berechtigt, zu

Ms-162b,39v

sagen: “ich kann mir ∣∣∣∣∣∣∣∣∣∣∣∣∣ nicht als Gestalt vorstellen” || “ich kann ∣∣∣∣∣∣∣∣ nicht als Gestalt sehen”? Was berechtigt mich dazu? (Was berechtigt den Blinden zu sagen, er könne nicht sehen?)

“Nun, – Dein Erlebnis, – daß Du ∣∣∣∣∣∣∣∣∣∣ nur als unbestimmte Menge siehst!” – Und was berechtigt mich das zu sagen? Wieder mein Erlebnis? – (Quelle des Mißverständnisses.)

Aber ich kann einem Andern || Einem antworten: “Nun ich sehe ∣∣∣∣∣∣∣∣∣∣∣ nur als unbestimmte

Ms-162b,40r

Menge, ich könnte z.B. nicht sagen, wo die Mitte ist, ich kann es nicht als das wiedererkennen, was sich so zerlegen läßt – – – ist das keine Rechtfertigung?” – Und der Andre könnte dann sagen: “Ja, das ist eine Rechtfertigung.”

The image corresponding to “I can't imagine” is a blank.

Ein Gesellschaftsspiel, in welchem es heißt: “Stell Dir das & das || … vor.” Z.B.: “Denk Dir eine

Ms-162b,40v

Zahl” etc. etc.¤ Wie lehrt man das Spiel. Wie weiß man ob Einer richtig spielt? Heißt “schwindeln”: sich etwas falsches vorstellen?

     Wozu sage ich: ich kann mir || wir können uns nicht vorstellen was man da für Empfindungen hat, wenn man jongliert wie Rastelli?

“Was ich kann, kann ich mir vorstellen.” – Inwiefern?
     Nun, ich kann es

Ms-162b,41r

tun, & ich kann mich dran erinnern, es getan zu haben.

“Das Gefühl, was ich (selber) || (selbst) hatte, kann ich mir vorstellen.” – Notwendigerweise? Wie, wenn ich's gänzlich vergessen habe? – Wenn ich mich aber daran erinnere – dann eher durch diese Erinnerung. – Wie aber wenn sich mein Gedächtnis irrt?

Wie, wenn Einer sagte: “ich kann mir nicht vorstellen, wie das ist, wenn

Ms-162b,41v

man einen Sessel sieht, außer, wenn ich ihn gerade sehe”? Wäre er || man berechtigt das zu sagen?

In welchen Zusammenhängen || Gesprächszusammenhängen sagt man: “Ich kann mir nicht vorstellen wie es Mozart erlebt hat als …”.

Die Erfahrung: neue Erfahrungen kennenzulernen. Etwa beim Schreiben. Wann sagt man, man habe eine neue Erfahrung kennengelernt? Wie gebraucht

Ms-162b,42r

man so einen Satz?

“Ich kann ∣∣∣∣∣∣∣∣ nicht als Gestalt sehen” – hat das einen Sinn, wenn's niemand kann? Hätte es einen Sinn von einem seelischen Phänomen zu sprechen das nicht existiert?

Wie gebraucht man tatsächlich “ich kann ∣∣∣∣∣∣∣∣∣ nicht als Gestalt sehen”, 1) wenn es einen gibt der's kann 2) wenn nicht. Wie weiß ich, daß diese Worte Sinn haben? Wenn ich auch versucht bin,

Ms-162b,42v

sie zu sagen. – (Ich kann mich nicht selbst einholen.)

‘Du kannst Dir's nicht vorstellen, denn Du kannst's nicht tun!’

Auf seinen Lorbeeren auszuruhen ist so gefährlich, wie auf einer Schneewanderung ausruhen. Du nickst ein & stirbst im Schlaf.

Ms-162b,43r

43

     Wo ist || liegt das Problem, das Sprechen zu sich selbst betreffend?
     Zweifle ich daran, daß Leute es tun?
     Zweifle ich daran, daß dieser Ausdruck einen Sinn hat? – – – Es besteht eine Schwierigkeit; die offenbar mit dem Vergleich des Gebrauchs dieses Ausdrucks & andrer Ausdrücke zu tun hat.

Erschwert wird dieser Vergleich durch Ausdrücke wie: “Ich bin absolut sicher, daß ich mir das vorgesagt habe” & “Ich

Ms-162b,43v

zweifle nicht daran, daß Du es getan hast”.

Beschreibe – erkläre nicht!

Wenn das Spiel ohne Ball gespielt wird, gewöhne Dich daran, es so zu beschreiben & nicht das Bild des Ballspiels zu gebrauchen.

“Ich glaube, daß Du es Dir vorgestellt hast.”

“Ich glaube, daß Du es wirklich glaubst.”

Bleib stehen, renn nicht

Ms-162b,44r

am philosophischen Ziel vorbei!

“Phantasievorstellungen sind blasser als Sinneswahrnehmungen! || .” – Kann man also dem, der die letzteren || ersteren || jene nicht kennt, sie durch diesen Satz erklären?

Ballspiel || Spiel, bei dem man sich einen Ball vorstellen muß.

‘Der Gegenstand, von dem wir reden, zerrinnt uns vor den Augen.’ – Was heißt das?

Ms-162b,44v

Es heißt: Wenn wir die Grammatik der physikalischen Gegenstände zum Vorbild nehmen, so haben wir uns hier Gegenstände zu denken, die alles oder nichts sein können.

In einem Ausdauerrennen gibt es kein Ziel.

Alle Menschen haben immer gelogen, wenn sie sagten daß sie Schmerzen fühlen.

Die Sprache ist eine Institution.

Ms-162b,45r

Beschreibung & Ausdruck eines Gefühls: Beschreibung nennen wir wesentlich etwas in einem System von Beschreibungen.

Denn die Beschreibung soll mich lehren, wie es ist: & wie es ist muß ich also anders ausdrücken können als durch die Wiederholung der Beschreibung selbst.

Wenn Einer behauptet “ich kann mir ganz vorstellen wie es ist,

Ms-162b,45v

absolutes Gehör zu haben” ohne daß er es hat, so würden wir ihm sagen, das sei nicht möglich. Wir würden ihm sagen: Wir verstehen Dich nicht. Und der Grund ist, daß wir seine Äußerung nicht anerkennen, wenn er Gewisses nicht tun kann.

Welche attitude unsrerseits ist gegen den Andern berechtigt: Er sagt, etwa, ich habe furchtbare Schmerzen, sagt es ohne äußeren Anlaß, & ohne andre Zeichen des Schmerzes, ist ein durchaus wahrheitsliebender

Ms-162b,46r

Mensch, weiß was ‘Schmerz’ heißt, wünscht kein Mitleid. Welche Attitude unsrerseits ist berechtigt || gerechtfertigt die des Glaubens, die des Unglaubens? Ursprünglich dachte man sich die Rechtfertigung in ihm; & nun fühlen wir sie liegt nicht mehr in ihm sondern außer ihm.
     Oder: Wir sahen die Rechtfertigung immer unter dem Bilde des innern Vorgangs: Wenn nur der der rechte ist, ist die Äußerung

Ms-162b,46v

gerechtfertigt; auf die äußern Zeichen kommt's nicht an.

“Wenn ein Mensch sagt ich habe Schmerzen so ist er dazu berechtigt, wenn er ein gewisses Gefühl hat, & nicht, wenn er es nicht hat.” Warum sagt man nicht: er ist berechtigt, wenn er Schmerzen hat? Weil man auf ein Ziel hinsteuert, welches man nicht erreicht. Unser Satz kann auch als grammatischer dienen.

Ms-162b,47r

“Der Richter ist berechtigt den Mann des Mordes schuldig zu sprechen, wenn der Mann gemordet hat.”
     “Der Richter ist berechtigt den Mann des Mordes schuldig zu sprechen, wenn der Mann eine bestimmte Tat vollbracht hat.”
     “…, wenn der Mann absichtlich getötet hat.” – Wie beurteilt der Richter die Absicht? Schaut er in den Mann hinein? Ja, er tut es! – Nun ist dies nicht, in gewissem Sinne wahr? – Aber

Ms-162b,47v

warum befriedigt es uns nicht?

Das Eisen ist, ist nicht, in FeS enthalten.

“Das Kind kann lesen aber nicht sprechen.”

‘Das Erlebnis wird zu einem x’ – Wie wird es das? Wie, wenn ich sagte: “Ich habe x Äpfel gekauft || gegessen & mir daher den Magen verdorben”? Ist dies eine Erklärung? Aber es kann die Einleitung zu einer sein.

Ms-162b,48r

     Warum hast Du verheimlicht, wie der Richter in den Verbrecher hineinschaut? War das nicht wichtig? – Warum sagst Du nicht, wie wir die Wahrhaftigkeit eines Menschen prüfen?

     Du willst doch nicht die Wahrheit; Du willst Dich selbst!

     Der Künstler sieht das Wesentliche? Er lehrt uns das Wesentliche sehen? – Er stellt etwas als das Wesen hin. Er

Ms-162b,48v

bringt uns dahin, nun das als wesentlich anzuerkennen.

“Beschreiben” heißt ein Beschreibungsspiel spielen. – Wie sieht so ein Spiel aus?
     Wir geben dem Andern eine Beschreibung & er soll irgendwie nach ihr handeln; & dadurch zeigen, daß er die Beschreibung verstanden hat. – Da gibt es sehr verschiedene Fälle! Beschreibungen

Ms-162b,49r

einer || von || einer Anordnung von Körpern, Beschreibung einer Farbe || Beschreibung von Farben, Beschreibungen von Körperempfindungen, von Stimmungen, etc.

“Beschreibe Deine Empfindungen bei der Zeile ‘In allen Wipfeln …’!” Ist es klar, was hier gemeint ist? Was hier als Kriterium dafür gilt, daß der Andere aufgefaßt hat?

Ich beschreibe Einem ein Zimmer & lasse ihn dann zum Zeichen,

Ms-162b,49v

daß er meine Beschreibung verstanden hat ein impressionistisches Bild dieser || nach dieser Beschreibung malen. – Er malt nun die Stühle die ich als grün beschrieben habe dunkelrot, wo ich gelb sagte, malt er ein Blau. Das ist der Eindruck, den er von diesem Zimmer erhielt. Und nun sage ich: “Ganz richtig – so sieht es aus.”

     “Aber kannst Du

Ms-162b,50r

die Atmosphäre beschreiben die diese Farbe (diese Zeile) umgibt?” – Warum soll ich nicht die Atmosphäre zur Farbe rechnen & sagen: wenn ich die Farbe beschreibe, beschreibe ich damit, was Du diese ‘Atmosphäre’ nennst. Will ich sie ‘ohne diese Atmosphäre’ beschreiben, dann muß ich der Beschreibung etwas hinzufügen.
     Aber die Frage ist: In welchem Falle sage ich, ich habe die Atmosphäre vermittelt,

Ms-162b,50v

& in welchem Falle, ich habe nur die Worte (Farbe), aber nicht ihre Atmosphäre vermittelt. Ich meine: in welchem Fall sage ich die Vermittlung sei || ist gelungen? Oder: wie unterscheiden sich die Fälle in denen das eine & in denen das andere (ich sage nicht: “nur das andre”) vermittelt wurde?

Wie_﹖ schaut das Beschreibungsspiel, auf das Du ausgehst || hinzielst || hinsteuerst,

Ms-162b,51r

(tatsächlich) aus?

     “Beschreibe, wie das ist, wenn Du Dich an … || daran erinnerst.” – “Beschreibe Dein Erinnerungserlebnis!” – Nun Du hast doch ein Erinnerungserlebnis! – läßt es sich nicht beschreiben? Wie, wenn ich sagte: “Es ist eine Atmosphäre um meine Worte – – – aber wie soll ich diese Atmosphäre übermitteln? Was wirst Du eine (solche) ‘Übermittelung’ nennen?” –

Ms-162b,51v

“Aber ist die Empfindung nicht nur dann übertragen, wenn der Andre sie (wirklich) hat? Die Kriterien seines Verhaltens sind nicht die Empfindung.” – Nein, sie sind es nicht – – – aber verschiedene Kriterien entsprechen doch der Übertragung verschiedener Empfindungen. – Oder wenn Du willst: diese Kriterien sind dann Kriterien dafür wie wir hier das Wort “gleich”

Ms-162b,52r

verwenden.

Wie, wenn ich Dir zugäbe: “ || , wenn ich Dir entgegenkäme & sagte: “ …Ja, eine Empfindung muß übertragen worden sein, – die Frage ist bloß, ob ich sie die ‘gleiche’, wie meine Empfindung, nennen soll.”

Was heißt es: eine Empfindung mit einem Wort bezeichnen, benennen? Gibt es da nichts zu untersuchen?
Denk Dir Du kämest von einem Sprachspiel mit Bausteinen – & nun hieße es, es werden

Ms-162b,52v

jetzt auch Empfindungen benannt. Wäre das nicht, als würde zuerst (nur) von einer Übertragung des Besitzes & dann auf einmal von einer Übertragung des Genusses || der Freude am Besitz oder des Stolzes auf den Besitz gesprochen. Müssen wir da nicht etwas Neues lernen? Etwas neues || Neues, was wir auch ‘übertragen’ nennen.

Der Vorteil der Betrachtung der Sprachspiele ist eben, daß

Ms-162b,53r

sie uns stufenweise erblicken läßt, was wir sonst nur in einem einzigen – verworrenen Knäuel sehen. || in einem Ganzen, und zwar, in einem verworrenen Knäuel sehen.

     Verstehen wir den Satz: ‘Ich habe soviel Paar Schuhe, als der Gleichung x²‒2x+2 = 0 genügen’?

Die ungeheure Eitelkeit der Wünsche zeigt sich z.B. darin, daß ich || dadurch, daß ich z.B. den Wunsch habe, ein schönes

Ms-162b,53v

Schreibebuch sobald wie möglich vollzuschreiben. Ich habe nichts davon; ich wünsche es nicht etwa, weil es nur meine Produktivität anzeigt; es ist bloß das Verlangen, etwas schon Gewohntes recht bald los zu werden; obwohl ja, sobald ich es los geworden bin, ein neues angefangen wird || ich ja, sobald ich es los geworden bin, ein neues anfangen werde & sich dasselbe wiederholen muß.

     ‘Sind Nachbilder Vorstellungen? Wo liegt der Unterschied?’

Ms-162b,54r

Ein gutes Motto für mein Buch wäre: “Ein Schuft: der mehr gibt, als er hat.”

     Wenn ich einen Mann für einen Mast halte, – habe ich ein ‘nn’ für ein ‘st’ gehalten? Und wie, wenn ich es so auszudrücken versucht wäre?

     Auf die Frage: verstehst Du diesen Satz bin ich geneigt ‘ja’ zu sagen, ich bin geneigt zu sagen, das Verstehen sei ein geistiger Akt, ich bin geneigt zu sagen … – Sind

Ms-162b,54v

wir nun befriedigt? || zu Ende?

     “Was besagt der Satz, dieser Blinde könne sich Farben vorstellen?” – Was für eine Art Antwort willst Du für so eine Frage gelten lassen?
     Was lassen wir gewöhnlich als Erklärung in so einem Fall gelten? D.h., welche Wirkung erwarten || fordern wir von einer Erklärung? Die Erklärung soll in die Ferne wirken.

Warum soll man

Ms-162b,55r

nicht sagen: “die Vorstellung ist privat”, “niemand kann wissen, was ich sehe” etc., etc.? Was schadet es, das zu sagen? Nehmen wir an, man würde sagen: ‘es führt zu Verwechslungen’ – wäre das wahr?! Führt es zu Verwechslungen? Man könnte aber z.B. sagen: es führt zu Beunruhigungen zu der Erfahrung || dazu, daß wir uns nicht auskennen, d.h., verwirrt werden. Manchmal dazu, daß wir gewissen Dingen unsre Aufmerksamkeit

Ms-162b,55v

schenken die sie sonst nicht angezogen hätten. Es führt dazu, daß es uns philosophisch vor den Augen flimmert. Daß wir im Kreise geführt werden. –– Aber was schadet das? –

     Schopenhauer, könnte man sagen, ist ein ganz roher Geist. D.h., er || : Er hat Verfeinerung, aber in einer gewissen Tiefe hört diese plötzlich auf & er ist so roh, wie der Roheste. Dort, wo eigentliche

Ms-162b,56r

Tiefe anfängt, hört die seine auf.

Man könnte von Schopenhauer sagen: er geht nie in sich.

Ich sitze auf dem Leben, wie der schlechte Reiter auf dem Roß. Ich verdanke es nur der Gutmütigkeit des Pferdes, daß ich jetzt gerade nicht abgeworfen werde.

‘Beschreibe mir, wie Du Dich jetzt fühlst! –

Ms-162b,56v

Nun, – fühlst Du Dich jetzt nicht irgendwie?!’

‘Beschreibe mir seinen Gesichtsausdruck! Nun – er hat doch irgendeinen Gesichtsausdruck!’

‘Welchen Eindruck macht Dir dieser Tisch?’ – ‘Keinen besonderen Eindruck.’
     Könnte man hier sagen: er müsse Einem irgend einen Eindruck machen?
     ‘Du hattest keinen besonderen Eindruck?! Aber

Ms-162b,57r

hast Du ihn z.B. nicht als den Tisch erkannt, & als den Tisch der hier immer steht, & als einen sehr gewöhnlichen Tisch etc. || u.a.?’

Die Beschreibung des Eindruckes. Wie verwenden wir Beschreibungen des Eindruckes? Im Gegensatz zu ‘Beschreibungen des Objekts’.

‘Diese Melodie macht mir einen starken Eindruck’ – Ist es klar, daß es eine Beschreibung dieses Eindrucks gibt?

Ms-162b,57v

Den Eindruck als Atmosphäre gesehen: ‘Diese Melodie ist mit einer starken Atmosphäre umgeben’.
     Aber mit welcher Atmosphäre? Was würden wir eine Angabe, Beschreibung dieser Atmosphäre nennen?

Die Beschreibung einer Atmosphäre ist eine spezielles Sprachspiel || spezielle Sprachanwendung, zu speziellen Zwecken.

     Deuten des ‘Verstehens’ als Atmosphäre; als geistiger || seelischer Akt. Man

Ms-162b,58r

kann zu allem, eine Atmosphäre hinzukonstruieren.

Beschreib das Aroma des Kaffees! – Warum geht es nicht? Fehlen uns die Worte? Und wofür fehlen sie uns? – Woher aber die Empfindung || der Gedanke, es müsse doch so eine Beschreibung möglich sein? || geben? Ist Dir so eine Beschreibung je abgegangen? Hast Du versucht das Aroma zu beschreiben & es ist Dir nicht gelungen?

Ms-162b,58v

     Verstehst Du den Satz || Befehl: “Beschreib das Aroma des Kaffees”?

Ich will unbedingt etwas sagen. Sagt das, als was der Andre es werten soll?

“Das Aroma beschreiben” nennen wir eine bestimmte Sprachverwendung. Z.B.: ‘Das Aroma dieses Kaffees ist ähnlich diesem aber stärker gebrannt.’ Wenn man glaubt, es gebe

Ms-162b,59r

abgesehen von solchen Beschreibungen noch etwas anderes was in einem eminenteren Sinn die Beschreibung des Aromas wäre, || : so läuft man einer philosophischen Schimäre nach.

     ‘Der Eindruck (den diese Melodie macht) ist völlig unbeschreibbar.’ – Das heißt: eine Beschreibung tut's (für meinen Zweck) nicht; Du mußt die Melodie hören.
     Wenn die Kunst dazu dient ‘Gefühle zu erzeugen’, ist, am

Ms-162b,59v

Ende, vielleicht ihre sinnliche Wahrnehmung auch unter diesen Gefühlen?

Kann man ein Erinnerungserlebnis beschreiben? – Gewiß. – Aber kann man das Erinnerungshafte an diesem Erlebnis beschreiben?
     Was heißt das?

     Wie weißt Du, daß es einen Sinn hat zu sagen, man beschreibe ein Gefühl?

     Meine Originalität,

Ms-162b,60r

(wenn das das richtige Wort ist), ist, glaube ich, eine Originalität des Bodens, nicht des Samens. (Ich habe vielleicht gar keinen eigenen Samen;) – aber, wirf || .) Wirf einen Samen in meinen Boden, & er wird anders wachsen, als in irgend einem andern. || Boden || Boden.
     Auch die Originalität Freud's war, glaube ich, von dieser Art. Ich habe immer geglaubt – ohne daß ich weiß, warum – daß der eigentliche Same der Psychoanalyse von

Ms-162b,60v

Breuer, nicht von Freud herrührt. Das Samenkorn Breuers kann natürlich nur ganz winzig gewesen sein.
     (Mut ist immer originell.)

     Die Menschen heute glauben, die Wissenschaft sei || Wissenschaftler seien da, sie zu belehren, die Dichter & Musiker etc., sie zu erfreuen. Daß diese sie etwas zu lehren haben; kommt ihnen nicht in dem Sinn.

     Das Klavierspielen,

Ms-162b,61r

ein Tanz der menschlichen Finger.

Was für eine Art Satz ist das: “Braun hat nicht den Charakter der primären Farben Rot, Blau, Grün, Gelb.”? Nun es ist eine Äußerung. Eine sehr wichtige Äußerung. Ein Anfang von Tätigkeiten.

Ja, – das sind wir geneigt zu sagen. – Und warum sage ich: wir sind ‘geneigt, das zu sagen’? –

Shakespeare, könnte man sagen, zeige || zeigt den Tanz der menschlichen Leidenschaften. Er muß daher

Ms-162b,61v

objektiv sein, sonst würde er ja nicht den Tanz der menschlichen Leidenschaften zeigen, – sondern etwa über ihn reden. Aber er zeigt sie uns im Tanz, nicht naturalistisch. (Diese Idee rührt von Paul Engelmann her.) || habe ich von Paul Engelmann.)

“Das Wort ‘rien’ ist dasselbe wie das Wort ‘res’.” Verstehst Du das? Ja. Aber verstehst Du es auch gewiß? Weißt Du, genau welche Art von Zusammenhang hier gemeint ist?

Ms-162b,62r

     Verstehst Du die Formel H₂O, wenn Du zwar weißt, sie sage daß ein Molekül Wasser aus 2 Atomen Sauerstoff … bestehe, aber nicht weißt, welche Art von Experiment, Verifikation, diesen Worten entspricht?

     Moore hat Gewissen; aber wenig Herz.

     Er ist, wahrscheinlich in seinen Zuneigungen & seinen Abneigungen pueril. Sein Herz ist also etwa eine Knospe

Ms-162b,62v

die nicht verdorrt, aber auch nie voll aufgeblüht ist.
     Er spornt niemand an.

Das spezifische Gewicht eines Satzes sieht man nicht– sein || . Sein || der Sätze sieht man nicht. Ihr Volumen sieht man.

Gute || Nützliche Gedanken in der Philosophie müssen von weither kommen.

     Denn nur was von weither genommen ist, kann unsern Gesichtspunkt ändern.

Ms-162b,63r

     Die Gleichnisse des N.T. lassen jede beliebige Tiefe der Interpretation || des Verstandes zu. Sie sind ohne Boden. || ohne einen Boden.

Auch im höchsten Kunstwerk ist noch etwas, was man ‘Stil’, ja auch, was man ‘Manier’ nennen kann. Sie haben weniger Stil, als das erste Sprechen eines Kindes. || Sie haben weniger Stil, als das erste Sprechen eines Kindes. Auch im höchsten Kunstwerk ist noch etwas, was man ‘Stil’, ja auch, was man ‘Manier’ nennen kann.

Mir ist, als lägen mir hundert Dinge vor den Augen, die nur beschrieben werden brauchen & es werden

Ms-162b,63v

wichtige Erkenntnisse an den Tag gefördert. Aber ich bin zu dumm, sie zu greifen.

– – – Ich kann z.B. sagen: ich bin in eine Rechnung hineingekommen, die || einen Kalkül hineingekommen, der mir verschiedene Resultate für eine Multiplikation, z.B., liefert. Ich kann diesen Kalkül daher für die Zwecke des Multiplizierens nicht verwenden. Ich weiß aber nicht,

Ms-162b,64r

was ich vermeiden muß, um im Eindeutigen zu bleiben, es sei denn ich vermeide alles Rechnen mit Klammer ausdrücken.
     Nun worin besteht dieses mich nicht Auskennen? Und soll ich nun sagen: hier habe ich überhaupt keinen Kalkül.

“Es sollte doch wieder das Gleiche herauskommen; & es kommt etwas

Ms-162b,64v

andres heraus!” – Ich muß mich verrechnet haben. Angenommen, dann finde ich, ich habe mich nicht verrechnet, sondern etwas in meinem Kalkül || in den Prinzipien meines Kalküls übersehen – was ist das für eine Änderung? Muß ich die neue Entdeckung annehmen?

     ‘Was halb voll ist, ist halb leer; darum ist, was ganz voll ist, ganz leer.’

Die Erfindung eines Mechanismus zur Erzeugung irgend

Ms-162b,65r

einer gewünschten Bewegung; ist sie auch eine physikalische Entdeckung? Sagt der, der auf die Idee kommt, Zahnräder, Hebel & Stangen so & so zu verbinden, er habe eine neue physikalische Entdeckung gemacht? Freilich entdeckt er daß sich Maschinenteile in dieser neuen Verbindung so wie gewöhnlich,

Ms-162b,65v

¤ & wie zu erwarten war, benehmen. Aber nennt man das: eine Entdeckung machen? Hat wer den Zipverschluß erfand, so eine Entdeckung gemacht? Ist so eine Erfindung nicht in gewissem Sinne || in einer Weise ähnlich der einer Rechnungsweise? Und verschieden, z.B., von der Erfindung des Schießpulvers.

     Die Inkonsistenz

Ms-162b,66r

der gewöhnlichen Sprache ist offenbar ganz harmlos. Das heißt aber nicht, daß Inkonsistenz in speziellen Fällen, für gewisse Techniken der Verwendung von Symbolen, nicht äußerst unerwünscht sein kann. Und man wird dann Vorsichtsmaßregeln ergreifen.

‘Was muß man aus der Logik ausschneiden || herausschneiden, um die Möglichkeit des Widerspruchs zu beseitigen?’

Ms-162b,66v

Was ist die Schwierigkeit? Die Schwierigkeit ist, den Fall mißzuverstehen, ihn nicht richtig zu verstehen. || . Warum ist es schwierig ihn richtig zu verstehen? Wir sehen ihn nicht durch das Medium der richtigen Beispiele. Wir sehen nicht die wichtigen Aspekte. Wir phrasieren das Thema nicht, wie es aufschlußreich wäre || ist, ¤ es zu phrasieren.

Die wichtigsten Aspekte

Ms-162b,67r

des Falles sind mir unzugänglich, weil ich die Möglichkeiten nicht übersehe.

Schau es auf eine neue Art, durch ein neues Schema an.

Mache || Mach eine andere || andre Art von Vergleich!

Das Verführerische der kausalen Betrachtungsweise ist, daß sie einen dazu führt zu sagen: “Natürlich, || – so

Ms-162b,67v

muß || mußte es geschehen.” Während man denken sollte: so, & auf viele andere Weisen || Arten kann es geschehen sein.

Wenn wir die ethnologische Betrachtungsweise verwenden, heißt das, daß wir die Philosophie für Ethnologie erklären? Nein es heißt nur, daß wir unsern Standpunkt weit draußen einnehmen, um die Dinge objektiver sehen zu können.

Ms-162b,68r

     Du zeigst mir einen neuen Gegenstand & sagst: “Was sagst Du nun dazu?” – Und ich: “Was kann ich dazu sagen? – doch nur daß …”.

Du kannst die Worte “consequent” & “inconsequent” nicht mathematisch definieren.

Eine Kontradiktion p ∙ ~p kann man doch immer auffassen als ~(p) ∙ ~(~p) & das als den Satz: ich will || kann weder p

Ms-162b,68v

noch ~p behaupten. || behaupten, noch ~p.

Eine meiner wichtigsten Methoden ist es mir den historischen Gang der Entwicklung unsrer Gedanken anders vorzustellen als er in Wirklichkeit verlaufen ist. || war. Tut man das so zeigt uns das Problem eine ganz neue Seite.

     Warum sollte ‘p ∙ ~p’ nicht p bedeuten?

Ms-162b,69r

Das ‘~’ im zweiten Teil ist nämlich ironisch gemeint. –

Kommt, was ich sagen will, nicht darauf hinaus, daß, an einem gewissen Punkt ein Beweis uns nicht größere Gewißheit gibt als die übrigen Umstände ohne einen Beweis? [Das ist elend ausgedrückt.] Aber es handelt sich um Gewißheit & Beweis. Und

Ms-162b,69v

darum: ob ein Beweis einen Kalkül admissibel machen kann.

     Dasjenige, wogegen ich mich wehre, ist die Idee || der Begriff einer vollkommenen || idealen Exaktheit der uns sozusagen a priori gegeben wäre. Zu verschiedenen Zeiten sind unsere Ideale der Exaktheit verschieden; & keines ist das höchste.

Was ist ‘der ideale

Ms-162b,70r

Kalkül’? Ideal zu welchem Ende?

Es ist oft nur sehr wenig unangenehmer die Wahrheit zu sagen, als eine Lüge; etwa nur so sehr wie bittern Kaffee zu trinken als süßen; & doch neige ich auch dann stark dazu, die Lüge zu sagen.

Ms-162b,70v

Ja, aber hat es nicht auch seinen Grund, warum dieses Bild den Satz rechtfertigt? – Dieser Grund liegt außerhalb der Lage.

Der Satz ist sozusagen die Moral an dem Beweis.

Warum Du geneigt bist den Satz auf diese formale Prüfung hin zu gebrauchen das hängt mit der Technik unseres || unsrer Technik des Gebrauchs der Sätze zusammen.

Ms-162b,71r

Ms-162b,71v

Ms-162b,72r

Ms-162b,72v

Ms-162b,BCr

Ms-162b,BCv