| |
| |
| / |
2
denn die Tabelle zwingt mich nicht
ihn zu machen
Ich mache ihn bei jeder Anwendung immer von
neuem
Er ist nicht quasi ein für alle mal in der Tabelle für mich
gemacht.
(Die Tabelle verleitet mich höchstens ihn so zu
machen)
[u|U]nd also richte ich mich doch unmittelbar nach dem secundären Zeichen wenn ich in der Tabelle von diesem secundären Zeichen gerade dorthin gehe |
| |
Nun könnte man freilich die Tabelle durch die ersten Anwendungen der
sekundären Zeichen ersetzen & man hätte sich in Zukunft nach diesen
ersten Anwendungen zu richten.
Und das geschieht bis zu einem
|
| |
Die Worte sind beliebig aus ihnen geht nicht hervor welche Farbe sie
meinen.
Aber
Hat es also wirklich nichts mit der Willkürlichkeit der Wörter auf sich? Ist das alles Unsinn? Nein. Und wo sie nötig ist können wir von primären & sekundären Zeichen sprechen. |
| / |
Welcher Art ist denn meine Aussage über die Tabelle „daß sie mich
nicht zwingt sie so & so zu gebrauchen”.
Und „daß die Anwendung durch
|
| / |
Woher nimmt diese Betrachtung ihre Wichtigkeit? da sie
doch nur alles Interessante zu zerstören scheint? –
|
| |
∣
The foundations we mean pervade rather than
underly mathematics & the
sciences.
(siehe Augustinus
et cum effunderis super nos, non tu iaces, sed erigis
nos.) ∣ |
| | ∣ Grillparzer: „Wie leicht bewegt man sich im Großen & im Fernen, wie schwer faßt sich, was nah & einzeln an ….” ∣ |
| | ∣
Woher nimmt die Betrachtung ihre Wichtigkeit die uns darauf
aufmerksam macht daß man eine Tabelle auf mehr als eine Weise
brauchen kann, daß man sich eine Tabelle als Anleitung zum Gebrauch einer
Tabelle
|
| / |
So ist also an der Bemerkung daß es in jeder Sprache primäre Zeichen geben
muß die die Wörter definieren das, daß man eine Tabelle aufstellen kann auf
deren beiden Seiten einerseits die Wörter anderseits Exempel ihrer
Anwendung stehen.
Und so ist das ist
|
| / |
Der Irrtum von den primären Zeichen gehört zu denen die die
Philosophie wie eine Art Physik behandeln indem sie einfachen Gesetzen
nachspüren wollen.
Prinzipia im Sinne
Newtons.
|
| / | „
|
| |
There is an infinity of things which you must notice about the
use of the simplest word.
The [G|g]rammar of every word is enormously complicated
& therefore enormously difficult to overlook & it is
just that you must try to do. |
| |
Methods of Projection for colours &
shapes. |
| |
Die Sprache hat für Alle die gleichen Fallen bereit, das gleiche
ˇungeheure Netz schon angelegter Irrwege.
Und so sehen wir also Einen nach dem Andern die gleichen Wege
gehn & wissen schon wo er jetzt abbiegen wird, welche
Abzweigung er nicht bemerken wird wo er
gera◇daus fortgehen wird ohne die Abzweigung zu
bemerken etc. etc.
Ich sollte also
|
| X |
∣
Es ist hier natürlich die Regel eine andere als im ersten Fall &
wenn sie nachgesehen wird so ist dadurch auch die Spielhandlung eine
andere.
Wie ist es aber, wenn sie nicht nachgesehen wird?
Dann lautet etwa der Befehl „bring mir eine rote Blume”
worin statt
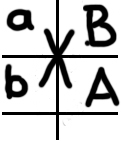 ein Quer-
ein Quer-
|
| |
Folgt nun aber daraus nicht daß die Definition die Wort mit Wort
(auch wenn dieses ein färbiges Täfelchen ist) von anderer Art, in
einem andern Sinne Definition ist als die welche ˇdas Wort mit einem
Muster verbindet.
Freilich erlaubt mir auch diese Definition das eine Zeichen an Stelle des
andern zu setzen das Muster an Stelle des
Wortes.
Aber die weitere Benützung des Zeichens ist ja jetzt ganz
anders.
Also ist wohl nicht
Kein Absatz Words are not paterns but paterns
are made out of words. Wir können allerdings sagen ˇd.h. es entspricht dem ganz der Sprachgebrauch daß wir uns ◇◇◇ durch Zeichen verständigen ob wir Wörter oder Muster gebrauchen aber das Muster ist kein Wort & das Spiel sich nach Worten (zu) richten ein anderes als das sich nach Mustern oder einem Muster zu richten. Wörter sind der Sprache nicht wesentlich. Die Frage war ursprünglich: muß ein rotes
|
| |
Meine Frage war aber eigentlich die: Kommt das Kopieren
überhaupt in Betracht wenn Worte definiert werden?
D.h. muß nicht alles wodurch ein Wort definiert
wird [ist] eo ipso ein Wort sein als Wort wirken
auch wenn es eine färbige Tafel ist & daher auch anders
funktionieren könnte nämlich als Muster?
Ist es also nicht
|
| |
Das Charakteristische an diesen
Projectionsmethoden ist daß sie in eine Tabelle
münden, was die räumlichen nicht tuen.
Daher sind sie eben
|
| |
Wird denn ein Wort eigentlich als Wort gebraucht wenn ich es dann
brauche nur in Verbindung mit einer Tabelle gebrauche die
es den Übergang zu Mustern macht?
|
| |
„Stell Deinen Fuß auf ellenhohe Socken, Du bleibst doch
immer was Du bist.” |
| |
Das Wort
|
| |
„I see that this p is the case”
„I know that p is the case” Does seeing depend on one of the senses? The subject in visual space. |
| |
Die Schwierigkeit die uns das [s|S]prechen über den
Gesichtsraum ohne Subject macht & über meine
& seine Zahnschmerzen ist die die Sprache einzurenken daß sie
richtig
|
| |
Wenn mir Herr N vorgestellt wird weiß ich jetzt etwas über ihn
nämlich wie er ausschaut etc oder verstehe
ich jetzt den Namen ‚N’?
D.h. war die Vorstellung ein Satz über N
oder eine Definition von ‚N’?
|
| |
Grund & Ursache. |
| |
Es ist als // Ich ver so
So verbinde ich So scheine ich ein (neues) Zeichen mit ihm
(wie wenn ich eine andere Art
|
| |
Don't say this is no explanation: This is
what we call an explanation. |
| | •
Es scheint aber
als sagten wir etwas anderes oder täten etwas anderes als ein Zeichen durch
ein anderes zu ersetzen.
Es ist als sagten wir nun etwas über das Z
über den Pfeil was seine Richtung bestimmt die
früher nicht bestimmt war
|
| |
– so gebe ich eine Definition während es scheint als
hätte ich sozusagen die Angabe des Pfeiles ergänzt.
Ich habe den Pfeil durch ein neues Zeichen ersetzt daß wir statt des
Pfeiles gebrauchen können. –
Gebrauchen
|
| |
Was Edington über die
‚Richtung der
|
| |
Untersuchen wir
|
| |
Finden wir irgendwo keine (festen) Regeln, nun so ist
das das Resultat. |
| |
Wie findet man denn die Regel eines Spiels bei einem fremden
Volk? |
| |
Einer teilt die Menschen ein in Käufer & Verkäufer &
vergißt, daß Käufer auch Verkäufer sind.
Wenn ich ihn daran erinnere, wird seine Grammatik
geändert? |
| |
Wenn ich sagte „ich sah einen Sessel” so widerspricht
dem
|
| |
Die meisten Menschen wenn sie eine philosophische Untersuchung
|
| |
„Das Stück war für Dich gemeint”; wie äußert sich das,
was ist die Verification dieses Satzes dann
werden wir wissen was er sagt. |
| |
Die philosophisch wichtigsten Aspekte der Dinge [ der
Sprache ]
Man kann es nicht bemerken weil man es immer ˇoffen vor Augen hat |
| |
(Das eigentliche Verdienst eines
Kopernicus oder Darwin
etc war nicht die Entdeckung einer wahren
Theorie sondern eines fruchtbaren Aspekts.) c a b b d
|
| |
Der Übergang von der Rechnung über Pflaumen zu einer Handlung mit den
Pflaumen & vom Wort Pflaume zum Ding. |
| |
Die Definition & die Namengebung ordnet einer Sache ein
Zeichen bei (im ersten Fall einem Zeichen). –
Aber ein Name wird dem Ding gegeben, daß ich von ihm sprechen
kann. –
Das klingt als wäre der Name wie ein Fernglas & der
obige Satz analog dem: Ein Fernglas wird mir
gegeben daß ich ihn sehen kann.
Aber das
Ich kann gewiß auch das sagen daß ich mich beim Einsetzen das definierende statt des definierten nach der according to Definition nach dem Zeichen richte & dasselbe wenn ich einen Befehl befolge. (Wenn ich einen Befehl in Gut, – was, wenn ich aber dem linken Zeichen jetzt einen Namen gebe, – wie kann der gebraucht werden, & kann er nicht gebraucht werden wie ‚M’? Geben wir ihm den Namen ‚A’. Wenn ich dann also sage „zeige
Die linke Seite der Definition steht (einfach) nicht im verhältnis zur rechten des Trägers eines Namens zum Namen. |
| |
Das heißt, der Übergang
|
| | ¤
∣ Welches Gefühl hätten wir wenn wir nicht von
Christus gehört
hätten?|
Hätten wir das Gefühl der Dunkelheit & Verlassenheit? Haben wir es nur insofern nicht als es ein Kind nicht hat wenn es weiß daß jemand mit ihm im Zimmer ist? Religiöser Wahnsinn ist Wahnsinn aus Irreligiosität. |
| |
Ist es denn aber nicht einfach so: Das Gleichheitszeichen
zwischen zwei
Ich
|
| | ¤
Difficulty of our investigations: great length of chain of
thoughts
The difficulty is here essential to the thought not as in the sciences
com due to its novelty.
It is a difficulty which I cann't remove if I try to
make you see the problems.
I cann't give you a startling solution which ◇ suddenly will remove all your difficulties. I cannt find one key which will unlock the door of our safe. The unlocking |
| | Wenn ich also einen Namen hinweisend definiere & einen zweiten durch den ersten so ist dieser zu jenem in anderem Verhaltnis als zum Zeichen das in der hinweisenden Def gegeben wurde. D.h. dieses letztere ist seinem Gebrauch nach wesentlich von dem Wie wirkt nun die hinweisende Erklärung? Sie erklärt den Gebrauch eines Zeichens; & das merkwürdige ist nur daß sie ihn auch für die Fälle zu lehren scheint in dem ein Zurückgehen auf das hinweisende Zeichen nicht möglich ist. Aber geschieht das nicht indem wir quasi die in der hinweisenden Def. gelernten Regeln in bestimmter Weise transformieren. (Wenn z.B. der Mann der mir vorgestellt wurde →
Vorlesg:
primary &
[S|s]e[k|c]ondary signs.
andere ersetzt werden könnte; oder: daß wenn wir sagen wir richten uns jetzt, nach einer Erklärung der Wortlaut jetzt anders lauten muß. Wir spielen jetzt nach einer andern Regel. Die wir nun tatsächlich aus der ersten erhalten haben. [Wie wirkt die hinweisende Erklärung weiter?] Es gibt offenbar ein Spiel worin ich immer
|
| | ¤ Das philosophische Problem ist ein Bewußtsein der Unordnung unsrer Begriffe & durch ordnen derselben zu heben. Es war also eine philosophische Frage, wenn die Schwester meines Bekannten E. dieses fragte: Was ist eigentlich ein Drittel? „Ein Apfel hat doch vier Teile”. Sie konnte sich im Augenblick offenbar nicht erklären wo die Bezeichnung „ein Drittel” herkomme da doch keine Zusammenstellung von Vierteln diesen Ausdruck Es hat einer gehört daß der Anker eines einem Schiffes durch eine Dampfmaschine aufgezogen werde. Er sa denkt nun ant die welche das Schiff treibt & kann sich was er gehört hat nicht erklären. (Vielleicht fällt ihm die Schwierigkeit auch erst später ein). Nun sagen wir ihm: Nein, es ist nicht diese Dampfmaschine sondern Die andere Beunru- Die Arbeit des Philosophen ist ein Zusammentragen von Wahrheiten zu einem bestimmten Zweck. We have to arrange evidence & do no Eine philosophische Frage ist ähnlich der nach der Verfassung einer bestimmten Gesellschaft. – Und es wäre etwa so als ob eine Gesellschaft ohne klar geschriebene Regeln zusammenkäme aber mit einem Bedürfnis nach solchen Ja auch mit einem Gefühl welches bewirke daß sie gewisse Regeln in ihren Zusammenkünften einhalten, nur daß dies dadurch erschwert wird weil nichts tigten Mitglieder
alle an einen Tisch etc. etc.. |
| |
„Etwas habe ich aber doch gemeint als ich das
sagte!”
Nun gut, aber wie können wir es herausbringen[;|?] doch
wohl nur dadurch daß wir ihn fragen.
Nicht Wenn wir nicht sein übriges
Verhalten zum Criterium des Sinnes nehmen sollen dann
also das was er uns erklärt. |
| |
Wenn man in der Philosophie [ den
Philosophen ] fragt „was ist –
z.B. – Substanz”
etc etc., so wird um eine Regel
gebeten |
| |
Sehe die Photographien von Corsischen Briganten und
denke mir: die Gesichter sind zu hart um das Christentum
& meines zu weich als daß das Christentum darauf schreiben
könnte.
Die Gesichter der Briganten sind schrecklich anzusehen & doch sind
sie gewiß nicht weiter von einem guten Leben entfernt & nur auf einer andern
Seite desselben gelegen als ich |
| |
Zwei Farben, zwei Dampfspannungen, zwei elektrische Ladungen
etc. etc. haben nicht zu gleicher Zeit an
einem [A|O]rt Platz.
Eine merkwürdige Gesellschaft die ich da aufzähle. [ die sich da zusammenfindet ] . Aber erst zu etwas Andrem: Wenn f(x) sagt x sei jetzt an diesem Ort & f(b) b sei so ist also fa ∙ fb ein Widerspruch. Warum nenne ich es so da doch fb nicht ~fa ist? p ∙ ~ p die Form des Widerspruchs ist? Es heißt wohl einfach daß das logische Produkt und sehr tief liegendes.
Die Entscheidung darüber ob fa ∙ fb Kann ich die Regel die dem allem zugrunde liegt so schreiben: fa = fa ∙ ~ fb? ◇ d.i.: aus fa folgt ~ fb |
| |
Wenn Leute sagen der Satz „es ist wahrscheinlich daß
p eintreffen wird” sage etwas über das Ereignis p so
vergessen sie
|
| |
Wir sagen mit dem Satz „p wird wahrscheinlich
eintreffen” zwar etwas über die Zukunft aber nicht etwas
„über das Ereignis p” wie die grammatische
Form ˇder Aussage uns glauben macht. |
| |
Wenn ich nach dem Grund einer Behauptung frage
„warum sagst Du glaubst Du das”
|
| |
Wenn ich sage: „das Wetter deutet auf Regen” sage
ich etwas über das ◇◇◇ zukünftige
Wetter?
Nein sondern über das gegenwärtige mit Hilfe eines
Gesetzes welches das Wetter zu einer Zeit mit dem in einer
Aber dasselbe könnte man dann auch für historische Aussagen sagen. Aber es war ja auch vorschnell zu sagen der Satz „das Wetter deutet auf Regen” sage nichts über das zukünftige Wetter. Das kommt darauf an was man darunter versteht „etwas über etwas aussagen”. Er sagt eben was seinen Wortlaut! |
| |
Der Satz ˇ„[p|e]s wird wahrsch.
eintreten” sagt nur etwas über die Zukunft in einem Sinn in
welchem
|
| |
Wenn wir sagen das Gewehr ziehlt jetzt auf
|
| |
Mit der Möglichkeit p ∙ q = p wenn sie nicht
aus der W-F Notation hervorgeht habe ich natürlich
eine ganz neues Element in den Kalkül eingeführt den
Kalkül ganz geändert. |
| |
Man kann definieren (∃x) φx (∃x,y) φx ∙ φ y ∙ ~ (∃ x,y,z) φx ∙ φ y ∙ φ z ≝ (∃n [φ|x],y) φx ∙ φ y = ∃n ❘ ❘x) φx ebenso (∃ x,y,z) φx ∙ φ y ∙ φ z ∙ ~ ‒ ‒ ‒ = (∃n ❘ ❘ ❘ x) φx etc. Man kann dann zeigen daß (∃n❘ ❘ ❘ ❘ ❘ x) φx ∙ (∃n ❘ ❘ ❘ x) ψ x ∙ ◇◇◇ ~ ∃ x) φx ∙ ψ x . ⊃ .
(∃n❘ ❘ ❘ ❘ ❘ x) φx ⌵ ψ
x eine Tautologie ist.
Hat man damit den Arithmetischen Satz ❘ ❘ & ❘ ❘ ❘ =
❘ ❘ ❘ ❘ ❘◇◇◇ gezeigt?
Nein Natürlich nicht.
Man hat ◇ auch nicht
(∃n ❘ ❘ x) φx ∙ (∃n ❘ ❘ ❘ x) φx ∙ Ind . ⊃ . (∃n ❘ ❘ +
❘ ❘ ❘ x) φx ⌵ ψx
eine Tautologie ist, denn von der
˃❘ Nun kann man aber
Taut.
macht immer dadurch erhält daß man in der
Klammer die Buchstaben setzt die durch den Kalkül
x y z u v w r s t x' y' x' y' z' gefunden werden (∃n n x) φ
x ‒ ‒ ‒ (∃n m x) –
⊃ (∃n n + m
x) φx ⌵ φ
[x|y] Hier hat es [s|S]inn die rechte Zahl m + n zu Schreiben denn dies drückt ein Gesetz aus. Dagegen hatte es keinen statt ❘ ❘ ❘ ❘ ❘ ❘ ❘ + ❘ ❘ ❘ zu schreiben dar man ebensogut ❘ + ❘ ❘ ❘ ❘ oder ❘ ❘ ❘ ❘ ❘ schreiben könnte. Es hat dagegen Sinn nach dieser allgemeinen (∃ 2x ‒ ‒ ‒ (∃
3x) (∃ 2 +
3x)
Wenn man (sozusagen) noch nicht weiß was
2 + 3 ergeben wird
denn 2 + 3 hat nur
sofern einen Sinn als es noch auszurechnen ist [ als es noch
ausgerechnet werden
Daher hat die Gleichung ❘ ❘ + ❘ ❘ ❘ = ❘ ❘ ❘ ❘ ❘ nur dann einen Sinn wenn das Zeichen ❘ ❘ ❘ ❘ ❘ so wiedererkannt
|
| |
Zu sagen „4 Gegenstände
|
| |
Von einem Teil meines Gesichtsfeldes zu sagen er habe keine Farben
Ich kann also in dem Satz „dieses Viereck hat mindestens zwei Farben” statt „zwei”, nicht „eine” einsetzen & im ˇSatz „es hat nur eine Farbe” nicht „0” statt 1 „eine”. Wenn nun die Frage wäre hat in so einem Satz 1 die gleiche Bedeutung wie dort wo |
| |
Wir brauchen nicht von Farben zu reden sondern ˇnur von der Teilung
einer Fläche im Gesichtsraum überhaupt. – – – – –
|
| |
D.h. Die Aussage „die
Fläche hat nur eine Farbe” enthält keine Aussage „die
Fläche ist färbig” welche ja Unsinn wäre.
Was gezählt wird sind die gleichfärbigen (einfarbigen) Flecken in
dem Viereck.
Es Und es können sehr wohl gar keine solche
Flecke in Viereck sein, wenn etwa das ganze Viereck von
|
| |
Wenn ich sage „alle diese Hüte sind von einer
Größe” so heißt das nicht „sie haben eine &
nur eine Größe” [ „sie haben eine Größe &
nur eine” ] |
| |
Soll ich nun den Satz alle diese Stäbe haben die gleiche Länge so
schreiben: „Es gibt eine Länge welche alle
diese Stäbe haben”? also:
(∃L): φx
. ⊃ x.x εL
→ Hier ist ein Fehler in der Auffassung. Das heißt ich kann natürlich (∃L): φx ⊃ x x ε L schreiben so
ε(1x)
φx ∙ ε(1x) ψx
ε(2x) φx ∙ ε(2x)
ψx ε(3x) φx ∙
ε(3x) ψx
u.s.w. zusammen.
Aber er ist nicht ein Satz dieser Form. Das sieht
man & auch nicht einer der
(ε x) φx ∙ (εx) ψx & das zeigt deutlich daß wir es hier nicht mehr mit einem log. Produkt zu tun haben (ahnlich wie der Differentialquotient kein Quotient ist). Und wie man dieses auch Z (φ(Z), ψ(Z)) (Was uns hier stört ist die ganz unnötige S Subjekt- Prädikat -Form.
Wir sagen doch nie a ist ein Apfel)
Es gilt dann natürlich für Z (φ Z,
ψ Z) die Regel daßZ (φ Z, ψ Z) ∙ (ε1 x) φx ∙ (ε 1 x) ψ x = = (ε 1 x) φx ∙ (ε 1 x) ψ x = u.s.w.. =
Z (φ Z, ψ Z) ∙ (ε 1 x) φx
=
u.s.w. in der Reihe der Kardinalzahlen. |
| |
∣ Die Gleichung p ∙ q =
p zeigt den eigentlichen Zusammenhang des Folgens & der
Wahrheitsfunktionen. ∣ |
| |
◇◇◇◇◇◇ a b b c d e f
a a a a a a a
a b c d e f g sind 7 Buchstaben da so können nicht mehr als 7 Typen von Buchstaben dasein & nicht weniger als eine. |
| |
Sind aber 0 Buchstaben da wieviel Tyen können dann
vorhanden sein?
Wir sagen: er hat Kappen & 3 Arten von Hüten aber auch
er verkauft Kappen & oder auch „Kappen &
eine Art von Hüten”, aber auch Kappen & keine Art
von Hüten. |
| |
Man könnte
|
| |
∣ Wird mit dem Beweis der Widerspruchsfreiheit ein
Satz bewiesen?
Und wie lautet der?
|
| |
Angenommen die Widerspruchsfreiheit ist bewiesen:
was haben wir gewonnen? |
| |
In wiefern ist denn der Widerspruch in den Axiomen schon
enthalten, wenn ich keine ◇ Methoden kenne ihn
hervorzuziehen? |
| |
„In den Regeln darf kein Widerspruch sein” das
klingt so wie eine Vorschrift wie: „in einem
Benzinmotor darf das Zahnrad auf der Kurbel-
|
| |
Könnte ich nun auch eine Zahlenart den Kardinalzahlen
|
| |
Zeigt sich hier nicht die Unsinnigkeit des Geredes von der
„Grundintuition”? |
| |
Regeln, die eine Verbindung zwischen Sprache und
Wirklich- Aber über diesen Unterschied besteht ein Irrtum durch den er von prinzipieller Art zu sein scheint. |
| |
Die Philosophen welche sagen: „nach dem
To[g|d] wird ein zeitloser Zustand eintreten”
oder „mit dem Tod
|
| |
„Das Viereck hat eine Farbe & nur
eine”.
Der erste Teil des Satzes darf dann nicht die grammatische Aussage der
färbigkeit sein.
(„Ich kann in dieser Fläche 3 Farben
unterscheiden”.) Es Ich weiß selbst nicht was mir an Wenn ich, daß ˇz.B. die Fläche schwarz⌊e⌋ ist Fläche farblos nenne so scheint alles ganz einfach zu werden. Man ist versucht zu glauben, daß zwar eine Länge nicht so ist |
| |
| |
Der aufregende Charakter der grammatischen Unklarheiten
|
| |
Den was
der Sinn der Musik ist
findet man wenn man sich fragt: wie weiß ich daß
einer Mensch ein Musikstück (also
„seinen Sinn”) versteht
Nun, wenn er bei jedem Ton sagen kann wie er gespielt werden soll, das
Tempo jedes Taktes angeben kann.
Eventuell auch, wenn er das begründen kann, indem er ˇeinmal
sagt: das ist so wie wenn jemand sagt … oder: das
entspricht diesem Tanzschritt, oder: das
ist die Antwort auf jenes oder
|
| |
| |
| |
Editorial notes
1) For the dating of Ms-153b see the corresponding parts in MSS 112-113.
2) Continuation from Ms-153a,BCr.
3) First drawing deleted, due to mistake in the drawing.
4) The bottom of the page contains some formulas which are difficult to read.
5) See facsimile; arrow pointing right, probably indicating that the indentation shall be increased.