genauen Kreis sehen bedeuten soll daß wir z.B. keine Gerade sehen die den Kreis in einem Punkt berührt (d.h. daß nichts in unserem Sehraum die Multiplizität der einen Kreis berührenden Gerade hat) dann ist zu dieser Ungenauigkeit nicht ein beliebig hoher Grad der Genauigkeit denkbar.
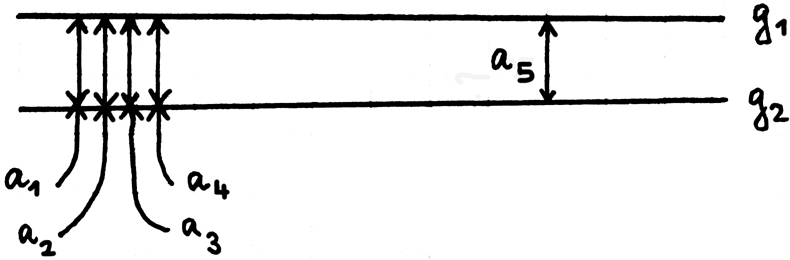
     Das Wort Gleichheit hat eine andere Bedeutung wenn wir es auf Strecken im physikalischen Sehraum anwenden als diejenige die es im || auf den physikalischen Raum angewendet hat. Die Gleichheit im Sehraum hat eine andere Multiplizität als die Gleichheit im physikalischen Raum, darum kann || können im Sehraum g₁ & g₂ Gerade (Sehgerade) sein & die Strecken a₁ = a₂, a₂ = a₃ etc. aber nicht a₁ = a₅ sein. Ebenso hat der Kreis & die Gerade im Gesichtsraum eine andere Multiplizität als Kreis & Gerade im physikalischen Raum denn ein kurzes Stück eines gesehenen Kreises kann gerade sein; „Kreis” & „Gerade” eben im Sinne der Gesichtsgeometrie angewandt.
     Die Gewöhnliche Sprache hilft sich hier mit dem Worte „scheint” oder „erscheint”. Sie sagt a₁ & a₂ scheinen gleich zu sein während zwischen a₁ & a₅ dieser Schein schon nicht mehr besteht. Aber sie benutzt das Wort Schein