(Das könnte z.B. tatsächlich die primitive Geometrie eines Volkes sein. Und für sie gälte das was ich über die Gleichberechtigung der Zahlenreihe „1, 2, 3, 4, 5, viele” mit der Reihe der Kardinalzahlen gesagt habe. Überhaupt ist es für unsere Untersuchungen ein guter Trick, sich die Mathematik Arithmetik oder Geometrie eines primitiven Volks

vorzustellen auszumalen

.
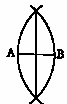
   Ich will diese Geometrie das System α nennen & fragen: „ist die 3 Teilung der Strecke im System α möglich?”
      Welche 3-Teilung ist in dieser Frage gemeint? – denn davon hängt offenbar der Sinn der Frage ab. Ist z.B. die physikalische 3-Teilung gemeint? d.h. die 3-Teilung durch Probieren & Nachmessen[?|.] In diesem Falle ist die Frage vielleicht zu be[g|j]ahen. Oder die optische Dreiteilung? d.h. die Teilung deren Resultat drei gleichlang aussehende Teile sind? Wenn wir z.B. durch ein verzerrendes Medium sehen so ist es ganz leicht vorstellbar daß uns die Teile 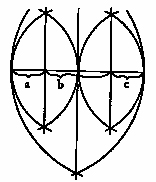a, b & c gleichlang erscheinen.
   Nun könnte man die Resultate der Teilungen im System α nach der Zahl der erzeugten Teile durch die Zahlen 2, 2², 2³, u.s.w. darstellen; & die Frage kon ob die 3-Teilung möglich ist könnte bedeuten: ist eine der Zahlen in dieser Reihe = 3. Diese Frage kann freilich nur gestellt werden wenn die 2, 2², 2³ etc in einem andern System (etwa den Kardinalzahlen) eingebettet sind; nicht, wenn sie selbst d unser Zahlensystem sind; denn dann kennen wir – oder unser System – eben die 3 nicht. – Aber wenn unsere Frage lautet ist eine der Zahlen 2, 2², ⌊2³,⌋ etc gleich ³ so ist hier eigentlich von einer 3-Teilung der Strecke nicht die Rede. Immerhin

könnte kann

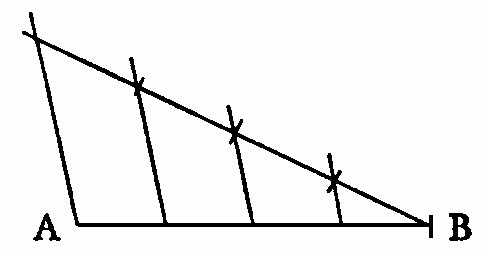die Frage nach der m Möglichkeit der 3-Teilung so aufgefaßt werden. – Eine andere Auffassung erhalten wir nun wenn wir dem System α ein System β hinzufügen worin ˇes die Streckenteilung nach Art dieser Figur gibt.
Es kann nun gefragt werden: ist die Teilung β in 108 Teile eine Teilung der Art α? Und diese Frage könnte wieder auf die hinauslaufen: ist 108 eine Potenz von 2? aber sie könnte auch auf eine andere Entscheidungsart hinweisen (einen andern Sinn haben) wenn wir die Systeme ˇα & β zu einem geometrischen Konstruktionssystem verbinden 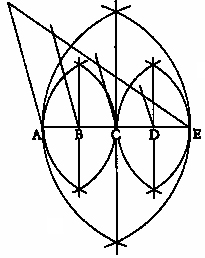so zwar, daß es sich nun in diesem System beweisen läßt, daß die beiden Konstruktionen „die gleichen Teilungspunkte B, C, D „liefern müssen”.
     

A B |–|–|–|–|–|–|–|–| ︸   ︸     ︸ a      b        c

^(Ƒ) Denken wir nun es h[ab|ätt]e Einer im System α eine Strecke ⌊AB⌋ in 8 Teile geteilt, nehme diese nun zu den Stre⌊c⌋ken a, b, c zusammen & fragte: ist das eine 3-Teilung [ eine

Teilung in 3 gleiche Teile ] (Wir könnten uns den Fall übrigens leichter mit einer größeren Anzahl von ursprünglicher Teilen vorstellen die es möglich macht, 3 gleichlang aussehende Gruppen von Teilen zu bilden.)
   Die Antwort auf diese Frage wäre der Beweis daß 2³ nicht durch 3 teilbar ist; oder der Hinweis darauf daß sich die Teile a, b, c wie 1:3:4 verhalten. Und nun könnte man fragen: habe ich also im System α nicht doch einen Begriff von der 3-Teilung, nämlich der Teilung, die die Teile a, b, c im Verhältnis 1:1:1 hervorbringt? Gewiß, ich habe nun einen neuen Begriff von ‘3-Teilung einer Strecke’ eingeführt; wir könnten ja sehr wohl sagen daß wir durch die 8-Teilung der Strecke AB die Strecke CB

A  C B |–|–|–|–|–|–|–|–|

in 3 gleiche Teile geteilt haben wenn das eben heißen soll: wir haben eine Strecke erzeugt die aus 3 gleichen Teilen besteht.¹