Denk Dir ein Material härter & fester als irgendein anderes. Aber wenn man einen Stab aus diesem Stoff aus der horizontalen in die Vertikale Lage bringt, so zieht er sich zusammen, oder denk Dir er bieg[t|e] sich, ˇwenn man ihn aufrichtet

& ist dabei so hart,
während man er so hart ist,

daß man ihn auf keine andre Weise biegen kann. Denk Dir [e|E]inen Mechanismus aus diesem

Stoff, etwa eine Kurbel Pleuelstange & Kreuzkopf. Andere Bewegungsweise des Kreuzkopfs. ⌊⌊

⌋⌋
Oder: eine Stange biegt sich, wenn ihr man ihr eine ˇgewisse gMasse nähert, gegen alle Kräfte aber die wir auf sie wirken lassen, ist sie

vollkommen
ganz

starr. Denk Dir die Führungsschienen des Kreuzkopfes biegen sich & strecken sich wieder wenn die Kurbel sich ihnen nähert & sich wieder entfernt. Ich nehme aber an daß keinerlei besondere äußere Kraft dazu nötig ist dies hervor-

zurufen.

Dieses
Das

Benehmen der Schienen würde

uns
einen

(in so einem Fall) wie das eines lebenden Wesens anmuten.
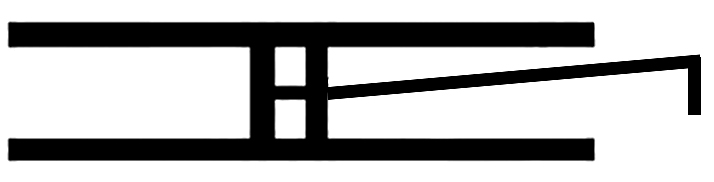
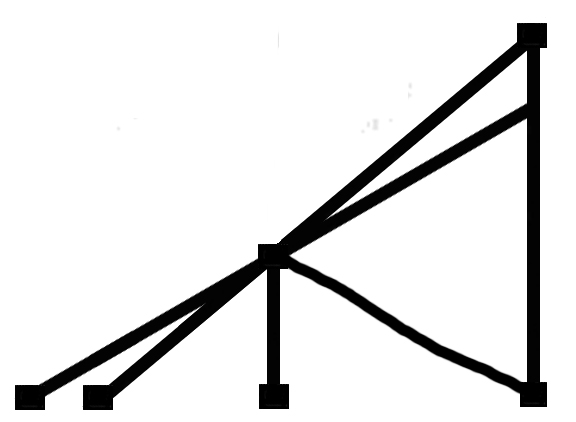
Wenn wir sagen “wenn die Glieder des Mechanismus ganz starr wären, würden sie sich so & so bewegen”, was ist das Kriterium dafür daß sie ganz starr sind? Ist es, daß sie gewissen Kräften widerstehen? Oder, daß sie sich so & so bewegen?
Denke, ich sage: “das ist das Bewegungsgesetz des Kreuzkopfes (die

Zuordnung seiner Lage zur Lage der Kurbel etwa, wenn sich die Länge der Kurbel & der Pleuelstange nicht ändern”. Das heißt wohl wenn sich die Lagen der Kurbel & des Kreuzkopfes so zueinander verhalten,

so
dann

sage ich, daß die Länge der Pleuelstange gleichbleibt
“Wenn die Teile ganz starr wären, würden sie sich so bewegen”: ist das eine Hypothese? Es scheint, nein. Denn wenn wir sagen: Wir Diese Gleichungen “die Kinematik beschreibt

die Bewegungen des Mechanismus unter der Voraussetzung daß seine Teile vollkommen starr sind”, so geben wir einerseits zu, daß diese Voraussetzung in der Wirklichkeit nie zutrifft, anderseits soll es keinem Zweifel unterliegen, daß vollkommen starre Teile sich so bewegen würden. Aber woher diese Sicherheit? Es handelt sich hier wohl nicht um Sicherheit sondern um eine Bestimmung, die wir getroffen haben. Wir wissen nicht, daß

Körper, wenn sie ( (nach den & den Kriterien) starr wären) sich so bewegen würden; wohl aber würden wir (unter Umständen) Teile “starr” nennen die sich so bewegen.

Denke ˇin so einem Fall immer daran daß ja die Geometrie (oder Kinematik) keine Meßmethode angibt // spezifiziert // , wenn sie von gleicher Länge oder vom Gleichbleiben einer Länge spricht.
Wenn wir also die Kinematik etwa die Lehre von der Bewegung vollkommen starrer Maschinenteile nennen, so liegt

hierin einerseits eine Andeutung über die (mathematische) Methode wir bestimmen gewisse Distanzen als die Längen von Maschinenteilen, die sich nicht ändern; anderseits eine Andeutung über die Anwendung des Kalküls.

(2015–) Wittgenstein Source Bergen Nachlass Edition (WS-BNE). Edited by the Wittgenstein Archives at the University of Bergen under the direction of Alois Pichler. In: Wittgenstein Source, curated by Alois Pichler (2009–) and Joseph Wang-Kathrein (2020–). (N) Bergen: WAB.