Logical constants can't be made into variables: because in them what symbolises is not the same; ◇◇◇ ˇall symbols ◇◇◇ for wh. a variable can be substituted symbolises in the same way.
We describe a symbol, & say This is a ˇarbitrarily ‘A symbol of this description is a tautology’. And then, it follows at once, both that any other symbol wh. answers to the same description is a tautology; & that any symbol which does not isn't. That is, we have arbitrarily fixed that that ˇany symbol of that description is to

be
shew

a tautology; & this being fixed it is no longer arbitrary with regard to all otherany other symbols whether they are it is a tautolog[ies|y] or not. We can get a contradiction of the same logical form as

a
our

tautology; but it won't answer our description.
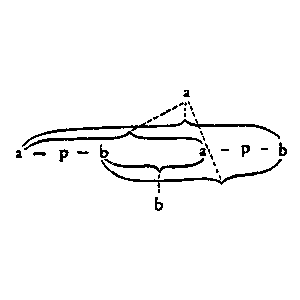
Having thus fixed what is a tautology & what is not, we can then, having fixed arbitrarily again that if the relation the relation a – b is transitive ◇◇◇ get from the 2 facts together that e.g. ‘p ≡ ~(~p)’ ˇis a taut.. For ~(~p) = a – b – apb – a – b. It follows from the fact that a – b is transitive, that where we have a – b – a, the first a has to the second the same relation that it has to b. It is just as from the fact that a–true implies b–false, & b–false implies ctrue, we get that a–true implies c–true. And we shall be able to see, having fixed the meaning description of a tautology that, p ≡ ~(~p) is a tautology.

That, when a

certain
given

rule is given, a symbol is tautological shews a logical truth.

  This symbol might be interpreted either as a tautology or as a contradiction.
  But now it is obvious that the a
  In settling that it is to be interpreted as a tautology & not as a contradiction, I am not assigning a meaning to a & b; i.e. saying that they symbolise different things but in the same way. What I am doing is to to say that the method way in wh. the a–pole is connected with the whole system symbol symbolises in a different way from that in which it would symbolise if the symbol were interpreted as a contradiction. And I add the scratches a & b merely in order to shew in which way the connection is symbolising, so that it may be evident that wherever the same scratch occurs in the corresponding place in another

symbol, there also the connection is symbolising in the same way.
We could, of course, symbolise

any a – b function
a tautology

without using 2 outside poles at all, merely, e.g., omitting the b–pole; & here what would symbolise would be that the ˇ3 pairs of inside poles of the props. were connected ˇin a certain way with the a–pole, while the other pair was not connected with it. And thus the difference between the scratches a & b, where we do use them, merely shews that it is a different state of things that is symbolising in the one case & the other: in the one case that certain inside poles are
Th connected in a certain way with an outside pole, in the other that they're not.
The symbol for a tautology, whatever we take to in whatever form we find put it, e.g. whether by omitting the a–pole or by omitting the ub, would always be capable of being used as the symbol for a contradiction; only not in the same language.

(2015–) Wittgenstein Source Bergen Nachlass Edition (WS-BNE). Edited by the Wittgenstein Archives at the University of Bergen under the direction of Alois Pichler. In: Wittgenstein Source, curated by Alois Pichler (2009–) and Joseph Wang-Kathrein (2020–). (N) Bergen: WAB.